Optical soliton for perturbed nonlinear fractional Schrödinger equation by extended trial function method

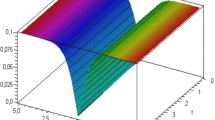
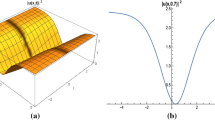
Abstract

This paper retrieves, bright, dark and singular optical solitons with the help of extended trial equation scheme. We consider Kerr law, power law and log law of nonlinearity. We find the solutions in terms of Jacobi elliptic functions and in the limiting cases of the modulus of ellipticity.

1 Introduction

Optical solitons have been the subjects of pervasive research in nonlinear optics due to their dormant applications in telecommunication and ultra fast signal processing systems (Agrawal 2007; Ekici et al. 2016, 2017a, b, c, d; Mirzazadeh et al. 2016; Eslami et al. 2014; Zhou et al. 2013, 2016a, b; Zhou 2014a, b; Zhou and Zhu 2015; Hao et al. 2017; Zhao et al. 2016, 2018; Guo et al. 2015; Guo and Liu 2015; Bekir and Guner 2013; Guner and Bekir 2016, 2017; Wang and Kara 2018; Guner et al. 2017). The dynamics of soliton pulses are described by nonlinear Schrödinger (NLS) equation with group velocity dispersion (GVD) and self-phase modulation (SPM). NLSE admits two distinct types of localized solutions, bright and dark soliton solutions. A renowned NLSE is nonlinear fractional Schrödinger equation (NFSE), which is the key equation in fractional quantum mechanics. Many soliton solutions have been found out for NFSE (Herzallah and Gepreel 2012; Taghizadeh and Foumani 2015; Pandir et al. 2013) . This equation was first derived by Laskin (2002). In this paper, we will find bright, dark, singular and Jacobi elliptic soliton solutions for perturbed nonlinear fractional Schrödinger equation (Taghizadeh et al. 2015) with Kerr law, power law and log nonlinearity by using extended trial equation method (Guner et al. 2017).

In the following section, we find the soliton solutions for perturbed nonlinear fractional Schrödinger equation with Kerr law, power law and log law nonlinearity.

2 Mathematical model

The time fractional perturbed nonlinear Schrödinger’s equation (Taghizadeh et al. 2015) is given as:

$$\begin{aligned} i\frac{\partial ^\alpha u}{\partial t^\alpha }+\frac{\partial ^2 u}{\partial x^2}+\gamma (F(|u|^2) u)+i\gamma _1 \frac{\partial ^3 u}{\partial x^3}+i\gamma _2F( |u|^2)\frac{\partial u}{\partial x}+i\gamma _3 \frac{\partial }{\partial x}(F(|u|^2))u=0 \end{aligned}$$

(1)

where $t>0$ and $0<\alpha \le 1$, $\gamma _1$ is third order dispersion, $\gamma _2$ and $\gamma _3$ are versions of nonlinear dispersions. We consider the transformation:

$$\begin{aligned} u(x,t)=u(\xi ), \quad \xi =kx+\frac{lt^\alpha }{\Gamma (\alpha +1)} \end{aligned}$$

(2)

where k and l are constants. By using Eq. (2) into Eq. (1), we obtain the following form;

$$\begin{aligned} ilu'+k^2u''+\gamma (F(|u|^2))u+i\gamma _1k^3u'''+i\gamma _2k(F(|u|^2))u'+i\gamma _3k(F(|u|^2))'u=0 \end{aligned}$$

(3)

2.1 Kerr law nonlinearity

Now by using the Kerr law nonlinearity,

$$\begin{aligned} F(u)=u \end{aligned}$$

(4)

After using Eq. (4) into Eq. (3), we get,

$$\begin{aligned} ilu'+k^2u''+\gamma (|u|^2)u+i\gamma _1k^3u'''+i\gamma _2k(|u|^2)u'+i\gamma _3k(|u|^2)'u=0 \end{aligned}$$

(5)

Here we use the complex transformation;

$$\begin{aligned} u(\xi )=\varphi (\xi )e^{i\beta \xi } \end{aligned}$$

(6)

where $\beta$ is a constant and $\varphi (\xi )$ is a real function. Now using Eq. (6) into Eq. (5), the real part is

$$\begin{aligned} (-l\beta -k^2\beta ^2+k^3\beta ^3\gamma _1)\varphi +(\gamma -k\beta \gamma _2)\varphi ^3+k^2(1-3k\beta \gamma _1)\varphi ''=0 \end{aligned}$$

(7)

and imaginary part is

$$\begin{aligned} (l+2k^2\beta -3k^3\beta ^2\gamma _1)\varphi '+k^3\gamma _1\varphi '''+k(\gamma _2+2\gamma _3)\varphi ^2\varphi '=0 \end{aligned}$$

(8)

By substituting $\gamma _1=0$ and $k(\gamma _2+2\gamma _3)=0$ in Eq. (8), we get

$$\begin{aligned} l=-\,2k^2\beta \end{aligned}$$

(9)

Thus, Eq. (7) becomes

$$\begin{aligned} k^2\beta ^2\varphi +(\gamma -k\beta \gamma _2)\varphi ^3+k^2\varphi ''=0 \end{aligned}$$

(10)

Now, we choose the following assumption (Guner et al. 2017) to get the soliton solution for Eq. (10)

$$\begin{aligned} \varphi =\sum \limits _{i=0}^{p}a_iy^i \end{aligned}$$

(11)

where

$$\begin{aligned} (y^{'})^{2}=\Phi (y)=\frac{f(y)}{g(y)}=\frac{b_qy^q+b_{q-1}y^{q-1}+ \cdots + b_1 y+b_0}{c_ry^r+c_{r-1}y^{r-1}+ \cdots + c_1 y+c_0} \end{aligned}$$

(12)

From Eqs. (11) and (12) we can write,

$$\begin{aligned} (\varphi ^{'})^{2}& {} = \frac{f(y)}{g(y)}\left( \sum \limits _{i=0}^{p}ia_i y^{i-1}\right) ^2 \end{aligned}$$

(13)

$$\begin{aligned} \varphi ^{''} & {}= \frac{f^{'}(y)g(y)-f(y) g^{'}(y)}{2g^{2}(y)}\left( \sum \limits _{i=0}^{p} ia_i y^{i-1}\right) +\frac{f(y)}{g(y)}\left( \sum \limits _{i=0}^{p}i(i-1)a_i y^{i-2}\right) \end{aligned}$$

(14)

Here f(y) and g(y) are the polynomials. Equation (12) can also be written in the form of the elementary integral

$$\begin{aligned} \pm (\xi -\xi _0)=\int \frac{dy}{\sqrt{\Phi (y)}}=\int \sqrt{\frac{g(y)}{f(y)}}dy \end{aligned}$$

(15)

By balancing the highest order nonlinear terms, we have

$$\begin{aligned} q=2p+r+2 \end{aligned}$$

(16)

Take $r=0$ , $p=1$, and $q=4$ so the result is given as,

$$\varphi = a_0+a_1y$$

(17)

$$\varphi ^{''} = \frac{a_1(4b_4y^3+3b_3y^2+2b_2y+b_1)}{2c_0}$$

(18)

By substituting Eqs. (17) and (18) into Eq. (10) and taking the free parameters,

$$\begin{aligned} a_0=a_0 ,\quad b_0=b_0 ,\quad c_0=c_0,\quad a_1=a_1,\quad b_4=b_4 \end{aligned}$$

We get set of algebraic equations which yields the solutions,

$$\beta = \frac{1}{\gamma _2}\left( \frac{\gamma }{k}+\frac{2kb_4}{a_1^2c_0}\right)$$

(19)

$$\begin{aligned} b_1 & {} = \frac{2a_0}{a_1}\left[ \frac{2a_0^2b_4}{a_1^2}-\frac{c_0}{\gamma _2^2}\left( \frac{\gamma }{k}+\frac{2kb_4}{a_1^2c_0}\right) ^2\right] \end{aligned}$$

(20)

$$\begin{aligned} b_2 & {} = \frac{6a_0^2b_4}{a_1^2}-\frac{c_0}{\gamma _2^2}\left( \frac{\gamma }{k}+\frac{2kb_4}{a_1^2c_0}\right) ^2 \end{aligned}$$

(21)

$$\begin{aligned} b_3 & {} = \frac{4a_0b_4}{a_1} \end{aligned}$$

(22)

Thus Eq. (15) takes the form,

$$\begin{aligned} \pm (\xi -\xi _0) = A\int \frac{dy}{\sqrt{\Phi (y)}} \end{aligned}$$

(23)

where

$$\begin{aligned} \Phi (y)=y^4+\frac{b_3}{b_4}y^3+\frac{b_2}{b_4}y^2+\frac{b_1}{b_4}y+\frac{b_0}{b_4}, \quad A=\sqrt{\frac{c_0}{b_4}} \end{aligned}$$

Hence, we obtain solutions for Eq. (6)

When $\Phi (y)=(y-d_1)^4$

$$\begin{aligned} u(x,t) & {} = \left[ a_0+a_1d_1\pm \frac{a_1A}{k\left( x-\frac{2(2k^2b_4+a_1^2c_0\gamma )}{a_1^2c_0\gamma _2\Gamma (\alpha +1)}t^\alpha \right) -\xi _0}\right] \nonumber \\&exp\left[ i\left( \frac{2k^2b_4+a_1^2c_0\gamma }{a_1^2c_0\gamma _2}\right) \left( x-\frac{2(2k^2b_4+a_1^2c_0\gamma )}{a_1^2c_0\gamma _2\Gamma (\alpha +1)}t^\alpha \right) \right] \end{aligned}$$

(24)

When $\Phi (y)=(y-d_1)^3(y-d_2)$; $d_2>d_1$

$$\begin{aligned} u(x,t) & {} = \left[ a_0+a_1d_1+\frac{4A^2(d_2-d_1)a_1}{4A^2-(d_1-d_2)^2\left( k\left( x-\frac{2(2k^2b_4+a_1^2c_0\gamma )}{a_1^2c_0\gamma _2\Gamma (\alpha +1)}t^\alpha \right) -\xi _0\right) ^2}\right] \nonumber \\&exp\left[ i\left( \frac{2k^2b_4+a_1^2c_0\gamma }{a_1^2c_0\gamma _2}\right) \left( x-\frac{2(2k^2b_4+a_1^2c_0\gamma )}{a_1^2c_0\gamma _2\Gamma (\alpha +1)}t^\alpha \right) \right] \end{aligned}$$

(25)

$$\begin{aligned} u(x,t) & {} = \left[ a_0+a_1d_1+\frac{(d_1-d_2)a_1}{exp\left( \frac{d_1-d_2}{A}\left( k\left( x-\frac{2(2k^2b_4+a_1^2c_0\gamma )}{a_1^2c_0\gamma _2\Gamma (\alpha +1)} t^\alpha \right) -\xi _0\right) \right) -1}\right] \nonumber \\&exp\left[ i\left( \frac{2k^2b_4+a_1^2c_0\gamma }{a_1^2c_0\gamma _2}\right) \left( x-\frac{2(2k^2b_4+a_1^2c_0\gamma )}{a_1^2c_0\gamma _2\Gamma (\alpha +1)}t^\alpha \right) \right] \end{aligned}$$

(26)

When $\Phi (y)=(y-d_1)(y-d_2)^3 ;~~ d_1>d_2$

$$\begin{aligned} u(x,t) & {} = \left[ a_0+a_1d_2+\frac{(d_2-d_1)a_1}{exp\left( \frac{d_1-d_2}{A}\left( k\left( x-\frac{2(2k^2b_4+a_1^2c_0\gamma )}{a_1^2c_0\gamma _2\Gamma (\alpha +1)} t^\alpha \right) -\xi _0\right) \right) -1}\right] \nonumber \\&exp\left[ i\left( \frac{2k^2b_4+a_1^2c_0\gamma }{a_1^2c_0\gamma _2}\right) \left( x-\frac{2(2k^2b_4+a_1^2c_0\gamma )}{a_1^2c_0\gamma _2\Gamma (\alpha +1)}t^\alpha \right) \right] \end{aligned}$$

(27)

When $\Phi (y)=(y-d_1)^2(y-d_2)(y-d_3)$; $d_1>d_2>d_3$

$$\begin{aligned} u(x,t) & {} = \left[ a_0+a_1d_1-\left[ 2a_1(d_1-d_2)(d_1-d_3)\left( 2d_1-d_2-d_3+(d_3-d_2) \right. \right. \right. \nonumber \\&\left. \left. \left. cosh\left[ \frac{\sqrt{(d_1-d_2)(d_1-d_3)}}{A}\left( k\bigg (x-\frac{2(2k^2b_4+a_1^2c_0\gamma )}{a_1^2c_0\gamma _2\Gamma (\alpha +1)} t^\alpha \bigg )-\xi _0\right) \right] \right) ^{-1}\right] \right] \nonumber \\&exp\left[ i\left( \frac{2k^2b_4+a_1^2c_0\gamma }{a_1^2c_0\gamma _2}\right) \left( x-\frac{2(2k^2b_4+a_1^2c_0\gamma )}{a_1^2c_0\gamma _2\Gamma (\alpha +1)}t^\alpha \right) \right] \end{aligned}$$

(28)

When $\Phi (y)=(y-d_1)(y-d_2)(y-d_3)(y-d_4);~~ d_1>d_2>d_3>d_4$

$$\begin{aligned} u(x,t) & {} = \left[ a_0+a_1d_1+\left[ a_1(d_1-d_2)(d_4-d_2)\left( d_4-d_2+(d_1-d_4) \right. \right. \right. \nonumber \\&\left. \left. \left. sn^2 \left[ \frac{\sqrt{(d_1-d_3)(d_2-d_4)}}{2A}\left( k\left( x-\frac{2(2k^2b_4+a_1^2c_0\gamma )}{a_1^2c_0\gamma _2\Gamma (\alpha +1)} t^\alpha \right) -\xi _0 \right) ,~\frac{(d_2-d_3)(d_1-d_4)}{(d_1-d_3)(d_2-d_4)}\right] \right) ^{-1}\right] \right] \nonumber \\&exp\left[ i\left( \frac{2k^2b_4+a_1^2c_0\gamma }{a_1^2c_0\gamma _2}\right) \left( x-\frac{2(2k^2b_4+a_1^2c_0\gamma )}{a_1^2c_0\gamma _2\Gamma (\alpha +1)}t^\alpha \right) \right] \end{aligned}$$

(29)

By setting, $a_0=-a_1d_1$ and $\xi _0=0$ into Eqs. (24)–(26), we obtain the rational function solutions:

$$\begin{aligned} u(x,t) =\pm \frac{B}{x-Ct^\alpha }exp\left( i D(x-Ct^\alpha )\right) \end{aligned}$$

(30)

and

$$\begin{aligned} u(x,t) & {} = \frac{E}{4A^2-F(x-Ct^\alpha )^2}exp\left( i D(x-Ct^\alpha )\right) \end{aligned}$$

(31)

$$\begin{aligned} u(x,t)& {} = \frac{G}{exp(H(x-Ct^\alpha ))-1}exp\left( i D(x-Ct^\alpha )\right) \end{aligned}$$

(32)

Also setting, $a_0=-a_1d_2$ and $\xi _0=0$ in Eq. (27), we get the following soliton solution;

$$\begin{aligned} u(x,t)=\frac{G}{1-exp(H(x-Ct^\alpha ))}exp\left( i D(x-Ct^\alpha )\right) \end{aligned}$$

(33)

After letting, $a_0=-a_1d_1$ and $\xi _0=0$ into Eqs. (28) and (29), we get bright soliton and the Jacobi elliptic function solutions respectively,

$$\begin{aligned} u(x,t)& {} = \frac{I}{J+Kcosh[L(x-Ct^\alpha )]} exp\left( i D(x-Ct^\alpha )\right) \end{aligned}$$

(34)

$$\begin{aligned} u(x,t)& {} = \frac{M}{N+Osn^2[P(x-Ct^\alpha ),Q]} exp\left( i D(x-Ct^\alpha )\right) \end{aligned}$$

(35)

where

$$\begin{aligned} C & {} = \frac{2(2k^2b_4+a_1^2c_0\gamma )}{a_1^2c_0\gamma _2\Gamma (\alpha +1)} ,~~ B = \frac{a_1A}{k} ,~~ D=\frac{2k^2b_4+a_1^2c_0\gamma }{a_1^2c_0\gamma _2}\\ E & {} = 4A^2(d_2-d_1)a_1 ,~~ F = k(d_1-d_2) ,~~ G = (d_1-d_2)a_1\\ H& {} = \frac{k(d_1-d_2)}{A} ,~~ I=-\,2a_1(d_1-d_2)(d_1-d_3) ,~~ J = 2d_1-d_2-d_3\\ K& {} = d_3-d_2 ,~~ L=\frac{\sqrt{k(d_1-d_2)(d_1-d_3)}}{A} ,~~ M =-a_1(d_1-d_2)(d_4-d_2)\\ N & {} = d_4-d_2 ,~~ O =d_1-d_4 ,~~ P = \frac{k\sqrt{(d_1-d_3)(d_2-d_4)}}{2A}\\ Q & {} = \frac{(d_2-d_3)(d_1-d_4)}{(d_1-d_3)(d_2-d_4)} \end{aligned}$$

Here, G and I are amplitude of soliton and H, L are inverse width of solitons.

Remark 1

We also get second form of dark optical soliton solutions, when modulus $Q \rightarrow 1$

$$\begin{aligned} u(x,t)=\frac{M}{N+Otanh^2[P(x-Ct^\alpha )]} exp\left( i D(x-Ct^\alpha )\right) \end{aligned}$$

(36)

Remark 2

We get periodic singular wave soliton solutions, when modulus $Q \rightarrow 0$

$$\begin{aligned} u(x,t)=\frac{M}{N+Osin^2[P(x-Ct^\alpha )]} exp\left( i D(x-Ct^\alpha )\right) \end{aligned}$$

(37)

2.2 Power law nonlinearity

The power law nonlinearity is

$$\begin{aligned} F(|u|)=|u|^n \end{aligned}$$

(38)

where n is the power law nonlinearity factor with $0<n<2$ and in particular $n\ne 2$ to avoid the self-focusing singularity. Using Eq. (38) in Eq. (3), we get

$$\begin{aligned} ilu'+k^2u''+\gamma |u|^{2n}u+i\gamma _1k^3u'''+i\gamma _2k|u|^{2n}u'+i\gamma _3k(|u|^{2n})'u=0 \end{aligned}$$

(39)

By using Eq. (6) in Eq. (39), the imaginary and real parts are

$$\begin{aligned} (l+2k^2\beta -3k^3\beta ^2\gamma _1)\varphi '+k^3\gamma _1\varphi '''+k(\gamma _2+2n\gamma _3)\varphi ^{2n}\varphi '=0 \end{aligned}$$

(40)

and

$$\begin{aligned} (-l\beta -k^2\beta ^2+k^3\beta ^3\gamma _1)\varphi +(\gamma -k\beta \gamma _2)\varphi ^{2n+1}+k^2(1-3k\beta \gamma _1)\varphi ''=0 \end{aligned}$$

(41)

By substituting $\gamma _1=0$ and $k(\gamma _2+2n\gamma _3)=0$ in Eq. (40), we get

$$\begin{aligned} l=-\,2k^2\beta \end{aligned}$$

(42)

Thus Eq. (41) becomes

$$\begin{aligned} k^2\beta ^2\varphi +(\gamma -k\beta \gamma _2)\varphi ^{2n+1}+k^2\varphi ''=0 \end{aligned}$$

(43)

By using $\varphi =\psi ^{\frac{1}{2n}}$ into Eq. (43), we get

$$\begin{aligned} 4n^2k^2\beta ^2\psi ^2+4n^2(\gamma -k\beta \gamma _2)\psi ^3+(1-2n)k^2(\psi ')^2+2nk^2\psi \psi ''=0 \end{aligned}$$

(44)

Now replace $\varphi$ by $\psi$ into Eqs. (11)–(14). After that, we use the resulting equations into Eq. (44) and by balancing the highest order nonlinear terms, we get,

$$\begin{aligned} q = p+r+2 \end{aligned}$$

(45)

Take $r=0$, $p=1$ and $q=3$ so the result is given as,

$$\begin{aligned} \psi & {} = a_0+a_1y \end{aligned}$$

(46)

$$\begin{aligned} \psi \psi ^{''} & {} = \frac{3a_1^2b_3y^3+(3a_0a_1b_3+2a_1^2b_2)y^2+(2a_0a_1b_2+a_1^2b_1)y+a_0a_1b_1}{2c_0} \end{aligned}$$

(47)

By substituting Eqs. (46) and (47) into Eq. (44) and taking the free parameters,

$$\begin{aligned} a_0=a_0,\quad c_0=c_0,\quad a_1=a_1,\quad b_3=b_3 \end{aligned}$$

we get set of algebraic equations which yields the solutions,

$$\begin{aligned} \beta & {} = \frac{1}{\gamma _2}\left( \frac{\gamma }{k}+\frac{(n+1)k b_3}{4n^2a_1c_0}\right) \end{aligned}$$

(48)

$$\begin{aligned} b_0 & {} = \frac{1}{k^2(2n-1)a_1^2}\left[ \frac{4n^2a_0^2c_0\gamma ^2}{\gamma _2^2}\left( 1-2nk^2a_1\right) +\frac{(n+1)^2k^4a_0^2b_3^2}{4n^2a_1^2c_0\gamma _2^2}\left( 1-2na_1\right) \right. \nonumber \\&\left. +\frac{(n+1)k^2a_0^2b_3}{a_1\gamma _2^2}\left( 2\gamma (1-2nk^2a_1)-a_0\gamma _2^2\right) +\frac{6n^3k^2a_0^3}{n-1}\left( k^2b_3+2a_1c_0\right) \right] \end{aligned}$$

(49)

$$\begin{aligned} b_1 & {} = \frac{a_0}{k^2a_1}\left[ \frac{6na_0}{n-1}\left( 2nc_0+\frac{k^2b_3}{a_1}\right) -\frac{1}{\gamma _2^2}\left( 8n^2c_0\gamma ^2 +\frac{(n+1)^2k^2b_3^2}{2n^2a_1^2c_0}\right. \right. \nonumber \\&\left. \left. +\frac{4(n+1)k^2\gamma b_3}{a_1}\right) \right] \end{aligned}$$

(50)

$$\begin{aligned} b_2 & {} = \frac{3a_0b_3}{a_1}-\frac{4n^2c_0\gamma ^2}{k^2\gamma _2^2}-\frac{(n+1)^2k^2b_3^2}{4n^2a_1^2c_0\gamma _2^2}-\frac{2(n+1)\gamma b_3}{a_1\gamma _2^2} \end{aligned}$$

(51)

Now the elementary integral becomes,

$$\begin{aligned} \pm (\xi -\xi _0) = {\widetilde{A}}\int \frac{dy}{\sqrt{\Pi (y)}} \end{aligned}$$

(52)

where

$$\begin{aligned} \Pi (y)=y^3+\frac{b_2}{b_3}y^2+\frac{b_1}{b_3}y+\frac{b_0}{b_3}, \quad {\widetilde{A}}=\sqrt{\frac{c_0}{b_3}} \end{aligned}$$

Thus solutions for Eq.(44) are given below, When $\Pi (y)=(y-e_1)^3$

$$\begin{aligned} u(x,t) & {} = \left[ a_0+a_1e_1+\frac{4{\widetilde{A}}^2a_1}{\left( k\left( x-\frac{2}{\Gamma (\alpha +1)}\left( \frac{\gamma }{\gamma _2}+ \frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}\right) t^\alpha \right) -\xi _0\right) ^2}\right] ^{\frac{1}{2n}}\nonumber \\&exp\left[ i\left( \frac{\gamma }{\gamma _2}+\frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}\right) \left( x-\frac{2}{\Gamma (\alpha +1)}\left( \frac{\gamma }{\gamma _2}+ \frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}\right) t^\alpha \right) \right] \end{aligned}$$

(53)

When $\Pi (y)=(y-e_1)^2(y-e_2);~~ e_2>e_1$

$$\begin{aligned} u(x,t)& {} = \left[ a_0+a_1e_1+a_1(e_2-e_1)sech^2\left( \frac{\sqrt{e_1-e_2}}{2{\widetilde{A}}} \left( k\left( x-\frac{2}{\Gamma (\alpha +1)}\left( \frac{\gamma }{\gamma _2}+ \frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}\right) t^\alpha \right) -\xi _0\right) \right) \right] ^{\frac{1}{2n}}\nonumber \\&exp\left[ i\left( \frac{\gamma }{\gamma _2}+\frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}\right) \left( x-\frac{2}{\Gamma (\alpha +1)}\left( \frac{\gamma }{\gamma _2}+ \frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}\right) t^\alpha \right) \right] \end{aligned}$$

(54)

When $\Pi (y)=(y-e_1)(y-e_2)^2;~~ e_1>e_2$

$$\begin{aligned} u(x,t)& {} = \left[ a_0+a_1e_1+a_1(e_1-e_2)cosech^2\left( \frac{\sqrt{e_1-e_2}}{2{\widetilde{A}}} \left( k\left( x-\frac{2}{\Gamma (\alpha +1)}\left( \frac{\gamma }{\gamma _2}+ \frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}\right) t^\alpha \right) -\xi _0\right) \right) \right] ^{\frac{1}{2n}}\nonumber \\&exp\left[ i\left( \frac{\gamma }{\gamma _2}+\frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}\right) \left( x-\frac{2}{\Gamma (\alpha +1)}\left( \frac{\gamma }{\gamma _2}+ \frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}\right) t^\alpha \right) \right] \end{aligned}$$

(55)

When $\Pi (y)=(y-e_1)(y-e_2)(y-e_3);~~ e_1>e_2>e_3$

$$\begin{aligned} u(x,t) & {} = \left[ a_0+a_1e_3+a_1(e_2-e_3)\left( sn^2\left( \pm \frac{\sqrt{e_1-e_3}}{2{\widetilde{A}}} \left( k\left( x-\frac{2}{\Gamma (\alpha +1)}\left( \frac{\gamma }{\gamma _2}+ \frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}\right) t^\alpha \right) -\xi _0\right) ,~~\frac{e_2-e_3}{e_1-e_3}\right) \right) ^{-1}\right] ^{\frac{1}{2n}}\nonumber \\&exp\left[ i\left( \frac{\gamma }{\gamma _2}+\frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}\right) \left( x-\frac{2}{\Gamma (\alpha +1)}\left( \frac{\gamma }{\gamma _2}+ \frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}\right) t^\alpha \right) \right] \end{aligned}$$

(56)

By letting, $a_0=-a_1e_1$ and $\xi _0=0$ in Eq. (53), we obtain rational function solution;

$$\begin{aligned} u(x,t)=\left[ \frac{{\widetilde{B}}}{(x-{\widetilde{C}}t^\alpha )}\right] ^{\frac{1}{n}}exp\left( i{\widetilde{D}}(x-{\widetilde{C}}t^\alpha )\right) \end{aligned}$$

(57)

and Eq. (54) gives bright soliton solution

$$\begin{aligned} u(x,t)=\frac{{\widetilde{E}}}{cosh^{\frac{1}{n}}({\widetilde{F}}(x-{\widetilde{C}}t^\alpha ))}exp\left( i{\widetilde{D}}(x-{\widetilde{C}}t^\alpha )\right) \end{aligned}$$

(58)

Also, Eq. (55) provides singular soliton solution

$$\begin{aligned} u(x,t)=\frac{{\widetilde{G}}}{sinh^{\frac{1}{n}}({\widetilde{F}}(x-{\widetilde{C}}t^\alpha ))}exp\left( i{\widetilde{D}}(x-{\widetilde{C}}t^\alpha )\right) \end{aligned}$$

(59)

Let $a_0=-a_1e_3$ and $\xi _0=0$, then the solution in Eq. (56) reduces to Jacobi elliptic function solution

$$\begin{aligned} u(x,t)=\frac{{\widetilde{H}}}{sn^{\frac{1}{n}}\left( {\widetilde{I_i}}(x-{\widetilde{E}}t^\alpha ),~{\widetilde{J}}\right) }exp\left( i{\widetilde{D}}(x-{\widetilde{C}}t^\alpha )\right) \end{aligned}$$

(60)

where

$$\begin{aligned} {\widetilde{B}} & = \frac{2{\widetilde{A}}\sqrt{a_1}}{k},\quad {\widetilde{C}} = \frac{2}{\Gamma (\alpha +1)}\left( \frac{\gamma }{\gamma _2}+ \frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}\right) , \quad {\widetilde{D}} = \frac{\gamma }{\gamma _2}+\frac{(n+1)k^2b_3}{4n^2a_1c_0\gamma _2}, \quad {\widetilde{E}}=\left( a_1(e_2-e_1)\right) ^{\frac{1}{2n}}\\ {\widetilde{F}} & = \frac{k\sqrt{e_1-e_2}}{2{\widetilde{A}}}, \quad {\widetilde{G}} = \left( a_1(e_1-e_2)\right) ^{\frac{1}{2n}}, \quad {\widetilde{H}} = \left( a_1(e_2-e_3)\right) ^{\frac{1}{2n}}\\ {\widetilde{J}} & = \frac{e_2-e_3}{e_1-e_3}, \quad {\widetilde{I_i} }= \frac{(-1)^ik\sqrt{e_1-e_3}}{2{\widetilde{A}}}, \quad i=1, 2 \end{aligned}$$

The solutions exist for $a_1>0$ while ${\widetilde{E}}, ~{\widetilde{G}}$ are amplitudes of soliton and ${\widetilde{F}}$ is the inverse width of the solitons.

Remark 1

The second form of dark optical soliton solutions can be obtained when modulus ${\widetilde{J}}\rightarrow 1$

$$\begin{aligned} u(x,t)={\widetilde{H}}tanh^{\frac{1}{n}}\left( {\widetilde{I_i}}(x-{\widetilde{E}}t^\alpha )\right) exp\left( i{\widetilde{D}}(x-{\widetilde{C}}t^\alpha )\right) \end{aligned}$$

(61)

Remark 2

The periodic singular wave soliton solutions are obtained, when modulus ${\widetilde{J}}\rightarrow 0$

$$\begin{aligned} u(x,t)=\frac{{\widetilde{H}}}{sin^{\frac{1}{n}}\left( {\widetilde{I_i}}(x-{\widetilde{E}}t^\alpha )\right) }exp\left( i{\widetilde{D}}(x-{\widetilde{C}}t^\alpha )\right) \end{aligned}$$

(62)

2.3 Log-law nonlinearity

The log-law nonlinearity is

$$\begin{aligned} F(|u|)=\ln |u| \end{aligned}$$

(63)

After using Eq. (63) in Eq. (3), we get

$$\begin{aligned} ilu'+k^2u''+\gamma u\ln |u|^2+i\gamma _1k^3u'''+i\gamma _2ku'\ln |u|^2+i\gamma _3ku(\ln |u|^2)'=0 \end{aligned}$$

(64)

By using Eq. (6) in Eq. (64), the imaginary and real parts are

$$\begin{aligned} (l+2k^2\beta -3k^3\beta ^2\gamma _1+2k\gamma _3)\varphi '+k^3\gamma _1\varphi '''+2k\gamma _2\varphi '\ln \varphi =0 \end{aligned}$$

(65)

and

$$\begin{aligned} (-l\beta -k^2\beta ^2+k^3\beta ^3\gamma _1)\varphi +(k^2-3\gamma _1k^3\beta )\varphi ''+2(\gamma -k\gamma _2\beta )\varphi \ln \varphi =0 \end{aligned}$$

(66)

By substituting $\gamma _1=0$ and $\gamma _2=0$ in Eq. (65), we get

$$\begin{aligned} l=-\,2k(k\beta +\gamma _3) \end{aligned}$$

(67)

Now, Eq. (66) implies

$$\begin{aligned} k\beta (k\beta +2\gamma _3)\varphi +k^2\varphi ''+2\gamma \varphi \ln \varphi =0 \end{aligned}$$

(68)

We use the transformation,

$$\begin{aligned} \varphi =exp(\psi ^{-1}) \end{aligned}$$

(69)

in Eq. (68), we get

$$\begin{aligned} k\beta (k\beta +2\gamma _3)\psi ^4+2\gamma \psi ^3-k^2\psi ^2\psi ''+2k^2\psi (\psi ')^2+k^2(\psi ')^2=0 \end{aligned}$$

(70)

By replacing $\varphi$ by $\psi$ into Eqs. (11)–(14), then by using the resulting equations into Eq. (70) and balancing the highest order nonlinear terms, we get,

$$\begin{aligned} q=p+r+2 \end{aligned}$$

(71)

Take $r=0$, $p=1$ and $q=3$ so the result is given as,

$$\begin{aligned} \psi =a_0+a_1y \end{aligned}$$

(72)

By substituting Eq. (72) into Eq. (70) and taking the free parameters,

$$\begin{aligned} a_0=a_0,\quad c_0=c_0,\quad a_1=a_1,\quad b_3=b_3 \end{aligned}$$

we get set of algebraic equations which yields the solutions,

$$\begin{aligned} \beta& {} = -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}} \end{aligned}$$

(73)

$$\begin{aligned} b_0 & {} = \frac{a_0^2}{3a_1^3(1+2a_0)}\left[ (1+3a_0^2)b_3+\frac{2a_1c_0\gamma (1-6a_0)}{k^2}\right] \end{aligned}$$

(74)

$$\begin{aligned} b_1 & {} = \frac{1}{3a_1^2}\left[ (2+3a_0^2)b_3+\frac{4a_1c_0\gamma (1-3a_0)}{k^2}\right] \end{aligned}$$

(75)

$$\begin{aligned} b_2 & {} = \left( \frac{3a_0-1}{a_1}\right) b_3-\frac{2\gamma c_0}{k^2} \end{aligned}$$

(76)

The elementary integral in Eq. (23) becomes,

$$\begin{aligned} \pm (\xi -\xi _0) = {\widehat{A}}\int {\frac{dy}{\sqrt{\Delta (y)}}} \end{aligned}$$

(77)

where

$$\begin{aligned} \Delta (y)=y^3+\frac{b_2}{b_3}y^2+\frac{b_1}{b_3}y+\frac{b_0}{b_3}, ~~{\widehat{A}}=\sqrt{\frac{c_0}{b_3}} \end{aligned}$$

Hence solutions are listed below When $\Delta (y)=(y-\delta _1)^3$

$$\begin{aligned} u(x, t) & {} = exp\left[ a_0+a_1\delta _1+\frac{4a_1{\widehat{A}}^2}{\left( k\left( x-\frac{2k}{\Gamma (\alpha +1)}\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) t^\alpha \right) -\xi _0\right) ^2}\right] ^{-1}\nonumber \\&exp\left[ ik\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) \left( x-\frac{2k}{\Gamma (\alpha +1)}\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) t^\alpha \right) \right] \end{aligned}$$

(78)

When $\Delta (y)=(y-\delta _1)^2(y-\delta _2) ;~~ \delta _2>\delta _1$

$$\begin{aligned} u(x,t) & {} = exp\left[ a_0+a_1\delta _1+a_1(\delta _2-\delta _1)\right. \nonumber \\&\left. sech^2\left( \frac{\sqrt{\delta _1-\delta _2}}{2{\widehat{A}}} \left( k\left( x-\frac{2k}{\Gamma (\alpha +1)}\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) t^\alpha \right) -\xi _0\right) \right) \right] ^{-1}\nonumber \\&exp\left[ ik\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) \left( x-\frac{2k}{\Gamma (\alpha +1)}\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) t^\alpha \right) \right] \end{aligned}$$

(79)

When $\Delta (y)=(y-\delta _1)(y-\delta _2)^2;~~ \delta _1>\delta _2$

$$\begin{aligned} u(x,t) & {} = exp\left[ a_0+a_1\delta _1+a_1(\delta _1-\delta _2)\right. \nonumber \\&\left. cosech^2\left( \frac{\sqrt{\delta _1-\delta _2}}{2{\widehat{A}}} \left( k\left( x-\frac{2k}{\Gamma (\alpha +1)}\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) t^\alpha \right) -\xi _0\right) \right) \right] ^{-1}\nonumber \\&exp\left[ ik\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) \left( x-\frac{2k}{\Gamma (\alpha +1)}\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) t^\alpha \right) \right] \end{aligned}$$

(80)

When $\Delta (y)=(y-\delta _1)(y-\delta _2)(y-\delta _3);~~ \delta _1>\delta _2>\delta _3$

$$\begin{aligned} u(x,t) & {} = exp\left[ a_0+a_1\delta _3+a_1(\delta _2-\delta _3)\right. \nonumber \\&\left. \left( sn^2\left( \pm \frac{\sqrt{\delta _1-\delta _3}}{2{\widehat{A}}} \left( k\left( x-\frac{2k}{\Gamma (\alpha +1)}\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) t^\alpha \right) -\xi _0\right) , ~~\frac{\delta _2-\delta _3}{\delta _1-\delta _3}\right) \right) ^{-1}\right] ^{-1}\nonumber \\&exp\left[ ik\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) \left( x-\frac{2k}{\Gamma (\alpha +1)}\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) t^\alpha \right) \right] \end{aligned}$$

(81)

We get the rational function solutions, by taking $a_0=-a_1\delta _1$ and $\xi _0=0$ into Eq. (78),

$$\begin{aligned} u(x,t)=exp\left[ \frac{{\widehat{B}}}{(x-{\widehat{C}}t^\alpha )^2}\right] ^{-1}exp\left( i{\widehat{D}}(x-{\widehat{C}}t^\alpha )\right) \end{aligned}$$

(82)

we get soliton solutions from Eq. (79),

$$\begin{aligned} u(x,t)=exp\left[ {\widehat{E}}cosh^2\left( ({\widehat{F}}(x-{\widehat{C}}t^\alpha ))\right) \right] exp\left( i{\widehat{D}}(x-{\widehat{C}}t^\alpha )\right) \end{aligned}$$

(83)

we also get singular soliton solution from Eq. (80),

$$\begin{aligned} u(x,t)=exp\left[ {\widehat{G}}sinh^2\left( ({\widehat{F}}(x-{\widehat{C}}t^\alpha ))\right) \right] exp\left( i{\widehat{D}}(x-{\widehat{C}}t^\alpha )\right) \end{aligned}$$

(84)

By setting, $a_0=-a_1\delta _3$ and $\xi _0=0$ into Eq. (81) we get Jacobi elliptic function solutions,

$$\begin{aligned} u(x,t)={\widehat{H}}sn^2\left[ {\widehat{I_i}}(x-{\widehat{E}}t^\alpha ),~{\widehat{J}}\right] exp\left( i{\widehat{D}}(x-{\widehat{C}}t^\alpha )\right) \end{aligned}$$

(85)

where

$$\begin{aligned} {\widehat{B}} & {} = \frac{4a_1{\widehat{A}}^2}{k^2},~~{\widehat{C}} = \frac{2k}{\Gamma (\alpha +1)}\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) , ~~{\widehat{D}}=k\left( -\frac{\gamma _3}{k}\pm \sqrt{\frac{\gamma _3^2}{k^2}-\frac{b_3}{2a_1c_0}}\right) \\ {\widehat{E}} & {} = \left( a_1(\delta _2-\delta _1)\right) ^{-1}, ~~ {\widehat{F}}=\frac{k\sqrt{\delta _1-\delta _2}}{2{\widehat{A}}}, ~~{\widehat{G}}=\left( a_1(\delta _1-\delta _2)\right) ^{-1}, ~~ {\widehat{H}}=\left( a_1(\delta _2-\delta _3)\right) ^{-1}\\ {\widehat{J}} & {} = \frac{\delta _2-\delta _3}{\delta _1-\delta _3}, ~~{\widehat{I_i}}=\frac{(-1)^ik\sqrt{\delta _1-\delta _3}}{2{\widehat{A}}}, \quad i=1, 2 \end{aligned}$$

The solutions exist for $a_1>0$ while ${\widehat{E}}, ~{\widehat{G}}$ are amplitudes of soliton and ${\widehat{F}}$ is the inverse width of the solitons.

Remark 1

The second form of dark optical soliton solutions can be obtained when modulus ${\widehat{J}}\rightarrow 1$

$$\begin{aligned} u(x,t)={\widehat{H}}tanh^2\left( {\widehat{I_i}}(x-{\widehat{E}}t^\alpha )\right) exp\left( i{\widehat{D}}(x-{\widehat{C}}t^\alpha )\right) \end{aligned}$$

(86)

Remark 2

The periodic singular wave soliton solutions are obtained, when modulus ${\widehat{J}}\rightarrow 0$

$$\begin{aligned} u(x,t)=\frac{{\widehat{H}}}{sin^2\left( {\widehat{I_i}}(x-{\widehat{E}}t^\alpha )\right) }exp\left( i{\widehat{D}}(x-{{\widehat{C}}}t^\alpha )\right) \end{aligned}$$

(87)

3 Conclusions

In this paper, we obtained bright, dark, singular, Gausson and Jacobi elliptic soliton solutions for perturbed nonlinear fractional Schrödinger equation. We used extended trial equation method with three types of nonlinearities, namely, Kerr law, power law and log law. Moreover, we obtained rational function and several other forms of solutions like cnoidal waves and plane waves.