Introduction

The most fundamental feature that sustains soliton formation and its stability is the existence of a delicate balance between chromatic dispersion (CD) and self-phase modulation (SPM). Once this balance is compromised, solitons fail to exist. Therefore, it is imperative to maintain the perfect harmony between the two key elements, CD and SPM. Occasionally, it may so happen that CD runs low. In such a situation, a new form of technology has been proposed. When CD was replaced by fourth-order dispersion (4OD), pure-quartic solitons were studied. However, for such solitons there is a limitation. No analytical closed-form soliton solution was available unless it is a stationary soliton. To overcome such shortcomings, cubic–quartic (CQ) solitons were proposed where, in addition to 4OD, third-order dispersion (3OD) effect was included. An abundance of results from CQ solitons have emerged and successfully floated across telecommunications industry, at least theoretically. Subsequently, the concept of CQ solitons, during such a crisis situation, was applied to a variety of other models that describe successful soliton transmission through optical fibers across trans-continental distances.

One of the models that describe soliton transmission through a variety of waveguides is perturbed Lakshmanan–Porsezian–Daniel (LPD) model, where the perturbation terms are all of Hamiltonian type [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. This model first appeared during 1988 in the context of Heisenberg spin chain [18]. Later, it gained popularity in soliton studies and has been extensively studied in various contexts using a wide variety of mathematical methodologies. These include rogue waves, Darboux transform, collective variables, Adomian decomposition, semi-inverse variational principle, Jacobi’s elliptic function expansion, exponential function expansion, trial equation approach, method of undetermined coefficients, Riccati equation approach and so on. The model was successfully studied in both contexts, namely polarization-preserving fibers as well as birefringent fibers. Today’s paper will be addressing CQ solitons with perturbed LPD model, in both such forms of fibers, for the very first time. Sine-Gordon equation approach will be the integration scheme that is adopted here. This will reveal a spectrum of soliton solutions in both such fibers that are exhibited along with their respective existence criteria. The algorithm is illustrated and the extensive details of the mathematical phenomenon follow through.

Optical solitons

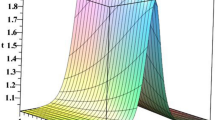
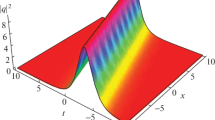
The retrieval of soliton solutions will be split into two subsections that deal with polarization-free fibers and when pulse polarization occurs. In both of the subsections, sine-Gordon equation approach will be employed to recover a wide spectrum of solitons. The details are exhibited in the next subsections.

Polarization-preserving fibers

The LPD equation in polarization-preserving fibers is:

$$\begin{aligned}&iu_{t}+iau_{xxx}+bu_{xxxx}+c\left| u\right| ^{2}u = \alpha \left( u_{x}\right) ^{2}u^{*}\nonumber \\&\quad +\beta \left| u_{x}\right| ^{2}u +\gamma \left| u\right| ^{2}u_{xx}+\lambda u^{2}u_{xx}^{*} \nonumber \\&\quad + \delta \left| u\right| ^{4}u \end{aligned}$$
(1)

where x and t that, respectively, stand for the spatial and temporal variables are independent variables. Linear temporal evolution is stood for the first term and \(i=\sqrt{-1}\). The complex valued function \(u\left( x,t\right)\) represents optical solitons in polarization-preserving fibers. a gives the coefficient of 3OD, while b is the coefficient of 4OD. Next, c stands for the coefficient of SPM and \(\delta\) corresponds to two-photon absorption. Lastly, \(\alpha\), \(\beta\), \(\gamma\) and \(\lambda\) are the coefficients of the nonlinear dispersion terms.

In presence of perturbation terms, the LPD equation for polarization-preserving fibers is:

$$\begin{aligned}&iu_{t}+iau_{xxx}+bu_{xxxx}+c\left| u\right| ^{2}u \nonumber \\&\quad =\alpha \left( u_{x}\right) ^{2}u^{*}+\beta \left| u_{x}\right| ^{2}u\nonumber \\&\qquad +\gamma \left| u\right| ^{2}u_{xx} + \lambda u^{2}u_{xx}^{*} +\delta \left| u\right| ^{4}u \nonumber \\&\qquad + i\left[ \zeta \left( \left| u\right| ^{2m}u\right) _{x} +\mu \left( \left| u\right| ^{2m}\right) _{x}u \right. \nonumber \\&\qquad \left. + \rho \left| u\right| ^{2m}u_{x}\right] \end{aligned}$$
(2)

where \(\zeta\) represents the self-steepening term, while \(\mu\) and \(\rho\) are, respectively, the coefficients of the higher-order dispersion and nonlinear dispersion effects. Finally, full nonlinearity parameter is indicated by m.

To obtain the soliton solution, we set

$$\begin{aligned} u(x,t)=U(\xi )e^{i\varphi },\ \ \xi =x-vt,\ \ \varphi (x,t)=-\kappa x+\omega t+\theta _{0} \end{aligned}$$
(3)

where the speed is denoted by v, while the frequency, wave number and phase center are stood for by \(\kappa ,\) \(\omega\) and \(\theta _{0}\), respectively. Also, the soliton amplitude and its phase component are, respectively, represented by \(U(\xi )\) and \(\varphi (x,t)\).

Plugging Eq. (3) into Eq. (2) yields the real equation

$$\begin{aligned}&bU^{\left( iv\right) }+\left( 3a\kappa -6b{\kappa }^{2}\right) U^{\prime \prime }-\left( \lambda +\gamma \right) U^{2}U^{\prime \prime }\nonumber \\&\quad -\left( \alpha +\beta \right) \left( U^{\prime }\right) ^{2}U+\left( c+\alpha { \kappa }^{2}+\gamma {\kappa }^{2}+\lambda {\kappa }^{2}-\beta {\kappa } ^{2}\right) U^{3}\nonumber \\&\quad +\left( b{\kappa }^{4}-a{\kappa }^{3}-\omega \right) U\nonumber \\&\quad -\delta U^{5}-\left( \kappa \zeta +\kappa \rho \right) U^{2m+1}=0 \end{aligned}$$
(4)

and the imaginary equation

$$\begin{aligned}&\left( a-4b\kappa \right) U^{\prime \prime \prime }+\left( 4b{\kappa }^{3}-3a {\kappa }^{2}-v\right) U^{\prime }\nonumber \\&\quad +2\kappa \left( \gamma +\alpha -\lambda \right) U^{\prime }U^{2} \nonumber \\&\quad -\left( \rho +\zeta +2m\mu +2m\zeta \right) U^{\prime }U^{2m}=0. \end{aligned}$$
(5)

Equations (4) and (5) are reduced to

$$\begin{aligned}&bU^{\left( iv\right) }+6b\kappa ^{2}U^{\prime \prime }-\left( 3b\kappa ^{4}+\omega \right) U\nonumber \\&\quad +\left( c-4\gamma {\kappa }^{2}+2\kappa \mu +2\kappa \zeta \right) U^{3}\nonumber \\&\quad -\delta U^{5}=0 \end{aligned}$$
(6)

with

$$\begin{aligned}&m=1, \end{aligned}$$
(7)
$$\begin{aligned}&a=4b\kappa , \end{aligned}$$
(8)
$$\begin{aligned}&\alpha =-2\gamma , \end{aligned}$$
(9)
$$\begin{aligned}&\rho =-2\mu -3\zeta , \end{aligned}$$
(10)
$$\begin{aligned}&\lambda =-\gamma , \end{aligned}$$
(11)
$$\begin{aligned}&\beta =2\gamma , \end{aligned}$$
(12)
$$\begin{aligned}&v=-8b\kappa ^{3}. \end{aligned}$$
(13)

Equation (6) can be integrated in order to designate the soliton profile, while Eq. (13) yields the soliton speed and Eqs. (7)–(12) gives the constraints.

The sine-Gordon equation method admits that the solution form of Eq. (6) is:

$$\begin{aligned}U\left( \xi \right) &=\sum _{i=1}^{N}\cos ^{i-1}(V\left( \xi \right) )[B_{i}\sin (V\left( \xi \right) )\nonumber \\&\quad +A_{i}\cos (V\left( \xi \right) )]+A_{0} \end{aligned}$$
(14)

where \(A_{i}\) and \(B_{i}\) \((0\le i\le N)\) are constants, N represents the balance number and \(V(\xi )\) ensures

$$\begin{aligned} V^{\prime }\left( \xi \right) =\sin \left( V\left( \xi \right) \right) \end{aligned}$$
(15)

with

$$\begin{aligned}&\sin \left( V\left( \xi \right) \right) =\text{ sech }\left( \xi \right) \text { or }\sin \left( V\left( \xi \right) \right) =\text {i}\text{ csh }\left( \xi \right) , \nonumber \\&\cos \left( V\left( \xi \right) \right) =\tanh \left( \xi \right) ,\ \ \ \text {or }\cos \left( V\left( \xi \right) \right) =\coth \left( \xi \right) . \end{aligned}$$
(16)

By virtue of the balancing principle applied in Eq. (6), Eq. (14) becomes

$$\begin{aligned} U\left( \xi \right) =B_{1}\sin (V\left( \xi \right) )+A_{1}\cos (V\left( \xi \right) )+A_{0}. \end{aligned}$$
(17)

Putting Eq. (17) with Eq. (15) into Eq. (6) leads to

Case-1

$$\begin{aligned}&\delta ={\frac{3\left( 4\gamma {\kappa }^{2}-c-2\kappa \mu -2\kappa \zeta \right) ^{2}}{2b\left( 3{\kappa }^{2}-10\right) ^{2}}},\ \ \omega \nonumber \\&\quad =-b\left( 3 {\kappa }^{4}+12{\kappa }^{2}-16\right) ,\ \ A_{{0}}=0, \nonumber \\&A_{{1}} =\pm \sqrt{-{\frac{4b\left( 3{\kappa }^{2}-10\right) }{c-4\gamma { \kappa }^{2}+2\kappa \left( \mu +\zeta \right) }}},\ \ B_{{1}}=0. \end{aligned}$$
(18)

Plugging Eq. (18) with Eq. (16) into Eq. (17) leads to the dark soliton

$$\begin{aligned}&u(x,t)=\pm \sqrt{-{\frac{4b\left( 3{\kappa }^{2}-10\right) }{c-4\gamma { \kappa }^{2}+2\kappa \left( \mu +\zeta \right) }}}\nonumber \\&\quad \tanh \left( x+8b{\kappa } ^{3}t\right) e^{i\left( -\kappa x-b\left( 3{\kappa }^{4}+12{\kappa } ^{2}-16\right) t+\theta _{0}\right) } \end{aligned}$$
(19)

and the singular soliton

$$\begin{aligned}&u(x,t)=\pm \sqrt{-{\frac{4b\left( 3{\kappa }^{2}-10\right) }{c-4\gamma { \kappa }^{2}+2\kappa \left( \mu +\zeta \right) }}}\nonumber \\&\quad \coth \left( x+8b{\kappa } ^{3}t\right) e^{i\left( -\kappa x-b\left( 3{\kappa }^{4}+12{\kappa } ^{2}-16\right) t+\theta _{0}\right) }. \end{aligned}$$
(20)

These solitons are valid for

$$\begin{aligned}&b\left( 3{\kappa }^{2}-10\right) \left( c-4\gamma {\kappa }^{2}+2\kappa \left( \mu +\zeta \right) \right) \nonumber \\&\quad <0. \end{aligned}$$
(21)

Case-2

$$\begin{aligned}&\delta ={\frac{3\left( 4\gamma {\kappa }^{2}-c-2\kappa \mu -2\kappa \zeta \right) ^{2}}{2b\left( 3{\kappa }^{2}+5\right) ^{2}}},\ \ \omega \nonumber \\&\quad =-b\left( 3{ \kappa }^{4}-6{\kappa }^{2}-1\right) ,\ \ A_{{0}}=0, \nonumber \\&A_{{1}} =0,\ \ B_{{1}}=\pm \sqrt{{\frac{4b\left( 3{\kappa }^{2}+5\right) }{ c-4\gamma {\kappa }^{2}+2\kappa \left( \mu +\zeta \right) }}}. \end{aligned}$$
(22)

Inserting Eq. (22) with Eq. (16) into Eq. (17) causes to the bright soliton

$$\begin{aligned}&u(x,t)=\pm \sqrt{{\frac{4b\left( 3{\kappa }^{2}+5\right) }{c-4\gamma {\kappa }^{2}+2\kappa \left( \mu +\zeta \right) }}}\nonumber \\&\quad \text{ sech }\left( x+8b{\kappa } ^{3}t\right) e^{i\left( -\kappa x-b\left( 3{\kappa }^{4}-6{\kappa } ^{2}-1\right) t+\theta _{0}\right) } \end{aligned}$$
(23)

and the singular soliton

$$\begin{aligned}&u(x,t)=\pm \sqrt{-{\frac{4b\left( 3{\kappa }^{2}+5\right) }{c-4\gamma { \kappa }^{2}+2\kappa \left( \mu +\zeta \right) }}}\nonumber \\&\quad \text{ csch }\left( x+8b{ \kappa }^{3}t\right) e^{i\left( -\kappa x-b\left( 3{\kappa }^{4}-6{\kappa } ^{2}-1\right) t+\theta _{0}\right) }. \end{aligned}$$
(24)

The bright soliton will exist provided the following constraint condition remains valid:

$$\begin{aligned} b\left( 3{\kappa }^{2}+5\right) \left( c-4\gamma {\kappa }^{2}+2\kappa \left( \mu +\zeta \right) \right) >0. \end{aligned}$$
(25)

while the singular soliton will exist provided the condition (26) holds:

$$\begin{aligned} b\left( 3{\kappa }^{2}+5\right) \left( c-4\gamma {\kappa }^{2}+2\kappa \left( \mu +\zeta \right) \right) <0. \end{aligned}$$
(26)

Case-3

$$\begin{aligned}&\delta ={\frac{6\left( 4\gamma {\kappa }^{2}-c-2\kappa \mu -2\kappa \zeta \right) ^{2}}{b\left( 6{\kappa }^{2}-5\right) ^{2}}},\ \ \omega \nonumber \\&\quad =-b\left( 3{ \kappa }^{4}+3{\kappa }^{2}-1\right) ,\ \ A_{{0}}=0, \nonumber \\&A_{{1}} =\pm \sqrt{-{\dfrac{b\left( 6{\kappa }^{2}-5\right) }{2\left( c-4\gamma {\kappa }^{2}+2\kappa \left( \mu +\zeta \right) \right) }}},\ \ B_{ {1}}\nonumber \\&\quad =\pm \sqrt{{\dfrac{b\left( 6{\kappa }^{2}-5\right) }{2\left( c-4\gamma { \kappa }^{2}+2\kappa \left( \mu +\zeta \right) \right) }}}. \end{aligned}$$
(27)

Inserting Eq. (27) with Eq. (16) into Eq. (17) yields the combo singular soliton

$$\begin{aligned}&u(x,t)\nonumber \\&\quad =\left\{ \begin{array}{l} \pm \sqrt{-{\dfrac{b\left( 6{\kappa }^{2}-5\right) }{2\left( c-4\gamma { \kappa }^{2}+2\kappa \left( \mu +\zeta \right) \right) }}}\coth \left( x+8b{ \kappa }^{3}t\right) \\ \\ \pm \sqrt{-{\dfrac{b\left( 6{\kappa }^{2}-5\right) }{2\left( c-4\gamma { \kappa }^{2}+2\kappa \left( \mu +\zeta \right) \right) }}}\text{ csch }\left( x+8b{\kappa }^{3}t\right) \end{array} \right\} \nonumber \\&\qquad e^{i\left( -\kappa x-b\left( 3{\kappa }^{4}+3{\kappa }^{2}-1\right) t+\theta _{0}\right) }. \end{aligned}$$
(28)

The combo singular soliton is valid for

$$\begin{aligned} b\left( 6{\kappa }^{2}-5\right) \left( c-4\gamma {\kappa }^{2}+2\kappa \left( \mu +\zeta \right) \right) <0. \end{aligned}$$
(29)

Birefringent fibers

The coupled system derived from the equation (2) for birefringent fibers without four-wave mixing is:

$$\begin{aligned}&iq_{t}+ia_{1}q_{xxx}+b_{1}q_{xxxx}+\left( c_{1}\left| q\right| ^{2}+d_{1}\left| r\right| ^{2}\right) q \nonumber \\&\quad = \left\{ \alpha _{1}\left( q_{x}\right) ^{2}+\beta _{1}\left( r_{x}\right) ^{2}\right\} q^{*} \nonumber \\&\qquad +\left( \gamma _{1}\left| q_{x}\right| ^{2}+\lambda _{1}\left| r_{x}\right| ^{2}\right) q+\left( \delta _{1}\left| q\right| ^{2}+\zeta _{1}\left| r\right| ^{2}\right) q_{xx}\nonumber \\&\qquad +\left( \mu _{1}q^{2}+\rho _{1}r^{2}\right) q_{xx}^{*}\nonumber \\&\qquad +\left( f_{1}\left| q\right| ^{4}+g_{1}\left| q\right| ^{2}\left| r\right| ^{2}+h_{1}\left| r\right| ^{4}\right) q \nonumber \\&\qquad +i\left[ \eta _{1}\left( \left| q\right| ^{2}q\right) _{x}+\vartheta _{1}\left( \left| r\right| ^{2}r\right) _{x}\right. \nonumber \\&\qquad +\left\{ \theta _{1}\left( \left| q\right| ^{2}\right) _{x}+\epsilon _{1}\left( \left| r\right| ^{2}\right) _{x}\right\} q\nonumber \\&\qquad \left. +\left( \tau _{1}\left| q\right| ^{2}+\sigma _{1}\left| r\right| ^{2}\right) q_{x}\right] , \end{aligned}$$
(30)
$$\begin{aligned}&ir_{t}+ia_{2}r_{xxx}+b_{2}r_{xxxx}+\left( c_{2}\left| r\right| ^{2}+d_{2}\left| q\right| ^{2}\right) r\nonumber \\&\quad =\left\{ \alpha _{2}\left( r_{x}\right) ^{2}+\beta _{2}\left( q_{x}\right) ^{2}\right\} r^{*} \nonumber \\&\qquad +\left( \gamma _{2}\left| r_{x}\right| ^{2}+\lambda _{2}\left| q_{x}\right| ^{2}\right) r+\left( \delta _{2}\left| r\right| ^{2}+\zeta _{2}\left| q\right| ^{2}\right) r_{xx}\nonumber \\&\qquad +\left( \mu _{2}r^{2}+\rho _{2}q^{2}\right) r_{xx}^{*}\nonumber \\&\qquad +\left( f_{2}\left| r\right| ^{4}+g_{2}\left| r\right| ^{2}\left| q\right| ^{2}+h_{2}\left| q\right| ^{4}\right) r \nonumber \\&\qquad +i\left[ \eta _{2}\left( \left| r\right| ^{2}r\right) _{x}+\vartheta _{2}\left( \left| q\right| ^{2}q\right) _{x}\right. \nonumber \\&\qquad +\left\{ \theta _{2}\left( \left| r\right| ^{2}\right) _{x}+\epsilon _{2}\left( \left| q\right| ^{2}\right) _{x}\right\} r\nonumber \\&\qquad \left. +\left( \tau _{2}\left| r\right| ^{2}+\sigma _{2}\left| q\right| ^{2}\right) r_{x}\right] \end{aligned}$$
(31)

where the complex valued functions \(q\left( x,t\right)\) and r(x, t) account for optical solitons in birefringent fibers. For \(l=1,2\), \(a_{l}\) are the coefficients of 3OD, while \(b_{l}\) represent the coefficients of 4OD. Then, \(c_{l}\) and \(f_{l}\) stands for the coefficients of SPM, while \(d_{l}\), \(g_{l}\) and \(h_{l}\) account for the coefficients of cross-phase modulation. Lastly, \(\alpha _{l}\), \(\beta _{l}\), \(\gamma _{l}\), \(\lambda _{l}\), \(\delta _{l}\), \(\zeta _{l}\), \(\mu _{l}\), \(\rho _{l}\), \(\eta _{l}\), \(\vartheta _{l}\), \(\theta _{l}\), \(\varepsilon _{l}\), \(\tau _{l}\) and \(\sigma _{l}\) are the coefficients of the nonlinear dispersion terms.

To look for soliton solution to the governing model, the solution hypothesis picked is:

$$\begin{aligned}&q(x,t)=U_{1}(\xi )e^{i\varphi },\ \ r(x,t)=U_{2}(\xi )e^{i\varphi },\ \ \xi \nonumber \\&\quad =x-vt,\ \ \varphi (x,t)=-\kappa x+\omega t+\theta _{0}. \end{aligned}$$
(32)

Inserting Eq. (32) into Eqs. (30) and (31) yields the real equation

$$\begin{aligned}&b_{{l}}U_{l}^{\left( iv\right) }+\left( 3\kappa a_{{l}}-6{\kappa }^{2}b_{{l} }\right) U_{l}^{\prime \prime }\nonumber \\&\quad -\left( \rho _{{l}}+\zeta _{{l}}\right) U_{ {\tilde{l}}}^{2}U_{l}^{\prime \prime }\nonumber \\&\quad -\left( \delta _{{l}}+\mu _{{l}}\right) U_{l}^{2}U_{l}^{\prime \prime }\nonumber \\&\quad -\left( \alpha _{{l}}+\gamma _{{l}}\right) \left( U_{l}^{\prime }\right) ^{2}U_{l} \nonumber \\&\quad -\left( \beta _{{l}}+\lambda _{{l}}\right) U_{l}\left( U_{{\tilde{l}}}^{\prime }\right) ^{2}+\left( {\kappa }^{2}\beta _{{l}}-{\kappa }^{2}\lambda _{{l}}\right. \nonumber \\&\quad \left. +{ \kappa }^{2}\zeta _{{l}}+{\kappa }^{2}\rho _{{l}}+d_{{l}}-\kappa \sigma _{{l} }\right) U_{l}U_{{\tilde{l}}}^{2}\nonumber \\&\quad +\left( {\kappa }^{4}b_{{l}}-{\kappa }^{3}a_{{ l}}-\omega \right) U_{l} \nonumber \\&\quad +\left( c_{{l}}+{\kappa }^{2}\delta _{{l}}+{\kappa }^{2}\alpha _{{l}}+{ \kappa }^{2}\mu _{{l}}\right. \nonumber \\&\quad \left. -{\kappa }^{2}\gamma _{{l}}-\kappa \eta _{{l}}-\kappa \tau _{{l}}\right) U_{l}^{3}-\kappa \vartheta _{{l}}U_{{\tilde{l}}}^{3}-h_{{l} }U_{l}U_{{\tilde{l}}}^{4}\nonumber \\&\quad -g_{{l}}U_{l}^{3}U_{{\tilde{l}}}^{2}-f_{{l}}U_{l}^{5}=0 \end{aligned}$$
(33)

and the imaginary equation

$$\begin{aligned}&\left( a_{{l}}-4\kappa b_{{l}}\right) U_{l}^{\prime \prime \prime }+\left( 4{ \kappa }^{3}b_{{l}}-3{\kappa }^{2}a_{{l}}-v\right) U_{l}^{\prime }\nonumber \\&\quad +\left( 2\kappa \zeta _{{l}}-2\kappa \rho _{{l}}-\sigma _{{l}}\right) U_{l}^{\prime }U_{{\tilde{l}}}^{2} \nonumber \\&\quad +\left( 2\kappa \alpha _{{l}}+2\kappa \delta _{{l}}-2\kappa \mu _{{l}}-3\eta _{{l}}-\tau _{{l}}-2\theta _{{l}}\right) U_{l}^{\prime }U_{l}^{2}\nonumber \\&\quad +\left( 2\kappa \beta _{{l}}-2\epsilon _{{l}}\right) U_{l}U_{{\tilde{l}}}^{\prime }U_{ {\tilde{l}}}-3\vartheta _{{l}}U_{{\tilde{l}}}^{\prime }U_{{\tilde{l}}}^{2}=0 \end{aligned}$$
(34)

where \(l=1,2\) and \({\tilde{l}}=3-l.\) Eqs. (33) and (34) reduce to

$$\begin{aligned}&b_{{l}}U_{l}^{\left( iv\right) }+6\kappa ^{2}b_{{l}}U_{l}^{\prime \prime }-\left( 3\kappa ^{4}b_{{l}}+\omega \right) U_{l} \nonumber \\&\quad +\left( d_{{l}}+c_{{l}}-4\left( \delta _{{l}}+\zeta _{{l}}\right) {\kappa } ^{2}\right. \nonumber \\&\quad \left. +2\kappa \left( \epsilon _{{l}}+\theta _{{l}}+\eta _{{l}}+\vartheta _{{l} }\right) \right) U_{l}^{3}\nonumber \\&\quad -\left( h_{{l}}+g_{{l}}+f_{{l}}\right) U_{l}^{5}=0 \end{aligned}$$
(35)

with

$$\begin{aligned}&U_{{\tilde{l}}}=U_{l}, \end{aligned}$$
(36)
$$\begin{aligned}&a_{{l}}=4\kappa b_{{l}}, \end{aligned}$$
(37)
$$\begin{aligned}\alpha _{{l}}&=-\beta _{{l}}-2\delta _{{l}}-2\zeta _{{l}}\nonumber \\&\quad +\frac{\tau _{{l} }+\sigma _{{l}}+2\epsilon _{{l}}+2\theta _{{l}}+3\eta _{{l}}+3\vartheta _{{l} }}{2\kappa }, \end{aligned}$$
(38)
$$\begin{aligned}\gamma _{{l}}&=-\lambda _{{l}}+2\delta _{{l}}+2\zeta _{{l}}\nonumber \\&\quad -\frac{\tau _{{l} }+\sigma _{{l}}+2\epsilon _{{l}}+2\theta _{{l}}+3\eta _{{l}}+3\vartheta _{{l} }}{2\kappa }, \end{aligned}$$
(39)
$$\begin{aligned}&\mu _{{l}}=-\rho _{{l}}-\delta _{{l}}-\zeta _{{l}}, \end{aligned}$$
(40)
$$\begin{aligned}&v=-8\kappa ^{3}b_{{l}}. \end{aligned}$$
(41)

Utilizing the balancing principle in Eq. (35), Eq. (14) changes to

$$\begin{aligned}U_{l}\left( \xi \right)& =B_{1}\sin (V_{l}\left( \xi \right) )\nonumber \\&\quad +A_{1}\cos (V_{l}\left( \xi \right) )+A_{0}. \end{aligned}$$
(42)

Substituting Eq. (42) with Eq. (15) into Eq. (35) leads to

Case-1

$$\begin{aligned}\omega &=-b_{{l}}\left( 3{\kappa }^{4}+12{\kappa }^{2}-16\right) ,\ \ A_{{0} }=0,\ \ B_{{1}}=0, \nonumber \\A_{{1}}&=\pm \sqrt{-{\frac{4b_{{l}}\left( 3{\kappa }^{2}-10\right) }{c_{{l} }+d_{{l}}-4{\kappa }^{2}\left( \delta _{{l}}+\zeta _{{l}}\right) +2\kappa \left( \epsilon _{{l}}+\eta _{{l}}+\theta _{{l}}+\vartheta _{{l}}\right) }}}, \nonumber \\f_{{l}}&=-\frac{1}{2b_{{l}}\left( 3{\kappa }^{2}-10\right) ^{2}}(-3{c_{{l}}} ^{2}-3{d_{{l}}}^{2}-12{\kappa }^{2}{\vartheta _{{l}}}^{2}-6c_{{l}}d_{{l}}\nonumber \\&\quad -48{ \kappa }^{4}{\delta _{{l}}}^{2}-48{\kappa }^{4}{\zeta _{{l}}}^{2}-12{\kappa } ^{2}{\epsilon _{{l}}}^{2} \nonumber \\&\quad -12{\kappa }^{2}{\eta _{{l}}}^{2}-12{\kappa }^{2}{\theta _{{l}}}^{2}+200b_{{l }}g_{{l}}+200b_{{l}}h_{{l}}+18{\kappa }^{4}b_{{l}}g_{{l}}\nonumber \\&\quad +18{\kappa }^{4}b_{{ l}}h_{{l}}-120{\kappa }^{2}b_{{l}}g_{{l}}-120{\kappa }^{2}b_{{l}}h_{{l}} \nonumber \\&\quad -12\kappa \,c_{{l}}\vartheta _{{l}}-12\kappa d_{{l}}\epsilon _{{l}}-12\kappa d_{{l}}\eta _{{l}}-12\kappa d_{{l}}\theta _{{l}}-12\kappa d_{{l}}\vartheta _{ {l}}\nonumber \\&\quad -96{\kappa }^{4}\delta _{{l}}\zeta _{{l}}+48{\kappa }^{3}\delta _{{l} }\epsilon _{{l}}+48{\kappa }^{3}\delta _{{l}}\eta _{{l}} \nonumber \\&\quad +48{\kappa }^{3}\delta _{{l}}\theta _{{l}}+48{\kappa }^{3}\delta _{{l} }\vartheta _{{l}}+48{\kappa }^{3}\epsilon _{{l}}\zeta _{{l}}\nonumber \\&\quad +48{\kappa } ^{3}\eta _{{l}}\zeta _{{l}}+48{\kappa }^{3}\theta _{{l}}\zeta _{{l}}+48{ \kappa }^{3}\zeta _{{l}}\vartheta _{{l}}+24{\kappa }^{2}c_{{l}}\delta _{{l} }+24{\kappa }^{2}c_{{l}}\zeta _{{l}} \nonumber \\&\quad +24{\kappa }^{2}d_{{l}}\delta _{{l}}+24{\kappa }^{2}d_{{l}}\zeta _{{l}}-24{ \kappa }^{2}\epsilon _{{l}}\eta _{{l}}-24{\kappa }^{2}\epsilon _{{l}}\theta _{{l}}\nonumber \\&\quad -24{\kappa }^{2}\epsilon _{{l}}\vartheta _{{l}}-24{\kappa }^{2}\eta _{{ l}}\theta _{{l}} \nonumber \\&\quad -24{\kappa }^{2}\eta _{{l}}\vartheta _{{l}}-24{\kappa }^{2}\theta _{{l} }\vartheta _{{l}}\nonumber \\&\quad -12\kappa c_{{l}}\epsilon _{{l}}-12\kappa c_{{l}}\eta _{{l} }-12\kappa c_{{l}}\theta _{{l}}). \end{aligned}$$
(43)

Plugging Eq. (43) with Eq. (16) into Eq. (42) leads to the dark solitons

$$\begin{aligned}&q(x,t)\nonumber \\&\quad =\pm \sqrt{-{\frac{4b_{{1}}\left( 3{\kappa }^{2}-10\right) }{c_{{1} }+d_{{1}}-4{\kappa }^{2}\left( \delta _{{1}}+\zeta _{{1}}\right) +2\kappa \left( \epsilon _{{1}}+\eta _{{1}}+\theta _{{1}}+\vartheta _{{1}}\right) }}} \nonumber \\&\qquad \tanh \left( x+8b_{{1}}\kappa ^{3}t\right) e^{i\left( -\kappa x-b_{{1} }\left( 3{\kappa }^{4}+12{\kappa }^{2}-16\right) t+\theta _{0}\right) }, \end{aligned}$$
(44)
$$\begin{aligned}&r(x,t)\nonumber \\&\quad =\pm \sqrt{-{\frac{4b_{{2}}\left( 3{\kappa }^{2}-10\right) }{c_{{2} }+d_{{2}}-4{\kappa }^{2}\left( \delta _{{2}}+\zeta _{{2}}\right) +2\kappa \left( \epsilon _{{2}}+\eta _{{2}}+\theta _{{2}}+\vartheta _{{2}}\right) }}} \nonumber \\&\qquad \tanh \left( x+8b_{{2}}\kappa ^{3}t\right) e^{i\left( -\kappa x-b_{{2} }\left( 3{\kappa }^{4}+12{\kappa }^{2}-16\right) t+\theta _{0}\right) } \end{aligned}$$
(45)

and the singular solitons

$$\begin{aligned}&q(x,t)\nonumber \\&\quad =\pm \sqrt{-{\frac{4b_{{1}}\left( 3{\kappa }^{2}-10\right) }{c_{{1} }+d_{{1}}-4{\kappa }^{2}\left( \delta _{{1}}+\zeta _{{1}}\right) +2\kappa \left( \epsilon _{{1}}+\eta _{{1}}+\theta _{{1}}+\vartheta _{{1}}\right) }}} \nonumber \\&\qquad \coth \left( x+8b_{{1}}\kappa ^{3}t\right) e^{i\left( -\kappa x-b_{{1} }\left( 3{\kappa }^{4}+12{\kappa }^{2}-16\right) t+\theta _{0}\right) }, \end{aligned}$$
(46)
$$\begin{aligned}&r(x,t)\nonumber \\&\quad =\pm \sqrt{-{\frac{4b_{{2}}\left( 3{\kappa }^{2}-10\right) }{c_{{2} }+d_{{2}}-4{\kappa }^{2}\left( \delta _{{2}}+\zeta _{{2}}\right) +2\kappa \left( \epsilon _{{2}}+\eta _{{2}}+\theta _{{2}}+\vartheta _{{2}}\right) }}} \nonumber \\&\qquad \tanh \left( x+8b_{{2}}\kappa ^{3}t\right) e^{i\left( -\kappa x-b_{{2} }\left( 3{\kappa }^{4}+12{\kappa }^{2}-16\right) t+\theta _{0}\right) }. \end{aligned}$$
(47)

These solitons are valid for

$$\begin{aligned} {b_{{l}}\left( 3{\kappa }^{2}-10\right) \left( c_{{l}}+d_{{l}}-4{\kappa } ^{2}\left( \delta _{{l}}+\zeta _{{l}}\right) +2\kappa \left( \epsilon _{{l} }+\eta _{{l}}+\theta _{{l}}+\vartheta _{{l}}\right) \right) <0}. \end{aligned}$$
(48)

Case-2

$$\begin{aligned}\omega &=-b_{{l}}\left( 3{\kappa }^{4}-6{\kappa }^{2}-1\right) ,\ \ A_{{0} }=0,\ \ A_{{1}}=0, \nonumber \\B_{{1}}&=\pm \sqrt{{\frac{4b_{{l}}\left( 3{\kappa }^{2}+5\right) }{c_{{l}}+d_{ {l}}-4{\kappa }^{2}\left( \delta _{{l}}+\zeta _{{l}}\right) +2\kappa \left( \epsilon _{{l}}+\eta _{{l}}+\theta _{{l}}+\vartheta _{{l}}\right) }}}, \nonumber \\f_{{l}}&=-\frac{1}{2b_{{l}}\left( 3\,{\kappa }^{2}+5\right) ^{2}}(-3{c_{{l}}} ^{2}-3{d_{{l}}}^{2}-12{\kappa }^{2}{\vartheta _{{l}}}^{2}-6c_{{l}}d_{{l}}\nonumber \\&\quad -48{ \kappa }^{4}{\delta _{{l}}}^{2}-48{\kappa }^{4}{\zeta _{{l}}}^{2}-12{\kappa } ^{2}{\epsilon _{{l}}}^{2} \nonumber \\&\quad -12{\kappa }^{2}{\eta _{{l}}}^{2}-12{\kappa }^{2}{\theta _{{l}}}^{2}+50b_{{l} }g_{{l}}+50b_{{l}}h_{{l}}+18{\kappa }^{4}b_{{l}}g_{{l}}\nonumber \\&\quad +18{\kappa }^{4}b_{{l} }h_{{l}}+60{\kappa }^{2}b_{{l}}g_{{l}}+60{\kappa }^{2}b_{{l}}h_{{l}} \nonumber \\&\quad -12\kappa c_{{l}}\vartheta _{{l}}-12\kappa d_{{l}}\epsilon _{{l}}-12\kappa d_{{l}}\eta _{{l}}-12\kappa d_{{l}}\theta _{{l}}-12\kappa d_{{l}}\vartheta _{ {l}}\nonumber \\&\quad -96{\kappa }^{4}\delta _{{l}}\zeta _{{l}}+48{\kappa }^{3}\delta _{{l} }\epsilon _{{l}}+48{\kappa }^{3}\delta _{{l}}\eta _{{l}} \nonumber \\&\quad +48{\kappa }^{3}\delta _{{l}}\theta _{{l}}+48{\kappa }^{3}\delta _{{l} }\vartheta _{{l}}+48{\kappa }^{3}\epsilon _{{l}}\zeta _{{l}}\nonumber \\&\quad +48{\kappa } ^{3}\eta _{{l}}\zeta _{{l}}+48{\kappa }^{3}\theta _{{l}}\zeta _{{l}}+48{ \kappa }^{3}\zeta _{{l}}\vartheta _{{l}}+24{\kappa }^{2}c_{{l}}\delta _{{l}} \nonumber \\&\quad +24{\kappa }^{2}c_{{l}}\zeta _{{l}}+24{\kappa }^{2}d_{{l}}\delta _{{l}}+24{ \kappa }^{2}d_{{l}}\zeta _{{l}}-24{\kappa }^{2}\epsilon _{{l}}\eta _{{l}}\nonumber \\&\quad -24{ \kappa }^{2}\epsilon _{{l}}\theta _{{l}}-24{\kappa }^{2}\epsilon _{{l} }\vartheta _{{l}}-24{\kappa }^{2}\eta _{{l}}\theta _{{l}} \nonumber \\&\quad -24{\kappa }^{2}\eta _{{l}}\vartheta _{{l}}-24{\kappa }^{2}\theta _{{l} }\vartheta _{{l}}\nonumber \\&\quad -12\kappa c_{{l}}\epsilon _{{l}}-12\kappa c_{{l}}\eta _{{l} }-12\kappa c_{{l}}\theta _{{l}}). \end{aligned}$$
(49)

Inserting Eq. (49) with Eq. (16) into Eq. (42) causes to the bright solitons

$$\begin{aligned}&q(x,t)\nonumber \\&\quad =\pm \sqrt{{\frac{4b_{{1}}\left( 3{\kappa }^{2}+5\right) }{c_{{1}}+d_{{ 1}}-4{\kappa }^{2}\left( \delta _{{1}}+\zeta _{{1}}\right) +2\kappa \left( \epsilon _{{1}}+\eta _{{1}}+\theta _{{1}}+\vartheta _{{1}}\right) }}} \nonumber \\&\qquad \text{ sech }\left( x+8b_{{1}}\kappa ^{3}t\right) e^{i\left( -\kappa x-b_{{1} }\left( 3{\kappa }^{4}-6{\kappa }^{2}-1\right) t+\theta _{0}\right) }, \end{aligned}$$
(50)
$$\begin{aligned}&r(x,t)\nonumber \\&\quad =\pm \sqrt{{\frac{4b_{{2}}\left( 3{\kappa }^{2}+5\right) }{c_{{2}}+d_{{ 2}}-4{\kappa }^{2}\left( \delta _{{2}}+\zeta _{{2}}\right) +2\kappa \left( \epsilon _{2}+\eta _{{2}}+\theta _{{2}}+\vartheta _{{2}}\right) }}} \nonumber \\&\qquad \text{ sech }\left( x+8b_{{2}}\kappa ^{3}t\right) e^{i\left( -\kappa x-b_{{2} }\left( 3{\kappa }^{4}-6{\kappa }^{2}-1\right) t+\theta _{0}\right) } \end{aligned}$$
(51)

and the singular solitons

$$\begin{aligned}&q(x,t)\nonumber \\&\quad =\pm \sqrt{-{\frac{4b_{{1}}\left( 3{\kappa }^{2}+5\right) }{c_{{1}}+d_{ {1}}-4{\kappa }^{2}\left( \delta _{{1}}+\zeta _{{1}}\right) +2\kappa \left( \epsilon _{{1}}+\eta _{{1}}+\theta _{{1}}+\vartheta _{{1}}\right) }}} \nonumber \\&\qquad \text{ csch }\left( x+8b_{{1}}\kappa ^{3}t\right) e^{i\left( -\kappa x-b_{{1} }\left( 3{\kappa }^{4}-6{\kappa }^{2}-1\right) t+\theta _{0}\right) }, \end{aligned}$$
(52)
$$\begin{aligned}&r(x,t)\nonumber \\&\quad =\pm \sqrt{-{\frac{4b_{{2}}\left( 3{\kappa }^{2}+5\right) }{c_{{2}}+d_{ {2}}-4{\kappa }^{2}\left( \delta _{{2}}+\zeta _{{2}}\right) +2\kappa \left( \epsilon _{2}+\eta _{{2}}+\theta _{{2}}+\vartheta _{{2}}\right) }}} \nonumber \\&\qquad \text{ csch }\left( x+8b_{{2}}\kappa ^{3}t\right) e^{i\left( -\kappa x-b_{{2} }\left( 3{\kappa }^{4}-6{\kappa }^{2}-1\right) t+\theta _{0}\right) }. \end{aligned}$$
(53)

The bright solitons are valid for

$$\begin{aligned}&b_{{l}}\left( c_{{l}}+d_{{l}}-4{\kappa }^{2}\left( \delta _{{l}}+\zeta _{{l} }\right) +2\kappa \left( \epsilon _{{l}}+\eta _{{l}}+\theta _{{l}}+\vartheta _{{l}}\right) \right) \nonumber \\&\quad >0 \end{aligned}$$
(54)

while the singular solitons are valid for

$$\begin{aligned}&b_{{l}}\left( c_{{l}}+d_{{l}}-4{\kappa }^{2}\left( \delta _{{l}}+\zeta _{{l} }\right) +2\kappa \left( \epsilon _{{l}}+\eta _{{l}}+\theta _{{l}}+\vartheta _{{l}}\right) \right) \nonumber \\&\quad <0. \end{aligned}$$
(55)

Case-3

$$\begin{aligned}\omega &=-b_{{l}}\left( 3{\kappa }^{4}+3{\kappa }^{2}-1\right) ,\ \ A_{{0}}=0, \nonumber \\A_{{1}}&=\pm \sqrt{-{\dfrac{b_{{l}}\left( 6{\kappa }^{2}-5\right) }{2\left( c_{{l}}+d_{{l}}-4{\kappa }^{2}\left( \delta _{{l}}+\zeta _{{l}}\right) +2\kappa \left( \epsilon _{{l}}+\eta _{{l}}+\theta _{{l}}+\vartheta _{{l} }\right) \right) }}}, \nonumber \\B_{{1}}&=\pm \sqrt{{\dfrac{b_{{l}}\left( 6{\kappa }^{2}-5\right) }{2\left( c_{ {l}}+d_{{l}}-4{\kappa }^{2}\left( \delta _{{l}}+\zeta _{{l}}\right) +2\kappa \left( \epsilon _{{l}}+\eta _{{l}}+\theta _{{l}}+\vartheta _{{l}}\right) \right) }}}, \nonumber \\f_{{l}}&=-\frac{1}{b_{{l}}\left( 6{\kappa }^{2}-5\right) ^{2}}(-6{c_{{l}}} ^{2}-6{d_{{l}}}^{2}-24{\kappa }^{2}{\vartheta _{{l}}}^{2}-12c_{{l}}d_{{l}}\nonumber \\&\quad -96 {\kappa }^{4}{\delta _{{l}}}^{2}-96{\kappa }^{4}{\zeta _{{l}}}^{2}-24{\kappa }^{2}{\epsilon _{{l}}}^{2} \nonumber \\&\quad -24{\kappa }^{2}{\eta _{{l}}}^{2}-24{\kappa }^{2}{\theta _{{l}}}^{2}+25b_{{l} }g_{{l}}+25b_{{l}}h_{{l}}+36{\kappa }^{4}b_{{l}}g_{{l}}\nonumber \\&\quad +36{\kappa }^{4}b_{{l} }h_{{l}}-60{\kappa }^{2}b_{{l}}g_{{l}}-60{\kappa }^{2}b_{{l}}h_{{l}} \nonumber \\&\quad -24\kappa c_{{l}}\vartheta _{{l}}-24\kappa d_{{l}}\epsilon _{{l}}-24\kappa d_{{l}}\eta _{{l}}-24\kappa d_{{l}}\theta _{{l}}-24\kappa d_{{l}}\vartheta _{ {l}}\nonumber \\&\quad -192{\kappa }^{4}\delta _{{l}}\zeta _{{l}}+96{\kappa }^{3}\delta _{{l} }\epsilon _{{l}}+96{\kappa }^{3}\delta _{{l}}\eta _{{l}} \nonumber \\&\quad +96{\kappa }^{3}\delta _{{l}}\theta _{{l}}+96{\kappa }^{3}\delta _{{l} }\vartheta _{{l}}+96{\kappa }^{3}\epsilon _{{l}}\zeta _{{l}}\nonumber \\&\quad +96{\kappa } ^{3}\eta _{{l}}\zeta _{{l}}+96{\kappa }^{3}\theta _{{l}}\zeta _{{l}}+96{ \kappa }^{3}\zeta _{{l}}\vartheta _{{l}}+48{\kappa }^{2}c_{{l}}\delta _{{l}} \nonumber \\&\quad +48{\kappa }^{2}c_{{l}}\zeta _{{l}}+48{\kappa }^{2}d_{{l}}\delta _{{l}}+48{ \kappa }^{2}d_{{l}}\zeta _{{l}}-48{\kappa }^{2}\epsilon _{{l}}\eta _{{l}}\nonumber \\&\quad -48{ \kappa }^{2}\epsilon _{{l}}\theta _{{l}}-48{\kappa }^{2}\epsilon _{{l} }\vartheta _{{l}}-48{\kappa }^{2}\eta _{{l}}\theta _{{l}} \nonumber \\&\quad -48{\kappa }^{2}\eta _{{l}}\vartheta _{{l}}-48{\kappa }^{2}\theta _{{l} }\vartheta _{{l}}\nonumber \\&\quad -24\kappa c_{{l}}\epsilon _{{l}}-24\kappa c_{{l}}\eta _{{l} }-24\kappa c_{{l}}\theta _{{l}}). \end{aligned}$$
(56)

Substituting Eq. (56) with Eq. (16) into Eq. (42) yields the combo singular solitons

$$\begin{aligned}&q(x,t)\nonumber \\&\quad =\left\{ \begin{array}{l} \pm \sqrt{-{\dfrac{b_{{1}}\left( 6{\kappa }^{2}-5\right) }{2\left( c_{{1} }+d_{{1}}-4{\kappa }^{2}\left( \delta _{{1}}+\zeta _{{1}}\right) +2\kappa \left( \epsilon _{{1}}+\eta _{{1}}+\theta _{{1}}+\vartheta _{{1}}\right) \right) }}}\coth \left( x+8b_{{1}}\kappa ^{3}t\right) \\ \\ \pm \sqrt{-{\dfrac{b_{{1}}\left( 6{\kappa }^{2}-5\right) }{2\left( c_{{1} }+d_{{1}}-4{\kappa }^{2}\left( \delta _{{1}}+\zeta _{{1}}\right) +2\kappa \left( \epsilon _{{1}}+\eta _{{1}}+\theta _{{1}}+\vartheta _{{1}}\right) \right) }}}\text{ csch }\left( x+8b_{{1}}\kappa ^{3}t\right) \end{array} \right\} \nonumber \\&\qquad e^{i\left( -\kappa x-b_{{1}}\left( 3{\kappa }^{4}+3{\kappa } ^{2}-1\right) t+\theta _{0}\right) }, \end{aligned}$$
(57)
$$\begin{aligned}&r(x,t)\nonumber \\&\quad =\left\{ \begin{array}{l} \pm \sqrt{-{\dfrac{b_{{2}}\left( 6{\kappa }^{2}-5\right) }{2\left( c_{{2} }+d_{{2}}-4{\kappa }^{2}\left( \delta _{{2}}+\zeta _{{2}}\right) +2\kappa \left( \epsilon _{{2}}+\eta _{{2}}+\theta _{{2}}+\vartheta _{{2}}\right) \right) }}}\coth \left( x+8b_{{2}}\kappa ^{3}t\right) \\ \\ \pm \sqrt{-{\dfrac{b_{{2}}\left( 6{\kappa }^{2}-5\right) }{2\left( c_{{2} }+d_{{2}}-4{\kappa }^{2}\left( \delta _{{2}}+\zeta _{{2}}\right) +2\kappa \left( \epsilon _{{2}}+\eta _{{2}}+\theta _{{2}}+\vartheta _{{2}}\right) \right) }}}\text{ csch }\left( x+8b_{{2}}\kappa ^{3}t\right) \end{array} \right\} \nonumber \\&\qquad e^{i\left( -\kappa x-b_{{2}}\left( 3{\kappa }^{4}+3{\kappa } ^{2}-1\right) t+\theta _{0}\right) }. \end{aligned}$$
(58)

The combo singular solitons are valid for

$$\begin{aligned}&b_{{l}}\left( 6{\kappa }^{2}-5\right) \left( c_{{l}}+d_{{l}}-4{\kappa } ^{2}\left( \delta _{{l}}+\zeta _{{l}}\right) +2\kappa \left( \epsilon _{{l} }+\eta _{{l}}+\theta _{{l}}+\vartheta _{{l}}\right) \right) \nonumber \\&\quad {<0}. \end{aligned}$$
(59)

Conclusions

This paper secures CQ solitons with perturbed LPD model for both polarization-preserving fibers and birefringent fibers. The sine-Gordon equation approach has made this retrieval of the complete spectrum of soliton solutions possible. The results thus form a new list in the data bank of nonlinear evolution equations and its soliton solutions. The list opens up a floodgate of opportunities with CQ solitons for LPD model. This would include locating the conservation laws and identifying the respective conservative quantities. One would also need to address the perturbation theory to form the adiabatic dynamics of soliton perturbation. Next, CQ solitons with Bragg gratings in presence of dispersive reflectivity for LPD model is a possibility. Additional integration methods, such as semi-inverse variational principle or Lie symmetry, would give a new perspectives to the model. A further extension is to address such dynamics with DWDM topology would be absolutely necessary. The results of such studies would gradually and sequentially be reported.