Exact solitary wave solutions to the (2 + 1)-dimensional generalised Camassa–Holm–Kadomtsev–Petviashvili equation

Abstract

In this paper, a ($2{+}1$)-dimensional nonlinear evolution equation (NLEE), namely the generalised Camassa–Holm–Kadomtsev–Petviashvili equation (gCHKP) or Kadomtsev–Petviashvili–Benjamin–Bona–Mahony equation (KP-BBM), is examined. After applying the newly developed generalised exponential rational function method (GERFM), 14 travelling wave solutions are formally generated. It is worth mentioning that by specifying values to free parameters some previously obtained solutions can be recovered. The simplest equation method (SEM) is used to prove that the solutions obtained by GERFM are good. With the aid of a symbolic computation system, we prove that GERFM is more efficient and faster.

1 Introduction

Many significant phenomena in physics and other related fields can be formulated using nonlinear evolution equations (NLEEs), which is the main reason for their importance in the past decades [1,2,3,4,5,6]. Accordingly, many different techniques have been developed to seek the associated exact solutions, including single solitary [7,8,9,10,11,12,13,14,15,16,17,18] and multisoliton solutions [1, 19,20,21,22,23]. Besides, as per mathematical physics, the exact solutions with variable coefficients can be used to simulate many experimental situations and they provide much more realistic models than their constant-coefficient counterparts, which are significantly useful to researchers to further study the nonlinear phenomena.

The present work is concerned with the ($2{+}1$)-dimensional generalised Camassa–Holm–Kadomtsev–Petviashvili equation (gCHKP) [24] which is well-known as the Kadomtsev–Petviashvili–Benjamin–Bona–Mahony equation (KP-BBM) [24,25,26,27,28,29,30,31,32] and constructed as

$$\begin{aligned} (u_t +u_x +\alpha uu_x +\beta u_{xxt} )_x +\gamma u_{yy} =0, \end{aligned}$$

(1.1)

where $\alpha ,\beta ,\gamma$ are arbitrary constants. This equation appears in the study of modern science and the role of dispersion in liquid drops. It is to be noted that for $\beta >0$, eq. (1.1) is called KP-BBM-I and for $\beta <0$ it is called KP-BBM-II [24] which is used to describe different physical phenomena.

Equation (1.1) is a modified form of the Benjamin–Bona–Mahony (BBM) equation formulated in the Kadomtsev–Petviashvili (KP) sense, where KP equation is then derived by examining the stability of the one-soliton solution of the KdV equation under transverse perturbations [5]. The BBM equation is better known as the regularised long-wave equation, which is used to describe long waves and model waves in plasma physics and other disciplines. In other words, KdV, KP and BBM equations are all used to study surface waves of long wavelength in liquids, acoustic-gravity waves in compressible fluids and waves in cold plasma [2]. So, the investigation of versions of exact solutions for KP-BBM equation turns into a vital and significant task.

In recent years, many powerful methods were applied to handle eq. (1.1) [24,25,26,27,28,29,30,31,32], such as the exp-function method applied by Yu et al [26], the bifurcation method applied by Song et al [27], the tan–cot method applied by Kumar et al [28], the generalised $({G}'/G)$-expansion method applied by Alam and Akbar [29], the factorisation method applied by Ganguly and Das [30], the modified simplest equation method (mSEM) method applied by Akter and Akbar [31], the improved $\tan (\frac{\phi (\xi )}{2})$-expansion method applied by Khan et al [32] and the homoclinic breather limit approach applied by Qin et al [24]. Consequently, a good understanding of the exact solutions is beneficial for researchers to concern the nonlinear wave model in real-world applications.

Therefore, the primary aim of this paper is to seek various versions of exact solutions for KP-BBM (1.1). The generalised exponential rational function method (GERFM) [33] and the simplest equation method (SEM) [34,35,36] are strong enough to deal with the variable-coefficient equations and naturally used to help achieve our goal. Here, in order to construct exact wave solutions, the travelling wave ansatz

$$\begin{aligned} \xi =kx+my-ct, \quad U(\xi )=u(x,y,t) \end{aligned}$$

is applied into eq. (1.1), to get

$$\begin{aligned} k(-cU_\xi +kU_\xi +\alpha kUU_\xi -c\beta k^{2}U_{\xi \xi \xi } )_\xi +\gamma m^{2}U_{\xi \xi } =0, \end{aligned}$$

(1.2)

where k, m are wave numbers and c is the wave speed. Then, integrating eq. (1.2) twice and letting the integral constants equal to zero yields

$$\begin{aligned} (k^{2}+\gamma m^{2}-ck)U+\frac{\alpha }{2}k^{2}U^{2}-c\beta k^{3}U_{\xi \xi } =0. \end{aligned}$$

(1.3)

The detail of handling eq. (1.3) will be demonstrated later. The organisation of the paper is as follows: Section 2 gives a short systematic description of GERFM and SEM. Then, these techniques are applied to solve eq. (1.3) in §3. Eventually, some discussion and conclusion are presented in §4.

2 The methods

2.1 The generalised exponential rational function method (GERFM)

In this subsection, we shall summarise the main algorithm of GERFM [33]:

Step 1:

Let us take into account a general NPDE as

$$\begin{aligned} \mathcal{N}\left( \psi (x,t),\frac{\partial \psi }{\partial x},\frac{\partial \psi }{\partial t},\frac{\partial ^{2}\psi }{\partial x^{2}},\ldots \right) =0. \end{aligned}$$

(2.1)

Using the new definition of the dependent variable as $\psi =\psi (\xi )$ with $\xi =kx+my-ct$, one can transform NPDE (2.1) into the following NODE:

$$\begin{aligned} \mathcal{N}\left( {\psi (\xi ),\frac{\mathrm{d}\psi }{\mathrm{d}\xi },\frac{\mathrm{d}^{2}\psi }{\mathrm{d}\xi ^{2}},\ldots } \right) =0, \end{aligned}$$

(2.2)

where the values of disposal parameters k, m, c will be found later.

Step 2:

Consider that eq. (2.2) has the solution of the following form:

$$\begin{aligned} \psi (\xi )=A_0 +\sum _{i=1}^M {A_i } \Phi (\xi )^{i}+\sum _{i=1}^M {B_k } \Phi (\xi )^{-i}, \end{aligned}$$

(2.3)

where

$$\begin{aligned} \Phi (\xi )=\frac{p_1 \mathrm{e}^{q_1 \xi }+p_2 \mathrm{e}^{q_2 \xi }}{p_3 \mathrm{e}^{q_3 \xi }+p_4 \mathrm{e}^{q_4 \xi }}. \end{aligned}$$

(2.4)

The values of constants $p_j ,q_j ~(1\le j\le 4), A_0 ,\ldots ,A_i$ and $B_i~ (1\le i\le M)$ are determined, in such a way that solution (2.3) always satisfies eq. (2.2). By considering the homogeneous balance principle, the value of M is determined.

Step 3:

Putting (2.3) into (2.2) and then collecting all terms, the left-hand side of eq. (2.2) gives us an algebraic equation $P(Z_1 ,Z_2 ,Z_3 ,Z_4 )=0$ in terms of $Z_i =\mathrm{e}^{q_i \xi }$ for $i=1,\ldots ,4$. Letting each coefficient of different powers in P to zero, we arrive at a system of a set of nonlinear equations regarding, k, m, c, $p_j ,q_j\, (1\le j\le 4),$ and $A_0 ,\ldots ,A_i$ and $B_i\, (1\le i\le M)$.

Step 4:

By solving the above system of equations using any symbolic computation software, the values of $p_i ,q_i\, (1\le i\le 4),A_0 ,\ldots ,A_k$ and $B_k\, (1\le k\le M)$ are determined, and replacing these values in eq. (2.3) we obtain the soliton solutions of eq. (2.1).

2.2 The simplest equation method (SEM)

In this subsection, we shall describe the main algorithm of the SEM [34,35,36]:

Step 1:

To solve eq. (2.2), the starting assumption for the solution of the equation is [5]

$$\begin{aligned} F(\xi )=\sum _{i=0}^M {a_i \left[ {Y(\xi )} \right] ^{i}} , \end{aligned}$$

(2.5)

where $a_{1,2...M}$ are parameters determined later, and Y satisfies in simplest equations reduced from the main ODE. Analogously, the value for the positive integer of M is obtained by using the balance technique.

Step 2:

Notably, the simplest equation is the crucial point for the SEM. In this work, to get new insights in solitary wave solutions and make a difference from GERFM the Bernoulli equation is considered as the simplest equation

$$\begin{aligned} Y_\xi =aY+bY^{2}. \end{aligned}$$

(2.6)

Equation (2.6) admits the following solution:

$$\begin{aligned} Y=\frac{a\mathrm{e}^{a(\xi )}}{1-b\mathrm{e}^{^{a(\xi )}}}. \end{aligned}$$

(2.7)

Step 3:

Note that according to the balance principle, one can determine the value of M from eq. (2.2). Then, the assumed solution (2.5) and the simplest equation (2.6) are substituted in (2.2). Thus, a polynomial of Y is given.

Step 4:

Finally, making the coefficients of the same powers of Y to zero, a system of algebraic equations with variables of $a_i$ ($i=0,...,M)$ is obtained. Replacing the results into expression (2.5) the soliton wave solutions of eq. (2.2) is achieved.

3 Applications of the methods

3.1 The solitary wave solutions by GERFM

In what follows, using GERFM various versions of travelling wave solutions of KP-BBM (1.1) are obtained.

First, applying the balance principle between the terms of $U^{2}$ and $U_{\xi \xi }$ in eq. (1.3) one has $2M=M+2$, i.e., $M=2$. Hence, eqs (2.3) and (2.4) suggest the following structure for the exact solutions:

$$\begin{aligned} u(\xi )= & {} A_0 +A_1 \Phi (\xi )+A_2 \Phi ^{2}(\xi )\nonumber \\&+\frac{B_1 }{\Phi (\xi )}+\frac{B_2 }{\Phi ^{2}(\xi )}. \end{aligned}$$

(3.1)

In what follows, under certain conditions, different solitary wave solutions are obtained.

Family 1: We obtain $p=[-1,1,1,1]$ and $q=[1,-1,1,-1]$, and so expression (2.4) turns to

$$\begin{aligned} \Phi \left( \xi \right) =-\frac{\sinh \left( \xi \right) }{\cosh \left( \xi \right) }. \end{aligned}$$

(3.2)

Case 1:

$$\begin{aligned}&c=\frac{\gamma m^{2}+k^{2}}{4\beta k^{3}+k},\,k=k,m=m, \\&A_0=-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{4\alpha \beta k^{2}+\alpha },\, A_1 =0, \\&A_2 =\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{4\alpha \beta k^{2}+\alpha },\, B_1 =B_1 , \, B_2 =B_2 . \end{aligned}$$

Substituting the above values and eq. (3.2) into eq. (3.1), we have

$$\begin{aligned} U\left( \xi \right) =-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{\alpha \left( {4\beta k^{2}+1} \right) \cosh ^{2}\left( \xi \right) }. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_1 \left( {x,y,t} \right) \\&\quad =-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{\alpha \left( {4\beta k^{2}+1} \right) \cosh ^{2}\left( {kx+my-\frac{\gamma m^{2}+k^{2}}{k\left( {4\beta k^{2}+1} \right) }t} \right) }. \end{aligned}$$

Case 2:

$$\begin{aligned}&c=\frac{-\gamma m^{2}-k^{2}}{4\beta k^{3}-k}, \,k=k, \,m=m, \\&A_0=\frac{4\left( {\gamma m^{2}+k^{2}} \right) \beta }{4\alpha \beta k^{2}-\alpha },\, A_1 =0,\\&A_2 = -\frac{12\left( {\gamma m^{2}+k^{2}} \right) \beta }{4\alpha \beta k^{2}-\alpha },\, B_1 =B_1 , \, B_2 =B_2 . \end{aligned}$$

Substituting the above values and eq. (3.2) into eq. (3.1), we have

$$\begin{aligned} U\left( \xi \right) =-\frac{\left( {\gamma m^{2}+k^{2}} \right) \beta \left( {8\cosh ^{2}\left( \xi \right) -12} \right) }{\alpha \left( {4\beta k^{2}-1} \right) \cosh ^{2}\left( \xi \right) }. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_2 \left( {x,y,t} \right) =-\frac{\left( {\gamma m^{2}+k^{2}} \right) \beta \left( {8\cosh ^{2}\left( {kx+my+\frac{\gamma m^{2}+k^{2}}{k\left( {4\beta k^{2}-1} \right) }t} \right) -12} \right) }{\alpha \left( {4\beta k^{2}-1} \right) \cosh ^{2}\left( {kx+my+\frac{\gamma m^{2}+k^{2}}{k\left( {4\beta k^{2}-1} \right) }t} \right) }. \end{aligned}$$

Case 3:

$$\begin{aligned}&c=\frac{\gamma m^{2}+k^{2}}{16\beta k^{3}+k},\quad k=k,\quad m=m, \\&A_0=-\frac{24\left( {\gamma m^{2}+k^{2}} \right) \beta }{16\alpha \beta k^{2}+\alpha },\quad A_1 =0,\\&A_2 =\frac{12\left( {\gamma m^{2}+k^{2}} \right) \beta }{16\alpha \beta k^{2}+\alpha }, \quad B_1 =0, \\&B_2=\frac{12\left( {\gamma m^{2}+k^{2}} \right) \beta }{16\alpha \beta k^{2}+\alpha }. \end{aligned}$$

Substituting the above values and eq. (3.2) into eq. (3.1), we have

$$\begin{aligned} U\left( \xi \right) =\frac{12\left( {\gamma m^{2}+k^{2}} \right) \beta \left( {\tanh ^{2}\left( \xi \right) -1} \right) ^{2}}{\alpha \left( {16\beta k^{2}+1} \right) \tanh ^{2}\left( \xi \right) }. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_3 \left( {x,y,t} \right) =\frac{12\left( {\gamma m^{2}+k^{2}} \right) \beta \left( {\tanh ^{2}\left( {kx+my-\frac{\gamma m^{2}+k^{2}}{k\left( {16\beta k^{2}+1} \right) }t} \right) -1} \right) ^{2}}{\alpha \left( {16\beta k^{2}+1} \right) \tanh ^{2}\left( {kx+my-\frac{\gamma m^{2}+k^{2}}{k\left( {16\beta k^{2}+1} \right) }t} \right) }. \end{aligned}$$

Case 4:

$$\begin{aligned}&c=\frac{-\gamma m^{2}-k^{2}}{16\beta k^{3}-k}, \quad k=k, \quad m=m,\\&A_0=-\frac{8\left( {\gamma m^{2}+k^{2}} \right) \beta }{16\alpha \beta k^{2}-\alpha }, \quad A_1 =0,\\&A_2 =-\frac{12\left( {\gamma m^{2}+k^{2}} \right) \beta }{16\alpha \beta k^{2}-\alpha },\quad B_1 =0,\\&B_2=-\frac{12\left( {\gamma m^{2}+k^{2}} \right) \beta }{16\alpha \beta k^{2}-\alpha }. \end{aligned}$$

Substituting the above values and eq. (3.2) into eq. (3.1), we have

$$\begin{aligned}&U\left( \xi \right) \\&\quad =-\frac{\left( {12\tanh ^{4}\left( \xi \right) {+}8\tanh ^{2}\left( \xi \right) {+}12} \right) \beta \left( {\gamma m^{2}{+}k^{2}} \right) }{\left( {\tanh \left( \xi \right) } \right) ^{2}\alpha \left( {16\beta k^{2}-1} \right) }. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_4 \left( {x,y,t} \right) =-\frac{\left( {12\tanh ^{4}\left( {kx+my+\frac{\gamma m^{2}+k^{2}}{k\left( {16\beta k^{2}-1} \right) }t} \right) +8\tanh ^{2}\left( {kx+my+\frac{\gamma m^{2}+k^{2}}{k\left( {16\beta k^{2}-1} \right) }t} \right) +12} \right) \beta \left( {\gamma m^{2}+k^{2}} \right) }{\alpha \left( {16\beta k^{2}-1} \right) \tanh ^{2}\left( {kx+my+\frac{\gamma m^{2}+k^{2}}{k\left( {16\beta k^{2}-1} \right) }t} \right) }. \end{aligned}$$

Family 2: We obtain $p=[i,-i,1,1]$ and $q=[i,-i,i,-i]$, and so expression (2.4) turns to

$$\begin{aligned} \Phi \left( \xi \right) =-\frac{\sin \left( \xi \right) }{\cos \left( \xi \right) }. \end{aligned}$$

(3.3)

Case 1:

$$\begin{aligned}&c=\frac{-\gamma m^{2}-k^{2}}{4\beta k^{3}-k},\quad k=k,\quad m=m,\\&A_0=-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{4\alpha \beta k^{2}-\alpha },\quad A_1 =A_1 ,\quad A_2 =A_2 ,\\&B_1 =0,\quad B_2 =-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{4\alpha \beta k^{2}-\alpha }. \end{aligned}$$

Substituting the above values and eq. (3.3) into eq. (3.1), we have

$$\begin{aligned} U\left( \xi \right) =-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{\alpha \left( {4\beta k^{2}-1} \right) \sin ^{2}\left( \xi \right) }. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_5 \left( {x,y,t} \right) \\&\quad =-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{\alpha \left( {4\beta k^{2}-1} \right) \sin ^{2}\left( {kx+my+\frac{\gamma m^{2}+k^{2}}{k\left( {4\beta k^{2}-1} \right) }t} \right) }. \end{aligned}$$

Case 2:

$$\begin{aligned}&c=\frac{\gamma m^{2}+k^{2}}{4\beta k^{3}+k},\,k=k,\,m=m,\\&A_0=\frac{4\beta \left( {\gamma m^{2}+k^{2}} \right) }{4\alpha \beta k^{2}+\alpha },\,A_1 =A_1 ,\,A_2 =A_2 ,\\&B_1 =0,\, B_2 =\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{4\alpha \beta k^{2}+\alpha }. \end{aligned}$$

Substituting the above values and eq. (3.3) into eq. (3.1), we have

$$\begin{aligned} U\left( \xi \right) =\frac{\left( {\gamma m^{2}+k^{2}} \right) \beta \left( {8\cos ^{2}\left( \xi \right) +4} \right) }{\left( {4\alpha \beta k^{2}+\alpha } \right) \sin ^{2}\left( \xi \right) }. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_6 \left( {x,y,t} \right) \\&\quad =\frac{\left( {\gamma m^{2}{+}k^{2}} \right) \beta \left( {8\cos ^{2}\left( {kx{+}my{-}\frac{\gamma m^{2}+k^{2}}{4\beta k^{3}{+}k}t} \right) +4} \right) }{\left( {4\alpha \beta k^{2}{+}\alpha } \right) \sin ^{2}\left( {kx+my-\frac{\gamma m^{2}+k^{2}}{4\beta k^{3}+k}t} \right) }. \end{aligned}$$

Case 3:

$$\begin{aligned}&c=\frac{\alpha B_2 }{12\beta k},\quad k=k,\\&m=-\frac{\sqrt{3}\sqrt{\alpha \left( {16\beta k^{2}-1} \right) B_2 +12\beta k^{2}}}{6\sqrt{-\beta \gamma }},\\&A_0 =2B_2 ,\quad A_1 {=}0,\quad A_2 =B_2 ,\quad B_1 {=}0,\quad B_2 {=}B_2 . \end{aligned}$$

Substituting the above values and eq. (3.3) into eq. (3.1), we have

$$\begin{aligned} U\left( \xi \right) =\frac{B_2 }{\cos ^{2}\left( \xi \right) \sin ^{2}\left( \xi \right) }. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_7 \left( {x,y,t} \right) =\frac{B_2 }{\cos ^{2}\left( {kx-\frac{\sqrt{3}\sqrt{\alpha \left( {16\beta k^{2}-1} \right) B_2 +12\beta k^{2}}}{6\sqrt{-\gamma \beta }}y-\frac{\alpha B_2 }{12\beta k}t} \right) \sin ^{2}\left( {kx-\frac{\sqrt{3}\sqrt{\alpha \left( {16\beta k^{2}-1} \right) B_2 +12\beta k^{2}}}{6\sqrt{-\gamma \beta }}y-\frac{\alpha B_2 }{12\beta k}t} \right) }. \end{aligned}$$

Case 4:

$$\begin{aligned}&c=\frac{\alpha B_2 }{12\beta k},\quad k=k,\\&m=\frac{\sqrt{3}\sqrt{\alpha \left( {16\beta k^{2}+1} \right) B_2 -12\beta k^{2}}}{6\sqrt{-\gamma \beta }},\\&A_0 {=}-2/3B_2 ,\;\; A_1 {=}0,\;\; A_2 {=}B_2 ,\;\; B_1 {=}0,\;\; B_2 {=}B_2 . \end{aligned}$$

Substituting the above values and eq. (3.3) into eq. (3.1), we have

$$\begin{aligned} U\left( \xi \right) =\frac{\left( {8\cos ^{4}\left( \xi \right) -8\cos ^{2}\left( \xi \right) +3} \right) B_2 }{3\cos ^{2}\left( \xi \right) \sin ^{2}\left( \xi \right) }. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_8 \left( {x,y,t} \right) \\&\quad =\frac{\left( {8\cos ^{4}\left( {kx+\frac{\sqrt{3}\sqrt{\alpha \left( {16\beta k^{2}{+}1} \right) B_2 {-}12\beta k^{2}}}{6\sqrt{-\gamma \beta }}y{-}\frac{\alpha B_2 }{12\beta k}t} \right) {-}8\cos ^{2}\left( {kx{+}\frac{\sqrt{3}\sqrt{\alpha \left( {16\beta k^{2}{+}1} \right) B_2 {-}12\beta k^{2}}}{6\sqrt{-\gamma \beta }}y{-}\frac{\alpha B_2 }{12\beta k}t} \right) \!\!{+}3} \right) B_2 }{3\cos ^{2}\left( {kx+\frac{\sqrt{3}\sqrt{\alpha \left( {16\beta k^{2}+1} \right) B_2 -12\beta k^{2}}}{6\sqrt{-\gamma \beta }}y-\frac{\alpha B_2 }{12\beta k}t} \right) \sin ^{2}\left( {kx+\frac{\sqrt{3}\sqrt{\alpha \left( {16\beta k^{2}+1} \right) B_2 -12\beta k^{2}}}{6\sqrt{-\gamma \beta }}y-\frac{\alpha B_2 }{12\beta k}t} \right) }. \end{aligned}$$

Family 3: We obtain $p=[1,1,-1,1]$ and $q=[1,-1,1,-1]$, and so expression (2.4) turns to

$$\begin{aligned} \Phi \left( \xi \right) =-\frac{\cosh \left( \xi \right) }{\sinh \left( \xi \right) }. \end{aligned}$$

(3.4)

Case 1:

$$\begin{aligned}&c=\frac{-\gamma m^{2}-k^{2}}{4\beta k^{3}-k},\quad k=k,\quad m=m,\\&A_0=\frac{4\left( {\gamma m^{2}+k^{2}} \right) \beta }{4\alpha \beta k^{2}-\alpha },\quad A_1 =0,\\&A_2 =-\frac{12\left( {\gamma m^{2}+k^{2}} \right) \beta }{4\alpha \beta k^{2}-\alpha },\quad B_1 =B_1 ,\quad B_2 =B_2 \end{aligned}$$

Substituting the above values and eq. (3.4) into eq. (3.1), we have

$$\begin{aligned} U\left( \xi \right) =-\frac{\left( {8\cosh ^{2}\left( \xi \right) +4} \right) \beta \left( {\gamma m^{2}+k^{2}} \right) }{\alpha \left( {4\beta k^{2}-1} \right) \sinh ^{2}\left( \xi \right) }. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_9 \left( {x,y,t} \right) \\&\quad =-\frac{\beta \left( {\gamma m^{2}{+}k^{2}} \right) \left( {8\cosh ^{2}\left( {kx{+}my{+}\frac{\gamma m^{2}{+}k^{2}}{k\left( {\beta k^{2}{-}1} \right) }t} \right) \!\!{+}4} \right) }{\alpha \left( {4\beta k^{2}-1} \right) \sinh ^{2}\left( {kx+my+\frac{\gamma m^{2}+k^{2}}{k\left( {\beta k^{2}-1} \right) }t} \right) }\!. \end{aligned}$$

Case 2:

$$\begin{aligned}&c=\frac{\gamma m^{2}+k^{2}}{4\beta k^{3}+k},\quad k=k,\quad m=m,\\&A_0=-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{4\alpha \beta k^{2}+\alpha },\quad A_1 =0,\\&A_2 =\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{4\alpha \beta k^{2}+\alpha },\quad B_1 =B_1 ,\quad B_2 =B_2 . \end{aligned}$$

Substituting the above values and eq. (3.4) into eq. (3.1), we have

$$\begin{aligned} U\left( \xi \right) =\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{\alpha \left( {4\beta k^{2}+1} \right) \sinh ^{2}\left( \xi \right) }. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_{10} \left( {x,y,t} \right) \nonumber \\&\quad =\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{\alpha \left( {4\beta k^{2}+1} \right) \sinh ^{2}\left( {kx+my-\frac{\gamma m^{2}+k^{2}}{k\left( {\beta k^{2}+1} \right) }t} \right) }. \end{aligned}$$

Table 1 The obtained solutions by GERFM.

Fig. 1

3D profile of $u_1(x,y,1)$ by selecting suitable parameters $\alpha =1,\gamma =0.5,\beta =3,m=0.1,k=2$.

Fig. 2

3D profile of $u_2 (x,y,1)$ by selecting suitable parameters $\alpha =1,\gamma =0.5,\beta =3,m=0.1,k=2$.

Fig. 3

3D profile of $u_4 (x,y,1)$ by selecting suitable parameters $\alpha =1,\gamma =0.5,\beta =3,m=0.1,k=2$.

Fig. 4

3D profile of $u_7 (x,y,1)$ by selecting suitable parameters $\alpha =4,\gamma =-0.5,\beta =10,B_2 =0.5,k=0.5$.

Fig. 5

3D profile of $u_8 (x,y,1)$ by selecting suitable parameters $\alpha =4,\gamma =-0.5,\beta =10,B_2 =0.5,k=0.5,m=0.1$.

Family 4: We obtain $p=[-1,0,1,1]$ and $q=[0,0,0,1]$, and so expression (2.4) turns to

$$\begin{aligned} \Phi \left( \xi \right) =-\frac{1}{1+\mathrm{e}^{\xi }}. \end{aligned}$$

(3.5)

Case 1:

$$\begin{aligned}&c=\frac{\gamma m^{2}+k^{2}}{k\left( {\beta k^{2}+1} \right) },\quad k=k,\quad m=m,\\&A_0 =0,\quad A_1 =\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{\alpha \left( {\beta k^{2}+1} \right) },\\&A_2=\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{\alpha \left( {\beta k^{2}+1} \right) },\quad B_1 =B_1 ,\quad B_2 =B_2 . \end{aligned}$$

Substituting the above values and eq. (3.5) into eq. (3.1), we have

$$\begin{aligned} U\left( \xi \right) =-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) \hbox {e}^{\xi }}{\alpha \left( {\beta k^{2}+1} \right) \left( {1+\hbox {e}^{\xi }} \right) ^{2}}. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_{11} \left( {x,y,t} \right) \\&\quad =-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) \hbox {e}^{kx+my-\frac{\gamma m^{2}+k^{2}}{k\left( {\beta k^{2}+1} \right) }t}}{\alpha \left( {\beta k^{2}+1} \right) \left( {1+\hbox {e}^{kx+my-\frac{\gamma m^{2}+k^{2}}{k\left( {\beta k^{2}+1} \right) }t}} \right) ^{2}}. \end{aligned}$$

Case 2:

$$\begin{aligned}&c=\frac{-\gamma m^{2}-k^{2}}{k\left( {\beta k^{2}-1} \right) },\quad k=k,\quad m=m,\\&A_0 =-\frac{2\beta \left( {\gamma m^{2}+k^{2}} \right) }{\alpha \left( {\beta k^{2}-1} \right) },\\&A_1 =-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{\alpha \left( {\beta k^{2}-1} \right) },\\&A_2 =-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{\alpha \left( {\beta k^{2}-1} \right) },\quad B_1 =B_1 ,\quad B_2 =B_2 . \end{aligned}$$

Substituting the above values and eq. (3.5) into eq. (3.1), we have

$$\begin{aligned} U\left( \xi \right) =-\frac{2\beta \left( {\gamma m^{2}+k^{2}} \right) \left( {\hbox {e}^{2{}\xi }-4\hbox {e}^{\xi }+1} \right) }{\alpha \left( {\beta k^{2}-1} \right) \left( {1+\hbox {e}^{\xi }} \right) ^{2}}. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_{12} \left( {x,y,t} \right) =-\frac{2\beta \left( {\gamma m^{2}+k^{2}} \right) \left( {\hbox {e}^{2{}\left( {kx+my+\frac{\gamma m^{2}+k^{2}}{k\left( {\beta k^{2}-1} \right) }t} \right) }-4\hbox {e}^{kx+my+\frac{\gamma m^{2}+k^{2}}{k\left( {\beta k^{2}-1} \right) }t}+1} \right) }{\alpha \left( {\beta k^{2}-1} \right) \left( {1+\hbox {e}^{kx+my+\frac{\gamma m^{2}+k^{2}}{k\left( {\beta k^{2}-1} \right) }t}} \right) ^{2}}. \end{aligned}$$

Fig. 6

3D profile of $u_{10} (x,y,1)$ by selecting suitable parameters $\alpha =4,\gamma =-0.5,\beta =10,k=0.5,m=0.1$.

Fig. 7

3D profile of $u_{12} (x,y,1)$ by selecting suitable parameters $\alpha =2,\gamma =1,\beta =1.5,k=0.2,m=0.3$.

Family 5: We obtain $p=[i,-i,1,1]$ and $q=[i,-i,i,-i]$, and so expression (2.4) turns to

$$\begin{aligned} \Phi \left( \xi \right) =-\frac{\sin \left( \xi \right) }{\cos \left( \xi \right) }. \end{aligned}$$

(3.6)

Case 1:

$$\begin{aligned}&c=\frac{-\gamma m^{2}-k^{2}}{4\beta k^{3}-k},\quad k=k,\quad m=m,\\&A_0=-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{4\alpha \beta k^{2}-\alpha },\quad A_1 =0,\\&A_2 =-\frac{12\beta \left( {\gamma m^{2}+k^{2}} \right) }{4\alpha \beta k^{2}-\alpha },\quad B_1 =B_1 ,\quad B_2 =B_2 . \end{aligned}$$

Substituting the above values and eq. (3.6) into eq. (3.1), we have

$$\begin{aligned} U\left( \xi \right) =-\frac{12\left( {\gamma m^{2}+k^{2}} \right) \beta }{\alpha \left( {4\beta k^{2}-1} \right) \cos ^{2}\left( \xi \right) }. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_{13} \left( {x,y,t} \right) \\&\quad =-\frac{12\left( {\gamma m^{2}+k^{2}} \right) \beta }{\alpha \left( {4\beta k^{2}-1} \right) \cos ^{2}\left( {kx+my+\frac{\gamma m^{2}+k^{2}}{4\beta k^{3}-k}t} \right) }. \end{aligned}$$

Case 2:

$$\begin{aligned}&c=\frac{\gamma m^{2}+k^{2}}{4\beta k^{3}+k},\quad k=k,\quad m=m,\\&A_0=\frac{4\left( {\gamma m^{2}+k^{2}} \right) \beta }{4\alpha \beta k^{2}+\alpha },\quad A_1 =0,\\&A_2 =\frac{12\left( {\gamma m^{2}+k^{2}} \right) \beta }{4\alpha \beta k^{2}+\alpha },\quad B_1 =B_1 ,\quad B_2 =B_2 . \end{aligned}$$

Substituting the above values and eq. (3.6) into eq. (3.1), we have

$$\begin{aligned} U\left( \xi \right) =-\frac{\left( {\gamma m^{2}+k^{2}} \right) \beta \left( {8\cos ^{2}\left( \xi \right) -12} \right) }{\left( {4\alpha \beta k^{2}+\alpha } \right) \cos ^{2}\left( \xi \right) }. \end{aligned}$$

So, one gets

$$\begin{aligned}&u_{14} \left( {x,y,t} \right) \\&\quad =-\frac{\left( {\gamma m^{2}+k^{2}} \right) \beta \left( {8\cos ^{2}\!\left( {kx{+}my{-}\frac{\gamma m^{2}{+}k^{2}}{4\beta k^{3}{+}k}t} \right) \!\!{-}12} \right) }{\left( {4\alpha \beta k^{2}{+}\alpha } \right) \cos ^{2}\left( {kx{+}my{-}\frac{\gamma m^{2}+k^{2}}{4\beta k^{3}+k}t} \right) }. \end{aligned}$$

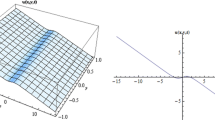
So far, 14 exact travelling wave solutions with free parameters are obtained. They have been verified by replacing them into the original equation and found correct. For particular values of these parameters, the periodic and solitary waves are derived, which are summarised in table 1 and depicted in figures 1–8.

3.2 The solitary wave solution by SEM

Taking into account the SEM, we seek exact solution of eq. (2.2) with the following formulation:

$$\begin{aligned} U=a_0 +a_1 Y+a_2 Y^{2}. \end{aligned}$$

(3.7)

Substituting eqs (3.7) and (2.6) into (1.3) and making the coefficient of the same power Y to zero, gives the following equations:

$$\begin{aligned}&Y^{0}:(k^{2}+\gamma m^{2}-ck)a_0 +\frac{\alpha k^{2}}{2}a_0^2 =0, \end{aligned}$$

(3.8)

$$\begin{aligned}&Y^{1}:(k^{2}+\gamma m^{2}-ck)a_1 \nonumber \\&\quad +\frac{\alpha k^{2}}{2}(2a_0 a_1 )-c\beta k^{3}a^{2}a_1 =0, \end{aligned}$$

(3.9)

$$\begin{aligned}&Y^{2}:(k^{2}+\gamma m^{2}-ck)a_2 \nonumber \\&\quad +\frac{\alpha k^{2}}{2}(a_1^2 +2a_0 a_2 )\nonumber \\&\quad -c\beta k^{3}(3aa_1 b+4a^{2}a_2 )=0, \end{aligned}$$

(3.10)

$$\begin{aligned}&Y^{3}:\frac{\alpha k^{2}}{2}2a_1 a_2 \nonumber \\&\quad -c\beta k^{3}(2a_1 b^{2}+10aba_2 )=0, \end{aligned}$$

(3.11)

$$\begin{aligned}&Y^{4}:\frac{\alpha k^{2}}{2}a_2^2 -c\beta k^{3}6a_2 b^{2}=0. \end{aligned}$$

(3.12)

Solving eqs (3.8)–(3.12) yields

Fig. 8

3D profile of $u_{13} (x,y,1)$ by selecting suitable parameters $\alpha =1,\gamma =0.5,\beta =0.1,k=0.2,m=0.01$.

Fig. 9

3D profile of $u_{15} (x,y,1)$ by selecting suitable parameters $\alpha =1, \gamma =0.5, \beta =0.1, k=0.2, a=0.1, b=0.1, m=0.01, c=0.7$.

Fig. 10

3D profile of $u_{15} (x,y,1)$ by selecting suitable parameters $\alpha =-3, \gamma =1.3, \beta =3.1, k=0.2, a=0.1, b=0.1, m=0.1, c=1$.

Table 2 The summary of the obtained solutions in this paper.

$$\begin{aligned}&a_0 =0, \nonumber \\{}&a_1 =\dfrac{12c\beta abk}{\alpha }, \nonumber \\{}&a_2 =\dfrac{12c\beta b^{2}k}{\alpha }, \nonumber \\&c=\dfrac{k^{2}+\gamma m^{2}}{k+\beta a^{2}k^{3}}. \end{aligned}$$

(3.13)

Using eqs (2.7) and (3.7) and by virtue of (3.13), we conclude the following novel solitary solution of eq. (2.2), as

$$\begin{aligned} u_{15} =\frac{12c\beta a^{2}bk}{\alpha }\frac{\mathrm{e}^{a(kx+my-ct)}}{(1-b\mathrm{e}^{kx+my-ct})^{2}}. \end{aligned}$$

(3.14)

The dynamical behaviour of solution (3.14) has been depicted in figures 9 and 10.

To our best knowledge, the solutions $u_{1-15}$ have never been reported before.This can be considered as one of the benefits of these methods. It is seen that the solution $u_{15}$ is consistent with $u_{11}$ by setting $a=1,b=-1$ into eqs (3.13) and (3.14). Besides, all generated solutions reveal that free parameters $\alpha ,\beta ,\gamma ,k,m,a,b$ influence the wave amplitude and $\beta ,\gamma ,k,m,a$ affect the wave speed. Meanwhile, as another advantage, it is clear that the GERFM is much more powerful than the other existing methods because it contains a lot of free parameters which give different types of assumed solution forms (3.2)–(3.6).

On the other hand, setting $\gamma =0$ reduces eq. (1.1) to the BBM equation [37] as

$$\begin{aligned} u_t +u_x +\alpha uu_x +\beta u_{xxt} =0. \end{aligned}$$

(3.15)

The related periodic and solitary solutions of eq. (3.15) can be correspondingly obtained by substituting $\gamma =0$ into $u_{1-15}$. Furthermore, specifying values to free parameters makes $u_{11}$ and $u_{15}$ to be the same as the 1-soliton solution (3.7) extracted by Hirota method in [37]. The summary of the obtained solutions is reported in table 2. Moreover, to help the readers for easy understanding, we have included a Maple code which we have used for the analysis of the acquired solutions in Appendix.

4 Conclusion

In this work, after applying GERFM and the SEM to handle the ($2+1$)-dimensional variable-coefficient KP-BBM equation, 15 versions of exact solutions are formally generated. All solutions are checked by Maple. Moreover, the solution $u_{11}$ obtained by GERFM and the solution $u_{15}$ obtained by SEM are consistent with the 1-soliton solution derived by Hirota method. In other words, all generated solutions are functional and physically meaningful. Thus, by specifying values to free parameters $\alpha ,\beta ,\gamma ,k,m,a,b$ in $u_{1-15}$ gives various versions of travelling waves, which may make outstanding contributions to the study of nonlinear wave science. It is highly anticipated that this investigation on the KP-BBM equation may have more ramifications in various physical models.

Appendix: Maple code