1 Introduction

Nonlinear dispersive partial differential equations have a long and rich history of study, which has continued to gain interest in recent years(Ablowitz et al. 2004, Ablowitz 2011; Akinyemi et al. 2021d, Akinyemi et al. 2021e; Biswas and Milovic 2010, Biswas et al. 2018; Biswas 2019; Dia Dai 1998; Hong 2001; Inc et al. 2020a; Karpman 1975; Mirzazadeh et al. 2021; Rezazadeh et al. 2020; Sulem and Sulem 1999; Triki and Biswas 2011; Vahidi et al. 2021; Wazwaz 2006, Wazwaz 2019, Wazwaz 2021; Zhou et al. 2016). One of the most important and fundamental tasks in applied sciences and engineering is the development of exact and analytical traveling wave solutions for nonlinear partial differential equations (NPDEs). There are several well-established techniques that have been used to study NPDEs, such as perturbation-iteration algorithm ( Senol and Dolapci 2016; Senol et al. 2019a), tanh method ( Wazwaz 2006), sine-Gordon method ( Ali Akbar et al. 2021), iterative shehu transform method (Akinyemi and Iyiola 2020a), residual power series method (Alquran et al. 2015; Senol et al. 2019b; Senol 2020b), variational iteration method ( He 1998), fractional reduced differential transform method ( Akinyemi 2020), \(\delta\)-homotopy perturbation transform method (Akinyemi et al. 2021a), q-homotopy analysis method ( Akinyemi 2019; Akinyemi et al. 2020a; El-Tawil and Huseen 2012), homogeneous balance method ( Jafari et al. 2014), F-expansion method ( Lu and Zhang 2017), \(G^{\prime }/{G}\)-expansion method ( Akinyemi et al. 2021c; Bekir and Guner 2013), q-homotopy analysis transform method (Akinyemi and Huseen 2020; Akinyemi and Iyiola 2020b), new extended direct algebraic method (Rezazadeh 2018; Senol 2020a), simple equation method ( Az-Zo’bi et al. 2021a), Jacobi elliptic function method (Az-Zo’bi et al. 2021b), functional variable method ( Inc et al. 2020b), and much more.

A fully integrated nonlinear dispersive partial differential equation, the nonlinear Schrödinger (NLS) equation proved instrumental in obtaining a deeper understanding of a wide variety of processes, from nonlinear optics and atomic physics to deep water waves, rogue waves, plasmas, and so on. The Korteweg-de Vries (KdV) equation is one of the most important nonlinear PDEs. In various fields of applied sciences and engineering, such as hydrodynamics, plasma physics, water waves, and quantum field theory, KdV equations play a prominent role. They define the interactions with distinct dispersion relations between two long waves. In mathematical physics, chemistry, and biology, several types of coupled nonlinear problems have emerged as models to describe the interacting wave phenomena. As a model to explain the interacting wave dynamics in the electromagnetic waves in plasma physics, dust-acoustic wave, and Langmuir wave, the coupled Schrödinger-KdV equations emerged as a model to describe different forms of wave phenomena in mathematical physics, etc. This study considers a generalized coupled NLS-KdV equations of the form:

$$\begin{aligned} \begin{aligned} iP_{t}+\uplambda _1\,P_{xx}+\uplambda _2|{P}|^2P+\uplambda _3PQ&=0,\\ Q_{t}+\beta _1\,QQ_{x}+\beta _2Q_{xxx}+\beta _3\big (|{P}|^2\big )_{x}&=0, \end{aligned} \end{aligned}$$
(1)

where \(\uplambda _1,\uplambda _2,\uplambda _3,\beta _1,\beta _2,\beta _3\) are real constants, \(P=P(x,t)\) is a complex function while \(Q=Q(x,t)\) is a real-valued function. Indeed, P simply represents the short wave, while Q represents the long wave. In fluid mechanics, like capillary gravity water wave interactions, these coupled equations occur in phenomena of interactions between short and long dispersive waves (Albert and Angulo Pava 2003; Corcho and Linares 2007; Funakoshi and Oikawa 1983). We also refer the readers to ( Deconinck et al. 2016; Nguyen and Liu 2020) for more detailed discussion. We observe that setting Q and \(\beta _3\) to zero in Eq. (1) yields the NLS equation:

$$\begin{aligned} iP_{t}+\uplambda _1\,P_{xx}+\uplambda _2|{P}|^2P=0. \end{aligned}$$
(2)

Also, setting \(P=0\) in Eq. (1) leads to the KdV equation:

$$\begin{aligned} Q_{t}+\beta _1\,QQ_{x}+\beta _2Q_{xxx}=0. \end{aligned}$$
(3)

In this study, our main aim is to analyze the solutions of the coupled NLS-KdV system with the help of Kudryashov and sub-equation techniques. The advantage of these two techniques over the other existing methods is that they provide the proposed system with some simple form of soliton solutions. Through these methods, we achieve trigonometric, hyperbolic, and rational type solutions containing the bright soliton, dark soliton, periodic, singular, and other soliton-type solutions. Relevantly, these kinds of solutions can help to understand some physical phenomena related to wave propagation. It is worth mentioning that the existence of solutions for the coupled system of NLS-KdV equations have been highlighted in (Colorado 2015, 2017). It should be noted that the retrieved findings are new and have not been published previously.

As follows, we organized the layout of the rest of our work: The explanation of the proposed methods are presented in Sect. 2. Finally, the discussion and conclusion of our work is given in Sect. 3.

2 The model’s mathematical analysis

Consider the generalized coupled system of NLS-KdV equations

$$\begin{aligned} \begin{aligned} iP_{t}+\uplambda _1\,P_{xx}+\uplambda _2|{P}|^2P+\uplambda _3PQ&=0,\\ Q_{t}+\beta _1\,QQ_{x}+\beta _2Q_{xxx}+\beta _3\big (|{P}|^2\big )_{x}&=0. \end{aligned} \end{aligned}$$
(4)

Since P is a complex function while Q is a real-valued function, we propose the transformation as:

$$\begin{aligned} \begin{aligned} P(x,t)&=P(\phi )e^{i(\omega _2x+\eta _2t)},\\ Q(x,t)&=Q(\phi ),\quad \phi =\omega _1x+\eta _1t, \end{aligned} \end{aligned}$$
(5)

where \(\omega _i\) and \(\eta _i,\,\,i=1,2\) are the speed of wave, wave number and frequency of the soliton respectively. Using the transformation defined in Eq. (5), we obtain the real and imaginary parts of Eq. (4) as follows:

$$\begin{aligned}&-(\eta _2+\uplambda _1\omega _2^2)P(\phi )+\uplambda _1\omega _1^2P^{\prime \prime }(\phi )+\uplambda _2P(\phi )^3+\uplambda _3P(\phi )Q(\phi )=0, \end{aligned}$$
(6)
$$\begin{aligned}&(\eta _1+2\uplambda _1\omega _1\omega _2)P^{\prime }(\phi )=0, \end{aligned}$$
(7)

and

$$\begin{aligned} \eta _1Q^{\prime }(\phi )+\beta _1\omega _1Q(\phi )Q^{\prime }(\phi )+\beta _2\omega _1^3Q^{\prime \prime \prime }(\phi )+2\beta _3\omega _1P(\phi )P^{\prime }(\phi )=0. \end{aligned}$$
(8)

Solving Eq. (7) yields

$$\begin{aligned} \eta _1=-2\uplambda _1\omega _1\omega _2. \end{aligned}$$
(9)

Substituting Eq. (9) into Eq. (8), then integrate once with zero constant of integration, we obtain

$$\begin{aligned} -2\uplambda _1\omega _2Q(\phi )+\frac{1}{2}\beta _1Q(\phi )^2+\beta _2\omega _1^2Q^{\prime \prime }(\phi )+\beta _3P(\phi )^2=0. \end{aligned}$$
(10)

Assume that the solutions of 6 and 10 are expressed respectively as

$$\begin{aligned} \begin{aligned} P(\phi )&=\sum _{m=0}^{\Lambda _1} g_m\Phi ^{m}(\phi ),\\ Q(\phi )&=\sum _{m=0}^{\Lambda _2} h_m\Phi ^{m}(\phi ),\,\,\,g_{\Lambda _1},\,h_{\Lambda _2}\ne {0}. \end{aligned} \end{aligned}$$
(11)

where the constants \(g_{m}\) and \(h_{m}\) are to be calculated respectively. With the use of the balance procedure (Malfliet 1992), balancing \(P^{\prime \prime }(\phi )\) with \(P(\phi )^3\) in Eq. (6) yields \(\Lambda _1=1\) and \(Q^{\prime \prime }(\phi )\) with \(Q(\phi )^2\) in Eq. (10) yields \(\Lambda _2=2.\)

2.1 The Kudryashov method

According to Kudryashov method (Kudryashov 2012, 2020a, b; Kudryashov and Antonova 2020; Rezazadeh et al. 2021), the solutions take the form

$$\begin{aligned} \begin{aligned} P(\phi )&=g_0+g_1\Phi {(\phi )},\\ Q(\phi )&=h_0+h_1\Phi {(\phi )}+h_2\Phi {(\phi )}^2. \end{aligned} \end{aligned}$$
(12)

The function \(\Phi {(\phi )}\) satisfies the ODE:

$$\begin{aligned} (\Phi ^{\prime }{(\phi )})^2=\Phi ^{2}(\phi )\big (1-\Omega \Phi ^{2}(\phi )\big ). \end{aligned}$$
(13)

The solution to the above ODE is given as

$$\begin{aligned} \Phi (\phi )=\frac{4{\mathcal {E}}_1}{\big (4{\mathcal {E}}_1^2-\Omega \big )\sinh {(\phi )}+\big (4{\mathcal {E}}_1^2+\Omega \big )\cosh {(\phi )}},\quad \Omega =4{\mathcal {E}}_1{\mathcal {E}}_2. \end{aligned}$$
(14)

Here, \({\mathcal {E}}_1\) and \({\mathcal {E}}_2\) are arbitrary constants. Inserting Eqs. (12) and (13) into Eqs. (6) and (10) respectively, collecting all the coefficient of \(\Phi ^{m}(\phi ),\,m=0,1,2,3,4\) and setting them to zero, we have

$$\begin{aligned} \begin{aligned} \Phi ^{0}(\phi )&:-g_0\eta _2+g_0h_0\uplambda _3-g_0\uplambda _1\omega _2^2+g_0^3\uplambda _2=0,\\&:\beta _3g_0^2+\frac{1}{2}\beta _1h_0^2-2h_0\uplambda _1 \omega _2=0,\\ \Phi ^{1}(\phi )&:-g_1\eta _2+g_0h_1\uplambda _3+g_1h_0\uplambda _3+g_1\uplambda _1\omega _1^2-g_1\uplambda _1\omega _2^2+3g_1g_0^2\uplambda _2=0,\\&:2\beta _3g_0g_1+\beta _2h_1\omega _1^2+\beta _1h_0h_1-2h_1\uplambda _1\omega _2=0,\\ \Phi ^{2}(\phi )&:g_1h_1\uplambda _3+g_0h_2\uplambda _3+3g_0g_1^2\uplambda _2=0,\\&:\beta _3g_1^2+4\beta _2h_2\omega _1^2+\frac{1}{2}\beta _1h_1^2+\beta _1h_0h_2-2h_2\uplambda _1\omega _2=0,\\ \Phi ^{3}(\phi )&:-2\Omega \,g_1\uplambda _1\omega _1^2+g_1h_2\uplambda _3+g_1^3\uplambda _2=0,\\&:\beta _1h_1h_2-2\Omega \beta _2h_1\omega _1^2=0,\\ \Phi ^{4}(\phi )&:\frac{1}{2}\beta _1h_2^2-6\Omega \beta _2h_2\omega _1^2=0. \end{aligned} \end{aligned}$$
(15)

The solutions of the above obtained algebraic equations with Eq. (9) results in the following cases:

Case 1

$$\begin{gathered} \eta _{1} = - 2\lambda _{1} \omega _{1} \omega _{2} ,\hfill \\ \eta _{2} = \frac{1}{{144\beta _{2}^{2} \lambda _{1} \lambda _{2}^{2} }}\left( { - 576\beta _{2}^{4} \lambda _{2}^{2} \omega _{1}^{4} + 144\beta _{2}^{2} \lambda _{1}^{2} \lambda _{2}^{2} \omega _{1}^{2} - 48\beta _{1} \beta _{2}^{2} \beta _{3} \lambda _{1} \lambda _{2} \omega _{1}^{2} + 288\beta _{2}^{3} \beta _{3} \lambda _{2} \lambda _{3} \omega _{1}^{2} - \beta _{1}^{2} \beta _{3}^{2} \lambda _{1}^{2} - 36\beta _{2}^{2} \beta _{3}^{2} \lambda _{3}^{2} + 12\beta _{1} \beta _{2} \beta _{3}^{2} \lambda _{1} \lambda _{3} } \right), \hfill \\ g_{0} = 0,{\mkern 1mu} {\mkern 1mu} g_{1} = \pm \omega _{1} \sqrt {\frac{{2\Omega (\beta _{1} \lambda _{1} - 6\beta _{2} \lambda _{3} )}}{{\beta _{1} \lambda _{2} }}} , \hfill \\ h_{0} = 0,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} h_{1} = 0,{\mkern 1mu} {\mkern 1mu} h_{2} = \frac{{12\Omega \beta _{2} \omega _{1}^{2} }}{{\beta _{1} }}, \hfill \\ \omega _{2} = \frac{{24\beta _{2}^{2} \lambda _{2} \omega _{1}^{2} + \beta _{1} \beta _{3} \lambda _{1} - 6\beta _{2} \beta _{3} \lambda _{3} }}{{12\beta _{2} \lambda _{1} \lambda _{2} }}. \hfill \\ \end{gathered}$$
(16)

By incorporating these parameters into Eq. (14), in addition to Eq. (12), we have the solutions

$$\begin{aligned} \begin{aligned} P_1(x,t)&=\pm \frac{\big (4{\mathcal {E}}_1\omega _1\sqrt{2\Omega (\beta _1\uplambda _1-6\beta _2\uplambda _3)}\big )e^{i(\omega _2x+\eta _2t)}}{\sqrt{\beta _1\uplambda _2}\big ((4{\mathcal {E}}_1^2-\Omega ) \sinh (\phi )+(4{\mathcal {E}}_1^2+\Omega )\cosh (\phi )\big )},\\ Q_1(x,t)&=\frac{192{\mathcal {E}}_1^2\Omega \beta _2\omega _1^2}{\beta _1\big ((4{\mathcal {E}}_1^2-\Omega )\sinh (\phi )+(4{\mathcal {E}}_1^2+\Omega )\cosh (\phi )\big )^2}. \end{aligned} \end{aligned}$$
(17)

Case 2

$$\begin{aligned} \begin{aligned} \eta _1&=-2\uplambda _1\omega _1\omega _2,\\ \eta _2&=\frac{1}{144\beta _1\beta _2^2\uplambda _1\uplambda _2^2}\Big (-576\beta _1\beta _2^4\uplambda _2^2\omega _1^4+144\beta _1\beta _2^2\uplambda _1^2\uplambda _2^2\omega _1^2-48\beta _1^2\beta _2^2\beta _3\uplambda _1\uplambda _2\omega _1^2\\&-\ 1152\beta _2^3\uplambda _1\uplambda _2^2\uplambda _3\omega _1^2+288\beta _1\beta _2^3\beta _3\uplambda _2\uplambda _3\omega _1^2-\beta _1^3\beta _3^2\uplambda _1^2-36\beta _1\beta _2^2\beta _3^2\uplambda _3^2\\&+\ 288\beta _2^2\beta _3\uplambda _1\uplambda _2\uplambda _3^2+12\beta _1^2\beta _2\beta _3^2\uplambda _1\uplambda _3-48\beta _1\beta _2\beta _3\uplambda _1^2\uplambda _2\uplambda _3\Big ),\\ g_0&=0,\,\,g_1=\pm \omega _1\sqrt{\frac{2\Omega (\beta _1\uplambda _1-6\beta _2\uplambda _3)}{\beta _1\uplambda _2}},\\ h_0&=\frac{-24\beta _2^2\uplambda _2\omega _1^2-\beta _1\beta _3\uplambda _1+6\beta _2\beta _3\uplambda _3}{3\beta _1\beta _2\uplambda _2},\,\,h_1=0,\,\,h_2=\frac{12\Omega \beta _2\omega _1^2}{\beta _1},\\ \omega _2&=\frac{-24\beta _2^2\uplambda _2\omega _1^2-\beta _1\beta _3\uplambda _1+6\beta _2\beta _3\uplambda _3}{12\beta _2\uplambda _1\uplambda _2}. \end{aligned} \end{aligned}$$
(18)

By incorporating these parameters into Eq. (14), in addition to Eq. (12), we have the solutions

$$\begin{aligned} \begin{aligned} P_2(x,t)&=\pm \frac{\big (4{\mathcal {E}}_1\omega _1\sqrt{2\Omega (\beta _1\uplambda _1-6\beta _2\uplambda _3)}\big )e^{i(\omega _2x+\eta _2t)}}{\sqrt{\beta _1\uplambda _2}\big ((4{\mathcal {E}}_1^2-\Omega ) \sinh (\phi )+(4{\mathcal {E}}_1^2+\Omega )\cosh (\phi )\big )},\\ Q_2(x,t)&=\frac{-24\beta _2^2\uplambda _2\omega _1^2-\beta _1\beta _3\uplambda _1+6\beta _2\beta _3\uplambda _3}{3\beta _1\beta _2\uplambda _2}+\frac{192{\mathcal {E}}_1^2\Omega \beta _2\omega _1^2}{\beta _1\big ((4{\mathcal {E}}_1^2-\Omega )\sinh (\phi )+(4{\mathcal {E}}_1^2+\Omega )\cosh (\phi )\big )^2}, \end{aligned} \end{aligned}$$
(19)

where \(\phi =\omega _1x+\eta _1t\) and \(\Omega =4{\mathcal {E}}_1{\mathcal {E}}_2.\)

Remark 1

It should be emphasized that the constraint for Eqs. (17) and (19) is that

$$\begin{aligned} \frac{\Omega (\beta _1\uplambda _1-6\beta _2\uplambda _3)}{\beta _1\uplambda _2}>0. \end{aligned}$$
(20)

Remark 2

For \({\mathcal {E}}_1={\mathcal {E}}_2=1,\) Eqs. (17) and (19) reduce to the bright soliton solutions of Eq. (4) as follows:

$$\begin{aligned} \begin{aligned} P(x,t)&=\pm {\omega _1}\sqrt{\frac{2(\beta _1\uplambda _1-6\beta _2\uplambda _3)}{\beta _1\uplambda _2}}{{\,\mathrm{sech}\,}}(\omega _1x+\eta _1t)e^{i(\omega _2x+\eta _2t)},\\ Q(x,t)&=\frac{12\beta _2\omega _1^2}{\beta _1}{{\,\mathrm{sech}\,}}^2(\omega _1x+\eta _1t), \end{aligned} \end{aligned}$$
(21)

and

$$\begin{aligned} \begin{aligned} P(x,t)&=\pm {\omega _1}\sqrt{\frac{2(\beta _1\uplambda _1-6\beta _2\uplambda _3)}{\beta _1\uplambda _2}}{{\,\mathrm{sech}\,}}(\omega _1x+\eta _1t)e^{i(\omega _2x+\eta _2t)},\\ Q(x,t)&=\frac{-24\beta _2^2\uplambda _2\omega _1^2-\beta _1\beta _3\uplambda _1+6\beta _2\beta _3\uplambda _3}{3\beta _1\beta _2\uplambda _2}+\frac{12\beta _2\omega _1^2}{\beta _1}{{\,\mathrm{sech}\,}}^2(\omega _1x+\eta _1t), \end{aligned} \end{aligned}$$
(22)

provided that

$$\begin{aligned} \frac{\beta _1\uplambda _1-6\beta _2\uplambda _3}{\beta _1\uplambda _2}>0. \end{aligned}$$
(23)

Remark 3

For \({\mathcal {E}}_1=1\) and \({\mathcal {E}}_2=-1,\) Eqs. (17) and (19) reduce to the singular soliton solutions of Eq. (4) as follows:

$$\begin{aligned} \begin{aligned} P(x,t)&=\pm {i\omega _1}\sqrt{\frac{2(\beta _1\uplambda _1-6\beta _2\uplambda _3)}{\beta _1\uplambda _2}}{{\,\mathrm{csch}\,}}(\omega _1x+\eta _1t)e^{i(\omega _2x+\eta _2t)},\\ Q(x,t)&=-\frac{12\beta _2\omega _1^2}{\beta _1}{{\,\mathrm{csch}\,}}^2(\omega _1x+\eta _1t), \end{aligned} \end{aligned}$$
(24)

and

$$\begin{aligned} \begin{aligned} P(x,t)&=\pm {i\omega _1}\sqrt{\frac{2(\beta _1\uplambda _1-6\beta _2\uplambda _3)}{\beta _1\uplambda _2}}{{\,\mathrm{csch}\,}}(\omega _1x+\eta _1t)e^{i(\omega _2x+\eta _2t)},\\ Q(x,t)&=\frac{-24\beta _2^2\uplambda _2\omega _1^2-\beta _1\beta _3\uplambda _1+6\beta _2\beta _3\uplambda _3}{3\beta _1\beta _2\uplambda _2}-\frac{12\beta _2\omega _1^2}{\beta _1}{{\,\mathrm{csch}\,}}^2(\omega _1x+\eta _1t), \end{aligned} \end{aligned}$$
(25)

provided that

$$\begin{aligned} \frac{\beta _1\uplambda _1-6\beta _2\uplambda _3}{\beta _1\uplambda _2}<0. \end{aligned}$$
(26)

2.2 The sub-equation method

Based on the sub-equation method (Akinyemi et al. 2021b; Senol et al. 2021), the solutions still take the form

$$\begin{aligned} \begin{aligned} P(\phi )&=g_0+g_1\Phi {(\phi )},\\ Q(\phi )&=h_0+h_1\Phi {(\phi )}+h_2\Phi {(\phi )}^2. \end{aligned} \end{aligned}$$
(27)

Here, the function \(\Phi (\phi )\) satisfies the Riccati equation defined by

$$\begin{aligned} \Phi ^{\prime }(\phi )=\varrho +\Phi ^{2}(\phi ), \end{aligned}$$
(28)

for constant \(\varrho .\) The category of solutions that certifies Eq. (28) are as follows:

$$\begin{aligned} \Phi (\phi )=\left\{ \begin{array}{lll} -\sqrt{-\varrho }\tanh ({\sqrt{-\varrho }\,\phi }), \qquad \qquad \varrho<0,\\ -\sqrt{-\varrho }\coth ({\sqrt{-\varrho }\,\phi }),\qquad \qquad \varrho <0,\\ \sqrt{\varrho }\tan ({\sqrt{\varrho }\,\phi }),\qquad \qquad \qquad \varrho>0,\\ -\sqrt{\varrho }\cot ({\sqrt{\varrho }\,\phi }),\qquad \qquad \qquad \varrho >0,\\ -\frac{1}{\phi +\phi _0},\quad \phi _0\,\text {is a constant,}\qquad \varrho =0. \end{array} \right. \end{aligned}$$
(29)

Putting Eqs. (27) and (28) into Eqs. (6) and (10) leads to the polynomial in \(\Phi ^{m}(\phi ).\) Gathering all of the \(\Phi ^{m}(\phi ),\,m=0,1,2,3,4\) coefficient and setting it to zero, one get

$$\begin{aligned} \begin{aligned} \Phi ^{0}(\phi )&:-g_0(\eta _2+\uplambda _1\omega _2^2)+g_0h_0\uplambda _3+g_0^3\uplambda _2=0,\\&:\beta _3g_0^2+2\beta _2h_2\varrho ^2\omega _1^2+\frac{1}{2}\beta _1h_0^2-2h_0\uplambda _1\omega _2=0,\\ \Phi ^{1}(\phi )&:-g_1(\eta _2+\uplambda _1\omega _2^2)+g_0h_1\uplambda _3+g_1h_0\uplambda _3+2g_1\uplambda _1\varrho \omega _1^2+3g_1g_0^2\uplambda _2=0,\\&:2\beta _3g_0g_1+2\beta _2h_1\varrho \omega _1^2+\beta _1h_0h_1-2h_1\uplambda _1\omega _2=0,\\ \Phi ^{2}(\phi )&:g_1h_1\uplambda _3+g_0h_2\uplambda _3+3g_0g_1^2\uplambda _2=0,\\&:\beta _3g_1^2+8\beta _2h_2\varrho \omega _1^2+\frac{1}{2}\beta _1h_1^2+\beta _1 h_0h_2-2h_2\uplambda _1\omega _2=0,\\ \Phi ^{3}(\phi )&:g_1h_2\uplambda _3+2g_1\uplambda _1\omega _1^2+g_1^3\uplambda _2=0,\\&:2\beta _2h_1\omega _1^2+\beta _1h_1h_2=0,\\ \Phi ^{4}(\phi )&:6\beta _2h_2\omega _1^2+\frac{1}{2}\beta _1h_2^2=0. \end{aligned} \end{aligned}$$
(30)

The solutions of the algebraic equations obtained above with Eq. (9) yields the following:

$$\begin{aligned} \begin{aligned} \eta _1&=-2\uplambda _1\omega _1\omega _2,\\ \eta _2&=\frac{1}{144\beta _2^2\uplambda _1\uplambda _2^2}\Big (-576\beta _2^4\uplambda _2^2\varrho ^2\omega _1^4\mp \frac{24\beta _2\uplambda _1\uplambda _2\uplambda _3\sqrt{(48\beta _2^2\beta _1\uplambda _2\varrho \omega _1^2+\beta _3\beta _1^2\uplambda _1-6\beta _2\beta _3\beta _1\uplambda _3)^2-1728\beta _1^2\beta _2^4\uplambda _2^2\varrho ^2\omega _1^4}}{\beta _1^2}\\&+\ 288\beta _2^2\uplambda _1^2\uplambda _2^2\varrho \omega _1^2-96\beta _1\beta _2^2\beta _3\uplambda _1\uplambda _2\varrho \omega _1^2+576\beta _2^3\beta _3\uplambda _2\uplambda _3\varrho \omega _1^2-\frac{1152\beta _2^3\uplambda _1\uplambda _2^2\uplambda _3\varrho \omega _1^2}{\beta _1}-\beta _1^2\beta _3^2\uplambda _1^2-36\beta _2^2\beta _3^2\uplambda _3^2\\&+\ \frac{144\beta _2^2\beta _3\uplambda _1\uplambda _2\uplambda _3^2}{\beta _1}+12\beta _1\beta _2\beta _3^2\uplambda _1\uplambda _3-24\beta _2\beta _3\uplambda _1^2\uplambda _2\uplambda _3\Big ),\\ g_0&=0,\,\,g_1=\pm \sqrt{\frac{2(6\beta _2\uplambda _3\omega _1^2-\beta _1\uplambda _1\omega _1^2)}{\beta _1\uplambda _2}},\,\,h_1=0,\,\,h_2=-\frac{12\beta _2\omega _1^2}{\beta _1},\\ h_0&=-\frac{\sqrt{(48\beta _2^2\beta _1\uplambda _2\varrho \omega _1^2+\beta _3\beta _1^2\uplambda _1-6\beta _2\beta _3\beta _1\uplambda _3)^2-1728\beta _1^2\beta _2^4\uplambda _2^2\varrho ^2\omega _1^4}-48\beta _2^2\beta _1\uplambda _2\varrho \omega _1^2+6\beta _2\beta _3\beta _1\uplambda _3-\beta _1^2\beta _3\uplambda _1}{6\beta _1^2\beta _2\uplambda _2},\\ \omega _2&=-\frac{\sqrt{(48\beta _2^2\beta _1\uplambda _2\varrho \omega _1^2+\beta _3\beta _1^2\uplambda _1-6\beta _2\beta _3\beta _1\uplambda _3)^2-1728\beta _1^2\beta _2^4\uplambda _2^2\varrho ^2\omega _1^4}}{12\beta _1\beta _2\uplambda _1\uplambda _2}. \end{aligned} \end{aligned}$$
(31)

By incorporating these parameters into Eq. (14), in addition to Eq. (12), we have the following solutions:

For \(\varrho <0,\) we have

$$\begin{aligned} \begin{aligned} P_3(x,t)&=\pm {\omega _1}\sqrt{-\frac{2\varrho (6\beta _2\uplambda _3-\beta _1\uplambda _1)}{\beta _1\uplambda _2}}\tanh (\sqrt{-\varrho }\phi )e^{i(\omega _2x+\eta _2t)},\\ Q_3(x,t)&=h_0+\frac{12\beta _2\varrho \omega _1^2}{\beta _1}\tanh ^2(\sqrt{-\varrho }\phi ), \end{aligned} \end{aligned}$$
(32)
$$\begin{aligned} \begin{aligned} P_4(x,t)&=\pm {\omega _1}\sqrt{-\frac{2\varrho (6\beta _2\uplambda _3-\beta _1\uplambda _1)}{\beta _1\uplambda _2}}\coth (\sqrt{-\varrho }\phi )e^{i(\omega _2x+\eta _2t)},\\ Q_4(x,t)&=h_0+\frac{12\beta _2\varrho \omega _1^2}{\beta _1}\coth ^2(\sqrt{-\varrho }\phi ). \end{aligned} \end{aligned}$$
(33)

For \(\varrho >0,\) we have

$$\begin{aligned} \begin{aligned} P_5(x,t)&=\mp {\omega _1}\sqrt{\frac{2\varrho (6\beta _2\uplambda _3-\beta _1\uplambda _1)}{\beta _1\uplambda _2}}\tan (\sqrt{\varrho }\phi )e^{i(\omega _2x+\eta _2t)},\\ Q_5(x,t)&=h_0-\frac{12\beta _2\varrho \omega _1^2}{\beta _1}\tan ^2(\sqrt{\varrho }\phi ), \end{aligned} \end{aligned}$$
(34)
$$\begin{aligned} \begin{aligned} P_6(x,t)&=\pm {\omega _1}\sqrt{\frac{2\varrho (6\beta _2\uplambda _3-\beta _1\uplambda _1)}{\beta _1\uplambda _2}}\cot (\sqrt{\varrho }\phi )e^{i(\omega _2x+\eta _2t)},\\ Q_6(x,t)&=h_0-\frac{12\beta _2\varrho \omega _1^2}{\beta _1}\cot ^2(\sqrt{\varrho }\phi ). \end{aligned} \end{aligned}$$
(35)

For \(\varrho =0,\) we have

$$\begin{aligned} \begin{aligned} P_7(x,t)&=\pm \frac{\omega _1\sqrt{2(6\beta _2\uplambda _3-\beta _1\uplambda _1)}}{\sqrt{\beta _1\uplambda _2}(\phi +\phi _0)}e^{i(\omega _2x+\eta _2t)},\\ Q_7(x,t)&=h_0-\frac{12\beta _2\omega _1^2}{\beta _1(\phi +\phi _0)^2}. \end{aligned} \end{aligned}$$
(36)

Remark 4

It should be noted that the additional constraint for Eqs. (32), (33), (34), (35) and (36) is that

$$\begin{aligned} \frac{6\beta _2\uplambda _3-\beta _1\uplambda _1}{\beta _1\uplambda _2}>0. \end{aligned}$$
(37)

3 Conclusion and discussion

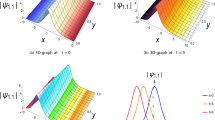
In conclusion, two novel methods, namely; the Kudryashov method and the sub-equation method have been successfully employed to obtain bright soliton, dark soliton, and other soliton-type solutions of the generalized nonlinear coupled Schrödinger-Korteweg-de Vries equations. The advantage of these two approaches over the other existing methods is that they present simple form soliton solutions to the proposed coupled system. The graphical representations in Figs. 1, 2, 3 and 4 of these solutions will undoubtedly play a prominent role in understanding the behavior and capture some of the physical characteristics of the coupled model. From these investigations, it can be projected that the results obtained may be useful for a better understanding of the interactive wave phenomena in any varied instance where the coupled model considered is applicable. Our results reinforced the fact that the methods suggested are an efficient, effective, and simple mathematical tool to handle various nonlinear problems in the fields of applied sciences and engineering. Furthermore, we have verified all the obtained solutions with the help of the Mathematica package software.

Fig. 1
figure 1

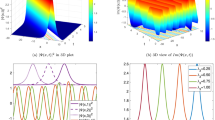
3D plots of the bright solitons (Eq. (21)) with \(\uplambda _1 = \beta _1 = -1,\,\uplambda _2 = \uplambda _3 = 1,\,\beta _2 = \beta _3 = 1,\) and \(\omega _1 = 0.1.\)

Full size image
Fig. 2
figure 2

2D plots of the bright solitons (Eq. 21) with different t when \(\uplambda _1 = \beta _1 =-1,\,\uplambda _2 = \uplambda _3 = 1,\,\beta _2 = \beta _3 = 1,\) and \(\omega _1 = 0.1.\)

Full size image
Fig. 3
figure 3

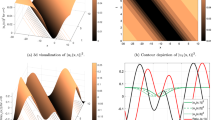
3D plots of the complex mixed dark-bright solitons (Eq. 32) and with \(\omega _1 = 0.1,\,\uplambda _1 = \uplambda _2 = \beta _1 = -1,\,\beta _2 = \beta _3 = \uplambda _3 = 1,\) and \(\varrho = -1.\)

Full size image
Fig. 4
figure 4

2D plots of the complex mixed dark-bright solitons (Eq. (32)) with different t when \(\omega _1 = 0.1,\,\uplambda _1 = \uplambda _2 = \beta _1 = -1,\,\beta _2 = \beta _3 = \uplambda _3 = 1,\) and \(\varrho = -1.\)

Full size image