1 Introduction

A wide range of complex phenomena in the fields of physics, engineering, chemistry, biology, and finance dynamics are modeled by nonlinear ordinary (NODEs) and partial (NPDEs) differential equations of integer and fractional orders (Wazwaz 2009; Kilbas et al. 2006; Owusu et al. 2020). Since there is no single method that can treat various kinds of nonlinear evolution equations (NLEEs), many techniques have been proposed, modified, and expanded for seeking exact analytic, semi-analytic and numerical solutions for NLEEs in conjunction with the development of software symbolic computations that helps researchers accomplish these tasks. Such solutions expand the area of understanding qualitative and measurable features of complex phenomena to draw efficient and appropriate conclusions. For this purpose, a variety of effective approaches have been suggested. The Darboux transformation (Gu et al. 1999), Bifurcation method (Song and Yang 2010), Hirota bilinear method (Hirota 2004), iterative shehu transform method (Akinyemi and Iyiola 2020b), expansion version of method (Wang et al. 2008), Adomian decomposition method and ifts extensions (Az-Zo’bi and Al-Khaled 2010; Az-Zo’bi 2013, 2014; Az-Zo’bi et al. 2019), Exp-function method (Ozis and Aslan 2018), F-expansion method (Seadawy and El-Rashidy 2018; Wang and Li 2005), He’s variational iteration method (Az-Zo’bi 2015), inverse scattering method (Biondini et al. 2016), reduced differential transform method (Az-Zo’bi et al. 2015, 2020; Az-Zo’bi 2014), homogeneous balance method (Rady et al. 2010), q-homotopy analysis method (Senol et al. 2019; Akinyemi et al. 2020; Akinyemi 2019), Lie symmetry method (Olver 1993), first integral method (Akram and Mahak 2018), residual power series method (Senol 2020; Az-Zo’bi 2018, 2019; Az-Zo’bi et al. 2019), simplest equation method (SEM) (Kudryashov 2005a, b), modified simplest equation method (MSEM) (Jawad et al. 2010), exp-\(\phi {(\xi )}\) method (Az-Zo’bi 2019), q-homotopy analysis transform method (Akinyemi 2020; Akinyemi and Huseen 2020; Akinyemi and Iyiola 2020a), sub-equation method (Kurt et al. 2020; Akinyemi et al. 2021), modified extended direct algebraic method (Arshad et al. 2017a), modified extended mapping method (Arshad et al. 2017b) and some others (Seadawy et al. 2019; Helal et al. 2014; Lu et al. 2018; Seadawy et al. 2020; Iqbal et al. 2020; Farah et al. 2020; Ahmad et al. 2020).

The simple equation method (SEM), derived by Kudryashov, and its expansions (Irshad et al. 2017; Arnous et al. 2017; Al-Amr and El-Ganaini 2017; Hossain et al. 2018; Zayed et al. 2019; Vitanov 2019; Az-Zo’bi 2019a, b) have succeeded in constructing solutions for several NLEEs. By means of the SEM and MSEM, this work will focus on constructing new analytic solutions for the time-fractional \((2+1)\)-dimensional Ito integro–differential equation in the conformable derivative sense:

$$\begin{aligned} \bigg (\partial _{t}^{2\rho }+\partial _{t}^{\rho }\partial _{x}^{3}+3u\,\partial _{t}^{\rho }{{\partial }_{x}}+3\bigg (\int \limits _{-\infty }^{x}{\partial _{t}^{\rho }u\,d{x}^{\prime }}\bigg )\partial _{x}^{2}+\alpha \,\partial _{t}^{\rho }{{\partial }_{y}}+\beta \,\partial _{t}^{\rho }{{\partial }_{x}}\bigg ) u+6\partial _{t}^{\rho }u{{\partial }_{x}}u=0, \end{aligned}$$
(1)

where \(\partial _{x}=\frac{\partial }{\partial {x}},\,\partial _{y}=\frac{\partial }{\partial {y}},\) \(\partial _{t}^{*\rho }\) is the conformable time-fractional derivative operator of order \(\rho \,(0<\rho \le {1}),\,\alpha\) and \(\beta\) are given constants, and u(x, y, t) denotes the relevant waves amplitude that approaches zero as x unboundedly decreases. By making use of differential operator \(u=\partial _{x}v\), Eq. 1 will be converted into the fifth-order NPDE

$$\begin{aligned} \Big (\partial _{t}^{2\rho }{{\partial }_{x}}+\partial _{t}^{\rho }\big (\partial _{x}^{4}+\alpha \,{{\partial }_{x}}{{\partial }_{y}}+\beta \,\partial _{x}^{2}\big )+3\big ({{\partial }_{x}}v\big )\,\partial _{t}^{\rho }{{\partial }_{x}}+\big (6\partial _{t}^{\rho }\,{{\partial }_{x}}v\big )\partial _{x}^{2}+3\big (\partial _{t}^{\rho }v\big )\partial _{x}^{3}\Big )v=0. \end{aligned}$$
(2)

The Ito model (Eq. 2) (or equivalently Eq. 1) was firstly derived by generalizing the well-known bilinear Korteweg-de Vries equation (Ito 1980). For \(\alpha =\beta =0\), we get the one-dimensional Ito equation. Recently, many authors have paid their concern to analytically process the (2+1)-dimensional Ito equation of integer time-derivative (\(\rho =1\)); Wazwaz (2008) applied the tanh-coth method to derive single soliton and periodic solutions. Also, N-solitons were derived by combining Hereman’s method and Hirota’s method. The extended homoclinic test technique and the bilinear method were performed to obtain single, two-solitons, periodic and doubly-periodic wave solutions (Li and Zhao 2009). Hyperbolic and periodic solutions were obtained using the extended F-expansion method (Bhrawy et al. 2012). The \(\left( {G}^{\prime }/G\right)\) method was used to carry out one-soliton solutions (Ebadi et al. 2012). Adem (2016) deduced multiple wave solutions by using the multiple exp-function algorithm. The Wronskian determinant technique was employed by Yildirim and Yasar (2018). Lump and stripe solutions with the diversity of interactions basing on the Hirota bilinear form were investigated by Ma et. al. in Yang et al. (2018), Ma et al. (2018), He et al. (2019).

This paper is prepared, in what follow, to present the basic concepts of conformable fractional calculus theory in Sect. 2. Mathematical analysis of the employed methods is included in Sect. 3. The derived exact analytic solutions for Eq. 1 by applying the proposed techniques are discussed in Sect. 4. Discussion and conclusions, with numerical simulations of some obtained solitons, are displayed in Sect. 5.

2 Conformable fractional derivative

Khalil et al. (2014) suggested the conformable fractional derivative (CFD) which satisfies the basic principles of normal derivative. In this section, the basic definition and necessary properties of the CFD are given. Suppose that \(u\left( t\right)\)is a function defined for \(t>0\). The CFD of order \(\rho\), \(0<\rho \le 1\), is defined as

$$\begin{aligned} D_{t}^{\rho }u=\underset{\hbar \rightarrow 0}{\lim }\,\frac{u(t+\hbar \,t^{1-\rho })-u(t) }{\hbar }. \end{aligned}$$
(3)

In the following theorem, the useful properties of the CFD are listed.

Theorem 2.1

(Ma et al. 2018; He et al. 2019; Abdeljawad 2015) Suppose that \(u_1(t)\) and \(u_2(t)\) are two \(\rho\)-differentiable functions on some interval I in the positive semi half space \((0,\infty ),\,\rho \in (0,1]\) and \(\nu\) are real numbers. Then

  1. 1.

    The CFD operator is linear,

  2. 2.

    \({\mathcal {D}}_{t}^{\rho }C=0,\)  C is constant.

  3. 3.

    \({\mathcal {D}}_{t}^{\rho }t^{\nu }=\nu \,t^{\nu -\rho }.\)

  4. 4.

    \({\mathcal {D}}_{t}^{\rho }(u_1\,u_2)=u_2\,{\mathcal {D}}_{t}^{\rho }u_1+u_1\,{\mathcal {D}}_{t}^{\rho }u_2.\)

  5. 5.

    \({\mathcal {D}}_{t}^{\rho }\left( \frac{u_1}{u_2}\right) =\frac{u_2\,{\mathcal {D}}_{t}^{\rho }u_1-u_1\,{\mathcal {D}}_{t}^{\rho }u_2}{u_2^{2}}.\)

  6. 6.

    \({\mathcal {D}}_{t}^{\rho }u_1(u_2(t))=t^{1-\rho }{u_2}^{\prime }(t){u_1}^{\prime }(v(t)).\)

  7. 7.

    \({\mathcal {D}}_{t}^{\rho }u_1=t^{1-\rho }u_1^{\prime }\) are satisfied for all \(t\in {I}.\)

Remark 1

Recently, several researchers have used the CFD when treating the fractional differential equations due to the efficiency and applicability of the CFD, which overcomes the existence complexity of other fractional derivatives such as Riemann-Liouville and Caputo. See Osman et al. (2019), Islama et al. (2019), Kurt et al. (2020), Zhu et al. (2019), Odabas (2020), Korpinar et al. (2020) for more detailed.

3 Mathematical analysis

In the current section, solution procedure to the constant-coefficients (2+1)-dimensional PDE

$$\begin{aligned} P\left( u,{{\partial }_{x}}u,{{\partial }_{y}}u,{\mathcal {D}}_{t}^{\rho }u,{{\partial }_{x}}{{\partial }_{y}}u,\cdots \right) =0, \end{aligned}$$
(4)

using the SEM and MSEM are outlined. P is assumed to be a polynomial \(u=u\left( x,y,t\right)\) and its derivatives including the highest derivative and the higher power of linear terms. The solution process also works for time-dependent coefficients NPDEs and systems. The SEM includes many other existing schemes; the Riccati equation, sub-equation, F-expansion, and \(\big (G^{\prime }/G\big )\) methods. The MSEM is considered here since it has a different procedure that used in the other one as will be shown in Sect. 3.2. To investigate Eq. 4, assume that its exact solution has the form

$$\begin{aligned} u\left( x,y,t\right) =u\left( \xi \right) , \end{aligned}$$
(5)

where \(\xi =x+y-\eta \,\frac{{{t}^{\rho }}}{\rho }\) is the wave variable, and \(\eta\) is the wave frequency. In the time-dependent case, we put \(\eta =\eta \left( t\right)\). Under this consideration, and by using of properties of the CFD in Theorem 2.1, Eq. 4 is reduced to be

$$\begin{aligned} F\left( u,{u}^{\prime },{u}^{\prime \prime },\ldots \right) =0, \end{aligned}$$
(6)

where \({{u}^{\left( i\right) }}=\frac{{{d}^{i}}u}{d{{\xi }^{i}}}\), \(i\ge 1\) . Taking integration of Eq. 6 as much as possible and setting the integration constants to zero, will reduce the transformed equation and keep the solution process as simple as possible. According to the aforementioned schemes, a positive integer M should be calculated by balancing the derivative with the highest order and the linear term of highest order in the completely-integrated form of Eq. 6. In what follow, the solution steps of each method will be discussed.

3.1 The simple equation method

The solution of Eq. 6 using the SEM (Kudryashov 2005a, b) can be expressed as

$$\begin{aligned} u(\xi )=\sum \limits _{i=0}^{M}B_{i}\,\phi ^{i}(\xi ),\quad \,B_{M}\ne {0}, \end{aligned}$$
(7)

where \(B_{i}(i=0,1,\ldots ,M)\) are the parameters to be calculated, the function \(\phi (\xi )\) is assumed to satisfy some solvable ODE of order less than the completely-integrated form of Eq. 6 known by the simplest equation. The simplest equations considered in this work are the Bernoulli and Riccati first order ODEs. By using the Bernoulli equation

$$\begin{aligned} \phi ^{\prime }(\xi )=\lambda \,\phi (\xi )+\mu \,\phi ^{2}(\xi ), \end{aligned}$$
(8)

as a simplest equation, the solution function \(\phi (\xi )\) will definitely possess

  1. i.

    the rational form

$$\begin{aligned} \phi \left( \xi \right) =\frac{1}{\mu \left( {{\xi }_{0}}-\xi \right) }, \text { if }\lambda =0, \end{aligned}$$
(9)
  1. ii.

    the rational-exponential form

$$\begin{aligned} \phi \left( \xi \right) =\frac{\,\lambda \,{{e}^{\left( \lambda \left( \xi +{ {\xi }_{0}}\right) \right) }}}{1-\mu \,{{e}^{\left( \lambda \left( \xi +{{ \xi }_{0}}\right) \right) }}},\,\text { if }\,\lambda >0\text { and }\mu <0, \end{aligned}$$
(10)

or,

$$\begin{aligned} \phi \left( \xi \right) =-\frac{\,\lambda \,{{e}^{\left( \lambda \left( \xi +{{\xi }_{0}}\right) \right) }}}{1+\mu \,{{e}^{\left( \lambda \left( \xi +{{\xi }_{0}}\right) \right) }}},\,\text { if }\,\lambda <0\,\text {and}\,\mu >0. \end{aligned}$$
(11)

In the case of using the simplest Riccati equation

$$\begin{aligned} \phi ^{\prime }(\xi )=\lambda \,\phi ^{2}(\xi )\,+\mu . \end{aligned}$$
(12)

\(\phi (\xi )\) will be in the following form:

  1. i.

    the hyperbolic form

    $$\begin{aligned} \phi (\xi )=-\frac{\sqrt{-\lambda \,\mu }}{\lambda }\tanh \left( \sqrt{-\lambda \,\mu }\,\xi +{{\xi }_{0}}\right) , \end{aligned}$$
    (13)

or,

$$\begin{aligned} \phi (\xi )=-\frac{\sqrt{-\lambda \,\mu }}{\lambda }\coth \big (\sqrt{-\lambda \,\mu }\,\xi +{{\xi }_{0}}\big ), \end{aligned}$$
(14)

if \(\lambda\,\mu<0,\) then

  1. ii.

    the periodic form

    $$\begin{aligned} \phi (\xi )=\frac{\sqrt{\lambda \,\mu }}{\lambda }\tan \Big (\sqrt{\lambda \,\mu }\,\xi +{{\xi }_{0}}\Big ), \end{aligned}$$
    (15)

    or,

    $$\begin{aligned} \phi (\xi )=-\frac{\sqrt{\lambda \,\mu }}{\lambda }\cot \left( \sqrt{\lambda \,\mu }\,\xi +{{\xi }_{0}}\right) , \end{aligned}$$
    (16)

if \(\lambda\,\mu>0\), where \(\xi _{0}\) is a constant comes from the integration. Via using of Bernoulli equation Eq. 8, substituting Eq. 7 into Eq. 6, and equating each coefficients with the same power in the resulted polynomial of \(\phi (\xi )\) to zero, a system of algebraic equations in the variables \(\mu ,\,\lambda\) and \(B_{i}\)’s would be resulted. Solving this system and substituting the obtained values of \(\mu ,\,\lambda\) and \(B_{i}\)’s, along with the general solutions of Eq. 8, into Eq. 7 gives the exact analytic solution in travelling-wave form for Eq. 4. Repeating this process with replacing Eq. 8 by Eq. 12, new classes of solutions could be derived. The simplest equation scheme is applicable while the gotten algebraic system is solvable in the undetermined parameters.

3.2 The modified simple equation method

The MSEM (Jawad et al. 2010) proceeds by considering the solution of Eq. 6 as

$$\begin{aligned} u(\xi )=\sum \limits _{i=0}^{M}{B_{i}{{\left( \frac{{\phi }^{\prime }(\xi )}{\phi (\xi )}\right) }^{i},}}\quad {B}_{M}\ne {0}, \end{aligned}$$
(17)

where \(B_{i},\,(i=0,1,\cdots ,M)\) are parameters to be calculated afterwards. M is the positive integer that obtained by the homogeneous balance principle. \(\phi (\xi )\) is an unknown function to be subsequently defined. Substituting the assumed anstanz in Eq. 17 into Eq. 6, a system of algebraic-differential system would be deduced. Forcing numerator of the resulting system to be vanished, and putting back the results into Eq. 17 will complete the determination of exact solution for the considered problem.

4 Applications for Ito equation

In this part, we investigate the \((2+1)\)-dimensional non-local Ito equation Eq. 1 by applying the Kudryashov simple equation Algorithms that discussed in the previous section. Along Eq. 5 and Theorem 2.1, Eq. 2 will be carried into the following NODE

$$\begin{aligned} (\eta -\alpha -\beta )\,v^{\prime \prime \prime }-6\big ((v^{\prime \prime })^{2}-v^{\prime }v^{\prime \prime \prime }\big )-v^{(5)}=0. \end{aligned}$$
(18)

In more compact form, Eq. 18 can be written as

$$\begin{aligned} (\eta -\alpha -\beta )\,v^{(\prime \prime \prime )}-3((v^{\prime })^{2})^{\prime \prime }-v^{(5)}=0. \end{aligned}$$
(19)

Integrating Eq. 19 twice with respect to \(\xi\) and setting the integration constants to be zeros gives the missing-v NODE

$$\begin{aligned} (\eta -\alpha -\beta )\,v^{\prime }-3(v^{\prime })^2-v^{(3)}=0. \end{aligned}$$
(20)

Let \(z(\xi )={v^{\prime }}(\xi )\) to get

$$\begin{aligned} (\eta -\alpha -\beta )\,z-3z^{2}-z^{\prime \prime }=0. \end{aligned}$$
(21)

Making balance between \(z^{\prime \prime }\) and \(z^{2}\) in Eq. 21 results \(M=2.\)

4.1 Using the SEM

Consequently, Eq. 21 owns the formal solution

$$\begin{aligned} z(\xi ) =B_{0}+B_{1}\,\phi (\xi )+B_{2}\,\phi {{(\xi )}^2}. \end{aligned}$$
(22)

Substituting Eq. 22 into Eq. 21, making use of the Bernoulli equation Eq. 8, and setting the coefficients of \(\phi ^{i}\),\(i=0,1,\cdots ,4\), to be zeros, gives the following simultaneous algebraic equations set in the sense of \(B_{0},\,B_{1},\,B_{2},\,\lambda ,\,\mu\) and \(\eta :\)

$$\begin{aligned}&B_{0}(3B_{0}+\alpha +\beta -\eta )=0, \end{aligned}$$
(23)
$$\begin{aligned}&\quad B_{1}(6B_{0}+\alpha +\beta -\eta +\lambda ^{2})=0, \end{aligned}$$
(24)
$$\begin{aligned}&\quad 3B_{1}(B_{1}+\lambda \,\mu )-B_{2}(6B_{0}+\alpha +\beta -\eta +4\lambda ^{2})=0, \end{aligned}$$
(25)
$$\begin{aligned}&\quad 2(3B_{1}B_{2}+5\lambda \,\mu \,B_{2}+\mu ^2B_{1})=0, \end{aligned}$$
(26)
$$\begin{aligned}&\quad 3B_{2}(B_{2}+2\mu ^{2})=0. \end{aligned}$$
(27)

Solving Eqs. 23–27 implies \(B_{0}=0,\,B_{1}=\frac{1}{3}\big ( \eta -\alpha -\beta \big )\) and \(B_{2}=-2\mu ^{2},\) where \(\mu\) is nonzero constant. As a consequence, the following exact moving wave solutions from Eq. 1 can be obtained as:

Case 1 If \(B_{0}=0,\,\eta =\alpha +\beta\) and \(\lambda =0,\) we get \(B_{1}=0\) and

$$\begin{aligned} u_{01}(x,y,t)=-\frac{2}{(\xi _{0}-\xi )^2}. \end{aligned}$$
(28)

Case 2 If \(B_{0}=0,\,\eta =\alpha +\beta +\lambda ^{2},\) and \(B_{1}=-2\,\lambda \,\mu\), we get

$$\begin{aligned}&u_{02}(x,y,t)=-\frac{2\lambda ^{2}{\mu }e^{\lambda \,\left( \xi +{{\xi }_{0}}\right) }}{{{\left( 1-\mu \,{{e}^{\lambda \,\xi +{{\xi }_{0}}}}\right) }^{2}}},\,\text {for }\lambda >0\,\text {and}\,\mu <0, \end{aligned}$$
(29)
$$\begin{aligned}&\quad u_{03}(x,y,t)=\frac{2\lambda ^{2}{\mu }e^{\lambda \,(\xi +{{\xi }_{0}})}}{{{\left( 1+\mu \,{{e}^{\lambda \,\xi +{{\xi }_{0}}}}\right) }^{2}}},\,\text { for }\lambda<0\,\text {and}\,\mu >0. \end{aligned}$$
(30)

Case 3 If \(B_{0}=\frac{1}{3}\left( \eta -\alpha -\beta \right) ,\,\eta =\alpha +\beta -\lambda ^{2}\) and \(B_{1}=-2\,\lambda \,\mu ,\) we get

$$\begin{aligned} u_{04}(x,y,t)=-\frac{\lambda ^{2}}{3}\left( 1+\frac{6\,{{e}^{\lambda \,(\xi +{\xi _{0}})}}}{{{\left( 1-\mu \,{{e}^{\lambda \,\xi +{{\xi }_{0}}}}\right) }^{2}}}\right),\,\text { for } \lambda>0\,\text {and}\, \mu <0, \end{aligned}$$
(31)
$$\begin{aligned} {{u}_{05}}(x,y,t) =-\frac{{{\lambda }^{2}}}{3}\left( 1-\frac{6\,{{e}^{\lambda \,(\xi +{{\xi }_{0}})}}}{{{(1+\mu \,{{e}^{\lambda \,\xi +{{\xi }_{0}}}})}^{2}}}\right),\,\text { for }\lambda<0\,\text {and}\,\mu >0. \end{aligned}$$
(32)

We get the following system of algebraic equations, as in the case of the Bernoulli equation, and using the Riccati equation Eq. 12:

$$\begin{aligned}&3B_{0}^{2}+B_{0}(\alpha \,+\beta \,-\eta ) +2\mu ^{2}B_{2}=0, \end{aligned}$$
(33)
$$\begin{aligned}&\quad B_{1}(6B_{0}+\alpha \,+\beta \,-\eta +2\,\lambda \,\mu )=0, \end{aligned}$$
(34)
$$\begin{aligned}&\quad 3B_{1}^{2}+B_{2}(6B_{0}+\alpha \,+\beta \,-\eta +8\,\lambda \,\mu )=0, \end{aligned}$$
(35)
$$\begin{aligned}&\quad 2B_{1}\left( 3B_{2}+{{\lambda }^{2}}\right) =0, \end{aligned}$$
(36)
$$\begin{aligned}&\quad 3B_{2}\left( B_{2}+2{{\lambda }^{2}}\right) =0. \end{aligned}$$
(37)

Eliminating the trivial solution, Eq. 33 and Eqs. 36–37 imply that \(B_{2}=-2\lambda ^{2},\,B_{1}=0\), and \(B_{0}=-\frac{1}{6}\big (\alpha +\beta -\eta +8\,\lambda \,\mu \big )\). The solutions can be classified as follows:

Case 4 If \(\eta =\alpha +\beta -4\lambda \mu\) and \(\lambda \,\mu <0\), we get

$$\begin{aligned} u_{06}(x,y,t)=-2\lambda \mu \,{{{\,{\mathrm{sech}}\,}}^{2}}\left( \sqrt{-\lambda \,\mu }\,\xi +{{\xi }_{0}}\right) , \end{aligned}$$
(38)

or,

$$\begin{aligned} {{u}_{07}}\left( x,y,t\right) =2\lambda \,\mu \,{{\,{\mathrm{csch}}\,}}^{2}\left( \sqrt{-\lambda \,\mu }\,\xi +{{\xi }_{0}}\right) . \end{aligned}$$
(39)

Case 5 If \(\eta =\alpha +\beta +4\,\lambda \,\mu\), and \(\lambda \,\mu <0\), we get

$$\begin{aligned} u_{08}(x,y,t)=-2\lambda \,\mu \left( \frac{1}{3}-\tanh ^{2}\left( \sqrt{-\lambda \,\mu }\,\xi +{{\xi }_{0}}\right) \right) , \end{aligned}$$
(40)

or,

$$\begin{aligned} u_{09}(x,y,t)=-2\lambda \,\mu \left( \frac{1}{3}-\coth ^{2}\Big (\sqrt{\lambda \,\mu }\,\xi +{{\xi }_{0}}\Big )\right) . \end{aligned}$$
(41)

Case 6 If \(\eta =\alpha +\beta -4\,\lambda \,\mu\), and \(\lambda \,\mu >0\), we get

$$\begin{aligned} u_{10}(x,y,t)=-2\lambda \,\mu \,\sec ^{2}\Big (\sqrt{\lambda \,\mu }\,\xi +{{\xi }_{0}}\Big ), \end{aligned}$$
(42)

or,

$$\begin{aligned} u_{11}( x,y,t)=-2\lambda \,\mu \,\csc ^{2}\Big ( \sqrt{\lambda \,\mu }\,\xi +{{\xi }_{0}}\Big ). \end{aligned}$$
(43)

Case 7 If \(\eta =\alpha +\beta +4\lambda \mu\) and \(\lambda \,\mu >0\), we get

$$\begin{aligned} u_{12}(x,y,t)=-2\lambda \,\mu \left( \frac{1}{3}+\tan ^{2}\Big (\sqrt{\lambda \,\mu }\,\xi +{{\xi }_{0}}\Big )\right) , \end{aligned}$$
(44)

or,

$$\begin{aligned} u_{13}(x,y,t)=-2\lambda \,\mu \left( \frac{1}{3}+\cot ^{2}\Big (\sqrt{\lambda \,\mu }\,\xi +{{\xi }_{0}}\Big )\right) . \end{aligned}$$
(45)

where \(\xi =x+y-\eta \,\frac{t^{\rho }}{\rho }.\)

4.2 Using the MSEM

By applying the MSEM for the Ito equation Eq. 2 with \(M=2,\) Eq. 21 gets the solution

$$\begin{aligned} z(\xi )=B_{0}+B_{1}\,\frac{{\phi }\prime (\xi )}{\phi (\xi )}+B_{2}{{\left( \frac{{\phi }\prime \left( \xi \right) }{\phi (\xi )}\right) }^{2}}. \end{aligned}$$
(46)

It is simple to find that

$$\begin{aligned}&z^{\prime }(\xi )=B_{1}\left( \frac{{{\phi }^{\prime \prime }}}{\phi }-{{\left( \frac{{{\phi }^\prime }}{\phi }\right) }^{2}}\right) +2B_{2}\left( \frac{{\phi }^{\prime }{\phi }^{\prime \prime }}{{{\phi }^{2}}}-{{\left( \frac{{{\phi }\prime }}{\phi }\right) }^{3}}\right) , \end{aligned}$$
(47)
$$\begin{aligned}&\quad z^{\prime \prime }(\xi )=B_{1}\left( \frac{{{\phi }^{\prime \prime \prime }}}{\phi }-3\frac{{\phi }^{\prime }\phi ^{\prime \prime }}{{{\phi }^{2}}}+2{{\left( \frac{{{\phi }^\prime }}{\phi }\right) }^{3}}\right) +2B_{2}\left( 2\frac{{{{{\phi }^{\prime \prime }}}^{2}}+{\phi }^{\prime }{\phi }^{\prime \prime \prime }}{{{\phi }^{2}}}-5\frac{{{{{\phi }^{\prime }}}^{2}}{\phi }^{\prime \prime }}{{{\phi }^{3}}}+3{{\left( \frac{{{\phi }^{\prime }}}{\phi }\right) }^{4}}\right) . \end{aligned}$$
(48)

Substituting Eqs. 47, 48 into Eq. 21 and equating the coefficients of \(\phi ^{-i}\,(i=0,\cdots ,4),\) to be vanished implies the algebraic-differential system:

$$\begin{aligned}&B_{0}(3B_{0}+\alpha +\beta -\eta )=0, \end{aligned}$$
(49)
$$\begin{aligned}&\quad 3B_{2}\left( 2+B_{2}\right) {\phi }^{\prime }{{\left( \xi \right) }^{4}}=0, \end{aligned}$$
(50)
$$\begin{aligned}&\quad 2\left( B_{1}{\phi }^{\prime }\left( \xi \right) \left( 1+3B_{2}\right) -5{\phi }^{\prime \prime }(\xi )\right) {\phi }^{\prime }{{(\xi )}^{2}}=0, \end{aligned}$$
(51)
$$\begin{aligned}&\quad B_{1}\left( {\phi }^{\prime }(\xi )(6B_{0}+\alpha +\beta -\eta )+{\phi }^{\prime \prime \prime }(\xi )\right) =0, \end{aligned}$$
(52)
$$\begin{aligned}&\quad 2B_{2}{\phi {^{\prime \prime }}}^{2}-(3B_{1}\,\phi ^{\prime \prime }-2B_{2}\,\phi ^{\prime \prime \prime })\phi ^{\prime }+(3B_{1}^{2}+B_{2}(6B_{0}+\alpha +\beta -\eta )){\phi ^{\prime }}^2=0. \end{aligned}$$
(53)

The Eqs. 49–50 with \(B_{2}\ne 0\) and \({\phi }^{\prime }(\xi )\ne {0}\) to avoid trivial solution, yields \(B_{0}=0,\,B_{1}=\frac{1}{3}\big (\eta -\alpha -\beta \big )\) and \(B_{2}=-2\) respectively. Accordingly, solving Eq. 51 (or equivalently Eq. 52) with nonzero arbitrary constant \(B_{1}\), exact solutions for Eq. 1 are listed as follows:

Case 8 If \(B_{0}=0,\)  \(\phi (\xi )=\frac{2{{e}^{\frac{B_{1} \,\xi }{2}}}\,}{B_{1}}{{\xi }_{1}}+{{\xi }_{2}}\) and \(\eta =\frac{1}{4}\big (B_{1}^{2}+4\alpha +4\beta \big ),\) we get

$$\begin{aligned} u_{14}(x,y,t)=\frac{{\xi _{1}}{{\xi }_{2}}B_{1}^{3}\,{e^{\frac{1}{2}B_{1}\,\xi }}}{{{\big (2{{\xi }_{1}}{{e}^{\frac{1}{2}B_{1}\,\xi }}+{{\xi }_{2}}B_{1}\big )}^{2}}}. \end{aligned}$$
(54)

Case 9 If \(B_{0}=\frac{1}{3}\left( \eta -\alpha -\beta \right) ,\) \(\phi (\xi )=\frac{2\,{e^{\frac{B_{1}\,\xi }{2}}}\,}{{B_{1}}}{{\xi }_{1}}+{\xi _{2}}\) and \(\eta =\frac{1}{4}\left( -B_{1}^{2}+4\alpha +4\beta \right) ,\) we get

$$\begin{aligned} u_{15}(x,y,t)=-\frac{B_{1}^{2}}{12}\,+\frac{{{\xi }_{1}}{{\xi }_{2}}B_{1}^{3}\,{{e}^{\frac{1}{2}B_{1}\,\xi }}}{{{\big (2{{\xi }_{1}}{{e}^{\frac{1}{2}B_{1}\,\xi }}+{{\xi }_{2}}B_{1}\big )}^2}}, \end{aligned}$$
(55)

where \(\xi _{1}\) and \(\xi _{2}\) are the constants of integration and \(\xi =x+y-\eta \,\frac{t^{\rho }}{\rho }.\)

Fig. 1
figure 1

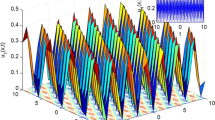
3D soliton profile of Eq. 31 in the xt-plane with \(\alpha =\beta =\lambda =1,\,\mu =-1\) and \(\xi _0=0\)

Full size image
Fig. 2
figure 2

3D corresponding contour plots to the soliton profiles in Fig. 1

Full size image
Fig. 3
figure 3

3D soliton profile of Eq. 40 in the xt-plane with \(\alpha =\beta =\mu =1,\,\lambda =-1\) and \(\xi _0=1.\)

Full size image
Fig. 4
figure 4

3D corresponding contour plots to the soliton profiles in Fig. 3

Full size image
Fig. 5
figure 5

3D soliton profile of Eq. 45 in the xt-plane with \(\alpha =\beta =\xi _0=1=1\) and \(\lambda =\mu =0.1.\)

Full size image
Fig. 6
figure 6

3D corresponding contour plots to the soliton profiles in Fig. 5

Full size image

5 Discussion and conclusion

In this work, the simple equation scheme (Kudryashov 2005a, b) and some of its variants developed by Jawad et al. (Az-Zo’bi 2019b) are successfully employed to analytically process the conformable time-fractional nonlinear \((2+1)\)-dimensional Ito equation (Eq. 1). Different types of travelling-wave solutions are formally extracted. The obtained solutions include one and multi-soliton wave solutions. The modified scheme outputs solutions of single soliton shapes coincide the obtained solutions in the SEM along Bernoulli equation with special choice of parameters. Some of these solutions are represented in Figs. 1, 2, 3, 4, 5, 6 for distinct values of the fractional order \(\rho .\) In Fig. 1, the xt-behavior of sound amplitude in soliton-like shape is shown for different fractional order. The corresponding Contour profiles are plotted in Fig. 2. In the same manner, singular kink-like (Eq. 40) are presented in Figs. 3, 4 while singular periodic sound amplitudes (Eq. 45) are illustrated in Figs. 5, 6 respectively. The order of derivative effect is clearly visible. Depending on the choice of free parameters, different physical structures could be suggested. As no researchers make consideration to solve time-fractional Ito equation, to the best of our knowledge, the solutions achieved throughout this paper are firstly presented and not published before. All of the obtained solutions are checked by replacing them back into the original equation. Because of the complexity of solving the NODEs result when applying the MSEM, as in Eq. 53, the results emphasize the effectiveness and powerful of the SEM. In general, the two methods are applicable to tackle several types of NLEEs with integer and fractional order derivatives.