A fractional analysis of Noyes–Field model for the nonlinear Belousov–Zhabotinsky reaction

Abstract

Nonlinear phenomena play an essential role in various field of natural sciences and engineering. In particular, the nonlinear chemical reactions are observed in various domains, as, for instance, in biological and chemical physics. For this reason, it is important to investigate the solution to this nonlinear phenomenon. This article investigates numerical solutions to a nonlinear oscillatory system called the Belousov–Zhabotinsky with Caputo fractional-time derivative. The simplified Noyes–Field fractional model reads

$$\begin{aligned} {\mathcal {D}}_t^{\mu }p= & {} \xi _1p_{xx}+\beta \delta {w}+p-p^2-\delta {pw},\quad 0<\mu \le 1,\\ {\mathcal {D}}_t^{\mu }w= & {} \xi _2w_{xx}+ \gamma {w}-\lambda {pw}, \end{aligned}$$

where $\xi _1$ and $\xi _2$ are the diffusing constants for the concentration p and w respectively, $\gamma$ and $\beta$ are given constants, $\lambda \ne 1$ and $\delta$ are positive parameters. The two iterative techniques used in this work are the fractional reduced differential transform method and q-homotopy analysis transform method. The outcomes using these two methods reveal an efficient numerical solution with high accuracy and minimal computations. Furthermore, to better understand the effect of the fractional order, we present the solution profiles which demonstrate the behavior of the obtained results.

1 Introduction

The applications of fractional calculus have been established in various connected bifurcation of science and engineering such as found in quantum mechanics Joseph (2012), random walk Hilfer and Anton (1995), astrophysics Tarasov (2006), chaos theory Baleanu et al. (2017), electrodynamics Nasrolahpour (2013), viscoelasticity Mainardi (2010), nanotechnology Baleanu et al. (2010), financial models Sweilam et al. (2017) and other fields Ali et al. (2019), Sun et al. (2018), Baleanu et al. (2011), Kilbas et al. (2006), Kumar et al. (2018a), Jaradat et al. (2018b), Jaradat et al. (2018c), Laskin and Zaslavsky (2006), Pu (2007), Ullah et al. (2017) and Zhang et al. (2012). In the twentieth century, Caputo Caputo (1969), Liao Liao (1998), Podlubny Podlubny (1999) and Miller and Ross (1993) have described the essential properties of fractional calculus. Nonlinear problems with fractional order are often more difficult to solve because its operator is defined by integral. However, different computational schemes are developed and have been used to investigate both the exact and numerical solution of the fractional problems. Some of the used methods are the Adomian decomposition method, (ADM) Ray and Bera (2006), Adomian (1994) and Wazwaz and Gorguis (2004) variational iteration method, (VIM) Das (2009) and He (1998) homotopy perturbation method, (HPM) He (1999) and He (2003) residual power series method, (RPSM) Alquran et al. (2015), Kurt et al. (2019), Şenol et al. (2019a) and Şenol et al. (2019b) Sumudu decomposition method, (SDM), Eltayeb and Kilicman (2012), homotopy analysis method, (HAM) Liao (2004) and Liao (1995) Laplace decomposition method, (LDM) Khuri (2001) and q-homotopy analysis method, (q-HAM) Akinyemi (2019), Akinyemi et al. (2020), El-Tawil and Huseen (2012), El-Tawil and Huseen (2013), Iyiola (2015), Iyiola et al. (2013), Iyiola (2016) and Soh et al. (2014).

In this present work, we consider a nonlinear oscillatory system called the Belousov–Zhabotinsky, (B–Z) with Caputo fractional-time derivative. The B–Z is a family of oscillating chemical reactions and is interesting because this reaction is a chemical reaction which can demonstrate both temporal oscillations and spatial traveling concentration waves that are accompanied with dramatic color changes Gibbs (1980). This reaction can generate up to numerous thousand oscillatory cycles in a closed system that enables examining the chemical waves and patterns without constant replenishment of reactants Zhabotinsky Anatol (2007). The simplified Noyes–Field fractional model for this B–Z is given as

$$\begin{aligned} {\mathcal {D}}_t^{\mu }p= & {} \xi _1p_{xx}+\beta \delta {w}+p-p^2-\delta {pw},\nonumber \\ {\mathcal {D}}_t^{\mu }w= & {} \xi _2w_{xx}+ \gamma {w}-\lambda {pw}, \end{aligned}$$

(1)

where $0<\mu \le 1$ in Caputo sense and $0<t<1.$ The motivation of this work is to study the numerical solutions of Eq. (1) with diffusing constants $\xi _1=\xi _2=1.$ Two distinct cases of Eq. (1) are considered.

• The first case is when $\gamma =\beta =0.$ This case has also been considered by Jaradat et al. (2018a) by means of generalized Taylor power series method with different initial conditions.

• The second case when $\gamma =\lambda$ and $\beta =1$ is study for the first time.

In addition, to also examine graphically the effect of the fractional order $\mu$ on the obtained numerical solutions. The two methods proposed for this present investigation are the fractional reduced differential transform method, (FRDTM) and q-homotopy analysis transform method, (q-HATM). The FRDTM was proposed by Keskin and Oturanc (2010) while the q-HATM which is a combination of q-HAM and Laplace transform was proposed by Singh et al. (2018). These two methods overcome a very huge computations that may arise in other methods used to obtain approximate and exact solutions to strong nonlinear problems with high accuracy and minimal computations.

The rest of the paper is organized as follows: Sect. 2 presents some important definitions and notations of fractional calculus and Laplace transform used in the present framework. In Sect. 3, the general idea of the proposed methods are detailed. Section 4 is concerned with the application of the proposed methods on two cases of time-fractional Belousov–Zhabotinsky system of equations. The numerical experiments and discussion are presented in Sect. 5. Finally, Sect. 6 gives the conclusion.

2 Preliminaries

Here, we present key concept of fractional calculus and Laplace transform, which are vital in the present framework.

Definition 1

Let $\eta \in {\mathbb {R}}$ and $\varphi \in {\mathbb {N}}.$ A function p is said to be in the space ${\mathbb {C}}_{\eta }$ if there exists $\alpha \in {\mathbb {R}},$$\alpha >\eta$ and $f\in C{[0, \infty )}$ such that $p(t)=t^{\alpha }f(t),\,\, \forall \,\,t\in {\mathbb {R}}^{+}.$ Furthermore, $p\in {\mathbb {C}}^{\varphi }_{\eta }$ if $p^{(\varphi )}\in {\mathbb {C}}_{\eta }$ Luchko and Srivastava (1995).

Definition 2

The Riemann–Liouville fractional integral of order $\mu \ (\mu \ge 0)$ of a function $p\in {\mathbb {C}}_{\eta },\ \eta \ge {-1},$ is given as Podlubny (1999), Luchko and Srivastava (1995) and Kilbas et al. (2006)

$$\begin{aligned} J^{\mu }_{t}p(t)=\frac{1}{\Gamma (\mu )}\int _{0}^{t}(t-\xi )^{\mu -1}\ p(\xi )\ {\text {d}}\xi ,\text { } \mu , \ t>0, \end{aligned}$$

(2)

where $\Gamma$ denoted the classical gamma function and $J_t^{0}p(t)=p(t)$. For example,

$$\begin{aligned} J_t^{\mu }t^{\nu }=\frac{\Gamma (\mu +1)}{\Gamma (\mu +1+ \nu )}t^{\mu +\nu }. \end{aligned}$$

(3)

Definition 3

In the Caputo’s sense, for $p\in {\mathbb {C}}_{\eta },\ \eta \ge {-1}$ and $\varphi -1<\mu \le \varphi ,$$\varphi \in {\mathbb {N}},$ the fractional derivative of p(t) (denoted by ${\mathcal {D}}^{\mu }_{t}p(t)$) is defined as Podlubny (1999); Kilbas et al. (2006)

$$\begin{aligned} {\mathcal {D}}^{\mu }_{t}p(t)=\left\{ \begin{array}{lll} p^{(\varphi )}(t),&{}\quad \mu =\varphi ,\\ J_t^{\varphi -\mu }p^{(\varphi )}(t),&{} \quad \varphi -1<\mu < \varphi ,\\ \end{array} \right. \end{aligned}$$

(4)

where

$$\begin{aligned} J^{\varphi -\mu }_{t}p^{(\varphi )}(t)=\frac{1}{\Gamma (\varphi -\mu )} \int _{0}^{t}(t-\xi )^{\varphi -\mu -1}p^{(\varphi )}(\xi )\ {\text {d}}\xi ,\text { } \mu ,\ t>0. \end{aligned}$$

(5)

Definition 4

The Laplace transform (denoted by ${\mathscr {L}}$) of a Riemann–Liouville fractional integral $\big (J_t^{\mu }p(t)\big )$ and Caputo fractional derivative $\big ({\mathcal {D}}_t^{\mu }p(t)\big )$ of a function $p\in {\mathbb {C}}_{\eta }\ (\eta \ge {-1})$ is given, respectively, as Caputo (1969) and Kilbas et al. (2006)

$$\begin{aligned} {\mathscr {L}}\big [J_t^{\mu }p(t)\big ]= & {} s^{-\mu }{\mathscr {L}}[p(t)],\nonumber \\ {\mathscr {L}}\big [{\mathcal {D}}_t^{\mu }p(t)\big ]= & {} s^\mu {\mathscr {L}}[p(t)]-\sum _{m=0}^{\varphi -1} s^{\mu -m-1}{p^{(m)}}(0^+), \quad \varphi -1< \mu \le \varphi , \end{aligned}$$

(6)

where s is a parameter.

3 Analysis of the proposed methods

Consider the time-fractional Belousov–Zhabotinsky, (TFB-Z) Eq. (1) with the diffusing constants for the concentration, $\xi _1=\xi _2=1$,

$$\begin{aligned} {\mathcal {D}}_t^{\mu }p= & {} \frac{\partial ^2 p}{\partial x^2}+\beta \delta {w}+p-p^2-\delta {pw}, \qquad 0<\mu \le 1,\nonumber \\ {\mathcal {D}}_t^{\mu }w= & {} \frac{\partial ^2 w}{\partial x^2}+ \gamma {w}-\lambda {pw}, \end{aligned}$$

(7)

subject to initial conditions

$$\begin{aligned} p(x,0)= & {} g_1(x),\nonumber \\ w(x,0)= & {} g_2(x),\quad x\in {\mathbb {R}}. \end{aligned}$$

(8)

3.1 Analysis of FRDTM

Let the functions p(x, t) and w(x, t) in Eq. (7) be analytic and continuously differentiable in the domain of investigation. In regard to the properties of differential transform, functions p(x, t) and w(x, t) can be express as

$$\begin{aligned} p(x,t)=\sum _{m=0}^{\infty }P_m(x)t^{m\mu },\nonumber \\ w(x,t)=\sum _{m=0}^{\infty }W_m(x)t^{m\mu }, \end{aligned}$$

(9)

where

$$\begin{aligned} P_m(x)= & {} \frac{1}{\Gamma {(m\mu +1)}}\bigg [\frac{\partial ^{m\mu } p(x,t)}{\partial t^{m\mu }}\bigg ]_{t=0},\nonumber \\ W_m(x)= & {} \frac{1}{\Gamma {(m\mu +1)}}\bigg [\frac{\partial ^{m\mu } w(x,t)}{\partial t^{m\mu }}\bigg ]_{t=0}. \end{aligned}$$

(10)

Here, $\mu$ is the fractional order and the t-dimensional spectrum functions $P_m(x)$ and $W_m(x)$ are, respectively, the transformed functions of p(x, t) and w(x, t). According to Table 1, the iteration formulas for Eq. (7) are

$$\begin{aligned} \frac{\Gamma {(m\mu +\mu +1)}}{\Gamma {(m\mu +1)}}P_{(m+1)}(x)= & {} \frac{\partial ^2 P_m}{\partial x^2}+\beta \delta W_m+P_m-\sum _{r=0}^{m} P_r P_{m-r}-\delta \sum _{r=0}^{m} P_r W_{m-r},\nonumber \\ \frac{\Gamma {(m\mu +\mu +1)}}{\Gamma {(m\mu +1)}}W_{(m+1)}(x)= & {} \frac{\partial ^2 W_m}{\partial x^2}+ \gamma {W_m}-\lambda \sum _{r=0}^{m} P_r W_{m-r},\qquad m=0,1,2,3,\ldots .\nonumber \\ \end{aligned}$$

(11)

Table 1 The essential operations of FRDTM

From initial condition Eq. (8), we write

$$\begin{aligned} P_{0}(x)= & {} p(x,0),\nonumber \\ W_{0}(x)= & {} w(x,0). \end{aligned}$$

(12)

Substituting Eqs. (12) into (11), we obtain the $P_m(x)$ and $W_m(x)$ values. The inverse transformation of the sets $\{P_m(x)\}_{m=0}^{K}$ and $\{W_m(x)\}_{m=0}^{K}$ are, respectively,

$$\begin{aligned} \mathrm {P}^{[K]}(x,t)= & {} \sum _{m=0}^{K}P_m(x)t^{m\mu },\nonumber \\ \mathrm {W}^{[K]}(x,t)= & {} \sum _{m=0}^{K}W_m(x)t^{m\mu } \end{aligned}$$

(13)

and

$$\begin{aligned} p(x,t)= & {} \lim _{k\rightarrow \infty }\mathrm {P}^{[K]}(x,t)=\sum _{m=0}^{\infty }P_m(x)t^{m\mu },\nonumber \\ w(x,t)= & {} \lim _{k\rightarrow \infty }\mathrm {W}^{[K]}(x,t)=\sum _{m=0}^{\infty }W_m(x)t^{m\mu }, \end{aligned}$$

(14)

which gives the exact solution of Eq. (7).

3.2 Fundamental idea of the q-HATM

Here, the central idea of q-HATM Kumara et al. 2017; Kumar et al. 2018b and Akinyemi (2020) to TFB-Z system of equations is presented. We first begin by applying Laplace transform to both sides of Eq. (7) and after simplifying, we obtain

$$\begin{aligned} {\mathscr {L}}[p(x,t)]-\frac{1}{s}\Big \{p(x,0)\Big \}-\frac{1}{s^\mu }{\mathscr {L}}\bigg [\frac{\partial ^2 p}{\partial x^2}+\beta \delta {w}+p-p^2-\delta {pw}\bigg ]= & {} 0,\nonumber \\ {\mathscr {L}}[w(x,t)]-\frac{1}{s}\Big \{w(x,0)\Big \}-\frac{1}{s^\mu }{\mathscr {L}}\bigg [\frac{\partial ^2 w}{\partial x^2}+ \gamma {w}-\lambda {pw}\bigg ]= & {} 0. \end{aligned}$$

(15)

To epitomize the idea of homotopy method Liao (1998), we construct zeroth-order deformation equations for $0\le {q}\le \frac{1}{n},\ \ n\ge {1},$ as

$$\begin{aligned} (1-nq){\mathscr {L}}\Big (\Phi _1(x,t;q)-p_0(x,t)\Big )= & {} \hbar {q}{\mathcal {H}}(x,t){\mathcal {N}}^{p}\big (\Phi _1(x,t;q),\Phi _2(x,t;q)\big ),\nonumber \\ (1-nq){\mathscr {L}}\Big (\Phi _2(x,t;q)-w_0(x,t)\Big )= & {} \hbar {q}{\mathcal {H}}(x,t){\mathcal {N}}^{w}\big (\Phi _1(x,t;q),\Phi _2(x,t;q)\big ),\nonumber \\ \end{aligned}$$

(16)

and define ${\mathcal {N}}^{p}\big (\Phi _1(x,t;q),\Phi _2(x,t;q)\big )$ and ${\mathcal {N}}^{w}\big (\Phi _1(x,t;q),\Phi _2(x,t;q)\big )$, respectively, as

$$\begin{aligned}&{\mathcal {N}}^{p}\big (\Phi _1(x,t;q),\Phi _2(x,t;q)\big )\nonumber \\&\quad ={\mathscr {L}}[\Phi _1(x,t;q)]-\frac{1}{s}\Big \{g_1(x)\Big \}-\frac{1}{s^\mu }{\mathscr {L}}\bigg [\frac{\partial ^2 \Phi _1(x,t;q)}{\partial x^2}\nonumber \\&\qquad +\ \beta \delta \Phi _2(x,t;q)+\Phi _1(x,t;q)-\Phi ^2_1(x,t;q)-\delta \Phi _1(x,t;q)\Phi _2(x,t;q)\bigg ],\nonumber \\&{\mathcal {N}}^{w}\big (\Phi _1(x,t;q),\Phi _2(x,t;q)\big )\nonumber \\&\quad ={\mathscr {L}}[\Phi _2(x,t;q)]-\frac{1}{s}\Big \{g_2(x)\Big \}-\frac{1}{s^\mu }{\mathscr {L}}\bigg [\frac{\partial ^2 \Phi _2(x,t;q)}{\partial x^2}\nonumber \\&\qquad +\ \gamma \Phi _2(x,t;q)-\lambda \Phi _1(x,t;q)\Phi _2(x,t;q)\bigg ], \end{aligned}$$

(17)

where q is the embedded parameter, the non-zero $\hbar$ is the auxiliary parameter, ${\mathscr {L}}$ is the Laplace transform and ${\mathcal {H}}(x,t)\ne 0$ represents the auxiliary function. Considering Eq. (16) with $q=0,\, \frac{1}{n}$, we get

$$\begin{aligned} \Phi _1\Big (x,t;0\Big )= & {} p_0(x,t),\qquad \Phi _1\Big (x,t;\frac{1}{n}\Big )=p(x,t),\nonumber \\ \Phi _2\Big (x,t;0\Big )= & {} w_0(x,t),\qquad \Phi _2\Big (x,t;\frac{1}{n}\Big )=w(x,t). \end{aligned}$$

(18)

When q rises from 0 to $\frac{1}{n}$, the solutions $\Phi _i(x,t;q),\ i=1,2,$ ranges from the initial guess $p_0$ and $w_0$ to the solution p and w. The Taylor series expansion of $\Phi _1(x,t;q)$ and $\Phi _2(x,t;q)$ are given as

$$\begin{aligned} \Phi _1(x,t;q)=p_0(x,t)+\sum _{m=1}^\infty p_m(x,t)q^m,\nonumber \\ \Phi _2(x,t;q)=w_0(x,t)+\sum _{m=1}^\infty w_m(x,t)q^m, \end{aligned}$$

(19)

where

$$\begin{aligned} p_m(x,t)=\left. \frac{1}{m!}\frac{\partial ^m\Phi _1(x,t;q)}{\partial q^m}\right| _{q=0},\nonumber \\ w_m(x,t)=\left. \frac{1}{m!}\frac{\partial ^m\Phi _2(x,t;q)}{\partial q^m}\right| _{q=0}. \end{aligned}$$

(20)

If we choose $p_0$, $w_0,$$\hbar ,$ and ${\mathcal {H}}$ adequately so that Eq. (19) converges at $q=\frac{1}{n},$ then we attain the following result for Eq. (7) as

$$\begin{aligned} p(x,t)= & {} p_0(x,t)+\sum _{m=1}^\infty p_m(x,t)\left( \frac{1}{n}\right) ^m,\nonumber \\ w(x,t)= & {} w_0(x,t)+\sum _{m=1}^\infty w_m(x,t)\left( \frac{1}{n}\right) ^m. \end{aligned}$$

(21)

Differentiating Eq. (16) m-times w.r.t to “q”, setting $q=0$ and lastly, multiply by $\frac{1}{m!}$ gives

$$\begin{aligned} {\mathscr {L}}\big [p_m(x,t)-\chi ^*_m p_{m-1}(x,t)\big ]= & {} \hbar {\mathcal {H}}(x,t){\mathcal {R}}_{1,m}\big (\mathbf {p}_{m-1}(x,t),\mathbf {w}_{m-1}(x,t)\big ),\nonumber \\ {\mathscr {L}}\big [w_m(x,t)-\chi ^*_{m}w_{m-1}(x,t)\big ]= & {} \hbar {\mathcal {H}}(x,t){\mathcal {R}}_{2,m}\big (\mathbf {p}_{m-1}(x,t),\mathbf {w}_{m-1}(x,t)\big ). \end{aligned}$$

(22)

Here, the vectors $\mathbf {p}_k$ and $\mathbf {w}_k$ is define as

$$\begin{aligned} \mathbf {p}_k(x,t)= & {} \left\{ p_0(x,t),p_1(x,t),\cdots ,p_k(x,t)\right\} ,\nonumber \\ \mathbf {w}_k(x,t)= & {} \left\{ w_0(x,t),w_1(x,t),\cdots ,w_k(x,t)\right\} . \end{aligned}$$

(23)

Application of inverse Laplace transform on Eq. (22) with ${\mathcal {H}}(x,t)=1$ gives

$$\begin{aligned} p_m(x,t)= & {} \chi ^*_m p_{m-1}(x,t)+\hbar {\mathscr {L}}^{-1}\big [{\mathcal {R}}_{1,m}\big (\mathbf {p}_{m-1}(x,t),\mathbf {w}_{m-1}(x,t)\big )\big ],\nonumber \\ w_m(x,t)= & {} \chi ^*_m w_{m-1}(x,t)+\hbar {\mathscr {L}}^{-1}\big [{\mathcal {R}}_{2,m}\big (\mathbf {p}_{m-1}(x,t),\mathbf {w}_{m-1}(x,t)\big )\big ], \end{aligned}$$

(24)

where ${\mathcal {R}}_{1,m}\big (\mathbf {p}_{m-1}(x,t),\mathbf {w}_{m-1}(x,t)\big )$ and ${\mathcal {R}}_{2,m}\big (\mathbf {p}_{m-1}(x,t),\mathbf {w}_{m-1}(x,t)\big )$ are defined, respectively, as follows:

$$\begin{aligned} {\mathcal {R}}_{1,m}\big (\mathbf {p}_{m-1},\mathbf {w}_{m-1}\big )= & {} {\mathscr {L}}\big [ p_{m-1}\big ]-\bigg (1-\frac{\chi ^*_m}{n}\bigg )\frac{1}{s}\Big \{g_1(x)\Big \}-\frac{1}{s^\mu }{\mathscr {L}}\Bigg [\frac{\partial ^2 p_{m-1}}{\partial x^2}\nonumber \\&+\ \beta \delta {w_{m-1}}+p_{m-1}-\sum _{r=0}^{m-1}p_{r}p_{(m-1-r)}-\delta \sum _{r=0}^{m-1}p_{r}w_{(m-1-r)}\Bigg ],\nonumber \\ {\mathcal {R}}_{2,m}\big (\mathbf {p}_{m-1},\mathbf {w}_{m-1}\big )= & {} {\mathscr {L}}\big [ w_{m-1}\big ]-\bigg (1-\frac{\chi ^*_m}{n}\bigg )\frac{1}{s}\Big \{g_2(x)\Big \}\nonumber \\&-\ \frac{1}{s^\mu }{\mathscr {L}}\Bigg [\frac{\partial ^2 w_{m-1}}{\partial x^2}+\gamma {w_{m-1}}-\lambda \sum _{r=0}^{m-1}p_rw_{(m-1-r)}\Bigg ], \end{aligned}$$

(25)

and

$$\begin{aligned} \chi ^*_m=\left\{ \begin{array}{lll} 0\,\,\,\,\,\,\,\,\,\,\,\,\,m\leqslant 1,\\ \\ n\,\,\,\,\,\,\,\,\,\,\,\,\,otherwise. \end{array} \right. \end{aligned}$$

(26)

Hence, Eqs. (24) and (25) reduces to

$$\begin{aligned} p_{m}(x,t)= & {} \big (\hbar +\chi ^*_m\big ) p_{m-1}-\hbar \bigg (1-\frac{\chi ^*_m}{n}\bigg ){\mathscr {L}}^{-1}\bigg [\frac{1}{s}\Big \{g_1(x)\Big \}\bigg ]-\hbar {\mathscr {L}}^{-1}\Bigg [\frac{1}{s^\mu }{\mathscr {L}}\bigg [\frac{\partial ^2 p_{m-1}}{\partial x^2}\nonumber \\&+\ \beta \delta {w_{m-1}}+p_{m-1}-\sum _{r=0}^{m-1}p_rp_{(m-1-r)}-\delta \sum _{r=0}^{m-1}p_{r}w_{(m-1-r)}\bigg ]\Bigg ],\nonumber \\ w_{m}(x,t)= & {} \big (\hbar +\chi ^*_m\big ) w_{m-1}-\hbar \bigg (1-\frac{\chi ^*_m}{n}\bigg ){\mathscr {L}}^{-1}\bigg [\frac{1}{s}\Big \{g_2(x)\Big \}\bigg ]\nonumber \\&-\ \hbar {\mathscr {L}}^{-1}\Bigg [\frac{1}{s^\mu }{\mathscr {L}}\bigg [\frac{\partial ^2 w_{m-1}}{\partial x^2}+\gamma {w_{m-1}}-\lambda \sum _{r=0}^{m-1}p_{r}w_{(m-1-r)}\bigg ]\Bigg ],\quad m=1,2,3,\ldots .\nonumber \\ \end{aligned}$$

(27)

The iterative terms of p(x, t) and w(x, t) are generated from simplifying Eq. (27) and the q-HATM series solution is

$$\begin{aligned} \mathrm {P}^{[K]}(x,t;n;\hbar )=\sum _{m=0}^K p_m(x,t)\left( \frac{1}{n}\right) ^m,\nonumber \\ \mathrm {W}^{[K]}(x,t;n;\hbar )=\sum _{m=0}^K w_m(x,t)\left( \frac{1}{n}\right) ^m. \end{aligned}$$

(28)

Then for a prescribed value of n and $\hbar ,$

$$\begin{aligned} p(x,t)=\lim _{k\rightarrow \infty }\mathrm {P}^{[K]}(x,t;n;\hbar )=\sum _{m=0}^\infty p_m(x,t)\left( \frac{1}{n}\right) ^m,\nonumber \\ w(x,t)=\lim _{k\rightarrow \infty }\mathrm {W}^{[K]}(x,t;n;\hbar )=\sum _{m=0}^\infty w_m(x,t)\left( \frac{1}{n}\right) ^m. \end{aligned}$$

(29)

Theorem 3.1

(El-Tawil and Huseen (2012) and Kumar et al. (2018b)) Suppose we can obtain real numbers ${\mathcal {M}}_1$ and ${\mathcal {M}}_2$ such that $0<{\mathcal {M}}_1<1$ and $0<{\mathcal {M}}_2<1$ satisfying

$$\begin{aligned} \left\Vert p_{m+1}(x,t)\right\Vert \le {\mathcal {M}}_1\left\Vert p_{m}(x,t)\right\Vert ,\,\,\left\Vert w_{m+1}(x,t)\right\Vert \le {\mathcal {M}}_2\left\Vert w_{m}(x,t)\right\Vert ,\quad \forall \, m\in {\mathbb {N}}. \end{aligned}$$

Furthermore, if the truncated series $\mathrm {P}^{[K]}(x,t;n;\hbar )$ and $\mathrm {W}^{[K]}(x,t;n;\hbar )$ defined in Eq. (28) are, respectively, used as an approximation to the solutions p(x, t) and w(x, t),  then the maximum absolute truncated errors are estimated, respectively, as

$$\begin{aligned} \left\Vert p(x,t)-\mathrm {P}^{[K]}(x,t;n;\hbar ) \right\Vert \le \frac{{\mathcal {M}}_1^{K+1}}{n^{K}(n-{\mathcal {M}}_1)}\left\Vert p_{0}(x,t)\right\Vert \end{aligned}$$

(30)

and

$$\begin{aligned} \left\Vert w(x,t)-\mathrm {W}^{[K]}(x,t;n;\hbar ) \right\Vert \le \frac{{\mathcal {M}}_2^{K+1}}{n^{K}(n-{\mathcal {M}}_2)}\left\Vert w_{0}(x,t)\right\Vert . \end{aligned}$$

(31)

Proof

For a prescribed value of n ($n\ge {1}$) and $\hbar$ ($\hbar \ne {0}$), we have

$$\begin{aligned} \left\Vert p(x,t)-\mathrm {P}^{[K]}(x,t;n;\hbar )\right\Vert= & {} \left\Vert \sum _{m=0}^{\infty } p_m(x,t)\left( \frac{1}{n}\right) ^m-\sum _{m=0}^K p_m(x,t)\left( \frac{1}{n}\right) ^m\right\Vert \\= & {} \left\Vert \sum _{m=K+1}^{\infty } p_m(x,t)\left( \frac{1}{n}\right) ^m\right\Vert \\\le & {} \sum _{m=K+1}^{\infty }\left\Vert p_m(x,t)\right\Vert \left( \frac{1}{n}\right) ^m\\\le & {} \sum _{m=K+1}^{\infty }{\mathcal {M}}_1^m\left\Vert p_{0}(x,t)\right\Vert \left( \frac{1}{n}\right) ^m\\\le & {} \sum _{m=K+1}^{\infty }\left( \frac{{\mathcal {M}}_1}{n}\right) ^m\left\Vert p_{0}(x,t)\right\Vert \\\le & {} \left( \frac{{\mathcal {M}}_1}{n}\right) ^{K+1} \bigg \{1+\Big (\frac{{\mathcal {M}}_1}{n}\Big ) +\Big (\frac{{\mathcal {M}}_1}{n}\Big )^2+\cdots \bigg \}\left\Vert p_{0}(x,t)\right\Vert \\\le & {} \frac{{\mathcal {M}}_1^{K+1}}{n^{K}(n-{\mathcal {M}}_1)}\left\Vert p_{0}(x,t)\right\Vert . \end{aligned}$$

By following the same approach, we also obtain

$$\begin{aligned} \left\Vert w(x,t)-\mathrm {W}^{[K]}(x,t;n;\hbar ) \right\Vert \le \frac{{\mathcal {M}}_2^{K+1}}{n^{K}(n-{\mathcal {M}}_2)}\left\Vert w_{0}(x,t)\right\Vert . \end{aligned}$$

This completes the proof. $\square$

4 Solution for TFB–Z system of equations

Here, application of the two proposed methods is tested on two cases of time-fractional Belousov–Zhabotinsky (TFB-Z) Eq. (7).

Case 1

Consider the nonlinear TFB-Z system with $\gamma =\beta =0,$ then Eq. (7) reduces to

$$\begin{aligned} \frac{\partial ^\mu p}{\partial t^\mu }= & {} \frac{\partial ^2 p}{\partial t^2}+p-p^2-\delta {pw}, \qquad 0<\mu \le 1,\nonumber \\ \frac{\partial ^\mu w}{\partial t^\mu }= & {} \frac{\partial ^2 w}{\partial t^2}-\lambda {pw}, \end{aligned}$$

(32)

with the initial conditions

$$\begin{aligned} p(x,0)= & {} \frac{1}{\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^2},\nonumber \\ w(x,0)= & {} \frac{(1-\lambda )e^{\sqrt{\frac{\lambda }{6}}x} \Big (e^{\sqrt{\frac{\lambda }{6}}x}+2\Big )}{\delta \Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^2}. \end{aligned}$$

(33)

The exact solution of Eq. (32) when $\mu = 1$ is

$$\begin{aligned} p(x,t)= & {} \frac{e^{\frac{5\lambda }{3}t}}{\Big (e^{\sqrt{\frac{\lambda }{6}}x}+e^{\frac{5\lambda }{6}t}\Big )^2},\nonumber \\ w(x,t)= & {} \frac{(1-\lambda )e^{\sqrt{\frac{\lambda }{6}}x}\Big (e^{\sqrt{\frac{\lambda }{6}}x}+2e^{\frac{5\lambda }{6}t}\Big )}{\delta \Big (e^{\sqrt{\frac{\lambda }{6}}x}+e^{\frac{5\lambda }{6}t}\Big )^2}. \end{aligned}$$

(34)

Here $\delta$ and $\lambda \ne 1$ are positive parameters.

Remark 1

The exact solution can also have the following form:

$$\begin{aligned} \frac{e^{\frac{5\lambda }{3}t}}{\Big (e^{\sqrt{\frac{\lambda }{6}}x}+e^{\frac{5\lambda }{6}t}\Big )^2}= & {} \frac{1}{4}\Bigg (\tanh ^2{\bigg (\sqrt{\frac{\lambda }{24}}x-\frac{5\lambda }{12}t\bigg )}-1\Bigg )^2,\nonumber \\ \frac{(1-\lambda )e^{\sqrt{\frac{\lambda }{6}}x}\Big (e^{\sqrt{\frac{\lambda }{6}}x}+2e^{\frac{5\lambda }{6}t}\Big )}{\delta \Big (e^{\sqrt{\frac{\lambda }{6}}x}+e^{\frac{5\lambda }{6}t}\Big )^2}= & {} \frac{\lambda -1}{4\delta }\Bigg (\tanh ^2{\bigg (\sqrt{\frac{\lambda }{24}}x-\frac{5\lambda }{12}t\bigg )}-2\tanh {\bigg (\sqrt{\frac{\lambda }{24}}x-\frac{5\lambda }{12}t\bigg )}-3\Bigg ).\nonumber \\ \end{aligned}$$

(35)

4.1 FRDTM solution

From Eq. (11) with $\gamma =\beta =0$, we have

$$\begin{aligned} P_{(m+1)}(x)= & {} \frac{\Gamma {(m\mu +1)}}{\Gamma {(m\mu +\mu +1)}}\Bigg \{\frac{\partial ^2 P_m}{\partial x^2}+P_m-\sum _{r=0}^{m} P_r P_{m-r}-\delta \sum _{r=0}^{m} P_r W_{m-r}\Bigg \},\nonumber \\ W_{(m+1)}(x)= & {} \frac{\Gamma {(m\mu +1)}}{\Gamma {(m\mu +\mu +1)}}\Bigg \{\frac{\partial ^2 W_m}{\partial x^2}-\lambda \sum _{r=0}^{m} P_r W_{m-r}\Bigg \},\qquad m=0,1,2,3,\ldots .\nonumber \\ \end{aligned}$$

(36)

Utilizing the initial condition Eq. (12), we obtain the successive solutions

$$\begin{aligned} P_0= & {} \frac{1}{\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^2},\\ W_0= & {} \frac{(1-\lambda )e^{\sqrt{\frac{\lambda }{6}}x}\Big (e^{\sqrt{\frac{\lambda }{6}}x}+2\Big )}{\delta \Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^2},\\ P_1= & {} \frac{5\lambda e^{\sqrt{\frac{\lambda }{6}}x}}{3\Gamma {(\mu +1)}\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^3},\\ W_1= & {} \frac{5\lambda (\lambda -1) e^{\sqrt{\frac{\lambda }{6}}x}}{3\delta \Gamma {(\mu +1)}\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^3},\\ P_2= & {} \frac{25\lambda ^2e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4},\\ W_2= & {} \frac{25\lambda ^2(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\delta \Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4},\\ P_3= & {} -\frac{25\lambda ^3\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}}{9\Gamma (\mu +1)^2\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}\\&-\frac{25\lambda ^3e^{\sqrt{\frac{\lambda }{6}}x}\Big (15e^{\sqrt{\frac{2\lambda }{3}}x}-20e^{\sqrt{\frac{3\lambda }{2}}x}+6e^{\sqrt{\frac{\lambda }{6}}x}-5\Big )}{108\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6},\\ W_3= & {} -\frac{25\lambda ^3(\lambda -1)\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}}{9\delta \Gamma (\mu +1)^2\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}\\&-\frac{25\lambda ^3(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (15e^{\sqrt{\frac{2\lambda }{3}}x}-20e^{\sqrt{\frac{3\lambda }{2}}x}+6e^{\sqrt{\frac{\lambda }{6}}x}-5\Big )}{108\delta \Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6},\\ P_4= & {} -\frac{25\lambda ^4\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (11e^{\sqrt{\frac{2\lambda }{3}}x}-5e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\Gamma (\mu +1)^2\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}\\&-\frac{125\lambda ^4\Gamma (3\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\Gamma (\mu +1)\Gamma (2\mu +1)\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^7}\\&+\ \frac{25\lambda ^4e^{\sqrt{\frac{2\lambda }{3}}x}\Big (124e^{\sqrt{\frac{2\lambda }{3}}x}+100e^{2\sqrt{\frac{2\lambda }{3}}x}+85e^{\sqrt{\frac{\lambda }{6}}x}-4\Big )}{324\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}\\&-\frac{625\lambda ^4e^{\sqrt{\frac{\lambda }{6}}x}\Big (17e^{2\sqrt{\frac{2\lambda }{3}}x}+1\Big )}{648\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8},\\ W_4= & {} -\frac{25\lambda ^4(\lambda -1)\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (11e^{\sqrt{\frac{2\lambda }{3}}x}-5e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\delta \Gamma (\mu +1)^2\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}\\&-\frac{125\lambda ^4(\lambda -1)\Gamma (3\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\delta \Gamma (\mu +1)\Gamma (2\mu +1)\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^7}\\&+\ \frac{25\lambda ^4(\lambda -1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (124e^{\sqrt{\frac{2\lambda }{3}}x}+100e^{2\sqrt{\frac{2\lambda }{3}}x}+85e^{\sqrt{\frac{\lambda }{6}}x}-4\Big )}{324\delta \Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}\\&-\frac{625\lambda ^4(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (17e^{2\sqrt{\frac{2\lambda }{3}}x}+1\Big )}{648\delta \Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}. \end{aligned}$$

Similar expression for $P_m(x,t)$ and $W_m(x,t)$, respectively, for $m=5,6,7,\ldots$ can be achieved. Then for system of Eq. (32), the FRDTM series solution is presented by Eq. (13).

4.2 q-HATM solution

From Eq. (27) with $\gamma =\beta =0$, we have

$$\begin{aligned} p_{m}(x,t)= & {} \big (\hbar +\chi ^*_m\big ) p_{m-1}-\hbar \bigg (1-\frac{\chi ^*_m}{n}\bigg ){\mathscr {L}}^{-1}\bigg [\frac{1}{s}\Big \{g_1(x)\Big \}\bigg ]\nonumber \\&-\ \hbar {\mathscr {L}}^{-1}\Bigg [\frac{1}{s^\mu }{\mathscr {L}}\bigg [\frac{\partial ^2 p_{m-1}}{\partial x^2}+p_{m-1}-\sum _{r=0}^{m-1}p_rp_{(m-1-r)}-\delta \sum _{r=0}^{m-1}p_rw_{(m-1-r)}\bigg ]\Bigg ],\nonumber \\ w_{m}(x,t)= & {} \big (\hbar +\chi ^*_m\big ) w_{m-1}-\hbar \bigg (1-\frac{\chi ^*_m}{n}\bigg ){\mathscr {L}}^{-1}\bigg [\frac{1}{s}\Big \{g_2(x)\Big \}\bigg ]\nonumber \\&-\ \hbar {\mathscr {L}}^{-1}\Bigg [\frac{1}{s^\mu }{\mathscr {L}}\bigg [\frac{\partial ^2 w_{m-1}}{\partial x^2}-\lambda \sum _{r=0}^{m-1}p_rw_{(m-1-r)}\bigg ]\Bigg ],\quad m=1,2,3,\ldots . \end{aligned}$$

(37)

On solving Eq. (37) with the aid of Eq. (26), we get the iterative terms of p and w as follows:

$$\begin{aligned} p_0= & {} \frac{1}{\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^2},\\ w_0= & {} \frac{(1-\lambda )e^{\sqrt{\frac{\lambda }{6}}x}\Big (e^{\sqrt{\frac{\lambda }{6}}x}+2\Big )}{\delta \Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^2},\\ p_1= & {} -\frac{5\hbar \lambda e^{\sqrt{\frac{\lambda }{6}}x}}{3\Gamma {(\mu +1)}\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^3}t^{\mu },\\ w_1= & {} -\frac{5\hbar \lambda (\lambda -1) e^{\sqrt{\frac{\lambda }{6}}x}}{3\delta \Gamma {(\mu +1)}\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^3}t^{\mu },\\ p_2= & {} (\hbar +n)p_1+\frac{25\hbar ^2\lambda ^2e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4}t^{2\mu },\\ w_2= & {} (\hbar +n)w_1+\frac{25\hbar ^2\lambda ^2(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\delta \Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4}t^{2\mu },\\ p_3= & {} (\hbar +n)p_2+\frac{25\hbar ^2(\hbar +n)\lambda ^2e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4}t^{2\mu }\\&+\frac{25\hbar ^3\lambda ^3\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}}{9\Gamma (\mu +1)^2\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu }\\&+\ \frac{25\hbar ^3\lambda ^3e^{\sqrt{\frac{\lambda }{6}}x}\Big (15e^{\sqrt{\frac{2\lambda }{3}}x}-20e^{\sqrt{\frac{3\lambda }{2}}x}+6e^{\sqrt{\frac{\lambda }{6}}x}-5\Big )}{108\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu },\\ w_3= & {} (\hbar +n)w_2+\frac{25\hbar ^2\lambda ^2(\hbar +n)(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\delta \Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4}t^{2\mu }\\&+\frac{25\hbar ^3\lambda ^3(\lambda -1)\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}}{9\delta \Gamma (\mu +1)^2\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu }\\&+\ \frac{25\hbar ^3\lambda ^3(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (15e^{\sqrt{\frac{2\lambda }{3}}x}-20e^{\sqrt{\frac{3\lambda }{2}}x}+6e^{\sqrt{\frac{\lambda }{6}}x}-5\Big )}{108\delta \Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu },\\ p_4= & {} (\hbar +n)p_3+\frac{25\hbar ^2(\hbar +n)^2\lambda ^2e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4}t^{2\mu }\\&+\frac{25(\hbar +n)\hbar ^3\lambda ^3\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}}{9\Gamma (\mu +1)^2\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu }\\&+\ \frac{25(\hbar +n)\hbar ^3\lambda ^3e^{\sqrt{\frac{\lambda }{6}}x}\Big (15e^{\sqrt{\frac{2\lambda }{3}}x}-20e^{\sqrt{\frac{3\lambda }{2}}x}+6e^{\sqrt{\frac{\lambda }{6}}x}-5\Big )}{108\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu }\\&-\frac{625\hbar ^4\lambda ^4e^{\sqrt{\frac{\lambda }{6}}x}\Big (17e^{2\sqrt{\frac{2\lambda }{3}}x}+1\Big )}{648\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}t^{4\mu }\\&-\ \frac{25\hbar ^4\lambda ^4\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (11e^{\sqrt{\frac{2\lambda }{3}}x}-5e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\Gamma (\mu +1)^2\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}t^{4\mu }\\&-\frac{125\hbar ^4\lambda ^4\Gamma (3\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\Gamma (\mu +1)\Gamma (2\mu +1)\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^7}t^{4\mu }\\&+\ \frac{25\hbar ^4\lambda ^4e^{\sqrt{\frac{2\lambda }{3}}x}\Big (124e^{\sqrt{\frac{2\lambda }{3}}x}+100e^{2\sqrt{\frac{2\lambda }{3}}x}+85e^{\sqrt{\frac{\lambda }{6}}x}-4\Big )}{324\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}t^{4\mu },\\ w_4= & {} (\hbar +n)w_3+\frac{25(\hbar +n)^2\hbar ^2\lambda ^2(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\delta \Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4}t^{2\mu }\\&+\frac{25(\hbar +n)\hbar ^3\lambda ^3(\lambda -1)\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}}{9\delta \Gamma (\mu +1)^2\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu }\\&+\ \frac{25(\hbar +n)\hbar ^3\lambda ^3(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (15e^{\sqrt{\frac{2\lambda }{3}}x}-20e^{\sqrt{\frac{3\lambda }{2}}x}+6e^{\sqrt{\frac{\lambda }{6}}x}-5\Big )}{108\delta \Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu }\\&-\frac{625\hbar ^4\lambda ^4(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (17e^{2\sqrt{\frac{2\lambda }{3}}x}+1\Big )}{648\delta \Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}t^{4\mu }\\&-\frac{25\hbar ^4\hbar ^4\lambda ^4(\lambda -1)\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (11e^{\sqrt{\frac{2\lambda }{3}}x}-5e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\delta \Gamma (\mu +1)^2\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}t^{4\mu }\\&-\frac{125\hbar ^4\lambda ^4(\lambda -1)\Gamma (3\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\delta \Gamma (\mu +1)\Gamma (2\mu +1)\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^7}t^{4\mu }\\&+\ \frac{25\hbar ^4\lambda ^4(\lambda -1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (124e^{\sqrt{\frac{2\lambda }{3}}x}+100e^{2\sqrt{\frac{2\lambda }{3}}x}+85e^{\sqrt{\frac{\lambda }{6}}x}-4\Big )}{324\delta \Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}t^{4\mu }. \end{aligned}$$

Similar expression for $p_m$ and $w_m$, respectively, for $m=5,6,7,\ldots$ can be achieved. Then, for system of Eq. (32), the q-HATM series solution is presented by Eq. (28).

Case 2

Consider the nonlinear TFB-Z system at $\gamma =\lambda$ and $\beta =1,$ then Eq. (7) reduced to

$$\begin{aligned} {\mathcal {D}}_t^{\mu }p= & {} \frac{\partial ^2 p}{\partial x^2}+\delta {w}+p-p^2-\delta {pw}, \qquad 0<\mu \le 1,\nonumber \\ {\mathcal {D}}_t^{\mu }w= & {} \frac{\partial ^2 w}{\partial x^2}+ \lambda {w}-\lambda {pw}, \end{aligned}$$

(38)

with the initial condition

$$\begin{aligned} p(x,0)= & {} \frac{1}{\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^2},\nonumber \\ w(x,0)= & {} \frac{\lambda -1}{\delta \Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^2}. \end{aligned}$$

(39)

The exact solution of Eq. (38) when $\mu = 1$ is

$$\begin{aligned} p(x,t)= & {} \frac{e^{\frac{5\lambda }{3}t}}{\Big (e^{\sqrt{\frac{\lambda }{6}}x}+e^{\frac{5\lambda }{6}t}\Big )^2},\nonumber \\ w(x,t)= & {} \frac{(\lambda -1)e^{\frac{5\lambda }{3}t}}{\delta \Big (e^{\sqrt{\frac{\lambda }{6}}x}+e^{\frac{5\lambda }{6}t}\Big )^2}, \end{aligned}$$

(40)

where $\lambda \ne 1$ is a positive parameter.

Remark 2

The exact solution can also have the following form:

$$\begin{aligned} \frac{e^{\frac{5\lambda }{3}t}}{\Big (e^{\sqrt{\frac{\lambda }{6}}x}+e^{\frac{5\lambda }{6}t}\Big )^2}= & {} \frac{1}{4}\Bigg (\tanh {\bigg (\sqrt{\frac{\lambda }{24}}x-\frac{5\lambda }{12}t\bigg )}-1\Bigg )^2,\nonumber \\ \frac{(\lambda -1)e^{\frac{5\lambda }{3}t}}{\delta \Big (e^{\sqrt{\frac{\lambda }{6}}x}+e^{\frac{5\lambda }{6}t}\Big )^2}= & {} \frac{\lambda -1}{4\delta }\Bigg (\tanh {\bigg (\sqrt{\frac{\lambda }{24}}x-\frac{5\lambda }{12}t\bigg )}-1\Bigg )^2.\nonumber \\ \end{aligned}$$

(41)

4.3 FRDTM solution

From Eq. (11) with $\gamma =\lambda$ and $\beta =1,$ we have

$$\begin{aligned} P_{(m+1)}(x)= & {} \frac{\Gamma {(m\mu +1)}}{\Gamma {(m\mu +\mu +1)}}\Bigg \{\frac{\partial ^2 P_m}{\partial x^2}+\delta W_m+P_m-\sum _{r=0}^{m} P_r P_{m-r}-\delta \sum _{r=0}^{m} P_r W_{m-r}\Bigg \},\nonumber \\ W_{(m+1)}(x)= & {} \frac{\Gamma {(m\mu +1)}}{\Gamma {(m\mu +\mu +1)}}\Bigg \{\frac{\partial ^2 W_m}{\partial x^2}+ \lambda {W_m}-\lambda \sum _{r=0}^{m} P_r W_{m-r}\Bigg \},\quad m=0,1,2,3,\ldots .\nonumber \\ \end{aligned}$$

(42)

Using the initial condition Eq. (12), we obtain the successive solutions

$$\begin{aligned} P_0= & {} \frac{1}{\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^2},\\ W_0= & {} \frac{\lambda -1}{\delta \Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^2},\\ P_1= & {} \frac{5\lambda e^{\sqrt{\frac{\lambda }{6}}x}}{3\Gamma {(\mu +1)}\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^3},\\ W_1= & {} \frac{5\lambda (\lambda -1) e^{\sqrt{\frac{\lambda }{6}}x}}{3\delta \Gamma {(\mu +1)}\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^3},\\ P_2= & {} \frac{25\lambda ^2e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4},\\ W_2= & {} \frac{25\lambda ^2(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\delta \Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4},\\ P_3= & {} -\frac{25\lambda ^3\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}}{9\Gamma (\mu +1)^2\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}\\&-\frac{25\lambda ^3e^{\sqrt{\frac{\lambda }{6}}x}\Big (15e^{\sqrt{\frac{2\lambda }{3}}x}-20e^{\sqrt{\frac{3\lambda }{2}}x}+6e^{\sqrt{\frac{\lambda }{6}}x}-5\Big )}{108\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6},\\ W_3= & {} -\frac{25(\lambda -1)\lambda ^3\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}}{9\delta \Gamma (\mu +1)^2\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}\\&-\frac{25(\lambda -1)\lambda ^3e^{\sqrt{\frac{\lambda }{6}}x}\Big (15e^{\sqrt{\frac{2\lambda }{3}}x}-20e^{\sqrt{\frac{3\lambda }{2}}x}+6e^{\sqrt{\frac{\lambda }{6}}x}-5\Big )}{108\delta \Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6},\\ P_4= & {} -\frac{25\lambda ^4\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (11e^{\sqrt{\frac{2\lambda }{3}}x}-5e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\Gamma (\mu +1)^2\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}\\&-\frac{125\lambda ^4\Gamma (3\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\Gamma (\mu +1)\Gamma (2\mu +1)\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^7}\\&+ \frac{25\lambda ^4e^{\sqrt{\frac{2\lambda }{3}}x}\Big (124e^{\sqrt{\frac{2\lambda }{3}}x}+100e^{2\sqrt{\frac{2\lambda }{3}}x}+85e^{\sqrt{\frac{\lambda }{6}}x}-4\Big )}{324\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}\\&-\frac{625\lambda ^4e^{\sqrt{\frac{\lambda }{6}}x}\Big (17e^{2\sqrt{\frac{2\lambda }{3}}x}+1\Big )}{648\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8},\\ W_4= & {} -\frac{25\lambda ^4(\lambda -1)\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (11e^{\sqrt{\frac{2\lambda }{3}}x}-5e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\delta \Gamma (\mu +1)^2\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}\\&-\frac{125\lambda ^4(\lambda -1)\Gamma (3\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\delta \Gamma (\mu +1)\Gamma (2\mu +1)\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^7}\\&+\ \frac{25\lambda ^4(\lambda -1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (124e^{\sqrt{\frac{2\lambda }{3}}x}+100e^{2\sqrt{\frac{2\lambda }{3}}x}+85e^{\sqrt{\frac{\lambda }{6}}x}-4\Big )}{324\delta \Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}\\&-\frac{625\lambda ^4(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (17e^{2\sqrt{\frac{2\lambda }{3}}x}+1\Big )}{648\delta \Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}. \end{aligned}$$

Similar expression for $P_m$ and $W_m$, respectively, for $m=5,6,7,\ldots$ can be achieved. Then for system of Eq. (38) with initial condition Eq. (39), the FRDTM series solution is presented by Eq. (13).

Fig. 1

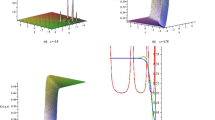
The 3D and 2D comparison of FRDTM, q-HATM ($n=1, \hbar =-1$) and exact solution for p(x, t) in a–e when $\mu =1,\ \delta =2$ and $\lambda =3$ for Case 1

Fig. 2

The 3D and 2D comparison of FRDTM, q-HATM ($n=1, \hbar =-1$) and exact solution for w(x, t) in a–e when $\mu =1,\ \delta =2$ and $\lambda =3$ for Case 1

Fig. 3

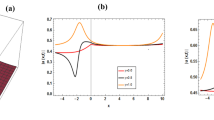
Solution profiles in a–d with different $\mu$ values when $x=3,\ \delta =2$ and $\lambda =3$ for Case 1

Fig. 4

Solution profiles in a–d with different $\mu$ values when $t=0.1,\ \delta =2$ and $\lambda =3$ for Case 1

Fig. 5

Solution profiles in a–d with different $\mu$ values when $t=0.5,\ \delta =2$ and $\lambda =3$ for Case 1

Fig. 6

The 3D and 2D comparison of FRDTM, q-HATM ($n=1, \hbar =-1$) and exact solution for p(x, t) when $\mu =1,\ \delta =2$ and $\lambda =2$ in a–e for Case 2

Fig. 7

The 3D and 2D comparison of FRDTM, q-HATM ($n=1, \hbar =-1$) and exact solution for w(x, t) when $\mu =1,\ \delta =2$ and $\lambda =2$ in a–e for Case 2

Fig. 8

Solution profiles in a–d with different $\mu$ values when $x=5,\ \delta =2$ and $\lambda =2$ for Case 2

Fig. 9

Solution profiles in a–d with different $\mu$ values when $t=0.1,\ \delta =2$ and $\lambda =2$ for Case 2

Fig. 10

Solution profiles in a–d with different $\mu$ values when $t=0.7,\ \delta =2$ and $\lambda =2$ for Case 2

Fig. 11

$\hbar$-curves plot in a, b for Case 1 and in c, d for Case 2 when $x=0.1,\ t=0.01$ with different $\mu$

4.4 q-HATM solution

From Eq. (27) with $\gamma =\lambda$ and $\beta =1,$ we have

$$\begin{aligned} p_{m}(x,t)= & {} \big (\hbar +\chi ^*_m\big ) p_{m-1}-\hbar \bigg (1-\frac{\chi ^*_m}{n}\bigg ){\mathscr {L}}^{-1}\bigg [\frac{1}{s}\Big \{g_1(x)\Big \}\bigg ]-\hbar {\mathscr {L}}^{-1}\Bigg [\frac{1}{s^\mu }{\mathscr {L}}\bigg [\frac{\partial ^2 p_{m-1}}{\partial x^2}\nonumber \\&+\ \delta {w_{m-1}}+p_{m-1}-\sum _{r=0}^{m-1}p_rp_{(m-1-r)}-\delta \sum _{r=0}^{m-1}p_{r}w_{(m-1-r)}\bigg ]\Bigg ],\nonumber \\ w_{m}(x,t)= & {} \big (\hbar +\chi ^*_m\big ) w_{m-1}-\hbar \bigg (1-\frac{\chi ^*_m}{n}\bigg ){\mathscr {L}}^{-1}\bigg [\frac{1}{s}\Big \{g_2(x)\Big \}\bigg ]\nonumber \\&-\ \hbar {\mathscr {L}}^{-1}\Bigg [\frac{1}{s^\mu }{\mathscr {L}}\bigg [\frac{\partial ^2 w_{m-1}}{\partial x^2}+\lambda {w_{m-1}}-\lambda \sum _{r=0}^{m-1}p_{r}w_{(m-1-r)}\bigg ]\Bigg ],\quad m=1,2,3,\ldots .\nonumber \\ \end{aligned}$$

(43)

On solving Eq. (43) with the aid of Eq. (26), we get the iterative terms of p and w as follows:

$$\begin{aligned} p_0= & {} \frac{1}{\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^2},\\ w_0= & {} \frac{\lambda -1}{\delta \Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^2},\\ p_1= & {} -\frac{5\hbar \lambda e^{\sqrt{\frac{\lambda }{6}}x}}{3\Gamma {(\mu +1)}\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^3}t^{\mu },\\ w_1= & {} -\frac{5\hbar \lambda (\lambda -1) e^{\sqrt{\frac{\lambda }{6}}x}}{3\delta \Gamma {(\mu +1)}\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^3}t^{\mu },\\ p_2= & {} (\hbar +n)p_1+\frac{25\hbar ^2\lambda ^2e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4}t^{2\mu },\\ w_2= & {} (\hbar +n)w_1+\frac{25\hbar ^2\lambda ^2(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\delta \Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4}t^{2\mu },\\ p_3= & {} (\hbar +n)p_2+\frac{25\hbar ^2(\hbar +n)\lambda ^2e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4}t^{2\mu }\\&+\frac{25\hbar ^3\lambda ^3\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}}{9\Gamma (\mu +1)^2\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu }\\&+\ \frac{25\hbar ^3\lambda ^3e^{\sqrt{\frac{\lambda }{6}}x}\Big (15e^{\sqrt{\frac{2\lambda }{3}}x}-20e^{\sqrt{\frac{3\lambda }{2}}x}+6e^{\sqrt{\frac{\lambda }{6}}x}-5\Big )}{108\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu },\\ w_3= & {} (\hbar +n)w_2+\frac{25\hbar ^2\lambda ^2(\hbar +n)(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\delta \Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4}t^{2\mu }\\&+\frac{25\hbar ^3\lambda ^3(\lambda -1)\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}}{9\delta \Gamma (\mu +1)^2\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu }\\&+\ \frac{25\hbar ^3\lambda ^3(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (15e^{\sqrt{\frac{2\lambda }{3}}x}-20e^{\sqrt{\frac{3\lambda }{2}}x}+6e^{\sqrt{\frac{\lambda }{6}}x}-5\Big )}{108\delta \Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu },\\ p_4= & {} (\hbar +n)p_3+\frac{25\hbar ^2(\hbar +n)^2\lambda ^2e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4}t^{2\mu }\\&+\frac{25(\hbar +n)\hbar ^3\lambda ^3\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}}{9\Gamma (\mu +1)^2\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu }\\&+\ \frac{25(\hbar +n)\hbar ^3\lambda ^3e^{\sqrt{\frac{\lambda }{6}}x}\Big (15e^{\sqrt{\frac{2\lambda }{3}}x}-20e^{\sqrt{\frac{3\lambda }{2}}x}+6e^{\sqrt{\frac{\lambda }{6}}x}-5\Big )}{108\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu }\\&-\frac{625\hbar ^4\lambda ^4e^{\sqrt{\frac{\lambda }{6}}x}\Big (17e^{2\sqrt{\frac{2\lambda }{3}}x}+1\Big )}{648\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}t^{4\mu }\\&-\ \frac{25\hbar ^4\lambda ^4\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (11e^{\sqrt{\frac{2\lambda }{3}}x}-5e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\Gamma (\mu +1)^2\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}t^{4\mu }\\&-\frac{125\hbar ^4\lambda ^4\Gamma (3\mu +1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\Gamma (\mu +1)\Gamma (2\mu +1)\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^7}t^{4\mu }\\&+\ \frac{25\hbar ^4\lambda ^4e^{\sqrt{\frac{2\lambda }{3}}x}\Big (124e^{\sqrt{\frac{2\lambda }{3}}x}+100e^{2\sqrt{\frac{2\lambda }{3}}x}+85e^{\sqrt{\frac{\lambda }{6}}x}-4\Big )}{324\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}t^{4\mu },\\ w_4= & {} (\hbar +n)w_3+\frac{25(\hbar +n)^2\hbar ^2\lambda ^2(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{18\delta \Gamma (2\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^4}t^{2\mu }\\&+\frac{25(\hbar +n)\hbar ^3\lambda ^3(\lambda -1)\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}}{9\delta \Gamma (\mu +1)^2\Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu }\\&+\ \frac{25(\hbar +n)\hbar ^3\lambda ^3(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (15e^{\sqrt{\frac{2\lambda }{3}}x}-20e^{\sqrt{\frac{3\lambda }{2}}x}+6e^{\sqrt{\frac{\lambda }{6}}x}-5\Big )}{108\delta \Gamma (3\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^6}t^{3\mu }\\&-\frac{625\hbar ^4\lambda ^4(\lambda -1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (17e^{2\sqrt{\frac{2\lambda }{3}}x}+1\Big )}{648\delta \Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}t^{4\mu }\\&-\frac{25\hbar ^4\hbar ^4\lambda ^4(\lambda -1)\Gamma (2\mu +1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (11e^{\sqrt{\frac{2\lambda }{3}}x}-5e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\delta \Gamma (\mu +1)^2\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}t^{4\mu }\\&-\frac{125\hbar ^4\lambda ^4(\lambda -1)\Gamma (3\mu +1)e^{\sqrt{\frac{\lambda }{6}}x}\Big (2e^{\sqrt{\frac{\lambda }{6}}x}-1\Big )}{27\delta \Gamma (\mu +1)\Gamma (2\mu +1)\Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^7}t^{4\mu }\\&+\ \frac{25\hbar ^4\lambda ^4(\lambda -1)e^{\sqrt{\frac{2\lambda }{3}}x}\Big (124e^{\sqrt{\frac{2\lambda }{3}}x}+100e^{2\sqrt{\frac{2\lambda }{3}}x}+85e^{\sqrt{\frac{\lambda }{6}}x}-4\Big )}{324\delta \Gamma (4\mu +1)\Big (e^{\sqrt{\frac{\lambda }{6}}x}+1\Big )^8}t^{4\mu }. \end{aligned}$$

Similar expression for $p_m$ and $w_m$, respectively, for $m=5,6,7,\ldots$ can be achieved. Then for the system of Eq. (38), the ${\hat{q}}$-HATM series solution is presented by Eq. (28).

Remark 3

If we let $w=\frac{\lambda -1}{\delta }p,$ in Eq. (38), then the system (Case 2) reduces to the fractional Fisher’s equation

$$\begin{aligned} {\mathcal {D}}_t^{\mu }p=\frac{\partial ^2 p}{\partial x^2}+\lambda {p}-\lambda {p^2}, \end{aligned}$$

(44)

which represents a model for the propagation of a mutant gene where p denotes the population density, $p(1-p)$ stand for the population supply due to births and deaths and $\lambda$ is the birth rate Fisher (1937). The exact solution of Eq. (44) for the case when $\mu =1$ can be obtained from Eq. (40) and is given for positive parameter $\lambda$ as

$$\begin{aligned} p(x,t)=\frac{e^{\frac{5\lambda }{3}t}}{\Big (e^{\sqrt{\frac{\lambda }{6}}x} +e^{\frac{5\lambda }{6}t}\Big )^2}=\frac{1}{4} \Bigg (\tanh {\bigg (\sqrt{\frac{\lambda }{24}}x-\frac{5\lambda }{12}t\bigg )}-1\Bigg )^2. \end{aligned}$$

(45)

Table 2 The comparison among FRDTM, q-HATM and the exact solution Eq. (34) for p(x, t) when $\mu =1,\ n=1,\ \hbar =-1,\ \lambda =3$ and $\delta =2$ for Case 1

Table 3 The comparison among FRDTM, q-HATM and the exact solution Eq. (34) for w(x, t) when $\mu =1,\ n=1,\ \hbar =-1,\ \lambda =3$ and $\delta =2$ for Case 1

Table 4 The comparison among FRDTM, q-HATM and the exact solution (Eq. (40)) for p(x, t) when $\mu =1,\ n=1,\ \hbar =-1,\ \lambda =2$ and $\delta =2$ for Case 2

Table 5 The comparison among FRDTM, q-HATM and the exact solution Eq. (40) for w(x, t) when $\mu =1,\ n=1,\ \hbar =-1,\ \lambda =2$ and $\delta =2$ for Case 2

Table 6 The error estimate for the time-fractional Fisher’s Eq. (44) when $\mu =1,\ n=1,\ \hbar =-1$ and $t=0.001$ for different $\lambda$

Table 7 The description of numerical solutions obtained from ADM Wazwaz and Gorguis (2004), HPSTM Abedle-Rady et al. (2014), q-HATM ($\mathrm {P}^{[3]}$) Veeresha et al. (2019), q-HATM ($\mathrm {P}^{[4]}$), FRDTM and the exact solution at $\mu =1,\ n=1,\ \hbar =-1,\ t=0.001$ and $\lambda =6$ for the time-fractional Fisher’s Eq. (44)

Table 8 The error estimate for the time-fractional Fisher’s Eq. (44) when $\mu =1,\ n=1,\ \hbar =-1,\ t=0.001$ and $\lambda =6$

5 Numerical results and discussion

Here, the numerical simulation of the obtained results by the two reliable techniques for TFB-Z system of equations is discussed. In Figs. 1, 2, 6 and 7, we observe that for the special case when $\mu =1$ the difference between the sets of numerical values obtained using the two proposed methods and the exact values are graphically almost indistinguishable. The solution profiles which described the effect and the behavior of the fractional order is presented in Figs. 3, 4, 5, 6, 7, 8, 9 and 10. These solution profiles reveal different behavior for different fractional order $\mu$ ($\mu =0.5,0.6,0.7,0.8,0.9,1$), thus assisting in understanding the nature of considered model. From these figures, we notice that as $\mu$ increases from 0.5 to 1, the solutions obtained by the two methods tends to the integer-order solution which are asymptotically continuously convergent to the exact solution ($\mu =1$).

To guarantee fast convergence of the series solutions obtained by q-HATM, the choice of the auxiliary parameter $\hbar$ is very vital. The $\hbar$-curves which guide the optimal choice of the values of $\hbar$ for Cases 1 and 2 are illustrated in Fig. 11. The horizontal line segment in the $\hbar$-curves presents the range for $\hbar$ (which verifies the choice of selecting $\hbar =-1$ in this present study). In Tables 2, 3, 4 and 5, we present the comparative study among the FRDTM, q-HATM and the exact solution which indicate the results obtained by the two techniques are very accurate and in agreement with the exact solution for the case when $\mu =1.$ We further present the absolute errors on the cited tables.

Remark 4

In Case 2, the numerical result for the case when $\lambda =3$ and $\delta =2$ is identical to the result obtained for p(x, t) in Case 1, so we switch attention to the case when $\lambda =2$ and $\delta =2$ instead.

Remark 5

It is worth looking into the numerical solution of the time-fractional Fisher’s Eq. (44). Table 6 reveals the absolute error for different $\lambda$ for the time-fractional Fisher’s Eq. (44). In Table 7, the numerical values of the proposed methods is compared to the obtained results by HPSTM Abedle-Rady et al. (2014), q-HATM Veeresha et al. (2019), ADM Wazwaz and Gorguis (2004) and the exact solution. Finally, the comparison in terms of absolute error is presented in Table 8.

6 Concluding remarks

In this paper, the time-fractional Belousov–Zhabotinsky system is solved using two reliable techniques, namely the fractional reduced differential transform method and q-homotopy analysis transform method. Two cases of the model are tested by the proposed methods. The effect of the fractional operator can be observed and capture more interesting physical behaviour of the considered model for diverse arbitrary order. The two methods reveal series form solutions which are stable while the values of the fractional order $\mu$ is approaching integer order 1. The outcomes of this study show that the result obtained by q-HATM is more general and contains the result of HAM, ADM, HATM, HPSTM, FRDTM, HPM and RPSM as a special case. The q-HATM uses two parameters $\hbar$ and n that provides flexibility in adjusting and controlling the convergence region of the solution. The choice of these two parameters give q-HATM advantage over these methods.

In Remark 3, it has been shown that the Belousov–Zhabotinsky system for Case 2 can be reduced to the fraction Fisher’s equation which represents a model for the propagation of a mutant gene. It is evidence from Tables 7, 8 that the proposed methods outperformed other methods used in obtaining approximate solution of the Fisher’s equation. Therefore, the proposed methods used in this present investigation are very effective, accurate and has a wide-ranging feasibility and can solve a lot of strong nonlinear fractional and classical PDEs that arise in physics, chemistry, biology, mathematics, and engineering. As for the future work, the author intend to explore other numerical methods, compare their computational time with the two methods used in this present investigation and study the noise effects with the aim to establish the robustness of the concerned algorithm.