1 Introduction

Fractional partial differential equations (FPDEs) appear in different field of science and engineering such as physics, biology, rheology, viscoelasticity, control theory, signal processing, systems identification and electrochemistry (Oldham and Spanier 1974; Miller and Ross 1993; Samko et al. 1993; Kiryakova 1994; Baleanu et al. 2017, 2018a, b; Inc et al. 2018). In order to describe nonlinear physical phenomena, obtaining exact solutions for nonlinear FPDEs is one of the most important aspect. This physical phenomenon may depend on both the time instant and the time history, which can be successfully modelled using the theory of derivatives and integrals of fractional order (Oldham and Spanier 1974; Miller and Ross 1993; Samko et al. 1993; Kiryakova 1994; Baleanu et al. 2017, 2018a, b; Inc et al. 2018). Recently, several methods have been applied to reach exact solutions of FPDEs in the literature. Among the techniques applied are the exp-function, fractional sub-equation, first integral, the \(G^{\prime} /G\)-expansion, Lie symmetry and many more (Eslami et al. 2016; Zhou et al. 2016; Mirzazadeh et al. 2014; Sonomezoglu et al. 2016; Islam et al. 2017; Ali et al. 2016; Cheema and Younis 2016a, b; Arnous et al. 2017; Sardar et al. 2015; Hosseini et al. 2017a, b, c, d; Korkmaz and Hosseini 2017; Younis 2017; Younis et al. 2017; Younis and Rizvi 2016; Sahar et al. 2017; Kalim and Younis 2017; Rizvi et al. 2017).

2 Conformable derivative

Recently, newly established definition of fractional derivative was introduced in (Abu Hammad and Khalil 2014; Khalil et al. 2014) and it is called conformable derivative. This definition gets rid of the deficiencies of the existing definitions.

Definition 1

Let \(f:\left( {0,\infty } \right) \to {\mathbb{R}}\), the conformable derivative of \(f\) of order \(\alpha\) is defined as

$$T_{\alpha } \left( f \right)\left( t \right) = \mathop {\lim }\limits_{\varepsilon \to 0} \frac{{f\left( {t + \varepsilon t^{1 - \alpha } - f\left( t \right)} \right)}}{\varepsilon },$$
(1)

for \(t > 0,\alpha \in \left( {0,1} \right)\). Conformable derivative has the following properties (Abu Hammad and Khalil 2014; Khalil et al. 2014; Abdeljawad 2015):

  1. 1.

    \(T_{\alpha } \left( {{\text{af}} + {\text{bg}}} \right) = {\text{a}}T_{\alpha } (f) + {\text{b}}T_{\alpha } ({\text{g}}),\;a,b \in {\mathbb{R}}\)

  2. 2.

    \(T_{\alpha } \left( {t^{\mu } } \right) = \mu \cdot t^{\mu - \alpha } ,\;\mu \in {\mathbb{R}}\)

  3. 3.

    \(T_{\alpha } \left( {\text{fg}} \right) = {\text{g}} T_{\alpha } \left( {\text{f}} \right) + {\text{f}} T_{\alpha } ({\text{g}}),\)

  4. 4.

    \(T_{\alpha } \left( {\frac{{{\text{f}} }}{\text{g}}} \right) = \frac{{{\text{g}} T_{\alpha } \left( {\text{f}} \right) - {\text{f}}\; T_{\alpha } \left( {\text{g}} \right) }}{{g^{2} }},\)

  5. 5.

    If \(f\) is differentiable, then \(T_{\alpha } \left( {\text{f}} \right)\left( {\text{t}} \right) = t^{1 - \alpha } \left( {\frac{\text{df }}{\text{dg}}} \right).\)

Theorem 1

Let \(f:\left( {0,\infty } \right) \to {\mathbb{R}}\) be a function such that \(f\) is differentiable and also \(\alpha\) differentiable. Let \(g\) be differentiable defined in the range of \(f\) and also differentiable, the we have then rule (Abdeljawad 2015) \(T_{\alpha } \left( {fog} \right)\left( t \right) = t^{1 - \alpha } g^{\prime} \left( t \right)f^{\prime} \left( {g\left( t \right)} \right).\)

3 Description of the method

Here, we present the procedure of the RB sub-ODE method (Yang et al. 2015) and the main steps

3.1 RB sub-ODE method

Consider a NLPDETFNDEs as follows,

$$P\left( {p,D^{\alpha}_{t}p ,D^{\alpha}_{x}p ,D^{2\alpha}_{x}p ,D^{\alpha}_{x}D^{\alpha}_{t}p , \ldots } \right) = 0,$$
(2)

where \(P\) is in general a polynomial function of its arguments, the subscripts denote the partial derivatives. The RB sub-ODE method consists of three steps.

  • Step 1 Convert \(x\) and \(t\) to one variable as follows

    $$p\left( {x,t} \right) = p\left( \xi \right),$$
    (3)

    and

    $$\xi = k\left( {x + l\left( {\frac{{t^{\alpha } }}{\alpha }} \right)} \right),$$
    (4)

    where the localized wave solution \(p\left( \xi \right)\) travels with speed \(l\), by using Eqs. (3) and (4), one can transform Eq. (2) to an ODE

    $$P\left( {p,p^{\prime} ,p^{\prime\prime},p^{\prime\prime\prime}, \ldots } \right) = 0.$$
    (5)

  • Step 2 Assume that Eq. (5) is the solution of the RB equation

    $$p^{\prime} = ap^{2 - m} + bp + cp^{m} .$$
    (6)

In Eq. (6), \(a\), \(b\), \(c\), and \(m\) are constants and will be found later. Taking the second and third derivatives of Eq. (6) yields

$$\begin{aligned} p^{\prime\prime} = & ab\left( {3 - m} \right)p^{2 - m} + a^{2} \left( {2 - m} \right)p^{3 - 2m} + mc^{2} p^{2m - 1} \\ & + bc\left( {m + 1} \right)p^{m} + \left( {2ac + b^{2} } \right)p, \\ \end{aligned}$$
(7)
$$\begin{aligned} p^{\prime \prime \prime}= & (ab\left( {2 - m} \right)\left( {3 - m} \right)p^{1 - m} + a^{2} \left( {2 - m} \right)\left( {3 - 2m} \right)p^{2 - 2m} \\ & + m\left( {2m - 1} \right)c^{2} p^{2m - 2} + bcm\left( {m + 1} \right)p^{m - 1} \\ & + \left( {2ac + b^{2} } \right))p^{\prime} . \\ \end{aligned}$$
(8)

One can obtain the solutions for Eq. (6) in the following forms:

Case 1 When \(m = 1\), the solution of Eq. (6) is

$$p\left( \xi \right) = Ce^{(a + b + c)\xi } .$$
(9)

Case 2 When \(m \ne 1\), \(b = 0\), and \(c = 0\), the solution of Eq. (6) is

$$p\left( \xi \right) = \left( {a(m - 1)\left( {\xi + C} \right)} \right)^{{\frac{1}{m - 1}}} .$$
(10)

Case 3 When \(m \ne 1\), \(b \ne 0\), and \(c = 0\), the solution of Eq. (6) is

$$p\left( \xi \right) = \left( { - \frac{a}{b} + Ce^{{b\left( {m - 1} \right)\xi }} } \right)^{{\frac{1}{m - 1}}} .$$
(11)

Case 4 When \(m \ne 1\), \(a \ne 0\), and \(b^{2} - 4ac < 0\), the solution of Eq. (6) is

$$p\left( \xi \right) = \left( { - \frac{b}{2a} + \frac{{\sqrt {4ac - b^{2} } }}{2a}\tan \left( {\frac{{\left( {1 - m} \right)\sqrt {4ac - b^{2} } }}{2}\left( {\xi + C} \right)} \right)} \right)^{{\frac{1}{1 - m}}} ,$$
(12)

and

$$p\left( \xi \right) = \left( { - \frac{b}{2a} - \frac{{\sqrt {4ac - b^{2} } }}{2a}\cot \left( {\frac{{\left( {1 - m} \right)\sqrt {4ac - b^{2} } }}{2}\left( {\xi + C} \right)} \right)} \right)^{{\frac{1}{1 - m}}} .$$
(13)

Case 5 When \(m \ne 1\), \(a \ne 0\), and \(b^{2} - 4ac > 0\), the solution of Eq. (6) is

$$p\left( \xi \right) = \left( { - \frac{b}{2a} - \frac{{\sqrt {b^{2} - 4ac} }}{2a}{ \coth }\left( {\frac{{\left( {1 - m} \right)\sqrt {b^{2} - 4ac} }}{2}\left( {\xi + C} \right)} \right)} \right)^{{\frac{1}{1 - m}}} ,$$
(14)

and

$$p\left( \xi \right) = \left( { - \frac{b}{2a} - \frac{{\sqrt {b^{2} - 4ac} }}{2a}\tanh \left( {\frac{{\left( {1 - m} \right)\sqrt {b^{2} - 4ac} }}{2}\left( {\xi + C} \right)} \right)} \right)^{{\frac{1}{1 - m}}} .$$
(15)

Case 6 When \(m \ne 1\), \(a \ne 0\), and \(b^{2} - 4ac = 0\), the solution of Eq. (6) is

$$p\left( \xi \right) = \left( {\frac{1}{{a\left( {m - 1} \right)\left( {\xi + C} \right)}} - \frac{b}{2a}} \right)^{{\frac{1}{1 - m}}} .$$
(16)

where \(C\) represents an arbitrary constant.

  • Step 3 Putting the derivatives of \(q\) in Eq. (5) gives an algebraic equation of \(q\). Setting the highest power exponents of \(q\) to their equivalence in Eq. (5), \(m\) is obtained. Comparing the coefficients of \(q_{i}\) gives a set of algebraic equations that includes \(a\), \(b\), \(c\), and \(V\). Finding the solutions of the obtained sets of algebraic equations and putting \(m\), \(a\), \(b\), \(c\), \(l\), and \(\xi = k\left( {x + l\left( {\frac{{t^{\alpha } }}{\alpha }} \right)} \right)\) into Eqs. (9)–(16), a soliton solutions can be obtained for Eqs. (2).

3.2 Bäcklund transformation of the RB equation

When \(p_{n - 1} \left( \xi \right)\) and \(p_{n} \left( \xi \right) = p_{n} \left( {p_{n - 1} \left( \xi \right)} \right)\) represent the solutions of Eq. (6)

$$\begin{aligned} \frac{{dp_{n} \left( \xi \right)}}{d\xi } & = \frac{{dp_{n} \left( \xi \right)}}{{dp_{n - 1} \xi }}\frac{{dp_{n - 1} \left( \xi \right)}}{d\xi } \\ & = \frac{{dp_{n} \left( \xi \right)}}{{dp_{n - 1} \xi }}\left( {ap_{n - 1}^{2 - m} + bp_{n - 1} + cp_{n - 1}^{m} } \right), \\ \end{aligned}$$
(17)

namely

$$\frac{{dp_{n} \left( \xi \right)}}{{ap_{n}^{2 - m} + bp_{n} + cp_{n}^{m} }} = \frac{{dp_{n - 1} \left( \xi \right)}}{{ap_{n - 1}^{2 - m} + bp_{n - 1} + cp_{n - 1}^{m} }}.$$
(18)

Taking the integral of the above equation one time with respect to \(\xi\) and solving it, we have

$$p_{n} \left( \xi \right) = \left( {\frac{{ - cA_{1} + aA_{2} \left( {p_{n - 1} \left( \xi \right)} \right)^{1 - m} }}{{bA_{1} + aA_{2} + aA_{1} \left( {p_{n - 1} \left( \xi \right)} \right)^{1 - m} }}} \right)^{{\frac{1}{1 - m}}} ,$$
(19)

where \(A_{1}\) and \(A_{2}\) are arbitrary constants. Equation (19) is the Bäcklund transformation of Eq. (6). If we obtain a solution of Eq. (6), we can find new infinite sequence of solutions of Eq. (6) by using Eq. (19).

4 Applications

In this section, the soliton structures for some TFNDEs are analyzed and investigated.

4.1 Time-fractional coupled Boussinesq equations with conformable derivative

The time-fractional coupled Boussinesq equations (Hosseini et al. 2017; Hosseini and Ansari 2017; Kheir et al. 2013) is given by

$$\begin{aligned} & u_{t}^{\alpha } + v_{x} = 0, \\ & v_{t}^{\alpha } + \gamma u_{x}^{2} - \beta u_{xxx} = 0, \\ \end{aligned}$$
(20)

where \((0 < \alpha \le 1)\) is a parameter describing the order of the fractional time derivative. Using the transformation

$$\begin{aligned} & u\left( {x,t} \right) = p\left( \xi \right), \\ & v\left( {x,t} \right) = q\left( \xi \right), \\ \end{aligned}$$
(21)

where \(\xi = x - l\left( {\frac{{t^{\alpha } }}{\alpha }} \right),\) Eq. (20) is reduces to the following systems of ODE

$$\begin{aligned} & - \;lp^{\prime} + q^{\prime} = 0, \\ & - \;lq^{\prime} + \gamma p\prime^{2} - \beta p^{\prime \prime \prime} = 0. \\ \end{aligned}$$
(22)

Substituting Eqs. (6) and (7) into Eq. (22), we have

$$\begin{aligned} & b_{2} p\left( \xi \right) - b_{1} lp\left( \xi \right) + a_{2} p(\xi )^{2 - m} - a_{1} lp(\xi )^{2 - m} + c_{2} p(\xi )^{m} - c_{1} lp(\xi )^{m} = 0, \\ & \beta b_{1}^{3} p\left( \xi \right) + 8\beta a_{1} b_{1} c_{1} p\left( \xi \right) + b_{2} lp\left( \xi \right) - 4\beta a_{1} b_{1} c_{1} mp\left( \xi \right) \\ & + 2\beta a_{1} b_{1} c_{1} m^{2} p\left( \xi \right) - \gamma b_{1}^{2} p(\xi )^{2} - 2a_{1} \gamma c_{1} p(\xi )^{2} + 6\beta a_{1}^{3} p(\xi )^{4 - 3m} \\ & - \;7\beta a_{1}^{3} mp(\xi )^{4 - 3m} + 2\beta a_{1}^{3} m^{2} p(\xi )^{4 - 3m} + 12\beta a_{1}^{2} b_{1} p(\xi )^{3 - 2m} \\ & - \,12\beta a_{1}^{2} b_{1} mp(\xi )^{3 - 2m} + 3\beta a_{1}^{2} b_{1} m^{2} p(\xi )^{3 - 2m} - a_{1}^{2} \gamma p(\xi )^{4 - 2m} \\ & + \;7\beta a_{1} b_{1}^{2} p(\xi )^{2 - m} + 8\beta a_{1}^{2} c_{1} p(\xi )^{2 - m} + a_{2} lp(\xi )^{2 - m} - 5\beta a_{1} b_{1}^{2} mp(\xi )^{2 - m} \\ & - \;7\beta a_{1}^{2} c_{1} mp(\xi )^{2 - m} + \beta a_{1} b_{1}^{2} m^{2} p(\xi )^{2 - m} + 2\beta a_{1}^{2} c_{1} m^{2} p(\xi )^{2 - m} \\ & - \;2a_{1} \gamma b_{1} p(\xi )^{3 - m} + \beta b_{1}^{2} c_{1} p(\xi )^{m} + 2\beta a_{1} c_{1}^{2} p(\xi )^{m} + c_{2} lp(\xi )^{m} \\ & + \;\beta b_{1}^{2} c_{1} mp(\xi )^{m} - \beta a_{1} c_{1}^{2} mp(\xi )^{m} + \beta b_{1}^{2} c_{1} m^{2} p(\xi )^{m} + 2\beta a_{1} c_{1}^{2} \\ & m^{2} p(\xi )^{m} - \gamma c_{1}^{2} p(\xi )^{2m} - 2\gamma b_{1} c_{1} p(\xi )^{1 + m} + 3\beta b_{1} c_{1}^{2} m^{2} p(\xi )^{ - 1 + 2m} \\ & - \;\beta c_{1}^{3} mp(\xi )^{ - 2 + 3m} + 2\beta c_{1}^{3} m^{2} p(\xi )^{ - 2 + 3m} = 0. \\ \end{aligned}$$
(23)

Setting \(m = 0\) in Eq. (23), we obtain

$$\begin{aligned} & c_{2} - c_{1} l + b_{2} p\left( \xi \right) - b_{1} lp\left( \xi \right) + a_{2} p(\xi )^{2} - a_{1} lp(\xi )^{2} = 0, \\ & \beta b_{1}^{2} c_{1} + 2\beta a_{1} c_{1}^{2} - \gamma c_{1}^{2} + c_{2} l + \beta b_{1}^{3} u\left[ r \right] + 8betaa_{1} b_{1} c_{1} p\left( \xi \right) - 2\gamma b_{1} c_{1} p\left( \xi \right) \\ & + \;b_{2} lp\left( \xi \right) + 7\beta a_{1} b_{1}^{2} p(\xi )^{2} - \gamma b_{1}^{2} p(\xi )^{2} + 8\beta a_{1}^{2} c_{1} p(\xi )^{2} - 2a_{1} \gamma c_{1} p(\xi )^{2} + a_{2} lp(\xi )^{2} \\ & + \;12\beta a_{1}^{2} b_{1} p(\xi )^{3} - 2a_{1} \gamma b_{1} p(\xi )^{3} + 6\beta a_{1}^{3} p(\xi )^{4} - a_{1}^{2} \gamma p(\xi )^{4} = 0. \\ \end{aligned}$$
(24)

Setting each of the coefficients of \(p^{i} \left( {i = 0,1,2,3,4} \right)\), we get the following algebraic systems:

$$c_{2} - c_{1} l = 0,$$
(25)
$$\left( {b_{2} - b_{1} l} \right) = 0,$$
(26)
$$\left( {a_{2} - a_{1} l} \right) = 0,$$
(27)
$$- \gamma c_{1}^{2} + \beta c_{1} \left( {b_{1}^{2} + 2a_{1} c_{1} } \right) + c_{2} l = 0,$$
(28)
$$\left( { - 2\gamma b_{1} c_{1} + \beta \left( {b_{1}^{3} + 8a_{1} b_{1} c_{1} } \right) + b_{2} l} \right) = 0,$$
(29)
$$\left( { - \gamma \left( {b_{1}^{2} + 2a_{1} c_{1} } \right) + \beta a_{1} \left( {7b_{1}^{2} + 8a_{1} c_{1} } \right) + a_{2} l} \right) = 0,$$
(30)
$$2a_{1} \left( {6\beta a_{1} - \gamma } \right)b_{1} = 0,$$
(31)
$$a_{1}^{2} \left( {6\beta a_{1} - \gamma } \right) = 0.$$
(32)

Solving Eqs. (25)–(32), we obtain the following sets of results

Result 1

\(c_{2} = 0,\;c_{1} = 0,\;a_{1} \ne 0,\;b_{2} = \frac{{a_{2} b_{1} }}{{a_{1} }},b_{1} \ne 0,\;\beta = - \frac{{a_{2}^{2} }}{{a_{1}^{2} b_{1}^{2} }},\gamma = 6\beta a_{1} ,\;l = \frac{{a_{2} }}{{a_{1} }}.\)

This result produces the following soliton solutions

$$u_{1} \left( {x,t} \right) = \left( { - \frac{{b_{1} }}{{2a_{1} }} - \frac{{b_{1} }}{{2a_{1} }}\tan \left[ { - \frac{{b_{1} }}{2}\left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right),$$
(33)
$$v_{1} \left( {x,t} \right) = \left( { - \frac{{b_{1} }}{{2a_{1} }} - \frac{{b_{1} }}{{2a_{1} }}\tan \left[ { - \frac{{b_{1} }}{2}\left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right).$$
(34)
$$u_{2} \left( {x,t} \right) = \left( { - \frac{{b_{1} }}{{2a_{1} }} + \frac{{b_{1} }}{{2a_{1} }}\cot \left[ { - \frac{{b_{1} }}{2}\left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right),$$
(35)
$$v_{2} \left( {x,t} \right) = \left( { - \frac{{b_{1} }}{{2a_{1} }} + \frac{{b_{1} }}{{2a_{1} }}\cot \left[ { - \frac{{b_{1} }}{2}\left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right).$$
(36)
$$u_{3} \left( {x,t} \right) = \left( { - \frac{{b_{1} }}{{2a_{1} }} - \frac{{b_{1} }}{{2a_{1} }}\coth \left[ {\frac{{b_{1} }}{2}\left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right),$$
(37)
$$v_{3} \left( {x,t} \right) = \left( { - \frac{{b_{1} }}{{2a_{1} }} - \frac{{b_{1} }}{{2a_{1} }}\coth \left[ {\frac{{b_{1} }}{2}\left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right).$$
(38)
$$u_{4} \left( {x,t} \right) = \left( { - \frac{{b_{1} }}{{2a_{1} }} - \frac{{b_{1} }}{{2a_{1} }}\tanh \left[ {\frac{{b_{1} }}{2}\left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right),$$
(39)
$$v_{4} \left( {x,t} \right) = \left( { - \frac{{b_{1} }}{{2a_{1} }} - \frac{{b_{1} }}{{2a_{1} }}\tanh \left[ {\frac{{b_{1} }}{2}\left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right).$$
(40)

Result 2

\(c_{1} \ne 0,\,a_{2} = \frac{{a_{1} c_{2} }}{{c_{1} }},\;a_{1} \ne 0,\;b_{2} = \frac{{a_{2} b_{1} }}{{a_{1} }},\; - b_{1}^{2} + 4a_{1} c_{1} \ne 0,\beta = \frac{{a_{2}^{2} }}{{a_{1}^{2} \left( { - b_{1}^{2} + 4a_{1} c_{1} } \right)}},\;\gamma = 6\beta a_{1} ,\,l = \frac{{a_{2} }}{{a_{1} }}\). This result produces the following solution

$$u_{5} \left( {x,t} \right) = \left( { - \frac{{b_{1} }}{{2a_{1} }} + \frac{{\sqrt {4a_{1} c_{1} - b_{1}^{2} } }}{{2a_{1} }}\tan \left[ {\frac{1}{2}\sqrt {4a_{1} c_{1} - b_{1}^{2} } \left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right),$$
(41)
$$v_{5} \left( {x,t} \right) = \left( { - \frac{{a_{2} b_{1} c_{1} }}{{2a_{1}^{2} c_{2} }} + \frac{{c_{1} }}{{a_{1} c_{2} }}\sqrt {\frac{{4a_{1}^{3} c_{1}^{2} - a_{2}^{2} c_{1} b_{1}^{2} }}{{a_{1}^{2} c_{1} }}} \tan \left[ {\frac{1}{2}\sqrt {\frac{{4a_{1}^{3} c_{1}^{2} - a_{2}^{2} c_{1} b_{1}^{2} }}{{a_{1}^{2} c_{1} }}} \left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right),$$
(42)

provided that \(4a_{1} c_{1} - b_{1}^{2} > 0,\) and \(\frac{{4a_{1}^{3} c_{1}^{2} - a_{2}^{2} c_{1} b_{1}^{2} }}{{a_{1}^{2} c_{1} }} > 0,\) respectively.

$$u_{6} \left( {x,t} \right) = \left( { - \frac{{b_{1} }}{{2a_{1} }} - \frac{{\sqrt {4a_{1} c_{1} - b_{1}^{2} } }}{{2a_{1} }}\cot \left[ {\frac{1}{2}\sqrt {4a_{1} c_{1} - b_{1}^{2} } \left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right),$$
(43)
$$v_{6} \left( {x,t} \right) = \left( { - \frac{{a_{2} b_{1} c_{1} }}{{2a_{1}^{2} c_{2} }} - \frac{{c_{1} }}{{a_{1} c_{2} }}\sqrt {\frac{{4a_{1}^{3} c_{1}^{2} - a_{2}^{2} c_{1} b_{1}^{2} }}{{a_{1}^{2} c_{1} }}} \cot \left[ {\frac{1}{2}\sqrt {\frac{{4a_{1}^{3} c_{1}^{2} - a_{2}^{2} c_{1} b_{1}^{2} }}{{a_{1}^{2} c_{1} }}} \left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right),$$
(44)

provided that \(4a_{1} c_{1} - b_{1}^{2} > 0,\) and \(\frac{{4a_{1}^{3} c_{1}^{2} - a_{2}^{2} c_{1} b_{1}^{2} }}{{a_{1}^{2} c_{1} }} > 0,\) respectively.

$$u_{7} \left( {x,t} \right) = \left( { - \frac{{b_{1} }}{{2a_{1} }} - \frac{{\sqrt {b_{1}^{2} - 4a_{1} c_{1} } }}{{2a_{1} }}\coth \left[ {\frac{1}{2}\sqrt {b_{1}^{2} - 4a_{1} c_{1} } \left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right),$$
(45)
$$v_{7} \left( {x,t} \right) = \left( { - \frac{{a_{2} b_{1} c_{1} }}{{2a_{1}^{2} c_{2} }} - \frac{{c_{1} }}{{a_{1} c_{2} }}\sqrt {\frac{{4a_{1}^{3} c_{1}^{2} - a_{2}^{2} c_{1} b_{1}^{2} }}{{a_{1}^{2} c_{1} }}} \coth \left[ {\frac{1}{2}\sqrt {\frac{{4a_{1}^{3} c_{1}^{2} - a_{2}^{2} c_{1} b_{1}^{2} }}{{a_{1}^{2} c_{1} }}} \left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right),$$
(46)

provided that \(b_{1}^{2} - 4a_{1} c_{1} > 0,\) and \(\frac{{4a_{1}^{3} c_{1}^{2} - a_{2}^{2} c_{1} b_{1}^{2} }}{{a_{1}^{2} c_{1} }} > 0,\) respectively.

$$u_{8} \left( {x,t} \right) = \left( { - \frac{{b_{1} }}{{2a_{1} }} - \frac{{\sqrt {b_{1}^{2} - 4a_{1} c_{1} } }}{{2a_{1} }}\tanh \left[ {\frac{1}{2}\sqrt {b_{1}^{2} - 4a_{1} c_{1} } \left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right),$$
(47)
$$v_{8} \left( {x,t} \right) = \left( { - \frac{{a_{2} b_{1} c_{1} }}{{2a_{1}^{2} c_{2} }} - \frac{{c_{1} }}{{a_{1} c_{2} }}\sqrt {\frac{{4a_{1}^{3} c_{1}^{2} - a_{2}^{2} c_{1} b_{1}^{2} }}{{a_{1}^{2} c_{1} }}} \tanh \left[ {\frac{1}{2}\sqrt {\frac{{4a_{1}^{3} c_{1}^{2} - a_{2}^{2} c_{1} b_{1}^{2} }}{{a_{1}^{2} c_{1} }}} \left( {x - \frac{{a_{2} t^{\alpha } }}{{a_{1} \alpha }} + C} \right)} \right]} \right),$$
(48)

provided that \(b_{1}^{2} - 4a_{1} c_{1} > 0,\) \(\frac{{4a_{1}^{3} c_{1}^{2} - a_{2}^{2} c_{1} b_{1}^{2} }}{{a_{1}^{2} c_{1} }} > 0,\) respectively.

4.2 Time-fractional Cahn–Allen equation with conformable derivative

The time-fractional Cahn–Allen equation (Hosseini et al. 2017; Esen et al. 2013; Rawashdeh 2017) is given by

$$u_{t}^{\alpha } - u_{xx} + u^{3} - u = 0,$$
(49)

where \((0 < \alpha \le 1)\) is a parameter describing the order of the fractional time derivative. Using the transformation

$$u\left( {x,t} \right) = p\left( \xi \right),\;\xi = kx - l\left( {\frac{{t^{\alpha } }}{\alpha }} \right),$$
(50)

we can reduce Eq. (49) to the following ODE

$$- lp^{\prime} - k^{2} p^{\prime \prime} - p + p^{3} = 0$$
(51)

Substituting Eqs. (6) and (7) into (51), we obtain

$$\begin{aligned} & p\left( \xi \right) + b^{2} k^{2} p\left( \xi \right) + 2ack^{2} p\left( \xi \right) + blp\left( \xi \right) - p(\xi )^{3} + 2a^{2} k^{2} p(\xi )^{3 - 2m} \\ & - \;a^{2} k^{2} mp(\xi )^{3 - 2m} + 3abk^{2} p(\xi )^{2 - m} + alp(\xi )^{2 - m} - abk^{2} mp(\xi )^{2 - m} + bck^{2} p(\xi )^{m} \\ & + \;clp(\xi )^{m} + bck^{2} mp(\xi )^{m} + c^{2} k^{2} mp(\xi )^{ - 1 + 2m} = 0 \\ \end{aligned}$$
(52)

Setting \(m = 0\) in Eq (52), we get

$$bck^{2} + cl + p\left( \xi \right) + b^{2} k^{2} p\left( \xi \right) + 2ack^{2} p\left( \xi \right) + blp\left( \xi \right) + 3abk^{2} p(\xi )^{2} + alp(\xi )^{2} - p(\xi )^{3} + 2a^{2} k^{2} p(\xi )^{3} = 0.$$
(53)

Setting each of the coefficients of \(p^{i} \left( {i = 0,1,2,3,4} \right)\), we get the following algebraic systems:

$$c\left( {bk^{2} + l} \right) = 0,$$
(54)
$$\left( {1 + \left( {b^{2} + 2ac} \right)k^{2} + bl} \right) = 0,$$
(55)
$$a\left( {3bk^{2} + l} \right) = 0,$$
(56)
$$\left( { - 1 + 2a^{2} k^{2} } \right) = 0.$$
(57)

Solving Eq. (54)–(57), we have the following

  • \(b = \pm a,\;c = 0,\;a \ne 0,\;l = - \frac{3b}{{2a^{2} }},\;k = \pm \frac{\sqrt 2 l}{3}\), which produces

    $$u_{9} \left( {x,t} \right) = \left( {\frac{1}{2} + \frac{1}{2}\tan \left[ {\frac{1}{2}\sqrt a \left( {\frac{3b\sqrt 2 }{{6a^{2} }}x - \frac{{3bt^{\alpha } }}{{2a^{2} \alpha }} + C} \right)} \right]} \right),$$
    (58)
    $$u_{10} \left( {x,t} \right) = \left( {\frac{1}{2} - \frac{1}{2}\cot \left[ {\frac{1}{2}\sqrt a \left( {\frac{3b\sqrt 2 }{{6a^{2} }}x - \frac{{3bt^{\alpha } }}{{2a^{2} \alpha }} + C} \right)} \right]} \right).$$
    (59)
    $$u_{11} \left( {x,t} \right) = \left( {\frac{1}{2} - \frac{1}{2}\coth \left[ {\frac{1}{2}\sqrt a \left( {\frac{3b\sqrt 2 }{{6a^{2} }}x - \frac{{3bt^{\alpha } }}{{2a^{2} \alpha }}} \right) + C} \right)]} \right),$$
    (60)
    $$u_{12} \left( {x,t} \right) = \left( {\frac{1}{2} - \frac{1}{2}{ \tanh }\left[ {\frac{1}{2}\sqrt a \left( {\frac{3b\sqrt 2 }{{6a^{2} }}x - \frac{{3bt^{\alpha } }}{{2a^{2} \alpha }} + C} \right)} \right]} \right),$$
    (61)

    provided that \(a > 0.\)

4.3 Time-fractional biological reaction–convection–diffusion model equations with conformable derivative

Consider the following time-fractional reaction–convection–diffusion equation as follows:

$$u_{t}^{\alpha } = \left( {\lambda + \lambda_{0} u} \right)u_{xx} + \lambda_{1} uu_{x} + \lambda_{2} u - \lambda_{3} u^{2} ,$$
(62)

where \(\lambda ,\lambda_{0} ,\lambda_{1} ,\lambda_{2} ,\) and \(\lambda_{3}\) are real constants (Javadi et al. 2013). Setting \(\lambda = 1\) and \(\lambda_{0} = 0\), the equation turns to the form of the time-fractional Murray (Yildirim and Pinar 2010) equation

$$u_{t}^{\alpha } = u_{xx} + \lambda_{1} uu_{x} + \lambda_{2} u - \lambda_{3} u^{2} ,$$
(63)

which is also a generalization of fishers equation when \(\lambda_{1} = 0\), where \((0 < \alpha \le 1)\) is a parameter describing the order of the fractional time derivative. When \(\lambda_{2} = \lambda_{3} = 0 {\text{and }}\alpha = 1\), the equation turns to the classical Burgers equation. By using the transformation in Eq. (50), one can reduces Eq. (63) to

$$lp^{\prime} - k^{2} p^{\prime \prime} - \lambda_{1} kpp^{\prime} - \lambda_{2} p + \lambda_{3} p^{2} .$$
(64)

Substituting Eqs. (6) and (7) into (64), we obtain

$$\begin{aligned} & 3abk^{2} p(\xi )^{2} - abk^{2} mp(\xi )^{2} - alp(\xi )^{2} + ak\lambda_{1} p(\xi )^{3} + 2a^{2} k^{2} p(\xi )^{3 - m} \\ & - \;a^{2} k^{2} mp(\xi )^{3 - m} + bck^{2} p(\xi )^{2m} + bck^{2} mp(\xi )^{2m} - cwp(\xi )^{2m} + b^{2} k^{2} p(\xi )^{1 + m} \\ & + \;2ack^{2} p(\xi )^{1 + m} - blp(\xi )^{1 + m} + \lambda_{2} p(\xi )^{1 + m} + bk\lambda_{1} p(\xi )^{2 + m} - \lambda_{3} p(\xi )^{2 + m} \\ & - \;\lambda_{3} u(\xi )^{2 + m} + ck\lambda_{1} u(\xi )^{1 + 2m} + c^{2} k^{2} mu(\xi )^{ - 1 + 3m} = 0 \\ \end{aligned}$$
(65)

Setting \(m = 0\) in Eq (65), we get

$$\begin{array}{*{20}l} {bck^{2} - cl + b^{2} k^{2} p\left( \xi \right) + 2ack^{2} p\left( \xi \right) - blp\left( \xi \right) + ck\lambda_{1} p\left( \xi \right) + \lambda_{2} p\left( \xi \right)} \hfill \\ { + 3abk^{2} p(\xi )^{2} - alp(\xi )^{2} + bk\lambda_{1} p(\xi )^{2} - \lambda_{3} p(\xi )^{2} + 2a^{2} k^{2} p(\xi )^{3} + ak\lambda_{1} p(\xi )^{3} = 0} \hfill \\ \end{array}$$
(66)

Setting each of the coefficients of \(p^{i} \left( {i = 0,1,2,3} \right)\), we get the following algebraic systems:

$$c\left( {bk^{2} - l} \right) = 0,$$
(67)
$$\left( {b^{2} k^{2} - bl + ck\left( {2ak + \lambda_{1} } \right) + \lambda_{2} } \right) = 0,$$
(68)
$$\left( {3abk^{2} - al + bk\lambda_{1} - \lambda_{3} } \right) = 0,$$
(69)
$$ak\left( {2ak + \lambda_{1} } \right) = 0.$$
(70)

Solving Eq. (67) to (70), we have the following

  • \(\lambda_{1}^{2} \lambda_{2} + 4\lambda_{3}^{2} \ne \, 0, \, k = \frac{{2 l \lambda_{1} \lambda_{3} }}{{\lambda_{1}^{2} \lambda_{2} + 4\lambda_{3}^{2} }}, \, a = - \frac{{\lambda_{1} }}{2k}, \, \lambda_{1} \ne 0, \, b = - \frac{{2\left( {a l + \lambda_{3} } \right)}}{{k\lambda_{1} }}, \, c = 0\), which produces

    $$u_{13} \left( {x,t} \right) = \left( - \frac{{\lambda_{1}^{2} l}}{{2\left( {2k\lambda_{3} - \lambda_{1} } \right)}} + Ce^{{\frac{{2\left( {al + \lambda_{3} } \right)}}{{k\lambda_{1} }}\left( {kx - l\left( {\frac{{t^{\alpha } }}{\alpha }} \right)} \right)}} \right)^{ - 1} .$$
    (71)
    $$u_{14} \left( {x,t} \right) = - \frac{{4\left( {2k\lambda_{3} - \lambda_{1} l} \right)}}{{\lambda_{1}^{2} }} + \frac{{\left( {2k\lambda_{3} - \lambda_{1} l} \right)}}{{\lambda_{1}^{2} }}{ \tan }\left( {\frac{{\left( {2k\lambda_{3} - \lambda_{1} l} \right)}}{{k\lambda_{1} }}\left( {kx - l\left( {\frac{{t^{\alpha } }}{\alpha }} \right) + C} \right)} \right),$$
    (72)

    and

    $$u_{15} \left( {x,t} \right) = - \frac{{4\left( {2k\lambda_{3} - \lambda_{1} l} \right)}}{{\lambda_{1}^{2} }} - \frac{{\left( {2k\lambda_{3} - \lambda_{1} l} \right)}}{{\lambda_{1}^{2} }}{ \cot }\left( {\frac{{\left( {2k\lambda_{3} - \lambda_{1} l} \right)}}{{k\lambda_{1} }}\left( {kx - l\left( {\frac{{t^{\alpha } }}{\alpha }} \right) + C} \right)} \right),$$
    (73)
    $$u_{16} \left( {x,t} \right) = - \frac{{4\left( {2k\lambda_{3} - \lambda_{1} l} \right)}}{{\lambda_{1}^{2} }} + \frac{{\left( {2k\lambda_{3} - \lambda_{1} l} \right)}}{{\lambda_{1}^{2} }}{ \coth }\left( {\frac{{\left( {2k\lambda_{3} - \lambda_{1} l} \right)}}{{k\lambda_{1} }}\left( {kx - l\left( {\frac{{t^{\alpha } }}{\alpha }} \right) + C} \right)} \right),$$
    (74)

    and

    $$u_{17} \left( {x,t} \right) = - \frac{{4\left( {2k\lambda_{3} - \lambda_{1} l} \right)}}{{\lambda_{1}^{2} }} + \frac{{\left( {2k\lambda_{3} - \lambda_{1} l} \right)}}{{\lambda_{1}^{2} }}{ \tanh }\left( {\frac{{\left( {2k\lambda_{3} - \lambda_{1} l} \right)}}{{k\lambda_{1} }}\left( {kx - l\left( {\frac{{t^{\alpha } }}{\alpha }} \right) + C} \right)} \right),$$
    (75)
    $$u_{18} \left( {x,t} \right) = \left( {\frac{2k}{{\lambda_{1} \left( {kx - l\left( {\frac{{t^{\alpha } }}{\alpha }} \right) + C} \right)}} + \frac{{4\left( {2k\lambda_{3} - \lambda_{1} l} \right)}}{{\lambda_{1}^{2} }}} \right).$$
    (76)

5 Numerical simulation

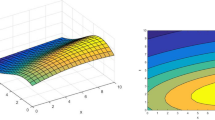
Herein, we present some three dimensional and two dimensional plots of some of the obtained results (see Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10). The construction of the Figures is carried out by taking suitable values of the parameters in order to see the mechanism of the original equations. From the Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 below, one can see that, the obtained solutions possess solutions such as periodic wave, bell-shaped, kink-type and singular soliton solutions.

Fig. 1
figure 1

Three and two dimensional plots for solution (33) with \(a_{1} = 1\), \(a_{2} = 1.9\), \(b_{1} = c_{1} = 12\), \(\alpha = 0.5\)

Full size image
Fig. 2
figure 2

Three and two dimentional plots for solution (34) with \(a_{1} = 5\), \(a_{2} = 3.9\), \(b_{1} = c_{1} = 2\), \(\alpha = 0.95\)

Full size image
Fig. 3
figure 3

Three and two dimentional plots for solution (39) with \(a_{1} = 10\), \(a_{2} = 1\), \(b_{1} = c_{1} = 2\), \(\alpha = 0.8\)

Full size image
Fig. 4
figure 4

Three and two dimensional plots for solution (40) with \(a_{1} = 10\), \(a_{2} = 1\), \(b_{1} = c_{1} = 2\), \(\alpha = 0.8\)

Full size image
Fig. 5
figure 5

Three and two dimensional plots for (45) with \(a_{1} = 5\), \(a_{2} = 12\), \(b_{1} = c_{1} = 4\), \(\alpha = 0.8\)

Full size image
Fig. 6
figure 6

Three and two dimentional plots for solution (46) with \(a_{1} = 4\), \(a_{2} = 1\), \(b_{1} = c_{1} = 4\), \(\alpha = 0.5\)

Full size image
Fig. 7
figure 7

Three and two dimentional plots for solution (47) with \(a_{1} = 4\), \(a_{2} = 1\), \(b_{1} = c_{1} = 4\), \(\alpha = 0.5\)

Full size image
Fig. 8
figure 8

Three and two dimentional plots for solution (48) with \(a_{1} = 4\), \(a_{2} = 1\), \(b_{1} = c_{1} = 4\), \(\alpha = 0.5\)

Full size image
Fig. 9
figure 9

Three and two dimentional plots for solution (60) with \(a = 1,b = 0.5,\alpha = 0.5\)

Full size image
Fig. 10
figure 10

Three and two dimensional plots for solution (61) with \(a = b = 10\), \(\alpha = 0.5\)

Full size image

6 Concluding remarks

This research presented soliton structures to some TFNDEs with conformable derivative. The powerful RB sub-ODE method was used to carry out the soliton solutions. Some of the obtained solutions include trigonometric, periodic wave and hyperpolic solutions. The constraint conditions were also presented. The RB sub-ODE method proved to be efficient and effective for the extraction of soliton structures for different types of TFNDEs. The obtained soliton solutions can be used for the interpretation of some physical phynomena in mathematical physics. Some interesting figures for the obtained solutions were presented in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.