Breather Wave Solutions for the (3+1)-D Generalized Shallow Water Wave Equation with Variable Coefficients

Abstract

The equation of the shallow water wave in oceanography and atmospheric science is extended to (3+1) dimensions, which is a known equation. To achieve this, an illustrative example of the VC generalized shallow water wave equation is provided to demonstrate the feasibility and reliability of the used procedure in this study. It is shown that Hirota bilinear method is an important scheme. So, it has plenty of classes of rational solutions by selecting the interaction breather and dark soliton solutions and homoclinic breather wave solutions. Here many types of rough and breather solutions are obtained. The mentioned equation is transformed into the Hirota bilinear form with help of the Hirota direct method. In this process, the Hirota bilinear operator plays a significant role. Based on the Hirota bilinear form, the breather wave forms solutions of the equation are obtained. Meanwhile, the figures of the breather wave forms solutions and periodic wave solutions are plotted. The trajectory solutions of the traveling waves are shown explicitly and graphically. The effect of the free parameters on the behavior of the acquired figures to a few of the obtained solutions for two nonlinear rational exact cases was also discussed. In addition to addressing a scientific explanation of the analytical work, the results are graphically presented to make it simple to recognize the dynamical aspects. Many new types of traveling-wave solutions are revealed, including the breather wave, the dark kink singular, the periodic solitary singular and the singular soliton solutions. By comparing the proposed method with the other existing methods, the results show that the execution of this method is concise, simple, and straightforward.

1 Introduction

Nonlinear shallow water wave (NSWW) equations generally are explained through flow under a pressure surface, and it transpires everywhere, closely in the domain of oceanography and atmospheric sciences; however, there is the horizontal structure of an atmosphere and the evolution of an incompressible fluid. The shallow water wave have used to many applications due to their importance in Rossby waves [1, 2], fluid dynamics [3, 4] and other subjects [5,6,7]. Alsu et al. [8] studied novel exact solutions of the (2+1)-dimensions extended shallow water wave equation by the Hirota bi-linear approach to find Lumps and interactions, fission and fusion phenomena in multi solitons. Third-order dispersive evolution equations were widely adopted to model one-dimensional long waves and have extensive applications in fluid mechanics, plasma physics and nonlinear optics by using complete integrability, Lax pairs and bi-Hamiltonian structure [9]. Solitons, lump solutions and lump-periodic solutions were obtained for the generalized (2+1)-dimensional shallow water wave equation via the Hirota bilinear method [10]. Authors of [11] used the the Hirota bilinear method to equation of the shallow water wave in oceanography and atmospheric science with variable coefficients and obtained interaction between the lump and soliton solutions. In [12], the solitary wave solutions by using the rogue wave and semi-inverse variational principle schemes to the generalized (2+1)-dimensional shallow water wave equation have been studied. M lump and interaction between M lump and N stripe solutions to the third-order evolution equation arising in the shallow water have been investigated [13].

In the last decades, researchers have developed numerous methods. One method is study on the nonlinear evolution equations. The study on the nonlinear evolution equations (NLEEs) has caused people’s attention in the last century. NLEEs have important applications in many subject areas, for example, theoretical physics, the multiple heaving wave energy [14], floating parabolic breakwaters [15], water environmental pollution [16], the Kudryashov’s quintuple self-phase modulation [17], particle physics, crystal physics, signal processing, chemistry, astronomy and so on. These fields are closely related to mathematics. The exact solutions of NLEEs have an important significance for applications in these fields, because researchers can explain so many natural phenomena through these exact solutions. Scholars and researchers have put forward a large number of methods to obtain solutions of NLEEs, including an integrated simulation–optimization framework [18], the Hirota’s bilinear method [19], the deep learning algorithm [20], the binary offset carrier signal capture algorithm [21], from van der Waals equation [22], free heat transfer properties of flat panel solar collectors [23], optimal bidding and offering strategies [24], a hybrid convolutional neural network [25], deep learning and modified african vulture optimization algorithm [26], optimal modeling of combined cooling [27], optimal economic scheduling method [28], a new combined energy system [29], a hybrid convolutional neural network and extreme [30], a robust optimization technique [31], a robust optimization based optimal method [32], a hybrid forecast engine based intelligent algorithm method [33], and so forth.

Here, the (3+1)-D variable coefficients generalized SWW equation is examined to use in ocean waves [34, 35] in the following

$$\begin{aligned} \alpha _1(t)\Phi _{yt}+\alpha _3(t)\Phi _x\Phi _{xy}+\alpha _3(t)\Phi _{y}\Phi _{xx}+\alpha _2(t)\Phi _{xxxy}+ \alpha _4(t)\Phi _{xz}=0, \end{aligned}$$

(1.1)

in which $\alpha _4(t)$ relates to the perturbed effects and $\alpha _2(t)$ and $\alpha _3(t)$ point to the dispersion and nonlinearity, respectively. Also, $\alpha _s(t) (s=1,\ldots ,4)$ is differentiable real function. Applications in weather simulations, tidal waves, tsunami prediction can be arisen in [36] with inserting $\alpha _1(t)=\alpha _2(t)=1, \alpha _3(t)=-3,\alpha _4(t)=-1$. Furthermore, by putting $\alpha _1(t)=2,\alpha _2(t)=1, \alpha _3(t)=3,\alpha _4(t)=-3$, the Eq. (1.1) will be replaced to (3+1)-dimensional Jimbo–Miwa equation [37]. Also, Eq. (1.1) can be substituted to the (3+1)-D constant coefficients generalized SWW equation [38] as follows

$$\begin{aligned} \Phi _{yt}-3\Phi _x\Phi _{xy}-3\Phi _{y}\Phi _{xx}+\Phi _{xxxy}- \Phi _{xz}=0, \end{aligned}$$

(1.2)

when $\alpha _1(t)=1, \alpha _3(t)=-3, \alpha _2(t)=1,\alpha _4(t)=-1$. Huang and co-authors [39, 40] investigated bilinear bäcklund transformation to Eq. (1.1) and obtained the soliton and periodic wave solutions.

Bright soliton, kink wave solution and traveling wave solutions were generated with the advantages of the generalized exponential rational function method to the $\left( 1+2\right)$-dimensional Zoomeron equation [41].

Among these methods, Hirota direct method is so prompt and effective. With this method, NLEEs are transformed into Hirota bilinear forms [42]. This form is so beautiful and beneficial to obtaining exact solutions, especially a kind of important solutions-soliton solutions [43,44,45]. In addition, lump solutions, breather solutions of NLEEs can be constructed. Lately, Ma developed this method, the proposed generalized bilinear differential operators, NLEEs can be transformed into generalized bilinear forms through this operators [46].

A new method named bilinear neural network and the corresponding tensor formula were proposed to obtain the exact analytical solutions of nonlinear partial differential equations [47]. Bilinear neural network method was introduced to solve the explicit solution of a generalized breaking soliton equation [48]. Based on bilinear neural network method, the generalized lump solution, classical lump solution and the novel analytical solution were constructed to the (2+1)-dimensional Caudrey–Dodd–Gibbon–Kotera–Sawada-like equation [49].

The Hamiltonian amplitude equation with the properties of truncated M-fractional derivative with different forms like, bright, dark, singular, combined and complex solitons were extracted by using the modified Sardar sub-equation method [50]. The three-component coupled nonlinear Schrödinger equation the optical solitons in fiber optics was studied by the extended direct algebraic method [51]. The double-chain DNA dynamical system was investigated using the the new auxiliary equation method and the extended sinh-Gordon equation expansion method [52]. The optical solitons to the Biswas–Arshed equation with third-order dispersion and self-steepening coefficients that communicate pulse propagation in fiber optics were obtained by using the extended Fan sub-equation method [53].

The exact solutions to one-dimensional long water wave propagation in a nonlinear medium simulated by the fractional-order modified equal-width equation were obtained [54]. The solitary dynamics including rogue wave, periodic wave solution, periodic combined singular soliton, combined singular soliton, and periodic wave solutions of the Biswas–Arshed model without self-phase modulation were investigated [55].

The analytical solutions of some nonlinear time-fractional partial differential equations were investigated by the direct algebraic method [56]. Analytical solutions and physical interpretations for the shallow water wave system were found using the modified expansion method [57]. The modulation instability was applied to study stability of the solutions of of (2+1)-Kadomtsev–Petviashvili equation [58].

The unified method to retrieve optical soliton solutions of the Biswas–Arshed model with the Kerr law nonlinearity was used [59]. The (2+1)-dimensional Benjamin–Bona–Mahony–Burgers model was considered and reduced to bilinear form by using the Hirota bilinear scheme to construct lump waves and collision of lump with periodic waves [60]. By the help of the Hirota bilinear formation and a trial function the novel collision solutions between the lump and kinky waves of the (3+1)-D Jimbo–Miwa-like model were studied [61]. The presence of stable kink soliton and kinky-periodic rogue wave solutions; unstable singular kink wave solutions of the biological dynamical models as a Cahn–Allen model and a diffusive predator–prey model was studied by modified simple equation scheme [62].

The dust ion-acoustic solitary wave in an unmagnetized collisional dusty plasma modeled by the damped modified Korteweg–de Vries equation by applying reductive perturbation technique was investigated [64]. The exact travelling and solitary wave solutions of the Kudryashov–Sinelshchikov equation by implementing the modified mathematical method were constructed [65]. The nonlinear longitudinal wave equation which involves mathematical physics with dispersal produced by the phenomena of transverse Poisson’s effect in a magneto-electro-elastic circular rod was investigated [66]. Also, the solitary wave solutions of generalized Kadomtsev–Petviashvili (KP) modified equal width equation with the help of modification form of extended auxiliary equation mapping method were obtained [67]. The exact traveling and solitary wave solutions of nonlinear diffusion reaction equation with quadratic and cubic nonlinearities were created by implementing a modified mathematical method [?].

This work successfully used the Hirota bilinear approach [34, 35] with Hirota direct method to the (3+1)-D generalized shallow water wave (GSWW) equation with variable coefficients for obtaining spatiotemporal breather soliton solutions and exact extended breather wave solutions. As a main result of this paper, theoretical analysis to get to exact solutions by bell polynomial method for a GSWW equation with distributed coefficients is investigated.

In the present work, we have constituted a used model in ocean waves by bilinear method. Due to the advantages of the logarithmic form of function in Hirota bilinear scheme, we have considered a binary bell polynomials to get to bilinear equation with logarithmic transformation in our study.

There are four sections in the paper, and the structure of this article is as follows: In Sect. 2, the basic concept related to Hirota bilinear operator is introduced and the Hirota bilinear form is derived. Meanwhile, with the help of Hirota analysis approach, we prove that the breather wave solutions can be derived from the extended breather wave solutions in Sect. 3. In Sect. 5, we give some conclusions.

2 Binary Bell Polynomials

Consider Ref. [68], take $b= b(x_1, x_2,\ldots ,x_n)$ be a $C^\infty$ with the below issues:

$$\begin{aligned} A_{n_1x_1,\ldots ,n_jx_j}(b)\equiv A_{n_1,\ldots ,n_j}(b_{l_1x_1,\ldots ,l_jx_j})=e^{-b}\partial _{x_1}^{n_1}\cdots \partial _{x_j}^{n_j}e^{b}, \end{aligned}$$

(2.1)

and

$$\begin{aligned} b_{l_1x_1,\ldots ,l_jx_j}=\partial _{x_1}^{l_1}\cdots \partial _{x_j}^{l_j}b, \ \ b_{0x_i}\equiv b, \ l_1=0,\ldots ,n_1;\ldots ;l_j=0,\ldots ,n_j, \end{aligned}$$

and we have

$$\begin{aligned} A_1(b)= & {} b_x,\quad A_2(b)=b_{2x}+b_x^2,\quad \nonumber \\ A_3(b)= & {} b_{3x}+3b_xb_{2x}+b_x^3,\ldots _,\quad b=b(x,t),\nonumber \\ A_{x,t}(b)= & {} b_{x,t}+b_xb_t,\quad A_{2x,t}(b)=b_{2x,t}+b_{2x}b_{t}+2b_{x,t}b_{x}+b_x^2b_t,\ldots _.\nonumber \\ \end{aligned}$$

(2.2)

The multi form of Bell polynomials is stated as

$$\begin{aligned} \sum _{n_1x_1,\ldots ,n_jx_j}(\mu _1,\mu _2)= & {} \left. \Upsilon _{n_{1},\ldots ,n_{j}}(b)\right| _{{b_{l_1x_1,\ldots ,l_jx_j}}}\nonumber \\= & {} \left\{ \begin{array}{ll} {\mu _1}_{l_1x_1,\ldots ,l_jx_j}, &{} l_1+l_2+\cdots +l_j, \hbox { is odd} \\ {\mu _2}_{l_1x_1,\ldots ,l_jx_j}, &{} l_1+l_2+\cdots +l_j, \hbox { is even.} \end{array} \right. \end{aligned}$$

(2.3)

The following issues are as

$$\begin{aligned} \sum _{x}(\mu _1)= & {} {\mu _1}_{x},\ \ \sum _{2x}(\mu _1,\mu _2)={\mu _2}_{2x}+{\mu _1}_{x}^2,\nonumber \\ \sum _{x,t}(\mu _1,\mu _2)= & {} {\mu _2}_{x,t}+{\mu _1}_{x}{\mu _1}_{t},\ldots _. \end{aligned}$$

(2.4)

Proposition 2.1

Suppose $\rho _1=\ln (\Theta _1/\Theta _2),\ \ \rho _2=\ln (\Theta _1\Theta _2),$ then the cases between binary Bell polynomials and Hirota operator will be appeared as

$$\begin{aligned}{} & {} \left. \sum _{n_1x_1,\ldots ,n_jx_j}(\rho _1,\rho _2)\right| _{\rho _1=\ln (\Theta _1/\Theta _2),\quad \rho _2=\ln (\Theta _1\Theta _2)}=(\Theta _1\Theta _2)^{-1}D_{x_1}^{n_1}\cdots D_{x_j}^{n_j}\Theta _1\Theta _2,\nonumber \\ \end{aligned}$$

(2.5)

with Hirota operator

$$\begin{aligned} \prod _{i=1}^{j}D_{x_i}^{n_i}g.\ \eta =\left. \prod _{i=1}^{j}\left( \frac{\partial }{\partial x_i}-\frac{\partial }{\partial x_i'}\right) ^{n_i}\Theta _1(x_1,\ldots ,x_j)\Theta _2(x_1',\ldots ,x_j')\right| _{x_1=x_1',\ldots ,x_j=x_j'}.\nonumber \\ \end{aligned}$$

(2.6)

Proposition 2.2

Take $\Xi (\gamma )=\sum _{i} \delta _i\mathfrak {P}_{l_1x_1,\ldots ,l_jx_j}=0$ and $\rho _1=\ln (\Theta _1/\Theta _2),\ \ \rho _1=\ln (\Theta _1\Theta _2),$ we have

$$\begin{aligned} \left\{ \begin{array}{ll} \sum _{i} \delta _{1i}\Upsilon _{n_1x_1,\ldots ,n_jx_j}(\rho _1,\rho _2)=0, \\ \sum _{i} \delta _{1i}\Upsilon _{l_1x_1,\ldots ,l_jx_j}(\rho _1,\rho _2)=0, \end{array} \right. \end{aligned}$$

(2.7)

in which the below relations are correct

$$\begin{aligned} \mathfrak {S}(\gamma ',\gamma )=\mathfrak {S}(\gamma ')-\mathfrak {S} (\gamma )=\mathfrak {S}(\rho _2+\rho _1)-\mathfrak {S}(\rho _2-\rho _1)=0. \end{aligned}$$

(2.8)

The generalized form of $\Upsilon _{n_1x_1,\ldots ,n_jx_j}(\xi )$ is presented as

$$\begin{aligned}{} & {} (\Theta _1\Theta _2)^{-1}D_{x_1}^{n_1}\cdots D_{x_j}^{n_j}\Theta _1\Theta _2= \left. \Sigma _{n_1x_1,\ldots ,n_jx_j}(\rho _1,\rho _2)\right| _{\rho _1=\ln (\Theta _1/\Theta _2),\ \ \rho _2=\ln (\Theta _1\Theta _2)}\nonumber \\{} & {} \quad =\left. \Sigma _{n_1x_1,\ldots ,n_jx_j}(\rho _1,\rho _1+\gamma )\right| _{\rho _1=\ln (\Theta _1/\Theta _2),\ \ \gamma =\ln (\Theta _1\Theta _2)}\nonumber \\{} & {} \quad =\sum _{k_1}^{n_1}\cdots \sum _{k_j}^{n_j}\prod _{i=1}^{j}\left( \begin{array}{c} n_i \\ k_i \end{array}\right) \mathfrak {P}_{k_1x_1,\ldots ,k_jx_j}(\gamma )\Upsilon _{(n_1-k_1)x_1,\ldots ,(n_j-k_j)x_j}(\rho _1). \end{aligned}$$

(2.9)

The Cole–Hopf relation in the following is given

$$\begin{aligned}{} & {} \Upsilon _{k_1x_1,\ldots ,k_jx_j}(\rho _1=\ln (\varphi ))=\frac{\varphi _{n_1x_1,\ldots ,n_jx_j}}{\varphi }, \end{aligned}$$

(2.10)

$$\begin{aligned}{} & {} \left. (\Theta _1\Theta _2)^{-1}D_{x_1}^{n_1}\cdots D_{x_j}^{n_j}\Theta _1\Theta _2 \right| _{\Theta _2=\exp (\gamma /2),\ \ \Theta _1/\Theta _2=\varphi }\nonumber \\{} & {} \qquad =\varphi ^{-1}\sum _{k_1}^{n_1}\cdots \sum _{k_j}^{n_j}\prod _{l=1}^{j}\left( \begin{array}{c} n_l \\ k_l \end{array}\right) \mathfrak {P}_{k_1x_1,\ldots ,k_lx_l}(\gamma )\varphi _{(n_1-k_1)x_1,\ldots ,(n_d-k_l)x_l},\nonumber \\ \end{aligned}$$

(2.11)

with

$$\begin{aligned} \Upsilon _{t}(\rho _1)= & {} \frac{\varphi _t}{\varphi },\quad \Upsilon _{2x}(\rho _1, \beta )=\gamma _{2x}+\frac{\varphi _{2x}}{\varphi },\nonumber \\ \Upsilon _{2x,y}(\rho _1,\rho _2)= & {} \frac{\gamma _{2x}\varphi _y}{\varphi }+ \frac{2\gamma _{x,y}\varphi _x}{\varphi }+\frac{\varphi _{2x,y}}{\varphi }. \end{aligned}$$

(2.12)

Inserting $\Phi =c(t)f_x+\Phi _0$ into Eq. (1.1), one gives $c(t)=2\alpha _0$. Hence, to more investigation the following theorem is taken.

Theorem 2.3

By the below issues, one gets

$$\begin{aligned} f=\ln (h)\Leftrightarrow \Phi =2\alpha _0\ln (h(x,y,z,t))_{x}-\omega (z), \end{aligned}$$

(2.13)

in which $\alpha _2=\alpha _0\alpha _3(t)/3$ and $\alpha _0$ is an nonzero constant and $\omega (z)$ is an free function into Eq. (1.1), the (3+1)-D VC generalized SWW equation can be expressed in the following

$$\begin{aligned} \mathfrak {R}(h)= & {} \alpha _1(t)(hh_{yt}-h_yh_t)+\alpha _4(t)(hh_{xz}-h_xh_z)\nonumber \\{} & {} +\,\alpha _2(t)(hh_{xxxy}-3h_xh_{xxy}+3h_{xy}h_{xx}-h_{y}h_{xxx})\nonumber \\= & {} \frac{1}{2} \left( \alpha _1(t)D_yD_t+\alpha _4(t)D_xD_z+\alpha _2(t)D_x^3D_y\right) h.h=0, \end{aligned}$$

(2.14)

where $h=h(x,y,z,t)$ and $f=f(x,y,z,t)$.

3 Two Types Solutions for VCSWW Equation

Two subsections containing the extended breather solutions and rational breather wave solutions are studied.

3.1 Extended Breather Wave Solutions

The following function for the extended breather wave solutions is offered as

$$\begin{aligned} h= & {} \textrm{e}^{a_1}+\textrm{e}^{a_2}+\tanh (a_3)+\tan (a_4),\nonumber \\ a_s= & {} m_sx+n_s(y)+p_sz+q_s(t),\quad s=1,2,3,4. \end{aligned}$$

(3.1)

Afterwards, the amounts $m_s,n_s(y),p_s(y), (s=1:2)$ will be determined. By making use of Eq. (3.1) into (2.14) and considering the coefficients the each powers of $\exp (a_s), s=1,2$ and $\tanh (a_3),\tan (a_4)$ to zero, reach a system of equations (algebraic) for $m_s,n_s(y),p_s, q_s(t), (s=1:4)$. Based on the (3.1) the solution $\Phi =2\alpha _0(\ln h)_{x}$ can be appeared as below:

$$\begin{aligned} \Phi= & {} {\frac{m_{{1}}{\textrm{e}^{a_{{1}}}}+m_{{2}}{\textrm{e}^{a_{{2}}}}+ \left( 1- \left( \tanh \left( a_{{3}} \right) \right) ^{2} \right) m_{{3}}+ \left( 1+ \left( \tan \left( a_{{4}} \right) \right) ^{2} \right) m_ {{4}}}{{\textrm{e}^{a_{{1}}}}+{\textrm{e}^{a_{{2}}}}+\tanh \left( a_{{3}} \right) +\tan \left( a_{{4}} \right) +q_{{5}} \left( t \right) }},\\ a_s= & {} m_sx+n_s(y)+p_sz+q_s(t), \quad s=1,2,3,4. \end{aligned}$$

3.1.1 Solution I

$$\begin{aligned} m_s= & {} m_s,\quad s=1,2,3,4,\quad n_s=p_s=0,\quad s=1,2,3,4,\nonumber \\ q_i(t)= & {} q_i(t),\quad i=1,2,3,4,\quad q_5(t)=C_5, \end{aligned}$$

(3.2)

in which $m_l, l=1,2,3,4$ are free constants and $q_l(t), l=1,2,3,4$ are parametric functions. The first solution of extended breather wave solution is obtained as

$$\begin{aligned} \Phi _1= & {} 2\,{\frac{\alpha _{{0}} \left( m_{{1}}{\textrm{e}^{m_{{1}}x+q_{{1}} \left( t \right) }}+m_{{2}}{\textrm{e}^{m_{{2}}x+q_{{2}} \left( t \right) }}+ \left( \omega ^-(x,t) \right) m_{{3}}+ \left( \omega ^+(x,t) \right) m_{{4}} \right) }{{\textrm{e}^{m_{{1}}x+q_{{1}} \left( t \right) }}+{\textrm{e}^{m_{{2}}x+q_{{2}} \left( t \right) }}+\tanh \left( m_{{3}}x+q_{{3}} \left( t \right) \right) +\tan \left( m_{{4} }x+q_{{4}} \left( t \right) \right) +q_{{5}} \left( t \right) }},\nonumber \\ \omega ^{\pm }(x,t)= & {} 1\pm \left( \tanh \left( m_{{3}}x+q_{{3}} \left( t \right) \right) \right) ^{2},\ \ a_1=m_{{l}}x+q_l t,\quad l=1,2,3,4.\nonumber \\ \end{aligned}$$

(3.3)

3.1.2 Solutions II

$$\begin{aligned} m_l= & {} n_l=0,\quad l=1,3,4,\quad m_2=m_2,\quad n_2=n_2,\quad p_i=p_i, \nonumber \\ i= & {} 1,2,3,4,\quad q_5(t)=C_5,\nonumber \\ q_{{i}} \left( t \right)= & {} \int \!-{\frac{\alpha _{{4}} \left( t \right) m_{{2}}p_{{i}}}{\alpha _{{1}} \left( t \right) n_{{2}}}} \,\textrm{d}t,\quad i=1,3,4, \nonumber \\ q_{{2}} \left( t \right)= & {} \int \!-{\frac{m_{{2}} \left( \alpha _{{2}} \left( t \right) {m_{{2}}}^{2}n_{{2}}+\alpha _{{4}} \left( t \right) p _{{2}} \right) }{\alpha _{{1}} \left( t \right) n_{{2}}}}\,\textrm{d}t, \end{aligned}$$

(3.4)

in which $m_2,n_2$ are free constants and $p_s,q_s(t), s=1,2,3,4$ are parametric functions. The rational extended breather wave solution is derived in the following form

$$\begin{aligned} \Phi _2= & {} \frac{2\,\alpha _{{0}}m_{{2}}F_{{1}}}{{\textrm{e}^{p_{{1}}z+\int \!-{\frac{\alpha _{{4}} \left( t \right) m_{{2 }}p_{{1}}}{\alpha _{{1}} \left( t \right) n_{{2}}}}\,\textrm{d}t}}+F_{{1}} +\tanh \left( p_{{3}}z+\int \!-{\frac{\alpha _{{4}} \left( t \right) m _{{2}}p_{{3}}}{\alpha _{{1}} \left( t \right) n_{{2}}}}\,\textrm{d}t\Lambda \right) +\tan \left( p_{{4}}z+\int \!-{\frac{\alpha _{{4}} \left( t \right) m_{{2}}p_{{4}}}{\alpha _{{1}} \left( t \right) n_{{2}}}} \,\textrm{d}t \right) +C_{{5}} },\nonumber \\ F_{{1}}= & {} {\textrm{e}^{m_{{2}}x+n_{{2}}y+p_{{2}}z+\int \!-{\frac{m_{{2}} \left( \alpha _{{2}} \left( t \right) {m_{{2}}}^{2}n_{{2}}+\alpha _{{4} } \left( t \right) p_{{2}} \right) }{\alpha _{{1}} \left( t \right) n_{ {2}}}}\,\textrm{d}t}}. \end{aligned}$$

(3.5)

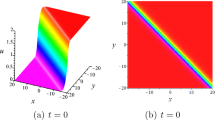
Figs. 1, 2  and 3, offer the behavior of interaction between breather and dark soliton solution with two wave solution in which the selected values for $\Phi _2$ are given in the following

$$\begin{aligned} m_2= & {} 2, n_2=1, p_1=3,p_2=2,p_3=3,p_4=4,C_5=\alpha _0 = 1,\nonumber \\ \alpha _1(t)= & {} t,\quad \alpha _2(t) = t,\quad \alpha _4(t) =-t^2,\quad x=y=1, \end{aligned}$$

(3.6)

$$\begin{aligned} m_2= & {} p_2=2,\quad p_1=p_3=3,\quad p_4=4,\quad n_2=C_5=\alpha _0 = 1, \nonumber \\ \alpha _1(t)= & {} \cos (t),\quad \alpha _2(t) = \cos (2t),\quad \alpha _4(t) =\sin (2t),\quad x=y=1, \end{aligned}$$

(3.7)

$$\begin{aligned} m_2= & {} p_2=2,\quad p_1=p_3=3,\quad p_4=4,\quad C_5=n_2=\alpha _0 = 1, \nonumber \\ \alpha _1(t)= & {} t^2,\alpha _2(t) = t^3,\quad \alpha _4(t) =t^2,\quad x=y=1, \end{aligned}$$

(3.8)

in Eq. (3.5). By using the above selected parameters the property interaction between breather and dark soliton solution is shown in Figs. 1, 2 and 3 with graphs to various times. It shown a kind of interaction between two exponential waves, hyperbolic wave and trigonometric waves.

Fig. 1

Plots of the extended breather wave solutions to GSWW equation with distributed coefficients (3.6) ($\Sigma _2$) with $\alpha _1(t) = t,\alpha _2(t) = t,\alpha _4(t) =-t^2$; Density map in the (z, t)-plane; Along plane: $x=y=1$

Fig. 2

Plots of the extended breather wave solutions to GSWW equation with distributed coefficients (3.7) ($\Sigma _2$) with $\alpha _1(t) = \cos (t),\alpha _2(t) = \cos (2t),\alpha _4(t) =\sin (2t)$; Density map in the (z, t)-plane; Along plane: $x=y=1$

Fig. 3

Plots of the extended breather wave solutions to GSWW equation with distributed coefficients (3.8) ($\Sigma _2$) with $\alpha _1(t) = t^2,\alpha _2(t) = t^3,\alpha _4(t) =t^2$; Density map in the (z, t)-plane; Along plane: $x=y=1$

3.1.3 Solution III

$$\begin{aligned} m_l= & {} n_l=0,\ \ l=1,4,\ \ m_2=m_2,\ \ n_2=n_2,\ \ m_3=m_3,\ \nonumber \\ n_3= & {} n_3,\ \ \ p_i=p_i,\ \ \ i=1,2,3,4,\ \ \ q_5(t)=C_5,\nonumber \\ q_{{i}} \left( t \right)= & {} \int \!-{\frac{m_{{2}} \left( \alpha _{{2}} \left( t \right) {m_{{2}}}^{2}n_{{2}}+\alpha _{{4}} \left( t \right) p _{{i}} \right) }{\alpha _{{1}} \left( t \right) n_{{2}}}}\,\textrm{d}t,\ \ i=1,2, \nonumber \\ q_{{i}} \left( t \right)= & {} \int \!-{\frac{\alpha _{{4}} \left( t \right) m_{{2}}p_{{i}}}{\alpha _{{1}} \left( t \right) n_{{2}}}} \,\textrm{d}t,\ \ i=1,2, \end{aligned}$$

(3.9)

in which $m_2,n_2,m_3,n_3$ are free values and $p_l, l=1,2,3,4$ are parametric functions. It derives the rational breather solution in the following way

$$\begin{aligned} \Phi _3= & {} \frac{2\,\alpha _{{0}}m_{{2}}F_{{1}}}{{\textrm{e}^{p_{{1}}z+\int \!-{\frac{\alpha _{{4}} \left( t \right) m_{{2 }}p_{{1}}}{\alpha _{{1}} \left( t \right) n_{{2}}}}\,\textrm{d}t}}+F_{{1}} +\tanh \left( p_{{3}}z+\int \!-{\frac{\alpha _{{4}} \left( t \right) m _{{2}}p_{{3}}}{\alpha _{{1}} \left( t \right) n_{{2}}}}\,\textrm{d}t \right) +\tan \left( p_{{4}}z+\int \!-{\frac{\alpha _{{4}} \left( t \right) m_{{2}}p_{{4}}}{\alpha _{{1}} \left( t \right) n_{{2}}}} \,\textrm{d}t \right) +C_{{5}} },\nonumber \\ F_{{1}}= & {} {\textrm{e}^{m_{{2}}x+n_{{2}}y+p_{{2}}z+\int \!-{\frac{m_{{2}} \left( \alpha _{{2}} \left( t \right) {m_{{2}}}^{2}n_{{2}}+\alpha _{{4} } \left( t \right) p_{{2}} \right) }{\alpha _{{1}} \left( t \right) n_{ {2}}}}\,\textrm{d}t}}. \end{aligned}$$

(3.10)

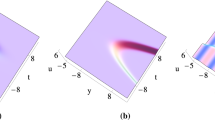
Figs. 4, 5 and 6, communicates interaction between breather and dark soliton solution with two wave solution when solution $\Phi _3$ are given with the below selected parameters

$$\begin{aligned} m_2= & {} 2,\quad n_2=1,\quad p_2=2, p_1=p_3=3,\quad p_4=4,\quad C_5=1,\quad \alpha _0 = 2,\nonumber \\ \alpha _1(t)= & {} t,\quad \alpha _2(t) = t,\quad \alpha _4(t) =-t^2,\quad x=y=1, \end{aligned}$$

(3.11)

$$\begin{aligned} m_2= & {} \alpha _0 = p_2=2,\quad p_1=p_3=3,\quad p_4=4,\quad \alpha _1(t) = \cos (t),\nonumber \\ \alpha _2(t)= & {} \cos (2t),\quad \alpha _4(t) =\sin (2t),\quad n_2=C_5=x=y=1, \end{aligned}$$

(3.12)

$$\begin{aligned} m_2= & {} 2,\quad n_2=1,\quad p_1=3,\quad p_2=2,\quad p_3=3,\quad p_4=4,\quad C_5=1,\nonumber \\{} & {} \alpha _0 = 2,\quad \alpha _1(t) = t^2,\quad \alpha _2(t) = t^3,\quad \alpha _4(t) =t^2,\quad x=y=1, \end{aligned}$$

(3.13)

in Eq. (3.10). By using the above amounts the property interaction between breather and dark soliton solution is presented in Figs. 4, 5 and 6 with plots with various times.

Fig. 4

Plots of the extended breather wave solutions to GSWW equation with distributed coefficients (3.11) ($\Sigma _3$) with $\alpha _1(t) = t,\alpha _2(t) = t,\alpha _4(t) =-t^2$; Density map in the (z, t)-plane; Along plane: $x=y=1$

Fig. 5

Plots of the extended breather wave solutions to GSWW equation with distributed coefficients (3.12) ($\Sigma _3$) with $\alpha _1(t) = \cos (t),\alpha _2(t) = \cos (2t),\alpha _4(t) =\sin (2t)$; Density map in the (z, t)-plane; Along plane: $x=y=1$

Fig. 6

Plots of the extended breather wave solutions to GSWW equation with distributed coefficients (3.13) ($\Sigma _3$) with $\alpha _1(t) = t^2,\alpha _2(t) = t^3,\alpha _4(t) =t^2$; Density map in the (z, t)-plane; Along plane: $x=y=1$

3.1.4 Solutions IV

$$\begin{aligned} m_l= & {} n_l=0,\ \ l=2,3,4,\ \ m_1=m_1,\ \ n_1=n_1,\ \ p_i=p_i,\nonumber \\ i= & {} 1,2,3,4,\ \ q_5(t)=C_5,\nonumber \\ q_{{1}} \left( t \right)= & {} \int \!-{\frac{m_{{1}} \left( \alpha _{{2}} \left( t \right) {m_{{1}}}^{2}n_{{1}}+\alpha _{{4}} \left( t \right) p _{{1}} \right) }{\alpha _{{1}} \left( t \right) n_{{1}}}}\,\textrm{d}t,\nonumber \\ q_{{i}} \left( t \right)= & {} \int \!-{\frac{\alpha _{{4}} \left( t \right) m_{{1}}p_{{i}}}{\alpha _{{1}} \left( t \right) n_{{1}}}} \,\textrm{d}t,\ \ i=2,3,4, \end{aligned}$$

(3.14)

in which $m_1,n_1$ are constants and $p_l, l=1,2,3,4$ the parametric functions. It derives the following rational breather solution

$$\begin{aligned} \Phi _4= & {} 2\,{\alpha _{{0}}m_{{2}}F_{{1}} \left( F_{{1}}+{\textrm{e}^{p_{{2}}z+\int \!-{\frac{\alpha _{{4}} \left( t \right) m_{{1}}p_{{2}}}{\alpha _{{1}} \left( t \right) n_{{1}}}}\,\textrm{d}t}}+\tanh \left( \omega _3(z,t)\right) +\tan \left( \omega _4(z,t) \right) +C_{{5}} \right) ^{- 1}},\nonumber \\ \omega _i(z,t)= & {} p_{{i}}z-\int \! {\frac{\alpha _{{4}} \left( t \right) m_{{1}}p_{{i}}}{\alpha _{{1}} \left( t \right) n_{{1}}}}\,\textrm{d}t,\ \ i=3,4,\nonumber \\ F_{{1}}= & {} {\textrm{e}^{m_{{2}}x+n_{{2}}y+p_{{1}}z+\int \!-{\frac{m_{{1}} \left( \alpha _{{2}} \left( t \right) {m_{{1}}}^{2}n_{{1}}+\alpha _{{4} } \left( t \right) p_{{1}} \right) }{\alpha _{{1}} \left( t \right) n_{ {1}}}}\,\textrm{d}t}}. \end{aligned}$$

(3.15)

3.1.5 Solutions V

$$\begin{aligned} m_l= & {} 0,\ \ l=2,3,4,\ \ m_1=m_1,\ \ n_l=n_l,\ \ l=1,2,3,4,\ \ \ q_1(t)=q_1(t),\ \nonumber \\ q_i(t)= & {} C_i,\ \ \ i=2,3,4,5,\nonumber \\ p_{{i}}= & {} -{\frac{n_{{i}} \left( \alpha _{{2}} \left( t \right) {m_{{1}} }^{3}+\alpha _{{1}} \left( t \right) {\frac{\textrm{d}}{{\textrm{d}}t}}q_{{1}} \left( t \right) \right) }{\alpha _{{4}} \left( t \right) m_{{1}}}},\ \ i=1,2,3,4, \end{aligned}$$

(3.16)

in which $n_l, l=1,2,3,4$ are constants. The exact solution is given as follows

$$\begin{aligned} {\Phi }_5= & {} \frac{2\,\alpha _{{0}}m_{{1}}F_{{1}}}{F_{{1}}+F_{{2}}+\tanh \left( \omega _3(y,z,t) \right) +\tan \left( \omega _4(y,z,t) \right) +C_{{5}}},\nonumber \\ \omega _{i}(y,z,t)= & {} n_{{i}}y-{\frac{n_{{i}} \left( \alpha _{{ 2}} \left( t \right) {m_{{1}}}^{3}+\alpha _{{1}} \left( t \right) { \frac{\textrm{d}}{{\textrm{d}}t}}q_{{1}} \left( t \right) \right) z}{\alpha _{{ 4}} \left( t \right) m_{{1}}}}+C_{{i}},\ \ i=3,4,\nonumber \\ F_{{1}}= & {} {{\textrm{e}}^{m_{{1}}x+n_{{1}}y-{\frac{n_{{1}} \left( \alpha _{{2} } \left( t \right) {m_{{1}}}^{3}+\alpha _{{1}} \left( t \right) {\frac{\textrm{d}}{{\textrm{d}}t}}q_{{1}} \left( t \right) \right) z}{\alpha _{{4}} \left( t \right) m_{{1}}}}+q_{{1}} \left( t \right) }},\nonumber \\ F_{{2}}= & {} {{\textrm{e}}^{n_{{2}}y-{\frac{n_{{2}} \left( \alpha _{{2}} \left( t \right) {m_{{1}}}^{3}+\alpha _{{1}} \left( t \right) {\frac{\textrm{d}}{ {\textrm{d}}t}}q_{{1}} \left( t \right) \right) z}{\alpha _{{4}} \left( t\right) m_{{1}}}}+C_{{2}}}}. \end{aligned}$$

(3.17)

Figs. 7, 8 and 9, express the behavior of interaction between breather and dark soliton solution with two wave solution to soltion $\Phi _5$ are given the following selected parameters

$$\begin{aligned} m_1= & {} n_2=\alpha _0 = 2,\quad n_1=n_3=3,\quad n_4=4,\quad C_i=1,\quad i=2,3,4,5,\ \nonumber \\ q_1(t)= & {} \alpha _1(t) =\alpha _2(t) = t,\quad \alpha _4(t) =2,\quad x=y=1,\end{aligned}$$

(3.18)

$$\begin{aligned} m_1= & {} 2,\quad n_1=3,\quad n_2=2,\quad n_3=3,\quad n_4=4,\quad C_i=1,\quad i=2,3,4,5, \nonumber \\ q_1(t)= & {} t,\quad \alpha _0 = 2,\nonumber \\ \alpha _1(t)= & {} \cos (t),\quad \alpha _2(t) = \sin (2t),\quad \alpha _4(t) =2+\cos (2t),\quad x=y=1,\end{aligned}$$

(3.19)

$$\begin{aligned} m_1= & {} n_2=\alpha _0 =\alpha _4(t) = 2,\quad n_1=n_3=3,\quad n_4=4,\quad q_1(t)=t, \nonumber \\ \alpha _1(t)= & {} t^2,\quad \alpha _2(t) = t^3,\quad C_i=x=y=1,\quad i=2,\ldots ,5, \end{aligned}$$

(3.20)

in Eq. (3.17). By utilizing the above parameters including trigonometric for time-variable functions as presented in Figs. 7, 8 and 9 with various times.

Fig. 7

Plots of the extended breather wave solutions to GSWW equation with distributed coefficients (3.18) ($\Sigma _5$) with $\alpha _0 = 2, \alpha _1(t) = t,\alpha _2(t) = t,\alpha _4(t) =2$; Density map in the (z, t)-plane; Along plane: $x=y=1$

Fig. 8

Plots of the extended breather wave solutions to GSWW equation with distributed coefficients (3.19) ($\Sigma _5$) with $\alpha _1(t) = \cos (t),\alpha _2(t) = \sin (2t),\alpha _4(t) =2+\cos (2t)$; Density map in the (z, t)-plane; Along plane: $x=y=1$

Fig. 9

Plots of the extended breather wave solutions to GSWW equation with distributed coefficients (3.20) ($\Sigma _5$) with $\alpha _0 = 2, \alpha _1(t) = t^2,\alpha _2(t) = t^3,\alpha _4(t) =2$; Density map in the (z, t)-plane; Along plane: $x=y=1$

3.1.6 Solutions VI

$$\begin{aligned}{} & {} m_l=0,\ \ l=3,4,\ \ m_1=m_1,\ \ m_2=m_2,\ \ n_l=n_l,\ \ l=1,2,3,4,\ \ \ q_1(t)=q_1(t),\nonumber \\{} & {} q_2(t)={\frac{q_{{1}} \left( t \right) m_{{2}}}{m_{{1}}}}+{\frac{m_{{2}}}{m _{{1}}}\int \!-{\frac{\alpha _{{2}} \left( t \right) m_{{1}}{m_{{2}}}^ {2}}{\alpha _{{1}} \left( t \right) }}+{\frac{\alpha _{{2}} \left( t \right) {m_{{1}}}^{3}}{\alpha _{{1}} \left( t \right) }}\,{\textrm{d}}t},\nonumber \\{} & {} q_i(t)=C_i,\ \ \ i=3,4,5, \nonumber \\{} & {} p_{{i}}=-{\frac{n_{{2}} \left( \alpha _{{2}} \left( t \right) {m_{{1}}}^{3}+ \alpha _{{1}} \left( t \right) {\frac{\textrm{d}}{{\textrm{d}}t}}q_{{1}} \left( t \right) \right) z}{\alpha _{{4}} \left( t\right) m_{{1}}}},\ \ i=1,2,\nonumber \\{} & {} p_{{i}}=-{\frac{n_{{i}} \left( \alpha _{{2}} \left( t \right) {m_{{1}}}^{3}+ \alpha _{{1}} \left( t \right) {\frac{\textrm{d}}{{\textrm{d}}t}}q_{{1}} \left( t \right) \right) z}{\alpha _{{4}} \left( t \right) m_{{1}}}},\ \ i=3,4, \end{aligned}$$

(3.21)

in which $m_1,m_2,n_l, l=1,2,3,4$ are parametric functions of t. The novel solution for the extended breather solution is given as follows

$$\begin{aligned}{} & {} \Phi _6=\frac{2\,\alpha _{{0}} \left( m_{{1}}F_{{1}}+m_{{2}}F_{{2}} \right) }{F_{{1}}+F_{{2}}+\tanh \left( \omega _3(y,z,t) \right) +\tan \left( \omega _4(y,z,t)\right) +C_{{5}}},\nonumber \\{} & {} \omega _i(y,z,t)=n_{{i}}y-{\frac{n_{{i}} \left( \alpha _{{ 2}} \left( t \right) {m_{{1}}}^{3}+\alpha _{{1}} \left( t \right) { \frac{\textrm{d}}{{\textrm{d}}t}}q_{{1}} \left( t \right) \right) z}{\alpha _{{ 4}} \left( t \right) m_{{1}}}}+C_{{i}},\ \ i=3,4\nonumber \\{} & {} F_{{1}}={{\textrm{e}}^{m_{{1}}x+n_{{2}}y-{\frac{n_{{2}} \left( \alpha _{{2} } \left( t \right) {m_{{1}}}^{3}+\alpha _{{1}} \left( t \right) {\frac{\textrm{d}}{{\textrm{d}}t}}q_{{1}} \left( t \right) \right) z}{\alpha _{{4}} \left( t \right) m_{{1}}}}+q_{{1}} \left( t \right) }},\nonumber \\{} & {} F_{{2}}={{\textrm{e}}^{m_{{2}}x+n_{{2}}y-{\frac{n_{{2}} \left( \alpha _{{2} } \left( t \right) {m_{{1}}}^{3}+\alpha _{{1}} \left( t \right) {\frac{\textrm{d}}{{\textrm{d}}t}}q_{{1}} \left( t \right) \right) z}{\alpha _{{4}} \left( t \right) m_{{1}}}}+{\frac{q_{{1}} \left( t \right) m_{{2}}}{ m_{{1}}}}+{\frac{m_{{2}}}{m_{{1}}}\int \!-{\frac{\alpha _{{2}} \left( t \right) m_{{1}}{m_{{2}}}^{2}}{\alpha _{{1}} \left( t \right) }}+{\frac{\alpha _{{2}} \left( t \right) {m_{{1}}}^{3}}{\alpha _{{1}} \left( t \right) }}\,\textrm{d}t}}}.\qquad \qquad \end{aligned}$$

(3.22)

3.1.7 Solutions VII

$$\begin{aligned} m_l= & {} 0,\ \ l=3,4,\ \ m_1=m_1,\ \ m_2=m_2,\ \ n_l=n_l,\ \ l=1,2,3,4,\nonumber \\ q_1(t)= & {} q_1(t),\ \ q_2(t)=q_2(t),\nonumber \\ q_i(t)= & {} C_i,\quad i=3,4,5,\quad p_{{i}}=-{\frac{n_{{i}} \left( \alpha _{{2}} \left( t \right) {m_{{2}}}^{3}+ \alpha _{{1}} \left( t \right) {\frac{\textrm{d}}{{\textrm{d}}t}}q_{{1}} \left( t \right) \right) }{\alpha _{{4}} \left( t \right) m_{{2}}}},\nonumber \\ i= & {} 1,2,3,4, \end{aligned}$$

(3.23)

in which $m_1,m_2,n_l, l=1,2,3,4$ are parametric functions of t. The novel solution for the extended breather solution is given as follows

$$\begin{aligned} \Phi _7= & {} \frac{2\,\alpha _{{0}} \left( m_{{2}}F_{{1}}+m_{{2}}F_{{2}} \right) }{F_{{1}}+F_{{2}}+\tanh \left( n_{{3}}y-{\frac{n_{{3}} \left( \alpha _{{ 2}} \left( t \right) {m_{{2}}}^{3}+\alpha _{{1}} \left( t \right) { \frac{\textrm{d}}{{\textrm{d}}t}}q_{{1}} \left( t \right) \right) z}{\alpha _{{ 4}} \left( t \right) m_{{2}}}}+C_{{3}} \right) +\tan \left( n_{{4}}y-{ \frac{n_{{4}} \left( \alpha _{{2}} \left( t \right) {m_{{2}}}^{3}+ \alpha _{{1}} \left( t \right) S_{{1}} \right) z}{\alpha _{{4}} \left( t \right) m_{{2}}}}+C_{{4}} \right) +C_{{5}}},\nonumber \\ F_{{1}}= & {} {{\textrm{e}}^{m_{{2}}x+n_{{1}}y-{\frac{n_{{1}} \left( \alpha _{{2} } \left( t \right) {m_{{2}}}^{3}+\alpha _{{1}} \left( t \right) {\frac{\textrm{d}}{{\textrm{d}}t}}q_{{1}} \left( t \right) \right) z}{\alpha _{{4}} \left( t \right) m_{{2}}}}+q_{{1}} \left( t \right) }},\ \ \ F_{{2}}={{\textrm{e}}^{m_{{2}}x+n_{{2}}y-{\frac{n_{{2}} \left( \alpha _{{2} } \left( t \right) {m_{{2}}}^{3}+\alpha _{{1}} \left( t \right) {\frac{\textrm{d}}{{\textrm{d}}t}}q_{{1}} \left( t \right) \right) z}{\alpha _{{4}} \left( t \right) m_{{2}}}}+q_{{2}} \left( t \right) }}. \end{aligned}$$

(3.24)

3.1.8 Solutions VIII

$$\begin{aligned} m_l= & {} 0,\ \ l=1,3,4,\ \ m_2=m_2,\ \ n_l=n_l,\ \ l=1,2,3,4,\ \ \nonumber \\ q_2(t)= & {} q_2(t),\ \ q_i(t)=C_i,\ \ \ i=1,3,4,5,\nonumber \\ p_{{i}}= & {} -{\frac{n_{{i}} \left( \alpha _{{2}} \left( t \right) {m_{{2}}}^{3}+ \alpha _{{1}} \left( t \right) {\frac{\textrm{d}}{{\textrm{d}}t}}q_{{2}} \left( t \right) \right) z}{\alpha _{{4}} \left( t \right) m_{{2}}}},\ \ i=1,2,3,4, \end{aligned}$$

(3.25)

in which $m_2,n_l, l=1,2,3,4$ parametric functions of t. The novel solution for the extended breather solution is given as follows

$$\begin{aligned} \Phi _{8}= & {} \frac{2\,\alpha _{{0}}m_{{2}}F_{{1}}}{F_{{2}}+F_{{1}}+\tanh \left( \omega _{3}(y,z,t) \right) +\tan \left( \omega _{4}(y,z,t) \right) +C_{{5}}},\nonumber \\ \omega _{i}(y,z,t)= & {} n_{{i}}y-{\frac{n_{{i}} \left( \alpha _{{ 2}} \left( t \right) {m_{{2}}}^{3}+\alpha _{{1}} \left( t \right) { \frac{\textrm{d}}{{\textrm{d}}t}}q_{{2}} \left( t \right) \right) z}{\alpha _{{ 4}} \left( t \right) m_{{2}}}}+C_{{i}},\ \ i=3,4,\nonumber \\ F_{{1}}= & {} {{\textrm{e}}^{m_{{2}}x+n_{{2}}y-{\frac{n_{{2}} \left( \alpha _{{2} } \left( t \right) {m_{{2}}}^{3}+\alpha _{{1}} \left( t \right) {\frac{\textrm{d}}{{\textrm{d}}t}}q_{{2}} \left( t \right) \right) z}{\alpha _{{4}} \left( t \right) m_{{2}}}}+q_{{2}} \left( t \right) }},\nonumber \\ F_{{2}}= & {} {{\textrm{e}}^{n_{{1}}y-{\frac{n_{{1}} \left( \alpha _{{2}} \left( t \right) {m_{{2}}}^{3}+\alpha _{{1}} \left( t \right) {\frac{\textrm{d}}{ {\textrm{d}}t}}q_{{2}} \left( t \right) \right) z}{\alpha _{{4}} \left( t \right) m_{{2}}}}+C_{{1}}}}. \end{aligned}$$

(3.26)

Figs. 10, 11 and 12, express the behavior of the obtained solution to $\Phi _8$ are given with the following selected parameters

$$\begin{aligned} m_2= & {} 2, n_1=1,n_2=3,n_3=2,n_4=3,C_i=1,\ \ i=1,3,4,5,\ \ q_2(t)=t,\ \ \alpha _0 = 2, \nonumber \\ \alpha _1(t)= & {} \frac{1}{1+t^2},\alpha _2(t) = \frac{4}{1+t^2},\alpha _4(t) =\frac{4t}{1+t^2}, x=y=1,\end{aligned}$$

(3.27)

$$\begin{aligned} m_2= & {} 2, n_1=1,n_2=3,n_3=2,n_4=3,C_i=1,\ \ i=1,3,4,5,\ \ q_2(t)=t,\ \ \alpha _0 = 2,\nonumber \\ \alpha _1(t)= & {} \cos (t),\alpha _2(t) = \sin (2t),\alpha _4(t) =2+\cos (2t), x=y=1,\end{aligned}$$

(3.28)

$$\begin{aligned} m_2= & {} 2, n_1=1,n_2=3,n_3=2,n_4=3,C_i=1,\ \ i=1,3,4,5,\ \ q_2(t)=t,\ \ \alpha _0 = 2,\nonumber \\ \alpha _1(t)= & {} \sinh (t),\alpha _2(t) = \sinh (2t),\alpha _4(t) =\cosh (2t), x=y=1, \end{aligned}$$

(3.29)

in Eq. (3.26). By employing the above amounts the the reached property are studied in Figs. 10, 11 and 12 with plots along with various times.

Fig. 10

Plots of the extended breather wave solutions to GSWW equation with distributed coefficients (3.27) ($\Sigma _8$) with $\alpha _1(t) = \frac{1}{1+t^2},\alpha _2(t) = \frac{4}{1+t^2},\alpha _4(t) =\frac{4t}{1+t^2}$; Density map in the (z, t)-plane; Along plane: $x=y=1$

Fig. 11

Plots of the extended breather wave solutions to GSWW equation with distributed coefficients (3.28) ($\Sigma _8$) with $\alpha _1(t) = \cos (t),\alpha _2(t) = \sin (2t),\alpha _4(t) =2+\cos (2t)$; Density map in the (z, t)-plane; Along plane: $x=y=1$

Fig. 12

Plots of the extended breather wave solutions to GSWW equation with distributed coefficients (3.29) ($\Sigma _8$) with $\alpha _1(t) =\sinh (t),\alpha _2(t) = \sinh (2t),\alpha _4(t) =\cosh (2t)$; Density map in the (z, t)-plane; Along plane: $x=y=1$

3.2 Rational Breather Wave

As last part of this section, the rational breather solutions and rational breather wave solutions are investigated.

$$\begin{aligned} h= & {} \cosh (a_1)+\lambda \cos (a_2)+\cosh (a_3)+q_4(t),\nonumber \\ a_s= & {} m_sx+n_sy+p_sz+q_s(t), \ \ \ s=1,2,3,4. \end{aligned}$$

(3.30)

Also, the amounts $m_s,n_s,p_s,q_s(t), (s=1,2,3,4)$ will be discovered. Inserting Eq. (3.30) into (2.14) get the coefficients powers of $\cosh (a_j), \cos (a_2),\cosh (a_3),j=1,2,3,4$ and $\sinh (a_j), \sin (a_2),\sinh (a_3),j=1,2,3,4$ to zero, conclude a system of equations to obtain the parameters $m_j,n_j,p_j,q_j(t), (j=1,2,3,4)$. Based on the (3.30) the solution $\Phi =2\alpha _0(\ln h)_{x}$ can be appeared as follow:

$$\begin{aligned} \Phi =2\,{\frac{\begin{aligned}\alpha _{{0}} \left( \sinh \left( m_{{1}}x+n_{{1}}y+p_{{1}}z +q_{{1}} \left( t \right) \right) m_{{1}}-\lambda \,\sin \left( m_{{2} }x+n_{{2}}y+p_{{2}}z\right. \right. \\ \left. \left. +q_{{2}} \left( t \right) \right) m_{{2}}+\sinh \left( m_{{3}}x+n_{{3}}y+p_{{3}}z+q_{{3}} \left( t \right) \right) m _{{3}} \right) \end{aligned}}{\begin{aligned}\cosh \left( m_{{1}}x+n_{{1}}y+p_{{1}}z+q_{{1}} \left( t \right) \right) +\lambda \,\cos \left( m_{{2}}x+n_{{2}}y+p_{ {2}}z+q_{{2}} \left( t \right) \right) \\ +\cosh \left( m_{{3}}x+n_{{3}} y+p_{{3}}z+q_{{3}} \left( t \right) \right) +q_{{4}} \left( t \right) \end{aligned}}}. \end{aligned}$$

3.2.1 First Solutions

$$\begin{aligned} m_j= & {} m_j,\ \ j=1,2,3,\ \ \ n_j=p_j=0,\ \ j=1,2,3,\ \ q_i(t)=q_i(t),\nonumber \\ i= & {} 1,2,3,4, \end{aligned}$$

(3.31)

in which $m_l, l=1,2$ are constants and $n_l(y), l=1,2,3,4$ parametric functions of y. The novel solution for the rational breather solution is given as follows

$$\begin{aligned} {\Phi }_1=2\,{\frac{\alpha _{{0}} \left( \sinh \left( m_{{1}}x+q_{{1}} \left( t \right) \right) m_{{1}}-\lambda \,\sin \left( m_{{2}}x+q_{{2}} \left( t \right) \right) m_{{2}}+\sinh \left( m_{{3}}x+q_{{3}} \left( t \right) \right) m_{{3}} \right) }{\cosh \left( m_{{1}}x+q_{ {1}} \left( t \right) \right) +\lambda \,\cos \left( m_{{2}}x+q_{{2}} \left( t \right) \right) +\cosh \left( m_{{3}}x+q_{{3}} \left( t \right) \right) +q_{{4}} \left( t \right) }}.\nonumber \\ \end{aligned}$$

(3.32)

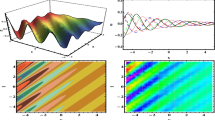
Figs. 13 and 14, express the behavior of interaction between a periodic wave and homoclinic wave solution with two wave solution to solution ${\Phi }_1$ are inserted with the following parameters

$$\begin{aligned} \lambda= & {} 2,m_1= 1, m_2=2, m_3=3, \alpha _0=2,q_1(t) = t,\nonumber \\ q_2(t)= & {} t^2+2t, q_3(t) = 2t, q_4(t) = t^2, \end{aligned}$$

(3.33)

$$\begin{aligned} \lambda= & {} 2,m_1= 1, m_2=2, m_3=3, \alpha _0=2,q_1(t) = \cos (t), \nonumber \\ q_2(t)= & {} \cos (2t), q_3(t) = \sin (2t), q_4(t) = \sin (2t). \end{aligned}$$

(3.34)

Some properties of interactions are presented in Figs. 13 and 14 with 3D, 2D, and density plots with different spaces.

Fig. 13

Plots of the rational breather wave solutions to GSWW equation with distributed coefficients (3.33) ($\Sigma _1$) with $q_1(t) = t, q_2(t) = t^2+2t, q_3(t) = 2t, q_4(t) = t^2$; Density map in the (x, t)-plane; Along plane: arbitrary (z, y)

Fig. 14

Plots of the rational breather wave solutions to GSWW equation with distributed coefficients (3.34) ($\Sigma _1$) with $q_1(t) = \cos (t), q_2(t) = \cos (2t), q_3(t) = \sin (2t), q_4(t) = \sin (2t)$; Density map in the (x, t)-plane; Along plane: arbitrary (z, y)

3.2.2 Second Solutions

$$\begin{aligned} m_j= & {} m_j,\ \ j=1,2,\ \ \ m_3=n_3=p_3=0,\ \ n_{{1}}=-{\frac{m_{{1}}n_{{2}}}{m_{{2}}}},\ \nonumber \\ q_{{1}} \left( t \right)= & {} \int {\frac{m_{{1}} \left( \alpha _{{ 2}} \left( t \right) {m_{{1}}}^{2}n_{{2}}+3\,\alpha _{{2}} \left( t \right) {m_{{2}}}^{2}n_{{2}}-2\,\alpha _{{4}} \left( t \right) p_{{2}} \right) }{2n_{{2}}\alpha _{{1}} \left( t \right) }}\,\textrm{d}t,\nonumber \\ q_{{2}} \left( t \right)= & {} \int \!{\frac{m_{{2}} \left( \alpha _{{2}} \left( t \right) {m_{{2}}}^{2}n_{{2}}-\alpha _{{4}} \left( t \right) p _{{2}} \right) }{n_{{2}}\alpha _{{1}} \left( t \right) }}\,\textrm{d}t,\ \ \ q_{{3}} \left( t \right) =C_3,\nonumber \\ q_{{4}} \left( t \right)= & {} C_4, \end{aligned}$$

(3.35)

where $m_l, m_2$ and $n_2$ are constants. The novel solution for the rational breather solution is given as follows

$$\begin{aligned} \Phi _2= & {} \frac{2\,\alpha _{{0}} \left( \sinh \left( F_{{1}} \right) m_{{1}}-{\frac{{m _{{1}}}^{2}}{m_{{2}}}\sin \left( m_{{2}}x+n_{{2}}y+p_{{2}}z+\int \!{ \frac{m_{{2}} \left( \alpha _{{2}} \left( t \right) {m_{{2}}}^{2}n_{{2 }}-\alpha _{{4}} \left( t \right) p_{{2}} \right) }{n_{{2}}\alpha _{{1}} \left( t \right) }}\,\textrm{d}t \right) } \right) }{\cosh \left( F_{{1}} \right) +{\frac{{m_{{1}}}^{2}}{{m_{{2}}}^{2}} \cos \left( m_{{2}}x+n_{{2}}y+p_{{2}}z+\int \!{\frac{m_{{2}} \left( \alpha _{{2}} \left( t \right) {m_{{2}}}^{2}n_{{2}}-\alpha _{{4}} \left( t \right) p_{{2}} \right) }{n_{{2}}\alpha _{{1}} \left( t \right) }}\,\textrm{d}t \right) }+\cosh \left( C_{{3}} \right) +C_{{4}} },\nonumber \\ F_{{1}}= & {} m_{{1}}x-{\frac{m_{{1}}n_{{2}}y}{m_{{2}}}}+1/2\,{\frac{m_{{1 }} \left( 3\,\alpha _{{2}} \left( t \right) {m_{{1}}}^{2}n_{{2}}+3\, \alpha _{{2}} \left( t \right) {m_{{2}}}^{2}n_{{2}}-2\,\alpha _{{4}} \left( t \right) p_{{2}} \right) z}{m_{{2}}\alpha _{{4}} \left( t \right) }}\nonumber \\{} & {} +\int \!1/2\,{\frac{m_{{1}} \left( \alpha _{{2}} \left( t \right) {m_{{1}}}^{2}n_{{2}}+3\,\alpha _{{2}} \left( t \right) {m_{{2} }}^{2}n_{{2}}-2\,\alpha _{{4}} \left( t \right) p_{{2}} \right) }{n_{{2 }}\alpha _{{1}} \left( t \right) }}\,\textrm{d}t. \end{aligned}$$

(3.36)

Figs. 15 and 16, express the behavior of interaction solutions with two wave solution to $\Phi _2$ are offered by the following parameters

$$\begin{aligned} m_1= & {} 1,\quad m_2= 2,\quad n_2=3,\quad p_2=4,\quad \alpha _0 = 2,\quad \alpha _1(t) = 1+t^2,\quad \alpha _2(t) = t,\nonumber \\ \alpha _4(t)= & {} 1+t^2,\quad C_3=1,\quad C_4=1,\quad z=y=1, \end{aligned}$$

(3.37)

$$\begin{aligned} m_1= & {} 1,\quad m_2= 2,\quad n_2=3,\quad p_2=4,\quad \alpha _0 = 2, \quad \alpha _1(t) = \exp (t),\nonumber \\ \alpha _2(t)= & {} \exp (t),\quad \alpha _4(t) =\exp (2t),\quad C_3=1,\quad C_4=1,\quad z=y=1. \end{aligned}$$

(3.38)

By considering the property interactions solution as presented in Figs. 15 and 16 with 3D, 2D, and density plots with various spaces.

Fig. 15

Plots of the rational breather wave solutions to GSWW equation with distributed coefficients (3.37) ($\Sigma _2$) with $\alpha _0 = 2, \ \alpha _1(t) = 1+t^2,\alpha _2(t) = t,\alpha _4(t) =1+t^2$; Density map in the (x, t)-plane; Along plane: $z=y=1$

Fig. 16

Plots of the rational breather wave solutions to GSWW equation with distributed coefficients (3.38) ($\Sigma _2$) with $\alpha _0 = 2, \ \alpha _1(t) = \exp (t),\alpha _2(t) = \exp (t),\alpha _4(t) =\exp (2t)$; Density map in the (x, t)-plane; Along plane: $z=y=1$

3.2.3 Third Solutions

$$\begin{aligned} m_s= & {} m_s,\ \ s=1,2,\ \ \ m_3=m_3,\ \ n_3=p_3=0,\ \ p_{{1}}={\frac{n_{{1}}p_{{2}}}{n_{{2}}}},\ \ q_{{1}} \left( t \right) =C_1,\nonumber \\ q_{{2}} \left( t \right)= & {} C_2,\nonumber \\ q_{{3}} \left( t \right)= & {} \int \!-{\frac{m_{{3}} \left( \alpha _{{2}} \left( t \right) {m_{{3}}} ^{2}n_{{2}}+\alpha _{{4}} \left( t \right) p_{{2}} \right) }{n_{{2}} \alpha _{{1}} \left( t \right) }}\,\textrm{d}t,\ \ \ q_{{4}} \left( t \right) =C_4, \end{aligned}$$

(3.39)

where $m_l, m_2$ and $n_2$ free parameters. The novel solution for the rational breather solution is given as follows

$$\begin{aligned} \Phi _3=\frac{2\,\alpha _{{0}}\sinh \left( m_{{3}}x+\int \!-{\frac{m_{{3}} \left( \alpha _{{2}} \left( t \right) {m_{{3}}}^{2}n_{{2}}+\alpha _{{4}} \left( t \right) p_{{2}} \right) }{n_{{2}}\alpha _{{1}} \left( t \right) }}\,\textrm{d}t \right) m_{{3}} }{\cosh \left( n_{{1}}y+{\frac{n_{{1}}p_{{2}}z}{n_{{2}}}}+C_{{1}} \right) +\lambda \,\cos \left( n_{{2}}y+p_{{2}}z+C_{{2}} \right) + \cosh \left( m_{{3}}x+\int \!-{\frac{m_{{3}} \left( \alpha _{{2}} \left( t \right) {m_{{3}}}^{2}n_{{2}}+\alpha _{{4}} \left( t \right) p _{{2}} \right) }{n_{{2}}\alpha _{{1}} \left( t \right) }}\,\textrm{d}t \right) +C_{{4}} }.\nonumber \\ \end{aligned}$$

(3.40)

Figs. 17 and 18, show the analysis of treatment of interaction between a periodic wave and homoclinic wave solution with two wave solution where graphs of ${\Phi }_3$ are given with the below selected parameters

$$\begin{aligned} \lambda= & {} 1,\quad n_1= 1, \quad n_2= 2,\quad m_3=3,\quad p_2=4,\quad \alpha _0 = 2, \quad \alpha _1(t) = 1+t^2,\nonumber \\ \alpha _2(t)= & {} t,\quad \alpha _4(t) =1+t^2,\quad C_1=1,\quad C_2=1,\quad C_4=1,\quad x=y=1, \end{aligned}$$

(3.41)

$$\begin{aligned} \lambda= & {} 1,\quad n_1= 1,\quad n_2= 2,\quad m_3=3,\quad p_2=4,\quad \alpha _0 = 2, \quad \ \alpha _1(t) = \cos (t),\nonumber \\ \alpha _2(t)= & {} \cos (t),\quad \alpha _4(t) =\sin (2t),\quad C_1=C_2=C_4=1,\quad x=y=1, \end{aligned}$$

(3.42)

in Eq. (3.40). By employing the above values the characteristic interaction between a periodic wave and homoclinic wave solution are expressed in Figs. 17 and 18 with 3D, 2D, and density plots with different spaces. It offers a type of interaction solutions between hyperbolic waves and trigonometric wave.

Fig. 17

Plots of the rational breather wave solutions to GSWW equation with distributed coefficients (3.41) ($\Sigma _3$) with $\alpha _0 = 2, \ \alpha _1(t) = 1+t^2,\alpha _2(t) = t,\alpha _4(t) =1+t^2$; Density map in the (y, t)-plane; Along plane: $x=y=1$

Fig. 18

Plots of the rational breather wave solutions to GSWW equation with distributed coefficients (3.42) ($\Sigma _3$) with $\alpha _0 = 2, \ \alpha _1(t) = \cos (t),\alpha _2(t) = \cos (t),\alpha _4(t) =\sin (2t)$; Density map in the (y, t)-plane; Along plane: $x=y=1$

4 Results and Discussion

In this section, the obtained solutions of the GSWW equation in (3+1)-dimensional with variable coefficients are illustrated by numerical simulation and physical interpretation. In order to describe the outcomes of the proposed technique, graphs of the surface soliton solutions to the governing equation have been displayed. The graphs in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 and 18 have been plotted for various values of the parameter $\alpha _i, i=1..4$ and the other parameters have fixed values. Thus, we have observed and discussed the effects of each parameter $\alpha _i, i=1..4$ on the stability of the model for the matter dominated era. Perhaps, the used value of one parameter by fixing the values of the other parameters is able to make our model stable. However, by taking suitable values of all the parameters as has been discussed above, the existence of the model can be achieved easily for the matter dominated era.

5 Conclusion

In this work, mainly the (2+1)-dimensional GSWW equation with variable coefficients was investigated. Also, the Hirota bilinear forms, extended breather solutions and rational breather wave solutions respectively were derived. This work was in order to obtain the exact solutions of the GSWW equation, the breather wave solutions and extended breather-wave solutions were studied. Using the Hirota bilinear method, two distinct types of solutions such as combination of exponential and hyperbolic, and also combination of trigonometric, and hyperbolic function solutions were achieved with unknown parameters. By demonstrating that the bilinear approach was highly efficient and suited for discovering the exact soliton solutions of nonlinear models. There were many new types of breather wave solutions that were discovered including the plenty of solutions as breather and extended breather wave solutions. Many other nonlinear evolution equations including coupled ones, were solved using this technique. From the results, we understood the Hirota direct method was really prompt and effective to obtain the exact solutions for some NLPDEs. Along with the scientific derivation for the analytical findings, the outcomes were graphically displayed to help identifying the dynamical aspects of solutions. Theoretical insights reported here may be helpful to future experimental studies. This proposed approach was extended to solve a wide variety of numerous nonlinear evolution equations that arise in mathematical physics since it is noteworthy and efficient. By Maple was shown in which the obtained results were correct. In the future, this research might be expanded to include the stochastic GSWW equation with variable coefficients.