Doubly periodic solutions and breathers of the Hirota equation: recurrence, cascading mechanism and spectral analysis

Abstract

The Hirota equation is an extension of the nonlinear Schrödinger equation by incorporating third-order dispersion. Doubly periodic solutions for the Hirota equation are established in terms of theta and elliptic functions. Cubic dispersion preserves numerical robustness, as slightly disturbed exact solutions as initial states still evolve to the analytical configurations. In contrast with the nonlinear Schrödinger case, the wavenumber of the envelope must satisfy an algebraic equation related to the magnitude of the quadratic / cubic terms and the period of the wave patterns. The long wave limits of these doubly periodic patterns will yield the widely studied Kuznetsov-Ma and Akhmediev breathers. A cascading mechanism for the Hirota equation is studied, which will elucidate the first formation of breather modes. Higher harmonics exponentially small initially will grow at a larger rate than the fundamental mode. Eventually the high frequency modes reach roughly the same magnitude at one moment in time (or spatial location), signifying the first occurrence of breather. Breathers then decay and modulation instability emerges again for sufficiently small amplitude. The cycle is repeated and constitutes a manifestation of the Fermi-Pasta-Ulam-Tsingou recurrence. These analytical doubly periodic solutions will permit the prediction of the period of recurrence. These results can be applied in hydrodynamic and optical contexts where third or higher-order dispersion is present.

1 Introduction

Instability, periodic arrays of modes and recurrence phenomenon are critical elements of many nonlinear dynamical systems. The nonlinear Schrödinger equation has been widely studied in many physical applications, e.g., fluid mechanics and optics [1, 2]. This equation describes the evolution of wave packets under the competition of quadratic dispersion and cubic nonlinearity. Analytically, many families of exact solutions have been established. A nonsingular rational solution was derived in the 1980s and has been widely adopted as a simple model of a rogue wave [3]. Review article on deterministic and probabilistic approaches of describing rogue wave has been written [4]. Extensions to vector and multi-dimensional systems have been made [5]. A unified approach to doubly periodic solutions, modulation instability and recurrence has been attempted [6].

Modulation instability of plane waves and the subsequent dynamics have attracted intensive attention. Here we focus on the formation of breathers and recurrence scenarios under periodic boundary conditions. Typically, these breathers decay after attaining maximum displacement. On reaching sufficiently small amplitude, modulation instability is triggered again, leading to the occurrence of breathers for the second time [7]. This cycle is repeated, and is taken as one manifestation of the Fermi-Pasta-Ulam-Tsingou recurrence (FPUT) in classical physics. A review on the progress made in the first fifty years since the 1950s had been written [8]. Discrete systems constitute an important direction of research for FPUT [9]. Indeed FPUT provides a fertile field of exploration for nonlinear dynamics/chaos [10], as well as diverse range of topics like ergodic behavior, oscillator chains and integrable equations [11]. Using a weakly anharmonic atomic chain model as example, the connection among the wavenumber, periodic orbit and breather is shown to be extremely intriguing [12]. Our objective is to extend this type of FPUT analysis to higher-order members of the Schrödinger family of evolution equations.

The instability of plane waves in free surface flows in hydrodynamics was first recognized in the 1960s, and is commonly known as the Benjamin-Feir (or modulation) instability in modern terminology [1]. Computational and experimental attempts produce evidence of one or the first few cycle(s) of FPUT [13]. In optics, similar FPUT patterns and the connection with the maximum compression distance in the context of optical fibers have been highlighted experimentally [14, 15]. As ‘time’ (t) and space (‘x’) take up different roles in the application of the nonlinear Schrödinger equation to fluid mechanics and optics, we shall adopt the terminology of ‘propagation’ variable (the one with the first derivative) and ‘transverse’ variable in subsequent discussions.

We shall be conducting the numerical computations under periodic boundary conditions. With instability and growth, we expect arrays of localized modes in the transverse coordinate of the nonlinear Schrödinger equation, i.e., occurrence of breathers. For FPUT patterns, we anticipate that these breathers will repeat in the direction of the propagation variable. Hence we require a ‘doubly periodic’ analytical solution to properly describe such FPUT dynamics. Such doubly periodic solutions have indeed been derived analytically in the literature. One route is based on the special relation between real and imaginary parts of the exact solutions [16,17,18]. Alternatively, sum and difference identities are employed to reduce bilinear derivatives of theta functions to products of theta functions themselves [19, 20]. This latter approach is adopted here, as bilinear forms are typically available for many ‘integrable’ equations.

Theta functions are Fourier series with exponentially decaying coefficients. Elliptic functions are meromorphic functions where the singularities in the complex plane are only simple and double poles [21, 22]. In terms of mathematical analysis, they possess a period in the real direction and another purely imaginary period. They will be utilized here to provide a description of doubly periodic profiles and thus FPUT patterns. Analytically, Jacobi elliptic functions of the propagation and the transverse variables are combined algebraically, leading to rational expressions of exact solutions periodic in both space and time (and hence a doubly periodic pattern physically).

Another class of modes to be studied here is the breathers, which are periodic in one direction but localized in the other. Commonly adopted names in the literature are the Akhmediev / Kuznetsov-Ma breathers for those periodic in the transverse / propagation variable, respectively. The connection between doubly periodic patterns and breathers will be scrutinized. We must emphasize that the word ‘breather’ will be used loosely here, representing a class of modes localized in one variable and periodic in the other. In subsequent sections, we establish analytical formulas for one class of breathers, but many such families of modes will exist.

The primary focus here will be the doubly periodic solutions, FPUT and breathers of one ‘integrable’ third-order envelope system, known as the Hirota equation and a special case, the complex modified Korteweg-de Vries equation. The ‘multi-soliton’ was first solved explicitly by Hirota himself in the 1970s [23]. Theoretical perspectives, such the Painlevé properties, are revealed later [24]. Rogue wave modes are derived [25, 26]. The classes of initial conditions likely to generate breathers are investigated. Connections with modulation instability are explained [27].

In this paper, we derive new doubly periodic solutions of the Hirota equation. Numerical robustness is demonstrated. The spectra are studied both analytically and computationally, which provide the motivation for introducing the ‘cascading mechanism’. This mechanism will elucidate the dynamics leading to the first formation of breathers. These breathers recur periodically and constitute a manifestation of FPUT. The analytic solutions can predict the period of recurrence of FPUT patterns.

Before discussing the main results, a few remarks on recent developments on solitons and localized modes are in order. Soliton interactions can be studied by symbolic computations and the knowledge gained may be used to enhance image processing in optics [28]. Solutions of coupled Schrödinger equations expressed via Jacobi elliptic functions can describe spatial, phase-modulated photovoltaic solitons [29]. The widely studied concept of PT-symmetric potential can describe tapered graded-index waveguide [30]. Similarly, current topics like neural networks and deep learning can be utilized for vector solitons [31]. Moreover, fractional Schrödinger equations can describe symmetric and asymmetric solitons [32].

The sequence of presentation of topics can now be described. We first review the derivation of one known doubly periodic solution of the Hirota equation using theta functions (Sect. 2). Next, we establish another doubly periodic solution (Sect. 3). For both cases, FPUT is demonstrated computationally. A breather mode, which is periodic in one direction and localized in the other, is derived through the Darboux transformation (Sect. 4). We establish solutions where the envelopes can move instead of being stationary. We also study the wavenumber spectrum and cascading mechanism (Sects. 4, 5). The growth of the higher-order harmonics can elucidate the formation of breathers. The evolution of the wave profile from random initial conditions is also considered (Sect. 6). Finally, conclusions are drawn (Sect. 7).

2 First family of doubly periodic solutions

2.1 Analytic formulation

The Hirota equation for a slowly varying, complex valued envelope A is

$$ iA_{t} + \, \lambda \left( {A_{xx} + \, 2A^{2} A^{*}} \right) \, + i\sigma \left( {A_{xxx} + \, 6AA^{*}A_{x} } \right) \, = \, 0. $$

(1)

The parameters λ, σ are real. The variables t, x are slow time / distance, group velocity coordinate / retarded time in fluid mechanics / optics, respectively. The choice of σ = 0 / λ = 0 will give the nonlinear Schrödinger / complex modified Korteweg-de Vries equation, respectively. A doubly periodic solution for Eq. (1) with λ = 1 is established earlier in the literature as [20]

$$ \begin{gathered} A = \frac{{{\upalpha }\theta_{2} \left( {0,{\uptau }} \right)\theta_{4} \left( {0,{\uptau }} \right)\theta_{3} \left( {0,{\uptau }_{1} } \right)}}{{\theta_{2}^{4} \left( {0,{\uptau }_{1} } \right)}} \hfill \\ \quad \times \left[ {\frac{{\theta_{3} \left( {{\upomega }t,{\uptau }_{1} } \right)\theta_{2} \left( {{\upalpha }x,{\uptau }} \right) + i\theta_{1} \left( {{\upomega }t,{\uptau }_{1} } \right)\theta_{4} \left( {{\upalpha }x,{\uptau }} \right)}}{{\theta_{4} \left( {{\upomega }t,{\uptau }_{1} } \right)\theta_{4} \left( {{\upalpha }x,{\uptau }} \right) - \theta_{2} \left( {{\upomega }t,{\uptau }_{1} } \right)\theta_{2} \left( {{\upalpha }x,{\uptau }} \right)}}} \right] \hfill \\ \quad \times \exp \left[ {i\left( {px - \Omega t} \right)} \right], \hfill \\ \end{gathered} $$

(2)

$$ p^{2} - \frac{2p}{{3{\upsigma }}} + \frac{{2{\upalpha }^{2} }}{3}\left[ {\theta_{2}^{4} \left( {0,{\uptau }} \right) - \theta_{4}^{4} \left( {0,{\uptau }} \right)} \right] = 0, $$

(3a)

$$ {\upomega } = \frac{{2{\upalpha }^{2} \left( {1 - 3{\upsigma }p} \right)\theta_{2}^{2} \left( {0,{\uptau }} \right)\theta_{4}^{2} \left( {0,{\uptau }} \right)}}{{\theta_{4}^{2} \left( {0,{\uptau }_{1} } \right)}}, $$

(3b)

$$ \Omega = \left( {1 - 3{\upsigma }p} \right){\upalpha }^{2} \left[ {\theta_{2}^{4} \left( {0,{\uptau }} \right) - \theta_{4}^{4} \left( {0,{\uptau }} \right)} \right] + p^{2} - {\upsigma }p^{3} , $$

(3c)

$$ \frac{{\theta_{4}^{4} \left( {0,{\uptau }} \right) - \theta_{2}^{4} \left( {0,{\uptau }} \right)}}{{2\theta_{2}^{2} \left( {0,{\uptau }} \right)\theta_{4}^{2} \left( {0,{\uptau }} \right)}} = \frac{{\theta_{2}^{2} \left( {0,{\uptau }_{1} } \right)}}{{\theta_{4}^{2} \left( {0,{\uptau }_{1} } \right)}}, $$

(3d)

where p/ω, Ω are the wavenumber/angular frequencies respectively and θ_n, n = 1, 2, 3, 4 are the theta functions (Appendix A). Mathematically there are two free parameters (degrees of freedom) for solutions Eqs. (2, 3). For convenience, we shall take α (wavenumber in the x direction) and τ (parameter governing the period of the theta function) as these two degrees of freedom. A corresponding representation in terms of the Jacobi elliptic functions is

$$ \begin{gathered} A = \frac{r}{\sqrt 2 }\left[ {\frac{{{\text{dn}}(st,k_{1} ){\text{cn}}(rx,k)/\,(\sqrt {1 + k_{1} } ) + i\,\sqrt {k_{1} } \,{\text{sn}}(st,k_{1} )}}{{1 - \sqrt {k_{1} } {\text{cn}}(st,k_{1} ){\text{cn}}(rx,k)/(\sqrt {1 + k_{1} } )}}} \right] \hfill \\ \times \exp ( - i\,\Omega \,t). \hfill \\ \end{gathered} $$

We must emphasize that τ and τ₁, parameters of the theta functions for x and t, are distinct. From a theoretical viewpoint, their relation constitutes a crucial, defining feature for such families of doubly periodic solutions. Physically, the wavelength of the breather pattern can be used to predict the period of the FPUT recurrence. An alternative representation can be obtained by the Jacobi elliptic functions. This scheme of describing the solutions will be illustrated when we derive the second family of exact solutions in the next section.

It is instructive to outline the method of derivation via the bilinear operator. On separating the wave envelope and the auxiliary dependent variables (g and f in Eq. 4a, g complex, f real), we get

$$ A = \exp \left[ {i\left( {p\,x - \Omega {\kern 1pt} \,t} \right)} \right]{g \mathord{\left/ {\vphantom {g f}} \right. \kern-\nulldelimiterspace} f} ,$$

(4a)

$$ \left( {D_{x}^{2} - C} \right)f \cdot f = 2gg^{*}, $$

(4b)

$$ \left\{ \begin{gathered} iD_{t} + i{\upsigma }D_{x}^{3} + \left( {{\uplambda } - 3{\upsigma }p} \right)D_{x}^{2} \hfill \\ + i\left[ {2{\uplambda }p - 3{\upsigma }\left( {p^{2} + C} \right)} \right]D_{x} - C_{0} \hfill \\ \end{gathered} \right\}g \cdot f = 0, $$

(4c)

$$ C_{0} = {\uplambda }\left( {p^{2} + C} \right) - {\upsigma }\left( {p^{3} + 3pC} \right) - \Omega .$$

(4d)

The bilinear operator is defined by

$$ D_{x}^{m} D_{t}^{n} g \cdot f = \left( {\frac{\partial }{\partial x} - \frac{\partial }{{\partial x^{\prime}}}} \right)^{m} \left( {\frac{\partial }{\partial t} - \frac{\partial }{{\partial t^{\prime}}}} \right)^{n} \left. {g\left( {x,t} \right)f\left( {x^{\prime},t^{\prime}} \right)} \right|_{{x = x^{\prime},t = t^{\prime}}} $$

and has been employed extensively in the literature of nonlinear waves [23]. The constants C, C₀ must be determined as part of the solution.

The scheme of solving the bilinear equations involving theta functions has been explained in our earlier works [19, 20], and hence the descriptions here will be brief. Theta functions have a huge variety of identities involving sum and difference of the argument variables (Appendix A). These identities are ideally suited for the bilinear operator, as conventional differentiation with the auxiliary variable will effectively convert bilinear derivatives of theta functions back into products of theta functions themselves. We outline illustrative cases of such calculations in Appendix A.

2.2 Structural robustness

The doubly periodic wave profile with typical values of input parameters is first illustrated (Fig. 1a). An illuminating perspective is to trace the time movements of the real and imaginary parts of the wave envelope A for one particular location (x = 0) (Fig. 1b). The ‘blue dot’ denotes the starting point, i.e., t = 0. The coordinate of this point also exhibits the amplitude of the doubly periodic solution. The arrows show the direction of increasing time. The periodic nature of the motion is clearly evident as the path traces itself indefinitely. However, for such solutions to be readily observable in practice, we need to test the structural robustness by performing a numerical simulation with slightly perturbed initial conditions. A random noise of 2% to 5% in amplitude is imposed. The computations are conducted with a split-step scheme, solving the linear part in Fourier space and the nonlinear part with a fourth-order Runge–Kutta method. The simulations result in doubly periodic patterns too (Fig. 1c). In terms of the wave profiles, the agreement between the wave profiles from analytical and numerical approaches is excellent (Fig. 1d, 1e). For a larger value of theta function parameter q (0 < q < 1, q = exp(πiτ), Eq. A5), the agreement is even better (Fig. 2). Physically, the wave profiles are manifestation of FPUT, as a suitably chosen initial condition evolves into a pattern periodic in time.

Fig. 1

a Doubly periodic solution; b Trajectories in the complex plane of doubly periodic solution at x = 0; c Numerical simulations; d-e Comparison between doubly periodic solution and numerical simulations along x and t directions. Parameters chosen are λ = 1, σ = 0.05, α = 1, q = 0.01 (Eq. A5)

Fig. 2

a Doubly periodic solution; b Numerical simulations; c Comparison between doubly periodic solution and numerical simulations along x direction at t = 4. Parameters chosen are λ = 1, σ = 0.05, α = 1, q = 0.04 (Eq. A5)

2.3 Recurrence with plane wave as initial condition

Before further comparisons between the numerically obtained FPUT patterns and the analytic doubly periodic solutions (Eqs. 2, 3), it is instructive to look at modulation instability first. A background plane wave for Eq. 1 is given by

$$ A_{0} \left( {x,t} \right) = {\upchi }\exp \left[ {i\left( {{\upgamma }_{1} x + {\upgamma }_{2} t} \right)} \right], $$

where χ is the amplitude, γ₁ denotes wavenumber, and the angular frequency is

$$ \gamma_{2} = - \gamma_{1}^{2} \lambda + \gamma_{1}^{3} \sigma + 2\lambda \chi^{2} - 6\gamma_{1} \chi^{2}. $$

A perturbed state is represented as

$$ A = \, [\chi \, + A^{\prime}\left( {x,t} \right)\left] {\text{ exp}} \right[i\left( {\gamma_{1} x + \, \gamma_{2} t} \right)], $$

where $A^{\prime}$ denotes the perturbation. Further modal separation

$$ A^{\prime} = A_{ + } {\text{exp}}\left[ {i\left( {\kappa x + \, \xi t} \right)} \right] \, + A_{-} {\text{exp}}\left[ {{-}i\left( {\kappa x + \, \xi t} \right)} \right] $$

is now taken. Modulation instability occurs whenever ξ has a nonzero imaginary part,

$$ G = \left| {{\text{Im}} \left( {\upxi } \right)} \right| = \left| {\upkappa } \right|\sqrt {\left( {{\uplambda } - 3{\upgamma }_{1} \sigma } \right)^{2} \left( {4{\upchi }^{2} - {\upkappa }^{2} } \right)} > 0 .$$

We now conduct a simulation where the perturbation is a cosine function

$$ A = A_{0} \left( {x,t} \right) \, + \, \mu \, \text{cos}\left( {\rho x} \right) \, , $$

(5)

where μ denotes the perturbation intensity and ρ represents the perturbation wavenumber. Starting with an arbitrary value of say ρ = 1, we obtain a breather mode first. The breather decays and modulation instability resumes at smaller amplitude. The breather emerges again, and thus the system exhibits FPUT (Fig. 3a).

Fig. 3

a Numerical simulations with λ = 1, σ = 0.05, χ = 0.65, γ₁ = 0, μ = 0.05, ρ = 1; b Comparison between numerical simulations and doubly periodic solution with parameters λ = 1, σ = 0.05, α = 1, q = 0.01 (Fig. 1a) at the peaks

As an attempt to model this with our analytic doubly periodic solution, we take parameter values to mimic the wave period and obtain reasonable fit (Fig. 3b, for λ = 1, σ = 0.05, χ = 0.65, γ₁ = 0, μ = 0.05, ρ = 1, q = 0.01). There is a phase shift between the peaks of the first and second breathers, numerically less than π/2 (or less than a quarter of a wavelength). This feature is different from the nonlinear Schrödinger case, where either a zero or π/2 phase shift occurs [6, 7].

3 Second family of doubly periodic solutions

3.1 Analytic formulation

A second family of exact solutions can be established by using a different choice of theta functions. The motivation arises from similar solutions for the nonlinear Schrödinger case. The calculations are again based on the simplification of bilinear derivatives of theta functions using identities listed in Appendix A [19, 20] and monographs of the subject [21, 22]. More precisely, an exact solution for the envelope A can be derived using different choices for the auxiliary functions f and g in Eq. 4:

$$ \begin{gathered} A = \frac{{A_{0} \left[ {\theta_{2} \left( {{\upomega }t,{\uptau }_{1} } \right)\theta_{2} \left( {{\upalpha }x,{\uptau }} \right) + i\theta_{1} \left( {{\upomega }t,{\uptau }_{1} } \right)\theta_{3} \left( {{\upalpha }x,{\uptau }} \right)} \right]}}{{\left[ {\theta_{3} \left( {{\upomega }t,{\uptau }_{1} } \right)\theta_{2} \left( {{\upalpha }x,{\uptau }} \right) - \theta_{4} \left( {{\upomega }t,{\uptau }_{1} } \right)\theta_{3} \left( {{\upalpha }x,{\uptau }} \right)} \right]}} \hfill \\ \times \exp \left[ {i\left( {px - \Omega t} \right)} \right], \hfill \\ \end{gathered} $$

(6)

with angular frequencies of the wave envelope (Ω)/wave profile (ω) given by

$$ \Omega = p^{2} \left( {{\uplambda } - {\upsigma }p} \right) - {\upalpha }^{2} \left( {{\uplambda } - 3{\upsigma }p} \right)\left[ {\theta_{2}^{4} \left( {0,\,{\uptau }} \right) + \theta_{3}^{4} \left( {0,\,{\uptau }} \right)} \right], $$

(7)

$$ {\upomega } = \frac{{{\upalpha }^{2} \left( {{\uplambda } - 3{\upsigma }p} \right)\left[ {\theta_{2}^{4} \left( {0,\,{\uptau }} \right) + \theta_{3}^{4} \left( {0,\,{\uptau }} \right)} \right]}}{{\theta_{3}^{2} \left( {0,\,{\uptau }_{1} } \right)}}. $$

(8)

The relation between the parameters of the two theta functions (τ, τ₁) is given by

$$ \frac{{\theta_{4}^{2} \left( {0,\,{\uptau }_{1} } \right)}}{{\theta_{3}^{2} \left( {0,\,{\uptau }_{1} } \right)}} = \frac{{2\theta_{2}^{2} \left( {0,\,{\uptau }} \right)\theta_{3}^{2} \left( {0,\,{\uptau }} \right)}}{{\theta_{2}^{4} \left( {0,\,{\uptau }} \right) + \theta_{3}^{4} \left( {0,\,{\uptau }} \right)}}, $$

(9)

and the amplitude A₀ is expressed as

$$ A_{0}^{2} = \frac{{{\upalpha }^{2} \left[ {\theta_{2}^{4} \left( {0,\,{\uptau }} \right) + \theta_{3}^{4} \left( {0,\,{\uptau }} \right)} \right]\theta_{2}^{2} \left( {0,\,{\uptau }_{1} } \right)}}{{2\theta_{3}^{2} \left( {0,\,{\uptau }_{1} } \right)}}. $$

(10)

The wavenumber of the envelope, p, is found as the roots of a quadratic equation,

$$ 3\sigma p^{2} - 2\lambda p - 2\sigma \alpha^{2} \left[ {\theta_{2}^{4} \left( {0,\tau } \right) + \theta_{3}^{4} \left( {0,\tau } \right)} \right] = 0 $$

(11)

and this generalizes the corresponding solutions for the nonlinear Schrödinger case (σ = 0). Equation 11 will degenerate to p = 0 for σ = 0, consistent with the known solution of stationary envelope packet. This governing equation for the wavenumber p will depend on the relative weight of the quadratic and cubic terms (λ, σ) as well as the period of the breather pattern (τ).

An alternative formulation, more convenient for computer algebra but perhaps less symmetric in terms mathematical appearance, is expressed in terms of the Jacobi elliptic functions:

$$ \begin{gathered} A = \frac{{rk_{1} }}{{\sqrt {1 + k_{1} } }} \hfill \\ \times \left[ {\frac{{{\text{cn}}(st,k_{1} )\,{\text{cn}}(rx,k) + i\sqrt {1 + k_{1} } \,{\text{sn}}(st,k_{1} )\,{\text{dn}}(rx,k)}}{{\sqrt {1 + k_{1} } \,{\text{dn}}(rx,k) - {\text{dn}}(st,k_{1} )\,{\text{cn}}(rx,k)}}} \right] \hfill \\ \times \exp \left[ {i\left( {px - \Omega t} \right)} \right]\,, \hfill \\ \end{gathered} $$

(12)

with the corresponding frequencies / amplitude, i.e., Ω, s / A₀ given by

$$ \Omega = p^{2} \left( {{\uplambda } - {\upsigma }p} \right) - \left( {{\uplambda } - 3{\upsigma }p} \right)\left( {1 + k^{2} } \right)r^{2} , $$

(13)

$$ s = \, \left( {\lambda \, {-} \, 3\sigma p} \right)\left( {1 \, + k^{2} } \right)r^{2}, $$

(14)

$$ A_{0}^{2} = \frac{{\left( {1 + k^{2} } \right)k_{1} r^{2} }}{2}. $$

(15)

Arguments of the theta functions and elliptic functions are different mathematically by a scale factor of (θ₃(0, τ))² and hence different symbols of r, s are used. The relationship between the moduli of the two elliptic functions, k, k₁, provides a more illuminating perspective than the counterpart for theta functions, i.e.,

$$ \sqrt {1 - k_{1}^{2} } = \frac{2k}{{1 + k^{2} }}. $$

(16)

3.2 A different recurrence pattern

The most remarkable difference between the first and the second families of exact solutions are in their FPUT patterns. Numerically we conduct a similar exercise as in Sect. 2, namely, solving a slightly perturbed initial state with a split-step Fourier scheme. Peaks of successive breathers are now aligned with those of the previous breather, i.e., there is no phase shift between two consecutive breather modes (Fig. 4).

Fig. 4

a Doubly periodic solution (Eq. 6); b Numerical simulations. Parameters chosen are λ = 1, σ = 0.05, α = 1, q = 0.01 (Eq. A5)

3.3 Connection with breather

For the long wave limit for one of the elliptic functions, e.g., k → 1, the modulus of the other elliptic functions must tend to zero (k₁ → 0) (Eq. 16). Mathematically, the elliptic functions in the k → 1 / k₁ → 0 limits will reduce to the hyperbolic / trigonometric functions, respectively. In other words, analytical expressions similar to the Kuznetsov-Ma and Akhmediev breathers will be obtained. As such modes have been studied intensively in the literature, we shall just give a quick derivation in terms of the Darboux transformation and concentrate instead on the cascading dynamics for the Hirota equation.

4 Breathers and spectral analysis

4.1 Theoretical formulation

A breather can be obtained by the Darboux transformation [25, 26], a recursive scheme to construct solutions of increasing complexity from ‘seed solutions’:

$$ A = A_{0} \left( {x,t} \right) + \frac{{2\left( {\eta^{ * } - \eta } \right)\varphi_{12} \varphi_{11}^{ * } }}{{\varphi_{11} \varphi_{11}^{ * } + \varphi_{12} \varphi_{12}^{ * } }}, $$

(17a)

$$ \begin{gathered} \varphi_{11} = \frac{1}{2\chi }\exp \left( { - \frac{1}{2}i\Theta_{11} } \right) \hfill \\ \times \left\{ {\left( {\gamma_{1} + 2\eta } \right)\left[ {1 + \exp \left( {i\Theta_{2} } \right)} \right] + \zeta \left[ { - 1 + \exp \left( {i\Theta_{2} } \right)} \right]} \right\} \hfill \\ \end{gathered}, $$

(17b)

$$ \varphi_{12} = \exp \left( { - \frac{1}{2}i\Theta_{12} } \right)\left[ {1 + \exp \left( {\Theta_{2} } \right)} \right], $$

(17c)

where ${\upeta } = {\upeta }_{R} + i{\upeta }_{I}$ is a complex number. The lengthy expressions for Θ₁₁, Θ₁₂, Θ₂, and ζ are fully tabulated in Appendix B. Our breather solution, Eq. 17, is different from those earlier in the literature [25, 27], as we incorporate a wavenumber dependence of the transverse variable in the formulation of the wave envelope. Mathematically, the parameter γ₁ permits larger flexibility in calculating the period and the velocity of the breather. The velocity of the breather is

$$ \begin{aligned} U_{0} &= {\uplambda }\frac{{ - {\upgamma }_{1} {\upzeta }_{I} + 2{\upzeta }_{R} {\upeta }_{I} + 2{\upzeta }_{I} {\upeta }_{R} }}{{{\upzeta }_{I} }} \hfill \\& + {\upsigma }\frac{{{\upgamma }_{1}^{2} {\upzeta }_{I} + 8{\upzeta }_{R} {\upeta }_{I} {\upeta }_{R} - 2{\upgamma }_{1} \left( {{\upzeta }_{R} {\upeta }_{I} + {\upzeta }_{I} {\upeta }_{R} } \right)}}{{{\upzeta }_{I} }} \hfill \\& - 2{\upsigma }\left( {2{\upeta }_{I}^{2} - 2{\upeta }_{R}^{2} + {\upchi }^{2} } \right). \hfill \end{aligned} $$

(18)

• When the speed of the breather U₀ is indefinitely large, i.e., ${\upeta }_{R} = - {\upgamma }_{1} /2,$ we recover the Akhmediev breather with wave profile periodic in the transverse variable x (Fig. 5a).

• When the speed of the breather U₀ is zero, we retrieve the configuration of a Kuznetsov–Ma breather, with wave profile periodic in the propagation variable t (Fig. 5b).

• Another penetrating insight can be obtained by allowing the variable x to be complex by analytic continuation. Remarkably, the location of maximum displacement in physical space is identical to the real part of the poles in the complex plane. For typical parameters chosen, λ = 1, σ = 0.05, χ = 1, γ₁ = 0, η = –0.5i, the locations of maximum displacements are (1.21 + 3.63n, 0), (n = 0, ± 1, ± 2, …). On the other hand, the poles, or the zeros of the denominator in Eq. 17a, are located at complex numbers with real parts identical to the expressions given (Table 1). Similar studies on pole trajectories have been conducted for the dynamics of solitons and rogue waves [33, 34].

Fig. 5

a The Akhmediev breather with parameters λ = 1, σ = 0.05, χ = 1, γ₁ = 0, η = –0.5i; Akhmediev breather with t = 0 (inset figure); b Fundamental Kuznetsov–Ma breather with parameters λ = 1, σ = 0.05, χ = 1, γ₁ = 0.5, η = 0.1 + 1.7538i; c-d Asymmetric energy spectra

Table 1 Correlation between the location of maximum displacement in physical space and the complex roots where poles occur

4.2 Spectral analysis

For the Akhmediev breather, the nonlinear dynamics can be elucidated more effectively through the frequency domain. The spectral modes can be calculated by

$$ f_{0} = \frac{1}{L}\int\limits_{ - L/2}^{L/2} {A\left( {x,t} \right)} dx, $$

(19a)

$$ f_{j} = \frac{1}{L}\int\limits_{ - L/2}^{L/2} {A\left( {x,t} \right)} \exp \left( { - ij\frac{{2{\uppi }}}{T}x} \right)dx, \, j = \pm 1,{\kern 1pt} \, \pm 2, \ldots $$

(19b)

where f₀ describes the temporal evolution of the pump mode, and f_j correspond to the harmonics (or sidebands). The time dependence of these components for j =  ± 1, ± 2, clearly illustrates the growth and decay of the breather (Fig. 5c). The spectral components should satisfy the constraint

$$ \left| {f_{0} \left( t \right)} \right|^{2} + \sum\limits_{j = 1}^{\infty } {\left| {f_{j} \left( t \right)} \right|^{2} + \sum\limits_{j = - 1}^{ - \infty } {\left| {f_{j} \left( t \right)} \right|^{2} } = 1} $$

(20)

as the total energy is conserved. From a plot of the individual spectral component versus time, we see clearly the central component contains the total energy for (numerically) large negative t, and transfers the energy to the sidebands before returning to the central mode for t >> 1. Moreover, the third-order dispersion operator destroys the symmetry of the system. The spectral components are asymmetric, which is different from the symmetric spectra of the nonlinear Schrödinger equation [35]. These spectra may appear to be identical, because the profile of Akhmediev breather at t = 0 is almost symmetric with respect to x except for a small phase shift (inset of Fig. 5a).

For the analytical Kuznetsov–Ma breather, the computation of the spectral components is similar to that for the Akhmediev breather. The asymmetric spectra are shown in Fig. 5d. As the total energy is conserved, the spectral components require

$$ \left| {f_{0} \left( x \right)} \right|^{2} + \sum\limits_{j = 1}^{\infty } {\left| {f_{j} \left( x \right)} \right|^{2} + \sum\limits_{j = - 1}^{ - \infty } {\left| {f_{j} \left( x \right)} \right|^{2} } = 0.1225} . $$

The first harmonic sideband with j = 1 serves as an illuminating example. The pump first conveys energy to the sidebands. The first sideband then transfers energy to the pump, which is dramatically different from that of Akhmediev breather in Fig. 5c.

Extensive numerical simulations have been conducted to investigate the stability of breathers. In particular, the split step method is utilized to test if the fundamental breather of Eq. 1 can be readily generated through realistic condition. For this purpose, we perturb a background plane wave by a cosine-type noise of strength μ = 0.01 with t = –2 as the initial condition. Typical simulation results are depicted in Fig. 6b with the identical parameters as Fig. 6a. After about four (non-dimensional) time units (t ≈ –2 to t ≈ 2), modulation instability has developed fully and the Akhmediev breather has emerged. At the formation of the breather, the numerical profile is compared with the analytical formulation (Fig. 6c). The agreement is highly satisfactory.

Fig. 6

a The analytical breather with parameters λ = 1, σ = 0.05, χ = 1, γ₁ = 0.5, η = –0.25 – 0.66i; b FPUT patterns with parameters λ = 1, σ = 0.05, χ = 1, γ₁ = 0.5, μ = 0.01, ρ = 1; c Comparison between the analytical breather and FPUT patterns at the formulation of the breather

5 Cascading mechanism

A conventional modulation instability analysis will only give the growth rate of a mode of one specified wavenumber. Higher-order harmonics are ignored. With the inherent limitation of linearization, exponential growth will continue indefinitely, but in reality this growth will be limited by nonlinear effects. A complete investigation on all the features of the nonlinearities may be exceedingly difficult. Here we hope to provide an illuminating perspective by studying a ‘cascading mechanism’ [7]. More precisely, we demonstrate that the instability of the higher-order sidebands (or harmonics) are ‘enslaved’ to or in ‘locked step’ with the growth of the fundamental mode. These higher-order sidebands are exponentially smaller initially, but they are amplified at a larger rate. Eventually all modes reach roughly the same order of magnitude at one instant in time (or one particular spatial location in the context of fiber optics), which signifies the first formation of a breather.

A quantitative treatment of the cascading mechanism will now be presented. We extend the modulation instability of the fundamental mode by considering a generalized asymptotic expansion. As example, the governing equations incorporating the second harmonic will be

$$ \begin{gathered} A\left( {x,t} \right) = {\upchi }\left[ \begin{gathered} B_{0} \left( t \right) + B_{1} \left( t \right)\exp \left( {i\Gamma x} \right) + B_{ - 1} \left( t \right)\exp \left( { - i\Gamma x} \right) \hfill \\ + B_{2} \left( t \right)\exp \left( {2i\Gamma x} \right) + B_{ - 2} \left( t \right)\exp \left( { - 2i\Gamma x} \right) \hfill \\ \end{gathered} \right] \hfill \\ \times \exp \left( {i{\upgamma }_{1} x} \right) \hfill \\ \end{gathered}, $$

(21a)

$$ B_{0} \left( t \right) = \exp \left( {i{\upgamma }_{2} t} \right), \, B_{ \pm 1} \left( t \right) = a_{1} \exp \left( {i{\upgamma }_{2} t \pm Gt} \right), $$

(21b)

where a₁ denotes the intensity of the perturbation. Physically, B₀ will be the background plane wave, while B₁ is the first harmonic. Substituting Eq. 21 into Eq. 1, we have

$$ \left( {2a_{1}^{2} \lambda \chi^{3} - 6a_{1}^{2} \gamma_{1} \sigma \chi^{3} - 6a_{1}^{2} \Gamma \sigma \chi^{3} } \right)\exp \left( {i\gamma_{2} t + 2Gt} \right) + i\chi B_{2}^{^{\prime}} \left( t \right) = 0, $$

(22a)

$$ \left( {2a_{1}^{2} \lambda \chi^{3} - 6a_{1}^{2} \gamma_{1} \sigma \chi^{3} + 6a_{1}^{2} \Gamma \sigma \chi^{3} } \right)\exp \left( {i\gamma_{2} t - 2Gt} \right) + i\chi B_{ - 2}^{^{\prime}} \left( t \right) = 0 .$$

(22b)

The exponential growth of $B_{ \pm 2} \left( t \right)$ can be separated as

$$ B_{2} \left( t \right) = \frac{{2ia_{1}^{2} {\upchi }^{2} \left[ {{\uplambda } - 3\left( {{\upgamma }_{1} + \Gamma } \right){\upsigma }} \right]\exp \left( {i{\upgamma }_{2} t + 2Gt} \right)}}{{i{\upgamma }_{2} + 2G}}, $$

(23a)

$$ B_{ - 2} \left( t \right) = \frac{{2a_{1}^{2} {\upchi }^{2} \left[ {{\uplambda } + 3\left( { - {\upgamma }_{1} + \Gamma } \right){\upsigma }} \right]\exp \left( {i{\upgamma }_{2} t - 2Gt} \right)}}{{{\upgamma }_{2} + 2iG}}. $$

(23b)

Similarly, we assume a formulation for the third-order sidebands as

$$ \begin{gathered} A\left( {x,t} \right) = {\upchi }\left[ \begin{gathered} B_{0} \left( t \right) + B_{1} \left( t \right)\exp \left( {i\Gamma x} \right) + B_{ - 1} \left( t \right)\exp \left( { - i\Gamma x} \right) \hfill \\ + B_{2} \left( t \right)\exp \left( {2i\Gamma x} \right) + B_{ - 2} \left( t \right)\exp \left( { - 2i\Gamma x} \right) \hfill \\ + B_{3} \left( t \right)\exp \left( {3i\Gamma x} \right) + B_{ - 3} \left( t \right)\exp \left( { - 3i\Gamma x} \right) \hfill \\ \end{gathered} \right] \hfill \\ \times \exp \left( {i{\upgamma }_{1} x} \right). \hfill \\ \end{gathered} $$

(24)

The quantities $B_{0} \left( t \right),\;B_{ \pm 1} \left( t \right),\;B_{ \pm 2} \left( t \right)$ are displayed in Eqs. 21 and 23. We can now compute $B_{3} \left( t \right)$ as

$$ B_{3} \left( t \right) = \frac{{4a_{1}^{3} {\upchi }^{4} \left[ {{{2\lambda }}^{{2}} - 3\left( {4{\upgamma }_{1} + 5\Gamma } \right)\lambda {{\sigma + 9}}\sigma^{{2}} \left( {2\gamma_{1}^{2} + 5\gamma_{1} \Gamma + 3\Gamma^{2} } \right)} \right]}}{{\left( {{\upgamma }_{2} - 2iG} \right)\left( {{\upgamma }_{2} - 3iG} \right)}}. $$

(25)

Repeating similar arguments for $B_{ \pm j} ,\;j = 1,\;2,\;3 \ldots$ yields

$$ B_{ \pm j} \left( t \right) = C_{ \pm j} \exp \left( { \pm jGt} \right), $$

(26)

where $C_{ \pm j}$ denote the initial amplitudes. Taking the logarithm for both sides of Eq. 26, dynamical evolution of the cascading process can be derived as

$$ H_{j} = \ln \left[ {\left| {B\left( t \right)} \right|} \right] = jG\left( {t - t_{j} } \right), \, t_{j} = - \frac{{\ln \left( {\left| {C_{j} } \right|} \right)}}{jG}. $$

(27)

To verify this prediction, we solve the governing system both analytically and numerically. The numerical approach is conducted by the split step Fourier scheme with a cosine initial profile (Eq. 5). A typical FPUT pattern is obtained (Fig. 7a). The numerical frequency domain spectral modes (or Fourier spectra) can be computed by

$$ F_{0} = \frac{1}{L}\int\limits_{ - L/2}^{L/2} {A\left( {x,t} \right)} dx, $$

(28a)

$$\begin{aligned}&F_{j} = \frac{1}{L}\int\limits_{ - L/2}^{L/2} {A\left( {x,t} \right)} \exp \left( - ij \rho x\right)dx, \, \\& \rm{j} = \pm 1,{\kern 1pt} \, \pm 2, \ldots \end{aligned}$$

(28b)

where the $F_{j}$ are supposed to be computed numerically but the $f_{j}$ should be associated with the analytical formula (Eq. 19). The comparison between the cascading prediction (Eq. 27), ‘star’ lines in Fig. 7b), and the logarithmic frequency domain spectral modes $\ln \left( {F_{j} } \right),\;j = 0,\; \pm 1,\; \pm 2,\; \pm 3$ (curves in Fig. 7b), attains excellent agreement. The analytical cascading predictions intersect at the first formation time $t_{j} \approx 5.3,\;j = 1,\;2,\;3$. The asymmetric numerical spectra exhibit a local minimum for the ‘pump’ wave and local maxima for high-order harmonics. This demonstrates the energy transfer among the modes. The term ‘pump’ is borrowed from the optical context where the background wave is termed the ‘pump beam’. As the total energy is conserved, the spectral components require

Fig. 7

a FPUT with parameters λ = 1, σ = 0.05, χ = 1, γ₁ = 0, μ = 0.0001, ρ = 1.4; b Comparison between the numerical spectra and the cascading mechanism prediction; c Breather with parameters λ = 1, σ = 0.05, χ = 1, γ₁ = 0, η = 0.73i; d Comparison between the analytical and numerical spectra; e Triangular spectrum of FPUT at t ≈ 5.3

$\left| {F_{0} \left( t \right)} \right|^{2} + \sum\limits_{j = 1}^{\infty } {\left| {F_{j} \left( t \right)} \right|^{2} + \sum\limits_{j = - 1}^{ - \infty } {\left| {F_{j} \left( t \right)} \right|^{2} } = 1}$.

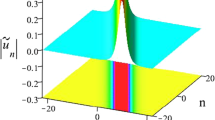
This cascading mechanism thus concretely highlights the growth of the higher-order harmonics. We select parameters for the analytical formulation which will fit the wave profile (Fig. 7a, c). The Fourier spectra of the analytical breather (circled curves) and numerical breather (solid curves) are compared (Fig. 7d). Moreover, as the higher-order harmonics start from a small amplitude initially, we also have a triangular spectrum (Fig. 7e).

6 Evolution from random initial conditions

When we choose one Fourier mode as the initial condition, periodic patterns and FPUT with a preferred wavelength can readily emerge. However, when the initial condition is taken as a random noise, an apparently chaotic wave field will be observed for small time. Eventually ‘rogue wave’ like mode can still arise. Strictly periodic condition is almost impossible to enforce, due to the large number of modes involved. Mathematically, we start the investigation by taking the initial condition as

$$ A = A_{0} \left( {x,t} \right) \, + \, \mu {\text{ Ran}}\left( x \right) $$

(29)

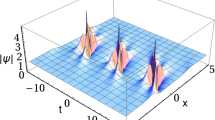
where Ran(x) denotes a random variable generated by a standard computer software, uniformly distributed over the interval of interest. The background is represented by A₀(x, t). Modulation instability is still operational as the random noise will nevertheless contain modes within the unstable band. Two typical examples with different values of γ₁ will be illustrated, namely γ₁ = 0 and γ₁ = 1 (Fig. 8a, b). These correspond to stationary / moving background carrier wave envelop, respectively. The background is mostly undisturbed before the onset of modulation instability (up to t ≈ 4 with input parameters chosen). Instability leads to the formation of ‘rogue wave’ modes (marked by the black rectangle in Fig. 8a). It will be instructive to compare the rogue modes obtained from a chaotic wave field with the analytical solution.

Fig. 8

Chaotic wave fields with a γ₁ = 0; b γ₁ = 1; c Probability density functions of the amplitudes in chaotic wave fields, green curve being the Rayleigh distribution. The vertical coordinate is set as a logarithmic scale. Parameters chosen are λ = 1, σ = 0.05, χ = 1, μ = 0.001

It is thus necessary to first derive the rogue wave by a generalized Darboux transformation. We start with a background plane wave as ‘seed’ and employ auxiliary functions ϕ_ij:

$$A = \exp \left( {i2{\uplambda }t} \right) - \frac{{4i\phi_{12} \phi_{11}^{*} }}{{\phi_{11} \phi_{11}^{*} + \phi_{12} \phi_{12}^{*} }},$$

(30a)

$$ \phi_{11} = i\exp \left( { - i{\uplambda }t} \right)\left( { - 1 + 2x + 4i{\uplambda }t - 12{\upsigma }t} \right), $$

(30b)

$$ \phi_{12} = i\exp \left( {i{\uplambda }t} \right)\left( {1 + 2x + 4i{\uplambda }t - 12{\upsigma }t} \right). $$

(30c)

Both the numerical and analytic rogue waves display the same ‘eye-shaped’ profile (a ‘peak’ with two adjacent ‘valleys’ (Fig. 8). The maximum displacements are almost the same too, and thus the agreements between the two approaches are highly satisfactory (Fig. 9).

Fig. 9

a ‘Zoom in’ view of the region marked by a black rectangle of Fig. 8a; b Analytic rogue wave with parameters λ = 1, σ = 0.05

The probability distribution of the amplitude displacement will provide an illuminating perspective of the dynamics, and also useful information for practitioners in physical applications. We attempt to construct such a distribution by performing a large number of simulations and recording the wave field. More precisely, we conduct 1,024 computer runs, each ranging from t = 0 to t = 10, with a time step of 0.005, i.e., 2,000 steps. From these 1,024 X 2,000 data points, histograms are constructed.

Such a model probability density function is illustrated for γ₁ = 0 / γ₁ = 1 (blue / red curve in Fig. 8c). The spectrum starts at value zero at the origin, attains a local maximum and decays in the far field. A Rayleigh distribution in probability theory, denoted by ‘Ray’ below, is used as a reference. With proper parameters to fit the shape of the curve, the approximation is taken as:

$$ {\text{Ray}}\left( {\left| A \right|} \right) = \frac{b\left| A \right|}{{{\upsigma }^{2} }}\exp \left( { - \frac{{\left| A \right|^{2} }}{{2{\upsigma }^{2} }}} \right), $$

where parameter values of b = 0.02, σ = 0.7 are used here (Fig. 8).

To avoid biased data trends, we remove the field amplitude in the small time regime (0 < t < 4). For field amplitude in the range of (2.3, 2.9), i.e., more than two times the background, chance of a rogue event for γ₁ = 1 is larger than that for γ₁ = 0. In other words, a moving background plane wave may favor the occurrence of abnormally large waves.

7 Discussions and conclusions

The properties and dynamics of breathers and doubly periodic solutions of the Hirota equation are studied. The Hirota equation with third-order dispersion represents an ‘integrable’ extension of the nonlinear Schrödinger equation, and includes the complex Korteweg-de Vries equation as a special case. Doubly periodic solutions are established by utilizing the bilinear derivatives of theta functions. We extend earlier results of our group by deriving a second, nonsingular exact solution. Theoretically, the crucial feature is that the wavenumber of the wave envelope cannot be arbitrary. It must satisfy an algebraic equation related to the magnitude of the quadratic / cubic terms and the periods of the wave patterns.

One important difference between these two doubly periodic solutions is the phase difference between peaks in the successive occurrence of breathers, namely, zero and π/2. In the literature on the nonlinear Schrödinger equation, the terminologies of ‘A-Type’ and ‘B-Type’ solutions have been proposed to describe these two scenarios. Both doubly periodic solutions of the Hirota equation display structural robustness. In other words, slightly perturbed wave profiles of the exact solutions will continue to evolve in shapes almost indistinguishable from the original form. Similar robustness to small perturbations has also been proven for the nonlinear Schrödinger case [36, 37]. We have thus demonstrated that the third-order dispersion operator does not modify this property. Physically these doubly periodic solutions constitute manifestation of the FPUT dynamics for these nonlinear systems. In this paper, we study the case where nonlinearity and dispersion are of the same sign. The case of opposite signs will be left for future study.

These analytic doubly periodic solutions can be used to study FPUT dynamics. Many ‘integrable’ equations possess bilinear forms. Hence the present line of investigation can be extended to FPUT studies for large sets of dynamical systems which are already amenable to theoretical treatment. In terms of physical applications, recurrence for picosecond pulses governed by the nonlinear Schrödinger equation has been observed in optical fibers [6, 14]. Pulses of shorter duration require the incorporation of third-order dispersion. The Hirota equation here provides a useful model for understanding the physics. Similar remarks apply to hydrodynamic waves up to the fourth order in wave steepness.

One simplifying perspective for these two doubly periodic solutions is their long wave limit. It is well established that theta or elliptic functions will degenerate to hyperbolic and trigonometric functions under such circumstances. We expect modes similar to the Kuznetsov-Ma and Akhmediev breathers will result. Instead, we give a quick derivation in terms of a Darboux transformation and concentrate on the cascading mechanism and spectral analysis. Nevertheless we have extended existing results in the literature by allowing a propagating envelope in the breather formulation.

The cascading mechanism can elucidate the first formation of a breather [7]. More precisely, higher-order harmonics exponentially small initially can nevertheless be amplified at a higher rate. Eventually, all these modes attain roughly the same magnitude at one instant of time (or one spatial location in the optical fiber setting), which signifies the first occurrence of a breather. We substantiate these assertions with a spectral analysis. The Hirota equation thus possesses similar properties as a few other members of this Schrödinger family of evolution equations [38, 39]. Contemporary studies on the pulsating modes of the focusing Schrödinger equation may also provide illuminating insights. The linear and nonlinear instabilities of the Akhmediev breathers of the Schrödinger equation have been formulated [40]. Given the recurrence observed for the Hirota equation, incorporating third-order dispersion will likely maintain the dynamical features and properties similar to those of the breather modes of the Schrödinger equation. From a theoretical perspective, the Lax pair formulations of breathers have been given for the nonlinear Schrödinger case [41]. A corresponding study for the Hirota equation and a scrutiny of the eigenvalue spectrum for instability would be valuable endeavor in future.

There are still many issues not completely understood. One scenario is the likely FPUT patterns resulting from arbitrary initial conditions, e.g., a plane wave or a random noise. For the random noise case, we have attempted to construct a probability density function. For the plane wave case, we show that doubly periodic patterns are still observed. However, the phase shift between peaks on consecutive breather modes may be neither zero nor π/2. Very likely general classes of doubly periodic solutions involving third and higher-order Lax-Novikov formulations must be investigated [42]. The corresponding distribution and properties of the eigenvalues should also be considered. An intriguing challenge is to study the occurrence of rogue waves on a doubly periodic background for the Hirota equation.

Another perspective is the introduction of dissipation or forcing in the evolution equation itself. In the context of water waves, additional terms mimicking the effects of the ‘Dysthe’s equation’ have been incorporated. A separatrix will occur and physically corresponds to a phase shift in the envelope [43]. Finally, from the perspective of nonlinear science, a study on the eigenvalue spectrum for the linear instability for these doubly periodic solutions may still reveal more information about the structure of the system [44]. Schrödinger equations and FPUT patterns will prove to be fruitful fields for research in continuum mechanics [45, 46] and discrete systems [47].

Appendices

Appendix A

Theta functions are defined by Fourier series with exponentially decaying coefficients. In mathematical analysis, the Jacobi elliptic functions, sn, cn, dn can be expressed as ratio of theta functions. In classical mathematical analysis, theta functions are usually expressed as Fourier series with a real parameter q (τ purely imaginary):

$$ \theta_{1} \left( {x,{\uptau }} \right) = 2\sum\limits_{n = 0}^{\infty } {\left( { - 1} \right)^{n} } q^{{\left( {n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \right)^{2} }} \sin \left( {2n + 1} \right)x $$

$$ = - \sum\limits_{m = - \infty }^{\infty } {\exp \left[ {{\uppi }i{\uptau }\left( {m + \frac{1}{2}} \right)^{2} + 2i\left( {m + \frac{1}{2}} \right)\left( {x + \frac{{\uppi }}{2}} \right)} \right]} , $$

(A1)

$$ \theta_{2} \left( {x,{\uptau }} \right) = 2\sum\limits_{n = 0}^{\infty } {q^{{\left( {n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \right)^{2} }} } \cos \left( {2n + 1} \right)x $$

$$ = \sum\limits_{m = - \infty }^{\infty } {\exp \left[ {{\uppi }i{\uptau }\left( {m + \frac{1}{2}} \right)^{2} + 2i\left( {m + \frac{1}{2}} \right)x} \right]} , $$

(A2)

$$ \theta_{3} \left( {x,{\uptau }} \right) = 1 + 2\sum\limits_{n = 1}^{\infty } {q^{{n^{2} }} } \cos 2nx $$

$$ = \sum\limits_{m = - \infty }^{\infty } {\exp \left( {{\uppi }i{\uptau }m^{2} + 2imx} \right)} , $$

(A3)

$$ \theta_{4} \left( {x,{\uptau }} \right) = 1 + 2\sum\limits_{n = 1}^{\infty } {\left( { - 1} \right)^{n} q^{{n^{2} }} } \cos 2nx $$

$$ = \sum\limits_{m = - \infty }^{\infty } {\exp \left[ {{\uppi }i{\uptau }m^{2} + 2im\left( {x + \frac{{\uppi }}{2}} \right)} \right]} , $$

(A4)

$$ 0 < q < 1, \, q = \exp \left( {{\uppi }i{\uptau }} \right), \, q = \exp \left( { - \frac{{{\uppi }K^{\prime}}}{K}} \right). $$

(A5)

K, K' are the complete elliptic integrals of the first kind with parameters k and (1 – k²)^1/2. In terms of the patterns in the summations, there is an extra minus sign in front of the function θ₁. In terms of basic mathematical properties, θ₁ is odd while the other three are even. The zeros or roots of θ₁, θ₂, θ₃, θ₄, are located at square grids in the complex plane at Mπ + Nπτ, (M + 1/2)π + Nπτ, (M + 1/2)π + (N + 1/2)πτ, Mπ + (N + 1/2)πτ respectively, with M, N integers. We can readily show by direct calculations that θ₁ and θ₂, as well as θ₃ and θ₄, are related by a phase shift of π/2.

The Jacobi elliptic functions can be expressed as ratios of theta functions with ‘stretched’ arguments or variables as (for simplicity, the dependence on the parameter τ in Eqs. A1-A4 has been dropped in Eqs. A6, A7:

$$ \begin{gathered} {\text{sn}}\left( u \right) = \frac{{\theta_{3} \left( 0 \right)\theta_{1} \left( z \right)}}{{\theta_{2} \left( 0 \right)\theta_{4} \left( z \right)}},{\text{ cn}}\left( u \right) = \frac{{\theta_{4} \left( 0 \right)\theta_{2} \left( z \right)}}{{\theta_{2} \left( 0 \right)\theta_{4} \left( z \right)}}, \, \hfill \\ {\text{dn}}\left( u \right) = \frac{{\theta_{4} \left( 0 \right)\theta_{3} \left( z \right)}}{{\theta_{3} \left( 0 \right)\theta_{4} \left( z \right)}}, \hfill \\ \end{gathered} $$

(A6)

$$ z = \frac{u}{{\theta_{3}^{2} \left( 0 \right)}}, \, k = \frac{{\theta_{2}^{2} \left( 0 \right)}}{{\theta_{3}^{2} \left( 0 \right)}}, \, k^{\prime} = \frac{{\theta_{4}^{2} \left( 0 \right)}}{{\theta_{3}^{2} \left( 0 \right)}}, \, k^{2} + \left( {k^{\prime}} \right)^{2} = 1. $$

(A7)

Theta functions possess many properties which make them ideal candidates for handling bilinear forms of evolution equations.

Sum and difference identities: Theta functions possess a huge varieties of identities:

$$ \theta_{3} \left( {x + y} \right)\theta_{3} \left( {x - y} \right)\theta_{2}^{2} \left( 0 \right) = \theta_{4}^{2} \left( x \right)\theta_{1}^{2} \left( y \right) + \theta_{3}^{2} \left( x \right)\theta_{2}^{2} \left( y \right), $$

(A8)

$$ \theta_{4} \left( {x + y} \right)\theta_{4} \left( {x - y} \right)\theta_{2}^{2} \left( 0 \right) = \theta_{4}^{2} \left( x \right)\theta_{2}^{2} \left( y \right) + \theta_{3}^{2} \left( x \right)\theta_{1}^{2} \left( y \right). $$

(A9)

By differentiating Eq. A8 with respect to y twice and setting y = 0,

$$ \begin{gathered} D_{x}^{2} \theta_{3} \left( x \right) \cdot \theta_{3} \left( x \right) = \frac{{2\theta_{2}^{\prime \prime } \left( 0 \right)\theta_{3}^{2} \left( x \right)}}{{\theta_{2} \left( 0 \right)}} + 2\theta_{3}^{2} \left( 0 \right)\theta_{4}^{2} \left( 0 \right)\theta_{4}^{2} \left( x \right), \hfill \\ D_{x}^{2} \theta_{4} \left( x \right) \cdot \theta_{4} \left( x \right) = 2\theta_{3}^{2} \left( 0 \right)\theta_{4}^{2} \left( 0 \right)\theta_{3}^{2} \left( x \right) + \frac{{2\theta_{2}^{\prime \prime } \left( 0 \right)\theta_{4}^{2} \left( x \right)}}{{\theta_{2} \left( 0 \right)}}, \hfill \\ \end{gathered} $$

i.e., the bilinear derivatives (‘D’ operator, defined below Eq. 4d) of theta functions can be expressed back in terms of the theta functions themselves through such ‘sum’ and ‘difference’ identities Eqs. A8, A9. Similar principles apply to the computations of

$$ D_{x} \theta_{m} \cdot \theta_{n} , \, D_{x}^{2} \theta_{m} \cdot \theta_{n} , $$

where m, n are integers.

Derivatives at specified values – By Taylor expansion of these sum and difference formulas and comparing powers, we relate the derivatives of theta functions to the functions themselves [20, 22], e.g.,

$$ \frac{{\theta_{4}^{\prime \prime } \left( 0 \right)}}{{\theta_{4} \left( 0 \right)}} - \frac{{\theta_{3}^{\prime \prime } \left( 0 \right)}}{{\theta_{3} \left( 0 \right)}} = \theta_{2}^{4} \left( 0 \right), \, \frac{{\theta_{4}^{\prime \prime } \left( 0 \right)}}{{\theta_{4} \left( 0 \right)}} - \frac{{\theta_{2}^{\prime \prime } \left( 0 \right)}}{{\theta_{2} \left( 0 \right)}} = \theta_{3}^{4} \left( 0 \right), $$

$$ \frac{{\theta_{3}^{\prime \prime } \left( 0 \right)}}{{\theta_{3} \left( 0 \right)}} - \frac{{\theta_{2}^{\prime \prime } \left( 0 \right)}}{{\theta_{2} \left( 0 \right)}} = \theta_{4}^{4} \left( 0 \right). $$

By differentiation using elementary calculus, we can simplify bilinear derivatives of products of exponential functions and the auxiliary variables, e.g.,

$$ \begin{gathered} D_{x} \left[ {\exp \left( {imx} \right)g \cdot \exp \left( {inx} \right)f} \right] \hfill \\ = \left[ {D_{x} g \cdot f + i\left( {m - n} \right)g\;f} \right]\exp \left[ {i\left( {m + n} \right)x} \right], \hfill \\ \end{gathered} $$

$$ \begin{aligned} & D_{x}^{2} \left[ {\exp \left( {imx} \right)g \cdot \exp \left( {inx} \right)f} \right] \hfill \\& = \left[ {D_{x}^{2} g \cdot f + 2i\left( {m - n} \right)D_{x} g \cdot f - \left( {m - n} \right)^{2} g\;f} \right] \hfill \\& \quad \times \exp \left[ {i\left( {m + n} \right)x} \right]. \hfill \\ \end{aligned} $$

These formulas will be especially relevant in the present wave packet type calculations, as the carrier wave envelope is expressed as a complex exponential function multiplied by the auxiliary functions governing the actual packet structure (Eq. 4).

Appendix B

The parameters of analytical breather are as follows:

$$ {\upzeta } = {\upzeta }_{R} + i{\upzeta }_{I} = \sqrt {{\upgamma }_{1}^{2} + 4{\upgamma }_{1} {\upeta } + 4\left( {{\upeta }^{2} + {\upchi }^{2} } \right)}, $$

(B1)

$$ \begin{gathered} \Theta_{11} = {\upgamma }_{1} x + \left( { - {{\lambda \gamma }}_{1}^{2} + {{\sigma \gamma }}_{1}^{3} + 2{{\lambda \chi }}^{2} - 6{{\sigma \gamma }}_{1} {\upchi }^{2} } \right)t + {\upzeta }x \hfill \\ \quad \quad + {\upzeta }t\left[ { - {\uplambda }\left( {{\upgamma }_{1} - 2{\upeta }} \right) + {\upsigma }\left( {{\upgamma }_{1}^{2} - 2{\upgamma }_{1} {\upeta } + 4{\upeta }^{2} - 2{\upchi }^{2} } \right)} \right] \hfill \\ \end{gathered} ,$$

(B2)

$$\begin{aligned} & \Theta_{12} = - {\upgamma }_{1} x + \left( {{{\lambda \gamma }}_{1}^{2} - {{\sigma \gamma }}_{1}^{3} - 2{{\lambda \chi }}^{2} + 6{{\sigma \gamma }}_{1} {\upchi }^{2} } \right)t + {\upzeta }x \\ & + {\upzeta }t\left[ { - {\uplambda }\left( {{\upgamma }_{1} - 2{\upeta }} \right) + {\upsigma }\left( {{\upgamma }_{1}^{2} - 2{\upgamma }_{1} {\upeta } + 4{\upeta }^{2} - 2{\upchi }^{2} } \right)} \right], \end{aligned}$$

(B3)

$$ \Theta_{2} = {\upzeta }\left\{ {x - t\left[ {{\uplambda }\left( {{\upgamma }_{1} - 2{\upeta }} \right) - {\upsigma }\left( {{\upgamma }_{1}^{2} - 2{\upgamma }_{1} {\upeta } + 4{\upeta }^{2} - 2{\upchi }^{2} } \right)} \right]} \right\}. $$

(B4)

Based on Eq. B1, ζ_R and ζ_I can be determined by

$$ \begin{gathered} {\upzeta }_{R}^{2} - {\upzeta }_{I}^{2} = {\upgamma }_{1}^{2} - 4{\upeta }_{I}^{2} + 4{\upgamma }_{1} {\upeta }_{R} + 4{\upeta }_{R}^{2} + 4{\upchi }^{2} , \, \hfill \\ 2{\upzeta }_{R} {\upzeta }_{I} = 4{\upgamma }_{1} {\upeta }_{I} + 8{\upeta }_{I} {\upeta }_{R} . \hfill \\ \end{gathered} $$

(B5)