1 Introduction

As the core part of the precision agriculture technology system, the automatic guidance of agricultural machinery has been widely used in agricultural production processes in recent years, mainly including farming, sowing, fertilizing, spraying, and harvesting, etc. [1, 2]. Meanwhile, the rapid update of some technologies has effectively promoted the intellectualization of modern agricultural machinery and equipment, which has also attracted widespread attention to the automatic driving technology of agricultural vehicles [3, 4]. These technologies involve control technology, sensor technology, information technology and microprocessor technology, etc. Actually, one of the most critical issues for autonomous agricultural vehicles is the path-tracking control [5], which refers to the use of RTK, lidar, camera and other sensors to get the vehicle’s operating environment and location information, and then under the action of the path-tracking control algorithms, the vehicle arrives and tracks the specified path. It should be further emphasized that the path-tracking errors (i.e., the lateral deviation and the orientation error) are required to be stabilized to the origin for the sake of accomplishing the task of path-tracking operation.

The high precision path-tracking capability of autonomous agricultural vehicles not only improves the quality of field operations, but also further reduces agricultural production costs [6]. Consequently, many research teams are focusing on the problem of the path-tracking control of farm vehicles. Actually, the reported path-tracking control approaches can achieve satisfactory tracking performance if the vehicle motion is almost pure rolling without slippage [7]. However, agricultural vehicles are inevitably affected by various uncertain factors in actual agricultural scenarios, such as tire slip and wheel deformation, etc., which means that the pure rolling constraints are usually not satisfied [8]. Under these circumstances, the automatic guidance performance and system stability of agricultural vehicles will severely degraded. In addition, the existence of the model uncertainties and external disturbances makes it extremely difficult to control autonomous agricultural vehicles [9]. It is notable that the model uncertainties are usually caused by changes in vehicles or environmental parameters and vehicle states.

To address the above-mentioned problems, some interesting research results have been put forward in the current literatures. For instance, the sliding effects considered in [10], which can be seen as an additional uncertain parameter, are introduced into the ideal kinematics model, and then a robust adaptive control scheme is proposed on account of the back-stepping control technique. In [11], the slipping is modeled as fast dynamics, and the robust tracking performance is achieved by adopting singular perturbation method when the sliding is small enough. In [12], the sliding effects are eliminated by re-planning predefined paths adaptively according to steady-state tracking errors which are usually caused by modeled slippage effects. Furthermore, the kinematic control law in combination with dynamic observers estimating slip parameters is used in [13, 14] to obtain suitable path-tracking precision. It is worth noting that the complete kinematic model and the offset model of the tractor-trailer system are obtained by utilizing engineering mechanics theory [15]. As a matter of fact, the kinematic model is used to predict the driving trajectory of agricultural vehicles in actual operation, and the offsets dynamics model is used to design path-tracking controllers for farm vehicles. For instance, the straight and circular forward or backward path-tracking problem of a tractor-trailer is solved in [16] by utilizing the Lyapunov method. Later, the kinematic and offset dynamics models for a tractor-trailer system with slips in practical farmland environment are proposed in [17] inspired by the practical work in [15]. Meanwhile, a robust controller is developed in [18] by combining a back-stepping and nonlinear PI control, which ensures that the tractors with steerable trailer can accurately track the desired trajectory under the influences of sideslip.

On the other hand, SMC has been considered as an excellent robust control method in dealing with the nonlinear characteristics of the model, parametric uncertainties and unknown external perturbations [19,20,21,22,23]. Therefore, SMC has been broadly applied in solving agricultural vehicle path tracking problems in recent years [24, 25]. In [26], the kinematic model of vehicles is converted to a perturbed chain system, and then a SMC strategy with robustness to sliding effects and input noise is proposed with the aid of the natural algebraic structure of chained systems. In [27], a nonlinear sliding mode (SM) controller is developed for an autonomous farming tractor with wheel slips and control input saturation. In [28], a composite SM control law is proposed to control the agricultural tractor to precisely track a specified path based on a novel disturbance observer. Moreover, other well-known path-tracking control algorithms, including proportional-integral-derivative control [29], fuzzy control [30] and model predictive control [31], have been applied to address the problem as well.

It should be pointed out that the path-tracking control laws usually contain the heading deviation information of the vehicle [32]. Unfortunately, due to the fact that the loss of GPS signal and the measurement noise of angle sensor always exist in the automatic guidance system, the measured heading deviation is usually inaccurate. Besides, the measurement noises may also lead to abnormal fluctuations of the control signal. From the perspective of real agricultural applications, as the feasible alternative control strategies, the output feedback control techniques can be applied to the path-tracking control design of autonomous agricultural vehicles, so as to attempt to circumvent the aforementioned problems.

Although numerous output feedback control approaches have been proposed in the current research works and widely applied to address the path-following control problem of vehicles [33, 34]. However, there are very few literature works simultaneously handled the sliding effects and the unknown heading deviation, along with the external interference, in the output feedback path-tracking control for autonomous agricultural vehicles. Motivated by the preceding discussion, we will present the robust output-feedback SM control schemes for path-tracking problems of automatics agricultural vehicles considering the external disturbances and sideslip effects. The proposed control methods can not only deal with unknown lump disturbance without using the information of the orientation angle measured by the sensor, but also can improve the transient performance of tracking and weaken the influences of chattering. Specifically, the path-tracking offset dynamics model is first transformed into a canonical form, where the unmodeled dynamics, unknown external disturbances, parameter perturbations in the derived system are seen as additive lumped term. The transformed canonical system then permits simultaneous reconstruction of unknown system state and estimation of unknown lumped disturbance by using second-order RED. Finally, two categories of output-feedback SM control methods are constructed by utilizing the estimated system states and lumped disturbance. Comprehensive simulation results are provided to verify the effectiveness of the proposed path-tracking control schemes.

The main contributions of this study are refined in three aspects:

  1. (1)

    The path-tracking error dynamics is converted to a strict-feedback form under the coordinate transformation, and then immeasurable system state and lumped disturbance are estimated by second-order RED. It is worth noting that using second-order RED can theoretically achieve the property of finite-time convergence, which ensures that the precondition of separation principle can be trivially satisfied.

  2. (2)

    Two robust output feedback controllers based on SM control algorithms and second-order RED are designed, which can guarantee that the lateral deviation and heading error are stabilized to the origin. It should be emphasized that the designed output feedback SOSM control algorithm can improve transient performance and obtain faster system response.

  3. (3)

    The designed control schemes only require the information about the deviation of vehicles’ position rather than the orientation error. In addition, the proposed control methods obviously reduce the effects of chattering. All these nice properties make the proposed controllers more attractive in practical control implementation.

The remainder of this paper are organized in the following manner. Section 2 presents the problem setup of the kinematic model and path-tracking offset dynamics model. The robust output feedback SM control approaches are designed in Sect. 3. Some comprehensive simulation results are given in Sect. 4 to validate the effectiveness of developed guidance approaches. The concluding remarks are provided in Sect. 5. An “Appendix” is attached at the end of the paper, which includes a definition and three key lemmas.

2 System description and modeling

2.1 Notation and problem formulation

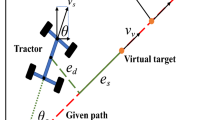
The autonomous agricultural vehicle is simplified by a bicycle model in this paper, and its path-tracking model is depicted in detail in Fig. 1. The steering of the vehicle is manipulated by the front wheels, which can be denoted by a unique virtual wheel along the longitudinal axis of the vehicle for the sake of simplicity. The vehicle is driven by the rear wheels of the agricultural vehicle. The vehicle has a body coordinate frame of \(O'X'Y'\) attached to the center point B of the rear axle of the vehicle with coordinates \(\zeta =(x_t,y_t)^T\) in global coordinate frame OXY. Some necessary variables appearing in the kinematic model and the offset dynamics model are displayed in Table 1.

Fig. 1
figure 1

Schematic diagram of path-tracking model

Full size image
Table 1 Description of variables and points
Full size table

Generally, the control target for path-tracking problem of autonomous agricultural vehicles is to design a suitable controller (i.e., front wheel steering angle \(\delta \)), which can ensure lateral deviation \(l_{os}\) and orientation error \(\theta _{os}\) approach to zero as closely as possible in presence of the external disturbances and wheel slips.

2.2 Kinematic model

In this paper, all angles in Fig. 1 are defined to be positive in the counterclockwise direction. Based on the modeling approach presented in [8], the ideal kinematic model of autonomous agricultural vehicles can be established as follows

$$\begin{aligned} \dot{x_t}&=v\cos \theta _t,~\nonumber \\ \dot{y_t}&=v\sin \theta _t,~\nonumber \\ \dot{\theta _t}&=\frac{v}{l_t}\tan \delta \end{aligned}$$
(1)

where \(x_t\) and \(y_t\) denote the position variables of the vehicle, \({\theta }_{t}\) denotes the orientation variable of the vehicle, and \(\delta \) represents front wheel steering angle, which is considered as the only control quantity. It should be noted here that the longitudinal velocity v is positive if the vehicle is controlled to move forward, and vice versa.

2.3 Offset model

In the light of the modeling method introduced in [16], the widely-used path-tracking offset model of the agricultural vehicles can be modeled as

$$\begin{aligned} {\dot{l}}_{o s}&=-\sigma \left| v\right| \sin \theta _{o s} \nonumber \\ {\dot{\theta }}_{o s}&= \frac{v}{l_{t}} \tan \delta -\sigma \left| v\right| \frac{c_{d} \cos \theta _{o s}}{1+c_{d} l_{o s}} \end{aligned}$$
(2)

where the variable \(\sigma \) denotes the direction parameter. Specifically, assuming that the autonomous agricultural vehicle follows the predefined path in a counterclockwise direction, then \(\sigma \) equals to \(+1\). Also, assuming that the autonomous agricultural vehicle follows the predefined path in a clockwise direction, then \(\sigma \) equals to \(-1\). It should be noted that the absolute value of the front wheel steering angle \(\delta \) is bounded and satisfies \(|\delta |\le {\frac{\pi }{2}}\) in many practical agricultural applications. In order to address the path-tracking control problem of autonomous agricultural vehicles, we will use offset dynamics (2) to complete the design of path-tracking control algorithm in the following section.

For a better interpretation, the vehicle is always considered to be moving forward, and the vehicle tracks the predefined path in a clockwise direction. Under this circumstances, the variable \(\sigma \) in (2) is equal to \(-1\), and the longitudinal speed v is deemed to be greater than zero. On the basis of the above assumptions, by letting \(x_1 = l_{os}\), \(x_2 = v\sin \theta _{os}\), \(u = \tan \delta \), the path-tracking dynamics (2) can be further expressed as follows:

$$\begin{aligned} {\dot{x}}_1&=x_2 \nonumber \\ {\dot{x}}_2&=\frac{v^2 c_d\left( 1-\frac{x_{2}^{2}}{v^{2}} \right) }{1+ c_dx_1}\nonumber \\&\quad +\frac{v^2\left( 1-\frac{x_{2}^{2}}{v^{2}} \right) ^{\frac{1}{2}}}{l_t}u+d_0(t) \end{aligned}$$
(3)

where \(x=[x_1,x_2]\in {\mathbb {R}}^2\) is the system state; \(u\in {\mathbb {R}}\) is the virtual controller; \(d_0(t)\) is unknown additive disturbance, which may be caused by unmodeled dynamics, unknown external disturbances, modeling uncertainties and sliding effects. Here, the control target in the work is to design an output-feedback control input u with access to only the measured output variable \(x_1\) such that the derived error variables \(x_1\) and \(x_2\) in system (3) will be converge to the origin as much as possible.

In what follows, we will give the basic assumptions about the unknown disturbance and desired path.

Assumption 1

The desired path and its first-order derivative are smooth, bounded and known.

Remark 1

It is important to note that, the desired path tracked by agricultural vehicles is generated by the path planner of the navigation system. In practical agricultural applications, the desired path either consists of circular arcs with a given radius or straight lines to be tracked at a specified reference velocity. Therefore, the desired path and its first derivative are usually smooth, bounded and known, which implies that Assumption 1 is reasonable.

Assumption 2

The unknown disturbance \(d_0(t)\) and its first-order derivatives \({\dot{d}}_0(t)\) are continuously bounded functions, i.e., \(\left| d_0(t)\right| \le \varGamma _0\) and \(\left| {\dot{d}}_0(t)\right| \le \varGamma _1\), where \(\varGamma _0\) and \(\varGamma _1\) are two positive constants.

Remark 2

It should be noted that Assumption 2 is frequently-used when dealing with disturbance in most practical scenarios, and similar assumptions can also be found in the references [24, 27]. The unknown disturbance \(d_0(t)\) in system (3) may be caused by unmodeled dynamics, unknown external disturbances, modeling uncertainties and sliding effects. As a matter of fact, the influence of \(d_0(t)\) on the path-tracking system always exists and is usually limited, which implies that \(d_0(t)\) can be regarded as a continuous and bounded signal. Meanwhile, it is noted that the actual operating speed of agricultural vehicles is usually slow, which will cause the disturbance \(d_0(t)\) to change slowly. Therefore, the derivative of \(d_0(t)\) can also be considered bounded. On these basis, Assumptions 2 is reasonable.

It should be pointed out that only the lateral deviation information can be obtained here, so we need to reconstruct the unknown state \(x_2\) in system (3) by designing a suitable state estimator. Consequently, in order to facilitate the design of estimator to deal with unknown system state \(x_2\), we can re-express the derivative of \(x_2\) as follows

$$\begin{aligned} {\dot{x}}_2&=\frac{v^2 c_d}{1+ c_dx_1}-\frac{ c_dx_{2}^{2}}{1+ c_dx_1} +d_0(t)+\frac{v^2}{l_t}u\nonumber \\&\quad +\frac{v^2}{l_t}\Big [\Big ( 1-\frac{x_{2}^{2}}{v^{2}} \Big )^{\frac{1}{2}}-1\Big ]u\nonumber \\&\quad =f(x_1)+g_mu +\varDelta \end{aligned}$$
(4)

where \(f(x_1)=\frac{v^2 c_d}{1+ c_dx_1}\), \(g_m=\frac{v^2}{l_t}\) and the unknown term \(\varDelta \) denotes the lumped disturbance, which can be expressed as follows

$$\begin{aligned} \varDelta&=-\frac{c_d{x_{2}^{2}}}{1+c_dx_1}\nonumber \\&\quad +\frac{v^2}{l_t}\left[ \left( 1-\frac{x_{2}^{2}}{v^{2}}\right) ^{\frac{1}{2}}-1\right] u +d_0(t). \end{aligned}$$
(5)

In this situation, the original offset dynamics (3) can be rewritten as follows

$$\begin{aligned} {\dot{x}}_1&=x_2 \nonumber \\ {\dot{x}}_2&=f(x_1)+g_mu +\varDelta . \end{aligned}$$
(6)

Obviously, system (6) can be regarded as the strict-feedback form. In what follows, we will design the output feedback path-tracking controller based on system (6), which not only greatly reduces the complexity of control design, but also uses only system output variable \(x_1\). Normally, the lumped disturbance \(\varDelta \) in system (6) is required to further satisfy the following assumption.

Assumption 3

Suppose that the lumped disturbance \(\varDelta \) is differentiable and bounded, and \({\dot{\varDelta }}\) is also bounded. i.e., there are two unknown positive constants \(\varDelta _0\) and \(\varDelta _1\) such that \(|\varDelta |\le \varDelta _0\) and \(|{\dot{\varDelta }}|\le \varDelta _1\), respectively.

Remark 3

Generally speaking, the system states \(x_1\) and \(x_2\) change very slowly and are bounded. The virtual control input u is always considered continuous and bounded from a practical application point of view, because u is related to the front wheel steering angle and only continuous control signals are allowed. Hence, Assumption 3 is valid in practical scenarios.

3 Design of output feedback controller

In this section, the output feedback SM controllers are designed for system (6) subject to the unknown bounded lumped disturbance. First of all, the second-order RED is constructed to simultaneously reconstruct the system full states in a finite time and provide an estimate of the unknown lumped disturbance in system (6). Then, two output feedback SM controllers are proposed to address the path-tracking control issue for autonomous agricultural vehicles without measuring the orientation angle information. Finally, the observer errors are taken into account during the stability analysis of the resulting closed-loop system.

3.1 Second-order RED

In order to reconstruct the unknown state \(x_2\) and estimate the lumped disturbance \(\varDelta \) in system (6), a second-order RED is given base on [36] in the following form

$$\begin{aligned} \dot{\hat{x}}_1&=L_1{\left\lfloor x_1-\hat{ x}_1\right\rceil }^{\frac{2}{3}}+\hat{x}_2 \nonumber \\ \dot{\hat{x}}_2&=f({x_1})+g_m u+L_2{\left\lfloor x_1-\hat{x}_1\right\rceil }^{\frac{1}{3}}+\hat{x}_3 \nonumber \\ \dot{\hat{x}}_3&=L_3{\left\lfloor x_1-\hat{x}_1\right\rceil }^{0}, \end{aligned}$$
(7)

where \(L_1\), \(L_2\) and \(L_3\) are positive observer parameters which need to be properly selected; \({\hat{x}}_1\), \({\hat{x}}_2\) and \({\hat{x}}_3\) denote the observed states of \(x_1\), \(x_2\) and \(\varDelta \), respectively. Then, a technical lemma will be presented in the following text.

Lemma 1

Provided that the second-order RED is constructed as (7), then there exists a time instant \(T_1\) such that the unknown state \(x_2\) and the unknown lump disturbance \(\varDelta \) can be estimated by \(\hat{x}_2\) and \(\hat{x}_3\) respectively when \(t\ge T_1\).

Proof

Define the error variables as \(e_1=x_1-\hat{x}_1\), \(e_2=x_2-\hat{x}_2\) and \(e_3=-\hat{x}_3+\varDelta \). Then, taking the time derivative of \(e_1\) along system (6) yields

$$\begin{aligned} {\dot{e}}_1&={\dot{x}}_1-\dot{\hat{x}}_1\nonumber \\&=-L_1{\left\lfloor x_1-\hat{x}_1\right\rceil }^{\frac{2}{3}}+x_2-\hat{x}_2\nonumber \\&=-L_1{\left\lfloor e_1\right\rceil }^{\frac{2}{3}}+e_2. \end{aligned}$$
(8)

Similarly, we can also easily obtain

$$\begin{aligned} {\dot{e}}_2&={\dot{x}}_2-\dot{\hat{x}}_2\nonumber \\&=-L_2{\left\lfloor x_1-\hat{x}_1\right\rceil }^{\frac{1}{3}}-\hat{x}_3+\varDelta \nonumber \\&=-L_2{\left\lfloor e_1\right\rceil }^{\frac{1}{3}}+e_3. \end{aligned}$$
(9)

By Assumption 3, we have

$$\begin{aligned} {\dot{e}}_3&=-\dot{\hat{x}}_3+{\dot{\varDelta }}\nonumber \\&=-L_3{\left\lfloor x_1-\hat{ x}_1\right\rceil }^{0}+{\dot{\varDelta }}. \end{aligned}$$
(10)

Then, the following error dynamics can be obtained as

$$\begin{aligned}&{\dot{e}}_1=-L_1{\left\lfloor e_1\right\rceil }^{\frac{2}{3}}+e_2\nonumber \\&{\dot{e}}_2=-L_2{\left\lfloor e_1\right\rceil }^{\frac{1}{3}}+e_3\nonumber \\&\dot{{e}}_3=-L_3{\left\lfloor {e_1}\right\rceil }^{0}+{\dot{\varDelta }}. \end{aligned}$$
(11)

Evidently, using Assumption 3 to the third equation of (11), we can easily obtain a differential inclusion as follows

$$\begin{aligned} {\dot{e}}_3\in -L_3{\left\lfloor e_1\right\rceil }^{0}+[-\varDelta _1,\varDelta _1]. \end{aligned}$$
(12)

This implies that the solutions of (11) can be understood in the Filippov sense [37]. Thus, the finite-time stability analysis of error dynamics (11) is not much different from the main result presented in [38] and is therefore omitted here for simplicity. As a result, it can be inferred that the error variables \(e_1\), \(e_2\) and \(e_3\) will be stabilized to the origin for \(t>T_1\) by choosing appropriate observer gains \(L_1\), \(L_2\) and \(L_3\). That is, once the error variables \(e_1\), \(e_2\) and \(e_3\) converge to the origin, it can be obtained that \(x_1=\hat{x}_1\), \(x_2=\hat{x}_2\) and \(\hat{x}_3=\varDelta \). This completes the proof of Lemma 1. \(\square \)

Remark 4

On the basis of the research results given in [36], it can be concluded that the observer parameters \(L_i(i=1,2,3)\) have an impact on the smoothness of the estimated state \(\hat{x}_i(i=1,2,3)\). It follows from [38] that in order to acquire the convergence of the observation errors, the sufficiently large parameters \(L_i\) should to be selected. Actually, the possible selection of these observer gains can be given as \(L_1=6{\root 3 \of {L}}\), \(L_2=11\root 2 \of {{L}}\) and \(L_3=6{L}\), which can well guarantee the the finite-time stabilization of observation errors. Here the variable parameter L is utilized to tune the transient performance of online observation process.

Remark 5

The necessity and advantages of designing a second-order RED in (7) can be summarized in the following three aspects. Firstly, due to the fact that the loss of GPS signal and the measurement noise of angle sensor always exist in the automatic guidance system, the measured heading deviation is usually inaccurate. However, the state \(x_2\) in system (3) is obviously related to the heading deviation, which means that \(x_2\) cannot be completely measurable. In this case, the state feedback controller previously designed based on system (3) will not work. Secondly, system (3) contains an unknown lumped disturbance \(\varDelta \), which causes serious negative effects (i.e. destroying system dynamic and steady-state performance) on the controlled system. Based on these points, the second-order RED in this paper is constructed to simultaneously rapidly reconstruct the full state variables of the system (3) and provides an accurate estimate for the unknown disturbance \(\varDelta \). Thirdly, using second-order RED can theoretically achieve the property of finite-time convergence, which ensures that the precondition of separation principle can be trivially satisfied. This indicates that the controller and second-order RED can be designed independently.

3.2 Design of output feedback FOSM controller

Since system state \(x_2\) is not available, we will use the observer state \(\hat{x}_2\) obtained by the second-order RED (7) in actual control. Note that the first step in designing a SM controller is to select a suitable SM surface. Hence, to achieve the control target of path tracking, we can choose the SM surface s as follows

$$\begin{aligned} {s}=\zeta x_1+\hat{x}_2 \end{aligned}$$
(13)

where \(\zeta >0\) is a weight coefficient, which represent the proportion of the lateral offset for the whole SM surface. Taking the derivative of (13) along system (6) and (7) produces

$$\begin{aligned} {\dot{s}}=\zeta \hat{x}_2+f({x_1}) +g_mu+L_2{\left\lfloor e_1\right\rceil }^{\frac{1}{3}}+\hat{x}_3+D_1(t) \end{aligned}$$
(14)

where \(g_m=\frac{v^2}{l_t}\) and \(D_1(t)=\zeta e_2\). Note that the bound of the observation error \(e_2\) is usually small due to the finite-time convergence property of second-order RED. Therefore, we can find a positive real number \({\bar{D}}_1\) such that \(|D_1(t)|\le {\bar{D}}_1\).

In view of the above detailed analysis, the output feedback FOSM control law can be constructed as

$$\begin{aligned} u&=-\frac{1}{g_m}\Big ( \zeta \hat{x}_2+f\left( {x}_1 \right) +L_2{\left\lfloor e_1\right\rceil }^{\frac{1}{3}}\Big .\nonumber \\&\quad +\int _0^t{L_3}{{\,\mathrm{\mathrm sign }\,}}\left( e_1 \right) d\tau \Big .+k_1\cdot {{\,\mathrm{\mathrm sign }\,}}({s})+k_2s \Big ) \end{aligned}$$
(15)

where \(k_1>{\bar{D}}_1\) and \(k_2>0\).

Now, we will give the first main result of this work, which can be expressed by the following theorem.

Theorem 1

Given path-tracking offset dynamic system (6) with unknown bounded lumped disturbance \(\varDelta \) under Assumption 3, the output feedback FOSM controller (15) guarantees that the system states \(x_1\) and \(x_2\) will be asymptotically stabilized to the origin.

Proof

: The detailed proof of Theorem 1 can be summarized into three steps. The first step is that the output feedback FOSM controller will be designed to finite-time stabilize the sliding variable s. We then analyze that the system states will not escape to infinity in a finite time. Finally, the rigorous theoretical analysis is given to demonstrate that the path-tracking errors are asymptotically stabilized to the origin.

Step 1: Finite-time stability of sliding variable

Putting controller (15) into (14) gives

$$\begin{aligned} {\dot{s}}=-k_1\cdot {{\,\mathrm{\mathrm sign }\,}}(s)-k_2s+D_1(t). \end{aligned}$$
(16)

We select a Lyapunov function candidate as \(V_1(s)=\frac{1}{2}s^2\). Then, differentiating the Lyapunov function \(V_1(s)\) along the SM dynamics (16) yields

$$\begin{aligned} {\dot{V}}_1(s)&=s\left( -k_1\cdot {{\,\mathrm{\mathrm sign }\,}}(s)-k_2s+D_1(t)\right) \nonumber \\&\le -\left( k_1-{\bar{D}}_1\right) |s|. \end{aligned}$$
(17)

Note that \(k_1>{\bar{D}}_1\) and \(k_2>0\). It can be shown that \({\dot{V}}_1(s)\le -\varrho V^\frac{1}{2}\) with \(\varrho =\sqrt{2}{(k_1-{\bar{D}}_1)}\) being a positive constant. With the fact \(0<\frac{1}{2}<1\) and the finite-time Lyapunov theory presented in [40] in mind, one can conclude that the sliding variable s is finite-time stabilized to the origin.

Step 2: Finite-time boundedness of system states

We select a finite-time bounded function inspired by [41] as

$$\begin{aligned} V_1(x_1,x_2,s)=\frac{1}{2}\left( x_1^2+x_2^2+s^2\right) . \end{aligned}$$
(18)

Differentiating the function \(V_1(x_1,x_2,s)\) along system (6) and (16) yields

$$\begin{aligned} {\dot{V}}_1(x_1,x_2,s)&=s {\dot{s}}+x_1{\dot{x}}_1+x_2{\dot{x}}_2\nonumber \\&=-(k_1|s|+k_2s^2-sD_1(t))+x_1{x}_2\nonumber \\&\quad +x_2({\dot{e}}_2+{\dot{s}}-\zeta {\dot{x}}_1). \end{aligned}$$
(19)

Note that the uncertainties \(D_1(t)\) and \({\dot{e}}_2\) are bounded satisfying \(|D_1(t)|\le {\bar{D}}_1\) and \(|{\dot{e}}_2|\le \eta _0\) with \(\eta _0\) being a positive constant. Therefore, it can be deduced from (19) that

$$\begin{aligned}&{\dot{V}}_1(x_1,x_2,s)\nonumber \\&\quad \le |k_1 s|+{k_2}s^2+|{{\bar{D}}_1}s| +\left| x_1x_2 \right| +\left| x_2\eta _0 \right| \nonumber \\&\qquad +\left| k_1x_2 \right| +{k_2}\left| x_2s \right| +\left| {\bar{D}}_1x_2 \right| +\zeta x_2^2\nonumber \\&\quad \le \frac{ k_1^2+s^2}{2}+{k_2}s^2+\frac{{\bar{D}}_1^{2} +s^{2}}{2}+\frac{x_{1}^{2}+x _{2}^{2}}{2}\nonumber \\&\qquad +\frac{\eta _{0}^{2}+x_{2}^{2}}{2}+\frac{k_{1}^{2} +x_{2}^{2}}{2}+{k_2}\frac{s^2+x_{2}^{2}}{2}\nonumber \\&\qquad +\frac{x_{1}^{2}+{\bar{D}}_1^{2}}{2}+\zeta x_2^2 \nonumber \\&\quad \le K_{v1}{V}_1(x_1,x_2,s)+L_{v1} \end{aligned}$$
(20)

where \(K_{v1}=\max \text {\{}\frac{4+2\zeta +k_2}{2},2+3k_2,1\}\) and \(L_{v1}=\frac{\eta _0^2+2k_1+2{\bar{D}}^2}{2}\) are two positive constants. Then, it can be concluded from (20) that

$$\begin{aligned}&{V_1}(x_1,x_2,s)\nonumber \\&\quad \le \Big ( V\Big ( x_1(0),x_2(0),s(0) \Big ) +\frac{L_{v1}}{K_{v1}} \Big ) e^{K_{v1}}-\frac{L_{v1}}{K_{v1}}. \end{aligned}$$
(21)

Therefore, it can be deduced from (21) that for any bounded time T, the function \(V(x_1,x_2,s)\) is bounded during [0, T], which means that system states \(x_1\), \(x_2\) and sliding variable s will not diverge to infinity for \(t\in (0,T]\). According to the definition of \(x_1\) and \(x_2\), it can be obtained that the lateral deviation \(l_{os}\) and the orientation error \(\theta _{os}\) cannot escape to infinity in finite time.

Step 3: Asymptotical stability of path-tracking errors

Since the sliding variable s converges to the origin in finite time, there is a time instant \(T_2\) after finite time \(t\ge T_2\), \(s=0\) is hold. Then, it can be derived from (13) that \(\hat{x}_2=-\zeta x_1\). Later, the following system dynamics can be further presented as follows

$$\begin{aligned} {\dot{x}}_1=-\zeta x_1+e_2,~~x_2=-\zeta x_1+e_2. \end{aligned}$$
(22)

Meanwhile, from (11), the observer error \(e_2\) converges to zero when \(t>T_1\). Hence, a time instant T can be defined as \(T=\max \{T_1,T_2\}\), one has for \(t>T\),

$$\begin{aligned}&{\dot{x}}_1=-\zeta x_1,~~x_2=-\zeta x_1, \end{aligned}$$
(23)

which implies that the system states \(x_1\) and \(x_2\) are asymptotically stable by selecting a suitable positive definite parameter \(\zeta \). By the fact that \(x_1 = l_{os}\) and \(x_2 = v\sin \theta _{os}\), it can also demonstrate that the output-feedback FOSM controller (15) can ensure that both lateral offset \(l_{os}\) and orientation error \(\theta _{os}\) converge to the origin in the presence of unknown bounded lumped disturbances. \(\square \)

Obviously, it can be seen that the discontinuous term existing in controller (15) can bring the undesirable chattering phenomenon, which may cause serious damage to the actuator and even destroy the system in a very short period. To alleviate the effect of chattering, the signum function can be approximated by the continuous hyperbolic tangent function such that \({{\,\mathrm{\mathrm sign }\,}}(s)=\tanh (\gamma _1 s)\) where \(\gamma _1\) is a positive constant. In addition, we can perform the inverse transformation of the virtual control input \(u= \tan \delta \), and then the actual front wheel steering angle can be generated as follows

$$\begin{aligned} \delta =&\arctan \left( -\frac{1}{g_m} \Big [\zeta \hat{x}_2 +\frac{v^2 c_d}{1+ c_dx_1} +L_2{\left\lfloor e_1\right\rceil }^{\frac{1}{3}}\Big .\right. \\&\quad +\int _0^t{L_3}{{\,\mathrm{\mathrm sign }\,}}\left( e_1 \right) d\tau \left. \Bigg .+k_1\cdot \tanh (\gamma _1\cdot {s})+k_2s \Big ]\right) . \end{aligned}$$

It can be clearly observed from (22) that the system state \(x_1\) is asymptotically stable only when the observation error \(e_2\) converges to zero for \(t>T_1\), which means that the lateral offset cannot converge to zero by utilizing the output feedback FOSM control algorithm during time interval \((0,T_1]\). As a matter of fact, the transient response of the lateral deviation has important implications for the crossing and turning operations of agricultural vehicles. In the next section, we will present a novel approach to further improve the transient path-tracking performance using the output feedback SOSM control strategy.

3.3 Design of output feedback SOSM controller

With the fact that \(e_1=x_1-\hat{x}_1\) and \(e_2=x_2-\hat{x}_2\), one has

$$\begin{aligned}&{\dot{x}}_1=\hat{x}_2+e_2\nonumber \\&\dot{\hat{x}}_2= f({x_1})+g_m u+L_2{\left\lfloor e_1\right\rceil }^{\frac{1}{3}}+\hat{x}_3, \end{aligned}$$
(24)

where \(f(x_1)=\frac{v^2 c_d}{1+ c_dx_1}\), \(g_m=\frac{v^2}{l_t}\) and \(\hat{x}_3=\int _0^t{L_3}{{\,\mathrm{\mathrm sign }\,}}\left( e_1 \right) d\tau .\)

First of all, considering the path-tracking control objective of agricultural vehicles, we can define lateral deviation \(x_1\) as sliding variable s. Then, we can directly calculate the two times derivative of the sliding variable s along system (24) as

$$\begin{aligned} \ddot{s}=f({x_1})+g_m u+L_2{\left\lfloor e_1\right\rceil }^{\frac{1}{3}}+\hat{x}_3+{\dot{e}}_2. \end{aligned}$$
(25)

Letting \({\tilde{x}}=(x_1,{e}_1)\), system (25) can be further expressed as follows

$$\begin{aligned} \ddot{s}=a(t,{\tilde{x}})+b(t,{\tilde{x}})u+{\dot{e}}_2 \end{aligned}$$
(26)

where \(b(t,{\tilde{x}})=g_m\), and \(a(t,{\tilde{x}})\) is expressed as

$$\begin{aligned} a(t,{\tilde{x}})=f({x_1})+L_2{\left\lfloor e_1\right\rceil }^{\frac{1}{3}} +\int _0^t{L_3}{{\,\mathrm{\mathrm sign }\,}}\left( e_1 \right) d\tau . \end{aligned}$$

For the sake of facilitating the subsequent control design, by setting \(s_1=s\) and \({s}_2={\dot{s}}_1\), then system (26) can be described by

$$\begin{aligned} {\dot{s}}_1&={s}_2\nonumber \\ \dot{{s}}_2&=a(t,\tilde{{x}})+b(t,{\tilde{x}})u+{\dot{e}}_2. \end{aligned}$$
(27)

Next, the second result of this work is given by the following theorem.

Theorem 2

Given path-tracking offset dynamic system (6) with unknown bounded lumped disturbance \(\varDelta \) under Assumption 3, if the output feedback SOSM controller is constructed as

$$\begin{aligned} u&=-\frac{1}{g_m}\Bigg (\beta _2{\left\lfloor {\left\lfloor {\dot{s}}\right\rceil }^{{\frac{3}{2}}} +\beta _1^{{\frac{3}{2}}}{s}\right\rceil }^{{\frac{1}{3}}}\nonumber \\&\quad +f({x_1})+L_2{\left\lfloor e_1\right\rceil }^{\frac{1}{3}}\Bigg .\Bigg .\nonumber \\&\quad +\int _0^t{L_3}{{\,\mathrm{\mathrm sign }\,}}\left( e_1 \right) d\tau +\beta _3\cdot {{\,\mathrm{\mathrm sign }\,}}\!\left( {\left\lfloor {\dot{s}}\right\rceil }^{{\frac{3}{2}}}+\beta _1^{{\frac{3}{2}}}{s}\right) \Bigg ) \end{aligned}$$
(28)

where the control gains \(\beta _1>2\), \(\beta _3\ge \eta _0=\sup (|{\dot{e}}_2|)\) and

$$\begin{aligned} \beta _2 \ge (1+ {\frac{32}{27}}+{\tilde{c}}_2) \end{aligned}$$
(29)

with \({\tilde{c}}_2= {\frac{5}{3}\times 2^{\frac{1}{3}}\beta _1^{\frac{3}{2}}+ \Big ( \frac{10}{9}\times 2^{\frac{1}{3}}\beta _1^{\frac{5}{2}}\Big )^{\frac{3}{2}}}\), then the system states \(x_1\) and \(x_2\) will be finite-time stabilized to the origin.

Proof

: The detailed proof of Theorem 2 can also be divided into three steps. First of all, the finite-time stability of the resulting closed-loop SM dynamics will be validated by using the modified API technique [39]. Then, we will further analyze that the corresponding system states are always bounded in a finite-time interval. Finally, the finite-time stability of the path-tracking errors will be verified to accomplish the proof.

Step 1: Finite-time stability of sliding variables

Let us select a Lyapunov function candidate as follows

$$\begin{aligned} V_1(s_1)=\frac{3}{7}|s_1|^{\frac{7}{3}}. \end{aligned}$$
(30)

Then, the time derivative of \(V_1(s_1)\) along SM dynamics (27) can be calculated as

$$\begin{aligned} {\dot{V}}_1(s_1)&= {\left\lfloor s_1\right\rceil }^{\frac{4}{3}}\cdot {s}_2\nonumber \\&={\left\lfloor s_1\right\rceil }^{\frac{4}{3}}{{s}_2^*}+ {\left\lfloor s_1\right\rceil }^{\frac{4}{3}}({{s}_2}-{{s}_2^*}) \end{aligned}$$
(31)

where \({{s}_2^*}\) is a virtual control input to be determined later.

By letting \(\xi _1=s_1\), the virtual control law \({{s}_2^*}\) can be designed as

$$\begin{aligned} {s}_2^*=-\beta _1 {\left\lfloor \xi _1\right\rceil }^{\frac{2}{3}} \end{aligned}$$
(32)

with \(\beta _1\ge 2\). Putting (32) into (31) yields

$$\begin{aligned} {\dot{V}}_1(s_1)\le -2 |\xi _1|^{2}+ {\left\lfloor \xi _1\right\rceil }^{\frac{4}{3}}({{s}_2}-{{s}_2^*}). \end{aligned}$$
(33)

In view of the virtual control law \({{s}_2^*}\), we define \(\xi _2={\left\lfloor s_2\right\rceil }^{\frac{3}{2}}-{\left\lfloor {s}_2^*\right\rceil }^{\frac{3}{2}}\) and let the function \(V_2(s_1, {{s}_2})\) be defined as

$$\begin{aligned} V_2(s_1, {{s}_2})=V_1(s_1)+W_2(s_1,{{s}_2}) \end{aligned}$$
(34)

where \(W_2(s_1, {{s}_2})=\int _{{s}_2^*}^{s_2}{\left\lfloor {\left\lfloor \mu \right\rceil }^{\frac{3}{2}} -{\left\lfloor {s}_2^*\right\rceil }^{\frac{3}{2}}\right\rceil }^{\frac{5}{3}}d\mu \). From Propositions B.1 and B.2 given in [35], we can easily obtain that \(V_2(s_1, {{s}_2})\) is continuously differentiable (i.e., \(C^1\)) and positive definite function. Therefore, the time derivative of the Lyapunov function \(V_2(s_1, {{s}_2})\) along system (27) can be calculated as follows

$$\begin{aligned} {\dot{V}}_2(s_1, {{s}_2})&\le -2 |\xi _1|^{{2}}+ {\left\lfloor \xi _1\right\rceil }^{{\frac{4}{3}}}({s_2}-{{s}_2^*})\nonumber \\&\quad + \frac{\partial W_2(s_1, {{s}_2})}{\partial s_1}{\dot{s}}_1 +\frac{\partial W_2(s_1, {{s}_2})}{\partial s_2}{\dot{s}}_2 \nonumber \\&=-2|\xi _1|^{{2}}+{\left\lfloor \xi _2\right\rceil }^{{\frac{5}{3}}}{\dot{{{s}}}_2} + {\left\lfloor \xi _1\right\rceil }^{{\frac{4}{3}}}({s_2}-{{s}_2^*})\nonumber \\&\quad +\frac{\partial W_2(s_1, {{s}_2})}{\partial s_1}{\dot{s}}_1. \end{aligned}$$
(35)

In the following, we will estimate the terms \({\left\lfloor \xi _1\right\rceil }^{\frac{4}{3}}({{s}_2}-{{s}_2^*})\) and \(\frac{\partial W_2(s_1, {s}_2)}{\partial s_1}{\dot{s}}_1\) in inequality (35) step by step.

By the fact that \(0<{\frac{2}{3}}< 1\), one can obtain from Lemma A.1 that

$$\begin{aligned} {\left\lfloor \xi _1\right\rceil }^{{\frac{4}{3}}}({{s}_2}-{{s}_2^*})&\le |\xi _1|^{{\frac{4}{3}}} \left| {\left\lfloor {s}_2\right\rceil }^{{\frac{3}{2}\cdot {\frac{2}{3}}}} -{\left\lfloor {{s}_2^*}\right\rceil }^{{\frac{3}{2}\cdot {\frac{2}{3}}}}\right| \nonumber \\&\le 2^{{\frac{1}{3}}} |\xi _1|^{{\frac{4}{3}}}|\xi _2|^{{\frac{2}{3}}}. \end{aligned}$$
(36)

Applying Lemma A.2 to (36) gets

$$\begin{aligned} {\left\lfloor \xi _1\right\rceil }^{{\frac{4}{3}}}({{s}_2}-{{s}_2^*}) \le \frac{1}{2} |\xi _1|^{{2}}+c_2|\xi _2|^{{2}} \end{aligned}$$
(37)

where \(c_2 = {\frac{32}{27}}.\)

On the other hand, one has from Lemma A.1 that

$$\begin{aligned} \left| \frac{\partial W_2(s_1, {s}_2)}{\partial s_1}{\dot{s}}_1\right|&\le {\frac{5}{3}}|{s}_2-{{s}_2^*}||\xi _2|^{\frac{2}{3}} \left| \frac{\partial {\left\lfloor {{s}_2^*}\right\rceil }^{{\frac{3}{2}}}}{\partial s_1}{\dot{s}}_1\right| \nonumber \\&\le {\frac{5}{3}\times } 2^{{\frac{1}{3}}}|\xi _2|^{{\frac{4}{3}}} \left| \frac{\partial {\left\lfloor {{s}_2^*}\right\rceil }^{{\frac{3}{2}}}}{\partial s_1}{\dot{s}}_1\right| . \end{aligned}$$
(38)

Taking \({{s}_2^*}=-\beta _1 {\left\lfloor \xi _1\right\rceil }^{{\frac{2}{3}}}\) into account, it can be shown that

$$\begin{aligned} \left| \frac{\partial {\left\lfloor {{s}_2^*}\right\rceil }^{\frac{3}{2}}}{\partial s_1}\right| \le \beta _1^{{\frac{3}{2}}}. \end{aligned}$$
(39)

By using Lemma A.3, one can get from (39) that

$$\begin{aligned} \left| \frac{\partial {\left\lfloor {{s}_2^*}\right\rceil }^{{\frac{3}{2}}}}{\partial s_1}{\dot{s}}_1\right| \le \beta _1^{{\frac{3}{2}}} \left( |\xi _2|^{{\frac{2}{3}}}+\beta _1|\xi _1|^{{\frac{2}{3}}}\right) . \end{aligned}$$
(40)

Putting (40) into (38) produces

$$\begin{aligned} \left| \frac{\partial W_2(s_1, {s}_2)}{\partial s_1}{\dot{s}}_1\right|&\le {\frac{5}{3}\times } 2^{{\frac{1}{3}}}|\xi _2|^{{\frac{4}{3}}} {\beta _1^{\frac{3}{2}}} \left( |\xi _2|^{{\frac{2}{3}}}+\beta _1|\xi _1|^{{\frac{2}{3}}}\right) . \end{aligned}$$
(41)

Applying Lemma A.2 for (41) leads to

$$\begin{aligned} \left| \frac{\partial W_2(s_1, {s}_2)}{\partial s_1}{\dot{s}}_1\right| \le \frac{1}{2} |\xi _1|^{{2}}+{\tilde{c}}_2 |\xi _2|^{{2}} \end{aligned}$$
(42)

where \({\tilde{c}}_2 = {\frac{5}{3}\times 2^{\frac{1}{3}}\beta _1^{\frac{3}{2}}+ \left( \frac{10}{9}\times 2^{\frac{1}{3}}\beta _1^{\frac{5}{2}}\right) ^{\frac{3}{2}}}.\)

Substituting (37) and (42) into (35) gets

$$\begin{aligned} {\dot{V}}_2(s_1,{s}_2) \le&-|\xi _1|^{{2}} + \left( c_2+{\tilde{c}}_2 \right) |\xi _2|^{{2}} +{\left\lfloor \xi _2\right\rceil }^{{\frac{5}{3}}}{{\dot{s}}_2} \nonumber \\ \le&-|\xi _1|^{{2}} + \left( c_2+{\tilde{c}}_2 \right) |\xi _2|^{{2}}\nonumber \\&+{\left\lfloor \xi _2\right\rceil }^{{\frac{5}{3}}}\left[ a(t,{\tilde{x}})+b(t,{\tilde{x}})u+{\dot{e}}_2\right] . \end{aligned}$$
(43)

Note that \({\dot{e}}_2\) usually is bounded and satisfies \(|{\dot{e}}_2|\le \eta _0\) with \(\eta _0\) being a positive constant. Design the controller u as

$$\begin{aligned} u=-\frac{1}{g_m}\left( \beta _2{\left\lfloor \xi _2\right\rceil }^{{\frac{1}{3}}} +a(t,{\tilde{x}})+{\beta _3}\cdot {{\,\mathrm{\mathrm sign }\,}}(\xi _2)\right) \end{aligned}$$
(44)

where \(\beta _2 \ge (1+ c_2+{\tilde{c}}_2)\) and \(\beta _3\ge \eta _0\).

Putting controller (44) into (43) arrives at

$$\begin{aligned}&{\dot{V}}_2(s_1, {s}_2)\le -\left( \left| \xi _1\right| ^{{2}} +\left| \xi _2\right| ^{{2}}\right) . \end{aligned}$$
(45)

By the definition of \(W_2(s_1, {{s}_2})\) and Lemma A.2, one has

$$\begin{aligned} W_2(s_1,{s}_2)&= \int _{{s}_2^*}^{{s}_2}{\left\lfloor {\left\lfloor \mu \right\rceil }^{\frac{3}{2}} -{\left\lfloor {s}_2^*\right\rceil }^{\frac{3}{2}}\right\rceil }^{\frac{5}{3}}d\mu \nonumber \\&\le |{s}_2-{s}_2^*||\xi _2|^{\frac{5}{3}} =2^{\frac{1}{3}}|\xi _2|^{\frac{7}{3}}. \end{aligned}$$
(46)

A careful observation on \(V_2(s_1, s_2)=V_1(s_1)+W_2(s_1,s_2)\) and (46) shows that

$$\begin{aligned} V_2(s_1, {{s}_2})&=\frac{3}{7}|\xi _1|^{\frac{7}{3}}+\int _{{s}_2^*}^{{s}_2} {\left\lfloor {\left\lfloor \mu \right\rceil }^{\frac{3}{2}}-{\left\lfloor {s}_2^*\right\rceil }^{\frac{3}{2}}\right\rceil }^{\frac{5}{3}}d\mu \nonumber \\&\le \frac{3}{7}|\xi _1|^{\frac{7}{3}}+2^{\frac{1}{3}}|\xi _2|^{\frac{7}{3}}\nonumber \\&\le 2^{\frac{1}{3}}\left( |\xi _1|^{\frac{7}{3}}+|\xi _2|^{\frac{7}{3}}\right) . \end{aligned}$$
(47)

Letting \(\lambda =2^{-\frac{2}{7}}\) and \({\bar{\alpha }}={\frac{6}{7}}\), it is clear that

$$\begin{aligned} {\dot{V}}_2(s_1, {s}_2)+\lambda V_2^{{\bar{\alpha }}}(s_1, {{s}_2})\le 0 \end{aligned}$$
(48)

With the fact \(0<{\bar{\alpha }}<1\) and the Lyapunov theory presented in [40] in mind, it can be obtained that SM dynamics (27) can be globally finite-time stabilized by controller (44). It is noted that controller (44) can be represented as (28). It also shows that system (27) can be globally finite-time stabilized by controller (28).

Step 2: Finite-time boundness of system states

Define a finite-time bounded function inspired by [41] for SOSM dynamics (27), which can be expressed as follows

$$\begin{aligned} {V}(s_1,s_2)={\frac{1}{2}}(s_1^2+s_2^2). \end{aligned}$$
(49)

Differentiating the function \({V}(s_1,s_2)\) along the closed-loop system (27) and (28) yields

$$\begin{aligned}&{\dot{V}}(s_1,s_2)=s_1{\dot{s}}_1+s_2{\dot{s}}_2\nonumber \\&\le |s_1s_2|+s_2\left( -\beta _2{\left\lfloor \xi _2\right\rceil }^{{\frac{1}{3}}} -\beta _3{{\,\mathrm{\mathrm sign }\,}}(\xi _2)+{\dot{e}}_2\right) . \end{aligned}$$
(50)

Note that \(\xi _2={\left\lfloor s_2\right\rceil }^{{\frac{3}{2}}}-{\left\lfloor {s}_2^*\right\rceil }^{{\frac{3}{2}}}\) can be further rewritten as \(\xi _2={\left\lfloor s_2\right\rceil }^{{\frac{3}{2}}}+\beta _1^{{\frac{3}{2}}}{s_1}\). Hence, one can conclude from Lemma A.3 that

$$\begin{aligned} |\xi _2|^{\frac{1}{3}}&=\left| {\left\lfloor s_2\right\rceil }^{{\frac{3}{2}}} +\beta _1^{{\frac{3}{2}}}{s_1}\right| ^{\frac{1}{3}}\nonumber \\&\le \big (|{s_2}|^{\frac{3}{2}}+\beta _1^{{\frac{3}{2}}}|{s_1}|\big )^{\frac{1}{3}}\le |{s_2}|^{\frac{1}{2}} +\beta _1^{{\frac{1}{2}}}|{s_1}|^{\frac{1}{3}}. \end{aligned}$$
(51)

Taking \(|{\dot{e}}_2|\le \eta _0\) into account, it can be shown that

$$\begin{aligned} {\dot{V}}(s_1,s_2)\le&\left| s_1s_2 \right| +\beta _2s_2\left( \left| s _{2} \right| ^{\frac{1}{2}} +\beta _{1}^{\frac{1}{2}}\left| s_1 \right| \right) \nonumber \\&+\left| \beta _3s_2\right| +\left| \eta _0s_2 \right| . \end{aligned}$$
(52)

By the fact that \(|{s_2}|^{\frac{1}{2}}<1+|{s_2}|\) and \(|{s_1}|^{\frac{1}{3}}<1+|{s_1}|\), one has

$$\begin{aligned} {\dot{V}}(s_1,s_2)&\le \frac{{s}_1^2+s _2^2}{2}+\beta _2\frac{1+ {s}_2^2}{2}+\beta _2{s}_2^2 \nonumber \\&\quad +\beta _2\beta _{1}^{\frac{1}{2}}\frac{s_2^2+{s}_1^2}{2}+\frac{\beta _3^2+s_2^2}{2} +\frac{s_2^2+\eta _0^2}{2} \end{aligned}$$
(53)

Next, we will rewrite inequality (53) in a compact form as follows

$$\begin{aligned} {\dot{V}}(s_1,s_2)\le {\bar{K}}_{v1}V(s_1,s_2)+{\bar{L}}_{v1} \end{aligned}$$
(54)

where the parameters \({\bar{K}}_{v1}=\max \{{1+\beta _2\beta _{1}^{\frac{1}{2}}},3+3\beta _2 +\beta _2\beta _{1}^{\frac{1}{2}}\}\) and \({\bar{L}}_{v1}=\frac{\beta _2+\beta _{2}^{3}+\eta _0}{2}\) are positive constants. Thus, it follows from (54) that

$$\begin{aligned} {V}(s_1,s_2)\le \left( V\left( (s_1(0),s_2(0) \right) +\frac{{\bar{L}}_{v1}}{{\bar{K}}_{v1}} \right) e^{{\bar{K}}_{v1}}-\frac{{\bar{L}}_{v1}}{{\bar{K}}_{v1}} \end{aligned}$$
(55)

Therefore, it can be concluded from (55) that for any finite time interval \((0, {\overline{T}}]\), the function \(V(s_1,s_2)\) is bounded, i.e., the sliding variables \(s_1\) and \(s_2\) will not diverge to infinity during the time interval \((0, {\overline{T}}]\). In addition, on the basis of the definition of \(s_1\) and \(s_2\), we can obtain that the state variables \(x_1\) and \(x_2\) are bounded during \((0,{\overline{T}}]\), which also means that lateral deviation \(l_{os}\) and orientation error \(\theta _{os}\) will not diverge to infinity in finite time.

Step 3: Finite-time stability of path-tracking errors

Note that the sliding variable s and its derivatives \({\dot{s}}\) finite-time converge to the origin, which implies that a time instant \(T_\sigma \) can be found such that for \(t\ge T_\sigma \), \(s={\dot{s}}=0\) can be kept. By the definition of sliding variables \(s_1\) and \(s_2\), we can define a time instant \({\overline{T}}\) as \({\overline{T}}\ge T_\sigma \). It is clear that when \(t\ge {\overline{T}}\), system (6) can be finite-time stabilized under controller (28). Similarly, by the fact \(x_1 = l_{os}\), \(x_2 = v\sin \theta _{os}\), it can be concluded that both lateral deviation \(l_{os}\) and orientation error \(\theta _{os}\) converge to the origin in finite time under the output feedback SOSM controller (28). Hence, this accomplishes the proof of Theorem 2. \(\square \)

In the same way, to reduce chattering problem in the output feedback SOSM controller (28), the signum function can also be approximated by the continuous hyperbolic tangent function such that \({{\,\mathrm{\mathrm sign }\,}}(\zeta _2)=\tanh (\gamma _2\zeta _2)\) with \(\gamma _2\) being a positive constant. Moreover, we can implement the inverse transformation of the virtual control input \(u=\tan \delta \), and then the actual front wheel steering angle can be provided as follows

$$\begin{aligned} \delta&=\arctan \Big (-\frac{1}{g_m}\Big [\beta _2{\left\lfloor {\left\lfloor {\dot{s}}\right\rceil }^{{\frac{3}{2}}}+\beta _1^{{\frac{3}{2}}}{s}\right\rceil }^{{\frac{1}{3}}}+\frac{v^2 c_d}{1+ c_dx_1} \\&\quad \Big .\Big . \Big .\Big .+L_2{\left\lfloor e_1\right\rceil }^{\frac{1}{3}}+\int _0^t{L_3}{{\,\mathrm{\mathrm sign }\,}}\left( e_1 \right) d\tau \\&\quad +\beta _3\cdot \tanh \left( \gamma _2\cdot \left( {\left\lfloor {\dot{s}}\right\rceil }^{{\frac{3}{2}}} +\beta _1^{{\frac{3}{2}}}{s}\right) \right) \Big ]\Big ). \end{aligned}$$

Remark 6

To implement the derived output feedback SOSM controller (28), some guidelines should be provided on how to select the control parameters in the work. The parameter \(\beta _1\) should meet \(\beta _1\ge 2\) and cannot be selected to be very small, because the convergence performance of the sliding variable \(s_1\) is affected by \(\beta _1\). When the value of \(\beta _1\) is selected smaller, it means that the convergence performance of the sliding variable \(s_1\) is slower. The parameter \(\beta _2\) should satisfy \(\beta _2 \ge (1+ {\frac{32}{27}}+{\tilde{c}}_2)\). And the parameter \(\beta _3\) should satisfy \(\beta _3\ge \eta _0\) to eliminate the adverse effects induced by the derivative of estimation error \(e_2\). It seems that the value of parameter \(\beta _2\) should be greater than a large positive constant. The reason is that the control design for the considered system utilizes a backstepping-like technique, which usually causes the value of the parameter \(\beta _2\) to be overestimated. Actually, the predetermined values of \(\beta _2\) could be gradually reduced until a good performance of the resulting closed-loop system is obtained.

Remark 7

In comparison with the output feedback FOSM control method, the advantages of the output feedback SOSM control method are described from two aspects. On the one hand, the closed-loop path-tracking offset dynamics under the derived output feedback SOSM controller will not only possess the strong robust property that the conventional SMC could provide, but also achieve good dynamic performance. On the other hand, the path-tracking error variables will be finite-time stabilized rather than asymptotically converge to the origin, because the stability of the tracking errors can be tested by utilizing the Lyapunov approach.

Table 2 Control parameters of different controllers
Full size table

4 Simulation results

To validate the effectiveness of the designed control methods for the path-tracking problem of autonomous agricultural vehicles, some comparative simulation results will be presented in this section. For this purpose, we will use the specified agricultural vehicle to follow two different desired paths consisting of straight lines and curves. One is an S-turn maneuver, and the other is a Multi-maneuver. It should be mentioned again that the path-tracking control objective of autonomous agricultural vehicles is to drive the vehicles to rapidly track the path planned in advance and drive along the specified path under the premise of ensuring stability.

In the following simulation, the wheelbase of the simulated agricultural vehicle is set as 1.69 m, and the maximum allowable threshold of the front wheel angle is defined as no more than 3 rad. The initial states of the simulated vehicle is set to be close to the reference path, i.e., \(x_t(0)=0\), \(y_t(0)=0.2\) and \(\theta _t(0)=0\). The starting point of the reference path is taken as the origin of the coordinate plane. The simulation is implemented by utilizing the Euler method, and the sampling interval is selected as 0.0001s. In addition, in order to test the robustness of the proposed path-tracking control schemes, we assume that the unknown additive disturbance in the path-tracking offset dynamics model (3) are given as

$$\begin{aligned} \begin{array}{c} d _0\left( t \right) =\left\{ \begin{array}{l} 0,\,\,\,\,0\le t<3\\ 0.5,\,\,\,\,3\le t<7\\ -\frac{t}{10}+0.5,\,\,\,\,7\le t<10\\ 0.5\sin \left( \frac{t-2}{4}\right) ,\ 10\le t<15\\ 0.5\cos \left( \pi t\right) ,\,\,\,t\ge 15\\ \end{array}\,\,\,\,\,\, \right. \\ \end{array} \end{aligned}$$
(56)

On the other hand, in order to further show the superiority of the designed path-tracking control strategies in this paper, a PD-type controller for the path-tracking error dynamics (3) proposed in [29] can also be tested for comparison.

$$\begin{aligned} u&=l_t\Big [ \frac{\varPsi _{1}^{3}}{\left( 1+x_1c_d \right) ^2}\Big ( -{\dot{c}}_dx_1\varPsi _2-K_d\left( 1-x_1c_d \right) \varPsi _2\Big .\Big . \Big .\Big .\nonumber \\&\quad -K_px_1-c_d\left( 1+x_1c_d \right) \varPsi _{2}^{2} \Big ) -\frac{c_d\varPsi _2}{1+x_1c_d} \Big ] \end{aligned}$$
(57)

where \(\varPsi _1=\left( 1-\frac{x_{1}^{2}}{v^2} \right) ^{\frac{1}{2}}\) and \(\varPsi _2={\frac{x_2}{v}}{\left( 1-\frac{x_{1}^{2}}{v^2} \right) ^{-\frac{1}{2}}}\). It should be noted that the control parameters \(K_p\) and \(K_d\) are usually gradually tuned from small values to appropriate values based on the trade-off between the steady-state performance and transient response (e.g., tracking error, overshoot and settling time). As a matter of fact, the following two situations should be emphasized. One is that the larger parameter \(k_p\) may lead to excessive and oscillated control response; The other is that the larger parameter \(k_d\) may make PD-type controller be sensitive to external noise, resulting in high frequency oscillation of the controlled system.

The control gains of the different controllers (15), (28), (57) and observer (7) are shown in Table 2.

4.1 S-Turn simulation

In the first simulation case, the agricultural vehicle is required to follow a clothoid curve at the reference speed \(v=1\) m/s, which is planned to approach an S-turn desired path.

Under the output feedback SM controllers (15) and (28) and the PD-type controller (57), the comparative simulation results for the lateral deviation and heading error are presented in Fig. 2a, b. From those figures, it can be seen that under the SM controllers (15) and (28), the path-tracking errors are stabilized, which means that the vehicle can follow desired path, and the vehicle is driven along the specified path. Since the PD-type controller (57) does not have a good anti-interference ability, it leads to unsatisfactory path-tracking accuracy. It should be emphasized that under the RED+SOSM controller (28), the transient performance of path-tracking errors’ response is significantly improved. As a matter of fact, the path-tracking error dynamics can obtain faster response with lower steady-state errors by using the RED+SOSM control method, which is an important index to evaluate the path tracking results of agricultural vehicles in the actual operation scenarios. In addition, it is clear that there exist small oscillations in the heading error within the first few seconds by using the SM controllers (15) and (28). This is because the gains \(L_1\), \(L_2\) and \(L_3\) of observer (7) in this paper are chosen sufficiently large to obtain shorter settling time and smaller tracking errors in the steady state.

Fig. 2
figure 2

The simulation results in the S-turn maneuver: a the lateral deviation; b the heading error; c the steering angle; d the path-tracking trajectory

Full size image

Figure 2c shows the front wheel steering angle in the S-turn simulation. It can obviously be observed from Fig. 2c that the control input is maintained in reasonable regions and does not exceed the saturation limit. Actually, the proposed SM controllers can achieve nice tracking performance because the unknown lumped disturbance \(\varDelta \) in the system (6) can be accurately estimated by using the proposed estimator (7) and then be compensated simultaneously. In addition, it can also be seen from the simulations that the steady-state tracking errors can be reduced by properly adjusting the control gains in practical agricultural applications. However, the excessive control gains may bring the undesirable oscillations in the control signals, which is undoubtedly harmful to the controlled system.

The path-tracking trajectory results are given in Fig. 2d. It can be observed that using SM controllers (15) and (28) will evidently decrease the overshoots of path-tracking errors and apparently improve the precision of path-tracking. Considering the great significance of the transient response of lateral deviation for autonomous agricultural vehicles in critical maneuvers, such as changing lanes or turning around in the field, the developed RED+SOSM control method can apparently improve the operational efficiency of agricultural vehicles. As a result, it can be concluded that the path-tracking control method using RED+SOSM can retain advantages of RED+FOSM controller, and the transient performance of path-tracking can be significantly improved.

4.2 Multi-turn simulation

In the second simulation case, the vehicle is controlled to track another realistic reference trajectory with two circular arc, which is designed to approach an Multi-turn desired path. Here, the reference speed is selected as v = 3m/s, which can be regarded as the common driving speed of the agricultural vehicle in actual agricultural applications.

Fig. 3
figure 3

The simulation results in the multi-turn maneuver: a the lateral deviation; b the heading error; c the steering angle; d the path-tracking trajectory

Full size image

The numerical simulation results for lateral deviation and heading error are plotted in Fig. 3a, b. It can be clearly seen that the path-tracking errors can be stabilized by controllers (15), (28) and (57). The lateral deviation and heading error converge to zero quickly based on the proposed control methods, which is very significant for improving the tracking accuracy of autonomous agricultural vehicles. Compared with the RED+SMC and PD control techniques, the RED+SOSM control can obtain fast system response and effectively reduce the steady-state error generated during the path- tracking process. Similarly, it is not difficult to find that there exists small oscillation in the first few seconds of the heading error by using the proposed control strategies. The reason for this phenomenon is that we pursue shorter settling time and smaller steady-state following error by adopting the larger control gains.

The simulation results for the front steering angle is displayed by Fig. 3c. It can be observed that the three control inputs are maintained within acceptable regions. A point should be mentioned is that under proposed methods, the front steering angle can be kept at reasonable magnitude without exceeding the saturation limit. Furthermore, the steady-state values of the front steering angle in the Multi-turn simulation are smaller than that in S-turn case.

The global path-tracking trajectory results are shown in Fig. 3d. It can evidently be observed that the overshoot of the global trajectory for path-tracking is significantly alleviated using the proposed SM controllers. Moreover, the path tracking target is accomplished satisfactorily using the proposed control methods, which illustrates that the actual operation quality of autonomous agricultural vehicles can be greatly guaranteed.

5 Conclusion

In this paper,considering that the precision of currently available sensors for vehicle heading angle measurement is easily affected by measurement noise and vehicle body vibration, the output feedback SM controllers are proposed to control the vehicle to track the desired path without using the vehicle heading deviation information. The vehicle’s path-tracking offset dynamics is first transformed into a strict standard form state-space equation to facilitate controller design, where the uncertainties are concentrated in an unknown nonlinear function. Then, we introduce second-order RED with attractive finite-time convergence to simultaneously reconstruct the unmeasured system state and estimate the unknown lumped disturbance in the transformed system. On this basis, two different types of output feedback SM control approaches are developed to improve the path-tracking performance of autonomous agricultural vehicles. The effectiveness of the designed control approaches is confirmed by two kinds of comparative simulation results. In our future research work, we hope to focus our efforts on experimental validation of the obtained results in the paper.