1 Introduction

The aging population and labor shortage are becoming increasingly serious around the world, and these phenomena promote the need for mechanization and automation in industry, agriculture, etc. [1, 2]. Benefits from the rapid development of global positioning systems, inertial navigation technology, and control theory, unmanned farm vehicles are gradually being utilized in agricultural activities such as plowing, harvesting, and spraying [3]. Precision, unmanned, and standardization are all trends in modern agriculture [4].

Path tracking control is one of the foundational technologies for unmanned agricultural vehicles [5]. The path tracking control of farm vehicles, i.e., forcing the vehicles to track the predetermined path [6]. Capabilities of autonomous high-precision tracking can increase operations quality and ecological benefit to some extent [7]. However, the agricultural environment is complex and full of unknown disturbances, as opposed to structured scenarios. For instance, the operating environment includes slippery slopes, sandy, sloppy grass grounds, and stony grounds [8]. The pure rolling constraint no longer exists, and the wheel slips are inevitable. Wheel slip, according to vehicle dynamic knowledge, is reflected in the influence on the speed of the front and rear wheels, i.e., it may exist uncertainties [9]. On the other hand, for instance, while plowing, the longitudinal dynamic model is impacted by the ground resistance, and perfect motion can hardly be maintained. Also, the kinematic model contains strong nonlinearity and unmodeled error, which might be viewed as the internal disturbance. As a result, it is eager to design a path tracking controller, which is easy to deploy and robust against unanticipated disturbances.

Massive control strategies for vehicles have been implemented in recent years, including optimal control (linear quadratic regulator [10], model predictive control [11,12,13]), control design via the Lyapunov method [14], Proportional-Integral-Differential (PID) control [15], and Pure Pursuit control (PPC) [16]. These methods are typically categorized as kinematic model-based or dynamic model-based. Among these studies mentioned above, the dynamic model is typically assumed to be precisely known. Unfortunately, factors such as wind forces, road adhesion, road surface conditions, and others make mathematical modeling of vehicle dynamics difficult. Furthermore, it has also been demonstrated that the path tracking controller developed using the kinematic model is appropriate for achieving satisfactory tracking accuracy for low-speed farm vehicles [17, 18]. Meanwhile, from a universal standpoint, the kinematic model-based controller is a better option for farm vehicles. The kinematic model-based robust path tracking controller design is still a hot open issue.

To the best of our knowledge, few papers took unknown disturbances into account. In [19], the kinematic model was developed with the lateral and longitudinal uncertainty velocities in mind. In [20], the nonlinear disturbance observer (NDO) was employed to reckon the influence of unknown disturbances, and an enhanced sliding mode controller was developed. However, disturbance suppression is dependent on high gain and high-frequency control, as well as the prior knowledge of the perturbation’s upper bound value. Active disturbance rejection control (ADRC) was employed by [21, 22] to accomplish lateral control under uncertainties, nonetheless, the converge rate is asymptotic. According to the aforementioned studies, the time-varying uncertainties and strong nonlinearity will act on the unmatched channel, indicating that the mismatched disturbance exists. However, the conventional control techniques can hardly handle the mismatched disturbance.

Sliding mode control (SMC) is an established method for rejecting disturbances. Due to its insensitivity to perturbations and ease of implementation, SMC has been implemented in a variety of fields, including power electronics [23], yaw moment control [24], motion control [25], etc. In addition, many excellent SMC theories have emerged [26,27,28,29,30, 43]. SMC has also been employed in farm vehicle path tracking control. Wu et al. [31] proposed extended state observer (ESO) based terminal sliding mode control (ESOB-TSMC). However, the convergence rate of ESO is asymptotic, and the hyperbolic tangent function suppressed the chattering at the expense of control accuracy. Experiments demonstrated the effectiveness of a novel continuous sliding surface designed for articulated vehicles in [32]. The aforementioned investigations demonstrated the feasibility and viability of SMC for farm vehicles’ path tracking control, yet some problems remain. As we all know, the traditional SMC suppressed disturbances by utilizing a discontinuous sign function, which made chattering inevitable [33]. Meanwhile, it is necessary to have the prior knowledge about the perturbation’s upper bound. In practice, obtaining the upper bound of the perturbation is challenging. Various techniques, such as the boundary-layer method [34] and the higher-order SMC method [35], have been developed to combat the chattering problem. However, due to the fact that sliding variable in a boundary layer has linear motion, the boundary-layer approach reduces control precision [34]. Higher-order SMC diminishes chattering while increasing the order of the considered system [35]. Notably, [36] developed a new adaptive sliding mode method in which the adaptive technology is used to determine the optimal value of the sliding mode controller’s gain, which inspired our research. In [36], a loss-pass filter (LPF) was used to accomplish the equivalent control; however, the LPF’s time constant will affect control accuracy as well as hardware performance requirements. On the other hand, time-varying uncertainties will cause mismatched disturbances in the lateral path tracking system. Disturbance observer-based SMC is an emerging technique for addressing mismatched disturbances. References [20, 37] all used NDO to estimate the mismatched disturbances, but the mismatched disturbance must be constant rather than time-varying. Linear ESO was applied in [21], and it has been proved to be asymptotically convergent. A precise and rapid estimation of mismatched disturbance is the perennial area of research interest.

This paper proposes a composite adaptive terminal sliding mode control (CATSMC) to address the previously listed issues. The FDO is employed to estimate the mismatched disturbance, which ensures that the disturbances are estimated in a finite time rather than asymptotically. Inspired by Uktin’s work, an adaptive law is used to construct the integral TSMC in order to achieve the least optimal control gain, which can significantly minimize the chattering issue. Finally, several simulation results under various scenarios are presented to prove the validity of the proposed control frame. This study’s creativity and significant contributions can be outlined as follows:

  1. (1)

    The path-tracking error model is converted to a second-order system, which includes both mismatched and matched disturbances. The FDO is capable of estimating the mismatched lump disturbance in a finite time as opposed to doing asymptotically.

  2. (2)

    An innovative FDOB-CATSMC technique for lateral path tracking of agricultural vehicles is proposed. It can provide a guarantee that the lateral deviation and the sliding variable will converge to stable in a finite time.

  3. (3)

    Combined with a high-frequency signal filter, the proposed adaptive controller can reduce chattering, and meanwhile maintaining the disturbance rejection ability.

This paper is structured as follows. In Sect. 2, we will describe the kinematic and error models of the path tracking system in presence of disturbances. The first-order SMC (FOSMC), the FDOB-CTSMC and the FDOB-CATSMC are all introduced, along with their respective designs and stabilities, in Sect. 3. The numerical simulations in Sect. 4 demonstrate the efficiency of the proposed composite control algorithm. Section 5 describes the conclusions.

2 System description and modeling

2.1 Notation and problem statement

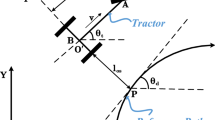
The Frenet–Serret frame, as shown in Fig. 1, is applied to delineate path tracking control for farm vehicles. XOY denotes the inertial coordinate frame, and the reference path is planned in the Frenet–Serret frame, which allows the longitudinal and lateral motions to be decoupled [38]. The variables and notations required for the kinematic model and the error model are listed in Table 1.

Fig. 1
figure 1

Sketch of the path following problem for farm vehicles

Full size image
Table 1 Variables in the kinematic model
Full size table

2.2 Kinematic model and error model

The kinematic model of the farm vehicles in inertial coordination can be described as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}\left( t \right) =v_s\cos \left( \theta \left( t \right) \right) ,\\ \dot{y}\left( t \right) =v_s\sin \left( \theta \left( t \right) \right) ,\\ \dot{\theta }\left( t \right) =\omega _s\left( t \right) .\\ \end{array} \right. \end{aligned}$$
(1)

Neglecting the longitudinal motion, one has

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}\left( t \right) =v_s\cos \left( \theta \left( t \right) \right) ,\\ \dot{\theta }\left( t \right) =\omega _s\left( t \right) .\\ \end{array} \right. \end{aligned}$$
(2)

The desired vehicle motion trajectory is set to

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_v\left( t \right) =v_v\cos \left( \theta ^*\left( t \right) \right) ,\\ \dot{y}_v\left( t \right) =v_v\sin \left( \theta ^*\left( t \right) \right) .\\ \end{array} \right. \end{aligned}$$
(3)

Decomposing in the Frenet–Serret frame, a more detailed error model is obtained as follows:

$$\begin{aligned} \left[ \begin{array}{c} e_s\left( t \right) \\ e_d\left( t \right) \\ \end{array} \right] =\left[ \begin{matrix} \cos \left( \theta ^*\left( t \right) \right) &{} \sin \left( \theta ^*\left( t \right) \right) \\ -\sin \left( \theta ^*\left( t \right) \right) &{} \cos \left( \theta ^*\left( t \right) \right) \\ \end{matrix} \right] \left[ \begin{array}{c} x\left( t \right) -x_v\left( t \right) \\ y\left( t \right) -y_v\left( t \right) \\ \end{array} \right] . \end{aligned}$$
(4)

In fact, it should be emphasized that in agricultural scenarios, uncertainties such as unexpected wheel slippage, different drivers’ driving skills, external environment influences, and road surface will influence the tracking accuracy. Thus, ideal vehicle motion is difficult to maintain. The above-mentioned uncertainties finally reflect on the lateral subsystem and heading angle velocity, respectively. Hence, taking disturbances into account, and based on (2) and (3), the following equation is obtained by differentiating (4)

$$\begin{aligned} \left\{ \begin{array}{l} \dot{e}_s\left( t \right) =0,\\ \dot{e}_d\left( t \right) =v_s\sin \left( \theta _e\left( t \right) \right) +f_0,\\ \dot{\theta }_e\left( t \right) =\omega _s\left( t \right) +\omega _d\left( t \right) ,\\ \end{array} \right. \end{aligned}$$
(5)

with \(f_0\) being the additive external time-varying disturbance, \(\omega _s(t)\) is the control input to be designed, and \(\omega _d\left( t \right) \) denotes the disturbance acts on the control input channel.

For the convenience of controller design, system (5) can be reformulated as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{e}_d\left( t \right) =\theta _e\left( t \right) +f_1,\\ \dot{\theta }_e\left( t \right) =\omega _s\left( t \right) +f_2,\\ \end{array} \right. \end{aligned}$$
(6)

where

$$\begin{aligned} f_1\triangleq v_s\sin \left( \theta _e\left( t \right) \right) -\theta _e\left( t \right) +f_0,\; f_2\triangleq \omega _d\left( t \right) . \end{aligned}$$
(7)

It should be noted that \(f_1\) is the mismatched disturbance in the \(e_d\) subsystem, which contains model nonlinearity and external disturbances, and the same concept can be found in [21, 31].

Assumption 1

The lumped disturbances \(f_1\), \(f_2\) satisfy the following requirements:

  1. (1)

    \(f_i\) is differentiable twice;

  2. (2)

    \(\left| f_i^{\left( j \right) } \right| \le \phi _i,\,\,i=1,2;\,\,j=0,1,2,\)

where \(\phi _i>0\) denote unknown constants.

Remark 1

In practice, the lumped disturbances \(f_1\), \(f_2\) are all bounded. For instance, according to the vehicle dynamic knowledge, the wheel slips will influence the rear and front wheel velocity, but it will be far less than the linear velocity. Similarly, the road resistances are all bounded, hence Assumption 1 is reasonable.

The work aims to construct a robust controller for a agriculture vehicle with the following characteristics:

  1. (1)

    Instead of asymptotic convergence, the lateral deviation can be forced to origin within a finite time when unknown disturbances are considered;

  2. (2)

    The proposed method not only can significantly reduce the influences of mismatched and matched disturbances, but also suppress the chattering problem.

Remark 2

In practice, the lateral deviation is the most important factor to consider, as it has a direct impact on operation quality, efficiency, production cost, and so on. It is difficult to control both the lateral deviation and the heading deviation to zero under these conditions at the same time. The nested frame is capable of accommodating both lateral and heading deviation.

3 Lateral path tracking controller design

In this section, the SMC approaches are utilized to design the lateral path tracking controller for farm vehicles in the presence of unknown disturbances. First of all, the FOSM method is used to build the path tracking lateral controller. The FDOB-CTSMC is subsequently constructed to accommodate the unknown mismatched disturbance. In conjunction with the sliding mode-based filter and the adaptive control technology, the composite control method is intended to significantly increase tracking accuracy and reduce chattering.

The following notations and lemmas are given prior to the controller design. The signum function is defined as follows:

$$\begin{aligned} \text {sign}\left( x \right) =\left\{ \begin{array}{ll} 1&{}\quad x >0\\ 0&{}\quad x=0\\ -1&{}\quad x<0\\ \end{array} \right. \end{aligned}$$

For the simplicity of expression, the fractional power is defined as \( \mathrm {sign}\left( x \right) ^r=\text {sign}\left( x \right) \left| x \right| ^r. \)

Notation \(\left[ x \right] _+\) denotes

$$\begin{aligned} \left[ x \right] _+=\left\{ \begin{array}{ll} 1,&{}\quad x\ge 0\\ 0,&{}\quad x<0.\\ \end{array} \right. \end{aligned}$$

Lemma 1

[39] For a continuous system \(\dot{x}\left( t \right) =f\left( x\left( t \right) \right) ,\, f\left( x(0) \right) =0,\, x\in {\mathbb {R}},\) suppose there exists a continuous positive definite function \(V: D\longrightarrow {\mathbb {R}}\), there exists real number \(\kappa _1>0,\,\,0<\alpha <1\), and an open neighborhood \({\mathscr {V}}\in \ D\) of the origin such that

$$\begin{aligned} \dot{V}\left( x \right) +\kappa _1V^{\alpha }\left( x \right) \leqslant 0, x\in {\mathscr {V}}\diagdown \left\{ 0 \right\} , \end{aligned}$$

then the origin is a finite-time stable equilibrium.

3.1 Design of FOSM lateral path tracking controller

For system (6), according to the control goal, the sliding manifold is chosen as

$$\begin{aligned} s=\varrho e_d\left( t \right) +\theta _e\left( t \right) , \end{aligned}$$
(8)

with \(\varrho >0\) is the design coefficient, which determines the convergence speed in the sliding manifold. Calculating the derivative of the sliding variable (8) and combining it with (6) yield

$$\begin{aligned} \dot{s}=\varrho \theta _e\left( t \right) +\omega _s\left( t \right) +\omega , \end{aligned}$$
(9)

where \(\omega \triangleq \varrho f_1+f_2\). According to Assumption 1, \(\omega \) satisfies \(\text {sup}\left| \omega \right| \le {\mathscr {W}}\) and \({\mathscr {W}}>0\) denotes a positive constant.

The following theorem depicts the finite-time convergence characteristic of the sliding variable s.

Theorem 1

If the FOSM lateral path tracking controller is designed as

$$\begin{aligned} \omega _s\left( t \right) =-\varrho \theta _e\left( t \right) -k_1\mathrm{sign}\left( s \right) , \end{aligned}$$
(10)

where \(k_1>{\mathscr {W}}\), it can conclude that the sliding variable s in (8) will converge to the equilibrium point within a finite time.

Proof

The first candidate Lyapunov function is chosen as \(V\left( s \right) =\frac{1}{2}s^2\), then taking the derivate and combining it with (10), we have

$$\begin{aligned} \dot{V}\left( s \right)&=s\left( -k_1\mathrm{sign}\left( s \right) +\omega \right) \nonumber \\&\le -k_1\left| s \right| +\omega \left| s \right| \nonumber \\&\le -\left( k_1-{\mathscr {W}} \right) \left| s \right| . \end{aligned}$$
(11)

With the given condition \(k_1>{\mathscr {W}}\), one can draw the conclusion \(\dot{V}\left( s \right) \le -\mu V^{\frac{1}{2}}\left( s \right) \) and \(\mu =\sqrt{2}\left( k_1-{\mathscr {W}} \right) \). By using Lemma 1, we can conclude that the sliding variable s will converge to the equilibrium within a finite time. This completes the proof. \(\square \)

Then, system (6) will be reduced to

$$\begin{aligned} \dot{e}_d\left( t \right) =-\varrho e_d\left( t \right) +f_1. \end{aligned}$$
(12)

According to the solution of (12), the lateral error cannot be driven to the equilibrium point. The suppression of disturbances influence is dependent on a high gain \(k_1\); therefore, chattering is serious in FOSM. Also, the prior upper bound information of the unknown total disturbance is notoriously difficult to obtain, hence FOSM cannot be applied to handle farm vehicle lateral path tracking control. In order to solve the chattering issue, the FDOB-CTSMC will be developed next.

3.2 Design of FDOB-CTSMC lateral path tracking controller

In this section, the FDOB-CTSMC will be developed to eliminate the impacts of mismatched disturbance. A novel terminal sliding manifold based on the integral operation is proposed, the lateral deviation and the sliding variable can converge to the equilibrium points within a finite time, which can be strictly proved by using the Lyapunov theory.

3.2.1 Design of FDO

First of all, the FDO is designed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{z}_1=v_1+\theta _e\left( t \right) ,\\ v_1=-L_1\mathrm {sign}\left( z_1-e_d\left( t \right) \right) ^{\frac{2}{3}}+z_2,\\ \dot{z}_2=v_2,\\ v_2=-L_2\mathrm {sign}\left( z_2-v_1 \right) ^{\frac{1}{2}}+z_3,\\ \dot{z}_3=-L_3\mathrm {sign}\left( z_3-v_2 \right) ,\\ \end{array} \right. \end{aligned}$$
(13)

where \(z_2\) and \(z_3\) are the estimations of \(f_1\) and \(\dot{f}_1\), respectively; \(L_i>0\,\,\left( i=1,2,3 \right) \) are the observer parameters which needed to be designed.

Lemma 2

If the observer is constructed as illustrated in (13) and the corresponding parameters are correctly specified, the mismatched disturbance and its derivate can be approximated by \(z_2\) and \(z_3\) in a finite time, i.e., it is possible to determine a time constant \(T_o\) such that

$$\begin{aligned} z_2=f_1,\; z_3=\dot{f}_1,\quad \forall t>T_o. \end{aligned}$$
(14)

Proof

The estimation errors are defined as

$$\begin{aligned} e_1=z_1-e_d\left( t \right) ,\quad e_2=z_2-f_1,\quad e_3=z_3-\dot{f}_1. \end{aligned}$$
(15)

Taking the derivate of \(e_1\) along system (13) yields

$$\begin{aligned} \dot{e}_1&=-L_1\mathrm {sign}\left( z_1-e_d\left( t \right) \right) ^{\frac{2}{3}}+z_2-f_1\nonumber \\&=-L_1\mathrm {sign}\left( z_1-e_d\left( t \right) \right) ^{\frac{2}{3}}+e_2\nonumber \\&=-L_1\mathrm {sign}\left( e_1 \right) ^{\frac{2}{3}}+e_2. \end{aligned}$$
(16)

Similarly, one can obtain

$$\begin{aligned} \dot{e}_2&=-L_2\mathrm {sign}\left( z_2-v_1 \right) ^{\frac{1}{2}}+e_3,\nonumber \\ \dot{e}_3&=-L_3\mathrm {sign}\left( z_3-v_2 \right) -\ddot{f}_1. \end{aligned}$$
(17)

Note that

$$\begin{aligned} e_2-\dot{e}_1&=z_2-v_1,\nonumber \\ e_3-\dot{e}_2&=z_3-v_2. \end{aligned}$$
(18)

Taking Eq. (18) into (17) along with Assumption 1, the following errors differential can be obtained

$$\begin{aligned} \left\{ \begin{array}{l} \dot{e}_1=-L_1\mathrm {sign}\left( e_1 \right) ^{\frac{2}{3}}+e_2,\\ \dot{e}_2=-L_2\mathrm {sign}\left( e_2-\dot{e}_1 \right) ^{\frac{1}{2}}+e_3,\\ \dot{e}_3\in -L_3\mathrm {sign}\left( e_3-\dot{e}_2 \right) +\left[ -\phi _1\,\,\phi _1 \right] .\\ \end{array} \right. \end{aligned}$$
(19)

This means that the solutions of differential (19) can be grasped under the Filippov sense, and the rigorous theoretical analysis of the FDO can be discovered in [40]. Then, Lemma 2 is proved. \(\square \)

Remark 3

FDO is based on the theory of Arie Levant’s differentiator [33], and the rigorous stability analysis of the FDO can be found in [33]. Levant has provided a detailed guideline for selecting observer parameters. Different from the observers such as ESO [31], NDO [37], etc., the estimation error of disturbance can be guaranteed to gather to the equilibrium point within finite time rather than asymptotically; meanwhile, the adopted FDO provides faster convergence rate of large initial error. In the following, the differentiator will also be used to filter the high-frequency control.

3.2.2 Design of FDOB-CTSMC

A new FDO-based integral terminal sliding surface is given below to drive the lateral error to zero within a finite time:

$$\begin{aligned} s&=\theta _e( t ) +z_2 +\int _0^t( \beta _1\mathrm {sign}( \theta _e( t ) +z_2 ) ^{\alpha _2}\nonumber \\&\quad +\beta _2\mathrm {sign}( e_d( t ) ) ^{\alpha _1}+z_3 ) d\tau , \end{aligned}$$
(20)

with \(\beta _i,\,\,\alpha _i\,\,\left( i=1,2 \right) \) denote positive control parameters, and \(\alpha _i\) are determined to satisfy

$$\begin{aligned} \left\{ \begin{array}{l} \alpha _1=\frac{\alpha _2}{2-\alpha _2},\\ \alpha _2=\alpha ,\,\,\alpha \in \left( 1-\delta ,\,\,1 \right) ,\,\,\delta \in \left( 0,1 \right) .\\ \end{array} \right. \end{aligned}$$
(21)

A composite terminal sliding mode controller is constructed as follows:

$$\begin{aligned} \omega _s\left( t \right) =-\left( \omega _1+\omega _2 \right) , \end{aligned}$$
(22)

where

$$\begin{aligned} \omega _1&=v_2+\beta _2\mathrm {sign}\left( \theta _e\left( t \right) +z_2 \right) ^{\alpha _2}\nonumber \\&\quad +\beta _1\mathrm {sign}\left( e_d\left( t \right) \right) ^{\alpha _1}+z_3. \end{aligned}$$
(23)

By substituting the expression of \(\dot{\theta }_e\left( t \right) \) in (6) and the controller (22) into the sliding manifold (20), we have

$$\begin{aligned} \dot{s}&=\dot{\theta }_e\left( t \right) +\dot{z}_2+\beta _2\mathrm {sign}\left( \theta _e\left( t \right) +z_2 \right) ^{\alpha _2}\nonumber \\&\quad +\beta _1\mathrm {sign}\left( e_d\left( t \right) \right) ^{\alpha _1}+z_3\nonumber \\&=\left[ \omega _s\left( t \right) +v_2+f_2 \right] +\beta _2\mathrm {sign}\left( \theta _e\left( t \right) +z_2 \right) ^{\alpha _2}\nonumber \\&\quad +\beta _1\mathrm {sign}\left( e_d\left( t \right) \right) ^{\alpha _1}+z_3 \nonumber \\&=-\omega _2+f_2. \end{aligned}$$
(24)

Based on (24), the following composite terminal sliding mode controller can be constructed for system (6)

$$\begin{aligned} \omega _s\left( t \right)&=-v_2-\beta _2\mathrm {sign}\left( \theta _e\left( t \right) +z_2 \right) ^{\alpha _2}\nonumber \\&\quad -\beta _1\mathrm {sign}\left( e_d\left( t \right) \right) ^{\alpha _1}-z_3-\beta ^{'}\mathrm{sign}\left( s \right) \end{aligned}$$
(25)

where \(\beta ^{'}>\phi _2+\eta , \eta >0\) is a constant.

Theorem 2

Under the FDOB-CTSMC (25), the lateral deviation in the system (6) will converge to zero along the terminal sliding manifold (20) within a finite time.

Proof

The Lyapunov function is chosen as \(V_s=\frac{1}{2}s^2\), such that

$$\begin{aligned} \dot{V}_s&=s\dot{s}=s\left( -\beta ^{'}\mathrm{sign}\left( s \right) +f_2 \right) \nonumber \\&\le \left( -\beta ^{'}+\phi _2 \right) \left| s \right| \nonumber \\&\le -\eta \left| s \right| . \end{aligned}$$
(26)

According to (26), one can obtain

$$\begin{aligned} \dot{V}_s\left( s \right) \le -\sqrt{2}\eta V_s^{\frac{1}{2}}\left( s \right) . \end{aligned}$$
(27)

Based on Lemma 1, the sliding variable s can reach sliding manifold (20) within a finite-time \(T_s\). Once the desired sliding mode occurs, the new state variables are defined as \(\tilde{e}_d\left( t \right) =e_d,\) and \(\tilde{\theta }_e\left( t \right) =\theta _e+z_2\). Then, the motion trajectories of the new states can be expressed as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\tilde{e}}_d\left( t \right) =\tilde{\theta }_e\left( t \right) -e_1,\\ \dot{\tilde{\theta }}_e\left( t \right) =-\beta _2\mathrm {sign}\left( \tilde{e}_d\left( t \right) \right) ^{\alpha _1}-\beta _1\mathrm {sign}\left( \tilde{\theta }_e\left( t \right) \right) ^{\alpha _2}+\dot{s}.\\ \end{array} \right. \end{aligned}$$
(28)

In the next, we will show that there will be no finite-time escape phenomenon in a finite-time \(T_e=\max \left\{ T_s,\,\,T_o \right\} \). A finite-time bounded (FTB) function is constructed for (28) as

$$\begin{aligned} \begin{array}{l} V_e\left( \tilde{e}_d\left( t \right) ,\,\,\tilde{\theta }_e\left( t \right) \right) =\frac{1}{2}\tilde{e}_d ^2\left( t \right) +\frac{1}{2}\tilde{\theta }_e ^2\left( t \right) . \end{array} \end{aligned}$$
(29)

Taking the derivate of (29) yields

$$\begin{aligned} \dot{V}_{e}&=\widetilde{e}_{d}(t) \dot{\tilde{e}}_{d}(t)+\widetilde{\theta }_{e}(t) \dot{\tilde{\theta }}_{e}(t) \nonumber \\&= \widetilde{e}_{d}(t)\left( \tilde{\theta }_{e}(t)-z_{2}\right) \nonumber \\&\quad +\widetilde{\theta }_{e}(t)\left\{ -\beta _{2} {\text {sgn}} \left( \widetilde{e}_{d}(t)\right) ^{\alpha _{1}}-\beta _{1} {\text {sgn}} \left( \tilde{\theta }_{e}(t)\right) { }^{\alpha _{2}}+\dot{s}\right\} \nonumber \\&\leqslant \left| \tilde{e}_{d}(t)\right| \left| \tilde{\theta }_{e}(t)\right| +\left| \tilde{e}_{d}(t)\right| \left| z_{2}\right| +\beta _{2}\left| \tilde{\theta }_{e}(t)\right| \left( 1+\left| \widetilde{e}_{d}(t)\right| \right) \nonumber \\&\quad +\beta _{1}\left| \tilde{\theta }_{e}(t)\right| \left( 1+\left| \tilde{\theta }_{e}(t)\right| \right) +\left| \tilde{\theta }_{e}(t)\right| |\dot{s}| \end{aligned}$$
(30)

By using inequality scaling and note that \(\left| \tilde{e}_d\left( t \right) \right| ^{\alpha _1}<1+\left| \tilde{e}_d\left( t \right) \right| \), for \(0<\alpha _1<1\), one can obtain

$$\begin{aligned} \dot{V}_{e}&\leqslant \left( \frac{1}{2} \widetilde{e}_{d}^{2}(t)+\frac{1}{2} \widetilde{\theta }_{e}^{2}(t)\right) +\left( \frac{1}{2} \widetilde{e}_{d}^{2}(t)+\frac{1}{2} z_{2}^{2}\right) \nonumber \\&\quad +\left( \frac{1}{2} \widetilde{\theta }_{e}^{2}(t)+\frac{1}{2} \dot{s}^{2}\right) +\left( \frac{1}{2} \tilde{\theta }_{e}^{2}(t)+\frac{1}{2}\left( \beta _{1}+\beta _{2}\right) ^{2}\right) \nonumber \\&\quad +\beta _{1}\left( \frac{1}{2} \widetilde{e}_{d}^{2}(t)+\frac{1}{2} \widetilde{\theta }_{e}^{2}(t)\right) +\beta _{2}\left( \frac{1}{2} \widetilde{e}_{d}^{2}(t)+\frac{1}{2} \widetilde{\theta }_{e}^{2}(t)\right) \nonumber \\&\leqslant K_{\max } V_{e}+L_{\max } \end{aligned}$$
(31)

where \(K_{\max }=2+\beta _1+\beta _2, L_{\max }=\frac{1}{2}\max \{ ( \beta _1+\beta _2 ) ^2+z_2^2+\dot{s}^2+ \widetilde{\theta }_{e}^{2}(t) \} \). It can be conclude that the states \(\tilde{e}_d\left( t \right) ,\,\,\tilde{\theta }_e\left( t \right) \) will not escape in a finite-time \(T_e\). According to (27) and Lemma 2, we have \(e_1=0\) and \(\dot{s}=0\) after \(T_e\), then the system (28) will reduce as

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} \dot{\tilde{e}}_d\left( t \right) =\tilde{\theta }_e\left( t \right) ,\\ \dot{\tilde{\theta }}_e\left( t \right) =-\beta _2\mathrm {sign}\left( \tilde{e}_d\left( t \right) \right) ^{\alpha _1}-\beta _1\mathrm {sign}\left( \tilde{\theta }_e\left( t \right) \right) ^{\alpha _2},\\ \end{array} \right. \end{array} \end{aligned}$$
(32)

according to Proposition 8.1 and its proof given in [41], the lateral deviation will converge to zero in a finite time. This completes the proof. \(\square \)

It should be noted in (25) that the controller contains the discontinuous signum function, controller chattering in FDOB-CTSMC remains severe. Inspired by Uktin’s work in [36], this research adopts and develops an adaptive control method that can greatly reduce controller chattering.

3.3 Design of FDOB-CATSMC lateral path tracking controller

In order to avoid the above questions, the FDOB-CATSMC scheme is proposed in this subsection. The FDOB-CATSMC is made up of the following components: finite-time disturbance observer; terminal sliding mode controller, and an adaptive control law. The control frame sketch of the FDOB-CATSMC is shown in Fig. 2.

Fig. 2
figure 2

Sketch of the FDOB-CATSMC control frame

Full size image

3.3.1 Equivalent control design

According to the definition of equivalent control theory [36], the equivalent control \(\tilde{\omega }_s\left( t \right) \) is

$$\begin{aligned} \left\{ \begin{array}{l} \tilde{\omega }_s\left( t \right) =-v_2-\beta _2\mathrm {sign}\left( \theta _e\left( t \right) +z_2 \right) ^{\alpha _2}\\ \quad \qquad \quad \; -\beta _1\mathrm {sign}\left( e_d\left( t \right) \right) ^{\alpha _1}-z_3-\omega _2,\\ \omega _2=f_2.\\ \end{array} \right. \end{aligned}$$
(33)

Due to the fact that the lumped matched disturbance \(f_2\) is unknown, (33) is often regarded as an abstract concept that cannot be implemented practically. After the system state variables have reached the sliding surface, the actual control (25) and the equivalent control (33) are equivalent. Therefore, by filtering the high-frequency control, it is possible to obtain that

$$\begin{aligned} \beta ^{'}\left[ \text {sign}\left( s \right) \right] _{av}=f_2, \end{aligned}$$
(34)

where \(\left[ \text {sign}\left( s \right) \right] _{av}\) denotes the evenness signal of \(\text {sign}\left( s \right) \).

Obviously, as indicated by the definition of signum function, \(\text {sign}\left( s \right) \) varies in the range \(\left[ -1,1 \right] \). Hence, we can conclude that its evenness value also changes between \(\left[ -1,1 \right] \). n addition, we have the following assumption:

Assumption 2

The two times derivative of variable \(\left[ \text {sign}\left( s \right) \right] _{av}\) is assumed to be bounded, i.e., \(\frac{\mathrm{d}^2}{\mathrm{d}t^2}\left[ \text {sign}\left( s \right) \right] _{av}\le \varGamma ,\,\,\varGamma >0\) is a positive constant.

3.3.2 High-frequency signal filter design

Arie Levant’s differentiator from [36] is used to derive the evenness signal of \(\left[ \text {sign}\left( s \right) \right] _{av}\), and the sliding mode-based filter is developed as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\upsilon }_{-1}=-\varOmega _2\varGamma ^{\frac{1}{3}}\mathrm {sign}\left( \upsilon _{-1} \right) ^{\frac{2}{3}}+\upsilon _0-\mathrm {sign}\left( s \right) ,\\ \dot{\upsilon }_0=-\varOmega _1\varGamma ^{\frac{2}{3}}\mathrm {sign}\left( \upsilon _{-1} \right) ^{\frac{1}{3}}+\upsilon _1,\\ \dot{\upsilon }_1=-\varOmega _0\varGamma \mathrm {sign}\left( \upsilon _{-1} \right) ^0,\\ \end{array} \right. \end{aligned}$$
(35)

where \(\varOmega _i,\,\,i=0,1,2\) are positive parameters to be designed, \(\upsilon _{-1}\) denotes the auxiliary internal variable, \(\upsilon _0\) and \(\upsilon _1\) are the estimation of \(\left[ \text {sign}\left( s \right) \right] _{av}\) and \(\frac{\mathrm{d}^2}{\mathrm{d}t^2}\left[ \text {sign}\left( s \right) \right] _{av}\), respectively.

Lemma 3

The output \(\upsilon _0\) of the high-frequency signal filter (35) can follow up the evenness signal \(\left[ \text {sign}\left( s \right) \right] _{av}\) .

Proof

Defining the following variables

$$\begin{aligned} \left\{ \begin{array}{l} q_{-1}=\left( \upsilon _{-1}+\varPsi \right) /\varGamma ,\\ q_0=\left( \upsilon _0-\left[ \text {sign}\left( s \right) \right] _{av} \right) /\varGamma ,\\ q_1=\left( \upsilon _1-\frac{\mathrm{d}}{\mathrm{d}t}\left[ \text {sign}\left( s \right) \right] _{av} \right) /\varGamma ,\\ \end{array} \right. \end{aligned}$$
(36)

with \(\varPsi \) being the auxiliary variable, which is generated by

$$\begin{aligned} \varPsi =\text {sign}\left( s \right) -\left[ \text {sign}\left( s \right) \right] _{av}-\varphi \varPsi ,\quad \varphi >0. \end{aligned}$$
(37)

According to Assumption 2, it can be easy to find \(| \text {sign}( s )\) \(-[ \text {sign}( s ) ] _{av} |\le \varepsilon _1\), \(\varepsilon _1>0\) with being a positive constant.

By integrating Eq. (37), we have

$$\begin{aligned} \left| \varPsi \right|&=e^{-\varphi t}\cdot \int _0^t{e^{\varphi t}\left| \text {sign}\left( s \right) -\text {sign}\left( s \right) _{av} \right| \mathrm{d}t}\nonumber \\&\le \varepsilon _1e^{-\varphi t}\int _0^t{e^{\varphi t}\mathrm{d}t}\nonumber \\&=\varepsilon _1e^{-\varphi t}\left( \varphi ^{-1}e^{\varphi t}-1 \right) \nonumber \\&\le \varepsilon _1\varphi ^{-1}, \end{aligned}$$
(38)

which also yields \(\left| \varphi \varPsi \right| \le \varepsilon _1,\,\,\left| \varPsi \right| \le \varepsilon _2\) with \(\varepsilon _2=\varepsilon _1\varphi ^{-1}\).

Taking the derivate of (36) along with (35), the following differential holds:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}_{-1} \in -\varOmega _2\mathrm {sign}\left( q_{-1}+\frac{\varepsilon _2}{\varGamma }[ -1,1 ] \right) ^{\frac{2}{3}}\\ \qquad \quad +\frac{\varepsilon _1}{\varGamma }[ -1,\,\,1 ] +q_0,\\ \dot{q}_0 \in -\varOmega _1\mathrm {sign}\left( q_{-1}+\frac{\varepsilon _2}{\varGamma }[ -1,1 ] \right) ^{\frac{1}{3}}+q_1,\\ \dot{q}_1 \in -\varOmega _0\mathrm {sign}\left( q_{-1}+\frac{\varepsilon _2}{\varGamma }[ -1,1 ] \right) ^0+[ -1,1 ] .\\ \end{array} \right. \end{aligned}$$
(39)

By defining \(\varepsilon =\max \left\{ \left( \frac{\varepsilon _2}{\varGamma } \right) ^{\frac{1}{3}},\,\,\left( \frac{\varepsilon _1}{\varGamma } \right) ^{\frac{1}{2}} \right\} \), which implies that \(\varepsilon _1\le \varGamma \varepsilon ^2,\,\,\varepsilon _2\le \varGamma \varepsilon ^3\).

According to the Filippov theory [40], we have

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}_{-1}\in -\varOmega _2\mathrm {sign}\left( q_{-1}+\varepsilon ^3\left[ -1,1 \right] \right) ^{\frac{2}{3}}\\ \qquad \quad +\varepsilon ^2\left[ -1,\,\,1 \right] +q_0,\\ \dot{q}_0\in -\varOmega _1\mathrm {sign}\left( q_{-1}+\varepsilon ^3\left[ -1,1 \right] \right) ^{\frac{1}{3}}+q_1,\\ \dot{q}_1\in -\varOmega _0\mathrm {sign}\left( q_{-1}+\varepsilon ^3\left[ -1,1 \right] \right) ^0+\left[ -1,1 \right] .\\ \end{array} \right. \end{aligned}$$
(40)

It can conclude that Eq. (40) is homogeneous of the degree \(-1\) with the weight \( \left( \text {deg}\,\,q_{-1},\,\,\text {deg}\,\,q_0,\,\,\text {deg}\,\,q_1 \right) =\left( 3,2,1 \right) . \) According to Theorem 1 in the work of [40,41,42,43,44], one can obtain that the following accuracy holds:

$$\begin{aligned} \left| \upsilon _0-\left[ \text {sign}\left( s \right) _{av} \right] \right| \le \mu _0\varGamma \varepsilon ^2, \end{aligned}$$
(41)

where \(\mu _0\) is a constant depends on \(\varOmega _i,\,\,i=0,1,2\). The inequality (41) means that the output variable \(\upsilon _0\) will converge to \(\left[ \text {sign}\left( s \right) \right] _{av}\). Then, we complete the proof. \(\square \)

3.3.3 Design of FDOB-CATSMC

Noting that the control gain \(\beta ^{'}\) in (25) is occasionally larger than the upper bound of the matched disturbance \(f_2\), the severe chattering problem cannot be avoided. Due to the time-varying operating environment, road surface, driving skills, etc., it is difficult to determine the upper limt of the disturbance. The fixed constant gain \(\beta ^{'}\) will be replaced with the following variable gain \(\beta \left( t \right) \) in the subsequent step. The FDOB-CATSMC is designed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \omega _s\left( t \right) =-(\omega _1+\omega _2),\\ \omega _1=v_2+\beta _2\mathrm {sign}\left( \theta _e\left( t \right) +z_2 \right) ^{\alpha _2}\\ \qquad \quad +\beta _1\mathrm {sign}\left( e_d\left( t \right) \right) ^{\alpha _1}+z_3,\\ \omega _2=\beta \left( t \right) \cdot \text {sign}\left( s \right) ,\\ \dot{\beta }\left( t \right) =\xi \cdot \beta \left( t \right) \cdot \text {sign}\left( \sigma \left( t \right) \right) -\varTheta \left[ \beta \left( t \right) -\beta ^+ \right] _+\\ \qquad \quad \;+\varTheta \left[ \beta ^--\beta \left( t \right) \right] _+,\\ \sigma \left( t \right) =\left| \left[ \text {sign}\left( s \right) \right] _{av} \right| -\vartheta ,\\ \end{array} \right. \end{aligned}$$
(42)

where \(\xi >\frac{\phi _2}{h\beta ^-}\) and \(\varTheta >\xi \beta ^+\); \(\beta ^->0\) and \(\beta ^+>\phi _2\) denote the bottom and upper limit bounds of the variable high gain \(\beta \left( t \right) \), we define \(\vartheta \in \left( 0,1 \right) \).

Theorem 3

Under the FDOB-CATSMC (42), the lateral deviation in the system (6) will converge to zero along the terminal sliding manifold (20) within a finite time. Meanwhile, the variagle high gain \(\beta \left( t \right) \) generated by (42) gathers to \(\frac{\left| f_2 \right| }{\vartheta }\) within a finite time, and it is limited between \(\left[ \beta ^-,\,\,\beta ^+ \right] \) to look for the best magnitude.

Proof

Primarily, we will prove the related properties of the adaptive gain \(\beta \left( t \right) \). According to the definition of equivalent control, we have the following relationship:

$$\begin{aligned} \beta \left( t \right) \left[ \text {sign}\left( s \right) \right] _{av}=f_2. \end{aligned}$$
(43)

The key concept of the adaptive technology is that the evenness value of the high frequency should be as close to 1 once the system state reaches the sliding surface. Hence, \(\beta \left( t \right) =\frac{f_2}{\left[ \text {sign}\left( s \right) \right] _{av}}>f_2\), the variable controller gain \(\beta \left( t \right) \) could approach \(f_2\).

Choosing the Lyapunov function as

$$\begin{aligned} V_{\sigma }=\frac{1}{2}\sigma ^2. \end{aligned}$$
(44)

Taking the derivate of (44) with (42) and (43) yields

$$\begin{aligned} \dot{V}_{\sigma }( \sigma )&= \sigma \dot{\sigma } \nonumber \\&=\sigma \frac{\mathrm{d}}{\mathrm{d}t}\left| \left[ \text {sign}\left( s \right) \right] _{av} \right| \nonumber \\&=\sigma \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\left| f_2 \right| }{\beta \left( t \right) } \right) \nonumber \\&=\sigma \beta ^{-1}\left( t \right) \cdot \dot{f}_2\cdot \text {sign}\left( f_2 \right) \nonumber \\&\quad -\sigma \xi \beta ^{-1}\left( t \right) \left| f_2 \right| \cdot \text {sign}\left( \sigma \left( t \right) \right) . \end{aligned}$$
(45)

It is evident that through the pursuit of dynamic gain, one has

$$\begin{aligned} \frac{\left| f_2 \right| }{\vartheta }>\beta ^-. \end{aligned}$$
(46)

Using Assumption 2 and (46), (45) can be transformed into

$$\begin{aligned} \dot{V}_{\sigma }\left( \sigma \right)&\le \left| \sigma \right| \beta ^{-1}\left( t \right) \cdot f_2-\xi \left| \sigma \right| \beta ^{-1}\left( t \right) \cdot \left( \vartheta \beta ^- \right) \nonumber \\&=-\left| \sigma \right| \beta ^{-1}\left( t \right) \cdot \left( \vartheta \beta ^-\xi -f_2 \right) \nonumber \\&\le -\frac{|\sigma |\left( \vartheta \beta ^-\xi -f_2 \right) }{\beta ^+}\nonumber \\&=-pV_{\sigma }^{^{\frac{1}{2}}}\left( \sigma \right) , \end{aligned}$$
(47)

where \(p=\frac{\sqrt{2}\left( \vartheta \beta ^-\xi -f_2 \right) }{\beta ^+}>0\). Based on Lemma 1, the variable \(\sigma \) will gather to the equilibrium point within a finite time, i.e., the evenness value of the high frequency will be close to \(\vartheta \) within a finite time. Finally, the dynamic adaptive gain \(\beta \left( t \right) \) can converge to \(\frac{\left| f_2 \right| }{\vartheta }\).

According to the adaptive law (42), the dynamic adaptive gain \(\beta \left( t \right) \) would not escape from the range \(\left[ \beta ^-,\,\,\beta ^+ \right] \). In fact, if \(\beta \left( t \right) \) increases to its maximum value \(\beta ^+\), one can obtain

$$\begin{aligned} \dot{\beta }\left( t \right) =\xi \beta ^+\cdot \text {sign}\left( \sigma \left( t \right) \right) -\varTheta , \end{aligned}$$
(48)

with \(\sigma \left( t \right) >0\) and \(\varTheta >\xi \beta ^+\), hence \(\dot{\beta }\left( t \right) \) would be negative, similarly, \(\beta \left( t \right) \) would not lower than \(\beta ^-\). Hence, the variable control gain \(\beta \left( t \right) \) will converges to \(\frac{\left| f_2 \right| }{\vartheta }\) in a finite time, and it is constrained in the region \(\left[ \beta ^-,\,\,\beta ^+ \right] \) to search for the minimum magnitude. It should be pointed out that the prior upper bound information of the unknown total disturbance \(f_1\) can be avoided to be exactly known by choosing a very large \(\beta ^+\), which will not affect the control performance.

Next, the finite-time convergence of the sliding variable and the lateral deviation will be proved. It should be noted that in (25) that \(\beta ^{'}>\phi _2+\eta ,\,\,\eta >0\). The constant \(\eta \) is only used to guarantee finite-time stability. Defining \(\tilde{f}_2=f_2+\eta \), indeed, \(\tilde{f}_2\) and \(f_2\) are essentially the same. Hence, it is reasonable to obtain the dynamic variable gain \(\beta \left( t \right) \) to track \(\tilde{f}_2\) in a finite time.

Choosing the Lyapunov function as

$$\begin{aligned} V_s\left( s \right) =\frac{1}{2}s^2. \end{aligned}$$
(49)

Based on (42), taking the derivate of (49) yields

$$\begin{aligned} \dot{V}_s\left( s \right)&=s\dot{s}\nonumber \\&=s\left( -\omega _2+f_2 \right) \nonumber \\&=s\left( -\beta \left( t \right) \cdot \text {sign}\left( s \right) +f_2 \right) \nonumber \\&\le \left| s \right| \left( -\beta \left( t \right) +f_2 \right) . \end{aligned}$$
(50)

According to (47) and (42), the inequality (50) can be further scaled into

$$\begin{aligned} \dot{V}_s\left( s \right)&=s\dot{s}\nonumber \\&\le \left| s \right| \left( -\beta \left( t \right) +f_2 \right) \nonumber \\&\le \left| s \right| \left( -\frac{\left| f_2+\eta \right| }{\vartheta }+\left| f_2 \right| \right) \nonumber \\&\le \left| s \right| \left( \frac{\vartheta \left| f_2 \right| -\left| f_2+\eta \right| }{\vartheta } \right) \nonumber \\&\le \left| s \right| \left( \frac{\left| f_2 \right| -\left| f_2+\eta \right| }{\vartheta } \right) \nonumber \\&\le -\frac{\sqrt{2}\eta }{\vartheta }V_s^{\frac{1}{2}}\left( s \right) . \end{aligned}$$
(51)

Based on Lemma 1, the sliding variable s will converge to the sliding manifold (20) in a finite time. Then, the finite-time convergence proof of lateral deviation resembles (28)\(\sim \)(32). This completes the proof. \(\square \)

4 Simulation and discussion

In this section, to verify the effectiveness of the proposed controller, comparative numerical simulations were conducted. The simulation is carried out by the Euler method, and the sampling time is set as 0.0001 s, the simulation time is 10 s. The desired path is chosen as a line \(y_v=x_v,\,\,\theta ^*=\frac{\pi }{4}\), as shown in Fig. 3. The set liner velocity of the farm vehicle is set as \(v_s=1\,\mathrm{m/s}\), and the initial states are selected as

$$\begin{aligned} x\left( 0 \right) =0.3\,\mathrm{m},\,\,y\left( 0 \right) =0\,\mathrm{m},\,\,\theta \left( 0 \right) =0\,\mathrm{rad}. \end{aligned}$$
(52)

In order to compare fairly and comprehensively, three cases under different disturbances are set.

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{l} {\textit{Case}}1:\,\omega _d\left( t \right) =2+\sin \left( 2t \right) ,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,f_0\left( t \right) =\left\{ \begin{array}{ll} -0.3&{}0\le t<1,\\ -0.3+0.6\left( t-1 \right) &{}1\le t<2,\\ 0.3&{}2\le t<3,\\ 0.3-0.6\left( t-3 \right) &{}3\le t<4,\\ -0.3&{}4\le t<5,\\ -0.3+0.6\left( t-5 \right) &{}5\le t<6,\\ 0.3&{}6\le t<7,\\ 0.3-0.6\left( t-7 \right) &{}7\le t<8,\\ -0.3&{}8\le t<9,\\ -0.3+0.6\left( t-9 \right) &{}t\ge 9,\\ \end{array} \right. \\ {\textit{Case}}2:\,\omega _d\left( t \right) =2+\sin \left( 2t \right) ,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,f_0\left( t \right) =0.1\left( 1+\sin \left( 2t \right) \right) ,\\ {\textit{Case}}3:\,\omega _d\left( t \right) =2+\sin \left( 2t \right) ,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,f_0\left( t \right) =0.3\cos \left( \sin \left( \pi t \right) \right) .\\ \end{array} \right. \end{array} \end{aligned}$$
(53)
Fig. 3
figure 3

The tracking results of reference path

Full size image

The parameters of FDO (13) are chosen as \(L_1=-4.5\cdot 2^{\frac{1}{3}}\), \(L_2=-4.5\cdot 2^{\frac{1}{2}}\) and \(L_3=-3\). The ESO proposed in [21] was used to make the comparison. As shown in Fig. 4, high-accuracy tracking of disturbances pertaining to the farm vehicle can be observed by the FDO within 0.7 s. The mismatched disturbance tracking performance of the FDO is better than the ESO; meanwhile, the adopted FDO provides faster convergence rate of large initial error.

Fig. 4
figure 4

Finite-time disturbance observer-based observations: a Time response of the disturbance tracking results; b Time response of the observation error

Full size image
Fig. 5
figure 5

History of control gain \(\beta \left( t \right) \)

Full size image

The parameters of the adaptive law (42) are set as \(\vartheta =0.999,\,\,\xi =1.3\), \(\beta ^+=15,\,\,\beta ^-=0.001\), \(\varTheta =30\). The parameters of (35) are \(\varGamma =250\), \(\varOmega _0=12\), and \(\,\,\varOmega _1=17,\,\,\varOmega _2=8\). Figure 5 depicts the trajectories of the variable control gain \(\beta \left( t \right) \). It can be seen that \(\beta \left( t \right) \) tends to but larger than the lumped matched disturbance \(f_2\). The controller parameters of different controllers are shown in Table 2.

Within the line tracking task of agricultural vehicles with unknown disturbances, the proposed FDOB-CATSMC strategy allows the vehicle to reach the target inspection path in less than 1 s, as shown in Fig. 6. By comparing Fig. 6, we can see that the FOSM technique struggles to trace the required trajectory, particularly in the presence of the fast time-varying mismatched disturbance, as in Case 3. The steady error in FOSM is about 0.045 m.

Figure 7 depicts the history of the control signals for three different controllers. Benefits from the adaptive law, the chattering in FDOB-CATSMC is less than that in FOSM and FDOB-CATSMC. As a result, the proposed FDOB-CATSMC is effective in reducing chattering. Meanwhile, the proposed method maintains the mismatched disturbance rejection ability.

Table 2 Parameters in the lateral path tracking controller
Full size table
Fig. 6
figure 6

Lateral errors under different controllers

Full size image
Fig. 7
figure 7

Time history of control inputs

Full size image

Remark 4

In practice, one solution to reduce the chattering existing in the traditional sliding mode controller is to replace the sign function with a saturation function, but the price paid is that the robustness of the resulting closed-loop system will be significantly weakened. As shown in Fig. 7, it is reasonable to claim that the FDOB-CATSMC can significantly reduce the chattering issue and also maintain the robustness.

5 Conclusion

In this paper, a composite adaptive terminal sliding mode controller for farm vehicles with unknown disturbances is constructed. The FDO is used to estimate the lumped mismatched disturbance, which is induced by model nonlinearity, and external disturbances. The integral terminal sliding surface is built by using the estimated value of disturbance. To suppress the chattering problem appearing in FOSM and FDOB-CTSMC, an adaptive control is used to search for the best value of the time-varying control gain, resulting in the least amount of chattering of the SMC. Numerical simulation results have proven the effectiveness and adaptability of the proposed FDOB-CATSMC.