A sliding mode controller with a nonlinear disturbance observer for a farm vehicle operating in the presence of wheel slip

Abstract

A sliding mode controller with a nonlinear disturbance observer is proposed and developed to control a farm vehicle to accurately track a specified path. The vehicle is subjected to lateral and longitudinal slips at front and rear wheels. The unpredictability of ground contact forces which occur at the wheels while traversing undulating, rough and sloping terrains require the controllers to be sufficiently robust to ensure stability. The work presented in this paper is directed at the practicality of its application with both matched and unmatched uncertainties considered in the controller design. The controller is designed using an offset model derived from the kinematic model and its operation is verified by simulation and field experiments. In the simulations, the kinematic model based controller is used to control both a kinematic model and a dynamic model of a tractor to verify the performance of the kinematic model based controller. The proposed controller is compared with two other nonlinear controllers, namely, back stepping control and model predictive control. In the field experiments, the three controller were used to control the physical tractor to follow a specified path. Simulation and experimental results are presented to show that the proposed controller demonstrated the required robustness and accuracy at all times.

1 Introduction

The use of autonomous systems in many industries is rapidly advancing. In the agricultural industry, the application of smaller modular autonomous vehicles is promising in delivering productivity advantages while they are operating with high accuracy on agricultural terrain. Among these are the ability to lay the crop highly accurately according to a pre-specified crop layout plan and to use the knowledge of crop location to manage the crop right throughout the cropping season. Similarly, knowing the crop locations also means knowing where crop has not been planted and hence herbicides can be accurately applied to where they are needed such as the inter-row space. The high accuracy autonomous path tracking capabilities not only bring in the cost savings, but also considerable ecological and environmental advantages. In general, large-scale agricultural activities are time-consuming, tedious, hazardous and the proposed path tracking accuracy is unable to be achieved by human operators. Without a sophisticated crop localization system, high precision path-tracking is essential for reliable maneuvering of an autonomous system in the field among the growing crop to ensure that the crop is not damaged. The aim of this study is to develop controllers that can deliver such accuracy. Although the focus of this paper is on farming vehicles, more specifically tractors, the presented approach is applicable to many other industries where high accuracy is required in the presence of disturbances and uncertainties.

Driver assistance devices and automatic steering systems are already in operation in the agricultural industry. By definition (Bell 2000), automatic vehicle guidance is ‘accurate automatic control of the vehicle or implement along a predefined trajectory’. Some realizations of such systems are presented in Keicher and Seufert (2000) and Reid et al. (2000). Many advanced approaches for path following control of wheeled vehicles [as presented in Bloch (2003) and Thuilot et al. (2001)] are based on the non-holonomic assumption, which makes the designed controllers vulnerable to lateral vehicle slip and uncertainties in the field. Similarly, for agricultural vehicles, the kinematic modeling in works related to a vehicle pulling a passive trailer (Rouchon et al. 1993; Ridley and Corke 2003) and many kinematic models of tractor-trailer systems (Hodo et al. 2007; Lamiraux et al. 1999) are based on the no-slip assumption. This assumption, however, is not valid in agricultural environment where undulating, sloping and very uncertain terrain with soft soil degrade the resemblance to pure rolling without slip.

The autonomous operation of a vehicle in a real agricultural environment exposes it to conditions that require a controller design that takes into account the lateral and longitudinal slips. The vehicles on agricultural fields are required to traverse non-smooth and undulating terrain where the ground conditions may change from soft soil to sealed road. Even the soil conditions may vary from soft sandy soil to sticky clay. If the designed controllers cannot handle these rough variable conditions, the autonomous operation will turn out to be ineffective and unreliable. In this study, vehicle slips are considered and the controller is designed to act robustly in the presence of considerable amount of slip in lateral and longitudinal directions.

The first step in designing a controller for path tracking of an autonomous vehicle is modeling. As discussed earlier the models must include vehicle slips. In this work, both kinematic and dynamic models are considered for comparative purposes. In dynamic models, slip forces are used and in the kinematic models slip velocities are used. Dynamic models are more comprehensive than kinematic models and are developed based on known, estimated and/or identified parameters. However, complexities in systems and uncertainties in parameters make the dynamic models somewhat inaccurate.

Dynamic models (Werner et al. 2012; Siew et al. 2009) are also more exclusive than the kinematic models, which degrades the generality of the models and the resulting controllers. Moreover, a dynamic model is most useful where high accelerations and velocities are involved and paths to be followed have significantly large curvatures. In agricultural scenarios, vehicles traverse at low speeds along straight paths and it is verified that the kinematic models act very similar to dynamic models (Werner et al. 2012).

In addition, kinematic modeling of unmanned vehicles enhanced by partial dynamic modeling and adaptive slip estimation in Lenain et al. (2012, 2010) demonstrate the applicability of kinematic models in off-road scenarios operating at high-speeds while following curved paths. In works of Werner et al. (2012) and Fang et al. (2011) kinematic models were developed taking into account the lateral and longitudinal slips, and in works of Werner et al. (2012) and Huynh et al. (2010) kinematic models have been developed for a steerable tractor-trailer system. In this paper, kinematic models are used for the design of the controllers. However, to simulate slip more accurately, a dynamic simulation platform was developed and the controllers were verified in dynamic simulation before evaluation in field experiments.

Before proceeding any further, it is important to describe the differences between the error model and the offset model. By definition an error model is a model that represents x, y and $\theta$ errors, with respect the the desired values $x_d, y_d$ and $\theta _d$. These models are generally used to develop trajectory tracking controllers where time plays an important role. The offset model is defined as the model describing the lateral position error and the heading error, with respect to those at the currently closest point on the desired path. These models are used in the design of path tracking controllers, where time is not considered. The aim of this work is path following and as such an offset model derived using a kinematic model, presented in Huynh et al. (2010) inspired by the work in Astolfi et al. (2004), has been used to design the controller (Huynh et al. 2012).

Design of the controllers in the presence of slip is considered in Thuilot et al. (2001), however, in them, they do not consider both longitudinal and lateral slips. In contrast, this work uses an offset model incorporating longitudinal and lateral slips representing the most general scenario.

In the context of nonlinear control, feedback linearization can be a viable method as shown in Bian et al. (2010) and Shu-qing and Sheng-xiu (2010). This approach has limitations and is not successful when there are uncertainties in dynamic modeling. Hence, such feedback linearization approaches lack robustness. Furthermore, they need to fulfill the zero dynamics stability requirement.

In nonlinear control design, most often Lyapunov stability criteria are used to prove stability of controllers. Back stepping control and sliding mode control (SMC) designs are based on Lyapunov’s second method of stability analysis. Both approaches are comprehensively used for the design of controllers for non-holonomic mobile vehicles. Back stepping control technique has been used in Huynh et al. (2012) and Fang (2004). However, as we show in this paper, the performance of the back stepping controller is more sensitive to the unmatched disturbances.

Model predictive control (MPC) is an advanced method of process control used in many industrial applications such as refining and petro-chemical industries (Qin and Badgwell 2003). Recently, it has also been used for autonomous guidance of vehicles. For farm vehicles, MPC can successfully achieve accurate path tracking due to receding optimization of both current and future states (Lenain et al. 2005). However, MPC is mostly for linear systems or linearized systems and also is not inherently a robust controller (Garcia et al. 1989). Moreover, precautions are needed in implementation and tuning of MPC for non-minimal phase systems (Maciejowski 2002).

The concept of SMC is well known in nonlinear control design. They are simple and practical, and are widely used in many industrial applications (Utkin 1977; Yu and Kaynak 2009; Yu et al. 2012). Although SMC acts robustly in the presence of uncertainties and disturbances, the original SMC is not reliable when unmatched uncertainties exist in the system. In an agricultural vehicle, unmatched uncertainties and disturbances are inherent. As reviewed in Yang et al. (2013), LMI-based, adaptive and Riccati approaches on one hand (Choi 1998; Cheng and Guo 2010), and integral sliding mode controllers (I-SMC) (Hu 2007) on the other hand, have been employed to address unmatched uncertainties. However, the first group is mostly applicable to linear systems. As for the second approach I-SMC, the integration has adverse influence on the closed-loop system’s performance causing phenomena such as large overshoots and long settling times.

In this work, the approach presented in Huynh et al. (2010) is used to derive the offset model for a farm vehicle. Then a new sliding mode controller incorporating a disturbance observer is presented. The stability analysis of the designed controller is then detailed. As dynamic models are also simulated in this work, the dynamic model of the tractor is also outlined referring to earlier literature. A raft of simulation results are presented by using the designed controller to control a kinematic model as well as a dynamic model and the results are compared with a well performing back stepping controller presented in the literature and a MPC controller based on kinematic model without slip inspired by Wang (2009). Finally the proposed controller is used to control a real tractor in a field experiment and the results are presented to verify the path tracking accuracy and robustness. Back stepping controller and MPC approaches are also implemented in the experiment for comparison purposes.

The content of the paper is laid out as follows. In Sect. 2, the kinematic and dynamic systems are presented. In Sect. 3, the proposed control law and stability analysis are presented. The experimental setup is introduced in Sect. 4. In Sect. 5, the simulation results that compare the proposed controller’s path following accuracy to the path following accuracy in Huynh’s back stepping controller (Huynh et al. 2012) and MPC controller inspired by Wang (2009) are presented. The DOB-SMC’s robustness and accuracy are verified by dynamic model simulation and compared with the back stepping controller and MPC in Sect. 6. In Sect. 6.2, the experimental results are presented. Conclusions are given in Sect. 7.

2 System description and modeling

In this section the kinematic and dynamic models used in the simulations are described.

2.1 Kinematic system description

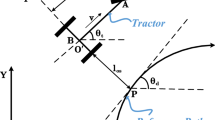
The kinematic model of the tractor is defined using a bicycle model with slip velocities incorporated in it. This arrangement is shown in Fig. 1 together with the desired path. The vehicle body coordinate frame is defined at the mid point of the rear axle. Note that only the front wheels are steered. The x-axis of the body coordinate frame coincides with the longitudinal axis of the tractor and points in the forward direction. The z-axis is pointing upwards and forms a right handed coordinate system. The offset model mentioned earlier will be developed with respect to this frame. The global coordinate frame is also shown in the figure. The desired path and the position and orientation of the body coordinate frame are represented with respect to the global frame.

Fig. 1

Tractor kinematic model

The variables and symbols in Fig. 1 are described in Table 1.

Table 1 The variables in the kinematic model

Throughout the paper $f(\cdot )$ and $g(\cdot )$ are nonlinear functions. It is assumed that all states are measurable and known, which is a valid assumption as the vehicle is equipped with two GPS units, both of them communicating with a base station in an RTK-GPS configuration. These GPS systems provide accurate measurement of the heading angle. Literature reports that RTK-GPS can provide accurate position readings (Lenain et al. 2003). In addition, the vehicle is equipped with an IMU and wheel encoders.

This work does not address the estimation of the slip velocities although plausible works in this regard have been done, (Taghia and Katupitiya 2013; Lenain et al. 2010, 2005), with considerable computational cost and complexity. The performance of the proposed controller was compared with a MPC. The MPC has been successfully used in Lenain et al. (2005), however, it has limitations such as negative effects of accuracy of sensors and ground irregularities in estimation approaches (Lenain et al. 2006). Furthermore, it has been shown that there are limitations in the estimation of slip using recursive approaches (Taghia and Katupitiya 2013). The goal of this research is the development of a SMC as a robust controller for a farm vehicle in the presence of lateral and longitudinal slips at the front and rear wheels of the vehicle. The controller is designed to drive the offsets, $l_{os}$ and ${\theta _{os}}$ to reach zero as time goes to infinity with the help of a nonlinear disturbance observer. In the next section, the kinematic model is derived using the above introduced parameters.

2.1.1 Kinematic model

By considering $x_t, y_t, \theta _t$ (easting, northing and heading of the vehicle) to be the vehicle states, the kinematic model (1) can be presented as in Lemma 1. The kinematic equations given in the following lemma are based on Huynh et al. (2010).

Lemma 1

The vehicle kinematic model

$$\begin{aligned} \begin{aligned} \dot{x}_t&=(V-V_{lr})\cos \theta _t-V_{sr}\sin \theta _t,\\ \dot{y}_t&=(V-V_{lr})\sin \theta _t+V_{sr}\cos \theta _t, \\ \dot{\theta }_t&=\frac{V-V_{lr}}{l_t}\tan (\delta +\beta _f)+\frac{V_{sr}}{l_t}. \end{aligned} \end{aligned}$$

(1)

Note that this model has the slip velocities incorporated.

2.1.2 Offset model

The path offset $l_{os}$ and the heading offset $\theta _{os}$ shown in Fig. 1 were chosen as the state variables to develop the offset model for the vehicle. The resulting state equations are given in (2).

Lemma 2

Offset model state space description

$$\begin{aligned} \begin{aligned} \dot{l}_{os}&=-\sigma |V-V_{lr}|\sin \theta _{os}-\sigma \zeta V_{sr}\cos \theta _{os},\\ \dot{\theta }_{os}&=\frac{V-V_{lr}}{l_t}\tan (\delta +\beta _f)+\frac{V_{sr}}{l_t}-\\ {}&\sigma |V-V_{lr}|\frac{c_d \cos \theta _{os}}{1+c_d l_{os}}+\sigma \zeta V_{sr} \frac{c_d\sin \theta _{os}}{1+c_dl_{os}}, \end{aligned} \end{aligned}$$

(2)

where $\sigma$ is considered $-1$ if the prescribed path curvature $c_d$ is counter-clockwise and it is $+1$ when the desired path’s curvature is clockwise. The tractor is always assumed to be moving in the forward direction and as such, $\zeta$ is always 1 and is therefore dropped for brevity. The offset model in (2) is a single input system. The derivation of this offset model can be found in Astolfi et al. (2004).

2.2 Dynamic system description

In order to simulate slip and verify the performance of the controllers in a more realistic simulation, a dynamic model of the vehicle was developed and simulated. For this purpose, a single-track nonlinear dynamic model (also known as a front wheel steered bicycle model) with longitudinal and lateral slips is formed. Dynamic modeling of the vehicle-road system allows for more accurate simulation and is formed by estimating various parameters of the vehicle, the road and the tires (Baffet et al. 2009). The simplified single-track nonlinear model of the vehicle similar to the one presented in Siew et al. (2009), is depicted in Fig. 2. The variables and symbols in Fig. 2 are described in Table 2.

Fig. 2

Depiction of single-track model

Table 2 The variables in the dynamic model

2.2.1 Dynamic model

The Euler equations describing the dynamic model shown in Fig. 2 are represented mathematically in (3) (Siew et al. 2009). This model can be summarized as the effect of the front and rear tire forces on the vehicle body itself with respect to the body’s mass and rotational inertia.

$$\begin{aligned} D\begin{bmatrix} \dot{v} - \omega \varOmega \\ \dot{\omega }+ v\varOmega \\ \dot{\varOmega } \end{bmatrix} + G_1 \begin{bmatrix} F_{lf} \\ F_{lr} \end{bmatrix} + G_2 \begin{bmatrix} T_{f} - R_{f} \\ T_{r} - R_{r} \end{bmatrix} = 0 \end{aligned}$$

(3)

where $R_f$ and $R_r$ are rolling resistances and

$$\begin{aligned} D= & {} \begin{bmatrix} m&0&0 \\ 0&m&0 \\ 0&0&J\end{bmatrix},\end{aligned}$$

(4)

$$\begin{aligned} G_1= & {} \begin{bmatrix} \sin \delta&0 \\ \cos \delta&1 \\ a\cos \delta&-b \end{bmatrix},\end{aligned}$$

(5)

$$\begin{aligned} G_2= & {} \begin{bmatrix} \cos \delta&1 \\ -sin \delta&0 \\ -a\sin \delta&0 \end{bmatrix}. \end{aligned}$$

(6)

To solve for the lateral forces on the front and rear tires, $F_{lf}$ and $F_{lr}$, the slip angles $\beta _f$ and $\beta _r$ are used with a lateral tire-force model shown in (7) based on Brach (2009) and Canudas-de Wit et al. (2003). Considering the tire orientation and its direction of travel, slip angles can be obtained. Tractive forces $T_f$ and $T_r$ require slip ratios $S_f$ and $S_r$ given in (8) and the longitudinal tire-force model shown in (9) which is also based on Brach (2009) and Canudas-de Wit et al. (2003). $R_f$ and $R_r$ are rolling resistances.

$$\begin{aligned} F(m, S)= & {} \left\{ \begin{array}{l l} \mu S / k_{sa} &{} \quad \text {if }|S| \le k_{sa}\\ \mu ~\text {sgn}(S) &{} \quad \text {if }|S| > k_{sa} \end{array} \right. \end{aligned}$$

(7)

$$\begin{aligned} S(V_r, V_{or})= & {} \left\{ \begin{array}{l l} (V_r / V_{or}) - 1 &{} \quad \text {if }V_r \le V_{or}\\ 1 - (V_{or} / V_r) &{} \quad \text {if }V_r > V_{or} \end{array} \right. \end{aligned}$$

(8)

$$\begin{aligned} T(m, S)= & {} \left\{ \begin{array}{l l} \mu S / k_{sr} &{} \quad \text {if }S \le k_{sr}\\ \mu ~\text {sgn}(S) &{} \quad \text {if }S > k_{sr} \end{array} \right. \end{aligned}$$

(9)

The purpose of the dynamic simulation is to verify the successful implementation of the kinematic model based controller to control a dynamic model. Furthermore, a dynamic simulation allows us to investigate the effect of slip on the performance of the kinematic model based controller. As such, the dynamic model parameters do not play a role in tuning of the back stepping controller, the MPC or the DOB-SMC. Hence a set of parameters (m, J, a and b) that approximately resemble a physical tractor was used in the dynamic simulation. Because of this reason the parameters in Table 2 do not need to be identified accurately.

3 Control methodology

SMCs are well known robust controllers used in practice to control non-linear systems with uncertainties. In general, they manage matched uncertainties very well, however, the management of unmatched uncertainties needs further work. In this paper, a nonlinear observer is added to the SMC in order to provide observations that can be used to adapt the sliding surface in (17) and hence the control law (16). In this section, DOB-SMC is derived based on (2), and its stability analysis is provided.

3.1 Control design

A nonlinear observer for estimating unmatched uncertainties is used in developing the DOB-SMC for this system.

Assumption 1

The velocity V is always greater than $V_{lr}$. Hence $-\sigma |V-V_{lr}|$ is equal to $-\sigma (V-V_{lr})$ and $V_{lr}$ is either measurable or can be estimated (Taghia and Katupitiya 2013). Thus

$$\begin{aligned} V_l=V-V_{lr}. \end{aligned}$$

(10)

This assumption is valid in most practical scenarios, although it may be violated in extreme circumstances. The slip velocity $V_{lr}$ is calculated based on the encoder readouts which give the wheel movement and the GPS and IMU readouts which give the real vehicle movement. With the proposed disturbance observer, any inaccuracy in the measurement of $V_{lr}$ is accommodated within the bounds of the unmatched and matched uncertainties as in (2).

Assumption 2

We can linearize $\tan (\delta + \beta _f)$ so that we have $\tan (\delta +\beta _f)=\tan \delta +\tan \beta _f$ and $\beta _f^*=\sup |\beta _f|$. By considering (10)

$$\begin{aligned} V_{l}+\tan \beta _f^* \geqslant 0. \end{aligned}$$

(11)

This assumption is valid because the angle $\beta _f$ is relatively small according to practical experience (Huynh et al. 2012; Fang et al. 2006), and the typical paths for farming activities mostly consist of straight line segments resulting in smaller slip. Given that $V_{l}$, which is a positive value sufficiently large when the vehicle is moving and that $\beta _f$ is small compared to $V_{l}$, (11) represents a valid assumption.

Assumption 3

We assume that the side slip velocity is bounded and is not greater than the real longitudinal speed of the vehicle, $\sup |V_{sr}|=V_l$.

This assumption means that the tractor’s forward velocity is larger than the lateral slip velocity. It means the tractor will move forward more than slip sideways, hence is a valid assumption for a tractor in a farm.

Accepting the Assumptions 1, 2 and 3, we define:

$$\begin{aligned} \begin{aligned}&x_1 = l_{os},\\&x_2 = -\sigma (V-V_{lr}) \sin \theta _{os} = -\sigma V_l \sin \theta _{os},\\&u = \tan \delta . \end{aligned} \end{aligned}$$

(12)

Based on the new states and input signal defined in (12), (2) can be rewritten as:

$$\begin{aligned} \begin{aligned} \dot{x}_1&=x_2+d_1, \\ \dot{x}_2&=a(x_1,x_2)+b(x_1,x_2)u+d_{2}. \end{aligned} \end{aligned}$$

(13)

where the parameters of (13) are as follows.

$$\begin{aligned} \begin{aligned} d_1&=-\sigma V_{sr}\cos \theta _{os}, \\ a(x_1,x_2)&=\frac{\sigma ^2 V_l^2 \left( 1-\frac{x_2^2}{\sigma ^2 V_l^2}\right) }{\frac{1}{c_d}+x_1},\\ b(x_1, x_2)&=\frac{-\sigma V_l \left( 1-\frac{x_2^2}{\sigma ^2 V_l^2}\right) ^{\frac{1}{2}}}{l_t},\\ d_{2_1}&=\frac{\sigma V_l }{l_t}\cos \theta _{os}(\tan \beta _f+V_{sr}),\\ d_{2_2}&=\frac{\sigma ^2 V_l V_{sr} \cos \theta _{os} \sin \theta _{os}}{\frac{1}{c_d}+x_1},\\ d_2&= d_{2_1}+d_{2_2}. \end{aligned} \end{aligned}$$

(14)

By re-arranging (13) in vector form the model is:

$$\begin{aligned} {\dot{\mathbf{x}}} = f(\mathbf{x})+g (\mathbf{x}) u+\mathbf{h} \; \mathbf{d}, \end{aligned}$$

(15)

where $\mathbf{x}=[x_1, x_2]^T$, $\mathbf{f} (\mathbf{x})=[x_2,a( \mathbf{x})]^T$, $\mathbf{g}(\mathbf{x})=[0,b(\mathbf{x})]^T$, $\mathbf{h}= \mathbf{I_{2 \times 2}}$ and $\mathbf{d}=[d_1,d_2]^T$.

In order to ensure Lyapunov stability of the system described by (13) in tracking the desired state values, $x_1 =0$ and $x_2=0$, the following control law is proposed:

$$\begin{aligned} u=-b^{-1}(\mathbf{x})[a(\mathbf{x})+c(x_2 + \Gamma {\hat{\mathbf{d}}})+k\;\text {sgn}(s)+\alpha _1 d_{2_1}^*+\alpha _2d_{2_2}^*], \end{aligned}$$

(16)

where s is a sliding surface and is defined as,

$$\begin{aligned} s=x_2+cx_1+\Gamma {\hat{\mathbf{d}}}, \end{aligned}$$

(17)

where c is the sliding surface gain, by using the Assumptions 2 and 3, $d_{2_1}^*$ is defined as:

$$\begin{aligned} \begin{aligned} d_{2_1}^*&=\frac{\sigma V_l \cos \theta _{os} (\tan \beta _f^*+ V_{l})}{l_t}\\ {}&=\sigma \sup \left| \frac{ V_l cos\theta _{os} (\tan \beta _f+V_{sr})}{l_t}\right| , \end{aligned} \end{aligned}$$

(18)

and similarly, $d_{2_2}^*$ is defined as,

$$\begin{aligned} \begin{aligned} d_{2_2}^*&=\frac{\sigma ^2 V_l^2 \cos \theta _{os}\sin \theta _{os}}{\frac{1}{c_d}+x_1}\\ {}&=\sup \left| \frac{\sigma ^2 V_l V_{sr}\cos \theta _{os}\sin \theta _{os}}{\frac{1}{c_d}+x_1}\right| . \end{aligned} \end{aligned}$$

(19)

The estimated disturbance ${\hat{\mathbf{d}}}$ in (16) and (17) is calculated using (20) given below (Yang et al. 2013; Chen 2003).

$$\begin{aligned} \begin{aligned} {\dot{\mathbf{p}}}&=-{\varvec{\Lambda }} \; \mathbf{h }\;\mathbf{p}-{\varvec{\Lambda }}[\mathbf{h }\; {\varvec{\Lambda }} \;{ \mathbf x}+\mathbf{f}(\mathbf{x})+\mathbf{g}(\mathbf{x})u], \\ {\hat{\mathbf{d}}}&=\mathbf{p}+{\varvec{\Lambda }} \; \mathbf{x}, \end{aligned} \end{aligned}$$

(20)

where ${\varvec{\Lambda }}=[\lambda _1,\lambda _2]^T$ is adjusted to ensure the estimator’s convergence while $\mathbf{p}=[p_1,p_2]^T$ are the internal states of the observer. They are used to calculate the disturbances ${\hat{\mathbf{d}}}=[\hat{d}_1, \hat{d}_2]^T$. If we define $e_{d_1}^* =\hat{ d_1}- d_1$, the derivative of $\hat{d}_1$ can now be calculated from (20) as follows:

$$\begin{aligned} \begin{aligned} \dot{ \hat{d_1}}&=-{\varvec{\Lambda }} \; \mathbf{g}(\hat{ d_1}- d_1)\\&=-{\varvec{\Lambda }} \; \mathbf{g}(e_{d_1}^*). \end{aligned} \end{aligned}$$

(21)

The control law (16) has a signum function that creates high frequency switching in the control command, which is well known as chattering (Fridman 2000). In many mechanical systems, actuators can be worn out and damaged if the control command has high frequency switching components. In this case the vehicles steering system is sensitive to chattering. To minimize chattering, the control law in (16) is smoothened by the use of a hyperbolic tangent function instead of signum function as follows:

$$\begin{aligned} \begin{aligned}&u=-b^{-1}({\mathbf{x}})[a({\mathbf{x}})+c(x_2+\Gamma {{\hat{\mathbf{d}}}})+k~\tanh \frac{k s}{\varrho }\\&\quad \qquad + \alpha _1 d_{2_1}^*+\alpha _2d_{2_2}^*], \end{aligned} \end{aligned}$$

(22)

where $\varrho >0$, $c>0$ and k are controller’s parameters. $\Gamma$ is chosen to be $\Gamma =[1,0]$ to limit the use of the estimator to admit only the unmatched uncertainties. The parameters $\alpha _1$ and $\alpha _2$ are defined as follows to ensure the stability of the system throughout.

$$\begin{aligned} \begin{aligned} \alpha _1&=\sigma ~\text {sgn}(\cos \theta _{os}),\\ \alpha _2&=\text {sgn}\left( \dfrac{\frac{-x_2}{\sigma V_l}}{\frac{1}{c_d}+x_1}\right) . \end{aligned} \end{aligned}$$

(23)

3.2 Stability analysis

Assumption 4

The error $e_{d_1}$ between the estimated value and actual value of $d_1$ is then $= d_1-\Gamma {\hat{\mathbf{d}}}$ and is considered bounded. This bound is denoted by $e_{d_1}^*=\sup |e_{d_1}|$.

The error between the estimated value and actual value of $d_1$ is bounded. This assumption relates to the bound on the error in the estimation of the disturbance. It is valid only if the disturbance observer is stable and converging. Then, since $d_1=-\sigma V_{sr} cos(\theta _{os})$ is a bounded sinusoidal signal with bound of $V_{sr}$, as per Assumption 3 the bound of $V_{sr}$ is $V_{l}$.

Theorem 1

For a tractor with a kinematic model given in (1), the proposed control law (16) brings Lyapunov stability if the Assumptions 1-4 are satisfied and k is chosen as:

$$\begin{aligned} k >(c+{\varvec{\Lambda }}{} \mathbf{g})e_{d_1}^*+e_{d_2}^*, \end{aligned}$$

(24)

where $e_{d_2}^*$ is defined as:

$$\begin{aligned} e^*_{d_2} = d_{2_1} + d_{2_2} -\alpha _1d^*_{21} - \alpha _2d^*_{2_2}. \end{aligned}$$

(25)

Note that based on the definitions of $d_{2_1}^*$ and $d_{2_2}^*$ given in (18) and (19), respectively, and $\alpha _1, \alpha _2$ given in (23), $e^*_{d_2} < 0$.

Proof

: We define the Lyapunov function,

$$\begin{aligned} V(s)=\frac{s^2}{2} \end{aligned}$$

(26)

the derivative of which is,

$$\begin{aligned} \dot{V}(s)=\dot{s} s. \end{aligned}$$

(27)

The derivative of the sliding surface in (17) is,

$$\begin{aligned} \dot{s}=\dot{x}_2+c \dot{x}_1+\dot{d}_1. \end{aligned}$$

(28)

By substituting state equation (13) and the control input u from (16) in (28), we get:

$$\begin{aligned} \begin{aligned} \dot{s}=-k\; \text {sgn}(s)+[\dot{ \hat{d_1}}+c(d_1-\hat{d}_1)]\\ +\,[d_{2_1}+d_{2_2}-\alpha _1 d_{2_1}^*-\alpha _2 d_{2_2}^*]. \end{aligned} \end{aligned}$$

(29)

The parameters, $\alpha _1$ and $\alpha _2$ in (29) are calculated to satisfy the stability of the controller and the observer. The derivative of $\hat{d_1}$ is defined in (21) and $e^*_{d_2}$ is defined in (25). Hence by substituting (21) and (25) in (29) the sliding surface’s derivative is defined as:

$$\begin{aligned} \dot{s}=-{\varvec{\Lambda }}\; \mathbf{g}(e_{d_1}^*)+e_{d_2}^*-k \; \text {sgn}(s). \end{aligned}$$

(30)

By substitution of (30) in (27), $\dot{V}$ is defined as:

$$\begin{aligned} \dot{V}=-k \; |s| + [(c+{\varvec{\Lambda }} \;{ \mathbf g})e_{d_1}^*+e_{d_2}^*]s \end{aligned}$$

(31)

Therefore, the whole closed loop is Lyapunov stable if:

$$\begin{aligned} k>(c+{\varvec{\Lambda }}\; { \mathbf g})e_{d_1}^*+e_{d_2}^*. \end{aligned}$$

(32)

$\square$

The condition (32) is more relaxed than the condition proposed in Yang et al. (2013) due to the fact that $e_{d_2}^*<0$ which reduces the total value of the right hand side of (32) and therefore stability is guaranteed with smaller k.

As for the tuning of the DOB-SMC, $\Gamma$ is a vector and its elements $[\gamma _1,\; \gamma _2]$ are the gains of the observer designed to estimate the unmatched and matched uncertainties, respectively. The condition $0 < \gamma _1 \le 1$ and $0 \le \gamma _2 \le 1$ are recommended based on practical experience (Yang et al. 2013).

4 Experimental setup

4.1 Hardware and the mechanical system

The DOB-SMC controller was implemented on an autonomous farm vehicle. The base tractor was a John Deere 4210 Compact Utility Tractor shown in Fig. 3. The fully autonomous system has been developed at the University of New South Wales, Sydney, Australia. More details about the hardware, safety system and sensors can be found in Matveev et al. (2013).

Fig. 3

Autonomous tractor

4.2 Software

The software architecture was first introduced in Matveev et al. (2013), however, new modules have been added and the software has been further improved to suit extensive experimentation with various control algorithms. The arrangement is shown in Fig. 4. Among the additions is a Window’s application to provide easier setup, tuning and monitoring and is shown in Fig. 5 . Another addition is an Android phone application that is written as a client to connect to the on-board control computer via internet, cellular network or wireless network, and is shown in Fig. 6. The Android app is able to access the shared memory to read or change the specified parameters. Moreover, it is able to provide three plots, two time based plots and one X–Y plot as the experiment progressed. The plots can be used as a guide to carry out speedy tuning of the controller being tested.

Fig. 4

Software modules and user interface

5 Control validation: kinematic simulation

First, in simulation, the proposed DOB-SMC controller was used to control the kinematic model and the performance is compared with the performance of the back stepping controller presented in Huynh et al. (2012) and MPC as per (Wang 2009) when used to control the same kinematic model. For designing MPC the offset model in (2) is simplified to a non-slip model (Wang 2009).

Both cases of without slip and with slip are simulated. The slip case takes into account the lateral and longitudinal slips at front and rear wheels. The slip velocities were considered constant and to be about 20 % of the vehicle speed which is 3 m/s.

Fig. 5

On-board user interface

Fig. 6

Three screen shots of the Android app for remote monitoring and tuning

The path used for simulations is shown in Fig. 7. This path consists of straight sections, curved sections and a sharp corner, which helps us to verify the controllers’ performance in coping with different types of path segments and segment to segment transition. Furthermore, a Bezier path is generated to ensure a smooth transition from the initial position and orientation of the vehicle on to the path. Note that the vehicle starts at the point denoted as the start point (0,0) of the figure and follows the entire path in the clockwise direction ending up at the point denoted as the finish point.

For the back stepping controller and the MPC, the tuning parameters were used based on the theory of these control approaches and recommendations in the cited sources [(Huynh et al. 2012) and MPC (Wang 2009)] with consideration of the experimental platform, and the bounds of uncertainties for the stability requirements. For DOB-SMC, SMC is tuned first without disturbance observation, then the observer is added during tuning to improve the performance. Tuning parameters have been verified to ensure they satisfy the bounds and stability requirements. The gains used for the DOB-SMC were; $c=25, k=5, {\varvec{\Lambda }}=[5,0]^T, \rho =1, \varrho =0.01$. In the simulation and experiments $[1,\; 0]$ is selected to compensate only for the unmatched uncertainties considering that SMC originally is able to deal with matched uncertainties. The controller parameters for the back stepping control law proposed in Huynh et al. (2012) are $c=0.6, k_1=0.6, a_1=0.01, a_2=1.05, \eta _0=1$ and $\epsilon =0.1$. Results obtained for both scenarios are presented and compared in sections below.

5.1 Back stepping controller, MPC and DOB-SMC without slip

Simulations have been carried out using the back stepping controller, MPC and DOB-SMC controllers to control the kinematic system to follow the reference path shown in Fig. 7, in the absence of slip. The comparison of the path offsets resulting from following the above mentioned reference path is plotted in Fig. 8. The comparison of the corresponding heading offsets is plotted in Fig. 9.

Fig. 7

The reference path

Fig. 8

Simulation of the kinematic model: path offset comparison without slip for back stepping controller, MPC and DOB-SMC

Fig. 9

Simulation of the kinematic model: heading offset comparison without slip for back stepping controller, MPC and DOB-SMC

5.2 Back stepping controller, MPC and DOB-SMC with slip

To take into account the effect of slip, the simulation has been repeated with wheel slip included in the model. Simulations have been carried out using the back stepping controller, MPC and DOB-SMC to control the kinematic model to follow the reference path shown in Fig. 7. The comparison of the path offsets is plotted in Fig. 10. The comparison of the corresponding heading offsets is plotted in Fig. 11.

Fig. 10

Simulation of the kinematic model: path offset comparison with slip for back stepping controller, MPC and DOB-SMC

Fig. 11

Simulation of the kinematic model: heading offset comparison with slip for back stepping controller, MPC and DOB-SMC

5.3 Analysis of kinematic model simulation results

Referring to Fig. 8, it can be seen that three controllers perform almost identically when there is no slip. However, it can be seen that there is a slight improvement of accuracy in the performance of MPC and DOB-SMC. The large errors that appear between the period form 25 to 30 s are due to the sharp corner in the reference path. Other smaller deviations occur when the path curvature is non-zero. Since, MPC is designed originally for a non-slip scenario and based on the prediction property of this controller, the performance at the curvy segments of the path is better. As for the case of heading offset comparison shown in Fig. 9, once again all three controllers performed equally well along straight path segments.

When slip is included in the kinematic model, the superiority of the DOB-SMC is clearly apparent in the path offset plot in Fig. 10. Unlike in the non-slip situation, the back stepping controller and the MPC show vulnerability to slip effects, even on straight path segments, while the DOB-SMC has successfully suppressed the effects of the slip for the majority of the time.

As shown in Fig. 11, as for the heading accuracy, the DOB-SMC out performs the back stepping controller and MPC. For these three controller, it can be seen that there exists a non-zero heading angle when traveling along straight path segments. This non-zero heading angle is unavoidable when lateral slip is present. This angle is called the crab angle.

Based on the above comparative study, it can be concluded that the DOB-SMC shows better performance with good stability in the presence of slip. The back stepping controller and MPC are compared in a dynamic simulation platform in a real field experiments.

Fig. 12

Illustration of the reference path in the field experiment according to Google earth

Fig. 13

Simulation of the dynamic model: a X–Y plot generated based on the performance of the controllers in the dynamic simulation. b The zoomed-in view of the far end of the path

Fig. 14

Simulation of the dynamic model: position offset results from the implementation of the controllers on the dynamic model subjected to slip

Fig. 15

Simulation of the dynamic model: heading offset results from the implementation of the controllers on the dynamic model subjected to slip

Fig. 16

Simulation of the dynamic model: steering command from the implementation of the controllers on the dynamic model subjected to slip

6 Control validation: dynamic model simulation and field experiment

The DOB-SMC, the back stepping controller and the MPC are implemented and validated in a dynamic simulation platform as well as in field experiments. The parameters for simulation and experiments are tuned to present good performance. For the back stepping controller and the MPC, the parameters are used based on the theory of this control approach and recommendations in Huynh et al. (2012) with consideration of our setup in the evaluation platform. For DOB-SMC, firstly, SMC is tuned without disturbance observation, then the observation part was added gradually to have a good performance. Tuning has been verified for different paths. Moreover, the bounds of uncertainties are considered and added to satisfy the stability conditions described in the paper.

6.1 Dynamic model simulation

To further investigate the DOB-SMC’s performance, a comprehensive simulation environment was developed. The reference path has been changed to a path that is typically used for farming operations, which is shown in Fig. 12. Then the back stepping controller and MPC as well as DOB-SMC that were used to control a dynamic model of a tractor that closely resembles the actual tractor, will eventually be used in the field experiment.

The X–Y plot generated by the simulation in the presence of slip are shown in Fig. 13. The path offsets are plotted in Fig. 14 and the heading offsets are plotted in Fig. 15. The steering commands are shown in Fig. 16.

Fig. 17

Field experiment: a X–Y plot generated based on the performance of the controllers in the field experiment. b The zoomed-in view of the far end of the path

6.2 Field experiment

Using the experimental set up described in Sect. 4, a field experiment was carried out using the DOB-SMC as the controller implemented in the module labeled “Path Following Control DOB-SMC” in Fig. 4.

The X–Y plots generated by the experiments are shown in Fig. 17. The path offsets are shown in Fig. 18, the heading offsets are shown in Fig. 19 and the steering angles are plotted in Fig. 20.

Fig. 18

Field experiment: position offset results from the implementation of the controllers on the real tractor

Fig. 19

Field experiment: heading offset results from the implementation of the controllers on the real tractor

Fig. 20

Field experiment: steering command from the implementation of the controllers on the real tractor

Fig. 21

Box plot of the path offsets for the controllers implemented on the real tractor in the field experiment

Fig. 22

Box plot of the heading offsets for the controllers implemented on the real tractor in the field experiment

Table 3 Position error RMS and standard deviation (SD) from the field experiment

Table 4 Heading offset RMS and standard deviation (SD) from the field experiment

6.3 Analysis of results

This section provides a brief analysis of the results obtained from the simulation of the dynamic model and the field experiment. In both cases DOB-SMC was used as the controller and compared with the back stepping controller and MPC. While the stability proofs have been provided earlier, from the plots it can be clearly seen that the DOB-SMC showed robustness against slip disturbances and parametric uncertainties in the dynamic simulation as well as in the field experiment. The path offset for the dynamic simulation is shown in Fig. 14 and for the field experiment in Fig. 18. In the dynamic simulation, the performance of the back stepping controller is very close to DOB-SMC, however, in the field experiments, DOB-SMC performs better and the reason is the sensitivity of the back stepping controller to the bounds of the errors. Moreover, as was expected the MPC did not perform well. The authors believe that the primary reason for the poor performance is that slip has not been taken into account in designing the MPC controller and it is not an easy matter to incorporate slip in the controller design. MPC performed better than other controllers in the no-slip simulation as shown in Figs. 8 and 9, however, when slip is present, MPCs performance degraded as shown in Figs. 10, 14, and 18. The superior performance of DOB-SMC is highlighted by the box plot shown in Fig. 22. The box plot is based on absolute value of the path offset. The red points indicate the outliers and the red line in the middle is the median, which is better when it is closer to zero with upper and lower quartiles shown in blue lines. As for the heading offsets of different controllers, the results are mostly consistent. However, as shown in the box plot in Fig. 22, the performance of DOB-SMC is slightly better than the performance of the other two controllers. The overall result based on DOB-SMC shows adequate settling time in the control of the farm vehicle and the smaller errors suggest good performance by the DOB-SMC. Moreover, due to the nature of the farming task, the farming operations are usually performed with relatively slower speeds, which makes the kinematic controller sufficiently robust and DOB-SMC is able to stabilize the system fast enough to maintain the desirable performance and precision (Fig. 21).

Apart from the comparisons, in an absolute sense the path tracking accuracy during the field experiment alone demonstrated high quality path tracking. The plot shows the position data generated using the GPS and IMU readings and it is very clear that the plot has high frequency components. A tractor which weighs more than a ton cannot follow these high frequency components. As such the actual path tracking has to be much smoother. In particular, as can be seen in Fig. 18, while the very high path tracking accuracy is shown along the straight line segments, the controller has also ensured very good stability when the curvature of the paths undergo sudden changes. To quantify the path tracking quality, the RMS errors of position offsets and heading offsets and their standard deviations for the straight line segments of the path and the entire path including curved and sharp turns are given in Tables 3 and 4, respectively. When traversing straight line path segments the RMS error for DOB-SMC is only 65.9 mm while the entire path including non-zero curvatures and sharp corners, shows an RMS value of 125 mm. The heading also shows very small errors.

7 Conclusion

This work presented a novel and very practical sliding mode controller backed by a disturbance observer, to control the steering of a field vehicle to ensure high accuracy path tracking. The controller was designed based on the kinematic model of a full scale tractor and then used to control three different types of systems. First, it was used to control the kinematic model, then it was used to control the dynamic model and finally it was used to control a real tractor in a field. The performance of the controller was compared against a back stepping controller and a model predictive controller from the literature. While all stability proofs are provided, it was shown that the new controller performed better under real field conditions, namely when subjected to slip. In an absolute sense the DOB-SMC performed very well in the field experiment showing very high accuracy path tracking along a path that contained circular segments on rough terrains. The accuracy was quantified by presenting statistical metrics. At all times the controller maintained stable operation.