1 Introduction

In recent decades, vibration suppression techniques have attracted broad research attention to solve problems like the failure of engineering structures, errors in manufacturing process, discomforts of transportation, etc. It is considered that the dynamic vibration absorbers have significant vibration suppression effect [1]. A traditional vibration absorber is designed to match the resonance frequency of the primary structure by designing the values of the mass, stiffness of the spring, and the damping coefficient of the damper, which make up a tuned-mass-damper (TMD). TMD is reported to be effective in the vibration suppression at its resonance frequency. For the case where excitation frequency varies, semi-/active control methods to improve the performances of vibration absorbers are proposed.

In active control loop, time delay is unavoidable due to data acquisition, signal transmission, mathematical calculation and force actuation. Time delay is treated as an unexpected factor since it may lead to the errors in control results, destabilization of systems, chaotic phenomenon, etc., and compensation methods [2, 3] are proposed to avoid the effect of time delay. Recently, researchers find that time delay is effective in the control of chaotic dynamic systems [4, 5], balancing of wheeled inverted pendulums [6, 7], vibration reduction of flexible beams [8, 9], chatter and flapping [10, 11], parametrically excited system [12], Jeffcott-rotor [13, 14], etc. Therefore, time delay is introduced intentionally into many vibration control problems. In vibration suppression problem, Sun et al. [15,16,17] proposed vibration isolators with multi-directional quasi-zero-stiffness adopting multiple time delays. The results show that time-delayed control (TDC) is able to tune the stiffness and damping properties of isolators, especially for low-frequency range. Cao et al. [18, 19] explored the effects of TDC on the vibration of a smooth and discontinuous (SD) oscillator, and established the relationship between the control parameters and vibration characteristics of the SD oscillator. The results show that the equivalent stiffness and damping characteristics are adjusted by the TDC which improves the vibration control effects.

Due to the advantages of TDC, it has been introduced to vibration absorber to improve it efficiency. Olgac et al. [20] proposed the delayed-resonator (DR) for vibration control. The time-delayed displacement signal is utilized to provide feedback control force for the improvement of vibration suppression of a linear dynamic system. The results show that the DR can tune the equivalent stiffness and damping properties of the primary system to realize the adjustment of vibration responses. And the vibration of the primary system can be totally eliminated when the control parameters is well designed. For multi-frequency external excitations, Olgac et al. [21] proposed two design methods of DR and focused on the design of the dual frequency fixed delayed resonator (DFFDR). The results show that the DFFDR is able to match the external excitation frequencies and anti-resonance frequencies of the main system when control gain and time delay are selected properly. At the resonance frequency, with absorber, the vibration of the primary system can be completely absorbed. Then, multiple DRs are applied for the multi-degree-of-freedom primary systems to suppress the vibration [22, 23]. In these study, multiple identical DRs are mounted on the multi-degree-of-freedom system to enhance the vibration suppression performances when the system is subjected to a primary resonance case. Also, centrifugal resonator with time delay is applied in the vibration suppression for the torsional systems. The proportional angular displacement is utilized in the feedback control with variable time-delay to achieve full absorption of torsional vibration of the structure [23,24,25]. Sun et al. [26, 27] design a time-delayed vibration absorber (TDVA) for the vibration of a linear system using acceleration signal to achieve anti-resonance phenomenon. The results show that the vibration of the primary system can be suppressed by about 80% with the proposed TDVA. Wang et al. [28, 29] proposed the parameter design criterions for TDVAs based on anti-resonance frequency analysis for linear and nonlinear systems. The research results show that the proposed TDVA is able to provide full elimination of vibrations for both linear and nonlinear primary systems. Zhao et al. [30] discuss the vibration suppression effects of TDC for nonlinear systems. The results show that TDVA can eliminate the torsional vibrating and parametrically excited systems. The study of TDVA with friction is carried out by Zhang et al. [31]. The authors reported that the stability boundaries of the control parameters depend on the excitation frequency due to the existence of non-smooth friction model. Based on the equal-peak phenomenon, Meng et al. [32, 33] proposed TDC method which utilized nonlinear TDVAs to design the control parameters for wide band vibration suppression. This method gives the design principle that the resonance peaks of the primary system should be equalized and minimized. Ji et al. [34, 35] analyzed the vibration suppression effects based on primary and super-harmonic resonances of the nonlinear primary system, and clarified the effectiveness of the vibration absorber on the above vibration suppression.

Multiple-layer structures have been found to be effective in vibration suppression. Deng et al. [36] proposed a bio-inspired multi-layer quasi-zero stiffness isolation system for suppression of micro-vibrations of low frequency and ultra-low frequency. Sun et al. [37] proposed a multi-layer structure with nonlinearity, which is bio-inspired by an avian neck structure, to realize dynamic stability and vibration isolation. For wide band vibration suppression, vibration absorbers have been adopted as inner resonators to form quasi-periodic structure. The band gap is determined by the physical parameters of the resonators in the units [38, 39]. Researcher have found the availability for the band gap achievement for systems with nonlinear stiffness [40, 41] and/or nonlinearity caused by rotation of pendulums [42, 43]. However, the position and width of the band gap are not adjustable after the decision of system parameters. To break this limitation, control mechanisms are needed to achieve adjustable band gaps for applications in various external environments. Practically, TDVA has been proven to be able to provide adjustable stiffness and damping simultaneously. Therefore, it is expected that TDVA can be adopted to realize vibration suppression within a wide low-frequency range.

In this study, a low-frequency multiple-layer metastructure is proposed for broadband vibration control and the effects of the TDVAs on the dynamic characteristics of a nonlinear metastructure are explored. First, in Sect. 2, the mathematical model is established. The response of the structure and stability of the system are studied. Then, in Sect. 3, the case with one TDVA is proposed. The optimum control parameters are given, and the vibration suppression effects are present. In Sect. 4, the effects of multiple TDVAs for vibration suppression are investigated. The relationship between the effective vibration control frequency band and the control parameters is given. In Sect. 5, conclusions are drawn and discussions are made. This study provides theoretical guidance for the application of TDVAs for nonlinear multiple degree of freedom systems.

2 Mathematical model

2.1 Equations of motion

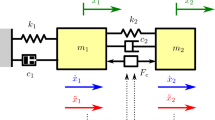
Figure 1 is a mechanical model proposed in this study that uses time-delay feedback control elements to achieve vibration suppression of multilayer nonlinear structures in the low-frequency range. As shown in Fig. 1a, the model consists of a multi-layer chain nonlinear structure coupled with the time-delayed vibration absorbers (TDVAs). In this study, the multilayer chain structure we studied is assumed to share the same physical parameters. The structure is arranged in the \(x\) direction, and the displacement of the n-th degree of freedom is defined as \(u_{n}\). In practice, the corresponding TDVA of the n-th degree of freedom may or may not exist. Here for the simplicity of the symbol, the displacement of the corresponding TDVA of \(u_{n}\) is defined as \(v_{n}\). Figure 1b shows the coupling mechanism between the last concentrated mass and the TDVA of the multi-layer chain structure, including the primary system with mass \(m_{1}\), a linear spring in the vertical direction \(k_{v}\) and a linear spring in the horizontal direction \(k_{h}\), and a rigid body with mass \(m_{2}\); and a TDVA composed of a spring \(k_{2}\) and active time-delayed control elements. The spring \(k_{v}\) provides the linear restoring force of the system, and the spring \(k_{h}\) provides the nonlinear restoring force. The deformation of the horizontal spring and vertical spring in Fig. 1b is shown in Fig. 1c. The original length of the horizontal spring is \(l\), and it is preloaded to the length \(l_{0}\). Assuming the displacement of \(m_{1}\) is \(u\), the restoring force provided by the horizontal spring and the vertical spring can be expressed as:

$$ f = k_{v} u - k_{h} u\left( {\frac{l}{{\sqrt {l_{0}^{2} + u^{2} } }} - 1} \right). $$
(1)

The restoring force in Eq. (1) can be expanded in Taylor series as

$$ \tilde{f} = k_{1} u + k_{3} u^{3} + \cdots . $$
(2)
Fig. 1
figure 1

Mechanical model of the multiple-layer metastructure with TDVAs

Full size image

Assuming that the nonlinear structure has N layers, the dynamic equation of the first layer structure of the time-delay coupled system shown in Fig. 1 can be written as:

$$ m_{1} \ddot{u}_{1} + k_{1} \left( {2u_{1} - u_{2} } \right) + \xi_{1} \left( {2\dot{u}_{1} - \dot{u}_{2} } \right) + k_{3} u_{1}^{3} + k_{3} \left( {u_{1} - u_{2} } \right)^{3} + f\left( {v_{1} ,\tau } \right) = F\cos \omega t. $$
(3)

The dynamic equation of the nth layer (\(1 < n < N\)) structure can be written as:

$$ \begin{aligned} & m_{1} \ddot{u}_{n} + k_{1} \left( {2u_{n} - u_{n - 1} - u_{n + 1} } \right) + \xi_{1} \left( {2\dot{u}_{n} - \dot{u}_{n - 1} - \dot{u}_{n + 1} } \right) \\ & \quad + k_{3} \left( {u_{n} - u_{n - 1} } \right)^{3} + k_{3} \left( {u_{n} - u_{n + 1} } \right)^{3} + f\left( {v_{n} ,\tau } \right) = 0. \\ \end{aligned} $$
(4)

The dynamic equation of the last layer is

$$ m_{1} \ddot{u}_{N} + k_{1} \left( {u_{N} - u_{N - 1} } \right) + \xi_{1} \left( {\dot{u}_{N} - \dot{u}_{N - 1} } \right) + k_{3} \left( {u_{N} - u_{N - 1} } \right)^{3} + f\left( {v_{N} ,\tau } \right) = 0. $$
(5)

The dynamic equation of the n-th TDVA is

$$ m_{2} \ddot{v}_{n} - f\left( {v_{n} ,\tau } \right) = 0. $$
(6)

In Eqs. (3)–(6), if \(v_{n}\) exists, then

$$ f\left( {v_{n} ,\tau } \right) = k_{2} \left( {u_{n} - v_{n} } \right) + \xi_{2} \left( {\dot{u}_{n} - \dot{v}_{n} } \right) + gk_{2} \left( {u_{n\tau } - v_{n\tau } } \right), $$
(7)

where \(u_{n\tau } = u_{n} \left( {t - \tau } \right)\), \(v_{n\tau } = v_{n} \left( {t - \tau } \right)\), \(g\) is the control gain, and \(\tau\) is the time delay. If \(v_{n}\) does not exist, then

$$ f\left( {v_{n} ,\tau } \right) = 0. $$
(8)

2.2 Response of the system

Suppose the response of the n-th layer structure is

$$ u_{n} = a_{n} \cos \omega t + b_{n} \sin \omega t,\;{\text{for}}\;n = 1,2, \ldots ,N, $$
(9)

and the response of the corresponding TDVA is

$$ v_{n} = c_{n} \cos \omega t + d_{n} \sin \omega t. $$
(10)

Substituting Eqs. (9) and (10) in Eqs. (3)–(6), one has

$$ \left\{ {\begin{array}{*{20}l} { - m_{1} \omega^{2} a_{1} + k_{1} \left( {2a_{1} - a_{2} } \right) + \xi_{1} \omega \left( {2b_{1} - b_{2} } \right) + f_{c1} } \hfill \\ {\quad + \frac{3}{4}k_{3} \left( {a_{1}^{3} + a_{1} b_{1}^{2} + \left( {a_{1} - a_{2} } \right)^{3} + \left( {a_{1} - a_{2} } \right)\left( {b_{1} - b_{2} } \right)^{2} } \right) = F,} \hfill \\ { - m_{1} \omega^{2} b_{1} + k_{1} \left( {2b_{1} - b_{2} } \right) - \xi_{1} \omega \left( {2a_{1} - a_{2} } \right) + f_{s1} } \hfill \\ {\quad + \frac{3}{4}k_{3} \left( {b_{1}^{3} + a_{1}^{2} b_{1} + \left( {b_{1} - b_{2} } \right)^{3} + \left( {b_{1} - b_{2} } \right)\left( {a_{1} - a_{2} } \right)^{2} } \right) = 0,} \hfill \\ \end{array} } \right. $$
(11)
$$ \left\{ {\begin{array}{*{20}l} { - m_{1} \omega^{2} a_{n} + k_{1} \left( {2a_{n} - a_{n - 1} - a_{n + 1} } \right) + \xi_{1} \omega \left( {2b_{n} - b_{n - 1} - b_{n + 1} } \right) + f_{cn} + \frac{3}{4}k_{3} [\left( {a_{n} - a_{n - 1} } \right)^{3} } \hfill \\ {\quad + \left( {a_{n} - a_{n - 1} } \right)\left( {b_{n - 1} - b_{n} } \right)^{2} + \left( {a_{n} - a_{n + 1} } \right)^{3} + \left( {a_{n} - a_{n + 1} } \right)\left( {b_{n} - b_{n + 1} } \right)^{2} ] = 0,} \hfill \\ { - m_{1} \omega^{2} b_{1} + k_{1} \left( {2b_{n} - b_{n - 1} - b_{n + 1} } \right) - \xi_{1} \omega \left( {2a_{n} - a_{n - 1} - a_{n + 1} } \right) + f_{s1} + \frac{3}{4}k_{3} [\left( {b_{n} - b_{n - 1} } \right)^{3} } \hfill \\ {\quad + \left( {b_{n} - b_{n - 1} } \right)\left( {a_{n - 1} - a_{n} } \right)^{2} + \left( {b_{n} - b_{n + 1} } \right)^{3} + \left( {b_{n} - b_{n + 1} } \right)\left( {a_{n} - a_{n + 1} } \right)^{2} ] = 0,} \hfill \\ \end{array} } \right. $$
(12)
$$ \left\{ {\begin{array}{*{20}l} { - m_{1} \omega^{2} a_{N} + k_{1} \left( {a_{N} - a_{n - 1} } \right) + \xi_{1} \omega \left( {b_{N} - b_{N - 1} } \right) + f_{cN} } \hfill \\ {\quad + \frac{3}{4}k_{3} [\left( {a_{N} - a_{N - 1} } \right)^{3} + \left( {a_{N} - a_{N - 1} } \right)\left( {b_{N - 1} - b_{N} } \right)^{2} ] = 0,} \hfill \\ { - m_{1} \omega^{2} b_{N} + k_{1} \left( {b_{N} - b_{n - 1} } \right) - \xi_{1} \omega \left( {a_{N} - a_{n - 1} } \right) + f_{sN} } \hfill \\ {\quad + \frac{3}{4}k_{3} [\left( {b_{N} - b_{N - 1} } \right)^{3} + \left( {b_{N} - b_{N - 1} } \right)\left( {a_{N - 1} - a_{N} } \right)^{2} ] = 0,} \hfill \\ \end{array} } \right. $$
(13)

and if \(v_{n}\) exists, then, respectively, for \(n = 1,2, \ldots ,N\)

$$ \left\{ \begin{gathered} - m_{2} \omega^{2} c_{n} - f_{cn} = 0, \hfill \\ - m_{2} \omega^{2} d_{n} - f_{sn} = 0, \hfill \\ \end{gathered} \right. $$
(14)

In Eqs. (11)–(14), the fcn and fsn can be solved as:

$$ \left\{ \begin{gathered} f_{cn} = k_{2} \left( {a_{n} - c_{n} } \right) + \xi_{2} \left( {b_{n} - d_{n} } \right) + \left( {a_{n} - c_{n} } \right)gk_{2} \;\cos \;\omega \tau - \left( {b_{n} - d_{n} } \right)gk_{2} \;\sin \;\omega \tau , \hfill \\ f_{sn} = \left( {b_{n} - d_{n} } \right)k_{2} - \xi_{2} \left( {a_{n} - c_{n} } \right) + \left( {b_{n} - d_{n} } \right)gk_{2} \;\cos \;\omega \tau + \left( {a_{n} - c_{n} } \right)gk_{2} \;\sin \;\omega \tau . \hfill \\ \end{gathered} \right. $$
(15)

If \(v_{n}\) does not exist, then Eq. (14) becomes

$$ f_{cn} = f_{sn} = 0. $$
(16)

It can be seen from Eqs. (11)–(16) that one can obtain \(2\left( {N + P} \right)\) equations about the unknown vibration amplitudes \(a_{n} ,b_{n} ,c_{p} ,d_{p}\), and control parameters \(g\) and \(\tau\), and external excitation amplitude \(F\), and frequency \(\omega\). By solving these equations, the response of the system can be obtained. Thus, the relationship between the response of any mass and the physical parameters, external excitation frequency and control parameters can be obtained. In this study, we define the frequency response curve (FRC) of the n-th mass as:

$$ {\text{FRC}} = 20\;\log \,(|u_{n} (t)|{/}|u_{1} (t)|). $$
(17)

2.3 Stability analysis

Consider the linearized autonomous system of Eqs. (3)–(6), the dynamic equation can be written as:

$$ {\mathbf{M\ddot{U}}} + {\mathbf{\Xi \dot{U}}} + {\mathbf{KU}} + {\mathbf{GU}}_{\tau } = 0, $$
(18)

where \({\mathbf{U}} = [\begin{array}{*{20}c} {u_{1} } & {u_{2} } & \cdots & {u_{N} } & {\underbrace {{\begin{array}{*{20}c} {v_{1} } & \cdots & {v_{N} } \\ \end{array} }}_{{{\text{Total Number }}P}}} \\ \end{array} ]^{T}\) is the displacement vector, \({\mathbf{M}}\), \({{\varvec{\Xi}}}\), \({\mathbf{K}}\), \({\mathbf{G}}\) are the matrix of mass, damping, stiffness and control gain, respectively. \(P\) is the total number of TDVAs. It can be easily found that

$$ {\mathbf{M}} = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{1} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{M}}_{2} } \\ \end{array} } \right]_{(N + P) \times (N + P)} , $$
(19)

where

$$ {\mathbf{M}}_{1} = m_{1} \left[ {\begin{array}{*{20}c} 1 & {} & 0 \\ {} & \ddots & {} \\ 0 & {} & 1 \\ \end{array} } \right]_{N \times N} ,\;\;{\mathbf{M}}_{2} = m_{2} \left[ {\begin{array}{*{20}c} 1 & {} & 0 \\ {} & \ddots & {} \\ 0 & {} & 1 \\ \end{array} } \right]_{P \times P} . $$
$$ {\mathbf{K}} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{1} } & {{\mathbf{K}}_{c} } \\ {{\mathbf{K}}_{c}^{T} } & {{\mathbf{K}}_{2} } \\ \end{array} } \right]_{{\left( {N + P} \right) \times \left( {N + P} \right)}} , $$
(20)

where

$$ {\mathbf{K}}_{1} = k_{1} \left[ {\begin{array}{*{20}c} 2 & { - 1} & 0 & \cdots & 0 \\ { - 1} & 2 & { - 1} & \ddots & \vdots \\ 0 & { - 1} & \ddots & \ddots & 0 \\ \vdots & \ddots & \ddots & 2 & { - 1} \\ 0 & \cdots & 0 & { - 1} & 1 \\ \end{array} } \right]_{N \times N} + k_{2} \left[ {\begin{array}{*{20}c} {\delta \left( {v_{1} } \right)} & {} & 0 \\ {} & \ddots & {} \\ 0 & {} & {\delta \left( {v_{N} } \right)} \\ \end{array} } \right]_{N \times N} ,\;\;{\mathbf{K}}_{2} = k_{2} \left[ {\begin{array}{*{20}c} 1 & {} & 0 \\ {} & \ddots & {} \\ 0 & {} & 1 \\ \end{array} } \right]_{P \times P} . $$

in which \(\delta (v_{n} ) = \left\{ \begin{array}{ll} 1,&\;\;{\text{if}}\; \, v_{n} \;{\text{exists,}} \hfill \\ 0,&\;\;{\text{if}}\;v_{n} \;{\text{doesn't exist.}} \hfill \\ \end{array} \right.\) Assuming the corresponding mass of the p-th TDVA is numbered as \(np\). Thus, for \(p = 1,2, \ldots ,P\), the element at the position of the \(np\)-th row and p-th column of the matrix in \({\mathbf{K}}_{c}\) is \(- k_{2}\), and the rest elements are zero. The matrix \({{\varvec{\Xi}}}\) shares the same form with \({\mathbf{K}}\), one can get the final expression of \({{\varvec{\Xi}}}\) by replacing the coefficients \(k_{1}\) and \(k_{2}\) with \(\xi_{1}\) and \(\xi_{2}\).

$$ {\mathbf{G}} = \left[ {\begin{array}{*{20}c} {{\mathbf{G}}_{1} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{G}}_{2} } \\ \end{array} } \right]_{{\left( {N + P} \right) \times \left( {N + P} \right)}} , $$
(21)

where \({\mathbf{G}}_{2} = gk_{2} \left[ {\begin{array}{*{20}c} 1 & {} & 0 \\ {} & \ddots & {} \\ 0 & {} & 1 \\ \end{array} } \right]_{P \times P}\). In \({\mathbf{G}}_{1}\), the element at the position of the \(np\)-th row and \(np\)-th column of the matrix is \(- g\), and the rest elements are zero.

Then, the characteristic equation of the system can be written as:

$$ \left| {\lambda^{2} {\mathbf{M}} + \lambda {{\varvec{\Xi}}} + {\mathbf{K}} + {\mathbf{G}}e^{ - \lambda \tau } } \right| = 0, $$
(22)

which can be expanded as:

$$ \left| {\left[ {\begin{array}{*{20}c} {\lambda^{2} {\mathbf{M}}_{1} + \lambda {{\varvec{\Xi}}}_{1} + {\mathbf{\rm K}}_{1} + {\mathbf{G}}_{1} e^{ - \lambda \tau } } & {\lambda {{\varvec{\Xi}}}_{c} + {\mathbf{K}}_{c} } \\ {\lambda {{\varvec{\Xi}}}_{c}^{T} + {\mathbf{K}}_{c}^{T} } & {\lambda^{2} {\mathbf{M}}_{2} + \lambda {{\varvec{\Xi}}}_{2} + {\mathbf{K}}_{2} + {\mathbf{G}}_{2} e^{ - \lambda \tau } } \\ \end{array} } \right]} \right| = 0. $$
(23)

Equation (23) contains the polynomial function of the \(2(N + P)\) degrees and the transcendental equation of \(e^{ - \lambda \tau }\), and it is difficult to obtain the accurate expression of the control parameters of the system for Hopf bifurcation. Instead, through the numerical method, the stability of the system can be obtained.

3 Vibration suppression effects of single TDVA

3.1 Model description

In this subsection, the total number of TDVA is assumed to be one and its position is located at the end of the multiple-layer metastructure. In this case, \(f_{cn}\) and \(f_{sn}\) in Eqs. (11)–(14) satisfy

$$ \left\{ \begin{array}{l} f_{cn} = f_{sn} = 0,\quad {\text{for}}\;n = 1,2, \ldots ,N - 1 \hfill \\ f_{cN} = k_{2} \left( {a_{N} - c_{N} } \right) + \xi_{2} \left( {b_{N} - d_{N} } \right) + \left( {a_{N} - c_{N} } \right)gk_{2} \;\cos \;\omega \tau - \left( {b_{N} - d_{N} } \right)gk_{2} \;{\text{sin}}\;\omega \tau , \hfill \\ f_{sN} = k_{2} \left( {b_{N} - d_{N} } \right) - \xi_{2} \left( {a_{N} - c_{N} } \right) + \left( {b_{N} - d_{N} } \right)gk_{2} \;\cos \;\omega \tau + \left( {a_{n} - c_{N} } \right)gk_{2} \;{\text{sin}}\;\omega \tau . \hfill \\ \end{array} \right. $$
(24)

The FRC of the n-th mass is the same as in Eq. (17). Without loss of generality, the parameters of the proposed system are selected as \(m_{1} = 1,\;k_{1} = 1,\;m_{2} = 0.1,\;k_{2} = 0.1,\;\xi_{1} = \xi_{2} = 0.01\) according to Ref. [33]. The mass and stiffness of the primary system are assumed to be unit. As a common practice, the mass and stiffness of the absorber are selected to be 10% of the values of the primary system. The stability boundary of the system is shown in Fig. 2. According to Eq. (24), the Hopf bifurcation occurs as the condition fcn = fsn = 0. In Fig. 2, the red, green and blue lines represent the critical values of time-delayed parameters as the positive real part of the eigenvalue occurs. In the area marked “Stable,” the real part of each eigenvalue of the system is negative, and the zero equilibrium point of the system is stable. In the shaded area, one or more pairs of characteristic roots containing positive real parts appear in the system, and the response of the system diverges with time. To verify the stability analysis and the stability partition, the vibration response of the primary system for different time-delayed parameters is shown in Fig. 3.

Fig. 2
figure 2

Stability boundary of the system

Full size image
Fig. 3
figure 3

Displacement response of the first mass for a g =  − 0.5 and τ = 1.5, b g =  − 0.5 and τ = 3.0 and c g = 0.5 and τ = 1.5

Full size image

In Fig. 3, the control gain g and time delay τ are selected such that {g, τ} = {− 0.5, 1.5}, {− 0.5, 3.0}, and {0.5, 1.5}, respectively. It can be obtained from Fig. 2 that for the case {g, τ} = {− 0.5, 1.5}, the zero equilibrium is unstable; and for the cases {g, τ} = {− 0.5, 3.0}, and {0.5, 1.5}, the zero equilibrium is stable. In Fig. 3a, the displacement of the mass gradually attenuates and eventually tends to zero, which means that the zero equilibrium point of the system is stable. In Fig. 3b, c, the displacement response of the mass increases exponentially with time, and the zero equilibrium point of the system becomes unstable. The results in Fig. 3 confirm the accuracy of the obtained bifurcation diagram given in Fig. 2.

3.2 Vibration suppression effect

According to Eq. (17), the suppression effect of a single TDVA on the vibration of the multiple-layer metastructure is obtained. First, when the time delay is zero, the control in this study becomes to proportional control. In Fig. 4, the FRCs of the last mass when the control gain is 0.5, 0 and − 0.5 are shown. As shown in Fig. 4, for different control gains g, the locations of anti-resonance point are different. For the three cases in Fig. 4, the anti-resonance points occur as the dimensionless frequency equals 1.22, 1 and 0.707. From the results in Fig. 4, it is found that as the gain decreases, the coupling stiffness between the vibration absorber and the mass decreases. Thus, the anti-resonance frequency point of the system gradually decreased. In fact, one can find that the frequency of the anti-resonance point is very close to the natural frequency of the vibration absorber. Therefore, changing the natural frequency of the vibration absorber through time-delayed feedback control is effective in suppressing the vibration of the multi-degree-of-freedom nonlinear system [33]. For different time-delayed parameters, the equivalent properties (including the equivalent stiffness and damping properties) of the local resonators and the coupling strength are adjusted. With positive control gain, the equivalent stiffness of the local resonators increases, while it decreases for negative control gain. Then, when the equivalent stiffness of the local resonators is close to one modal of the primary system, the anti-resonance frequency point would occur there. As shown in Fig. 4a, the anti-resonance point is located between the fourth- and fifth-order resonance frequencies; in Fig. 4b, the anti-resonance point is within the third- and fourth-order resonance frequencies; while in Fig. 4c, the anti-resonance frequency is moved between the second- and third-order resonance frequencies. It can be seen that the TDVA proposed in this study can realize the adjustment of cross-modal anti-resonance and vibration suppression in a wide frequency band.

Fig. 4
figure 4

FRCs of the last mass with single TDVA when the control gain \(g\) is a 0.5, b 0 and c − 0.5 (solid lines correspond to stable responses and dashed black lines correspond to unstable ones)

Full size image

From Fig. 4, one can see that the response of this mass is very small near the anti-resonance area. Similar to the previous study [29], the comparison between the dynamic responses of the system with or without nonlinearity is shown in Fig. 5. It can be seen that there is a big difference between the two FRCs where the response amplitude is large. The existence of nonlinearity leads to multiple steady-state solutions for the system. When the response amplitude is small, the difference between the two FRCs is very small, and the nonlinear behavior is not obvious. At the anti-resonance, the two FRCs are almost in the same position, which is induced by the fact that the nonlinearity on the system is very weak for low vibration amplitude. Based on this finding, adopting the optimal control parameters in the linear case to realize the vibration control of the nonlinear system at the anti-resonance is worth studying.

Fig. 5
figure 5

Comparison between the dynamic responses of the system with single TDVA with or without nonlinearity (solid lines correspond to stable responses and dashed black lines correspond to unstable ones)

Full size image

For a linear system, the optimal time-delayed control parameter of the last mass at a given frequency satisfies

$$ - m_{2} \omega^{2} + k_{{2}} + i\zeta_{2} \omega + gk_{2} e^{ - i\omega \tau } = 0. $$
(25)

From Eq. (25), one has

$$ g_{{{\text{opt}}}} = \pm {{\sqrt {\left( {\zeta_{2} \omega } \right)^{2} + \left( {m_{2} \omega^{2} - k_{2} } \right)^{2} } } \mathord{\left/ {\vphantom {{\sqrt {\left( {\zeta_{2} \omega } \right)^{2} + \left( {m_{2} \omega^{2} - k_{2} } \right)^{2} } } {k_{2} }}} \right. \kern-\nulldelimiterspace} {k_{2} }}, $$
(26)

and

$$ \tau_{{{\text{opt}}}} = \left\{ \begin{gathered} {{\left[ {\arcsin \left( {\frac{{\zeta_{2} \omega }}{{g_{opt} k_{2} }}} \right) + 2r\pi } \right]} \mathord{\left/ {\vphantom {{\left[ {\arcsin \left( {\frac{{\zeta_{2} \omega }}{{g_{opt} k_{2} }}} \right) + 2r\pi } \right]} \omega }} \right. \kern-\nulldelimiterspace} \omega }, \hfill \\ {{\left[ { - \arcsin \left( {\frac{{\zeta_{2} \omega }}{{g_{opt} k_{2} }}} \right) + \left( {2r + 1} \right)\pi } \right]} \mathord{\left/ {\vphantom {{\left[ { - \arcsin \left( {\frac{{\zeta_{2} \omega }}{{g_{opt} k_{2} }}} \right) + \left( {2r + 1} \right)\pi } \right]} \omega }} \right. \kern-\nulldelimiterspace} \omega }, \hfill \\ \end{gathered} \right.\quad r = 1,2, \ldots $$
(27)

For a linear multi-degree-of-freedom system, when the control parameters satisfying Eqs. (26) and (27) are used, the response at the corresponding frequency is exactly zero. Figure 6 shows the relationship between the optimal control parameters and the external excitation frequency.

Fig. 6
figure 6

Relationship between the optimal a control gain and b time delay with the external excitation frequency

Full size image

Figure 7 shows the FRCs of the last mass when the optimal control parameters for the external excitation frequency are 0.9 and 1.1. It can be seen from Fig. 7 that when the above optimal control parameters are used, the corresponding external excitation frequency becomes the anti-resonance frequency, and the response at this frequency is very small. In this study, when the above optimal control parameters are selected, the response magnitude of the end mass at the anti-resonance point is below \(10^{ - 10}\). It is shown that the optimal control parameters satisfying the conditions as Eqs. (26) and (27) are effective on the vibration suppression of a nonlinear multiple-degrees-of-freedom system.

Fig. 7
figure 7

FRCs of the last mass with single TDVA for cases where the external excitation frequencies are 0.9 and 1.1 (solid lines correspond to stable responses and dashed black lines correspond to unstable ones)

Full size image

In this subsection, the influence of a single TDVA on the dynamic response of a multi-degree-of-freedom nonlinear system is explored. The stability distribution of the delay-coupled system is proven by numerical calculations to verify the correctness of the stability partition. The FRCs of the system under linear and nonlinear conditions are compared, and it is found that the nonlinear performance is very weak in the anti-resonance region. Taking the last mass as an example, the relationship between the anti-resonance point in the FRC and the time-delayed control parameter is obtained. The relationship satisfied by the optimal control parameters is obtained. It is found that the response at the anti-resonance point is close to zero when the optimal parameters are used. Therefore, the time-delay feedback control can greatly improve the effect of the vibration absorber on the dynamic response of the multi-degree-of-freedom nonlinear system.

4 Vibration suppression effects of multiple TDVAs

4.1 Model description

In this section, the case where corresponding TDVAs for all \(u_{n}\) exist will be explored. The simplified structure is shown in Fig. 8. From Fig. 8, the metastructure can be expressed as a mechanical model consisting of a chain with a two-degree-of-freedom units made up of a mass and a TDVA. In practice, any position can contain a vibration absorber, and its parameters can be arbitrarily selected. In this section, the effect of TDVAs with the same parameters on the response of a multi-degree-of-freedom system is studied.

Fig. 8
figure 8

Simplified model of the quasi-periodic structure with TDVAs

Full size image

4.2 Effective band

Considering the structure shown in Fig. 8, which can be approximated as a periodic structure, the band gap problem of the corresponding infinite long chain linear structure can be analyzed through wave conduction theory [44]. Therefore, the harmonic solution is set as:

$$ \left\{ \begin{gathered} u_{j + n} = U\exp \left[ {i\left( {qx_{j} + nql_{c} } \right) + \lambda t} \right], \hfill \\ v_{j + n} = V\exp \left[ {i\left( {qx_{j} + nql_{c} } \right) + \lambda t} \right], \hfill \\ \end{gathered} \right. $$
(28)

where \(q\) is the wave vector and \(l_{c}\) is the length of the unit.

Substituting Eq. (28) in Eqs. (4) and (6), and ignoring the nonlinear and damping terms, one has

$$ \left[ {\begin{array}{*{20}c} {\lambda^{2} m_{1} + 2k_{1} (1 - \cos ql_{c} ) + k_{2} + gk_{2} e^{ - \lambda \tau } } & { - k_{2} - gk_{2} e^{ - \lambda \tau } } \\ { - k_{2} - gk_{2} e^{ - \lambda \tau } } & {\lambda^{2} m_{2} + k_{2} + gk_{2} e^{ - \lambda \tau } } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} U \\ V \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right\}. $$
(29)

The characteristic equation of Eq. (29) is

$$ A_{4} \lambda^{4} + A_{2} \lambda^{2} + A_{0} + (B_{2} \lambda^{2} + B_{0} )e^{ - \lambda \tau } = 0, $$
(30)

where

$$ \begin{aligned} A_{4} & = m_{1} m_{2} , \\ A_{2} & = 2k_{1} m_{2} (1 - \cos (ql_{c} )) + k_{2} (m_{1} + m_{2} ), \\ A_{0} & = 2k_{1} k_{2} (1 - \cos (ql_{c} )), \\ B_{2} & = gk_{2} (m_{1} + m_{2} ), \\ B_{0} & = 2k_{1} gk_{2} (1 - \cos (ql_{c} )). \\ \end{aligned} $$

For the case without control, the analytical expression of the characteristic frequency obtained from Eq. (30) is

$$ \lambda_{1,2} = \sqrt {\frac{{A_{2} }}{{2A_{4} }} \mp \sqrt {\frac{{A_{2}^{2} }}{{4A_{4}^{2} }} - \frac{{A_{0} }}{{A_{4} }}} } . $$
(31)

The real parts of the Bloch wave vector \({\text{Re}} (q)\) corresponding to the start and cut-off frequencies of the band gap are \({\pi \mathord{\left/ {\vphantom {\pi {l_{c} }}} \right. \kern-\nulldelimiterspace} {l_{c} }}\) and 0, respectively. Substituting \(ql_{c} = \pi\) and \(ql_{c} = 0\) in Eq. (31), the analytical expressions of the band gap's start and cut-off frequencies are

$$ \left\{ \begin{gathered} \Omega_{{{\text{start}}}} = \omega_{2} \sqrt {2\frac{{\omega_{1}^{2} }}{{\omega_{2}^{2} }} + \frac{1}{2}\left( {1 + \mu } \right) - \sqrt {\left[ {2\frac{{\omega_{1}^{2} }}{{\omega_{2}^{2} }} + \frac{1}{2}\left( {1 + \mu } \right)} \right]^{2} - 4\frac{{\omega_{1}^{2} }}{{\omega_{2}^{2} }}} } , \hfill \\ \Omega_{{\text{cut - off}}} = \omega_{2} \sqrt {1 + \mu } , \hfill \\ \end{gathered} \right. $$
(32)

where \(\omega_{1} = \sqrt {{{k_{1} } \mathord{\left/ {\vphantom {{k_{1} } {m_{1} }}} \right. \kern-\nulldelimiterspace} {m_{1} }}}\), \(\omega_{2} = \sqrt {{{k_{2} } \mathord{\left/ {\vphantom {{k_{2} } {m_{2} }}} \right. \kern-\nulldelimiterspace} {m_{2} }}}\), and \(\mu = {{m_{2} } \mathord{\left/ {\vphantom {{m_{2} } {m_{1} }}} \right. \kern-\nulldelimiterspace} {m_{1} }}\).

Figure 9a shows the relationship between the start and cut-off frequencies of the band gap of the last mass with different parameters. It can be seen that when the mass of the vibration absorber is fixed, for decreasing the stiffness of the vibration absorber, the start and cut-off frequencies of the band gap gradually decrease, and the width of the band gap also gradually narrows. When the stiffness of the absorber is the same, the larger absorber brings a lower band gap frequency. Therefore, suitable vibration absorber parameters can be selected to achieve vibration suppression within a specific frequency band. Figure 9b presents the normalized bandwidth which is defined as \({\text{NW}} = 2{{\left( {\Omega_{{\text{cut - off}}} - \Omega_{{{\text{start}}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\Omega_{{\text{cut - off}}} - \Omega_{{{\text{start}}}} } \right)} {\left( {\Omega_{{\text{cut - off}}} + \Omega_{{{\text{start}}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\Omega_{{\text{cut - off}}} + \Omega_{{{\text{start}}}} } \right)}}\) according to Ref. [45, 46]. For \(m_{2} = 0.1\), the normalized bandwidth varies from 5 to 20% with the increase in \(k_{2}\). The changing rate of the normalized bandwidth for \(m_{2} = 0.2\) is less than that for \(m_{2} = 0.1\).

Fig. 9
figure 9

a Start and cut-off frequencies and b normalized bandwidth of the band gap of the last mass with respect to \(k_{2}\)

Full size image

Considering the case when the time delay is small, in Eq. (30), \(e^{ - \lambda \tau } \approx 1\). Then, Eq. (30) becomes

$$ A_{4} \lambda^{4} + \left( {A_{2} + B_{2} } \right)\lambda^{2} + \left( {A_{0} + B_{0} } \right) = 0. $$
(33)

The analytical expression of the characteristic frequency obtained from Eq. (33) is

$$ \lambda_{1,2} = \sqrt {\frac{{\left( {A_{2} + B_{2} } \right)}}{{2A_{4} }} \mp \sqrt {\frac{{\left( {A_{2} + B_{2} } \right)^{2} }}{{4A_{4}^{2} }} - \frac{{A_{0} + B_{0} }}{{A_{4} }}} } . $$
(34)

Similar to the derivation of Eq. (32), substituting \(ql_{c} = \pi\) and \(ql_{c} = 0\) in Eq. (34) and considering the expressions of the coefficients in Eq. (30), the start and cut-off frequencies correspond to \(\lambda_{1}\) and \(\lambda_{2}\) for the controlled case are

$$ \left\{ \begin{gathered} \Omega_{{{\text{start}}}} = \omega_{2} \sqrt {\frac{{2\omega_{1}^{2} }}{{\omega_{2}^{2} }} + \frac{1}{2}\left( {1 + g} \right)\left( {1 + \mu } \right) - \sqrt {\left[ {\frac{{2\omega_{1}^{2} }}{{\omega_{2}^{2} }} + \frac{1}{2}\left( {1 + g} \right)\left( {1 + \mu } \right)} \right]^{2} - \left( {1 + g} \right)\frac{{4\omega_{1}^{2} }}{{\omega_{2}^{2} }}} } , \hfill \\ \Omega_{{\text{cut - off}}} = \omega_{2} \sqrt {\left( {1 + g} \right)\left( {1 + \mu } \right)} , \hfill \\ \end{gathered} \right. $$
(35)

Figure 10 shows the curve of the start and cut-off frequencies and normalized bandwidth of the band gap for the last mass with the control gain under different parameters for \(m_{2} = 0.1\). It can be seen that as the control gain decreases, the start and cut-off frequencies of the band gap gradually decrease, and the width of the band gap gradually narrows. Therefore, the conclusion that the position of the band gap in the FRC can be changed by adjusting the control gain is drawn. However, for vibration in the low-frequency range, although a low-frequency band gap can be achieved, its width gradually narrows and the normalized bandwidth gets smaller. It should be considered whether the resonance peak near the band gap can be reduced through the damping effect of the time delay to achieve broadband vibration suppression.

Fig. 10
figure 10

a Start and cut-off frequencies and b normalized bandwidth of the band gap of the last mass with the change of control gain

Full size image

Without considering the nonlinearity, the FRCs of the last mass under several sets of parameters are shown in Fig. 11. When the time delay is zero, according to Eq. (35), when the corresponding gains are − 0.5, 0 and 0.5, the frequency range of the band gap is [0.7021, 0.7416], [0.9839, 1.0488] and [1.1907, 1.2845]. As shown in Fig. 11, under the above parameters, the band gap position of the amplitude and frequency agrees very well with the theoretical value. After introducing the time delay, it is found that the band gap position of the amplitude frequency moves only slightly, and the resonance peak near the band gap was weakened. However, the frequency band for effective vibration suppression can be broadened. Although the effect of vibration suppression in the effective control band will be reduced, the substantial broadening of the vibration suppression frequency band brought about by the time delay is very worthwhile.

Fig. 11
figure 11

Band structure and FRCs of the last mass for control gain g as a − 0.5, b 0, and c 0.5

Full size image

4.3 Vibration suppression effect

The discussion on the effective bandwidth position and width in the previous subsection is based on the linearized system. Next, we will discuss the effective bandwidth position and width of the nonlinear system. In Fig. 12, the FRCs of the last mass when the control gain is 0.5, 0 and − 0.5 are shown. In Fig. 12a, the response of the last mass is lower than 0 dB in the frequency band of approximately [1.1907, 1.2845]; in Fig. 12b, the frequency band is [0.9839, 1.0488]; in Fig. 12c, the frequency band is [0.7021, 0.7416]. From the results in Fig. 12, it can be seen that as the gain decreases, the coupling stiffness between the vibration absorber and the mass gradually decreases; the band gap position of the system response also gradually decreases, and its width gradually narrows. These results are consistent with the analysis of the band gap position and width of the linearized system in the previous subsection. In fact, the band gap position and width can be adjusted by changing the strength of the time-delayed feedback control. This adjustment is still effective in suppressing the vibration of the multi-degree-of-freedom nonlinear system. Therefore, the parameter selection method for the band gap position control of the nonlinear multi-degree-of-freedom system is similar to the linear case.

Fig. 12
figure 12

FRCs of the last mass with multiple TDVAs when the control gain is a 0.5, b 0 and c − 0.5 (solid lines correspond to stable responses and dashed black lines correspond to unstable ones)

Full size image

Similar to the previous subsection, in Fig. 12a, the band gap is located between the fourth- and fifth-order resonance frequencies; in Fig. 12b, the band gap is within the third- and fourth-order resonance frequencies; in Fig. 12c, the band gap has moved between the second and third resonant frequencies. Therefore, the TDVAs can also achieve cross-modal band gap position adjustment, which provides a basis for achieving vibration suppression in a large frequency band.

From Fig. 12, one can find that within the band gap, the response of the last mass is very small. Therefore, the nonlinearity has a very small effect on the system's FRC and the band gap position. In Fig. 13, FRCs of the last mass considering linearity and nonlinearity are compared. In fact, similar to the above study, there is a big difference between the two FRCs at the peaks of the response, while in the band gap the two curves almost overlap where the response is small.

Fig. 13
figure 13

Comparison between the dynamic responses of the system with multiple TDVAs with or without nonlinearity (solid lines correspond to stable responses and dashed black lines correspond to unstable ones)

Full size image

As known that the existence of time delay will bring equivalent damping, in order to clarify the influence of the parameters of TDVAs on the system response, in Fig. 14, the FRCs of the last mass under different time delays are present. In Fig. 14, the time delays are \(\tau = 0\), 0.1, and 0.2, respectively, and the gains corresponding to the blue, orange, green, and red lines in Fig. 14d–f are 0, − 0.25, − 0.5, and − 0.75, respectively. It can be seen that when the gain gradually becomes smaller, the position of the effective vibration control frequency band gradually moves to the low frequency. Comparing Fig. 14d–f, it is found that as the time delay increases, the position of the effective vibration suppression band does not change much, but its width has been greatly widened. As mentioned earlier, although the effect of vibration suppression in the band gap has deteriorated, the vibration suppression frequency band has been greatly broadened.

Fig. 14
figure 14

FRCs of the last mass with multiple TDVAs, a–c density plots and d–f with different gains for time delay as 0, 0.1 and 0.2, respectively (solid lines correspond to stable responses and dashed black lines correspond to unstable ones)

Full size image

From Fig. 14, it is known that time delay can greatly broaden the width of the effective vibration suppression frequency band. In Fig. 15, the changing trend of FRCs of the last mass with respect to time delay is present. In Fig. 15, the control gains are \(g = - 0.25\) and 0.50, respectively. The time delays corresponding to the blue, orange, green and red lines in Fig. 15c, d are 0, 0.02, 0.1, and 0.2, respectively. In Fig. 15a, it can be seen that when the time delay is small, the FRCs in two frequency bands inside the band gap are greater than 0 dB, corresponding to the FRC in Fig. 15c where the time delay is zero. It can be seen that there is a resonance peak in each of these two frequency bands. As the time delay increases to 0.02, the resonance peak at about 0.92 is gradually lower than 0 dB. Compared with the case without time delay, the effective frequency band is significantly broadened. As the time delay continues to increase, the resonance peak at the frequency of about 0.83 gradually disappears, and the effective bandwidth is further expanded to more than twice the original width. Similarly, in Fig. 15d, as the time delay gradually increases, the resonance peak near the frequency of 0.75 also gradually disappears, and the effective bandwidth can also be expanded to about twice the original width. Although the response in the effective frequency band has been increased, the effective bandwidth can be broadened to about twice the original width, which makes this attempt very worthwhile.

Fig. 15
figure 15

Changing trend of FRCs of the last mass with respect to time delay for control gain as a, c − 0.25 and b, d − 0.50

Full size image

In Fig. 16, the effective vibration suppression bandwidth ratio with respect to time delay is shown. The width ratio is defined as the ratio of the continuous effective bandwidth to the bandwidth without time-delayed control, so that the ratio is 1 when there is no time delay. In Fig. 16, for \(g = - 0.25\), it can be seen that the effective bandwidth width ratio suddenly increases when the time delay is around 0.01 and 0.03. This is because the values of the two resonance peaks are equal to zero under these two conditions. After the time delay exceeds these values, the original effective frequency band is connected to the band outside the peak and forms a wider one. It can be seen that the effective vibration suppression frequency band can be broadened to more than 2.2 times of its original width. In Fig. 16, for \(g = - 0.50\), it can be seen that the effective bandwidth width ratio also suddenly increases when the time delay is around 0.02. As the time delay increases, the width of the effective bandwidth does not increase all the time. In addition, as mentioned above, the increase in time delay will weaken the vibration suppression effect in the effective vibration suppression band. Therefore, it is necessary to consider both the width of the effective bandwidth and the quality of vibration suppression when choosing the control parameters.

Fig. 16
figure 16

Change trend of the effective vibration suppression bandwidth ratio with respect to time delay

Full size image

5 Conclusions and discussions

In this study, the effects of the TDVAs on the dynamic characteristics of a nonlinear metastructure are explored. First, the effect of using a single TDVA on the metastructure for vibration suppression is studied. The results show that the introduction of time-delayed feedback control is beneficial to improve the vibration suppression of the metastructure in the anti-resonance range. Then, the relationship between the dynamic response of the metastructure and the control parameters of the multiple TDVAs which are evenly distributed is explored, and the relationship between the effective vibration suppression frequency band and the control parameters is given.

The research results in this study show that the TDVA can be used to suppress the vibration of the proposed metastructure. Anti-resonance phenomenon at a specific external excitation frequency can be achieved by using a single TDVA, and the vibration suppression effect can be greatly improved when the optimal time-delay control parameters are selected. For vibration suppression of the metastructure within a broad band, multiple TDVAs are found to be effective. In addition, the selection of appropriate time-delay control parameters is available in the adjustment of the position and width of the band gap in which the vibration can be suppressed to low level. This study presents a novel exploration on the wide band vibration suppression of TDVAs and provides guidance of applications of time-delayed control in the multi-degree-of-freedom nonlinear system and the parameter selection method.