1 Introduction

The control of chaotic behavior can be applied to a variety of systems to provide flexibility switching from different periodic responses. In essence, the idea is to take advantage of unstable periodic orbits embedded on the chaotic attractor that can be stabilized with low energy consumption. This can be used to stabilize high-power lasers [1], communication systems [2], mechanical systems [3, 4] and energy-harvesting systems [5]. Chaos control is related to several techniques varying from discrete to continuous approaches [3, 6].

The use of smart material remarkable properties for actuation purposes is an interesting idea due to the coupling between different physical fields. This coupling characteristic allows one to convert different kinds of energy, conferring adaptive capacity to the system. Shape memory alloys (SMAs) belong to this class of material presenting solid phase transformations. Among other interesting properties, SMAs present pseudoelastic and shape memory effects that have been applied on dynamical systems [7], associated with vibration control [8], origami structures [9], robotics [10] and energy harvesting [11, 12]. Systems with this type of material have intrinsic nonlinearities usually presenting chaotic behavior [7]. This characteristic opens the possibility to implement chaos control strategies for stabilization on desirable situations [4, 13].

SMAs have an increasing importance on applied dynamics exploiting either property changes due to temperature variations or hysteretic dissipation [7]. The use and characterization of SMAs as actuators are discussed in some references [14,15,16] that focus on their thermomechanical modeling. An essential problem to the use of SMAs in dynamical systems is their actuation frequency that is limited due to heat transfer issues. This subject is discussed in only few works in the literature, and its connection with control approaches is not treated. In this regard, it is important to evaluate the real capacity of SMA actuators to provide control efforts and their applicability in different controllers.

This work investigates the thermal control of an SMA system considering heat transfer constraints. Basically, an extended time-delayed feedback control is applied by SMA thermal actuation on an SMA–pendulum system composed of a nonlinear pendulum coupled with SMA springs. Nonlinear dynamics of this system is previously addressed on reference [17] that shows the system ability to change equilibrium point structure and responses due to temperature variations. Floquet theory is employed to define controller parameters. Discussions about energy consumption and stabilization time are presented establishing a comparison between controllers with and without heat transfer constraints, respectively named as constrained and ideal controllers. Numerical simulations show the possibility of using shape memory alloy actuators to control chaotic behavior using temperature variations.

After this introduction, the paper presents a discussion about the delayed feedback control approach and the use of Floquet theory to estimate controller parameters. The next section presents the mathematical modeling of the SMA–pendulum system and the thermal actuation of the controller. Afterward, numerical simulations of the uncontrolled system are discussed and the chaotic response is analyzed identifying UPOs embedded on the attractor. On the following section, the identification of the controller parameters is performed and a discussion about the differences between constrained and ideal controllers is presented. Concluding remarks are then presented.

2 Chaos control method

Chaos control has as its main goal the stabilization of unstable periodic orbits (UPOs) embedded on chaotic attractor using discrete or continuous methods [18]. Basically, it consists of a two-stage method composed of a learning stage, where UPOs are identified and controller parameters are defined, and a stabilization stage, where UPO stabilization is performed. De Paula and Savi [3, 6] presented a general overview of chaos control methods establishing a comparative analysis of the capability of each one of them to stabilize a desired UPO.

The extended time-delayed feedback control (ETDF) [19] is an interesting continuous approach that has been successfully used in various experimental applications in electrical systems [20,21,22,23]. The controlled system is governed by the following equation:

$$\begin{aligned}&\dot{\varvec{x}}={\varvec{f}}({\varvec{x}},t)+{\varvec{p}}({\varvec{y}},{\varvec{y}} (t-\tau ), {\varvec{y}}(t-2\tau ),\ldots ), \nonumber \\&{\varvec{y}}(t)={\varvec{Cx}}, \end{aligned}$$
(1)

where \({\varvec{x}}\in \mathbb {R}^{N}\) is the system state, t is the time, \({\varvec{f}}\left( {{\varvec{x}},t} \right) \in \mathbb {R}^{N}\) defines the system dynamics, and \((\dot{~})\) represents time derivative; \({\varvec{y}}\in \mathbb {R}^{M}\) is the system observation provided by the operator \({\varvec{C}}={\varvec{C}}\left( {\varvec{x}} \right) \in \mathbb {R}^{M\times N}\) applied to state variables; \({\varvec{p}}\in \mathbb {R}^{N}\) is the control signal defined as follows

$$\begin{aligned} {\varvec{p}}\left( {y,t} \right) ={\varvec{K}}\left[ {\left( {1-R} \right) \mathop \sum \limits _{n=1}^\infty R^{n-1}{\varvec{y}}\left( {t-n\tau } \right) -{\varvec{y}}\left( t \right) } \right] , \nonumber \\ \end{aligned}$$
(2)

where \({\varvec{K}}\in \mathbb {R}^{N\times M}\) is a proportional gain and \(R\in \mathbb {R} \) is a controller parameter; \(\tau \) is the period of the target UPO to be controlled.

Controller parameters \({\varvec{K}}\) and R are defined from the analysis of the UPO stability under control action. For the sake of simplicity, \({\varvec{K}}\) is assumed to be a scalar, \(K\in \mathbb {R}\), indicating that only one state is accessible to the controller \(\left( {p\in \mathbb {R}} \right) \) and only one output is used as feedback \(\left( {y\in \mathbb {R}} \right) \). Although parameters K and R can be estimated using a try and error strategy, the formal estimation needs to evaluate the UPO stability under control action. In this regard, either Lyapunov exponents [4, 21, 24] or Floquet exponents [20, 25] can be employed to define controller parameters.

Floquet exponents are useful to analyze the stability of a general periodic orbit as their calculation requires only one integration period. As a matter of fact, it constitutes a spectrum \({\varvec{\mu }} \in \mathbb {C}^{N}\) of values \(\mu _j \in \mathbb {C}\) for each system dimension. In brief, these exponents measure how a solution on the neighborhood of a periodic orbit, \({\varvec{\delta x}}\), diverges during one period. If all exponents have a negative real part, the solution converges to the orbit. On the other hand, if any Floquet exponent has a positive real part, the solution diverges from the orbit. As chaos control methods have the goal to stabilize a UPO, Floquet exponents can be employed to evaluate the stability of that controlled UPO.

Floquet exponents of a target UPO are estimated following the procedure presented in reference [20]. It considers a time evolution linearization around a reference path \({\varvec{x}}_\mathbf{0} ={\varvec{x}}_{\mathbf{0}} \left( t \right) \), leading to a displacement \({\varvec{\delta }} {\varvec{x}}={\varvec{x}}-{\varvec{x}}_{\mathbf{0}} \) of the path. This leads to a time evolution given by:

$$\begin{aligned} {\varvec{\delta }} \dot{{\varvec{x}}}= & {} {\varvec{Df}}(t; {\varvec{x}}_{\mathbf{0}}){\varvec{\delta x}}(t)\nonumber \\&+\,K{\varvec{B}}\left[ (1-R)\sum _{n=1}^{\infty } R^{n-1}{\varvec{\delta x}}(t-n\tau )-{\varvec{\delta x}}(t)\right] , \nonumber \\ \end{aligned}$$
(3)

where \({\varvec{Df}}\) is the Jacobian matrix and \({\varvec{B}}\) is the gradient of the function \({\varvec{C}}\) with respect to its variables.

Since Eq. 3 has the form \(\dot{{\varvec{x}}}={\varvec{Ax}}\), with a period-\(\tau \) such that, \({\varvec{A}}\left( {\varvec{t}} \right) ={\varvec{A}}\left( {t+\tau } \right) \), Floquet theory establishes that:

$$\begin{aligned} {\varvec{\delta }} {\varvec{x}}=e^{{\varvec{H}}t}{\varvec{q}}, \end{aligned}$$
(4)

where \({\varvec{q}}={\varvec{q}}\left( t \right) \) is a period-\(\tau \) function and \({\varvec{H}}={\varvec{H}}\left( {\varvec{\mu }} \right) \) is a matrix that has the spectrum of the Floquet exponents as eigenvalues. Under this assumption, delayed and present states are related as follows:

$$\begin{aligned} {\varvec{\delta x}}\left( {t-n\tau } \right) =e^{-{\varvec{H}}n\tau } {\varvec{\delta x}}\left( t \right) . \end{aligned}$$
(5)

Equation 5 allows one to calculate the infinite sum of Eq. 3, which leads to:

$$\begin{aligned} {\varvec{\delta \dot{x}}}=\left[ {\varvec{Df}}(t;{\varvec{x}}_\mathbf{0})+K{\varvec{B}}\left( {\mathbb {I}-e^{-{\varvec{H}}\tau }} \right) \left( {\mathbb {I}-Re^{-{\varvec{H}}\tau }} \right) ^{-1}\right] {\varvec{\delta x}}, \nonumber \\ \end{aligned}$$
(6)

where \(\mathbb {I}\) is the identity matrix. Note that Eq. 5 correlates delayed states reducing the dimension of Eq. 6 from infinity to the uncontrolled system dimension N. Nevertheless, this reduction makes the displacement time evolution to be dependent on the Floquet exponents.

By considering the evolution of a single period, Eq. 5 can be rewritten as:

$$\begin{aligned} {\varvec{\delta x}}\left( \tau \right) =e^{{\varvec{H}}\tau }{\varvec{\delta }} {\varvec{x}}\left( 0 \right) . \end{aligned}$$
(7)

Therefore, Floquet exponent calculations can be done using the following equation:

$$\begin{aligned} {\varvec{\delta x}}\left( t \right) ={\varvec{\psi }} \left( t \right) {\varvec{\delta x}}\left( 0 \right) , \end{aligned}$$
(8)

where \({\varvec{\psi }} \) is the fundamental matrix and \({\varvec{\psi }} \left( 0 \right) =\mathbb {I}\). The time evolution of the fundamental matrix can be obtained by replacing Eq. 8 with Eq. 6:

$$\begin{aligned}&\varvec{\dot{\psi }} =\left[ {\varvec{Df}}(t;{\varvec{x}}_\mathbf{0})+K{\varvec{B}}\left( {\mathbb {I}-e^{-{\varvec{H}}\tau }} \right) \left( {\mathbb {I}-Re^{-{\varvec{H}}\tau }} \right) ^{-1}\right] {\varvec{\psi }}. \nonumber \\ \end{aligned}$$
(9)

Under these assumptions, Floquet exponents can be calculated as follows:

$$\begin{aligned} {\varvec{\psi }} \left( {\tau ;{\varvec{\mu }} } \right) -e^{\mu _j \tau }\mathbb {I}=\mathbf{0}. \end{aligned}$$
(10)

Since matrix \({\varvec{\psi }} ={\varvec{\psi }} \left( {t;{\varvec{\mu }} } \right) \) depends on the Floquet exponents themselves (Eq. 9), it is necessary to establish a proper procedure for their calculation. In this regard, Floquet exponents are estimated using a differential evolution-based algorithm [26], presented in Fig. 1. This optimization scheme considers, on its kth iteration, a population of trial values of Floquet exponents \({\varvec{\mu }} ^{{\varvec{trial}}}\left[ k \right] \). Afterward, the fundamental matrix \({\varvec{\psi }} \) is estimated from the integration of Eq. 9 using a fourth-order Runge–Kutta method and the trial exponents. After obtaining \({\varvec{\psi }} ={\varvec{\psi }} \left( {\tau ;{\varvec{\mu }} ^{{\varvec{trial}}}\left[ k \right] } \right) \), Floquet exponents, \({\varvec{\mu }} \left[ k \right] \), are recalculated with Eq. 10 and compared with the initial trial values using an Euclidean metric on the complex plane. This metric, \(\delta \mu \), is used as a measure for each individual. Lower values of \(\delta \mu \) indicate a high level of fitness and probability to leave descendants. The stop criteria are defined by comparing the fitness of the individuals with a tolerance value, \(\delta _\mathrm{Tol} .\) If the fitness of some population individuals is smaller than the tolerance, the process ends and the best individuals \({\varvec{\mu }} ^{{\varvec{best}}}\) are chosen. If the criteria are not satisfied, the algorithm [26] selects the population individuals and create a new generation \({\varvec{\mu }}^{{\varvec{trial}}}\left[ {k+1} \right] \).

It should be pointed out that under an uncontrolled situation \(\left( {K=R=0} \right) \), Eq. 9 becomes independent of the Floquet multipliers, allowing one to calculate their values by a straight time integration of \({\varvec{\psi }}\).

Fig. 1
figure 1

Algorithm to calculate the Floquet exponents with ETDF control. \({\varvec{\mu }} ^{{\varvec{trial}}}\left[ k \right] \) indicates the kth population, \({\varvec{\mu }} \left[ k \right] \) is the calculated Floquet exponent population after temporal evolution of the UPO’s period, \(\delta \mu \) is the fitness value, \(\delta _\mathrm{Tol} \) is the stopping criteria tolerance, and \({\varvec{\mu }} ^{{\varvec{best}}}\) is the best individual on the selected population

Full size image

3 SMA–pendulum system

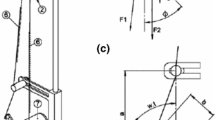
Consider a nonlinear pendulum system, shown in Fig. 2, which is formed by a disk of diameter D (1) and a lumped mass m (2). The excitation is provided by a motor–spring–string system where a DC motor (7) is connected to a string–spring system. The spring is made of SMA providing an adaptive behavior to the system. The string–spring system has two springs (6) connected by a string. One end of the first spring is connected to the DC motor, while the other end is connected to a string that involves a disk of diameter d and, finally, reaches the end of the second spring. The other end of the second spring is connected to an anchor (5). A magnetic device provides a controlled dissipation to the apparatus (3). Costa and Savi [17] analyzed the nonlinear dynamics of this system with special attention on temperature-dependent behavior. De Paula et al. [27] discussed the analysis of a similar system, using elastic springs instead of SMA springs, considering both numerical and experimental approaches.

Fig. 2
figure 2

Nonlinear pendulum: a physical model (1) metallic disk; (2) lumped mass; (3) magnetic damping device; (4) rotary motion sensor; (5) anchor; (6) SMA spring; (7) electric motor. b Parameters and forces on the metallic disk. c Parameters for driving device [27]. d Picture of the experimental setup

Full size image

By considering that \({\varvec{\phi }} \) is the angle of the pendulum and assuming that dissipation is a combination of linear viscous and dry friction, respectively, represented by coefficients \(\vartheta \) and \(\xi \), the equation of motion is given by [17, 27]:

$$\begin{aligned} {\phi }''= & {} -\frac{\vartheta }{J \omega _{0}}\phi ^{\prime }-\frac{\xi }{mgD}\hbox {sign}(\phi ^{\prime })\nonumber \\&-\frac{sin(\phi )}{2}+\frac{d}{2mgD}(F_{m}-s_{m}), \end{aligned}$$
(11)

where J is the pendulum angular inertia, g is the acceleration of gravity, and \(\omega _0 \) is a reference frequency defined as follows,

$$\begin{aligned} \omega _0 =\sqrt{\frac{mgD}{J}}. \end{aligned}$$
(12)

Time derivative \(\left( \right) ^{\prime }\) is related to a dimensionless time defined by \(t^{*}=t\omega _0 \). Moreover, \(s_m \) is the force of the anchored spring and \(F_m \) is the excitation force of the spring connected to the motor.

The displacement due to the motor movement is given by:

$$\begin{aligned} u= & {} \sqrt{\left( {a^{2}+b^{2}-2ab\hbox {cos}\left( {\frac{\omega t^{*}}{\omega _0 }+\theta } \right) } \right) }\nonumber \\&-\left( {a-b} \right) -\frac{d\phi }{2}, \end{aligned}$$
(13)

where a is the distance between the center of the disk and the center of the rotor, \(\theta \) is the initial phase of the motor, \(\omega \) is the excitation frequency, and b is the motor arm length.

A polynomial constitutive model describes the general SMA thermomechanical behavior. Basically, a polynomial stress–strain–temperature (\(\sigma -\varepsilon -T\)) relation is considered as follows,

$$\begin{aligned} \sigma =\alpha _m \left( {T-T_\mathrm{M} } \right) \varepsilon -\beta _m \varepsilon ^{3}+\frac{\beta _m^2 }{\alpha _m \left( {T_\mathrm{A} -T_\mathrm{M} } \right) }\varepsilon ^{5}, \nonumber \\ \end{aligned}$$
(14)

where \(\alpha _m \) and \(\beta _m \) are material parameters, T is the temperature, \(T_\mathrm{M} \) is the temperature below which only martensitic phase is stable, and \(T_\mathrm{A} \) is the temperature above which only austenitic phase is stable (at stress-free state). This equation is based on a potential energy that presents two minimum points at temperatures below \(T_\mathrm{M} \), representing two martensitic phases (tension induced and compression induced); three minimum points at temperatures between \(T_\mathrm{M} \) and \(T_\mathrm{A} \), representing the stability of austenite and both martensitic variants; and finally one minimum point at temperatures above \(T_\mathrm{A} \), representing the stability of austenite on a stress-free state.

Spring behavior description is done, assuming that phase transformation is homogeneous on the spring cross section. Under this assumption, it is possible to write a force–displacement–temperature equation that is similar to the stress–strain–temperature expression [28]. Hence, the terms related to equations of motion, Eq. 11, can be written as follows,

$$\begin{aligned} F_m= & {} a_m \left( {T-T_\mathrm{M} } \right) u -b_m u^{3} \nonumber \\&+\frac{b_m ^{2}}{a_m \left( {T_\mathrm{A} -T_\mathrm{M} } \right) }u^{5} \end{aligned}$$
(15)
$$\begin{aligned} s_m= & {} a_m \left( {T-T_\mathrm{M} } \right) \frac{\phi d}{2}-b_m \left( {\frac{\phi d}{2}} \right) ^{3} \nonumber \\&+\frac{b_m ^{2}}{a_m \left( {T_\mathrm{A} -T_\mathrm{M} } \right) }\left( {\frac{\phi d}{2}} \right) ^{5}. \end{aligned}$$
(16)

It should be highlighted that springs need to be prestressed, working in a stretched configuration. More details of the system modeling can be seen in reference [17].

4 Thermal actuation modeling

The controller is designed in order to use SMA spring temperature changes as actuation. This is achieved by the application of an electric current providing heat through Joule effect. The thermal actuator is modeled by considering an SMA spring force, \(F_\mathrm{thermo} \), given by:

$$\begin{aligned} F_\mathrm{thermo} =a_m \left[ {\left( {T_1 -T_\mathrm{ref} } \right) u} \right] , \end{aligned}$$
(17)

where \(T_1 \) is the spring temperature and \(T_\mathrm{ref} \) is a reference temperature.

An ideal controller is the one where temperature can be altered without heat transfer constraints. Hence, the controller is able to apply any force and therefore always applies the calculated control force estimated by the ETDF method. On the other hand, a constrained controller has restrictions related to heat transfer and electrical power.

The definition of the constrained controller considers that temperature \(T_1 \) is estimated from the energy equation. By assuming homogeneous temperature distributions and similar resistance for all SMA phases and neglecting thermomechanical coupling terms, the energy equation is built as a balance of convective dissipation and Joule effect, being written as follows:

$$\begin{aligned} T_1^{\prime }=-\frac{h}{c_p \omega _0 }\left( {T_1 -T_\infty } \right) +\frac{\left( {I_1 +I_\mathrm{ref} } \right) ^{2}R_\mathrm{ohn} }{c_p \omega _0 }, \end{aligned}$$
(18)

where \(T_\infty \) is the ambient temperature, \(I_1 \) is the current on the forcing spring, \(I_\mathrm{ref} \) is a reference current which maintains the system on the reference temperature \(T_\mathrm{ref} \), \(R_\mathrm{ohn} \) is the spring resistance, \(c_p \) is the spring thermal capacity, and h is the convection dissipation coefficient. Note that a dimensionless time was considered, being defined in a similar way of the equations of motion.

It should be pointed out that energy equation defines constraints that limit the SMA temperature. Besides, current \(I_1 \) is also restricted between limit values (from 0 to 5 A, for instance).

Under these assumptions, the controller has constraints that limit actuation. The difference between the calculated control force using ETDF, ideal controller and the constrained one, defined by the constrained controller, is expressed by variable \(\left( {e_T } \right) \) that can be seen as an error, expressed by a percentage of the maximum applied force:

$$\begin{aligned} e_T =\frac{F_\mathrm{thermo} -p}{\max \left( p \right) }. \end{aligned}$$
(19)

Moreover, it is interesting to evaluate the power consumed by the controller given by:

$$\begin{aligned} P_w =I_1^2 R_\mathrm{ohn}. \end{aligned}$$
(20)

5 Uncontrolled system dynamics

Numerical simulations of the uncontrolled system are carried out in order to evaluate system dynamics. Fourth-order Runge–Kutta method is employed with time steps that lead to errors smaller than \(10^{-8}\) estimated by a fifth-order method.

System parameters are the ones experimentally identified in reference [27]: \(m=1.47 \times 10^{-2}\hbox {kg}\), \(D=9.5\,\hbox {cm}\), \(d=4.8\,\hbox {cm}\), \(b=1.5\,\hbox {cm}\), \(a=16\,\hbox {cm}\), \(\xi =1.272 10^{-4}\,\hbox {Nm}\), \(\vartheta =2.368 10^{-5}\frac{\hbox {kg m}^{2}}{\hbox {s}}\) and \(g=9.81\,\hbox {m}/\hbox {s}^{2}\). SMA parameters are adjusted with experimental data related to Nitinol: \(T_\mathrm{A} =289.35\,\hbox {K}\), \(T_\mathrm{M} =282.45\,\hbox {K}\), \(a_m =0.4375\,\hbox {N}/\hbox {mK}\) and \(b_m =150\,\hbox {Pa}/\hbox {m}\). Thermal parameters are: \(T_\mathrm{ref} =283.15 \hbox {K}\), \(c_p =5\,\hbox {J}/\hbox {K}\) and \(T_\infty =281.15\,\hbox {K}\). The convection coefficient h is chosen on a range of typical experimental values, with a reference value \(h=17.76\,\hbox {W}/\hbox {K}\), that can be varied in order to evaluate the influence of control constraints.

By considering a forcing frequency \(\omega =8.5\,\hbox {rad}/\hbox {s}\) and initial conditions of \({\varvec{x}}\left( 0 \right) =\left( {-\,6\hbox { rad}, 0\,\hbox {rad}/\hbox {s}\omega _\mathrm{0} } \right) \), the system presents a chaotic response (Fig. 3). In order to assure the chaotic behavior, it is necessary to calculate the system greatest Lyapunov exponent. If this value is positive, chaotic regime is confirmed. The exponent is calculated employing the algorithm proposed by Wolf et al. [29] presenting a positive value of \(\lambda =+2.86\pm 0.01\,\hbox {bits}\), confirming the chaotic behavior.

An essential part of chaos control is the learning stage where UPOs embedded on chaotic attractor are identified. The forthcoming analysis presents this UPO identification for the mentioned chaotic attractor, performed with the algorithm proposed by Auerbach et al. [30] that searches for periodic orbits through Poincaré map time series.

The basic idea of this algorithm is to search for a period-P UPO in time series with \(N_{p}\) data points, represented by state vectors. The search is carried out for pairs of points that satisfy the condition \(\left| {x_i -x_{i+P} } \right| _{i=1}^{N_p -P} \le r_1 \), where \(r_{1}\) is the identification radius value for distinguishing return points. After this analysis, all points that belong to a period-P cycle are grouped together. During the search, the vicinity of a UPO may be visited many times, and it is necessary to distinguish each orbit, remove any cycle permutation and to average them in order to improve estimations. In this regard, separation radius \(r_2 \) needs to be defined.

Fig. 3
figure 3

Phase space and Poincaré section of the chaotic response

Full size image

Basically, the SMA–pendulum system is analyzed considering a Poincaré map with 25,000 points, identification radius of \(r_1 =0.04\) and separation radius of \(r_2 =0.15\). After the identification, Floquet exponents \(\left( {\varvec{\mu }} \right) \) of each orbit are calculated employing the procedure described in Sect. 2 via straight integration of \({\varvec{\psi }} \) (\(K=R=0)\) [20]. Figure 4 shows three identified UPOs: period-1, period-2 and period-3. Table 1 presents Floquet exponents of each one of these orbits. It is important to highlight that each orbit has a Floquet exponent with positive real part indicating its instability.

Fig. 4
figure 4

Phase space and Poincaré sections: a period-1 UPO, b period-2 UPO, c period-3 UPO

Full size image
Table 1 Identified UPO’s Floquet exponent values without control
Full size table

6 Controlling the system with thermal actuation

Thermal control is now in focus for the stabilization of UPOs. SMA–pendulum velocity is considered as the only observable variable, being also employed to define controller actuation. Numerical simulations are carried out with Runge–Kutta method, considering an approximation of the delayed equations using the first ten terms [15]. Initial conditions of \({\varvec{x}}\left( 0 \right) =\left( {-\,6\hbox { rad}, 0\,\hbox {rad}/\hbox {s}\omega _0 } \right) \) are employed for all simulations. The controller is turned on after 75 periods, which means that delayed states are known.

Initially, a period-1 UPO stabilization is analyzed. Controller parameters K and R are estimated using Floquet exponents, considering ideal actuation. Figure 5 shows the maximum real part of the Floquet exponents \(\mu ^\mathrm{max}=\max (\hbox {Re}\left( {\varvec{\mu }} \right) ) \) for several values of K and R. Note that for each value R, curves present a minimum optimum value, \(\mu ^\mathrm{opt}\), that decreases and translate to the right as R increases. The optimum Floquet exponent is considered to be the one with the most negative real part, and values in this neighborhood are chosen for the UPO stabilization. The UPO is considered to be stabilized after the temperature variations during one period, which are less than 0.2 K.

Figure 6 shows the UPO stabilization with ideal controller and parameters \(K=0.4\) and \(R=0.3\), condition close to the optimum value indicated in Fig. 5. Note that the control starts around \(t^{*}=500\) with a peak on its power and stabilizes the UPO after 36 periods, when the actuation power consumption starts to decrease until it vanishes. One may also notice an exponential envelope when the system response is close to the UPO (Fig. 6d). This decay furnishes a good approximation of the largest Floquet exponent real part and can be clearly identified considering an exponential fit on the Poincaré section (Fig. 6e) resulting on a Floquet exponent of \(\mu ^\mathrm{max}=-\,0.13\pm 0.01\) that agrees with the predicted Floquet exponent (Fig. 5). The Poincaré section also shows that the system converges to the period-1 UPO throughout a period 2 orbit, which means that the Floquet exponent with maximum real part has an imaginary part, \(\hbox {Im}\left( {\mu ^\mathrm{max}} \right) =\pi /\tau \).

Fig. 5
figure 5

Real part of period-1 UPO’s Floquet exponents for various values of K and R

Full size image
Fig. 6
figure 6

Ideal controller (standard ETDF) applied to a period-1 UPO. The Floquet exponents encapsulation is calculated using an exponential fitting \(A_0 +A_1 e^{-\mu ^\mathrm{max}t^{*}}\) which displays the same value for the Floquet multiplier: \(\mu ^\mathrm{max}=-\,0.13 \pm 0.01\). a Pendulum position. b Controller energy consumption. c Stabilized orbit. d Temperature. e Position of Poincaré section versus time and exponential fitting

Full size image

Constrained controller is now in focus considering different convection coefficients: \(h=17.76\,\hbox {W}/\hbox {K }\) (Fig. 7) and \(h=13.32\,\hbox {W}/\hbox {K}\) (Fig. 8). Note that controller stabilizes the orbit after 19 UPO periods for the first case and 36 UPO periods for the second. After this stabilization, the power consumption vanishes for both cases, in the same way of the ideal controller. Nevertheless, the exponential envelope appears just closer to the UPO when compared with the ideal one. Poincaré section of both cases indicates an exponential convergence of the period-1 UPO through a period-2 orbit. Floquet exponents are still approximated with the exponential decay, presenting the same results for calculated and fitted values. They also indicate the thermal constraints influence on controlled UPO stability as they are greater than the ideal controller. When \(h=17.76\,\hbox {W}/\hbox {K}\), it presents \(\mu ^\mathrm{max}=-0.12 \pm 0.01\), while \(\mu ^\mathrm{max}=-\,0.10 \pm 0.01\) when \(h=13.32\,\hbox {W}/\hbox {K}\).

The power consumption after stabilization is similar for both cases. This occurs since the control signal tends to vanish after the stabilization and therefore, minimizing the temperature variation needed to generate the actuation force and the influence of the thermal constraints. The stabilization convergence is evident on the controller actuation error plots shown in Figs. 7 and 8.

Fig. 7
figure 7

Constrained controller applied to a period-1 UPO with \(h=17.76\,\hbox {W}/\hbox {K}\). The Floquet exponents encapsulation is calculated using an exponential fitting \(A_0 +A_1 e^{-\mu ^\mathrm{max}t^{*}}\) which displays the same value for the Floquet multiplier: \(\mu ^\mathrm{max}=-\,0.13 \pm 0.01\). a Pendulum position. b Controller energy consumption. c Stabilized orbit. d Control signal. e Position Poincaré section versus time and exponential fitting. f Controller actuation error against time

Full size image
Fig. 8
figure 8

Constrained controller applied to a period-1 UPO with \(h=13.32\,\hbox {W}/\hbox {K}\). The Floquet exponents encapsulation is calculated using an exponential fitting \(A_0 +A_1 e^{-\mu ^\mathrm{max}t^{*}}\) which displays the same value for the Floquet multiplier: \(\mu ^\mathrm{max}=-\,0.10 \pm 0.01\). a Pendulum position. b Controller energy consumption. c Stabilized orbit. d Control signal. e Position Poincaré section versus time and exponential fitting. f Controller actuation error against time

Full size image

A comparison between both controller behaviors shows that the constrained controller stabilizes the system faster than the ideal one, but this is not always the case. This stabilization time is dependent on the initial conditions. For instance, by considering initial condition to be \({\varvec{x}}\left( 0 \right) =\left( {-\,7\hbox { rad}, 0\,\hbox {rad}/{\hbox {s}\omega }_0 } \right) \) and \(h=17.76\,\hbox {W}/\hbox {K}\), the ideal controller stabilizes the system after 20 periods, while the constrained controller stabilizes after 24 periods. A possible explanation for this is that the controller can effectively stabilize the UPO only when the system solution visits the UPO neighborhood. As a matter of fact, on discrete techniques such as OGY, the control is only turned on when the system solution is on the neighborhood of the UPO leading to a waiting time. Although this waiting time is not necessary to be considered for continuous techniques, it can be an interesting approach to minimize control energy consumption, to increase the controller efficacy [3, 6] and enlarge the basin of attraction of the controlled UPO [31].

The idea that chaos control confers flexibility to the system can be shown by considering a control rule that makes the system switches from one UPO to another. In this regard, a test is performed to evaluate the controller performance to follow a control rule: During the first 75 periods, controller is turned off. After that, it is turned on to stabilize a period-1 UPO (UPO-1) using \(K=0.4,R=0.3\); control parameters are changed on the 300th period to stabilize a period-2 UPO \((K=0.2,R=0.1)\) (UPO-2); finally, a period-3 UPO is targeted after the 600th period \((K=0.1,R=0.1)\) (UPO-3). The control strategy is performed with both controllers, ideal and constrained (with \(h=17.76\,\hbox {W}/\hbox {K}\)).

Figure 9 shows the Poincaré section and control current \(\left( {I_1 } \right) \) for the ideal controller, while Fig. 10 shows results for the constrained controller. The comparison of these results makes possible to identify that the ideal controller has a more evident exponential envelope associated with the control signal on the transitions between each UPO, while the constrained controller signal envelope is restricted to a smaller neighborhood of the UPO. It is also noticeable that the constrained controller has greater control signal amplitude after stabilization due to its restrictions, but needs a smaller time to perform the transition from period-1 UPO to period-2 UPO.

The maximum real-part Floquet exponents for each UPO, employing the ideal controller, are: \(\mu _{\mathrm{UPO}\hbox {-}1}^\mathrm{max} =-\,0.05, \quad \mu _{\mathrm{UPO}\hbox {-}2}^\mathrm{max} =-\,0.15\) and \(\mu _{\mathrm{UPO}\hbox {-}3}^\mathrm{max} =-\,0.14\), with a precision of \(\pm \,0.01.\) Using the constrained controller, the maximum Floquet exponents real parts are: \(\mu _\mathrm{UPO-1}^\mathrm{max} =-\,0.05, \quad \mu _{\mathrm{UPO}\hbox {-}2}^\mathrm{max} =-\,0.15\) and \(\mu _{\mathrm{UPO}\hbox {-}3}^\mathrm{max} =-\,0.09\) with a precision of \(\pm \, 0.03\).

Fig. 9
figure 9

Multi-orbit stabilization with ideal controller: a Poincaré map position against time and b controller power consumption against time

Full size image

Since the essential thermal controller constraint is represented by the convection coefficient, h, it is expected that the increase in this coefficient tends to eliminate the constraint, making both controllers similar. In order to verify this behavior, an analysis of the influence of h over the constrained controller is performed. The controller is employed to stabilize a period-1 UPO considering \(K=0.42\) and \(R=0.3\). Figure 11 shows the stabilization of a period-1 orbit together with associated errors. Results show that the constrained controller transient errors decrease with the increase in h values but, after stabilization, all results present the same error and control effort. This behavior is explained by considering that the control effort tends to vanish after stabilization, which facilitates the constrained actuation to provide the force needed.

Fig. 10
figure 10

Multi-orbit stabilization with constrained controller, with parameter \(h=17.76\,\hbox {W}/\hbox {K}\): a Poincaré map position against time and b controller power consumption against time

Full size image

Figure 12 shows the influence of thermal convection h on the controller behavior showing Floquet exponents as a function of \(h/\omega _0 c_p \). Note that the controller tends to loose stability with the decrease in \(h/\omega _0 c_p \), which is associated with the increase in actuation errors. This is related to the trend of \(\mu ^\mathrm{max}\) to become positive. On the other hand, as \(h/\omega _0 c_p \) tends to infinity, the constrained controller tends to a behavior similar to the ideal one. This can be clearly observed by the convergence of the UPO Floquet exponent values to the value of the ideal controller (dashed dotted line).

Fig. 11
figure 11

Influence of convection coefficient h during a period-1 stabilization. Time history of errors and stabilized orbit for different values of the parameter h. a, b \(h=4440.00\,\hbox {W}/\hbox {K}\); c, d \(h=444.00\,\hbox {W}/\hbox {K}\); e, f \(h=44.40\,\hbox {W}/\hbox {K}\); g, h \(h=17.76\,\hbox {W}/\hbox {K}\)

Full size image

Based on this analysis, it is possible to define three different situations. The first one (right-side region, green diagonal lines) is related to situations where both controllers are similar, being delimited by a saturation point where the Floquet exponent of the constrained controller is 99% of the ideal one. This region is characterized by the fact that variations in \(h/\omega _0 c_p \) do not affect the control. The second situation (central part region, yellow vertical lines) defines cases where the constrained controller is still effective to stabilize the UPO, but with different behavior compared with ideal controller, which is expressed by changes in Floquet exponents. Finally, the third situation (left-side region, red horizontal lines) is where the controller is not able to stabilize the UPO.

Fig. 12
figure 12

Analysis of Floquet exponents as a function of the convection coefficient \(h/\omega _0 c_p \) using control parameters \(K=0.42\) and \(R=0.3\). Dashed dotted line (green) represents the ideal controller. (Color figure online)

Full size image

7 Conclusions

This work deals with the application of chaos control to smart adaptive systems considering thermal actuation constraints defined by heat transfer issues. An SMA–pendulum system is analyzed considering the stabilization of unstable periodic orbits using extended time-delayed feedback control. Thermal constraints are defined by the energy equation. Control parameters are evaluated by calculating the target UPO Floquet exponents. Performance of the constrained controller is compared with the ideal controller, without constraints. Results indicate that the constrained controller is able to perform UPO stabilization. Both controllers have similar behaviors after stabilization since control force tends to vanish. The difference between both controllers is essentially defined by the heat convection coefficient, and the errors tend to vanish when it tends to infinity, increasing when it tends to zero. This analysis allows one to define three regions of effectiveness for the constrained controller: a region where the controller is not able to stabilize UPOs; a region where constrained controller is similar to the ideal one; and an intermediate region where the controller is able to stabilize UPOs, but with different costs.