1 Introduction

Vibration control is extensively used in modern engineering. One of the well-established devices of vibration control is the vibration absorber. The fundamentals of vibration absorbers were established by Den Hartog [1]. A mass-spring system attached to a primary system usually works as a passive absorber. The high-efficiency passive absorber removes all vibrations of the harmonically excited primary system when the excitation frequency equals the natural frequency of the passive absorber [2]. If the excitation frequency is variable, the passive absorber is invalid. As a result, the active absorber has been proposed by several researchers. The active absorber is regarded as a passive absorber with an actuator attached. The actuator force is determined by various control laws. These include proportional integral derivative (PID) [3], robust [4], positive position feedback (PPF) [5], and fuzzy control [6]. Although it has better vibration suppression performance than the passive one, the active absorber has not been widely used due to higher energy consumption, more complex structure and larger actuation force. The semi-active absorber is a trade-off between the passive and the active ones, which possesses the perfect combination of performance improvement and simplicity of implementation. The highlight of the semi-active absorber is the adjustment of its resonant frequency to track the excitation frequency in real time. There are three types of semi-active absorbers: variable inertia [7], variable stiffness [8], and variable damping absorbers [9].

It should be noted that time delay is unavoidable in active vibration control. It mainly comes from the process of signal acquiring and processing, computing, and applying the control force [10]. Although the value of time delay is small in most situations, it still results in complex dynamic behaviors of the controlled system [11–14]. The time delay was initially regarded as a negative factor in active vibration control. It may give rise to the degradation of the control performance and even destabilize the controlled system. Hence, several methods are employed to compensate the influence of the time delay. These include the Smith predictor method [15], the phase-shift method [16], and the recursive response method [17]. However, in the past three decades, many investigations have shown that the intentional introduction of time delay in the feedback control loop also improves the control performance or system stability [18–21]. The time-delayed absorber has attracted considerable attention in the field of active vibration control. The core idea of the time-delayed absorber is the introduction of an actuator controlled via state feedback with the adjustable time delay. It is easy to implement, real-time tunable, and effective within a wide frequency band. There has been tremendous interest in the application of the time-delayed absorber. A delayed resonator was invented by Olgac [22] to suppress the vibration of a finite freedom degree system. The design idea of the delayed resonator is that the utilization of a time-delayed position feedback converts a passive absorber into a resonator at the desired frequency. With proper selections of the feedback gain coefficient and time delay, the delayed resonator eliminates tonal vibrations of the primary structure. For extension of the delayed resonator, Olgac [23] developed a delayed resonator with delayed acceleration feedback to rest a clamped-clamped beam at the point of attachment. The theoretical and experimental results validated the effectiveness of the delayed resonator in absorbing the vibration of distributed structures. In view of the fact that time delay plays an important role in the system stability, the direct method [24] is employed for the linear time invariant time-delayed system to determine the exact boundaries of stable and unstable regions in time delay. Wang [25] investigated the effect of the feedback form on the performance of the delayed resonator. It is found that for stability the delayed acceleration feedback is superior to the delayed position feedback. The delayed resonator was used by Tootoonchi and Gholami [26] to minimize relative vibration between the cutting tool and work piece during machining process. The work done by Liu [27] showed that the delayed resonator is a special case of the proportional derivative (PD) controller if the control objective is to suppress a steady-state response to a harmonic excitation. The effect of a nonlinear time-delayed absorber on suppressing the vertical vibration of a primary system was studied by Zhao and Xu [28]. Effects of both positive and negative feedback control are observed at simultaneous primary resonance and a 1:1 internal resonance condition. The efficacy of the time-delayed absorber for controlling the self-excited vibration of a mechanical oscillator was investigated by Chatterjee and Mahata [29]. Their work revealed the possibility of using a time-delayed absorber to control any form of self-excited vibration of an elastic system. The availability of the time-delayed absorber for suppressing the vibration due to rotor blade flapping motion was found by El-Sayed and Bauomy [30]. In another work, El-Gohary and El-Ganaini [31] studied the performance of the time-delayed absorber on the control of a beam subjected to multi-parametric excitation forces. It should be pointed out that a great deal of effort has been devoted to the theoretical and numerical study of the time-delayed absorber. Limited work has been done on experiments [32, 33].

As mentioned above, the passive absorber is quite effective within a narrow and fixed frequency band. The effectiveness of the passive absorber reduces sharply outside the effective frequency band. In addition, the attachment of a passive absorber to a single degree of freedom (SDOF) linear primary system introduces two new resonant frequencies. When the excitation frequency is close to either of the two resonant frequencies, the vibration of the primary system with an absorber attached is much worse than that of the primary system alone. In this case, the passive absorber totally fails. Motivated by the above facts, we will here design a time-delayed acceleration feedback control to convert a passive absorber into a time-delayed one. The intentional time delay used in the time-delayed feedback may not necessarily be small compared to the natural periods of the system. The feedback gain coefficient may be positive or negative. We focus attention on answers to the following questions: (1) Does the time-delayed absorber broaden the effective frequency band of vibration absorption? (2) Does the time-delayed absorber suppress the resonant response of the primary system when the passive absorber totally fails?

The present paper is organized as follows. Section 2 presents the mechanical model of a 2-DOF system consisting of the primary system and the time-delayed absorber. The forced response and its stability analysis are given. In Sect. 3, the efficiency of the time-delayed absorber is illustrated experimentally, analytically, and numerically. The effects of the feedback gain coefficient and time delay on the performance of the time-delayed absorber are investigated. Section 4 concludes the study.

2 Modeling and stability analysis

In this section, the model describing the motions of the 2-DOF linear system with time-delayed feedback is firstly established. The periodic responses are obtained to predict the dynamic behaviors of the coupled system. Since the introduction of the time-delayed feedback affects the stability of the system, the stability of the system is then shown.

Fig. 1
figure 1

Mechanical model

Full size image

2.1 Modeling

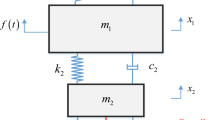
Figure 1 depicts the mechanical model of the 2-DOF vibration system. The system consists of the primary system and the time-delayed absorber. \(m_1 ,k_1, \hbox {and} \,c_1\) represent the mass, stiffness, and damping of the absorber respectively. \(m_2 ,k_2,\, \hbox {and}\,c_2 \) represent the mass, stiffness, and damping of the primary system, respectively. \(x_1 \,\hbox {and}\,x_2\) denote the absolute displacements of the absorber mass and the primary mass. An actuator located between the absorber and the primary system provides the time-delayed feedback control force. Applying the base excitation to the primary system, the vibrations of the system are described by the following two equations

$$\begin{aligned}&m_1 \ddot{x}_1 +k_1 \left( {x_1 -x_2 } \right) +c_1 \left( {\dot{x}_1 -\dot{x}_2 } \right) -g\ddot{x}_1 \left( {t-\tau } \right) =0,\quad \end{aligned}$$
(1)
$$\begin{aligned}&m_2 \ddot{x}_2 +k_2 \left( {x_2 -u} \right) +c_2 \left( {\dot{x}_2 -\dot{u}} \right) +k_1 \left( {x_2 -x_1 } \right) \nonumber \\&\quad +\,c_1 \left( {\dot{x}_2 -\dot{x}_1 } \right) +g\ddot{x}_1 \left( {t-\tau } \right) =0, \end{aligned}$$
(2)

\(\hbox {where}\,g\) is feedback gain coefficient. \(\tau \, \hbox {is}\) the sum of the inherent and intentional time delay. \(u\,\hbox {represents}\) the base excitation. In the following experiments, a base acceleration excitation is used. To make the description of the base excitation consistent in theory and experiment, we introduce the change of variables

$$\begin{aligned} y_1 =x_1 -u, y_2 =x_2 -u, \end{aligned}$$
(3)

\(y_1\, \hbox {and}\,y_2 \) represent the relative displacements of the absorber mass and the primary mass, respectively.

Substituting Eq. (3) into Eqs. (1) and (2) yields

$$\begin{aligned}&m_1 \ddot{y}_1 +k_1 \left( {y_1 -y_2 } \right) +c_1 \left( {\dot{y}_1 -\dot{y}_2 } \right) -g\ddot{y}_1 \left( {t-\tau } \right) \nonumber \\&\quad =g\ddot{u}\left( {t-\tau } \right) -m_1 \ddot{u}, \end{aligned}$$
(4)
$$\begin{aligned}&m_2 \ddot{y}_2 +k_2 y_2 +c_2 \dot{y}_2 +k_1 \left( {y_2 -y_1 } \right) +c_1 \left( {\dot{y}_2 -\dot{y}_1 } \right) \nonumber \\&\quad +\,g\ddot{y}_1 \left( {t-\tau } \right) =-g\ddot{u}\left( {t-\tau } \right) -m_2 \ddot{u}. \end{aligned}$$
(5)

It is easy to see from Eqs. (4) and (5) that the base excitation is \(\ddot{u}\). Suppose that the base excitation has the following form

$$\begin{aligned} \ddot{u}=u_0 \sin \left( {\omega t} \right) , \end{aligned}$$
(6)

and hence the solutions of Eqs. (4)–(5) are

$$\begin{aligned} y_1= & {} a_1 \sin \left( {\omega t} \right) +b_1 \cos \left( {\omega t} \right) , \end{aligned}$$
(7)
$$\begin{aligned} y_2= & {} a_2 \sin \left( {\omega t} \right) +b_2 \cos \left( {\omega t} \right) . \end{aligned}$$
(8)

By substituting Eqs. (6)–(8) into Eqs. (4)–(5) and extracting the coefficients of \(\sin \left( {\omega t} \right) \, \hbox {and}\cos \left( {\omega t} \right) \)from both sides of the equations, we obtain the linear algebraic equations \(\hbox {about}\,a_1 ,b_1 ,a_2 \,\hbox {and}\,b_2 \)

$$\begin{aligned} {\varvec{D}} \left\{ {a_1 ,b_1 ,a_2 ,b_2 } \right\} ^\mathrm{T}={{\varvec{f}}_1 } , \end{aligned}$$
(9)

in which

Solving Eq. (9) gives

$$\begin{aligned} \left\{ {a_1 ,b_1 ,a_2 ,b_2 } \right\} ^\mathrm{T}={\varvec{D}}^{-1} {{\varvec{f}}_1 }. \end{aligned}$$
(10)

Using Eq. (10) in Eqs. (7) and (8), we have, in light of Eq. (3)

$$\begin{aligned} \ddot{x}_1= & {} \sqrt{\left( {-a_1 \omega ^{2}+u_0 } \right) ^{2}+\left( {-b_1 \omega ^{2}} \right) ^{2}}\sin \left( {\omega t+\varphi _1 } \right) , \end{aligned}$$
(11)
$$\begin{aligned} \ddot{x}_2= & {} \sqrt{\left( {-a_2 \omega ^{2}+u_0 } \right) ^{2}+\left( {-b_2 \omega ^{2}} \right) ^{2}}\sin \left( {\omega t+\varphi _2 } \right) , \end{aligned}$$
(12)

where \(\varphi _i =\arctan \left( {\frac{-b_i \omega ^{2}}{-a_i \omega ^{2}+u_0 }} \right) \,\left( {i=1,2} \right) \).

We define \(H_1 \) and \(H_2 \) to be the acceleration transfer rate of the absorber and the primary system

$$\begin{aligned} H_i \!=\!\frac{\left\| {\ddot{x}_i } \right\| }{u_0 }\!=\!\frac{\sqrt{\left( {-a_i \omega ^{2}+u_0 } \right) ^{2}+\left( {-b_i \omega ^{2}} \right) ^{2}}}{u_0 },\quad {i=1,2}. \end{aligned}$$
(13)

2.2 Stability analysis

In the above section, we established the mechanical model of the coupled vibration systems and obtained the periodic responses. It is well known that time delay has a significant effect on the stability of the system responses. Hence, it is desirable to analyze the stability of the periodic responses under different values of \(g\) and \(\tau \). In the Laplace domain, Eqs. (1) and (2) become

$$\begin{aligned} \, {\varvec{A}}\left( {s} \right) {{\varvec{X}}} \left( {s} \right) ={\varvec{F}}\left( {s} \right) , \end{aligned}$$
(14)

in which

$$\begin{aligned}&{\varvec{A}}\left( {s} \right) =\left[ {\left( {a_{ij} } \right) _{4\times 4} } \right] ,\\&a_{11} =m_1 s^{2}+k_1 +c_1 s-gs^{2}\mathrm{e}^{-s\tau },\\&a_{12} =-k_1 -c_1 s, a_{21} =-k_1 -c_1 s+gs^{2}\mathrm{e}^{-s\tau },\\&a_{22} =m_2 s^{2}+k_1 +k_2 +c_1 s+c_2 s,\\&{{\varvec{X}}}({s})=[x_1 (s),x_2 (s)]^\mathrm{T}, {{\varvec{F}}}({s})=[0,f(s)]^\mathrm{T}. \end{aligned}$$

The characteristic equation of the coupled system is \(\left| {{{\varvec{A}}}\left( {s} \right) } \right| =0\), that is

$$\begin{aligned} P\left( s \right) +Q\left( s \right) \mathrm{e}^{-s\tau }=0, \end{aligned}$$
(15)

in which

$$\begin{aligned} P\left( s \right)= & {} k_1 k_2 +\left( {c_2 k_1 +c_1 k_2 } \right) s\\&+\,\left( {c_1 c_2 +k_1 m_1 +k_2 m_1 +k_1 m_2 } \right) s^{2}\\&+\,\left( {c_1 m_1 +c_2 m_1 +c_1 m_2 } \right) s^{3}+m_1 m_2 s^{4},\\ Q\left( s \right)= & {} -gk_2 s^{2}-c_2 gs^{3}-gm_2 s^{4}. \end{aligned}$$

The system is stable if and only if all characteristic roots of Eq. (15) have negative real parts. Hence, we firstly consider the critical stable state, letting

$$\begin{aligned} s=\omega _c i. \end{aligned}$$
(16)

Substituting Eq. (16) into Eq. (15) and separating the real and imaginary parts give rise to

$$\begin{aligned}&\left[ {-c_1 c_2 -k_1 m_1 -k_2 m_1 -k_1 m_2 +gk_2 \cos \left( {\omega _c \tau } \right) } \right] \omega _c ^{2}\nonumber \\&\quad +c_2 g\sin \left( {\omega _c \tau } \right) \omega _c ^{3} +\left[ {m_1 m_2 -gm_2 \cos \left( {\omega _c \tau } \right) } \right] \omega _c ^{4}\nonumber \\&\quad +k_1 k_2 =0,\end{aligned}$$
(17)
$$\begin{aligned}&\left( {c_2 k_1 +c_1 k_2 } \right) \omega _c -gk_2 \sin \left( {\omega _c \tau } \right) \omega _c ^{2}\nonumber \\&\quad +\left[ {-c_1 m_1 -c_2 m_1 -c_1 m_2 +c_2 g\cos \left( {\omega _c \tau } \right) } \right] \omega _c ^{3}\nonumber \\&\quad +\,gm_2 \sin \left( {\omega _c \tau } \right) \omega _c ^{4}=0. \end{aligned}$$
(18)

\(\hbox {Using}\sin ^{2}\left( {\omega _c \tau } \right) +\cos ^{2}\left( {\omega _c \tau } \right) =1\), we obtain

$$\begin{aligned} a_8 \omega _c ^{8}+a_6 \omega _c ^{6}+a_4 \omega _c ^{4}+a_2 \omega _c ^{2}+a_0 =0, \end{aligned}$$
(19)

in which

$$\begin{aligned} a_8= & {} \left( {m_1 ^{2}-g^{2}} \right) m_2 ^{2},\\ a_6= & {} 2c_1 c_2 m_1 ^{2}+\left( {c_2 ^{2}-2k_2 m_2 } \right) \left( {m_1 ^{2}-g^{2}} \right) \\&-2k_1 m_1 m_2 \left( {m_1 +m_2 } \right) +c_1 ^{2}\left( {m_1 +m_2 } \right) ^{2},\\ a_4= & {} c_1 ^{2}c_2 ^{2}+k_2 ^{2}\left( {m_1 ^{2}-g^{2}} \right) -2c_1 ^{2}k_2 \left( {m_1 +m_2 } \right) \\&-\,2k_1 m_1 \left( {c_2 ^{2}-k_2 m_1 -2k_2 m_2 } \right) +k_1 ^{2}\left( {m_1 +m_2 } \right) ^{2},\\ a_2= & {} c_2 ^{2}k_1 ^{2}+c_1 ^{2}k_2 ^{2}-2k_1 k_2 ^{2}m_1 -\,2k_1 ^{2}k_2 \left( {m_1 +m_2 } \right) ,\\ a_0= & {} k_1 ^{2}k_2 ^{2}. \end{aligned}$$

For a certain gain coefficient \(g=g_1 \), we \(\hbox {use}\,l\, \hbox {denote}\) the number of the positive real root of Eq. (19). The value \(\hbox {of} \ l\,\hbox {is}\) decided by the coefficient of Eq. (19). \(\hbox {When}\,l=0\), there is no stability switch. The stability of the coupled system remains the same for \(\hbox {all}\,\tau \in \mathfrak {R}^{+}\). \(\hbox {When}\,l\ne 0\), we \(\hbox {have}\,\left\{ {\omega _{c1} ,\omega _{c2} ,\ldots ,\omega _{cl} } \right\} \). For each \(\omega _{cp} \left( {p=1,\ldots ,l} \right) \), we have \(\hbox {infinite}\,\tau \, \hbox {values}\,\left\{ {\tau _{p1} ,\tau _{p2} ,\ldots ,\tau _{p\infty } } \right\} \). The transition direction of the roots \(\hbox {at}\,\omega _{cp} \,\hbox {as}\,\tau \) increases \(\hbox {from}\,\tau _{pq} -\varepsilon \, \hbox {to}\,\tau _{pq} +\varepsilon \quad \left( {0<\varepsilon \ll 1,q=1,2,\ldots ,\infty } \right) \) is determined by the following expression

$$\begin{aligned} \hbox {RT}=\hbox {sgn}\left[ {\hbox {Re}\left( {\left. {\frac{\partial s}{\partial \tau }} \right| _{s=\omega _{cp} i} } \right) } \right] . \end{aligned}$$
(20)

\(+\)1 and \(-\)1 values of \(\hbox {RT}\) represent destabilizing and stabilizing transitions, respectively.

Through the above analysis, the stable and unstable intervals \(\hbox {of}\,\tau \, \hbox {for}\,g=g_1 \) are divided. Performing the same procedure for other values \(\hbox {of}\,g\), the stable and unstable regions on the \(\hbox {plane}\left( {g,\tau } \right) \,\hbox {are}\) plotted.

3 Experimental results

In this section, a 2-DOF experimental structure is designed and assembled. Firstly, the experimental setup is introduced in detail. Secondly, the design of the control parameters is conducted, which guide the choices of feedback gain and time delay. Thirdly, the vibration suppression effect of the time-delayed absorber is investigated experimentally, numerically, and theoretically.

Fig. 2
figure 2

Photo of the experimental structure (1 vibrating table, 2 base, 3 primary mass, 4 absorber mass, 5 servo motor, 6 controlled steel sheet, 7 and 8 acceleration sensors)

Full size image

3.1 Experimental setup

The photo of the experimental structure is shown in Fig. 2. The base (2) is fixed on the vibrating table (1). The primary mass (3) is supported upon the base via four steel sheets. A servo motor (5) is mounted on the primary mass. The absorber mass (4) connects to the primary mass via five steel sheets. A controlled steel sheet (6) is used to implement time-delayed feedback control. Its upper end is fixed on the absorber mass and its lower end is connected with the shaft of the servo motor through a wire rope.

The schematic view of the time-delayed feedback control experiment is plotted in Fig. 3. The experimental system consists of three parts: excitation source, signal acquisition, and time-delayed feedback control loop.

Fig. 3
figure 3

A schematic of the feedback control (1–3 acceleration sensor, 4 absorber mass, 5 primary mass, 6 servo motor, 7 controlled steel sheet)

Full size image

(I) Excitation source The vibrating table provides the sinusoidal acceleration excitation to the base. The amplitude and frequency of the excitation are set in M\(+\)p vib-pilot 1, which works as the signal generator.

(II) Signal acquisition Three acceleration sensors (1–3) are used to monitor the acceleration of vibrating table, absorber mass (4), and primary mass (5), respectively. The three acceleration signals are transmitted to M\(+\)p vib-pilot2, which acts as signal acquisition device. The sampling rate is 512 Hz in all experiments.

(III) Feedback control loop The acceleration signal of the absorber mass firstly enters into the signal conditioning instrument. The low-pass filter and signal amplification functions of the signal conditioning instrument are used to improve signal-to-noise ratio. Second, the processed signal goes into the Trio motion controller via the voltage lifting circuit. The feedback control command is created in the Trio motion controller and then transmitted into the servo motor controller, which guides the rotation of the shaft of the servo motor (6). Finally, the low end of the controlled steel sheet (7) moves horizontally under the drive of the servo motor and applies the control force.

The physical parameters of the coupled system are: \(m_1 =0.68\,\hbox {kg},m_2 =6.70\,\hbox {kg}, k_1 =2817.23\,\hbox {N/m},k_2 =12932.87\,\hbox {N/m},c_1 =0.21\,\hbox {N}\, \hbox {s/m},c_2 =4.33\,\hbox {N}\, \hbox {s/m}\). Applying a random base excitation to the coupled system, the amplitude-frequency plots of the system without feedback control are shown in Fig. 4. \(\varOmega \) denotes the excitation frequency. The circles represent the experimental result. The solid lines represent the analytical result obtained by Eq. (13). Obviously, the experimental result agrees well with the analytical one. It is seen that the two resonant frequencies of the coupled system are 6.5 and 11.125 Hz. The anti-resonant frequency of the coupled system is 10.25 Hz. This means that the passive absorber totally fails \(\hbox {when}\,\varOmega =6.5\, \hbox {and}\) 11.125 Hz. The passive absorber is mostly effective and minimizes the vibration of the primary system when \(\varOmega =10.25\,\hbox {Hz}\). For simplicity of presentation, we hereinafter \(\hbox {use}\,\varOmega _\mathrm{{a}}\, \hbox {to}\) denote the anti-resonant frequency of the coupled system.

Fig. 4
figure 4

Acceleration transfer rate versus excitation frequency plots \(\hbox {for}\,g=0\), a absorber, b primary system

Full size image

Before introducing the intentional time delay, the value of the inherent time delay is obtained by a hammer test. When the primary mass is excited by hammer impact, a sensor is used to acquire the acceleration of the absorber mass. This acceleration signal is divided into two branches. One branch goes directly into channel 1 of M+p vib-pilot 2. The other branch goes successively into the signal conditioning instrument, voltage lifting device, and Trio motion controller. A control command is written into the Trio motion controller and then transmitted into the servo controller. Driven by the servo controller, the servo motor shaft begins to rotate. The tangential acceleration signal of the servo motor shaft is acquired by a three-phase acceleration sensor and then transmitted into channel 2 of M+p vib-pilot 2. In this way, the inherent time delay is regarded as the time lag between the signals from channel 2 and channel 1. It is observed from the time histories that the value of the inherent time delay is 63 ms. The value of the intentional time delay is set by the Trio motion controller. The value of the intentional time delay is limited to an integral multiple of sampling period. Moreover, the values of sampling period and the multiple could be changed artificially. The desired value of the intentional time delay could be reached by choosing proper sampling period and multiple.

As a premise, the stability chart is plotted in Fig. 5. The coupled system is stable when the values \(\hbox {of}\,g\,\hbox {and}\,\tau \, \hbox {locate}\) in the shaded region, while unstable when the values \(\hbox {of}\,g\,\hbox {and}\,\tau \,\hbox {locate}\) in the blank region.

Fig. 5
figure 5

Stability chart of the coupled system

Full size image

3.2 Design of the control parameters

As stated in the previous section, the passive absorber minimizes the vibration of the primary system when the excitation frequency equals the anti-resonant frequency of the coupled system. When the excitation frequency is disturbed and deviates from the anti-resonant frequency, selecting reasonable values of feedback gain and time delay to ensure that the anti-resonant frequency always equals the excitation frequency will be considered.

The anti-resonant frequency of the coupled system satisfies the following two conditions

$$\begin{aligned} {\begin{array}{l} \left. {\frac{\hbox {d}H_2 \left( {\varOmega ;g,\tau } \right) }{\hbox {d}\varOmega }} \right| _{\varOmega \,=\, \varOmega _\mathrm{{a}} ,\left( {g,\tau } \right) \in S} \,=\,0, \\ \left. {\frac{\hbox {d}^{2}H_2 \left( {\varOmega ;g,\tau } \right) }{\hbox {d}\varOmega ^{2}}} \right| _{\varOmega \,=\,\varOmega _\mathrm{{a}} ,\left( {g,\tau } \right) \in S} >0, \\ \end{array}} \end{aligned}$$
(21)

\(\hbox {where}\,S\,\hbox {denote}\) the stable region of Fig. 5.

For a certain excitation frequency, Eq. (21) establishes the relationship among control effectiveness, feedback gain and time delay. When changing the excitation frequency, the values of time delay and feedback gain should be accordingly adjusted to guarantee the control effectiveness of the absorber.

Fig. 6
figure 6

Relationship \(\hbox {of}\,g\,\hbox {and}\,\tau \,\hbox {satisfying} \) a \(\varOmega _\mathrm{{a}} =10\,\hbox {Hz}\), b \(\varOmega _\mathrm{{a}} = 9.8\,\hbox {Hz}\), c \(\varOmega _\mathrm{{a}} =9.625\,\hbox {Hz}\), d \(\varOmega _\mathrm{{a}} =9.5\,\hbox {Hz}\), shaded region represent stable one of the period responses

Full size image

The heavy lines in Fig. 6 show the plots \(\hbox {of}\,g\,\hbox {and}\,\tau \hbox {satisfying} \) Eq. (21) \(\hbox {for}\,\varOmega _\mathrm{{a}} =10\), 9.8, 9.625 and 9.5Hz. It is apparent from Fig. 6 that for a certain anti-resonant frequency, there are groups \(\hbox {of}\,\left( {g,\tau } \right) \) satisfying Eq. (21). Figure 6 will provide the theoretical guidance for selecting the values of feedback gain and time delay in the following experiments.

3.3 Effect of time-delayed absorber

The emphasis of this section is to discuss the vibration suppression effect of the time-delayed absorber. Both negative and positive feedback control are taken into consideration.

Case 1 \(g=-0.036\,\hbox {kg},\tau =0.1\,\hbox {s}\)

Figure 7 shows the acceleration transfer rate versus excitation frequency \(\hbox {for}\,g=-0.036\,\hbox {kg}\,\hbox { and}\,\tau =0.1\,\hbox {s}\). \(H_{i\mathrm{{e}}} \,\left( {i=1,2} \right) \) denote the experimental results of the acceleration transfer rate. \(H_{i\mathrm{{a}}} \,\left( {i=1,2} \right) \) denote the analytical results of the acceleration transfer rate. The following three points are seen from Fig. 7: (1) The experimental results agree with the theoretical prediction. Compared with those of the coupled system without control, the anti-resonant frequency, and the second-order resonant frequency of the coupled system with control are clearly stepped down. (2) The time-delayed absorber is mostly effective and greatly absorbs the vibration of the primary system \(\hbox {when}\,\varOmega =\varOmega _\mathrm{{a}} =10\,\hbox {Hz}\). (3) The passive absorber totally fails \(\hbox {when}\,\varOmega =11.125\,\hbox {Hz}\). Fortunately, the introduction of the time-delayed feedback greatly improves the vibration suppression effect when \(\varOmega =11.125\,\hbox {Hz}\).

Fig. 7
figure 7

Comparison of the experimental and the analytical results \(\hbox {of}\,H_i \hbox {--}\varOmega \,\hbox {plots for}\,g=-0.036\,\hbox {kg}, \tau =0.1\,\hbox {s}\)

Full size image
Fig. 8
figure 8

Experimental vibration suppression effect \(\hbox {for}\,g=-0.036\,\hbox {kg},\tau =0.1\,\hbox {s}\), a absorber, b–d primary system \(\hbox {for}\,\varOmega \in \left[ {5, 10.0625} \right] \, \hbox {Hz},\varOmega \in \left[ {10.125, 10.875} \right] \,\hbox {Hz} \, \hbox {and}\,\varOmega \in \left[ {11,~12}\right] \,\hbox {Hz}\, \hbox {respectively}\)

Full size image

Figure 8 shows the vibration suppression performance of the time-delayed absorber, \(\hbox {where }\,D_i =\frac{\left. {H_{i\mathrm{{e}}} } \right| _{g=0} -\left. {H_{i\mathrm{{e}}} } \right| _{g=-0.036\,\mathrm {kg},\tau =0.1\,\mathrm {s}} }{\left. {H_{i\mathrm{{e}}} } \right| _{g=0} }\times 100~\%~\left( {i=1,2} \right) \). The following points are observed from Fig. 8: (1) Energy transfer between the primary system and the absorber occurs \(\hbox {for}\,\varOmega \in \left[ {8,10.0625}\right] \,\hbox {Hz}\). In other words, the vibrationamplitude of the primary system decreases and that of the absorber increases when the time-delayed feedback control is applied. It is noted that the vibration amplitude of the primary system decreases 80.03 % and that of the absorber increases 22.19 % \(\hbox {for}\,\varOmega =10\,\hbox {Hz}\). (2) Vibration amplitudes of both the primary system and the absorber decrease \(\hbox {for}\,\varOmega \in \left[ {11, 12}\right] \,\hbox {Hz}\). Especially, vibration amplitudes of the primary system and the absorber, respectively, decrease 73.19 % and 79.79 % for \(\varOmega =11.125\,\hbox {Hz}\). (3) Due to the step-down of the anti-resonant frequency, the vibration amplitude of the primary dramatically increases 597.58 % \(\hbox {for}\,\varOmega =10.25\,\hbox {Hz}\).

Figure 9 shows the measured system responses \(\hbox {for}\,\varOmega =10\,\hbox {Hz}, \hbox {where}\,u_0 =1\,\hbox {m/s}^{{2}}\). The total sampling time is 160 s. The time-delayed feedback control is activated at \(t=9\,\hbox {s}\). After an initial transient, the acceleration amplitude of the primary system decreases from   \(0.18\,\hbox {to}\,0.036\,\hbox {m/s}^{{2}}\,\hbox {and}\) the acceleration amplitude of the absorber increases \(\hbox {from 3.84}\) to \(4.69\,\hbox {m/s}^{{2}}\). The time-delayed feedback control is deactivated \(\hbox {at}\,t = 108\,\hbox {s}\,\hbox {and}\) the coupled system is restored to the initial uncontrolled state after a transient period. Figure 10 shows the measured system responses \(\hbox {for}\,\varOmega =10.25\,\hbox {Hz}, \hbox {where}\,u_0 =1\,\hbox {m/s}^{{2}}\). When the feedback control works, the acceleration amplitude of the primary system and the absorber, respectively, increase from \(0.041\,\hbox {to 0.29}\,\hbox {m/s}^{{2}}\), and from \(4.54\,\hbox {to 5.96}\,\hbox {m/s}^{{2}}\).

Fig. 9
figure 9

Measured acceleration responses \(\hbox {for}\,\varOmega =10\,\hbox {Hz},u_0 =1\,\hbox {m/s}^{{2}}\, (\hbox {for}\,t<9\,\hbox {s}\,\hbox {and}\,t>108\,\hbox {s},g=0\); for \(9\,\hbox {s}\le t\le 108\,\hbox {s},g=-0.036\,\hbox {kg},\tau =0.1\,\hbox {s})\), a absorber, b primary system

Full size image
Fig. 10
figure 10

Measured acceleration responses \(\hbox {for}\,\varOmega =10.25\,\hbox {Hz},u_0 =1\,\hbox {m/s}^{{2}}\, (\hbox {for}\,t<21\,\hbox {s}\,\hbox {and}\,t>120\,\hbox {s},g=0\); for \(21\,\hbox {s}\le t\le 120\,\hbox {s},g=-0.036\,\hbox {kg},\tau =0.1\,\hbox {s})\), a absorber, b primary system

Full size image

To validate further the analytical and experimental results, numerical results are derived by numerical integration of Eqs. (1) and (2). Figures 11 and 12, respectively, show the numerical simulations of acceleration responses for \(\varOmega =10\) and 10.25 Hz, \(\hbox {where}\, u_0 =1\,\hbox {m/s}^{{2}}\). It is seen that the numerical simulations agree with the analytical and experimental results.

Fig. 11
figure 11

Numerical simulations of acceleration responses \(\hbox {for}\,\varOmega =10\,\hbox {Hz},u_0 =1\,\hbox {m/s}^{{2}}\), a absorber, b primary system, dashed lines \(\hbox {represent}\,g=0\), solid lines \(\hbox {represent}\,g=-0.036\,\hbox {kg},\tau =0.1\,\hbox {s}\)

Full size image
Fig. 12
figure 12

Numerical simulations of acceleration responses \(\hbox {for}\,\varOmega =10.25\,\hbox {Hz},u_0 =1\,\hbox {m/s}^{{2}}\), a absorber, b primary system, dashed lines \(\hbox {represent}\,g=0\), solid lines \(\hbox {represent}\,g=-0.036\,\hbox {kg},\tau =0.1\,\hbox {s}\)

Full size image

Case 2 \(g=-0.063\,\hbox {kg},\tau =0.204\,\hbox {s}\)

Similar to Case 1, the variations of the acceleration transfer rate versus excitation frequency \(\hbox {for}\,g=-0.063\,\hbox {kg}\,\hbox {and} \,\tau =0.204\,\hbox {s}\,\hbox {are}\) shown in Fig. 13. It is seen that the anti-resonant frequency of the coupled system is stepped down from 10.25 to 9.8 Hz. The time-delayed absorber absorbs the vibration of the primary system to the maximum extent \(\hbox {when}\,\varOmega =9.8\,\hbox {Hz}\).

Figure 14 shows the vibration suppression effect of the time-delayed absorber. It is seen that energy transfer comes up \(\hbox {for}\,\varOmega \in \left[ {9, 9.875} \right] \,\hbox {Hz}\). It is attractive that the acceleration amplitudes of the primary system, respectively, decrease 33.87 %, 89.49 % and 86.48 % \(\hbox {for}\,\varOmega =6.5, 9.8\,\hbox {and}11.125\,\hbox {Hz}\).

Fig. 13
figure 13

Comparison of the experimental and the analytical results \(\hbox {of}\,H_i -\varOmega \, \hbox {plots}\) for \(g=-0.063\,\hbox {kg}, \tau =0.204\,\hbox {s}\)

Full size image
Fig. 14
figure 14

Experimental vibration suppression effect \(\hbox {for}\,g=-0.063\,\hbox {kg}\,\hbox {and}\,\tau =0.204\,\hbox {s}\), a absorber, b–d primary system \(\hbox {for}\,\varOmega \in \left[ {5, 10\,} \right] \,\hbox {Hz},\varOmega \in \left[ {10.125, 10.875} \right] \,\hbox {Hz}\, \hbox {and}\,\varOmega \in \left[ {11, 12\,}\right] \,\hbox {Hz}\, \hbox {respectively}\)

Full size image

Figure 15 shows the measured system responses \(\hbox {for}\,\varOmega =9.8\,\hbox {Hz}, \hbox {where}\,u_0 =1\,\hbox {m/s}^{{2}}\). The feedback control works when \(14\,\hbox {s}\le t\le 118\,\hbox {s}\). In this duration, the acceleration amplitude of the primary system decreases from \(0.25 \,\hbox {to 0.026}\,\hbox {m/s}^{{2}}\,\hbox {and}\) that of the absorber increases from \(3.49\) to \(4.81\,\hbox {m/s}^{{2}}\). Figure 16 shows the measured system responses \(\hbox {for}\,\varOmega =6.5\,\hbox {Hz}, \hbox {where}\,u_0 =0.1\,\hbox {m/s}^{{2}}\). It is observed that the acceleration amplitudes of both the primary system and the absorber decrease in different degrees when the feedback control is implemented.

Fig. 15
figure 15

Measured acceleration responses \(\hbox {for}\,\varOmega =9.8\,\hbox {Hz},u_0=1\,\hbox {m/s}^{{2}}\,(\hbox {for}\,\, t<14\,\hbox {s}\,\hbox {and}\,t>118\,\hbox {s},g = 0\); for \(14\,\hbox {s}\le t\le 118\,\hbox {s},g=-0.063\,\hbox {kg},\tau =0.204\,\hbox {s})\), a absorber, b primary system

Full size image
Fig. 16
figure 16

Measured acceleration responses \(\hbox {for}\,\varOmega =6.5\,\hbox {Hz},u_0 =0.1\,\hbox {m/s}^{{2}}\,(\hbox {for}\,\,t<17\,\hbox {s}\,\hbox {and}\,t>121\,\hbox {s},g=0\); for \(17\,\hbox {s}\le t\le 121\,\hbox {s},g=-0.063\,\hbox {kg},\tau =0.204\,\hbox {s})\), a absorber, b primary system

Full size image

Figures 17 and 18 show the numerical simulations of acceleration responses \(\hbox {for}\,\varOmega =9.8\,\hbox {and}\,\hbox {6.5}\, \hbox {Hz}\), respectively. Obviously, the experimental results agree with the numerical ones qualitatively, although there is a bit difference quantitatively.

Fig. 17
figure 17

Numerical simulations of acceleration responses \(\hbox {for}\,\varOmega =9.8\,\hbox {Hz},u_0 =1\,\hbox {m/s}^{{2}}\), a absorber, b primary system, dashed lines \(\hbox {represent}\,g=0\), solid lines \(\hbox {represent}\,g=-0.063\,\hbox {kg},\tau =0.204\,\hbox {s}\)

Full size image
Fig. 18
figure 18

Numerical simulations of acceleration responses \(\hbox {for}\,\varOmega =6.5\,\hbox {Hz},u_0 =0.1\,\hbox {m/s}^{{2}}\), a absorber, b primary system, dashed lines \(\hbox {represent}\,g=0\), solid lines \(\hbox {represent}\,g=-0.063\,\hbox {kg},\tau =0.204\,\hbox {s}\)

Full size image

Case 3 \(g=0.09\,\hbox {kg},\tau =0.156\,\hbox {s}\)

In the above two cases, negative feedback control has been discussed and its effectiveness has been verified. In Case 3, the performance of positive feedback control will be investigated. Figure 19 shows how the values of the acceleration transfer rate change as a function of excitation frequency.It is seen that the anti-resonant frequency of the coupled system in this case is 9.625 Hz.

Fig. 19
figure 19

Comparison of the experimental and the analytical results of \(H_i -\varOmega \,\hbox {plots for}\,g=0.09\,\hbox {kg}, \tau =0.156\,\hbox {s}\)

Full size image

Figure 20 shows the experimental vibration suppression effect of the time-delayed absorber \(\hbox {for}\,g=0.09\,\hbox {kg}\,\hbox {and}\,\tau =0.156\,\hbox {s}\). It is seen that the time-delayed absorber absorbs the vibration of the primary system \(\hbox {for}\,\varOmega \in \left[ {8.5, 9.75} \right] \,\hbox {Hz}\). The acceleration amplitude of the primary system decreases 91.90 % \(\hbox {when}\,\varOmega =9.625\,\hbox {Hz}\). The acceleration amplitudes of both the primary system and the time-delayed absorber are suppressed \(\hbox {for}\,\varOmega \in \left[ {10.875, 11.5} \right] \,\hbox {Hz}\). The acceleration amplitudes of the primary system and the absorber, respectively, decrease 87.85 % and 91.88 % when \(\varOmega =11.125\,\hbox {Hz}\). However, the acceleration amplitude of the primary system increases 1808.92 % \(\hbox {when}\,\varOmega =10.25\,\hbox {Hz}\).

Fig. 20
figure 20

Experimental vibration suppression effect \(\hbox {for}\,g=0.09\,\hbox {kg}\,\hbox {and}\,\tau =0.156\,\hbox {s}\), a absorber, b–d primary system \(\hbox {for}\,\varOmega \in \left[ {5, 10} \right] \,\hbox {Hz},\varOmega \in \left[ {10.25, 10.75} \right] \,\hbox {Hz}\,\hbox {and}\,\varOmega \in \left[ {10.875, 12} \right] \,\hbox {Hz}\,\hbox {respectively}\)

Full size image

Figures 21 and 22, respectively, show the measured acceleration responses of the coupled system \(\hbox {for}\,\varOmega =9.625\,\hbox {and}\) 11.125 Hz. It is apparent that once the time-delayed feedback is activated, the acceleration amplitude of the primary system rapidly and significantly decreases. The numerical simulations shown in Figs. 23 and 24 well validate the experimental results.

Fig. 21
figure 21

Measured acceleration responses \(\hbox {for}\,\varOmega =9.625\,\hbox {Hz},u_0 =1\,\hbox {m/s}^{{2}}\,(\hbox {for}\,\,t<18\,\hbox {s}\,\hbox {and}\,t>117\,\hbox {s},g=0\); for \(18\,\hbox {s}\le t<117\hbox {s},g=0.09\,\hbox {kg},\tau =0.156\,\hbox {s})\), a absorber, b primary system

Full size image
Fig. 22
figure 22

Measured acceleration responses \(\hbox {for}\,\varOmega =11.125\,\hbox {Hz},u_0 =0.1\,\hbox {m/s}^{{2}}\,(\hbox {for}\,\,t<10\,\hbox {s}\,\hbox {and}\,t>109\,\hbox {s},g=0\); for \(10\,\hbox {s}\le t\le 109\,\hbox {s},g=0.09\,\hbox {kg},\tau =0.156\,\hbox {s})\), a absorber, b primary system

Full size image
Fig. 23
figure 23

Numerical simulations of acceleration responses \(\hbox {for}\,\varOmega =9.625\,\hbox {Hz},u_0 =1\,\hbox {m/s}^{{2}}\), a absorber, b primary system, dashed line \(\hbox {represent}\,g = 0\), solid line \(\hbox {represent}\,g = 0.09\,\hbox {kg},\tau = 0.156\,\hbox {s}\)

Full size image
Fig. 24
figure 24

Numerical simulations of acceleration responses \(\hbox {for}\,\varOmega =11.125\,\hbox {Hz},u_0 =0.1\,\hbox {m/s}^{{2}}\), a absorber, b primary system, dashed line \(\hbox {represent}\,g=0\), solid line \(\hbox {represent}\,g = 0.09\,\hbox {kg},\tau =0.156\,\hbox {s}\)

Full size image

Case 4 \(g=0.114\,\hbox {kg},\tau =0.157\,\hbox {s}\)

Figure 25 shows the variation of the acceleration transfer rate versus excitation frequency \(\hbox {for}\,g=0.114\,\hbox {kg}\,\hbox {and}\,\tau =0.157\,\hbox {s}\). The anti-resonant frequency of the coupled system is further stepped down from 9.625 to 9.5 Hz by increasing the value of the feedback gain coefficient.

Fig. 25
figure 25

Comparison of the experimental and the analytical results \(\hbox {of}\,H_i-\varOmega \,\hbox {plots for}\,g=0.114\,\hbox {kg}, \tau =0.157\,\hbox {s}\)

Full size image

The vibration suppression effect of the time-delayed absorber \(\hbox {for}\,g=0.114\,\hbox {kg}, \tau =0.157\,\hbox {s}\) is shown in Fig. 26. It is seen that the energy transfer between the primary system and the absorber occurs \(\hbox {for}\,\varOmega \in \left[ {8.5, 9.625} \right] \,\hbox {Hz}\). It is amazing that the time-delayed absorber almost rests the primary system \(\hbox {when}\,\varOmega =9.5\,\hbox {Hz}\).

Fig. 26
figure 26

Experimental vibration suppression effect \(\hbox {for}\,g=0.114\,\hbox {kg}\,\hbox {and}\,\tau =0.157\,\hbox {s}\), a absorber, b–d primary system \(\hbox {for}\,\varOmega \in \left[ {5, 10} \right] \,\hbox {Hz},\varOmega \in \left[ {10.25, 10.75} \right] \,\hbox {Hz}\,\hbox {and}\,\varOmega \in \left[ {10.875, 12} \right] \,\hbox {Hz}\,\hbox {respectively}\)

Full size image
Fig. 27
figure 27

Measured acceleration responses \(\hbox {for}\,\varOmega =9.5\,\hbox {Hz},u_0 =1\,\hbox {m/s}^{{2}}\,(\hbox {for}\,t<14\,\hbox {s}\,\hbox {and}\,t>113\,\hbox {s}, g = 0\); for \(14\,\hbox {s}\le t\le 113\,\hbox {s},g=0.114\,\hbox {kg},\tau =0.157\,\hbox {s})\), a absorber, b primary system

Full size image
Fig. 28
figure 28

Measured acceleration responses \(\hbox {for}\,\varOmega =11.125\,\hbox {Hz},u_0 =0.1\,\hbox {m/s}^{{2}}\,(\hbox {for}\,t<10\,\hbox {s}\,\hbox {and}\,t>109\,\hbox {s},g = 0\); for \(10\,\hbox {s}\le t\le 109\,\hbox {s},g=0.114\,\hbox {kg},\tau =0.157\,\hbox {s})\), a absorber, b primary system

Full size image
Fig. 29
figure 29

Numerical simulations of acceleration responses \(\hbox {for}\,\varOmega =9.5\,\hbox {Hz},u_0 =1\,\hbox {m/s}^{{2}}\), a absorber, b primary system, dashed line \(\hbox {represent}\,g = 0\), solid line \(\hbox {represent}\,g = 0.114\,\hbox {kg},\tau =0.157\,\hbox {s}\)

Full size image
Fig. 30
figure 30

Numerical simulations of acceleration responses \(\hbox {for}\,\varOmega =11.125\,\hbox {Hz},u_0 =0.1\,\hbox {m/s}^{{2}}\), a absorber, b primary system, dashed line \(\hbox {represent}\,g = 0\), solid line \(\hbox {represent}\,g = 0.114\,\hbox {kg},\tau =0.157\,\hbox {s}\)

Full size image
Fig. 31
figure 31

Comparison of the experimental and the analytical results \(\hbox {of}\,H_1 -\varOmega \,\hbox {plots} \)

Full size image
Fig. 32
figure 32

Comparison of the experimental and the analytical results \(\hbox {of}\,H_2 -\varOmega \,\hbox {plots}\)

Full size image

Figures 27 and 28, respectively, show the measured acceleration responses for \(\varOmega = 9.5\) and 11.125 Hz, which agree well with the numerical simulations shown in Figs. 29 and 30.

3.4 Summary

In the above studies, the vibration suppression performances of the time-delayed absorber with different values of feedback gain and time delay have been investigated. Figures 31 and  32, respectively, show the experimental and the analytical results \(\hbox {of}\,H_1-\varOmega \,\hbox {and}\,H_2 -\varOmega \, \hbox {plots}\) corresponding to the above four cases. It is seen that both the anti-resonant and the second-order resonant frequencies of the coupled system, respectively, corresponding to the four cases are stepped down. This way, the effect frequency band of vibration absorption is broadened. Moreover, the second-order resonant responses of the uncontrolled system are sharply suppressed in all four cases.

Tables  1, 2, 3 and 4, respectively, show the vibration suppression effect of the time-delayed absorber \(\hbox {for}\,\varOmega =\varOmega _\mathrm{{a}} \), 10.25, 6.5 and 11.125 Hz. It is seen from Table 1 \(\hbox {that}\,D_2 \,\hbox {is}\) inversely proportional \(\hbox {to}\,D_1\,\hbox {when} \) the excitation frequency equals the anti-resonant frequency. Table 2 shows that the acceleration amplitude of the primary system respectively corresponding to the four cases dramatically increases \(\hbox {for}\,\varOmega =10.25\,\hbox {Hz}\). This phenomenon is due to the step-down of the anti-resonant frequency of the coupled system when the time-delayed feedback control is implemented. As indicated in Tables 3 and 4, the feedback control with reasonable values of feedback gain and time delay substantially improves the vibration suppression effect when the passive absorber totally fails.

Table 1 Effect of vibration suppression at the new anti-resonant frequency
Full size table
Table 2 Effect of vibration suppression \(\hbox {for}\,\varOmega =10.25\,\hbox {Hz}\)
Full size table
Table 3 Effect of vibration suppression \(\hbox {for}\,\varOmega =6.5\,\hbox {Hz}\)
Full size table
Table 4 Effect of vibration suppression \(\hbox {for}\,\varOmega =11.125\,\hbox {Hz}\)
Full size table

4 Conclusions and extensions

In this paper, we propose a time-delayed absorber with delayed acceleration feedback. This absorber is used to mitigate the vibration of an SDOF system under base excitation. The design of control parameters is conducted to guarantee the control effectiveness. An experimental device is constructed to observe the performance of the time-delayed absorber. Both analytical and experimental results indicate that the time-delayed absorber significantly absorbs the vibration of the primary system in a wide frequency band. In addition, when the passive absorber completely fails, the time-delayed feedback control with a proper choice of time delay and feedback gain can recover the absorber to be valid.