Nonlinear resonances of axially functionally graded beams rotating with varying speed including Coriolis effects

Abstract

The purpose of the current study was to develop an accurate model to investigate the nonlinear resonances in an axially functionally graded beam rotating with time-dependent speed. To this end, two important features including stiffening and Coriolis effects are modeled based on nonlinear strain relations. Equations governing the axial, chordwise, and flapwise deformations about the determined steady-state equilibrium position are obtained, and the rotating speed variation is considered as a periodic disturbance about this equilibrium condition. Multi-mode discretization of the equations is performed via the spectral Chebyshev approach and the method of multiple scales for gyroscopic systems is employed to study the nonlinear behavior. After determining the required polynomial number based on convergence analysis, results obtained are verified by comparing to those found in literature and numerical simulations. Moreover, the model is validated based on simulations carried out by commercial finite element software. Properties of the functionally graded material and the values of average rotating speed leading to 2:1 internal resonance in the system are found. Time and steady-state responses of the system under primary and parametric resonances caused by the time-dependent rotating speed are investigated when the system is tuned to 2:1 internal resonance. A comprehensive study on the time response, frequency response, and stability behavior shows that the rotating axially functionally graded beam exhibits a complicated nonlinear behavior under the effect of the rotating speed fluctuation frequency, damping coefficient, and properties of the functionally graded material.

1 Introduction

Vibration analysis of rotating beams has drawn the attention of many researchers due to their numerous engineering applications in turbomachinery, aircraft propellers, rotors, etc. Recent developments in material technology have also contributed to the construction of rotating beams composed of advanced materials to achieve more reliable, cost-effective, and optimal designs. Functionally graded materials (FGMs) as one of these advanced materials provide more design parameters to achieve unique properties of the rotating beams, for instance, high stiffness, low density, and tunable natural frequencies or other dynamic features. In this regard, understanding the dynamics of rotating functionally graded (FG) beams and developing precise models to evaluate the vibration characteristics are important ongoing research topics. One of the important issues in modeling rotating beams is including the stiffening effect in the model appropriately, which can be classified into three categories. The first is considering stretch variable instead of axial deformation [1,2,3,4,5,6]. In the second approach, which results in the same modeling equations as in the first category, equivalent time-independent centrifugal force is added to the model [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. The modeling approaches of the third category employ nonlinear strain relations to consider the stiffening effect as a time-dependent axial force in the system [24,25,26,27,28,29,30,31,32]. This approach results in nonlinear modeling of the problem, in which the nonlinearity is due to kinematic relations inducing coupling between the axial, chordwise, and flapwise deformations. Kim et al. [28] showed that the results based on models of the third category exhibit significant differences to those of the first and second categories, especially as the rotating speed increases. Moreover, in this approach, the steady-state condition, in which the beam is rotating with a constant speed, should be determined to derive the governing equations about the equilibrium position. Therefore, any external force or rotation speed variation can be exerted as a disturbance to this equilibrium condition. However, as claimed by [28], models based on the time-independent axial force are not acceptable for dynamic analysis of rotating beams with varying speed or under external forces. In this regard, in the current study, the dynamic behavior of the rotating FG beam is modeled by nonlinear strain relations based on the approaches of the third category. Thus, some of the literature regarding the nonlinear vibrations of rotating beams are discussed in the following. There exist several studies on the nonlinear vibrations of rotating beams. Almost all of these studies consider nonlinearity due to large amplitude vibrations in the system, and thus they do not necessarily fall into the third category. Younesian and Esmailzadeh [4] investigated the large amplitude vibrations of a beam under varying rotating speed. They simplified the model to transverse vibrations by assuming zero stretching and used single-mode discretization to apply the method of multiple scales (MMS). For the same problem, parametric instability analysis of the axial and chordwise motions was performed via applying MMS directly to the governing equations in [5]. Various applications of rotating beams have encouraged the researchers to study the different aspects of large amplitude vibrations of these systems. For instance, primary and 1:1 internal resonances under supersonic gas flow [9], hardening and softening behavior under harmonic force [11], 2:1 internal resonances under gas pressure [12], saturation phenomenon under thermal gradient [13], sub-harmonic and combination resonances [14], and super-harmonic and 2:1 internal resonances under gas pressure [15]. In all these studies the Coriolis effects were neglected in the nonlinear analysis, and a constant centrifugal force was used to model the stiffening effect. Pesheck et al. [24] used the approaches of the third category to construct reduced-order models for axial-transverse vibrations of rotating beams based on nonlinear strain relations. They determined static elongation for the beam as a steady-state equilibrium condition. Similarly, Arvin and Bakhtiari-Nejad [27] derived the governing equations of rotating beams about equilibrium condition and applied MMS to study the large amplitude vibrations of the system. Recently, Tian et al. [29] introduced a modified variational method to model the vibrations of rotating beams including Coriolis effects based on nonlinear strain relations. In the case of rotating FG beams, there are a number of studies on the vibration analysis of such systems in the literature. Oh and Yoo [6] revealed the effect of FGM parameters on the natural frequencies and mode shapes of pre-twisted rotating FG beams. The vibration behavior of rotating FG beams under thermal loadings and the effect of temperature on the natural frequencies were investigated by [18,19,20]. Zarrinzadeh et al. [21] examined the effect of rotating speed on the natural frequencies and mode shapes of FG tapered beams. In another study, Chen et al. [23] performed isogeometric nonlinear analysis to study large amplitude vibrations of rotating FG porous micro-beams. The time response and natural frequencies of rotating FG beams including Coriolis effects were investigated in [25] based on finite element (FE) method. Tian et al. [30] investigated the free vibration of rotating FG double-tapered beams with porosity based on nonlinear strain relations. They discussed modal couplings and the effect of FGM parameters on the natural frequencies of the system. More observations on the effect of FGM properties on the natural frequencies, time response, and frequency veering regions of rotating FG beams can be found in [31, 32]. According to the literature, the main features in modeling the rotating beams are stiffening and Coriolis effects. It has already been shown that the Coriolis effects significantly influence the natural frequencies and dynamic behavior of the system at high rotating speeds. Including Coriolis effects in the model results in gyroscopic terms which necessitate the use of approaches for gyroscopic systems to study the nonlinear behavior of the system. However, to the best of our knowledge, investigation on the nonlinear resonances of rotating FG beams has not been addressed to date and studies found in the literature regarding nonlinear resonances of rotating beams have neglected Coriolis effects. Accordingly, this work is devoted to studying the nonlinear behavior including primary, principal parametric, and 2:1 internal resonances of an axially FG beam rotating with harmonically varying speed in the presence of Coriolis effects. The mathematical model of the problem is developed based on the approaches of the third category by employing nonlinear strain relations and equations governing the axial, flapwise, and chordwise motions are derived. After discretizing the equations by the means of the spectral Chebyshev approach, the MMS for gyroscopic systems is employed to study the nonlinear behavior of the system. The results are verified by comparing to those available in the literature and obtained by numerical methods. Also, the model is validated by comparing the natural frequencies of the linear system to those derived through commercial FE software. Then, the effects of FGM parameters, damping, and varying rotating speed on the internal resonance conditions, time response, modal amplitudes, frequency response, and primary and parametric instabilities are investigated.

2 Model development

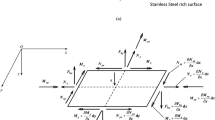
The basic configuration of the system considered here is a rotating axially FG beam clamped to a rigid hub of radius, $r_h$, as shown in Fig. 1. The beam has length L, cross-sectional area A, mass density $\rho (x)$, and Young’s modulus E(x), where x is the axis along the beam. Moreover, the hub is rotating about its axis with velocity of ${\dot{\psi }}$, and acceleration of $\ddot{\psi }$.

Fig. 1

Schematic of a rotating axially FG beam

As aforementioned, the effective material properties (e.g., Young’s modulus E), vary continuously along the beam and are functions of volume fractions of the constituent materials. Considering material A matrix, and material B inclusions as the constituents, and implementing the rule of mixtures, the effective material property, P, can be given by $P=P_AV_A+P_BV_B$, where $P_A$ and $P_B$ are the material properties of the constituents A and B. Also, $V_A$ and $V_B$ denote the corresponding volume fractions of the constituents, satisfying the relation $V_A+V_B=1$ at each cross-section. In this research, the inclusions volume fraction, $V_B$, is expressed by a four-parameter distribution relation as

$$\begin{aligned} V_B=\bigg [1-a\bigg (\frac{x}{L}\bigg )+b\bigg (\frac{x}{L}\bigg )^c\bigg ]^p \end{aligned}$$

(1)

where the parameters a, b, c, and the volume fraction index $p\ (0\le p\le \infty )$ compose the material variation profile along the beam. For $p=0$ or $p\rightarrow \infty$, a homogeneous isotropic material profile is obtained as a special case of the FGM [33, 34]. For a better insight, examples of material profiles for the FG beam are illustrated in “Appendix 1.” .

2.1 Kinematics of deformation

As shown in Fig. 2, to develop the kinematics of deformation of the rotating beam, four Cartesian coordinate systems defined by the right-hand rule are utilized. $O_IXYZ$ is the fixed inertial coordinate system, Z axis of which coincides with the rotation axis. $O_Rxyz$ is the rotating coordinate system, where $O_R$ and z axis coincide with $O_I$ and Z axis, respectively. For the cross section of the undeformed and deformed rotating beam, local coordinate systems $O_Ux_1y_1z_1$ and $O_Dx_2y_2z_2$ are defined, respectively.

Fig. 2

Coordinate systems used to model the rotating axially FG beam

Accordingly, the position vector of a generic point B on the cross section of the undeformed and deformed beam can be expressed, respectively, as

$$\begin{aligned} {\mathbf {r}}= & {} \begin{Bmatrix}r_h+x;&y_1;&z_1\end{Bmatrix} \end{aligned}$$

(2)

$$\begin{aligned} {\mathbf {R}}= & {} \begin{Bmatrix}r_h+x+{\bar{u}};&{\bar{v}};&{\bar{w}}\end{Bmatrix} +{\mathbf {D}}\begin{Bmatrix}0;&y_1;&z_1\end{Bmatrix} \end{aligned}$$

(3)

where ${\bar{u}}$, ${\bar{v}}$, and ${\bar{w}}$ are deformations of a generic point along the x, y, and z axes, sequentially representing the axial, the chordwise, and the flapwise deformations. Moreover, ${\mathbf {D}}$ is the transformation matrix, rotating the cross-section of the beam from $O_Ux_1y_1z_1$ to $O_Dx_2y_2z_2$. The beam cross section is assumed to be doubly symmetric, and as a result, the coupling between the torsional and bending deformations is negligible [28], and the torsional behavior is not investigated here. In this regard, the transformation matrix includes rotations due to the in-plane bending (chordwise motion) and the out-of-plane bending (flapwise motion), in the following form:

$$\begin{aligned} {\mathbf {D}}= & {} \begin{bmatrix} \cos \theta _y &{} 0 &{} -\sin \theta _y\\ 0 &{} 1 &{} 0\\ \sin \theta _y &{} 0 &{} \cos \theta _y\end{bmatrix} \begin{bmatrix} \cos \theta _z &{} -\sin \theta _z &{} 0\\ \sin \theta _z &{} \cos \theta _z &{} 0\\ 0 &{} 0 &{} 1\end{bmatrix} \end{aligned}$$

(4)

here, $\theta _y$ and $\theta _z$ are the flapwise and the chordwise rotations, respectively. Making use of the approximations $\cos \theta _y=\cos \theta _z\approx 1$, $\sin \theta _y\approx {\bar{w}}_{,x}$, and $\sin \theta _z\approx {\bar{v}}_{,x}$ in Eq. (4), the position vector of an arbitrary point on the cross section of the deformed beam can be obtained as

$$\begin{aligned} {\mathbf {R}} \!=\!\begin{Bmatrix}r_h\!+\!x\!+\!{\bar{u}}-y_1{\bar{v}}_{,x}-z_1{\bar{w}}_{,x};&y_1\!+\!{\bar{v}};&z_1+{\bar{w}}\!-\!y_1{\bar{v}}_{,x}{\bar{w}}_{,x}\end{Bmatrix}\nonumber \\ \end{aligned}$$

(5)

where, $[\ ]_{,x}$ denotes the derivative of $[\ ]$ with respect to x. In order to add the effect of rotation to the deformed position vector of the beam, the following transformation is employed [29, 30, 35]

$$\begin{aligned} {\mathbf {R}}_{rot}={\mathbf {D}}^{IR}{\mathbf {R}}=\begin{bmatrix} \cos \psi &{} -\sin \psi &{} 0\\ \sin \psi &{} \cos \psi &{} 0\\ 0 &{} 0 &{} 1\end{bmatrix}{\mathbf {R}} \end{aligned}$$

(6)

In Eq. (6), ${\mathbf {D}}^{IR}$ is the rotation transformation matrix, which implements the rotation from the coordinate system $O_IXYZ$ to $O_Rxyz$, and $\psi$ is the rotation angle of the hub. In this paper, the rotating speed of the hub is assumed to include an average value $\omega _0$, and small periodic fluctuation in the following form

$$\begin{aligned} {\dot{\psi }}=\omega _0+\omega (t)=\omega _0+\gamma \sin \Omega t \end{aligned}$$

(7)

where $\Omega$ is the rotating speed fluctuation frequency, and $\gamma$ is the small perturbed fluctuation amplitude.

2.2 The elastic strain and kinetic energies of the system

To model the stiffening effect in the rotating beam and include time-dependent axial centrifugal force, linear stress, and nonlinear strain relations are utilized. By assuming a long and slender geometry for the rotating beam and using Green’s strain definition, one can express the nonlinear x-directional strain in the following form [26, 28]

$$\begin{aligned} \varepsilon _{x}^{nl} = {\bar{u}}_{,x}+\frac{1}{2}({\bar{v}}_{,x}^2+{\bar{w}}_{,x}^2)-y_1{\bar{v}}_{,xx}-z_1{\bar{w}}_{,xx} \end{aligned}$$

(8)

Also by defining the linear axial stress as $\sigma _x^l=E(x)\varepsilon _{x}^l$, the variations of the elastic strain energy is calculated by [28]

$$\begin{aligned} \delta U_s = \int _{0}^{L}\int _{A} E(x)\sigma _{x}^l\delta \varepsilon _{x}^{nl}\mathrm {d}A\mathrm {d}x \end{aligned}$$

(9)

where $\delta$ is the variational parameter. The variations of the kinetic energy of the system can also be written in the following form

$$\begin{aligned} \delta U_k = -\int _{0}^{L}\int _{A} \rho (x){\ddot{\mathbf {R}}}_{rot}^\mathrm {T}\delta {\mathbf {R}}_{rot}\mathrm {d}A\mathrm {d}x \end{aligned}$$

(10)

where the dot notation denotes derivative with respect to time, and ${\ddot{\mathbf {R}}}_{rot}$ is the acceleration vector given by [35]

$$\begin{aligned} {\ddot{\mathbf {R}}}_{rot} = {\mathbf {D}}^{IR}({\ddot{\mathbf {R}}}+2\varvec{\omega }{\dot{\mathbf {R}}}+\varvec{\omega }\varvec{\omega }{\mathbf {R}}+\varvec{\alpha }{\mathbf {R}}) \end{aligned}$$

(11)

in which $\varvec{\omega }$ and $\varvec{\alpha }$ are the second-order skew-symmetric tensors of the angular velocity and acceleration vectors, respectively, given by

$$\begin{aligned} \varvec{\omega }=\begin{bmatrix} 0 &{} -{\dot{\psi }} &{} 0\\ {\dot{\psi }} &{} 0 &{} 0\\ 0 &{} 0 &{} 0\end{bmatrix}, \qquad \qquad \varvec{\alpha }=\begin{bmatrix} 0 &{} -\ddot{\psi } &{} 0\\ \ddot{\psi } &{} 0 &{} 0\\ 0 &{} 0 &{} 0\end{bmatrix} \end{aligned}$$

(12)

2.3 Governing equations

Once the elastic strain and kinetic energies are calculated, the equations governing the axial, chordwise, and flapwise motions are obtained using the Hamilton’s principle as

$$\begin{aligned}&\rho A({\bar{u}}_{,tt}-{\dot{\psi }}^2{\bar{u}}-2{\dot{\psi }}{\bar{v}}_{,t} -\ddot{\psi }{\bar{v}})-A(E{\bar{u}}_{,x})_{,x}\nonumber \\&\quad =\rho A{\dot{\psi }}^2(r_h+x) \end{aligned}$$

(13)

$$\begin{aligned}&\rho A({\bar{v}}_{,tt}-{\dot{\psi }}^2{\bar{v}}+2{\dot{\psi }}{\bar{u}}_{,t} +\ddot{\psi }{\bar{u}})-I_z(\rho {\bar{v}}_{,xtt})_{,x}\nonumber \\&\qquad +I_z{\dot{\psi }}^2(\rho {\bar{v}}_{,x})_{,x}\nonumber \\&\qquad +I_z(E{\bar{v}}_{,xx})_{,xx}-A(E{\bar{u}}_{,x}{\bar{v}}_{,x})_{,x}\nonumber \\&\quad =I_z\rho ^{'}\ddot{\psi }-\rho A\ddot{\psi }(r_h+x) \end{aligned}$$

(14)

$$\begin{aligned}&\rho A{\bar{w}}_{,tt}-I_y(\rho {\bar{w}}_{,xtt})_{,x}+I_y{\dot{\psi }}^2(\rho {\bar{w}}_{,x})_{,x}\nonumber \\&\quad +I_y(E{\bar{w}}_{,xx})_{,xx}-A(E{\bar{u}}_{,x}{\bar{w}}_{,x})_{,x}=0 \end{aligned}$$

(15)

here, $I_y$ and $I_z$ represent the second moment of cross-sectional area with respect to $y_1$- and $z_1$-axis, respectively. In addition, prime symbol shows the total derivative of a parameter with respect to x. In Eqs. (13–15), $2{\dot{\psi }}{\bar{u}}_{,t}$ and $2{\dot{\psi }}{\bar{v}}_{,t}$ are the Coriolis effect terms, and $I_z(\rho {\bar{v}}_{,xtt})_{,x}$, $I_z{\dot{\psi }}^2(\rho {\bar{v}}_{,x})_{,x}$, $I_y(\rho {\bar{w}}_{,xtt})_{,x}$, and $I_y{\dot{\psi }}^2(\rho {\bar{w}}_{,x})_{,x}$ show the rotary inertia terms. Additionally, term $EA{\bar{u}}_{,x}$ in the chordwise and flapwise equations represents the time-dependent axial force in the rotating FG beam causing the stiffening effect in the system. The associated boundary conditions are also expressed as:

$$\begin{aligned}&{\bar{u}}={\bar{v}}={\bar{w}}={\bar{v}}_{,x}={\bar{w}}_{,x}=0\ \mathrm {at}\ x=0,\quad {\bar{u}}_{,x}={\bar{v}}_{,xx}\nonumber \\&\quad ={\bar{w}}_{,xx}={\bar{v}}_{,xxx}={\bar{w}}_{,xxx}=0\ \mathrm {at}\ x=L \end{aligned}$$

(16)

For the undisturbed motion of the rotating beam, the steady-state equilibrium deformations must be obtained from Eqs. (13–15). In this regard, deformations of the beam are considered as the sum of steady-state equilibrium deformations, $(u_s,v_s,w_s)$, and disturbed deformations about the equilibrium position, $(\Delta u,\Delta v,\Delta w)$, in the following forms

$$\begin{aligned}&{\bar{u}}(x,t)=u_s(x)+\Delta u(x,t),\nonumber \\&{\bar{v}}(x,t)=v_s(x)+\Delta v(x,t), \nonumber \\&{\bar{w}}(x,t)=w_s(x)+\Delta w(x,t) \end{aligned}$$

(17)

by inserting Eqs. (17) into Eqs. (13–15), making use of Eq. (7), and ignoring the fluctuation in the rotating speed, one can derive the equations governing the steady-state equilibrium condition of the rotating axially FG beam as

$$\begin{aligned}&\rho A\omega _0^2u_s+A(Eu_s^\prime )^\prime =-\rho A\omega _0^2(r_h+x) \end{aligned}$$

(18)

$$\begin{aligned}&\rho A\omega _0^2v_s-I_z\omega _0^2(\rho v_s^\prime )^\prime -I_z(Ev_s^{\prime \prime })^{\prime \prime }+A(Eu_s^\prime v_s^\prime )^\prime =0\nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned}&I_y\omega _0^2(\rho w_s^\prime )^\prime +I_y(Ew_s^{\prime \prime })^{\prime \prime }+A(Eu_s^\prime w_s^\prime )^\prime =0 \end{aligned}$$

(20)

Boundary conditions for these equations are the same as (16); applying these conditions and using a numerical method based on midpoint rule enhanced by Richardson extrapolation algorithm [36], the following solutions are obtained

$$\begin{aligned} u_s=\sum _{j=1}^Jc_jx^j,\quad v_s=w_s=0 \end{aligned}$$

(21)

here, $u_s$ is expressed in a polynomial form with coefficients $c_j$, and polynomial degree J, both of which are determined to reconstruct the numerical solution. Once the equilibrium position is determined, by inserting Eq. (17) into Eqs. (13–15), and using Eqs. (18–21), the governing axial, chordwise, and flapwise equations about the equilibrium position are obtained as

$$\begin{aligned}&\rho A(u_{,tt}-{\dot{\psi }}^2u-2{\dot{\psi }}v_{,t}-\ddot{\psi }v)-A(Eu_{,x})_{,x}=0\nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned}&\rho A(v_{,tt}-{\dot{\psi }}^2v+2{\dot{\psi }}u_{,t}+{\ddot{\psi }}u)-I_z(\rho v_{,xtt})_{,x}\nonumber \\&\quad +I_z{\dot{\psi }}^2(\rho v_{,x})_{,x}+I_z(Ev_{,xx})_{,xx}\nonumber \\&\quad -A(Eu_s^{\prime }v_{,x})_{,x}-A(Eu_{,x}v_{,x})_{,x}=I_z\rho ^{'}\ddot{\psi }\nonumber \\&\quad -\rho A\ddot{\psi }(r_h+x+u_s) \end{aligned}$$

(23)

$$\begin{aligned}&\rho Aw_{,tt}-I_y(\rho w_{,xtt})_{,x}+I_y{\dot{\psi }}^2(\rho w_{,x})_{,x}\nonumber \\&\quad +I_y(Ew_{,xx})_{,xx}-A(Eu_s^{\prime }w_{,x})_{,x}\nonumber \\&\quad -A(Eu_{,x}w_{,x})_{,x}=0 \end{aligned}$$

(24)

where $\Delta$ is omitted for the sake of brevity. It can be observed from Eqs. (22–24) that the chordwise and flapwise equations include quadratic nonlinearities due to the coupling to axial deformation via time-dependent axial force terms. Generally, such quadratic nonlinearities are associated with vibrations of rotating elements about a static equilibrium position [37]. Moreover, the presence of terms ${\dot{\psi }}$ and $\ddot{\psi }$, which are time-dependent due to the fluctuation of the rotating speed, leads to parametric excitation in the system. On the other hand, the external excitation of the chordwise motion is due to the inertial forces stemming from the variation of the rotating speed.

3 Discretization of the equations

To obtain the discretized equations of motion, the following scaled Chebyshev polynomials are used [38, 39]

$$\begin{aligned} C_k(\xi ) = \cos \big (k\cos ^{-1}(\xi )\big ),\ k=0,1,2,... \end{aligned}$$

(25)

These recursive, orthogonal, and exponentially convergent polynomials form a complete set on the interval $[-1,1]$, and therefore, the spatial domain x that lies on the arbitrary interval [0, L] is mapped to $\xi \in [-1,1]$. In this interval, one can approximate any square-integrable function in terms of these polynomials [40, 41]. For each deformation $q_i$ of the rotating axially FG beam ($q_1=u$, $q_2=v$, $q_3=w$), the following Chebyshev series expansion is expressed

$$\begin{aligned} q_i(\xi ) = \sum _{k=1}^{N}a_{i_{k-1}}C_{k-1}(\xi ),\ i=1,2,3 \end{aligned}$$

(26)

where $a_i$’s are the coefficients of the expansion in the domain $\xi$, which is discretized by N Gauss–Lobatto sampling points [42, 43]. According to the above equation, each deflection is expressed by N number of polynomials, which can be rewritten in the following matrix form

$$\begin{aligned} {\mathbf {q}}_i = {\varvec{\Gamma }}_B{\mathbf {a}}_i,\ i=1,2,3 \end{aligned}$$

(27)

where ${\mathbf {q}}_i$ is the vector of mapped deflection, $q_i$, at sampling points, and ${\varvec{\Gamma }}_B$ is the backward transformation matrix defined by

$$\begin{aligned} \Gamma _{B_{mn}}=C_{n-1}(\xi _m),\ m,n=1,2,...,N \end{aligned}$$

(28)

Next, to implement the spatial derivatives defined in the governing equations, the coefficients $a_{i_{k-1}}$ are related to coefficients of the spatial derivative expansion, $b_{i_{k-1}}$, via [44]

$$\begin{aligned} {\mathbf {b}}_i = {\mathbf {D}}{\mathbf {a}}_i,\ i=1,2,3 \end{aligned}$$

(29)

here ${\mathbf {D}}$ is derivative matrix with respect to $\xi$. Accordingly, by using Eqs. (27) and (29), the differentiation matrix ${\mathbf {Q}}$ in the sampled domain can be defined as

$$\begin{aligned} \frac{{\partial {\mathbf {q}}_i}}{\partial \xi }={\varvec{\Gamma }}_B{\mathbf {b}}_i={\varvec{\Gamma }}_B{\mathbf {D}}{\mathbf {a}}_i={\varvec{\Gamma }}_B{\mathbf {D}}{\varvec{\Gamma }}_B^{-1}{\mathbf {q}}_i={\mathbf {Q}}{\mathbf {q}}_i \end{aligned}$$

(30)

By making use of inner product definition, definite integral of functions $f(\xi )$ and $g(\xi )$ that can be expressed by Chebyshev polynomials can be written as

$$\begin{aligned} \int _{\xi }f(\xi )g(\xi )\mathrm {d}\xi = {\mathbf {f}}^{\mathrm {T}}\mathbf {Vg} \end{aligned}$$

(31)

in which ${\mathbf {V}}$ is the inner product matrix, and ${\mathbf {f}}$ and ${\mathbf {g}}$ are the sampled functions values. (Readers are gently invited to see [40] for the detailed derivation of the inner product matrix). Finally, to impose the essential boundary conditions, basis recombination is used [45, 46]

$$\begin{aligned} {\mathbf {q}}_i={\mathbf {P}}_i{\mathbf {q}}_{d_i},\ i=1,2,3 \end{aligned}$$

(32)

here, ${\mathbf {P}}_i$’s are the projection matrices that are obtained via singular value decomposition of the boundary condition matrix $\varvec{\beta }_i$, such that $\varvec{\beta }_i{\mathbf {q}}_i={\mathbf {0}}$. By using the series expansion for each deformation in Eqs. (22–24), substituting differentiation matrices, and applying Galerkin’s method, one can derive the discretized equations of motion as

$$\begin{aligned}&\mathbf {M}{\ddot{\mathbf{q}}}_s+(2{\dot{\psi }}{\mathbf {G}}+{\mathbf {C}}){{\dot{\mathbf{q}}}}_s +({\mathbf {K}}_1+{\dot{\psi }}^2{\mathbf {K}}_2+\ddot{\psi }{\mathbf {K}}_3){\mathbf {q}}_s\nonumber \\&\quad +\mathbf {NL}({\mathbf {q}}_s)=\ddot{\psi }{\mathbf {f}} \end{aligned}$$

(33)

where ${\mathbf {q}}_s = \{{\mathbf {q}}_{d_1};{\mathbf {q}}_{d_2};{\mathbf {q}}_{d_3}\}$, and ${\mathbf {M}}$, ${\mathbf {G}}$, and ${\mathbf {K}}_i$’s are respectively mass, gyroscopic, and stiffness matrices. Damping effect is also added to the model by inserting ${\mathbf {C}}$ as a damping matrix proportional to ${\mathbf {K}}_1+\omega _0^2{\mathbf {K}}_2$. Moreover, $\mathbf {NL}({\mathbf {q}}_s)$, and ${\mathbf {f}}$ are internal nonlinear forcing, and generalized force vectors, respectively. Details of these matrices are given in “Appendix 1.”

3.1 Preliminaries for nonlinear analysis

In this research, the MMS for gyroscopic systems is used to solve the governing equations of motion. To this end, the linear stiffness part of equations is decoupled via implementing linear modal analysis. To obtain equations governing the linear system, Eq. (7) is inserted into Eq. (33), then by ignoring the fluctuation in the rotating speed, damping effect, and the nonlinear forcing $\mathbf {NL}$, the following linear matrix form equations of motion are derived

$$\begin{aligned} {\mathbf {M}\ddot{\mathbf{q}}}_s+2\omega _0\mathbf {G}{\dot{\mathbf{q}}}_s+({\mathbf {K}}_1+\omega _0^2{\mathbf {K}}_2){\mathbf {q}}_s={\mathbf {0}} \end{aligned}$$

(34)

by solving state-space eigenvalue problem for Eq. (34), complex eigenvalues are obtained, where their imaginary parts are natural frequencies including Coriolis effects denoted by $\omega _n^{c}$. To decouple the linear stiffness part of equations, the following transformation is also introduced [47]

$$\begin{aligned} {\mathbf {q}}_s=\varvec{\Phi }\varvec{\eta } \end{aligned}$$

(35)

where $\varvec{\Phi }$ is the matrix of normalized eigenvectors associated with the problem (34) when ${\mathbf {G}}={\mathbf {0}}$, such that $\varvec{\Phi }^\mathrm {T}{\mathbf {M}}\varvec{\Phi }$ yields an identity matrix. By inserting transformation (35) into Eq. (33), and premultiplying it by $\varvec{\Phi }^\mathrm {T}$, one obtains

$$\begin{aligned}&\ddot{\eta }_i+2{\dot{\psi }}\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}{\dot{\eta }}_j+\lambda \omega _i^2{\dot{\eta }}_i\nonumber \\&\qquad +\omega _i^2\eta _i+({\dot{\psi }}^2-\omega _0^2) \sum _{j=1}^{N_e}{\hat{k}}_{2_{i,j}}\eta _j\nonumber \\&\qquad +\ddot{\psi }\sum _{j=1,j\ne i}^{N_e}{\hat{k}}_{3_{i,j}}\eta _j+\sum _{j=1}^{N_e} \sum _{l=1}^{N_e}{\hat{f}}_{nl_{i,j,l}}\eta _j\eta _l\nonumber \\&\quad =\ddot{\psi }{\hat{f}}_i,\ i=1,2,...,N_e \end{aligned}$$

(36)

where $\lambda$ is damping coefficient, $\omega _i^2$’s are eigenvalues of (34) when ${\mathbf {G}}={\mathbf {0}}$, (equal to natural frequencies of the system when neglecting Coriolis effects), $N_e$ is the number of equations, and ${\hat{g}}_{i,j}$, ${\hat{k}}_{2_{i,j}}$, ${\hat{k}}_{3_{i,j}}$, and ${\hat{f}}_i$’s are, respectively, elements of ${\hat{\mathbf {G}}}$, ${\hat{\mathbf {K}}}_2$, ${\hat{\mathbf {K}}}_3$, and $\hat{{\mathbf {f}}}$, given by

$$\begin{aligned}&{\hat{\mathbf {G}}}={\varvec{\Phi }}^\mathrm {T}{\mathbf {G}}{\varvec{\Phi }},\quad {\hat{\mathbf {K}}}_2={\varvec{\Phi }}^\mathrm {T}{\mathbf {K}}_2{\varvec{\Phi }},\nonumber \\&\quad {\hat{\mathbf {K}}}_3={\varvec{\Phi }}^\mathrm {T}{\mathbf {K}}_3{\varvec{\Phi }},\quad {\hat{\mathbf {f}}}=\varvec{\Phi }^\mathrm {T}{\mathbf {f}} \end{aligned}$$

(37)

in addition, ${\hat{f}}_{nl_{i,j,l}}$’s are coefficients of $\eta _j\eta _l$ in $i^{th}$ element of ${\hat{\mathbf {NL}}}$, defined by

$$\begin{aligned} {\hat{\mathbf {NL}}}={\varvec{\Phi }}^\mathrm {T}\mathbf {NL}(\varvec{\Phi }\varvec{\eta }) \end{aligned}$$

(38)

4 Applying multiple scales method

To implement the MMS to solve the set of Eq. (36), damping coefficient is rescaled as $\lambda \rightarrow \epsilon \lambda$, where, $\epsilon$ is a positive small parameter used as a bookkeeping device. Moreover, for all the terms containing parametric excitation and the nonlinear forcing function, the following transformations are used [37, 48, 49]:

$$\begin{aligned}&\omega (t)\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}{\dot{\eta }}_j \rightarrow \epsilon \omega (t)\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}{\dot{\eta }}_j,\nonumber \\&\quad \omega (t)\sum _{j=1}^{N_e}{\hat{k}}_{2_{i,j}}\eta _j\rightarrow \epsilon \omega (t)\sum _{j=1}^{N_e}{\hat{k}}_{2_{i,j}}\eta _j,\quad \nonumber \\&\quad \omega (t)^2\sum _{j=1}^{N_e}{\hat{k}}_{2_{i,j}}\eta _j\rightarrow \epsilon ^2\omega (t)^2\sum _{j=1}^{N_e}{\hat{k}}_{2_{i,j}}\eta _j,\nonumber \\&\quad \sum _{j=1}^{N_e}\sum _{l=1}^{N_e}{\hat{f}}_{nl_{i,j,l}}\eta _j\eta _l\rightarrow \epsilon \sum _{j=1}^{N_e}\sum _{l=1}^{N_e}{\hat{f}}_{nl_{i,j,l}}\eta _j\eta _l \end{aligned}$$

(39)

For the external excitation terms, such transformations might be used depending on the resonance condition in the system. Due to the presence of both parametric and external excitation in the system, regardless of internal resonances, many possible resonant combinations of $\Omega$ with natural frequencies of the system can occur. For instance, because of the external excitation, conditions like $\Omega \approx \omega _n^c$, $\Omega \approx 2\omega _n^c$, and $\Omega \approx \frac{1}{2}\omega _n^c$, and due to the parametric excitation, conditions such as $\Omega \approx 0$, $\Omega \approx 2\omega _n^c$, $\Omega \approx \omega _n^c +\omega _{m}^c$, and $\Omega \approx \omega _{m}^c -\omega _{n}^c$ can result in different resonant cases. Some of the important resonant cases are discussed in the following subsections for systems with/without internal resonances.

4.1 The case with non-resonant $\Omega$

Based on the MMS, a first-order uniform expansion of the solution for generalized coordinate $\eta _i$ is considered as

$$\begin{aligned}&\eta _i(T_0,T_1)=\eta _{i,0}(T_0,T_1)+\epsilon \eta _{i,1}(T_0,T_1)+...,\nonumber \\&\quad i=1,2,...,N_e \end{aligned}$$

(40)

where $T_n=\epsilon ^nt$. Substituting solution (40) into Eqs. (36), after implementing transformations (39), and equating coefficients of similar powers of $\epsilon$ yield

$$\begin{aligned}&\mathrm {O}(\epsilon ^0):\quad \mathrm {D}_0^2\eta _{i,0}+2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mathrm {D}_0\eta _{j,0}+\omega _i^2\eta _{i,0}\nonumber \\&\quad =\gamma \Omega {\hat{f}}_i\cos \Omega T_0, \end{aligned}$$

(41)

$$\begin{aligned}&\mathrm {O}(\epsilon ^1):\quad \mathrm {D}_0^2\eta _{i,1}+2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mathrm {D}_0\eta _{j,1}+\omega _i^2\eta _{i,1}\nonumber \\&\quad =-2\mathrm {D}_0\mathrm {D}_1\eta _{i,0}-2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mathrm {D}_1\eta _{j,0}\nonumber \\&\qquad -\lambda \omega _i^2\mathrm {D}_0\eta _{i,0}-2\gamma \sin \Omega T_0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mathrm {D}_0\eta _{j,0}\nonumber \\&\qquad -2\gamma \omega _0\sin \Omega T_0\sum _{j=1}^{N_e}{\hat{k}}_{2_{i,j}}\eta _{j,0}\nonumber \\&\qquad -\gamma \Omega \cos \Omega T_0\sum _{j=1,j\ne i}^{N_e}{\hat{k}}_{3_{i,j}}\eta _{j,0}\nonumber \\&\qquad -\sum _{j=1}^{N_e}\sum _{l=1}^{N_e}{\hat{f}}_{nl_{i,j,l}}\eta _{j,0}\eta _{l,0}, \end{aligned}$$

(42)

in which, $\mathrm {D}_n\equiv \partial /\partial T_n$. The solutions of equations of order $\epsilon ^0$ are expressed as

$$\begin{aligned} \eta _{1,0}(T_0,T_1)&=\sum _{j=1}^{N_e}A_j(T_1)\exp (I\omega _j^cT_0)\nonumber \\&\quad + \Delta _1\exp (I\Omega T_0) + cc \end{aligned}$$

(43)

$$\begin{aligned} \eta _{i,0}(T_0,T_1)&=\sum _{j=1}^{N_e}\mu _{i,j}A_j(T_1)\exp (I\omega _j^cT_0)\nonumber \\&\quad + \Delta _i\exp (I\Omega T_0) + cc,\quad i=2,3,...,N_e\nonumber \\ \end{aligned}$$

(44)

In the above solutions, $I=\sqrt{-1}$, $\omega _j^c$’s are eigenvalues of Eq. (41), which are equal to natural frequencies of the rotating axially FG beam including Coriolis effects. $A_j$’s are complex amplitudes that need to be determined. Moreover, $\mu _{i,j}$, and $\Delta _i$’s are vibration amplitude coefficients that balance the harmonics in Eq. (41) after inserting the solution (See Appendix 1 for more details). For Eq. (42), the following solution is considered

$$\begin{aligned}&\eta _{i,1}(T_0,T_1)=\sum _{j=1}^{N_e}B_{i,j}(T_1)\exp (I\omega _j^cT_0)\nonumber \\&\quad + cc,\quad i=1,2,...,N_e \end{aligned}$$

(45)

by inserting Eqs. (43–44) and Eq. (45) respectively to the right-hand side and left-hand side of Eq. (42), and applying the same balancing mentioned earlier for $\mu$ and $\Delta$, the following $N_e$ number of linear algebraic systems including $N_e$ number of equations are obtained

$$\begin{aligned}&2I\omega _0\sum _{j=1,j\ne i}^{N_e}\omega _l^c{\hat{g}}_{i,j}B_{j,l}+(\omega _i^2-{\omega _l^c}^2)B_{i,l}=R_{i,l},\nonumber \\&\quad i,l = 1,2,...,N_e \end{aligned}$$

(46)

here $R_{i,l}$’s are right-hand side terms which are given in Appendix 1. Equation (46) shows the ith equation in the lth linear algebraic system. The lth system of equations can be written in the form $\mathbf {[C]}_l\mathbf {\{B\}}_l=\mathbf {\{R\}}_l$. The coefficient matrices $\mathbf {[C]}_l$’s are singular, since they represent the characteristic equation of the eigenvalue problem in Eq. (41). Therefore, one can conclude that $\det (\mathbf {[C]}_{l_{N_e}})$ is also equal to zero, in which $\mathbf {[C]}_{l_{N_e}}$ is the matrix formed by replacing the $N_e$th column of $\mathbf {[C]}_l$ by the right-hand side column vector $\mathbf {\{R\}}_l$. By setting this determinant equal to zero for lth system of equations, the equation governing $A_l(T_1)$ can be obtained as

$$\begin{aligned} \mathrm {D}_1A_l+\Gamma _lA_l=0,\quad l=1,2,...,N_e \end{aligned}$$

(47)

where $\Gamma _l$’s are real valued functions of all the system parameters present in Eq. (46). The solutions of Eq. (47) can be expressed in polar form as

$$\begin{aligned} A_l(T_1)=\frac{1}{2}a_l\exp (-\Gamma _lT_1+I\theta _l),\quad l=1,2,...,N_e\nonumber \\ \end{aligned}$$

(48)

where the $a_l$ and $\theta _l$ are real-valued constants determined by initial conditions $\varvec{\eta }(0)=\varvec{{{\dot{\eta }}}}(0)={\mathbf {0}}$. The solution above indicates that the modal amplitudes will decay over time to zero due to the damping effect, and the steady-state solution is a stable solution including particular parts of Eqs. (43–44). For the case of a system with internal resonance, detuning parameter $\sigma _0$ is introduced such that

$$\begin{aligned} \omega _m^c = 2\omega _n^c+\epsilon \sigma _0,\ m>n \end{aligned}$$

(49)

representing modal interactions between modes m and n. Based on this assumption, by reconstructing new right-hand side term in Eq. (46), the procedure mentioned above results in the following equations

$$\begin{aligned}&\mathrm {D}_1A_l+\Gamma _lA_l=0,\nonumber \\&\mathrm {D}_1A_n+\Gamma _nA_n+\Gamma _{nm}A_m{\bar{A}}_n\exp (I\sigma _0T_1)=0,\nonumber \\&\mathrm {D}_1A_m+\Gamma _mA_m+\Gamma _{nn}A_n^2\exp (-I\sigma _0T_1)=0,\nonumber \\&l=1,2,...,N_e,\ l\ne m,n,\ 2\le m\le N_e,\ \nonumber \\&1\le n\le N_e-1 \end{aligned}$$

(50)

where overbar indicates complex conjugate. For $A_l$ amplitudes, solutions in the form of Eq. (48) are valid; however, for $A_n$ and $A_m$ amplitudes, solutions in the form $\frac{1}{2}a_i\exp (I\theta _i)$ are considered, where $a_i$ and $\theta _i$ are real valued functions of $T_1$. Using these solutions, one obtains

$$\begin{aligned}&a^\prime _n+\Gamma _na_n+\frac{\Gamma _{nm}}{2}a_ma_n\cos \nu _1=0,\nonumber \\&a^\prime _m+\Gamma _ma_m+\frac{\Gamma _{nn}}{2}a_n^2\cos \nu _1=0,\nonumber \\&a_m\nu ^\prime _1-a_m\sigma _0-\bigg (\frac{\Gamma _{nn}}{2}a_n^2+\Gamma _{nm}a_m^2\bigg )\sin \nu _1=0 \end{aligned}$$

(51)

where, $\nu _1=\theta _m-2\theta _n+\sigma _0T_1$. Solutions of these equations result in oscillatory modal amplitudes that decay over time. These solutions are bounded if $\frac{\Gamma _{nm}}{\Gamma _{nn}}<0$, and may be unbounded if $\frac{\Gamma _{nm}}{\Gamma _{nn}}>0$. Since the system does not contain any regenerative element, ${\Gamma _{nn}}$ and ${\Gamma _{nm}}$ have opposite signs, and the vibration response is always bounded.

4.2 The case with $\Omega$ near $\omega _n^c$

One of the important resonant cases for the current system is the external primary resonance occurring when the rotating speed fluctuation frequency is close to one of the chordwise natural frequencies of the system. In this case, transformation ${\hat{f}}_n\rightarrow \epsilon {\hat{f}}_n$ is used, and detuning parameter $\sigma _1$ is defined such that

$$\begin{aligned} \Omega = \omega _n^c+\epsilon \sigma _1 \end{aligned}$$

(52)

here n is the vibration mode regarding the chordwise motion of the system. By reobtaining Eqs. (41–42) accordingly, solutions in the form of Eqs. (43–44) are valid for $i\ne n$, and for $\eta _{n,0}$, we have

$$\begin{aligned} \eta _{n,0}(T_0,T_1)=\sum _{j=1}^{N_e}\mu _{n,j}A_j(T_1)\exp (I\omega _j^cT_0) + cc\nonumber \\ \end{aligned}$$

(53)

using these solutions, re-obtaining the right-hand side of Eq. (46), and setting $\det (\mathbf {[C]}_{i_{N_e}})$ equal to zero for the ith system of equations $(i=1,2,...,N_e)$, governing equations of modal amplitudes are derived as

$$\begin{aligned}&\mathrm {D}_1A_l+\Gamma _lA_l=0,\nonumber \\&\mathrm {D}_1A_n+\Gamma _nA_n+I\Gamma _{f_n}\gamma \Omega {\hat{f}}_n\exp (I\sigma _1T_1)=0,\nonumber \\&l=1,2,...,N_e,\ l\ne n,\ 1\le n\le N_e \end{aligned}$$

(54)

For $A_l$ amplitudes, solutions in the form of Eq. (48) are valid; however, for $A_n$, one can obtain

$$\begin{aligned}&A_n(T_1)=\frac{1}{2}a_n\exp (-\Gamma _nT_1+I\theta _n)-I\Gamma _{f_n}\gamma \Omega {\hat{f}}_n\nonumber \\&\quad (\Gamma _n+I\sigma _1)^{-1}\exp (I\sigma _1T_1),\ 1\le n\le N_e \end{aligned}$$

(55)

where the $a_n$ and $\theta _n$ are real constants determined by initial conditions. In this case, if 2:1 internal resonance as defined in Eq. (49) is present in the system, Eq. (54) becomes

$$\begin{aligned}&\mathrm {D}_1A_l+\Gamma _lA_l=0,\nonumber \\&\mathrm {D}_1A_n\!+\!\Gamma _nA_n\!+\!\Gamma _{nm}A_m{\bar{A}}_n\exp (I\sigma _0T_1)\nonumber \\&\quad +I\Gamma _{f_n}\gamma \Omega {\hat{f}}_n\exp (I\sigma _1T_1)=0,\nonumber \\&\mathrm {D}_1A_m+\Gamma _mA_m+\Gamma _{nn}A_n^2\exp (-I\sigma _0T_1)=0,\nonumber \\&\quad l=1,2,...,N_e,\ l\ne m,n,\ 2\le m\le N_e,\nonumber \\&\quad 1\le n\le N_e-1 \end{aligned}$$

(56)

similarly, by considering $A_i=\frac{1}{2}a_n(T_1)\exp (I\theta _i(T_1))$ for $i = n,m$, one obtains

$$\begin{aligned}&a^\prime _n+\Gamma _na_n+\frac{\Gamma _{nm}}{2}a_ma_n\cos \nu _1-2\Gamma _{f_n}\gamma \Omega {\hat{f}}_n\nonumber \\&\quad \sin \nu _2=0,\nonumber \\&a^\prime _m+\Gamma _ma_m+\frac{\Gamma _{nn}}{2}a_n^2\cos \nu _1=0,\nonumber \\&\quad a_ma_n\nu ^\prime _1-a_ma_n\sigma _0-\bigg (\frac{\Gamma _{nn}}{2}a_n^3 +\Gamma _{nm}a_m^2a_n\bigg )\sin \nu _1\nonumber \\&\quad -4a_m\Gamma _{f_n}\gamma \Omega {\hat{f}}_n\cos \nu _2=0,\nonumber \\&\quad a_n\nu ^\prime _2-a_n\sigma _1-\frac{\Gamma _{nm}}{2}a_ma_n\sin \nu _1\nonumber \\&\quad -2\Gamma _{f_n}\gamma \Omega {\hat{f}}_n\cos \nu _2=0 \end{aligned}$$

(57)

where $\nu _1=\theta _m-2\theta _n+\sigma _0T_1$, and $\nu _2 = \sigma _1T_1-\theta _n$. For the transient vibration response, these equations can be solved numerically. For the case of steady-state response, solution is obtained by assuming $a^\prime _n=a^\prime _m=\nu ^\prime _1=\nu ^\prime _2=0$, and the stability analysis is performed by assuming Cartesian notation of the solutions as [50, 51]

$$\begin{aligned}&A_n(T_1) = \frac{1}{2}(x_n-Iy_n)\exp (I\sigma _1T_1),\nonumber \\&\quad A_m(T_1) = \frac{1}{2}(x_m-Iy_m)\exp (2I\sigma _1T_1-I\sigma _0T_1)\nonumber \\ \end{aligned}$$

(58)

By inserting these solutions into the governing equations of $A_n$ and $A_m$, and separating the real, and imaginary parts, a system of algebraic equations are obtained. Then, Jacobian matrix of these equations are constructed and Routh–Hurwitz criterion is applied to its characteristic equation to obtain the following conditions for the stability of the solution

$$\begin{aligned}&s_1>0,\ s_1s_2-s_3>0,\ s_3(s_1s_2-s_3)-s_1^2s_4>0,\nonumber \\&\quad \ s_4>0 \end{aligned}$$

(59)

where

$$\begin{aligned} s_1&=\Gamma _n+\Gamma _m,\nonumber \\ s_2&=\frac{1}{4}\Gamma _{nn}\Gamma _{nm}a_n^2+\frac{1}{16}\Gamma _{nm}^2a_m^2 -\frac{1}{4}(\Gamma _n^2+\Gamma _m^2)\nonumber \\&\quad -\Gamma _n\Gamma _m-\frac{5}{4}\sigma _1^2-\frac{1}{4}\sigma _0^2+\sigma _0\sigma _1,\nonumber \\ s_3&=\frac{1}{16}\Gamma _{nm}^2\Gamma _ma_m^2+\frac{1}{8}\Gamma _{nn}\Gamma _{nm} (\Gamma _n+\Gamma _m)a_n^2\nonumber \\&\quad -\frac{1}{4}\Gamma _n\Gamma _m(\Gamma _n+\Gamma _m) -(\Gamma _n+\frac{1}{4}\Gamma _m)\sigma _1^2\nonumber \\&\quad -\Gamma _n\sigma _0 (\frac{1}{4}\sigma _0-\sigma _1),\nonumber \\ s_4&=\frac{1}{64}\Gamma _{nn}^2\Gamma _{nm}^2a_n^4 -\frac{1}{64}\Gamma _{nm}^2a_m^2(\Gamma _m^2+\sigma _0^2\nonumber \\&\quad -4\sigma _0\sigma _1 +4\sigma _1^2)-\frac{1}{16}\Gamma _{nn}\Gamma _{nm}a_n^2(\Gamma _n\Gamma _m\nonumber \\&\quad -2\sigma _1^2 +\sigma _0\sigma _1)\nonumber \\&\quad +\frac{1}{16}\gamma _n^2(\Gamma _m^2+\sigma _0^2-4\sigma _0\sigma _1+4\sigma _1^2)\nonumber \\&\quad +\frac{1}{16}\sigma _1^2(\Gamma _m^2+\sigma _0^2-4\sigma _0\sigma _1+4) \end{aligned}$$

(60)

4.3 The case with $\Omega$ near $2\omega _n^c$

This resonance case corresponds to the principal parametric resonance in the system. Moreover, if the $n^{th}$ vibration mode is a chordwise motion, the resonance case corresponds to the sub-harmonic resonance besides the parametric one. Similar to the previous case, transformation ${\hat{f}}_n\rightarrow \epsilon {\hat{f}}_n$ is used, and detuning parameter $\sigma _2$ is defined as

$$\begin{aligned} \Omega = 2\omega _n^c+\epsilon \sigma _2 \end{aligned}$$

(61)

By re-obtaining Eqs. (41–42) accordingly, the solutions in the form of Eqs. (43–44) are valid for $i\ne n$, and for $\eta _{n,0}$, solution given by Eq. (53) must be used. By using these solutions, re-obtaining the right-hand side of Eq. (46), and based on the procedure discussed earlier, equations governing modal amplitudes are derived as

$$\begin{aligned}&\mathrm {D}_1A_l+\Gamma _lA_l=0,\nonumber \\&\mathrm {D}_1A_n+\Gamma _nA_n+{\tilde{\Gamma }}_{n}\gamma \Omega {\bar{A}}_n\exp (I\sigma _2T_1)=0,\nonumber \\&l=1,2,...,N_e,\ l\ne n,\ 1\le n\le N_e \end{aligned}$$

(62)

For $A_l$ amplitudes solutions in the form of Eq. (48) are valid; however, for $A_n$, one can obtain

$$\begin{aligned}&a^\prime _n+\Gamma _na_n+{\tilde{\Gamma }}_{n}\gamma \Omega a_n\cos \nu _3=0,\nonumber \\&\quad \nu ^\prime _3-\sigma _2-2{\tilde{\Gamma }}_{n}\gamma \Omega \sin \nu _3=0 \end{aligned}$$

(63)

where the $a_n$ and $\theta _n$ are amplitude and phase of polar form vibration response of $A_n$, and $\nu _3=\sigma _2T_1-2\theta _n$. The transient response can be obtained by numerical integration of these equations; however, for steady-state response and stability analysis, the following solution is considered

$$\begin{aligned} A_n(T_1) = \frac{1}{2}(x_n-Iy_n)\exp (\frac{1}{2}I\sigma _2T_1) \end{aligned}$$

(64)

Similar to the procedure mentioned earlier, Routh-Hurwitz criterion yields

$$\begin{aligned}&{\tilde{\Gamma }}_n\gamma \Omega>0,\nonumber \\&\quad {\tilde{\Gamma }}_n^2\gamma ^2\Omega ^2-\Gamma _n^2-\frac{1}{4}\sigma _2^2>0 \end{aligned}$$

(65)

According to these conditions, the value of rotating speed fluctuation amplitude that results in transition of the bounded time response into the unbounded one can be obtained. For the rotating axially FG beam under parametric and 2:1 internal resonances, Eq. (62) becomes

$$\begin{aligned}&\mathrm {D}_1A_l+\Gamma _lA_l=0,\nonumber \\&\mathrm {D}_1A_n\!+\!\Gamma _nA_n\!+\!\Gamma _{nm}A_m\bar{A}_n\exp (I\sigma _0T_1) \!+\!{\tilde{\Gamma }}_{n}\gamma \Omega {\bar{A}}_n\nonumber \\&\exp (I\sigma _2T_1)=0,\nonumber \\&\mathrm {D}_1A_m+\Gamma _mA_m+\Gamma _{nn}A_n^2\exp (-I\sigma _0T_1)=0,\nonumber \\&l=1,2,...,N_e,\ l\ne m,n,\ 2\le m\le N_e,\nonumber \\&\ 1\le n\le N_e-1 \end{aligned}$$

(66)

by considering $A_i=\frac{1}{2}a_i(T_1)\exp (I\theta _i(T_1))$, for $i = n,m$, one obtains

$$\begin{aligned}&a^\prime _n+\Gamma _na_n+\frac{\Gamma _{nm}}{2}a_ma_n\cos \nu _1+{\tilde{\Gamma }}_n\gamma \Omega a_n\cos \nu _3=0,\nonumber \\&\quad a^\prime _m+\Gamma _ma_m+\frac{\Gamma _{nn}}{2}a_n^2\cos \nu _1=0,\nonumber \\&\quad a_ma_n\nu ^\prime _1-a_ma_n\sigma _0-\bigg (\frac{\Gamma _{nn}}{2}a_n^3 +\Gamma _{nm}a_m^2a_n\bigg )\nonumber \\&\quad \sin \nu _1-2{\tilde{\Gamma }}_n\gamma \Omega a_ma_n \sin \nu _3=0,\nonumber \\&\quad a_n\nu ^\prime _2-a_n\sigma _2-\Gamma _{nm}a_ma_n\sin \nu _1-2{\tilde{\Gamma }}_n\gamma \Omega a_n\nonumber \\&\quad \sin \nu _3=0 \end{aligned}$$

(67)

For the steady-state response, $a^\prime _n$, $a^\prime _m$, $\nu ^\prime _1$, and $\nu ^\prime _3$ are set to zero and two set of trivial and nontrivial solutions are obtained. For the case of nontrivial solutions, the stability analysis is performed based on Jacobian matrix of Eqs. (67); however, for the case of trivial solutions, Routh–Hurwitz stability criteria are obtained based on the following Cartesian notation solutions

$$\begin{aligned}&A_n(T_1) = \frac{1}{2}(x_n-Iy_n)\exp (\frac{1}{2} I\sigma _2T_1), \nonumber \\&A_m(T_1) = \frac{1}{2}(x_m-Iy_m)\exp (I\sigma _2T_1-I\sigma _0T_1) \end{aligned}$$

(68)

It is worth mentioning that in all the governing equations of the modal amplitudes $A_l$, coefficients $\Gamma$ are real valued functions of system parameters present in Eq. (46), in which right-hand side terms $R_{i,l}$’s are given in “Appendix 1”. Moreover, to obtain the steady-state solutions, the nonlinear algebraic forms of Eqs. (51), (57), and (67) are solved by utilizing Newton’s method [52].

5 Results and discussion

In this section, the dynamic behavior of rotating axially FG beams including natural frequencies, transient time response, and steady-state response resulting from the fluctuation in the rotating speed are investigated via several numerical examples. To verify the accuracy of the obtained results, comparisons are made to those available in the literature and obtained from numerical solutions of Eq. (33). Also, to validate the proposed model, natural frequencies are compared to those obtained from commercial FE software (COMSOL Multiphysics $^\circledR$ v5.5). For more general results and convenience of comparison, the following dimensionless parameters are introduced

$$\begin{aligned}&\tau = \frac{t}{T},\quad \delta =\frac{r_h}{L},\quad \alpha = \sqrt{\frac{AL^2}{I_z}},\nonumber \\&\quad \quad {\hat{\lambda }}=\frac{\lambda }{T},\nonumber \\&\quad {\hat{\omega }}_n^c=T\omega _n^c,\quad {\hat{\omega }}_0=T\omega _0, \nonumber \\&\quad {\hat{\Omega }}=T\Omega ,\quad {{\hat{\gamma }}}=T\gamma \end{aligned}$$

(69)

where

$$\begin{aligned} T=L^2\sqrt{\frac{\rho _cA}{E_cI_z}} \end{aligned}$$

(70)

In addition, the constituents of the FGM are taken to be aluminium (metal) as the matrix, and zirconia (ceramic) as the inclusions with $\rho _A=\rho _m=2707\ \mathrm {kg/m}{^3}$, $E_A=E_m=70\ \mathrm {GPa}$, $\rho _B=\rho _c = 5700\ \mathrm {kg/m}{^3}$, and $E_B=E_c=168\ \mathrm {GPa}$, here subscripts m and c stand for metal and ceramic, respectively. To determine the required number of polynomials along x direction, a convergence analysis is performed. Based on this analysis, N is set to 11, which results in 23 number of discretized equations after implementing boundary conditions, i.e. $N_e=23$ (See “Appendix 1” for the details).

5.1 Natural frequencies

Here, the effect of different FGM profiles on the natural frequencies of rotating axially FG beam is studied. To this end, at first step verification and validation are performed. The first 11 dimensionless natural frequencies of a rotating isotropic beam obtained from current work and those available in [28] are compared in Table 1. Relative difference between the results and types of motion in each mode are also provided in this table. It can be observed that there is an excellent agreement between the results.

Table 1 The comparison of dimensionless natural frequencies of isotropic rotating beam to those of previous study for $\delta =0$, ${\hat{\omega }}_0=10$, and $\alpha =70$

According to Table 1, the obtained results for homogeneous isotropic rotating beam are verified. For the case of FG beam, and validating FG model, first six dimensionless natural frequencies are compared to those of FE modeling. This modeling is performed in COMSOL Multiphysics$^\circledR$ based on three-dimensional solid mechanics. Comparing the results of a stubby beam to those of such FE model may require theories including higher order deformation, and torsional effect, which are neglected in the current work. Thus, to compare the results in this case, a long slender beam is considered. The beam has thickness $0.004\ \mathrm {m}$, and length $1\ \mathrm {m}$, and is analyzed based on 20 elements. Accordingly, Fig. 3 shows the dimensionless natural frequencies as a function of dimensionless rotating speed for two different material gradations. The provided results are in good agreement with each other, validating the developed dynamic model of the rotating axially FG beam. In this figure, the type of motion in each mode is the same as the sequence reported in Table 1.

Fig. 3

First six dimensionless natural frequencies of a rotating axially FG beam as functions of dimensionless rotating speed for $\delta =0$, and $\alpha =885$: a $\mathrm {FGM}_{(a=1.8/b=1.8/c=2/p=3)}$, and b $\mathrm {FGM}_{(a=1.8/b=1/c=2/p=1)}$

Fig. 4

Variations of dimensionless natural frequencies of a rotating axially FG beam in modes i, j, and k as a function of volume fraction index for different values of rotating speed, $\delta =0$, and $\alpha =70$: a $\mathrm {FGM}_{(a=1.8/b=1.8/c=2/p)}$, b $\mathrm {FGM}_{(a=2/b=2/c=3/p)}$, and c $\mathrm {FGM}_{(a=1.8/b=1.6/c=5/p)}$

Fig. 5

Variations of $r_{mn}$ parameter as a function of volume fraction index for different values of rotating speed, $\delta =0$, and $\alpha =70$: a $\mathrm {FGM}_{(a=1.8/b=1.8/c=2/p)}$, b $\mathrm {FGM}_{(a=1.8/b=1.6/c=5/p)}$, c $\mathrm {FGM}_{(a=2/b=2/c=3/p)}$, and d $\mathrm {FGM}_{(a=1.5/b=0.8/c=2/p)}$ (red line: $r_{21}$, orange dashed line: $r_{32}$, greed dash-dotted line: $r_{42}$, blue dash-double-dotted line: $r_{53}$, purple double-dash–dotted line: $r_{54}$, and black dotted line: $r_{63}$)

The effect of different system parameters on the dynamic behavior of the rotating axially FG beam, leading to significant variations of the natural frequencies, is of high importance. However, such analyses have been already conducted in abundant number of research works based on linear models (See Refs. [6, 18,19,20]). Thus, in the current study, the effect of rotating speed, and FGM parameters is investigated as an instance, and further investigations on the effect of system parameters on the natural frequencies are avoided. Figure 4 shows variations of dimensionless natural frequencies of the system in different modes as a function of volume fraction index. The results are provided for different values of rotating speed and three sets of volume fraction parameters a, b, and c. Modes i, j, and k are chosen such that coupling and crossing modes phenomena are distinguished. Natural frequencies of different motions get close to each other in the case of coupling modes, and for the case of crossings, this closeness is accompanied by mode crossover and re-ordering. In this figure, types of motions before couplings and crossings are specified by initial letters of axial, chordwise, and flapwise terms. For instance, in the case of $i=4$, $j=5$, and ${\hat{\omega }}_0=44$, second flapwise mode, F2, crosses second axial mode, A2, at $p=3.2$.

Fig. 6

Normalized time response of the rotating axially FG beam at $x=L$, for the non-resonant case based on MS and numerical solutions for $\mathrm {FGM}_{(a=2/b=2/c=3/p=0.5)}$, $\alpha =70$, ${\hat{\lambda }}=10^{-6}$, $\delta =0$, ${\hat{\omega }}_0=10$, ${\hat{\Omega }}=3$, and ${\hat{\gamma }}=0.1$, (black lines: MS solution, and red dotted lines: numerical solution)

In this research, the dynamic behavior of the system is investigated under different resonant conditions of rotating speed fluctuation frequency with/without internal resonance. As shown in Fig. 4, the rotating speed, and FGM parameters have significant effect on the variations of natural frequencies of the system, which can lead to commensurable frequencies causing internal resonances in the system. In this regard, conditions leading to 2:1 internal resonances caused by system parameters are examined by defining $r_{mn}={\omega _m^c}/{\omega _n^c}$. Figure 5 shows variations of $r_{mn}$ parameter as a function of volume fraction index for different values of rotating speed and four sets of a, b, and c parameters. Accordingly, values of $r_{mn}$ close to 2.0 represent commensurable frequencies that cause internal resonance in the system.

5.2 Time response

The time response of the system for any prescribed rotating speed can be obtained by solving the discretized form of Eqs. (13–15). By defining a realistic rotating speed profile, the prescribed speed increases gently from zero to reach a constant value ${\hat{\omega }}_0$ at steady-state, such time response analyses are available in [2, 28]. However, in the present work, it is assumed that the system has already reached a constant rotating speed, and the axial, chordwise, and flapwise deformations are at their steady-state conditions. Then, by including a small fluctuation in the value of ${\hat{\omega }}_0$, the dynamic behavior of the rotating axially FG beam is investigated. The fluctuation plays the role of a disturbance to the steady condition of the system and generates a transient time response that decays over time to a new forced steady-state response. Accordingly, in this subsection, the time responses of the system based on the solutions of Eqs. (22–24) are discussed to study the effect of rotating speed fluctuation on the dynamics of the rotating axially FG beam. The steady-state responses and the stability analysis are discussed in the next subsection. The time response of the system at the end of the beam is obtained for non-resonant case of ${\hat{\Omega }}$ and shown in Fig. 6. For a reasonable framework, displacements are normalized by thickness of the beam. In this figure, results based on the MMS and time integration solutions of Eq. (33) are included. The flapwise deformation is undisturbed during the variations of the rotating speed and is equal to zero, therefore, it is not included in the illustrations. However, both axial and chordwise motions are affected by the fluctuations. The chordwise motion is affected by the external force term in Eq. (23), and the axial deformation is nonzero due to the linear coupling of the chordwise motion as in Eq. (22). Consequently, the axial deformation has smaller vibration amplitude, and approximately resembled appearance when compared to the chordwise motion. The provided time integration solutions are based on the fourth-order Runge–Kutta method, and it is observed that there is a good agreement between the solutions. It should be mentioned that this agreement might deteriorate for the resonant cases as the vibration amplitude is larger and nonlinear terms are stronger.

For the resonant cases, normalized time responses of the system for the chordwise motion are shown in Fig. 7 for different FGM profiles and rotating speed fluctuation functions. In this figure, time integration solutions are also provided to be compared to those of the MMS. For a better comparison, time responses are plotted for a short dimensionless time range. Thus, for more information on the vibration behavior over time, the responses for longer time span are also provided on each plot. The time response of the system under primary resonance is depicted in Fig. 7a, where the rotating speed fluctuation frequency is close to the first natural frequency of the system. In this case, the beam experiences high vibration amplitude containing beating-like behavior even for a low fluctuation amplitude ${\hat{\gamma }}=0.02$. In Figs. 7b and 7c, the rotating axially FG beam is under parametric resonance with two different fluctuation amplitudes, where the rotating speed fluctuation frequency is close to twice the first natural frequency of the system. For the higher value of ${\hat{\gamma }}$, the time response becomes unbounded as the time passes, due to the instability in the contributed vibration mode(s). Moreover, as mentioned above, for the vibration responses with higher amplitudes, the agreement between the results deteriorates due to the approximate nature of the perturbation technique.

Fig. 7

Normalized time response of the rotating axially FG beam at $x=L$ based on MS and numerical solutions for $\mathrm {FGM}_{(a=2/b=2/c=3/p)}$, $\alpha =70$, ${\hat{\lambda }}=10^{-6}$, $\delta =0$, ${\hat{\omega }}_0=10$: a Primary resonance condition with $p=1$, ${\hat{\Omega }}=4\approx {\hat{\omega }}_1^c$, and ${\hat{\gamma }}=0.02$, b Parametric resonance condition with $p=1.4$, ${\hat{\Omega }}=10\approx 2{\hat{\omega }}_1^c$, and ${\hat{\gamma }}=0.02$, and c Parametric resonance condition with $p=1.4$, ${\hat{\Omega }}=10\approx 2{\hat{\omega }}_1^c$, and ${\hat{\gamma }}=0.1$, (black lines: MS solution, and red dotted lines: numerical solution)

Fig. 8

Normalized modal amplitudes of the rotating axially FG beam under primary and internal resonances for different values of volume fraction index, $\mathrm {FGM}_{(a=2/b=2/c=3/p)}$, $\alpha =70$, ${\hat{\lambda }}=0.5\times 10^{-6}$, $\delta =0$, ${\hat{\omega }}_0=10$, ${\hat{\gamma }}=0.1$, and ${\hat{\omega }}_2^c\approx 2{\hat{\omega }}_1^c$: a $p=1.6$, b $p=1.8$, and c $p=2$

Fig. 9

Normalized modal amplitudes of the rotating axially FG beam under primary and internal resonances for different values of damping coefficients and fluctuation amplitudes, $\mathrm {FGM}_{(a=1.8/b=1.8/c=2/p=1)}$, $\alpha =70$, $\delta =0$, ${\hat{\omega }}_0=8$, and ${\hat{\omega }}_2^c\approx 2{\hat{\omega }}_1^c$: a ${\hat{\lambda }}=10^{-7}$, ${\hat{\gamma }}=0.05$, b ${\hat{\lambda }}=10^{-6}$, ${\hat{\gamma }}=0.05$, c ${\hat{\lambda }}=2\times 10^{-6}$, ${\hat{\gamma }}=0.05$, d ${\hat{\lambda }}=10^{-7}$, ${\hat{\gamma }}=0.1$, e ${\hat{\lambda }}=10^{-6}$, ${\hat{\gamma }}=0.1$, and f ${\hat{\lambda }}=2\times 10^{-6}$, ${\hat{\gamma }}=0.1$

5.3 Steady-state response and stability analysis

Generally, the vibration response of the system is in the form of Eqs. (43–44), which includes the contribution of modal amplitudes $A_n$ and forced response amplitudes $\Delta _n$. These amplitudes have an important role in constructing the transient and steady-state response of the system. As discussed in the previous subsection, obtaining the vibration response of the system can reveal different aspects of the dynamic behavior and effects of different system parameters on the vibrations of the rotating beam both in the transient and steady-state time spans. However, obtaining these time responses for different system parameters and long time spans is time-consuming. In addition, the time response does not capture the whole possible steady-state solutions due to the nonlinear nature of the problem. In this regard, studying the steady-state response of the system based on solving the algebraic form of governing equations for modal amplitudes is of high importance. Frequency response curves of the system based on modal amplitudes that are normalized by the thickness of the beam are illustrated in Fig. 8. In this figure, the rotating axially FG beam is under primary resonance and tuned to 2:1 internal resonance between the first and second vibration modes, which respectively correspond to the chordwise and flapwise motions. The frequency response curves are provided for three different values of volume fraction index, respectively, resulting in ${\hat{\omega }}_2^c/2{\hat{\omega }}_1^c$ values of 1.061, 1.003, and 0.958. It is observed that material gradation significantly affects the frequency response. Moreover, the value of modal amplitude $a_2$ is very smaller than $a_1$. It is worth mentioning that the contribution of these modal amplitudes to the vibration response is via functions $\mu _{i,1}A_1$ and $\mu _{i,2}A_2$ to all the generalized coordinate responses, i.e. $\eta _i$’s. It should be noted that this complexity is the result of the gyroscopic nature of the system. To investigate the effect of the damping coefficient and rotating speed fluctuation amplitude on these modal amplitudes, results in Fig. 9 are provided. It can be observed that higher damping reduces the vibration amplitude and damps the hardening and softening branches of the frequency response. However, for higher fluctuation amplitude, the damping effect on the frequency response branches weakens.

Fig. 10

Normalized modal amplitudes of the rotating axially FG beam under primary and internal resonances, with and without Coriolis effects, $\mathrm {FGM}_{(a=2/b=2/c=3/p=1.6)}$, $\alpha =70$, $\delta =0$, ${\hat{\omega }}_0=10$, ${\hat{\lambda }}=10^{-6}$, ${\hat{\gamma }}=0.1$ and ${\hat{\omega }}_2^c\approx 2{\hat{\omega }}_1^c$: a First mode, and b Second mode

Fig. 11

Stability boundary curves of the rotating axially FG beam under parametric resonance for $\mathrm {FGM}_{(a=1.5/b=0.8/c=2/p)}$, $\alpha =70$, and $\delta =0$: a ${\hat{\omega }}_0=10$, $p=1$, b ${\hat{\lambda }}=10^{-7}$, $p=1$, c ${\hat{\omega }}_0=10$, ${\hat{\lambda }}=10^{-7}$, and d ${\hat{\omega }}_0=10$, ${\hat{\lambda }}=10^{-6}$

One of the main purposes of the current work is the inclusion of Coriolis effects in the dynamic modeling of the system. Including these effects in the model results in gyroscopic terms, and necessitates the use of nonlinear analysis for gyroscopic systems, which leads to a complex procedure. According to Eq. (46), the developed analysis is based on two eigenvalues with and without Coriolis effects. These eigenvalues represent the natural frequencies of the system with and without Coriolis effects, i.e. ${\hat{\omega }}^c_n$, and ${\hat{\omega }}_n$, respectively. Hence, for a model that neglects these effects, (i.e. ${\mathbf {G}}={\varvec{0}}$), the current approach cannot be implemented, since the mentioned eigenvalues coincide in that case, and the left-hand side of Eq. (46) is equal to zero. Meaning that the coefficient matrices $\mathbf {[C]}_l$’s cannot be constructed. However, to investigate the effect of neglecting gyroscopic term, $2\omega {\mathbf {G}}$, on the nonlinear dynamics of the system, this term is weakened such that $2\omega {\mathbf {G}} \rightarrow {\mathbf {0}}$. Accordingly, frequency response curves of the system under primary and 2:1 internal resonances, with and without Coriolis effects are obtained and shown in Fig. 10. For the system in this figure, the used system parameters in the presence of gyroscopic term, result in: ${\hat{\omega }}_2^c/2{\hat{\omega }}_1^c = 1.061$, ${\hat{\omega }}^c_1=5.368$, and ${\hat{\omega }}_1=5.459$. However, as the gyroscopic term is weakened, these values are obtained as: ${\hat{\omega }}_2^c/2{\hat{\omega }}_1^c = 1.048$, ${\hat{\omega }}^c_1=5.436$, and ${\hat{\omega }}_1=5.459$. It can be seen from this figure that the frequency response curves are highly affected by Coriolis effects, and the energy transferred to the second mode in the absence of these effects highly decreases.

For the system under parametric resonance, as the rotating speed fluctuation amplitude increases, the time response of the system becomes unbounded and unstable. Accordingly, stability boundary curves of the rotating axially FG beam are shown in Fig. 11 for different values of damping, average rotating speed, and volume fraction index. Figure 11a shows the effect of damping on these curves, it can be seen that as the damping increases, the system becomes unstable at higher fluctuation amplitudes; hence, stability region increases as expected. The effect of average rotating speed on these curves in Fig. 11b also represents the same behavior; as the rotating speed increases the system experiences instability at higher fluctuation amplitudes. Figures 11c and d show the effect of volume fraction index on the stability boundary curves for two different damping coefficient values. It is observed that the effect of FGM profile parameter increases at higher damping coefficient.

Fig. 12

Normalized modal amplitudes of the rotating axially FG beam under parametric and 2:1 internal resonances for $\mathrm {FGM}_{(a=1.8/b=1.8/c=2/p=1)}$, $\alpha =70$, $\delta =0$, ${\hat{\omega }}_0=8$, and ${\hat{\lambda }}=5\times 10^{-7}$: a ${\hat{\gamma }}=0.04$, b ${\hat{\gamma }}=0.043$, c ${\hat{\gamma }}=0.045$, and d ${\hat{\gamma }}=0.1$

Frequency response curves based on modal amplitudes for the system under parametric and 2:1 internal resonances are shown in Fig. 12. In this figure, the axially FG beam has an FGM profile of $\mathrm {FGM}_{(a=1.8/b=1.8/c=2/p=1)}$, rotating with ${\hat{\omega }}_0=8$, and representing ${\hat{\omega }}_2^c/2{\hat{\omega }}_1^c=0.9969$. The results are provided for different values of dimensionless fluctuation amplitudes. For the lowest value of the fluctuation amplitude, Fig. 12a, the stable trivial solution becomes unstable at a frequency ratio of 0.999, where bifurcations of modal amplitudes to nontrivial solutions occur. At this bifurcation point, two stable and one unstable solutions representing softening and hardening behaviors appear. By increasing the frequency ratio to 1.001, the trivial solution regains stability and bifurcations of nontrivial unstable solutions occur. By increasing the fluctuation amplitude in Fig. 12b-d, two obvious phenomena take place. First, additional branches of modal amplitudes for both modes appear on the frequency response plots. These curves are located away from the bifurcation points in the case of ${\hat{\gamma }}=0.043$; however, for ${\hat{\gamma }}=0.045$ and 0.1, they are located between the bifurcation branches. These additional curves are stable for frequency ranges with lower vibration amplitudes, and become unstable as the amplitude increases. The second important phenomenon is that by increasing the fluctuation amplitude, the vibration amplitude increases and as a result the stable regions become narrower. For the case of ${\hat{\gamma }}=0.1$, the stable solutions vanish at the first bifurcation point.

The effect of volume fraction index on the frequency response curves of the system with $\mathrm {FGM}_{(a=1.8/b=1.8/c=2/p)}$, under parametric and 2:1 internal resonances are shown in Fig. 13. By varying the volume fraction index, the frequency range of unstable trivial solution is not affected significantly; however, the aforementioned additional branches move from a higher frequency range to a lower one as p increases.

Fig. 13

Normalized modal amplitudes of the rotating axially FG beam under parametric and 2:1 internal resonances for $\mathrm {FGM}_{(a=2/b=2/c=3/p)}$, $\alpha =70$, $\delta =0$, ${\hat{\omega }}_0=10$, ${\hat{\gamma }}=0.1$, and ${\hat{\lambda }}=5\times 10^{-7}$: a $p=1.7$, b $p=1.8$, and c $p=1.9$

6 Conclusions

In this paper, nonlinear vibration of axially FG beams rotating with time-dependent speed is investigated. The nonlinearity is quadratic and due to coupling between axial, chordwise, and flapwise motions. Multimode discretization based on the spectral Chebyshev approach is performed and the MMS for gyroscopic systems is used to solve the problem. The system is tuned to 2:1 internal resonance via varying FGMs’ properties and average rotating speed. Then, primary and parametric resonances based on time response and steady-state modal amplitudes are investigated. Several conclusions are obtained as follow:

• 1. Rotating FG beam with constant speed experiences static elongation with zero chordwise and flapwise deformations. Periodic disturbance in the rotating speed induces vibrations in the axial and chordwise deformations, while the flapwise deformation is intact. This variation causes parametric excitation in all of the motions, and external excitation in the chordwise motion.

• 2. Including Coriolis effects in the model necessitates the use of nonlinear analysis for gyroscopic systems, which leads to a complex procedure. The analysis is based on two eigenvalues with and without Coriolis effects. These eigenvalues sequentially represent the natural frequencies of the system with and without Coriolis effects. Hence, for a model that neglects these effects, the current approach cannot be implemented, since the mentioned eigenvalues coincide in that case. In other words, the left-hand side of Eq. (46) is equal to zero. However, to investigate the effect of neglecting gyroscopic term on the nonlinear dynamics of the system, this term is weakened such that $2\omega {\mathbf {G}} \rightarrow {\mathbf {0}}$. Accordingly, it is shown that the frequency response curves are highly affected by Coriolis effects, and the energy transferred to the second mode in the absence of these effects highly decreases.

• 3. The natural frequencies of the linear rotating FG beam are obtained with the maximum convergence error of 0.4%. The maximum relative difference to the results of a previous study is also 1%. The commensurable frequencies causing 2:1 internal resonance in the system are found as functions of rotating speed and FGM parameters.

• 4. The implemented approach for nonlinear analysis based on the MMS is verified by comparing the time response of the system to numerical results for different non-resonant and resonant conditions.

• 5. The primary resonance occurs when the rotating speed fluctuation frequency is close to one of the chordwise natural frequencies of the system. The modal amplitudes under such a condition are obtained and investigated in this work. It is shown that the volume fraction index highly affects these frequency response curves. According to [37], for such systems with quadratic nonlinearity, the primary resonance of the second frequency represents saturation phenomenon. However, the important note to mention is that in the current system, the second natural frequency represents flapwise motion, which is not under external excitation. Therefore, the saturation phenomenon is not possible to occur for the current system.

• 6. When the rotating speed fluctuation frequency is close to twice the natural frequency of the system, parametric resonance occurs. Due to the presence of external excitation in the chordwise motion, if the natural frequency represents a chordwise motion, the parametric resonance coincides with the sub-harmonic resonance of the system. Modal amplitude curves for such condition are discussed in this paper and the effect of FGM parameters are studied. One might conclude that in these frequency responses, the bifurcation of stable/unstable curves from points at which the trivial solution loses/regains stability represents the parametric resonance curves. However, the additional branches can be considered as the consequence of sub-harmonic resonance in the system.

• 7. A comprehensive study on the dynamic behavior of the rotating axially FG beam under the effect of the rotating speed fluctuation frequency, damping coefficient, and FGM properties is carried out. Functionally graded materials properties can be considered as important design parameters for desired vibration behavior of rotating beams, due to their significant effect on the frequency response and stability behavior.

Appendices

Appendix A: FGM profiles

Some of FGM profiles used in this research are illustrated via numerical examples in Fig. 14. In this figure variations of the ceramic volume fraction are provided for six sets of a, b, and c parameters as a function of the volume fraction index p. It can be seen that the exploited distribution function can construct symmetric/asymmetric volume fraction variations along the beam.

Fig. 14

Variations of the ceramic volume fraction $V_c$ along the beam for different values of the parameters a, b, c and the volume fraction index p: a $\mathrm {FGM}_{(a=1/b=0.8/c=1/p=0.1k)}$, b $\mathrm {FGM}_{(a=1.5/b=0.8/c=2/p=0.1k)}$, c $\mathrm {FGM}_{(a=1.8/b=1.8/c=2/p=0.1k)}$, d $\mathrm {FGM}_{(a=2/b=2/c=3/p=0.1k)}$, e $\mathrm {FGM}_{(a=1.8/b=1.6/c=5/p=0.1k)}$, and f $\mathrm {FGM}_{(a=4/b=3/c=3/p=2k)}$, for $k=0,1,2,...,50$

Appendix B: Matrix elements

Here, the details of the matrices in Eq. (33) are given:

$$\begin{aligned}&{\mathbf {M}}=\begin{bmatrix} \mathbf {M_{uu}} &{} {\mathbf {0}} &{} {\mathbf {0}}\\ {\mathbf {0}} &{} \mathbf {M_{vv}} &{} {\mathbf {0}}\\ {\mathbf {0}} &{} {\mathbf {0}} &{} \mathbf {M_{ww}}\end{bmatrix},\ {\mathbf {G}}=\begin{bmatrix} {\mathbf {0}} &{} \mathbf {G_{uv}} &{} {\mathbf {0}}\\ \mathbf {G_{vu}} &{} {\mathbf {0}} &{} {\mathbf {0}}\\ {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}}\end{bmatrix},\nonumber \\&{\mathbf {K}}_1=\begin{bmatrix} {\mathbf {K}}_{\mathbf {uu}_1} &{} {\mathbf {0}} &{} {\mathbf {0}}\\ {\mathbf {0}} &{} {\mathbf {K}}_{\mathbf {vv}_1} &{} {\mathbf {0}}\\ {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {K}}_{\mathbf {ww}_1}\end{bmatrix},\nonumber \\&{\mathbf {K}}_2=\begin{bmatrix} {\mathbf {K}}_{\mathbf {uu}_2} &{} {\mathbf {0}} &{} {\mathbf {0}}\\ {\mathbf {0}} &{} {\mathbf {K}}_{\mathbf {vv}_2} &{} {\mathbf {0}}\\ {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {K}}_{\mathbf {ww}_2}\end{bmatrix},\ {\mathbf {K}}_3=\begin{bmatrix} {\mathbf {0}} &{} \mathbf {K_{uv}} &{} {\mathbf {0}}\\ \mathbf {K}_\mathbf{vu} &{} {\mathbf {0}} &{} {\mathbf {0}}\\ {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}}\end{bmatrix},\nonumber \\&{\mathbf {C}}\!=\!\lambda ({\mathbf {K}}_1\!+\!\omega _0^2{\mathbf {K}}_2),\ \mathbf {NL}({\mathbf {q}}_s)\!=\!\begin{Bmatrix} {\mathbf {0}}\\ \mathbf {NL_{v}}\\\mathbf {NL_{w}}\end{Bmatrix},\ {\mathbf {f}}\!=\!\begin{Bmatrix} {\mathbf {0}}\\ \mathbf {f_{v}}\\{\mathbf {0}}\end{Bmatrix} \end{aligned}$$

(B.1)

where the elements are calculated by

$$\begin{aligned}&\mathbf {M_{uu}}=-{\mathbf {K}}_{\mathbf {uu}_2}=A{\mathbf {P}}_1^\mathrm {T}{\mathbf {V}}_1{\mathbf {P}}_1 \end{aligned}$$

(B.2)

$$\begin{aligned}&\mathbf {M_{vv}}=-{\mathbf {K}}_{\mathbf {vv}_2}=A{\mathbf {P}}_2^\mathrm {T} {\mathbf {V}}_1{\mathbf {P}}_2-I_z({\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_1 {\mathbf {Q}}_2{\mathbf {P}}_2\nonumber \\&\quad +{\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_2{\mathbf {Q}}_1 {\mathbf {P}}_2) \end{aligned}$$

(B.3)

$$\begin{aligned}&\mathbf {M_{ww}}=A{\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_1{\mathbf {P}}_3-I_y({\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_1{\mathbf {Q}}_2{\mathbf {P}}_3+{\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_2{\mathbf {Q}}_1{\mathbf {P}}_3) \end{aligned}$$

(B.4)

$$\begin{aligned}&\mathbf {G_{uv}}=\mathbf {K_{uv}}=-A{\mathbf {P}}_1^\mathrm {T}{\mathbf {V}}_1{\mathbf {P}}_2 \end{aligned}$$

(B.5)

$$\begin{aligned}&\mathbf {G_{vu}}=\mathbf {K_{vu}}=A{\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_1{\mathbf {P}}_1 \end{aligned}$$

(B.6)

$$\begin{aligned}&{\mathbf {K}}_{\mathbf {uu}_1}=-A({\mathbf {P}}_1^\mathrm {T}{\mathbf {V}}_3{\mathbf {Q}}_2{\mathbf {P}}_1+{\mathbf {P}}_1^\mathrm {T}{\mathbf {V}}_4{\mathbf {Q}}_1{\mathbf {P}}_1) \end{aligned}$$

(B.7)

$$\begin{aligned}&{\mathbf {K}}_{\mathbf {vv}_1}=I_z({\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_3{\mathbf {Q}}_4{\mathbf {P}}_2+2{\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_4{\mathbf {Q}}_3{\mathbf {P}}_2+{\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_5{\mathbf {Q}}_2{\mathbf {P}}_2)\nonumber \\&\qquad \qquad -A({\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_6{\mathbf {Q}}_2{\mathbf {P}}_2+{\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_7{\mathbf {Q}}_1{\mathbf {P}}_2+{\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_8{\mathbf {Q}}_1{\mathbf {P}}_2) \end{aligned}$$

(B.8)

$$\begin{aligned}&{\mathbf {K}}_{\mathbf {ww}_1}=I_y({\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_3 {\mathbf {Q}}_4{\mathbf {P}}_3+2{\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_4 {\mathbf {Q}}_3{\mathbf {P}}_3+{\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_5 {\mathbf {Q}}_2{\mathbf {P}}_3)\nonumber \\&\qquad -A({\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_6{\mathbf {Q}}_2{\mathbf {P}}_3 +{\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_7{\mathbf {Q}}_1{\mathbf {P}}_3 +{\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_8{\mathbf {Q}}_1{\mathbf {P}}_3)\nonumber \\ \end{aligned}$$

(B.9)

$$\begin{aligned}&{\mathbf {K}}_{\mathbf {ww}_2}=I_y({\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_1 {\mathbf {Q}}_2{\mathbf {P}}_3+{\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_2{\mathbf {Q}}_1 {\mathbf {P}}_3) \end{aligned}$$

(B.10)

$$\begin{aligned}&\mathbf {NL}_{\mathbf {v}}({\mathbf {q}}_s) =-A{\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_3\big [({\mathbf {Q}}_2{\mathbf {P}}_1 {\mathbf {q}}_{d_1})\circ ({\mathbf {Q}}_1{\mathbf {P}}_2{\mathbf {q}}_{d_2})\big ]\nonumber \\&-A{\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_3\big [({\mathbf {Q}}_1{\mathbf {P}}_1 {\mathbf {q}}_{d_1})\circ ({\mathbf {Q}}_2{\mathbf {P}}_2{\mathbf {q}}_{d_2})\big ]\nonumber \\&\qquad \qquad -A{\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_4 \big [({\mathbf {Q}}_1{\mathbf {P}}_1{\mathbf {q}}_{d_1})\circ ({\mathbf {Q}}_1{\mathbf {P}}_2 {\mathbf {q}}_{d_2})\big ] \end{aligned}$$

(B.11)

$$\begin{aligned}&\mathbf {NL}_{\mathbf {w}}({\mathbf {q}}_s)=-A{\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_3 \big [({\mathbf {Q}}_2{\mathbf {P}}_1{\mathbf {q}}_{d_1})\circ ({\mathbf {Q}}_1{\mathbf {P}}_3 {\mathbf {q}}_{d_3})\big ]\nonumber \\&\qquad -A{\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_3 \big [({\mathbf {Q}}_1{\mathbf {P}}_1{\mathbf {q}}_{d_1})\circ ({\mathbf {Q}}_2{\mathbf {P}}_3 {\mathbf {q}}_{d_3})\big ]\nonumber \\&\qquad -A{\mathbf {P}}_3^\mathrm {T}{\mathbf {V}}_4 \big [({\mathbf {Q}}_1{\mathbf {P}}_1{\mathbf {q}}_{d_1})\circ ({\mathbf {Q}}_1{\mathbf {P}}_3 {\mathbf {q}}_{d_3})\big ] \end{aligned}$$

(B.12)

$$\begin{aligned}&\mathbf {f_v}\!=\!(I_z{\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_2\!-\!Ar_h{\mathbf {P}}_2^\mathrm {T} {\mathbf {V}}_1-A{\mathbf {P}}_2^\mathrm {T}{\mathbf {V}}_9){\mathbf {f_I}} \end{aligned}$$

(B.13)

In all the above equations, ${\mathbf {Q}}_i$ is the differentiation matrix representing the ith derivative with respect to $\xi$, $\circ$ symbol shows the element-wise multiplication, ${\mathbf {f_I}}$ is a vector of ones, and weighted inner product matrices are defined by

$$\begin{aligned}&\int _{\xi }\big \{\rho (\xi ),\rho ^\prime (\xi ),E(\xi ),E^\prime (\xi ), E^{\prime \prime }(\xi ),\nonumber \\&\qquad E(\xi )u_s^\prime (\xi ),E(\xi )u_s^{\prime \prime }(\xi ), E^{\prime }(\xi )u_s^{\prime }(\xi ),\nonumber \\&\qquad \rho (\xi )(\xi +u_s(\xi ))\big \}f(\xi )g(\xi )\mathrm {d}\xi \nonumber \\&\quad = {\mathbf {f}}^\mathrm {T}\big \{{\mathbf {V}}_1,{\mathbf {V}}_2,{\mathbf {V}}_3, {\mathbf {V}}_4,{\mathbf {V}}_5,{\mathbf {V}}_6,{\mathbf {V}}_7,{\mathbf {V}}_8, {\mathbf {V}}_9\big \}{\mathbf {g}} \end{aligned}$$

(B.14)

Appendix C: Coefficients $\mu$ and $\Delta$

By inserting solutions (43) and (44) into Eq. (41) for $i=1,2,..N_e-1$, and equating the coefficients of $\exp (I\omega _n^cT_0)$ on both sides of the resulting equations for $n=1,2,...,N_e$, $N_e$ number of linear algebraic systems including $N_e-1$ number of equations are derived as

$$\begin{aligned}&2I\omega _0\sum _{j=1,j\ne i}^{N_e}\omega _n^c{\hat{g}}_{i,j}\mu _{j,n}+(\omega _i^2-{\omega _n^c}^2)\mu _{i,n}=0,\nonumber \\&\quad n = 1,2,...,N_e,\ i =1,2,...,N_e-1 \end{aligned}$$

(C.1)

One should note that according to the assumed solutions $\mu _{1,n} = 1$. Based on the same balancing for coefficients of $\exp (I\Omega T_0)$, we have

$$\begin{aligned}&2I\omega _0\Omega \sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\Delta _j+(\omega _i^2-\Omega ^2)\Delta _i=\frac{\gamma \Omega {\hat{f}}_i}{2},\nonumber \\&\quad i = 1,2,...,N_e \end{aligned}$$

(C.2)

By solving these linear algebraic systems of equations, coefficients $\mu _{i,j}$ and $\Delta _i$ can be determined.

Appendix D: Right-hand side terms

• For non-resonant $\Omega$ without internal resonance:

$$\begin{aligned}&R_{i,l}=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mu _{j,l}\mathrm {D}_1A_l+2I{\omega _l^c}\mu _{i,l}\mathrm {D}_1A_l\nonumber \\&\quad +\lambda I\omega _i^2\omega _l^c\mu _{i,l}A_l,\quad i,l = 1,2,...,N_e \end{aligned}$$

(D.1)

• For non-resonant $\Omega$ with internal resonance ($\omega _m^c = 2\omega _n^c+\epsilon \sigma _0$):

$$\begin{aligned} R_{i,l}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mu _{j,l}\mathrm {D}_1A_l\nonumber \\&\quad +2I{\omega _l^c}\mu _{i,l}\mathrm {D}_1A_l\nonumber \\&\quad +\lambda I\omega _i^2\omega _l^c\mu _{i,l}A_l,\nonumber \\ R_{i,n}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mu _{j,n}\mathrm {D}_1A_n+2I{\omega _n^c}\mu _{i,n}\mathrm {D}_1A_n\nonumber \\&\quad +\lambda I\omega _i^2\omega _n^c\mu _{i,n}A_n\nonumber \\&\quad +\exp (I\sigma _0T_1)\sum _{j=1}^{N_e}\sum _{k=1}^{N_e}{\hat{f}}_{nl_{i,j,k}} {\bar{\mu }}_{k,n}{\bar{A}}_n\mu _{j,m}A_m,\nonumber \\ R_{i,m}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mu _{j,m}\mathrm {D}_1A_m\nonumber \\&\quad +2I{\omega _m^c}\mu _{i,m}\mathrm {D}_1A_m\nonumber \\&\quad +\lambda I\omega _i^2\omega _m^c\mu _{i,m}A_m\nonumber \\&\quad +\exp (-I\sigma _0T_1)\sum _{j=1}^{N_e}\sum _{k=1}^{N_e}{\hat{f}}_{nl_{i,j,k}}\mu _{j,n}\mu _{k,n}A_n^2,\nonumber \\&\quad i,l=1,2,...,N_e,\ l\ne m,n,\ 2\le m\le N_e,\nonumber \\&\quad 1\le n\le N_e-1 \end{aligned}$$

(D.2)

• For case with $\Omega$ near $\omega _n^c$ ($\Omega = \omega _n^c+\epsilon \sigma _1$):

$$\begin{aligned} R_{i,l}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mu _{j,l} \mathrm {D}_1A_l+2I{\omega _l^c}\mu _{i,l}\mathrm {D}_1A_l\nonumber \\&\quad +\lambda I\omega _i^2\omega _l^c\mu _{i,l}A_l,\nonumber \\ R_{n,n}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{n,j}\mu _{j,n}\mathrm {D}_1A_n+2I{\omega _n^c}\mu _{n,n}\mathrm {D}_1A_n\nonumber \\&\quad +\lambda I\omega _n^2\omega _n^c\mu _{n,n}A_n-\exp (I\sigma _1T_1)\frac{\gamma {\hat{f}}_n\Omega }{2},\nonumber \\&i,l=1,2,...,N_e,\ i\ne n,\ 1\le n\le N_e \end{aligned}$$

(D.3)

• For case with $\Omega$ near $\omega _n^c$ and internal resonance ($\Omega = \omega _n^c+\epsilon \sigma _1$, $\omega _m^c = 2\omega _n^c+\epsilon \sigma _0$):

$$\begin{aligned} R_{i,l}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mu _{j,l} \mathrm {D}_1A_l+2I{\omega _l^c}\mu _{i,l}\mathrm {D}_1A_l\nonumber \\&\quad +\lambda I\omega _i^2\omega _l^c\mu _{i,l}A_l,\nonumber \\ R_{i,n}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mu _{j,n}\mathrm {D}_1A_n\nonumber \\&\quad +2I{\omega _n^c}\mu _{i,n}\mathrm {D}_1A_n+\lambda I\omega _i^2\omega _n^c\mu _{i,n}A_n\nonumber \\&+\exp (I\sigma _0T_1)\sum _{j=1}^{N_e}\sum _{k=1}^{N_e}{\hat{f}}_{nl_{i,j,k}}{\bar{\mu }}_{k,n}{\bar{A}}_n\mu _{j,m}A_m,\nonumber \\ R_{n,n}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{n,j}\mu _{j,n}\mathrm {D}_1A_n+2I{\omega _n^c}\mu _{n,n}\mathrm {D}_1A_n\nonumber \\&\quad +\lambda I\omega _n^2\omega _n^c\mu _{n,n}A_n\nonumber \\&\quad +\exp (I\sigma _0T_1)\sum _{j=1}^{N_e}\sum _{k=1}^{N_e}{\hat{f}}_{nl_{n,j,k}}{\bar{\mu }}_{k,n}{\bar{A}}_n\mu _{j,m}A_m\nonumber \\&\quad -\exp (I\sigma _1T_1)\frac{\gamma {\hat{f}}_n\Omega }{2},\nonumber \\ R_{i,m}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mu _{j,m}\mathrm {D}_1A_m\nonumber \\&\quad +2I{\omega _m^c}\mu _{i,m}\mathrm {D}_1A_m+\lambda I\omega _i^2\omega _m^c\mu _{i,m}A_m\nonumber \\&\quad +\exp (-I\sigma _0T_1)\sum _{j=1}^{N_e}\nonumber \\&\quad \sum _{k=1}^{N_e}{\hat{f}}_{nl_{i,j,k}}\mu _{j,n}\mu _{k,n}A_n^2,\nonumber \\&\quad i,l=1,2,...,N_e,\ i\ne n,\ l\ne m,n,\nonumber \\&\quad 2\le m\le N_e,\ 1\le n\le N_e-1 \end{aligned}$$

(D.4)

• For case with $\Omega$ near $2\omega _n^c$ ($\Omega = 2\omega _n^c+\epsilon \sigma _2$):

$$\begin{aligned} R_{i,l}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mu _{j,l}\mathrm {D}_1A_l\nonumber \\&\quad +2I{\omega _l^c}\mu _{i,l}\mathrm {D}_1A_l+\lambda I\omega _i^2\omega _l^c\mu _{i,l}A_l,\nonumber \\ R_{i,n}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mu _{j,n}\mathrm {D}_1A_n\nonumber \\&\quad +2I{\omega _n^c}\mu _{i,n}\mathrm {D}_1A_n+\lambda I\omega _i^2\omega _n^c\mu _{i,n}A_n\nonumber \\&\quad -\exp (I\sigma _2T_1)\bigg (\gamma \omega _n^c\sum _{j=1,j\ne i}^{N_e}\nonumber \\&\quad {\hat{g}}_{i,j}{\bar{\mu }}_{j,n}{\bar{A}}_n+I\gamma \omega _0\sum _{j=1}^{N_e}{\hat{k}}_{2_{i,j}}{\bar{\mu }}_{j,n}{\bar{A}}_n\nonumber \\&-\frac{1}{2}\gamma \Omega \sum _{j=1,j\ne i}^{N_e}{\hat{k}}_{3_{i,j}}{\bar{\mu }}_{j,n}{\bar{A}}_n\nonumber \\&\quad -\sum _{j=1}^{N_e}\sum _{k=1}^{N_e}{\hat{f}}_{nl_{i,j,k}}\Delta _j{\bar{\mu }}_{k,n}{\bar{A}}_n\bigg ),\nonumber \\&\quad i,l=1,2,...,N_e,\ l\ne n,\ 1\le n\le N_e \end{aligned}$$

(D.5)

• For case with $\Omega$ near $2\omega _n^c$ and internal resonance ($\Omega = 2\omega _n^c+\epsilon \sigma _2$, $\omega _m^c = 2\omega _n^c+\epsilon \sigma _0$):

$$\begin{aligned} R_{i,l}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mu _{j,l}\mathrm {D}_1A_l\nonumber \\&\quad +2I{\omega _l^c}\mu _{i,l}\mathrm {D}_1A_l+\lambda I\omega _i^2\omega _l^c\mu _{i,l}A_l,\nonumber \\ R_{i,n}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mu _{j,n}\mathrm {D}_1A_n\nonumber \\&\quad +2I{\omega _n^c}\mu _{i,n}\mathrm {D}_1A_n+\lambda I\omega _i^2\omega _n^c\mu _{i,n}A_n\nonumber \\&\quad -\exp (I\sigma _2T_1)\bigg (\gamma \omega _n^c\nonumber \\&\quad \sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}{\bar{\mu }}_{j,n}{\bar{A}}_n\nonumber \\&\quad +I\gamma \omega _0\sum _{j=1}^{N_e}{\hat{k}}_{2_{i,j}}{\bar{\mu }}_{j,n}{\bar{A}}_n-\frac{1}{2}\gamma \Omega \nonumber \\&\quad \sum _{j=1,j\ne i}^{N_e}{\hat{k}}_{3_{i,j}}{\bar{\mu }}_{j,n}{\bar{A}}_n\nonumber \\&\quad -\sum _{j=1}^{N_e}\sum _{k=1}^{N_e}{\hat{f}}_{nl_{i,j,k}}\Delta _j{\bar{\mu }}_{k,n} {\bar{A}}_n\bigg )\nonumber \\&\quad +\exp (I\sigma _0T_1)\sum _{j=1}^{N_e}\sum _{k=1}^{N_e}{\hat{f}}_{nl_{i,j,k}}{\bar{\mu }}_{k,n}{\bar{A}}_n\mu _{j,m}A_m,\nonumber \\ R_{i,m}&=2\omega _0\sum _{j=1,j\ne i}^{N_e}{\hat{g}}_{i,j}\mu _{j,m}\mathrm {D}_1A_m\nonumber \\&\quad +2I{\omega _m^c}\mu _{i,m}\mathrm {D}_1A_m+\lambda I\omega _i^2\omega _m^c\mu _{i,m}A_m\nonumber \\&\quad +\exp (-I\sigma _0T_1)\sum _{j=1}^{N_e}\nonumber \\&\quad \sum _{k=1}^{N_e}{\hat{f}}_{nl_{i,j,k}}\mu _{j,n}\mu _{k,n}A_n^2,\nonumber \\&\quad i,l=1,2,...,N_e,\ l\ne m,n,\ 2\le m\le N_e,\ \nonumber \\&\quad 1\le n\le N_e-1 \end{aligned}$$

(D.6)

Appendix E: Convergence analysis

To determine the number of polynomials used in the solution technique, a convergence analysis is carried out. In this analysis, the polynomial number is gradually increased, and the predicted natural frequencies are compared with a reference values calculated using a large polynomial number. To quantitatively assess the level of convergence, a relative logarithmic assessment approach given by the following equation is used

$$\begin{aligned} LCV_N = \log \bigg (\frac{1}{K}\sum _{i=1}^K\frac{\big |\omega _{i_N}^c-\omega _{i_{ref}}^c\big |}{\omega _{i_{ref}}^c}\bigg ) \end{aligned}$$

(E.1)

Here, LCV is the logarithmic convergence value, $\omega _{i_N}^c$ refers to the natural frequency of the $i^{th}$ vibration mode calculated using N number of polynomials, $\omega _{i_{ref}}^c$ is the natural frequency of the reference case (obtained using large polynomial numbers), and K shows the number of interested modes. Note that this convergence analysis can be performed for a single mode or several selected modes of the system. To determine the sufficient number of polynomials, $LCV_N<\varepsilon$ should be satisfied (where $\varepsilon$ is the threshold value selected by the user).

Fig. 15

Convergence plots for dimensionless natural frequencies of an axially FG rotating beam based on spectral Chebyshev approach as a function of dimensionless rotating speed for $\delta =0$, ${\hat{\omega }}_0=10$, and $\alpha =70$: a Isotropic material i.e. $p=0$, b $\mathrm {FGM}_{(a=1/b=0.8/c=1/p=0.4)}$, c $\mathrm {FGM}_{(a=1/b=1/c=2/p=1)}$, and d $\mathrm {FGM}_{(a=1.5/b=0.8/c=2/p=1.6)}$

Convergence plots for different volume fraction parameters as a function of dimensionless angular velocity are depicted in Fig. 15. Note that, to present the convergence in terms of contour plots, a linear interpolation is used since LCVs are defined only for integer number of polynomials. In this figure, LC values are obtained as an average of the convergence of the first eight natural frequencies in the system, i.e. $K=8$, and for the reference case, $N=30$ is considered. Each colored contour corresponds to a level of LCV, and the numbers are the corresponding values. According to this figure, the FGM distribution parameters does not affect the convergence behavior; however, as the rotating velocity increases, the number of polynomials necessary to obtain results with the same convergence performance increases. Accordingly, by considering the minimum error threshold to be $0.01\%$ ($LCV = -4$) and maximum value to be $0.4\%$ ($LCV = -2.4$), the number of polynomials is set to 11 shown with red horizontal line.