1 Introduction

Rotating blades are present in many industry applications. The aircraft engine is one of the most important instances. Blade vibration failure due to resonance and flutter occupies a large proportion of the total engine failure. A better understanding of the resonance mechanism and dynamic behavior of rotating blades is helpful to reduce blade vibration failure.

In the early studies [1,2,3,4,5,6] of this field, researchers presented numerous dynamic modeling methodologies of rotating blades and investigated the dynamic characteristics of such structures with only some classical effects taken into consideration in the framework of small-deformation theory. Afterwards, some researchers also paid their attention to some nonclassical effects on the dynamic characteristics of rotating blade. Qin et al. [7] addressed the influence of hygrothermal environment on a rotating composite blade. Liang et al. [8] clarified the contributions of gyroscopic term and dynamic centrifugal terms on a rotating blade. Niu et al. [9] built a dynamic model for a rotating functionally graded cylindrical panel reinforced with graphene platelets (GPLs). Zhang et al. [10] examined the natural frequencies of the rotating blade with different distribution patterns, weight fractions and geometric characteristics of the GPLs. Guo et al. [11] studied the coupling effects among six displacement components based on the Timoshenko beam theory. Xie et al. [12] modeled a rotating blade with a breathing crack.

In reality, the engine blade often serves under the extreme environment. The flow field around the rotating blades is highly unsteady and turbulent. The large amplitude vibration is unavoidable under strong periodic gas flow disturbance [13]. Results and conclusions obtained based on the small-deformation theory seem to be inadequate. Hence, an increasing number of researchers have been focusing their attention on the nonlinear dynamic behavior of such structures nowadays, especially on the internal resonance behavior due to its potential threat to the fatigue life of rotating blades [14]. Li et al. [15] modeled a wind turbine blade considering the geometric nonlinearities and studied the effects of aerodynamic loads on the dynamic characteristics of the blade. Recently, Yao et al. [16] established a dynamic model of a pre-twisted blade based on the shell theory and reported the influences of system parameters on the nonlinear dynamic response of the blade. Thomas et al. [17] studied the nonlinear vibration of a rotating blade considering the large deformation. They reported that rotating speed could affect the hardening/softening behavior and the jumping phenomena. Wang et al. [18] studied the 1:1 internal resonance of a turbine blade considering the fluid-structure interactions. Zhang et al. [19] established a nonlinear dynamic model of rotating pre-twisted blade considering the pre-deformation caused by the thermal gradient. They verified the possibility of the occurrence of 2:1 internal resonance and conducted parameter studies to reveal the nonlinear dynamic behavior of the blade. Zhang et al. [20] explored the second primary resonance of the same blade and presented a saturation phenomenon.

In the above studies, researchers studied the dynamic behavior of rotating blades when primary resonance occurs, that is, the exciting frequency is near one of the natural frequencies of the blade. There exist more complex resonance mechanisms in the nonlinear system. Other exciting frequencies could also result in resonance, such as super-harmonic resonance, subharmonic resonance and combination resonance. Cao et al. [21] constituted the Campbell diagram of a pre-twisted rotating plate to demonstrate the possibility of complex harmonic resonances in such structures when nonlinearities are taken into account. Inoue et al. [22] validated the occurrence of super-harmonic resonance of a wind turbine blade in their experiment. Recently, Zhang et al. [23] studied the super-harmonic resonance of a rotating blade based on the previous dynamic model [19]. Shahgholi et al. [24] utilized the harmonic balance method to address the combination and subharmonic resonances of a rotating shaft. From the literature review, it could be concluded that although the subharmonic resonance [25] and combination resonance [26, 27] have been studied for various structures, the related theoretical analyses of the dynamic responses of pre-deformed rotating blades, especially those subjected to high gas pressure, are rather limited. To close the gap, we consider four cases of resonances, including two subharmonic resonances and two combination resonances, and calculate the corresponding steady-state response of a rotating blade in this study.

2 Equations of Motion and Analytical Solutions

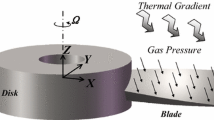
Consider a rotating pre-twisted blade attached to a disk with a certain setting angle, as shown in Fig. 1. The rotating speed of the disk is \(\varOmega \). A strong harmonic gas pressure \(P_\mathrm{gas}\) is acted on the blade. The blade serves in a thermal gradient environment. The notations \(g_{y}\) and \(g_{z}\) denote the thermal gradients in two principle directions, i.e., the width direction and the thickness direction of the blade section, respectively. It must be mentioned that the present load status of the blade is rather idealized, and is a simplification of the real one. In reality, the turbine blade suffers from complex loads, for example, the blade-casing impact and rubbing, the air blast loads, etc. The detailed consideration of the complex loads exerted on the turbine blade exceeds the scope of the present investigation, which, however, is a challenging and rewarding research direction. For details of the force state on blades, readers are referred to [16, 28, 29].

The governing equation of the blade, including the effects of geometric large deformation and the pre-deformation caused by thermal gradient, could be derived via Lagrange principle and modal transformation [20].

$$\begin{aligned} \ddot{{\tilde{{q}}}}_{i} +c_{d} \dot{{\tilde{{q}}}}_{i} +\omega _{i} ^{2}\tilde{{q}}_{i} =\tilde{{f}}_{i} \cos \left( {\omega t} \right) +\sum \limits _{j=1}^{n_{2} +n_{3} } {\sum \limits _{k=1}^{n_{2} +n_{3} } {\eta _{ijk} \tilde{{q}}_{j} \tilde{{q}}_{k} } } +\sum \limits _{j=1}^{n_{2} +n_{3} } {\sum \limits _{k=1}^{n_{2} +n_{3} } {\sum \limits _{l=1}^{n_{2} +n_{3} } {\xi _{ijkl} \tilde{{q}}_{j} \tilde{{q}}_{k} \tilde{{q}}_{l} } } } \quad \left( {i=1,2\ldots ,n_{2} +n_{3} } \right) \end{aligned}$$
(1)

in which, \(\tilde{{q}}_{i} \) and \(\tilde{{f}}_{i} \) denote the system response and the excitation amplitude in modal space, respectively. Here, \(\tilde{{f}}_{i} \) are proportional to the gas pressure amplitude \(P_\mathrm{gas}\). The symbols \(c_{d}\) and \(\omega _{i}\) are the dimensionless damping coefficient and the blade dimensionless natural frequencies, respectively. \(\eta _{ijk}\) are the quadratic nonlinear coefficients introduced by the pre-deformation. \(\xi _{ijkl}\) are the cubic nonlinear coefficients introduced by the large deformation, which is proved to be ignorable, especially in the presence of 2:1 internal resonance in the previous study [20]. \(n_{{2}}\) and \(n_{{3}}\) are the numbers of trial functions assumed chordwise and flapwise, respectively.

Fig. 1
figure 1

The model of a rotating pre-deformed blade subjected to gas pressure

Full size image

The previous studies [19, 20] were confined to the resonance mechanism and dynamic behavior of rotating blade under weak excitation. In the present study, a strong gas pressure is applied to the blade. Hence, the excitation amplitude is assumed to have the same order as the blade response [30]. The vibration response, damping coefficient and gas pressure are rescaled as follows.

$$\begin{aligned} \tilde{{q}}_{i} \leftrightarrow \varepsilon \tilde{{q}}_{i} ,c_{d} \leftrightarrow \varepsilon c_{d} ,\tilde{{f}}_{i} \leftrightarrow \varepsilon \tilde{{f}}_{i} \end{aligned}$$
(2)

where \(\varepsilon \) is a small dimensionless parameter. The solution of the system is assumed to have the following form

$$\begin{aligned} \tilde{{q}}_{i} \left( t \right) =\tilde{{q}}_{i0} \left( {T_{0} ,T_{1} } \right) +\varepsilon \tilde{{q}}_{i1} \left( {T_{0} ,T_{1} } \right) +O\left( {\varepsilon ^{2}} \right) \end{aligned}$$
(3)

in which \(T_{{0}} = t\) and \(T_{{1}} = \varepsilon t\) are the fast and slow time scales, respectively. Then we substitute Eqs. (2) and (3) into Eq.(1) and set the coefficients of each power of \(\varepsilon \) to be zero. The following equations can be obtained.

$$\begin{aligned}&\text {D}_{0}^{2} \tilde{{q}}_{i0} +\omega _{i}^{2} \tilde{{q}}_{i0} =\tilde{{f}}_{i} \cos \left( {\omega T_{0} } \right) \end{aligned}$$
(4)
$$\begin{aligned}&\text {D}_{0}^{2} \tilde{{q}}_{i1} +\omega _{i}^{2} \tilde{{q}}_{i1} =-2\text {D}_{0} \text {D}_{1} \tilde{{q}}_{i0} -c_{d} \text {D}_{0} \tilde{{q}}_{i0} +\sum \limits _{j=1}^{n_{2} +n_{3} } {\sum \limits _{k=1}^{n_{2} +n_{3} } {\eta _{ijk} \tilde{{q}}_{j0} \tilde{{q}}_{k0} } } \end{aligned}$$
(5)

where D\(_{i}\) (\(i =\) 0, 1) represents the derivative operator \(\partial /{\partial T_{i} }\). It should be noted that the derivative operator will also get perturbed after the multiple time scales are introduced. The solution to Eq. (4) holds the following form.

$$\begin{aligned} \tilde{{q}}_{i0} =A_{i} \left( {T_{1} } \right) \text {exp}\left( {\text {i}\omega _{i} T_{0} } \right) +B_{i} \text {exp}\left( {\text {i}\omega T_{0} } \right) +\text {cc} \end{aligned}$$
(6)

which consists of the general solution (i.e. the free vibration component) and the particular solution (i.e. the forced vibration component). \(A_{i}\) and \(B_{i}\) denote the corresponding amplitudes. The symbol cc denotes the complex conjugate of the terms ahead. \(A_{i}\) and \(B_{i}\) can be written as:

$$\begin{aligned} A_{i} \left( {T_{1} } \right) =\frac{a_{i} \left( {T_{1} } \right) }{2}\text {exp}\left( {\text {i}\zeta _{i} \left( {T_{1} } \right) } \right) ,B_{i} =\frac{\tilde{{f}}_{i} }{2\left( {\omega _{i}^{2}-\omega ^{2}} \right) } \end{aligned}$$
(7)

\(A_{i}(T_{{1}})\) is an undetermined complex function of \(T_{{1}}\), while \(B_{i}\) is a real. \(a_{i}\) and \(\zeta _{i}\) stand for the magnitude and phase angle of \(A_{i}(T_{{1}})\), respectively. Substituting Eq. (6) into Eq. (5) yields

$$\begin{aligned} \begin{aligned} \text {D}_{0}^{2} \tilde{{q}}_{i1} +\omega _{i}^{2} \tilde{{q}}_{i1}&=-\text {i}\omega _{i} \left( {2\text {D}_{1} A_{i} +c_{d} A_{i} } \right) \text {exp}\left( {\text {i}\omega _{i} T_{0} } \right) -\text {i}\omega c_{d} B_{i} \text {exp}\left( {\text {i}\omega T_{0} } \right) \\&\quad +\sum \limits _{j=1}^{n_{2} +n_{3} } {\sum \limits _{k=1}^{n_{2} +n_{3} } {\eta _{ijk} } } \left\{ {B_{j} B_{k} \text {exp}\left( {\text {2i}\omega T_{0} } \right) } \right. \\&\quad +A_{j} A_{k} \text {exp}\left( {\text {i}\left( {\omega _{j} +\omega _{k} } \right) T_{0} } \right) +A_{j} \bar{{A}}_{k} \text {exp}\left( {\text {i}\left( {\omega _{j} -\omega _{k} } \right) T_{0} } \right) +A_{j} B_{k} \text {exp}\left( {\text {i}\left( {\omega _{j} +\omega } \right) T_{0} } \right) \\&\quad +\bar{{A}}_{j} B_{k} \text {exp}\left( {\text {i}\left( {\omega -\omega _{j} } \right) T_{0} } \right) \left. {+B_{j} A_{k} \text {exp}\left( {\text {i}\left( {\omega _{k} +\omega } \right) T_{0} } \right) +B_{j} \bar{{A}}_{k} \text {exp}\left( {\text {i}\left( {\omega -\omega _{k} } \right) T_{0} } \right) } \right\} +\text {cc} \\ \end{aligned} \end{aligned}$$
(8)

The possibility of the 2:1 internal resonance, i.e. 2\(\omega _{{1}} \approx \omega _{{2}}\), has been confirmed in the present model [19]. The internal detuning parameter \(\sigma _{{1}}\) is introduced to describe the nearness between \(\omega _{{2}}\) and 2\(\omega _{{1}}\), \(\omega _{{2}} =\) 2\(\omega _{{1}} + \varepsilon \sigma _{{1}}\). Hence, the term\(A_{j} \bar{{A}}_{k} \text {exp}\left( {\text {i}\left( {\omega _{j} -\omega _{k} } \right) T_{0} } \right) \) (\(j = 2, k = 1\)) and the term\(A_{j} A_{k} \text {exp}\left( {\text {i}\left( {\omega _{j} +\omega _{k} } \right) T_{0} } \right) \) (\(j = k =\) 1) will contribute to the secular terms for the first and the second modes, respectively. In the present study, our attention is focused on the cross terms, such as the term \(A_{j} B_{k} \text {exp}\left( {\text {i}\left( {\omega _{j} +\omega } \right) T_{0} } \right) \) and the term \(\bar{{A}}_{j} B_{k} \text {exp}\left( {\text {i}\left( {\omega -\omega _{j} } \right) T_{0} } \right) \). When the excitation frequency \(\omega \) is set as several special values, the cross terms can also contribute to the secular terms.

2.1 The Case of \(\pmb {\omega }\) Being Close to 2\(\pmb {\omega _{{{1}}}}\)

When \(\omega \) is close to 2\(\omega _{{1}}\), the term \(\bar{{A}}_{j} B_{k} \text {exp}\left( {\text {i}\left( {\omega -\omega _{j} } \right) T_{0} } \right) \) (\(j =\) 1, \(k =\) 1 or 2) contributes to the secular terms of the first mode. In addition, the term \(-\text {i}\omega c_{d} B_{i} \exp \left( {\text {i}\omega T_{0} } \right) \) (\(i =\) 1) can also contribute to the secular terms of the second mode due to the presence of the 2:1 internal resonance. In the present case, \(B_{{2}}\) is a small divisor term. This resonance is often defined as the subharmonic resonance of the first mode. The external detuning parameter \(\sigma _{{2}}\) is introduced as \(\omega =\) 2\(\omega _{{1}} + \varepsilon \sigma _{{2}}\). Eliminating the secular terms of the first two modes yields the solvability conditions.

$$\begin{aligned} \begin{aligned} \text {D}_{1} A_{1}&=\varGamma _{11} A_{1} +\varGamma _{12} \bar{{A}}_{1} A_{2} \exp (i\sigma _{1} T_{1} )+\varGamma _{13} \bar{{A}}_{1} \text {exp}\left( {\text {i}\sigma _{2} T_{1} } \right) \\ \text {D}_{1} A_{2}&=\varGamma _{21} A_{2} +\varGamma _{22} A_{1}^{2} \exp (-i\sigma _{1} T_{1} )+\varGamma _{23} \exp (i\left( {\sigma _{2} -\sigma _{1} } \right) T_{1} ) \\ \end{aligned} \end{aligned}$$
(9)

where

$$\begin{aligned} \begin{aligned} \varGamma _{11}&=\varGamma _{21} =-{c_{d} } / 2,\varGamma _{12} ={\left( {\eta _{121} +\eta _{112} } \right) } /{\left( {2\text {i}\omega _{1} } \right) },\varGamma _{22} ={\eta _{211} } / {\left( {2\text {i}\omega _{2} } \right) },\varGamma _{13} ={B_{1} \sum \limits _{k=1}^{n_{2} +n_{3} } {\left( {\eta _{11k} +\eta _{1k1} } \right) } } /{\text {2i}\omega _{1} }, \\ \varGamma _{23}&=-{\omega c_{d} B_{2} } /{2\omega _{2} } \\ \end{aligned} \end{aligned}$$
(10)

Separating the real from the imaginary part on both sides of Eq. (9), one can derive the autonomous modulation equations.

$$\begin{aligned} \begin{aligned} \frac{\text {d}a_{1} }{\text {d}T_{1} }&=\left( {\varGamma _{12}^{R} \cos \psi _{1} -\varGamma _{12}^{I} \sin \psi _{1} } \right) \frac{a_{1} a_{2} }{2}+\left( {\varGamma _{13}^{R} \cos \psi _{2} } {-\varGamma _{13}^{I} \sin \psi _{2} } \right) a_{1} +\varGamma _{11}^{R} a_{1} \\ \frac{\text {d}a_{2} }{\text {d}T_{1} }&=2\left[ {\varGamma _{23}^{R} \cos (\psi _{2} -\psi _{1} )-\varGamma _{23}^{I} \sin (\psi _{2} -\psi _{1} )} \right] +\varGamma _{21}^{R} a_{2} +\left( {\varGamma _{22}^{R} \cos \psi _{1} +\varGamma _{22}^{I} \sin \psi _{1} } \right) \frac{a_{1}^{2} }{2} \\ \frac{\text {d}\psi _{1} }{\text {d}T_{1} }&=\left[ {\varGamma _{23}^{R} \sin (\psi _{2} -\psi _{1} )+\varGamma _{23}^{I} \cos (\psi _{2} -\psi _{1} )} \right] \frac{2}{a_{2} }-\left( {\varGamma _{22}^{R} \sin \psi _{1} -\varGamma _{22}^{I} \cos \psi _{1} } \right) \frac{a_{1}^{2} }{2a_{2} }-\left( {\varGamma _{12}^{R} \sin \psi _{1} } \right. \\&\quad \left. {+\varGamma _{12}^{I} \cos \psi _{1} } \right) a_{2} -2\left( {\varGamma _{13}^{R} \sin \psi _{2} +\varGamma _{13}^{I} \cos \psi _{2} } \right) +\sigma _{1} +\varGamma _{21}^{I} -2\varGamma _{11}^{I} \\ \frac{\text {d}\psi _{2} }{\text {d}T_{1} }&=-\left( {\varGamma _{12}^{R} \sin \psi _{1} +\,\varGamma _{12}^{I} \cos \psi _{1} } \right) a_{2} -2\left( {\varGamma _{13}^{R} \sin \psi _{2} } {+\varGamma _{13}^{I} \cos \psi _{2} } \right) +\sigma _{2} -2\varGamma _{11}^{I} \\ \end{aligned} \end{aligned}$$
(11)

where \(\psi _{{1}}= \sigma _{{1}}T_{{1}}\) – 2\(\zeta _{{1}}+ \zeta _{{2}}\), \(\psi _{{2}} = \sigma _{{2}}T_{{1}}\) – 2\(\zeta _{{1}}\), and the real part and imaginary part of coefficients \(\varGamma _{ij}\) are denoted by superscripts R and I, respectively. Given that the left side of Eq. (11) is equal to 0 in the steady state, the modulation equations lead to a set of nonlinear quaternary algebraic equations. Apparently, the solutions of the algebraic equations include two types: the single-mode solution (\(a_{{1}} =\) 0 and \(a_{{2}} \ne \) 0), and the coupled-mode solution (\(a_{{1}} \ne \) 0 and \(a_{{2}} \ne \) 0). Substituting \(a_{{1}} =\) 0 into the right side of Eq. (11), one can obtain the single-mode solution as follows.

$$\begin{aligned} a_{1l} =0,\;a_{2l} ={2\left| {\varGamma _{23} } \right| } / {\sqrt{\left( {\varGamma _{21}^{{R}} } \right) ^{2}+\left( {\sigma _{2} -\sigma _{1} -\varGamma _{21}^{{I}} } \right) ^{2}} } \end{aligned}$$
(12)

In the present case, it is hard to derive the analytical expressions of the coupled-mode solution. The command “NSolve” in Mathematica is employed to find numerical approximations of the corresponding equations.

In order to determine the stability of these two types of solution, it is convenient to cast the modulation equations into the Cartesian form as follows.

$$\begin{aligned} \begin{aligned} \frac{\text {d}x_{1} }{\text {d}T_{1} }&=\left( {\varGamma _{11}^{R} +\varGamma _{13}^{R} } \right) x_{1} +\left( {\varGamma _{11}^{I} -\varGamma _{13}^{I} } \right) y_{1} -\nu _{1} y_{1} +\frac{1}{2}\varGamma _{12}^{R} \left( {x_{1} x_{2} } {+y_{1} y_{2} } \right) +\frac{1}{2}\varGamma _{12}^{I} \left( {x_{1} y_{2} -x_{2} y_{1} } \right) \\ \frac{\text {d}y_{1} }{\text {d}T_{1} }&=-\left( {\varGamma _{11}^{I} +\varGamma _{13}^{I} } \right) x_{1} +\left( {\varGamma _{11}^{R} -\varGamma _{13}^{R} } \right) y_{1} +\nu _{1} x_{1} -\frac{1}{2}\varGamma _{12}^{I} \left( {x_{1} x_{2} } {+y_{1} y_{2} } \right) +\frac{1}{2}\varGamma _{12}^{R} \left( {x_{1} y_{2} -x_{2} y_{1} } \right) \\ \frac{\text {d}x_{2} }{\text {d}T_{1} }&=\varGamma _{21}^{R} x_{2} +\varGamma _{21}^{I} y_{2} -\nu _{2} y_{2} +\frac{1}{2}\varGamma _{22}^{R} \left( {x_{1} ^{2}-y_{1}^{2}} \right) +\varGamma _{22}^{I} x_{1} y_{1} +2\varGamma _{22}^{R} \\ \frac{\text {d}y_{2} }{\text {d}T_{1} }&=-\varGamma _{21}^{I} x_{2} +\varGamma _{21}^{R} y_{2} +\nu _{2} x_{2} -\frac{1}{2}\varGamma _{22}^{I} \left( {x_{1} ^{2}-y_{1}^{2}} \right) +\varGamma _{22}^{R} x_{1} y_{1} -2\varGamma _{22}^{I} \\ \end{aligned} \end{aligned}$$
(13)

in which \(\nu _{{1}} = \sigma _{{2}}\)/2, \(\nu _{{2}} = \sigma _{{2}}--\sigma _{{1}}\). The eigenvalues of the Jacobian matrix of Eq. (13) are calculated at the steady-state solutions. If there exist positive real parts among the eigenvalues, the corresponding solution is unstable.

Ultimately, the first approximate solutions can be written as

$$\begin{aligned} \begin{aligned} \tilde{{q}}_{1}&=a_{1} \cos \left( {{\omega t} / 2-{\psi _{2} } /2} \right) +2B_{1} \cos \left( {\omega t} \right) +O\left( {\varepsilon ^{2}} \right) \\ \tilde{{q}}_{2}&=a_{2} \cos \left( {\omega t\text {+}\left( {\psi _{1} -\psi _{2} } \right) } \right) +2B_{2} \cos \left( {\omega t} \right) +O\left( {\varepsilon ^{2}} \right) \\ \tilde{{q}}_{i}&=0\quad \left( {i=3,4,\cdots ,n_{2} +n_{3} } \right) \\ \end{aligned} \end{aligned}$$
(14)

2.2 The Case of \(\pmb {\omega } \) Being Close to 2\(\pmb {\omega _{{{2}}}}\)

When \(\omega \) is close to 2\(\omega _{{2}}\), the term \(\bar{{A}}_{j} B_{k} \text {exp}\left( {\text {i}\left( {\omega -\omega _{j} } \right) T_{0} } \right) \) (\(j =\) 2, \(k =\) 1 or 2) contributes to the secular terms of the second mode. This resonance is often defined as the subharmonic resonance of the second mode. The external detuning parameter \(\sigma _{{2}}\) is introduced as \(\omega = 2\omega _{{2}} + \varepsilon \sigma _{{2}}\). After the mathematic manipulations similar to those in subsection 2.1, we can obtain the polar form of modulation equations

$$\begin{aligned} \begin{aligned} \frac{\text {d}a_{1} }{\text {d}T_{1} }&=\varGamma _{11}^{R} a_{1} +\left( {\varGamma _{12}^{R} \cos \psi _{1} -\varGamma _{12}^{I} \sin \psi _{1} } \right) \frac{a_{1} a_{2} }{2} \\ \frac{\text {d}a_{2} }{\text {d}T_{1} }&=\varGamma _{21}^{R} a_{2} +\left( {\varGamma _{22}^{R} \cos \psi _{1} +\varGamma _{22}^{I} \sin \psi _{1} } \right) \frac{a_{1}^{2} }{2}+\left( {\varGamma _{24}^{R} \cos \psi _{2} } {-\varGamma _{24}^{I} \sin \psi _{2} } \right) a_{2} \\ \frac{\text {d}\psi _{1} }{\text {d}T_{1} }&=\sigma _{1} +\varGamma _{21}^{I} -\left( {\varGamma _{22}^{R} \sin \psi _{1} -\varGamma _{22}^{I} \cos \psi _{1} } \right) \frac{a_{1}^{2} }{2a_{2} }+\left( {\varGamma _{24}^{R} \sin \psi _{2} } {+\varGamma _{24}^{I} \cos \psi _{2} } \right) -2\varGamma _{11}^{I} \\&\quad -\left( {\varGamma _{12}^{R} \sin \psi _{1} } {+\varGamma _{12}^{I} \cos \psi _{1} } \right) a_{2} \\ \frac{\text {d}\psi _{2} }{\text {d}T_{1} }&=\sigma _{2} -2\varGamma _{21}^{I} +\left( {\varGamma _{22}^{R} \sin \psi _{1} -\varGamma _{22}^{I} \cos \psi _{1} } \right) \frac{a_{1}^{2}}{a_{2} }-2\left( {\varGamma _{24}^{R} \sin \psi _{2} } {+\varGamma _{24}^{I} \cos \psi _{2} } \right) \\ \end{aligned} \end{aligned}$$
(15)

where

$$\begin{aligned} \psi _{1} =\sigma _{1} T_{1} -2\zeta _{1} +\zeta _{2} ,\psi _{2} =\sigma _{2} T_{1} -2\zeta _{2} ,\varGamma _{24} ={\sum \limits _{k=1}^{n_{2} +n_{3} } {\left( {\eta _{22k} +\eta _{2k2} } \right) } B_{k} } / {2\text {i}\omega _{2} } \end{aligned}$$
(16)

The solutions of the corresponding algebraic equation include two types: the trivial solution (\(a_{{1}} =\) 0 and \(a_{{2}} =\) 0), and the non-trivial solution or coupled-mode solution (\(a_{{1}} \ne \) 0 and \(a_{{2}} \ne \) 0). Eliminating \(\psi _{{1}}\) and \(\psi _{{2}}\), we conclude that the steady-state response of the first mode is the root of the following frequency response equation. Due to the limitation of space, the explicit analytical expressions of \(a_{{1}}\) and \(a_{{2}}\) are not recorded here. Ultimately, the first approximate solutions can be written as

$$\begin{aligned} \begin{aligned} \tilde{{q}}_{1}&=a_{1} \cos \left( {{\omega t} / 4-{\left( {2\psi _{1} +\psi _{2} } \right) } /4} \right) +2B_{1} \cos \left( {\omega t} \right) +O\left( {\varepsilon ^{2}} \right) \\ \tilde{{q}}_{2}&=a_{2} \cos \left( {{\omega t} / 2-{\psi _{2} } /2} \right) +2B_{2} \cos \left( {\omega t} \right) +O\left( {\varepsilon ^{2}} \right) \\ \tilde{{q}}_{i}&=0\quad \left( {i=3,4,\cdots ,n_{2} +n_{3} } \right) \\ \end{aligned} \end{aligned}$$
(17)

2.3 The Case of \(\omega \) Being Close to \(\pmb {\omega _{{{2}}}}\) \(\pmb {+ \omega _{{{1}}}}\)

When \(\omega \) is close to \(\omega _{{2}} + \omega _{{1}}\), the term\(\bar{{A}}_{j} B_{k} \text {exp}\left( {\text {i}\left( {\omega -\omega _{j} } \right) T_{0} } \right) (j =\) 2, \(k =\) 1 or 2) contributes to the secular terms of the first mode, and in the same time, the term \(\bar{{A}}_{j} B_{k} \text {exp}\left( {\text {i}\left( {\omega -\omega _{j} } \right) T_{0}} \right) \)( \(j =\) 1, \(k =\) 1 or 2) contributes to the secular terms of the second mode. This resonance is often defined as the combination resonance of summed type. The external detuning parameter \(\sigma _{{2}}\) is introduced as \(\omega = \omega _{{2}} + \omega _{{1}} + \varepsilon \sigma _{{2}}\). After the mathematical manipulations similar to those in subsection 2.1, we can obtain the polar form of modulation equations.

$$\begin{aligned} \begin{aligned} \frac{\text {d}a_{1} }{\text {d}T_{1} }&=\left( {\varGamma _{12}^{R} \cos \psi _{1} -\varGamma _{12}^{I} \sin \psi _{1} } \right) \frac{a_{1} a_{2} }{2}+\left( {\varGamma _{16}^{R} \cos \psi _{2} } {-\varGamma _{16}^{I} \sin \psi _{2} } \right) a_{2} +\varGamma _{11}^{R} a_{1} \\ \frac{\text {d}a_{2} }{\text {d}T_{1} }&=\left( {\varGamma _{22}^{R} \cos \psi _{1} +\varGamma _{22}^{I} \sin \psi _{1} } \right) \frac{a_{1}^{2} }{2}+\left( {\varGamma _{26}^{R} \cos \psi _{2} } {-\varGamma _{26}^{I} \sin \psi _{2} } \right) a_{1} +\varGamma _{21}^{R} a_{2} \\ \frac{\text {d}\psi _{1} }{\text {d}T_{1} }&=\sigma _{1} +\varGamma _{21}^{I} -2\varGamma _{11}^{I} -\left( {\varGamma _{12}^{R} \sin \psi _{1} +\varGamma _{12}^{I} \cos \psi _{1} } \right) a_{2} +\left( {\varGamma _{26}^{R} \sin \psi _{2} } {+\varGamma _{26}^{I} \cos \psi _{2} } \right) \frac{a_{1} }{a_{2} } \\&\quad -\left( {\varGamma _{16}^{R} \sin \psi _{2} +\varGamma _{16}^{I} \cos \psi _{2} } \right) \frac{2a_{2} }{a_{1} }\;-\left( {\varGamma _{22}^{R} \sin \psi _{1} } {-\varGamma _{22}^{I} \cos \psi _{1} } \right) \frac{a_{1}^{2} }{2a_{2} } \\ \frac{\text {d}\psi _{2} }{\text {d}T_{1} }&=\sigma _{2} -\varGamma _{21}^{I} -\left( {\varGamma _{12}^{R} \sin \psi _{1} +\varGamma _{12}^{I} \cos \psi _{1} } \right) \frac{a_{2} }{2}-\varGamma _{11}^{I} -\left( {\varGamma _{16}^{R} \sin \psi _{2} +\varGamma _{16}^{I} \cos \psi _{2} } \right) \frac{a_{2} }{a_{1} } \\&\quad +\left( {\varGamma _{22}^{R} \sin \psi _{1} } {-\varGamma _{22}^{I} \cos \psi _{1} } \right) \frac{a_{1}^{2}}{2a_{2} }-\left( {\varGamma _{26}^{R} \sin \psi _{2} +\varGamma _{26}^{I} \cos \psi _{2} } \right) \frac{a_{1} }{a_{2} } \\ \end{aligned} \end{aligned}$$
(18)

where

$$\begin{aligned} \psi _{1} =\sigma _{1} T_{1} -\text { }2\zeta _{1} +\zeta _{2} ,\psi _{2} =\sigma _{2} T_{1} -\zeta _{1} -\zeta _{2} ,\varGamma _{16} =\frac{\sum \nolimits _{k=1}^{n_{2} +n_{3} } {\left( {\eta _{12k} +\eta _{1k2} } \right) B_{k} } }{2\text {i}\omega _{1} },\varGamma _{26} =\frac{\sum \nolimits _{k=1}^{n_{2} +n_{3} } {\left( {\eta _{21k} +\eta _{2k1} } \right) B_{k} } }{2\text {i}\omega _{2} } \end{aligned}$$
(19)

The solutions of the corresponding algebraic equation include two types the same as the previous subsection. Ultimately, the first approximate solutions can be written as

$$\begin{aligned} \begin{aligned} \tilde{{q}}_{1}&=a_{1} \cos \left( {\frac{\omega t}{3}-\frac{\psi _{1} +\psi _{2} }{3}} \right) +2B_{1} \cos \left( {\omega t} \right) +O\left( {\varepsilon ^{2}} \right) \\ \tilde{{q}}_{2}&=a_{2} \cos \left( {\frac{2\omega t}{3}+\frac{\psi _{1} -2\psi _{2} }{3}} \right) +2B_{2} \cos \left( {\omega t} \right) +O\left( {\varepsilon ^{2}} \right) \\ \tilde{{q}}_{i}&=0\quad \left( {i=3,4,\ldots ,n_{2} +n_{3} } \right) \\ \end{aligned} \end{aligned}$$
(20)

2.4 The Case of \(\omega \) Being Close to \({\omega _{{{2}}}}\)–\(\omega _{{{1}}}\)

When \(\omega \) is close to \(\omega _{{2}}\)–\(\omega _{{1}}\), the term \(A_{j} B_{k} \text {exp}\left( {\text {i}\left( {\omega _{j} +\omega } \right) T_{0} } \right) \) (\(j =\) 1, \(k =\) 1 or 2) contributes to the secular terms of the second mode. This resonance is often defined as the combination resonance of difference type. The external detuning parameter \(\sigma _{{2}}\) is introduced as \(\omega =\omega _{{2}}--\omega _{{1}} + \varepsilon \sigma _{{2}}\). After the mathematical manipulations similar to those in subsection 2.1, we can obtain the polar form of modulation equations.

$$\begin{aligned} \begin{aligned} \frac{\text {d}a_{1} }{\text {d}T_{1} }&=\varGamma _{11}^{R} a_{1} +\left( {\varGamma _{12}^{R} \cos \psi _{1} -\varGamma _{12}^{I} \sin \psi _{1} } \right) \frac{a_{1} a_{2} }{2}+\left( {\varGamma _{17}^{R} \cos \psi _{2} } {-\varGamma _{17}^{I} \sin \psi _{2} } \right) a_{2} \\&\quad +2\left( {\varGamma _{18}^{R} \cos \left( {\psi _{1} -\psi _{2} } \right) -\varGamma _{18}^{I} \sin \left( {\psi _{1} -\psi _{2} } \right) } \right) \\ \frac{\text {d}a_{2} }{\text {d}T_{1} }&=\varGamma _{21}^{R} a_{2} +\left( {\varGamma _{22}^{R} \cos \psi _{1} +\varGamma _{22}^{I} \sin \psi _{1} } \right) \frac{a_{1}^{2} }{2}+\left( {\varGamma _{27}^{R} \cos \psi _{2} } {+\varGamma _{27}^{I} \sin \psi _{2} } \right) a_{1} \\ \frac{\text {d}\psi _{1} }{\text {d}T_{1} }&=\sigma _{1} +\varGamma _{21}^{I} -2\varGamma _{11}^{I} -\left( {\varGamma _{12}^{R} \sin \psi _{1} +\varGamma _{12}^{I} \cos \psi _{1} } \right) a_{2} -\left( {\varGamma _{17}^{R} \sin \psi _{2} } {+\varGamma _{17}^{I} \cos \psi _{2} } \right) \frac{2a_{2} }{a_{1} }-\left( {\varGamma _{27}^{R} \sin \psi _{2} } \right. \\&\quad \left. {-\varGamma _{27}^{I} \cos \psi _{2} } \right) \frac{a_{1} }{a_{2} }-\left( {\varGamma _{22}^{R} \sin \psi _{1} } {-\varGamma _{22}^{I} \cos \psi _{1} } \right) \frac{a_{1}^{2} }{2a_{2} }-\left( {\varGamma _{18}^{R} \sin \left( {\psi _{1} -\psi _{2} } \right) +\varGamma _{18}^{I} \cos \left( {\psi _{1} -\psi _{2} } \right) } \right) \frac{4}{a_{1} } \\ \frac{\text {d}\psi _{2} }{\text {d}T_{1} }&=\varGamma _{21}^{I} -\varGamma _{11}^{I} -\sigma _{2} -\left( {\varGamma _{12}^{R} \sin \psi _{1} +\varGamma _{12}^{I} \cos \psi _{1} } \right) \frac{a_{2} }{2}-\left( {\varGamma _{18}^{R} \sin \left( {\psi _{1} -\psi _{2} } \right) } {+\varGamma _{18}^{I} \cos \left( {\psi _{1} -\psi _{2} } \right) } \right) \frac{2}{a_{1}} \\&\quad -\left( {\varGamma _{22}^{R} \sin \psi _{1} } {-\varGamma _{22}^{I} \cos \psi _{1} } \right) \frac{a_{1}^{2} }{2a_{2} }-\left( {\varGamma _{27}^{R} \sin \psi _{2} } {-\varGamma _{27}^{I} \cos \psi _{2} } \right) \frac{a_{1} }{a_{2} }-\left( {\varGamma _{17}^{R} \sin \psi _{2} +\varGamma _{17}^{I} \cos \psi _{2} } \right) \frac{a_{2} }{a_{1} } \\ \end{aligned} \end{aligned}$$
(21)

where

$$\begin{aligned} \begin{aligned} \psi _{1}&=\sigma _{1} T_{1} -2\zeta _{1} +\zeta _{2} ,\psi _{2} =-\sigma _{2} T_{1} -\zeta _{1} +\zeta _{2} ,\varGamma _{17} ={\sum \limits _{k=1}^{n_{2} +n_{3} } {\left( {\eta _{12k} +\eta _{1k2} } \right) B_{k} } } / {2\text {i}\omega _{1} } \\ \varGamma _{18}&={\omega c_{d} B_{1} } /{2\omega _{1} },\varGamma _{27} ={\sum \limits _{k=1}^{n_{2} +n_{3} } {\left( {\eta _{21k} +\eta _{2k1} } \right) B_{k} } } /{2\text {i}\omega _{2} } \\ \end{aligned} \end{aligned}$$
(22)

In the present case, it is hard to derive the analytical expressions of the coupled-mode solution due to the same reason as the subharmonic resonance of the first mode. The numerical approximate solution and the corresponding stability of the solutions can be determined following subsection 2.1. Ultimately, the first approximate solutions can be written as

$$\begin{aligned} \begin{aligned} \tilde{{q}}_{1}&=a_{1} \cos \left( {\omega t-\left( {\psi _{1} -\psi _{2} } \right) } \right) +2B_{1} \cos \left( {\omega t} \right) +O\left( {\varepsilon ^{2}} \right) \\ \tilde{{q}}_{2}&=a_{2} \cos \left( {2\omega t-\left( {\psi _{1} -2\psi _{2} } \right) } \right) +2B_{2} \cos \left( {\omega t} \right) +O\left( {\varepsilon ^{2}} \right) \\ \tilde{{q}}_{i}&=0\quad \left( {i=3,4,\cdots ,n_{2} +n_{3} } \right) \\ \end{aligned} \end{aligned}$$
(23)

3 Validation and Perturbation Curves

In this section, the validation of free vibration component (\(a_{{1}}\) and \(a_{{2}})\) is conducted through the 4\(^{\mathrm {th}}\)-order Runge-Kutta method [31] and the frequency response and the force response curves are presented for the aforementioned four resonance cases. The equation of motion is integrated numerically. Only the past-transient motion is picked up to verify the analytical results. In the present study, parameters are chosen following the previous paper [20], namely \(n_{{2}} = n_{{3}} =\) 10, \(\varPsi = 10^{\circ } , \varTheta = 30^{\circ } , \kappa = 0.25, \delta = 0\), \(g_{y} =\) 0, \( g_{z} =\) 0.032, \(\eta =\) 200, \(c_{d} =\) 0.1, and \(\varepsilon =\) 0.01. For the complete 2:1 internal resonance (\(\sigma _{{1}} =\) 0) of this rotating blade, the critical rotating speed is \(\gamma _{\mathrm {in}} =\) 6.5798, and the corresponding first two natural frequencies are \(\omega _{{1}} = 4.4873\) and \(\omega _{{2}} = 8.9746\).

3.1 Subharmonic Resonance of the First Mode

From the first equation in Eq. (14), it is found that the free vibration component of the first mode response, namely the frequency component of \(\omega \)/2, is separated from the forced vibration component, namely the frequency component of \(\omega \). So the free vibration component amplitude \(a_{{1}}\) can be determined directly from the fast Fourier transform (FFT) of the blade response. However, the situation is more complicated for the second mode response. The free vibration component and the forced vibration component share the same frequency \(\omega \). To verify the free vibration component amplitude \(a_{{2}}\), the second equation of Eq. (14) is cast into

$$\begin{aligned} \tilde{{q}}_{2} =Q_{2} \cos \left( {\omega t+\nu _{2} } \right) +O\left( {\varepsilon ^{2}} \right) \end{aligned}$$
(24)

in which \(Q_{{2}}\) and \(\nu _{{2}}\) stand for the magnitude and phase angle of the frequency component of \(\omega \), respectively, and hold the following relationships.

$$\begin{aligned} \begin{aligned} Q_{2}&=\sqrt{a_{2}^{2}+4B_{2}^{2}+4a_{2} B_{2} \cos \left( {\psi _{1} -\psi _{2} } \right) } \\ \cos \nu _{2}&=\frac{a_{2} \cos \left( {\psi _{1} -\psi _{2} } \right) +2B_{2} }{Q_{2} } \\ \end{aligned} \end{aligned}$$
(25)

Eliminating \(\psi _{{1}}\) and \(\psi _{{2}}\) yields

$$\begin{aligned} a_{2} =\sqrt{4B_{2}^{2}+Q_{2}^{2}-4B_{2} Q_{2} \cos \nu _{2} } \end{aligned}$$
(26)

In the equation above, \(B_{{2}}\) is calculated from Eq. (7), \(Q_{{2}}\) and \(\nu _{{2}}\) are determined from the FFT. Eq. (26) can be used to verify the free vibration component amplitude \(a_{{2}}\). The comparison between the frequency responses obtained from theoretical analysis and numerical integrations is displayed in Fig. 2. The solid and dotted lines denote the stable and unstable solutions calculated by the method of multiple scales, respectively. The hollow circles and asterisks denote the results obtained from the numerical integrations of the original system and the modulation equations, respectively. As seen in Fig. 2, the steady solutions seem to be attracted to the single-mode solution near the jumping [32]. The theoretical results are well consistent with the numerical integrations.

Fig. 2
figure 2

The comparison between the frequency responses obtained from theoretical analysis and numerical integrations in the case of subharmonic resonance of the first mode (\(P_\mathrm{gas} = 10^{{-4}})\): a the first mode; b the second mode

Full size image
Fig. 3
figure 3

Parameter study of frequency response curves in the case of subharmonic resonance of the first mode: a, b the influence of thermal gradient; c, d the influence of rotating speed; e, f the influence of damping coefficient; g, h the influence of gas pressure

Full size image

The influences of system parameters on frequency response curves are illustrated in Fig. 3. The response curves tend to bend more to both sides and the peak responses are enlarged with the increase of thermal gradient. Actually, the thermal gradient presents quadratic nonlinearities of the system in some sense. The response curves will tilt to the right with the increase of rotating speed across the internal critical rotating speed \(\gamma _\mathrm{in}\). It has been reported in the literature [17, 19] that the variation in rotating speed will result in the variation in nonlinear hardening/softening behavior of the rotating blade. The jumping phenomena are limited by the damping. With the increase of damping coefficient, the peak responses are reduced and the multi-valued ranges are narrowed. The response curves tend to be flattened for large damping coefficient. However, as expected, the gas pressure seems to have an opposite influence on the response curves. The jumping phenomena become dramatic with the increase of the gas pressure. Both the peak response and the multi-valued ranges are enlarged by the gas pressure. The variation trends of the frequency response curve with parameters in other resonance cases are similar to the present one. Hence, the related results are not displayed herein.

The force response curves of the first and the second modes are plotted together in Fig. 4. A hysteresis phenomenon occurs. The single-mode solution turns unstable when the gas pressure increases beyond the first limit point. Compared with the coupled-mode solution, the single-mode solution of the second mode is quite small and negligible.

Fig. 4
figure 4

The subharmonic force response curves of the first and the second modes in the case of subharmonic resonance of the first mode (\(\sigma _{{1}} =\) 0, \(\sigma _{{2}} =\) 1)

Full size image
Fig. 5
figure 5

The comparison between the frequency responses obtained from theoretical analysis and numerical integrations in the case of subharmonic resonance of the second mode (\(P_\mathrm{gas} =\) 0.5): a the first mode; b the second mode

Full size image
Fig. 6
figure 6

The subharmonic force response curves of the first and the second modes in the case of subharmonic resonance of the second mode (\(\sigma _{{1}} =\) 0, \(\sigma _{{2}} =\) 5)

Full size image

3.2 Subharmonic Resonance of the Second Mode

For the first two modes of response, the free vibration components are separated from the forced vibration components in the case of subharmonic resonance of the second mode. So the free vibration component amplitudes \(a_{{1}}\) and \(a_{{2}}\) can be determined directly from FFT of the blade response. The comparisons between the frequency responses obtained from the theoretical analysis and the numerical integrations are displayed in Fig. 5. The theoretical results agree well with the numerical simulation. The non-trivial solutions of the first two modes are both v-shaped. Both the trivial and non-trivial solutions are unstable near the totally external resonance. In order to present the full view of the dynamic behavior, the gas pressure is set as a quite large value, \(P_\mathrm{gas} =\) 0.5. To a certain extent, this indicates that the subharmonic resonance of the second mode is hard to excite.

The force response curves are plotted in Fig. 6. A saturation phenomenon [33] can be observed. There exist two critical values of gas pressure, \(P_{cr1}\) and \(P_{cr2}\), between which there exist two non-trivial solutions for \(a_{{1}}\) (the lager one is stable) and the second-mode response keeps constant. It seems that the external energy is only imported into the first mode.

3.3 Combination Resonance of Summed Type

The free vibration components are separated from the forced vibration components in the case of combination resonance of summed type. So the free vibration component amplitudes \(a_{{1}}\) and \(a_{{2}}\) can be determined directly from FFT of the blade response. The comparison between the frequency responses obtained from theoretical analysis and numerical integrations is displayed in Fig. 7. It can be found that the non-trivial equilibrium points have strong attraction and several trivial equilibrium points are attracted to the non-trivial ones. The gas pressure here is quite strong as the previous case. The trivial solution is unstable near the total external resonance (\(\sigma _{{2}} =\) 0). There exist certain ranges, in which both the non-trivial and the trivial solutions are unstable and the response will be quasi-periodic motion or chaos.

Fig. 7
figure 7

The comparison between the frequency responses obtained from theoretical analysis and numerical integrations in the case of combination resonance of summed type (\(P_\mathrm{gas} =\) 1): a the first mode; b the second mode

Full size image

Figure 8 shows the force response curves for certain values of \(\sigma _{{2}}\). In the flapwise primary resonance under low gas pressure [20], the second-mode response is independent of gas pressure after saturated. In the present case, after a certain value, the second-mode response changes rather slightly with gas pressure when compared with the first-mode response. The vast majority of the external energy carried in the gas pressure pours into the first mode. A quasi-saturation phenomenon can be found. The prefix “quasi-” is used to emphasize the difference between the present phenomenon and the saturation phenomenon [20]. The quasi-saturation phenomenon can only occur at high gas pressure. The limit value of the second-mode response can be reduced by decreasing the external detuning parameter \(\sigma _{{2}}\). In the design stage of such structure, engineers may utilize the quasi-saturation phenomenon to control the quantity and direction of energy transfer from the gas excitation to the vibration of the blade.

Fig. 8
figure 8

The force response curves of the first and the second modes in the case of combination resonance of summed type (\(\sigma _{{1}} =\) 0): a the first mode; b the second mode

Full size image
Fig. 9
figure 9

The comparison between the frequency responses obtained from theoretical analysis and numerical integrations in the case of combination resonance of difference type (Pgas \(=\) 0.01): a the first mode; b the second mode

Full size image
Fig. 10
figure 10

The force response curves of the first and the second modes in the case of combination resonance of difference type (\(\sigma _{{1}} = 0\)): a the first mode; b the second mode

Full size image

3.4 Combination Resonance of Difference Type

From Eq. (23), it is found that for the second-mode response, the free vibration component is separated from the forced vibration components in the case of combination resonance of difference type. While the free vibration of the first mode share the same frequency with the forced vibration component. Hence, the free vibration component amplitude \(a_{{2}}\) can be determined directly from FFT of the blade response, and \(a_{{1}}\) can be verified following subsection 3.1. The comparison between the frequency responses obtained from theoretical analysis and numerical integrations is displayed in Fig. 9. There exist three solutions in most situations. The minimum changes slightly with the external detuning parameter and approximates to zero solution. Both the maximum and the minimum are stable. The response depends on the initial conditions. The theoretical analysis is in agreement with the numerical integrations.

The force response curves for several different values of \(\sigma _{{2}}\) are presented in Fig. 10. A quasi-saturation phenomenon can be found, which is similar to subsection 3.3.

4 Conclusion

In this paper, we consider four resonance cases of a rotating blade subjected to harmonic gas pressure in the presence of 2:1 internal resonance. The method of multiple scales is applied to obtain the steady-state response. The theoretical results are supported by the numerical simulation. For the case of the subharmonic resonance of the first mode, a hysteresis phenomenon occurs and the single-mode solution of the second mode is negligible when compared with the coupled-mode solution. The quasi-saturation phenomenon of the rotating blade only occurs with high gas pressure. The limit value of the second mode response can be reduced by decreasing the external detuning parameter in the two cases of combination resonance. The dynamic behavior observed is expected to be useful for the design of such structure.