Nonlinear vibration of rotating pre-deformed blade with thermal gradient

Abstract

In this paper, the nonlinear dynamic behavior is investigated for a rotating pre-deformed pre-twisted blade subjected to harmonic gas pressure. The pre-deformation curve produced by thermal gradient is derived. A novel nonlinear vibration system is established by considering the influence of pre-deformation. The combination of the Lagrange principle and the assumed modes method is utilized to obtain the motion equations, and then the equations are transformed into a dimensionless form through introducing a set of dimensionless parameters. For the purpose of ensuring high precision in determination of the internal resonance condition, the equations of motion are discretized by adequate trial functions. An eigenvalue analysis is conducted on the corresponding linear system to obtain the natural frequencies and examine the possibility of the 2:1 internal resonance. The method of multiple scales is developed to solve the resulting multi-degree-of-freedom nonlinear ordinary differential equations. A numerical integration by means of Runge–Kutta is performed to establish the validity of the derived formulations. The evolution of frequency response curves with the rotating speed is observed. The influences of the thermal gradient, gas pressure and damping coefficient on the resonant dynamics of the system are investigated in detail. For the purpose of comparison, another distribution profile of pre-deformation, which is frequently used in previous literature, is also examined. It could be found that not only the amplitude but also the distribution of the initial deflection could influence the steady-state nonlinear response of the pre-deformed blade. A series of interesting nonlinear dynamic phenomena are discovered from the results.

1 Introduction

Blade is a vital component in the turbomachine. It is well known that blades are often exposed under a severe thermal load and periodic gas pressure, especially in the gas turbines. To design such structures properly, we need a better understanding of their dynamic characteristics to avoid some undesirable disasters such as the resonance phenomena.

In the early studies, researchers focused their attention on the linear dynamic characteristics of various rotating blade in order to obtain their natural frequencies and mode shapes during past three decades. An extensive list of the related papers was well reviewed by Rao [1]. Yoo et al. [2] established the model for pre-twisted rotating blades with a concentrated mass and analyzed the vibration characteristics of a rotating blade. Ramesh and Rao [3] extended the Yoo’s modeling method for estimating the natural frequencies of a functionally graded rotating pre-twisted cantilever beam. Piovan and Sampaio [4] made use of the finite-element method and Hamilton’s principle to examine the nonlinear dynamics of the rotating beam made of the functionally graded materials. Banerjee [5–8] applied the dynamic stiffness method combined with the Wittrick and Williams’ algorithm to study the modal characteristics of the rotating tapered Euler–Bernoulli, Timoshenko and Rayleigh beams, respectively. Chu et al. [9] studied the impact of vibration characteristics on a shrouded blade under wake flow excitations. Chiu and Yang [10] revealed the effects of lacing wire on the natural frequencies of shift–disk–blade system.

In recent years, more and more reports on nonlinear behavior of the rotating structures have appeared in the literature. Zhang and Li [11] observed a series of perturbation frequency components in the nonlinear dynamic response of a rotating cracked shaft. Hamdan and Al-Bedoor [12] studied the free vibrations of a rotating beam with nonlinear curvature via a single-degree-of-freedom model by using a time transformation method. Turhan and Bulut [13] investigated the in plane nonlinear bending vibrations of a rotating beam. The integro-partial differential equation was discretized by means of Galerkin’s method. They studied the frequency responses on the single- and two-degree-of-freedom models. Yao et al. [14] adopted the method of multiple scales to study the 1:1 internal resonance of the rotating blade with varying speed. They observed the periodic and chaotic motions in the nonlinear vibrations. In their latter research work [15], the frequency response curves are obtained for the 2:1 internal resonance of rotating blade. In these two helpful works, the authors used only one term of Galerkin truncation for both the flapwise and chordwise vibrations and derived a two-degree-of-freedom nonlinear motion equation. This is a brief way to describe the vibration of the blade. However, this will result in a rough estimation for the equation coefficients and the internal resonance condition. It will be demonstrated latter that the dynamic behavior is very sensitive to the coefficients of governing equation, especially near the internal resonance condition. So it is necessary to discretize the governing equation to a higher-order degree-of-freedom system. In the view of analytical approaches of nonlinear vibration, the two-degree-of-freedom is quite different from the higher-number-degree-of-freedom system. Nayfeh [16] pointed that the solvability condition in the method of multiple scales may cast into different forms, and it can be mathematically proved that the different forms are equivalent only in the two-degree-of-freedom systems. Recently, Chen and Zhang [17] developed a general framework of multiple scales analysis on the nonlinear gyroscopic system for the first time, and they observed that the different forms of the solvability condition for a four-degree-of-freedom system are equivalent when studied the forced vibration of pipes conveying fluid [18, 19]. In the present paper, Chen and Zhang’s general framework is developed to analysis a higher degree-of-freedom vibration system.

In all above valuable studies on rotating blade, the axis of the blade is assumed to be perfectly straight. However, during the operation of the gas turbine, high-temperature-burned gas have impacts directly on the concave airfoil surface of blade; however, the gas temperature near the convex surface is relatively low. Hence, there will exist a great thermal gradient along the blade thickness, and slender blade will be pre-deformed. The pre-deformation due to the dead load, geometric imperfection or environmental factors has been recognized for a long time as having a significant effect on the linear and nonlinear dynamic behavior. The initial deflections are usually of the order of the structure thickness and sometimes even greater. So influence of initial deflections has to be studied within the framework of large deflection theory. Wedel-Heinen [20] proposed a general theory for analysis of the effect of initial geometrical imperfection on natural frequencies of linear elastic beam. Takabatake [21] proposed the conception of pre-deformation induced stiffness matrix in the early 1990s. In his work, the combination of linear small deflection theory and nonlinear large deflection theory is adopted to study the effect of pre-deformation on the natural frequencies of a simply supported beam. Based on Takabatake’s conception, Zhou and Zhu [22] developed a finite-element techniques for beam element subjected to the dead load. Oz et al. [23] considered two types of initial curvature, sinusoidal and parabolic curvatures, and studied the 2:1 internal resonance case of curved shallow beams. Nowadays, Ghayesh and his colleagues [24–28] highlighted the effect of geometrical imperfection on the nonlinear resonant dynamics of microbeam, microplate by the means of the pseudo-arc-length continuation technique. Hence, it is more practical to examine the dynamic characteristics of pre-deformed rotating blade.

The objective of the present paper is to investigate the nonlinear 2:1 internal resonance of a rotating pre-deformed slender blade under harmonic gas pressure. In Sect. 2, the rotating pre-deformed pre-twisted blade model is described and the corresponding nonlinear motion equations are derived. In Sect. 3, the method of multiple scales is developed to solve the multi-degree-of-freedom nonlinear equations. In Sect. 4, convergence test and eigenvalue analysis are conducted on the corresponding linear system to obtain the suitable number of trial functions and to examine the possibility of the 2:1 internal resonance. In Sect. 5, the derived formulations are verified by a numerical integration and a series of parameter studies are performed. Finally, the major conclusions are summarized in Sect. 6.

2 Dynamic modeling

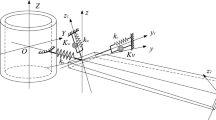
The configuration of the system is illustrated in Fig. 1, showing a rotating pre-twisted slender blade of length L, Young’s modulus E, rectangular cross-sectional area A. The blade is assembled on a rigid hub with a stagger angle. The hub, with radius r, is rotating about its central axis at a constant speed of $\varOmega$. The blade is subjected to a uniform harmonic gas pressure and thermal gradient.

Fig. 1

The sketch of a gas turbine blade

Two types of coordinate system, the global inertial coordinate XYZ and the rotating blade coordinate xyz, are considered (see Fig. 2). Associated with these two coordinate systems xyz and XYZ, we define the unit vectors i, j, k and I, J, K, respectively. The coordinate xyz is attached at the center of root section and rotates with the blade. The axis x is along the centroid axes of the undeformed blade. The axis y is chordwise direction of the rotating blade. The axis z, the flapwise direction, is parallel to the axis Z of the inertial coordinate. The axis $y^{r}$ and $z^{r}$ denote the two principal axes of root section. Similarly, $y^{t}z^{t}$ and $y^{p}z^{p}$ represent those of the tip section and a general section, respectively. An arbitrary point P is placed on the general section. $\varPsi$ denotes the blade stagger angle. The blade presents a twisted shape in its natural state. The pretwist angle between the root section and the general section is $\theta$, which is a function of the total pre-twist angle $\varTheta$ and the position of the section. Due to initial geometric imperfection or environmental factors, the blade is pre-deformed during operation. The amount of axis pre-deformation is $u_{20}$ in chordwise and $u_{30}$ in flapwise direction, respectively. The variables $u_{1}$, $u_{2}$ and $u_{3}$ are employed to describe the axial, chordwise and flapwise deformation components of the blade centroid axis, respectively.

In this study, following assumptions are made to establish the dynamic modal. (1) The Euler–Bernoulli beam theory is employed, and the effects of the shear deformation, the rotary inertia and the warping are not taken into account. (2) The material of the beam is homogeneous and isotropic linear elastic. (3)The variation of pre-twist angle is uniform along the longitudinal axis. (4) The longitudinal component of pre-deformation is ignored.

Fig. 2

The coordinate systems and a general cross section

By considering the initial deflection $u_{20}$ and $u_{30}$, the strain-displacement relation for a pre-deformed beam[20, 23] is extended to describe the three-dimensional vibration. One could obtain the axis strain at an arbitrary point of the blade as

$$\begin{aligned} \varepsilon _{x}= & {} u_{1,x} +\frac{1}{2}u_{2,x}^2 +\frac{1}{2}u_{\mathrm{3,x}}^{2}\nonumber \\&+\,u_{20,x} u_{2,x} +u_{30,x} u_{3,x}-yu_{2,xx}-zu_{3,xx} \end{aligned}$$

(1)

where a comma followed by a subscript denotes the differentiation with respect to the subscript. With the assumption of isotropic linear elastic material, the strain energy of the system can be formulated as

$$\begin{aligned} U_\sigma= & {} \frac{1}{2}\int _V {\sigma _{ij} \varepsilon _{ij}} \hbox {d}V \nonumber \\= & {} \frac{1}{2}\int _{0}^{L} {EI_{3} u_{2,xx}^{2}} \hbox {d}x+\frac{1}{2}\int _{0}^{L} {EI_{2} u_{3,xx}^{2}} \hbox {d}x\nonumber \\&+\,\int _{0}^{L} {EI_{23} u_{2,xx} u_{3,xx}} \hbox {d}x \nonumber \\&+\,EA\int _{0}^{L} \frac{1}{8}u_{2,x}^{4}+\frac{1}{8}u_{3,x}^{4} +\frac{1}{4}u_{2,x}^{2}u_{3,x}^{2}\nonumber \\&+\,\frac{1}{2}u_{20,x} u_{2,x}^{3} +\frac{1}{2}u_{30,x} u_{3,x}^{3} \nonumber \\&+\,\frac{1}{2}u_{1,x} u_{2,x}^{2}+\frac{1}{2}u_{1,x} u_{3,x}^{2}+\frac{1}{2}u_{30,x} u_{2,x}^{2}u_{3,x}\nonumber \\&+\,\frac{1}{2}u_{20,x} u_{2,x} u_{3,x}^{2} \nonumber \\&+\,\frac{1}{2}u_{1,x}^{2}+\frac{1}{2}u_{20,x}^{2}u_{2,x}^{2} +\frac{1}{2}u_{30,x}^{2}u_{3,x}^{2}\nonumber \\&+\,u_{20,x} u_{1,x} u_{2,x} +u_{30,x} u_{1,x} u_{3,x} \nonumber \\&+\,u_{20,x} u_{30,x} u_{2,x} u_{3,x} \;\hbox {d}x \end{aligned}$$

(2)

in which ${\varvec{\sigma }}$ and ${\varvec{\varepsilon }}$ represent the stress and strain tensors, respectively, and

$$\begin{aligned} I_{2} =\int _{{A_{P}}} {z^{2}\hbox {d}A} ,\quad I_{3} =\int _{{A_{P}}} {y^{2}\hbox {d}A} ,\quad I_{23} =\int _{{A_{P}}} {yz\hbox {d}A} \end{aligned}$$

(3)

are the second moments of area and the mixed second moment of area of the general section $A_{P}$ in the rotating frame. They can be calculated with rotation transform matrix as following.

$$\begin{aligned} I_{2} (x)= & {} \frac{I_{2}^{*}+I_{3}^{*}}{2} +\frac{I_{2}^{*}-I_{3}^{*} }{2}\cos \left[ {2(\theta +\varPsi )} \right] \end{aligned}$$

(4)

$$\begin{aligned} I_{3} (x)= & {} \frac{I_{2}^{*}+I_{3}^{*}}{2} -\frac{I_{2}^{*}-I_{3}^{*}}{2} \cos \left[ {2(\theta +\varPsi )} \right] \end{aligned}$$

(5)

$$\begin{aligned} I_{23} (x)= & {} \frac{I_{2}^{*}-I_{3}^{*}}{2}\sin \left[ {2(\theta +\varPsi )} \right] \end{aligned}$$

(6)

in which $I_{2}^{*}$ and $I_{3}^{*}$ are the principal second moments of area for the section. Upon the assumption of linear variation, the pre-twist angle $\theta$ in the equations above could be expressed as:

$$\begin{aligned} \theta =\frac{x}{L}\varTheta \end{aligned}$$

(7)

The axial shortening potential energy due to centrifugal force [29–31] can be written as:

$$\begin{aligned} U_{as}= & {} \frac{1}{2}\int _{0}^{L} \left[ \rho A\varOmega ^{2}\left( {L^{2}-x^{2}} \right) \right. \nonumber \\&\left. -2\rho A\Omega ^{2}r\left( {L-x} \right) \right] \left( {u_{2,x}^{2}+u_{3,x}^{2}} \right) \hbox {d}x \end{aligned}$$

(8)

So the total potential energy is

$$\begin{aligned} U=U_{\sigma } +U_{as} \end{aligned}$$

(9)

The kinetic energy of the rotating blade could be established as [32]

$$\begin{aligned} K= & {} \frac{1}{2}\int _{0}^{L} \rho A\left[ \left( {\dot{u}_{1} -\Omega u_{2} } \right) ^{2}\right. \nonumber \\&\left. +\left( {\dot{u}_{2} +\Omega u_{1} +\left( {r+x} \right) \Omega }\right) ^{2}+\dot{u}_{3}^{2}\right] \hbox {d}x \end{aligned}$$

(10)

The dot represents the differentiation with respect to time t. The external forces acting on the blade consist of harmonic gas pressure and the viscous damping force. In this study, the damping effect results from the interaction between the blade and the surrounding medium (the air). Hence, the damping force is proportional to the three velocity components. The variation of the work done by these external forces can be expressed as:

$$\begin{aligned} \delta W_{e}= & {} \int _{0}^{L} wP_{gas} \cos \left( {\omega t} \right) \left[ \sin \left( {{\varTheta x}/L+\varPsi } \right) \delta u_{2}\right. \nonumber \\&\left. -\cos \left( {{\varTheta x}/L+\varPsi } \right) \delta u_{3} \right] \hbox {d}x \nonumber \\&-\sum _{i=1}^{3} {\int _{0}^{L} {c_{d} \dot{u}_{i} \delta u_{i} \hbox {d}x}} \end{aligned}$$

(11)

where $P_{gas}$ is the gas pressure, w is the width of blade, $\omega$ is the excitation frequency and $c_{d}$ represents the viscous damping coefficient, $-c_{d}\dot{u}_{i} \;\left( {i=1,2,3} \right)$ represent the damping forces on unit length in x, y and z direction, respectively.

The assumed modes method (AMM) is used to discretizing the three displacement components. The displacement functions are separated into products of spatial and temporal functions.

$$\begin{aligned} u_{i} \left( {x,t}\right) =\sum _{j=1}^{{n_{i}}} {\phi _{ij} \left( x \right) q_{ij} \left( t \right) } \end{aligned}$$

(12)

For the displacement component $u_{i}$ ($i=1, 2, 3$), $n_{i}$ is the number of assumed trial functions, $q_{ij}(t)$ is generalized coordinate and $\phi _{ij} \left( x \right)$ is a set of linear independent admissible functions which satisfy the geometric boundary conditions but not necessarily the natural boundary conditions of the system. In the present study, the eigenfunctions of a non-rotating cantilever beam are chosen as the admissible function set.

By rotating coordinates, the curvature functions of uniform beam under thermal gradient [33] is developed to obtain those of a pre-twisted blade subjected to thermal gradients along two principal axes of general section.

$$\begin{aligned} u_{20,xx}= & {} -\alpha g_{y} \cos \left( {{\varTheta x}/L+\varPsi } \right) \nonumber \\&+\,\alpha g_{z} \sin \left( {{\varTheta x}/L+\varPsi } \right) \nonumber \\ u_{30,xx}= & {} -\alpha g_{y} \sin \left( {{\varTheta x}/L+\varPsi } \right) \nonumber \\&-\,\alpha g_{z} \cos \left( {{\varTheta x}/L+\varPsi }\right) \end{aligned}$$

(13)

In these equations, $\alpha$ is the coefficient of thermal expansion, $g_{y}$ and $g_{z}$ are the thermal gradients along two principal axes of a general section. Keep the boundary condition in mind:

$$\begin{aligned} u_{20} \left( 0\right) =u_{30} \left( 0\right) =u_{20,x} \left( 0 \right) =u_{30,x} \left( 0\right) =0 \end{aligned}$$

(14)

One can integrate the curvature equations to obtain the slopes and deflections.

If $\varTheta \ne 0$,

$$\begin{aligned} u_{20,x}= & {} -\left[ g_{y} \sin \left( {{\varTheta x}/L+\varPsi } \right) +g_z \cos \left( {{\varTheta x}/L+\varPsi }\right) \right. \nonumber \\&\left. -\,g_{y} \sin \left( \varPsi \right) -g_{z} \cos \left( \varPsi \right) \right] {L\alpha }/\varTheta \nonumber \\ u_{30,x}= & {} \left[ g_{y} \cos \left( {{\varTheta x}/L+\varPsi } \right) -g_{z} \sin \left( {{\varTheta x}/L+\varPsi } \right) \right. \nonumber \\&\left. +\,g_{z} \sin \left( \varPsi \right) -g_{y} \cos \left( \varPsi \right) \right] {L\alpha }/\varTheta \nonumber \\ u_{20}= & {} -\left[ g_z \sin \left( {{\varTheta x}/L+\varPsi } \right) -g_{y} \cos \left( {{\varTheta x}/L+\varPsi }\right) \right. \nonumber \\&\left. -\,g_{z} \sin \left( \varPsi \right) +g_{y} \cos \left( \varPsi \right) \right] {L^{2}\alpha }/{\varTheta ^{2}} \nonumber \\&+\,\left[ {g_{y} \sin \left( \varPsi \right) x-g_{z} \cos \left( \varPsi \right) x} \right] {L\alpha }/\varTheta \nonumber \\ u_{30}= & {} \left[ g_z \cos \left( {{\varTheta x}/L+\varPsi } \right) +g_{y} \sin \left( {{\varTheta x}/L+\varPsi } \right) \right. \nonumber \\&\left. -\,g_{y} \sin \left( \varPsi \right) -g_{z} \cos \left( \varPsi \right) \right] {L^{2}\alpha }/{\varTheta ^{2}} \nonumber \\&+\,\left[ {g_{z} \sin \left( \varPsi \right) x-g_{y} \cos \left( \varPsi \right) x} \right] {L\alpha }/\varTheta \nonumber \\ \end{aligned}$$

(15)

If $\varTheta = 0$ then,

$$\begin{aligned} u_{20,x}= & {} \alpha \left( {-g_y \cos \left( \varPsi \right) +g_{z} \sin \left( \varPsi \right) } \right) x \nonumber \\ u_{30,x}= & {} -\alpha \left( {g_{y} \sin \left( \varPsi \right) +g_{z} \cos \left( \varPsi \right) } \right) x \nonumber \\ u_{20}= & {} \frac{\alpha }{2}\left( {-g_{y} \cos \left( \varPsi \right) +g_{z} \sin \left( \varPsi \right) } \right) x^{2} \nonumber \\ u_{30}= & {} -\frac{\alpha }{2}\left( {g_{y} \sin \left( \varPsi \right) +g_{z} \cos \left( \varPsi \right) } \right) x^{2} \end{aligned}$$

(16)

To study the influence of the distribution of pre-deformation on the dynamic behavior, another pre-deformation profile is also taken into consideration, which is frequently adopted in the previous literature [20, 24, 26, 27]. The initial deflection is assumed to be of the same shape as the first vibration mode, so

$$\begin{aligned} u_{i0} =d_{0} \phi _{i1} \quad \left( {i=2,3} \right) \end{aligned}$$

(17)

in which $d_{0}$ stands for the amplitude of pre-deformation.

Substitution of Eq. (12) into Eqs. (2), (8), (10) and (11), gives the potential, kinetic energies and external work as functions of the generalized coordinates. These equations are then substituted into the Lagrange equations resulting into a nonlinear coupled ordinary differential equation. For the sake of generality, following dimensionless variables are introduced.

$$\begin{aligned} \bar{{t}}= & {} t\sqrt{\frac{EI_{3}^{*}}{\rho AL^{4}}},\bar{{x}}=\frac{x}{L},\bar{{u}}_{i} =\frac{u_{i}}{L}\;\left( {i=1,2,3} \right) ,\nonumber \\ \bar{{u}}_{i0}= & {} \frac{u_{i0} }{L}\;\left( {i=2,3} \right) , \nonumber \\ \bar{{g}}_{a}= & {} \alpha g_{a} L\;\left( {a=x\;or\;y} \right) ,\bar{{P}}_{gas} =\frac{P_{gas} wL^{3}}{EI_{3}^{*} },\nonumber \\ \bar{{c}}_{d}= & {} \frac{c_d L^{4}}{EI_{3}^{*}}\sqrt{\frac{EI_{3}^{*} }{\rho AL^{4}}}, \nonumber \\ \bar{{\omega }}= & {} \omega \sqrt{\frac{\rho AL^{4}}{EI_{3}^{*}}},\kappa =\left( {\frac{h}{w}} \right) ^{2}=\frac{I_{2}^{*}}{I_{3}^{*}},\eta =\sqrt{\frac{AL^{2}}{I_{3}^{*}}},\nonumber \\ \gamma= & {} \Omega \sqrt{\frac{\rho AL^{4}}{EI_{3}^{*}}}, \nonumber \\ \delta= & {} \frac{r}{L},J_{2} =\frac{I_{2}}{I_{3}^{*}},J_{23} =\frac{I_{23} }{I_{3}^{*}},J_{3} =\frac{I_{3}}{I_{3}^{*}} \end{aligned}$$

(18)

In the following equations of this paper, the overbar notation is disregarded for briefness. After the application of the dimensionless variables, the equation of motion is recast into followings.

$$\begin{aligned}&\sum _{j=1}^{{n_{1}}} {\left( {\int _{0}^{1}{\phi _{1i}\phi _{1j} \hbox {d}x}} \right) \ddot{q}_{1j}}+c_{d} \sum _{j=1}^{{n_{1}}} \left( {\int _{0}^{1} {\phi _{1i} \phi _{1j} \hbox {d}x}}\right) \dot{q}_{1j}\nonumber \\&\quad -\,2\gamma \sum _{j=1}^{{n_{2}}} {\left( {\int _{0}^{1} {\phi _{1i} \phi _{2j} \hbox {d}x}}\right) \dot{q}_{2j}} \nonumber \\&\quad -\,\gamma ^{2}\sum _{j=1}^{{n_{1}}}{\left( {\int _{0}^{1} {\phi _{1i} \phi _{1j} \hbox {d}x}}\right) q_{1j}}\nonumber \\&\quad +\,\eta ^{2}\left[ \sum _{j=1}^{n_{1} }{\left( {\int _{0}^{1}{{\phi }'_{1i}{\phi }'_{1j} \hbox {d}x}} \right) q_{1j}}\right. \nonumber \\&\quad +\,\sum _{j=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{u}'_{20} {\phi }'_{1i} {\phi }'_{2j} \hbox {d}x}} \right) q_{2j}} \nonumber \\&\quad +\,\sum _{j=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{30} {\phi }'_{1i} {\phi }'_{3j} \phi \hbox {d}x}} \right) q_{3j}}\nonumber \\&\quad +\,\frac{1}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{\phi }'_{1i} {\phi }'_{2j} {\phi }'_{2k} \hbox {d}x}} \right) q_{2j} q_{2k} } } \nonumber \\&\left. \quad +\,\frac{1}{2}\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{\phi }'_{1i} {\phi }'_{3j} {\phi }'_{3k} \hbox {d}x} } \right) q_{3j} q_{3k}}}\right] \nonumber \\&\quad =\gamma ^{2}\int _{0}^{1} {\phi _{1i} \left( {\delta +x} \right) \hbox {d}x} ,\quad i=1,2,\ldots ,n_{1} \end{aligned}$$

(19)

$$\begin{aligned}&\sum _{j=1}^{n_2 } {\left( {\int _{0}^{1} {\phi _{2i} \phi _{2j} \hbox {d}x} } \right) \ddot{q}_{2j}}+2\gamma \sum _{j=1}^{{n_{1}}} {\left( {\int _{0}^{1} {\phi _{2i} \phi _{1j} \hbox {d}x}} \right) \dot{q}_{1j} }\nonumber \\&\quad +\,c_{d} \sum _{j=1}^{{n_{2}}} {\left( {\int _{0}^{1} {\phi _{2i} \phi _{2j} \hbox {d}x}} \right) \dot{q}_{2j}} \nonumber \\&\quad +\,\sum _{j=1}^{{n_{2}}} {\left( {\int _{0}^{1} {J_{3} {\phi }''_{2i} {\phi }''_{2j} \hbox {d}x}} \right) q_{2j}}\nonumber \\&\quad +\,\sum _{j=1}^{{n_{3}}} {\left( {\int _{0}^{1} {J_{23} {\phi }''_{2i} {\phi }''_{3j} \hbox {d}x} } \right) q_{3j}}\nonumber \\&\quad -\gamma ^{2}\sum _{j=1}^{{n_{2}}} {\left( {\int _{0}^{1} {\phi _{2i} \phi _{2j} \hbox {d}x} } \right) q_{2j}} \nonumber \\&\quad +\,\frac{1}{2}\gamma ^{2}\sum _{j=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{\phi }'_{2i} {\phi }'_{2j} \left( {1-x^{2}+2\delta -2\delta x} \right) \hbox {d}x} } \right) q_{2j} }\nonumber \\&\quad +\,\eta ^{2}\left[ \sum _{j=1}^{{n_{1}}} {\left( {\int _{0}^{1} {{u}'_{20} {\phi }'_{2i} {\phi }'_{1j} \hbox {d}x} } \right) q_{1j} } \right. \nonumber \\&\quad +\,\sum _{j=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{u}'_{20} {u}'_{20} {\phi }'_{2i} {\phi }'_{2j} \hbox {d}x}} \right) q_{2j}}\nonumber \\&\quad +\,\sum _{j=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{20} {u}'_{30} {\phi }'_{2i} {\phi }'_{3j} \hbox {d}x} } \right) q_{3j} } \nonumber \\&\quad +\,\frac{3}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{u}'_{20} {\phi }'_{2i} {\phi }'_{2j} {\phi }'_{2k} \hbox {d}x} } \right) q_{2j} q_{2k}}}\nonumber \\&\quad +\,\frac{1}{2}\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{20} {\phi }'_{2i} {\phi }'_{3j} {\phi }'_{3k} \hbox {d}x} } \right) q_{3j} q_{3k} } } \nonumber \\&\quad +\,\sum _{j=1}^{{n_{1}}} {\sum _{k=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{\phi }'_{2i} {\phi }'_{1j} {\phi }'_{2k} \hbox {d}x} } \right) q_{1j} q_{2k} } }\nonumber \\&\quad +\,\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{30} {\phi }'_{2i} {\phi }'_{2j} {\phi }'_{3k} \hbox {d}x} } \right) q_{2j} q_{3k} } } \nonumber \\&\quad +\,\frac{1}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\sum _{l=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{\phi }'_{2i} {\phi }'_{2j} {\phi }'_{2k} {\phi }'_{2l} \hbox {d}x} } \right) q_{2j} q_{2k} q_{2l} } } } \nonumber \\&\left. \quad +\,\frac{1}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\sum _{l=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{\phi }'_{2i} {\phi }'_{2j} {\phi }'_{3k} {\phi }'_{3l} \hbox {d}x} } \right) q_{2j} q_{3k} q_{3l} } } } \right] \nonumber \\&\quad =\left( {\int _0^1 {\phi _{2i} P_{gas} \sin \left( {\varTheta x+\varPsi } \right) \hbox {d}x} } \right) \cos \left( {\omega t} \right) ,\nonumber \\&\qquad i=1,2,\ldots ,n_{2} \end{aligned}$$

(20)

$$\begin{aligned}&\sum _{j=1}^{{n_{3}}} {\left( {\int _{0}^{1} {\phi _{3i} \phi _{3j} \hbox {d}x} } \right) \ddot{q}_{3j} } +c_{d} \sum _{j=1}^{{n_{3}}} {\left( {\int _{0}^{1} {\phi _{3i} \phi _{3j} \hbox {d}x} } \right) \dot{q}_{3j}}\nonumber \\&\quad +\,\sum _{j=1}^{{n_{3}}} {\left( {\int _{0}^{1} {J_{2} {\phi }''_{3i} {\phi }''_{3j} \hbox {d}x} } \right) q_{3j} } \nonumber \\&\quad +\,\sum _{j=1}^{n_2 } {\left( {\int _{0}^{1} {J_{23} {\phi }''_{3i} {\phi }''_{2j} \hbox {d}x} } \right) q_{2j}}\nonumber \\&\quad +\,\frac{1}{2}\gamma ^{2}\sum _{j=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{\phi }'_{3i} {\phi }'_{3j} \left( {1-x^{2}+2\delta -2\delta x} \right) \hbox {d}x} } \right) q_{3j} } \nonumber \\&\quad +\,\eta ^{2}\left[ \sum _{j=1}^{n_1 } {\left( {\int _{0}^{1} {{u}'_{30} {\phi }'_{3i} {\phi }'_{1j} \hbox {d}x} } \right) q_{1j} }\right. \nonumber \\&\quad +\,\sum _{j=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{u}'_{20} {u}'_{30} {\phi }'_{3i} {\phi }'_{2j} \hbox {d}x} } \right) q_{2j} }\nonumber \\&\quad +\,\sum _{j=1}^{n_3 } {\left( {\int _{0}^{1} {{u}'_{30} {u}'_{30} {\phi }'_{3i} {\phi }'_{3j} \hbox {d}x} } \right) q_{3j}}\nonumber \\&\quad +\,\frac{1}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{u}'_{30} {\phi }'_{3i} {\phi }'_{2j} {\phi }'_{2k} \hbox {d}x} } \right) q_{2j} q_{2k} } } \nonumber \\&\quad +\,\frac{3}{2}\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{30} {\phi }'_{3i} {\phi }'_{3j} {\phi }'_{3k} \hbox {d}x} } \right) q_{3j} q_{3k} } }\nonumber \\&\quad +\,\sum _{j=1}^{{n_{1}}} {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{\phi }'_{3i} {\phi }'_{1j} {\phi }'_{3k} \hbox {d}x} } \right) q_{1j} q_{3k} } } \nonumber \\&\quad +\,\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{20} {\phi }'_{3i} {\phi }'_{2j} {\phi }'_{3k} \hbox {d}x} } \right) q_{2j} q_{3k} } }\nonumber \\&\quad +\,\frac{1}{2}\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {\sum _{l=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{\phi }'_{3i} {\phi }'_{3j} {\phi }'_{3k} {\phi }'_{3l} \hbox {d}x} } \right) q_{3j} q_{3k} q_{3l} } } } \nonumber \\&\left. \quad +\,\frac{1}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\sum _{l=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{\phi }'_{3i} {\phi }'_{2j} {\phi }'_{2k} {\phi }'_{3l} \hbox {d}x} } \right) q_{2j} q_{2k} q_{3l} } } } \right] \nonumber \\&\quad =\left( {-\int _{0}^{1} {\phi _{3i} P_{gas} \cos \left( {\varTheta x+\varPsi } \right) \hbox {d}x} } \right) \cos \left( {\omega t} \right) ,\nonumber \\&\qquad i=1,2,\ldots ,n_{3} \end{aligned}$$

(21)

The first set governs the longitudinal motion, and the last two sets describe the chordwise and flapwise motion. It is easy to find that the pre-deformation introduces a series of coupling terms and quadratic nonlinearities. If the pre-deformations, $u_{20}$ and $u_{30}$, are set to 0 and other nonlinear terms are dropped, these equations will be reduced to the Yoo’ modal [32]. As Yoo explained, for Euler-Bernoulli beam, the coupling effect between the stretching and the bending motions is negligible, and the first axial natural frequency is far from the bending natural frequencies. So the coupling effects of the longitudinal motion is ignored in the present study. Equations (20) and (21) could be written in matrix form for briefness.

$$\begin{aligned} {{\varvec{M}}}\ddot{{\varvec{q}}}+{{\varvec{C}}}\dot{{{\varvec{q}}}}+{{\varvec{Kq}}}={{\varvec{Q}}} \end{aligned}$$

(22)

In which M, C, K, Q are mass matrix, damping matrix, stiffness matrix and nonlinear load vector. They are listed in Appendix. At this point we have obtained a set of motion equation consisting of $n_{2}+n_{3}$ nonlinear coupled second-order ordinary differential equations.

3 Internal resonance response

In the present study, the method of multiple scales is developed to solve the nonlinear coupled ordinary differential equations (22). To balance the nonlinearity and describe the smallness of vibration amplitude, gas pressure and, following rescaling is introduced.

$$\begin{aligned} {{\varvec{q}}}\leftrightarrow \varepsilon {{\varvec{q}}}, \quad P_{gas} \leftrightarrow \varepsilon ^{2}P_{gas},\quad c_{d} \leftrightarrow \varepsilon c_{d} \end{aligned}$$

(23)

in which $\varepsilon$ is a small dimensionless perturbation parameter. The equation of motion (22) is rearranged and cast into following form.

$$\begin{aligned} {{\varvec{M}}}\ddot{{\varvec{q}}}+{{\varvec{Kq}}}=\varepsilon {\varvec{\lambda }} \left( t,{{\varvec{q}}},\dot{{\varvec{q}}}\right) +{{\varvec{O}}}\left( {\varepsilon ^{2},\varepsilon ^{3},\ldots } \right) \end{aligned}$$

(24)

where O($\varepsilon ^{2}$,$\varepsilon ^{3}$,...) are the higher-order terms, which are omitted in subsequent analysis, the vector ${\varvec{\lambda }}$ is a nonlinear function with respect to t, q and $\dot{{\varvec{q}}}$. The elements in the vector ${\varvec{\lambda }}$ take the form as:

$$\begin{aligned} {\varvec{\lambda }}= & {} \left( {\left[ {\varvec{\lambda }}_{2} \right] ^{\mathrm{T}},\left[ {\varvec{\lambda }}_{3} \right] ^{\mathrm{T}}} \right) ^{\mathrm{T}} \nonumber \\ \lambda _{2i}= & {} f_{2i} \cos \left( {\omega t} \right) +\sum _{j=1}^{{n_{2}}} {\alpha _{ij}^{21} \dot{q}_{2j}} +\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\alpha _{ijk}^{22} q_{2j} q_{2k} } }\nonumber \\&+\sum _{j=1}^{{n_{3}}}{\sum _{k=1}^{{n_{3}}} {\alpha _{ijk}^{23} q_{3j} q_{3k} } } \nonumber \\&+\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{ijk}^{24} q_{2j} q_{3k} }} \nonumber \\ \lambda _{3i}= & {} f_{3i} \cos \left( {\omega t} \right) +\sum _{j=1}^{{n_{3}}} {\alpha _{ij}^{31} \dot{q}_{3j}} +\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\alpha _{ijk}^{32} q_{2j} q_{2k} } }\nonumber \\&+\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_3}} {\alpha _{ijk}^{33} q_{3j} q_{3k} } } \nonumber \\&+\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{ijk}^{34} q_{2j} q_{3k}}} \end{aligned}$$

(25)

The first term represents harmonic gas pressure, the second is damping force, and the others are quadratic nonlinear terms. The coefficients in Eq. (25) are listed in Appendix.

According to multiple scales method, the steady-state solution can be expanded as:

$$\begin{aligned} {{\varvec{q}}}\left( t \right) ={{\varvec{q}}}_{0} \left( {T_{0} ,T_{1}} \right) +\varepsilon {{\varvec{q}}}_{1} \left( {T_{0} ,T_{1} } \right) +{{\varvec{O}}}\left( {\varepsilon ^{2},\varepsilon ^{3},\ldots } \right) \end{aligned}$$

(26)

where $T_{0}=t$ is a fast time scale characterizing motions with frequencies of the linear derived system and $T_{1}=\varepsilon t$ is a slow timescale. Therefore, the time derivatives can be written as follows:

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}= & {} \frac{\partial }{\partial T_{0} }+\varepsilon \frac{\partial }{\partial T_{1}}+\cdots =D_{0} +\varepsilon D_{1} +\cdots \nonumber \\ \frac{\hbox {d}^{\hbox {2}}}{\hbox {d}t^{2}}= & {} \frac{\partial ^{2}}{\partial T_{0}^{2}}+2\varepsilon \frac{\partial ^{2}}{\partial T_{0} \partial T_{1} }+\cdots =D_0^{2}+2\varepsilon D_{0} D_{1} +\cdots \nonumber \\ \end{aligned}$$

(27)

Substituting Eqs. (26) and (27) into Eq. (24) and equating the coefficients of like powers $\varepsilon$ of result in the following equations:

$$\begin{aligned}&{{\varvec{M}}}D_{0}^{2}{{\varvec{q}}}_{{\varvec{0}}} +{{\varvec{Kq}}}_{{\varvec{0}}} ={{\varvec{0}}} \end{aligned}$$

(28)

$$\begin{aligned}&{{\varvec{M}}}D_0^{2}{{\varvec{q}}}_{{{\varvec{1}}}} +{{\varvec{Kq}}}_{{\varvec{1}}} =-2{{\varvec{M}}}D_{0} D_{1} {{\varvec{q}}}_{{\varvec{0}}} +{\varvec{\lambda }}\left( t,{{\varvec{q}}}_{{\varvec{0}}} , D_{0} {{\varvec{q}}}_{{\varvec{0}}} \right) \nonumber \\ \end{aligned}$$

(29)

The solution of Eq. (28) can be assumed as:

$$\begin{aligned} {{\varvec{q}}}_{{\varvec{0}}} \left( {T_{0} ,T_{1}}\right) =\sum _{r=1}^{{n_{2} +n_{3}}} {A_{r} \left( {T_1 } \right) {{\varvec{p}}}_{r} e^{{i\omega _{r} T_{0}}}} +cc \end{aligned}$$

(30)

where $A_{r}$ is a complex function of $T_{1}$, $\omega _{r}$ stands for the $r^{\mathrm{th}}$ natural frequency, ${{\varvec{p}}}_{{\varvec{r}}}$ is the corresponding mode vector and cc represents the complex conjugate of the preceding terms. The complex function $A_{r}$ could also be written in the polar form:

$$\begin{aligned} A_{r} \left( {T_{1}} \right) =\frac{a_{r}\left( {T_{1}} \right) }{2}e^{{i\zeta _{r} \left( {T_{1}} \right) }} \end{aligned}$$

(31)

in which $a_{r}$ and $\zeta _{r}$ are amplitude and phrase angle, respectively, and both of them are real functions of $T_{1}$. Through substituting Eq. (30) into Eq. (29), one could obtain

$$\begin{aligned} {{\varvec{M}}}D_{0}^{2}{{\varvec{q}}}_{{\varvec{1}}} +{{\varvec{Kq}}}_{{\varvec{1}}}= & {} -2{{\varvec{M}}} \sum _{r=1}^{{n_{2} +n_{3}}} {i\omega _{r} D_{1} A_{r} {{\varvec{p}}}_{r} e^{{i\omega _{r} T_{0}}}}\nonumber \\&+\,{\varvec{\lambda }} \left( t,\sum _{r=1}^{{n_{2} +n_{3}}} {A_{r} {{\varvec{p}}}_{r} e^{{i\omega _{r} T_{0}}}} +cc,\right. \nonumber \\&\quad \left. \sum _{r=1}^{{n_{2} +n_{3}}} {i\omega _{r} A_{r} {{\varvec{p}}}_{r} e^{{i\omega _{r} T_{0}}}} +cc \right) +cc\nonumber \\ \end{aligned}$$

(32)

One assumes $\omega _{2} =2\omega _{1} +\varepsilon \sigma _{1} ,\omega =\omega _{1} +\varepsilon \sigma _{2}$ to study the first primary resonance with 2:1 internal resonance. Two detuning parameters, $\sigma _{1}$ and $\sigma _{2}$, are introduced to describe the nearness of the second natural frequency to the two times of the first one and the nearness of the excitation frequency to the first natural frequency, respectively. To separate the secular terms from the right side, Eq. (32) is rearranged and written as:

$$\begin{aligned} {{\varvec{M}}}D_{0}^{2}{{\varvec{q}}}_{{\varvec{1}}} +{{\varvec{Kq}}}_{{\varvec{1}}} =\sum _{r=1}^{{n_{2}+n_{3}}} {{{\varvec{R}}}_{r} e^{{i\omega _{r} T_{0}}}} +NST+cc \end{aligned}$$

(33)

where ${{\varvec{R}}}_{{{\varvec{r}}}}$ is the coefficient vector of the secular term corresponding to $exp(i\omega _{r}T_{0})$, NST stands for the terms that will not results in the secular terms. The secular terms corresponding the first several modes are paid for special attention. For the first mode, the components of vector ${{\varvec{R}}}_{{{\varvec{1}}}}$ share the same pattern as:

$$\begin{aligned} R_{1s}= & {} \beta _{10s} D_{1} A_{1} +\beta _{11s} A_{1} +\beta _{12s} \bar{{A}}_{1} A_{2} e^{{i\sigma _{1} T_{1}}}\nonumber \\&+\,\beta _{13s} e^{{i\sigma _{2} T_{1}}} \end{aligned}$$

(34)

For the second mode:

$$\begin{aligned} R_{2s} =\beta _{20s} D_{1} A_{2} +\beta _{21s} A_{2} +\beta _{22s} A_{1}^{2}e^{{-i\sigma _{1} T_{1}}} \end{aligned}$$

(35)

The nonlinear coupled terms vanish for the third mode, and the components of ${{\varvec{R}}}_\mathbf{3 }$ take the following form:

$$\begin{aligned} R_{3s} =\beta _{30s} D_{1} A_{3} +\beta _{31s} A_{3} \end{aligned}$$

(36)

For the mode $r>$ 3, the pattern of secular term is similar to the case r = 3. The coefficients in Eqs. (34)–(36) are documented in Appendix.

Assume that solution of Eq. (33) has following form:

$$\begin{aligned} {{\varvec{q}}}_{1} \left( {T_{0} ,T_{1}}\right) =\sum _{r=1}^{{n_{2} +n_{3}}} {{{\varvec{P}}}_{r} \left( {T_{1} } \right) e^{{i\omega _{r} T_{0}}}}+cc \end{aligned}$$

(37)

where ${{\varvec{P}}}_{{{\varvec{r}}}}$ is vector function with respect to $T_{1}$. Substitution of Eq. (37) into (33) and then the equalization of each coefficient of term $exp(i\omega _{r}T_{0})$ yield

$$\begin{aligned} \left( -\omega _{r}^{2}{{\varvec{M}}}+{{\varvec{K}}} \right) {{\varvec{P}}}_{{\varvec{r}}} = {{\varvec{R}}}_{{\varvec{r}}} \end{aligned}$$

(38)

which could be regarded as a set of linear algebraic equations with unknown vector ${{\varvec{P}}}_{{\varvec{r}}}$. According to the definition of natural frequency, coefficient determinant of Eq. (38) should be zero. Keep the Cramer’s Rule in mind, to guarantee the existence of solution ${{\varvec{P}}}_{{\varvec{r}}}$, a series of new matrices ${\varvec{\varDelta }}_{{\varvec{rk}}}$ ($k = 1, 2, {\ldots }$, $n_{2}+n_{3})$ must be singular, where the matrix ${\varvec{\varDelta }}_{{\varvec{rk}}}$ is formed from the coefficient matrix of Eq. (38) by replacing column k with the vector ${{\varvec{R}}}_{{\varvec{r}}}$. The solvability conditions are obtained

$$\begin{aligned} \det \left( {{\varvec{\varDelta }}}_{{\varvec{rk}}} \right) =0 \end{aligned}$$

(39)

So one has

$$\begin{aligned} \sum _{s=1}^{{n_{2} +n_{3}}}{\left[ {{{\varvec{Z}}}_{r}^{*}}\right] _{ks} R_{rs} =0} \end{aligned}$$

(40)

in which ${{\varvec{Z}}}_{r}^{*}$ is the adjoint matrix of the coefficient matrix of Eq. (38). As Chen and Zhang commented in Ref. [17], for each k, Eq. (39) yields a solvability condition consisting of a set of ordinary differential equations of $A_{r}(T_{1})$. For the first three modes:

$$\begin{aligned} D_{1} A_{1}= & {} \varGamma _{11} A_{1} +\varGamma _{12} \bar{{A}}_{1} A_{2} e^{{i\sigma _{1} T_{1}}}+\varGamma _{13} e^{{i\sigma _{2} T_{1}}} \end{aligned}$$

(41)

$$\begin{aligned} D_{1} A_{2}= & {} \varGamma _{21} A_{2} +\varGamma _{22} A_{1}^{2}e^{{-i\sigma _{1} T_{1}}} \end{aligned}$$

(42)

$$\begin{aligned} D_{1} A_{3}= & {} \varGamma _{31} A_{3} \end{aligned}$$

(43)

where the coefficients could be calculated from:

$$\begin{aligned} \varGamma _{rj} =-\frac{\sum \limits _{s=1}^{{n_{2} +n_{3}}} {\left[ {{{\varvec{Z}}}_{r}^{*}} \right] _{ks} \beta _{rjs}}}{\sum \limits _{s=1}^{{n_{2} +n_{3}}} {\left[ {\mathbf{Z}_{r}^{*}}\right] _{ks} \beta _{r0s}}} \end{aligned}$$

(44)

From Eq. (43), it is easy to found that the $3^{\mathrm{rd}}$ and higher modes are not coupled with first two modes, and they will decay with time due to the damping. So only the first two modes are paid for special attention. Keep the Eq. (31) in mind, and equalize the real and imaginary part on both sides of the Eqs. (41) and (42), respectively. One obtains

$$\begin{aligned} D_{1} a_{1}= & {} \varGamma _{11}^{R} a_{1} +\frac{1}{2}a_{1} a_{2} \left( {\varGamma _{12}^{R} \cos \psi _{1} -\varGamma _{12}^{I} \sin \psi _{1}} \right) \\&+\,2\left( {\varGamma _{13}^{R} \cos \psi _2 -\varGamma _{13}^{I} \sin \psi _{2}} \right) \end{aligned}$$

$$\begin{aligned} a_{1} a_{2} D_{1} \psi _{1}= & {} a_{1} a_{2} \left( {\sigma _{1} -2\varGamma _{11}^{I}+\varGamma _{21}^{I}} \right) \\&-\,a_{1} a_{2}^{2}\left( {\varGamma _{12}^{R} \sin \psi _{1} +\varGamma _{12}^{I} \cos \psi _{1}} \right) \\&-\,4a_2 \left( {\varGamma _{13}^R \sin \psi _{2} +\varGamma _{13}^{I} \cos \psi _{2} } \right) \\&-\,\frac{1}{2}a_{1}^{3}\left( {\varGamma _{22}^{R} \sin \psi _{1} -\varGamma _{22}^{I} \cos \psi _{1}} \right) \end{aligned}$$

$$\begin{aligned} D_{1} a_{2}= & {} \varGamma _{21}^{R} a_{2} +\frac{1}{2}a_{1}^{2}\left( {\varGamma _{22}^{I} \sin \psi _{1} +\varGamma _{22}^{R} \cos \psi _{1}}\right) \end{aligned}$$

$$\begin{aligned} a_{1} D_{1} \psi _{2}= & {} a_{1} \left( {\sigma _{2} -\varGamma _{11}^{I}} \right) \nonumber \\&-\,\frac{1}{2}a_{1} a_{2} \left( {\varGamma _{12}^{R} \sin \psi _{1} +\varGamma _{12}^{I} \cos \psi _{1}} \right) \nonumber \\&-\,2\left( {\varGamma _{13}^{R} \sin \psi _{2} +\varGamma _{13}^{I} \cos \psi _{2}} \right) \end{aligned}$$

(45)

where $\psi _{1}=\sigma _{1}T_{1}-2\zeta _{1}+\zeta _{2}$, $\psi _{2}= \sigma _{2}T_{1}-\zeta _{1}$, the superscripts R and I represent the real part and the imaginary part, respectively. To study the steady-state response, the fixed points of the autonomous system Eq. (45), the left side of Eq. (45) should be set to 0. After eliminating $\psi _{1}$, $\psi _{2}$ and $a_{2}$, one obtains the frequency–amplitude relationship for the first mode.

$$\begin{aligned} \varLambda _{1} a_{1}^{6}+\varLambda _{2} a_{1}^{4}+\varLambda _{3} a_{1}^{2}+\varLambda _{4}=0 \end{aligned}$$

(46)

in which,

$$\begin{aligned} \varLambda _{1}= & {} \frac{1}{8}\left| {\varGamma _{12} } \right| ^{2}\left| {\varGamma _{22}} \right| ^{2} \nonumber \\ \varLambda _2= & {} \left( \sigma _1 \sigma _2 -2\sigma _2^{2}\right) \left( \varGamma _{12}^I \varGamma _{22}^{I} -\varGamma _{12}^{R} \varGamma _{22}^{R} \right) \nonumber \\&-\,\sigma _1 \left( \varGamma _{11}^{I} \varGamma _{12}^{I} \varGamma _{22}^{I} +\varGamma _{11}^{R} \varGamma _{12}^{R} \varGamma _{22}^{I} +\varGamma _{11}^{R} \varGamma _{12}^{I} \varGamma _{22}^{R} \right. \nonumber \\&\left. -\,\varGamma _{11}^{I} \varGamma _{12}^{R} \varGamma _{22}^{R}\right) +\sigma _{2} (2\varGamma _{11}^{I} \varGamma _{12}^{I} \varGamma _{22}^{I}\nonumber \\&+\,2\varGamma _{11}^{R} \varGamma _{12}^{R} \varGamma _{22}^{I} +\varGamma _{12}^{I} \varGamma _{21}^{I} \varGamma _{22}^{I} +\varGamma _{12}^{R} \varGamma _{21}^{R} \varGamma _{22}^{I} \nonumber \\&+\,2\varGamma _{11}^{R} \varGamma _{12}^{I} \varGamma _{22}^{R}-2\varGamma _{11}^{I} \varGamma _{12}^{R} \varGamma _{22}^{R}-\varGamma _{12}^{R} \varGamma _{21}^{I} \varGamma _{22}^{R}\nonumber \\&+\,\varGamma _{12}^{I} \varGamma _{21}^{R} \varGamma _{22}^{R} )-\varGamma _{11}^{I} (\varGamma _{12}^{I} \varGamma _{21}^I \varGamma _{22}^{I} \nonumber \\&+\,\varGamma _{12}^{R} \varGamma _{21}^R \varGamma _{22}^I -\varGamma _{12}^{R} \varGamma _{21}^{I} \varGamma _{22}^R +\varGamma _{12}^I \varGamma _{21}^{R} \varGamma _{22}^R )\nonumber \\&-\,\varGamma _{11}^R (\varGamma _{12}^R \varGamma _{21}^{I} \varGamma _{22}^I -\varGamma _{12}^I \varGamma _{21}^R \varGamma _{22}^I \nonumber \\&+\,\varGamma _{12}^{I} \varGamma _{21}^I \varGamma _{22}^R +\varGamma _{12}^{R} \varGamma _{21}^R \varGamma _{22}^R ) \nonumber \\ \varLambda _{3}= & {} 2\left( {\left( {\sigma _1 -2\sigma _2 +\varGamma _{21}^{I}} \right) ^{2}+\left( {\varGamma _{21}^R } \right) ^{2}} \right) \left( \left( {\sigma _2 -\varGamma _{11}^I } \right) ^{2}\right. \nonumber \\&\left. +\left( {\varGamma _{11}^R } \right) ^{2} \right) \nonumber \\ \varLambda _4= & {} -8\left| {\varGamma _{13} } \right| ^{2}\left( {\left( {\sigma _1 -2\sigma _2 +\varGamma _{21}^I } \right) ^{2}+\left( {\varGamma _{21}^{R}} \right) ^{2}} \right) \nonumber \\ \end{aligned}$$

(47)

Then the amplitude of second mode can be expressed by $a_{1}$ as following:

$$\begin{aligned} a_{2} =\frac{\left| {\varGamma _{22}} \right| a_1^{2}}{2\sqrt{\left( {\sigma _{1} -2\sigma _2 +\varGamma _{21}^{I}} \right) ^{2}+\left( {\varGamma _{21}^R } \right) ^{2}}} \end{aligned}$$

(48)

Equation (46) could be analytically solved based on the general roots formula for cubic equation. And then $a_{2}$ could be calculated. In addition, the stability of the steady-state response is determined according to Lyapunov theory.

4 Convergence test and eigenvalue analysis

In the numerical investigation of the present study, unless special description, the dimensionless parameters are set as: $\varPsi =10^{\circ }$, $\varTheta = 30^{\circ }$, $\kappa = 0.25$, $\delta = 0$, $g_{y} = 0$, $\eta = 200$, $c_{d} = 0.1$, $P_{gas}= 0.01$, and $\varepsilon = 0.01$.

Table 1 Convergence characteristics for first two natural frequencies and critical rotating speed

Fig. 3

The variation of the first two natural frequencies with thermal gradient along the blade thickness: a non-rotating $\gamma = 0$, b dimensionless rotating speed $\gamma = 5$

In this section, an eigenvalue analysis is conducted on the corresponding linear system of Eq. (24) (Ignoring the nonlinear terms) to obtain the natural frequencies and to examine the possibility of the modal interactions and the internal energy transfer. Firstly, a convergence test is performed for the natural frequencies and the critical rotating speed $\gamma _{in}$ which satisfies the internal resonance condition as shown in Table 1. The same number of trial functions are employed in both the chordwise and flapwise vibrations. The second and third columns of Table 1 are the first two natural frequencies of the given pre-twisted blade with dimensionless rotating speed $\gamma = 5$, and the critical rotating speed for the given blade is listed in last column. As it is seen, when the number of trial functions approaches 10, both the natural frequencies and critical rotating speed show a good convergence. Therefore, the first 10 shape functions are applied in both flapwise and chordwise vibrations to guarantee the accuracy in the further computations, i.e., the vibration system has 20 degree of freedoms.

Figure 3 displays the variation of the first two natural frequencies with thermal gradient $g_{z}$. To identify the possibility of the internal resonant, the curve of $2\omega _{1}$ is also plotted in the figure. It could be observed that for a wide range of thermal gradient, the second natural frequency increases with $g_{z}$ more quickly than the first one. And there is an intersection between the curves for $\omega _{2}$ and $2\omega _{1}$. For the non-rotating blade (Fig. 3a), the influence of thermal gradient $g_{z}$ on the first natural frequency seems to disappear for higher thermal gradient range (when thermal gradient $g_{z}$ is greater than 0.02). With the variation of the thermal gradient, a weak veering phenomenon occurs between the first two natural frequency curves in the range of [0.01, 0.02]. For the case of $\gamma$ = 5 (Fig. 3b), the veering phenomenon disappears and the effect of thermal gradient on the first natural frequency is even more invisible.

Fig. 4

The variation of the first two natural frequencies with rotating speed: a without thermal gradient $g_{z} = 0$, b $g_{z} =0.032$

Fig. 5

Frequency–response curves of the rotating blade for $g_{z} = 0.0365$ and $\gamma = 5$: a the first mode response, b the second mode response

The variation of the first two natural frequencies with rotating speed is shown in Fig. 4. Without the thermal gradient, the increasing rate of the second natural frequency is lower than that of the first one for lower rotating speed. However, the scenario reverses for higher rotating speed. An obvious veering phenomenon in natural frequency curves with the growth of rotating speed could be found (Fig. 4a), and this phenomenon is weakened as the increase in thermal gradient (Fig. 4b). The detailed discussion on the veering phenomena is beyond the scope of the present study. The second natural frequency is close to 2 $\omega _{1}$ for a wide range of rotating speed when the thermal gradient is set to 0.032 (Fig. 4b). It should be remarked that for the given parameters the second natural frequency of the non-rotating blade is just twice the first one. We won’t intend to pay any further attention to this case in this study. The pentagrams in Figs. 3 and 4 indicate that the 2:1 internal resonant $(\varepsilon \sigma _{1}= 0)$ would occur when the parameters are set properly. In the following numerical calculations, the nonlinear vibration behavior is investigated in a small range in vicinity of the 2:1 the internal resonant cases.

5 Numerical results and discussion

From Eqs. (46) and (48), the steady-state amplitudes $a_{1}$ and $a_{2}$ could be solved. Obviously, they are the functions of the coefficients $\varGamma _{rj}$ which are dependent on which solvability condition (the subscript k in Eq. (44)) is applied. So firstly, the solutions obtained with different solvability conditions are examined.

Figure 5 shows the frequency–response curves constructed with some different solvability conditions for the case of the intersection in Fig. 3b ($g_{z} = 0.0365$). For the purpose of briefness, the subscript k in Eq. (44) is only set to some representative values of k. And for other k’s, the results coincide with the present curves. In these figures and the followings, the solid line represents the stable solutions and the dashed line represents the unstable ones. As shown in Fig. 5, different solvability conditions result in a same steady-state response. With the increase and decrease of gas pressure frequency, the jumping phenomena occurs two times. There are two peaks bending to the opposite directions in the frequency–response curves. And the curves are symmetrical about $\varepsilon \sigma _{2}$ = 0.

Fig. 6

The evolution of frequency response with the varying of rotating speed: a1, a2 the first and second mode responses for rotating speed $\gamma = 0.97\gamma _{in}$ ($\varepsilon \sigma _{1}= -0.0508$); b1, b2 those for $\gamma = 0.99\gamma _{in}$ ($\varepsilon \sigma _{1}= -0.0173)$; c1, c2 those for $\gamma =\gamma _{in}$ ($\varepsilon \sigma _{1}= 0$); d1, d2 those for $\gamma = 1.01\gamma _{in}$ ($\varepsilon \sigma _{1}= 0.0176$); e1, e2 those for $\gamma = 1.03\gamma _{in}$ ($\varepsilon \sigma _{1}= 0.0540$)

Fig. 7

The variation of frequency–response curves at inertial resonant with thermal gradient: a the first mode response, b the second mode response

Fig. 8

The variation of frequency–response curves at inertial resonant with pre-deformation amplitude: a the first mode response, b the second mode response

Fig. 9

The variation of frequency–response curves at inertial resonant with gas pressure for $g_{z} = 0.032$: a the first mode response, b the second mode response

Fig. 10

The variation of frequency–response curves at inertial resonant with damping coefficients for $g_{z} = 0.032$: a the first mode response, b the second mode response

Fig. 11

Force–response curves of the rotating blade for different external resonance detuning parameters $\sigma _{2}$: a1, a2 the first and second mode responses for internal resonance detuning parameter $\sigma _{1}=-3$; b1, b2 those for internal resonance detuning parameter $\sigma _{1}=3$

To verify the derived formulations, the rearranged equation of motion Eq. 24, is integrated numerically with the variable-step Runge–Kutta method. It’s worth mentioning that the higher-order term is omitted in both numerical and analytical method for the purpose of comparability. Introducing the general velocity variable vector to Eq. 24 through

$$\begin{aligned} {{\varvec{v}}}=\dot{{\varvec{q}}} \end{aligned}$$

(49)

results in:

$$\begin{aligned} \dot{{\varvec{v}}}=-{{\varvec{M}}}^{-1}{{\varvec{Kq}}}+\varepsilon {{\varvec{M}}}^{-1} {\varvec{\lambda }}\left( {t,{{\varvec{q}}},{{\varvec{v}}}} \right) \end{aligned}$$

(50)

The Eq. (49) combined with Eq. (50) represents a set of first-order nonlinear ordinary differential equations of degree $2(n_{2}+n_{3})$. This set of equations is integrated numerically with zero initial condition, i.e., $\dot{{\varvec{v}}}={{\varvec{v}}}=\dot{{{\varvec{q}}}}={{\varvec{q}}}={{\varvec{0}}}$. The frequency of the gas pressure traverses from a set of given values near the first natural frequency. Other parameters are set as those used in analytical method. The simulation is conducted for adequately long time to make sure the initial effects can be attenuated and the system is running under steady state. The response amplitude is calculated as the half of the difference between the maximum and minimum displacement in steady-state response [34]. A program is written to implement this process in Matlab platform. Please note that only the stable solutions of periodic motion could be obtained by numeric simulation.

The evolution of frequency response with the varying of the rotating speed nearby the 2:1 internal resonant (for case of the intersection in Fig. 4b) is illustrated in Fig. 6, in which the hollow triangles represent the solutions obtained by numerical integration and the lines represent those furnished by method of multi-scale (MMS). For the parameters of Fig. 4b, the 2:1 internal resonant occurs at the critical rotating speed of $\gamma _{in} = 6.5840$. Here, the rotating speed is set to $0.97 \gamma _{in}$, $0.99\gamma _{in}$, $\gamma _{in}$, $1.01\gamma _{in}$ and $1.03\gamma _{in}$, respectively. And the corresponding dynamic responses are examined. It is easy to find that the results obtained by two methods show a good agreement.

For the rotating speed lower than $\gamma _{in}$, internal resonant detuning parameters $\varepsilon \sigma _{1}$ is negative (Fig. 4b), the frequency–response curves bend to the higher frequency direction and show a stiffening effect (Fig. 6a1, a2). With a slight increment of rotating speed, the curves seem to bend more to the right side and the stiffening effect becomes stronger. In addition, there is a small peak appears before the main peak in the second mode response (Fig. 6b2), at the same time a little flat peak appears in the first mode, and it is almost invisible (Fig. 6b1). For the case of complete internal resonant, there are two peaks bending to the opposite directions in the frequency–response curves. There is an unstable region near the middle dip of response curves (Fig. 6c1, c2). When the rotating speed exceeds $\gamma _{in}$, internal resonant detuning parameters $\varepsilon \sigma _{1}$ turns to positive, the right peak becomes small and disappear at last. So there is only one main peak bending to lower frequency direction (Fig. 6d1, d2) and the curves show a softening effect. With a further increment in rotating speed, the softening effect becomes smaller (Fig. 6e1, e2). One could conclude that the dynamic behavior is very sensitive to the rotating speed, especially near the internal resonant. From the overall view of the evolution, one could also observe the following phenomenon. When the rotating speed raises from a value lower than $\gamma _{in}$, the peak value of the first mode resonant response decreases firstly and increases afterward, on the contrary, the peak value of the second mode increases firstly and decreases afterward. Hence, when the complete internal resonant occurs, the first and second mode response obtain their minimum and maximum value, respectively, and the internal energy transfer between first two modes is the strongest. As the vibration system approaches internal resonant condition, the response curves bend more to one side and the unstable regions become lager. One can imagine that when the rotating speed is far away from $\gamma _{in}$, the response curves will reduce to those of linear system.

Figure 7 reveals the effects of thermal gradient on frequency response of rotating blade in the presence of internal resonant. As show in Fig. 7a, the peak values of both modes decrease when the thermal gradient is increased from 0.028 to 0.036. This is mainly due to that the amplitude of pre-deformation increases linearly with thermal gradient. And the increase in pre-deformation will improve the stiffness of the rotating blade. Moreover, with increase in thermal gradient, the curves tend to bend more to two sides and the unstable region is enlarged. The second mode response (Fig. 7b) shows a similar trend.

For the purpose of comparison, the pre-deformation of the same shape with the first mode shape is considered. And the effects of the pre-deformation amplitude $d_{0}$ on the internal resonant response are shown in Fig. 8. The increase in $d_{0}$ will lead to decrease in vibration amplitude and narrowing in unstable region. The response curves get their peak value at smaller external resonance tune parameter for larger $d_{0}$. However, for different $d_{0}$’s, the upper branches of the multi-value region nearly coincide with each other. From the comparison between Figs. 7 and 8, it could be concluded that not only the amplitude but also the distribution of the pre-deformation field could influence the nonlinear dynamic behavior of the rotating blade.

The effect of the gas pressure amplitude on the resonant dynamic is investigated by plotting the frequency–response curves for different gas pressure together in Fig. 9. The blade is pre-deformed due to the thermal gradient of $g_{z} = 0.032$. The dimensionless gas pressure $P_{gas}$ is set to 0.005, 0.01 and 0.015, respectively. It is observed that the increase in gas pressure will lead to an improvement in vibration amplitude and an enlargement in unstable region.

The frequency–response curves at internal resonant condition for various dimensionless damping coefficients ($c_{d} = 0.1, 0.2, 0.25, 0.3$) are compared in Fig. 10. From the global point of view, the frequency–response curves become flatter with the increment of the damping coefficient. For small damping coefficients ($c_{d} = 0.1$), the response curves show a strong double-jumping phenomenon. This jumping phenomenon is weakened by the increase of damping coefficient ($c_{d} = 0.2$). For even lager damping coefficient ($c_{d} = 0.25$) the jumping phenomenon disappears in the response curves but the steady response is still unstable near external resonant ($\varepsilon \sigma _{2}= 0$). With the further increase in the damping coefficient ($c_{d} = 0.3$), the response near external resonant becomes stable.

Force–response curves of first two modes could be obtained by varying the gas pressure amplitude and solving the Eqs. (46) and (48). The force–response curves of the system for several values of the external resonance detuning parameters are plotted in Fig. 11. As shown in this figure, multi-valuedness does not exist in the complete external resonance ($\sigma _{2}= 0$). The steady response is stable for small gas pressure and unstable for large gas pressure. For other cases, there are two limit point bifurcations and an unstable portion between them. The external resonant detuning parameters are denoted near the first limit point for each curve. With the increment of the deviation from the complete external resonance, the first limit points are delayed remarkably. However, the second ones are changed slightly. Therefore, the unstable region is enlarged by the deviation from the resonance frequency. It could be also observed that in the second mode response the second limit points for different cases almost coincide with each other. Moreover, a positive external resonant detuning parameter $\sigma _{2}$ results in a larger unstable region when $\sigma _{1}$ is negative (Fig. 10a1, a2); a opposite scenario could be observed for the positive internal resonant detuning parameter (Fig. 10b1, b2).

6 Conclusion

The nonlinear forced vibration of a pre-deformed rotating blade subjected to uniform distributed gas pressure under thermal gradient is analyzed in this study. A novel nonlinear vibration system is established by considering the influence of pre-deflection of the rotating blade.

The proper number of trial function is determined through the convergence test for natural frequencies and the critical rotating speed. From the eigenvalue analysis, it is showed that the natural frequencies increase with both thermal gradient and rotating speed, and the influence in second mode is more pronounced. The possibility of the modal interaction is also confirmed.

The method of multiple scales is developed to solve the multi-degree-of-freedom nonlinear system. It is showed that the different solvability conditions result in the same steady response for the present problem. The analytical results furnished by method of multiple scales are consistent with the numerical integration using Runge–Kutta method. It is discovered that variation in rotating speed near $\gamma _{in}$ will lead to an interesting evolution in the frequency–response curves. The internal energy transfer between modes is observed. The peak value of the frequency response curve decreases with the amplitude of the pre-deformation for both types of pre-deformation distribution. However, the variation in width of unstable region with the pre-deformation amplitude is opposite for different deformation distribution profiles. The influences of the gas pressure and damping coefficients on the nonlinear behavior of rotating blade are also examined. The present study is expected to be helpful to understanding the nonlinear resonant characters of rotating blade.

Appendix

The matrices and their components in Eq. (22) are derived as:

$$\begin{aligned} {{\varvec{M}}}= & {} \left[ {{\begin{array}{cc} {\left[ {{\varvec{M}}}^{{{\varvec{22}}}} \right] _{{n_{2} \times n_{2}}} }&{} \quad 0 \\ 0&{}\quad {\left[ {{\varvec{M}}}^{{{\varvec{33}}}} \right] _{{n_{3} \times n_{3}}} } \\ \end{array} }} \right] \end{aligned}$$

(51)

$$\begin{aligned} {{\varvec{C}}}= & {} \left[ {{\begin{array}{cc} {\left[ {{\varvec{C}}}^{{{\varvec{22}}}} \right] _{{n_{2} \times n_{2}}} }&{}\quad 0\\ 0&{}\quad {\left[ {{{\varvec{C}}}}^{{{\varvec{33}}}} \right] _{{n_{3} \times n_{3}}}} \\ \end{array} }} \right] \end{aligned}$$

(52)

$$\begin{aligned} {{\varvec{K}}}= & {} \left[ {{\begin{array}{cc} {\left[ {{{\varvec{K}}}^{22}} \right] _{{n_{2} \times n_{2}}} }&{}\quad {\left[ {{{\varvec{K}}}^{23}} \right] _{{n_{2} \times n_{3}}} } \\ {\left[ {{{\varvec{K}}}^{32}} \right] _{{n_{3} \times n_{2}} }}&{}\quad {\left[ {{{\varvec{K}}}^{33}} \right] _{{n_{3} \times n_{3}}}} \\ \end{array} }} \right] \end{aligned}$$

(53)

$$\begin{aligned} {{\varvec{q}}}= & {} \left( {q_{21} ,\ldots ,q_{{2n_{2}}} ,q_{31} ,\ldots ,q_{{3n_{3}}} } \right) ^\mathrm{T} \end{aligned}$$

(54)

$$\begin{aligned} {{\varvec{Q}}}= & {} \left( {\left[ {{{\varvec{Q}}}^{2}} \right] _{{n_{2} \times 1}}^\mathrm{T} ,\left[ {{{\varvec{Q}}}^{3}} \right] _{{n_{3} \times 1}}^\mathrm{T}} \right) ^{\mathrm{T}} \end{aligned}$$

(55)

whose components are:

$$\begin{aligned}&M_{ij}^{22} =\int _{0}^{1} {\phi _{2i} \phi _{2j} \hbox {d}x} , \quad M_{ij}^{33} =\int _{0}^{1} {\phi _{3i} \phi _{3j} \hbox {d}x} \end{aligned}$$

(56)

$$\begin{aligned}&C_{ij}^{22} =c_{d}\int _0^1 {\phi _{2i} \phi _{2j} \hbox {d}x} , \quad C_{ij}^{33} =c_{d} \int _{0}^{1} {\phi _{3i} \phi _{3j} \hbox {d}x}\nonumber \\ \end{aligned}$$

(57)

$$\begin{aligned} K_{ij}^{22}= & {} \int _{0}^{1} {J_{3} {\phi }''_{2i} {\phi }''_{2j} \hbox {d}x} +\eta ^{2}\int _{0}^{1} {{u}'_{20} {u}'_{20} {\phi }'_{2i} {\phi }'_{2j} \hbox {d}x} \nonumber \\&-\,\gamma ^{2}\int _0^1 {\phi _{2i} \phi _{2j} \hbox {d}x}\nonumber \\&+\,\frac{1}{2}\gamma ^{2}\int _0^1 {{\phi }'_{2i} {\phi }'_{2j} \left( {1-x^{2}+2\delta -2\delta x} \right) \hbox {d}x}\nonumber \\ \end{aligned}$$

(58)

$$\begin{aligned}&K_{ij}^{23} =\int _0^1 {J_{23} {\phi }''_{2i} {\phi }''_{3j} \hbox {d}x} +\eta ^{2}\int _0^1 {{u}'_{20} {u}'_{30} {\phi }'_{2i} {\phi }'_{3j} \hbox {d}x}\nonumber \\ \end{aligned}$$

(59)

$$\begin{aligned} K_{ij}^{32}= & {} \int _{0}^{1} {J_{23} {\phi }''_{3i} {\phi }''_{2j} \hbox {d}x} +\eta ^{2}\int _0^1 {{u}'_{20} {u}'_{30} {\phi }'_{3i} {\phi }'_{2j} \hbox {d}x} \nonumber \\\end{aligned}$$

(60)

$$\begin{aligned} K_{ij}^{33}= & {} \int _{0}^{1} {J_2 {\phi }''_{3i} {\phi }''_{3j} \hbox {d}x} +\eta ^{2}\int _0^1 {{u}'_{30} {u}'_{30} {\phi }'_{3i} {\phi }'_{3j} \hbox {d}x} \nonumber \\&+\,\frac{1}{2}\gamma ^{2}\int _0^1 {{\phi }'_{3i} {\phi }'_{3j} \left( {1-x^{2}+2\delta -2\delta x} \right) \hbox {d}x}\nonumber \\ \end{aligned}$$

(61)

$$\begin{aligned} Q_{i}^{2}= & {} \int _{0}^{1} {\phi _{2i} P_{gas} \sin \left( {\varTheta x+\varPsi } \right) \hbox {d}x} \cos \left( {\omega t} \right) \nonumber \\&-\,\eta ^{2}\left[ \frac{3}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{u}'_{20} {\phi }'_{2i} {\phi }'_{2j} {\phi }'_{2k} \hbox {d}x} } \right) q_{2j} q_{2k}} }\right. \nonumber \\&+\,\frac{1}{2}\sum _{j=1}^{n_3 } {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{20} {\phi }'_{2i} {\phi }'_{3j} {\phi }'_{3k} \hbox {d}x} } \right) q_{3j} q_{3k}} }\nonumber \\&+\,\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{30} {\phi }'_{2i} {\phi }'_{2j} {\phi }'_{3k} \hbox {d}x} } \right) q_{2j} q_{3k} } } \nonumber \\&+\,\frac{1}{2}\sum _{j=1}^{n_2 } {\sum _{k=1}^{{n_{2}}} {\sum _{l=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{\phi }'_{2i} {\phi }'_{2j} {\phi }'_{2k} {\phi }'_{2l} \hbox {d}x} } \right) q_{2j} q_{2k} q_{2l} } } } \nonumber \\&\left. +\,\frac{1}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\sum _{l=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{\phi }'_{2i} {\phi }'_{2j} {\phi }'_{3k} {\phi }'_{3l} \hbox {d}x} } \right) q_{2j} q_{3k} q_{3l} } } } \right] ,\nonumber \\&\qquad i=1,2,\ldots , n_{2} \end{aligned}$$

(62)

$$\begin{aligned} Q_{i}^{3}= & {} -\int _0^1 {\phi _{3i} P_{gas} \cos \left( {\varTheta x+\varPsi } \right) \hbox {d}x} \cos \left( {\omega t} \right) \nonumber \\&-\,\eta ^{2}\left[ \frac{1}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{u}'_{30} {\phi }'_{3i} {\phi }'_{2j} {\phi }'_{2k} \hbox {d}x} } \right) q_{2j} q_{2k} } } \right. \nonumber \\&+\,\frac{3}{2}\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{30} {\phi }'_{3i} {\phi }'_{3j} {\phi }'_{3k} \hbox {d}x} } \right) q_{3j} q_{3k}}}\nonumber \\&+\,\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{20} {\phi }'_{3i} {\phi }'_{2j} {\phi }'_{3k} \hbox {d}x}}\right) q_{2j} q_{3k} } } \nonumber \\&+\,\frac{1}{2}\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {\sum _{l=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{\phi }'_{3i} {\phi }'_{3j} {\phi }'_{3k} {\phi }'_{3l} \hbox {d}x} } \right) q_{3j} q_{3k} q_{3l}} } } \nonumber \\&\left. +\,\frac{1}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\sum _{l=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{\phi }'_{3i} {\phi }'_{2j} {\phi }'_{2k} {\phi }'_{3l} \hbox {d}x} } \right) q_{2j} q_{2k} q_{3l}} } } \right] ,\nonumber \\&\qquad i=1,2,\ldots ,n_{3} \end{aligned}$$

(63)

The coefficients in Eq.(25) are written as followings.

$$\begin{aligned} f_{2i}= & {} \int _0^1 {\phi _{2i} P_{gas} \sin \left( {\varTheta x+\varPsi } \right) \hbox {d}x} ,f_{3i}\nonumber \\= & {} -\int _{0}^{1} {\phi _{3i} P_{gas} \cos \left( {\varTheta x+\varPsi } \right) \hbox {d}x} \end{aligned}$$

(64)

$$\begin{aligned} \alpha _{ij}^{21}= & {} -c_d \int _{0}^{1} {\phi _{2i} \phi _{2j} \hbox {d}x} ,\alpha _{ij}^{31} =-c_{d} \int _{0}^{1} {\phi _{3i} \phi _{3j} \hbox {d}x} \nonumber \\\end{aligned}$$

(65)

$$\begin{aligned} \alpha _{ijk}^{22}= & {} -\frac{3}{2}\eta ^{2}\int _{0}^{1} {{u}'_{20} {\phi }'_{2i} {\phi }'_{2j} {\phi }'_{2k} \hbox {d}x} ,\alpha _{ijk}^{32}\nonumber \\= & {} -\frac{1}{2}\eta ^{2}\int _{0}^{1} {{u}'_{30} {\phi }'_{3i} {\phi }'_{2j} {\phi }'_{2k} \hbox {d}x} \end{aligned}$$

(66)

$$\begin{aligned} \alpha _{ijk}^{23}= & {} -\frac{3}{2}\eta ^{2}\int _{0}^{1} {{u}'_{20} {\phi }'_{2i} {\phi }'_{3j} {\phi }'_{3k} \hbox {d}x} ,\alpha _{ijk}^{33}\nonumber \\= & {} -\frac{1}{2}\eta ^{2}\int _{0}^{1} {{u}'_{30} {\phi }'_{3i} {\phi }'_{3j} {\phi }'_{3k} \hbox {d}x} \end{aligned}$$

(67)

$$\begin{aligned} \alpha _{ijk}^{24}= & {} -\eta ^{2}\int _{0}^{1} {{u}'_{30} {\phi }'_{2i} {\phi }'_{2j} {\phi }'_{3k} \hbox {d}x} ,\alpha _{ijk}^{34}\nonumber \\= & {} -\eta ^{2}\int _{0}^{1} {{u}'_{20} {\phi }'_{3i} {\phi }'_{2j} {\phi }'_{3k} \hbox {d}x} \end{aligned}$$

(68)

The coefficients in Eqs. (34)–(36) are listed as following formulation.

For 1 $\le s \le n_{2}$,

$$\begin{aligned} \beta _{10s}= & {} -\sum _{j=1}^{{n_{2}}} {2i\omega _1 M_{sj}^{22} p_{12j}} \end{aligned}$$

(69)

$$\begin{aligned} \beta _{11s}= & {} \sum _{j=1}^{{n_{2}}} {i\omega _1 \alpha _{sj}^{21} p_{12j}} \end{aligned}$$

(70)

$$\begin{aligned} \beta _{12s}= & {} \sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {2\alpha _{sjk}^{22} \bar{{p}}_{12j} p_{22k} } } +\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {2\alpha _{sjk}^{23} \bar{{p}}_{13j} p_{23k}}}\nonumber \\&+\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{sjk}^{24} \left( {\bar{{p}}_{12j} p_{23k} +p_{22j} \bar{{p}}_{13k} } \right) } } \end{aligned}$$

(71)

$$\begin{aligned} \beta _{13s}= & {} \frac{f_{2s} }{2} \end{aligned}$$

(72)

$$\begin{aligned} \beta _{20s}= & {} -\sum _{j=1}^{{n_{2}}} {2i\omega _{2} M_{sj}^{22} p_{22j}} \end{aligned}$$

(73)

$$\begin{aligned} \beta _{21s}= & {} \sum _{j=1}^{{n_{2}}} {i\omega _2 \alpha _{sj}^{21} p_{22j}} \end{aligned}$$

(74)

$$\begin{aligned} \beta _{22s}= & {} \sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\alpha _{sjk}^{22} p_{12j} p_{12k} } } +\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{sjk}^{23} p_{13j} p_{13k}}}\nonumber \\&+\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{sjk}^{24} p_{12j} p_{13k}}} \end{aligned}$$

(75)

$$\begin{aligned} \beta _{30s}= & {} -\sum _{j=1}^{{n_{2}}} {2i\omega _3 M_{sj}^{22} p_{32j}} \end{aligned}$$

(76)

$$\begin{aligned} \beta _{31s}= & {} \sum _{j=1}^{{n_{2}}} {i\omega _{3} \alpha _{sj}^{21} p_{32j}} \end{aligned}$$

(77)

For $n_{2}+1 \le s \le \quad n_{2} + n_{3}$, assume that ${s}'=s-n_2$, then

$$\begin{aligned} \beta _{10s}= & {} -\sum _{j=1}^{{n_{3}}} {2i\omega _1 M_{{s}'j}^{33} p_{13j}} \end{aligned}$$

(78)

$$\begin{aligned} \beta _{11s}= & {} \sum _{j=1}^{{n_{3}}} {i\omega _1 \alpha _{{s}'j}^{31} p_{13j}} \end{aligned}$$

(79)

$$\begin{aligned} \beta _{12s}= & {} \sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {2\alpha _{{s}'jk}^{32} \bar{{p}}_{12j} p_{22k} } }\nonumber \\&+\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {2\alpha _{{s}'jk}^{33} \bar{{p}}_{13j} p_{23k}}} \nonumber \\&+\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{{s}'jk}^{34} \left( {\bar{{p}}_{12j} p_{23k} +p_{22j} \bar{{p}}_{13k} } \right) } } \end{aligned}$$

(80)

$$\begin{aligned} \beta _{13s}= & {} \frac{f_{3{s}'} }{2} \end{aligned}$$

(81)

$$\begin{aligned} \beta _{20s}= & {} -\sum _{j=1}^{{n_{3}}} {2i\omega _{2} M_{{s}'j}^{33} p_{23j}} \end{aligned}$$

(82)

$$\begin{aligned} \beta _{21s}= & {} \sum _{j=1}^{{n_3}} {i\omega _{2} \alpha _{{s}'j}^{31} p_{23j}} \end{aligned}$$

(83)

$$\begin{aligned} \beta _{22s}= & {} \sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\alpha _{{s}'jk}^{32} p_{12j} p_{12k}}} +\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{{s}'jk}^{33} p_{13j} p_{13k}}}\nonumber \\&+\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{{s}'jk}^{34} p_{12j} p_{13k}}} \end{aligned}$$

(84)

$$\begin{aligned} \beta _{30s}= & {} -\sum _{j=1}^{{n_{3}}} {2i\omega _3 M_{{s}'j}^{33} p_{33j}} \end{aligned}$$

(85)

$$\begin{aligned} \beta _{31s}= & {} \sum _{j=1}^{{n_{3}}} {i\omega _{3} \alpha _{{s}'j}^{31} p_{33j}} \end{aligned}$$

(86)

In Eqs. (69)–(86), the notation $p_{r2j}$ (r = 1, 2, 3; $j= 1, 2,{\ldots }$, $n_{2})$ represents the $j^{\mathrm{th}}$ component in the $r^{\mathrm{th}}$ mode vector of the chrodwise vibration, and $p_{r3j}$ ($r = 1, 2, 3; j = 1, 2, \ldots ,n_{3})$ represents that of the flapwise vibration.