Gradient-optimized physics-informed neural networks (GOPINNs): a deep learning method for solving the complex modified KdV equation

Abstract

Recently, the physics-informed neural networks (PINNs) have received more and more attention because of their ability to solve nonlinear partial differential equations via only a small amount of data to quickly obtain data-driven solutions with high accuracy. However, despite their remarkable promise in the early stage, their unbalanced back-propagation gradient calculation leads to drastic oscillations in the gradient value during model training, which is prone to unstable prediction accuracy. Based on this, we develop a gradient optimization algorithm, which proposes a new neural network structure and balances the interaction between different terms in the loss function during model training by means of gradient statistics, so that the newly proposed network architecture is more robust to gradient fluctuations. In this paper, we take the complex modified KdV equation as an example and use the gradient-optimized PINNs (GOPINNs) deep learning method to obtain data-driven rational wave solution and soliton molecules solution. Numerical results show that the GOPINNs method effectively smooths the gradient fluctuations and reproduces the dynamic behavior of these data-driven solutions better than the original PINNs method. In summary, our work provides new insights for optimizing the learning performance of neural networks and improves the prediction accuracy by a factor of 10 to 30 when solving the complex modified KdV equation.

1 Introduction

With the rapid development of computational science, deep learning has achieved great success in many fields, which include computer vision (CV), natural language processing (NLP), recommender systems, protein structure prediction, and so on [1,2,3,4]. There is an important reason behind these successes: neural network models are good approximators of complex functions. And using this property of neural networks, numerous data-driven methods have been proposed to solve nonlinear partial differential equations (NPDEs) [5,6,7,8], among which the physics-informed neural networks (PINNs) method proposed by Raissi et al. [8] stand out with its high prediction accuracy and good generalization ability in solving NPDEs. It does this by efficiently designing the network loss of the function approximator so that it is constrained by the underlying NPDEs and boundary conditions. That is, it respects the given physics theorems described by the general NPDEs as constraints for supervised learning. Subsequently, many improved deep learning frameworks based on the PINNs have emerged to improve its robustness as well as generalization capabilities for use in other fields. For example, Raissi et al. [9] proposed a minimization-based forward–backward stochastic neural networks model to solve coupled forward–backward stochastic differential equations; Jagtap et al. [10] proposed cPINNs that conforms to various conservation laws, solving problems on multiple subdomains and ensuring flux continuity on subdomain boundaries; Mattey et al. [11] proposed backward compatible PINNs, which can effectively address large domains or multi-scale solutions. These methods were developed to be applied in other different situations and even in different domains.

In recent decades, the numerical solution of NPDEs has always been a hot topic in the field of mathematical physics. After the PINNs were proposed, their related variants have been uninterruptedly applied in the direction of solving NPDEs, such as function approximation of unknown solutions [12], and data-driven discovery [7, 13]. It is worth noting that there are some scholars who have done a lot of meaningful work in the field of mathematical physics. Chen and his group solved local wave solution of NPDEs of second and third order, and some classical mathematical physics equations such as the Sine-Gordon, nonlinear Schrödinger, and derivative nonlinear Schrödinger equations, and obtained important breather, rogue waves, and other soliton solutions for these equations in the field of mathematical physics [14,15,16,17,18,19]. Yan and Dai et al. studied data-driven solutions of related equations and parameter discovery using PINNs [20,21,22,23]. Bai et al. solved Huxley equation using an improved PINN method [24]. Wu et al. predicted the dynamic process and model parameters of the vector optical solitons in birefringent fibers via the modified PINN [25]. Marcucci et al. proposed a novel deep learning computational model driven by nonlinear waves as a ‘hidden layer’ [26].

Based on the idea of gradient-balanced optimization, we propose a gradient-optimized PINNs (GOPINNs). Specifically, the gradient descent update process is optimized by balancing the interactions between different terms in the loss function during model training through gradient statistics on the original PINNs method and changing its fully connected feed-forward neural network architecture. This improved approach has two main motivations: (1) Automatically adjust the penalty term coefficients during model training using back-propagation gradient statistics [27] to equilibrate the interactions among the terms of the loss function; (2) The idea comes from the recent frequent use of neural network attention mechanisms for CV and NLP researches [28], where two transformer networks are added to a traditional neural network to update the hidden layers and augment the hidden state using residual connections. In summary, we can smooth the gradient statistics on the hidden layers of the neural networks to make the novel neural network architecture with better stability and prediction accuracy.

In this article, by comparing the numerical results of the PINNs and GOPINNs methods, we verify the good learning performance of the newly method by taking the rational wave and soliton molecules solutions of the complex modified KdV equation as examples.

The paper is organized as follows. In Sect. 2, we review the PINNs model and propose the GOPINNs model by gradient analysis. In Sect. 3, we use PINNs and GOPINNs methods to compare the dynamical behaviors of the rational wave solution and the soliton molecules solution of the modified KdV equation, and the learning performance is also evaluated by comparing the numerical results of the two methods. Finally, the conclusions and discussion are given in Sect. 4.

2 Methods

2.1 The PINNs method

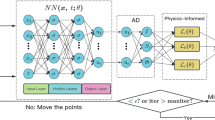
Firstly, let’s briefly review the PINNs, which is a deep learning framework designed to infer the latent function q(t, x) of the NPDEs of general form [8]

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} q_t + \mathcal {N}_{x}[q] = 0, &{} (t, x) \in T \times \Omega ,\\ q(0, x) = \mathcal {I}(x), &{} x \in \Omega ,\\ q(t, x) = \mathcal {B}(t, x), &{} (t, x) \in T \times \partial \Omega , \end{array}\right. } \end{aligned} \end{aligned}$$

(1)

where variables t and x denote time and space coordinates, T and $\Omega$ stand for their value range, respectively, $\partial \Omega$ is the boundary of the spatial domain $\Omega$, subscripts represent partial differentiation. $\mathcal {N}_{x}[\cdot ]$ is the combination of linear and nonlinear operators, $\mathcal {I}[\cdot ]$ and $\mathcal {B}[\cdot ]$ are the initial and boundary conditions (IBCs) operators. Then, we use a deep neural networks $f_{\theta }(t,x)$ to approach the latent solution q(t, x), here the residuals of Eq. (1) are defined as

$$\begin{aligned} \begin{aligned} \mathcal {R}_{\theta }(t,x) = [f_{\theta }(t,x)]_{t} + \mathcal {N}_{x}[f_{\theta }(t,x)]. \end{aligned} \end{aligned}$$

(2)

Generally, partial differential calculations can be done automatically in neural networks by automatic backward differentiation operations [27], and the parameters $\theta$ in PINNs are shared among the latent solutions and the residuals of NPDEs. And our aim is to filter a good set of optimized parameters by the stochastic gradient descent (SGD) calculation and set the general form of the suitable loss function [30] as follows

$$\begin{aligned} \begin{aligned} \mathcal {L}(\theta ) = \mathcal {L}_{\mathcal {R}}(\theta ) + \sum ^{N}_{j=1}\lambda _{j}\mathcal {L}_{j}(\theta ), \end{aligned} \end{aligned}$$

(3)

where $\mathcal {L}_{\mathcal {R}}(\theta )$ is a loss term that penalizes the residuals of the NPDEs, and $\mathcal {L}_{j}(\theta )$ represents that penalty items of the other data for $f_{\theta }(t,x)$ (e.g., initial or boundary conditions, etc.). What is noted here is that in PINNs [8], all $\lambda _j$ are equal to 1. In this paper, based on the classical initial value and boundary problem, the terms of the loss function (3) are defined as follows

$$\begin{aligned} \mathcal {L}_{\mathcal {R}}= & {} \frac{1}{N_{\mathcal {R}}}\sum ^{N_{\mathcal {R}}}_{j=1} [\mathcal {R}_{\theta }(t^{j}_{\mathcal {R}}, x^{j}_{\mathcal {R}})]^2,\nonumber \\ \mathcal {L}_{\mathcal {I}}= & {} \frac{1}{N_{\mathcal {I}}}\sum ^{N_{\mathcal {I}}}_{j=1} [q(0, x^{j}_I) - \mathcal {I}^{j}]^2, \nonumber \\ \mathcal {L}_{\mathcal {B}}= & {} \frac{1}{N_{\mathcal {B}}}\sum ^{N_{\mathcal {B}}}_{j=1} [q(t^{j}_{\mathcal {B}}, x^{j}_{\mathcal {B}}) - \mathcal {B}^{j}]^2, \end{aligned}$$

(4)

here $\{x_{\mathcal {I}}^{j}, \mathcal {I}^{j} \}_{j=1}^{N_{\mathcal {I}}}$ and $\{t_{\mathcal {B}}^{j}, x_{\mathcal {B}}^{j}, \mathcal {B}^{j} \}_{j=1}^{N_{\mathcal {B}}}$ represent the initial value and boundary datasets, and $\{ t^{j}_{\mathcal {R}}, x^{j}_{\mathcal {R}} \}_{j=1}^{N_{\mathcal {R}}}$ denotes the random collocation points used to minimize the residuals of NPDEs inside the solution domain. In addition, $\mathcal {L}_{\mathcal {R}}$ represents the punishment of the NPDEs that not being satisfied the random collocation points, subsequently, $\mathcal {L}_{\mathcal {I}}$ and $\mathcal {L}_{\mathcal {B}}$ denote the loss on the IBCs, respectively. The ultimate goal of these designs is to construct the deep neural networks $f_{\theta }(t,x)$ such that the loss function (3) is as close to 0 as possible.

2.2 Gradient analysis for the PINNs method

Although there are some positive results [31,32,33], the PINNs still present some unexpected difficulties in approximating the latent solution q(t, x). In this paper, let’s take the complex modified KdV equation [34] as an example, which widely used in the fields of dynamic evolution of ultrashort pulses, nonlinear lattices, fluid dynamics, etc. The general form is as follows

$$\begin{aligned} \begin{aligned} q_t + 6 |q|^2 q_x + q_{xxx} = 0, \end{aligned} \end{aligned}$$

(5)

where $q = q(t, x)$ denotes a complex field. Here, we can use PINNs to approximate the latent solution of Eq. 5 by the deep neural networks $f_{\theta }(t,x)$, and the parameters could be obtained by minimizing the suitable loss function (3) that meet the IBCs and the punishment of the residuals of the complex modified KdV equation inside the spatiotemporal domain $T \times \Omega$. At first, we investigate the rational wave solution [34] of Eq. 5 with the IBCs as follows

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} q_t + 6 |q|^2 q_x + q_{xxx} = 0, &{} (t,x) \in [0, 10] \times [0, 30]\\ \mathcal {I}(x) = -c + \frac{4 c}{4 c^2 (s \ + \ x)^2\ + \ 1}, \\ \mathcal {B}(t, 0) = -c + \frac{4 c}{4 c^2 (6 c^2 t \ - \ s)^2 \ + \ 1}, &{} \mathcal {B}(t, 30) = -c + \frac{4 c}{4 c^2 (6 c^2 t \ - \ s \ - \ 30)^2 \ + \ 1}. \end{array}\right. } \end{aligned} \end{aligned}$$

(6)

Here, we set $c = \frac{1}{2 \sqrt{6}}, s = -14$. Without loss of generality, the $f_{\theta }(t, x)$ is defined as a deep fully connected neural networks including eight hidden layers and 50 neurons in each hidden layer, and the nonlinear activation function is designated as a hyperbolic tangent function. Then, we use the Adam optimizer [27] to minimize the loss function of Eq. 6 with 40000 iterations of SGD.

Fig. 1

(Color online) Rational wave solution (PINNs): The exact solution and predicted solution |q(t, x)|, and their absolute error with the above parameter settings (relative $\mathbb {L}_2$ error: $\mathrm {6.45e-02}$)

Fig. 2

(Color online) Rational wave solution (PINNs): Histograms of the back-propagation gradients distribution of $\nabla _\theta \mathcal {L}_{\mathcal {I}}, \nabla _\theta \mathcal {L}_{\mathcal {B}}$ and $\nabla _\theta \mathcal {L}_{\mathcal {R}}$ at per hidden layer

In Fig. 1, comparing the difference among the exact solution and predicted solution, we could see from the absolute error plot that most of error points appear in the central crest region, while the larger error points appear at the right boundary and the peak of the rational line wave from the combination of the three plots. Clearly, the PINNs method cannot do the job in adapting to the sharper areas and boundaries, which results in a relative $\mathbb {L}_2$ prediction error of $10.01\%$.

In order to investigate why the PINNs method does not obtain more accurate predictions, we took inspiration from Glorot and Bengio’s interesting work [35], which is monitoring the back-propagation gradient fluctuations of the neural network parameters in each hidden layer of our model for the training process. It is important to note here that we are not tracking the gradients of the total loss function, but the gradients of each individual items $\nabla _{\theta } \mathcal {L}_{\mathcal {I}}(\theta ), \nabla _{\theta } \mathcal {L}_{\mathcal {B}}(\theta )$ and $\nabla _{\theta } \mathcal {L}_{\mathcal {r}}(\theta )$ that denote the shared parameters in per hidden layer of the deep neural networks.

Seeing Fig. 2, the gradients values represent the IBCs terms $\nabla _{\theta } \mathcal {L}_{\mathcal {I}}(\theta )$ and $\nabla _{\theta } \mathcal {L}_{\mathcal {B}}(\theta )$ in per hidden layer, respectively, which are sharply concentrated around zero and formation of spikes, which is likely to be the cause of the gradient imbalance. In addition, the gradients corresponding to the NPDE residuals $\nabla _{\theta } \mathcal {L}_{\mathcal {R}}(\theta )$ keep large values, especially in the later layers, is related to the back-propagation computation mechanism. And it’s always known that when the gradient $\nabla _{\theta } \mathcal {L}_r(\theta )$ is big, the deep neural networks will easily infer to any solutions that satisfies the NPDEs. Therefore, the model we train should strictly return a solution of the NPDE with residuals as close to zero as possible, otherwise it is easy to return wrong prediction.

Fig. 3

(Color online) Rational wave solution (PINNs): Loss curves of $\mathcal {L}_{\mathcal {R}}(\theta )$ and $\mathcal {L}_{q}(\theta )$, respectively, with 40000 iterations of the stochastic gradient descent via Adam optimizer

The variation of the loss with different iterations is shown in Fig. 3, where $\mathcal {L}_{\mathcal {R}}$ represents the residuals of the NPDE, and $\mathcal {L}_{q}$ represents the error of the NPDE on the initial value and the boundary. Obviously, we can see that $\mathcal {L}_{\mathcal {R}}$ is still relatively smooth, but $\mathcal {L}_{q}$ is very unstable during the iterations, which also explains from the side that the unstable gradient can lead to poor prediction accuracy of PINNs at the boundary.

2.3 A gradient-optimized fully connected network architecture

Network architecture optimization is an important research idea in deep learning, and the general approximation theorems for physics-informed neural networks are usually lacking in solving NPDEs, so whether the standard fully connected architecture can provide flexible enough representations to infer more complex NPDEs is a question we need to focus on. Inspired by neural networks attention mechanisms that has been widely used in CV and NLP [28], we have made a simple adaptation of the standard fully connected network architecture and proposed a new network architecture with the following features: the gradient equalization effect is enhanced by using residual connections through element multiplicative interactions between different hidden layers, and numerical results show that the inference performance of the newly proposed architecture seems to be better than the results obtained by the original PINNs method. As shown below, the key to adapting the traditional fully connected neural network is to introduce two transformer network terms to smooth the diffusion term of the NPDE, and then the hidden layers are updated using a point-by-point multiplication operation according to the following feed-forward propagation rules.

$$\begin{aligned} \begin{aligned}&U = \sigma (W^1X + b^1), \quad V = \sigma (W^2X + b^2) \\&Q^{(1)} = \sigma (W^{s,1}X + b^{s,1}), \\&P^{(l)} = \sigma (W^{s,l}Q^{(l)} + b^{s,l}), \quad l = 1, ..., K, \\&Q^{(l+1)} = (1 - P^{(l)}) \odot U + P^{(l)} \odot V, \quad l = 1, ..., K, \\&f_{\theta }(t, x) = WQ^{(K+1)} + b, \end{aligned} \end{aligned}$$

(7)

here X represents the $(n \times d)$ dimensional matrix of the input points data, $\sigma$ denotes nonlinear activation function and $\odot$ represents element multiplication. All parameters of the new fully connected architectures are substantially the same as the traditional fully connected model, except that the weights and biases added to the two transformer networks.

$$\begin{aligned} \begin{aligned} \theta = \{ W^1,\ b^1,\ W^2,\ b^2,\ (W^{s,l},\ b^{s,l})_{l=1}^K,\ W,\ b \}. \end{aligned} \end{aligned}$$

(8)

Here, it’s also worth noting that the new proposed architecture and the forward propagation rules lead to relatively small computational and memory overheads, while significantly improving the prediction accuracy.

Fig. 4

(Color online) Rational wave solution (GOPINNs): The exact solution and predicted solution |q(t, x)|, and their absolute error with the above parameter settings (relative $\mathbb {L}_2$ error: $\mathrm {3.87e-03}$)

For consistency, we also set the deep neural networks with eight hidden layers and 50 neurons per hidden layer, and use a hyperbolic tangent as the nonlinear activation function. After 40000 iterations of SGD with Adam optimizer, the numerical prediction results of the newly proposed fully connected structure are shown in Fig. 4. It is clear that the proposed training scheme can properly balance the interaction between the initial and boundaries, and reduce the relative prediction $\mathbb {L}_2$ error $(0.60\%)$ by one order of magnitude. Compared with the original PINNs scheme in Fig. 1, we can see by the two figures that the absolute error on the boundary and the crest area are effectively reduced. By tuning the traditional fully connected feed-forward neural networks architecture, the prediction accuracy of the new model is more than ten times better than that of PINNs method.

Fig. 5

(Color online) Rational wave solution (GOPINNs): (a) Histograms of the back-propagation gradients distribution of $\nabla _\theta \mathcal {L}_{\mathcal {I}}, \nabla _\theta \mathcal {L}_{\mathcal {B}}$ and $\nabla _\theta \mathcal {L}_{\mathcal {R}}$ at per hidden layer; (b) Evolution of constraint values $\lambda _{\mathcal {I}}$ and $\lambda _{\mathcal {B}}$ in Eq. 3 with the iterations applied to minimize the IBCs loss terms $\mathcal {L}_{\mathcal {I}}(\theta )$ and $\mathcal {L}_{\mathcal {B}}(\theta )$; (c) The loss values of $\mathcal {L}_{\mathcal {R}}(\theta )$ and $\mathcal {L}_{q}(\theta )$ with 40000 iterations of the SGD via Adam optimizer

The other numerical results of solving the rational wave solution using GOPINNs model are shown in Fig. 5. Comparing Figs. 5a and 2, it is found that the distribution of the gradients is significantly improved and becomes smoother. From Fig. 5b, with the addition of the constraint values, comparing Figs. 5c and 3, it can be seen that the loss values become smaller, especially the error loss term $\mathcal {L}_q$, which represents the initial value and the boundary, becomes smoother and more stable, and all these are finally reflected in the more accurate prediction solution of GOPINNs model.

3 Numerical results of the complex modified KdV equation

In this section, we provide the results of a more comprehensive numerical study aimed at evaluating the performance of a fully connected deep neural network model using gradient optimization to infer the NPDEs. In all cases, we use neural networks with 8 hidden layers and 50 neurons per hidden layer, the nonlinear activation function defined as hyperbolic tangent, and train the deep neural networks using a SGD algorithm with Adam optimizer. Moreover, the train datasets initialization is performed in all neural networks using Xavier [35] and we do not use any additional regularization techniques. All algorithms were implemented in TensorFlow [36], and all numerical experiments run on the ACER Aspire E5-571G laptop with 2.20 GHz 4-cores i5 CPU.

3.1 Rational wave solution

Firstly, we review the numerical results of the rational wave solution in Sect. 2.3. In this subsection, our goal is to systematically analyze the performance of these two models by setting a uniform criterion and quantify their prediction results.

We conducted independent numerical experiments using random weight initialization, after 40000 Adam iterations in disparate numbers of hidden layers and different numbers of neurons each hidden layer, all numerical results (relative $\mathbb {L}_2$ errors) are presented in Table 1. Apparently, the PINNs are sensitive to the connectivity architecture of the neural networks, which leads it to be very unstable in terms of prediction accuracy, producing relative $\mathbb {L}_2$ errors in the range of $5.56\%$–$15.09\%$. In contrast, the newly proposed GOPINNs show great robustness in terms of neural network architectures and have a positive correlation in terms of improved prediction accuracy as disparate number of hidden layers and neurons in per layer increases. This suggests that the newly proposed neural networks architectures may be stronger able to predict complex nonlinear partial differential equations instead of the traditional fully connected neural networks, which may also result in a more SGD. Ultimately, our newly proposed model obtains relatively accurate results on this problem (relative $\mathbb {L}_2$ error between $0.31\%$ and $3.30\%$).

3.2 Soliton molecules solution

To further study the learning performance of the newly proposed model in dealing with the evolutionary NPDEs, we chose the soliton molecules solution of the complex modified KdV equation with more complex dynamical behavior. Soliton molecules have been a very popular research topic in recent years. It’s a bound state of solitons and has been discovered experimentally in nonlinear optical systems. In 2012, numerical predictions of soliton molecules were obtained in Bose–Einstein condensates [37]. In 2018, Liu et al. [38] observed experimentally for the first time the real-time dynamics of stable soliton molecules throughout the buildup process. Recently, Lou [39] proposed a velocity resonance mechanism and obtained theoretically the soliton molecules and asymmetric solitons in three fifth-order systems. In this subsection, we set the IBCs of soliton molecules solution as the following form

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} q_t + 6 |q|^2 q_x + q_{xxx} = 0, \quad (t,x) \in [0, 1] \times [-15, 15]\\ \mathcal {I}(x) = {\frac{2\,i \left( i{\mathrm{e}^{12+ix}}-i{\mathrm{e}^{12-ix+2\,x}}+i{ \mathrm{e}^{ \left( 2+i \right) x}}+{\mathrm{e}^{12+ix}}-{\mathrm{e}^{12-ix+2\, x}}-i{\mathrm{e}^{-ix}}-{\mathrm{e}^{ \left( 2+i \right) x}}+{\mathrm{e}^{-ix}} \right) {\mathrm{e}^{-x+6}}}{2\,{\mathrm{e}^{12}}\cos \left( 2\,x \right) + 2\,{\mathrm{e}^{24}}+{\mathrm{e}^{2\,x+12}}+{\mathrm{e}^{-2\,x+12}}+2}}, \\ \mathcal {B}(t, -15) = {\frac{-2\,i{\mathrm{e}^{21-2\,t}} \left( i{\mathrm{e}^{2\,it-18+15\,i+4\,t }}-i{\mathrm{e}^{-2\,it-30-15\,i+4\,t}}-i{\mathrm{e}^{12-15\,i-2\,it}}+{ \mathrm{e}^{2\,it-18+15\,i+4\,t}}+{\mathrm{e}^{-2\,it-30-15\,i+4\,t}}-{ \mathrm{e}^{12-15\,i-2\,it}}+i{\mathrm{e}^{i \left( 2\,t+15 \right) }}-{ \mathrm{e}^{i \left( 2\,t+15 \right) }} \right) }{{\mathrm{e}^{4\,it+12+30\, i}}+{\mathrm{e}^{-4\,it+12-30\,i}}+2\,{\mathrm{e}^{24}}+{\mathrm{e}^{42-4\,t}}+ {\mathrm{e}^{-18+4\,t}}+2}},\\ \mathcal {B}(t, 15) = {\frac{-2\,i{\mathrm{e}^{-9-2\,t}} \left( i{\mathrm{e}^{2\,it+42-15\,i+4\,t }}-i{\mathrm{e}^{-2\,it+30+15\,i+4\,t}}-i{\mathrm{e}^{12+15\,i-2\,it}}+{ \mathrm{e}^{2\,it+42-15\,i+4\,t}}+{\mathrm{e}^{-2\,it+30+15\,i+4\,t}}-{ \mathrm{e}^{12+15\,i-2\,it}}+i{\mathrm{e}^{i \left( 2\,t-15 \right) }}-{ \mathrm{e}^{i \left( 2\,t-15 \right) }} \right) }{{\mathrm{e}^{4\,it+12-30\, i}}+{\mathrm{e}^{-4\,it+12+30\,i}}+2\,{\mathrm{e}^{24}}+{\mathrm{e}^{-18-4\,t}} +{\mathrm{e}^{42+4\,t}}+2}}. \end{array}\right. } \end{aligned} \end{aligned}$$

(9)

Here, we set a suitable loss function as

$$\begin{aligned} \begin{aligned} \mathcal {L}(\theta ) = \mathcal {L_{\mathcal {R}}}(\theta ) + \lambda _{\mathcal {I}}\mathcal {L}_{\mathcal {I}}(\theta ) + \lambda _{\mathcal {B}}\mathcal {L}_{\mathcal {B}}(\theta ), \end{aligned} \end{aligned}$$

(10)

where $\mathcal {L_{\mathcal {R}}}(\theta ), \mathcal {L}_{\mathcal {I}}(\theta ), \mathcal {L}_{\mathcal {B}}(\theta )$ are defined in Eq. (4). We recall the PINNs method in Sect. 2.1, here, it is worth noting that when $\lambda _{\mathcal {I}}(\theta ) = \lambda _{\mathcal {B}}(\theta ) = 1$, the loss function Eq. (10) degenerates to the original form of the loss function calculation for PINNs. Without loss of generality, here the various parameter settings of our network parameters are consistent with the rational wave solution. Let’s first look at the results of training using the PINNs scheme.

Table 1 Rational wave solution: The relative $\mathbb {L}_2$ error among the exact solution and the predicted solution |q(t, x)| for the two models at disparate numbers of hidden layers and different numbers of neurons in each hidden layer

Fig. 6

(Color online) Soliton molecules solution (PINNs): Histograms of the back-propagation gradients distribution of $\nabla _\theta \mathcal {L}_{\mathcal {I}}, \nabla _\theta \mathcal {L}_{\mathcal {B}}$ and $\nabla _\theta \mathcal {L}_{\mathcal {R}}$ at per hidden layer

The results shown in Fig. 6 indicate that $\nabla _\theta \mathcal {L}_{\mathcal {I}}, \nabla _\theta \mathcal {L}_{\mathcal {B}}$ and $\nabla _\theta \mathcal {L}_{\mathcal {R}}$ rapidly converge near the origin and form spikes, but $\nabla _\theta \mathcal {L}_{\mathcal {R}}$ remains smooth, which means that the gradient of $\nabla _\theta \mathcal {L}_{\mathcal {R}}$ is almost decreasing compared to $\nabla _\theta \mathcal {L}_{\mathcal {I}}$ and $\nabla _\theta \mathcal {L}_{\mathcal {B}}$. This is a clear manifestation of gradient imbalance, and therefore it is not possible to fit the data for the IBCs accurately, which we can consider as the main reason for the failure of the original PINNs, and the relative $\mathbb {L}_2$-norm error of $7.72\%$ for the soliton molecules solution. In our experience, this behavior is very commonly seen in systems of NPDEs that use traditional PINNs models to solve more complex dynamical behaviors [8].

Now, what we obviously want to know is whether the newly raised model can effectually alleviate the gradient unbalance and thus obtain more robust and accurate prediction results. For this purpose, the gradient distributions obtained using the GOPINNs method are shown in Fig. 7. Comparing with each hidden layer corresponding to the network structure used above, we find that the gradient distribution becomes smoother and the gradient imbalance is significantly improved. In Table 2, we give the relative $\mathbb {L}_2$ errors of these two models and the training time taken to complete their learning performance. Clearly, we can see that GOPINNs not only outperform PINNs in terms of accuracy, but also have a significant advantage in terms of training time.

Fig. 7

(Color online) Soliton molecules solution (GOPINNs): Histograms of the back-propagation gradients distribution of $\nabla _\theta \mathcal {L}_{\mathcal {I}}, \nabla _\theta \mathcal {L}_{\mathcal {B}}$ and $\nabla _\theta \mathcal {L}_{\mathcal {R}}$ at per hidden layer

Figures 8 and 9 show a detailed visual assessment of the predictability of the PINNs and GOPINNs models. From Fig. 8, the PINNs model cannot get an accurate predicted solution, which its absolute error is magnified at the boundary and the crest of the wave on the lower side. As shown in Fig. 9, we can discover that the volatility of the absolute error becomes significantly smaller, especially at the boundary, and the maximum is 0.0040 and the relative $\mathbb {L}_2$ error is $0.26\%$, whose prediction accuracy is about 30 times better than PINNs. Finally, Fig. 10a and b shows the evolution of the constraint values and loss function during the continuous iteration via GOPINNs method, respectively.

Fig. 8

(Color online) Soliton molecules solution (PINNs): The exact solution and predicted solution |q(t, x)|, and their absolute error with the above parameter settings (relative $\mathbb {L}_2$ error: $\mathrm {8.11e-02}$)

Fig. 9

(Color online) Soliton molecules solution (GOPINNs): The exact solution and predicted solution |q(t, x)|, and their absolute error with the above parameter settings (relative $\mathbb {L}_2$ error: $\mathrm {2.73e-03}$)

Table 2 Soliton molecules solution: Relative $\mathbb {L}_2$ errors among the exact solution and predicted solution |q(t, x)| for these two models, and the training time for 40000 iterations of SGD with Adam optimizer

Fig. 10

(Color online) Soliton molecules solution (GOPINNs): a Evolution of constraint values $\lambda _{\mathcal {I}}$ and $\lambda _{\mathcal {B}}$ in Eq. 10 with the iterations applied to minimize the IBCs loss terms $\mathcal {L}_{\mathcal {I}}(\theta )$ and $\mathcal {L}_{\mathcal {B}}(\theta )$; b The loss values of $\mathcal {L}_{\mathcal {R}}(\theta )$ and $\mathcal {L}_{q}(\theta )$ with 40000 iterations of the SGD via Adam optimizer

4 Conclusions and discussion

Despite recent successes in some applications, PINNs often have difficulty in approximating the solutions of NPDEs exactly. In this paper, we supervise and analyze the underlying pattern of failure of PINNs related to gradient dynamics in neural networks that leads to gradient imbalance in the hidden layer when training the model via automatic back-propagation. For a deeper understanding, we quantitatively analyze the gradient dynamics in each hidden layer and clarify the troubles with training PINNs by SGD algorithm. In order to obtain a more stable gradient model, we balance the interaction between different terms in the loss function during model training by means of gradient statistics and come up with a new neural networks structure that can improve the generalization and accuracy via smoothing the distribution of gradients. We take the data-driven rational wave solution and soliton molecules solution of the complex modified KdV equation as examples, and the experimental results show that the newly proposed architecture can play an important role in the PINNs model. In summary, our study provides new insights into the development of PINNs and continuously improves their prediction accuracy by a factor of 10–30 when solving the complex modified KdV equation.

Despite some recent progress, it must be acknowledged that we are in an initial stage of comprehending the limitations of the PINNs model. To close this gap, we still have many questions to explore further: (1) What’s the relationship among the gradient fluctuations of a given NPDEs and the gradient dynamics for corresponding PINNs method? (2) How to effectively reduce these gradient fluctuations (e.g., by choosing different loss functions, more efficient neural network architectures, etc.)? (3) What else could we do to increase the generalization and prediction accuracy during training? These interesting discussions will be further explored in future work.