Enhancing PINNs for solving PDEs via adaptive collocation point movement and adaptive loss weighting

Abstract

Physics-informed neural networks (PINNs) are an emerging method for solving partial differential equations (PDEs) and have been widely applied in the field of scientific computing. In this paper, we introduce a novel adaptive PINN model for solving PDEs. The model draws on the idea of traditional adaptive methods and incorporates the adaptive collocation point movement method into the PINNs model. It can use residual information from the PDE or characteristics of the solution function itself to guide the movement of collocation points, giving an appropriate distribution of collocation points for specific problems, improving the predictive accuracy of the model, and avoiding overfitting. Additionally, the model introduces an adaptive loss weighting strategy, which updates adaptive weights continuously by minimizing negative log-likelihood estimation to achieve adaptive weighting of the loss function, thereby improving the convergence rate and accuracy of the model. Finally, we conduct extensive experiments, including the one-dimensional Poisson equation, two-dimensional Poisson equation, Burgers equation, Klein–Gordon equation, Helmholtz equation, and Lid-Driven problem, to demonstrate the effectiveness and accuracy of the proposed model. The experimental results show that the model can significantly improve predictive accuracy and generalization ability. The data and code can be found at https://github.com/hsbhc/AMAW-PINN.

1 Introduction

PDEs [1, 2] are an important mathematical tool for describing a variety of physical and engineering phenomena, including heat conduction, sound waves, electromagnetic waves, and fluid flow [3, 4]. The applications of PDEs are extensive in natural and engineering sciences, involving numerous practical problems in weather forecasting, astrophysics [5, 6], fluid dynamics [7, 8], chemical reactions, and materials science, among others [9]. However, since analytical solutions of PDEs are usually only obtainable in special cases, numerical methods have become the primary approach for solving PDEs. Traditional numerical methods have strict theoretical foundations, high accuracy, and reliability [10,11,12]. Nonetheless, these methods can be computationally expensive and typically require specific treatment for dealing with complex problems.

In recent years, deep neural networks (DNNs) [13] have become a focal point of research across nearly all scientific and engineering domains, exhibiting remarkable capabilities for tackling a variety of challenging problems. In fields such as image recognition [14], natural language processing [15], speech recognition [16], medical image diagnosis [17], and cancer discovery [18, 19], DNNs have achieved substantial success. In the field of scientific computing, DNNs also have shown great potential in solving both forward and inverse problems of PDEs [20, 21]. Many researchers have investigated methods for solving PDEs based on deep neural networks, such as the deep Galerkin method (DGM) [22], physics-informed neural networks (PINNs) [23], auxiliary physics-informed neural networks (A-PINN) [24], gradient-enhanced physics-informed neural networks (gPINNs) [25], the DeepONet operator learning framework [26, 27], and the PDE-Net framework [28]. As a result, DNNs have emerged as important tools for solving mathematical and physical equations as well as various engineering problems.

PINNs suggested by Raissi et al. [23] as a representative model have been proven to be a flexible and effective approach. In PINNs, the governing equation of PDE is encoded as a loss function that is integrated into the neural network architecture. By optimizing this loss function, the governing equations are satisfied after training the neural network, thereby enforcing the physical constraints of the problem. This approach provides a flexible and computationally efficient way to incorporate prior knowledge about physics into the neural network training process, allowing for accurate and robust solutions to be obtained for a wide range of PDE problems. PINNs and their variants [29,30,31,32,33,34,35] have achieved promising results in solving both forward and inverse PDE problems, including Navier–Stokes equations [36], fractional PDEs [37], differential-integral equations [24], stochastic differential equations [38], high-dimensional PDEs [39], and more. Moreover, PINNs have been applied to a range of engineering problems and achieved significant results, including fluid simulation [40], materials [41], thermal simulation [42], medical applications [43], and geological surveying [44], among others [45, 46].

Despite their remarkable success, PINNs still face challenges in solving complex problems. Therefore, further refinement and targeted improvements are necessary to enhance their adaptability to specific problems, accuracy, computational efficiency, and generalization capabilities [47]. Continuous refinement and optimization can lead to significant improvements in the performance of PINNs and enable them to play a more important role in a wider range of scientific and engineering applications. Recently, researchers have found that when the number of collection points is insufficient, the loss function of PINNs may become an under-constrained optimization problem, resulting in training errors that approach zero but the solution differs significantly from the true solution [48]. To address this issue, the researchers proposed a novel coupled-automatic-numerical differentiation method (CAN-PINN), which combines automatic differentiation and numerical differentiation techniques to accurately solve the problem even with an insufficient number of collection points. It is worth noting that the collection points in the PINNs model resemble the grid points in traditional numerical methods, their positions have an important impact on the performance of the model [49].

Therefore, there have been efforts to develop adaptive methods for the distribution of collection points in PINNs. Lu et al. [21] proposed a residual-based adaptive refinement (RAR) method that adds new collection points to locations with high PDE residuals. Nabian et al. [50] proposed a collection point resampling strategy that resamples all residual points according to a probability density function proportional to their PDE residuals. Additionally, Wu et al. [49] conducted a comprehensive study on non-adaptive and residual-based adaptive sampling in PINNs and proposed two unified methods, residual-based adaptive distribution (RAD) and residual-based adaptive refinement with distribution (RAR-D), which include the collection point sampling strategies proposed in studies [51,52,53,54,55]. These residual-based adaptive methods have improved the performance of PINNs, especially in shock problems. However, these methods only focus on the residuals and overlook the inherent characteristics of the solution function. They only attend to locations with large residuals, which may lead to an excessive number of collocation points at these locations while leaving other locations with insufficient collocation points, thus affecting the generalization capability of the model. In addition, these methods usually require computing the residuals, which increases the computational and time costs. Therefore, more efficient and accurate methods are needed to adapt to different types of PDE problems.

Currently, most research focuses on developing residual-based adaptive algorithms, and there is little attention paid to the role of solution characteristics in guiding the distribution of collection points, such as the gradient information of the solution. In traditional adaptive methods [56, 57], grid refinement or coarsening can be performed in corresponding regions based on the error indicators, which can be defined by the variation of the numerical solution on the grid, the gradient of the numerical solution [58], etc. This paper draws inspiration from traditional adaptive mesh refinement methods and proposes a new adaptive collection point movement method. This method can ensure that collection points are more densely distributed in regions with rapid changes, while being evenly distributed in smooth regions, thereby improving the predictive accuracy of the model, avoiding the neural network paying extreme attention to difficult-to-fit regions, and preventing overfitting.

Different from previous adaptive collocation point methods, the method proposed in this paper that divides collocation points into fixed and movable sets. During the adaptive process, only movable collocation points are updated to provide a suitable distribution of the collocation points, and without increasing the number of collocation points. In the proposed method, in addition to using residual information to guide collocation point movement, we also fully consider the characteristics of the solution itself and design a sampling method based on gradient information. In addition, the convergence of PINNs models can be effectively accelerated and their accuracy can be improved by appropriately balancing different loss terms through the use of suitable weights [59, 60]. Hence, this paper integrates the adaptive collection point movement method with the adaptive loss weighting technique proposed by Kendall et al. [61] and introduces the adaptive collection point movement and adaptive loss weighting for physics-informed neural network (AMAW-PINN) to improve the performance of the model, resulting in enhanced prediction accuracy, improved computational efficiency, and increased training robustness.

The model has a wide range of extended applications for solving complex partial differential equations and related problems in the fields of science, engineering, and applied mathematics. In particular, the model shows significant advantages in dealing with shock wave problems. With the model, we can obtain accurate numerical solutions, which provide powerful tools and methods for solving practical problems.

Specifically, our main contributions can be summarized as follows:

• A new adaptive collection point movement method is proposed, which can provide a suitable distribution of collection points according to the specific problem, improving the accuracy of the model.

• The adaptive process for the collection points can be guided by the gradient information of the solution, which is more in line with the physical characteristics of the problem and has a smaller computational cost.

• The utilization of adaptive loss weighting technology to balance the weight of the loss function improves prediction accuracy and convergence rate.

The remaining parts of this paper are organized as follows. Section 2 first reviews the principle of PINNs, then introduces in detail the proposed adaptive collection point movement method and model details. In Sect. 2.3, the principle of adaptive loss weighting technology is introduced, and it is combined with the adaptive collection point movement method. In Sect. 3, we conduct a number of numerical experiments on benchmark problems to evaluate the efficiency and precision of the proposed method. In Sects. 4 and 5, we discuss the advantages of this work and summarize this work.

2 Methods

2.1 The brief overview of PINNs

In this section, we give a quick introduction to PINNs, which are used to solve nonlinear PDEs. PINNs can infer a continuous solution function $u(\varvec{x}, t)$ based on physical equations. Consider a general nonlinear PDE:

$$\begin{aligned} \begin{array}{l} u_{t}+\mathcal {N}_{\varvec{x}}[u]=0,\ \ \quad \varvec{x} \in \Omega , t \in [0, T], \\ u(\varvec{x}, 0)=I(\varvec{x}), \ \ \ \quad \varvec{x} \in \Omega , \\ u(\varvec{x}, t)=B(\varvec{x}, t), \quad \varvec{x} \in \partial \Omega , t \in [0, T], \end{array} \end{aligned}$$

(1)

where $\varvec{x}$ and t represent the spatial and temporal coordinates, respectively. $u_{t}$ is the time derivative term, and $\mathcal {N}_{\varvec{x}}[\cdot ]$ is a differential operator. The aim is to find the solution function $u(\varvec{x}, t)$ under these known conditions.

Based on the original work of PINNs, we utilize a neural network $f(\varvec{x}, t;\theta )$ to approximate the solution function $u(\varvec{x}, t)$, where $\theta$ denotes the set of parameters for the neural network. We can express a neural network with an input layer, $L-1$ hidden layers, and an output layer as follows:

$$\begin{aligned} \textbf{x}^{0}= & {} [\varvec{x}, t]^{T}, \nonumber \\ \mathscr {L}_{l}\left( \textbf{x}^{l-1}\right)= & {} \textbf{w}^{(l)} \textbf{x}^{l-1}+\textbf{b}^{(l)}, l=1, \ldots , L. \nonumber \\ f(\varvec{x}, t;\theta )= & {} \left( \mathscr {L}_{L} \circ \cdots \circ \sigma \circ \mathscr {L}_{1}\right) \left( \textbf{x}^{0}\right) , \end{aligned}$$

(2)

where $\textbf{x}^{0}$ is the input vector, $\theta =\{\textbf{w}^{(l)}, \textbf{b}^{(l)}\}_{l=1}^{L}$ is the collection of weights and biases in the neural network, $\circ$ denotes the composition operator, and $\sigma$ is the activation function. The activation function commonly used in PINNs is the hyperbolic tangent function, denoted as tanh(x).

Subsequently, we substitute $f(\varvec{x}, t;\theta )$ into Eq. (1) and define the residual:

$$\begin{aligned} r(\varvec{x}, t;\theta ):=\frac{\partial }{\partial t} f(\varvec{x}, t;\theta )+\mathcal {N}_{\varvec{x}}\left[ f(\varvec{x}, t;\theta )\right] , \end{aligned}$$

(3)

where the partial derivatives concerning the variables can be effortlessly obtained utilizing automatic differentiation. The loss function of the PINNs model consists of multiple loss components, and its general form is expressed as:

$$\begin{aligned} \mathcal {L}(\theta )=\lambda _{i} \mathcal {L}_{i}(\theta ) + \lambda _{b} \mathcal {L}_{b}(\theta ) +\lambda _{r} \mathcal {L}_{r}(\theta ), \end{aligned}$$

(4)

where $\lambda _{i}, \lambda _{b}$, and $\lambda _{r}$ are the weight parameters for the corresponding loss terms, while $\mathcal {L}_{i}(\theta ), \mathcal {L}_{b}(\theta )$, and $\mathcal {L}_{r}(\theta )$ represent the initial condition loss term, boundary condition loss term, and residual loss term, respectively. The specific forms of these loss terms are:

$$\begin{aligned} \begin{array}{l} \left. \mathcal {L}_{i}(\theta )=\frac{1}{N_{i}} \sum _{j=1}^{N_{i}}\left[ f\left( \varvec{x}_{i}^{j}, 0;\theta \right) -I(\varvec{x}_{i}^{j})\right) \right] ^{2},\\ \mathcal {L}_{b}(\theta )=\frac{1}{N_{b}} \sum _{j=1}^{N_{b}}\left[ f\left( \varvec{x}_{b}^{j}, t_{b}^{j};\theta \right) -B\left( \varvec{x}_{b}^{j}, t_{b}^{j}\right) \right] ^{2}, \\ \mathcal {L}_{r}(\theta )=\frac{1}{N_{r}} \sum _{j=1}^{N_{r}}\left[ r\left( \varvec{x}_{r}^{j}, t_{r}^{j};\theta \right) \right] ^{2}, \\ \end{array} \end{aligned}$$

(5)

where $\{\varvec{x}_{i}^{j}, I(\varvec{x}_{i}^{j})\}_{j=1}^{N_{i}}$ denotes the initial point data, $\{(\varvec{x}_{b}^{j}, t_{b}^{j}), B(\varvec{x}_{b}^{j}, t_{b}^{j})\}_{j=1}^{N_{b}}$ represents the boundary point data, and $\{\varvec{x}_{r}^{j}, t_{r}^{j}\}_{j=1}^{N_{r}}$ refers to the internal collocation points, $N_{i}, N_{b}, N_{r}$ are the respective number of data points. The initial point data serves to enforce the initial condition on the neural network, while the boundary point data is used to ensure that the neural network satisfies the boundary condition. The internal collocation points are randomly selected coordinate points from the domain $\Omega$ to compute the residual loss, which forces the neural network $f(\varvec{x}, t;\theta )$ to fulfill the governing equation. Once the training data is prepared, we can employ gradient descent methods commonly used in deep learning, such as Adam, SGD, or L-BFGS, to optimize the neural network parameters. By minimizing the loss function and bringing $\mathcal {L}(\theta )$ as close to zero as possible, we can consider the neural network $f(\varvec{x}, t;\theta )$ as an approximate solution function $u(\varvec{x}, t)$ for Eq. (1) when the loss reaches a minimum value.

Fig. 1

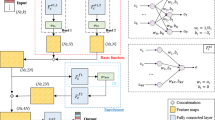
AM-PINN: Adaptive collocation point movement for PINNs. $P_{N_\textrm{rn}}$ is the set of fixed collocation points, which are fixed during the model training and generated by the uniform sampling strategy. $P_{N_\textrm{rm}}$ is the set of movable collocation points which can be dynamically changed during the training process

2.2 Adaptive collocation point movement for PINNs

The PINNs model is highly concise and efficient, and has been widely applied to the solution of various PDEs with good results. However, in some cases, the solution obtained by PINNs may not be ideal. By observing the form of the PINNs loss function, it can be seen that the initial and boundary conditions belong to the labeled learning in traditional machine learning, which is a typical supervised training. Neural networks easily converge in supervised learning. However, the residual loss term has no labels, and it is a soft constraint. This soft constraint may lead to the neural network being unable to optimize in the right direction when there are few collocation points or the collocation point distribution is unreasonable [62]. On the other hand, the importance of each region in the computational domain is different. In some regions, the solution function is relatively smooth, and the neural network can easily fit it; while in other regions, the solution function has strong nonlinearity, and more points are needed in these difficult-to-fit regions to obtain good solution results. Therefore, when the distribution of collocation points cannot adapt to the specific problem, PINNs cannot provide good solutions, especially when there are few collocation points. Therefore, a reasonable strategy for selecting collocation points tailored to the specific problem is crucial, and the distribution of collocation points can be adjusted through adaptive methods to obtain better solution results.

In traditional numerical methods, adaptive moving mesh technology can continuously adjust the mesh in regions with significant variations, refine the mesh points during the iteration process, couple the distribution of mesh points with the physical solution, and thus improve the accuracy and resolution of the solution without increasing the number of mesh points. In the PINNs model framework, we do not need to consider the issue of mesh partitioning and only need to focus on the positions of the collocation points. Therefore, adaptive technology can be easily introduced.

Inspired by traditional moving mesh methods, this paper introduces adaptive moving mesh technology into the PINNs model and proposes an iterative model of adaptive collocation point movement PINN (AM-PINN). This model allows the dynamic movement of collocation points during the training process, making the collocation points densely distributed in important areas and uniformly distributed in regular areas, thus finding a suitable collocation point distribution for specific problems. The AM-PINN framework is illustrated in Fig. 1.

Specifically, we denote the initial point set as $P_{N_{i}}$, the boundary point set as $P_{N_{b}}$, and the set of $N_{r}$ collocation points as $P_{N_{r}}$. Thus,

$$\begin{aligned} P_{N_{r}} = \left\{ \varvec{x}_{r}^{j}, t_{r}^{j}\right\} _{j=1}^{N_{r}}. \end{aligned}$$

(6)

Then, the collocation points $P_{N_{r}}$ are divided into two parts, $P_{N_\textrm{rn}}$ and $P_{N_\textrm{rm}}$.

$$\begin{aligned} P_{N_{r}} = P_{N_\textrm{rn}} \cup P_{N_\textrm{rm}}, \end{aligned}$$

(7)

where $P_{N_\textrm{rn}} = \{\varvec{x}_\textrm{rn}^{j}, t_\textrm{rn}^{j}\}_{j=1}^{N_\textrm{rn}}$ refers to a fixed set of collocation points that remain unchanged during the model training process. These points are generated through a uniform sampling strategy. On the other hand, $P_{N_\textrm{rm}} = \{\varvec{x}_\textrm{rm}^{j}, t_\textrm{rm}^{j}\}_{j=1}^{N_\textrm{rm}}$ represents a set of movable collocation points that gradually aggregate to the important computing areas during the training process, similar to the grid moving process in the moving mesh method (i.e., gradually aggregating in regions with large gradients of the solution). By combining these two sets of collocation points, we can achieve adaptive movement of the collocation points that participate in the training process. We demonstrate the approach using a simple 2D function, as shown in Fig. 2.

$$\begin{aligned} u(x,y) = 100e^{-10(x^2+y^2)}. \end{aligned}$$

(8)

The movement of movable collocation points is achieved by resampling this set of points during the training process, similar to the process of grid refinement or coarsening in the moving mesh method based on the error estimator. Many works [21, 49] have shown that adding collocation points with larger residuals can help the PINN model converge quickly during the training process. Therefore, some adaptive PINN training methods that use the residual of collocation points as an error estimator have been designed, such as RAR and RAD. RAR requires constantly adding points with larger residuals to the collocation point set, while RAD resamples the collocation points across the entire domain based on the residual distribution.

Fig. 2

An example of collocation points: $P_{N_{r}} = P_{N_\textrm{rn}} \cup P_{N_\textrm{rm}}$, $N_r = 2000,N_\textrm{rn} = N_\textrm{rm} = 1000$

In contrast to previous approaches in adaptive collocation point methods, this paper introduces a novel adaptive collocation point movement. This method divides the collocation points into two sets: fixed and movable. Unlike traditional methods, where all collocation points are updated during the adaptive process, our approach focuses solely on updating the movable collocation points. The proposed method not only utilizes residual information to guide the movement of collocation points but also takes into account the characteristics of the solution itself. Firstly, we define Eq. (9) as an indicator of the variation of the solution function.

$$\begin{aligned} \omega = \sqrt{1+\alpha |u|^2 + \beta \left\| \nabla u \right\| ^2+\gamma \left\| \nabla ^2 u \right\| ^2}, \end{aligned}$$

(9)

where $\alpha$, $\beta$, and $\gamma$ are adjustable coefficients. This formula includes the function value, gradient value, and second-order derivative value, which is sufficient to measure the variation of the solution in the local area and is highly flexible. For most problems, the commonly used gradient indicator is sufficient, which means that we only need to set $\alpha = 0$, $\beta = 1$, and $\gamma = 0$. Thus,

$$\begin{aligned} \omega (\varvec{x}) = \sqrt{1+ \left\| \nabla u(\varvec{x}) \right\| ^2}. \end{aligned}$$

(10)

Next, we define a probability density function and resample the movable collocation points in the computational domain based on the probability density function:

$$\begin{aligned} p(\varvec{x}) = \frac{w^{k}(\varvec{x})}{\sum w^{k}(\varvec{x})}, \end{aligned}$$

(11)

where k is a hyperparameter. $p(\varvec{x})$ becomes a uniform distribution when $k = 0$, and as k increases, the sampling points will be more concentrated in the high-gradient areas. We still use the simple two-dimensional function Eq. (8) as an example to demonstrate the effect of the parameter k on sampling, as shown in Fig. 3. Additionally, if we replace $w(\varvec{x})$ with the absolute value of the collocation point residual $\vert r(\varvec{x})\vert$, where $r(\varvec{x})$ is calculated by Eq. (3), the gradient indicator can be replaced by the residual indicator. In this paper, the adaptive collocation point movement based on the residual indicator is called RAM, while that based on the gradient indicator is called WAM.

Fig. 3

The parameter k can control the degree of concentration of sampling points, where $\omega (x,y) = u(x,y)$ and $k=0.5,1,2$

The movement of movable collocation points $P_{N_\textrm{rm}}$ during model training is achieved by resampling based on the probability density function $p(\varvec{x})$, which results in the aggregation of collocation points in important computational areas. Additionally, fixed collocation points $P_{N_\textrm{rn}}$ ensure that collocation points are evenly distributed in regular computational areas, preventing the model from focusing too much on difficult-to-fit areas and ignoring smooth areas. By combining $P_{N_\textrm{rn}}$ and $P_{N_\textrm{rm}}$, collocation points can achieve adaptive movement, with uniform distribution in smooth areas and dense distribution in difficult-to-fit areas, thus adapting to specific problems and automatically providing appropriate collocation point distributions to improve model accuracy.

During the specific iterative training, we move the collocation points $P_{N_\textrm{rm}}$ every certain number of training iterations. A more general approach is to use the L-BFGS optimizer for optimization, which will automatically stop training after convergence, allowing for the movement of collocation points and the start of the next round of training. However, the L-BFGS optimizer is prone to falling into local minima. Therefore, in each training round, we can first use the Adam optimizer to optimize for a certain number of iterations to update the parameters to appropriate initial values, and then use the L-BFGS optimizer to converge [63]. The specific algorithm of AM-PINN is shown in Algorithm 1. AM-count is the number of rounds for adaptive collocation point movement.

Training for AM-PINN

2.3 Adaptive loss weighting for AM-PINN

In the previous section, we introduced the AM-PINN model in detail. In this section, to achieve automatic weighting of the loss function, we introduce the adaptive loss weighting technique into AM-PINN and propose the AMAW-PINN model to further improve performance. The model structure of AMAW-PINN is shown in Fig. 4.

The loss function of AM-PINN is the same as that of PINNs, consisting of multiple loss terms. Many studies have shown that the loss function of PINNs is a multi-task loss function, and balancing the different loss terms using appropriate weights ${\lambda _{i},\lambda _{b},\lambda _{r}}$ can effectively accelerate the convergence of the PINNs model and improve its accuracy [59, 60]. It is essential to introduce the adaptive loss weighting technique in the AM-PINN model. This technique eliminates the tedious and time-consuming process of manually tuning the loss weights. Moreover, when one round of training AM-PINN converges, and the movable collocation points $P_{N_\textrm{rm}}$ get updated, the distribution of the collocation points changes, resulting in a change of the training data used to compute the residual loss $\mathcal {L}_{r}(\theta )$. Thus, AM-PINN requires constantly using an adaptive loss balancing technique to determine appropriate weights ${\lambda _{i},\lambda _{b},\lambda _{r}}$ that can adapt to the entire training iteration process of the AM-PINN model.

In this paper, to balance the loss of each task, we use the multi-task learning approach described in [61]. The homoscedastic uncertainty of each task is used to modify the weights of the loss function. Specifically, this method updates the adaptive weights through maximum likelihood estimation to automatically weight the loss of each task. We incorporate this method into the AM-PINN model and propose AMAW-PINN. The specific adaptive weight algorithm is as follows.

Fig. 4

AMAW-PINN: Adaptive loss weighting for AM-PINN. $s_i,s_b,s_r$ are trainable adaptive parameters

First, we model the output of the neural network as a Gaussian probability distribution:

$$\begin{aligned} p(u|NN(\varvec{x},t,\theta )) = \mathcal {N}(u|NN(\varvec{x},t,\theta ),\sigma ^2), \end{aligned}$$

(12)

where $\sigma$ is the noise parameter, representing the uncertainty of the task. Assuming there are K tasks in total, we maximize the joint probability distribution of all tasks.

$$\begin{aligned} p(u_{1},u_{2},...,u_{K}|NN(\varvec{x},t,\theta )) = \prod _{k=1}^{K} p(u_{k}|NN(\varvec{x},t,\theta )). \end{aligned}$$

(13)

Next, we take the negative logarithm of the likelihood function to get the negative log-likelihood as the desired loss function.

$$\begin{aligned}&-\log p(u_{1},u_{2},...,u_{K}|NN(\varvec{x},t,\theta ))\nonumber \\&\quad = -\sum _{k=1}^{K} \log p(u_{k}|NN(\varvec{x},t,\theta )) \end{aligned}$$

(14)

$$\begin{aligned}&\quad = -\sum _{k=1}^{K} \log \mathcal {N}(u_{k}|NN(\varvec{x},t,\theta ),\sigma _{k}^2) \end{aligned}$$

(15)

$$\begin{aligned}&\quad \propto \ \ \ \sum _{k=1}^{K} \left( \frac{1}{2\sigma _{k}^{2}}\mathcal {L}_{k} + \frac{1}{2}\log \sigma _{k}^2\right) . \end{aligned}$$

(16)

The first term in Eq. (16) represents the weighted loss function for each task, and the second term is a regularization term that penalizes tasks with high uncertainty. Minimizing Eq. (16) is equivalent to maximizing the joint probability distribution of all tasks, thereby adaptively assigning appropriate weight coefficients to each task to balance their loss functions. Each task corresponds to an uncertainty parameter $\sigma$, and if a task is easy to learn with low uncertainty, it will be assigned a higher weight, while a task with high uncertainty will have its weight reduced. The regularization term ensures that $\sigma$ does not become too large and prevents the model from ignoring difficult tasks.

In summary, the final adaptive loss function of AMAW-PINN based on uncertainty is given by:

$$\begin{aligned} \mathcal {L}(\theta ,\sigma )&= \frac{1}{2\sigma _{i}^{2}} \mathcal {L}_{i}(\theta )+ \frac{1}{2\sigma _{b}^{2}}\mathcal {L}_{b}(\theta ) +\frac{1}{2\sigma _{r}^{2}} \mathcal {L}_{r}(\theta )\nonumber \\&\quad + \frac{1}{2}\log \sigma _{i}^2 + \frac{1}{2}\log \sigma _{b}^2 + \frac{1}{2}\log \sigma _{r}^2 , \end{aligned}$$

(17)

where trainable uncertainty parameters $\sigma = {\sigma _{i},\sigma _{b},\sigma _{r}}$ are added. During actual training, in order to avoid the denominator becoming zero as much as possible and since $\log \sigma ^2$ is more stable than $\sigma ^2$, we introduce trainable adaptive parameters $s = \{s_{i},s_{b},s_{r}\}$, where $s_{k} = \log \sigma _{k}^2$. Then, the adaptive loss function of AMAW-PINN can be expressed as:

$$\begin{aligned}&\mathcal {L}(\theta ,s) = \frac{1}{2}e^{(-s_{i})} \mathcal {L}_{i}(\theta )+ \frac{1}{2}e^{(-s_{b})}\mathcal {L}_{b}(\theta ) \nonumber \\&\qquad +\frac{1}{2} e^{(-s_{r})}\mathcal {L}_{r}(\theta )\nonumber \\&\qquad + \frac{1}{2}s_{i} + \frac{1}{2}s_{b} + \frac{1}{2}s_{r} \end{aligned}$$

(18)

$$\begin{aligned}&\quad \propto e^{(-s_{i})} \mathcal {L}_{i}(\theta )+ e^{(-s_{b})}\mathcal {L}_{b}(\theta ) +e^{(-s_{r})}\mathcal {L}_{r}(\theta )\nonumber \\&\qquad + s_{i} +s_{b} + s_{r}. \end{aligned}$$

(19)

We use Eq. (19) as the final loss function for AMAW-PINN. The trainable parameters $s = \{s_{i},s_{b},s_{r}\}$ are incorporated into the model, and they can be optimized using gradient-based optimizers such as SGD or Adam, and can have different learning rates(denoted as AW-lr) than the network parameters $\theta$. In comparison with the standard PINNs model, $\lambda _{k}$ corresponds to $e^{(-s_{k})}$. Algorithm 2 shows the training algorithm for AMAW-PINN. $Adam-iters$ is the number of Adam optimizations per training round.

AMAW-PINN

3 Results

In this section, we consider a variety of partial differential equations and provide a series of numerical experiments to verify the efficacy of the proposed methods. We use standard PINN as the baseline, and name the adaptive collocation point movement PINN as AM-PINN (based on residual sampling referred to as RAM and based on gradient sampling referred to as WAM). Additionally, we name the model with the introduction of adaptive loss weighting as AMAW-PINN (based on residual sampling referred to as RAM-AW and based on gradient sampling referred to as WAM-AW). In the WAM and WAM-AW models, we use a uniform gradient indicator to compute $\omega (\varvec{x})$. The formula is as follows:

$$\begin{aligned} \omega (\varvec{x}) = \sqrt{1+ [u_{x_{1}}(\varvec{x};\theta )]^{2} +\dots + [u_{x_{n}}(\varvec{x};\theta )]^{2}} \end{aligned}$$

(20)

In the RAM and RAM-AW models, the formula for calculating $\omega (\varvec{x})$ is as follows:

$$\begin{aligned} \omega (\varvec{x}) = \mid r(\varvec{x};\theta )\mid \end{aligned}$$

(21)

We first study the performance of the AM-PINN model on a one-dimensional Poisson equation. The results show that the predictions given by the AM-PINN model are more accurate. Then, we study the performance of both the AM-PINN and AMAW-PINN models on a two-dimensional Poisson equation. The experiments not only validate the effectiveness of the AM-PINN model but also demonstrate that the adaptive weights can automatically balance the loss functions, improving the accuracy of the model. Next, we conduct experiments on a series of benchmark examples, including the Burgers equation, Klein–Gordon equation, and Helmholtz equation. Finally, we use the WAM-AW model to solve the Navier–Stokes equation in fluid dynamics, which serves to further validate the efficacy of our proposed model.

The prediction accuracy is measured by the relative L2 error. To compare the performance of different models fairly, all comparative experiments are conducted under the same conditions. Key parameters such as Adam-iters (number of Adam iterations), Adam-lr (Adam learning rate), LBFGS-iters (maximum number of L-BFGS iterations), AM-k (parameter k of the probability density function $p(\varvec{x})$), and AW-lr (learning rate of the adaptive weight parameter s) are kept the same across all experiments. The values are listed in Table 1. Table 8 shows the summary of the main symbols and notations used in this work. PyTorch is used to implement the neural network.

$$\begin{aligned} \text {L2error }=\frac{\sqrt{\sum _{i=1}^{N}\left| \widehat{u}\left( x_{i}, t_{i}\right) -u\left( x_{i}, t_{i}\right) \right| ^{2}}}{\sqrt{\sum _{i=1}^{N}\left| u\left( x_{i}, t_{i}\right) \right| ^{2}}} \end{aligned}$$

(22)

3.1 One-dimensional Poisson equation

We first consider the one-dimensional Poisson equation with Dirichlet boundary conditions:

$$\begin{aligned} \left\{ \begin{array}{lll} u_{xx} =g(x),&{} x \in \Omega = [-1,1] \\ u = h(x),&{} x\in \partial \Omega \\ \end{array}\right. \end{aligned}$$

(23)

where the boundary function h(x) and forcing term g(x) are known. We aim to solve for the function u(x) in the domain $x \in [-1,1]$ that satisfies the Poisson equation with Dirichlet boundary conditions.

The solution to this equation is chosen as $u(x) = 0.1 \sin (4 \pi x) + \tanh (50 x)$, which exhibits a steep change near $x=0$. In this example, we utilize a fully connected neural network $f(x;\theta )$ to approximate the function u(x), which has four hidden layers and each layer is composed of 20 neurons. Subsequently, the residual of the PDE can be expressed as:

$$\begin{aligned} r(x;\theta ):=f_{xx}(x;\theta ) - g(x) \end{aligned}$$

(24)

The loss function $\mathcal {L}(\theta )$ is constructed using the equation and boundary conditions, and it consists of two components:

$$\begin{aligned} \mathcal {L}(\theta )=\lambda _{b} \mathcal {L}_{b}(\theta ) +\lambda _{r} \mathcal {L}_{r}(\theta ) \end{aligned}$$

(25)

where

$$\begin{aligned} \mathcal {L}_{b}(\theta )= & {} \frac{1}{N_{b}} \sum _{j=1}^{N_{b}}\left[ f\left( x_{b}^{j};\theta \right) -h\left( x_{b}^{j}\right) \right] ^{2} \end{aligned}$$

(26)

$$\begin{aligned} \mathcal {L}_{r}(\theta )= & {} \frac{1}{N_{r}} \sum _{j=1}^{N_{r}}\left[ r(x_{r}^{j};\theta )\right] ^{2} \end{aligned}$$

(27)

Table 1 Uniform hyperparameter values

Fig. 5

The solution results of the one-dimensional Poisson equation, with a total of 60 collocation points

Fig. 6

The changes in relative L2 error and test residual for the four models

In this example, we conduct experiments using PINN, WAM, and RAM, respectively. To better illustrate the positive effect of adaptive collocation point movement on the solution accuracy, we also set up a randomly uniform sampled Random-PINN model by setting the probability density function parameter k to 0. In this experiment, all neural network structures are identical, and the weights of the loss function are set to ${\lambda _{b} = 10,\lambda _{r}=1}$. The boundary points $\{x_{b}^{j}\}_{j=1}^{N_{b}}, N_{b} = 2$ are the two endpoints of the computational domain, and the internal collocation points $P_{N_{r}}$ are divided into two parts, $P_{N_\textrm{rn}}$ and $P_{N_\textrm{rm}}$, where $N_{r} = N_\textrm{rn}+N_\textrm{rm} = 60, N_\textrm{rn}=N_\textrm{rm} = 30$. The fixed collocation points $P_{N_\textrm{rn}}$ are chosen as equidistant points within the $[-1,1]$ interval. During the training of PINN, we use 60 equidistant collocation points. The training process employs the Adam optimizer with a 0.001 learning rate, and each model is optimized for a total of 100,000 epochs. For the WAM, RAM, and Random models, the collocation points $P_{N_\textrm{rm}}$ are moved every 10,000 epochs. To compare the accuracy of different models, we sample 10,000 test points at equal intervals within the $[-1,1]$ range and calculate the test loss and the relative L2 error every 2,000 epochs.

Table 2 The one-dimensional Poisson equation: the relative L2 error of the four methods with $N_{r}$ equal to 30, 50, 70, 90, and 110

Fig. 7

The test residual and the relative L2 error of the four models as the number of collocation points varies

The experimental results are shown in Figs. 5 and 6. Both the standard PINN and Random-PINN cannot accurately solve the equation. They fail to fit the true solution in the vicinity of $x=0$ where the function has large gradients. In contrast, the RAM and WAM methods can solve the problem well, and can obtain accurate results even near $x=0$, thanks to the fact that they move a portion of the collocation points close to $x=0$. In addition, it can be observed from Fig. 5 that after training, the residuals of the four models near $x=0$ are relatively higher compared to other regions. Compared with PINN, the RAM and WAM models have smaller residuals near $x=0$. This fully demonstrates that the AM-PINN can adjust the distribution of collocation points according to specific problems, so that the distribution of collocation points adapts to the problem to be solved, and thereby improves the accuracy of solutions. Figure 6 shows the testing results of the four models during training. The relative L2 error and residual of the standard PINN experience a phenomenon of first decreasing and then increasing, which indicates that these collocation points cannot provide more information for training and the model suffers from overfitting. Since the collocation points used by Random-PINN are randomly sampled, its relative L2 error and residual fluctuate greatly. In contrast, the AM-PINN method has a lower testing error and test residual, and its residual decreases more steadily.

To further demonstrate the advantages of the AM-PINN model, we varied the number of collocation points. Specifically, we start with 30 points and increase them by 20 at each step, up to a maximum of 110 points. In each configuration, we keep the number of fixed and movable collocation points equal, that is, $N_\textrm{rn}=N_\textrm{rm} = \frac{1}{2}N_{r}$, while keeping other settings constant. The results are presented in Table 2 and Fig. 7. The AM-PINN approach attains greater precision compared to alternative models, both for RAM and WAM cases. With the increase in collocation points, the differences in accuracy among the four models become smaller. From the testing residual in Fig. 7, the AM-PINN method has a smaller test residual, which indicates that its results are more reliable and the model has better generalization ability.

3.2 Two-dimensional Poisson equation

Fig. 8

Two-dimensional Poisson equation: the absolute error, cross-sectional views, and distribution of movable collocation points for PINN and AM-PINN

Next, let us consider the following two-dimensional Poisson equation to further test the model proposed in this paper:

$$\begin{aligned} \left\{ \begin{array}{lll} u_{xx} + u_{yy} =g(x,y),&{} x,y \in \Omega = [-1,1]^2, \\ u = h(x,y),&{} x,y\in \partial \Omega , \\ \end{array}\right. \end{aligned}$$

(28)

where g(x, y) and h(x, y) are known functions. We assume that the solution to this problem has two peaks, with the form given as:

$$\begin{aligned} u(x,y) = e^{-k [(x - x_1)^2 + (y - y_1)^2]} + e^{-k [(x - x_2)^2 + (y - y_2) ^2]}, \end{aligned}$$

(29)

where the magnitude of k represents the steepness of the function, and $(x_1, y_1), (x_2, y_2)$ are the coordinates of the two peaks. In this experiment, we choose k to be 500, with the peak coordinates set as (0.5, 0.5) and $(-0.5, -0.5)$.

We employ a fully connected neural network, denoted as $f(x, y; \theta )$, to approximate u(x, y). The residual expression for this problem is as follows:

$$\begin{aligned} r(x,y;\theta ):=f_{xx}(x,y;\theta ) + f_{yy}(x,y;\theta ) - g(x,y) \end{aligned}$$

(30)

Following this, we formulate the loss function as follows:

$$\begin{aligned} \mathcal {L}(\theta )=\lambda _{b} \mathcal {L}_{b}(\theta ) +\lambda _{r} \mathcal {L}_{r}(\theta ) \end{aligned}$$

(31)

where

$$\begin{aligned} \mathcal {L}_{b}(\theta )= & {} \frac{1}{N_{b}} \sum _{j=1}^{N_{b}}\left[ f\left( x_{b}^{j},y_{b}^{j};\theta \right) -h\left( x_{b}^{j},y_{b}^{j}\right) \right] ^{2} \end{aligned}$$

(32)

$$\begin{aligned} \mathcal {L}_{r}(\theta )= & {} \frac{1}{N_{r}} \sum _{j=1}^{N_{r}}\left[ r(x_{r}^{j},y_{r}^{j};\theta )\right] ^{2} \end{aligned}$$

(33)

In this example, the loss function weights are set as ${\lambda _{b} = 100, \lambda _{r} = 1}$, and the training data configuration is defined as $N_b = 400, N_r = 2000$. Specifically, 100 data points are uniformly sampled at each boundary, resulting in a total of 400 boundary data points. $N_\textrm{rn}$ and $N_\textrm{rm}$ are both chosen as 1000, with collocation points initialized as uniformly sampled points within the computational domain. The number of iteration rounds for AM-PINN is set to 10. For testing, a $256 \times 256$ uniform grid is used to compute the relative L2 error.

Figure 8 illustrates the absolute error, cross-sectional views, and distribution of movable collocation points for PINN and AM-PINN. As seen in 8, the adaptive movement of collocation points leads to their clustering in steep regions, which reduces the error of the model. In RAM, movable collocation points are more dispersed and gather in areas with larger residuals, while in WAM, they are more densely distributed in regions where the function is steep and uniformly distributed in other areas. Both RAM and WAM models achieve a good approximation of the solution function. Additionally, Fig. 9 shows the convergence curves of AM-PINN with iterations increases. It can be observed that both RAM and WAM converge quickly to minimal error.

Fig. 9

The relative L2 error of the two-dimensional Poisson problem with the number of iterative rounds

To further demonstrate the effectiveness of AM-PINN, we conduct experiments with varying numbers of collocation points. In these experiments, we change the number of fixed collocation points while keeping the number of movable collocation points constant, and set the number of iteration rounds for AM-PINN to 5. The experimental results are shown in Table 3, indicating that AM-PINN can achieve higher accuracy.

Table 3 The relative L2 error of the two-dimensional Poisson equation with $N_\textrm{rm} = 1000$ movable collocation points

Fig. 10

Left: $N_\textrm{rn} = 500$, a comparison between RAM and RAM-AW models. Right: $N_\textrm{rn} = 1000$, a comparison between WAM and WAM-AW models

Fig. 11

Left: $N_\textrm{rn} = 500$, the change in weights $e^{(-s)}$ for RAM-AW. Right: $N_\textrm{rn} = 1000$, the change in weights $e^{(-s)}$ for WAM-AW

Table 4 the relative L2 errors for various models with $N_\textrm{rm} = 1000$

In previous experiments, we manually set the loss function weights as ${\lambda _{b} = 100, \lambda _{r} = 1}$. Now, instead of manually setting the weights, we employ an adaptive loss weighting method to automatically learn appropriate weights. According to the AMAW-PINN model, we modify the loss function as follows:

$$\begin{aligned} \mathcal {L}(\theta ,s) = e^{(-s_{b})}\mathcal {L}_{b}(\theta ) +e^{(-s_{r})}\mathcal {L}_{r}(\theta )+ s_{b} + s_{r} \end{aligned}$$

(34)

where $s = \{s_{b}, s_{r}\}$ are both initialized as 0, which is equivalent to setting the weights to 1 in the standard loss function. The parameters s are optimized using the Adam optimizer with a learning rate of AW-lr = 0.001. The number of movable collocation points is still set as $N_\textrm{rm} = 1000$, and experiments are conducted for $N_\textrm{rn} = 500$ and $N_\textrm{rn} = 1000$, respectively.

Figure 10 presents the iteration convergence curves for both the RAM-AW and WAM-AW models. As seen in Fig. 10, incorporating the adaptive loss weighting technique into the AM-PINN model significantly improves the accuracy of the model and convergence speed. As shown in Fig. 11, adaptive weights gradually change with iterations and ultimately converge. Consequently, AMAW-PINN can adaptively allocate weights to the loss terms, which enhances the solution accuracy of the model. Observing Fig. 11, it can be seen that the weight of the boundary condition is significantly larger than the weight of the internal collocation point residual loss, which validates the effectiveness of the adaptive loss weighting. By employing adaptive weighting, the model can dynamically adjust the weights, which enables it to focus more on learning easier tasks while still addressing tasks with higher uncertainty. This approach helps the model strike a balance between all the tasks and optimize its performance.

The relative L2 error of the experiments is shown in Table 4. The standard PINN cannot correctly solve the problem when the loss function weights are set as ${\lambda _{b} = 1, \lambda _{r} = 1}$, regardless of whether $N_\textrm{rn} = 500$ or $N_\textrm{rn} = 1000$. However, using the adaptive collocation point movement model can improve the accuracy by an order of magnitude. The integration of adaptive weights in the model can further improve accuracy by another order of magnitude. This fully validates the effectiveness of the AMAW-PINN model, which can not only find suitable collocation point distributions for specific tasks but also automatically weight the loss function, balancing the loss of each task and achieving the desired prediction accuracy.

Next, we give a series of benchmark numerical experiments to investigate the effectiveness and high performance of the AMAW-PINN model. This includes testing the performance of the proposed model on shockwave problems and strongly time-dependent problems.

3.3 Burgers equation

Initially, we examine the Burgers equation, which is a fundamental partial differential equation in fluid dynamics, describing the dynamics of viscous fluids [64, 65]. It exhibits shockwave behavior, making it analytically challenging to solve and a research focus in the field of nonlinear dynamics. The equation is given as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} u_t + u u_x = \mu u_{xx},\ \ x \in [-1,1],\ t \in [0,1], \\ u(0,x) = -\sin (\pi x),\\ u(t,-1) = u(t,1) = 0,\\ \end{array}\right. \end{aligned}$$

(35)

Fig. 12

The exact solution and predicted solution of Burgers equation

Fig. 13

Predicted cross-sectional plots of Burgers equation using RAM-AW and WAM-AW

Fig. 14

The weight variation of the loss function and iteration convergence curves of RAM-AW and WAM-AW for Burgers equation

Fig. 15

Burgers equation: the absolute error, residual, and distribution of movable collocation points for PINN and AMAW-PINN

In this work, $\mu = \frac{0.01}{\pi }$ is taken. The AMAW-PINN model is used to solve this equation with a network structure consisting of 4 hidden layers, each with 20 neurons. The equation’s residual is defined as follows:

$$\begin{aligned} r(x,t;\theta ):=f_{t} + f f_{x} - \frac{0.01}{\pi } f_{xx} \end{aligned}$$

(36)

The derivative terms in $r(x,t;\theta )$ can be obtained using automatic differentiation. The loss function is defined as follows:

$$\begin{aligned} \mathcal {L}(\theta ,s)&= e^{(-s_{i})}\mathcal {L}_{i}(\theta )+e^{(-s_{b})}\mathcal {L}_{b}(\theta ) +e^{(-s_{r})}\mathcal {L}_{r}(\theta )\nonumber \\&\quad +s_{i}+ s_{b} + s_{r} \end{aligned}$$

(37)

where

$$\begin{aligned} \mathcal {L}_{i}(\theta )= & {} \frac{1}{N_{i}} \sum _{j=1}^{N_{i}}\left[ f\left( x_{i}^{j},0;\theta \right) +\sin (\pi x_{i}^{j})\right] ^{2} \end{aligned}$$

(38)

$$\begin{aligned} \mathcal {L}_{b}(\theta )= & {} \frac{1}{N_{b}} \sum _{j=1}^{N_{b}}\left[ f\left( x_{b}^{j},t_{b}^{j};\theta \right) \right] ^{2} \end{aligned}$$

(39)

$$\begin{aligned} \mathcal {L}_{r}(\theta )= & {} \frac{1}{N_{r}} \sum _{j=1}^{N_{r}}\left[ r(x_{r}^{j},t_{r}^{j};\theta )\right] ^{2} \end{aligned}$$

(40)

where $\{x_{i}^{j}\}_{j=1}^{N_{i}}$ represents the initial points, $\{x_{b}^{j},t_{b}^{j}\}_{j=1}^{N_{b}}$ represents the boundary points, and $\{x_{r}^{j},t_{r}^{j}\}_{j=1}^{N_{r}}$ represents the randomly sampled collocation points within the computational domain.

In this experiment, we initialize $s_{i}=s_{b}=s_{r}=0$. The training data is composed of 100 initial points ($N_{i} = 100$), 200 boundary points ($N_{b} = 200$) randomly sampled at each of the two boundaries $x=-1$ and $x=1$, and 2000 collocation points ($N_{r} = 2000$) within the computational domain, with 1500 fixed collocation points ($N_\textrm{rn} = 1500$) and 500 movable collocation points ($N_\textrm{rm} = 500$). The weight parameters s are optimized by the Adam optimizer. The total number of iteration rounds for adaptive movement is set to 10.

Table 5 The relative L2 error for Burgers equation when $N_\textrm{rm}=500$

Figures 12 and 13 show the comparison between the predicted solutions by RAM-AW and WAM-AW models and the exact solution for the Burgers equation. The results demonstrate that AMAW-PINN can effectively solve Burgers equation. From Fig. 14a and b, it can be observed that the convergence paths of the loss function weights of RAM-AW and WAM-AW models are quite similar, with the weights of the boundary and initial conditions becoming larger. Figure 14c indicates that, compared with the standard PINN, AMAW-PINN can achieve an error level of $10^{-4}$ using only 2000 collocation points, while PINN can only reach an error level of $10^{-2}$. Additionally, after the first training iteration, it can be seen that the error of AMAW-PINN is larger than that of PINN, which may be because the weights of the loss function have not yet converged. Figure 15 shows the absolute error, residual, and distribution of movable collocation points for PINN, RAM-AW, and WAM-AW models. RAM-AW and WAM-AW models have smaller errors and residuals, and the movable collocation points are concentrated at the location of the shock.

We also conduct on the AMAW-PINN model with varying numbers of fixed points $N_\textrm{rn}$ while maintaining a constant count of 500 movable points ($N_\textrm{rm} = 500$). Training the model for 10 iteration rounds, the prediction accuracy is assessed by computing the arithmetic mean and standard deviation of the relative L2 errors over the final 5 iteration rounds. The results are recorded in Table 5. WAM-AW achieves good results when $N_\textrm{rn}$ is set to 1000, 1500, and 2000, with a prediction accuracy about two orders of magnitude higher than that of the baseline model under the same conditions. The RAM-AW model obtains relatively poor results when $N_\textrm{rn}=1000$, but achieves the best prediction accuracy at $N_\textrm{rn}=1500$ and $N_\textrm{rn}=2000$.

3.4 Klein–Gordon equation

In the experiment on the Burgers equation, we validate the capacity of the proposed method to handle nonlinear shock problems. We further validate the ability of AMAW-PINN to handle time-dependent problems by considering the Klein–Gordon equation. The problem not only provides the initial values of the solution but also the first-order time derivative at the initial time. The Klein–Gordon equation is the most basic equation in relativistic quantum mechanics and quantum field theory, and it is a nonlinear equation that plays an important role in many scientific fields such as quantum mechanics, particle physics, and nonlinear optics [66, 67]. The problem can be expressed as:

$$\begin{aligned} \left\{ \begin{array}{lll} u_{tt}+\alpha \Delta u+\beta u + \gamma u^{k} = g(x,t),&{} x \in [0,1],t \in [0,1] \\ u(x,0) = h_{1}(x)\\ u_{t}(x,0) = h_{2}(x)\\ u(0,t)=h_{3}(t)\\ u(1,t)=h_{4}(t)\\ \end{array}\right. \end{aligned}$$

(41)

where $\alpha ,\beta ,\gamma$, and k are known constants, and $\Delta$ is the Laplacian operator acting on the spatial variable. The parameter k indicates that this equation is k-th order nonlinear. The functions $g(x,t),h_{1}(x),h_{2}(x),h_{3}(t),h_{4}(t)$ are known functions, and the function u(x, t) is the solution to the problem. In this experiment, we choose $\alpha =-1,\beta =0,\gamma =1,k=3$. The following function is used as the solution to Eq. (41) to evaluate our model:

$$\begin{aligned} u(x,t) = x\cos (5\pi t)+(xt)^{3}. \end{aligned}$$

(42)

The external forcing term g(x, t) and the initial and boundary conditions $h_{1}(x)$,$h_{2}(x)$,$h_{3}(t),h_{4}(t)$ can all be obtained from Eqs. (41) to (42).

Fig. 16

The exact solution and predicted solution of Klein–Gordon equation

Fig. 17

Predicted cross-sectional views of Klein–Gordon equation using PINN, RAM-AW, and WAM-AW

Fig. 18

The weight variation of the loss function and iteration convergence curves of RAM-AW and WAM-AW for Klein–Gordon equation

Fig. 19

Klein–Gordon: the absolute error, residual, and distribution of movable collocation points for PINN and AMAW-PINN

The equation is solved using the RAM-AW and WAM-AW models, with a fully connected neural network $f(x,t;\theta )$ with 4 hidden layers, each containing 20 neurons, used to approximate u(x, t). The residual of the equation is defined as follows:

$$\begin{aligned} r(x,t;\theta ):=f_{tt} - \Delta f+ f^{3} - g(x,t). \end{aligned}$$

(43)

The various derivative terms in the equation can be obtained using automatic differentiation. We then define the loss function, which is given by:

$$\begin{aligned} \mathcal {L}(\theta ,s)&= e^{(-s_{i})}\mathcal {L}_{i}(\theta )+e^{(-s_{it})}\mathcal {L}_{it}(\theta )+e^{(-s_{b})}\mathcal {L}_{b}(\theta ) \nonumber \\&\quad +e^{(-s_{r})}\mathcal {L}_{r}(\theta )+s_{i}+s_{it}+ s_{b} + s_{r}, \end{aligned}$$

(44)

where

$$\begin{aligned} \mathcal {L}_{i}(\theta )= & {} \frac{1}{N_{i}} \sum _{j=1}^{N_{i}}\left[ f\left( x_{i}^{j},0;\theta \right) -h_1(x_{i}^{j}) \right] ^{2}, \end{aligned}$$

(45)

$$\begin{aligned} \mathcal {L}_{it}(\theta )= & {} \frac{1}{N_{it}} \sum _{j=1}^{N_{it}}\left[ f_{t}\left( x_{it}^{j},0;\theta \right) -h_2(x_{it}^{j}) \right] ^{2}, \end{aligned}$$

(46)

$$\begin{aligned} \mathcal {L}_{b}(\theta )= & {} \frac{1}{N_{b}} \sum _{j=1}^{N_{b}}\left[ f\left( x_{b}^{j},t_{b}^{j};\theta \right) -u(x_{b}^{j},t_{b}^{j})\right] ^{2}, \end{aligned}$$

(47)

$$\begin{aligned} \mathcal {L}_{r}(\theta )= & {} \frac{1}{N_{r}} \sum _{j=1}^{N_{r}}\left[ r\left( x_{r}^{j},t_{r}^{j};\theta \right) \right] ^{2}, \end{aligned}$$

(48)

where $\{x_{i}^{j}\}_{j=1}^{N_{i}}$ and $\{x_{it}^{j}\}_{j=1}^{N_{it}}$ are the initial points, $\{x_{b}^{j},t_{b}^{j}\}_{j=1}^{N_{b}}$ are the boundary points, and $\{x_{r}^{j},t_{r}^{j}\}_{j=1}^{N_{r}}$ are the collocation points.

In this experiment, we initialize the adaptive weight parameters $s_{i}=s_{it}=s_{b}=s_{r}=0$. The training data consist of $N_{i}=N_{it} = 100$ initial points, $N_{b} = 200$ boundary points, and $N_{r} = 2000$ internal collocation points. The initial points are evenly spaced on the interval [0, 1], and the boundary points consist of 100 randomly sampled points on each of the two boundaries. Among the internal collocation points, $N_\textrm{rn} = 1500$ are fixed and $N_\textrm{rm} = 500$ are movable. The weight parameters s are optimized using the Adam optimizer, and the total number of iteration rounds for adaptive movement is set to 10.

Table 6 The relative L2 error for Klein–Gordon equation with $N_\textrm{rm}=500$

Figure 16 shows the true solution and predicted solution by the model. Figure 17 shows the predicted slices of PINN, RAM-AW, and WAM-AW. From the experimental results, we can see that both RAM-AW and WAM-AW can correctly solve the problem. Figure 18a and b shows the changes in adaptive weights, and we find that RAM-AW and WAM-AW have similar trends, with the internal residual loss having the lowest weight after weight convergence. Figure 18c shows the convergence curves of the relative L2 error for RAM-AW and WAM-AW with iteration rounds. From the curves, we can see that RAM-AW and WAM-AW can quickly reach a minimum error. Figure 19 shows the absolute error, residual, and distribution of movable collocation points for PINN, RAM-AW, and WAM-AW. From Fig. 19, we can see that the errors and residuals of RAM-AW and WAM-AW are relatively low. Observing the distribution of movable collocation points, we found that $P_{N_\textrm{rm}}$ of RAM-AW mainly distributes in the lower right corner, and the residual plot of the model shows that the residual in the lower right corner is relatively large. The distribution of $P_{N_\textrm{rm}}$ of WAM-AW is closely related to the gradient of the function, and it is denser in the area with a larger gradient.

In addition, tests are conducted on the RAM-AW and WAM-AW models with different fixed points $N_\textrm{rn}$ and a constant number of movable points $N_\textrm{rm}=500$. Table 6 reports the relative L2 error and its standard deviation for each model. The PINN model fails to learn the correct solution when $N_\textrm{rn}=1500$. The results show that both RAM-AW and WAM-AW achieve good results when $N_\textrm{rn}$ is set to 500, 1000, and 1500, with a prediction accuracy of about 1–2 orders of magnitude higher than the baseline model under the same conditions.

3.5 Helmholtz equation

In this section, we consider the two-dimensional second-order Helmholtz equation. The Helmholtz equation is fundamental in physics, engineering, and mathematics, and can be used to describe various wave phenomena, including sound waves, electromagnetic waves, and heat conduction [68]. The equation takes the form of:

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta u(x,y)+k^{2}u(x,y)=q(x,y),&{} x,y \in \Omega = [-1,1]^2 \\ u = h(x,y),&{} x,y\in \partial \Omega \\ \end{array}\right. \end{aligned}$$

(49)

where $\Delta$ is the Laplace operator, and k is a constant. For this problem, we can easily construct a solution as follows:

$$\begin{aligned} u(x,y) = \sin (a_{1}\pi x)\sin (a_{2}\pi y) \end{aligned}$$

(50)

where $a_1$ and $a_2$ are parameters. By substituting this solution function into Eq. (49), we can obtain the source term q(x, y) and the boundary condition h(x, y). q(x, y) has the following forms:

$$\begin{aligned} q(x,y)=-(a_{1}\pi )^{2}u-(a_{2}\pi )^{2}u+k^{2}u \end{aligned}$$

(51)

In this experiment, we choose $k=1$, $a_1=1$, and $a_2=4$. We use the RAM-AW and WAM-AW models to solve this equation. We use a fully connected neural network $f(x,y;\theta )$ with 4 hidden layers, each containing 20 neurons, to approximate u(x, y). The residual of the equation is defined as follows:

$$\begin{aligned} r(x,y;\theta ):=\Delta f(x,y;\theta )+ f(x,y;\theta ) - q(x,y) \end{aligned}$$

(52)

The term $\Delta f$ can be obtained using automatic differentiation. The loss function is defined as follows:

$$\begin{aligned} \mathcal {L}(\theta ,s) = e^{(-s_{b})}\mathcal {L}_{b}(\theta ) +e^{(-s_{r})}\mathcal {L}_{r}(\theta )+s_{b} + s_{r} \end{aligned}$$

(53)

where

$$\begin{aligned} \mathcal {L}_{b}(\theta )= & {} \frac{1}{N_{b}} \sum _{j=1}^{N_{b}}\left[ f\left( x_{b}^{j},t_{b}^{j};\theta \right) -h\left( x_{b}^{j},t_{b}^{j}\right) \right] ^{2} \end{aligned}$$

(54)

$$\begin{aligned} \mathcal {L}_{r}(\theta )= & {} \frac{1}{N_{r}} \sum _{j=1}^{N_{r}}\left[ r\left( x_{r}^{j},t_{r}^{j};\theta \right) \right] ^{2} \end{aligned}$$

(55)

where the set $\{x_{b}^{j},t_{b}^{j}\}_{j=1}^{N_{b}}$ represents the boundary points, and $\{x_{r}^{j},t_{r}^{j}\}_{j=1}^{N_{r}}$ represents randomly sampled collocation points within the computation domain.

Fig. 20

The exact solution and predicted solution of Helmholtz equation

Fig. 21

Predicted cross-sectional views of Helmholtz equation using RAM-AW and WAM-AW

Fig. 22

The weight variation of the loss function and iteration convergence curves of RAM-AW and WAM-AW for Helmholtz equation

Fig. 23

Helmholtz equation: the absolute error, residual, and distribution of movable collocation points for PINN and AMAW-PINN

Table 7 The relative L2 error for Helmholtz equation with $N_\textrm{rm}=500$

In this experiment, we initialize the adaptive weight parameters $s_{b}=s_{r}=0$. The training data consists of 400 boundary points and 800 interior points. The boundary points consist of 100 randomly sampled points on each of the four boundaries. In the interior points, 300 points are fixed and 500 points are movable. We use the Adam optimizer for updating the weight parameters s, and the total number of iteration rounds for adaptive movement is set to 10.

Figure 20 shows the true solution and the predicted solution given by the model. Figure 21 compares the true solution and the predicted solution on the cutting plane. The results show that RAM-AW and WAM-AW can solve the Helmholtz equation well. From Fig. 22a and b, we can see that the weight changes of the loss function of RAM-AW and WAM-AW are similar, and after convergence, the weight of the boundary condition is much larger than that of the residual loss. Figure 22c shows that compared with the standard PINN, RAM-AW and WAM-AW can quickly reduce the relative L2 error to around $10^{-3}$ with only 800 collocation points, while PINN can only achieve $10^{-2}$. Figure 23 plots the absolute error, residual, and distribution of movable collocation points for the PINN, RAM-AW, and WAM-AW models. It can be seen that the errors and residuals of RAM-AW and WAM-AW are smaller, and the movable collocation points of RAM-AW are distributed in areas with relatively large residuals, while the movable collocation points of WAM-AW are distributed in areas with larger function gradients.

In addition, we conduct tests on the RAM-AW and WAM-AW models with different values of the fixed points $N_\textrm{rn}$ while keeping the movable points $N_\textrm{rm}=500$ fixed. Table 7 records the relative L2 error and its standard deviation for each model. From Table 7, we can see that RAM-AW and WAM-AW achieve good results when $N_\textrm{rn}$ is set to 300, 500, and 1000, with a prediction accuracy at least one order of magnitude higher than that of the baseline model under the same conditions.

3.6 Flow in a lid-driven cavity

Finally, we apply the proposed method to study the Lid-Driven cavity flow problem, which is a benchmark problem in computational fluid dynamics and has a wide range of applications in engineering and scientific fields. In the Lid-Driven flow [69], the upper boundary of the cavity is given a fixed x-direction velocity, while the other edges of the cavity are stationary and do not move. The incompressible Navier–Stokes equations may be used to analyze this example and can be expressed as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} \varvec{u} \cdot \nabla \varvec{u} + \nabla p = \frac{1}{Re} \Delta \varvec{u},&{} \text {in} \ \ \Omega \\ \nabla \cdot \varvec{u} = 0,&{} \text {in} \ \ \Omega \\ \varvec{u}(\varvec{x}) = (1,0),&{} \text {on} \ \ \Gamma _1\\ \varvec{u}(\varvec{x}) = (0,0),&{} \text {on} \ \ \Gamma _2\\ \end{array}\right. \end{aligned}$$

(56)

where $\varvec{u}(x,y)=(u(x,y),v(x,y))$ is the velocity vector field, p is the scalar pressure field, and Re is the Reynolds number. In this paper, the Reynolds number is 100. The computational domain $\Omega$ is a two-dimensional cavity, where $(x,y)\in \Omega = [0,1]^2$. $\Gamma _1$ is the upper boundary of the cavity with a velocity of 1 in the x-direction, and $\Gamma _2$ represents the other three boundaries with a velocity of 0. By solving this equation, the motion state of the fluid inside the cavity, such as the distribution of the velocity and pressure fields, can be obtained.

In this problem, three unknown scalar functions need to be solved: u(x, y), v(x, y), and p(x, y). Therefore, we use a fully connected neural network $f(x,y;\theta )$ with 5 hidden layers, each containing 20 neurons, and 3 output neurons to approximate the solution of the problem. In this case, the neural network needs to learn all three unknown functions simultaneously, that is,

$$\begin{aligned} f(x,y;\theta ) = (u(x,y),v(x,y),p(x,y)). \end{aligned}$$

(57)

Next, we express Eq. (56) in scalar form:

$$\begin{aligned}&u u_{x} + v u_{y} + p_{x} = \frac{1}{Re}\Delta u \end{aligned}$$

(58)

$$\begin{aligned}&u v_{x} + v v_{y} + p_{x} = \frac{1}{Re}\Delta v \end{aligned}$$

(59)

$$\begin{aligned}&u_{x} + v_{y} = 0 \end{aligned}$$

(60)

The residual is defined as:

$$\begin{aligned} r^{u}(x,y;\theta )&:= u u_{x} + v u_{y} + p_{x}- \frac{1}{Re}\Delta u \end{aligned}$$

(61)

$$\begin{aligned} r^{v}(x,y;\theta )&:=u v_{x} + v v_{y} + p_{x} - \frac{1}{Re}\Delta v \end{aligned}$$

(62)

$$\begin{aligned} r^{c}(x,y;\theta )&:=u_{x} + v_{y} \end{aligned}$$

(63)

where terms (u, v, p) are outputs of the neural network, and their derivatives can be obtained using automatic differentiation. Then, we define the loss function for the neural network as:

$$\begin{aligned} \mathcal {L}(\theta ,s) = e^{(-s_{b})}\mathcal {L}_{b}(\theta ) +e^{(-s_{r})}\mathcal {L}_{r}(\theta )+s_{b} + s_{r} \end{aligned}$$

(64)

where

$$\begin{aligned} \mathcal {L}_{b}(\theta ) =&\frac{1}{N_{b}} \sum _{j=1}^{N_{b}}\{[u(x_{b}^{j},y_{b}^{j};\theta )-u_{b}^{j})]^{2} \nonumber \\&+[v(x_{b}^{j},y_{b}^{j};\theta )-v_{b}^{j})]^{2}\} \end{aligned}$$

(65)

$$\begin{aligned} \mathcal {L}_{r}(\theta ) =&\frac{1}{N_{r}} \sum _{j=1}^{N_{r}}\{[r^{u}(x_{r}^{j},y_{r}^{j};\theta )]^{2} \nonumber \\&+[r^{v}(x_{r}^{j},y_{r}^{j};\theta )]^{2} \nonumber \\&+[r^{c}(x_{r}^{j},y_{r}^{j};\theta )]^{2}\} \end{aligned}$$

(66)

where $\{(x_{b}^{j},y_{b}^{j}),(u_{b}^{j},v_{b}^{j}\}_{j=1}^{N_{b}}$ are the boundary data of the velocity vector, and $\{x_{r}^{j},y_{r}^{j}\}_{j=1}^{N_{r}}$ are the interior collocation points used for minimizing the residual.

Fig. 24

The reference solution and predicted solution of Lid-Driven problem

Fig. 25

The weight variation of the loss function, distribution of movable collocation points of WAM-AW for Lid-Driven problem

In this experiment, the WAM-AW model is utilized to solve the problem. The adaptive weight parameters $s_b$ and $s_r$ are initialized to zero. The training data consists of 400 boundary points and 1000 interior points, where the former are randomly sampled with 100 points on each of the four boundaries. Among the interior points, 500 are fixed and the remaining 500 are movable. The Adam optimizer is employed to update the weight parameters s, and the total number of iteration rounds for adaptive movement is set to 4.

Figure 24 shows $\mid \varvec{u}(x,y)\mid =\sqrt{u^{2}(x,y)+v^{2}(x,y)}$ the reference and the predicted velocity fields by the PINN and WAM-AW models. From the experimental results, it can be seen that the PINN model does not fully capture the flow velocity changes, while the WAM-AW model successfully predicts the accurate velocity field. Figure 25a illustrates the changes in the loss function weights, and for this problem, the weights of the boundary conditions and residual terms are not significantly different. Figure 25b shows the distribution of the movable collocation points in the WAM-AW model. It can be observed that the movable collocation points are mainly concentrated near the upper boundary, indicating that the neural network will pay more attention to the areas with dramatic velocity changes. Therefore, the WAM-AW model has effectively learned the solution to the problem.

4 Discussion

In this work, we propose an AMAW-PINN model for solving partial differential equations. We perform a series of numerical tests, which demonstrate that the proposed model can significantly improve generalization ability and prediction accuracy. This work provides a new model that can adaptively offer suitable collocation point distributions for specific problems. Due to the introduction of adaptive loss weighting techniques, the model can also adaptively allocate weights to the loss function. The proposed model can effectively solve various partial differential equations and can well address shock wave and interface problems. The proposed model displays significant advantages, particularly when the number of collocation points is limited.

Despite the promising progress made in the current research, there are still some open questions to be addressed. How should the number of fixed and movable collocation points be selected when facing a specific problem? Can residual information and gradient information be combined to provide a more suitable collocation point distribution for the problem? We believe that the distribution of collocation points and the weighting of loss terms play a crucial role in the performance of the model. Exploring and researching these issues can not only help us better understand the mechanisms of models and equations but also provide more reliable theories and methods for key applications in the field of scientific computing and engineering.

5 Conclusion

In this paper, we propose a novel adaptive PINN method for solving partial differential equations, called AMAW-PINN. Firstly, we introduce the adaptive collocation point movement PINN (AM-PINN). AM-PINN has the ability to autonomously move collocation points throughout the training process, which enables dense distribution in difficult-to-fit regions and even distribution in smooth areas. This results in a suitable collocation point distribution tailored to specific problems and improving model performance. In the AM-PINN model, we can use common residual information to guide the movement of collocation points. Furthermore, inspired by traditional adaptive techniques, we propose that using the characteristics of the solution function itself to guide the movement of collocation points and design a gradient-based collocation point movement method. Secondly, to achieve adaptive weighting of the loss function, we introduce adaptive loss weighting techniques into the AM-PINN model and propose the AMAW-PINN model. This model can automatically assign weights to the losses of respective tasks based on their uncertainties, which enables adaptive weighting of the loss function and enhances model convergence rate and accuracy.

To investigate the efficiency and accuracy of the proposed method, we first conduct ablation experiments on one-dimensional Poisson equations and two-dimensional Poisson equations to verify the effectiveness of each part of the proposed model. Subsequently, we conduct experimental studies on Burgers equations, Klein–Gordon equations, Helmholtz equations, and Lid-Driven problems. The experimental results demonstrate that the proposed method can improve the prediction accuracy and generalization ability of the model. It is worth noting that the current model still uses either residual information or gradient information separately to guide the movement of collocation points. Effectively combining both to provide a more efficient collocation point distribution will be discussed in future research reports.

6 Nomenclature

See Table 8.

Table 8 Nomenclature Summary of the main symbols and notations used in this work