A color image encryption algorithm based on hyperchaotic map and Rubik’s Cube scrambling

Abstract

At present, many encryption algorithms for color images either decompose color images into three gray images and encrypt them, respectively, or combine R, G, B channels into a two-dimensional image matrix before encryption. These methods break the internal link between the three colors and reduce the efficiency of encryption. Here, to address these shortcomings, a new hyperchaotic system two-dimension Chebyshev–Sine coupling map (2D-CSCM) is proposed to improve the security of the encryption algorithm, and the dynamic behaviors of the system are analyzed by phase diagram, bifurcation diagram, Lyapunov exponent spectra information entropy and 0–1 test. We propose a Rubik's Cube scrambling method to scramble a three-dimensional bit-level matrix of the color image directly. Then the pixel values of the scrambled image matrix are diffused by two rounds of different operations based on chaotic sequences. The parameters and initial values of the chaotic system are derived from the secret key generated by the hash function SHA-512. Simulation results and security analysis demonstrate that the proposed algorithm has high efficiency and security to resist various common attacks.

1 Introduction

With the rapid development of artificial intelligence, multimedia communication and Internet technology, information security has become a serious problem in modern society. Image is one of the main carriers of multimedia information, which conveys more information than sound and text. Image contains information related to personal privacy, trade secrets, national security and other aspects. Therefore, it is essential to adopt an encryption technology to prevent images from being leaked and attacked in the process of storage and transmission [1,2,3,4,5,6,7,8,9].

Several traditional encryption algorithms are gradually replaced in the field of image encryption with a large amount of data, such as data encryption standard (DES) [10], advanced encryption standard (AES) [11], RSA [12] and so on. With the continuing research, DNA coding [13, 14], cellular automata [15, 16], Fourier transform [17, 18], chaos [19, 20] and other new image encryption technologies have emerged [21,22,23]. Among them, taking chaos as the core of the cryptosystem can greatly improve the performance of the encryption algorithm.

Chaos is a long-term unpredictable behavior produced by deterministic nonlinear systems, and its unpredictability comes from the instability of the internal motion of the system [24,25,26]. Chaotic system has the characteristics of sensitivity to the initial value, ergodicity, internal stochastic [27,28,29,30,31], so it has a favorable prospect in the field of cryptography. In recent years, many scholars have proposed image encryption technology based on chaos theory [32,33,34,35]. For instance, Liu et al. [36] proposed a new two-dimensional Sine ICMIC (iterative chaotic map with infinite collapse) modulation map based on the close-loop modulation coupling model and a chaotic shift transform for image encryption. Hu et al. [37] established a fractional-order chaotic circuit with different coupled memristors and applied it to image encryption. Wang et al. [38] used the chaotic sequences generated by Chen hyperchaotic system to perform inter-block index scrambling and intra-block Fisher-Yates scrambling. Chen et al. [39] generalized the two-dimensional chaotic cat map to 3D for designing a real-time secure symmetric encryption scheme. Haq et al. [40] constructed a 4D mixed chaotic map with hyperchaotic properties and high randomness behavior by using the 1D Sine map and the 2D Thinker bell map and then introduced a novel image encryption scheme based on the proposed chaotic system and symmetric group S8 permutation. According to the above research, it is found that these methods adopt chaotic systems of different orders, and the performance of these image encryption methods is closely related to the dynamic characteristics of chaotic systems [41, 42]. Some encryption methods have poor performance because of the small distribution range of attractors and the poor unpredictability of chaotic sequences generated by the chaotic map. In this paper, we aim to design a new hyperchaotic system with better ergodicity and unpredictability of sequence and apply it to a high-security image encryption method.

The images transmitted in the network are mainly color images. Most encryption algorithms for color images include two types. One is to encrypt the R, G, B color channels, respectively, which breaks the internal link between the three color channels of the image. Gao et al. [43] divided color image into R, G, B primary colors and then scrambled and diffused three primary colors by the improved Hénon sequences. Noura et al. [44] used a hybrid 2D composite chaotic map combined with a sine–cosine cross-chaotic map to encrypt three color channels, respectively. The other is to transform the three-dimensional image matrix of a color image into a two-dimensional matrix before encryption, which increases the number of iterations of chaotic system and encryption and reduces the efficiency of encryption. Teng et al. [45] vertically combined the R, G, B matrixes of color images into a two-dimensional matrix and then perform cycle shift scrambling and selecting diffusion based on a cross 2D hyperchaotic map. The purpose of this paper is to design a more efficient and secure color image encryption method.

In this paper, we propose a cross-operation coupling model and construct a novel hyperchaotic system (2D-CSCM) through the Chebyshev map and Sine map. The better hyperchaotic properties of the system are proved by phase diagram, bifurcation diagram, Lyapunov exponent spectra, information entropy and 0–1 test. Considering the features of a color image matrix, a Rubik's Cube scrambling method is proposed in this paper. The three-dimensional bit-level matrix of a color image is randomly scrambled by row transform and column transform similar to the Rubik's Cube. Pixel values of the scrambled image matrix are diffused by three-dimensional row diffusion and column diffusion. Simulation experiments and analysis show that this algorithm improves the efficiency and security of color image encryption.

The remainder of this paper is organized as follows. Section 2 proposes the model of the novel two-dimensional hyperchaotic map 2D-CSCM; then the dynamic behaviors are analyzed. In Sect. 3, a novel color image encryption algorithm is proposed. Section 4 introduces the decryption algorithm. Section 5 analyzes the simulation results and security analysis of the proposed algorithm. In Sect. 6, the conclusion is given.

2 Chaotic system

2.1 Definition of 2D-CSCM

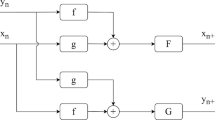
Some existing chaotic cryptosystems have many shortcomings because of the uncomplex dynamic characteristics of the chaotic system. In view of this situation, the cross-operation coupling model is proposed in this chapter to construct a novel hyperchaotic map, which is shown in Fig. 1.

Fig. 1

Structural diagram of the cross-operation coupling mode

In the structure diagram, there are two input signals $x_{n}$, $y_{n}$ and two output signals $x_{n + 1}$, $y_{n + 1}$. $F$ and $G$ are chaotic maps, $f$ is a nonlinear function, and $\oplus$ and ${\ominus }$ represent the addition and subtraction of the input signals, respectively. The expression of the model is given as

$$ \left\{ {\begin{array}{*{20}l} {x_{n + 1} = F\left( {f\left( {x_{n} - y_{n} } \right)} \right)} \hfill \\ {y_{n + 1} = G\left( {x_{n} + y_{n} } \right)} \hfill \\ \end{array} } \right. $$

(1)

In the model of cross-operation coupling, the nonlinear function $f$ is chosen as $\cos \left( x \right)$, and the chaotic maps $F$ and $G$ are set as the Chebyshev map and Sine map. Chebyshev map and Sine map are two classical one-dimensional chaotic maps, whose expressions are, respectively, defined as Eqs. (2) and (3).

$$ x_{n + 1} = \cos \left( {\alpha \cos^{ - 1} \left( {x_{n} } \right)} \right) $$

(2)

$$ y_{n + 1} = \beta \sin \left( {\pi y_{n} } \right),\beta \in \left( {0,1} \right] $$

(3)

Then a novel two-dimensional Chebyshev–Sine coupling map (2D-CSCM) is obtained as

$$ \left\{ {\begin{array}{*{20}l} {x_{n + 1} = \cos \left( {\alpha \cos^{ - 1} \left( {\sin \left( {x_{n} - y_{n} } \right)} \right)} \right)} \hfill \\ {y_{n + 1} = \beta \sin \left( {\pi \left( {x_{n} + y_{n} } \right)} \right)} \hfill \\ \end{array} } \right. $$

(4)

where $\alpha$, $\beta$ are control parameters, and $\alpha ,\beta \in \left[ {2, + \infty } \right)$.

2.2 Performance analysis of 2D-CSCM

2.2.1 Phase diagram

The dynamic behavior of chaotic system can be observed directly from phase diagram. The phase trajectory of chaotic motion is an unclosed curve that can be observed through the phase plane graph. Attractors of a chaotic system with good chaotic behaviors usually occupy a large area in the phase diagram. For the chaotic system proposed in this chapter, we set the initial values $\left( {x_{0} ,y_{0} } \right) = \left( {1,1} \right)$, set the control parameters $\alpha = 5$, $\beta = 5$, and iterate the system 50,000 times; the generated phase diagram of 2D-CSCM is shown in Fig. 2a. It can be seen that the system exhibits chaotic behavior under the parameters set above, and the trajectory of the system completely covers the whole phase plane, which indicates the output variables of this system have excellent ergodicity.

Fig. 2

Phase diagrams of chaotic maps. a 2D-CSCM with $\alpha = 5,\beta = 5$. b 2D-SIMM with $\alpha = 1,\beta = 5$. c 2D-SLMM with $\alpha = 1,\beta = 3$. d 2D-Logistic with $r = 1.19$

In addition, phase diagram analysis is also carried out for several 2D chaotic maps in use, and the optimal initial states and control parameters are selected for each chaotic map to obtain the best chaotic performance. The phase diagrams of 2D-SIMM [36], 2D- SLMM [7] and 2D-Logistic [41] are shown in Fig. 2b–d, respectively. It can be seen that the attractor range of 2D-CSCM is much larger than that of 2D-SIMM, 2D-SLMM and 2D-Logistic, indicating that 2D-CSCM has better ergodicity.

2.2.2 Bifurcation diagram

Bifurcation diagram is another important method to analyze the dynamic behavior of chaotic system. The motion state of the system will be different along with the change of control parameters, which can be demonstrated by bifurcation diagram. For the 2D-CSCM proposed in this chapter, setting the initial values $\left( {x_{0} ,y_{0} } \right) = \left( {1,1} \right)$, the bifurcation diagrams of 2D-CSCM are illustrated in Fig. 3. Setting the control parameter $\alpha = 4$, when $\beta$ in the range of $\left( {2,6} \right)$, the corresponding bifurcation diagram is illustrated in Fig. 3a. Similarly, setting the control parameter $\beta = 4$, when $\alpha$ in the range of $\left( {2,6} \right)$, the result is illustrated in Fig. 3b. It can be seen that there is no periodic state in both bifurcation diagrams, indicating that the system exhibits the chaotic state in a wide range of parameters.

Fig. 3

Bifurcation diagram of 2D-CSCM

2.2.3 Lyapunov exponent spectrum

The Lyapunov exponent spectrum of the chaotic system can effectively represent the sensitivity of the system to the initial value when the system evolves over time. For a high-order chaotic system, the number of Lyapunov exponents is equal to the number of orders, so the 2D-CSCM proposed in this chapter has two Lyapunov exponents. When setting $\beta = 4$, the Lyapunov exponent spectrum of 2D-CSCM is illustrated in Fig. 4a. It can be observed that when $\alpha \in \left( {2,6} \right)$, the chaotic system has two positive Lyapunov exponents, indicating that the system is in the hyperchaotic state. Similarly, setting control parameter $\alpha = 4$, when $\beta \in \left( {2,6} \right)$, the system is in the hyperchaotic state, which is illustrated in Fig. 4b. It can be seen that the system always exhibits the hyperchaotic state within the parameters set above, which indicates that it has complex dynamic behavior and is suitable for a cryptosystem.

Fig. 4

Lyapunov exponents spectrum of 2D-CSCM

2.2.4 Complexity analysis

The complexity of the chaotic system is one of the important methods to describe the dynamic characteristics of the chaotic system. The complexity analysis of chaotic system is used to measure the degree to which chaotic sequences approximate to random sequences [46, 47]. The main idea of the image encryption method based on the chaotic system is to apply the pseudo-random sequence generated by a chaotic system to the process of image encryption, so the complexity of the chaotic sequence will greatly affect the security of encryption algorithm. Therefore, we analyze the complexity of our chaotic system in this section to demonstrate its superior performance. Notably, the larger the complexity value is, the more chaotic sequence is approximate to the random sequence, and the higher the security of the corresponding application system will be. At present, there are many algorithms to calculate the complexity of chaotic pseudo-random sequences. In this chapter, the permutation entropy (PE) algorithm is chosen to evaluate the complexity of 2D-CSCM. The PE complexity graph of control parameters $\alpha$ and $\beta$ is shown in Fig. 5. As can be seen from the graphs, permutation entropy proves that 2D-CSCM has large sequence complexity value which is close to ideal value 1. Figure 6 shows the comparison of permutation entropy between 2D-CSCM and different chaotic maps. It is obvious that the complexity of 2D-CSCM is greater than that of several classical 1D chaotic maps and other newly proposed 2D chaotic maps. As a result, the chaotic sequence generated by 2D-CSCM shows better complexity and unpredictability and can generate more secure key sequences.

Fig. 5

Complexity graph of 2D-CSCM

Fig. 6

Permutation entropy of different maps. a 2D-CSCM, ICMIC map, Logistic map and Sine map. b 2D-CSCM, 2D-LSCM, 2D-SLMM and 2D-Logistic

2.2.5 0–1 test

Gottwald GA and Melbourne I proposed a reliable binary test method for determining whether a given deterministic dynamical system is chaotic or non-chaotic [48, 49]. Different from the usual method of calculating the maximal Lyapunov exponent, this method is applied directly to the time series data without phase space reconstruction and is generally suitable for any deterministic dynamical system. To comprehensively reflect the dynamic characteristics of the proposed system, we conduct 0–1 test and show the chaotic behaviors of our system through the test results in this section. It can be seen from the trajectory of the 0–1 test result that the trajectory of a regular system is bounded, while that of a chaotic system is unbounded which is similar to the Brownian motion. Setting the initial values $\left( {x_{0} ,y_{0} } \right) = \left( {1,1} \right)$ and control parameters $\left( {\alpha ,\beta } \right) = \left( {4,4} \right)$, the 0–1 test result of the sequence $x$ and $y$ is shown in Fig. 7a, b. The test results show that the trajectory of the sequence $x$ and $y$ is Brownian motion, indicating the proposed system is a chaotic system.

Fig. 7

0–1 test result of 2D-CSCM

3 Proposed encryption algorithm

Based on the chaotic sequences generated by the proposed two-dimensional hyperchaotic system, a novel color image encryption algorithm is proposed in this chapter. The proposed algorithm includes Rubik's Cube scrambling and two rounds of three-dimensional matrix diffusion, the flowchart of which is shown in Fig. 8.

Fig. 8

Flowchart of the proposed encryption algorithm

3.1 Generation of key and system parameters

Hash algorithm is extremely sensitive to change of input and can resist plaintext attack effectively, the output of the hash algorithm is irreversible. The secret key of the encryption algorithm proposed in this paper is generated by the hash algorithm because of its security. Input the pixel value of the plaintext image into the SHA-512 function to produce a 128-bit string key $K$. The key is divided into eight 16-bit strings and then converted into eight decimal sub-keys $k_{1} ,k_{2} ...k_{8}$ according to Eq. (5).

$$ k_{i} = {\text{hex}}2{\text{dec}}\left( {K\left( {16 \times i - 15:16 \times i} \right)} \right),\;i = 1 \cdots 8 $$

(5)

where ${\text{hex}}2{\text{dec}}\left( x \right)$ represents converting the hexadecimal character $x$ to a decimal number, $K\left( {x:y} \right)$ represents taking the $x - {\text{th}}$ to $y - {\text{th}}$ value of K.

The control parameters $\alpha ,\beta$ and initial values $x_{0} ,y_{0}$ of 2D-CSCM are obtained by processing the sub-keys:

$$ \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\alpha = \bmod \left( {{\text{sqrt}}\left( {k_{1} \times M \times N} \right)/k_{8} \times 10^{10} ,0.5} \right) + 4} \\ {\beta = \bmod \left( {{\text{sqrt}}\left( {k_{2} \times M \times N} \right)/k_{7} \times 10^{10} ,0.5} \right) + 4} \\ \end{array} } \\ {\begin{array}{*{20}c} {x_{0} = \bmod \left( {{\text{sqrt}}\left( {k_{3} \times M \times N} \right)/k_{6} \times 10^{10} ,0.5} \right) + 1} \\ {y_{0} = \bmod \left( {{\text{sqrt}}\left( {k_{4} \times M \times N} \right)/k_{5} \times 10^{10} ,0.5} \right) + 1} \\ \end{array} } \\ \end{array} } \right. $$

(6)

where ${\text{mod}}()$ represents the modulo operation, ${\text{sqrt}}\left( x \right)$ represents the square root of $x$, $M$ is the number of rows, and $N$ is the number of columns.

3.2 Rubik's Cube scrambling

The purpose of scrambling is to average the image statistics and make the image information uniform by changing the position of image pixels. We introduced the concept of Rubik's Cube into the process of color image matrix scrambling and proposed a Rubik's Cube scrambling method for color images, which shuffles the 3D bit-level matrix of the color image directly.

Step 1. The color plaintext image is input to get an image matrix $P$ with the size of $M \times N \times 3$. Convert pixel values in matrix $P$ into 8-bit binary values and obtain the binary matrix $P^{\prime}$ with the size of $M \times 8N \times 3$.

Step 2. The control parameters and initial values of 2D-CSCM are generated from Eq. (6). Iterate the 2D-CSCM $M \times N \times 3 + t$ times, and discard the first $t$ values to prevent transient effect, where $t = 500$. Then we get two chaotic sequences $x,y$. The two chaotic sequences $x,y$ are further processed to obtain two shuffling sequences $X$, $Y$ and a selecting sequence $Z$ according to Eq. (7).

$$ \left\{ {\begin{array}{*{20}l} {X = \bmod \left( {{\text{ceil}}\left( {x\left( {1:3M} \right) \times 10^{14} } \right),3M} \right)} \hfill \\ {Y = \bmod \left( {{\text{ceil}}\left( {y\left( {1:3 \times 8N} \right) \times 10^{14} } \right),3 \times 8N} \right)} \hfill \\ {Z = \bmod \left( {{\text{ceil}}\left( {x\left( {3M + 1:3M + M + 8N} \right) \times 10^{14} } \right),M + 8N} \right)} \hfill \\ \end{array} } \right. $$

(7)

where ${\text{ceil}}\left( x \right)$ represents rounding element $x$ to the nearest integer greater than or equal to $x$.

Then obtain the index order $S$ of selecting sequence $Z$ from $\left[ {{\text{Z}}1,{\text{S}}} \right] = {\text{sort}}\left( {\text{Z}} \right)$, where ${\text{sort}}\left( Z \right)$ represents sorting the elements of $Z$ in ascending order.

Step 3. The Rubik's Cube scrambling method proposed in this section is mainly divided into row scrambling and column scrambling. The total number of rows and columns in the matrix $P^{\prime}$ is $M + 8N$. Traverse elements in index order sequence $S\left( i \right)$, $i = 1,2, \ldots ,M + 8N$, pixel values of the $S\left( i \right) - M$-th column in the matrix $P^{\prime}$ are scrambled when $S\left( i \right) > M$, otherwise, pixel values of the $S\left( i \right)$-th row are scrambled.

Step 4. When pixel values of the $S\left( i \right) - M$-th column are scrambled, the pixel values of the $S\left( i \right) - M$-th column in the three dimensions of $P^{\prime }$ are scanned into an array $P_{1}$ with the length of $3 \times M$ as $\left[ {P^{\prime } \left( {:,S\left( i \right) - M,1} \right),P^{\prime } \left( {:,S\left( i \right) - M,2} \right),P^{\prime } \left( {:,S\left( i \right) - M,3} \right)} \right]$. $P_{1}$ is scrambled by a chaos-based shuffle algorithm. The process is to swap the number at a random position with the last number in the unprocessed array each time until all positions have been processed. The random position is obtained by chaotic sequences $X$, which is described as Eq. (8).

$$ \left\{ {\begin{array}{*{20}l} {{\text{Exchange}}\left( {P_{1} \left( i \right),P_{1} \left( {RP_{1} \left( i \right)} \right)} \right),\,i = 3 \times M,3 \times M - 1, \ldots 2} \hfill \\ {RP_{1} \left( i \right) = \bmod \left( {X\left( i \right),i - 1} \right) + 1,\,i = 3 \times M,3 \times M - 1, \ldots 2} \hfill \\ \end{array} } \right. $$

(8)

Similarly, when pixel values of the $S\left( i \right)$-th row are scrambled, the pixel values of the $S\left( i \right)$-th row in the three dimensions are scanned into an array $P_{2}$ with the length of $3 \times 8N$ as $\left[ {P^{\prime } \left( {S\left( i \right),:,1} \right),P^{\prime } \left( {S\left( i \right),:,2} \right),P^{\prime } \left( {S\left( i \right),:,3} \right)} \right]$, then $P_{2}$ is scrambled by chaos-based shuffle algorithm, the process of row scrambling is described as Eq. (9).

$$ \left\{ {\begin{array}{*{20}l} {{\text{Exchange}}\left( {P_{2} \left( i \right),P_{2} \left( {RP_{2} \left( i \right)} \right)} \right),\,i = 3 \times 8N,3 \times 8N - 1, \ldots 2} \hfill \\ {RP_{2} \left( i \right) = \bmod \left( {Y\left( i \right),i - 1} \right) + 1,\,i = 3 \times 8N,3 \times 8N - 1, \ldots 2} \hfill \\ \end{array} } \right. $$

(9)

Assume a color image matrix with the size of $4 \times 4 \times 3$ and two chaotic sequences $X,Y$, the scrambling process of the first row and then the fourth column is shown in Fig. 9. It can be seen that the pixels in the first row and the fourth column have changed a lot.

Fig. 9

Rubik's Cube scrambling

Step 5. Convert pixel values in the scrambled matrix $P^{\prime }$ into decimal values and obtain the scrambled integer matrix $P^{\prime \prime }$ with the size of $M \times N \times 3$. The position and value of the pixels in the image matrix are changed to a great extent by the bit-level scrambling process.

3.3 Diffusion process

We proposed a color image diffusion method in which pixel values are diffused through three-dimensional row diffusion and three-dimensional column diffusion.

Step 1. The two chaotic sequences $x,y$ are further processed to obtain two diffusion matrixes $X^{\prime},Y^{\prime}$ with the size of $M \times N \times 3$ according to Eqs. (10) and (11).

$$ \left\{ {\begin{array}{*{20}c} {X^{\prime } = \bmod \left( {{\text{ceil}}\left( {x\left( {1:3 \times M \times N} \right) \times 10^{13} } \right),256} \right)} \\ {Y^{\prime } = \bmod \left( {{\text{ceil}}\left( {y\left( {1:3 \times M \times N} \right) \times 10^{13} } \right),256} \right)} \\ \end{array} } \right. $$

(10)

$$ \left\{ {\begin{array}{*{20}c} {X^{\prime } = {\text{reshape}}\left( {X^{\prime } ,M,N,3} \right)} \\ {Y^{\prime } = {\text{reshape}}\left( {Y^{\prime } ,M,N,3} \right)} \\ \end{array} } \right. $$

(11)

where ${\text{reshape}}\left( {A,s1,s2, \ldots ,sk} \right)$ represents reshaping the array $A$ into a $s1 \times s2 \times \cdots \times sk$ model array.

Step 2. In the process of row diffusion, the pixel values of each row in the three dimensions of the matrix $P^{\prime \prime }$ are diffused with the pixel values in the previous dimension and the values of the corresponding row in the diffusion matrix $X^{\prime }$. Row diffusion is described as Eq. (12).

$$ \left\{ {\begin{array}{*{20}l} {D\left( {1,:,1} \right) = \left( {P^{\prime \prime } \left( {1,:,1} \right) < < 3} \right) \oplus X^{\prime } \left( {1,:,1} \right)} \hfill \\ {D\left( {i,:,k} \right) = \left( {\left( {P^{\prime \prime } \left( {i,:,k} \right) \oplus D\left( {i,:,k - 1} \right)} \right) < < 3} \right) \oplus X^{\prime } \left( {i,:,k} \right),k \ne 1} \hfill \\ {D\left( {i,:,k} \right) = \left( {\left( {P^{\prime \prime } \left( {i,:,k} \right) \oplus D\left( {i - 1,:,3} \right)} \right) < < 3} \right) \oplus X^{\prime } \left( {i,:,k} \right),k = 1,i \ne 1} \hfill \\ \end{array} } \right. $$

(12)

where $D()$ is the result of row diffusion, $A < < m$ represents that the binary of $A$ is cyclically shifted to the left by m-bit, $\oplus$ represents XOR operation, $i = 1,2 \cdots M,k = 1,2,3$.

Step 3. In the process of column diffusion, the pixel values of each column in the three dimensions of the matrix $D$ are diffused with the pixel values in the previous dimension and the values of the corresponding column in the diffusion matrix $Y^{\prime }$. Column diffusion is described as Eq. (13).

$$ \left\{ {\begin{array}{*{20}l} {C\left( {:,1,1} \right) = \left( {D\left( {:,1,1} \right) < < 3} \right) \oplus Y^{\prime } \left( {:,1,1} \right)} \hfill \\ {C\left( {:,j,k} \right) = \left( {\left( {D\left( {:,j,k} \right) \oplus C\left( {:,j,k - 1} \right)} \right) < < 3} \right) \oplus Y^{\prime } \left( {:,j,k} \right),k \ne 1} \hfill \\ {C\left( {:,j,k} \right) = \left( {\left( {D\left( {:,j,k} \right) \oplus C\left( {:,j - 1,3} \right)} \right) < < 3} \right) \oplus Y^{\prime } \left( {:,j,k} \right),k = 1,j \ne 1} \hfill \\ \end{array} } \right. $$

(13)

where $C()$ is the result of column diffusion, $j = 1,2 \ldots N,k = 1,2,3$.

Step 4. After the above steps, the final ciphertext image $C$ is obtained.

4 Decryption algorithm

Step 1. The reverse of three-dimensional column diffusion is described as Eq. (14).

$$ \left\{ {\begin{array}{*{20}l} {C^{\prime } \left( {:,1,1} \right) = \left( {C\left( {:,1,1} \right) \oplus Y^{\prime } \left( {:,1,1} \right)} \right)} \hfill \\ {C^{\prime } \left( {:,j,k} \right) = \left( {\left( {C\left( {:,j,k} \right) \oplus Y^{\prime } \left( {:,j,k} \right)} \right) > > 3} \right) \oplus C\left( {:,j,k - 1} \right),k \ne 1} \hfill \\ {C^{\prime } \left( {:,j,k} \right) = \left( {\left( {C\left( {:,j,k} \right) \oplus Y^{\prime } \left( {:,j,k} \right)} \right) > > 3} \right) \oplus C\left( {:,j - 1,3} \right),k = 1,j \ne 1} \hfill \\ \end{array} } \right. $$

(14)

where $A > > m$ represents the binary of $A$ is cyclically shifted to the right by m-bit.

Step 2. The reverse of three-dimensional row diffusion is described as Eq. (15).

$$ \left\{ {\begin{array}{*{20}l} {C^{\prime \prime } \left( {1,:,1} \right) = \left( {C^{\prime } \left( {1,:,1} \right) \oplus X^{\prime } \left( {1,:,1} \right)} \right)} \hfill \\ {C^{\prime \prime } \left( {i,:,k} \right) = \left( {\left( {C^{\prime } \left( {i,:,k} \right) \oplus X^{\prime } \left( {i,:,k} \right)} \right) > > 3} \right) \oplus C^{\prime } \left( {i,:,k - 1} \right),k \ne 1} \hfill \\ {C^{\prime \prime } \left( {i,:,k} \right) = \left( {\left( {C^{\prime } \left( {i,:,k} \right) \oplus X^{\prime } \left( {i,:,k} \right)} \right) > > 3} \right) \oplus C^{\prime } \left( {i - 1,:,3} \right),k = 1,j \ne 1} \hfill \\ \end{array} } \right. $$

(15)

Step 3. The pixel values in the matrix $C^{\prime \prime }$ are converted into 8-bit binary values to obtain the binary matrix $D^{\prime }$ with the size of $M \times 8N \times 3$. Traverse elements in index order sequence $S\left( i \right)$, $i = M + 8N,M + 8N - 1, \ldots ,1$, pixel values of the $S\left( i \right) - M$-th column are scanned into an array $P_{1}^{^{\prime}}$ and then reverse shuffled based on chaotic sequences $X$ when $S\left( i \right) > M$, otherwise, pixel values of the $S\left( i \right)$-th row are scanned into an array $P_{2}^{\prime }$ and then reverse shuffled based on sequences $Y$. The reverse column scrambling and reverse row scrambling are described as Eqs. (16) and (17).

$$ \left\{ {\begin{array}{*{20}l} {{\text{Exchange}}\left( {P_{1}^{\prime } \left( i \right),P_{1}^{\prime } \left( {RP_{1}^{\prime } \left( i \right)} \right)} \right),i = 2,3, \ldots ,3 \times M} \hfill \\ {RP_{1}^{\prime } \left( i \right) = \bmod \left( {X\left( i \right),i - 1} \right) + 1,i = 2,3, \ldots ,3 \times M} \hfill \\ \end{array} } \right. $$

(16)

$$ \left\{ {\begin{array}{*{20}l} {{\text{Exchange}}\left( {P_{2}^{\prime } \left( i \right),P_{2}^{\prime } \left( {RP_{2}^{\prime } \left( i \right)} \right)} \right),i = 2,3, \ldots ,3 \times 8N} \hfill \\ {RP_{2}^{\prime } \left( i \right) = \bmod \left( {Y\left( i \right),i - 1} \right) + 1,i = 2,3, \ldots ,3 \times 8N} \hfill \\ \end{array} } \right. $$

(17)

Step 4. The matrix $D^{\prime }$ is converted into a decimal matrix and then the decryption image $D$ is obtained.

5 Experimental results and security analysis

In this chapter, the performance of the proposed encryption algorithm is analyzed from many aspects by testing several color images of different sizes. The color images tested in the experiment include $256 \times 256$ Lena, $512 \times 512$ Baboon, $512 \times 768$ Motorcycle, $768 \times 512$ Sailboat and $1024 \times 1024$ Pepper. The plain images, encrypted images and decrypted images are shown in Fig. 10. It can be seen from the test results that the encrypted images hide the plaintext information well, indicating that the proposed algorithm has a good encryption effect on color images of any sizes.

Fig. 10

Encryption and decryption results of color images

5.1 Key space

A large key space ensures that the encryption algorithm can effectively resist violent attacks. From the perspective of cryptography, the key space should be greater than $2^{100}$ to provide high-security performance. The encryption algorithm proposed in this paper contains a 512-bit secret key, so the key space of the algorithm is $2^{512}$, which is obviously greater than $2^{100}$. Therefore, the encryption algorithm proposed in this paper has a better ability to resist violent attacks.

5.2 Histogram

For a digital image, the histogram is the statistics of gray level distribution in the image, which can intuitively reflect the number of different gray levels, so the histogram of the plaintext image has statistical significance. After encryption, the resulting ciphertext image should break the statistical distribution of the plaintext image. In the histogram of the encrypted image, the frequency of each gray level should be as equal as possible, so that the histogram is uniform. Evenly distributed histograms indicate that image information is well hidden. Figure 11 shows the histograms of the plaintext images and ciphertext images tested in this chapter. The histograms of the encrypted image are all well-distributed enough to resist statistical attacks.

Fig. 11

Histogram of original image and encrypted image

5.3 Differential attack analysis

Differential attack is a kind of selective plaintext attack, in which the attacker obtains two ciphertext images by making a slight change to the plaintext image and using the encryption algorithm to process two different plaintext images, respectively. By comparing and analyzing the differences between the two ciphertext images, the attacker can find the connection between the plaintext image and the ciphertext image. For a secure encryption algorithm, when the plaintext image changes slightly, the corresponding ciphertext should change significantly, which means that it has good resistance to differential attacks. The ability to resist the differential attack is measured by the number of pixels change rate (NPCR) and the unified average changing intensity (UACI). The formula of NPCR and UACI is defined by Eqs. (18)–(20).

$$ {\text{NPCR}} = \frac{{\mathop \sum \nolimits_{ij} D\left( {i,j} \right)}}{M \times N} \times 100\% $$

(18)

$$ D\left( {i,j} \right) = \left\{ {\begin{array}{*{20}c} {1,C_{1} \left( {i,j} \right) \ne C_{2} \left( {i,j} \right)} \\ {0,C_{1} \left( {i,j} \right) = C_{2} \left( {i,j} \right)} \\ \end{array} } \right. $$

(19)

$$ {\text{UACI}} = \frac{1}{M \times N}\left[ {\mathop \sum \limits_{ij} \frac{{\left| {C_{1} \left( {i,j} \right) - C_{2} \left( {i,j} \right)} \right|}}{255}} \right] \times 100\% $$

(20)

where $C_{1}$ and $C_{2}$, respectively, represent the ciphertext images generated by the encryption algorithm for the plaintext images with only one pixel difference. $M$ and $N$ indicate the number of rows and columns of the ciphertext image, respectively. For a digital image with a gray level of 256, the ideal NPCR value and UACI value are 99.6094% and 33.4635%, respectively.

The NPCR and UACI results of different tested images in this chapter are listed in Table 1. Table 2 shows the NPCR and UACI performance comparison of our algorithm with other methods. The comprehensive performance of NPCR and UACI of our algorithm is closer to the ideal theoretical value. Therefore, our algorithm has a better ability to resist differential attacks.

Table 1 Results of NPCR and UACI performance

Table 2 Comparison of NPCR and UACI performance with other methods

5.4 The correlation between adjacent pixels

To prevent attackers from obtaining effective information of the image by analyzing the correlation between adjacent pixels, the adjacent pixels in the ciphertext image must be as irrelevant as possible, that is, the correlation coefficient between adjacent pixels should be close to 0. The formula of the correlation coefficient $r_{xy}$ is defined as Eq. (21).

where $x$ and $y$ are the gray values of two adjacent pixels in the image, $E\left( x \right)$ and $D\left( x \right)$ are the mathematical expectation and variance of $x$, respectively, $cov\left( {x,y} \right)$ is the covariance of $x$ and $y$, and $r_{xy}$ is the correlation coefficient.

$$ \left\{ {\begin{array}{*{20}l} {r_{xy} = \frac{{{\text{cov}} \left( {x,y} \right)}}{{\sqrt {D\left( x \right)D\left( y \right)} }}} \\ {E\left( x \right) = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} x_{i} } \\ {D\left( x \right) = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left[ {x_{i} - E\left( x \right)} \right]^{2} } \\ {{\text{cov}} \left( {x,y} \right) = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left[ {x_{i} - E\left( x \right)} \right]\left[ {y_{i} - E\left( y \right)} \right]} \\ \end{array} } \right. $$

(21)

Randomly select adjacent pixels from plaintext Lena image and ciphertext image in the horizontal, vertical and diagonal directions, the corresponding correlation distributions of R, G, B channels are shown in Fig. 12. Table 3 lists the correlation coefficients of adjacent pixels in plaintext images and ciphertext images. It can be found that the proposed algorithm greatly reduces the correlation between adjacent pixels in ciphertext images. The comparison of the correlation coefficients between the proposed algorithm and other methods in horizontal, vertical and diagonal directions is indicated in Table 4. It can be seen that although some methods have better correlation coefficients in a certain direction, the comprehensive performance of our algorithm in three directions is better than that of most other methods.

Fig. 12

Correlation distribution of plaintext image and encrypted image

Table 3 Correlation coefficients of ciphertext image and plaintext image

Table 4 Comparison of correlation coefficient with other methods

5.5 Information entropy

Information entropy is used to measure the uncertainty of digital images, and is an important indicator of randomness. The larger the information entropy of the image, the higher the uncertainty of the information it contains. The mathematical expression of information entropy is defined as Eq. (22).

$$ H\left( m \right) = - \mathop \sum \limits_{i = 1}^{L} p\left( {m_{i} } \right)\log_{2} p\left( {m_{i} } \right) $$

(22)

where $m_{i}$ represents the $i - {\text{th}}$ pixel value, $p\left( {m_{i} } \right)$ is the probability of the symbol $m_{i}$, $L$ is the gray level of image pixels. For a digital image with a gray level of 256, the ideal value of information entropy is 8. When the information entropy value of the ciphertext image is close to 8, it indicates that the encryption algorithm has high security.

Table 5 calculates the information entropy of the encrypted images, and Table 6 shows the comparison of the information entropy between the proposed algorithm and other methods. The information entropy of R, G, B channels of our algorithm is quite close to the ideal value, which indicates that the proposed algorithm is highly secure.

Table 5 Information entropy analysis

Table 6 Comparison of information entropy with other methods

5.6 Cropping and noise attacks

In the process of ciphertext image transmission, it is likely that partial data will be lost or disturbed by noise, which causes the receiver to fail to decrypt the correct plaintext image quickly.

A secure encryption algorithm must be able to resist data loss and cropping attacks. The test results of the image Lena subjected to data loss and noise attack are shown in Fig. 13. It can be seen that the image can still be decrypted and the main information of the image can be recognized regardless of the degree of data loss and noise attack. The test results prove that the proposed algorithm has high robustness.

Fig. 13

Test results of cropping and noise attacks

5.7 Key sensitivity

Key sensitivity is one of the important indexes of secure cryptosystem. Due to the sensitivity of the chaotic system to initial values, a small change in the key will lead to significant changes in the encrypted image and failure of decryption. Figure 14 shows the decryption results when the initial values and parameters of the chaotic system are changed slightly, respectively. It can be found that slight changes in each parameter will lead to decryption failure. The test results show that the proposed algorithm is very sensitive to secret key.

Fig. 14

Test results of key sensitivity

5.8 Running performance

The proposed algorithm directly scrambles and transforms the three-dimensional matrix of the color image, avoiding the process of matrix transformation and reducing the number of iterations of the chaotic system. Therefore, the proposed algorithm exhibits rapid encryption and decryption efficiency. The running performance was tested on MATLAB 2020b, Intel Core i7-8750H CPU @2.20 GHz with 8 GB RAM and Windows 10 operating system. Table 7 lists the encryption and decryption times for tested images of different sizes. It can be seen that the proposed algorithm completes image encryption and decryption in a few seconds. Table 8 shows the running time of our algorithm compared with other methods when encrypting and decrypting images of size $512 \times 512$. Obviously, our color image encryption algorithm has a better comprehensive running performance.

Table 7 Encryption and decryption time analysis

Table 8 Comparison of encryption and decryption time with other methods

6 Conclusion

In this paper, the cross-operation coupling model is proposed to design a new hyperchaotic system. Derived from the Chebyshev map, Sine map and a nonlinear function $\cos \left( x \right)$, this paper constructs a novel two-dimensional Chebyshev-Sine coupling map (2D-CSCM). Phase diagram, bifurcation diagram, Lyapunov exponent spectra, information entropy analysis and 0–1 test illustrate that the proposed hyperchaotic system exhibits complex hyperchaotic behavior. The key of the proposed encryption algorithm is generated by the hash function SHA-512 to improve the sensitivity to the plaintext image. In the process of encryption, the 3D bit-level matrix of color plaintext image is directly shuffled by Rubik's Cube scrambling method. Then the scrambled matrix is diffused by three-dimensional row diffusion and three-dimensional column diffusion based on chaotic sequences. Test results and security analysis of different sizes of color image encryption prove that the proposed algorithm has high security and efficiency and can resist various attacks.