1 Introduction

Over the past three decades, the chaos theory and its application have attracted frequently of consideration [25, 36, 42]. It is extremely rapid for chaotic systems, multifarious dissipative and conservative, to design and come true [28, 29, 44, 53,54,55]. In 2021, Han Xin-tong et al. designed a new fractional order system and implemented it with DSP [21]. Yang Yan et al. proposed and designed a multidimensional system with multiple equilibrium points [59]. In 2022, Bao Bo-cheng et al. designed no-argument memristive hyper-jerk system and its coexisting chaotic bubbles boosted by initial conditions [5]. Chen Ming-shu et al. found a novel memristive chaotic system without any equilibrium point [14]. These works have contributed considerably to the aspect of chaos, both in terms of system construction methods and applications of the system. However, the dynamical representation of some of the systems has remained up until now relatively less in terms of dynamics and lacks some properties. This paper refers to some classical systems, like Chen system [11], Lü system [39], Sprott system [47], Rucklidge system [62], etc. After understanding a variety of methods to construct the system, a novel asymmetric two-wing hyperchaotic system with multiple attractors is proposed, which contains some basic dynamical manifestations. In addition, it has some properties such as multistability, attractor coexistence, multiple state transitions.

Since hyperchaotic systems exhibit the following characteristics: autonomous systems with at least four-dimensional phase space are dissipative and possess at least two or more positive Lyapunov exponents. Therefore, hyperchaotic systems have higher unpredictability, greater randomness, more key parameters, and more complex topology and evolutionary behavior than low-dimensional chaotic systems [17]. On the other hand, their phase space is more difficult in reconstruction due to the existence of multiple positive Lyapunov exponents, and thus they are reliably secure in use for signal encryption, confidential communication and system synchronization. There is still a little less research on the aspect of hyperchaotic systems than chaotic systems, so there is a need for more research on hyperchaotic systems. After considering the comparative methods in some literatures [6, 7, 9], this paper also compares the systems in much literature. Moreover, the asymmetric double-wing system proposed in this paper obtains a hyperchaotic system, which can be studied more.

Chaotic synchronization is one of the considerable fields of chaotic systems. Synchronization methods are principally known in the following categories, for instance, adaptive synchronization [37], intermittent feedback synchronization [51], state observer synchronization [20], chaos observer synchronization [60], projective synchronization [63]. However, the aforementioned studies are all involved asymptotic synchronization and infinite convergence time [34]. Sun Jun-wei et al. realized finite time synchronization of two sophisticated systems by using sliding mode control method [48]. Shi Lei, Wang Lei-min et al., studied the finite time synchronization between multidimensional systems [4, 45, 52]. However, there are few related research, so it is of considerable value to further study the synchronization method of chaotic system. In this paper, the novel hyperchaotic system is combined with a finite time synchronization method to realize its finite time synchronization.

Chaotic systems have various real-world applications, like random number generators, communication, synchronization, and image encryption [16, 50]. Digital images are characterized by large amount of data and direct correlation between pixels and chaotic system has randomness, so it has certain advantages to apply chaotic system to image encryption [35]. Cun Qi-qi et al. proposed an innovative alternative method of DNA encryption [15]. Uzair Aslam Bhatti has delivered many contributions to image encryption algorithms, such as the hybrid watermarking algorithm using Clifford algebra, Arnold perturbation and chaotic encryption [8], and hyperspectral image classification based on spatial and spectral fusion of local similarity [10]. Gurpreet Kaur et al. studied fractional and based color image encryption algorithm [31]. Tanveer et al. discovered and studied 4D chaotic system and successfully developed it in the field of image encryption [22]. These works represent enormous contributions to chaotic digital image encryption. However, some of them still need continuing to optimize their image encryption methods, and some literature does not provide a comprehensive analysis of the encrypted images.

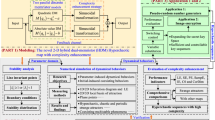
Based on the foregoing considerations, we present a novel asymmetrical double-wing third order hyperchaotic system in this paper. There are many special dynamics phenomena in this new system, like multi-stability, control of different initial values, high complexity, polymorphic transition. At the same time, this system has multiple equilibrium points, which means it has good homogeneous multiple stabilities and multiple attractors. This has been unobserved before in other hyperchaotic systems. In addition, the physical circuit of the system is designed and implemented. Last but not the least, a new image encryption algorithm is designed by combining the sequence of hyperchaotic system with DNA dynamic coding.

The rest of the paper is organized as follows. In the Section 2, the equation model, phase diagram and sequence diagram of the new system are introduced. Section 3 analyzes in detail the dynamical properties of the system and the state changes of the attractor of the chaotic system. Section 4 implements the physical circuit of the hyperchaotic system. In the Section 5, finite-time synchronization of the chaotic system is designed and implemented. Section 6 is the complete image encryption algorithm for the new system. Section 7 is the performance analysis of the encrypted images and the comparison with other algorithms. Finally, the results of the study are summarized, and conclusions are drawn.

2 New hyperchaotic system

The three-dimensional hyperchaotic system is designed in this paper which has good chaotic behavior, and its system equation is as follows:

$$ \left\{\begin{array}{l}\frac{dx}{dt}=- ax+ by- yz-c\\ {}\frac{dy}{dt}= dx+y\\ {}\frac{dz}{dt}=x-z+{y}^2\end{array}\right. $$
(1)

Where x, y and z are system variables, a, b, c, and d are system parameters. The choice of parameters is of immense importance for system, and nonlinear systems with independent parameters will be in diverse states. To enrich the states of chaotic systems, we combine chaotic circuits, phase diagrams, bifurcation diagrams, Lyapunov exponential spectra to determine the system parameters in a comprehensive way. The chaotic dynamics of a nonlinear system occur only at some specific parameters. When changing the system parameters, the nonlinear system can be in a periodic, quasi-periodic or chaotic state.

When the parameters of the system are a = 4, b = 10, c = 1, d = 1 and the initial value is (1, 1, 0), complex hyper-chaos exists in the system. The chaotic attractor of the system is shown in Fig. 1. It can be discovered that the phase diagram of the system is asymmetric with two vortexes, one is tremendous, and the other is small. In addition, the sequence diagram of each variable can equally be seen. At the same instant, the system proposed in this paper is compared with other systems in some respects as shown in Table 1, which also demonstrates the rich dynamic behavior of the system from the side.

Fig. 1
figure 1

Hyperchaotic systems with fixed initial values and parameters. (a) Spatial phase diagram of the system. (b) Sequence diagram of chaotic variables

Full size image
Table 1 Comparison of dynamic behavior of other systems
Full size table

3 Dynamical analysis of hyperchaotic system

3.1 Dissipation of attractor

The divergence (∇V) for the system (1) is obtained from the system eq. (1)

$$ \nabla V=\frac{\partial \overset{\cdotp }{x}}{\partial x}+\frac{\partial \overset{\cdotp }{y}}{\partial y}+\frac{\partial \overset{\cdotp }{z}}{\partial z}=-a+1-1=-4 $$
(2)

The ∇V< 0, so the system is dissipative and \( \frac{dv}{dt}={e}^{-4t} \) converges exponentially. When t → ∞, every trajectory of the system shrinks exponentially to zero. At this point, all the system orbits will ultimately be limited to a set of limit points with zero volume, and its progressive dynamic will be stuck on an attractor, which indicates the existence of the attractor.

3.2 Equilibrium point

To find the equilibrium point of the system, set system equation equal to zero. The system as follows:

$$ \left\{\begin{array}{l}- ax+ by- yz-c=0\\ {} dx+y=0\\ {}x-z+{y}^2=0\end{array}\right. $$
(3)

When variables for the system are a = 4, b = 10, c = 1, d = 1, the equilibrium set of the system are S1=(3.31467, −3.31467,14.3017); S2=(−4.24357, 4.24357, 13.7643); S3= (−0.071093, 0.071093, −0.06603). The Jacobian matrix obtained by linearizing the system.

$$ J=\left[\begin{array}{ccc}-a& b-z& -y\\ {}d& 1& 0\\ {}1& 2y& -1\end{array}\right] $$
(4)

Let det (J − λI) = 0, I is the identity matrix. The eigenvalues of the three equilibrium points for the system are obtained respectively, and the specific values are shown in Table 2. There is a real eigenvalues λ1 and a pair of complex conjugate characteristic roots λ2, λ3 in the equilibrium points of S1 and S2. According to Lyapunov stability theory, S1 and S2 are saddle focal equilibrium points, which are very important for chaotic system. For many chaotic systems, such equilibrium points are the prerequisite for the generation of vortex motion. In equilibrium point S3, λ1, λ3 are negative and λ2 is positive, so this equilibrium point is an unstable saddle point.

Table 2 Eigenvalues of each equilibrium point
Full size table

3.3 Lyapunov exponent, dimension, and bifurcation

Lyapunov index can quantitatively represent the motion state characteristics of the system and vividly describe the degree of attraction and repulsion between adjacent trajectories of the system, which is the most important physical quantity for describing chaotic systems. When the parameters in the system change, the curve in the Lyapunov exponential spectrum of the system describes the change of the system’s motion state. When the parameters are set, a = 4, b = 10, c = 1, d = 1 in the system, Lyapunov index (LEi) is calculated by MATLAB and obtained: LE1=0.7291, LE2=0.3993, LE3=-4.12. The Lyapunov dimension (DL) of the system is DL = 2.2738, indicating that the system is in the fractal dimension. At the same time，it can also be shown that the system is in hyperchaotic state by the Lyapunov exponent.

$$ {D}_L=j+\frac{1}{\left|{LE}_{j+1}\right|}\sum \limits_{i=1}^j{LE}_i=2+\frac{LE_1+{LE}_2}{LE_3}=2.2738 $$
(5)

Bifurcation refers to the phenomenon that the dynamic state of the system will change with the change of the system parameters or the initial value of the state variable. Lyapunov exponential spectrum and bifurcation diagram of the system change with the change of different parameters. When other parameters of the system remain unchanged, parameter c is selected to analyze the dynamic behavior. Figure 2 shows the Lyapunov exponential spectrum and bifurcation diagram of the system with c as a variable. The curves in the Fig. 2 are downward as LE1, LE2 and LE3.

Fig. 2
figure 2

System bifurcation diagram and Lyapunov exponential spectrum with parameter c. (a) Bifurcation diagram, (b) Lyapunov exponents spectra

Full size image

In addition, different periodic bifurcation also appears in the variation of system parameter c. The various variations of the chaotic attractor (x-y plane) are shown in Fig. 3. It can be seen from the observation of the curves that when c∈(−10,-5.5), the curves LE1 and 0 are basically in coincidence state, and LE1, LE2 and LE3 are both less than 0. When c∈(−5.2,-2.95), the curve LE1 continues to rise, the curve LE2 tends to be flat, but both are still greater than 0, LE3 less than 0, the system is hyperchaotic. When c∈[−2.95,-2.9], the curve LE1 is still greater than 0, and the curve LE2 drops rapidly and less than 0, LE3 is less than 0, the system is chaotic. Furthermore, when c∈[1.65,1.7], or c∈ [3.3,3.4), or c∈ [6.55,7.05], the system is chaotic. When c = −7.5, the system is in the period state (Fig. 3a). When c = −5.5, single wing transient chaotic state (Fig. 3b) is observed in the system. When c = −5.3, The system changes from single wing transient chaotic state to double wing transient chaotic state (Fig. 3c). When the value of c increases to −1, the system becomes double wing hyperchaotic state (Fig. 3d). When c = 3.5, the system is in a double wing periodic state (Fig. 3e). When increasing c = 6, single wing periodic oscillation (Fig. 3f) is observed in the system. When c = 10, single wing periodic state (Fig. 3g) appears in the system. Continue to increase parameter c to c = 15, the system evolves into quasi-periodic state (Fig. 3h). When c∈[15.1,20], the curve LE1 tends to a flat straight-line state, and curve LE2 drops gently. The system gradually enters a limit period state. As the parameter c changes, it is found that the system exhibits various chaotic attractors.

Fig. 3
figure 3

System attractor diagram with parameter c. (a) Single-wing period state attractor for c = −7.5, (b) Single-wing transient chaos state attractor for c = −5.5, (c) Transient transition attractor for c = −5.3, (d) Hyperchaotic attractor for c = −1, (e) Double-wing periodic state attractor for c = 3.5, (f) Single-wing periodic attractor for c = 6, (g) Periodic attractor for c = 10, (h) Quasi-periodic state attractor for c = 15

Full size image

3.4 System complexity

The study of the complexity of chaotic systems is regarded as an important part of system dynamics analysis. The complexity algorithm is used to try out the closeness between chaotic sequence and random sequence. The higher the complexity, the better the system. According to the complexity of correlation algorithm, the more similar it is to a random sequence, the higher the complexity of the system. The complexity of chaotic sequences can be divided into behavior complexity and structure complexity. Among them, C0 and SE algorithms belong to structural complexity, and their results have global statistical significance compared with behavior complexity.

In Fig. 4, the system complexity under a single parameter is first tested. On the premise that other system parameters remain unchanged, the complexity of C0 and SE of the system can be obtained by changing system parameter b, as shown in Fig. 4a and b respectively. As can be seen from the figure, when b = 10, the C0 complexity of the system is 0.06410, and the SE complexity is 0.397. Similarly, when we change the system parameter c, we can see that its complexity is not as high as that of b, but the complexity of C0 is generally above 0.04, and the complexity of SE fluctuates greatly, but it is also above 0.25. The complexity of the system was also tested for different initial values, when the system parameters were a = 4, b = 10, c = 1, and d = 1. The test values are shown in Table 3. It is found that no matter how the initial value of the system changes, the C0 complexity of the system is stable above 0.06400. In addition, after comparing the complexity of other literature systems, it is found that the complexity of this system is greater than that of other systems, indicating that the complexity of other systems is higher.

Fig. 4
figure 4

System complexity. (a) The C0 complexity of parameter b. (b) SE complexity with b. (c) C0 complexity with c. (d) SE complexity with c

Full size image
Table 3 C0 complexity of initial-controlled chaotic sequences
Full size table

Moreover, two system parameters are selected to calculate the complexity of the system. In the Fig. 5, the darker the color, the more complex the system. In addition, C0 complexity and SE complexity have good consistency in the same parameter variation. In the Fig. 5a and b, when the system parameters c∈(8, 10) and d∈(8, 9), the highly complex region is mainly on c∈(8, 9.8), d∈(8.1, 9). According to the multivariable complex chaos diagram, the change of the system can be seen more concretely. When other parameters remain unchanged and system parameters b and c are changed, the complexity of C0 and SE of the system is shown in Fig. 5c and d. It can be observed that the complexity graph of system parameters b and c is darker than that of parameters c and d, indicating that the complexity of b and c is higher.

Fig. 5
figure 5

System complexity. (a) C0 complexity, c∈(8,10), d∈(8,9). (b) SE complexity, c∈(8,10), d∈(8,9). (c) C0 complexity, b∈(0,10), c∈(0,2). (d) SE complexity, b∈(0,10), c∈(0,2)

Full size image

4 Circuit design and realization

After the theoretical analysis and numerical simulation, the circuit design is typically started in this completed the section to further observe the dynamic behavior of the complex system. When properly designing the independent circuit, the system eq. (1) is firstly transformed by proportional compression. Set RX → X, RY → Y, RZ → Z, R is the variable proportional compression factor. Correctly assuming R = 0.5, the changed equation in common is eq. (6).

$$ \left\{\begin{array}{l}\frac{dX}{dt}=- ax+ by- eyz-c\\ {}\frac{dY}{dt}= dx+y\\ {}\frac{dZ}{dt}=x-z+f{y}^2\end{array}\right. $$
(6)

The system parameters are a = 4, b = 10, c = 1, d = 1, e = 2, f = 2, respectively. Time scale transformation is performed on eq. (6), let T = τ0t and \( {\tau}_0=\frac{1}{R_5{C}_1}=\frac{1}{R_{11}{C}_2}=\frac{1}{R_{18}{C}_3} \), where τ0 is the time scale change factor. The transformed equation and schematic diagram are obtained.

$$ \left\{\begin{array}{l}\frac{dX}{dT}=\frac{1}{R_5{C}_1}\cdot \frac{R_7}{R_6}\left(-\frac{R_4}{R_1}X+\frac{R_4}{R_3}Y-0.1\frac{R_4}{R_2}Y\cdot Z-1\cdot \frac{R_4}{R_{21}}\right)\\ {}\frac{dY}{dT}=\frac{1}{R_{11}{C}_2}\cdot \frac{R_{13}}{R_{12}}\left(\frac{R_{10}}{R_8}X+\frac{R_{10}}{R_9}Y\right)\\ {}\frac{dZ}{dT}=\frac{1}{R_{18}{C}_3}\cdot \frac{R_{20}}{R_{19}}\left(\frac{R_{17}}{R_{16}}X-\frac{R_{17}}{R_{15}}Z+0.1\frac{R_{17}}{R_{14}}Y\cdot Y\right)\end{array}\right. $$
(7)

Set C1 = C2 = C3 = 33nF, the following parameter values, R5 = R11 = R18 = 50KΩ, R3 = R6 = R7 = 10KΩ, R12 = R13 = R19 = R20 = 10KΩ and R4 = R8 = R9 = R10 = R21 = 100KΩ, R15 = R16 = R17 = 100KΩ and R1 = 25KΩ, R2 = R14 = 5KΩ, can be obtained by comparing eqs. (6) and (7).

Through simulation verification on circuit simulation software Multisim, the phase diagram of the system is sufficiently shown in Fig. 6. The theoretical attractor is similar to the circuit attractor by carefully comparing the Fig. 1 and the Fig. 6. Therefore, the possible existence of attractors is confirmed by numerical analysis and experimental study.

Fig. 6
figure 6

System circuit schematic diagram and simulation diagram

Full size image

5 Synchronization implementation

In this section, system (8) is taken as the drive system and system (9) as the response system, a finite time synchronization mode of the system is realized. The model parameters in system (9) are the same as those in system (8), and U1, U2 and U3 are the control inputs. The specific synchronization method is as instantly follows:

$$ \left\{\begin{array}{l}\overset{\cdotp }{x_1}=-a{x}_1+b{x}_2-{x}_2{x}_3-c\\ {}\overset{\cdotp }{x_2}=d{x}_1+{x}_2\\ {}\overset{\cdotp }{x_3}={x}_1-{x}_3+{x_2}^2\end{array}\right. $$
(8)
$$ \left\{\begin{array}{l}\overset{\cdotp }{y_1}=-a{y}_1+b{y}_2-{y}_2{y}_3-c+{u}_1\\ {}\overset{\cdotp }{y_2}=d{y}_1+{y}_2+{u}_2\\ {}\overset{\cdotp }{y_3}={y}_1-{y}_3+{y_2}^2+{u}_3\end{array}\right. $$
(9)

In this synchronization, the error is defined as ei = yi − xi(i = 1, 2, 3), and the error dynamic system is system (10)

$$ \left\{\begin{array}{c}{e}_1={y}_1-{x}_1\\ {}{e}_2={y}_2-{x}_2\\ {}{e}_3={y}_3-{x}_3\end{array}\right. $$
(10)
$$ \left\{\begin{array}{l}\overset{\cdotp }{e_1}=-a{e}_1+b{e}_2-{y}_2{y}_3+{x}_2{x}_3+{u}_1\\ {}\overset{\cdotp }{e_2}=d{e}_1+{e}_2+{u}_2\\ {}\overset{\cdotp }{e_3}={e}_1-{e}_3+{y_2}^2-{x_2}^2+{u}_3\end{array}\right. $$
(11)

The controller design is as follows:

$$ \left\{\begin{array}{l}{u}_1=-{k}_1{e}_1-{k}_2\operatorname{sgn}\left({e}_1\right){\left|{e}_1\right|}^{\mu }+\left({y}_2{y}_3-{x}_2{x}_3\right)\\ {}{u}_2=-{k}_1{e}_2-{k}_2\operatorname{sgn}\left({e}_2\right){\left|{e}_2\right|}^{\mu }-\left(d+b\right){e}_1\\ {}{u}_3=-{k}_1{e}_3-{k}_2\operatorname{sgn}\left({e}_3\right){\left|{e}_3\right|}^{\mu }+\left({x_2}^2-{y_2}^2-{e}_1\right)\end{array}\right. $$
(12)

k1, k2 is a constant, 0 < μ < 1. sgn is the step function, if the parameters satisfy k1 ≥ max {a, 0}, k2 > 0, then the finite time synchronization can be fulfilled for the system through the controller. Now, using the Lyapunov function and eq. (11), its derivative can be obtained.

$$ {\displaystyle \begin{array}{l}v=\frac{1}{2}\sum \limits_{i=1}^3{e_i}^2\\ {}\begin{array}{l}\overset{\cdotp }{v}={e}_1{\overset{\cdotp }{e}}_1+{e}_2{\overset{\cdotp }{e}}_2+{e}_3{\overset{\cdotp }{e}}_3\\ {}={e}_1\left[-a{e}_1+b{e}_2-{y}_2{y}_3+{x}_2{x}_3+{u}_1\right]\\ {}+{e}_2\left[d{e}_1+{e}_2+{u}_2\right]+{e}_3\left[{e}_1-{e}_3+{y_2}^2-{x_2}^2+{u}_3\right]\\ {}={e}_1\left[-a{e}_1+b{e}_2-{y}_2{y}_3+{x}_2{x}_3\right]+{e}_2\left[d{e}_1+{e}_2\right]+\\ {}{e}_3\left[{e}_1-{e}_3+{y_2}^2-{x_2}^2\right]+{e}_1{u}_1+{e}_2{u}_2+{e}_3{u}_3\end{array}\end{array}} $$
(13)

Plug U1, U2 and U3 into eq. (13), get

$$ {\displaystyle \begin{array}{l}\overset{\cdotp }{v}=-a{e_1}^2+b{e}_1{e}_2-{y}_2{y}_3{e}_1+{x}_2{x}_3{e}_1+\\ {}d{e}_1{e}_2+{e_2}^2+{e}_1{e}_3-{e_3}^2+{e}_3{y_2}^2-{e}_3{x_2}^2+\\ {}\left[-{k}_1{e_1}^2+{e}_1{y}_2{y}_3-{e}_1{x}_2{x}_3-{e}_1{k}_2\operatorname{sgn}\left({e}_1\right){\left|{e}_1\right|}^{\mu}\right]\\ {}+\left[-{k}_1{e_2}^2-\left(d+b\right){e}_1{e}_2-{e}_2{k}_2\operatorname{sgn}\left({e}_2\right){\left|{e}_2\right|}^{\mu}\right]+\\ {}\left[-{k}_1{e_3}^2+{x_2}^2{e}_3-{y_2}^2{e}_3-{e}_1{e}_3-{e}_3{k}_2\operatorname{sgn}\left({e}_3\right){\left|{e}_3\right|}^{\mu}\right]\Big]\\ {}=-\left(k+a\right){e_1}^2+\left(1-k\right){e_2}^2-\left(1+k\right){e_3}^2-\\ {}{k}_2\left({\left|{e}_1\right|}^{\mu +1}+{\left|{e}_2\right|}^{\mu +1}+{\left|{e}_3\right|}^{\mu +1}\right)\end{array}} $$
(14)

Here, two lemmas are introduced as follows [51]:

  • Lemma 1

If there is a constantt1 > 0, such that\( \underset{t\to {t}_1}{\lim}\left|{e}_i\right|=0 \) and whent ≥ t1, |ei| ≡ 0(i = 1, 2, 3), finite time synchronization is implemented.

If there is a positive definite differential function V(t) that satisfies eq. (15):

$$ \overset{\cdotp }{V}(t)\le \varepsilon {V}^{\theta }(t),\forall t{\ge}_0,V\left({t}_0\right)\ge 0 $$
(15)

Where ε and θ are constants, in addition ε > 0, 0 < θ < 1, then the function ∀t satisfies.

$$ {V}^{1-\theta }(t)\le {V}^{1-\theta}\left({t}_0\right)-\varepsilon \left(1-\theta \right)\left(t-{t}_0\right),{t}_0\le t\le {t}_1 $$
(16)

and when ∀t ≥ t1,

$$ V(t)\equiv 0, $$
(17)
$$ {t}_1\le {t}_0+\frac{V^{1-\theta}\left({t}_0\right)}{\varepsilon \left(1-\theta \right)}. $$
(18)

  • Lemma 2

For any real numbers τ1, …, τn and 0 < α < 1, there are the following inequalities

$$ \sum \limits_{i=1}^n{\left|{\tau}_i\right|}^{\alpha +1}\ge {\left(\sum \limits_{i=1}^n{\left|{\tau}_i\right|}^2\right)}^{\frac{\alpha +1}{2}} $$
(19)

According to Lemma 1 and 2

$$ \overset{\cdotp }{v}\le -{k}_2\left({\left|{e}_1\right|}^{\mu +1}+{\left|{e}_2\right|}^{\mu +1}+{\left|{e}_3\right|}^{\mu +1}\right) $$
(20)

then

$$ {\displaystyle \begin{array}{l}\left({\left|{e}_1\right|}^{\mu +1}+{\left|{e}_2\right|}^{\mu +1}+{\left|{e}_3\right|}^{\mu +1}\right)\ge {\left({\left|{e}_1\right|}^2+{\left|{e}_2\right|}^2+{\left|{e}_3\right|}^2\right)}^{\frac{\mu +1}{2}}\\ {}\dot{v}\le -{k}_2{\left({\left|{e}_1\right|}^2+{\left|{e}_2\right|}^2+{\left|{e}_3\right|}^2\right)}^{\frac{\mu +1}{2}}\\ {}\begin{array}{l}\le -{k}_2{(2v)}^{\frac{\mu +1}{2}}\\ {}\le -{2}^{\frac{\mu +1}{2}}{k}_2{v}^{\frac{\mu +1}{2}}\end{array}\end{array}} $$
(21)

then

$$ {t}_1\le \frac{{\left(v\left({t}_0\right)\right)}^{\frac{1-\mu }{2}}}{2^{\frac{\mu -1}{2}}{k}_2\left(1-\mu \right)}\le \frac{{\left[\frac{1}{2}\sum \limits_{i=1}^3{e_i}^2(0)\right]}^{\frac{1-\mu }{2}}}{2^{\frac{\mu -1}{2}}{k}_2\left(1-\mu \right)} $$
(22)

Based on the lemma above, the system can achieve finite synchronization. If constants (x1, x2, x3) = (1, 1, 0), (y1, y2, y3) = (35, 20, −1), \( \mu =\frac{1}{2} \), k1 = 4, \( {k}_2=\frac{1}{4} \) are set, the synchronization time of the system is calculated as t≤21.714 according to eq. (22). It can be perceived from Fig. 7 that the error state converges to zero in finite time, so finite time synchronization, the driving system (8) and the response system (9), can be achieved.

Fig. 7
figure 7

System finite-time synchronization errors e1, e2, e3

Full size image

6 System image encryption

As shown in Fig. 8, the image encryption algorithm is mainly divided into three key parts in this paper: generating initial chaotic values related to chosen plaintext and generating pseudo-random sequences; Local Graph Structure (LGS) algorithm is intentionally used to select the region of the explicit image; and then finally, DNA encryption and secondary scrambling.

Fig. 8
figure 8

Image encryption flowchart

Full size image

6.1 LGS selection algorithm

LGS image selection was proposed by Eimad Abdu Abusham [1], and the specific formula is as follows:

$$ \left\{\begin{array}{l} LGS\left({\chi}_d,{y}_d\right)=\sum \limits_{k=0}^0s\left({g}_{d+1+p}-{g}_{d+p}\right){2}^{7-p}\\ {}s(x)=\Big\{\begin{array}{c}1,x\ge 0\\ {}0,x<0\end{array}\\ {}p=7,\dots, 0\end{array}\right. $$
(23)

Where (xd,yd) represents any two adjacent pixel values in the picture. Since more image details can be preserved by the algorithm and there are exactly 8 binary sequences. The principle of the LGS algorithm is described below. In Fig. 9a, When the pixel value is 125, the consecutiveness begins along the red arrow path in the upper left corner. As it moves along, if the next value is greater than the current value, zero is going to represent it, otherwise one will represent it. Finally, a binary sequence is obtained, and it became decimal by converting. In addition, we set the threshold for image selection as 128. In the image selection, if last decimal value is equivalent or greater than the set value, the initial information of the image is preserved. The binary sequence ‘10101011’ is generated at pixel 125 in Fig. 9b. It is converted to decimal to 171 greater than the threshold of 128 for this article. In this manner, the pixel value for this point should be retained. The binary sequence selected by LGS algorithm for pixel value 90 is ‘00101001’, and the final decimal is 41. Since it is less than 128, zero is set to be the value at this point. This manipulation is repeated, resulting in a vivid text image of the selected region.

Fig. 9
figure 9

LGS algorithm selection process

Full size image

6.2 Full encryption algorithm

Step1: According to the original image, the plaintext matrix is obtained and then converted into the corresponding plaintext sequence.

Step 2: Ode45 algorithm is used to calculate the initial value of the chaotic system and iterate the chaotic system. For better randomness, the first 1500 terms were removed, resulting in three chaotic sequences{xi, yi, zi}.

Step 3: Because 0–255 is the pixel value of the image, therefore the pseudo-random sequence {xi, yi, zi} are converted to 0–255 values. Sequence Zi can be applied in DNA encryption operations, Ziis converted to 1–3. The expression is shown below.

$$ \left\{\begin{array}{c}{X}_i=\operatorname{mod}\left(\mathrm{floor}\left(\left(50+a\sin \left({x}_i\right)/\pi \right)\times 65536\right),256\right)\\ {}{Y}_i=\operatorname{mod}\left(\mathrm{floor}\left(\left(50+a\sin \left({y}_i\right)/\pi \right)\times 65536\right),256\right)\\ {}{Z}_i=\operatorname{mod}\left(\mathrm{floor}\left(\left(50+a\sin \left({z}_i\right)/\pi \right)\times 65536\right),3\right)+1\end{array}\right. $$
(24)

Where floor() stands for taking the whole function.

Step 4: LGS algorithm and the above formula are used to process the plaintext image, which is converted into binary and then into decimal, and a matrix H of M × N is obtained.

Step 5: Eq. (25) determines the formation of H matrix. The matrix contains selected areas and unselected areas of the image.

$$ p\left(i,j\right)=\left\{\begin{array}{l}H\left(i,j\right),H\left(i,j\right)\ge 128\\ {}0,H\left(i,j\right)<128\end{array}\right. $$
(25)

Step 6: The matrix H is preprocessed with pseudo random sequence Yi, and the two-dimensional matrix E is output. Then, formula (25), (26) and (27) are used to encode the DNA of the selected region and sequence Xi.

$$ {E}_1\left(i,j\right)=\left\{\begin{array}{c} DNA\_ code\left(E\left(i,j\right), code\_ number\right),P\left(i,j\right)\ne 0\\ {}E\left(i,j\right),P\left(i,j\right)=0\end{array}\right. $$
(26)
$$ {X_i}^{\prime }(k)= DNA\_ code\Big({X}_i(k), code\_{number}^{\prime } $$
(27)

Where code _ number ≠ code _ number', but it’s all part of the eight ways DNA codes.

Step 7: Sequence Zi is used for DNA manipulation of selected regions and sequenceXi.

$$ {E}_2\left(i,j\right)=\left\{\begin{array}{c} DNA\_ operation\left({E}_1\left(i,j\right),{X}_i(k),{Z}_i\right),P\left(i,j\right)\ne 0\\ {}E\left(i,j\right),P\left(i,j\right)=0\end{array}\right. $$
(28)

The addition, subtraction, XOR and other operations are determined by sequence Zi in DNA encryption. Tables 4, 5, 6, and 7 show the detailed operation rules.

Table 4 DNA coding rules
Full size table
Table 5 DNA addition rule
Full size table
Table 6 DNA subtraction rule
Full size table
Table 7 DNA XOR rule
Full size table

Step 8: Decode according to the decoding number decode _ number.

$$ {E}_3\left(i,j\right)=\left\{\begin{array}{c} DNA\_ decode\left({E}_2\left(i,j\right), decode\_ number\right),P\left(i,j\right)\ne 0\\ {}E\left(i,j\right),p\left(i,j\right)=0\end{array}\right. $$
(29)

Where decode _ number also belongs to the eight encoding methods of DNA, butdecode _ number ≠ code _ number, decode _ number ≠ code _ number'. This step is equivalent to encrypting the image for the selected region again.

Step 9: The two-dimensional matrix R of M × N is obtained by transforming the sequence Zi. Then perform XOR operations on E3 and the matrix Zi.

$$ {E}_4\left(i,j\right)={E}_3\left(i,j\right)\oplus R\left(i,j\right) $$
(30)

Step 10: Finally, the whole image is scrambled without repetition to obtain the encrypted image H. For encryption algorithm, its reverse process is decryption algorithm.

Specific standard 256 × 256 Lena, Baboon and familiar Peppers images are ordinarily used in the image encryption experiment. The encrypted image is shown in Fig. 10. Accurately compared with the original image, no image features are invariably found.

Fig. 10
figure 10

Image encryption effect. (a), (d), (g) is the original image. (b), (e), (h) is encryption image. (c), (f), i is decrypted image

Full size image

7 Image security performance analysis

7.1 Key space analysis

Key space refers to the set of all legitimate keys. When the key space is large enough, exhaustive attack can be effectively resisted. Generally speaking, when the key space is larger than 2100, the security and adequate reliability of the encryption system will be guaranteed [61]. In this encryption system, the private key is the initial value of the hyperchaotic system (X0, Y0, Z0), and the size for the calculated key space is 2 × 1060, which is far larger than the above requirements.

7.2 Sensitivity analysis

Whether the encryption algorithm is sensitive to the key is also one of the good performances. According to the encryption algorithm in this paper, the key parameter is (X0, Y0, Z0). On the premise of keeping two of them unchanged, the original image can be decrypted when Y0 becomes Y0 + 10−16. But when Y0 changes to Y0 + 10−15 and is denoted as Y0', the plaintext image cannot be decrypted. In the same way, when Z0 becomes Z0 + 10−15, is called Z0', the original image can’t be decrypted. The results are presented Fig. 11, and similar results occur when the remaining key parameters are tested. The consequences show that the proposed image encryption algorithm includes extraordinary key sensitivity.

Fig. 11
figure 11

Images decrypted with the wrong key and the right key respectively. (a) Decryption image of error key Y0', (b) Decryption image of error keyZ0'. (c) Decryption image of the correct key

Full size image

7.3 Image histogram analysis

It is a dominant statistical feature for the image. The histogram of the plaintext image is evenly undistributed, which shows the statistical features of the pixel. On the direct contrary, the histogram distribution of ciphertext image is more uniform. Figure 12 of this system also conforms to the above characteristics.

Fig. 12
figure 12

Histogram of image. (a) Raw Lena image, (b) Encrypted Lena image

Full size image

7.4 Correlation coefficient calculation and analysis

Correlation between images is equally significant for encryption algorithms. Principally, plaintext image has strong correlation between adjacent pixels in horizontal, vertical, and diagonal directions, while ciphertext image should have no correlation between adjacent pixels. The calculation formula remain as follows.

$$ \left\{\begin{array}{l}\gamma =\frac{\mathit{\operatorname{cov}}\left(u,v\right)}{\sqrt{D(u)}\sqrt{D(v)}}\\ {}\mathit{\operatorname{cov}}\left(u,v\right)=\frac{1}{N}{\sum}_{i=1}^N\left({u}_i-E(u)\right)\left({v}_i-E(v)\right)\\ {}D(u)=\frac{1}{N}{\sum}_{i=1}^N{\left({u}_i-E(u)\right)}^2\\ {}E(u)=\frac{1}{N}{\sum}_{i=1}^N\left({u}_i\right)\end{array}\right. $$
(31)

Where Uand V stand for the values of any two adjacent pixels, E(U) and D(U)show the expectation and variance respectively. The previous Lena images before and after encryption are selected for correlation coefficient calculation, and the correlation coefficient diagram of the images before and after encryption is shown in Fig. 13. The plaintext images provide obvious correlation, while the corresponding ciphertext images are evenly distributed. The correlation coefficients of the image in horizontal, vertical, and diagonal directions before and after encryption were calculated. As shown in Table 8, the archetypal image has a strong correlation close to one in three directions, while the corresponding ciphertext image has uniformly distributed pixels and its correlation coefficient is close to zero.

Fig. 13
figure 13

Correlation coefficient of image. (a) Plaintext horizontal, (b) Plaintext vertical direction, (c) Plaintext is diagonal, (d) Clear opposition to angular direction, (e) Ciphertext horizontal direction, (f) Ciphertext vertical direction, (g) The ciphertext is in the diagonal direction, (h) Ciphertext is opposed to angular direction

Full size image
Table 8 Correlation coefficient comparison
Full size table

7.5 Difference analysis

A secure image encryption algorithm is exceptionally sensitive to any minor change in the plaintext image. That is, any change in a single pixel of the plaintext image will produce a completely different ciphertext image. Broadly, the sensitivity of encryption algorithm to plaintext information is measured by two indexes: pixel change rate (NPCR) and average change intensity of normalized pixel value (UACI). The calculation formula of NPCR and UACI is described as follows:

$$ NPCR=\frac{1}{M\times N}\sum \limits_{i=1}^M\sum \limits_{j=1}^ND\left(i,j\right)\times 100\% $$
(32)
$$ UACI=\frac{1}{M\times N}\sum \limits_{i=1}^M\sum \limits_{j=1}^N\frac{\mid {C}^{\prime}\left(i,j\right)-C\left(i,j\right)\mid }{255}\times 100\% $$
(33)

Where, C(i, j) and C(i, j) respectively represent the pixel gray values of the two ciphertext images at coordinates (i, j); M and N represent the height and width of the image, respectively. D(i, j) is defined as follows: if C(i, j) = C(i, j), D(i, j) = 1; Otherwise, D(i, j) = 0.

The ciphertext image can be obtained by encrypting the image with the key in the algorithm. Subsequently arbitrarily select a pixel in the plaintext image, change its pixel value and get a new plaintext image. The similar key is used to encrypt the changed plaintext image to obtain another ciphertext image. According to eq. (32) and eq. (33), a set of NPCR and UACI values can be obtained by calculating the above two ciphertext images, and the results are shown in Table 9. After performing the previous method several times, the average value of NPCR and UACI can be obtained. The outstanding value of NPCR and UACI obtained by using the proposed algorithm is 99.62% and 33.43%, which is very close to the ideal expected value of NPCR and UACI.

Table 9 NPCR and UACI test results
Full size table

7.6 Robustness analysis

Robustness analysis is the most essential criterion to measure the anti-interference capability of an encryption algorithm. In this paper, Lena image is selected for experimental analysis, and noise attack and shear attack are used to test the robustness of the algorithm. 0.2 time and 0.05 time of salt and pepper noise were applied to the encrypted image respectively, and the decrypted image was shown in Fig. 14b and d. The decryption results of one-eighth and one-fourth encrypted images are shown in Fig. 14f and h. Compared with the experimental consequences, the encryption algorithm in this paper can still recover most of the original image information. It shows the algorithm can resist noise and shear attacks to a certain extent and has good robustness.

Fig. 14
figure 14

Robustness analysis of image. (a) Apply 0.2 times salt and pepper noise, (b) Decrypted image, (c) Apply 0.05 times salt and pepper noise, (d) Decrypted image, (e) Crop 1/8 of the encrypted image, (f) Decrypted image, (g) Crop a quarter of the encrypted image, (h) Decrypted image

Full size image

7.7 The information entropy

The uncertainty of image is usually known by information entropy. The greater the entropy of information, the more information, the less visual information. The calculation formula of information entropy is as follows.

$$ H=-{\sum}_{i=0}^{2^{\mathrm{n}}-1}p\left({\mathrm{s}}_{\mathrm{i}}\right){\log}_2p\left({\mathrm{s}}_{\mathrm{i}}\right) $$
(34)

Where, 2n shows all states for the pixel value in the image, and p(si) is the possibility of the pixel value in the whole image. If there are 2n states of information, the entropy of information is n. For a standard image with 256 states, 8 would be ideal for its entropy of information. The encrypted image entropy of the system is 7.9986, which is very close to the theoretical value 8.

7.8 Comparison of different algorithms

To compare the performance of different literature algorithms, Table 8 shows the comparison of correlation coefficients of different literature algorithms. After comparison, it is discovered that the correlation coefficient of this algorithm is better than that of most literature algorithms. Table 9 shows the comparison of the results of NPCR and UACI. The NPCR of this algorithm is the highest and the value of UACI is only lower than the UACI of the literature [23, 56]. The information entropy of this algorithm is the highest after comparing the information entropy of other literature in Table 10. Therefore, the algorithm in this paper boasts an intense comprehensive performance compared with other algorithms in the literature.

Table 10 Information entropy comparison
Full size table

8 Conclusion

In this paper, a current hyperchaotic system of third order non-autonomous is constructed. The dynamic behavior of the system is analyzed by the spatial phase diagram, bifurcation diagram, Lyapunov exponential spectrum, Poincare cross section diagram and complexity. It is uncovered that the system has abundant dynamic behaviors and good topological structure. In addition, the system additionally accepts the extraordinary circumstances which asymmetrical double wing is converted to single wing, but it is affected by changes in system initialization and system parameters. When analyzing the influence of nonlinear term c, we observe several phenomena of chaotic attractors. For instance, from chaos to chaos, or from chaos to period. And tested the C0 and SE complexity of the system with different initial values and parameters. Compared with the complexity of other systems, the complexity of this system is relatively high. Furthermore, the system circuit is designed and verified in Multisim circuit simulation software. At the same instant, finite time synchronization of the system is achieved by selecting the appropriate controller. Moreover, a new image encryption algorithm is designed based on the system, DNA encryption and LGS image selection. By comparing it with most of the other algorithms, this one can select and encrypt each region of the image accurately. At the last moment, the security performance of encrypted image is analyzed, and it is found that it has good encryption effect and can be widely used in the field of image encryption in the future. In future work, we plan to apply the hyperbolic sine function to this hyperchaotic system. In the circuit design of the novel chaotic system, the circuit structure is optimized, and some circuit elements are reduced. In addition, it is expected that the system can be successfully applied to the field of signal detection.