1 Introduction

Soliton equations have been widely used and deeply studied in the fields of fluid mechanics, physics, mathematics, communication and other natural disciplines from the discovery of solitons to the present. On the one hand, the content of soliton theory is to develop systematic methods for solving nonlinear equations [1,2,3,4,5,6]. The other is to study the algebraic and geometric properties of integrable systems [7, 8]. With the continuous development of integrable systems, the theory of integrable systems is also gradually applied to discrete systems. Then, the discrete integrable systems have attracted more and more attention because of their wide application in many fields in recent decades. The research of the discrete integrable systems can be traced back to the works of Ablowitz, Ladik [9, 10] and Hirota in the 1970s. Hirota firstly discretized the nonlinear partial difference KdV equation [11], the discrete-time Toda equation [12] and other soliton equations. Then, the properties and exact solutions of some discrete equations have been discussed [13,14,15,16]. Date et al proposed a method of discrete soliton equation by means of the transformation group theory, which gives a great number of integrable discretizations of soliton equations [17]. A case in point is the quantum field theory, in which discretization provides a strong implement for building models of quantum gravity [18]. Suris developed a universal Hamiltonian method for integrable discretization [19]. After this pioneering work of integrable discretization, the research of discrete integrable systems has gradually extended to other mathematical fields. For instance, numerical analysis and its various applications are largely dependent on the discretization of the related partial differential equations (PDEs) [20]. Integrable discrete system promotes the development of new core mathematical tools for the discrete complex analysis, the discrete differential geometry and the theoretical physics. And it provides an effective way to study the difference equation and the general theory of discrete system.

In 1992, Matveev firstly proposed the positon solutions of the KdV equation [21], which is a kind of singular real solution, and has obvious connection with the super transparent potential in quantum physics. The results shown that the positon solution is a class of slowly damped oscillation solution widely existing in nonlinear integrable equations and it has the special property of being superreflectionless [22]. Unlike the exponentially decaying soliton solution, the positons are weakly localized. In particular, the solitons do not experience any phase shift in a collision with the positons, whereas the positons produce two additional but always finite phase shifts in collision with solitons. The positons themselves remain unchanged in the collision [23,24,25]. Especially, when Matveev gave positon and soliton-positon solutions of the KdV equation by means of the exact Wronskian expression [22], the positon solutions were quickly taken into account in other nonlinear evolution equations, such as the Sine-Gordon (SG) equation [26], the defocusing modified KdV (mKdV) equation [27, 28], the Toda-lattice [29], the extended KdV equation [30] and the Hirota–Satsuma coupled KdV system [31]. However, all of the above literatures on positon are singular functions. For many soliton equations with complex values, the existence of smooth positon solutions becomes a question worthy studying. Recently, some papers have constructed the smooth positon for continuous equations of the focusing mKdV equation [25], the complex mKdV equation [32], the second-type derivative nonlinear Schrödinger (DNLSII) equation [33], the derivative nonlinear Schrödinger (DNLS) equation [34]. Besides, as a potential in quantum mechanics, the positon solution of the KdV equation is expected to be realized by band engineering in practical application [35].

In this paper, the spatial discretization equation of Hirota equation [36] is discussed,

$$\begin{aligned} \begin{aligned} \frac{\hbox {d}}{\hbox {d}t}u_{n}=&\;\alpha (1+|u_{n}|^2)[u_{n+2}-u_{n-2}+2u_{n-1}\\&-2u_{n+1}+u_{n}^{*}(u_{n+1}^2-u_{n-1}^2)\\&-|u_{n-1}|^2u_{n-2}+|u_{n+1}|^2u_{n+2}\\&+u_{n}(u_{n-1}^{*}u_{n+1}-u_{n+1}^{*}u_{n-1})]\\&-i\beta (1+|u_{n}|^2)(u_{n+1}+u_{n-1})+2i\beta u_{n}, \end{aligned} \end{aligned}$$
(1)

where \(\alpha \) and \(\beta \) are two real constants and the \(*\) denotes the complex conjugation. The spatially discrete Hirota equation was derived from the reduction of an Ablowitz–Ladik hierarchy matrix. The order-n soliton solution and continuous limit theory of Eq. (1) have been discussed in Ref. [36]. In Ref. [37], the rogue wave solutions of Eq. (1) were studied. Moreover, There are two special forms of the spatial discrete Hirota equation. The spatial discrete complex mKdV equation can be simplified from Eq. (1) when \(\beta =0\), and Eq. (1) can be reduced to the spatial discrete NLS equation when \(\alpha =0\). And the rational solution, breather solution and continuous limit theory of the spatial discrete complex mKdV equation have been investigated [15]. However, to our knowledge, the smooth positon solutions of the spatial discrete Hirota equation (1) have not been reported. Positon solution can be derived from the degenerate of soliton solution. Therefore, we consider whether we can use this degenerated idea to construct the degenerate solutions of the discrete equation. The purpose of this paper is constructed the degenerate solutions of the spatial discrete Hirota equation.

This paper is organized as follows. In Sect. 2, the smooth positon solution under the zero seed solution is given by using the degenerate Darboux transformation (DT). In Sect. 3, the breather solution of Eq. (1) is constructed from the nonzero seed solution. In Sect. 4, the breather-positon solutions of Eq. (1) are generated by a degenerated process based on breather solution. The conclusion is provided in the last section.

2 Positons of the spatial discrete Hirota equation

The Lax pairs of the spatial discrete Hirota equation (1) are [36]:

$$\begin{aligned} \varphi _{n+1}=L_{n}\varphi _{n}, \quad \frac{\hbox {d}\varphi _{n}}{\hbox {d}t}=M_{n}\varphi _{n}, \end{aligned}$$
(2)

where the matrices \(L_{n}\) and \(M_{n}\) have the following forms:

$$\begin{aligned} L_{n}= & {} \left( \begin{matrix} \lambda &{}\quad u_{n} \\ -u_{n}^{*} &{}\quad \lambda ^{-1} \end{matrix}\right) ,\\ M_{n}= & {} \alpha \left( \begin{matrix}A_{n}(\lambda ,\lambda ^{-1},u_{n})&{}\quad B_{n}(\lambda ,\lambda ^{-1},u_{n})\\ -B_{n}(\lambda ^{-1},\lambda ,u_{n}^{*})&{}\quad A_{n}(\lambda ^{-1},\lambda ,u_{n}^{*})\end{matrix}\right) \\&\quad +\,i\beta \left( \begin{matrix}C_{n}(\lambda ,\lambda ^{-1},u_{n})&{}\quad D_{n}(\lambda ,\lambda ^{-1},u_{n})\\ D_{n}(\lambda ^{-1},\lambda ,u_{n}^{*})&{}\quad -C_{n}(\lambda ^{-1},\lambda ,u_{n}^{*})\end{matrix}\right) , \end{aligned}$$

where

$$\begin{aligned} A_{n}(\lambda ,\lambda ^{-1},u_{n})&= \frac{\lambda ^{4}-\lambda ^{-4}}{2}-\lambda ^{2}+\lambda ^{-2}+\lambda ^{2}u_{n}u_{n-1}^{*}\\&-\lambda ^{-2}u_{n-1}u_{n}^{*}-2u_{n}u_{n-1}^{*}\\&+(u_{n}u_{n-1}^{*})^{2}+(1\\&+|u_{n-1}|^{2})u_{n}u_{n-2}^{*}\\&+(1+|u_{n}|^{2})u_{n+1}u_{n-1}^{*},\\ B_{n}(\lambda ,\lambda ^{-1},u_{n})&= \lambda ^{3}u_{n}+\lambda ^{-3}u_{n-1}+\lambda [(1\\&+|u_{n}|^{2})u_{n+1}+u_{n}^{2}u_{n-1}^{*}-2u_{n}]\\&+\lambda ^{-1}[(1+|u_{n-1}|^{2})u_{n-2}\\&+u_{n-1}^{2}u_{n}^{*}-2u_{n-1}],\\ C_{n}(\lambda ,\lambda ^{-1},u_{n})&= -u_{n}u_{n-1}^{*}-\frac{(\lambda -\lambda ^{-1})^{2}}{2},\\ D_{n}(\lambda ,\lambda ^{-1},u_{n})&= -\lambda u_{n}+\lambda ^{-1}u_{n-1}. \end{aligned}$$

Here, \(\lambda \) is the eigenvalue parameter independent of n and t and \(\varphi _{n}=(\varphi _{n,1},\varphi _{n,2})^{T}\) is the eigenfunction related to \(\lambda \). According to the compatibility condition of Eq. (1), the zero curvature equation is

$$\begin{aligned} L_{n,t}=M_{n+1}L_{n}-L_{n}M_{n}. \end{aligned}$$
(3)

The determinant representation of the N-fold Darboux transformation (DT) for Eq. (1) has been expressed by [36]

$$\begin{aligned} u_{n}^{[N]}=u_{n}\frac{\omega _{n+1}^{{[N]}_{1}}}{\omega _{n+1}^{[N]}}+\frac{\omega _{n+1}^{{[N]}_{2}}}{\omega _{n+1}^{[N]}}, \end{aligned}$$
(4)

where

$$\begin{aligned} \tiny \omega _{n}^{[N]} =\tiny \begin{vmatrix} \lambda _{1}^{-N}\varphi _{n,1}^{(1)}&\quad \lambda _{1}^{-N+1}\varphi _{n,2}^{(1)}&\quad \lambda _{1}^{-N+2}\varphi _{n,1}^{(1)}&\quad \cdots&\quad \lambda _{1}^{N-2}\varphi _{n,1}^{(1)}&\quad \lambda _{1}^{N-1}\varphi _{n,2}^{(1)} \\ \lambda _{2}^{-N}\varphi _{n,1}^{(2)}&\quad \lambda _{2}^{-N+1}\varphi _{n,2}^{(2)}&\quad \lambda _{2}^{-N+2}\varphi _{n,1}^{(2)}&\quad \cdots&\quad \lambda _{2}^{N-2}\varphi _{n,1}^{(2)}&\quad \lambda _{2}^{N-1}\varphi _{n,2}^{(2)} \\ \vdots&\quad \vdots&\quad \vdots&\quad \vdots&\quad \vdots&\quad \vdots \\ \lambda _{N}^{-N}\varphi _{n,1}^{(N)}&\quad \lambda _{N}^{-N+1}\varphi _{n,2}^{(N)}&\quad \lambda _{N}^{-N+2}\varphi _{n,1}^{(N)}&\quad \cdots&\quad \lambda _{N}^{N-2}\varphi _{n,1}^{(N)}&\quad \lambda _{N}^{N-1}\varphi _{n,2}^{(N)}\\ (\lambda _{1}^{*})^{N}\varphi _{n,2}^{*(1)}&\quad -(\lambda _{1}^{*})^{N-1}\varphi _{n,1}^{*(1)}&\quad (\lambda _{1}^{*})^{N-2}\varphi _{n,2}^{*(1)}&\quad \cdots&\quad (\lambda _{1}^{*})^{-N+2}\varphi _{n,2}^{*(1)}&\quad -(\lambda _{1}^{*})^{-N+1}\varphi _{n,1}^{*(1)}\\ (\lambda _{2}^{*})^{N}\varphi _{n,2}^{*(2)}&\quad -(\lambda _{2}^{*})^{N-1}\varphi _{n,1}^{*(2)}&\quad (\lambda _{2}^{*})^{N-2}\varphi _{n,2}^{*(2)}&\quad \cdots&\quad (\lambda _{2}^{*})^{-N+2}\varphi _{n,2}^{*(2)}&\quad -(\lambda _{2}^{*})^{-N+1}\varphi _{n,1}^{*(2)}\\ \vdots&\quad \vdots&\quad \vdots&\quad \vdots&\quad \vdots&\quad \vdots \\ (\lambda _{N}^{*})^{N}\varphi _{n,2}^{*(N)}&\quad -(\lambda _{N}^{*})^{N-1}\varphi _{n,1}^{*(N)}&\quad (\lambda _{N}^{*})^{N-2}\varphi _{n,2}^{*(N)}&\quad \cdots&\quad (\lambda _{N}^{*})^{-N+2}\varphi _{n,2}^{*(N)}&\quad -(\lambda _{N}^{*})^{-N+1}\varphi _{n,1}^{*(N)} \end{vmatrix}, \end{aligned}$$

here, replace the first column and the second column, respectively, in \(\omega _{n}^{[N]}\) with \((\lambda _{1}^{N}\varphi _{n,1}^{(1)},\lambda _{2}^{N}\varphi _{n,1}^{(2)},\ldots ,\lambda _{N}^{N}\varphi _{n,1}^{(N)},(\lambda _{1}^{*})^{-N}\varphi _{n,2}^{*(1)}, (\lambda _{2}^{*})^{-N}\varphi _{n,2}^{*(2)}, \ldots , (\lambda _{N}^{*})^{-N}\varphi _{n,2}^{*(N)})^{T}\), which is \(\omega _{n}^{{[N]}_{1}}\) and \(\omega _{n}^{{[N]}_{2}}\).

Taking a seed solution \(u_{n}=0\), the corresponding spectral equation becomes,

$$\begin{aligned} \varphi _{n+1}= & {} \left( \begin{matrix} \lambda &{}\quad 0 \\ 0 &{}\quad \lambda ^{-1} \end{matrix}\right) \varphi _{n}, \quad and\nonumber \\ \frac{\hbox {d}\varphi _{n}}{\hbox {d}t}= & {} \left( \begin{matrix} \chi (\lambda ) &{}\quad 0 \\ 0 &{}\quad \omega (\lambda ) \end{matrix}\right) \varphi _{n}, \end{aligned}$$
(5)

where

$$\begin{aligned} \lambda&=e^{a+ib},\\ \chi (\lambda )&= \alpha \left( \frac{\lambda ^{4}-\lambda ^{-4}}{2}-\lambda ^{2}+\lambda ^{-2}\right) -\frac{i\beta }{2}(\lambda -\lambda ^{-1})^2,\\ \omega (\lambda )&=-\chi (\lambda ), \end{aligned}$$

then obtain the eigenfunction

$$\begin{aligned} \varphi _{n,1}=c_{1}e^{Z(\lambda )}, \quad \varphi _{n,2}=c_{2}e^{-Z(\lambda )}, \end{aligned}$$
(6)
Fig. 1
figure 1

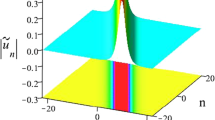
The evolution of two-positon \(|u_{n-p}^{[2]}|\) with \(a_{1}=0.8\), \(b_{1}=0.6\), \(c_{1}^{(1)}=1\), \(c_{2}^{(1)}=0.78\), \(c_{1}^{(2)}=1.2\), \(c_{2}^{(2)}=0.9\), \(\alpha =0.6\) and \(\beta =1.98\) of the spatial discrete Hirota equation on (n, t)-plane. Panel (a) is the discrete 3D plot, Panel (b) is the continuous 3D plot, panel (c) is the density plot

Full size image
Fig. 2
figure 2

The evolution of three-positon \(|u_{n-p}^{[3]}|\) with \(a_{1}=0.8\), \(b_{1}=0.09\), \(c_{1}^{(1)}=0.6\), \(c_{2}^{(1)}=0.8\), \(c_{1}^{(2)}=0.7\), \(c_{2}^{(2)}=1.1\), \(c_{1}^{(3)}=0.6\), \(c_{2}^{(3)}=1.2\), \(\alpha =0.6\) and \(\beta =0.6\) of the spatial discrete Hirota equation on (n, t)-plane. Panel (a) is the discrete 3D plot, Panel (b) is the continuous 3D plot, panel (c) is the density plot

Full size image

where a and b are real constants and \(Z(\lambda )=n\ln \lambda +\chi (\lambda )t\) and \(c_{j}\) \((j=1,2)\) are arbitrary complex parameters. Therefore, when \(N=1\), taking the eigenfunctions \(\varphi _{n,1}^{(1)}=c_{1}^{(1)}e^{Z(\lambda _{1})}, \varphi _{n,2}^{(1)}=c_{2}^{(1)}e^{-Z(\lambda _{1})}\) are substituted into Eq. (4), the explicit formula of order-one soliton solution is follows:

$$\begin{aligned} u_{n}^{[1]}= & {} \frac{\lambda _{1}(\lambda _{1}^{*})^{-2}(|\lambda _{1}|^{4}-1)\varphi _{n,1}^{(1)}\varphi _{n,2}^{*(1)}}{|\lambda _{1}|^{2}|\varphi _{n,1}^{(1)}|^{2}+|\varphi _{n,2}^{(1)}|^{2}},\nonumber \\= & {} \frac{(1-|\lambda _{1}|^{-4})\lambda _{1}^{2}}{2}e^{2iZ_{I}(\lambda _{1})}sech(2Z_{R}(\lambda _{1}), \end{aligned}$$
(7)

here \(Z_{R}(\lambda _{1})\) and \(Z_{I}(\lambda _{1})\) are the real and imaginary parts of \(Z(\lambda _{1})\), respectively, and they are given by

$$\begin{aligned} Z_{R}(\lambda _{1})= & {} a_{1}n+\{\alpha [\cos (4b_{1})\sinh (4a_{1})\\&-\,2\cos (2b_{1})\sinh (2a_{1})]\\&+\,\beta \sin (2b_{1})\sinh (2a_{1})\}t,\\ Z_{I}(\lambda _{1})= & {} b_{1}n+\{\alpha [\sin (4b_{1})\cosh (4a_{1})\\&-\,2\sin (2b_{1})\cosh (2a_{1})]\\&-\,\beta \cos (2b_{1})\cosh (2a_{1})+\beta \}t. \end{aligned}$$

Similar to solving the order-one soliton solution, the order-two soliton solution \(u_{n}^{[2]}\) can be obtained when \(N=2\). It can be seen that the denominator of \(u_{n}^{[2]}\) is zero when the eigenvalue \(\lambda _{2}=\lambda _{1}\) from the expression of \(u_{n}^{[2]}\). In general, the soliton solution \(u_{n}^{[N]}\) becomes an indeterminate form \(\frac{0}{0}\) through the degenerate N-fold DT obtained by setting the degenerate limit \(\lambda _{j}\rightarrow \lambda _{1}(j=2,3,4, \ldots ,N)\). Then, by performing the high-order Taylor expansion of \(\lambda _{j}=\lambda _{1}+\varepsilon (j=2,3,4, \ldots ,N)\) in Eq. (4), the n-positon solution of the spatial discrete Hirota equation given in the following content.

Example 2.1

The n-positon solution of Eq. (1) generated by the degenerated N-fold DT from the zero seed solution \(u_{n}=0\) is expressed as

$$\begin{aligned} u_{n-p}^{[N]}=\frac{{\omega _{n+1}^{[N]_{2}}}'}{{\omega _{n+1}^{[N]}}'}, \end{aligned}$$
(8)

where

$$\begin{aligned} {\omega _{n+1}^{[N]}}'=(\frac{\partial ^{N_{i}-1}}{\partial \epsilon ^{N_{i}-1}}|_{\epsilon =0}(\omega _{n+1}^{[N]})_{ij}(\lambda _{1}+\epsilon ))_{2N\times 2N}, \end{aligned}$$
$$\begin{aligned} {\omega _{n+1}^{[N]_{2}}}'=(\frac{\partial ^{N_{i}-1}}{\partial \epsilon ^{N_{i}-1}}|_{\epsilon =0}(\omega _{n+1}^{[N]_{2}})_{ij}(\lambda _{1}+\epsilon ))_{2N\times 2N}, \end{aligned}$$

and

$$\begin{aligned} N_{i}= {\left\{ \begin{array}{ll} i, &{} i\le N\\ i-N, &{} i> N. \end{array}\right. } \end{aligned}$$

The positon solution is smooth, which is expressed as a mixed form of exponential function and polynomial of n and t. Two-positon solution \(u_{n-p}^{[2]}\) can be calculated by the formula (8) when \(N=2\). Since the exact form of the two-positon solution is complex, we do not write its explicit expression but plotted it in Fig. 1. And Similar to the two-positon solution, the three-positon solution is plotted in Fig. 2. The discrete 3D plot of positons is given in Figs. 1 and 2, respectively. Their continuous 3D plots are also given to give their density plots. The smooth positon solution is not a traveling wave solution whose trajectory is not a straight line but a slowly changing curve. And it can be seen that neither the carrier wave nor the envelope has changed from Figs. 1 and 2.

3 Breather solution

Breather solutions to the spatial discrete Hirota equation based on the Darboux transformation (4) are presented in this section. For this purpose, take a nonzero seed solution—plane wave solution

$$\begin{aligned} u_{n}=ce^{iwt}{,} \end{aligned}$$
(9)

where

$$\begin{aligned}w=-2\beta c^{2},\end{aligned}$$

and c is a real constant. Introducing a transformation related to the seed solution (9)

$$\begin{aligned} \varphi _{n} = \left( \begin{matrix} e^{\frac{1}{2}iwt} &{}\quad 0 \\ 0 &{}\quad e^{-\frac{1}{2}iwt} \end{matrix}\right) \widetilde{\varphi }_{n}, \end{aligned}$$
(10)

then we can map the variable coefficient differential-difference equation (2) to constant coefficient differential-difference equation,

$$\begin{aligned} \widetilde{\varphi }_{n+1}=\widetilde{L}_{n}\widetilde{\varphi }_{n}, \quad \frac{\hbox {d}\widetilde{\varphi }_{n}}{dt}=\widetilde{M}_{n}\widetilde{\varphi }_{n}, \end{aligned}$$
(11)

where

$$\begin{aligned} \widetilde{L}_{n}&= \left( \begin{matrix} \lambda &{}\quad c \\ -c &{}\quad \lambda ^{-1} \end{matrix}\right) ,\\ \widetilde{M}_{n}&= \alpha [(\lambda +\lambda ^{-1})\widetilde{L}_{n}^{3}+(3\lambda c^{2}+3\lambda ^{-1}c^{2}-3\lambda \\&-3\lambda ^{-1})\widetilde{L}_{n}+(-\frac{1}{2}\lambda ^{4}-\frac{1}{2}\lambda ^{-4}\\&+\lambda ^{2}+\lambda ^{-2}+3c^{4}+3)I]+i\beta [(-\lambda +\lambda ^{-1})\widetilde{L}_{n}\\&+(\frac{1}{2}\lambda ^{2}-\frac{1}{2}\lambda ^{-2})I]. \end{aligned}$$

In order to find the fundamental solution of the last linear system, we ought to solve the eigenvalues of the matrix \(\widetilde{L}_{n}\). This is the characteristic equation

$$\begin{aligned} det(pI-\widetilde{L}_{n})=p^{2}-(\lambda +\lambda ^{-1})p+1+c^{2}=0{.} \end{aligned}$$
(12)

When there are two different eigenvalues \(p_{1}\) and \(p_{2}\) in the matrix \(\widetilde{L}_{n}\), the corresponding eigenfunction is

$$\begin{aligned} \varphi _{n}(\lambda )= & {} \left( \begin{matrix} \varphi _{n,1}(\lambda ) \\ \varphi _{n,2}(\lambda ) \end{matrix}\right) \nonumber \\= & {} \left( \begin{matrix} e^{\frac{1}{2}iwt}(K_{1}p_{1}^{n}e^{\theta _{1}t}+K_{2}p_{2}^{n}e^{\theta _{2}t}) \\ e^{-\frac{1}{2}iwt}(p_{1}^{n}e^{\theta _{1}t}+p_{2}^{n}e^{\theta _{2}t}) \end{matrix}\right) , \end{aligned}$$
(13)

where

$$\begin{aligned} K_{j}=&\; -\frac{p_{j}-\lambda ^{-1}}{c}, \quad (j=1,2),\\ \theta _{j}=&\; \alpha [(\lambda +\lambda ^{-1})p_{j}^{3}+(3\lambda c^{2}+3\lambda ^{-1}c^{2}-3\lambda \\&-3\lambda ^{-1})p_{j}+(-\frac{1}{2}\lambda ^{4}-\frac{1}{2}\lambda ^{-4}\\&+\lambda ^{2}+\lambda ^{-2}+3c^{4}+3)]\\&+i\beta [(-\lambda +\lambda ^{-1})p_{j}+(\frac{1}{2}\lambda ^{2}-\frac{1}{2}\lambda ^{-2})]. \end{aligned}$$

Next, substitute the plane wave solution (9) as the seed solution and eigenfunction (13) into the N-fold DT (4) to construct the breather solution of (1), then the order-n breather solution of the spatial discrete Hirota equation (1) as

$$\begin{aligned} u_{n-b}^{[N]}=ce^{iwt}\frac{\omega _{n+1}^{[N]_{1}}}{\omega _{n+1}^{[N]}}+\frac{\omega _{n+1}^{[N]_{2}}}{\omega _{n+1}^{[N]}}{.} \end{aligned}$$
(14)

Example 3.1

The order-one breather solution with nonzero constant c and eigenvalue \(\lambda _{1}\) is obtained by letting \(N=1\) in the upper formula (14) is

$$\begin{aligned} u_{n-b}^{[1]}= & {} ce^{iwt}\frac{\omega _{n+1}^{[1]_{1}}}{\omega _{n+1}^{[1]}}+\frac{\omega _{n+1}^{[1]_{2}}}{\omega _{n+1}^{[1]}}{,}\nonumber \\= & {} \frac{\varDelta _{n}}{\varTheta _{n}}e^{iwt}{,} \end{aligned}$$
(15)

where

$$\begin{aligned} \varTheta _{n}= & {} (|K_{1}|^{2}\lambda _{1}^{-1}+\lambda _{1}^{*})|p_{1}|^{2n+2}e^{(\theta _{1}+\theta _{1}^{*})t}\\&+ (|K_{2}|^{2}\lambda _{1}^{-1}+\lambda _{1}^{*})|p_{2}|^{2n+2}e^{(\theta _{2}+\theta _{2}^{*})t}\\&+ (K_{1}K_{2}^{*}\lambda _{1}^{-1}+\lambda _{1}^{*})(p_{1}p_{2}^{*})^{n+1}e^{(\theta _{1}+\theta _{2}^{*})t}\\&+ (K_{2}K_{1}^{*}\lambda _{1}^{-1}+\lambda _{1}^{*})(p_{2}p_{1}^{*})^{n+1}e^{(\theta _{2}+\theta _{1}^{*})t}{,}\\ \end{aligned}$$

and

$$\begin{aligned} \varDelta _{n}=&\; (K_{1}|\lambda _{1}|^{2}+c|K_{1}|^{2}\lambda _{1}+c(\lambda _{1}^{*})^{-1}\\&-K_{1}|\lambda _{1}|^{-2})|p_{1}|^{2n+2}e^{(\theta _{1}+\theta _{1}^{*})t}\\&+(K_{2}|\lambda _{1}|^{2}+c|K_{2}|^{2}\lambda _{1}+c(\lambda _{1}^{*})^{-1}\\&-K_{2}|\lambda _{1}|^{-2})|p_{2}|^{2n+2}e^{(\theta _{2}+\theta _{2}^*)t}\\&+(K_{1}|\lambda _{1}|^{2}+cK_{1}K_{2}^{*}\lambda _{1}+c(\lambda _{1}^{*})^{-1}\\&-K_{1}|\lambda _{1}|^{-2})(p_{1}p_{2}^{*})^{n+1}e^{(\theta _{1}+\theta _{2}^*)t}\\&+(K_{2}|\lambda _{1}|^{2}+cK_{2}K_{1}^{*}\lambda _{1}+c(\lambda _{1}^{*})^{-1}\\&-K_{2}|\lambda _{1}|^{-2})(p_{2}p_{1}^{*})^{n+1}e^{(\theta _{2}+\theta _{1}^*)t}{.}\\ \end{aligned}$$

Specially, setting \(\lambda =e^{a}\), the characteristic equation reduce to

$$\begin{aligned} p^{2}-(e^{a}+e^{-a})p+1+c^{2}=0, \end{aligned}$$
(16)
Fig. 3
figure 3

Dynamical evolution of order-one breather solution \(|u_{n-b}^{[1]}|\) in the spatial discrete Hirota equation

Full size image
Fig. 4
figure 4

The evolution of order-two breather \(|u_{n-b}^{[2]}|\) with \(a_{1}=1.01\), \(b_{1}=1.03\), \(a_{2}=1.1\), \(b_{2}=1.2\), \(c=1\), \(\alpha =0.1\) and \(\beta =1\) of the spatial discrete Hirota equation on (n, t)-plane. Panel (a) is the 3D plot, panel (b) is the density plot

Full size image

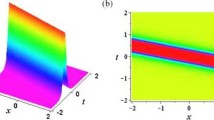
where the roots are either real roots or complex conjugation root pairs. To obtain the space-periodic breather, we need to choose the pair of conjugate complex roots, that is \((e^{a}+e^{-a})^{2}-4(1+c^{2})<0\). On the other hand, when \((e^{a}+e^{-a})^{2}-4(1+c^{2})>0\) the solution becomes time-periodic breather. For illustration, we plot the dynamics of the breather solution for parameters \(a_{1}=0.6\), \(b_{1}=0.58\), \(c=1\), \(\alpha =2\) and \(\beta =1\) in Fig. 3a, dynamical evolution of the time-periodic Kuznetsov–Ma breather solution for parameters \(a_{1}=0.6\), \(c=0.58\), \(\alpha =0.01\) and \(\beta =3\) in Fig. 3b and the dynamical evolution of the space-periodic Akhmediev breather solution for parameters \(a_{1}=0.2\), \(c=2\), \(\alpha =0.01\) and \(\beta =3\) in Fig. 3c. Figure 3d, e and f, respectively, shows their density plots.

Fig. 5
figure 5

The evolution of the interaction of Kuznetsov–Ma breather and Akhmediev breather with \(a_{1}=0.8\), \(a_{2}=1.1\), \(c=1\), \(\alpha =0.001\) and \(\beta =1\) of the spatial discrete Hirota equation on (n, t)-plane. Panel (a) is the 3D plot, panel (b) is the density plot

Full size image
Fig. 6
figure 6

The evolution of the order-two breather-positon of the spatial discrete Hirota equation on (n, t)-plane, the parameters of (a) are \(a_{1}=0.8\), \(b_{1}=0.9\), \(c=1\), \(\alpha =0.6\) and \(\beta =1.98\); the parameters of (b) are \(a_{1}=0.8\), \(b_{1}=1.8\), \(c=0.8\), \(\alpha =0.7\) and \(\beta =0.4\); the parameters of (c) are \(a_{1}=0.6\), \(b_{1}=0.2\), \(c=0.58\), \(\alpha =0.02\) and \(\beta =1.98\). Panel (a) (b) and (c) are the 3D plots, panel (d), (e) and (f) are the density plots

Full size image

Example 3.2

Similarly, the order-two breather solution obtained when \(N=2\) can be expressed as

$$\begin{aligned} u_{n-b}^{[2]}=ce^{iwt}\frac{\omega _{n+1}^{[2]_{1}}}{\omega _{n+1}^{[2]}}+\frac{\omega _{n+1}^{[2]_{2}}}{\omega _{n+1}^{[2]}}, \end{aligned}$$
(17)

where

$$\begin{aligned} \omega _{n}^{[2]}=\begin{vmatrix} \lambda _{1}^{-2}\varphi _{n,1}^{(1)}&\quad \lambda _{1}^{-1}\varphi _{n,2}^{(1)}&\quad \varphi _{n,1}^{(1)}&\quad \lambda _{1}\varphi _{n,2}^{(1)}\\ \lambda _{2}^{-2}\varphi _{n,1}^{(2)}&\quad \lambda _{2}^{-1}\varphi _{n,2}^{(2)}&\quad \varphi _{n,1}^{(2)}&\quad \lambda _{2}\varphi _{n,2}^{(2)}\\ (\lambda _{1}^{*})^{2}\varphi _{n,2}^{*(1)}&\quad -(\lambda _{1}^{*})\varphi _{n,1}^{*(1)}&\quad \varphi _{n,2}^{*(1)}&\quad -(\lambda _{1}^{*})^{-1}\varphi _{n,1}^{*(1)}\\ (\lambda _{2}^{*})^{2}\varphi _{n,2}^{*(2)}&\quad -(\lambda _{2}^{*})\varphi _{n,1}^{*(2)}&\quad \varphi _{n,2}^{*(2)}&\quad -(\lambda _{2}^{*})^{-1}\varphi _{n,1}^{*(2)} \end{vmatrix}, \end{aligned}$$
$$\begin{aligned} \omega _{n}^{[2]_{1}}=\begin{vmatrix} \lambda _{1}^{2}\varphi _{n,1}^{(1)}&\quad \lambda _{1}^{-1}\varphi _{n,2}^{(1)}&\quad \varphi _{n,1}^{(1)}&\quad \lambda _{1}\varphi _{n,2}^{(1)}\\ \lambda _{2}^{2}\varphi _{n,1}^{(2)}&\quad \lambda _{2}^{-1}\varphi _{n,2}^{(2)}&\quad \varphi _{n,1}^{(2)}&\quad \lambda _{2}\varphi _{n,2}^{(2)}\\ (\lambda _{1}^{*})^{-2}\varphi _{n,2}^{*(1)}&\quad -(\lambda _{1}^{*})\varphi _{n,1}^{*(1)}&\quad \varphi _{n,2}^{*(1)}&\quad -(\lambda _{1}^{*})^{-1}\varphi _{n,1}^{*(1)}\\ (\lambda _{2}^{*})^{-2}\varphi _{n,2}^{*(2)}&\quad -(\lambda _{2}^{*})\varphi _{n,1}^{*(2)}&\quad \varphi _{n,2}^{*(2)}&\quad -(\lambda _{2}^{*})^{-1}\varphi _{n,1}^{*(2)} \end{vmatrix}, \end{aligned}$$

and

$$\begin{aligned} \omega _{n}^{[2]_{2}}=\begin{vmatrix} \lambda _{1}^{-2}\varphi _{n,1}^{(1)}&\quad \lambda _{1}^{2}\varphi _{n,1}^{(1)}&\quad \varphi _{n,1}^{(1)}&\quad \lambda _{1}\varphi _{n,2}^{(1)}\\ \lambda _{2}^{-2}\varphi _{n,1}^{(2)}&\quad \lambda _{2}^{2}\varphi _{n,1}^{(2)}&\quad \varphi _{n,1}^{(2)}&\quad \lambda _{2}\varphi _{n,2}^{(2)}\\ (\lambda _{1}^{*})^{2}\varphi _{n,2}^{*(1)}&\quad (\lambda _{1}^{*})^{-2}\varphi _{n,2}^{*(1)}&\quad \varphi _{n,2}^{*(1)}&\quad -(\lambda _{1}^{*})^{-1}\varphi _{n,1}^{*(1)}\\ (\lambda _{2}^{*})^{2}\varphi _{n,2}^{*(2)}&\quad (\lambda _{2}^{*})^{-2}\varphi _{n,2}^{*(2)}&\quad \varphi _{n,2}^{*(2)}&\quad -(\lambda _{2}^{*})^{-1}\varphi _{n,1}^{*(2)} \end{vmatrix}. \end{aligned}$$

An order-two breather is formed by two order-one breathers superimposed on each other, and different parameters have different effects on the dynamic evolution of the order-two breather. Figure 4 describes a dynamic evolution of the order-two breather solution. Figure 5 describes the interaction of Kuznetsov–Ma breather and Akhmediev breather. In addition, both the first-order and the second-order breather solutions show their periodicity. Hence, the breather solution is a periodic traveling wave solution of the spatial discrete Hirota equation.

Fig. 7
figure 7

The evolution of the space-periodic order-two breather-positon of the spatial discrete Hirota equation on (n, t)-plane. the parameters of (a) are \(a_{1}=0.8\), \(c=1\), \(\alpha =0.5\) and \(\beta =1.98\); the parameters of (c) are \(a_{1}=0.6\), \(c=1\), \(\alpha =0.02\) and \(\beta =1.98\); Panel (a) and (c) are the 3D plots, panel (b) and (d) are the density plots

Full size image

Compared with the spatial discrete complex mKdV equation [15], not only the time-period Kuznetsov–Ma breather solution of Eq. (1) is derived from Eqs. (15) and (16), but also the order-two breather solution and the order-two breather solution of the interaction of Kuznetsov–Ma breather and Akhmediev breather are obtained by Eq. (17).

4 Breather-positon solution

In fact, the method of breather-positon solution constructed in this part is the same as the positon solution described in Example 2.1. That is to say, using the degenerate limit \(\lambda _{j}\rightarrow \lambda _{1}(j=2, 3, \ldots , N)\) and high-order Taylor expansion of the eigenvalues in the breather solution to construct the breather-positon solution. The determinant representation of the breather-positon is slightly different from the positon owing to the different seed solutions.

Fig. 8
figure 8

The evolution of time-periodic the order-two breather-positon with \(a_{1}=0.92\), \(c=0.91\), \(\alpha =0.01\) and \(\beta =3\) of the spatial discrete Hirota equation on (n, t)-plane. Panel (a) is the 3D plot, panel (b) is the density plot

Full size image

Example 4.1

Under the limit \(\lambda _{j}\rightarrow \lambda _{1}(j=2, 3, \ldots , N)\), an indeterminate form \(\frac{0}{0}\) associated with \(u_{n-b}^{[N]}\) yield an order-n breather-positon by higher-order Taylor expansion, namely

$$\begin{aligned} u_{n-bp}^{[N]}=ce^{iwt}\frac{{\omega _{n+1}^{[N]_{1}}}'}{{\omega _{n+1}^{[N]}}'}+\frac{{\omega _{n+1}^{[N]_{2}}}'}{{\omega _{n+1}^{[N]}}'}{,} \end{aligned}$$
(18)

where

$$\begin{aligned} {\omega _{n+1}^{[N]}}'=(\frac{\partial ^{N_{i}-1}}{\partial \epsilon ^{N_{i}-1}}|_{\epsilon =0}(\omega _{n+1}^{[N]})_{ij}(\lambda _{1}+\epsilon ))_{2N\times 2N}, \end{aligned}$$
$$\begin{aligned} {\omega _{n+1}^{[N]_{1}}}'=(\frac{\partial ^{N_{i}-1}}{\partial \epsilon ^{N_{i}-1}}|_{\epsilon =0}(\omega _{n+1}^{[N]_{1}})_{ij}(\lambda _{1}+\epsilon ))_{2N\times 2N}, \end{aligned}$$
$$\begin{aligned} {\omega _{n+1}^{[N]_{2}}}'=(\frac{\partial ^{N_{i}-1}}{\partial \epsilon ^{N_{i}-1}}|_{\epsilon =0}(\omega _{n+1}^{[N]_{2}})_{ij}(\lambda _{1}+\epsilon ))_{2N\times 2N}, \end{aligned}$$

and

$$\begin{aligned} N_{i}= {\left\{ \begin{array}{ll} i, &{} i\le N\\ i-N, &{} i> N. \end{array}\right. } \end{aligned}$$

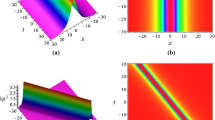
Breather-positon solution is not only a new type of breather solution but also an extension of positon solution. Different breathers of multi-breathers have different periods, unlike a single breather have only one period (or equivalent frequencies) and can be adjusted effectively in experiments [38,39,40,41]. The breather-positon can be reduced to the rogue wave through further degenerate \(\lambda _{1}\rightarrow \lambda _{0}\) \((\varphi _{n}(\lambda _{0})=0)\); thus, the order-n breather-positon is the intermediate state of the order-n-breather transformation to the order-n rogue wave. In this state, different breathers have the same period (or velocity), and they can have different phases. Different phase combinations can produce different modes in the strong interaction region. It is easy to find that an order-one breather-positon is the order-one breather solution in Eq. (15). The first nontrivial breather-positon is the order-2 breather-positon \(u_{n-bp}^{[2]}\), which is the limit of the order-two breather on the limit \(\lambda _{2}\rightarrow \lambda _{1}\). Figure 6 shows the order-two breather-positon dynamic evolution under different parameters, and Figs. 7 and 8 show the dynamic evolution of space-periodic breather-positon and time-periodic breather-positon with special parameters, respectively.

The positon and breather-positon solutions derived in this paper are exact solutions that have never been discussed in two special forms[15, 42, 43] of the spatial discrete Hirota equations (1). So far, we all know that the Positon solution, the breather-positon solution and the rogue wave solution can be obtained by taking the limit of the eigenvalue, but they have the following differences: 1: The positon solution is obtained under the background that the seed solution is zero; 2: The breather-positon solution is based on the nonzero seed solution; 3: The rogue wave solution is a double degenerated limit to the breather solution, i.e., the breather-positon solution is an intermediate state from the breather solution to the rogue wave solution.

5 Conclusions

We first provide the n-positon solution of Eq. (1) by using the degenerate limit \(\lambda _{j}\rightarrow \lambda _{1}\) \((j=2, 3, \ldots , N)\) and higher-order Taylor expansion in the corresponding determinant representation of the multi-soliton solution. They are smooth solution expressed as a mixed form of exponential function and polynomial of n and t, which is similar to the multi-pole solutions of the mKdV equation [44,45,46,47,48] and the NLS equation [49] reported by the Hirota method and the classical inverse scattering method in the past three decades. The eigenfunction under the nonzero seed solution is derived by means of the variables separation method and the superposition principle, and then the breather solution of the spatial discrete Hirota equation is obtained by the Darboux transformation method. The breather solution is periodic. Finally, using the same method as positon solution, a new type of breather solution is derived from the breather solution, namely breather-positon. It is very meaningful to use the breather-positon to explore the modes and properties of the rogue wave solution as in Ref [50]. Because on the basis of the degenerate limit \(\lambda _{j}\rightarrow \lambda _{1}\) \((j=2, 3, \ldots , N)\) of the breather solution, the rogue wave solution can be derived from the further degenerate step \(\lambda _{1}\rightarrow \lambda _{0}\) (\(\lambda _{0}\) is the zero point of the eigenfunction, i.e., \(\varphi _{n}(\lambda _{0})=0\)). The soliton-positon solution of this equation is also very interesting, which is similar to the soliton-position solution in the derivative nonlinear Schrödinger equation [34]. Besides the results of the spatial discrete equation obtained in this paper, it is worth studying the decomposition process, bent trajectory and phase shift of the positon solutions in the near future.