Several categories of exact solutions of the third-order flow equation of the Kaup–Newell system

Abstract

In this paper, we introduce the third-order flow equation of the Kaup–Newell (KN) system. We study this equation, and we obtain different types of solutions by using the Darboux transformation (DT) and the extended DT of the KN system, such as solitons, positons, breathers, and rogue waves. The extended DT is obtained by taking the degenerate eigenvalues $\lambda _{i} \rightarrow \lambda _{1} (i=3,5,7,\ldots ,2k-1)$ and by performing the Taylor expansion near $\lambda _{1}$ of the determinants of DT. Some analytic expressions are explicitly given for the first-order solutions. We study the unique waveforms of both the first-order and higher-order rogue-wave solutions for special choices of parameters, and we find different types of such wave structures: fundamental pattern, triangular, modified-triangular, pentagram, ring, ring-triangular, and multi-ring wave patterns. We conclude that the third-order dispersion and quintic nonlinear term of the KN system modify both the trajectories and speeds of the solutions as compared with those corresponding to the second-order flow equation of the KN system.

1 Introduction

In recent decades, the soliton concept plays an increasing role in mathematics, physical sciences, and in other areas of science and engineering. From the perspectives of soliton theory and real-world applications, many different types of solitons have been extensively studied under various physical conditions [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. The soliton is a category of special localized solutions of nonlinear partial differential equations and is also one of the abstract mathematical concepts that can be directly transformed into crucial technological advances [17]. For instance, due to the fact that the optical soliton can maintain its shape and energy during long-distance propagation, it is considered to be the ideal information carrier in modern optical fiber communications systems [17,18,19,20,21,22].

When a picosecond optical pulse propagates in a single-mode fiber, the soliton solution of the famous nonlinear Schrödinger (NLS) equation is considered to be the result of the delicate balance between dispersion and cubic (Kerr) nonlinearity without the inclusion of higher-order nonlinear effects into the dynamical model [23, 24]. However, in optical fibers, other physical effects such as self-steepening, self-frequency shift, and self-phase modulation have a great impact on the propagation dynamics of optical pulses in these nonlinear and dispersive optical media [7, 25]. With the development of high-bit-rate optical fiber communication system and laser technology, higher-order nonlinear effects should be taken into account when modeling the propagation of ultra-short and high-intensity optical pulse in nonlinear optical media. Thus, during the past decades, several types of nonlinear partial differential equations that include the effects of third-order dispersion, quintic nonlinear terms, and other effects have been investigated, such as Kundu–Eckhaus equation [26, 27], Hirota equation [28, 29], generalized NLS equation [30, 31], and derivative NLS equation (which is also the second-order flow of the KN system) [32, 33]. For instance, a generalized NLS equation with the fourth-order dispersion and quintic nonlinear terms to describe the optical pulse propagation in nonlinear metamaterials has been studied [34]. Meanwhile, the equation investigated in Ref. [34] can be extended to a more general model with the fourth-order dispersion $\dfrac{\partial ^{4}q}{\partial x^{4}}$ and a quintic nonlinear term having the form $\dfrac{\partial ({\left| q \right| }^{4}q )}{\partial x}$, which this quintic nonlinear term accounts for the self-steepening effect related to the higher-order quintic optical nonlinearity [35].

Many works have been devoted to the study of higher-order nonlinearities and generalized (higher-order) NLS equations. For example, in Ref. [36] the problem of wave train generation of solitons in systems with higher-order nonlinearities has been investigated and in Ref. [37] the impact of dispersion and non-Kerr nonlinearity on the modulational instability of the higher-order nonlinear Schrödinger equation has been studied in detail. However, the effect of the fifth-order nonlinear term of the Ginzburg–Landau (GL) equation has been observed experimentally in mode-locked fiber lasers [38, 39]. Although the third-order GL equation and the fifth-order GL equation have both of them stable solutions whose amplitudes are arbitrary (the so-called flat-top solutions) [40, 41], the stable fixed amplitude solution only exists in the fifth-order GL equation. This means that the fifth-order nonlinear term is useful to improve the stability of the solution [42, 43]. Very recently, several NLS-type models were extended and studied in detail [44,45,46,47].

In this paper, we study the third-order flow equation of the Kaup–Newell system (TOFKN equation) that contains the third-order dispersion and quintic nonlinear terms. It is an integrable system that is obtained from the coupled TOFKN equation proposed by Kenji Imai in 1999 [48]. We reduce the coupled TOFKN equation by imposing the condition $r=-q^{*}$ and some special values of the parameters, and then, we get the general form of the TOFKN equation:

$$\begin{aligned} q_{t}+q_{xxx}-3i(|q|^{2}q_{x})_{x}-\frac{3}{2}(|q|^{4}q)_{x}=0. \end{aligned}$$

(1)

To the best of our knowledge, Eq. (1) is new and thus deserves further studies in this paper.

During the past 2 decades, rogue waves have attracted considerable attention in many research fields, such as oceanography [49], optical fibers [5, 50], plasma physics [51], and Bose–Einstein condensates [52]. The rogue waves, or freak waves, were originally used to describe extraordinarily high and steep waves in deep ocean, and their appearance or disappearance is always sudden and traceless [53,54,55,56,57,58,59,60,61,62,63]. Although the intrinsic nature of the rogue waves is elusive and they are essentially difficult to monitor due to their fleeting existences, satellite monitoring has confirmed that they wander in deep oceans [49]. When rogue wave occasionally encounter ships, huge casualties and losses will occur. The first experimental observation of a rogue wave in an optical system was reported in 2007 [50], and in 2011, the rogue wave formation in a water wave tank was reported [64]. We point out that the rogue waves can create conditions for generating highly energetic pulses in different optical settings [50, 65, 66].

The purpose of this paper is to generate various types of solutions of the TOFKN equation by using the Darboux transformation (DT), and to discuss the effects of fifth-order nonlinear terms on the KN system by comparing the obtained results with those corresponding to the solutions of the derivative nonlinear Schrödinger equation (DNLS) equation [32, 33]. First, we introduce the DT and the extended DT of the KN system [32, 33]. The extended DT [67] is obtained via taking the degenerate eigenvalues $\lambda _{i} \rightarrow \lambda _{1} (i=3,5,7,\ldots ,2k-1)$ of the determinant formula of the DT and by performing the Taylor expansion near $\lambda _{1}$ of the determinants of DT. Second, we directly obtain several categories of solutions of the TOFKN equation, such as solitons, positons, breathers, rogue waves, and rational solutions. The detailed analytical expressions of some obtained solutions and their dynamics are given. Third, we arrive at the conclusion that the fifth-order nonlinear term of the KN system can affect the trajectory and the speed of the obtained solutions and we compare this result with that corresponding to the second-order flow equation of the KN system.

The organization of this paper is as follows: In Sect. 2, we present the coupled TOFKN equation, the Lax pair, and the formula of the nth-order solutions of the TOFKN equation, see also Refs. [32, 33, 48]. Through the application of the obtained formula, some analytic expressions of different types of solutions from zero seed solution are given, which include solitons, positons, and rational solutions. In Sect. 3, we obtain both the breather solutions and the rogue wave solutions from the nonzero seed solution by using the DT and we plot these types of solutions. In Sect. 4, by modifying the coefficients of eigenfunctions, we generate different types of multiple-rogue waves. For special choices of the parameters, we obtain seven types of higher-order rogue waves having fundamental pattern, triangular, modified-triangular, pentagram, ring, ring-triangular, and multi-ring structures. We point out that the pentagram waveform is investigated here for the first time, to the best of our knowledge. Finally, summary and discussion are given in Sect. 5.

2 Solutions of the TOFKN equation from zero seed solution

Let us start from the second non-trivial flow (the third-order flow) of the KN system [48]:

$$\begin{aligned} \left\{ \begin{aligned}&q_{t}+q_{xxx}+3i(qrq_{x})_{x}-\frac{3}{2}(q^{3}r^{2})_{x}=0,\\&r_{t}+r_{xxx}-3i(qrr_{x})_{x}-\frac{3}{2}(q^{2}r^{3})_{x}=0. \end{aligned} \right. \end{aligned}$$

(2)

This system of coupled equations can be generated by the integrability condition, i.e., the zero curvature equation $M_{t}-N_{x}+[M,N]=0$ of the KN spectral problem (Lax pair) [48]:

$$\begin{aligned} \left\{ \begin{aligned}&\varPsi _{x}=M\varPsi =(J\lambda ^{2}+Q\lambda )\varPsi ,\\&\varPsi _{t}=N\varPsi =(V_{6}\lambda ^{6}+V_{5}\lambda ^{5}+V_{4}\lambda ^{4}+V_{3}\lambda ^{3}+V_{2}\lambda ^{2}+V_{1}\lambda )\varPsi . \end{aligned} \right. \nonumber \\ \end{aligned}$$

(3)

with

$$\begin{aligned} \begin{aligned}&J=\begin{pmatrix} i &{} 0 \\ 0 &{} -i\end{pmatrix} ,\quad Q=\begin{pmatrix} 0 &{} q \\ r &{} 0\end{pmatrix},\\&V_{6}=4J, \quad V_{5}=4Q,\quad V_{4}=2qrJ,\\&V_{3}=\begin{pmatrix} 0 &{} -2iq_{x}+2q^{2}r \\ 2ir_{x}+2qr^{2} &{} 0\end{pmatrix},\\&V_{2}=\left( \frac{3}{2}q^{2}r^{2}+i(qr_{x}-q_{x}r)\right) J,\\&V_{1}=\begin{pmatrix} 0 &{} \frac{3}{2}q^{3}r^{2}-3iqrq_{x}-q_{xx} \\ \frac{3}{2}q^{2}r^{3}+3iqrr_{x}-r_{xx} &{} 0\end{pmatrix}. \end{aligned} \end{aligned}$$

Here, $\lambda \in {\mathbb {C}}$, $\varPsi \in {\mathbb {C}}^{2}$, and $\varPsi$ is the eigenfunction associated with eigenvalue $\lambda$ of the KN system.

When $r=-q^{*}$, Eq. (2) can be reduced to Eq. (1), and ‘$*$’ denotes the complex conjugation here.

2.1 The formula for the nth-order solutions of the TOFKN equation

In order to obtain different solutions of the TOFKN equation, we refer to the DT and extended DT formulae of the second-order flow of the KN system, i.e., the DNLS equation in [32, 33]. It is easy to see that the DT is also applicable to the TOFKN equation. Further, the formulae for the nth-order solutions of the TOFKN equation are provided as follows:

Lemma 1

[32] We set $\varPsi _{i}=\begin{pmatrix} f_{i} \\ g_{i}\end{pmatrix}(i=1,2,\ldots ,n)$, which is the eigenfunction corresponding to eigenvalue $\lambda _{i}$ of the spectral equation (3), and then, the new nth-order solutions $(q^{[n]},r^{[n]})$ of Eq. (2) are directly obtained by the DT formulae:

$$\begin{aligned} \left\{ \begin{aligned}&q^{[n]}=\dfrac{\varOmega _{11}^{2}}{\varOmega _{21}^{2}}q+2i\dfrac{\varOmega _{11}\varOmega _{12}}{\varOmega _{21}^{2}},\\&r^{[n]}=\dfrac{\varOmega _{21}^{2}}{\varOmega _{11}^{2}}r-2i\dfrac{\varOmega _{21}\varOmega _{22}}{\varOmega _{11}^{2}}. \end{aligned} \right. \end{aligned}$$

(4)

Here, for $n=2k$, we have the following formulae of the determinants:

$$\begin{aligned}&\varOmega _{11}=\begin{vmatrix} \lambda _{1}^{n-1}g_{1}&\lambda _{1}^{n-2}f_{1}&\lambda _{1}^{n-3}g_{1}&\cdots&\lambda _{1}g_{1}&f_{1} \\ \lambda _{2}^{n-1}g_{2}&\lambda _{2}^{n-2}f_{2}&\lambda _{2}^{n-3}g_{2}&\cdots&\lambda _{2}g_{2}&f_{2}\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ \lambda _{n}^{n-1}g_{n}&\lambda _{n}^{n-2}f_{n}&\lambda _{n}^{n-3}g_{n}&\cdots&\lambda _{n}g_{n}&f_{n}\end{vmatrix} ,\\&\varOmega _{12}=\begin{vmatrix} \lambda _{1}^{n}f_{1}&\lambda _{1}^{n-2}f_{1}&\lambda _{1}^{n-3}g_{1}&\cdots&\lambda _{1}g_{1}&f_{1} \\ \lambda _{2}^{n}f_{2}&\lambda _{2}^{n-2}f_{2}&\lambda _{2}^{n-3}g_{2}&\cdots&\lambda _{2}g_{2}&f_{2}\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ \lambda _{n}^{n}f_{n}&\lambda _{n}^{n-2}f_{n}&\lambda _{n}^{n-3}g_{n}&\cdots&\lambda _{n}g_{n}&f_{n}\end{vmatrix} ,\\&\varOmega _{21}=\begin{vmatrix} \lambda _{1}^{n-1}f_{1}&\lambda _{1}^{n-2}g_{1}&\lambda _{1}^{n-3}f_{1}&\cdots&\lambda _{1}f_{1}&g_{1} \\ \lambda _{2}^{n-1}f_{2}&\lambda _{2}^{n-2}g_{2}&\lambda _{2}^{n-3}f_{2}&\cdots&\lambda _{2}f_{2}&g_{2}\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ \lambda _{n}^{n-1}f_{n}&\lambda _{n}^{n-2}g_{n}&\lambda _{n}^{n-3}f_{n}&\cdots&\lambda _{n}f_{n}&g_{n}\end{vmatrix} ,\\&\varOmega _{22}=\begin{vmatrix} \lambda _{1}^{n}g_{1}&\lambda _{1}^{n-2}g_{1}&\lambda _{1}^{n-3}f_{1}&\cdots&\lambda _{1}f_{1}&g_{1} \\ \lambda _{2}^{n}g_{2}&\lambda _{2}^{n-2}g_{2}&\lambda _{2}^{n-3}f_{2}&\cdots&\lambda _{2}f_{2}&g_{2}\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ \lambda _{n}^{n}g_{n}&\lambda _{n}^{n-2}g_{n}&\lambda _{n}^{n-3}f_{n}&\cdots&\lambda _{n}f_{n}&g_{n}\end{vmatrix} .\\ \end{aligned}$$

And for $n=2k+1$, we have the following formulae for the determinants:

$$\begin{aligned}&\varOmega _{11}=\begin{vmatrix} \lambda _{1}^{n-1}g_{1}&\lambda _{1}^{n-2}f_{1}&\lambda _{1}^{n-3}g_{1}&\cdots&\lambda _{1}f_{1}&g_{1} \\ \lambda _{2}^{n-1}g_{2}&\lambda _{2}^{n-2}f_{2}&\lambda _{2}^{n-3}g_{2}&\cdots&\lambda _{2}f_{2}&g_{2}\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ \lambda _{n}^{n-1}g_{n}&\lambda _{n}^{n-2}f_{n}&\lambda _{n}^{n-3}g_{n}&\cdots&\lambda _{n}f_{n}&g_{n}\end{vmatrix} ,\\&\varOmega _{12}=\begin{vmatrix} \lambda _{1}^{n}f_{1}&\lambda _{1}^{n-2}f_{1}&\lambda _{1}^{n-3}g_{1}&\cdots&\lambda _{1}f_{1}&g_{1} \\ \lambda _{2}^{n}f_{2}&\lambda _{2}^{n-2}f_{2}&\lambda _{2}^{n-3}g_{2}&\cdots&\lambda _{2}f_{2}&g_{2}\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ \lambda _{n}^{n}f_{n}&\lambda _{n}^{n-2}f_{n}&\lambda _{n}^{n-3}g_{n}&\cdots&\lambda _{n}f_{n}&g_{n}\end{vmatrix} ,\\&\varOmega _{21}=\begin{vmatrix} \lambda _{1}^{n-1}f_{1}&\lambda _{1}^{n-2}g_{1}&\lambda _{1}^{n-3}f_{1}&\cdots&\lambda _{1}g_{1}&f_{1} \\ \lambda _{2}^{n-1}f_{2}&\lambda _{2}^{n-2}g_{2}&\lambda _{2}^{n-3}f_{2}&\cdots&\lambda _{2}g_{2}&f_{2}\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ \lambda _{n}^{n-1}f_{n}&\lambda _{n}^{n-2}g_{n}&\lambda _{n}^{n-3}f_{n}&\cdots&\lambda _{n}g_{n}&f_{n}\end{vmatrix} ,\\&\varOmega _{22}=\begin{vmatrix} \lambda _{1}^{n}g_{1}&\lambda _{1}^{n-2}g_{1}&\lambda _{1}^{n-3}f_{1}&\cdots&\lambda _{1}g_{1}&f_{1} \\ \lambda _{2}^{n}g_{2}&\lambda _{2}^{n-2}g_{2}&\lambda _{2}^{n-3}f_{2}&\cdots&\lambda _{2}g_{2}&f_{2}\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ \lambda _{n}^{n}g_{n}&\lambda _{n}^{n-2}g_{n}&\lambda _{n}^{n-3}f_{n}&\cdots&\lambda _{n}g_{n}&f_{n}\end{vmatrix}. \end{aligned}$$

Under the reduction condition $q^{[n]}=-r^{([n])^{*}}$, we take

$$\begin{aligned} \lambda _{2l}=-\lambda ^{*}_{2l-1}, \quad \varPsi _{2l}=\begin{pmatrix} f_{2l} \\ g_{2l}\end{pmatrix}=\begin{pmatrix} g^{*}_{2l-1} \\ f^{*}_{2l-1}\end{pmatrix},\quad (l=1,2,\ldots ,k), \end{aligned}$$

and one eigenvalue is pure imaginary:

$$\begin{aligned} \lambda _{2k+1}=i\beta _{2k+1},\quad \varPsi _{2k+1}=\begin{pmatrix} f_{2k+1} \\ g_{2k+1}\end{pmatrix}=\begin{pmatrix} f_{2k+1} \\ f^{*}_{2k+1}\end{pmatrix}. \end{aligned}$$

Lemma 2

[33] Suppose $\lambda _{1}=\alpha _{1}+i\beta _{1},\lambda _{2}=-\lambda _{1}^{*}$, and take the degenerate limit $\lambda _{i} \rightarrow \lambda _{1} (i=3,5,7,\ldots ,2k-1)$, then a new nth-order $(n=2k)$ solution $q^{[n]}$ of the TOFKN equation can be calculated by the formula (4) generated at the same eigenvalue and Taylor expansion, where

$$\begin{aligned} \begin{aligned} q^{[n]}=\dfrac{\varDelta _{11}^{2}}{\varDelta _{21}^{2}}q+2i\dfrac{\varDelta _{11}\varDelta _{12}}{\varDelta _{21}^{2}}, \end{aligned} \end{aligned}$$

(5)

with

$$\begin{aligned}&\varDelta _{11}=\begin{vmatrix} g[1,n-1,0]&f[1,n-2,0]&\cdots&g[1,1,0]&f[1,0,0] \\ g[2,n-1,0]&f[2,n-2,0]&\cdots&g[2,1,0]&f[2,0,0] \\ g[1,n-1,1]&f[1,n-2,1]&\cdots&g[1,1,1]&f[1,0,1] \\ g[2,n-1,1]&f[2,n-2,1]&\cdots&g[2,1,1]&f[2,0,1] \\ \vdots&\vdots&\ddots&\vdots&\vdots \\ g[1,n-1,k-1]&f[1,n-2,k-1]&\cdots&g[1,1,k-1]&f[1,0,k-1] \\ g[2,n-1,k-1]&f[2,n-2,k-1]&\cdots&g[2,1,k-1]&f[2,0,k-1] \\ \end{vmatrix},\\&\varDelta _{12}=\begin{vmatrix} f[1,n,0]&f[1,n-2,0]&g[1,n-3,0]&\cdots&g[1,1,0]&f[1,0,0] \\ f[2,n,0]&f[2,n-2,0]&g[2,n-3,0]&\cdots&g[2,1,0]&f[2,0,0] \\ f[1,n,1]&f[1,n-2,1]&g[1,n-3,1]&\cdots&g[1,1,1]&f[1,0,1] \\ f[2,n,1]&f[2,n-2,1]&g[2,n-3,1]&\cdots&g[2,1,1]&f[2,0,1] \\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ f[1,n,k-1]&f[1,n-2,k-1]&g[1,n-3,k-1]&\cdots&g[1,1,k-1]&f[1,0,k-1] \\ f[2,n,k-1]&f[2,n-2,k-1]&g[2,n-3,k-1]&\cdots&g[2,1,k-1]&f[2,0,k-1] \\ \end{vmatrix}, \end{aligned}$$

$$\begin{aligned}&\varDelta _{21}=\begin{vmatrix} f[1,n-1,0]&g[1,n-2,0]&\cdots&f[1,1,0]&g[1,0,0] \\ f[2,n-1,0]&g[2,n-2,0]&\cdots&f[2,1,0]&g[2,0,0] \\ f[1,n-1,1]&g[1,n-2,1]&\cdots&f[1,1,1]&g[1,0,1] \\ f[2,n-1,1]&g[2,n-2,1]&\cdots&f[2,1,1]&g[2,0,1] \\ \vdots&\vdots&\ddots&\vdots&\vdots \\ f[1,n-1,k-1]&g[1,n-2,k-1]&\cdots&f[1,1,k-1]&g[1,0,k-1] \\ f[2,n-1,k-1]&g[2,n-2,k-1]&\cdots&f[2,1,k-1]&g[2,0,k-1] \\ \end{vmatrix}. \end{aligned}$$

Here, the new functions $\varPsi [i,j,k]$ are defined as follows:

$$\begin{aligned} \begin{aligned}&\lambda ^{j}_{i}\varPsi =\varPsi [i,j,0]+\varPsi [i,j,1]\epsilon +\varPsi [i,j,2]\epsilon ^{2}\\&\qquad \qquad \, +\,\cdots +\varPsi [i,j,k]\epsilon ^{k}+\cdots ,\\&\varPsi [i,j,k]=\frac{1}{k!}\frac{\partial ^{k} (\lambda _{i}^{j}\varPsi (\lambda _{i}))}{\partial \lambda _{i}^{k}}, \quad \varPsi [1,1,0]\\&\qquad \qquad \quad \,\,=\lambda _{1}\varPsi (\lambda _{1}), \quad \varPsi [i,j,0]=\lambda _{i}^{j}\varPsi (\lambda _{i}), \end{aligned} \end{aligned}$$

(6)

where the eigenfunction $\varPsi =\varPsi (\lambda )$ corresponding to eigenvalue $\lambda$ is similar to that of Lemma 1.

2.2 Solutions from zero seed solution

Here, by the application of the above DT and its extended method, we will discuss several types of solutions from zero seed solution.

For $q=r=0$, we can generate the following eigenfunction related to $\lambda$:

$$\begin{aligned}&\varPsi =\begin{pmatrix} f \\ g \end{pmatrix}, \nonumber \\&f=\exp (i(4\lambda ^{6}t+\lambda ^{2}x)), \nonumber \\&g=\exp (-i(4\lambda ^{6}t+\lambda ^{2}x)). \end{aligned}$$

(7)

Case 1 $(n=1)$. Assuming $\lambda _{1}=i\beta _{1}$, then a solution of the TOFKN equation can be simply obtained by Eq. (4):

$$\begin{aligned} q^{[1]}=-2\beta _{1}\exp (2i(4\beta _{1}^{6}t+\beta _{1}^{2}x)). \end{aligned}$$

(8)

This simple solution is a plane wave with a constant amplitude.

Case 2 $(n=2)$. Setting $\lambda _{1}=i(l+m),\lambda _{2}=i(l-m)$, and substituting the eigenfunctions in Eq. (7) back in Eq. (4), we can generate a quasi-periodic solution:

$$\begin{aligned} \begin{aligned} { q^{[2]}}=-4lm{\dfrac{\left( m\cos \left( 2\,G \right) +il\sin \left( 2\,G \right) \right) ^{3}{\mathrm{\exp (-2iF)}}}{ \left( \left( -{l}^{2}+{m}^{2} \right) \left( \cos \left( 2\,G \right) \right) ^{2 }+{l}^{2} \right) ^{2}}}, \end{aligned}\nonumber \\ \end{aligned}$$

(9)

where

$$\begin{aligned}&G= \left( 24{l}^{5}m+80\,{m}^{3}{l}^{3}+24\,l{m}^{5} \right) t+2lmx,\\&F= \left( 4\,{l}^{6}+60\,{l}^{4}{m}^{2}+60\,{l}^{2}{m}^{4}+4\,{m}^{6}\right) t+ \left( {l}^{2}+{m}^{2} \right) x. \end{aligned}$$

Next, supposing $\lambda _{1}=\alpha _{1}+i\beta _{1},\lambda _{2}=-\alpha _{1}+i\beta _{1}$, and substituting the eigenfunctions (7) in formula (4), the following solution of the TOFKN equation can be simply obtained by the twofold DT:

$$\begin{aligned} \begin{aligned}&{ q^{[2]}}\\&\quad = -\,4\alpha _{1}\beta _{1}{\dfrac{\left( \alpha _{1}\,\cosh \left( 2\,{ H} \right) +i\beta _{1}\,\sinh \left( 2\,{ H} \right) \right) ^{3 }{\mathrm{\exp (2i h)}}}{ \left( \left( {\alpha _{1}}^{2}+{\beta _{1}}^{2} \right) \left( \cosh \left( 2\,{ H} \right) \right) ^{2}-{\beta _{1} }^{2} \right) ^{2}}}, \end{aligned}\nonumber \\ \end{aligned}$$

(10)

with

$$\begin{aligned} H=&\left( 24\,{\alpha _{1}}^{5}\beta _{1}-80\,{\alpha _{1}}^{3}{\beta _{1}}^{3}+24\,\alpha _{1}\,{\beta _{1}}^{5}\right) t+2\,\alpha _{1}\,\beta _{1}\,x,\\ h=&\left( 4\,{\alpha _{1}}^{6}-60\,{\alpha _{1}}^{4}{\beta _{1}}^{2}+60\,{\alpha _{1}}^{2}{\beta _{1}}^{4}-4\,{\beta _{1}}^{6} \right) t\\&+ \left( {\alpha _{1}}^{2}-{\beta _{1}}^{2} \right) x, \end{aligned}$$

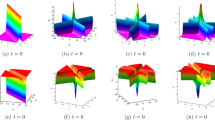
which is a bright one-soliton solution. We plot its three-dimensional waveform and its density plot in Fig. 1a, b, respectively.

Fig. 1

a The three-dimensional profile of the bright one-soliton solution $\left| q^{[2]} \right| ^{2}$ with parameters $\alpha _{1}=0.1, \beta _1=0.2$. Its peak trajectory is $x=0$ in the $(x-t)$ plane. b The density plot of the bright one-soliton solution with $\alpha _{1}=0.1, \beta _1=0.2$. c The three-dimensional profile of the rational solution $\left| q^{[2]} \right| ^{2}$ with $\beta _{1}=0.5$. d The density plot of the rational solution with $\beta _{1}=0.5$

Furthermore, if we assume $\alpha _{1} \rightarrow 0$ in the above equations, we obtain a rational soliton solution:

$$\begin{aligned} \begin{aligned}&{q^{[2]}}\\&\quad =-\,4\beta _{1}\,{\frac{{\mathrm{e}^{-2\,i{\beta _{1}}^{2} \left( 4\,{\beta _{1}}^{4}t+x\right) }} \left( 4\,i{\beta _{1}}^{2} \left( 12\,{\beta _{1}}^{4}t+x \right) +1 \right) ^{3}}{ \left( 16\,{\beta _{1}}^{4}\left( 12\,{\beta _{1}}^{4}t+x\right) ^{2}+1 \right) ^{2}}}, \end{aligned}\nonumber \\ \end{aligned}$$

(11)

with an arbitrary real constant $\beta _{1}$. This rational solution is a line-type soliton and is plotted in Fig. 1c, d. The peak trajectory of this rational solution is obtained by analyzing the analytic expression of Eq. (11). Thus, the soliton trajectory is the line $x=-12\beta _{1}^{4}t$ on the $(x-t)$ plane.

Remark 2.1

We point out that the coefficient of the independent variable t in the above expression of the rational solution is different to that corresponding to the first-order rational solution of the DNLS equation in Ref. [32]. In other words, the propagation speed of the above first-order rational soliton solution of the TOFKN equation is different to that corresponding to the rational solution of the DNLS equation, under the same conditions. The propagation speed of the rational solution of the TOFKN equation is $-12\beta _{1}^{4}$, which is less than zero, whereas the propagation speed of the rational solution of the DNLS equation is $4\beta _{1}^{2}$, which is greater than zero. Therefore, we find that their peak trajectories are different, but their peak amplitudes are equal under the same conditions.

Case 3 $(n=4)$. Let $\lambda _{1}=\alpha _{1}+i\beta _{1},\lambda _{2}=-\lambda _{1}^{*},\lambda _{3}=\alpha _{3}+i\beta _{3},\lambda _{4}=-\lambda _{3}^{*}$, then a new solution, the second-order soliton solution, can be obtained by the fourfold DT and substituting the eigenfunctions in Eq. (7) in formula (4). Because the analytical expression of the second-order soliton solution is very complicated, it is omitted here, but we show its three-dimensional plot in Fig. 2a. The typical third-order soliton is shown in Fig. 2b (see also the discussion in Case 4 $(n=6)$). The very complicated form of its analytical expression is also omitted here.

Fig. 2

a The second-order soliton solution $\left| q^{[4]} \right| ^{2}$ with parameters: $\alpha _{1}=0.3, \beta _1=0.3,\alpha _{3}=0.1,\beta _{3}=0.4$. b The third-order soliton solution with parameters: $\alpha _{1}=0.2, \beta _{1}=-0.45, \alpha _{3}=0.2, \beta _{3}=-0.6, \alpha _{5}=0.3, \beta _{5}=-0.35$

Furthermore, when $\lambda _{1}=\alpha _{1}+i\beta _{1},\lambda _{2}=-\lambda _{1}^{*}$ and taking the degenerate limit $\lambda _{3} \rightarrow \lambda _{1}$, a two-positon solution can be generated by applying Lemma 2 and substituting the eigenfunction (7) in the formula (5). The analytical expression of the two-positon solution is as follows:

$$\begin{aligned} \begin{aligned} { q^{[4]}_{positon}}={\dfrac{L_{1}^{*}L_{2}}{L_{1}^{2}}}, \end{aligned} \end{aligned}$$

(12)

where

$$\begin{aligned} L_{1}&=P_{1}-iP_{2},\\ L_{2}&=(-\cos ({Q_{2}}) +i\sin ( {Q_{2}}))(2{h_{1}}\cosh ({Q_{1}}) \\&\quad + 2\,{h_{2}}\,\sinh ({Q_{1}})),\\ P_{1}&={\alpha }^{4}_{1}+{\beta }^{4}_{1}+4608{\alpha }^{2}_{1}{\beta }^{2}_{1}({\alpha }^{2}_{1}\\&\quad +\,{\beta }^{2}_{1})^{6}{t}^{2} +32{\alpha }^{2}_{1}{\beta }^{2}_{1}({\alpha }^{2}_{1} + {\beta }^{2}_{1})^{2}{x}^{2}\\&\quad +768{\alpha }^{2}_{1}{\beta }^{2}_{1}({\alpha }^{2}_{1}-2\alpha _{1}\beta _{1} -\,{\beta }^{2}_{1})({\alpha }^{2}_{1}+2\alpha _{1}\beta _{1}-{\beta }^{2}_{1})\\&\quad ({\alpha }^{2}_{1} +{\beta }^{2}_{1})^{2}xt +({\alpha }^{4}_{1}-{\beta }^{4}_{1}) \cosh (2 Q_{1}),\\ P_{2}&=16{\alpha }^{2}_{1}{\beta }^{2}_{1}(\alpha _{1}-\beta _{1})(\alpha _{1}+\beta _{1})(12{\alpha }^{4}_{1}\\&\quad -168{\beta }^{2}_{1}{\alpha }^{2}_{1}+12{\beta }^{4}_{1})t\\&\quad +16{\alpha }^{2}_{1}{\beta }^{2}_{1}\left( \alpha _{1}-\beta _{1}\right) \left( \alpha _{1}+\beta _{1}\right) x\\&\quad +2\alpha _{1}\beta _{1}({\alpha }^{2}_{1}+{\beta }^{2}_{1})\sinh (2{ Q_{1}}),\\ Q_{1}&=4\alpha _{1}\beta _{1}((12{\alpha }^{4}_{1}-40{\beta }^{2}_{1}{\alpha }^{2}_{1}+12{\beta }^{4}_{1})t+x),\\ Q_{2}&=2({\alpha }^{2}_{1}-{\beta }^{2}_{1})((4{\alpha }^{4}_{1}-56{\beta }^{2}_{1}{\alpha }^{2}_{1} +4{\beta }^{4}_{1})t+x), \\ h_{1}&=-32i{\alpha }^{2}_{1}{\beta }^{3}_{1}({\alpha }^{2}_{1}+{\beta }^{2}_{1})(60{\alpha }^{4}_{1}t\\&\quad -120{\alpha }^{2}_{1}{\beta }^{2}_{1}t+12{\beta }^{4}_{1}t+x)+8{\alpha }^{4}_{1}\beta _{1},\\ h_{2}&=-32{\alpha }^{3}_{1}{\beta }^{2}_{1}({\alpha }^{2}_{1}+{\beta }^{2}_{1})(12{\alpha }^{4}_{1}t\\&\quad -120{\alpha }^{2}_{1}{\beta }^{2}_{1}t+60{\beta }^{4}_{1}t+x)+8i\alpha _{1}{\beta }^{4}_{1}. \end{aligned}$$

When $x=0,t=0,\left| q_{positon}^{[4]}\right| ^{2}=64\beta _{1}^{2}$. It is easy to find that this positon solution possesses a phase shift relative to the two-soliton solution when $t\rightarrow \pm \infty$. The evolution of positon solution of the TOFKN equation with $\alpha _{1}=0.5,\beta _{1}=0.35$ is shown in Fig. 3a, d.

Fig. 3

a, d The two-positon solution $\left| q_{positon}^{[4]} \right| ^{2}$ with $\alpha _{1}=0.5, \beta _1=0.35$. b, e The second-order rational traveling wave solution $\left| q^{[4]} \right| ^{2}$ of the TOFKN equation with $\beta _{1}=0.3$. c, f The three-positon solution $\left| q_{positon}^{[6]} \right| ^{2}$ with $\alpha _{1}=0.5,\beta _{1}=0.2$

Remark 2.2

A simple comparison between the above positon solution of the TOFKN equation and the corresponding positon solution of the DNLS equation [33] shows that their explicit analytic expressions are different only in terms of the coefficient of the variable t. This leads to different propagation speeds of these solutions under the same conditions. Thus, their trajectories are different, but their peak amplitudes are equal for the same set of parameters.

Next, let $\alpha _{1}\rightarrow 0$ in the above procedure of calculating the two-positon solution, then we obtain the second-order rational traveling wave solution. Its analytical expression can also be reduced to the same form as Eq. (12), but the values of the parameters $L_{1}$ and $L_{2}$ are as follows:

$$\begin{aligned} L_{1}&=P_{1}-iP_{2},\\ L_{2}&={\mathrm{e}^{-2i\beta _{1}^{2}(4{\beta }_{1}^{4}t+x)}}(-884736i{\beta }_{1}^{19}{t}^{3}\\&\quad +\,(-221184i{\beta }_{1}^{15}x-276480{\beta }_{1}^{13}) {t}^{2}\\&\quad +\,(-18432i{\beta }_{1}^{11}{x}^{2}-27648{\beta }_{1}^{9}x+6528i{\beta }_{1}^{7})t\\&\quad -\,512i{\beta }_{1}^{7}{x}^{3}-384{\beta }_{1}^{5}{x}^{2} - 96i{\beta }_{1}^{3}x+24\beta _{1}),\\ P_{1}&=5308416{\beta }_{1}^{24}{t}^{4}+1769472{\beta }_{1}^{20}x{t}^{3}\\&\quad +\,221184{\beta }_{1}^{16}{x}^{2}{t}^{2}+12288{\beta }_{1}^{12}{x}^{3}t\\&\quad -\,87552{\beta }_{1}^{12}{t}^{2}+256{\beta }_{1}^{8}{x}^{4}\\&\quad +\,768{\beta }_{1}^{8}xt-96{\beta }_{1}^{4}{x}^{2}-3,\\ P_{2}&=-442368{\beta }_{1}^{18}{t}^{3}-110592{\beta }_{1}^{14}x{t}^{2}\\&\quad -9216{\beta }_{1}^{10}{x}^{2}t-256{\beta }_{1}^{6}{x}^{3}-3648{\beta }_{1}^{6}t -48{\beta }_{1}^{2}x. \end{aligned}$$

This second-order rational traveling wave solution is plotted in Fig. 3b, e.

Case 4 $(n=6)$. Setting $\lambda _{1}=\alpha _{1}+i\beta _{1},\lambda _{2}=-\lambda _{1}^{*},\lambda _{3}=\alpha _{3}+i\beta _{3},\lambda _{4}=-\lambda _{3}^{*},\lambda _{5}=\alpha _{5}+i\beta _{5},\lambda _{6}=-\lambda _{5}^{*}$, we get the third-order soliton solution of the TOFKN equation by substituting the eigenfunctions (7) in formula (4) in Lemma 1. Its analytical expression is omitted here because it is very complicated, but we present here its three-dimensional plot in Fig. 2b.

Further, when we set $\lambda _{1}=\alpha _{1}+i\beta _{1}$ and eigenfunction (7), a three-positon solution of the TOFKN equation can be generated by applying Lemma 2. Its evolution is shown in Fig. 3c, f, and its complicated analytical expression is also omitted here. Obviously, the evolution of the three-positon solutions in Fig. 3 shows phase shifts when $t\rightarrow \pm \infty$, as compared with the corresponding three-soliton solutions.

3 Solutions of the TOFKN equation from nonzero seed solution

In this section, we will discuss some solutions of the TOFKN equation from nonzero seed solution that are obtained via the above-described method. We will obtain two types of breather solutions and rogue wave solutions. First, we must find a special nonzero seed solution (a plane wave solution) and spectral eigenfunctions associated with eigenvalues.

We set a nonzero periodic solution

$$\begin{aligned}&q=ce^{i(ax+bt)},\quad b=a\left( \frac{3}{2} c^{4}-3c^{2}a+a^{2}\right) ,\nonumber \\&\quad a,c\in {\mathbb {R}}, \end{aligned}$$

(13)

and substitute Eq. (13) in the spectral problem (3). After that, the eigenfunction $\varPsi =\begin{pmatrix} f\\ g \end{pmatrix}$ associated with the eigenvalue $\lambda$ is given by using the method of separation of variables and the superposition principle.

$$\begin{aligned}&\begin{pmatrix}f(x,t,\lambda _{k})\\ g(x,t,\lambda _{k})\end{pmatrix}=\begin{pmatrix} D_{1}\varpi _{1k}^{1}(x,t,\lambda _{k})+D_{2}\varpi _{1k}^{2}(x,t,\lambda _{k})+D_{1}{\varpi _{2k}^{1}}^{*}(x,t,-\lambda _{k}^{*})+D_{2}{\varpi _{2k}^{2}}^{*}(x,t,-\lambda ^{*}_{k})\\ D_{1}\varpi _{2k}^{1}(x,t,\lambda _{k})+D_{2}\varpi _{2k}^{2}(x,t,\lambda _{k})+D_{1}{\varpi _{1k}^{1}}^{*}(x,t,-\lambda _{k}^{*})+D_{2}{\varpi _{1k}^{2}}^{*}(x,t,-\lambda ^{*}_{k}) \end{pmatrix},\qquad \end{aligned}$$

(14)

where

$$\begin{aligned} \begin{aligned}&\left\{ \begin{aligned}&D_{1}\,=\,1, \\&D_{2}\,=\,1, \end{aligned} \right. \\&\begin{pmatrix} \varpi _{1k}^{1}(x,t,\lambda _{k}) \\ \varpi _{2k}^{1}(x,t,\lambda _{k}) \end{pmatrix}\\&=\begin{pmatrix} \exp (s(x+(4\lambda _{k}^{4}+2(a-c^{2})\lambda _{k}^{2}+a^{2}-3ac^{2}+\frac{3}{2}c^{4})t)+\frac{1}{2}(i(ax+bt)))\\ \frac{ia-2i\lambda _{k}^{2}+2s}{2c\lambda _{k}}\exp (s(x+(4\lambda _{k}^{4}+2(a-c^{2})\lambda _{k}^{2}+a^{2}-3ac^{2}+\frac{3}{2}c^{4})t)-\frac{1}{2}(i(ax+bt))) \end{pmatrix},\\&\begin{pmatrix} \varpi _{1k}^{2}(x,t,\lambda _{k}) \\ \varpi _{2k}^{2}(x,t,\lambda _{k}) \end{pmatrix}\\&=\begin{pmatrix} \exp (-s(x+(4\lambda _{k}^{4}+2(a-c^{2})\lambda _{k}^{2}+a^{2}-3ac^{2}+\frac{3}{2}c^{4})t)+\frac{1}{2}(i(ax+bt)))\\ \frac{ia-2i\lambda _{k}^{2}-2s}{2c\lambda _{k}}\exp (-s(x+(4\lambda _{k}^{4}+2(a-c^{2})\lambda _{k}^{2}+a^{2}-3ac^{2}+\frac{3}{2}c^{4})t)-\frac{1}{2}(i(ax+bt))) \end{pmatrix},\\&\varpi ^{1}(x,t,\lambda _{k})= \begin{pmatrix} \varpi _{1k}^{1}(x,t,\lambda _{k})\\ \varpi _{2k}^{1}(x,t,\lambda _{k}) \end{pmatrix}, \qquad \varpi ^{2}(x,t,\lambda _{k})= \begin{pmatrix} \varpi _{1k}^{2}(x,t,\lambda _{k})\\ \varpi _{2k}^{2}(x,t,\lambda _{k}) \end{pmatrix},\\&s=\frac{\sqrt{-a^{2}-4\lambda _{k}^{4}-4\lambda _{k}^{2}(c^{2}-a)}}{2}. \end{aligned} \end{aligned}$$

(15)

In order to obtain the breather solutions and rogue wave solutions, we have to set $n=2k$, i.e., the value of n is even.

3.1 The breather solutions of the TOFKN equation

Case 5 $(n=2)$. Let $\lambda _{1}=\alpha _{1}+i\beta _{1}, \lambda _{2}=-\lambda _{1}^{*}$, and we substitute their eigenfunctions (14) in the formula (4).

(1) For simplicity, we set $a=c^{2}+2\alpha _{1}^{2}-2\beta _{1}^{2}$ so that Im$(-a^{2}-4\lambda _{1}^{4}-4\lambda _{1}^{2}(c^{2}-a))=0$, and then, a new solution can be obtained as follows:

$$\begin{aligned} \begin{aligned} {\left| q^{[2]}\right| }^{2}={c}^{2} -\frac{\omega _{1}(c\alpha _{1}\cos ({F_{2}})\cosh ({F_{1}}) -c\beta _{1}\sin ({F_{2}}) \sinh ( {F_{1}}) +2\alpha _{1}\beta _{1})}{\omega _{2}\cos ({F_{2}})\cosh ({F_{1}})+\omega _{3}\sin ({F_{2}})\sinh ({F_{1}})+\omega _{4}\cosh (2{F_{1}})+\omega _{5}\cos (2{F_{2}})+\omega _{6}}, \end{aligned} \end{aligned}$$

(16)

with

$$\begin{aligned}&\omega _{1}=16\alpha _{1}\beta _{1}(c^{2}+4\alpha _{1}^{2})(c^{2}-4\beta _{1}^{2}),\\&\omega _{2}=8c{\alpha _{1}}^{2}\beta _{1}({c}^{2}+4{\alpha _{1}}^{2}),\\&\omega _{3}=-8c\alpha _{1}{\beta _{1}}^{2}({c}^{2}-4{\beta _{1}}^{2}),\\&\omega _{4}=16{\alpha _{1}}^{2}{\beta _{1}}^{2}({\alpha _{1}}^{2}+{\beta _{1}}^{2}),\\&\omega _{5}={c}^{2}({\alpha _{1}}^{2}+{\beta _{1}}^{2})({c}^{2}+4{\alpha _{1}}^{2}-4{\beta _{1}}^{2}),\\&\omega _{6}={c}^{4}({\alpha _{1}}^{2}-{\beta _{1}}^{2})+4{c}^{2}({\alpha _{1}}^{2}+{\beta _{1}}^{2})^{2}\\&\quad +16{\alpha _{1}}^{2}{\beta _{1}}^{2}({\alpha _{1}}^{2}-{\beta _{1}}^{2}),\\&F_{1}=K\{[12{\alpha _{1}}^{4}-2{\alpha _{1}}^{2}({c}^{2}+20{\beta _{1}}^{2})-\frac{{c}^{4}}{2}\\&\quad +2{c}^{2}{\beta _{1}}^{2}+12{\beta _{1}}^{4}]t+x\},\\&F_{2}=24K\alpha _{1}\beta _{1}({\alpha _{1}}^{2}-{\beta _{1}}^{2})t,\\&K=\sqrt{-({c}^{2}+4{\alpha _{1}}^{2})({c}^{2}-4{\beta _{1}}^{2})}. \end{aligned}$$

If $K^{2}>0$, the trajectory of this solution is defined specifically by $x=-[12{\alpha _{1}}^{4}-2{\alpha _{1}}^{2}({c}^{2}+20{\beta _{1}}^{2})-\frac{{c}^{4}}{2}+2{c}^{2}{\beta _{1}}^{2}+12{\beta _{1}}^{4}]t$ from $F_{1}=0$. If $K^{2}<0$ , the trajectory of this solution is defined explicitly by $t=0$ from $F_{2}=0$. Then, the dynamics of ${\left| q^{[2]}\right| }^{2}$ in Eq. (16) with different parameters is shown in Fig. 4a, b.

Remark 3.1

It is easy to find that for the same conditions the propagation speeds and the trajectories of the first-order breather solutions of the TOFKN equation and of the DNLS equation [32] are different; see also Remark 2.1 and Remark 2.2.

(2) When $a=\frac{c^{2}}{2}$, we can get two sets of eigenfunctions from Eq. (14) without difficulty,

$$\begin{aligned} \begin{aligned} \begin{pmatrix} \varpi _{1k}^{1}(x,t,\lambda _{k}) \\ \varpi _{2k}^{1}(x,t,\lambda _{k}) \end{pmatrix}\, and \, \begin{pmatrix} {\varpi _{1k}^{2}}^{*}(x,t,-\lambda ^{*}_{k}) \\ {\varpi _{2k}^{2}}^{*}(x,t,-\lambda ^{*}_{k}) \end{pmatrix}, \end{aligned} \end{aligned}$$

(17)

$$\begin{aligned} \begin{aligned} \begin{pmatrix} \varpi _{1k}^{2}(x,t,\lambda _{k}) \\ \varpi _{2k}^{2}(x,t,\lambda _{k}) \end{pmatrix}\, and \, \begin{pmatrix} {\varpi _{1k}^{1}}^{*}(x,t,-\lambda ^{*}_{k}) \\ {\varpi _{2k}^{1}}^{*}(x,t,-\lambda ^{*}_{k}) \end{pmatrix}. \end{aligned} \end{aligned}$$

(18)

Thus, in this case, the eigenfunction $\varPsi _{k}$ corresponding to $\lambda _{k}$ is obtained by

$$\begin{aligned} \begin{pmatrix} f(x,t,\lambda _{k})\\ g(x,t,\lambda _{k}) \end{pmatrix}= \begin{pmatrix} \varpi _{1k}^{1}(x,t,\lambda _{k})+{\varpi _{1k}^{1}}^{*}(x,t,-\lambda ^{*}_{k}) \\ \varpi _{2k}^{1}(x,t,\lambda _{k})+{\varpi _{2k}^{1}}^{*}(x,t,-\lambda ^{*}_{k}) \end{pmatrix},\nonumber \\ \end{aligned}$$

(19)

with

$$\begin{aligned}&\begin{pmatrix} \varpi _{1k}^{1}(x,t,\lambda _{k}) \\ \varpi _{2k}^{1}(x,t,\lambda _{k}) \end{pmatrix}\\&\quad = \begin{pmatrix} \exp (i(\lambda _{k}^{2}x+\frac{1}{2}c^{2}x+4\lambda _{k}^{6}t+\frac{1}{8}c^{6}t))\\ \frac{ic}{2\lambda _{k}}\exp (i(\lambda _{k}^{2}x+4\lambda _{k}^{6}t)) \end{pmatrix}. \end{aligned}$$

After that, it is not difficult to generate another first-order breather solution $q^{[2]}$ with $\lambda _{1}=\alpha _{1}+i\beta _{1},\lambda _{2}=-\lambda _{1}^{*}$ by the formula (4). Its evolution is shown in Fig. 4c.

Fig. 4

a The first-order breather solution $\left| q^{[2]}\right| ^{2}$ with $\alpha _{1}=\beta _{1}, \alpha _{1}=0.3, c=0.5$. b The first-order breather solution $\left| q^{[2]}\right| ^{2}$ with $\alpha _{1}=0.6, \beta _{1}=0.2, c=0.6$. Its trajectory is the line $t=0$. c The first-order breather solution $\left| q^{[2]}\right| ^{2}$ with $\alpha _{1}=0.5, \beta _{1}=0.6, c=1.2$

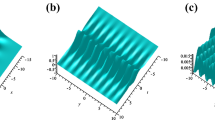
Case 6 $(n=4)$. Let $\lambda _{1}=\alpha _{1}+i\beta _{1},\lambda _{2}=-\lambda _{1}^{*},\lambda _{3}=\alpha _{3}+i\beta _{3},\lambda _{4}=-\lambda _{3}^{*}$, then we obtain the new solution $q^{[4]}$ using the above method, that is using the fourfold DT and substituting $\varPsi _{1}$ and $\varPsi _{2}$ in Eq. (4). Here, the analytical expression of $q^{[4]}$ is omitted, but ${\left| q^{[4]}\right| }^{2}$ is plotted in Fig. 5: (a) let $a=c^{2}+2\alpha _{i}^{2}-2\beta _{i}^{2}, i=1,3$, so that $Im(-a^{2}-4\lambda _{i}^{4}-4\lambda _{i}^{2}(c^{2}-a))=0$; (b) let $a=\frac{c^{2}}{2}$. The elastic collision between the two breathers can be clearly observed in Fig. 5.

Fig. 5

a The second-order breather solution $\left| q^{[4]}\right| ^{2}$ with $c=0.6, \alpha _{1}=0.6, \beta _{1}=0.35, \alpha _{3}=0.5, \beta _{3}=\frac{\sqrt{125}}{100}$. b The second-order breather solution $\left| q^{[4]}\right| ^{2}$ with $\ c=1.2, \alpha _{1}=0.8, \beta _{1}=0.4, \alpha _{3}=0.5, \beta _{3}=0.75$

3.2 The rogue wave solutions of the TOFKN equation

Here, we obtain the formula for generating rogue waves of the TOFKN equation by looking at the generating mechanism of the higher-order rogue waves of the NLS equation [67] and the DNLS equation [33], as follows:

Lemma 3

[33] Supposing $\lambda _{1}=\frac{1}{2}\sqrt{-c^{2}+2a}-\frac{ic}{2}, \lambda _{2}=-\lambda _{1}^{*}$, then the kth-order rogue wave solution $q^{[n]}(n=2k)$ can generated by the following formula:

$$\begin{aligned} \begin{aligned} q^{[n]}=\dfrac{\delta _{11}^{2}}{\delta _{21}^{2}}q+2i\dfrac{\delta _{11}\delta _{12}}{\delta _{21}^{2}}, \end{aligned} \end{aligned}$$

(20)

with

$$\begin{aligned} \begin{aligned}&\delta _{11}=\begin{vmatrix} g[1,n-1,1]&f[1,n-2,1]&\cdots&g[1,1,1]&f[1,0,1] \\ g[2,n-1,1]&f[2,n-2,1]&\cdots&g[2,1,1]&f[2,0,1] \\ g[1,n-1,2]&f[1,n-2,2]&\cdots&g[1,1,2]&f[1,0,2] \\ g[2,n-1,2]&f[2,n-2,2]&\cdots&g[2,1,2]&f[2,0,2] \\ \vdots&\vdots&\ddots&\vdots&\vdots \\ g[1,n-1,k]&f[1,n-2,k]&\cdots&g[1,1,k]&f[1,0,k] \\ g[2,n-1,k]&f[2,n-2,k]&\cdots&g[2,1,k]&f[2,0,k] \\ \end{vmatrix},\\&\delta _{12}=\begin{vmatrix} f[1,n,1]&f[1,n-2,1]&g[1,n-3,1]&\cdots&g[1,1,1]&f[1,0,1] \\ f[2,n,1]&f[2,n-2,1]&g[2,n-3,1]&\cdots&g[2,1,1]&f[2,0,1] \\ f[1,n,2]&f[1,n-2,2]&g[1,n-3,2]&\cdots&g[1,1,2]&f[1,0,1] \\ f[2,n,2]&f[2,n-2,2]&g[2,n-3,2]&\cdots&g[2,1,2]&f[2,0,2] \\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ f[1,n,k]&f[1,n-2,k]&g[1,n-3,k]&\cdots&g[1,1,k]&f[1,0,k] \\ f[2,n,k]&f[2,n-2,k]&g[2,n-3,k]&\cdots&g[2,1,k]&f[2,0,k] \\ \end{vmatrix},\\&\delta _{21}=\begin{vmatrix} f[1,n-1,1]&g[1,n-2,1]&\cdots&f[1,1,1]&g[1,0,1] \\ f[2,n-1,1]&g[2,n-2,1]&\cdots&f[2,1,1]&g[2,0,1] \\ f[1,n-1,2]&g[1,n-2,2]&\cdots&f[1,1,2]&g[1,0,2] \\ f[2,n-1,2]&g[2,n-2,2]&\cdots&f[2,1,2]&g[2,0,2] \\ \vdots&\vdots&\ddots&\vdots&\vdots \\ f[1,n-1,k]&g[1,n-2,k]&\cdots&f[1,1,k]&g[1,0,k] \\ f[2,n-1,k]&g[2,n-2,k]&\cdots&f[2,1,k]&g[2,0,k] \\. \end{vmatrix}. \end{aligned} \end{aligned}$$

Thus, the higher-order rogue wave solutions of the TOFKN equation are given by the above formula (20).

Case 7 $(n=2)$. We easily get the first-order rogue wave solution via substituting the eigenfunctions (14) in the above formula (20):

$$\begin{aligned} q^{[2]}_{RW}=\dfrac{R_{1}^{*}R_{2}}{R_{1}^{2}}c\exp \left( ia\left( x+\left( \frac{3}{2} c^{4}-3c^{2}a+a^{2}\right) t\right) \right) , \end{aligned}$$

(21)

where

$$\begin{aligned} R_{1}&=u_{1}+iu_{2}, \, R_{2}=u_{3}+iu_{4},\\ u_{1}&=24{c}^{2}a\sqrt{-{c}^{2}+2a}\left( \frac{5}{2}{c}^{4}t-4a{c}^{2}t+{a}^{2}t+\frac{1}{3}x\right) ,\\ u_{2}&=2a\sqrt{-{c}^{2}+2a}(45a{c}^{10}{t}^{2}-180{a}^{2}{c}^{8}{t}^{2}\\&\quad +\,252{c}^{6}{a}^{3}{t}^{2}-144{c}^{4}{a}^{4}{t}^{2}+36{c}^{2}{a}^{5}{t}^{2}\\&\quad +\,36{c}^{6}atx-72{c}^{4}{a}^{2}tx+24{c}^{2}{a}^{3}tx\\&\quad +\,4{c}^{2}a{x}^{2}+2),\\ u_{3}&=2a\sqrt{-{c}^{2}+2a}(-30{c}^{6}t\\&\quad +\,96a{c}^{4}t-60{a}^{2}{c}^{2}t-4{c}^{2}x),\\ u_{4}&=2a\sqrt{-{c}^{2}+2a}(45a{c}^{10}{t}^{2}-180{a}^{2}{c}^{8}{t}^{2}\\&\quad +\,252{c}^{6}{t}^{2}{a}^{3}-144{c}^{4}{a}^{4}{t}^{2} +36{c}^{2}{a}^{5}{t}^{2}\\&\quad +\,36{c}^{6}atx-72{c}^{4}{a}^{2}tx+24{c}^{2}{a}^{3}tx + 4{c}^{2}a{x}^{2}-6). \end{aligned}$$

A simple analysis shows that the first-order rogue wave solution ${\left| q^{[2]}_{RW}\right| }^{2}\rightarrow c^{2}$ when $x\rightarrow \infty , t\rightarrow \infty$, and the maximum amplitude of ${\left| q^{[2]}_{RW}\right| }^{2}$ equals $9c^{2}$ and appears at the origin of the $(x-t)$ plane. The first-order rogue wave solution is plotted in Fig. 6.

Fig. 6

a, b The first-order rogue wave solution ${\left| q_{RW}^{[2]}\right| }^{2}$ of the TOFKN equation with $a=1, c=\frac{1}{\sqrt{3}}$. c The first-order rogue wave solution ${\left| q_{RW}^{[2]}\right| }^{2}$ of the DNLS equation with $a=1, c=\frac{1}{\sqrt{3}}$

Remark 3.2

We also plot the first-order rogue wave solution of the DNLS equation [33] to compare it with the first-order rogue wave solution of the TOFKN equation under the same conditions. From Fig. 6b, c, we see that their directions and lengths are different under the same parameter conditions. We point out that these dissimilarities between the first-order rogue wave solutions of the TOFKN equation and of the DNLS equation were also discussed in Ref. [66], by using the contouring method.

Case 8 $(n=4)$. Assume $a=1$ and $c=\dfrac{1}{\sqrt{3}}$ in order to simplify the analytical expressions. Then, the second-order rogue wave solution is given by the formula (20):

$$\begin{aligned} \begin{aligned} q^{[4]}_{RW}=\dfrac{R_{1}^{*}R_{2}}{R_{1}^{2}}\dfrac{1}{\sqrt{3}}\exp (i(x+\frac{1}{6}t)), \end{aligned} \end{aligned}$$

(22)

where

$$\begin{aligned} R_{1}&=u_{1}+iu_{2}, \, R_{2}=u_{3}+iu_{4},\\ u_{1}&=704969{t}^{6}+855468{t}^{5}x+1201500{x}^{2}{t}^{4}\\&\quad +738720{x}^{3}{t}^{3}+486000{x}^{4}{t}^{2}\\&\quad +\,139968t{x}^{5}+46656{x}^{6}+6514614{t}^{4}\\&\quad -9954576{t}^{3}x-1854576{t}^{2}{x}^{2}\\&\quad +\,1446336{x}^{3}t+69984{x}^{4}\\&\quad +36137988{t}^{2}-4094064tx+3464208{x}^{2}\\&\quad +\,1417176,\\ u_{2}&=142578{t}^{5}-740124{t}^{4}x-553392{x}^{2}{t}^{3}\\&\quad -785376{t}^{2}{x}^{3}-256608t{x}^{4}\\&\quad -\,139968{x}^{5}+10546848{t}^{3}-46656{t}^{2}x\\&\quad -3079296{x}^{2}t-559872{x}^{3}\\&\quad +\,6351048t-2834352x,\\ u_{3}&=704969{t}^{6}+855468{t}^{5}x+1201500{x}^{2}{t}^{4}\\&\quad +738720{x}^{3}{t}^{3}+486000{x}^{4}{t}^{2}\\&\quad +\,139968t{x}^{5}+46656{x}^{6}-19841490{t}^{4}\\&\quad -28228176{t}^{3}x-17670960{t}^{2}{x}^{2}\\&\quad -\,2472768{x}^{3}t-769824{x}^{4}-1093500{t}^{2}\\&\quad +19420560tx-6613488{x}^{2}\\&\quad +\,7085880,\\ u_{4}&=6701166{t}^{5}+6276636{t}^{4}x+7209648{x}^{2}{t}^{3}\\&\quad +3024864{t}^{2}{x}^{3}+1376352t{x}^{4}\\&\quad +\,139968{x}^{5}-10912320{t}^{3}-49362048{t}^{2}x\\&\quad -9517824{x}^{2}t-1119744{x}^{3}\\&\quad -\,32805000t-4723920x. \end{aligned}$$

Furthermore, the higher-order rogue wave solutions are also calculated by the same method as above. However, their analytic expressions are omitted here because of their very complicated forms. But they are plotted in Fig. 7. The plots show that the higher-order rogue wave solutions are all equal to $c^{2}$ when $x\rightarrow \infty , t\rightarrow \infty$, and the maximum amplitude of the kth-order rogue wave is $\frac{(2k+1)^{2}}{c^{2}}$ in the origin of the $(x-t)$ plane, for the value $a=1$ of the parameter a. By comparing to Ref. [33], we find that the result is consistent with the maximum amplitude of the kth-order rogue wave of the DNLS equation with respect to variables a and c. Therefore, we make a guess that the energy of the central peak of the rogue wave of the TOFKN equation is the same with that corresponding to the DNLS equation, but is larger than that corresponding to the NLS equation. But like in Remark 3.2, the directions of propagation of the higher-order rogue waves of the TOFKN equation and of the DNLS equation are different.

4 The different types of rogue wave solutions by changing the parameters

In Ref. [33], the different waveforms of the higher-order rogue wave solutions of the DNLS equation were obtained. Next, we investigate how the waveforms of the solutions of the TOFKN equation will modify with the change of the parameters as compared to the corresponding solutions of the DNLS equation. In this section, we will discuss the dynamics of the rogue wave solutions of the TOFKN equation for different choices of the parameters. First, let the coefficients $D_{1}$ and $D_{2}$ of the eigenfunction (14) as follows:

$$\begin{aligned} \begin{aligned}&\left\{ \begin{aligned}&D_{1}\,=\,\exp (-is(S_{0}+S_{1}\epsilon +S_{2}\epsilon ^{2}+S_{3}\epsilon ^{3}+\cdots +S_{k-1}\epsilon ^{k-1})), \\&D_{2}\,=\,\exp (is(S_{0}+S_{1}\epsilon +S_{2}\epsilon ^{2}+S_{3}\epsilon ^{3}+\cdots +S_{k-1}\epsilon ^{k-1})). \end{aligned} \right. \end{aligned}\nonumber \\ \end{aligned}$$

(23)

Here, $S_{0}, S_{1}, S_{2}, S_{3},\ldots , S_{k-1}\in {\mathbb {C}}$, which have a crucial influence on the structure of the rogue wave solutions. Generally, we set $(k-1)$ free parameters for the kth-order rogue wave solution, and we obtain various structures of the solutions by setting different values of the parameters $S_{i}$.

Fig. 7

The higher-order rogue wave solutions ${\left| q_{RW}^{[2]}\right| }^{2}$ with $a=1, c=\frac{1}{\sqrt{3}}$

4.1 The rogue wave solutions with one nonzero parameter value

In this subsection, when just one of the parameters $S_{i}$ has a nonzero value, we obtain five typical waveforms: fundamental pattern, triangular, modified-triangular, pentagram, and ring structures.

4.1.1 (1) Fundamental pattern

For $n=2$, we can obtain different first-order rogue waves with $S_{i}=0$ excepting $S_{0}$ that has a nonzero value. We show them in Fig. 8. We can see that this solution is in fact that plotted in Fig. 6, but displaced about the origin. Furthermore, the first-order rogue wave and the higher-order rogue wave can all be displaced to any position in the $(x-t)$ plane, but this result is rather trivial.

Fig. 8

Different types of first-order rogue wave solutions with parameters $a=1, c=\frac{1}{\sqrt{3}}$, and for $S_{0}$ different from zero. a The first-order rogue wave with $S_{0}=10$. b The first-order rogue wave with $S_{0}=-10$

4.1.2 (2) Triangular structure

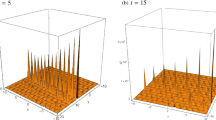
Let $S_{i}=0$, $(i\ne 1)$, and we show the evolution of the rogue waves of orders $k=2, 3, 4, 5$ in Fig. 9. We explicitly observe from Fig. 9 that the structures of all higher-order rogue wave are triangular ones. There are, respectively, three peaks, six peaks, ten peaks, and fifteen peaks in Fig. 9, in which every peak constitutes a first-order rogue wave. Thus, we conclude that the triangular structure of the kth-order rogue wave is composed of $\frac{k(k+1)}{2}$ peaks, which are arranged in k rows as in an arithmetic progression.

Fig. 9

The triangular structures of higher-order rogue waves with parameters $a=1$ and $c=\frac{1}{\sqrt{3}}$

4.1.3 (3) Modified-triangular structure

Moreover, by altering the coefficients of Eq. (14), the inner part of the above triangular structure shown in Fig. 9 can be converted into a higher-order peak that constitutes a higher-order rogue wave.

For $k=5$, let

$$\begin{aligned} \begin{aligned}&\begin{pmatrix}f(x,t,\lambda _{k})\\ g(x,t,\lambda _{k})\end{pmatrix}=\begin{pmatrix} D_{1}\varpi _{1k}^{1}(x,t,\lambda _{k})+D_{1}\varpi _{1k}^{2}(x,t,\lambda _{k})+D_{2}{\varpi _{2k}^{1}}^{*}(x,t,-\lambda _{k}^{*})+D_{2}{\varpi _{2k}^{2}}^{*}(x,t,-\lambda ^{*}_{k})\\ D_{1}\varpi _{2k}^{1}(x,t,\lambda _{k})+D_{1}\varpi _{2k}^{2}(x,t,\lambda _{k})+D_{2}{\varpi _{1k}^{1}}^{*}(x,t,-\lambda _{k}^{*})+D_{2}{\varpi _{1k}^{2}}^{*}(x,t,-\lambda ^{*}_{k}) \end{pmatrix}, \end{aligned} \end{aligned}$$

(24)

with

$$\begin{aligned}&\left\{ \begin{aligned}&D_{1}\,=\,\exp (-is^{2}(S_{0}+S_{1}\epsilon +S_{2}\epsilon ^{2}\\&+S_{3}\epsilon ^{3}+\cdots +S_{k-1}\epsilon ^{k-1})), \\&D_{2}\,=\,\exp (is^{2}(S_{0}+S_{1}\epsilon +S_{2}\epsilon ^{2}\\&+S_{3}\epsilon ^{3}+\cdots +S_{k-1}\epsilon ^{k-1})); \end{aligned} \right. \end{aligned}$$

thus, a new pattern, the modified-triangular structure, is generated in this way. This structure has at its periphery the form of a triangle of twelve first-order rogue waves and has a central peak in the interior of the triangle, which is in fact a second-order rogue wave. This modified-triangular structure is shown in Fig. 10 for a special choice of the parameters.

Fig. 10

The modified-triangular structures of the fifth-order rogue waves with parameters $a=1, c=\frac{1}{\sqrt{3}}$, and $S_{1}=1000$

Fig. 11

The pentagram structures of higher-order rogue waves with parameters $a=1$, $c=\frac{1}{\sqrt{3}}$, and $S_{2}=20000$

Fig. 12

The ring structures of the higher-order rogue waves with parameters $a=1$ and $c=\frac{1}{\sqrt{3}}$

Fig. 13

The ring-triangular structure of higher-order rogue waves with parameters $a=1, c=\frac{1}{\sqrt{3}}$

4.1.4 (4) Pentagram structure

Let $S_{i}=0$, $(i\ne 2)$, then we get a new type of wave structure, namely the pentagram waveform, which is shown in Fig. 11. We point out that this type of wave structure has not been discovered before, to the best of our knowledge. From Fig. 11, we observe that the fourth-order rogue wave and the fifth-order rogue wave are divided into ten peaks and fifteen peaks, respectively, when the parameter $S_{2}$ has a nonzero value. We also point out that every peak in Fig. 11 is a first-order rogue wave. Thus, we obtain the general result that the pentagram structure of the kth-order rogue wave is composed of $\frac{k(k+1)}{2}$ peaks, and all of them are first-order rogue waves.

4.1.5 (5) Ring structure

We suppose $S_{i}=0$, excepting $S_{k-1}$. Then, when $S_{k-1}$ is sufficiently large with increasing the value of k, a ring structure of the kth-order rogue wave is obtained, which is plotted in Fig. 12. We can clearly observe that $(2k-1)$ first-order rogue waves locate on the outer shell of the ring and one $(k-2)$th-order peak, which is in fact a $(k-2)$th-order rogue wave, locates in the center of the ring; see the three different ring structures plotted in Fig. 12.

4.2 The rogue wave solutions with more than one nonzero parameter

In the above subsection, five types of patterns depending on only one nonzero parameter are described. Next, we will discuss the solutions with two or more nonzero parameters.

4.2.1 (6) Ring-triangular structure

In the above subsection, a ring structure of the fourth-order rogue wave solution has been generated with $S_{3}\ne 0$, whose outer shell is a ring that is composing of seven first-order rogue waves and the center of the ring structure is a second-order rogue wave. Thus, when we continue to set $S_{1}\ne 0$, we obtain the result that the outer shell maintains as it is and the central peak can be split into a triangular structure. This kind of pattern is shown in Fig. 13. Furthermore, a similar ring-triangular structure of more higher-order rogue wave solutions of the TOFKN equation can be also obtained if we proceed in the same way. Therefore, we conclude that the central $(k-2)$th-order rogue wave of the ring structure of the kth-order rogue wave solution is able to be divided up into a triangular structure when $S_{k-1}$ is sufficiently large with increasing k.

Fig. 14

a The multi-ring structure of fifth-order rogue waves with parameter $a=1, c=\frac{1}{\sqrt{3}}, S_{2}=5\times 10^{5},$ and $S_{4}=1\times 10^{12}$. b The inside of the multi-ring structure

4.2.2 (7) Multi-ring structure

Moreover, the central higher-order peak of the ring structure of the higher-order rogue wave can also be divided up into a ring structure. For $k=5$, the ring structure of this solution is shown for $S_{4}\ne 0$ in Fig. 12c. Then, if we continue to assume $S_{2}\ne 0$ and $S_{4}\gg 0$, the inner third-order rogue wave will be divided up into a ring waveform. This structure is plotted in Fig. 14. Obviously, the outer part of the multi-ring structure is consistent with that of the ring structure shown in Fig. 12c, and a new ring composed of five first-order rogue waves is added to the inner part. Meanwhile, there is also a first-order peak in the center of the new ring. Therefore, we can guess that the center of the more higher-order solutions will continue to be split into a multi-ring structure.

5 Summary and discussion

In this paper, we have studied the third-order flow of the KN system (TOFKN equation) with third-order dispersion and quintic nonlinearity. By applying the DT and the Taylor expansion, from different seed solutions, i.e., zero seed solution and nonzero seed solution (plane wave solution), we have explicitly generated the soliton, rational, positon, breather, and rogue wave solutions of the TOFKN equation. The detailed analytic expressions of some of the obtained solutions and their dynamics for some special choices of the parameters have been also given. Our results prove again the usefulness of the DT method for solving integrable nonlinear partial differential equations. Moreover, we obtain the rogue wave solutions with different waveforms by properly choosing the coefficients $D_{1}$ and $D_{2}$ of the eigenfunctions. Notably, we have obtained several distinct patterns of first-order and higher-order rogue wave solutions of the TOFKN equation via selecting different parameter values: fundamental pattern, triangular, modified-triangular, pentagram, ring, ring-triangular, and multi-ring structures. The pentagram structure is firstly discovered here, to the best of our knowledge.

In conclusion, the comparison made between the solutions of the TOFKN equation and the DNLS equation shows that the third-order dispersion and quintic nonlinear term of the KN system can affect both the trajectory and the speed of the solutions. The exact analytical results obtained in this paper might have a reference value for the study of the higher-order flows of other integrable nonlinear dynamical systems and provide a theoretical basis for possible experimental studies and applications.