1 Introduction

Recent years have witnessed the rapid development of the fractional derivative concept in the whole scientific community. An increasing number of researchers have devoted themselves to the study of fractional derivatives. Fractional derivatives have been applied in mathematics, physics, biology, electrical engineering, control and other fields, and achieved abundant research results [1,2,3,4,5,6,7,8]. Fractional-order derivatives are most widely used in fractional-order systems, which are worthy of research since many systems in nature are of non-integer order. There are often factors interfering with the study process of a variety of fractional-order systems, such as neural network systems [4, 5], gene regulation network systems [9, 10], HIV systems [11, 12], and Lorenz dynamical systems [8, 13], which necessitates the investigation of the stability and stabilization of fractional-order systems. Scholars have put forward different stability conditions and controllers of the fractional-order systems after years of research. These methods can be roughly divided into two types, with one based on a Lyapunov function and the other based on eigenvalue judgment. Since this paper focuses on the use of the Lyapunov-like function and the vector Lyapunov function to solve the problem, the method based on eigenvalue judgment is adopted [14, 15]. Li et al. derived the stability conditions for fractional-order systems via a Lyapunov function [16], and other stability conditions via the Lyapunov direct method [17]. Tuan et al. put forward a novel stability judgment method based on the fractional-order Lyapunov function [18], and investigated the asymptotic stability of nonlinear fractional-order differential equations next year [19]. The method of relaxing piecewise quadratic Lyapunov function was used to study the stability and stabilization problems for a class of switched discrete-time nonlinear systems by Zhu et al. [20]. Next year, Zhu et al. investigated the problem of quasi-synchronization for a class of discrete-time Lur’e-type switched systems via virtue of the semi-time-varying Lyapunov function [21]. The application of the Lyapunov function was extended to a variety of fractional-order derivatives by Wei et al. [22, 23]. Cao et al. obtained the sufficient criteria of asymptotic stability based on fractional-order Lyapunov functional [24]. However, the above-mentioned studies only focused on the sufficient conditions of asymptotic stability of the fractional-order system, without solving the instability problem of the fractional-order system itself. In other words, the asymptotic stabilization of the fractional-order system was achieved by the corresponding control strategy. Moreover, these methods ignored a more complicated situation, i.e., multiple time delays of the fractional-order system. The comparison theorem is a widely used and effective method to solve the stability and stabilization of fractional-order systems at present. For instance, the comparison theorem was used to discuss asymptotic stability of multivariable fractional-order systems with different fractional-orders in the paper of Lenka [25], to deduce sufficient conditions of a fractional-order neural network with multiple time delays in the study of Cao et al. [26], and to address the global stabilization of fractional-order memristor-based neural networks with time delays in the article of Jia et al. [27] However, the comparison theorem method has a extremely complicated stability proof process, conservative confinement conditions, and a relatively low convergence rate, as indicated by the experimental results. Motivated by works related to the comparison theorem, we proposed two new control methods based on a Lyapunov-like function and a vector Lyapunov function separately, attempting to overcome the deficiencies of the comparison theorem and solve the asymptotic stabilization problem of general fractional-order nonlinear systems with multiple time delays. Compared with the comparison theorem, the first proposed integer-order Lyapunov function-based method solved the problem of fractional-order systems through a series of transformations, with less restriction, greatly enhancing the physical meaning of the study. The M-matrix introduced by the second proposed method tremendously reduced the complexity of the derivation process with a faster convergence rate.

The M-matrix was first introduced in [28] for the stability analysis and control of integer-order systems, which has lower conservatism and less restriction than negative definite matrices. In this paper, the M-matrix was generalized to the stabilization control of fractional-order systems for the first time. The vector Lyapunov function was employed to solve the asymptotic stability problem of nonlinear fractional-order composite systems [29]. However, the asymptotic stabilization of the general nonlinear fractional-order system with multiple time delays was never solved. In this paper, we extended the vector Lyapunov function method to the asymptotic stabilization of the general nonlinear fractional-order system with multiple delays for the first time, and applied the Lyapunov-like function to the asymptotic stabilization of general fractional-order nonlinear systems. The two methods greatly reduce the control limitation and afford a wider stability domain.

This paper has two main contributions. On the one hand, the Lyapunov-like function was generalized to general nonlinear fractional-order systems, and a new control criterion for asymptotic stabilization of the nonlinear fractional-order systems was put forward. With this approach, asymptotic stabilization problems of different kinds of nonlinear fractional-order systems can be solved. On the other hand, the vector Lyapunov function and M-matrix were introduced to solve the asymptotic stability of nonlinear fractional-order systems with multiple time delays for the first time. Moreover, a new asymptotic stability criterion applicable to all nonlinear fractional-order systems with multiple time delays is put forward.

The rest of the paper was organized as follows. Section 2 reviews some definitions and lemmas. The results of this paper are stated in Sect. 3. Section 4 covers some numerical simulations to illustrate the correctness and feasibility of the proposed controllers. Section 5 presents the conclusion of the paper.

2 Preliminaries

For a general nonlinear fractional-order system

$$ {}^{C}D^{\varsigma } x(t) = f(x(t)), $$
(2.1)

where the \( x(t) \in {\mathbb{R}}^{n} \) is the state of Eq. (2.1) and the function \( f:{\mathbb{R}}^{n} \to {\mathbb{R}}^{n} \) satisfies \( f(0) = 0 \) and locally Lipschitz continuous condition, the following lemmas hold.

Lemma 1

[30] If \( f(x(t)) \) is an continuous in the time dimension, then there exists a unique solution to the fractional-order system (2.1), the unique solution is as follow

$$ x(t) = x_{0} + \int_{0}^{\infty } {\xi_{\varsigma } (\omega )\varphi (\omega ,t)} {\text{d}}\omega , $$
(2.2)

where \( \varphi (\omega ,t) \) is the solution of the initial value to the fractional-order system (2.1), and \( \omega \in \left( {0,\infty } \right). \)

$$ \frac{\partial \varphi (\omega ,t)}{\partial t} = - \omega \varphi (\omega ,t) + f\left( {x(t)} \right),\varphi (0,t) = 0, $$
(2.3)

where \( \xi_{\varsigma } (\omega ) = [\sin (\pi \varsigma )/\pi ]\omega^{ - \varsigma } ,\omega \in \left( {0,\infty } \right). \)

Lemma 2

[18] If the Lyapunov function \( V:{\mathbb{R}}^{n} \to {\mathbb{R}} \) of (2.1) be a convex and continuously differentiable function such that \( V(0) = 0. \) Then, the following inequality holds for all \( t \ge 0. \)

$$ {}^{C}D^{\varsigma } V(x) \le \frac{\partial V(x)}{\partial x}{}^{C}D^{\varsigma } x, $$
(2.4)

Lemma 3

[29] If \( P = \left[ {p_{ij} } \right] \) is an \( M{\text{ - matrix,}} \) there exists a diagonal matrix \( Q = {\text{diag}}\left\{ {q_{1} ,q_{2} , \ldots q_{N} } \right\} \) with elements \( q_{i} > 0, \, i \in N, \) such that the matrix \( Z \) satisfies the following equation

$$ Z = P^{\rm T} Q + QP, $$
(2.5)

Lemma 4

[16] If the convex and continuously differentiable Lyapunov function \( V:{\mathbb{R}}^{n} \to {\mathbb{R}} \) of (2.1) satisfies

$$ \beta_{1} (\left\| x \right\|) \le V(x) \le \beta_{2} (\left\| x \right\|), $$
(2.6)
$$ D^{\varsigma } V(x) \le - \beta_{3} (\left\| x \right\|), $$
(2.7)

\( \forall t \ge 0, \) where \( \beta_{i} (i = 1,2,3) \) are \( {\text{class - }}\kappa \) functions and the fractional-order operator is \( \varsigma \in \left( {0,1} \right), \) then the fractional-order system (2.1) is asymptotically stable.

3 Main result

In this section, we will solve the stability and stabilization problems of nonlinear fractional-order systems via two different methods.

3.1 Stability analysis of nonlinear fractional-order system

In this section, we derive a novel stability theorem of the asymptotic stabilization of nonlinear fractional-order systems via Lyapunov-like function and diffusive realization. The Lyapunov-like function was first appeared in [31]. Then, in [30], Wu et al. extended the Lyapunov-like function method to analyze the external stability of Caputo fractional-order system. First of all, the general form of the all fractional-order nonlinear system can be expressed as follows

$$ {}^{C}D^{\alpha } x_{i} (t) = a_{i} x_{i} (t) + f_{i} (x_{i} (t)) + g_{i} (x(t)),\quad i \in \left\{ {1,2, \ldots ,N} \right\}, $$
(3.1)

where \( x_{i} (t) \in R^{{n_{i} }} \) is the state of the \( \, i{\text{ - th}} \) subsystem and is a differentiable vector, the function \( f_{i} :{\mathbb{R}}^{{n_{i} }} \to {\mathbb{R}}^{{n_{i} }} \) are the nonlinear part of the systems and the function \( g_{i} :{\mathbb{R}}^{{\sum\limits_{i = 1}^{N} {n_{i} } }} \to {\mathbb{R}}^{{n_{i} }} ,\quad i \in \left\{ {1,2, \ldots ,N} \right\} \) refers to the nonlinear part of interconnections between the state \( x_{i} (t) \) and other state \( x_{j} (t). \)

We can rewrite the fractional-order system (3.1) to the compact form as follows.

$$ {}^{C}D^{\alpha } x = Ax + f(x) + g(x), $$
(3.2)

where

$$ \begin{aligned} A & = {\text{diag}}\{ a_{1} ,a_{2} , \ldots ,a_{N} \} ,x = \left[ {x_{1} ,x_{2} , \ldots ,x_{N} } \right]^{\text{T}} , \\ f(x) & = \left[ {f_{1} (x_{1} (t)),f_{2} (x_{{}} (t)), \ldots ,f_{N} (x_{N} (t))} \right]^{\text{T}} , \\ g(x) & = \left[ {g_{1} (x(t)),g_{2} (x(t)), \ldots ,g_{N} (x(t))} \right]^{\rm T} . \\ \end{aligned} $$
(3.3)

Assumption 1

We assume the nonlinear function \( f(x),g(x) \) are all continuous in \( t \) and satisfies a locally Lipschitz condition of \( x(t), \) whose Lipschitz parameters are \( L_{1} \) and \( L_{2} \), and \( f(0) = g(0) = 0. \)

Theorem 1

If the nonlinear fractional-order system (3.1) satisfies Assumption 1, and for positive definite constant \( \kappa_{f} ,\kappa_{g} > 0 \) and a positive definite matrix \( P \) with all elements \( p_{ij} > 0 \) for all \( i,j \in 1,2, \ldots ,n, \) make the following matrix inequality hold, then the fractional-order nonlinear system (3.1) is asymptotically stable.

$$ \left[ {\begin{array}{*{20}c} {\varTheta_{ 1} } & P \\ * & { - \kappa_{f} I} \\ \end{array} } \right] < 0, $$
(3.4)

where

$$ \varTheta_{ 1} = PA + A^{\rm T} P + 2\kappa_{f} L_{1}^{2} I + 2\kappa_{g} L_{2}^{2} I, $$
(3.5)

Proof

We choose the following Lyapunov-like function which is convex and continuously differentiable of Eq. (3.1).

$$ V(x) = \int_{0}^{\infty } {\xi_{\alpha } (\omega )\varphi^{\text{T}} (\omega ,t)P\varphi (\omega ,t)} {\text{d}}\omega , $$
(3.6)

Then we take the derivative of (3.6), we have

$$ \dot{V}(x) = \int_{0}^{\infty } {\xi_{\alpha } (\omega )\left( {\frac{{\partial \varphi^{\text{T}} (\omega ,t)}}{\partial t}P\varphi (\omega ,t) + \varphi^{\text{T}} (\omega ,t)P\frac{\partial \varphi (\omega ,t)}{\partial t}} \right)} {\text{d}}\omega , $$
(3.7)

Then, according to the Lipschitz condition, for any positive definite constant \( \kappa_{f} ,\kappa_{g} > 0, \) we can obtain

$$ \begin{aligned} & \kappa_{f} \left( {f^{\text{T}} (x(t))f(x(t)) - f^{\text{T}} (x(t))f(x(0)) - f(x(t))f^{\text{T}} (x(0)) + f^{\text{T}} (x(0))f(x(0))} \right) \\ & \quad \le 2\kappa_{f} L_{1}^{2} \left( {x^{\text{T}} (t)x(t) - x^{\text{T}} (t)x(0) - x(t)x^{\text{T}} (0) + x^{\text{T}} (0)x(0)} \right) \\ & \quad 2\kappa_{f} L_{1}^{2} x^{\rm T} (t)x(t) - \kappa_{f} f^{\text{T}} (x(t))f(x(t)) \ge 0, \\ \end{aligned} $$
(3.8)

and

$$ \begin{aligned} & \kappa_{g} \left( {g^{\text{T}} (x(t))g(x(t)) - g^{\text{T}} (x(t))g(x(0)) - g(x(t))g^{\text{T}} (x(0)) + g^{\text{T}} (x(0))g(x(0))} \right) \\ & \quad \le 2\kappa_{g} L_{2}^{2} \left( {x^{\text{T}} (t)x(t) - x^{\text{T}} (t)x(0) - x(t)x^{\text{T}} (0) + x^{\text{T}} (0)x(0)} \right) \\ & \quad 2\kappa_{g} L_{2}^{2} x^{\rm T} (t)x(t) - \kappa_{g} g^{\text{T}} (x(t))g(x(t)) \ge 0, \\ \end{aligned} $$
(3.9)

Then, according to Lemma 1, we have

$$ \begin{aligned} \dot{V}(x) & = \int_{0}^{\infty } {\xi_{\alpha } (\omega )\left( {\frac{{\partial \varphi^{\text{T}} (\omega ,t)}}{\partial t}P\varphi (\omega ,t) + \varphi^{\text{T}} (\omega ,t)P\frac{\partial \varphi (\omega ,t)}{\partial t}} \right)} {\text{d}}\omega \\ & = \int_{0}^{\infty } {\xi_{\alpha } (\omega )(( - \omega \varphi^{\text{T}} (\omega ,t) + A^{\text{T}} x + f^{\text{T}} (x(t)) + g^{\text{T}} (x(t)))P\varphi (\omega ,t)} \\ & \quad + \varphi^{\text{T}} (\omega ,t)P( - \omega \varphi (\omega ,t) + Ax + f(x(t)) + g(x(t))){\text{d}}\omega \\ & = - \int_{0}^{\infty } {\xi_{\alpha } (\omega )\omega \varphi^{\text{T}} (\omega ,t)P\varphi (\omega ,t){\text{d}}\omega + \int_{0}^{\infty } {\xi_{\alpha } (\omega )(x^{\text{T}} A^{\text{T}} + f^{\text{T}} (x(t)) + g^{\text{T}} (x(t)))P\varphi (\omega ,t){\text{d}}\omega } } \\ & \quad - \int_{0}^{\infty } {\xi_{\alpha } (\omega )\varphi^{\text{T}} (\omega ,t)P\omega \varphi (\omega ,t){\text{d}}\omega + \int_{0}^{\infty } {\xi_{\alpha } (\omega )\varphi^{\text{T}} (\omega ,t)P(Ax + f(x(t)) + g(x(t))){\text{d}}\omega } } \\ & = x^{\text{T}} (t)(PA + A^{\text{T}} P)x + x^{\text{T}} (t)Pf(x(t)) + x^{\text{T}} (t)Pg(x(t)) + f^{\text{T}} (x(t))Px(t) + g^{\text{T}} (x(t))Px(t) \\ & \quad - 2\int_{0}^{\infty } {\xi_{\alpha } (\omega )\omega \varphi^{\text{T}} (\omega ,t)P\varphi (\omega ,t){\text{d}}\omega } \\ & \le x^{\text{T}} (t)(PA + A^{\text{T}} P)x + x^{\text{T}} (t)Pf(x(t)) + x^{\text{T}} (t)Pg(x(t)) + f^{\text{T}} (x(t))Px(t) + g^{\text{T}} (x(t))Px(t) \\ & \quad + 2\kappa_{f} L_{1}^{2} x^{\text{T}} (t)x(t) - \kappa_{f} f^{\text{T}} (x(t))f(x(t)) + 2\kappa_{g} L_{2}^{2} x^{\text{T}} (t)x(t) - \kappa_{g} g^{\text{T}} (x(t))g(x(t)) \\ & = \psi^{\text{T}} (t)\left[ {\begin{array}{*{20}c} {\varTheta_{ 1} } & P & P \\ * & { - \kappa_{f} I} & 0 \\ * & 0 & { - \kappa_{g} I} \\ \end{array} } \right]\psi (t), \\ \end{aligned} $$
(3.10)

where

$$ \psi (t) = [x^{\text{T}} (t),f^{\text{T}} (x(t)),g^{\text{T}} (x(t))]^{\text{T}} . $$
(3.11)

According to the conditions of Theorem 1, we can obtain

$$ \begin{aligned} \dot{V}(x) & = \psi^{\rm T} (t)\left[ {\begin{array}{*{20}c} {\varTheta_{ 1} } & P & P \\ * & { - \kappa_{f} I} & 0 \\ * & 0 & { - \kappa_{g} I} \\ \end{array} } \right]\psi (t) \\ & < 0, \\ \end{aligned} $$
(3.12)

The fractional-order nonlinear system (3.1) is asymptotically stable, which completes the proof. □

Remark 1

Compared with the method of integration from 0 to T of the Lyapunov-like function in [30, 31], we obtained the asymptotically stability criterion of fractional-order nonlinear system via directly differentiating the Lyapunov-like function is conciser and more convenient.

3.2 Stabilization analysis of nonlinear fractional-order system

Next, we will address the problem of stabilization of nonlinear fractional-order system with multiple time delay or not, respectively. First, we consider the case that the nonlinear fractional-order system is without time delay. A feedback controller is added to the system (3.1) as follow,

$$ {}^{C}D^{\alpha } x = Ax + f(x) + g(x) + Bu(t), $$
(3.13)

where, the feedback controller is

$$ u(t) = - Kx(t), $$
(3.14)

where, the \( K = \left( {k_{ij} } \right)_{n \times n} , \) then, the (3.1) can be rewritten as follow

$$ {}^{C}D^{\alpha } x = (A - BK)x + f(x) + g(x), $$
(3.15)

Theorem 2

If the controlled nonlinear fractional-order system with control (3.15) satisfies Assumption 1, and for positive definite constant \( \kappa_{f} ,\kappa_{g} > 0 \) and a positive definite matrix \( P \) with all elements \( p_{ij} > 0 \) for all \( i,j \in 1,2, \ldots ,n, \) and a matrix \( X > 0 \) such that (3.16), then the fractional-order system (3.15) is asymptotically stabilization.

$$ \left[ {\begin{array}{*{20}c} {\varTheta_{ 2} } & P \\ * & { - \kappa_{f} I} \\ \end{array} } \right] < 0, $$
(3.16)

where \( \varTheta_{ 2} = PA - X + A^{\rm T} P - X^{\rm T} + 2\kappa_{f} L_{1}^{2} I + 2\kappa_{g} L_{2}^{2} I, \) the feedback gain matrix can be obtained by solving \( BK = P^{ - 1} X. \)

Proof

We choose the same Lyapunov-like function as (3.7), and then we take the derivative as follow,

$$ \begin{aligned} \dot{V}(x) & = \int_{0}^{\infty } {\xi_{\alpha } (\omega )(( - \omega \varphi^{\text{T}} (\omega ,t) + (A - BK)^{\text{T}} x + f^{\text{T}} (x(t - \tau )) + g^{\text{T}} (x(t)))P\varphi (\omega ,t)} \\ & \quad + \varphi^{\text{T}} (\omega ,t)P( - \omega \varphi (\omega ,t) + (A - BK)x + f(x(t - \tau )) + g(x(t))){\text{d}}\omega \\ & = - \int_{0}^{\infty } {\xi_{\alpha } (\omega )\omega \varphi^{\text{T}} (\omega ,t)P\varphi (\omega ,t){\text{d}}\omega + \int_{0}^{\infty } {\xi_{\alpha } (\omega )(x^{\text{T}} (A - BK)^{\text{T}} + f^{\text{T}} (x(t)) + g^{\text{T}} (x(t)))P\varphi (\omega ,t){\text{d}}\omega } } \\ & \quad - \int_{0}^{\infty } {\xi_{\alpha } (\omega )\varphi^{\text{T}} (\omega ,t)P\omega \varphi (\omega ,t){\text{d}}\omega + \int_{0}^{\infty } {\xi_{\alpha } (\omega )\varphi^{\text{T}} (\omega ,t)P((A - BK)x + f(x(t)) + g(x(t))){\text{d}}\omega } } \\ & = x^{\text{T}} (t)(PA - PBK + A^{\text{T}} P - K^{\text{T}} B^{\text{T}} P)x + x^{\text{T}} (t)Pf(x(t)) \\ & \quad + x^{\text{T}} (t)Pg(x(t)) + f^{\text{T}} (x(t))Px(t) + g^{\text{T}} (x(t))Px(t) - 2\int_{0}^{\infty } {\xi_{\alpha } (\omega )\omega \varphi^{\text{T}} (\omega ,t)P\varphi (\omega ,t){\text{d}}\omega } \\ & \le x^{\text{T}} (t)(PA - PBK + A^{\text{T}} P - K^{\text{T}} B^{\text{T}} P)x(t) + x^{\text{T}} (t)Pf(x(t)) + x^{\text{T}} (t)Pg(x(t)) \\ & \quad + f^{\text{T}} (x(t))Px(t) + g^{\text{T}} (x(t))Px(t) + 2\kappa_{f} L_{1}^{2} x^{\text{T}} (t)x(t) \\ & \quad - \kappa_{f} f^{\text{T}} (x(t))f(x(t)) + 2\kappa_{g} L_{2}^{2} x^{\text{T}} (t)x(t) - \kappa_{g} g^{\text{T}} (x(t))g(x(t)) \\ & = \psi^{\text{T}} (t)\left[ {\begin{array}{*{20}c} {\varTheta_{ 2} } & P & P \\ * & { - \kappa_{f} I} & 0 \\ * & 0 & { - \kappa_{g} I} \\ \end{array} } \right]\psi (t), \\ \end{aligned} $$
(3.17)

we make \( X = PBK \), and then according to (3.16), one has

$$ \begin{aligned} \dot{V}(x) & = \psi^{\text{T}} (t)\left[ {\begin{array}{*{20}c} {\varTheta_{4} } & P & P \\ * & { - \kappa_{f} I} & 0 \\ * & 0 & { - \kappa_{g} I} \\ \end{array} } \right]\psi (t) \\ & < 0. \\ \end{aligned} $$
(3.18)

The fractional-order nonlinear system controlled is asymptotically stabilization, which completes the proof. □

Then, we consider the stabilization of the fractional-order systems with multiple time delay. It is unable to solve fractional-order systems with time delay by using Lyapunov-like function functions. Thus, we take a new approach based on the vector Lyapunov function and the M-matrix. First we convert the general fractional-order nonlinear system into a form of which has multiple time delay as follow

$$ {}^{C}D^{\alpha } x_{i} (t) = a_{i} x_{i} (t) + b_{i} x_{i} (t - \tau ) + f_{i} (x_{i} (t - \tau )) + g_{i} (x(t)) + c_{i} u_{i} (t),\quad i \in \left\{ {1,2, \ldots ,N} \right\}, $$
(3.19)

then, we design the following distributed feedback controller for each fractional-order subsystem

$$ u_{i} (t) = k_{i} x_{i} (t),\quad i \in {\rm N}, $$
(3.20)

The fractional-order nonlinear system (3.1) can be rewritten as follows

$$ {}^{C}D^{\alpha } x_{i} (t) = \left( {a_{i} - c_{i} k_{i} } \right)x_{i} (t) + b_{i} x_{i} (t - \tau ) + f_{i} (x_{i} (t - \tau )) + g_{i} (x(t)),\quad i \in \left\{ {1,2, \ldots ,N} \right\}, $$
(3.21)

Assumption 2

There exists some constant \( \vartheta_{i} > 0 \) such that

$$ \frac{{\partial V_{i} (x_{i} (t))}}{{\partial x_{i} (t)}}f_{i} (x_{i} (t - \tau )) \le \vartheta_{i} \Phi_{3i}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {\left\| {x_{i} } \right\|} \right)\Phi_{3i}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {\left\| {x_{i} (t - \tau )} \right\|} \right),\quad i \in \left\{ {1,2, \ldots ,N} \right\}, $$
(3.22)

Assumption 3

There exists a continuous nondecreasing function \( \zeta_{i} (u) > u \) for \( u > 0 \) such that:

$$ \left\| {f_{i} (x(t - \tau ))} \right\| < \zeta_{i} \left( {\left\| {f_{i} (x(t))} \right\|} \right) ,\quad i \in \left\{ {1,2, \ldots ,N} \right\}, $$
(3.23)
$$ \Phi_{3i}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {\left\| {x_{i} (t - \tau )} \right\|} \right) < \zeta_{i} \left( {\Phi_{3i}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {\left\| {x_{i} (t)} \right\|} \right)} \right) ,\quad i \in \left\{ {1,2, \ldots ,N} \right\}, $$
(3.24)

Assumption 4

Consider some nonnegative real numbers \( \varXi_{ij} , \, \varUpsilon_{ij} ,(i,j = 1,2, \ldots ,N), \) which can make the following inequality hold

$$ \left\| {\frac{{\partial V_{i} (x_{i} )}}{{\partial x_{i} }}g_{i} (x(t))} \right\| \le \sqrt {\gamma_{3i} (\left\| {x_{i} } \right\|)} \sum\limits_{j = 1}^{N} {\varXi_{ij} } \varUpsilon_{ij} \sqrt {\gamma_{3j} (\left\| {x_{j} } \right\|)} , $$
(3.25)

Theorem 3

For any nonlinear fractional-order system composition of (3.19) which is controlled by the decentralized feedback controller (3.20) satisfies from Assumption 2 to 4, if the following judgment matrix \( W \) is an \( M{\text{ - matrix,}} \) it is asymptotically stabilization.

$$ W = \left[ {\begin{array}{*{20}c} {w_{11} } & {w_{12} } & \cdots & {w_{1j} } \\ {w_{21} } & {w_{22} } & \cdots & {w_{2j} } \\ \vdots & \vdots & \ddots & \vdots \\ {w_{i1} } & {w_{i2} } & \cdots & {w_{ij} } \\ \end{array} } \right]_{i \times j} , \, w_{ij} = \left\{ {\begin{array}{*{20}l} {( - a_{i} + c_{i} k_{i} - \left\| {b_{i} } \right\|\zeta_{i} - \vartheta_{i} \zeta_{i} ) - \varXi_{ij} \varUpsilon_{ij} ,} \hfill & {{\text{if }}i = j,} \hfill \\ { - \varXi_{ij} \varUpsilon_{ij} ,} \hfill & {{\text{otherwise}},} \hfill \\ \end{array} } \right. $$
(3.26)

Proof

We select a series of positive definite function \( V_{i} (x_{i} ) \) which satisfies the following conditions based on Lemma 4 as the Lyapunov function of the controlled nonlinear fractional-order system (3.21)

$$ \sigma_{1i} (\left\| {x_{i} } \right\|) \le V_{i} (x_{i} ) \le \sigma_{2i} (\left\| {x_{i} } \right\|), $$
(3.27)
$$ D^{\varsigma } V_{i} (x_{i} ) \le - \sigma_{3i} (\left\| {x_{i} } \right\|), $$
(3.28)

where \( \sigma_{i} (i = 1,2,3) \) are \( {\text{class - }}\kappa \) functions and the fractional-order operator is \( \varsigma \in \left( {0,1} \right). \) Then, we choose the following vector function as the Lyapunov function of the whole fractional-order system with a set of positive definite constants \( q_{i} > 0 \),

$$ V(x) = \sum\limits_{i = 1}^{N} {q_{i} V_{i} (x_{i} )} , $$
(3.29)

then, we take the fractional-order derivative of (3.29), according to Lemma 2, the following inequality is derived

$$ \begin{aligned} {}^{C}D^{\alpha } V(x(t)) & \le \sum\limits_{i = 1}^{N} {q_{i} \frac{{\partial V_{i} (x_{i} )}}{{\partial x_{i} }}} {}^{C}D^{\alpha } x_{i} (t) \\ & = \sum\limits_{i = 1}^{N} {q_{i} \frac{{\partial V_{i} (x_{i} )}}{{\partial x_{i} }}} \left[ {a_{i} x_{i} (t) + b_{i} x_{i} (t - \tau ) + f_{i} (x_{i} (t - \tau )) + g_{i} (x(t)) + c_{i} u_{i} (t)} \right] \\ & = \sum\limits_{i = 1}^{N} {q_{i} \frac{{\partial V_{i} (x_{i} )}}{{\partial x_{i} }}} \left[ {\left( {a_{i} - c_{i} k_{i} } \right)x_{i} (t) + b_{i} x_{i} (t - \tau ) + f_{i} (x_{i} (t - \tau )) + g_{i} (x(t))} \right] \\ & \le \sum\limits_{i = 1}^{N} {q_{i} [\frac{{\partial V_{i} (x_{i} )}}{{\partial x_{i} }}\left( {a_{i} - c_{i} k_{i} } \right)x_{i} (t) + \left\| {b_{i} } \right\|\sigma_{3i}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {\left\| {x_{i} } \right\|} \right)\sigma_{3i}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {\left\| {x_{i} (t - \tau )} \right\|} \right)} \\ & \quad + \vartheta_{i} \sigma_{3i}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {\left\| {x_{i} } \right\|} \right)\sigma_{3i}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {\left\| {x_{i} (t - \tau )} \right\|} \right) + \frac{{\partial V_{i} (x_{i} )}}{{\partial x_{i} }}g_{i} (x(t))] \\ & \le \sum\limits_{i = 1}^{N} {q_{i} [\left( {a_{i} - c_{i} k_{i} } \right)\sigma_{3i} \left( {\left\| {x_{i} (t)} \right\|} \right) + b_{i} \zeta_{i} \sigma_{3i} \left( {\left\| {x_{i} (t)} \right\|} \right)} \\ & \quad + \vartheta_{i} \zeta_{i} \sigma_{3i} \left( {\left\| {x_{i} } \right\|} \right) + \sqrt {\sigma_{3i} (\left\| {x_{i} } \right\|)} \sum\limits_{j = 1}^{N} {\varXi_{ij} } \varUpsilon_{ij} \sqrt {\sigma_{3j} (\left\| {x_{j} } \right\|)} ] \\ & \le - \frac{1}{2}\sigma_{3}^{\rm T} \left( {\left\| {x(t)} \right\|} \right)\left( {W^{\rm T} Q + QW} \right)\sigma_{3} \left( {\left\| {x(t)} \right\|} \right), \\ \end{aligned} $$
(3.30)

we can always find a diagonal matrix \( Q = {\text{diag}}\{ q_{1} ,q_{2} \ldots ,q_{N} \} \) with elements \( q_{i} > 0, \, i \in N, \) such that the matrix \( Z = W^{\rm T} Q + QW \) is positive definite. Then, based on Lemma 3, the following inequality is derived

$$ \begin{aligned} {}^{C}D^{\alpha } V(x(t)) & \le - \frac{1}{2}\sigma_{3}^{\rm T} \left( {\left\| {x(t)} \right\|} \right)Z\sigma_{3} \left( {\left\| {x(t)} \right\|} \right) \, \\ & < 0,\quad {\text{if }}x(t) \ne 0, \\ \end{aligned} $$
(3.31)

where

$$ \sigma_{3} \left( {\left\| {x(t)} \right\|} \right) = \left[ {\sigma_{31}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {\left\| {x_{1} } \right\|} \right),\sigma_{32}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {\left\| {x_{2} } \right\|} \right), \ldots ,\sigma_{3N}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {\left\| {x_{N} } \right\|} \right)} \right]^{\rm T} . $$
(3.32)

According to the Lemma 4, we can obtain that the controlled nonlinear fractional-order system is asymptotically stabilization, which completes the proof. □

4 Numerical simulation of several common fractional-order systems

In this section, we will demonstrate the effectiveness and feasibility of our proposed control methods for general nonlinear fractional-order systems through several common fractional-order chaotic systems

Example 1

First the effectiveness of the proposed controller based on Lyapunov-Like function is verified by a fractional-order Chua’s circuit system, the model of which without control is as follows

$$ \left\{ \begin{array}{l} D^{\alpha } x(t) = a\left[ {(b(y(t) - x(t)) + bx(t) - c(\left| {x(t) + 1} \right| - \left| {x(t) - 1} \right|)} \right], \hfill \\ D^{\alpha } y(t) = x(t) - y(t) + z(t), \hfill \\ D^{\alpha } z(t) = - dy(t), \hfill \\ \end{array} \right. $$
(4.1)

where the coefficient parameters \( a,b,c,d \) are constants, and we choose them:\( a = 12,b = 1,c = 0.3,d = 17, \) with the fractional-order parameter \( \alpha = 0.98, \) and the initial values are \( \left[ {0.1,0.1,0.1} \right]. \) Then, we rewrite the fractional-order Chua’s circuit system (4.1) to a matrix form

$$ {}^{C}D^{\alpha } v(t) = Av(t) + f(v(t)) + g(v(t)), $$
(4.2)

where

$$ v(t) = \left[ {\begin{array}{*{20}c} {x(t)} \\ {y(t)} \\ {z(t)} \\ \end{array} } \right],A = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & { - 1} & 0 \\ 0 & 0 & 0 \\ \end{array} } \right],f(v(t)) = \left[ {\begin{array}{*{20}c} { - ac(\left| {x(t) + 1} \right| - \left| {x(t) - 1} \right|)} \\ 0 \\ 0 \\ \end{array} } \right],g(v(t)) = \left[ {\begin{array}{*{20}c} {aby(t)} \\ {x(t) + z(t)} \\ { - dy(t)} \\ \end{array} } \right], $$
(4.3)

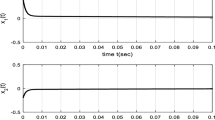
Next, the time responses and phase diagrams of the fractional-order Chua’s circuit system without control are shown in Fig. 1.

Fig. 1
figure 1

The time responses and phase diagrams of (4.1) without control

Full size image

It is obvious that the fractional-order Chua’s circuit system without control presents an unstable state. Then we add the control input to the fractional-order Chua’s circuit system

$$ {}^{C}D^{\alpha } v(t) = Av(t) + f(v(t)) + g(v(t)) + Bu(t), $$
(4.4)

where \( u(t) = - Kv(t), \) and we have

$$ {}^{C}D^{\alpha } v = (A - BK)v + f(v) + g(v), $$
(4.5)

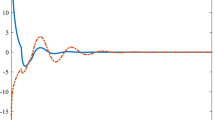
By calculating, we can obtain \( L_{1} = \frac{24}{7},L_{2} = 17, \)\( \kappa_{f} = 0.1,\kappa_{g} = 0.042. \) And according to the control conditions of the proposed controller based on Lyapunov-Like function, the conditions of Theorem 2, via calculation, we have \( K = {\text{diag}}(1.3,1.3,1.3) \). Then the contrast time responses of the fractional-order Chua’s circuit system with control or not are shown in Fig. 2.

Fig. 2
figure 2

The contrast time responses of the (4.1) and (4.5)

Full size image

It is obvious that the system is asymptotically stabilization after applying the proposed controller based on Lyapunov-Like function. Compared with the controller in other papers, the controller proposed in this paper has a wider application range and can play a role in different fractional-order parameters. Next we illustrate the time responses of the fractional-order Chua’s circuit system (4.1) with different fractional-order parameters and the time responses of it with control are shown in Fig. 3.

Fig. 3
figure 3

The time responses of (4.5) with different fractional parameters

Full size image

Obviously, for the fractional-order operators selected randomly, the controller which satisfies the conditions of Theorem 2 can effectively act on the fractional-order Chua’s circuit system to make it asymptotically stabilization.

Example 2

Then, the effectiveness and universality of another proposed controller based on vector Lyapunov function will be fully demonstrated through the example of fractional-order Lorentz system with time delay. First, we transform the traditional fractional-order Lorentz system into a form with time delay, which is shown as follow

$$ \begin{aligned} D^{\alpha } x_{1} (t) & = a(x_{2} (t) - x_{1} (t)), \\ D^{\alpha } x_{2} (t) & = - x_{1} (t - \tau )x_{2} (t - \tau ) + bx_{1} (t) - x_{1} (t)x_{3} (t), \\ D^{\alpha } x_{3} (t) & = cx_{3} (t) + x_{1} (t)x_{2} (t), \\ \end{aligned} $$
(4.6)

where \( a = 10,b = 28,c = - \frac{8}{3},\tau = 1 \) with the fractional-order parameter \( \alpha = 0.98, \) and the initial values are \( \left[ {0.1,0.1,0.1} \right]. \) Then, the time responses of the fractional-order Lorentz system without control are shown in Fig. 4.

Fig. 4
figure 4

The time responses and phase diagrams of (4.6) without control

Full size image

It is obvious that the time delayed fractional-order Lorentz system without control presents an unstable state. Then, we add controllers, and then the (4.6) can be rewritten to the follow form

$$ \begin{aligned} D^{\alpha } x_{1} (t) & = - 10x_{1} (t) + 10x_{2} (t) + c_{1} u_{1} (t), \\ D^{\alpha } x_{2} (t) & = - x_{1} (t - 1)x_{2} (t - 1) + 28x_{1} (t) - x_{1} (t)x_{3} (t) + c_{2} u_{2} (t), \\ D^{\alpha } x_{3} (t) & = - \frac{8}{3}x_{3} (t) + x_{1} (t)x_{2} (t) + c_{3} u_{3} (t), \\ \end{aligned} $$
(4.7)

where \( u_{i} (t) = - k_{i} x_{i} (t), \, i = 1,2,3, \) we select the input coefficient \( c_{1} = c_{2} = c_{3} = 1 \) and the vector Lyapunov function of Eq. (4.7) is as follow

$$ V(x(t)) = x_{1}^{2} + x_{2}^{2} + x_{3}^{2} . $$
(4.8)

According to the requirements of Theorem 3, we select \( \zeta_{2} = \frac{3}{2} > 1, \) and the following inequality can be obtained

$$ \begin{aligned} \frac{{\partial V_{2} (x_{2} (t))}}{{\partial x_{2} (t)}}f_{2} (x_{2} (t - 1)) & \le 2\left\| {x_{2} (t)} \right\|^{2} \left\| {x_{2} (t - 1)} \right\|, \\ & \le 3\left\| {x_{2} (t)} \right\|^{3} , \\ \end{aligned} $$
(4.9)

by calculating, we have

$$ \left\{ \begin{array}{l} \frac{{\partial V_{1} (x_{1} (t))}}{{\partial x_{1} (t)}}g_{1} (x(t)) \le 2\left\| {x_{1} (t)} \right\|\left\| {x_{2} (t)} \right\|, \hfill \\ \frac{{\partial V_{2} (x_{2} (t))}}{{\partial x_{2} (t)}}g_{2} (x(t)) \le 56\left\| {x_{1} (t)} \right\|\left\| {x_{2} (t)} \right\| + 2\left\| {x_{1} (t)} \right\|\left\| {x_{2} (t)} \right\|\left\| {x_{3} (t)} \right\|, \hfill \\ \frac{{\partial V_{3} (x_{3} (t))}}{{\partial x_{3} (t)}}g_{3} (x(t)) \le 2\left\| {x_{1} (t)} \right\|\left\| {x_{2} (t)} \right\|\left\| {x_{3} (t)} \right\|. \hfill \\ \end{array} \right. $$
(4.10)

Then, according to the conditions of Theorem 3, through calculation, we have

$$ k_{1} = 4,k_{2} = 15,k_{3} = \frac{4}{3}, $$
(4.11)

then, we can deduce the decision matrix \( W \) as follows

$$ W = \left[ {\begin{array}{*{20}c} {( - a_{1} + c_{1} k_{11} - \vartheta_{1} \zeta_{1} ) - \varXi_{11} \varUpsilon_{11} } & { - \varXi_{12} \varUpsilon_{12} } & { - \varXi_{13} \varUpsilon_{13} } \\ { - \varXi_{21} \varUpsilon_{21} } & {( - a_{2} + c_{2} k_{2} - \vartheta_{2} \zeta_{2} ) - \varXi_{22} \varUpsilon_{22} } & { - \varXi_{23} \varUpsilon_{23} } \\ { - \varXi_{31} \varUpsilon_{31} } & { - \varXi_{32} \varUpsilon_{32} } & {( - a_{3} + c_{3} k_{3} - \vartheta_{3} \zeta_{3} ) - \varXi_{33} \varUpsilon_{33} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {14} & { - 2} & 0 \\ { - 56} & {12} & { - 2} \\ { - 2} & { - 2} & 4 \\ \end{array} } \right]. $$
(4.12)

It is obvious that the matrix \( W \) is an \( M{\text{ - matrix}} . \) With the same advantages as the previous proposed control method based on Lyapunov-like function, this controller based on vector Lyapunov function proposed in this paper also has a wide application range and can work in different fractional-order parameters. In the same way, we illustrate the time responses of the system (4.7) with different fractional-order parameters and the time responses of the fractional-order Lorentz system with control are shown in Fig. 5.

Fig. 5
figure 5

The time responses of (4.7) with different fractional parameters

Full size image

The results show that, for randomly selected fractional-order parameters, the proposed controller based on vector Lyapunov function satisfies the conditions of Theorem 3 can achieve satisfactory result.

In addition to its wide application in the selection of fractional-order parameters, this control method also has the advantages of being applicable to different initial values. Without loss of generality, we illustrate the time responses of the system (4.7) with different initial values and the time responses of the fractional-order Lorentz system with control are shown in Fig. 6.

Fig. 6
figure 6

The time responses of (4.7) with different initial values

Full size image

The results show that, for randomly selected initial values, the proposed controller based on vector Lyapunov function satisfies the conditions of Theorem 3 can be also valid.

Remark 2

Although the previous method based on Lyapunov-like function can solve the stability problem of fractional-order derivative into integer-order derivative, which can greatly simplify the complexity of the stability problem, it cannot solve the stability problem of the fractional-order system with time delay. The method based on vector Lyapunov function can not only solve the stability problem of the fractional-order system without time delay, but also with time delay even multiple time delays. Thus, compared with the previous method based on Lyapunov-like function, this method based on vector Lyapunov function is more widely used and less limited.

Example 3

Then, an example of fractional-order Liu system is given to illustrate that the proposed control method can solve the problem of multiple time delays. First, we transform the traditional fractional-order Liu system into a form with multiple time delays, which is shown as follow

$$ \begin{aligned} D^{\alpha } x_{1} (t) & = - x_{1} (t - \tau ) + x_{2}^{2} (t), \\ D^{\alpha } x_{2} (t) & = ax_{2} (t - \tau ) + bx_{1} (t)x_{3} (t), \\ D^{\alpha } x_{3} (t) & = cx_{3} (t - \tau ) + {\text{d}}x_{1} (t)x_{2} (t), \\ \end{aligned} $$
(4.13)

where \( a = 2.5,b = - 4,c = - 5,d = 4,\tau = 1, \) and the initial values are \( \left[ {0.1,0.1,0.1} \right]. \) Then, the time responses of the fractional-order Liu system without control are shown in Fig. 7.

Fig. 7
figure 7

The time responses and phase diagrams of (4.13) without control

Full size image

It is obvious that the time delayed fractional-order Liu system without control presents an unstable state. Then, we add controllers, and then the (4.13) can be rewritten to the follow form

$$ \begin{aligned} D^{\alpha } x_{1} (t) & = - x_{1} (t - \tau ) + x_{2}^{2} (t) + e_{1} u_{1} (t), \\ D^{\alpha } x_{2} (t) & = 2.5x_{2} (t - \tau ) - 4x_{1} (t)x_{3} (t) + e_{2} u_{2} (t), \\ D^{\alpha } x_{3} (t) & = - 5x_{3} (t - \tau ) + 4x_{1} (t)x_{2} (t) + e_{3} u_{3} (t), \\ \end{aligned} $$
(4.14)

where \( u_{i} (t) = - k_{i} x_{i} (t), \, i = 1,2,3, \) we select the input coefficient \( e_{1} = e_{2} = e_{3} = 1 \) and the vector Lyapunov function of Eq. (4.14) is as follow

$$ V(x(t)) = x_{1}^{2} + x_{2}^{2} + x_{3}^{2} . $$
(4.15)

We select \( \zeta_{2} = \frac{3}{2} > 1, \) which satisfy the requirements of Theorem 3, and the following inequality can be obtained

$$ \begin{aligned} \frac{{\partial V_{i} (x_{i} (t))}}{{\partial x_{i} (t)}}x_{i} (t - 1) & \le 2\left\| {x_{i} (t)} \right\|\left\| {x_{i} (t - 1)} \right\|, \\ & \le 3\left\| {x_{i} (t)} \right\|^{2} , \\ \end{aligned} $$
(4.16)

by calculating, we have

$$ \left\{ \begin{array}{l} \frac{{\partial V_{1} (x_{1} (t))}}{{\partial x_{1} (t)}}g_{1} (x(t)) \le 2\left\| {x_{1} (t)} \right\|\left\| {x_{2} (t)} \right\|^{2} , \hfill \\ \frac{{\partial V_{2} (x_{2} (t))}}{{\partial x_{2} (t)}}g_{2} (x(t)) \le 8\left\| {x_{1} (t)} \right\|\left\| {x_{2} (t)} \right\|\left\| {x_{3} (t)} \right\|, \hfill \\ \frac{{\partial V_{3} (x_{3} (t))}}{{\partial x_{3} (t)}}g_{3} (x(t)) \le 8\left\| {x_{1} (t)} \right\|\left\| {x_{2} (t)} \right\|\left\| {x_{3} (t)} \right\|. \hfill \\ \end{array} \right. $$
(4.17)

Then, according to the conditions of Theorem 3, through calculation, we have

$$ k_{1} = 9,k_{2} = 15,k_{3} = 13, $$
(4.18)

then, we can deduce the decision matrix \( W \) as follows

$$ W = \left[ {\begin{array}{*{20}c} {( - a_{1} + c_{1} k_{1} - \left\| {b_{1} } \right\|\zeta_{1} ) - \varXi_{11} \varUpsilon_{11} } & { - \varXi_{12} \varUpsilon_{12} } & { - \varXi_{13} \varUpsilon_{13} } \\ { - \varXi_{21} \varUpsilon_{21} } & {( - a_{2} + c_{2} k_{2} - \left\| {b_{2} } \right\|\zeta_{2} ) - \varXi_{22} \varUpsilon_{22} } & { - \varXi_{23} \varUpsilon_{23} } \\ { - \varXi_{31} \varUpsilon_{31} } & { - \varXi_{32} \varUpsilon_{32} } & {( - a_{3} + c_{3} k_{3} - \left\| {b_{3} } \right\|\zeta_{3} ) - \varXi_{33} \varUpsilon_{33} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 8 & { - 2} & 0 \\ { - 8} & {12.5} & { - 8} \\ { - 8} & { - 8} & 8 \\ \end{array} } \right]. $$
(4.19)

It is obvious that the matrix \( W \) is an \( M{\text{ - matrix}} . \) In the same way, we illustrate the time responses of the system (4.14) with different fractional-order parameters and different initial value. Then, the time responses of the fractional-order Lorentz system with control are shown in Figs. 8 and 9.

Fig. 8
figure 8

The time responses of (4.14) with different fractional parameters

Full size image
Fig. 9
figure 9

The time responses of (4.14) with different initial values

Full size image

The results show that, for randomly selected fractional-order parameters and initial values, the proposed controller based on vector Lyapunov function satisfy the conditions of Theorem 3 can also achieve satisfactory result.

5 Conclusion

In this paper, new stabilization conditions are acquired using two different control strategies based on a Lyapunov-like function and a vector Lyapunov function separately, capable of solving both the asymptotic stability problem of nonlinear fractional-order systems and the asymptotic stabilization problem of nonlinear fractional-order systems with multiple time delays. The correctness and validity of the proposed novel control methods are verified by the simulating results of several common nonlinear fractional-order systems, including the fractional-order Chua’s circuit system, the fractional-order Lorentz system and the fractional-order Liu system. In particular, the control technology of the fractional-order Chua’s circuit system is already highly developed in the actual circuit system engineering. The new methods put forward in this paper can provide new directions and ideas for the control of the fractional-order Chua’s circuit in practice, and they are applicable to many other practical fractional nonlinear systems, such as fractional gene regulatory network systems, fractional HIV systems, fractional financial systems, fractional-order switched PWA systems, fractional-order switched Lur’e systems, etc. Therefore, the new methods have effective practical value and important practical significance. In the future research, we will extend the proposed control methods to all fractional-order operators.