1 Introduction

Past several years have witnessed the wide applications of fractional calculus, involving biology [1,2,3], physics [4, 5], psychology [6], engineering [7, 8], etc. Compared with integer-order derivatives, fractional derivatives have the superiority of accuracy and flexibility when they are used to describe the mathematical models of phenomena in the real world. From the perspectives of the mathematical and systematical science, the fractional-order systems depicted by dynamical equations with fractional orders will emerge many dynamical behaviors, which are of great value to be investigated.

The rapid growth of Internet has brought a series of drawbacks in the past two decades, among which the congestion problem has been intriguing many scholars. To overcome that, some congestion control schemes were studied deeply [9,10,11]. Especially, many results were given about the dynamic properties of the congestion control systems, including the stability [12,13,14,15], Hopf bifurcations [16,17,18,19,20], and chaos [21,22,23]. For a single resource and single-user system, some criteria for the local stability and the rate of convergence were proposed in [12]. Then, the congestion control systems with multiple sources, which are more common in Internet networks, were discussed also from the view of stability [14]. On the other hand, it was also shown in [17] that the variations of some system parameters would lead to the loss of stability, which causes the bifurcation and chaos.

In various kinds of dynamic systems like congestion control systems, bifurcations are not always desired and probably do harm to our systems. Thus, some control schemes are designed to change the bifurcation characteristics of systems, which are often referred to bifurcation control. In general, bifurcation control means the control of bifurcation properties of nonlinear dynamic systems, thereby inducing some desired output behaviors of the systems [24]. Different from other control schemes, bifurcation control usually aims to delay the onset of an inherent bifurcation, change the critical values of an existing bifurcation, and stabilize an unstable bifurcated solution or branch [24]. In addition, unlike many control schemes, most bifurcation control schemes will not change the properties of the original system.

Especially, to improve the bifurcation characteristics for congestion control systems, various bifurcation control schemes were proposed, such as the time-delay feedback control [25,26,27], the state feedback control [24, 28, 29], and the hybrid control strategy [30, 31]. It is shown that under these control strategies, the stability regions of congestion systems are extended and the occurrences of undesired Hopf bifurcations are delayed.

It is known that conventional integer-order dynamical systems will turn to fractional-order ones when we replace the integer-order derivatives with fractional-order derivatives. It is noted that fractional-order dynamical systems are quite different from integer-order counterparts [32, 33]. For instance, a main difference is that the fractional-order derivatives of a periodic function with a specific period cannot be a periodic function with the same period [33]. However, current studies about fractional-order dynamical systems are insufficient and many characteristics of these fractional-order systems have not been revealed.

Moreover, fractional-order derivatives are non-local, integro-differential operators, while integer-order ones are local operators [34]. Therefore, fractional-order derivatives are suitable for simulating infinite memory effects and long-range dispersion processes. Considering that congestion control systems include round trip communication delays, the application of memory module will bring great improvement to congestion control systems [35]. Additionally, the introduction of fractional calculus can make the congestion control models more accurate than conventional integer-order systems in depicting realistic systems. Hence, it is more meaningful to investigate fractional-order congestion control systems than integer-order counterparts.

However, nearly all efforts on the stability and Hopf bifurcations are limited to the integer-order model of congestion control systems. Moreover, the qualitative theory for bifurcations in fractional-order systems is still an open problem. Thus, it is of great significance to investigate the bifurcations for fractional-order congestion control system. To the best of the authors’ knowledge, few work on the bifurcations has been reported for fractional-order congestion control systems.

As a category of typical proportional–integral–derivative (PID) control, proportional–derivative (PD) control has been widely applied, especially in robotic systems [36,37,38]. Dupont [37] studied the question of how to achieve steady motion at very low velocities using PD control and figured out that stick-slip can be avoided only through velocity feedback. From the view of bifurcation and bifurcation control, the effects of PD controller on the bifurcations of dynamic systems have been investigated in [39,40,41]. Bucklaew et al. [39] studied Hopf bifurcations in a parametrically forced pendulum or manipulator with a PD controller. It is noted that a PD control strategy was recently used in a small-world network to improve its dynamic behaviors [40]. The results show that one can easily advance or delay the onset of Hopf bifurcations just by changing the control parameters, including the proportional control parameter and the derivative control parameter.

In the past few years, some kinds of fractional-order proportional–integral–derivative (PID) controllers, which own fractional-order integral and derivative terms, have been designed to improve fractional-order systems [42,43,44,45,46]. Using a fractional-order \(PI^{\lambda }D^{\mu }\) controller, Hamamci [42] stabilized a delayed fractional-order system and determined a set of global stability domains in the control parameter space. In [45], a fractional-order PID controller with the employment of particle swarm optimization was designed to improve the robustness of an automatic voltage regulator. Based on user-specified peak overshoot and rise time, the fractional-order closed-loop transfer function of the designed plant was realized in [44], where the Tustin operator-based continuous fraction expansion scheme was adopted. To optimize the multi-objective functions for an automatic voltage regulator system, Pan and Das [46] proposed a fractional-order \(PI^{\lambda }D^{\mu }\) controller with an improved evolutionary non-dominated sorting genetic algorithm, where a chaotic map was adopted for greater effectiveness.

Motived by the works on bifurcation control with the application of conventional PD controllers and the massive applications of fractional-order PID controllers, in this paper, we adopt a fractional-order PD control strategy as a bifurcation control method to control the Hopf bifurcations in fractional-order congestion control systems. The superiorities of the fractional-order PD controller over the fractional-order congestion control system are obvious. The onset of Hopf bifurcations of fractional-order congestion control system is adjustable; namely, the stability domain of the system is flexible. Thus, by choosing proper values of control parameters, fractional-order congestion control systems will work stably even under strict conditions. Moreover, the fractional-order PD controller is more universal than its conventional integer-order counterpart, due to its flexible fractional-order parameter. Therefore, investigating the effects of the fractional-order PD controller over fractional-order dynamic systems is of great value, and fractional-order congestion control systems are such typical fractional-order dynamic systems.

It is also worth mentioning that the problems of bifurcation control in fractional-order dynamical systems have been investigated recently [47,48,49]. A novel incommensurate fractional-order predator–prey system with time delay was discussed in [48], and the investigation showed that time delay can heavily influence the dynamics of the proposed system and each order has a major influence on the creation of bifurcation simultaneously. Chen et al. [47] successfully applied an innovative bifurcation control method by using a weakly fractional-order feedback controller to eliminate the stochastic jump in the forced response for a bounded noise excited Duffing oscillator. A dynamic state feedback was applied to control Hopf bifurcations arising from a fractional-order Van Der Pol oscillator, the stability domain is extended, and the system possesses the stability in a larger parameter range [49]. Although some results have emerged, the bifurcation characteristics of controlled systems and the effects of bifurcation control are far from totally understood. In addition, many kinds of dynamic systems and bifurcation control methods have not been covered yet. Thus, bifurcation control in fractional-order dynamical systems is still an open problem. In this paper, we extend the conventional PD controller into a novel fractional-order PD controller and use it to control the bifurcations of a category of fractional-order congestion control systems. To the best of the authors’ knowledge, such bifurcation control method has not been reported.

This paper is dedicated to studying the stability and bifurcation control in a delayed fractional-order congestion control system under the fractional-order PD controller. Some conditions of the stability and Hopf bifurcation are derived where the communication delay is chosen as a bifurcation parameter. Then, for the controlled fractional-order model, we identify the critical value where a Hopf bifurcation occurs and a family of oscillations bifurcate from the equilibrium. It is also shown that, by choosing proper control parameters in our fractional-order PD controller, the critical value can be adjusted in a large area and the stability domain for the controlled system is flexible. Thus, the original fractional-order congestion control system is improved in dynamic behaviors.

The paper is organized as follows. Section 2 presents some preliminaries and some pioneering results. The target congestion control system and some pioneering results about it are introduced in Sect. 3. In Sect. 4, a fractional-order PD controller is designed and the controlled system is studied in respect of the stability and Hopf bifurcation, where the stability condition is derived and the existence of Hopf bifurcation is proved. Section 5 provides some numerical results to verify the effectiveness of the controller. Finally, some conclusions are drawn in Sect. 6.

2 Preliminaries

It is known that three main fractional derivative definitions have been proposed, including the Riemann–Liouville fractional derivative, the Grunwald–Letnikov fractional derivative, and the Caputo fractional derivative [34]. Considering that the Caputo fractional derivative only needs initial conditions which can be easily obtained in physical situations, it is more applicable in engineering. Therefore, we discuss the Caputo fractional derivative merely.

The Caputo derivative can be defined as follows:

$$\begin{aligned} { }_a^C D_t^\alpha f\left( t \right) =\frac{1}{\Gamma \left( {n-\alpha } \right) }\int _a^t {\left( {t-\tau } \right) } ^{n-\alpha -1}f^{\left( n \right) }\left( \tau \right) \mathrm{d}\tau , \end{aligned}$$
(1)

where \(n-1<\alpha \le n,n\in N\) and \(\Gamma \left( \cdot \right) \) is the Gamma function. The value of the fractional order is denoted by \(\alpha \) and is generally in the domain of \(\left( {0,1} \right] \) in engineering.

Deng et al. [50] introduced a category of n-dimensional linear fractional-order systems with multiple time delays which can be expressed as follows:

$$\begin{aligned} \frac{\mathrm{d}^{\alpha _1}x_{1}}{\mathrm{d}t^{\alpha _1}}= & {} a_{11}x_{1}\left( t-\tau _{11}\right) +a_{12}x_{2}\left( t-\tau _{12}\right) +\ldots \nonumber \\&\quad +\,a_{1n}x_{n}\left( t-\tau _{1n}\right) ,\nonumber \\ \frac{\mathrm{d}^{\alpha _2}x_{2}}{\mathrm{d}t^{\alpha _2}}= & {} a_{21}x_{1}\left( t-\tau _{21}\right) +a_{22}x_{2}\left( t-\tau _{22}\right) +\ldots \nonumber \\&\quad +\,a_{2n}x_{n}\left( t-\tau _{2n}\right) ,\nonumber \\ \frac{\mathrm{d}^{\alpha _n}x_{2}}{\mathrm{d}t^{\alpha _n}}= & {} a_{n1}x_{1}\left( t-\tau _{n1}\right) +a_{n2}x_{2}\left( t-\tau _{n2}\right) +\ldots \nonumber \\&\quad +\,a_{nn}x_{n}\left( t-\tau _{nn}\right) , \end{aligned}$$
(2)

where \(0<\alpha _i \le 1\) for \(i=1,2,\ldots ,n,\) and the notation \(\mathrm{d}^{\alpha _i }/\mathrm{d}t^{\alpha _i }\) is chosen as the Caputo fractional derivative (1). We choose the initial values \(x_i \left( t \right) =\varphi _i \left( t \right) \) in the domain \(-\tau _{\max } \le t\le 0,i=1,2,\ldots ,n,\) where \(\tau _{\max } =\mathop {\max }\limits _{1\le i,j\le n} \left\{ {\tau _{ij} } \right\} \). The associated characteristic equation for system (2) is displayed as follows:

$$\begin{aligned} \det \left( \! {{\begin{array}{llll} {s^{\alpha _1 }-a_{11} e^{-s\tau _{11} }}&{}\quad {-a_{12} e^{-s\tau _{12} }}&{}\quad \cdots &{}\quad {-a_{1n} e^{-s\tau _{1n} }} \\ {-a_{21} e^{-s\tau _{21} }}&{}\quad {s^{\alpha _2 }-a_{22} e^{-s\tau _{22} }}&{}\quad \cdots &{}\quad {-a_{2n} e^{-s\tau _{2n} }} \\ \quad \vdots \quad &{}\quad \vdots \quad &{}\quad \ddots \quad &{}\quad \quad \vdots \\ {-a_{n1} e^{-s\tau _{n1} }}&{}\quad {-a_{n2} e^{-s\tau _{n2} }}&{}\quad \cdots &{}\quad {s^{\alpha _n }-a_{nn} e^{-s\tau _{nn} }} \\ \end{array} }} \!\right) =0. \end{aligned}$$
(3)

Then, we state some stability results for (2) obtained in [50].

Theorem 1

([50]) Given that all the roots of the characteristic equation (3) have negative real parts, the zero solution of system (2) is Lyapunov globally asymptotically stable.

Corollary 1

([50]) Suppose that \(\tau _{ij} =0,i,j=1,2,\ldots ,n\) and \(\alpha _i =\alpha \in \left( {0,1} \right] ,i=1,2,\ldots ,n.\) If \(\left| {\arg \left( \lambda \right) } \right| >\alpha \pi /2\) is satisfied for all roots of the characteristic equation \(\det \left( {\lambda I-A} \right) =0\) , the zero solution of system (2) is Lyapunov globally asymptotically stable, where \(A=(a_{ij} )_{n\times n}\) is the coefficient matrix and \(\lambda =s^{\alpha }.\)

Corollary 2

([50]) Given \(\alpha _i =\alpha \in \left( {0,1} \right] \). If all the characteristic equation (3) has no purely imaginary roots for any \(\tau _{ij} >0,i,j=1,2,\ldots ,n\) and \(\left| {\arg \left( \lambda \right) } \right| >\alpha \pi /2\) is satisfied for all the eigenvalues \(\lambda s\) of A, then the zero solution of system (2) is Lyapunov globally asymptotically stable.

Although the conclusions for Hopf bifurcations in integer-order dynamical systems are well known, we cannot simply extend most of them to fractional-order systems due to huge substantial differences between these two kinds of systems. Since most corresponding investigations have been made only based on numerical simulations, the Hopf bifurcation theory for fractional-order dynamical systems is still an open problem. Next, we will introduce some conditions of Hopf bifurcation for a typical n-dimensional fractional-order system with the time delay as a bifurcation parameter.

Theorem 2

([35]) Consider the following system:

$$\begin{aligned} \frac{\mathrm{d}^{\alpha }x_i }{\mathrm{d}t^{\alpha }}=f_i \left( {x_1 ,x_2 ,\ldots ,x_n ;\tau } \right) ,{}{}{}{}{}{}{}i=1,2,\ldots ,n, \end{aligned}$$
(4)

where \(0<\alpha \le 1\) and the time delay \(\tau \ge 0\). A Hopf bifurcation will occur at the equilibrium when \(\tau =\tau _0 \) if the following conditions are satisfied:

  1. (1)

    The inequality \(\left| {\arg \left( \lambda \right) } \right| >\alpha \pi /2\) is satisfied for all the eigenvalues of the coefficient matrix of the linearized system of (4).

  2. (2)

    The characteristic equation of system (4) has a purely imaginary root \(\pm i\omega \) when \(\tau =\tau _0 .\)

  3. (3)

    The transversality condition \([\mathrm{dRe}(s(\tau ))/\mathrm{d}\tau ]_{\tau =\tau _0} >0\) is satisfied, where \(\mathrm{Re}(\cdot )\) represents the real part of the complex eigenvalue.

3 Model descriptions

As a kind of congestion mechanisms, the dual algorithms have been analyzed in many aspects, involving the stability and bifurcations. It is noted that a typical fair dual congestion control model was introduced in [17], which can be represented as the following differential equation:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}p\left( t \right) =\kappa p\left( t \right) \left( {x\left( {t-\tau } \right) -C} \right) , \end{aligned}$$
(5)

where the variable p represents the price at the link, \(\tau \) is the communication delay, \(\kappa >0\) is the gain parameter and the scalar C is the capacity. Additionally, \(x\left( t \right) =D\left( {p\left( t \right) } \right) \) is a nonnegative continuous, strictly decreasing demand function.

The integer-order system (5) has been investigated by some scholars from the aspects of stability and bifurcations in past few years [17, 18, 30]. Choosing the non-dimensional parameter \(\kappa \) as the bifurcation parameter, Raina [17] studied the local stability and Hopf bifurcation for the integer-order system (5). Some conditions of the stability and Hopf bifurcation were obtained, and the direction of Hopf bifurcations was determined. The local Hopf bifurcation for system (5) was also analyzed when the communication delay \(\tau \) was selected as the bifurcation parameter [18]. It was shown that when \(\tau \) passes through a threshold, system (5) loses its stability and a Hopf bifurcation occurs.

It is also noted that some control strategies will help improve the characteristics of system (5), such as delaying the occurrence of Hopf bifurcations and extending the stability domain. Applying a hybrid control strategy, Ding et al. [30] investigated the local Hopf bifurcation for the controlled congestion system and the effectiveness of the hybrid controller was validated.

Substituting the fractional-order Caputo derivative (1) for the usual integer-order derivative, the integer-order congestion system (5) was extended into the following fractional-order congestion system:

$$\begin{aligned} \frac{\mathrm{d}^{\alpha }p\left( t \right) }{\mathrm{d}t^{\alpha }}=\kappa p\left( t \right) \left( {x\left( {t-\tau } \right) -C} \right) , \end{aligned}$$
(6)

where \(\alpha \in \left( {0,1} \right] \) and other system parameters share the same meanings with those in system (5). It easy to see that system (6) has a nonzero equilibrium \(p^{*}\) satisfying the following equation:

$$\begin{aligned} D(p^{*})=C. \end{aligned}$$

It should be mentioned that the fractional-order system (6) has the same equilibrium to that of the integer-order system (5).

Theorem 3

([35]) The equilibrium \(p^{*}\) of system (6) is Lyapunov asymptotically stable if the following condition holds:

$$\begin{aligned} \left[ {-\kappa p^{*}{D}'\left( {p^{*}} \right) } \right] ^{1/\alpha }\ne \frac{1}{\tau }\left[ {\left( {2k+1} \right) \pi -\alpha \pi /2} \right] , \end{aligned}$$

where \(k\in \mathrm{Z}.\)

Theorem 4

([35]) The equilibrium \(p^{*}\) of system (6) is asymptotically stable when \(\tau \in \left[ {0,\tau _0 } \right) \) and is unstable if \(\tau >\tau _0 \). A Hopf bifurcation occurs at the equilibrium \(p^{*}\) when \(\tau =\tau _0 \). Here,

$$\begin{aligned} \tau _0 =\frac{\left( {1-\alpha /2} \right) \pi }{\left[ {-\kappa p^{*}{D}'\left( {p^{*}} \right) } \right] ^{1/\alpha }}, \end{aligned}$$

and \(\tau _0 \) is the critical value of the communication delay for system (6).

4 Analysis for controlled system via a fractional-order PD controller

In this section, a novel fractional-order PD control strategy is used to control the bifurcation in the fractional-order system (6). It is worth mentioning that when it comes to engineering, the fractional-order derivative part in an electronic circuit is usually realized by a generalized capacitor called fractance [51]. Using this method, we can freely adjust the controller to improve the parameters and characteristics of the controlled systems. For the convenience of calculation, we will use the fractional order \(\alpha \) of system (6) to set the fractional order of the differentiator. Then, we will study the stability and Hopf bifurcation for the controlled model.

For the delayed fractional-order system (6), we propose a fractional-order PD controller with single input and single output as follows:

$$\begin{aligned} u=k_p \left( {p\left( t \right) -p^{*}} \right) +k_d \frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}\left( {p\left( t \right) -p^{*}} \right) , \end{aligned}$$
(7)

where \(k_p \) is the proportional control parameter and \(k_d \) is the derivative control parameter.

Remark 1

It is known that a traditional PD control scheme usually consists of a proportional term, which is related to the current error value, and a derivative term, which helps limit the high-frequency gain and noise. In this paper, we choose \(k_p <1\) and \(k_d <1\) as [40].

Applying the fractional-order PD controller (7) to the fractional-order congestion system (6), we get the controlled fractional-order system as follows:

$$\begin{aligned} \frac{\mathrm{d}^{\alpha }p\left( t \right) }{\mathrm{d}t^{\alpha }}= & {} \kappa p\left( t \right) \left( {x\left( {t-\tau } \right) -C} \right) +k_p \left( {p\left( t \right) -p^{*}} \right) \\&\quad +\,k_d \frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}\left( {p\left( t \right) -p^{*}} \right) , \end{aligned}$$

which is equivalent to

$$\begin{aligned} \frac{\mathrm{d}^{\alpha }p\left( t \right) }{\mathrm{d}t^{\alpha }}= & {} \frac{1}{1-k_d }\left[ \kappa p\left( t \right) \left( {x\left( {t-\tau } \right) -C} \right) \right. \nonumber \\&\quad \left. +\,k_p \left( {p\left( t \right) -p^{*}} \right) \right] . \end{aligned}$$
(8)

Remark 2

It is obvious that in the controlled fractional-order system (8), the application of the controller will not carry an influence in the equilibrium, which is still located in \(p^{*}\). Thus, the bifurcation control can be realized without destroying the properties of the original system (6).

Remark 3

Although various controllers have been designed for the problems of the bifurcation control in integer-order systems [21, 24], only few control schemes have been reported to control the bifurcations embedded in fractional-order systems [3]. In this paper, we have first introduced a novel fractional-order PD controller to improve the bifurcation characteristics of the fractional-order congestion control system (6).

4.1 Stability analysis

Letting \(u\left( t \right) =p\left( t \right) -p^{*}\), we can expand (8) by the Taylor expansion around the equilibrium point \(p^{*}\), and obtain the corresponding linear equation:

$$\begin{aligned} \frac{\mathrm{d}^{\alpha }u}{\mathrm{d}t^{\alpha }}=\frac{1}{1-k_d }\left( {k_p u\left( t \right) +\kappa p^{*}{D}'\left( {p^{*}} \right) u\left( {t-\tau } \right) } \right) ,\nonumber \\ \end{aligned}$$
(9)

whose characteristic equation is

$$\begin{aligned} s^{\alpha }-\frac{1}{1-k_d }\left( {k_p +\kappa p^{*}{D}'\left( {p^{*}} \right) e^{-s\tau }} \right) =0. \end{aligned}$$
(10)

Then, let us make the following hypothesis:

\((\hbox {H}_{1}): k_p <\kappa p^{*}{D}'\left( {p^{*}} \right) .\)

Theorem 5

If (H\(_{1}\)) holds, then the equilibrium \(p^{*}\) of the controlled fractional-order system (8) is Lyapunov asymptotically stable.

Proof

Let \(s=i\omega =\omega \left( {\cos \frac{\pi }{2}+i\sin \frac{\pi }{2}} \right) \left( {\omega >0} \right) \) be a root of (10). We can get

$$\begin{aligned}&\omega ^{\alpha }\left( {\cos \frac{\alpha \pi }{2}+i\sin \frac{\alpha \pi }{2}} \right) \nonumber \\&\quad -\,\frac{1}{1-k_d }\left( k_p +\kappa p^{*}{D}'\left( {p^{*}} \right) \left( \cos \left( {\omega \tau } \right) \right. \right. \nonumber \\&\quad \left. \left. -\,i\sin \left( {\omega \tau } \right) \right) \right) =0. \end{aligned}$$
(11)

Separating the real and imaginary parts, we get

$$\begin{aligned} \omega ^{\alpha }\cos \frac{\alpha \pi }{2}-a_1= & {} a_2 \cos \omega \tau , \nonumber \\ \omega ^{\alpha }\sin \frac{\alpha \pi }{2}= & {} -a_2 \sin \omega \tau , \end{aligned}$$
(12)

where

$$\begin{aligned} a_1 =\frac{k_p }{1-k_d },a_2 =\frac{\kappa p^{*}{D}'\left( {p^{*}} \right) }{1-k_d }. \end{aligned}$$

Taking square on both sides of (12) and summing up the results, we obtain

$$\begin{aligned} \left( {\omega ^{\alpha }} \right) ^{2}-2a_1 \cos \frac{\alpha \pi }{2}\cdot \omega ^{\alpha }+a_1^2 -a_2^2 =0. \end{aligned}$$
(13)

Note that \(\kappa>0,p^{*}>0,{D}'\left( {p^{*}} \right) <0.\) This implies that \(a_1^2 -a_2^2 >0\) and \(a_1 \cos \frac{\alpha \pi }{2}<0\) when (H\(_{1})\) holds. Thus, (13) has no positive roots, meaning that (10) has no purely imaginary roots with positive imaginary parts.\(\square \)

Similarly, (10) has no purely imaginary roots with negative imaginary parts under the hypothesis (H\(_{1})\). Therefore, if (H\(_{1})\) holds, then the characteristic equation (10) has no purely imaginary roots.

On the other side, it is obvious that when (H\(_{1})\) holds, the coefficient matrix of the linearized system (9) has one eigenvalue \(\lambda =\frac{1}{1-k_d }\left( {k_p +\kappa p^{*}{D}'\left( {p^{*}} \right) } \right) <0,\) which satisfies \(\left| {\arg \left( \lambda \right) } \right| >\alpha \pi /2.\)

Then, using Corollary 2, we obtain that the equilibrium \(p^{*}\) of system (8) is Lyapunov asymptotically stable.

For the illustration of Theorem 5, according to [35] and [40], we suppose \(D\left( p \right) =1/p\) and choose the parameters \(\kappa =0.01,C=50,k_p =-0.8,k_d =-0.5,\) and \(\tau =1.\) Then, we have the equilibrium \(p^{*}=0.02\) and \(\kappa p^{*}{D}'\left( {p^{*}} \right) =-0.5.\) Obviously, (H\(_{1})\) is satisfied. Figure 1 shows that the state \(p\left( t \right) \) of the controlled fractional-order system (8) is asymptotically converging to the equilibrium \(p^{*}.\)

Fig. 1
figure 1

Waveform plot of \(p\left( t \right) \) in the controlled system (8) with \(\kappa =0.01,C=50,D\left( p \right) =1/p,k_p =-0.8,k_d =-0.5,\) and \(\tau =1.\) The equilibrium \(p^{{*}}\)is asymptotically stable

Full size image

4.2 Hopf bifurcation

Generally speaking, the Hopf bifurcation refers to the phenomena that a limit cycle emerges from an equilibrium and the stability of the equilibrium changes. The analysis for Hopf bifurcation can be operated by choosing different parameters, and we will select the time delay as the bifurcation parameter for the controlled fractional-order system (8).

We make the following hypothesis:

(H\(_{2})\): \(\left| {k_p } \right| <-\kappa p^{*}{D}'\left( {p^{*}} \right) \).

Lemma 1

If (H\(_{2}\)) holds and \(\tau =\tau _k^c ,k=0,1,2\ldots \), then the characteristic equation (10) has a pair of purely imaginary roots \(\pm i\omega _0^c \left( {\omega _0^c >0} \right) \), where

$$\begin{aligned} \omega _0^c= & {} \left( {a_1 \cos \frac{\alpha \pi }{2}+\sqrt{a_2^2 -a_1^2 \sin ^{2}\frac{\alpha \pi }{2}}} \right) ^{1/\alpha }, \nonumber \\ \tau _k^c= & {} \frac{1}{\omega _0^c }\left( \arccos \left( {\frac{\left( {\omega _0^c } \right) ^{\alpha }\cos \frac{\alpha \pi }{2}-a_1 }{a_2 }} \right) +2k\pi \right) ,\nonumber \\ \end{aligned}$$
(14)

where \(\tau _k^c \) is the critical value of the communication delay for system (8) and \(\tau _0^c \) is the smallest positive value of \(\tau _k^c \) in particular, name \(\tau _0^c \hbox {=}\left. {\tau _k^c } \right| _{k=0} .\)

Proof

Based on the discussion in the stability analysis, we can figure out that if (H\(_{2})\) holds, which means that \(a_1^2 -a_2^2 <0\), (13) has at least one positive root. This indicates that the characteristic equation (10) has a pair of purely imaginary roots.

Solving (13) gives

$$\begin{aligned} \omega _0^c =\left( {a_1 \cos \frac{\alpha \pi }{2}+\sqrt{a_2^2 -a_1^2 \sin ^{2}\frac{\alpha \pi }{2}}} \right) ^{1/\alpha }. \end{aligned}$$

Then, it follows from (12) that

$$\begin{aligned} \tau _k^c =\frac{1}{\omega _0^c }\left( {\arccos \left( {\frac{\left( {\omega _0^c } \right) ^{\alpha }\cos \frac{\alpha \pi }{2}-a_1 }{a_2 }} \right) +2k\pi } \right) . \end{aligned}$$

\(\square \)

Remark 4

Lemma 1 demonstrates that condition (2) of Hopf bifurcations in Theorem 2 is satisfied for the controlled fractional-order system (8).

In what follows, we need to check the transversality condition of Hopf bifurcations.

Lemma 2

Let \(h=\left( {1-k_d } \right) \left( {\omega _0^c } \right) ^{\alpha }+k_p \sin \left( {\alpha -1} \right) \frac{\pi }{2}\). The following results hold:

  1. (1)

    If \(\kappa p^{*}{D}'\left( {p^{*}} \right) <k_p \le 0\),    then \(h>0.\)

  2. (2)

    If \(0<k_p <-\frac{1}{2}\kappa p^{*}{D}'\left( {p^{*}} \right) \),    then \(h\ne 0.\)

  3. (3)

    If \(-\frac{1}{2}\kappa p^{*}{D}'\left( {p^{*}} \right)<k_p <-\kappa p^{*}{D}'\left( {p^{*}} \right) \) , the sign of h depends on the values of \(\alpha ,k_d \) and \(k_p .\)

Proof

Notice that \(k_d <1,\omega _0^c >0\) and \(0<\alpha \le 1.\) Therefore, it is easy to see that \(\left( {1-k_d } \right) \left( {\omega _0^c } \right) ^{\alpha }>0\) and \(\sin \left( {\alpha -1} \right) \frac{\pi }{2}\le 0.\)

  1. (1)

    If \(\kappa p^{*}{D}'\left( {p^{*}} \right) <k_p \le 0\), then we have that \(k_p \sin \left( {\alpha -1} \right) \frac{\pi }{2}\ge 0.\) Thus, h is positive.

  2. (2)

    Supposing that \(h=0\), we obtain \(\left( {\omega _0^c } \right) ^{\alpha }=-k_p \sin \left( {\alpha -1} \right) \frac{\pi }{2}/{\left( {1-k_d } \right) }\). By substituting \(\left( {\omega _0^c } \right) ^{\alpha }\) into (13), we can get that

    $$\begin{aligned}&k_p^2 \left[ 1+\left( {\sin \left( {\alpha -1} \right) \frac{\pi }{2}} \right) \left( \sin \left( {\alpha -1} \right) \frac{\pi }{2}\nonumber \right. \right. \\&\quad \left. \left. +\,2\cos \frac{\alpha \pi }{2} \right) \right] =\left( {\kappa p^{*}{D}'\left( {p^{*}} \right) } \right) ^{2} \end{aligned}$$
    (15)

    It is clear that the left side of (15) falls in \(\left[ {0,4k_p^2 } \right) .\) Moreover, it is known that the right side of (15) belongs to \(\left( {4k_p^2 ,\infty } \right) \) under the condition \(0<k_p <-\frac{1}{2}\kappa p^{*}{D}'\left( {p^{*}} \right) .\) This is contradictory. Hence, the conclusion follows.

  3. (3)

    From the proof of conclusion (2) of Lemma 2, it is figured out that if the condition \(-\frac{1}{2}\kappa p^{*}{D}'\left( {p^{*}} \right)<k_p <-\kappa p^{*}{D}'\left( {p^{*}} \right) \) holds, the values of \(\alpha ,k_d ,k_p \) can have an effect on the sign of h. This completes the proof.

Next, we make the following hypothesis:

(H\(_{3})\): \(h=\left( {1-k_d } \right) \left( {\omega _0^c } \right) ^{\alpha }+k_p \sin \left( {\alpha -1} \right) \frac{\pi }{2}>0.\) \(\square \)

Lemma 3

Let \(s\left( \tau \right) =\rho \left( \tau \right) +i\omega \left( \tau \right) \) be the root of (10) satisfying \(\rho \left( {\tau _k^c } \right) =0\) and \(\omega \left( {\tau _k^c } \right) =\omega _0^c >0,k=0,1,2\ldots \). If (H\(_{3}\)) holds, then

$$\begin{aligned} \left. {\frac{{ dRe}\left[ {s\left( \tau \right) } \right] }{{d}\tau }} \right| _{\tau =\tau _k^{c} } >0. \end{aligned}$$

Proof

Substituting \(s\left( \tau \right) \) into (10) and differentiate both sides of the resulting equation with respect to \(\tau ,\) then

$$\begin{aligned} \frac{\mathrm{d}s}{\mathrm{d}\tau }=\frac{-\kappa p^{*}{D}'\left( {p^{*}} \right) se^{-s\tau }}{\alpha \left( {1-k_d } \right) s^{\alpha -1}+\kappa p^{*}{D}'\left( {p^{*}} \right) \tau e^{-s\tau }}. \end{aligned}$$

Note that \(s\left( \tau \right) =\rho \left( \tau \right) +i\omega \left( \tau \right) =r\left( {\cos \theta +i\sin \theta } \right) \) is the root of (10). Thus

$$\begin{aligned}&\frac{\mathrm{d}s}{\mathrm{d}\tau } =\frac{-\kappa p^{*}{D}'\left( {p^{*}} \right) \left( {\rho +i\omega } \right) e^{-\rho \tau }\left[ {\cos \left( {\omega \tau } \right) -i\sin \left( {\omega \tau } \right) } \right] }{\alpha \left( {1-k_d } \right) \left( {\rho +i\omega } \right) ^{\alpha -1}+\kappa p^{*}{D}'\left( {p^{*}} \right) \tau e^{-\rho \tau }\left[ {\cos \left( {\omega \tau } \right) -i\sin \left( {\omega \tau } \right) } \right] }. \end{aligned}$$

Then, it follows that

$$\begin{aligned} \frac{\mathrm{dRe}\left[ {s\left( \tau \right) } \right] }{\mathrm{d}\tau }= & {} -\kappa p^{*}{D}'\left( {p^{*}} \right) e^{-\rho \tau }\\&\times \frac{P\left( \tau \right) M\left( \tau \right) +Q\left( \tau \right) N\left( \tau \right) }{M^{2}\left( \tau \right) +N^{2}\left( \tau \right) }, \end{aligned}$$

where

$$\begin{aligned} P\left( \tau \right)= & {} \rho \cos \left( {\omega \tau } \right) +\omega \sin \left( {\omega \tau } \right) , \\ Q\left( \tau \right)= & {} \omega \cos \left( {\omega \tau } \right) -\rho \sin \left( {\omega \tau } \right) ,\\ M\left( \tau \right)= & {} \alpha \left( {1-k_d } \right) r^{\alpha -1}\cos \left[ {\left( {\alpha -1} \right) \theta } \right] \\&\quad +\,\kappa p^{*}{D}'\left( {p^{*}} \right) \tau e^{-\rho \tau }\cos \left( {\omega \tau } \right) , \\ N\left( \tau \right)= & {} \alpha \left( {1-k_d } \right) r^{\alpha -1}\sin \left[ {\left( {\alpha -1} \right) \theta } \right] \\&\quad -\,\kappa p^{*}{D}'\left( {p^{*}} \right) \tau e^{-\rho \tau }\sin \left( {\omega \tau } \right) . \end{aligned}$$

When \(\tau =\tau _k^c \), it is easy to obtain

$$\begin{aligned}&\left. {\frac{\mathrm{dRe}\left[ {s\left( \tau \right) } \right] }{\mathrm{d}\tau }} \right| _{\tau =\tau _k^c } \\&\quad =\alpha \left( {1-k_d } \right) \left( {\omega _0^c } \right) ^{\alpha }\frac{\left( {1-k_d } \right) \left( {\omega _0^c } \right) ^{\alpha }+k_p \sin \left( {\alpha -1} \right) \frac{\pi }{2}}{M^{2}\left( {\tau _k^c } \right) N^{2}\left( {\tau _k^c } \right) }. \end{aligned}$$

Combining the hypothesis (H\(_{3})\), \(\alpha>0,\left( {\omega _0^c } \right) ^{\alpha }>0\) and \(1-k_d >0\), we obtain

$$\begin{aligned} \left. {\frac{{dRe}\left[ {s\left( \tau \right) } \right] }{{d}\tau }} \right| _{\tau =\tau _k^{c} } >0. \end{aligned}$$

\(\square \)

Remark 5

Lemma 3 illustrates that condition (3) of Hopf bifurcations in Theorem 2 is satisfied for the controlled fractional-order system (8).

Theorem 6

If (H\(_{2}), (H_{3}\)) hold, the following statements are true for the controlled fractional-order congestion system (8):

  1. (1)

    For \(\tau \in \left[ {0,\tau _0^c } \right) \) , the equilibrium \(p^{*}\) of system (8) is asymptotically stable.

  2. (2)

    For \(\tau >\tau _0^c \) , the equilibrium \(p^{*}\) of system (8) is unstable.

  3. (3)

    When \(\tau =\tau _0^c \) , system (8) undergoes a Hopf bifurcation at the equilibrium \(p^{*}.\)

Proof

  1. (1)

    It is easy to see that when \(\tau =0\), all the roots of (10) have negative real parts. It follows from Lemma 1 that all the roots of (10) also have negative real parts for \(\tau \in \left[ {0,\tau _0^c } \right) .\) Thus, the equilibrium \(p^{*}\) of system (8) is stable.

  2. (2)

    The conclusion in Lemma 3 implies that if (H\(_{3})\) holds, then (10) has at least one root with positive real part when \(\tau >\tau _0^c .\) So, the equilibrium \(p^{*}\) of system (8) is unstable.

  3. (3)

    Since the coefficient matrix of the linearized system (9) has the eigenvalue \(\lambda =\left[ {k_p +\kappa p^{*}{D}'\left( {p^{*}} \right) } \right] /(1-k_d )<0\) when (H\(_{2})\) holds, the inequality \(\left| {\arg \left( \lambda \right) } \right| >\alpha \pi /2\) follows. Therefore, condition (1) of Hopf bifurcations in Theorem 2 is reached for the controlled fractional-order system (8). From Lemmas 1 and 3, conditions (2) and (3) of Hopf bifurcations in Theorem 2 are also satisfied for the controlled fractional-order system (8). Thus, system (8) undergoes a Hopf bifurcation at the equilibrium \(p^{*}\) when \(\tau =\tau _0^c .\) \(\square \)

Remark 6

Equation (14) gives that the critical value \(\tau _0^c \) of the controlled fractional-order congestion system (8) that varies with the control parameters \(k_d \) and \(k_p\). Accordingly, the effectiveness of the fractional-order PD controller on the dynamic behaviors of system (8) is validated; namely, the fractional-order congestion control system (8) will maintain a stationary sending rate in a flexible domain of the communication delay.

Remark 7

Theorem 6 shows that the onset of Hopf bifurcations of the original fractional-order congestion control system (6) has been changed by the fractional-order PD controller. Therefore, the fractional-order PD controller has successfully realize the aim of bifurcation control.

Remark 8

Apart from the time delay, some other parameters in system (8) also play an important role in affecting the system’s dynamic characteristics. Thus, they can be also selected as the bifurcation parameters, such as the fractional order \(\alpha \) and the gain parameter \(\kappa .\)

Fig. 2
figure 2

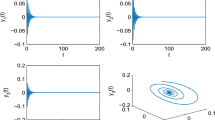
Waveform plot and phase portrait of the controlled fractional-order system (8) with \(\kappa =0.01,C=50,D(p)=1/p,\alpha \)=0.92,  and \(k_p =-0.1,k_d =-0.2.\) The equilibrium \(p^{{*}}\) is asymptotically stable, where \(\tau =4.5<\tau _0^c =5.1626\)

Full size image
Fig. 3
figure 3

Waveform plot and phase portrait of the controlled fractional-order system (8) with \(\kappa =0.01,C=50,D(p)=1/p,\alpha =0.92,\) and \(k_p =-0.1,k_d =-0.2.\) A periodic oscillation bifurcates from the equilibrium \(p^{{*}},\) where \(\tau =5.3>\tau _0^c =5.1626\)

Full size image
Fig. 4
figure 4

Waveform plot and phase portrait of the controlled fractional-order system (8) with \(\kappa =0.01,C=50,D(p)=1/p,\alpha =0.92,\) and \(k_p =0.1,k_d =0.2.\) The equilibrium \(p^{{*}}\) is asymptotically stable, where \(\tau =2.3<\tau _0^c =\hbox {2.4807}\)

Full size image
Fig. 5
figure 5

Waveform plot and phase portrait of the controlled fractional-order system (8) with \(\kappa =0.01,C=50,D(p)=1/p,\alpha \)=0.92,  and \(k_p =0.1,k_d =0.2.\) A periodic oscillation bifurcates from the equilibrium, where \(\tau =2.7>\tau _0^c =\hbox {2.4807}\)

Full size image

5 Numerical simulations

This section will provide some numerical results to illustrate the analytical results obtained in the previous section and validate the effectiveness of the fractional-order PD controller.

For the purpose of comparison, we choose the same parameters \(\kappa =0.01,C=50, \) and the proportional fairness \(D\left( p \right) =1/p\) used in [18, 35, 52]. Then, the controlled fractional-order congestion system (8) has a unique nonzero equilibrium \(p^{*}=0.02,\) which is the same as that of the uncontrolled system (6). By a simple calculation, we have \(\kappa p^{*}{D}'\left( {p^{*}} \right) =-0.5.\)

We will show the dynamics of Hopf bifurcation for the controlled fractional-order congestion system (8) when \(\alpha \in \left( {0,1} \right] .\) For a consistent comparison, we will take \(\alpha =0.92\) for an example, which is used in [35].

Now, we will use our fractional-order PD scheme with two different control parameters to control the Hopf bifurcation of the controlled fractional-order system (8) and observe the change of the bifurcation characteristics.

Firstly, we choose the fractional-order PD controller (7) with \(k_p =-0.1,k_d =-0.2\) (\(k_p<0,k_d <0\) in order to delay the bifurcation [40]). It follows from (14) that

$$\begin{aligned} \tau _0^c =5.1626,\omega _0^c =0.3673. \end{aligned}$$

It is easy to verify that conditions (H\(_{2})\) and (H\(_{3})\) are satisfied under the controller (7) with \(k_p =-0.1,k_d =-0.2.\) By Theorem 6, the equilibrium \(p^{*}\) of the controlled system (8) is stable when \(\tau =4.5<\tau _0^c \) (see Fig. 2), while \(p^{*}\) loses its stability when \(\tau =5.3>\tau _0^c \) (see Fig. 3). Therefore, the controlled system (8) generates a Hopf bifurcation at the equilibrium \(p^{*}\) when \(\tau \) is increased over the critical value \(\tau _0^c .\)

Secondly, we choose the fractional-order PD controller (7) with \(k_p =0.1,k_d =0.2\) (\(0<k_p<1,0<k_d <1\) in order to advance the Hopf bifurcation [40]) for the controlled fractional-order system (8). From (14), we have

$$\begin{aligned} \tau _0^c =\hbox {2.4807},\omega _0^c =\hbox {0.6034.} \end{aligned}$$

Under the controller parameters \(k_p =0.1,k_d =0.2, \) conditions (H\(_{2})\) and (H\(_{3})\) hold. Figures 4 and 5 display the dynamical behaviors of system (8). From Theorem 6, it is illustrated that the equilibrium \(p^{*}\) of the controlled system (8) is stable when \(\tau =2.3<\tau _0^c \) (see Fig. 4), while \(p^{*}\) loses its stability and a Hopf bifurcation occurs when \(\tau =2.7>\tau _0^c \) (see Fig. 5). Based on the results discussed above, Theorem 6 is verified to be correct.

Fig. 6
figure 6

Waveform plots of the uncontrolled integer-order system (5) (left) and the controlled integer-order system (16) (right) when \(4.3409=\tau _0^c>\tau =4>\tau _0 =3.1416,\) where \(\kappa =0.01,C=50,D(p)=1/p,\) and \(k_p =-0.1,k_d =-0.2\)

Full size image
Fig. 7
figure 7

Waveform plots of the uncontrolled integer-order system (5) (left) and the controlled integer-order system (16) (right) when \(2.2363=\tau _0^c<\tau =2.6<\tau _0 =3.1416,\) where \(\kappa =0.01,C=50,D(p)=1/p,\) and \(k_p =0.1,k_d =0.2\)

Full size image

Next, we will examine the effectiveness of the fractional-order PD control strategy in changing the onset of Hopf bifurcations. For the uncontrolled fractional-order system (6) with \(\kappa =0.01,C=50, D\left( p \right) =1/p,\) and \(\alpha =0.92,\) it follows from Theorem 4 that

$$\begin{aligned} \tau _0 =3.6037,\omega _0 =0.4708. \end{aligned}$$

It can be seen that under the action of the fractional-order PD control, the bifurcation characteristics of the original fractional-order congestion system (6) have been changed. Specifically, the fractional-order PD controller (7) with \(k_p =-0.1,k_d =-0.2\) increases the critical value \(\tau _0 \) from 3.6037 to 5.1626, which implies that the onset of Hopf bifurcation is delayed and the stability domain of the original fractional-order system (6) is expanded, while the fractional-order PD controller (7) with \(k_p =0.1,k_d =0.2\) decreases the critical value \(\tau _0 \) from 3.6037 to 2.4807, which means that the onset of Hopf bifurcation is advanced and the stability region of the original fractional-order system (6) is reduced. It is observed that when \(5.1626=\tau _0^c>\tau >\tau _0 =3.6037,\) the equilibrium \(p^{*}\) of the uncontrolled fractional-order system (6) is unstable and a Hopf bifurcation occurs early (see Fig. 6 in [35]), while the equilibrium \(p^{*}\) of the controlled system (8) remains stable under the control parameters \(k_p =-0.1,k_d =-0.2\) (see Fig. 2). Therefore, the stability and the onset of Hopf bifurcations of system (8) have been changed by our fractional-order PD controller; namely, one can efficiently manipulate these dynamic characteristics of system (8) by choosing proper values of the control parameters \(k_p ,k_d \) and the order \(\alpha .\)

Since the proposed fractional-order PD controller (7) with \(\alpha =1\) will degenerate to a normal integer-order PD controller, our fractional-order PD controller is a general case of the integer-order PD controller. Meanwhile, both the uncontrolled fractional-order system (6) and the controlled fractional-order system (8) will become the integer-order counterparts when \(\alpha =1.\)

For the uncontrolled integer-order congestion system (5) with \(\kappa =0.01,C=50, \) and \(D\left( p \right) =1/p, \) the onset of Hopf bifurcation is as follows [18]:

$$\begin{aligned} \tau _0 =\hbox {3.1416, }\quad \omega _0 =\hbox {0.5.} \end{aligned}$$

Moreover, the controlled congestion system (8) can be represented by the following integer-order differential equation:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}p\left( t \right)= & {} \frac{1}{1-k_d }\left[ \kappa p\left( t \right) \left( {x\left( {t-\tau } \right) -C} \right) \right. \nonumber \\&\left. +\,k_p \left( {p\left( t \right) -p^{*}} \right) \right] . \end{aligned}$$
(16)

By choosing the control parameters \(k_p =-0.1,k_d =-0.2\), we can apply (14) to obtain the critical value of system (16):

$$\begin{aligned} \tau _0^c =\hbox {4.3409,}\quad \omega _0^c =\hbox {0.4082.} \end{aligned}$$

Similarly, under the control parameters \(k_p =0.1,k_d =0.2\), the critical value of system (16) can be calculated as follows:

$$\begin{aligned} \tau _0^c =\hbox {2.2363,} \quad \omega _0^c =\hbox {0.6124.} \end{aligned}$$
Fig. 8
figure 8

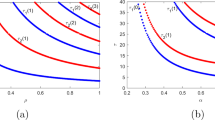
Relationship between \(\tau _0^c \) and \(k_d \) for \(k_p =-0.1,\alpha =0.92\), and \(k_p =-0.1,\alpha =1\) given by the controlled fractional-order system (8) with \(\kappa =0.01,C=50,D(p)=1/p\)

Full size image
Fig. 9
figure 9

Relationship between \(\tau _0^c \) and \(k_p \) for \(k_d =-0.2,\alpha =0.92\), and \(k_d =-0.2,\alpha =1\) given by the controlled fractional-order system (8) with \(\kappa =0.01,C=50,D(p)=1/p\)

Full size image

Figure 6 shows that when \(\tau =4\), the equilibrium \(p^{*}\) of the uncontrolled integer-order congestion system (5) is unstable, while that of the controlled integer-order system (16) is stable. It is demonstrated that the onset of Hopf bifurcation is postponed. From Fig. 7, we observe that when \(\tau =2.6\), the integer-order PD controller with \(k_p =0.1,k_d =0.2\) may advance the onset of Hopf bifurcation.

Fig. 10
figure 10

Relationship between \(\tau _0^c \) and \(\alpha \) for the controlled fractional-order system (8) with \(k_p =-0.1,k_d =-0.2\) and the uncontrolled system (6), both of which have the same system parameters \(\kappa =0.01,C=50,D(p)=1/p\)

Full size image

For the controlled fractional-order system (8) with \(\kappa =0.01,C=50, \) and \(D\left( p \right) =1/p, \) Figs. 8, 9, and 10 visualize the relationships between the critical value \(\tau _0^c \) and the parameters \(k_d ,k_p ,\) and \(\alpha ,\) respectively. To be specific, as the parameter \(k_d ,k_p ,\) or \(\alpha \) increases, respectively, the value of \(\tau _0^c \) decreases. Moreover, some differences of the effectiveness between fractional-order PD controller and conventional PD controller are also illustrated in Figs. 8, 9 and 10. Particularly, our fractional-order PD controller with the control parameters \(k_p =-0.1,k_d =-0.2\) is more effective in delaying the onset of Hopf bifurcations when the fractional order is smaller.

6 Conclusions

In this paper, we have addressed the problem of controlling Hopf bifurcations in fractional-order congestion control systems. Without using conventional bifurcation control methods, we have extended the integer-order PD controller to the fractional-order PD controller and have first applied it to control the Hopf bifurcation of a delayed fractional-order dual model of congestion control algorithms.

Using the communication delay as the bifurcation parameter, we have investigated the stability and Hopf bifurcations for the controlled fractional-order congestion system. Some conditions for the stability are derived for the controlled fractional-order congestion system by using the stability theory of fractional-order systems. It is demonstrated that a Hopf bifurcation will occur at the equilibrium when the communication delay passes through a critical value. It has also been shown that the fractional-order PD controller can successfully control the Hopf bifurcations of fractional-order congestion control system. Concretely, by choosing proper control parameters, one can effectively change the critical value for the communication delay and accordingly postpone or advance the onset of the inherent bifurcation of the original fractional-order congestion system. Therefore, for such a fractional-order congestion control system under our fractional-order PD controller, a stationary sending rate is guaranteed for a larger (or more flexible) domain for the communication delay, due to the variation of the critical value.

Although conventional bifurcation control schemes have been successfully applied in various integer-order dynamic systems, few investigations are reported about the bifurcation control in fractional-order systems. Our future works will focus on the bifurcation control for high-dimensional fractional-order systems using the proposed fractional-order PD control strategy.