1 Introduction

Recently fractional-order systems have attracted increasing interests from scientists and engineers. The essential difference between the fractional-order derivation model and integer-order derivation lies in the following two aspects. First, the integer-order derivative indicates a variation or certain attribute at particular time for a physical or mechanical process, while fractional-order derivative is concerned with the whole time domain. Second, integer-order derivative describes the local properties of a certain position for a physical process, while fractional-order derivative is related to the whole space. It is therefore that many real-world physical systems are well characterized by fractional-order state equations [1–4], for example, fractional-order Schrödinger equation [5] in quantum mechanics, fractional-order oscillator equation [6] in damping vibration, fractional Lotka–Volterra equation [7] in biological systems, fractional Langevin equation [8] in anomalous diffusion and so on. In particularly, stability analysis is one of the most fundamental and important issues for systems. In spite of extensive researches, nonlinear stability of fractional order systems remains a formidable problem. In recent years, there are many results about the stability of fractional-order linear time invariant systems [9–15]. However, only in certain cases or under some special circumstances, the practical problems may be regarded as linear systems. Therefore, research on nonlinear dynamics not only is of great significance, but also has important value in application.

It is well known that the analysis on stability of fractional-order systems is more complex than that of classical differential equations, since fractional derivatives are nonlocal and have weakly singular kernels. Especially, the development on stability of nonlinear fractional-order equations is a bit slow [16]. Up to now, few authors investigated the stability of fractional-order nonlinear system and obtained some useful results. Li et al proposed the definition of Mittag–Leffler stability and introduced the fractional Lyapunov direct method to discuss stability of fractional-order nonlinear systems [17]. Then Sadati et al. [18] and Liu et al. [19] studied Mittag–Leffler stability of the fractional nonlinear delayed systems and fractional nonlinear neutral singular systems, respectively. By using Bihari’s inequality and Bellman–Gronwall’s inequality, rather than Laplace transform and inverse Laplace transform, Delavari et al. presented an extension of Lyapunov direct method for the Caputo type fractional-order nonlinear system [20], which overcome some limitations in [17] and have important values in theory. However, in practice, to select a suitable Lyapunov function and calculate its fractional derivative for fractional-order system are very inconvenient. Wen et al. considered the stability and stabilization of nonlinear fractional-order dynamical systems with fractional-order α:0<α<1 [21]. Deng derived sufficient conditions for the local asymptotical stability of nonlinear fractional-order systems with fractional-order α:0<α<1 [22]. Chen et al. obtained two sufficient criteria on the asymptotical stability and stabilization of a class of fractional-order nonlinear systems with fractional-order α:0<α<1 and α:1<α<2, respectively [23]. Zhao et al. studied the stabilization of nonlinear fractional order dynamic systems [24].

Note that these literatures on the stability of fractional order systems mainly concentrated on fractional-order α belonging to 0<α<1. In fact, not all the fractional differential systems have fractional orders in 0<α<1. There exist fractional-order models described by fractional order α lying in 1<α<2, for example, super-diffusion [25]. However, as far as we know, there are few results on stability and stabilization of fractional-order nonlinear systems with the order α belonging to 1<α<2. [23] obtained sufficient conditions for such asymptotical stability of fractional-order nonlinear systems, but these results are local. Here, by using Mittag–Leffler function, Laplace transform, and the Gronwall inequality, two sufficient conditions for the local and global asymptotic stability and stabilization of a class of fractional-order nonlinear systems with fractional-order α:1<α<2 are presented, respectively.

The remainder of this paper is organized as follows. In Sect. 2, some necessary definitions, lemmas are presented. Main results are proposed in Sect. 3. In Sect. 4, two examples and corresponding numerical simulations are used to illustrate the validity and feasibility of the proposed method. Finally, conclusions are drawn in Sect. 5.

2 Preliminaries

There are some definitions for fractional derivatives. The commonly used definitions are Grunwald–Letnikov (GL), Riemann–Liouville (RL), and Caputo (C) definitions.

Definition 1

The fractional integral (Riemann–Liouville integral) \(D_{t_{0}, t}^{-\alpha}\) with fractional order α∈R + of function x(t) is defined as

$$\begin{aligned} D_{t_0, t}^{-\alpha}x(t)=\frac{1}{\varGamma(\alpha)}\int_{t_0}^t(t- \tau)^{\alpha-1}x(\tau)\,d\tau, \end{aligned}$$
(1)

where Γ(⋅) is the gamma function, \(\varGamma(\tau)= \int_{0}^{\infty}t^{\tau-1}e^{-t}\,dt\).

Definition 2

The Riemann–Liouville derivative of fractional order α of function x(t) is given as

$$\begin{aligned} {}_{RL}D_{t_0,t}^\alpha x(t) & =\frac{d^n}{dt^n}D_{t_0,t}^{-(n-\alpha)} x(t) \\ & =\frac{d^n}{dt^n}\frac{1}{\varGamma(n-\alpha)}\!\int_{t_0}^t(t- \tau)^{n-\alpha-1}x(\tau)\,d\tau, \end{aligned}$$
(2)

where n−1≤α<n∈Z +.

Definition 3

The Caputo derivative of fractional order α of function x(t) is defined as follows:

$$\begin{aligned} \begin{aligned}[b] {}_{C}D_{t_0,t}^\alpha x(t)&=D_{t_0,t}^{-(n-\alpha)}\frac{d^n}{dt^n}x(t) \\ &=\frac{1}{\varGamma(n-\alpha)}\int_{t_0}^t(t- \tau)^{n-\alpha-1}x^{(n)}(\tau)\,d\tau, \end{aligned} \end{aligned}$$
(3)

where n−1≤α<n∈Z +.

The Laplace transform of Caputo fractional derivatives \(_{C}D_{t_{0},t}^{\alpha}x(t)\) is given as follows:

$$\begin{aligned} &\int_0^\infty e^{-st} {_{C}D_{0,t}^\alpha x(t)}\,dt \\ &\quad =s^\alpha X(s)-\sum_{k=0}^{n-1}s^{\alpha -k-1}x^{(k)}(t)\bigg|_{t=0} \\ &\qquad (n-1\leq \alpha<n). \end{aligned}$$
(4)

Grunwald–Letnikov (GL) definition is difference scheme and suitable for numerical calculations, Riemann–Liouville (RL) definition takes the form of differential-integral and plays an important role in theory analysis. Throughout the paper, only the Caputo definition is used since this Laplace transform allows for initial conditions taking the same forms as those for integer-order derivatives, which have clear physical interpretations and have a wide range of applications in the process of factual modeling. The notation \(\frac{d^{\alpha}}{dt^{\alpha}}\) is chosen as the Caputo fractional derivative operator \({}_{C}D_{0,t}^{\alpha}\).

In order to obtain main results, the following definitions and lemmas are presented firstly.

Similar to the exponential function frequently used in the solutions of integer-order systems, a function frequently used in the solutions of fractional order systems is the Mittag–Leffler function.

Definition 4

Mittag–Leffler function is defined as

$$\begin{aligned} E_\alpha(z)=\sum_{k=0}^\infty \frac{z^k}{\varGamma(k\alpha+1)}, \end{aligned}$$
(5)

where α>0 and z∈C.

The Mittag–Leffler function with two parameters appears most frequently and has the following form:

$$\begin{aligned} E_{\alpha,\beta}(z)=\sum_{k=0}^\infty \frac{z^k}{\varGamma(k\alpha+\beta)}, \end{aligned}$$
(6)

where α>0,β>0, and z∈C. When β=1, one has E α (z)=E α,1(z), further, E 1,1(z)=e z.

Moreover, the Laplace transform of Mittag–Leffler function in two parameters is

$$\begin{aligned} \mathcal {L}\bigl\{t^{\beta-1}E_{\alpha,\beta}\bigl(-\lambda t^\alpha\bigr)\bigr\} =\frac{s^{\alpha-\beta}}{s^\alpha+\lambda}\quad \bigl(\mathcal {R}(s)>| \lambda|^{\frac{1}{\alpha}}\bigr), \end{aligned}$$
(7)

where t and s are, respectively, the variables in the time domain and Laplace domain, \(\mathcal {L}\{\cdot\}\) stands for the Laplace transform.

Lemma 1

([1])

If 0<α<2, β is an arbitrary real number, μ satisfies \(\pi\alpha/2<\mu<\rm min\{\pi, \pi\alpha\}\), and C 1,C 2 are real constants, then

$$\begin{aligned} \bigl|E_{\alpha,\beta}(z)\bigr|&\leq C_1\bigl(1+|z|\bigr)^{(1-\beta)/\alpha}\exp\bigl( \mathit{Re}\bigl(z^{1/\alpha}\bigr)\bigr) \\ &\quad {}+\frac{C_2}{1+|z|}, \end{aligned}$$
(8)

where |arg(z)|≤μ, |z|≥0.

Lemma 2

([26])

The following properties hold.

  1. (i)

    There exist finite real constants M 1,M 2≥1 such that for any 0<α<1,

    $$\begin{aligned} \begin{aligned} &E_{\alpha,1}\bigl(At^\alpha\bigr)\leq M_1 \bigl\|e^{At}\bigr\|, \\ &E_{\alpha,\alpha}\bigl(At^\alpha\bigr)\leq M_2\bigl\|e^{At}\bigr\|, \end{aligned} \end{aligned}$$
    (9)

    where A denotes matrix, ∥⋅∥ denotes any vector or induced matrix norm.

  2. (ii)

    If α≥1, then for β=1,2,α

    $$\begin{aligned} E_{\alpha,\beta}\bigl(At^\alpha\bigr)\leq \bigl\|e^{At^{\alpha}}\bigr\|. \end{aligned}$$
    (10)

Lemma 3

([27])

Suppose α>0, a(t) is a nonnegative function locally integrable on 0≤t<T (some T≤+∞) and g(t) is a nonnegative, nondecreasing continuous function defined on 0≤t<T, g(t)≤M(constant), and suppose u(t) is nonnegative and locally integrable on 0≤t<T with

$$\begin{aligned} u(t)\leq a(t)+g(t)\int_{0}^t(t-s)^{\alpha-1}u(s) \,ds, \end{aligned}$$
(11)

on this interval. Then

$$\begin{aligned} u(t)&\leq a(t) \\ &\quad {}+\int_{0}^t \Biggl[\sum _{n=1}^{\infty}\frac{(g(t)\varGamma(\alpha))^n}{\varGamma (n\alpha)}(t-s)^{n\alpha-1} a(s) \Biggr]\,ds. \end{aligned}$$
(12)

Moreover, if a(t) is a nondecreasing function on [0,T), then

$$\begin{aligned} u(t)\leq a(t)E_{\alpha,1}\bigl(g(t)\varGamma(\alpha)t^\alpha\bigr). \end{aligned}$$
(13)

3 Main results

Consider the following fractional-order nonlinear system:

$$\begin{aligned} \frac{d^\alpha x(t)}{dt^\alpha}=f\bigl(x(t)\bigr)=Ax(t)+h\bigl(x(t)\bigr), \end{aligned}$$
(14)

where x(t)=(x 1(t),x 2(t),…,x n (t))T∈R n denotes the state vector of the state system, f:R n→R n defines a nonlinear vector field in the n-dimensional vector space, fractional-order α belongs to 1<α<2. A∈R n×n is a constant matrix, Ax(t) and h(x(t)) denote linear and nonlinear parts of f(x(t)).

3.1 Stability of fractional-order nonlinear systems

Theorem 1

System (14) is locally asymptotically stable, if

  1. (i)

    h(x(t)) satisfies h(0)=0 and \(\lim_{x\rightarrow 0}\frac{\|h(x(t))\|}{\|x(t)\|} =0\);

  2. (ii)

    Reλ(A)<0 and ω=−max{Reλ(A)}>(Γ(α))1/α.

Proof

Assume the initial conditions be x (k)(0)=x k (k=0,1), the solution of (14) can be obtained by taking the Laplace transform and inverse Laplace transform on (14)

$$\begin{aligned} x(t)&=E_{\alpha,1}\bigl(At^\alpha\bigr)x_0+tE_{\alpha,2} \bigl(At^\alpha\bigr)x_1 \\ &\quad {}+\int_{0}^t(t-\tau)^{\alpha-1}E_{\alpha,\alpha} \bigl(At^\alpha\bigr)h\bigl(x(\tau)\bigr)\,d\tau. \end{aligned}$$
(15)

From Lemma 2, one has

$$\begin{aligned} \begin{aligned} \bigl\|x(t)\bigr\|&\leq \bigl\|e^{At^\alpha}\bigr\|\|x_0\|+\bigl\|e^{At^\alpha}\bigr\| \|x_1\|t \\ &\quad {}+\int_0^t(t-\tau)^{\alpha-1} \bigl\|e^{A(t-\tau)^\alpha}\bigr\| \bigl\|h\bigl(x(\tau)\bigr)\bigr\|\,d\tau. \end{aligned} \end{aligned}$$
(16)

Since A is a stability matrix, there exists N>0 such ∥e At∥≤Ne −ωt and

$$\begin{aligned} \bigl\|e^{At^\alpha}\bigr\|\leq Ne^{-\omega t^\alpha}\leq Ne^{-\omega t}. \end{aligned}$$
(17)

Combining (16) with (17), one obtains

$$\begin{aligned} \bigl\|x(t)\bigr\|&\leq Ne^{-\omega t}\|x_0\|+Ne^{-\omega t} \|x_1\|t \\ &\quad {}+N\int_0^t(t-\tau)^{\alpha-1}e^{-\omega(t-\tau)} \bigl\|h\bigl(x(\tau)\bigr)\bigr\|\,d\tau. \end{aligned}$$
(18)

Multiplying by e ωt both sides of (18), one yields

$$\begin{aligned} e^{\omega t}\bigl\|x(t)\bigr\|&\leq N\|x_0\|+N\|x_1\|t \\ &\quad {}+N\int_0^t(t-\tau)^{\alpha-1}e^{\omega\tau} \bigl\|h\bigl(x(\tau)\bigr)\bigr\|\,d\tau. \end{aligned}$$
(19)

Based on the properties of \(\lim_{x\rightarrow 0}\frac{\|h(x(t))\|}{\|x(t)\|}=0\), there exists a constant δ>0, such that

$$\begin{aligned} \bigl\|h\bigl(x(t)\bigr)\bigr\|\leq \frac{1}{N}\bigl\|x(t)\bigr\| \quad \mbox{as}\ \bigl\|x(t)\bigr\|< \delta. \end{aligned}$$
(20)

Substituting (20) into (19), one gets

$$\begin{aligned} e^{\omega t}\bigl\|x(t)\bigr\|&\leq N\|x_0\|+N\|x_1\|t \\ &\quad {}+\int_0^t(t-\tau)^{\alpha-1}e^{\omega\tau} \bigl\|x(\tau)\bigr\|\,d\tau. \end{aligned}$$
(21)

According to Lemma 3, and denote a(t)=N∥x 0∥+N∥x 1∥t, g(t)=1, u(t)=e ωt∥x(t)∥, one obtains

$$ e^{\omega t}\bigl\|x(t)\bigr\|\leq \bigl(N\|x_0\|+N\|x_1 \|t\bigr)E_{\alpha,1}\bigl(\varGamma(\alpha)t^\alpha\bigr). $$
(22)

Then it follows from Lemma 1 that there exist two real constants C 1,C 2>0 such that

$$\begin{aligned} e^{\omega t}\bigl\|x(t)\bigr\| \leq& \bigl(N\|x_0\|+N\|x_1 \|t\bigr)E_{\alpha,1}\bigl(\varGamma(\alpha)t^\alpha\bigr) \\ \leq&C_1\bigl(N\|x_0\|+N\|x_1 \|t\bigr)e^{(\varGamma(\alpha))^{1/\alpha}t} \\ &{}+\frac{C_2(N\|x_0\|+N\|x_1\|t)}{1+\varGamma(\alpha)t^\alpha}. \end{aligned}$$
(23)

That is,

$$\begin{aligned} \bigl\|x(t)\bigr\| \leq&C_1\bigl(N\|x_0\|+N\|x_1 \|t\bigr)e^{[(\varGamma(\alpha))^{1/\alpha}-\omega]t} \\ &{}+\frac{C_2(N\|x_0\|+N\|x_1\|t)}{(1+\varGamma(\alpha)t^\alpha)e^{\omega t}}. \end{aligned}$$
(24)

Based on Condition (ii), ∥x(t)∥→0 as t→+∞, which implies that system (14) is locally asymptotically stable. □

Theorem 2

System (14) is globally asymptotically stable, if

  1. (i)

    h(x(t)) satisfies h(0)=0, and is global Lipschitz with Lipschitz constant L, i.e., |h(x 1)−h(x 2)|≤L|x 1−x 2| for ∀x 1,x 2∈R;

  2. (ii)

    Reλ(A)<0 and ω=−max{Reλ(A)}>(NLΓ(α))1/α, in which N satisfies ∥e At∥≤Ne −ωt.

Proof

Similar to Theorem 1, the solution of (14) can be obtained by taking the Laplace transform and inverse Laplace transform on (14)

$$\begin{aligned} x(t) =&E_{\alpha,1}\bigl(At^\alpha\bigr)x_0+tE_{\alpha,2} \bigl(At^\alpha\bigr)x_1 \\ &{}+\int_{0}^t(t-\tau)^{\alpha-1}E_{\alpha,\alpha} \bigl(At^\alpha\bigr)h\bigl(x(\tau)\bigr)\,d\tau. \end{aligned}$$
(25)

It follows from Lemma 2 and Condition (i) that

$$\begin{aligned} \bigl\|x(t)\bigr\|&\leq \bigl\|e^{At^\alpha}\bigr\|\|x_0\|+\bigl\|e^{At^\alpha}\bigr\| \|x_1\|t \\ &\quad {}+L\int_0^t(t-\tau)^{\alpha-1} \bigl\|e^{A(t-\tau)^\alpha}\bigr\| \bigl\|x(\tau)\bigr\|\,d\tau. \end{aligned}$$
(26)

Due to A is a stability matrix, then ∥e At∥≤Ne −ωt and

$$\begin{aligned} \bigl\|e^{At^\alpha}\bigr\|\leq Ne^{-\omega t^\alpha}\leq Ne^{-\omega t}. \end{aligned}$$
(27)

Substituting (27) into (26), one gets

$$\begin{aligned} \bigl\|x(t)\bigr\|&\leq Ne^{\omega t}\|x_0\|+Ne^{\omega t} \|x_1\|t \\ &\quad {}+LN\int_0^t(t-\tau)^{\alpha-1}e^{-\omega(t-\tau)} \bigl\|x(\tau)\bigr\|\,d\tau. \end{aligned}$$
(28)

Multiplying by e ωt both sides of (28), one has

$$\begin{aligned} \begin{aligned} e^{\omega t}\bigl\|x(t)\bigr\|&\leq N\|x_0\|+N\|x_1\|t \\ &\quad {}+LN\int_0^t(t-\tau)^{\alpha-1}e^{\omega\tau} \bigl\|x(\tau)\bigr\|\,d\tau. \end{aligned} \end{aligned}$$
(29)

Based on Lemma 3, and let a(t)=N∥x 0∥+N∥x 1∥t, g(t)=LN, u(t)=e ωt∥x(t)∥, it yields

$$ e^{\omega t}\bigl\|x(t)\bigr\|\leq \bigl(N\|x_0\|+N\|x_1 \|t\bigr)E_{\alpha,1}\bigl(LN\varGamma(\alpha)t^\alpha\bigr). $$
(30)

Then, according to Lemma 1, there exist two real constants C 1,C 2>0 such that

$$\begin{aligned} e^{\omega t}\bigl\|x(t)\bigr\|&\leq \bigl(N\|x_0\|+N\|x_1 \|t\bigr)E_{\alpha,1}\bigl(LN\varGamma(\alpha)t^\alpha\bigr) \\ &\leq C_1\bigl(N\|x_0\|+N\|x_1 \|t\bigr)e^{(LN\varGamma(\alpha))^{1/\alpha}t} \\ &\quad {}+\frac{C_2(N\|x_0\|+N\|x_1\|t)}{1+LN\varGamma(\alpha)t^\alpha}, \end{aligned}$$
(31)

which is equivalent to

$$\begin{aligned} \bigl\|x(t)\bigr\|&\leq C_1\bigl(N\|x_0\|+N\|x_1 \|t\bigr)e^{[(LN\varGamma(\alpha))^{1/\alpha}-\omega]t} \\ &\quad {}+\frac{C_2(N\|x_0\|+N\|x_1\|t)}{(1+LN\varGamma(\alpha)t^\alpha)e^{\omega t}}. \end{aligned}$$
(32)

Therefore, from Condition (ii), when t→+∞, ∥x(t)∥→0, which implies system (14) is globally asymptotically stable. □

3.2 Stabilization of fractional-order nonlinear systems

The fractional-order system (14) is said to be stabilization via linear state-feedback control if there exists a state-feedback controller u(t)=Kx(t) such that the closed-loop system

$$\begin{aligned} \frac{d^\alpha x(t)}{dt^\alpha} =&Ax(t)+h\bigl(x(t)\bigr)+Bu(t) \\ =&(A+BK)x(t)+h\bigl(x(t)\bigr) \\ =&\tilde{A}x(t)+h\bigl(x(t)\bigr), \end{aligned}$$
(33)

is asymptotically stable, where feedback gains K need to be determined, \(\tilde{A}=A+BK\).

Therefore, our aim is to design a suitable feedback gain matrix K such that the controlled system (33) is asymptotically stable.

Theorem 3

If feedback gains K is chosen such that the following conditions hold:

  1. (i)

    h(x(t)) satisfies h(0)=0 and \(\lim_{x\rightarrow 0}\frac{\|h(x(t))\|}{\|x(t)\|}=0\);

  2. (ii)

    \(\mathit{Re}{\lambda(\tilde{A})}<0\) and \(\omega=-\max \{\mathit{Re}{\lambda(\tilde{A})}\}> (\varGamma(\alpha))^{1/\alpha}\), then controlled system (33) is locally asymptotically stable.

Proof

The process of the proof is similar to that of Theorem 1, so we omit it here. □

Theorem 4

If feedback gains K is chosen such that the following conditions hold,

  1. (i)

    h(x(t)) satisfies h(0)=0 and is global Lipschitz with Lipschitz constant L, i.e., |h(x 1)−h(x 2)|≤L|x 1−x 2| for ∀x 1,x 2∈R;

  2. (ii)

    \(\mathit{Re}{\lambda(\tilde{A})}<0\) and \(\omega=-\max \{\mathit{Re}{\lambda(\tilde{A})}\}> (NL\varGamma(\alpha))^{1/\alpha}\), in which N satisfies \(\|e^{\tilde{A}t}\|\leq Ne^{-\omega t}\), then controlled system (33) is globally asymptotically stable.

Proof

The process of the proof is similar to that of Theorem 2, it is omitted here. □

Remark 1

Although [23] obtained the sufficient conditions for ensuring the asymptotical stability and stabilization of system (14) and controlled system (33), respectively, these results are also local. Here, we derive the sufficient conditions on the global asymptotic stability of fractional order nonlinear systems.

4 Numerical examples

In this section, to verify and demonstrate the effectiveness of the proposed method, we apply them to stabilizing fractional-order chaotic Lü system with fractional-order α=1.1 and fractional-order chaotic Lorenz system with fractional-order α=1.05, respectively. Here, an improved predictor-corrector algorithm proposed by Deng [28] is applied.

The so-called Lü system is known as a bridge between the Lorenz system and Chen system [29]. Its fractional version [30] is described as follows:

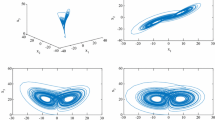
$$ \left \{ \begin{aligned} &\frac{d^{\alpha} x_1}{dt^{\alpha}}=a(x_2-x_1), \\ &\frac{d^{\alpha} x_2}{dt^{\alpha}}=-x_1x_3+cx_2, \\ &\frac{d^{\alpha} x_3}{dt^{\alpha}}=x_1x_2-bx_3, \end{aligned} \right . $$
(34)

when the parameters are chosen as a=36, b=3, c=20, and α=1.1, system (34) displays a chaotic attractor, as shown in Fig. 1.

Fig. 1
figure 1

Chaotic behaviors of fractional-order chaotic Lü system (34) with fractional-order α=1.1

Full size image

System (34) can be also rewritten as (14), in which

$$\begin{aligned} A=\begin{bmatrix} -a & a & 0\\ 0 & c & 0\\ 0 & 0 & -b \end{bmatrix},\qquad h(x)=\begin{bmatrix} 0\\ -x_1x_3\\ x_1x_2 \end{bmatrix}. \end{aligned}$$
(35)

It is very easy to verify that

$$\begin{aligned} \lim_{x\rightarrow 0} \frac{\|h(x(t))\|}{\|x(t)\|} =&\lim_{x\rightarrow0} \frac{\sqrt{(x_1x_3)^2+(x_1x_2)^2}}{\sqrt{x_1^2+x_2^2+x_3^2}} \\ \leq&\lim_{x\rightarrow 0}|x_1|=0, \end{aligned}$$
(36)

which implies that h(x) satisfies Conditions (i). It follows from Theorem 3 and pole placement technique that feedback gain is selected as

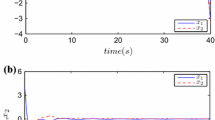
$$K=\left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 34 & -36 & 0 \\ 0& -21 & 0 \\ 0 & 0 &0 \\ \end{array} \right ], $$

which satisfies the conditions Re(λ(A))<0 and ω=−max{λ(A+BK)}=1>0.9557=(Γ(α))1/α. Simulation results are depicted in Fig. 2, which show that the zero solution of the controlled system is locally asymptotically stable.

Fig. 2
figure 2

Stabilization of fractional-order chaotic Lü system (34)

Full size image

Fractional-order Lorenz system[31] can be described by

$$ \left \{ \begin{aligned} &\frac{d^{\alpha} x_1}{dt^{\alpha}}=a(x_2-x_1), \\ &\frac{d^{\alpha} x_2}{dt^{\alpha}}=bx_1-x_1x_3-x_2, \\ &\frac{d^{\alpha} x_3}{dt^{\alpha}}=x_1x_2-cx_3, \end{aligned} \right . $$
(37)

when the parameters are chosen as a=10, b=28, c=8/3, and α=1.05, system (37) displays a chaotic attractor, as shown in Fig. 3.

Fig. 3
figure 3

Chaotic behaviors of fractional-order chaotic Lorenz system (37) with fractional-order α=1.05

Full size image

Systems (37) can also be rewritten as (14), in which

$$\begin{aligned} A=\begin{bmatrix} -a & a & 0\\ b & -1 & 0\\ 0 & 0 & -c \end{bmatrix},\qquad h(x)=\begin{bmatrix} 0\\ -x_1x_3\\ x_1x_2 \end{bmatrix}. \end{aligned}$$
(38)

Based on the boundedness of chaotic systems, there exist a real constant L such that

$$\begin{aligned} \begin{aligned}[b] \bigl\|h(x)\bigr\|&=\sqrt{(x_1x_3)^2+(x_1x_2)^2} \\ &=|x_1|\sqrt{x_1^2+x_2^2+x_3^2} \leq L\|x\|, \end{aligned} \end{aligned}$$
(39)

which implies that h(x) satisfies Lipschitz-conditions. From phase diagram, L is taken to be 20. In the simulation, according to Theorem 4, feedback gain is selected as

$$K=\left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} -8 & -10 & 0 \\ -28& -16 & 0 \\ 0 & 0 &-15 \\ \end{array} \right ]. $$

By using simple calculation, ∥e (A+BK)∥≤e −17.6667t and ω=−max{Reλ(A+BK)}=17.6667>16.9032=(20×Γ(1.05))1/1.05, which satisfies Conditions (i). Simulation results are displayed in Fig. 4, which show that the zero solution of the controlled system is globally asymptotically stable.

Fig. 4
figure 4

Stabilization of fractional-order chaotic Lorenz system (37)

Full size image

5 Conclusion

In this paper, based on the Mittag–Leffler function, the generalized Gronwall inequality and property of fractional calculus, two sufficient stability theorems of a class of nonlinear fractional-order differential systems with fractional-order α:1<α<2 have been given. It should be pointed out that the global stability of such systems is investigated for the first time. And the corresponding criteria have been derived to construct the linear state feedback controller that can stabilize such systems. Simulation results have illustrated the effectiveness of the results and the proposed control method.