1 Introduction

Nonlinear springs can be constructed from many types of physical systems that take advantage of geometric nonlinearities. Important applications of nonlinear springs that have received notable attention in recent years are nonlinear energy sinks (NESs) and energy harvesting systems. The former are basically nonlinear springs that can be attached to primary vibratory systems as nonlinear passive vibration dampers, to which the vibratory energy is pumped from the primary oscillator. However, the latter is implemented for an inverse purpose, i.e., the energy generated in the spring is stored by conveying it to an accumulation system.

Several classes of physical realizations of NES devices based on nonlinear spring systems have been reported in the literature over the past twenty years. In a recent review paper, Lu provides a comprehensive overview of the contributions in the field of NES [10]. Amongst NES devices, a widely studied and physically implemented prototype is the wire NES, reported in the literature by several scholars [11, 21, 25, 29]. However, other classes of nonlinear springs based on different physical phenomena have also been extensively reported [27, 28, 30]. More recent developments in nonlinear springs have been proposed by several researchers. Rivlin used a type of nonlinear spring based on the concept of a cantilevered beam with specially shaped (indented) lateral boundaries for applications in gap-closing electrostatic actuators and mechanical batteries [13, 14, 19, 20]. Wang et al. proposed a similar application of a wideband piezoelectric energy harvester using a quadruple-well potential, induced by a combination of boundary contact and magnetoelasticity [26]. Similarly, Liu compared the effect that different curvature fixtures have on energy harvesters based on cantilevered beams [9]. Kluger used a similar concept for energy harvesting and high-resolution load cells [6, 7]. An interesting application related to automotive vibration reduction was proposed by Spreeman where he imposed a hardening behavior to a spring by adding a boundary of predefined characteristic [22]. In a recent study, Yuan et al. implemented a merged model joining stiffness curves of two different source generators through the use of a cantilever of similar characteristics as those described herein [31]. All these developments used the approach of modeling the dynamics of the spring quasi-statically. Despite not being an exact approach, this methodology has proved to be powerful as the behavior of the nonlinear spring can be accurately described by its force–displacement characteristic previously determined in a force–displacement analysis.

This concept of a cantilever beam bounded by specially shaped rigid surfaces is not new. In fact, the first scholar who proposed a similar idea was Huygens in 1659, later reported in his famous Horologium Oscillatorium in 1672 [1]. In his design, Huygens used specially shaped boundaries around a pendulum to enhance the isochronism of the pendulum, where a strictly identical oscillation period regardless of the amplitude was guaranteed. More recently, Timoshenko included a particular mechanism consisting of a beam with cylindrical boundaries as an example of a nonlinear spring in his book Strength of Materials [24], while Keer & Silva provided an analytical solution for such a problem and compared the solution obtained using theory of elasticity concepts, with that obtained from beam theory [5].

A considerable amount of research on a somewhat similar problem regarding centrifugal pendulum vibration absorbers can be found in the literature. After the first attempt in proposing a centrifugal pendulum vibration absorber, made in France in 1935, whose purpose was to control torsional vibrations in radial aircraft engine propellers [15], Shaw and collaborators in a series of papers reported on the theoretical dynamics, bifurcations and chaotic motion of these types of systems, followed by their industrial use as torsional vibration absorbers for automotive engine crankshafts. The centrifugal pendulum vibration absorber is a combination of a tuned device with nonlinear characteristics, but with a featured tautochronicity in its design that allows it to remain tuned regardless of the disturbance torque [2, 4, 15,16,17,18]. Several other researchers have also proposed nonlinear springs based on beams and pendulums, but based on different mechanics principles. Canturu et al. reported on shape-varying cantilevered beams for obtaining different spring characteristics depending on the chosen beam surface profile [3].

In this study, a model and experimental verification of the above mentioned nonlinear beam spring is developed. This model is able to capture the dynamics of the beam element under reasonably large deformations. The nonlinear characteristics of the beam is provided by two rigid boundaries placed on both sides of the beam, thus limiting the free length of the beam as it gradually wraps around said boundaries. These boundaries have a carefully selected surface order in their shape profile, so the beam fully wraps around them when oscillating. This constraint to the lateral vibration produces a variable nature on the modal characteristics of the system as the beam does not have a preferred vibration frequency and it is highly sensitive to initial conditions and the amplitude of excitation. The model developed is obtained in two stages: (1) the force–displacement (F–D) characteristic obtained from a quasi-static analysis, which allows to generating an appropriate restoring spring force term for the equation of motion of the device; and (2) the derivation of the entire equation of motion (EOM) of the device, using concepts from plane kinematics of rigid bodies, assuming that the system behaves like a bar pivoted on a moving end, and rotating around a fixed axis. This model is then numerically simulated using sine dwell signals that provide a reasonable approximation of the response of the system at its dominant harmonic at each frequency of interest, thus obtaining frequency response functions. Furthermore, the model is experimentally verified using a set of devices fabricated for this purpose and tested using base excitations generated by a shake table. The results demonstrate that the proposed device possesses a frequency response broadband in nature. This suggests that the device has the capacity to engage in TET (targeted energy transfer) regimes, suitable for applications of nonlinear energy transfer such as vibration attenuation.

2 Semi-analytical model

The EOM of the nonlinear spring is derived in this section, first by studying the static behavior of the spring with respect to the imparted force, and then, with the obtained quasi-static behavior, a mathematical expression of the response of the system is obtained.

2.1 Quasi-static analysis

Consider a cantilever beam supported by a smooth rigid curved boundary of height \(H_{\mathrm {S}}\), and length \(L_{\mathrm {S}}\), and with a prescribed shape, described by a function \(f(l-x)\), as shown in Fig. 1. The quantity l is the total length of the beam, x is the length of the free end of the beam beyond the last point of contact between itself and the boundary surface (labeled contact point in Fig. 1), \(u'\) is the transverse displacement of the neutral axis of the beam at its joint with the tip mass, and u is the displacement of the center of mass of the tip mass. For the sake of clarity in the figure, only half of the system is shown as another curved boundary is present on the upper side of the beam, completely bounding its lateral vibration. The beam is loaded by a concentrated load P at the tip and, as it deflects, becomes gradually in contact with the rigid support, such that part of the beam is resting on the support (portion \(l-x\)), and the remaining portion is free (portion x), working as a regular cantilevered beam but with a shorter length, and slightly tilted.

Fig. 1
figure 1

Schematic and dimensions of the nonlinear spring

Full size image

Depending on the applied load and order of curvature, the beam will wrap around a certain portion of the rigid support, and beyond the contact point, it will deflect a certain distance \(u'\) given by

$$\begin{aligned} u' = f(l-x) + \frac{\hbox {d}[f(l-x)]}{\hbox {d}(x)} x + \frac{Px^3}{3EI}. \end{aligned}$$
(1)

The first term in Eq. (1) is associated with the vertical distance from the equilibrium position to the contact point, and it is equivalent to evaluating the surface function f at point \((l-x)\). The second term is the additional vertical distance due to the slope of the beam at the contact point. After the beam wraps around portion \(l-x\), the free portion of the beam x becomes a new inclined cantilever beam with initial slope given by \(\frac{\hbox {d}[f(l-x)]}{\hbox {d}(x)}\). The distance between the equilibrium position and the tip of this inclined beam is calculated by multiplying the slope by the free end x. The third term is the static deflection of the free portion x due to bending, where E and I are the modulus of elasticity of the material, and the second moment of area of the cross section, respectively. An additional component of the deflection is also contributed by the deflection of the tip of the mass (quantity \(u'-u\)), which results from the multiplication of half the mass length \(l_m\) by the cantilever slope. By combining Eq. (1) with the expression of the slope of a cantilever beam, the mass deflection is given by

$$\begin{aligned} u = u' + \frac{Px^2}{2EI}+ \frac{\hbox {d}[f(l-x)]}{\hbox {d}(l-x)} x, \end{aligned}$$
(2)

where \(u, \, u'\) and x are clearly indicated in Fig. 1. Four examples of surfaces with different orders of curvature are shown in Fig. 2, to give the reader an idea of the topological differences between surface orders.

Fig. 2
figure 2

Effect of order n on the boundary surface curvature

Full size image

A general expression for the curvature function of the boundary surface is given by

$$\begin{aligned} f(l-x) = d(l-x)^n, \end{aligned}$$
(3)

where

$$\begin{aligned} d = \frac{H_{_{\mathrm {S}}}}{L_{_{\mathrm {S}}}^n}, \end{aligned}$$
(4)

The quantities \(H_{_{\mathrm {S}}}\) and \(L_{_{\mathrm {S}}}\) (depicted in Fig. 1) are the height and length of the rigid surface, and n is the surface order function of the boundary. In this analysis, n ranges from 3 to 5 as it was demonstrated that the spring achieves strongly nonlinear characteristics for \(n\ge 3\) [6]. Depending on the order of the surface function, the length of the beam l is adjusted accordingly to set it equal to the arc length AD, such that a theoretical infinite stiffness is achieved when the beam completely wraps around the surface, leaving no portion of the beam extending beyond the boundary edge.

To determine the characteristic of the nonlinear spring, the force–displacement relationship must be obtained. Thus, the location of the contact point is required for a given applied load. Since the deflection of the beam in this system is not a function of the applied force alone but of the contact point, the calculation is carried out in two steps: (1) determination of the contact point; and (2) determination of the deflection as a function of the contact point. The contact point is obtained by equating the radius of curvature of the surface, approximated by the second derivative of the surface profile function, and the radius of curvature of the beam at the contact point, given by the known expression of radius of curvature for a cantilever beam:

$$\begin{aligned} \frac{\hbox {d}^{2}}{\hbox {d}x^2} [d(l-x)^n] = n(n-1)d(l-x)^{n-2} = \frac{Px}{EI}. \end{aligned}$$
(5)

Equation (5) has a single-valued solution for \(n\le 3\). For \({n>3}\), distance x must be obtained using numerical techniques as the expressions for x become polynomials of order \(n-2\). Thus, a closed-form expression for the deflection as a function of the applied force is not realizable for a beam of any order greater than 3, and a calculation of the total deflection must be carried out for each surface order case, n, according to Table 1:

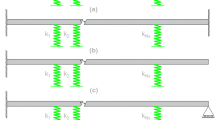
Table 1 Contact point x expressions for each order of n
Full size table

The nonlinear spring defined in Sect. 2.1 has several parameters that can be selected to produce different effects in the static and dynamic responses of the system. Obvious choices are those related to the geometry of the problem including the surface order of the boundary, n, the aspect ratio d, and the length of the beam, l. Moreover, non-geometrical parameters such as the material properties and inertia of the beam will also play a role. The resulting force–displacement curve (P vs u) of the nonlinear spring is a function of the contact point location x which is expressed implicitly in the equation of motion of the system. An schematic diagram of the nonlinear spring, considering base excitation, is presented in Fig. 3.

Fig. 3
figure 3

Proposed nonlinear spring subjected to base excitation

Full size image

The behavior of this spring can be described by a general nonlinear function:

$$\begin{aligned} f_{_{\mathrm {sp}}}= f(u). \end{aligned}$$
(6)

This spring force is equivalent to variable P in Sect. 2.1, which is obtained by solving a two-step problem: (1) finding the solution to the corresponding equation of Table 1, for x; and (2) replacing this solution from step (1) into Eq.(1) for \({f_{_{\mathrm {sp}}}}\). This result is then used to compute a force versus deformation (F-D) characteristic of the spring. The resulting nonlinear stiffness curve is bounded by the surface height \(H_{\mathrm {S}}\) on one axis, and the maximum applied force \(P_{\mathrm {max}}\) on the other axis, as indicated in Fig. 4.

Fig. 4
figure 4

Variation of hardening behavior with the order of surface curvature

Full size image

For a higher-order boundary surface, a higher force is needed to reach the edge, which in practice means that such system would produce a higher nonlinear stiffness. Because of the nature of this problem, where the stiffness theoretically reaches infinity when the beam fully wraps around the surface and no portion of the beam extends beyond the boundary edge, the F-D diagram has an asymptotic behavior toward the maximum beam deflection (at \(u = \pm H_{\mathrm {s}}\)). This behavior is difficult to interpolate into an analytic function that can be incorporated into the \({f_{_{\mathrm {sp}}}}\) term in Eq. (6). One approach is to model this system with an interpolation lookup table as the source of the nonlinear stiffness, and the other, to approximate this behavior with a general power series of the form:

$$\begin{aligned} f_{sp} = \sum _{j=1}^N k_j u^j, \end{aligned}$$
(7)

where N is the order of nonlinearity. The resulting expression consists of odd powers only (\(j = 1, 3, 5, \dots \)) as the nonlinearity is assumed to be an odd function (e.g., for a cubic nonlinearity, the spring force is \({{f}_{_{\mathrm {sp}}} = k_1 u + k_3 u^3}\), for a quintic nonlinearity, it would be \({{f}_{_{\mathrm {sp}}} = k_1 u + k_3 u^3 + k_5 u^5}\), and so forth). The order of nonlinearity is to be determined in a later section.

2.2 Dynamic model

A simple and reasonably accurate way to model this system would be to use the beam model of a cantilever beam with a mass on its tip, attached to a nonlinear spring that captures the nonlinearities described in Eq. (7). However, to account for the additional inertia, the fact that the beam is bending, and the possible gravitational implications of the device (if configured in a vertical direction), a model is proposed based on a concept, similar to Huygen’s pendulum clock with the main difference being in the rigid boundary surface order. The EOMs are derived using the equations of plane kinematics of rigid bodies.

Fig. 5
figure 5

Beam NES schematic idealization

Full size image

The system is idealized as massless bar of length l, pivoted at point A with a concentrated mass m at the tip (point B), and constrained by a spring force \(f_\mathrm {sp}\) of nonlinear characteristics, given by the general expression in Eq. (7), and a damping force \(f_\mathrm {d}\) of viscous characteristics. The pivot point is fixed to a moving cart representing the host structure base acceleration \(\ddot{u}_{\mathrm {b}}\). The motion of the bar is defined completely by its rotation angle from the vertical equilibrium position, \(\phi \). This system is shown schematically in Fig. 5.

Several assumptions need to be made, namely that: (1) the beam is rigid, so all bending characteristics from its elastic physical features are assumed to be captured by the nonlinear spring characteristic; (2) the radius of curvature of the path described by the mass is constant, which is not true in reality as the length of the beam changes progressively as it wraps around the curved surface of the boundary; and, (3) the beam is massless, as its actual mass is much smaller than the concentrated mass at its tip.

Consider the free body diagram shown in Fig. 6. The external forces that produce a moment around point B are the spring force (\(f_{\mathrm {sp}}\)), damping force (\(f_{\mathrm {d}}\)), and the gravitational force (mg), each one multiplied by the appropriate moment arm length to A.

Fig. 6
figure 6

Beam NES free body diagram

Full size image

The vector equation of the acceleration of point B, accounting for its relative motion with respect to point A, is given by:

$$\begin{aligned} \mathbf {a}_B&= \mathbf {a}_A + \upalpha \times \mathbf {r}_{B/A}-\omega ^2\mathbf {r}_{B/A} \nonumber \\&= {\mathbf {a}}_{_{\mathrm {A}}} \hat{\mathbf {i}}+ \ddot{\phi }\hat{\mathbf {k}} \times [-l \sin (\phi ) \hat{\mathbf {i}} +l \cos {\phi } \hat{\mathbf {j}}] \nonumber \\&\quad +[\dot{\phi }^2 l\sin (\phi )\hat{\mathbf {i}}-\dot{\phi }^2l\cos (\phi )\hat{\mathbf {j}}], \end{aligned}$$
(8)

where \(\mathbf {r}_{B/A}\) is the position vector from point B to point A, \(\upalpha \) is the angular acceleration vector of the beam, \(\omega \) is the scalar angular velocity of the beam, and \(\mathbf {a}\) is an acceleration vector of its corresponding point in the diagram indicated by the subscript. Note that bold letters represent vector quantities. Now, expanding the cross-products of the rightmost side of Eq.(8) produces:

$$\begin{aligned} \mathbf {a}_B&= [\mathbf {a}_A - \ddot{\phi } l \cos {\phi }+\dot{\phi }^2 l\sin (\phi )] \hat{\mathbf {i}} \nonumber \\&\quad +[-\dot{\phi }^2 l\cos (\phi )- \ddot{\phi }l \sin (\phi ) ]\hat{\mathbf {j}}, \end{aligned}$$
(9)

and, enforcing Newton’s second law for rotational motion, yields the angular acceleration relationship:

$$\begin{aligned} \sum \mathbf {M}_A = I_B \mathbf {\upalpha } + \mathbf {r}_{B/A} \times m \mathbf {a}_B, \end{aligned}$$
(10)

where \(I_B\) is the rotational moment of inertia of the mass, \(\upalpha = \ddot{\phi }\hat{\mathbf {k}}\), and the sign convention for positive moments is in the counterclockwise sense. Once more, from the free body diagram, one obtains:

$$\begin{aligned}&(mgl\sin {\phi } + f_{\mathrm {sp}} l \cos {\phi } + f_\mathrm {d} l \cos {\phi }) \hat{\mathbf {k}} = I_G \ddot{\phi } \hat{\mathbf {k}} \nonumber \\&\quad +(-l \sin {\phi } \hat{\mathbf {i}} + l \cos {\phi } \hat{\mathbf {j}})\nonumber \\&\quad \times m [(\mathbf {a}_A -\ddot{\phi } l \cos {\phi }) \hat{\mathbf {i}} -\ddot{\phi }l \sin {\phi } \hat{\mathbf {j}}]. \end{aligned}$$
(11)

After computing all the cross-products, the resulting expression is only in the \(\hat{\mathrm {k}}\) direction, as expected for planar rotation, so the directional unit vector is dropped:

$$\begin{aligned}&(mgl\sin {\phi } + {f}_{\mathrm {sp}} l \cos {\phi } + {f}_{\mathrm {d}} l \cos {\phi }) \nonumber \\&\quad = I_B \ddot{\phi } + m\ddot{\phi }l^2 - m a_A l \cos {\theta }. \end{aligned}$$
(12)

The remaining quantity to be determined is the form of the nonlinear spring force. For the purpose of expressing the nonlinearity in the equation, the general expression \({f}_{_{\mathrm {sp}}}\), which is a function of \((l\phi )\), is included. The base acceleration variable name is changed to \(\ddot{u}_{\mathrm {b}}\), thus producing an equation in terms of angular moments, and assuming small angle approximations yields:

$$\begin{aligned} (I_B + ml^2) \ddot{\phi } + cl (l \dot{\phi }) + {f}_{_{\mathrm {sp}}}(l \phi ) -m g l (l \phi ) = -m l \ddot{u}_{\mathrm {b}}. \end{aligned}$$
(13)

This constitutes the equation of motion (EOM) of this class of nonlinear spring in terms of angular states. For the present study, the gravitational effects included in Eq. (13) are neglected as the device is oriented in a horizontal plane, thus gravity points toward the paper plane in Fig. 6. To retrieve the motion states in the u direction, a simple substitution derived from the kinematics of the problem has to be made to the \(\phi \) quantity, recalling that \(u = l \phi \). Thus the angular and linear quantities are related by:

$$\begin{aligned} u = l \phi , \quad \dot{u} = l \dot{\phi }, \quad \ddot{u} = l \ddot{\phi }. \end{aligned}$$

3 Approximate analytical solution

An approximation of the analytical solution of the developed EOMs is presented. A preliminary step in determining a set of adequate parameters for having a fully described system is also required.

3.1 Parametric design

With the EOM and F-D characteristics completed, a parametric model is generated from physical constraints defined beforehand for this nonlinear spring, mainly ensuring that it would be easy to build, from commercially available materials, and that it shall produce relevant results when attached to existing physical components available in the laboratory, which are expected to be used during the experimental verification of the model. Thus, physical characteristics for the spring are defined accordingly and shown in Table 2. The rigid boundaries are defined and assumed to be of a material such that elasticity does not play a role when interacting with the beams, and friction implications are considered to be within the status of a lightly damped system. It should also be mentioned that the tip mass considers the additional weight of the instrumentation and bolts that will be used in the physical realization of the experiments.

Table 2 Material and geometric properties of the nonlinear spring
Full size table

With all the constant parameters defined and assumed, MATLAB interpolation capabilities through the function cftool.m are used to obtain a fit to the curves generated in the static analysis. From the combined use of Eq. (5), Table 1, and subsequent fitting of the F-D curve, the resulting form of the nonlinear stiffness defined in the power series of Eq. (7) is:

$$\begin{aligned} f_{_{\mathrm {sp}}} = k_{\mathrm {L}} u + k_{\mathrm {NL}} u^9, \end{aligned}$$
(14)

where \(k_{\mathrm {L}}\) and \(k_{\mathrm {NL}}\) are the linear and nonlinear stiffness coefficients, respectively. Several candidates for the spring force were considered here, from a purely cubic, to a quintic, an order 7 and an order 9 expression, and also to different combinations thereof. The criteria for selecting the final shape included the smoothness of the interpolation, the coefficient of determination given by the \(R^2\), and the root mean-squared error to evaluate the degree of correlation between the calculated and interpolated F-D curves. The expression that produced the highest \(R^2\) value with smoother behavior was a ninth-order polynomial nonlinear force. It should be mentioned that a combined polynomial including intermediate powers of u would produce an undesired wiggly behavior in the interpolated curve. The coefficients corresponding to two boundary surface order cases (\(n=3\), and \(n=5\)) extracted from interpolating the F-D curves of Fig. 7 are shown in Table 3.

Fig. 7
figure 7

Nonlinear spring polynomial stiffness interpolation

Full size image

Once these preliminary steps are completed, numerical simulations of the determined nonlinear spring of 9\(^{\mathrm {th}}\) order, using the derived EOM corresponding to the two cases in hand (\(n=3\) and \(n=5\)), are carried out using Simulink [23], with a Runge–Kutta (ode45) integrator, running at a variable time step within the ode45.m environment. Three numerically generated sine dwell diagrams are run between frequencies of interest: from 3.0 to 5Hz, for the case of \(n=3\), and from 4 to 6Hz, for the case of \(n=5\) surface curvature order. Each run is carried out at amplitudes of 0.8 and 1.2mm. To generate the frequency domain response numerically, the integration is performed in ascending order of frequencies (forward integration), and then in descending order of frequencies (backward integration) at each excitation frequency point, using the last steady-state maximum amplitude as the initial condition for the next frequency point.

3.2 Damping identification

In order to identify the linear damping and linear natural frequency of the system, the cantilevered oscillator with mass attached is clamped horizontally to the table and given an initial excitation (hammer hit) (Table 4). The response is recorded and shown in Fig. 8.

Table 3 Non-dimensional parameters for different curvature cases
Full size table
Table 4 Damping and natural frequency estimates due to small perturbation
Full size table
Fig. 8
figure 8

Time waveform for linear fit of \(\omega _n\) and \(\zeta \)

Full size image

Once these preliminary steps are completed, numerical simulations of the determined nonlinear spring of 9\(^{\mathrm {th}}\) order, using the derived EOM corresponding to the two cases in hand (\(n=3\) and \(n=5\)) are carried out using Simulink [23], with a Runge–Kutta integrator, running at a variable time step within the ode45.m environment. Three numerically generated sine dwell diagrams are run between frequencies of interest: from 3.0 to 5Hz, for the case of \(n=3\), and from 4 to 6Hz, for the case of \(n=5\) surface order. Each run is carried out at amplitudes of 0.8, and 1.2 mm. To generate the frequency domain response numerically, the integration is performed in ascending order of frequencies (forward integration), and then in descending order of frequencies (backward integration) at each excitation frequency point, using the last steady state maximum amplitude as the initial condition for the next frequency point.

3.3 Non-dimensionalization

With the obtained expression of the nonlinear force of the spring, Eq. (13) can be rewritten as

$$\begin{aligned}&(I_G + ml^2) \ddot{\phi } + cl (l \dot{\phi }) \nonumber \\&\quad + {k}_{_{\mathrm {L}}}l (l \phi ) + {k}_{_{\mathrm {NL}}}l (l \phi )^9 -m g l (l \phi ) = -m l \ddot{u}_{\mathrm {b}}. \end{aligned}$$
(15)

Here, the input excitation is given by

$$\begin{aligned} {\ddot{u}}_{\mathrm {b}}=F_0\omega ^2\cos {\omega t}, \end{aligned}$$
(16)

where \(F_0\) is the amplitude and \(\omega \), the frequency of excitation. Also, the gravitational term \(mgl(l\phi )\) is neglected as the configuration of the device is in the horizontal plane. The relative contribution of constant terms in Eq. (15) must be evaluated through non-dimensionalization. By scaling the time variable by a characteristic time, \(T_{\mathrm {c}}\), and noting that the displacement is already in non-dimensional form (radians), let

$$\begin{aligned} \tau = \frac{t}{T_{\mathrm {c}}} \implies \quad \phi (t) = \varphi (T_{\mathrm {c}} \tau ), \end{aligned}$$
(17)

thus,

$$\begin{aligned} \dot{\phi } = \frac{1}{T_{\mathrm {c}}}\varphi ', \quad \ddot{\phi } = \frac{1}{T_{\mathrm {c}}^2} \varphi '', \end{aligned}$$
(18)

with

$$\begin{aligned} T_c=\sqrt{\frac{I_G+ml^2}{{k}_{_{\mathrm {L}}} l^2}} = \frac{1}{{\omega }_{\mathrm {n}}}, \end{aligned}$$
(19)

where \({\omega }_{\mathrm {n}}\) is the linear natural frequency of the spring. Substituting Eqs. (16), (17), (18), and (19) in Eq. (15) yields:

$$\begin{aligned}&\varphi ''+\mu \varphi '+\lambda \varphi +\epsilon \varphi ^9=\varLambda \varOmega ^2\cos (\varOmega \tau ), \end{aligned}$$
(20)

where

$$\begin{aligned} \mu&= \frac{cl}{\sqrt{(I_G+ml^2){k}_{_{\mathrm {L}}}}}, \quad \varepsilon = \frac{{k}_{_{\mathrm {NL}}}}{{k}_{_{\mathrm {L}}}}l^{8}, \quad \varLambda = \frac{mF_0}{{k}_{_{\mathrm {L}}}l}\varOmega . \end{aligned}$$
(21)

The quantity \(\varOmega \) is the forcing frequency normalized by the first linear natural frequency of the spring, \(\varOmega = \frac{\omega }{{\omega }_{\mathrm {n}}}\). The relative difference between the linear and nonlinear term of the stiffness confirms indeed that the system is highly nonlinear.

3.4 System response near resonance

Due to the high-order terms present in the EOM, a closed-form solution is rather difficult to obtain. Therefore, a numerical approximation through perturbation methods, specifically the method of harmonic balance, is posted as an alternative as this method is suitable for systems with polynomial nonlinear terms and strong nonlinearities (hardening type). Therefore, a solution to Eq. (20) is assumed of the form

$$\begin{aligned} \varphi (t) \approx \varphi _{\mathrm {h}} = A \cos (\varOmega \tau ) + B \sin (\varOmega \tau ), \end{aligned}$$
(22)

where A and B are the Fourier coefficients. Here, single frequency is assumed as we are only interested in low-frequency harmonics. The detailed procedure of derivation is mathematically extensive, yielding long expressions. Therefore, some steps of the procedure are briefly mentioned herein. Substituting Eq. (22) in Eq. (20) yields an expression in terms of powers of sines and cosines:

$$\begin{aligned}&-\, A \varOmega ^2 \cos (\varOmega \tau )- B \varOmega ^2 \sin (\varOmega \tau )-\lambda A \varOmega \sin (\varOmega \tau ) \nonumber \\&+\,\lambda B \varOmega \cos (\varOmega \tau )+ A \cos (\varOmega \tau )+B \sin (\varOmega \tau ) \nonumber \\&+\,\varepsilon A^9 \cos (\varOmega \tau )^9+9 \varepsilon A^8 \cos (\varOmega \tau )^8 B \sin (\varOmega \tau ) \nonumber \\&+\,36 \varepsilon A^7 \cos (\varOmega \tau )^7 B^2 \sin (\varOmega \tau )^2 \nonumber \\&+ \,84 \varepsilon A^6 \cos (\varOmega \tau )^6 B^3 \sin (\varOmega \tau )^3 \nonumber \\&+ \,126 \varepsilon A^5 \cos (\varOmega \tau )^5 B^4 \sin (\varOmega \tau )^4 \nonumber \\&+\, 126 \varepsilon A^4 \cos (\varOmega \tau )^4 B^5 \sin (\varOmega \tau )^5 \nonumber \\&+\,84 \varepsilon A^3 \cos (\varOmega \tau )^3 B^6 \sin (\varOmega \tau )^6 \nonumber \\&+\,36 \varepsilon A^2 \cos (\varOmega \tau )^2 B^7 \sin (\varOmega \tau )^7 \nonumber \\&+\, 9 \varepsilon A \cos (\varOmega \tau ) B^8 \sin (\varOmega \tau )^8 \nonumber \\&+\,\varepsilon B^9 \sin (\varOmega \tau )^9+\varOmega ^2 \varLambda \sin (\varOmega \tau ) = 0. \end{aligned}$$
(23)

Expanding and using multiple-angle trigonometric identities (e.g., \({\sin ^3(\varOmega \tau ) = \frac{3}{4}\sin (\varOmega \tau ) - \frac{1}{4} \sin (3 \varOmega \tau )}\), and so on), produces an expression in terms of sines and cosines of multiple angles up to \((9 \varOmega \tau )\). All the higher-order terms greater than \(3 \varOmega \tau \) are dropped as only lower harmonics are of interest here. Next, collecting the fundamental sine harmonics yields:

$$\begin{aligned}&A+(63/128) \varepsilon A^9+(63/32) \varepsilon A^3 B^6 \nonumber \\&+ (63/128) \varepsilon A B^8-M A \varOmega ^2+C B \varOmega \nonumber \\&+ (63/32) \varepsilon A^7 B^2+(189/64) \varepsilon A^5 B^4 = 0, \end{aligned}$$
(24)

and collecting the fundamental cosine harmonics, produces:

$$\begin{aligned}&B+(63/128) \varepsilon B^9+(189/64) \varepsilon A^4 B^5 \nonumber \\&\quad + (63/32) \varepsilon A^2 B^7-M B \varOmega ^2-C A \varOmega \nonumber \\&\quad + (63/128) \varepsilon A^8 B+(63/32) \varepsilon A^6 B^3 = -\varOmega ^2 \varLambda . \end{aligned}$$
(25)

At this point, a polar substitution is made such that \({A = a \cos (\theta )}\), and \({B = b \cos (\theta )}\), to both Eq. (24), and Eq. (25). This produces two expressions in power terms of \(\sin (\theta )\), and \(\cos (\theta )\), let us call them \(h_1\) and \(h_2\), respectively. Now, equation \(h_1\) is again multiplied by \(\sin (\theta )\) to produce equation \(f_1\), and by \(\cos (\theta )\) to produce equation \(f_2\). Similarly, equation \(h_2\) is also multiplied by \(\sin (\theta )\) to produce equation \(g_1\), and by \(\cos (\theta )\) to produce equation \(g_2\). The reason for doing these artifices is to eliminate trigonometric terms by combining the formed equations. After combining and reducing, using trigonometric identities, equations \(f_1 + f_2\), and \(g_1 + g_2\), two-phase equations are generated, which are given by:

$$\begin{aligned} a+\frac{63}{128} \varepsilon a^9 -M a \varOmega ^2 = \varOmega ^2 \varLambda \cos (\theta ), \end{aligned}$$
(26)

and

$$\begin{aligned} \lambda a \varOmega = \varOmega ^2 \varLambda \cos (\theta ). \end{aligned}$$
(27)

Squaring and adding Eqs. (26) and (27), and recalling the relationship \(\sin ^2(\theta ) + \cos ^2(\theta ) = 1\), the final simplified expression of the frequency–amplitude relationship is

$$\begin{aligned} \begin{aligned}&\frac{3969}{16384}\,{a}^{18}{\varepsilon }^{2}- \frac{63}{64}\,{a}^{10} \varepsilon {\varOmega }^{2}+ \frac{63}{64}\,{a}^{10} \, \varepsilon \\&\quad +{a}^{2} {\varOmega }^{4}- 2\,a^2 \varOmega ^2+ {a}^{2} + \lambda ^2 a^2{\varOmega }^{2} = \varLambda ^2 \varOmega ^4. \end{aligned} \end{aligned}$$
(28)

This equation produces a polynomial of order 18 in a that can be solved numerically for the roots that constitute the amplitude response level of the system for different forcing frequencies \(\varOmega \). At each frequency point, the polynomial produces nine roots, which contain both real and imaginary values. From these, only the real roots are of relevance in the present analysis for constructing the frequency response curve.

3.5 Stability analysis

Floquet theory is used to evaluate the stability of the periodic solutions derived from the harmonic balance technique in Sect. 3.4. The periodic solution \(\phi (t)\) is perturbed by a disturbance \(\xi (t)\), such that \(\phi _{\mathrm {h}}\) becomes \(\phi _{\mathrm {h}}+\xi (t)\) (subscript \(()_h\) denotes ‘harmonic’). Then, the system is expressed as a set of first-order differential equations

$$\begin{aligned} \begin{aligned} \ddot{\varphi }_1&= \varphi _2\\ \ddot{\varphi }_2&= -\lambda \phi _2 - \varphi _1 - \varepsilon \varphi _1^9. \end{aligned} \end{aligned}$$
(29)

Now, let us perturb the solutions to the system of Eq. (29) by a small perturbation \(\xi \), such that

$$\begin{aligned} \phi _1(t)&= \phi _{1,0} + \xi _1 (t) \nonumber \\ \phi _2(t)&= \phi _{1,0} + \xi _1 (t), \end{aligned}$$
(30)

and noting that

$$\begin{aligned} \phi _{1,0}(t)&= b \cos {\omega t} \nonumber \\ \phi _{2,0}(t)&= \dot{u}_{1,0}(t) = -b \omega \sin {\omega t}. \end{aligned}$$
(31)

After replacing Eq. (31) into Eq. (30), a system of two first-order differential equations with state variables \([\xi _1 \quad \xi _2]^\intercal \) is obtained. Then, rearranging and simplifying such that only first-order terms of \(\xi _1\), and \(\xi _2\) are retained, the perturbed system can be expressed in state-space form as

$$\begin{aligned} \begin{bmatrix} \dot{\xi }_1\\ \dot{\xi }_2 \end{bmatrix} = \begin{bmatrix} 0 &{} 1\\ - 1 - 9\varepsilon u_{10}^8 &{} -\lambda \end{bmatrix} \begin{bmatrix} \xi _1 \\ \xi _2 \end{bmatrix}. \end{aligned}$$
(32)

To assess the stability of the linearized equations, the monodromy matrix is obtained by integrating system (32) from \(t=0\) to \(t=T=2\pi /\omega \), i.e., a full period of the excitation. This is accomplished by determining two solution vectors

$$\begin{aligned} \varvec{\xi _1}(t)= \begin{bmatrix} \xi _{11}(t)\\ \xi _{12}(t) \end{bmatrix}\quad \text {and}\quad \varvec{\xi _2}(t)= \begin{bmatrix} \xi _{21}(t)\\ \xi _{22}(t) \end{bmatrix} \end{aligned}$$
(33)

which satisfy the following initial conditions

$$\begin{aligned} \begin{bmatrix} \xi _{11}(0)\\ \xi _{12}(0) \end{bmatrix}=\begin{bmatrix} 1\\ 0 \end{bmatrix}\quad \text {and}\quad \begin{bmatrix} \xi _{21}(0)\\ \xi _{22}(0) \end{bmatrix}=\begin{bmatrix} 0\\ 1 \end{bmatrix}; \end{aligned}$$
(34)

The identity matrix is used as initial condition. This allows the monodromy matrix to be

$$\begin{aligned} \varPhi = \begin{bmatrix} \xi _{11}(T)&{}\xi _{21}(T)\\ \xi _{12}(T)&{}\xi _{22}(T) \end{bmatrix}. \end{aligned}$$
(35)

The eigenvalues of \(\varPhi \), known as the Floquet or characteristic multipliers, indicate whether the solution corresponding to the associated frequency is stable, according to the next criteria:

  1. 1.

    The Floquet multiplier leaves the unit circle through \({\mathrm {Re} = +1}\), resulting in a transcritical (TC), symmetry breaking (SB), and cyclic fold (CF) bifurcation.

  2. 2.

    The Floquet multiplier leaves the unit circle through \({\mathrm {Re} = -1}\), resulting in a period doubling bifurcation (PD).

  3. 3.

    The Floquet multiplier in the form of a pair of complex conjugates leave the unit circle away from the real axis resulting in a secondary Hopf or Neimark-Sacker bifurcation [8, 12]

It is expected that for the present case, the Floquet multipliers start occurring within the unit circle as pairs of complex conjugates, progressing toward \(\mathrm {Re}+1\) at which point they leave the unit circle the moment that the system bifurcates into two solutions. They remain outside of the unit circle, while the system is unstable (in the folding region), and return inside the unit circle once the system again reaches stability. This will be apparent in the results section.

4 Numerical and experimental outcomes

The proposed dynamics of the ninth-order nonlinear spring are numerically simulated and are conducted using appropriate computational tools, and their response is examined both in frequency and time domains. Then, an experimental verification of the strength of the model is provided.

4.1 Computational simulations

With the dynamic model constructed and its corresponding numerical constants and parameters properly determined, numerical simulations of the ninth-order spring corresponding to the two cases in hand (\(n=3\) and \(n=5\)) are carried out using Simulink [23], with a Runge–Kutta (ode4) integrator, running at a variable time step within the ode45.m environment. Two numerically generated sine dwell diagrams are run between the frequencies of interest: from 3.0 to 6Hz, for both cases of surface curvature order. Each run is conducted at amplitudes of 0.8 and 1.2mm. To generate the frequency domain response numerically, the integration is performed in the ascending order of frequencies (forward integration), with a simulation time to reach steady state estimated in 500 cycles of oscillation at each frequency point, using the last steady-state maximum amplitude as the initial condition for the next frequency point. The same procedure is followed in descending order of frequencies (backward integration). The reason to run simulations in ascending and descending orders is to capture the unstable regions of the plot. The obtained frequency responses are then correlated both with the approximated analytical solution obtained in Sec. 3.4, and with the experimental measurements to be explained in the next section.

4.2 Experimental measurements

To demonstrate the applicability of this dynamic model, a set of experiments is conducted in the Intelligent Infrastructure Systems Laboratory at Purdue University. First, a prototype device is designed and fabricated, sized properly to fit and use the existing facilities available in the lab. Next, a series of sine sweeps are applied as base excitation to the device. Then, data are collected for use in the process of model verification. This process is repeated for both the \(n=3\) and \(n=5\) cases described in Sect. 4. Data are collected using a VibPilot8 DAQ data acquisition box, manufactured by m+p International, with built-in anti-aliasing filtering and the capability to sample at frequencies up to 10kHz. For these experiments, data are acquired at a sampling rate of 256Hz to minimize large data set sizes. The acceleration transducers utilized for this test were two PCB Piezoelectric accelerometers model 333B40, adequate for frequencies in the range of [0.5Hz to 10kHz], with ICP® type excitation. Base displacement data are also collected along the acceleration records, and were measured with a built-in LVDT in the actuator of the shake table.

The nonlinear spring is designed in such a way that it can be mounted on any flat surface of appropriate dimensions. A mounting bracket is used to attach the device to any base structure with a flat face, on any configuration. This bracket also works as a mounting vise to fix the device to the rigid surfaces while applying pressure to the beam to maintain a tight cantilevered boundary condition. The device is fabricated in a CNC machine at the Mechanical Engineering Machine Shop and is shown in Fig. 9.

Fig. 9
figure 9

Physical realization of the nonlinear device

Full size image

The spring assembly is mounted on a six-DOF servo hydraulic shake table manufactured by Shore Western Manufacturing, controlled by a SC-6000 PID-type servo controller at each DOF. The shake table dimensions are 760 \(\times \) 760mm, with a maximum payload capacity of 200kg. The acceleration transducers are tightly glued to the mass on the tip of the beam, for recording the acceleration of the motion in both directions of the trajectory. Because the actual motion of the mass travels on a curved trajectory, and the transducers used are single direction, it is not possible to directly record measurements in the rectilinear directions (u and v), rather accelerations are recorded in normal and tangential coordinates, which are later corrected with the appropriate angle to horizontal and vertical components (Fig. 10). It should be mentioned that although only the horizontal component (\(\ddot{x}\)) is being compared in the present study, both components are collected for completeness.

Fig. 10
figure 10

Angle correction of the measured data to convert acceleration from normal tangential to Euclidean

Full size image

Post-processing of the collected data includes a step of two-way (ascending and descending direction of the data set) low-pass filtering to eliminate high-frequency noise, and minimize phase shifts to the signals. The filter used is a Butterworth low-pass filter of order 8 and a cutoff frequency of 12Hz.

The rigid surface is interchangeable to different sets, depending on the case of interest. For the present experiment, following the numerical cases mentioned earlier, two sets of surfaces are fabricated: one for curvature degree \(n=3\) and the other for curvature \(n=5\). The mass is attached as a separate insert and can conveniently slide the beam in or out to accommodate the appropriate length, as the arc lengths of the boundaries are different, depending on the order of curvature. The fabricated pairs of boundaries are shown in Fig. 11.

Fig. 11
figure 11

Physical realization of boundary surfaces

Full size image

The verification procedure starts by subjecting the specimen to sine dwells at very slow frequency rates, allowing the system to reach steady state and recording the amplitude before a frequency step is made. The excitation is imposed replicating the numerical simulations (i.e., from 3 to 6Hz with increments of 0.1Hz). The excitation time at each frequency point is set such that the device completes 250 to 400 cycles, depending on the level of transiency (approximately from 45 to 70s).

The steady-state acceleration amplitudes measured during the experiments are correlated with those found in the numerical simulations, both in the forward and backward integration schemes, and then compared with the approximated analytical solution found from the method of harmonic balance. All of the quantities were corrected such that they could be depicted in the u direction, as the experimental measurements were made with linear directional accelerometers instead of angular. The responses of the tested cases corresponding to boundary curvature order \(n=3\) are presented in Fig. 12, with the following clarifications: (1) Each plot contains the numerical simulations both in forward and backward integration fashion, superimposed to the experimental measurements, limited to the first Fourier frequency component in each frequency step, to produce a fair comparison with the approximate analytical solution obtained in the same fashion (just the first harmonic) from the harmonic balance, and the approximated solution, as indicated in the legends; (2) the top plot corresponds to the low amplitude case (\(A=0.8\)mm); and, (3) the bottom row corresponds to the high amplitude case (\(A=1.2\)mm).

Fig. 12
figure 12

Approximated analytical, simulated and experimental responses of the dynamic nonlinear spring system, \(n=3\)

Full size image

The simulation results for \(n=3\) offer a reasonably close match between the approximate analytical solution of the harmonic balance method for all of the cases, both in frequency (peaking at approximately 4.3Hz on all cases), and in amplitude, differing only at the end of the hardening peak, which is expected as the harmonic balance shows a trend in hardening toward higher frequencies. Moreover, the model developed earlier and the analytical solution compare reasonably well both in frequency and amplitude. However, the measured response does not agree as close to the analytical response as would be expected. Several possible causes can be attributed for this outcome, some of which include (1) unmodeled dynamics in the chosen modeling approach; (2) measurement errors and uncertainties in several parameters, such as the effective beam length, the actual mass, including the added dynamics produced by the transducer cables; (3) truncation of the approximate analytical solution to the first Fourier harmonic only; (4) errors associated with reaching steady state in the sine-dwell experiments; (5) frequency stepping up during the sine-dwell experiments, which includes a fast ramp to zero between frequency points; (6) possible inhomogeneity of the beam material properties; (7) differences between command and measured displacement in the shake table likely due to measurement noise introduced by the system in general, or by the hydraulic system in particular (both base displacement and acceleration are measured quantities) and; (8) the resolution of the experiment, which is not very high, and may cause the system to loose the continuity of amplitude at those locations. Higher resolution in these types of experiments is difficult to achieve due to the length needed for each sine dwell to reach steady state. A trade-off between dwell time and resolution is always a challenge. The stability of these results is also checked by monitoring the evolution of the Floquet multipliers, in a unit circle diagram where they are traced as the frequency of excitation is increased. This can be observed in Fig. 12c, where the leaving and reentry of the multipliers from the unit circle occurs at 4.2 and 4.4Hz, respectively, which is consistent with the simulated, experimental and analytical results.

Fig. 13
figure 13

Approximated analytical, simulated and experimental responses of the dynamic nonlinear spring system, \(n=5\)

Full size image

Similarly, the simulation results for case \(n=5\), presented in the pair of plots in Fig. 13, show a close correlation between the solution from harmonic balance with the results of the simulations, both in ascending and descending integration order. The resonant peak occurs at around 4.9Hz with a slight divergence toward higher amplitudes, returning to its stable branch at around 5.2Hz. This result is also confirmed by looking at the evolution of the Floquet multipliers (see Fig. 13c, where the occurrence of the values leaving and reentering the unit circle happens at exactly the same frequencies listed above. Another interesting observation that can be derived from the results presented in Figs. 12 and 13 is that the model is able to capture the energy threshold in a similar way as the device behaves in reality. Though the system is essentially nonlinear, as at every amplitude of vibration the beam is oscillating at a different frequency within the frequencies of study, it is expected that at low amplitudes, the device would behave more closely to a linear cantilever. Nevertheless, for the two cases presented here, the nonlinearity appears clearly both in the modeled as well as in the measured responses.

5 Conclusions

The application of a nonlinear spring, based on a cantilever beam with a concentrated mass at the tip, whose transverse vibration is constrained by a specially shaped rigid boundary, is proposed here as a suitable candidate for vibration attenuation applications as a nonlinear spring. A semi-analytical dynamic model is developed based on the equations of plane kinematics of rigid bodies. First, a static analysis is performed to determine that the nonlinearity can be described as a ninth-order spring, due to the pronounced F-D behavior; and second, equations of motion are derived inserting this F-D characteristic. Numerical simulations demonstrate that the model captures the amplitudes and frequencies of oscillation reasonably well when the device is subjected to different amplitudes of excitation, if compared to the approximate analytical solution obtained from the harmonic balance approximation. However, these results compare in less degree with the experimental measurements due to various possible reasons, some of which include unmodeled dynamics and uncertainties in the experimental setup, and truncation of the solution obtained the harmonic balance. The broadband capacity of the nonlinear spring is demonstrated in the frequency domain, for two amplitudes of excitation for two selected surface curvature orders, one low and one high. Finally, a series of laboratory experiments are conducted for the two physical realizations of the proposed device. The observed results as compared with the simulations and with the approximate analytical solution show an acceptable match in amplitude and frequency, after extracting the first Fourier component of the measured signal for each case of physical realization. These results suggest that this class of spring behaves as a nonlinear element suited for potential vibration absorption applications as a nonlinear energy sink. From the performed experimental studies, it became apparent that as the surface order of the limiting boundary grows, the nonlinear behavior of the spring also increases (behavior hardens), which in turn demonstrate the intrinsic amplitude dependency of most nonlinear systems of this class.