Free Vibration of Compliant Mechanisms Based on Euler-Bernoulli-Beams

Abstract

This paper presents an analytical approach for computing the natural frequencies of planar compliant mechanisms consisting of any number of beam segments. The approach is based on the Euler-Bernoulli Beam theory and the transfer matrix method (TMM), which means there is no need for a global dynamics equation, but instead low-order matrices are used which result in high computational efficiency. Each beam segment is elastic, thin, has a different rectangular cross-section or a different orientation and is treated as an Euler-Bernoulli beam. The approach in principle does not differentiate between the flexure hinges, and the more rigid beam sections, both are treated as beams. The difference in stiffness solely results from the changes in the cross sections and length. A finite element analysis (FEA), as often used in practical applications, has been carried out for various geometries to serve as state-of-the-art reference models to which the results obtained by the presented analytical method could be compared. Various test specimens (TS) consisting of concentrated and distributed compliance in various degrees of complexity were produced and measured in free- and forced vibration testing. The results from experiments and the FEA compared to those of the proposed method are in very good correlation with an average deviation of 1.42%. Furthermore, the analytical method is implemented into a readily accessible computer-based calculation tool which allows to calculate the natural frequencies efficiently and to easily vary different parameters.

1 Introduction

Compliant mechanisms gain their mobility partially or exclusively from the compliance of its flexible members rather than from traditional joints. Nowadays this compliance is no longer seen as just a disadvantage but is used in a targeted manner in many areas of application. While lots of progress has been made in the static analysis of such systems in recent years, their dynamic behaviour has been subject to little research to date. Dynamic analysis is indispensable especially for systems that are exposed to high dynamic processes.

So far, pseudo-rigid-body models (PRBM), FEA and beam models are the most common approaches for calculating the natural frequencies of compliant mechanisms. For example, Lyon et al. [10] and Yu et al. [14] used PRBM to predict the first modal response of compliant mechanisms. Liu and Yan [9] used a modified PRBM approach by considering also the nonlinear effects and Vedant and Allison [12] propose a general pseudo-rigid body dynamic model for n-links. A hybrid compliant mechanism with a flexible central chain and a cantilever is examined through a PRBM by Zheng et al. [16].

As for the FEA Li et al. [8] and Wang et al. [13] both propose an approach based on it for the dynamic analysis of compliant mechanisms.

Concerning the classical Euler-Bernoulli beam theory, an approach is proposed for example by Vaz and de Lima Junior [3], where multi-stepped beams with changing cross sections, material properties or different boundary conditions were considered.

A different approach to obtain the vibration frequencies for uniform or non-uniform beams is the transfer-matrix-method (TMM). It is commonly used, for instance by Boiangiu et al. [2] to calculate the natural frequencies and observe the relation between them and the geometric parameters for multi-step beams. Khiem et al. [5, 6] as well as Attar [1] use this method for crack detection and investigation of damaged beams. Obradovic et al. [11] represents an analytical treatise, where the TMM is used on rigid bodies in conjunction with elastic beam sections and Hu et al. [4] propose a new closed-form dynamic model for describing the vibration characteristics of actual compliant mechanisms with serial and parallel configuration by using the TMM.

Despite extensive research, the authors are not aware of any widely applicable analytical method or standalone tool for the calculation of the natural frequencies for compliant mechanisms.

Therefore, the purpose of this paper is the development of an analytical method (Sect. 2) and its implementation into a time efficient, intuitively operable tool (Sect. 3) for determining the transverse vibration of planar compliant mechanisms with minimum input data. This will enable the analysis of the dynamic behaviour of compliant mechanisms from the design phase to its application. Thus, the natural frequencies can easily be taken into account which can safe a lot time and money. The method is validated through several experiments and FEA (Sect. 4), the results are presented and discussed (Sects. 5 and 6) and finally conclusions are drawn (Sect. 7).

2 Analytical Method

2.1 Differential Equations of Motion

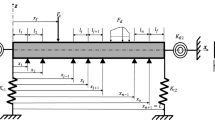
Different forms of the following compliant mechanism, as shown in Fig. 1, are evaluated in this paper, consisting of n beam segments and joints.

Fig. 1.

Compliant mechanism consisting of n beam and joint segments

The partial differential equations of motion of an elastic Euler-Bernoulli beam can be expressed as

$$\begin{aligned} \text {transversal}\quad&k_i^4 \frac{\partial ^2 w_i(x,t)}{\partial t^2}+p_i^2 \frac{\partial ^4 w_i(x,t)}{\partial x^4}=0,&i=1,\ldots ,n{} & {} \end{aligned}$$

(1a)

$$\begin{aligned} \text {axial}\quad&k_i^4 \frac{\partial ^2 u_i(x,t)}{\partial t^2}-p_i^2 \frac{\partial ^2 u_i(x,t)}{\partial x^2}=0,&i=1,\ldots ,n{} & {} \end{aligned}$$

(1b)

$$\begin{aligned} \text {with the relations} \quad&k_i^4 = \frac{\rho _i A_i}{E_i I_x(i)}\omega ^2 \quad p_i^2=\frac{\rho _i}{E_i}\omega ^2.{} & {} {}&\end{aligned}$$

(1c)

The following notations are used: $E_i$-Young modulus, $I_x(i)$-second moment of area, $\rho _i$-density, $A_i$-area surface, $\omega$-frequency, $\alpha _i$-angle between $x_i$ and $x_{i-1}$ in a positive sense, $w_i (x,t)$-transversal displacement and $u_i (x,t)$-axial displacement of the ith beam segment at axial coordinate x and time t, $x_i$-coordinate axis of the beam segments. The considered compliant mechanisms are monolithic structures; therefore, all segments are from the same material and have the same Young modulus and density. Later in this paper the Lagrange’s and Newton’s notations are used for differentiation.

Applying Bernoulli’s commonly used method of separation of variables and using the approach $W(x)= e^{\lambda x}$, the general solutions for the transversal W(x) and axial displacement U(x) are

$$\begin{aligned} W_i(x_i)=C_{1i}&\cos (k_i x_i)+C_{2i}\sin (k_i x_i)+C_{3i}\cosh (k_i x_i)+C_{4i}\sinh (k_i x_i), \end{aligned}$$

(2)

$$\begin{aligned} U_i(x_i)=C_{5i}&\cos (p_i x_i)+C_{6i}\sin (p_i x_i), \\ \text {with}\quad&i=1,\ldots ,n \nonumber \end{aligned}$$

(3)

in which $C_{1i} - C_{6i}$ are unknown constants.

2.2 Boundary Conditions

In order to solve these differential equations (2) and (3), boundary conditions are used. The boundary conditions at the beginning describe the slopes and displacement at $x_i=0$ and $i=1$, and at the end at $x_i=L_i$ and $i=n$.

Table 1. Boundary conditions, beginning and end

2.3 Continuity Conditions

The continuity conditions describe the relations of force and deformation quantities at the junction of two beam segments, see Fig. 2.

Fig. 2.

Connecting point of two adjacent beams with internal forces and moments

All internal forces must occur in collinear pairs, according to Newton’s Third Law, and must be equal in magnitude and opposite in direction. Taking further into account the following relations

$$\begin{aligned} N=U^{\prime }EA, \quad -Q=W^{\prime \prime \prime }EI_z, \quad M=W^{\prime \prime }EI_z, \end{aligned}$$

(5)

we obtain the continuity conditions regarding the internal forces and moments at the connecting point:

$$\begin{array}{l} N:\,\,\,\,\,\,\quad \quad U_i^\prime ({L_i}){A_i} = U_{i + 1}^\prime (0){A_{i + 1}}\cos {\alpha _i} + W_{i + 1}^{\prime \prime \prime }(0){I_{z,i + 1}}\sin {\alpha _i},\\ Q:\,\,\,\,\quad - W_i^{\prime \prime \prime }({L_i}){I_{z,i}} = U_{i + 1}^\prime {A_{i + 1}}\sin {\alpha _i} - W_{i + 1}^{\prime \prime \prime }(0){I_{z,i + 1}}\cos {\alpha _i},\\ M:\,\,\,\quad \quad W_i^{\prime \prime }({L_i}){I_{z,i}} = W_{i + 1}^{\prime \prime }(0){I_{z,i + 1}}.\end{array}$$

(6)

Slopes as well as axial and transversal displacements at the connecting point must be continuous, which leads to the following continuity conditions:

$$\begin{aligned} \begin{aligned} U_i(L_i)&=U_{i+1}(0)\cos {\alpha _i}-W_{i+1}(0)\sin {\alpha _i},\\ -W_i(L_i)&=U_{i+1} \sin {\alpha _i}+W_{i+1}(0)\cos {\alpha _i},\\ W_i^{\prime }(L_i)&=W_{i+1}^{\prime }(0). \end{aligned} \end{aligned}$$

(7)

2.4 Matrix Form

To describe the motion of a compliant mechanism Eqs. (1a)–(7) can be written in a simple yet ineffective matrix form as follows.

$$\begin{aligned} \left( \begin{matrix} x_{1,1} &{} x_{1,2} &{} \cdots &{} x_{1,n}\\ x_{2,1} &{} x_{2,2} &{} \cdots &{} x_{2,n}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ x_{m,1} &{} x_{m,2} &{} \cdots &{} x_{m,n} \end{matrix}\right) \begin{pmatrix} C_{11}\\ \cdots \\ C_{61}\\ C_{12}\\ \cdots \\ C_{6n} \end{pmatrix}&= \begin{pmatrix} 0\\ 0\\ \cdots \\ \cdots \\ 0 \end{pmatrix} \end{aligned}$$

(8)

$$\begin{aligned} {\textbf {T}} {\textbf {C}}&={\textbf {0}} \end{aligned}$$

(9)

where $m =n$. The second index of the vector C indicates the corresponding segment and the first index, ranging from 1–6, symbolises the coefficient. The square matrix T grows in correlation to the number of segments of the mechanism. The first 3 rows are the initial conditions for the first beam and the last 3 rows for the ending conditions of the last beam, see (5) in Table 1. In between are 6 rows each for the continuity conditions (6) and (7) of the individual connecting points. For each additional segment six new rows and columns are added to the matrix.

In order to find the natural frequency of the mechanism under consideration the non-trivial solutions of its system (8) are calculated. To do this, the determinant of the matrix T is calculated as a function of the frequency $\omega$. The values for $\omega$, for which the determinant is equal to zero, are the natural frequencies of the mechanism. The determinant calculation of such huge matrices soon exceeds the computing capacity of common computers, which makes this approach unsuitable and impractical for the calculation of compliant mechanisms with already more than three segments.

2.5 Transfer Matrices

To be able to perform the calculation faster and for compliant mechanisms with an arbitrary number of beams and joints, each segment must be considered individually—individual matrices and sets of equations must be derived and then put in relation to each other. Instead of one big matrix for the whole mechanism, the boundary and continuity conditions for each beam and connection point are set up individually and then multiplied together. This always results in one single matrix T with the size 3$\times$3, regardless of the number of segments within the mechanism. The matrix multiplication and the calculation of the determinant of the 3$\times$3 matrix can be done with high computational efficiency.

First Beam Analysing for instance the motion of the mechanism in Fig. 1, the starting point is the clamped beam 1. Respectively using the boundary conditions (4a) combined with Eqs. (2) and (3), a set of equations is formed and can be written in matrix form as follows:

$$\begin{aligned} C_{11}+C_{31}=0, \quad C_{21}+C_{41}&=0, \quad C_{51}=0,\end{aligned}$$

(10)

$$\begin{aligned} \left( \begin{matrix} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ -1 &{} 0&{} 0\\ 0 &{}-1 &{} 0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 \end{matrix}\right) \begin{pmatrix} C_{11}\\ C_{21}\\ C_{61} \end{pmatrix},&= \begin{pmatrix} C_{11}\\ C_{21}\\ C_{31}\\ C_{41}\\ C_{51}\\ C_{61} \end{pmatrix}\\ \scriptstyle (6 \times 3) \cdot (3 \times 1)&= \scriptstyle (6 \times 1) \nonumber \end{aligned}$$

(11)

$$\begin{aligned} {\textbf {T}}_0{\textbf {C}}_0&={\textbf {C}}_1. \end{aligned}$$

(12)

${\textbf {T}}_0$ for pinned and free boundary conditions are obtained in the same way. The matrices ${\textbf {T}}_i$ are called transfer matrices and the vectors ${\textbf {C}}_i$ coefficient vectors.

Last Beam Moving on to the end of the last beam of the mechanism, which is free, Eqs. (2) and (3) are combined with the boundary condition (4f). This results in the following set of equations and can also be written in matrix form:

$$\begin{aligned} \begin{aligned} -C_{1n}k_n^2 c(k_n l_n)-C_{2n}k_n^2\,s(k_n l_n)+C_{3n}k_n^2 ch(k_n l_n)+C_{4n} k_n^2 sh(k_n l_n)&=0,\\ C_{1n}k_n^3\,s(k_n l_n)-C_{2n}k_n^3 c(k_n l_n)+C_{3n}k_n^3 sh(k_n l_n)+C_{4n}k_n^3 ch(k_n l_n)&=0,\\ -C_{5n}p_n s(p_n l_n)+C_{6n}p_n c(p_n l_n)&=0. \end{aligned} \end{aligned}$$

(13)

Instead of $\texttt{sin}$ and $\texttt{sinh}$ it is $\texttt{s}$ and $\texttt{sh}$; instead of $\texttt{cos}$ and $\texttt{cosh}$ it is $\texttt{c}$ and $\texttt{ch}$. The set of equations for clamped and pinned boundary conditions are obtained in the same way. These equations, describing the end of the last beam, can also be written in matrix form, such as

$$\begin{aligned} \begin{aligned} {\textbf {T}}_n {\textbf {C}}_n&={\textbf {0}}.\\ \scriptstyle (3 \times 6) \cdot (6 \times 1)&= \scriptstyle (3 \times 1) \end{aligned} \end{aligned}$$

(14)

Connecting Point This leaves the evaluation of the two connecting points within the mechanism. Equations (6), (7) and (2), (3) lead to a set of equations, with k is a substitute for $k_i l_i$ and p for $p_i l_i$, which can be written in matrix form as demonstrated in (15)–(17).

$$\begin{aligned}&\text {T}_{iL}={\left( \begin{matrix} 0 &{} 0 &{} 0 &{} 0 &{} -A_ip_is(p) &{} A_ip_ic(p)\\ -I_ik_i^3s(k) &{} I_ik_i^3c(k) &{} -I_ik_i^3sh(k) &{} -I_ik_i^3ch(k) &{} 0 &{} 0\\ -I_ik_i^2c(k) &{} -I_ik_i^2s(k) &{} I_ik_i^2ch(k) &{} I_ik_i^2sh(k) &{} 0 &{} 0 \\ -k_is(k) &{} k_ic(k) &{} k_ish(k) &{} k_ich(k) &{} 0 &{} 0\\ c(k) &{} s(k) &{} ch(k) &{} sh(k) &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} c(p) &{} s(p) \end{matrix}\right) }\\ \nonumber \end{aligned}$$

(15)

$$\begin{aligned}&\text {T}_{iR}= \nonumber \\&{\left( \begin{matrix} 0 &{} -I_{i+1}k_{i+1}^3s(\alpha _i) &{} 0 &{} I_{i+1}k_{i+1}^3s(\alpha _i)&{} 0 &{} A_{i+1}p_{i+1}c(\alpha _i)\\ 0 &{} +I_{i+1}k_{i+1}^3c(\alpha _i)&{} 0 &{} -I_{i+1}k_{i+1}^3c(\alpha _i)&{} 0 &{} A_{i+1}p_{i+1}s(\alpha _i)\\ -I_{i+1}k_{i+1}^2 &{} 0 &{} I_{i+1}k_{i+1}^2 &{} 0 &{} 0 &{} 0 \\ 0 &{} k_{i+1} &{} 0 &{} k_{i+1} &{} 0 &{} 0\\ c(\alpha _i) &{} 0 &{} c(\alpha _i) &{} 0 &{} s(\alpha _i) &{} 0\\ -s(\alpha _i) &{} 0 &{} -s(\alpha _i) &{} 0 &{} c(\alpha _i) &{} 0 \end{matrix}\right) } \end{aligned}$$

(16)

$$\begin{array}{*{20}{c}} {}&{\quad \quad \;\;\;\;{{\bf{T}}_{iL}}{{\bf{C}}_i} = {{\bf{T}}_{iR}}{{\bf{C}}_{i + 1}}}\\ {}&{\quad \quad \quad \;{\bf{T}}_{iR}^{ - 1}{{\bf{T}}_{iL}}{{\bf{C}}_i} = {\bf{T}}_{iR}^{ - 1}{{\bf{T}}_{iR}}{{\bf{C}}_{i + 1}}}\\ {{\rm{Which\,can\,be\,written\,as}}}&{\quad \quad \;\;{{\bf{T}}_i}{{\bf{C}}_i} = {{\bf{C}}_{i + 1}}.}\\ {}&{(6 \times 6)(6 \times 1) = (6 \times 1)} \end{array}$$

(17)

2.6 Equation of the Natural Frequencies

Inserting Eqs. (11), (14) and (17) into one another leads to the following equation

$${{\textbf{T}}_n}{{\textbf{T}}_{n - 1}} \cdots {{\textbf{T}}_{i + 1}}{{\textbf{T}}_i}{{\textbf{T}}_0}{{\textbf{C}}_0} = {\textbf{0}}$$

(18)

$$\begin{aligned} \Rightarrow {\textbf {T}} {\textbf {C}}_0&=0. \end{aligned}$$

(19)

$$\begin{aligned} \text {det}({\textbf {T}})&=0. \end{aligned}$$

(20)

The natural frequencies of the mechanism correspond to the values for $\omega$ for which det(T)=0.

2.7 First Verification of the Analytical Approach

In order to prove the presented analytical method a numerical verification is carried out through FEA. For this purpose eleven mechanisms with different dimensions and angles are examined, such as the mechanism in Fig. 3. It consists of three beams with the angles $\alpha _{1,2}=\frac{\pi }{6}$ and dimensions 5$\times$5$\times$50 mm$^3$, 1$\,\times \,$1$\times$10 mm$^3$ and 5$\,\times \,$5$\times$40 mm$^3$. The material of the mechanisms is structural steel with a density of $\rho$=7850 $\frac{kg}{m^3}$ and Young’s modulus E=200,000 MPa.

Table 2. Natural frequencies of Fig. 3; results and deviation (dev.)

Fig. 3.

Exemplary mechanism, beginning clamped, end free

The Program Wolfram Mathematica 9 is used to calculate the natural frequencies with the given Eqs. (18)–(20) and the numerical analysis is carried out as a modal analysis with FEA-models using ANSYS Workbench 2019 R3.

As one can see in Table 2 the deviations of the first five natural frequencies of the mechanism shown in Fig. 3 between the analytical and numerical calculation are in a range of less than 4%. Similar deviations are obtained for the other calculated mechanisms.

3 Design of the Calculation Tool

The derived analytical method can be easily implemented into a calculation tool, due to the pre defined boundary conditions and the consistent calculation of the matrices.

3.1 Programming Language Python

For programming the graphical user interface the programming language Python was chosen with its library Tkinter. It is a universal, usually interpreted, higher programming language, which can be run platform independent. One of the great advantages of Python is the extreme variety of freely available standard libraries, which allow the language’s range of functions to be extended at will. The majority of the libraries are also platform independent, so that even larger Python programs run on Unix, Windows, macOS and other platforms without any changes.

The Python program is split into several files, for example the language-dependent terms, standard values, colours of the controls etc., making it easy to make changes to the standard configuration of the program.

3.2 Design of the Graphical User Interface for the Calculation Tool

The concept behind the structure of the user interface is a large drawing area for the two-dimensional graphical representation of the current beam configuration on the right-hand side, with all operating tools of the program on the left-hand side, see Fig. 4.

Fig. 4.

Screenshot of the calculation tool LeViTho

The two-dimensional drawing of the beams shows the width, length and angle of each beam segment. Furthermore, a graphic representation of the respective boundary conditions at the start and end is implemented. On the left side of the program the parameters are added. The Young’s-Modulus and density are defined for the whole mechanisms, whereas the geometric parameters for the beam segments are assigned individually. The program supports entering the angle in both degrees and radians, which can be selected via an associated checkbox. The selection of the beam segment can be changed using a drop-down menu or by clicking the respective segment with the mouse. Changes to the width, length or angle of a segment are shown in real time on the drawing area. Furthermore, checkboxes for the display of the coordinate system for the first segment as well as a short explanation of the dimensions and numbering of each beam segment are featured. In the lower section of the input area the user can input the frequency range, in which the calculation function will search for the natural frequencies. Below the input fields there is a button to start the calculation and another one to cancel the calculation.

Invalid entries are checked before the actual calculation is started and corresponding error messages are displayed in the result text field. During the calculation, all the solutions found in the given frequency range are displayed in the results text field, while the progress bar below shows the current calculation progress in percent as well as a rough estimate of the remaining calculation time in seconds.

Finally, the program offers the possibility to export the entered parameters (Young’s-Modulus, density, boundary conditions, geometry of each beam segment, frequency range) as well as the corresponding natural frequencies resulting from the calculation in form of a .csv file.

4 Validation and Verification

To create an assortment of reference models on which the proposed analytical method can be assessed various Test Specimens (TS) are designed and manufactured. The tests for the validation are carried out as free and forced vibration tests. The verification is then done by FEA and the parameters used can be found in the appendix Table 7.

4.1 Test Specimen Design

The TS are plane symmetric in respect to the XY-plane and the XZ-plane. For compliance with the TMM the TS have a rectangular cross section, though for mechanical and manufacturing reasons the corners of the flexure hinges are filleted, characterized as corner-filleted notch hinges, see Fig. 5.

Fig. 5.

Visual representation of test specimens parameters, see Table 3

The specimens have a constant width in the Z-direction, so they are biased to oscillate around this axis. The dimensions of the four TS are specified in Table 3. All values are within ± 0.020 the nominal value if not stated differently. Due to the immense influence of the notch height of the flexure hinge, the actual height was measured and later used for the calculations with LeViTho and for the FEA.

Table 3. Geometric dimensions of TS: L-length of whole mechanism, l-length of compliant segment, w-width, H-height, h-height compliant segment, r-radius

Compliant mechanisms can be categorized to have concentrated or distributed compliance. Specimens with a dimensionless ratio of $\frac{L}{l}\ge$ 10 are defined to have Concentrated Compliance (CC), specimens with a ratio of $\frac{L}{l}<$ 10 are defined to have Distributed Compliance (DC) [15]. Thus, TS 1 and 3 feature CC, TS 2 and 4 DC.

4.2 Material Choice and Manufacturing

To guarantee the longevity and avoid deterioration of the TS a cold work tool steel, 100MnCrW4 (DIN EN ISO 4957; 1.2510) was picked. To avoid creeping of the TS during the cutting process due to releasing internal stresses the material was annealed twice by the supplier. The Youngs-Modulus was specified by the supplier as E= 193 000 MPa, the density is measured to be 7776 $\frac{kg}{m^3}$. The TS were cut on a Wire Erosion Discharge Machine (WEDM) Charmilles Robofill 240 with a single rough cut ($v_c$= 3 $\frac{mm}{min}$).

4.3 Free Vibration Testing

The test setup for measuring the first natural frequency can be seen in Fig. 6. The TS are treated as cantilever beams. The fixed end is clamped with a set of wedges in a force-fitting manner in a clamping device. The XY-Plane is oriented parallel to the ground to avoid interaction with gravity.

Fig. 6.

Free vibration test setup with a triangulation displacement sensor

Every TS is deflected to a specified value and then released to start the oscillation. The procedure is repeated six times for every test set up, the Standard Deviation (SD) is deducted. The amplitudes are recorded over time by the laser triangulation displacement sensor (LTD) Micro Epsilon optoNCDT 1420-100, its parameters can be found in the appendix, see Table 6. The Fast Fourier Transformation (FFT) is applied to the raw data, which shows the amplitudes and corresponding frequencies.

4.4 Dynamic Vibration Testing

To recover the second natural frequency the TS are additionally examined with a Laser-Doppler-Scanning-Vibrometer. The TS are clamped in a cantilever manner to the shaker and are agitated along a band of frequencies while the Vibrometer scans the respond on the surface of the TS. The system is set to a sampling rate of 5.12 kHz at a sweep resolution of 625 mHz. The shaker is set to sweep a frequency band from 1 Hz to 1.6 kHz in a time frame of 4 seconds. Once again, the first natural frequencies are really evident. The frequency of the second planar eigenmode is found for the 2nd and 4th test specimen (DC), see Fig. 7. The 1st and 3rd specimen (CC) showed no clear frequency respond for the second planar eigenmode.

Fig. 7.

First (left) and second (right) planar normal mode of test specimen 4, excitation through Vibrometer

4.5 Verification Through Finite Element Analysis

To verify the results obtained by the TMM, the models of the test specimen are analysed with the commercial software SolidWorks with the simulation add-on. The first 5 normal modes are calculated, those corresponding with the transversal vibration on the XY-plane, see Fig. 8, are used as comparative values for the evaluation.

Fig. 8.

1st (left) and 2nd (right) planar natural frequency of TS 4 in FEM

5 Results

The prismatic TS were examined by free vibration testing. The first natural frequency is found by processing the signal from the LTD sensor with FFT. The elastic behaviour of the flexure hinge results in a well-defined peak in the amplitude spectrum, as shown for TS1 in Fig. 9, corresponding to the frequency of the first mode shape of the investigated specimen. The first natural frequency is very evident for all specimens, the second natural frequency around the Z-direction (the 3rd or 4th spatial natural frequency) though is very small and not clearly distinguishable from the background noise.

Fig. 9.

Frequency spectrum of TS1

The oscillation of the test specimen is subject to losses which results is the decay of the amplitudes over time. Energy dissipation occurs externally due to air resistance and internally due to internal friction resulting in a dampened system. From the decay of the amplitudes the logarithmic decrement $\delta$ is calculated, as shown in (21).

$$\begin{aligned} \delta =\frac{1}{i} ln\left( \frac{x(t)}{x(t+iT)}\right) \end{aligned}$$

(21)

i is an integer defining the number of consecutive positive peaks occurring within a decrement of 10 dB, x(t) is the amplitude peak value at time t, T is the period duration. From the logarithmic decrement the damping ratio $\xi$ is found in (22).

$$\xi = \left( \frac{\delta }{\sqrt{4{\pi ^{2}} + {\delta ^{2}}} } \right)$$

(22)

The damping ratio as well as the logarithmic decrement for the results of the first natural frequencies of the free vibration tests are listed in the appendix, see Table 5.

To reveal the second natural frequency of the prismatic TS a modal-analysis is carried out with a Vibrometer. The second mode shape for the specimens with DC is identified as well as the related natural frequency. The first two planar natural frequencies are also calculated for all four TS with the LeViTho tool and through FEA.

The results for free and forced vibration tests as well as the FEA and their respective deviations to LeViTho are listed in Table 4.

Table 4. Comparison of results of free and forced vibration test (V.T.) and FEA to LeViTho results; N.F.-natural frequency, $\Delta$-devitation to LeViTho

6 Discussion

As can be seen in Table 4 and is visualized in Fig. 10, the results from the experiments and the finite element analysis compared to the results obtained with the proposed analytical method implemented in the programm LeViTho are mostly in very good correlation with an average deviation of 1.42%.

Fig. 10.

Comparison of results of free and forced vibration testing, LeViTho and FEA: 1st N.F.-first natural frequency, 2nd N.F.-second natural frequency, free V.T.-free vibration test, forced V.T.-forced vibration test

The experimental results from TS 4 show comparably large deviations for the first natural frequency. As mentioned, the TS were cut via WEDM process, though they were only rough cut. This may have led to many imperfections in the surface and dimensional inaccuracy which leads to larger deviations between the experiment and the calculation with the ideal geometry (LeViTho). Another factor which would influence the natural frequency of the TS could be stress within the material, due to manufacturing processes.

Furthermore, the properties of the rim zone that was altered by the cut might have influenced the results to a certain degree, as stated by [7]. The dimensional inaccuracies were compensated in the calculations as good as possible by measuring the deviation from the nominal value, see Table 3. The calculations depend on the geometrical dimensions as well as the physical quantities of Young’s-Modulus and the density. The density was calculated from the theoretical volume of the TS and their measured weight. The Young’s-Modulus was taken as indicated by the supplier, but it was not independently measured.

Additionally, the different orientation of the TS during the two testing setups may influence the measured natural frequency. In the free vibration test run the vibration axis was oriented in line with the gravitational vector. This was not possible in the forced vibration test run due to the setup of the Vibrometer, the specimen were therefore oriented perpendicular. The somewhat larger deviations in the forced V.T. might be attributable to the acting gravity. The damping ratio was calculated for the free vibration, it is small enough to be neglected comparing to other influence factors. Furthermore, neither LeViTho nor the FEA take into consideration the filleted corners of the TS.

7 Conclusion and Outlook

This paper shows that the proposed analytical approach can be legitimately applied to compliant mechanisms for calculating their natural frequencies. Several single flexure hinges with CC and DC were designed, manufactured and tested. The frequency values obtained by this method are in very good correlation to the measured frequencies and to the results from the FEA. With the development of LeViTho a handy tool with practical application was created. It might be used in the design stage of compliant machines to prevent harmonic reactions or it could be applied to troubleshoot when existing machines show signs of harmonic interaction. The big advantage beside the reasonably precise calculations, is the fast and intuitive handling of the software, which compared to the FEA has the potential to save a good amount of time. As observed in the testing phase, compliant mechanisms are very sensible to manufacturing tolerances, in this case LeViTho can be used to simulate the consequences deriving from manufacturing variations. The current state of the analytical method implemented in LeViTho is that it is only applicable for planar continuous systems, even though the calculation of merged systems, i.e. the segments can have different material properties, is possible with few modifications. In the future, further investigations will be carried out to calculate spatial systems, systems with branching points and possibly flexure hinges.

8 Appendix

Table 5. Free vibration test results; N.F.-natural frequency, SD-standard deviation, $\delta$-logarithmic decrement, $\xi$-damping ratio

Table 6. Sensor parameters Micro Epsilon optoNCDT 1420-100

Table 7. FEA parameters