Vibration control for nonlinear overhead crane bridge subject to actuator failures and output constraints

Abstract

An active robust adaptive fault-tolerant control protocol is studied for reducing vibration of crane bridge system and handling actuator faults and output constraints simultaneously based on a partial differential equation model. The closed-loop system subject to environmental perturbations and actuator failures can be stabilized with proposed control laws. Furthermore, output constraints of trolley can always be ensured via employing barrier Lyapunov function (BLF), and uncertain actuator faults can also be compensated availably using developed adaptive control laws without any knowledge of actuator fault information. Finally, numerical simulation is provided for illustrating performance of the proposed control method.

1 Introduction

Overhead crane systems universally exist in many industrial sites such as warehouses, workshop halls, and harbors to lift and transport the cargo to the desired position. Since it is expected to fast and precisely transport the payload, assorted control methods are investigated for overhead cranes [1,2,3,4,5].

It is noteworthy that [1,2,3,4,5] all focus on oscillation elimination of the cable and position regulation of the trolley, and the influence of undesirable vibration of crane bridge is seriously neglected. However, as a matter of fact, the vibration of overhead crane bridge will bring undesirable interference to both the cable and trolley of overhead crane, which may negatively affect control performance in [1,2,3,4,5] and result in inaccurate positioning. Regarding the vibration of overhead crane bridge as general phenomenon existing in control systems, structural analysis, modeling method, and control strategy are thus investigated. In [6], a bivariate polynomial model is developed for estimating offset of main beam of gantry crane considering dynamics of payload. In [7], the 3D parametric finite element model is carried out for a crane girder, and its load-bearing ability is predicted applying finite element analysis and numerical methods. In [8], utilizing moving finite element approximation, dynamic characteristics of a main beam of crane are investigated with considering motion effect of a mass. A suspension weight-bridge crane is abstracted as a model of a mass with suspension weight moving on a supported main beam, and its vibration responses are analyzed in [9]. Nevertheless, although a small amount of researches on control design of crane bridges are done, such as [6,7,8,9], they all center on ordinary differential equation (ODE) methods.

It is generally known that the dynamic characteristics of infinite-dimensional distributed parameter systems are traditionally represented by finite critical modes to simplify control design. As a result, control and observer spillover problems may arise by using ODE model-based control methods, which need to be further resolved by developing related methods [10,11,12]. However, the additional methods in [10,11,12] will place additional difficulty on control application. To avoid spillover problem induced by the ODE model, partial differential equation (PDE) model-based control thus becomes one of research hot spots in recent years. In [13], a PDE boundary iterative learning control is addressed for flexible structures subject to input saturation and external disturbances. In [14], a robust adaptive control algorithm is proposed for a moving perturbed string. In [15], offset of flexible string with input hysteresis is successfully eliminated adopting an adaptive control. In [16], unit quaternion is employed to establish a PDE model for a 3D robot link, and control laws are addressed for regulating its orientation and restricting its elastic vibration with interferences. However, up to now, the research on vibration control of overhead bridge systems is still insufficient.

During operating safety-critical control systems, actuator failure may cause unacceptable control performance degradation and even lead to devastating effect. Consequently, the problem of actuator fault accommodation is of significant importance and required to be resolved imperatively. Compared with conservative passive fault-tolerant control [17,18,19,20,21], active adaptive tolerant control has received tremendous attention for decades due to its better capability of failure compensation and performance maintenance. Since the control reconfiguration is used in active fault-tolerant control schemes to adjust controllers in real time, active tolerant control can effectively enhance the adaptability and robustness of the system. In [22], a robust adaptive fault-tolerant control is investigated for coupled ODE beams for vibration attenuation. For linear time-invariant plants subject to uncertain actuator stuck faults, an active control strategy is addressed for asymptotic-state tracking in [23]. In [24], an adaptive backstepping control algorithm is investigated for ensuring system transient performance even when actuator faults occur. Note that controllers in [22,23,24] all need to know control directions of the system. To remove this restriction, [25] proposes a control scheme to handle unknown actuator failures without any information on control directions.

Output constraint is a significant and widespread problem in engineering practice [26, 27]. Once output constraints of control objects are exceeded, serious harm, such as sharp friction, high-speed impact, and strong extrusion, may occur and directly affects the lifetime of the system. As a result, a considerable amount of related control strategies are addressed for limiting output signals. In [28], problem of output constraints is studied in vibration control design of an Euler–Bernoulli beam considering parametric uncertainties. In [29], time-varying output restrictions are considered in control design of strict-feedback nonlinear systems by utilizing BLFs. In [30], a switching strategy with actuator redundancy is proposed for uncertain nonlinear systems with constraints as well as actuator faults.

Research done in this paper is motivated by the great inadequacy of control design of crane bridges. Main contributions of the paper are highlighted as: (1) To make up deficiency of ODE models and avoid spillover problems, a PDE model is adopted in this paper for depicting dynamics of crane bridge consisted by a Timoshenko beam and a middle rigid body with preserving all modal information; (2) a PDE model-based active robust adaptive fault-tolerant control is developed against actuator failures in terms of both total loss of effectiveness (TLOE) and partial loss of effectiveness (PLOE), and failure information does not need to be collected in the control process; (3) by applying proposed control laws, vibration and rotation of the system can be suppressed. Besides, output constraints of the middle trolley are effectively ensured with actuator faults and environmental disturbances.

It should be pointed out that problems of actuator failures and output constraints of crane bridges are first considered and resolved by this paper.

Fig. 1

An overhead crane bridge

Fig. 2

A simplified diagram of an overhead crane bridge

Besides, the high nonlinearity of the system and strong coupling effect between main beam and trolley greatly complicate control design. Consideration of shearing deformation and rotational inertia effects of bridge beam also adds difficulties to the control design of this paper. The guarantee of output constraints of the trolley and robust adaptive actuator failure compensation make this paper have certain practical application meaning, and pave the way for later researches.

This paper is organized as follows. PDE model of crane bridge is formulated in Sect. 2. In Sect. 3, an active robust adaptive fault-tolerant control scheme is addressed for stabilizing system and ensuring output constraints of the trolley. Section 4 conducts a simulation example for demonstrating validity of designed control method. Conclusions are briefly summed up in Sect. 5.

2 PDE model description and preliminaries

2.1 PDE model description

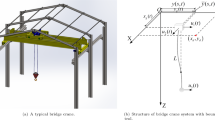
The whole system is illustrated in Fig. 1 for following modeling and control design, and a simplified system diagram is given in Fig. 2. As we have seen, the configuration in Fig. 2 represents a crane bridge consisted by a main beam which is considered as a Timoshenko beam whose density is denoted by $\rho$, and a trolley considered as a rigid body with lumped mass M as well as inertia J. Elastic deformation and rotation of beam’s cross section on the left-hand side of trolley are defined by ${{v}_{L}}\left( s,t \right)$ as well as ${{\theta }_{L}}\left( s,t \right)$, respectively, at position s. Similarly, to definitions of left ones, right ones are, respectively, represented by ${{v}_{R}}\left( s,t \right)$ and ${{\theta }_{R}}\left( s,t \right)$. Let ${{l}_{1}}$ and ${{l}_{2}}$ be the beam’s length on left and right sides of trolley, and total length of beam is denoted by l, which satisfies $l={{l}_{1}}+{{l}_{2}}$. Mass moment of inertia of main beam’s cross section is given by ${{I}_{p}}$. Bending stiffness of main beam is expressed by ${\mathrm{EI}}$. Friction coefficients due to elastic deformation and rotation of the main beam are denoted by ${{\sigma }_{1}}$ and ${{\sigma }_{2}}$, respectively. We denote offset of central body as $v\left( {{l}_{1}},t \right)$, and its rotation angle is expressed by $\theta \left( {{l}_{1}},t \right)$. Force $u\left( t \right)$ and torque $\tau \left( t \right)$ are control signals flowing from actuators into the control system for eliminating bending and rotation deflections, respectively.

The system kinetic energy ${{E}_{k}}\left( t \right)$ and potential energy ${{E}_{p}}\left( t \right)$ are given by

$$\begin{aligned} {{E}_{k}}\left( t \right) \,&=\frac{1}{2}\rho \int _{0}^{{{l}_{1}}}{{\dot{v}}_{L}^{2}\left( s,t \right) {\mathrm{d}s}} \nonumber \\&\quad +\frac{1}{2}\rho \int _{{{l}_{1}}}^{l}{{\dot{v}}_{R}^{2}\left( s,t \right) {\mathrm{d}s}}+\frac{1}{2}M{\dot{v}}_{{}}^{2}\left( {{l}_{1}},t \right) \nonumber \\&\quad +\frac{1}{2}I_{p}^{{}}\int _{0}^{{{l}_{1}}}{{\dot{\theta }}_{L}^{2}\left( s,t \right) {\mathrm{d}s}} \nonumber \\&\quad +\frac{1}{2}I_{p}^{{}}\int _{{{l}_{1}}}^{l}{{\dot{\theta }}_{R}^{2}\left( s,t \right) {\mathrm{d}s}}+\frac{1}{2}J{\dot{\theta }}_{{}}^{2}\left( {{l}_{1}},t \right) \end{aligned}$$

(1)

and

$$\begin{aligned} {{E}_{p}}\left( t \right) \,&= \frac{1}{2}K\int _{0}^{{{l}_{1}}} {{{\left( v_{Ls}^{{}}\left( s,t \right) -\theta _{L}^{{}}\left( s,t \right) \right) }^{2}}\text {d}}\text {s}\nonumber \\&\quad +\frac{1}{2}K\int _{{{l}_{1}}}^{l}{{{\left( v_{Rs}^{{}}\left( s,t \right) -\theta _{R}^{{}}\left( s,t \right) \right) }^{2}}{\mathrm{d}s}} \nonumber \\&\quad +\frac{1}{2}{\mathrm{EI}}\int _{0}^{{{l}_{1}}}{\theta _{Ls}^{2}\left( s,t \right) {\mathrm{d}s}} \nonumber \\&\quad +\frac{1}{2}{\mathrm{EI}}\int _{{{l}_{1}}}^{l}{\theta _{Rs}^{2}\left( s,t \right) \text {d}}\text {s} \end{aligned}$$

(2)

where $K=kGA$, in which k is a positive constant related to shape of main beam’s cross section; G is shear modulus; and A is cross-section area of main beam.

The virtual work is given by

$$\begin{aligned} W\left( t \right) \,&=\left( u\left( t \right) +{{d}_{1}}\left( t \right) \right) v\left( {{l}_{1}},t \right) \nonumber \\&\quad +\left( \tau \left( t \right) +{{d}_{2}}\left( t \right) \right) \theta \left( {{l}_{1}},t \right) \nonumber \\&\quad -{{\sigma }_{1}}\int _{0}^{{{l}_{1}}}{{{{\dot{v}}}_{L}}\left( s,t \right) {{v}_{L}}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\quad -{{\sigma }_{1}}\int _{{{l}_{1}}}^{l}{{{{\dot{v}}}_{R}}\left( s,t \right) {{v}_{R}}\left( s,t \right) }{\mathrm{d}s}\nonumber \\&\quad -{{\sigma }_{2}}\int _{0}^{{{l}_{1}}}{{{\theta }_{L}}\left( s,t \right) {{{{\dot{\theta }}}}_{L}}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\quad -{{\sigma }_{2}}\int _{{{l}_{1}}}^{l}{{{\theta }_{R}}\left( s,t \right) {{{{\dot{\theta }}}}_{R}}\left( s,t \right) }{\mathrm{d}s} \end{aligned}$$

(3)

where ${{d}_{1}}\left( t \right)$ and ${{d}_{2}}\left( t \right)$ are input disturbances.

Applying following Hamilton’s principle

$$\begin{aligned} \int _{{{t}_{1}}}^{{{t}_{2}}}{\left( \delta {{E}_{k}}\left( t \right) -\delta {{E}_{p}}\left( t \right) +\delta W\left( t \right) \right) }\text {d}t=0 \end{aligned}$$

(4)

in which $\delta$ denotes variational operator; ${{t}_{1}}$ and ${{t}_{2}}$ are time constants satisfying ${{t}_{1}}<t<{{t}_{2}}$; then, governing equations can be achieved as

$$\begin{aligned}&\rho {{\ddot{v}}_{L}}\left( s,t \right) -K{{v}_{Lss}}\left( s,t \right) +K{{\theta }_{Ls}}\left( s,t \right) \nonumber \\&\quad +{{\sigma }_{1}}{{\dot{v}}_{L}}\left( s,t \right) =0 \end{aligned}$$

(5)

$$\begin{aligned}&{{I}_{p}}{{{{\ddot{\theta }}}}_{L}}\left( s,t \right) -{\mathrm{EI}}{{\theta }_{Lss}}\left( s,t \right) \nonumber \\&\quad -K{{v}_{Ls}}\left( s,t \right) +K{{\theta }_{L}}\left( s,t \right) +{{\sigma }_{2}}{{{{\dot{\theta }}}}_{L}}\left( s,t \right) =0 \end{aligned}$$

(6)

for $\forall \left( s,t \right) \in \left( 0,{{l}_{1}} \right) \times \left[ 0,\infty \right)$,

$$\begin{aligned}&\rho {{\ddot{v}}_{R}}\left( s,t \right) -K{{v}_{Rss}}\left( s,t \right) +K{{\theta }_{Rs}}\left( s,t \right) \nonumber \\&\quad +{{\sigma }_{1}}{{\dot{v}}_{R}}\left( s,t \right) =0 \end{aligned}$$

(7)

$$\begin{aligned}&{{I}_{p}}{{{{\ddot{\theta }}}}_{R}}\left( s,t \right) -{\mathrm{EI}}{{\theta }_{Rss}}\left( s,t \right) -K{{v}_{Rs}}\left( s,t \right) \nonumber \\&\quad +K{{\theta }_{R}}\left( s,t \right) +{{\sigma }_{2}}{{{{\dot{\theta }}}}_{R}}\left( s,t \right) =0 \end{aligned}$$

(8)

for $\forall \left( s,t \right) \in \left( {{l}_{1}},l \right) \times \left[ 0,\infty \right)$, and boundary conditions are

$$\begin{aligned}&M{\ddot{v}}\left( {{l}_{1}},t \right) +K{{v}_{Ls}}\left( {{l}_{1}},t \right) -K{{v}_{Rs}}\left( {{l}_{1}},t \right) \nonumber \\&\quad -u\left( t \right) -{{d}_{1}}\left( t \right) =0 \end{aligned}$$

(9)

$$\begin{aligned}&J{\ddot{\theta }}\left( {{l}_{1}},t \right) +{\mathrm{EI}}{{\theta }_{Ls}}\left( {{l}_{1}},t \right) -{\mathrm{EI}}{{\theta }_{Rs}}\left( {{l}_{1}},t \right) \nonumber \\&\quad -\tau \left( t \right) -{{d}_{2}}\left( t \right) =0 \end{aligned}$$

(10)

$$\begin{aligned}&{{v}_{L}}\left( 0,t \right) ={{v}_{R}}\left( l,t \right) ={{\theta }_{L}}\left( 0,t \right) ={{\theta }_{R}}\left( l,t \right) =0 \end{aligned}$$

(11)

$$\begin{aligned}&{{v}_{L}}\left( {{l}_{1}},t \right) ={{v}_{R}}\left( {{l}_{1}},t \right) =v\left( {{l}_{1}},t \right) , \nonumber \\&{{\theta }_{L}}\left( {{l}_{1}},t \right) ={{\theta }_{R}}\left( {{l}_{1}},t \right) ={\theta }\left( {{l}_{1}},t \right) \end{aligned}$$

(12)

for $\forall t\in \left[ 0,\infty \right)$.

Remark 1

The crane bridge is treated as a Timoshenko beam equipped with a rigid body representing dynamics of the middle trolley. As shown in Eqs. (5)–(12), the effects of the shearing deformation and rotational inertia of the bridge beam are taken into account in PDE model in Eqs. (5)–(12). For practical consideration, if the bridge beam is characterized with large slender ratio, an Euler–Bernoulli beam can be used to approximately describe beam’s dynamics with ignoring the rotational inertia and shear deformation effects.

Remark 2

Environmental disturbances may be caused by the effect of the sway of the payload and wind effect on the trolley, such as vortex shedding, flutter, and buffeting, which may aggravate the vibration of the crane bridge.

2.2 Preliminaries

Some lemmas and assumptions are introduced as below to lay the foundation for following stability analysis.

Assumption 1

Upper bounds of additional disturbances on crane bridge are also bounded and set as $\left| {{d}_{1}}\left( t \right) \right| \le {{\bar{D}}_{1}}$, $\left| {{d}_{2}}\left( t \right) \right| \le {{\bar{D}}_{2}}$, in which ${{\bar{D}}_{1}}$ and ${{\bar{D}}_{2}}$ are positive constants.

Lemma 1

[31] Let ${{{\varPhi }}_{1}}\left( s,t \right)$, ${{{\varPhi }}_{2}}\left( s,t \right) \in R$ with $s\in \left[ 0,L \right]$ and $t\in \left[ 0,\infty \right)$, the inequality holds as:

$$\begin{aligned} {{{\varPhi }}_{1}}\left( s,t \right) {{{\varPhi }}_{2}}\left( s,t \right) \le \frac{1}{\gamma }{\varPhi }_{1}^{2}\left( s,t \right) +\gamma {\varPhi }_{2}^{2}\left( s,t \right) \end{aligned}$$

(13)

in which $\gamma >0$.

Lemma 2

[32] Let ${\varPhi }\left( s,t \right) \in R$ be a function defined on $s\in \left[ 0,L \right]$ and $t\in \left[ 0,\infty \right)$ which has boundary condition ${\varPhi }\left( 0,t \right) =0$, then following inequality holds:

$$\begin{aligned} {{{\varPhi }}^{2}}\left( s,t \right) \le L\int _{0}^{L}{{\varPhi }_{s}^{2}\left( s,t \right) }{\mathrm{d}s}, \forall s\in \left[ 0,L \right] . \end{aligned}$$

(14)

Remark 3

From the deduction process of Lemma 2 in [32], it can be easily derived that inequality (14) also holds when the function ${\varPhi }\left( s,t \right)$ defined in Lemma 2 satisfies ${\varPhi }\left( L,t \right) =0$ for $\forall t\in \left[ 0,\infty \right)$.

Lemma 3

For any $\vartheta \left( s,t \right)$ continuously differentiable on $s\in \left[ {{L}_{1}},{{L}_{2}} \right]$, we have following inequalities

$$\begin{aligned} \int _{{{L}_{1}}}^{{{L}_{2}}}{{{\vartheta }^{2}} \left( s,t \right) \mathrm{d}}s&\le 2\left( {{L}_{2}}-{{L}_{1}} \right) {{\vartheta }^{2}}\left( {{L}_{2}},t \right) \nonumber \\&\quad +4{{\left( {{L}_{2}}-{{L}_{1}} \right) }^{2}}\int _{{{L}_{1}}}^{{{L}_{2}}}{{{{{\vartheta }_{s}^{2}} }}\left( s,t \right) {\mathrm{d}s}} \end{aligned}$$

(15)

$$\begin{aligned} \int _{{{L}_{1}}}^{{{L}_{2}}}{{{\vartheta }^{2}} \left( s,t \right) \mathrm{d}s}&\le 2\left( {{L}_{2}}-{{L}_{1}} \right) {{\vartheta }^{2}}\left( {{L}_{1}},t \right) \nonumber \\&\quad +4{{\left( {{L}_{2}}-{{L}_{1}} \right) }^{2}}\int _{{{L}_{1}}}^{{{L}_{2}}}{{{{{\vartheta }_{s}^{2}} }}\left( s,t \right) {\mathrm{d}s}}. \end{aligned}$$

(16)

Remark 4

The proof of Lemma 3 is replenished in this remark. Utilizing integration by part, we have

$$\begin{aligned}&2\int _{{{L}_{1}}}^{{{L}_{2}}}{\left( s-{{L}_{1}} \right) \vartheta \left( s,t \right) {{\vartheta }_{s}}\left( s,t \right) {\mathrm{d}s}} \nonumber \\&\quad =\left( {{L}_{2}}-{{L}_{1}} \right) \vartheta _{{}}^{2}\left( {{L}_{2}},t \right) -\int _{{{L}_{1}}}^{{{L}_{2}}}{\vartheta _{{}}^{2}\left( s,t \right) }{\mathrm{d}s}. \end{aligned}$$

(17)

Then, we get

$$\begin{aligned}&\int _{{{L}_{1}}}^{{{L}_{2}}}{{{\vartheta }^{2}}\left( s,t \right) {\mathrm{d}s}} \nonumber \\&\quad = \left( {{L}_{2}}-{{L}_{1}} \right) \vartheta _{{}}^{2}\left( {{L}_{2}},t \right) \nonumber \\&\qquad -2\int _{{{L}_{1}}}^{{{L}_{2}}}{\left( s-{{L}_{1}} \right) \vartheta \left( s,t \right) {{\vartheta }_{s}}\left( s,t \right) {\mathrm{d}s}} \nonumber \\&\quad \le \left( {{L}_{2}}-{{L}_{1}} \right) \vartheta _{{}}^{2}\left( {{L}_{2}},t \right) +\frac{1}{2}\int _{{{L}_{1}}}^{{{L}_{2}}}{{{\vartheta }^{2}}\left( s,t \right) {\mathrm{d}s}} \nonumber \\&\qquad +2{{\left( {{L}_{2}}-{{L}_{1}} \right) }^{2}}\int _{{{L}_{1}}}^{{{L}_{2}}}{\vartheta _{s}^{2}\left( s,t \right) {\mathrm{d}s}}. \end{aligned}$$

(18)

From inequality (18), one can attain

$$\begin{aligned} \int _{{{L}_{1}}}^{{{L}_{2}}}{{{\vartheta }^{2}}\left( s,t \right) {\mathrm{d}s}}\,&\le 2\left( {{L}_{2}}-{{L}_{1}} \right) \vartheta _{{}}^{2}\left( {{L}_{2}},t \right) \nonumber \\&\quad +4{{\left( {{L}_{2}}-{{L}_{1}} \right) }^{2}}\int _{{{L}_{1}}}^{{{L}_{2}}}{\vartheta _{s}^{2}\left( s,t \right) {\mathrm{d}s}}. \end{aligned}$$

(19)

Inequality (16) can be achieved in a similar way.

Remark 5

From Lemma 3 and boundary conditions in Eq. (11), we have

$$\begin{aligned}&\int _{0}^{{{l}_{1}}}{v_{L}^{2}}\left( s,t \right) {\mathrm{d}s}\le 4l_{1}^{2}\int _{0}^{{{l}_{1}}}{v_{Ls}^{2}\left( s,t \right) \text {d}}\text {s},\nonumber \\&\int _{{{l}_{1}}}^{l}{v_{R}^{2}}\left( s,t \right) {\mathrm{d}s}\le 4l_{2}^{2}\int _{{{l}_{1}}}^{l}{v_{Rs}^{2}\left( s,t \right) \text {d}}\text {s} \end{aligned}$$

(20)

$$\begin{aligned}&\int _{0}^{{{l}_{1}}}{\theta _{L}^{2}}\left( s,t \right) {\mathrm{d}s}\le 4l_{1}^{2}\int _{0}^{{{l}_{1}}}{\theta _{Ls}^{2}\left( s,t \right) {\mathrm{d}s}}, \nonumber \\&\int _{{{l}_{1}}}^{l}{\theta _{R}^{2}}\left( s,t \right) {\mathrm{d}s}\le 4l_{2}^{2}\int _{{{l}_{1}}}^{l}{\theta _{Rs}^{2}\left( s,t \right) \text {d}}\text {s}. \end{aligned}$$

(21)

Assumption 2

System initial conditions are bounded, and initial conditions of trolley satisfy $\left| v\left( {{l}_{1}},0 \right) \right| <k_{1}^{{}}$ and $\left| \theta \left( {{l}_{1}},0 \right) \right| <k_{2}^{{}}$, where $k_{1}^{{}}$ and $k_{2}^{{}}$ are positive limitations of $v\left( {{l}_{1}},t \right)$ and $\theta \left( {{l}_{1}},t \right)$, respectively.

Remark 6

Assumption 2 is raised according to the definition of BLF and its features mentioned by [29, 33] such that the output constraints can be ensured when the initial states of the crane bridge system satisfy Assumption 2.

Lemma 4

[34] Let $\digamma \in {\mathbb {R}}_{+}$ be a nonnegative function of time. If ${\dot{\digamma }}\le -r$ where r is a nonnegative time-related function, and ${\dot{r}}\in {{\mathcal {L}}_{\infty }}$, then we have $\lim \nolimits _{t\rightarrow \infty }\,r=0$.

3 Controller design

We first propose a robust control scheme utilizing BLF [35] to resolve output constraint problems with healthy actuators and disturbances. Then, an active robust adaptive fault-tolerant control is developed for crane bridge with output constraints of the middle trolley to compensate for actuator failures in terms of TLOE and PLOE.

3.1 Robust controller design for system with output constraints and healthy actuators

In this part, with fault-free actuators, a BLF-based robust control protocol is designed using backstepping technology to handle disturbances and output constraints of middle trolley.

First, the following transform of coordinate is made

$$\begin{aligned} {{\eta }_{1}}\left( t \right)&=v\left( {{l}_{1}},t \right) , {{\eta }_{2}}\left( t \right) =\theta \left( {{l}_{1}},t \right) \end{aligned}$$

(22)

$$\begin{aligned} {{\eta }_{3}}\left( t \right)&={{{\dot{\eta }}}_{1}}\left( t \right) +{{\varpi }_{1}}\left( t \right) , {{\eta }_{4}}\left( t \right) ={{{\dot{\eta }}}_{2}}\left( t \right) +{{\varpi }_{2}}\left( t \right) \end{aligned}$$

(23)

in which ${{\varpi }_{1}}\left( t \right)$ and ${{\varpi }_{2}}\left( t \right)$ are virtual control laws designed as

$$\begin{aligned} {{\varpi }_{1}}\left( t \right)&=\frac{\alpha }{\beta }{{\eta }_{1}}\left( t \right) \end{aligned}$$

(24)

$$\begin{aligned} {{\varpi }_{2}}\left( t \right)&=\frac{\alpha }{\beta }{{\eta }_{2}}\left( t \right) \end{aligned}$$

(25)

in which $\alpha >0$ as well as $\beta >0$.

We define

$$\begin{aligned} {{\mu }_{1}}\left( t \right)&={{k}_{3}}{{\eta }_{3}}\left( t \right) \text {+}{{{\bar{D}}}_{1}} {\mathrm{sgn}} \left( {{\eta }_{3}}\left( t \right) \right) \nonumber \\&\quad -A\left( t \right) +M\frac{\alpha }{\beta }{\dot{v}}\left( {{l}_{1}},t \right) \nonumber \\&\quad +\frac{{{k}_{5}}{{\eta }_{3}}\left( t \right) +{{k}_{1}}v\left( {{l}_{1}},t \right) +A\left( t \right) }{a\left( t \right) } \nonumber \\&\quad +\frac{M{{\eta }_{3}}\left( t \right) }{a\left( t \right) }\frac{v\left( {{l}_{1}},t \right) {\dot{v}}\left( {{l}_{1}},t \right) }{k_{1}^{2}-v_{{}}^{2}\left( {{l}_{1}},t \right) } \end{aligned}$$

(26)

$$\begin{aligned} {{\mu }_{2}}\left( t \right)&={{k}_{4}}{{\eta }_{4}}\left( t \right) \text {+}{{{\bar{D}}}_{2}}{\mathrm{sgn}} \left( {{\eta }_{4}}\left( t \right) \right) -B\left( t \right) \nonumber \\&\quad +J\frac{\alpha }{\beta }{\dot{\theta }}\left( {{l}_{1}},t \right) \nonumber \\&\quad +\frac{{{k}_{6}}{{\eta }_{4}}\left( t \right) +{{k}_{2}}\theta \left( {{l}_{1}},t \right) +B\left( t \right) }{b\left( t \right) } \nonumber \\&\quad +\frac{J{{\eta }_{4}}\left( t \right) }{b\left( t \right) }\frac{\theta \left( {{l}_{1}},t \right) {\dot{\theta }}\left( {{l}_{1}},t \right) }{k_{2}^{2}-\theta _{{}}^{2}\left( {{l}_{1}},t \right) } \end{aligned}$$

(27)

where ${{k}_{3}},{{k}_{4}},{{k}_{5}},{{k}_{6}}>0$, $A\left( t \right) =K{{v}_{Ls}}\left( {{l}_{1}},t \right) -K{{v}_{Rs}}\left( {{l}_{1}},t \right)$, and $B\left( t \right) ={\mathrm{EI}}{{\theta }_{Ls}}\left( {{l}_{1}},t \right) -{\mathrm{EI}}{{\theta }_{Rs}}\left( {{l}_{1}},t \right)$.

Then, controllers are designed as

$$\begin{aligned} u\left( t \right)&=-{{\mu }_{1}}\left( t \right) \end{aligned}$$

(28)

$$\begin{aligned} \tau \left( t \right)&=-{{\mu }_{2}}\left( t \right) . \end{aligned}$$

(29)

Remark 7

BLF has wide utilization on handling constraints for systems, and it yields a value which approaches infinity as its arguments approach some limits, which can be regarded as the main feature of BLF. Inspired by this idea, BLF has been applied for the control of overhead crane bridge subject to output constraints, which fully embodies the innovative use of BLF in this paper. The definition and properties of BLF can be found in [29, 33], which is considered as the significant theoretical support of this paper.

Remark 8

All control signals in Eqs. (26)–(29) are measurable and implementable. For instance, $v\left( {{l}_{1}},t \right)$ and $\theta \left( {{l}_{1}},t \right)$ can be measured using laser displacement sensor and inclinometer, respectively. Furthermore, other control signals can also be achieved via backward difference algorithm of $v\left( {{l}_{1}},t \right)$ as well as $\theta \left( {{l}_{1}},t \right)$ with respect to time or space, respectively. Besides, the input signal $u\left( t \right)$ can be generated by using a flap-based effector [36] or a micro-trailing edge effector [37], and input $\tau \left( t \right)$ can be realized by the permanent magnet acting on the trolley applying an electromagnet [36].

We design $v\left( s,t \right) =\left\{ \begin{matrix} {{v}_{L}}\left( s,t \right) ,\text { 0}\le s<{{l}_{1}}\text { } \\ v\left( {{l}_{1}},t \right) ,\text { }s={{l}_{1}} \\ {{v}_{R}}\left( s,t \right) ,\text { }{{l}_{1}}\text {}<s\le l \\ \end{matrix} \right.$ and $\theta \left( s,t \right) =\left\{ \begin{matrix} {{\theta }_{L}}\left( {{l}_{1}},t \right) ,\text { 0}\le s<{{l}_{1}}\text { } \\ \theta \left( {{l}_{1}},t \right) ,\text { }s={{l}_{1}} \\ {{\theta }_{R}}\left( {{l}_{1}},t \right) ,\text { }{{l}_{1}}\text {}<s\le l \\ \end{matrix} \right.$, and the control scheme in Eqs. (26)–(29) has the following desired property.

Theorem 1

Under Assumptions 1 and 2, robust control laws in Eqs. (26)–(29) ensure the boundedness of closed-loop signals of overhead crane bridge system in Eqs. (5)–(12) subject to disturbances. The closed-loop system is exponentially stable with output constraints of middle trolley, which means that $\lim \nolimits _{t\rightarrow \infty } \,v\left( s,t \right) = \lim \nolimits _{t\rightarrow \infty } \,\theta \left( s,t \right) =0$ holds for $\forall s\in \left[ 0,l \right]$, and $\left| v\left( {{l}_{1}},t \right) \right| <k_{1}^{{}}$, $\left| \theta \left( {{l}_{1}},t \right) \right| <k_{2}^{{}}$ hold for $\forall t\in \left[ 0,\infty \right)$.

Proof

First, define a Lyapunov function as

$$\begin{aligned} {{V}_{a}}\left( t \right) =\frac{\beta }{2}{{k}_{1}}\eta _{1}^{2}\left( t \right) +\frac{\beta }{2}{{k}_{2}}\eta _{2}^{2}\left( t \right) \end{aligned}$$

(30)

where ${{k}_{1}}>0$, ${{k}_{2}}>0$ and its time derivative is calculated as

$$\begin{aligned} {{{\dot{V}}}_{a}}\left( t \right) =\beta {{k}_{1}}v\left( {{l}_{1}},t \right) {\dot{v}}\left( {{l}_{1}},t \right) +\beta {{k}_{2}}\theta \left( {{l}_{1}},t \right) {\dot{\theta }}\left( {{l}_{1}},t \right) . \end{aligned}$$

(31)

To ensure output constraints, BLF is introduced to Lyapunov function and let

$$\begin{aligned} {{V}_{1}}\left( t \right) ={{V}_{a}}\left( t \right) +\frac{\beta }{2}M\eta _{3}^{2}\left( t \right) a\left( t \right) +\frac{\beta }{2}J\eta _{4}^{2}\left( t \right) b\left( t \right) \end{aligned}$$

(32)

where $a\left( t \right) =\ln \frac{2k_{1}^{2}}{k_{1}^{2}-v_{{}}^{2}\left( {{l}_{1}},t \right) }$ and $b\left( t \right) =\ln \frac{2k_{2}^{2}}{k_{2}^{2}-\theta _{{}}^{2}\left( {{l}_{1}},t \right) }$.

Taking time derivative of ${{V}_{1}}\left( t \right)$, we achieve

$$\begin{aligned} {{{\dot{V}}}_{1}}\left( t \right)&={{{\dot{V}}}_{a}}\left( t \right) +\beta M\eta _{3}^{{}}\left( t \right) {\dot{\eta }}_{3}^{{}}\left( t \right) a\left( t \right) \nonumber \\&\quad +\,\beta J\eta _{4}^{{}}\left( t \right) {\dot{\eta }}_{4}^{{}}\left( t \right) b\left( t \right) \nonumber \\&\quad +\,\frac{\beta }{2}M\eta _{3}^{2}\left( t \right) \dot{a}\left( t \right) +\frac{\beta }{2}J\eta _{4}^{2}\left( t \right) {\dot{b}}\left( t \right) \nonumber \\&=\beta \eta _{3}^{{}}\left( t \right) \nonumber \\&\quad \left( -K{{v}_{Ls}}\left( {{l}_{1}},t \right) +K{{v}_{Rs}}\left( {{l}_{1}},t \right) +u\left( t \right) \right. \nonumber \\&\qquad \left. +\,{{d}_{1}}\left( t \right) +M\frac{\alpha }{\beta }{\dot{v}}\left( {{l}_{1}},t \right) \right) a\left( t \right) +\beta \eta _{4}^{{}}\left( t \right) \nonumber \\&\quad \left( -{\mathrm{EI}}{{\theta }_{Ls}}\left( {{l}_{1}},t \right) +{\mathrm{EI}}{{\theta }_{Rs}}\left( {{l}_{1}},t \right) \right. \nonumber \\&\qquad \left. +\,\tau \left( t \right) +{{d}_{2}}\left( t \right) +J\frac{\alpha }{\beta }{\dot{\theta }}\left( {{l}_{1}},t \right) \right) b\left( t \right) \nonumber \\&\quad +\,\beta M\eta _{3}^{2}\left( t \right) \frac{v\left( {{l}_{1}},t \right) {\dot{v}}\left( {{l}_{1}},t \right) }{k_{1}^{2}-v_{{}}^{2}\left( {{l}_{1}},t \right) } \nonumber \\&\quad +\,\beta J\eta _{4}^{2}\left( t \right) \frac{\theta \left( {{l}_{1}},t \right) {\dot{\theta }}\left( {{l}_{1}},t \right) }{k_{2}^{2}-\theta _{{}}^{2}\left( {{l}_{1}},t \right) } \nonumber \\&\quad +\,\beta {{k}_{1}}v\left( {{l}_{1}},t \right) {\dot{v}}\left( {{l}_{1}},t \right) \nonumber \\&\quad +\,\beta {{k}_{2}}\theta \left( {{l}_{1}},t \right) {\dot{\theta }}\left( {{l}_{1}},t \right) . \end{aligned}$$

(33)

Then, substitute Eqs. (26)–(29) into Eq. (33)

$$\begin{aligned} {{{\dot{V}}}_{1}}\left( t \right)&\le \beta \eta _{3}^{{}}\left( t \right) \nonumber \\&\quad \left( -{{k}_{3}}{{\eta }_{3}}\left( t \right) -\frac{{{k}_{5}}{{\eta }_{3}}\left( t \right) +{{k}_{1}}v\left( {{l}_{1}},t \right) +A\left( t \right) }{a\left( t \right) } \right. \nonumber \\&\qquad \left. -\,\frac{M{{\eta }_{3}}\left( t \right) }{a\left( t \right) }\frac{v\left( {{l}_{1}},t \right) {\dot{v}}\left( {{l}_{1}},t \right) }{k_{1}^{2}-v_{{}}^{2}\left( {{l}_{1}},t \right) }\right) a\left( t \right) +\beta \eta _{4}^{{}}\left( t \right) \nonumber \\&\quad \left( -{{k}_{4}}{{\eta }_{4}}\left( t \right) -\frac{{{k}_{6}}{{\eta }_{4}}\left( t \right) +{{k}_{2}}\theta \left( {{l}_{1}},t \right) +B\left( t \right) }{b\left( t \right) } \right. \nonumber \\&\qquad \left. -\,\frac{J{{\eta }_{4}}\left( t \right) }{b\left( t \right) }\frac{\theta \left( {{l}_{1}},t \right) {\dot{\theta }}\left( {{l}_{1}},t \right) }{k_{2}^{2}-\theta _{{}}^{2}\left( {{l}_{1}},t \right) }\right) b\left( t \right) \nonumber \\&\quad +\beta M\eta _{3}^{2}\left( t \right) \frac{v\left( {{l}_{1}},t \right) {\dot{v}}\left( {{l}_{1}},t \right) }{k_{1}^{2}-v\left( {{l}_{1}},t \right) } \nonumber \\&\quad +\beta J\eta _{4}^{2}\left( t \right) \frac{\theta \left( {{l}_{1}},t \right) {\dot{\theta }}\left( {{l}_{1}},t \right) }{k_{2}^{2}-{{\theta }^{2}}\left( {{l}_{1}},t \right) } \nonumber \\&\quad +\beta {{k}_{1}}v\left( {{l}_{1}},t \right) {\dot{v}}\left( {{l}_{1}},t \right) \nonumber \\&\quad +\,\beta {{k}_{2}}\theta \left( {{l}_{1}},t \right) {\dot{\theta }}\left( {{l}_{1}},t \right) . \end{aligned}$$

(34)

Thus, from inequality (34) and designed controllers in Eqs. (26)–(29), it produces

$$\begin{aligned} {{{\dot{V}}}_{1}}\left( t \right) \le -\beta {{k}_{3}}\eta _{3}^{2}\left( t \right) a\left( t \right) -\beta {{k}_{4}}\eta _{4}^{2}\left( t \right) b\left( t \right) +D \end{aligned}$$

(35)

where

$$\begin{aligned} D&=-\beta \eta _{3}^{{}}\left( t \right) \left( {{k}_{5}}{{\eta }_{3}}\left( t \right) +{{k}_{1}}v\left( {{l}_{1}},t \right) \right) -\beta \eta _{3}^{{}}\left( t \right) A\left( t \right) \nonumber \\&\quad -\beta \eta _{4}^{{}}\left( t \right) \left( {{k}_{6}}{{\eta }_{4}}\left( t \right) +{{k}_{2}}\theta \left( {{l}_{1}},t \right) \right) -\beta \eta _{4}^{{}}\left( t \right) B\left( t \right) \nonumber \\&\quad +\beta {{k}_{1}}v\left( {{l}_{1}},t \right) {\dot{v}}\left( {{l}_{1}},t \right) +\beta {{k}_{2}}\theta \left( {{l}_{1}},t \right) {\dot{\theta }}\left( {{l}_{1}},t \right) \nonumber \\&=-\,{{k}_{5}}\beta \eta _{3}^{2}\left( t \right) -\alpha {{k}_{1}}v_{{}}^{2}\left( {{l}_{1}},t \right) -\beta \eta _{3}^{{}}\left( t \right) A\left( t \right) \nonumber \\&\quad -{{k}_{6}}\beta \eta _{4}^{2}\left( t \right) -\alpha {{k}_{2}}{{\theta }^{2}}\left( {{l}_{1}},t \right) -\beta \eta _{4}^{{}}\left( t \right) B\left( t \right) . \end{aligned}$$

(36)

$\square$

The system stability can be analyzed by designing following Lyapunov function

$$\begin{aligned} V\left( t \right) ={{V}_{1}}\left( t \right) +{{V}_{2}}\left( t \right) +{{V}_{3}}\left( t \right) +{{V}_{4}}\left( t \right) \end{aligned}$$

(37)

in which

$$\begin{aligned} {{V}_{2}}\left( t \right)&=\frac{\beta }{2}\rho \int _{0}^{{{l}_{1}}}{{\dot{v}}_{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\beta }{2}K\int _{0}^{{{l}_{1}}}{{{\left( \theta _{L}^{{}}\left( s,t \right) -{{v}_{Ls}}\left( s,t \right) \right) }^{2}}}{\mathrm{d}s} \nonumber \\&\quad +\frac{\beta }{2}{{I}_{p}}\int _{0}^{{{l}_{1}}}{{\dot{\theta }}_{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\beta }{2}{\mathrm{EI}}\int _{0}^{{{l}_{1}}}{\theta _{Ls}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\beta }{2}\rho \int _{{{l}_{1}}}^{l}{{\dot{v}}_{R}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\beta }{2}K\int _{{{l}_{1}}}^{l}{{{\left( \theta _{R}^{{}}\left( s,t \right) -{{v}_{Rs}}\left( s,t \right) \right) }^{2}}}{\mathrm{d}s} \nonumber \\&\quad +\frac{\beta }{2}{{I}_{p}}\int _{{{l}_{1}}}^{l}{{\dot{\theta }}_{R}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\beta }{2}{\mathrm{EI}}\int _{{{l}_{1}}}^{l}{\theta _{Rs}^{2}}\left( s,t \right) {\mathrm{d}s} \end{aligned}$$

(38)

$$\begin{aligned} {{V}_{3}}\left( t \right)&=\alpha \rho \int _{0}^{{{l}_{1}}}{{\dot{v}}_{L}^{{}}}\left( s,t \right) v_{L}^{{}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\alpha {{I}_{p}}\int _{0}^{{{l}_{1}}}{{\dot{\theta }}_{L}^{{}}}\left( s,t \right) \theta _{L}^{{}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\alpha \rho \int _{{{l}_{1}}}^{l}{{\dot{v}}_{R}^{{}}}\left( s,t \right) v_{R}^{{}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\alpha {{I}_{p}}\int _{{{l}_{1}}}^{l}{{\dot{\theta }}_{R}^{{}}}\left( s,t \right) \theta _{R}^{{}}\left( s,t \right) {\mathrm{d}s} \end{aligned}$$

(39)

$$\begin{aligned} {{V}_{4}}\left( t \right)&=\frac{\alpha {{\sigma }_{1}}}{2}\int _{0}^{{{l}_{1}}}{v_{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\alpha {{\sigma }_{2}}}{2}\int _{0}^{{{l}_{1}}}{\theta _{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\alpha {{\sigma }_{1}}}{2}\int _{{{l}_{1}}}^{l}{v_{R}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\alpha {{\sigma }_{2}}}{2}\int _{{{l}_{1}}}^{l}{\theta _{R}^{2}}\left( s,t \right) {\mathrm{d}s}. \end{aligned}$$

(40)

To verify the positive definiteness of $V\left( t \right)$, we define

$$\begin{aligned} \chi \left( t \right)&=\int _{0}^{{{l}_{1}}}{{\dot{v}}_{L}^{2}}\left( s,t \right) {\mathrm{d}s}+\int _{0}^{{{l}_{1}}}{{\dot{\theta }}_{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\int _{0}^{{{l}_{1}}}{\theta _{Ls}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\int _{0}^{{{l}_{1}}}{v_{Ls}^{2}\left( s,t \right) }{\mathrm{d}s}+\int _{0}^{{{l}_{1}}}{\theta _{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\int _{0}^{{{l}_{1}}}{v_{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\int _{{{l}_{1}}}^{l}{{\dot{v}}_{R}^{2}}\left( s,t \right) {\mathrm{d}s}+\int _{{{l}_{1}}}^{l}{{\dot{\theta }}_{R}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\int _{{{l}_{1}}}^{l}{\theta _{Rs}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\int _{{{l}_{1}}}^{l}{v_{Rs}^{2}\left( s,t \right) }{\mathrm{d}s}+\int _{{{l}_{1}}}^{l}{\theta _{R}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\int _{{{l}_{1}}}^{l}{v_{R}^{2}}\left( s,t \right) {\mathrm{d}s}. \end{aligned}$$

(41)

From Eqs. (38) and (40) and inequalities (20) and (21), we can obtain

$$\begin{aligned} {{V}_{2}}\left( t \right) +{{V}_{4}}\left( t \right)&\ge \frac{\beta }{2}\rho \int _{0}^{{{l}_{1}}}{{\dot{v}}_{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\alpha {{\sigma }_{1}}}{2}\int _{0}^{{{l}_{1}}}{v_{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\beta }{2}{{I}_{p}}\int _{0}^{{{l}_{1}}}{{\dot{\theta }}_{L}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\frac{\beta }{4}{\mathrm{EI}}\int _{0}^{{{l}_{1}}}{\theta _{Ls}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\int _{0}^{{{l}_{1}}}{{\varvec{{\varOmega }}}_{1}^{\text {T}}\left( s,t \right) }{{{\varvec{{\varXi }}}}_{1}}{\varvec{{\varOmega }}}_{1}^{{}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\frac{\beta }{2}\rho \int _{{{l}_{1}}}^{l}{{\dot{v}}_{R}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\alpha {{\sigma }_{1}}}{2}\int _{{{l}_{1}}}^{l}{v_{R}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\frac{\beta }{2}{{I}_{p}}\int _{{{l}_{1}}}^{l}{{\dot{\theta }}_{R}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\beta }{4}{\mathrm{EI}}\int _{{{l}_{1}}}^{l}{\theta _{Rs}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\int _{{{l}_{1}}}^{l}{{\varvec{{\varOmega }}}_{2}^{\text {T}}\left( s,t \right) }{{{\varvec{{\varXi }}}}_{2}}{\varvec{{\varOmega }}}_{2}^{{}}\left( s,t \right) {\mathrm{d}s} \end{aligned}$$

(42)

in which ${{{\varvec{{\varOmega }}}}_{1}}\left( s,t \right) ={{\left[ \begin{matrix} \theta _{L}^{{}}\left( s,t \right) &{} v_{Ls}^{{}}\left( s,t \right) \\ \end{matrix} \right] }^{\text {T}}}$, ${{{\varvec{{\varOmega }}}}_{2}}\left( s,t \right) ={{\left[ \begin{matrix} \theta _{R}^{{}}\left( s,t \right) &{} v_{Rs}^{{}}\left( s,t \right) \\ \end{matrix} \right] }^{\text {T}}}$, and ${{{\varvec{{\varXi }}}}_{c}}=\left[ \begin{matrix} {\frac{\beta {\mathrm{EI}}}{16l_{c}^{2}}+\frac{\beta }{2}K+\frac{\alpha {{\sigma }_{2}}}{2}} &{} -\frac{\beta }{2}K \\ {-\frac{\beta }{2}K} &{} \frac{\beta }{2}K \\ \end{matrix} \right]$ is a positive definite matrix for $c=1,2$.

Thus, we have

$$\begin{aligned} {{V}_{2}}\left( t \right) +{{V}_{4}}\left( t \right) \ge {{\lambda }_{1}}\chi \left( t \right) \end{aligned}$$

(43)

where ${{\lambda }_{1}}=\min \left\{ \frac{\beta }{2}\rho ,\frac{\beta }{2}{{I}_{p}},\frac{\beta }{4}{\mathrm{EI}},{{\lambda }_{\min }}\left( {{{\varvec{{\varXi }}}}_{1}} \right) ,{{\lambda }_{\min }}\left( {{{\varvec{{\varXi }}}}_{2}} \right) ,\frac{\alpha {{\sigma }_{1}}}{2} \right\} >0$, and ${{\lambda }_{\min }}\left( {{{\varvec{{\varXi }}}}_{c}} \right)$ is defined as the minimal eigenvalue of ${{{\varvec{{\varXi }}}}_{c}}$, $c=1,2$.

According to Eqs. (38) and (40) and inequalities (20) and (21), we achieve

$$\begin{aligned} {{V}_{2}}\left( t \right) +{{V}_{4}}\left( t \right)&\le \frac{\beta }{2}\rho \int _{0}^{{{l}_{1}}}{{\dot{v}}_{L}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\frac{\alpha {{\sigma }_{1}}}{2}\int _{0}^{{{l}_{1}}}{v_{L}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\beta K\int _{0}^{{{l}_{1}}}{v_{Ls}^{2}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\quad +\frac{\beta }{2}{{I}_{p}}\int _{0}^{{{l}_{1}}}{{\dot{\theta }}_{L}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\frac{\beta }{2}{\mathrm{EI}}\int _{0}^{{{l}_{1}}}{\theta _{Ls}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\left( \beta K+\frac{\alpha {{\sigma }_{2}}}{2} \right) \int _{0}^{{{l}_{1}}}{\theta _{L}^{2}\left( s,t \right) }{\mathrm{d}s}\nonumber \\&\quad +\frac{\beta }{2}\rho \int _{{{l}_{1}}}^{l}{{\dot{v}}_{R}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\alpha {{\sigma }_{1}}}{2}\int _{{{l}_{1}}}^{l}{v_{R}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\beta K\int _{{{l}_{1}}}^{l}{v_{Rs}^{2}\left( s,t \right) }{\mathrm{d}s}\nonumber \\&\quad +\frac{\beta }{2}{{I}_{p}}\int _{{{l}_{1}}}^{l}{{\dot{\theta }}_{R}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\beta }{2}{\mathrm{EI}}\int _{{{l}_{1}}}^{l}{\theta _{Rs}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\left( \beta K+\frac{\alpha {{\sigma }_{2}}}{2} \right) \int _{{{l}_{1}}}^{l}{\theta _{R}^{2}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\le {{\lambda }_{2}}\chi \left( t \right) \end{aligned}$$

(44)

where ${{\lambda }_{2}}=\max \left\{ \frac{1}{2}\beta \rho ,\frac{\beta }{2}{{I}_{p}},\frac{\beta }{2}{\mathrm{EI}},\beta K+\frac{\alpha {{\sigma }_{2}}}{2},\frac{\alpha {{\sigma }_{1}}}{2} \right\} >0$.

Using Eq. (39), we can get the following inequality

$$\begin{aligned} \left| {{V}_{3}}\left( t \right) \right|&\le \frac{\alpha \rho }{2}\int _{0}^{{{l}_{1}}}{{\dot{v}}_{L}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\frac{\alpha \rho }{2}\int _{0}^{{{l}_{1}}}{v_{L}^{2}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\quad +\frac{\alpha {{I}_{p}}}{2}\int _{0}^{{{l}_{1}}}{{\dot{\theta }}_{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad +\frac{\alpha {{I}_{p}}}{2}\int _{0}^{{{l}_{1}}}{\theta _{L}^{2}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\quad +\frac{\alpha \rho }{2}\int _{{{l}_{1}}}^{l}{{\dot{v}}_{R}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\frac{\alpha \rho }{2}\int _{{{l}_{1}}}^{l}{v_{R}^{2}\left( s,t \right) }{\mathrm{d}s}\nonumber \\&\quad +\frac{\alpha {{I}_{p}}}{2}\int _{{{l}_{1}}}^{l}{{\dot{\theta }}_{R}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\frac{\alpha {{I}_{p}}}{2}\int _{{{l}_{1}}}^{l}{\theta _{R}^{2}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\le {{\lambda }_{3}}\chi \left( t \right) \end{aligned}$$

(45)

in which ${{\lambda }_{3}}=\max \left\{ \frac{1}{2}\alpha {{I}_{p}},\frac{1}{2}\alpha \rho \right\} >0$.

If $\alpha$ and $\beta$ are selected to meet ${{\lambda }_{1}}>{{\lambda }_{3}}$, we have

$$\begin{aligned} 0&<\left( {{\lambda }_{1}}-{{\lambda }_{3}} \right) \chi \left( t \right) \le {{V}_{2}}\left( t \right) +{{V}_{3}}\left( t \right) +{{V}_{4}}\left( t \right) \nonumber \\&\le \left( {{\lambda }_{2}}+{{\lambda }_{3}} \right) \chi \left( t \right) . \end{aligned}$$

(46)

Then, we can further attain

$$\begin{aligned} 0<{{\lambda }_{4}}\left( \chi \left( t \right) +{{V}_{1}}\left( t \right) \right) \le V\left( t \right) \le {{\lambda }_{5}}\left( \chi \left( t \right) +{{V}_{1}}\left( t \right) \right) \end{aligned}$$

(47)

where ${{\kappa }_{1}}={{\lambda }_{1}}-{{\lambda }_{3}}>0$, ${{\kappa }_{2}}={{\lambda }_{2}}+{{\lambda }_{3}}>0$, ${{\lambda }_{4}}=\min \left\{ {{\kappa }_{1}},1 \right\} >0$, and ${{\lambda }_{5}}=\max \left\{ {{\kappa }_{2}},1 \right\} >0$.

Differentiating Eq. (38) and substituting Eqs. (5)–(8) lead to

$$\begin{aligned} {{{{\dot{V}}}}_{2}}\left( t \right)&=\beta K{\dot{v}}_{L}^{{}}\left( {{l}_{1}},t \right) \left( {{v}_{Ls}}\left( {{l}_{1}},t \right) -{{\theta }_{L}}\left( {{l}_{1}},t \right) \right) \nonumber \\&\quad +\beta {\mathrm{EI}}{{{{\dot{\theta }}}}_{L}}\left( {{l}_{1}},t \right) {{\theta }_{Ls}}\left( {{l}_{1}},t \right) \nonumber \\&\quad -\beta K{\dot{v}}_{R}^{{}}\left( {{l}_{1}},t \right) \left( {{v}_{Rs}}\left( {{l}_{1}},t \right) -{{\theta }_{R}}\left( {{l}_{1}},t \right) \right) \nonumber \\&\quad -\beta {\mathrm{EI}}{{{{\dot{\theta }}}}_{R}}\left( {{l}_{1}},t \right) {{\theta }_{Rs}}\left( {{l}_{1}},t \right) \nonumber \\&\quad -\beta {{\sigma }_{1}}\int _{0}^{{{l}_{1}}}{{\dot{v}}_{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad -\beta {{\sigma }_{2}}\int _{0}^{{{l}_{1}}}{{\dot{\theta }}_{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad -\beta {{\sigma }_{1}}\int _{{{l}_{1}}}^{l}{{\dot{v}}_{R}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad -\beta {{\sigma }_{2}}\int _{{{l}_{1}}}^{l}{{\dot{\theta }}_{R}^{2}}\left( s,t \right) {\mathrm{d}s}. \end{aligned}$$

(48)

Substituting Eqs. (5)–(8) into derivative of Eq. (39) and using integration by parts, one gets

$$\begin{aligned} {{{{\dot{V}}}}_{3}}\left( t \right)&=\alpha K{{v}_{L}}\left( {{l}_{1}},t \right) {{v}_{Ls}}\left( {{l}_{1}},t \right) \nonumber \\&\quad -\alpha K\int _{0}^{{{l}_{1}}}{v_{Ls}^{2}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\quad -\alpha K{{v}_{L}}\left( {{l}_{1}},t \right) {{\theta }_{L}}\left( {{l}_{1}},t \right) \nonumber \\&\quad +\alpha \rho \int _{0}^{{{l}_{1}}}{{\dot{v}}_{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad -\alpha {{\sigma }_{1}}\int _{0}^{{{l}_{1}}}{{{v}_{L}}\left( s,t \right) {{{\dot{v}}}_{L}}\left( s,t \right) {\mathrm{d}s}}\nonumber \\&\quad +\alpha {\mathrm{EI}}{{\theta }_{L}}\left( {{l}_{1}},t \right) {{\theta }_{Ls}}\left( {{l}_{1}},t \right) \nonumber \\&\quad -\alpha {\mathrm{EI}}\int _{0}^{{{l}_{1}}}{\theta _{Ls}^{2}\left( s,t \right) }{\mathrm{d}s}\nonumber \\&\quad +2\alpha K\int _{0}^{{{l}_{1}}}{\theta _{L}^{{}}\left( s,t \right) {{v}_{Ls}}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\quad -\alpha K\int _{0}^{{{l}_{1}}}{\theta _{L}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\alpha {{I}_{p}}\int _{0}^{{{l}_{1}}}{{\dot{\theta }}_{L}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad -\alpha {{\sigma }_{2}}\int _{0}^{{{l}_{1}}}{\theta _{L}^{{}}\left( s,t \right) {{{{\dot{\theta }}}}_{L}}\left( s,t \right) }{\mathrm{d}s}\nonumber \\&\quad -\alpha K{{v}_{R}}\left( {{l}_{1}},t \right) {{v}_{Rs}}\left( {{l}_{1}},t \right) \nonumber \\&\quad -\alpha K\int _{{{l}_{1}}}^{l}{v_{Rs}^{2}\left( s,t \right) }{\mathrm{d}s}\nonumber \\&\quad +\alpha K{{v}_{R}}\left( {{l}_{1}},t \right) {{\theta }_{R}}\left( {{l}_{1}},t \right) \nonumber \\&\quad +\alpha \rho \int _{{{l}_{1}}}^{l}{{\dot{v}}_{R}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad -\alpha {{\sigma }_{1}}\int _{{{l}_{1}}}^{l}{{{v}_{R}}\left( s,t \right) {{{\dot{v}}}_{R}}\left( s,t \right) {\mathrm{d}s}} \nonumber \\&\quad -\alpha {\mathrm{EI}}{{\theta }_{R}}\left( {{l}_{1}},t \right) {{\theta }_{Rs}}\left( {{l}_{1}},t \right) \nonumber \\&\quad -\alpha {\mathrm{EI}}\int _{{{l}_{1}}}^{l}{\theta _{Rs}^{2}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\quad +2\alpha K\int _{{{l}_{1}}}^{l}{\theta _{R}^{{}}\left( s,t \right) {{v}_{Rs}}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\quad -\alpha K\int _{{{l}_{1}}}^{l}{\theta _{R}^{2}\left( s,t \right) {\mathrm{d}s}} \nonumber \\&\quad +\alpha {{I}_{p}}\int _{{{l}_{1}}}^{l}{{\dot{\theta }}_{R}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad -\alpha {{\sigma }_{2}}\int _{{{l}_{1}}}^{l}{\theta _{R}^{{}}\left( s,t \right) {{{{\dot{\theta }}}}_{R}}\left( s,t \right) }{\mathrm{d}s}. \end{aligned}$$

(49)

Time derivative of ${{{V}}_{4}}\left( t \right)$ is supposed to be

$$\begin{aligned} {{{\dot{V}}}_{4}}\left( t \right)&=\alpha {{\sigma }_{1}}\int _{0}^{{{l}_{1}}}{v_{L}^{{}}}\left( s,t \right) {\dot{v}}_{L}^{{}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\alpha {{\sigma }_{2}}\int _{0}^{{{l}_{1}}}{\theta _{L}^{{}}}\left( s,t \right) {\dot{\theta }}_{L}^{{}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\alpha {{\sigma }_{1}}\int _{{{l}_{1}}}^{l}{v_{R}^{{}}}\left( s,t \right) {{{\dot{v}}}_{R}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad +\alpha {{\sigma }_{2}}\int _{{{l}_{1}}}^{l}{\theta _{R}^{{}}}\left( s,t \right) {\dot{\theta }}_{R}^{{}}\left( s,t \right) {\mathrm{d}s}. \end{aligned}$$

(50)

Combining inequality (35), Eqs. (48)–(50) and utilizing Lemma 1 yield

$$\begin{aligned} {\dot{V}}\left( t \right)&\le -\left( \beta {{\sigma }_{1}}-\alpha \rho \right) \int _{0}^{{{l}_{1}}}{{\dot{v}}_{L}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad -\left( \alpha K-2\alpha K{{\delta }_{1}} \right) \int _{0}^{{{l}_{1}}}{v_{Ls}^{2}\left( s,t \right) }{\mathrm{d}s}\nonumber \\&\quad -\left( \beta {{\sigma }_{2}}-\alpha {{I}_{p}} \right) \int _{0}^{{{l}_{1}}}{{\dot{\theta }}_{L}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad -\left( \alpha K-\frac{2\alpha K}{{{\delta }_{1}}} \right) \int _{0}^{{{l}_{1}}}{\theta _{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad -\alpha {\mathrm{EI}}\int _{0}^{{{l}_{1}}}{\theta _{Ls}^{2}\left( s,t \right) }{\mathrm{d}s}\nonumber \\&\quad -\left( \beta {{\sigma }_{1}}-\alpha \rho \right) \int _{{{l}_{1}}}^{l}{{\dot{v}}_{R}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad -\left( \alpha K-2\alpha K{{\delta }_{2}} \right) \int _{{{l}_{1}}}^{l}{v_{Rs}^{2}\left( s,t \right) }{\mathrm{d}s}\nonumber \\&\quad -\left( \beta {{\sigma }_{2}}-\alpha {{I}_{p}} \right) \int _{{{l}_{1}}}^{l}{{\dot{\theta }}_{R}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad -\left( \alpha K-\frac{2\alpha K}{{{\delta }_{2}}} \right) \int _{{{l}_{1}}}^{l}{\theta _{R}^{2}\left( s,t \right) {\mathrm{d}s}}\nonumber \\&\quad -\alpha {\mathrm{EI}}\int _{{{l}_{1}}}^{l}{\theta _{Rs}^{2}\left( s,t \right) }{\mathrm{d}s}-\beta {{k}_{3}}\eta _{3}^{2}\left( t \right) a\left( t \right) \nonumber \\&\quad -\beta {{k}_{4}}\eta _{4}^{2}\left( t \right) b\left( t \right) -\alpha {{k}_{1}}v_{{}}^{2}\left( {{l}_{1}},t \right) \nonumber \\&\quad -\alpha {{k}_{2}}{{\theta }^{2}}\left( {{l}_{1}},t \right) \end{aligned}$$

(51)

in which ${{\delta }_{1}}>0$ and ${{\delta }_{2}}>0$.

Utilizing inequalities (20) and (21), we have

$$\begin{aligned} {\dot{V}}\left( t \right)&\le -\left( \beta {{\sigma }_{1}}-\alpha \rho \right) \int _{0}^{{{l}_{1}}}{{\dot{v}}_{L}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad -{{\zeta }_{1}}\int _{0}^{{{l}_{1}}}{v_{L}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad -\left( \alpha K-2\alpha K{{\delta }_{1}}-4l_{1}^{2}{{\zeta }_{1}} \right) \int _{0}^{{{l}_{1}}}{v_{Ls}^{2}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\quad -\left( \beta {{\sigma }_{2}}-\alpha {{I}_{p}} \right) \int _{0}^{{{l}_{1}}}{{\dot{\theta }}_{L}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad -\left( \alpha K+\frac{\alpha }{8l_{1}^{2}}{\mathrm{EI}}-\frac{2\alpha K}{{{\delta }_{1}}} \right) \int _{0}^{{{l}_{1}}}{\theta _{L}^{2}}\left( s,t\right) {\mathrm{d}s} \nonumber \\&\quad -\frac{\alpha }{2}{\mathrm{EI}}\int _{0}^{{{l}_{1}}}{\theta _{Ls}^{2}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\quad -\left( \beta {{\sigma }_{1}}-\alpha \rho \right) \int _{{{l}_{1}}}^{l}{{\dot{v}}_{R}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad -{{\zeta }_{2}}\int _{{{l}_{1}}}^{l}{v_{R}^{2}}\left( s,t \right) {\mathrm{d}s} \nonumber \\&\quad -\left( \alpha K-2\alpha K{{\delta }_{2}}-4l_{2}^{2}{{\zeta }_{2}} \right) \int _{{{l}_{1}}}^{l}{v_{Rs}^{2}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\quad -\left( \beta {{\sigma }_{2}}-\alpha {{I}_{p}} \right) \int _{{{l}_{1}}}^{l}{{\dot{\theta }}_{R}^{2}}\left( s,t \right) {\mathrm{d}s}\nonumber \\&\quad -\frac{\alpha }{2}{\mathrm{EI}}\int _{{{l}_{1}}}^{l}{\theta _{Rs}^{2}\left( s,t \right) }{\mathrm{d}s} \nonumber \\&\quad -\left( \alpha K+\frac{\alpha }{8l_{2}^{2}}{\mathrm{EI}}-\frac{2\alpha K}{{{\delta }_{2}}} \right) \int _{{{l}_{1}}}^{l}{\theta _{R}^{2}\left( s,t \right) {\mathrm{d}s}} \nonumber \\&\quad -\beta {{k}_{3}}\eta _{3}^{2}\left( t \right) a\left( t \right) -\beta {{k}_{4}}\eta _{4}^{2}\left( t \right) b\left( t \right) \nonumber \\&\quad -\alpha {{k}_{1}}v_{{}}^{2}\left( {{l}_{1}},t \right) -\alpha {{k}_{2}}{{\theta }^{2}}\left( {{l}_{1}},t \right) \end{aligned}$$

(52)

where ${{\zeta }_{1}}>0$, ${{\zeta }_{2}}>0$, and ${{\delta }_{1}}$, ${{\delta }_{2}}$, ${{\zeta }_{1}}$, ${{\zeta }_{2}}$, $\alpha$, $\beta$ are chosen for satisfying $\beta {{\sigma }_{1}}-\alpha \rho >0$, $\beta {{\sigma }_{2}}-\alpha {{I}_{p}}>0$, $\alpha K+\frac{\alpha }{8l_{1}^{2}}{\mathrm{EI}}-\frac{2\alpha K}{{{\delta }_{1}}}>0$, $\alpha K+\frac{\alpha }{8l_{2}^{2}}{\mathrm{EI}}-\frac{2\alpha K}{{{\delta }_{2}}}>0$, $\alpha K-2\alpha K{{\delta }_{1}}-4l_{1}^{2}{{\zeta }_{1}}>0$, and $\alpha K-2\alpha K{{\delta }_{2}}-4l_{2}^{2}{{\zeta }_{2}}>0$.

Then, ${\dot{V}}\left( t \right)$ is rewritten as

$$\begin{aligned} {\dot{V}}\left( t \right) \le -{{\lambda }_{6}}\left( \chi \left( t \right) +{{V}_{1}}\left( t \right) \right) \end{aligned}$$

(53)

where ${{\lambda }_{6}}=\min \left\{ \beta {{\sigma }_{1}}-\alpha \rho ,{{\zeta }_{1}},\alpha K-2\alpha K{{\delta }_{1}}-4l_{1}^{2}{{\zeta }_{1}}, \right. \beta {{\sigma }_{2}}-\alpha {{I}_{p}},\alpha K+\frac{\alpha }{8l_{1}^{2}}{\mathrm{EI}}-\frac{2\alpha K}{{{\delta }_{1}}}, \frac{\alpha }{2}{\mathrm{EI}}, {{\zeta }_{2}},\alpha K-2\alpha K{{\delta }_{2}}-4l_{2}^{2}{{\zeta }_{2}},\alpha K+\frac{\alpha }{8l_{2}^{2}}{\mathrm{EI}}-\frac{2\alpha K}{{{\delta }_{2}}},\frac{2\alpha }{\beta }, \frac{2{{k}_{3}}}{M},\frac{2{{k}_{4}}}{J}\}.$

Remark 9

According to the definition of ${{\lambda }_{6}}$ given above, ${{\lambda }_{6}}$ can be obtained by picking out the minimum of $\beta {{\sigma }_{1}}-\alpha \rho ,{{\zeta }_{1}},\alpha K-2\alpha K{{\delta }_{1}}-4l_{1}^{2}{{\zeta }_{1}},\beta {{\sigma }_{2}}-\alpha {{I}_{p}},\alpha K+\frac{\alpha }{8l_{1}^{2}}{\mathrm{EI}}-\frac{2\alpha K}{{{\delta }_{1}}},\frac{\alpha }{2}{\mathrm{EI}},{{\zeta }_{2}},\alpha K-2\alpha K{{\delta }_{2}}-4l_{2}^{2}{{\zeta }_{2}},\frac{2\alpha }{\beta },\frac{2{{k}_{3}}}{M},$$\frac{2{{k}_{4}}}{J},\alpha K+\frac{\alpha }{8l_{2}^{2}}{\mathrm{EI}}-\frac{2\alpha K}{{{\delta }_{2}}}$, where $\rho$, ${{\sigma }_{1}}$, ${{\sigma }_{2}}$, K, ${{I}_{p}}$, ${\mathrm{EI}}$, $l_{1}^{{}}$, $l_{2}^{{}}$ are system parameters; $\beta$, $\alpha$ are parameters of controllers; and ${{\zeta }_{1}}$, ${{\zeta }_{2}}$, ${{\delta }_{1}}$, ${{\delta }_{2}}$ are positive constants satisfying $\alpha K+\frac{\alpha }{8l_{1}^{2}}{\mathrm{EI}}-\frac{2\alpha K}{{{\delta }_{1}}}>0$, $\alpha K+\frac{\alpha }{8l_{2}^{2}}{\mathrm{EI}}-\frac{2\alpha K}{{{\delta }_{2}}}>0$, $\alpha K-2\alpha K{{\delta }_{1}}-4l_{1}^{2}{{\zeta }_{1}}>0$, $\alpha K-2\alpha K{{\delta }_{2}}-4l_{2}^{2}{{\zeta }_{2}}>0$.

From inequalities (47) and (53), one has

$$\begin{aligned} {\dot{V}}\left( t \right) \le -\lambda V\left( t \right) \end{aligned}$$

(54)

in which $\lambda =\frac{{{\lambda }_{6}}}{{{\lambda }_{5}}}>0$.

Multiplying inequality (54) by ${{\mathrm{e}}^{\lambda t}}$ yields

$$\begin{aligned} V\left( t \right) \le V\left( 0 \right) {{\mathrm{e}}^{-\lambda t}}. \end{aligned}$$

(55)

Based on inequalities (55), (47), Lemma 2, and Remark 3, we have

$$\begin{aligned} \frac{1}{{{l}_{1}}}\theta _{L}^{2}\left( s,t \right)&\le \frac{1}{{{\lambda }_{4}}}V\left( 0 \right) {{\mathrm{e}}^{-\lambda t}}, \nonumber \\ \frac{1}{{{l}_{2}}}\theta _{R}^{2}\left( s,t \right)&\le \frac{1}{{{\lambda }_{4}}}V\left( 0 \right) {{\mathrm{e}}^{-\lambda t}} \end{aligned}$$

(56)

$$\begin{aligned} \frac{1}{{{l}_{1}}}v_{L}^{2}\left( s,t \right)&\le \frac{1}{{{\lambda }_{4}}}V\left( 0 \right) {{\mathrm{e}}^{-\lambda t}}, \nonumber \\ \frac{1}{{{l}_{2}}}v_{R}^{2}\left( s,t \right)&\le \frac{1}{{{\lambda }_{4}}}V\left( 0 \right) {{\mathrm{e}}^{-\lambda t}} \end{aligned}$$

(57)

$$\begin{aligned} \frac{\beta }{2}{{k}_{1}}v_{{}}^{2}\left( {{l}_{1}},t \right)&\le \frac{1}{{{\lambda }_{4}}}V\left( 0 \right) {{\mathrm{e}}^{-\lambda t}}, \nonumber \\ \frac{\beta }{2}{{k}_{2}}\theta _{{}}^{2}\left( {{l}_{1}},t \right)&\le \frac{1}{{{\lambda }_{4}}}V\left( 0 \right) {{\mathrm{e}}^{-\lambda t}}. \end{aligned}$$

(58)

Then, it is obvious that

$$\begin{aligned} \left| v_{L}^{{}}\left( s,t \right) \right| ,\left| \theta _{L}^{{}}\left( s,t \right) \right|&\le \sqrt{\frac{{{l}_{1}}}{{{\lambda }_{4}}}V\left( 0 \right) {{\mathrm{e}}^{-\lambda t}}} \end{aligned}$$

(59)

$$\begin{aligned} \left| v_{R}^{{}}\left( s,t \right) \right| ,\left| \theta _{R}^{{}}\left( s,t \right) \right|&\le \sqrt{\frac{{{l}_{2}}}{{{\lambda }_{4}}}V\left( 0 \right) {{\mathrm{e}}^{-\lambda t}}} \end{aligned}$$

(60)

$$\begin{aligned} \left| v\left( {{l}_{1}},t \right) \right|&\le \sqrt{\frac{2}{\beta {{k}_{1}}{{\lambda }_{4}}}V\left( 0 \right) {{\mathrm{e}}^{-\lambda t}}}, \nonumber \\ \left| \theta \left( {{l}_{1}},t \right) \right|&\le \sqrt{\frac{2}{\beta {{k}_{2}}{{\lambda }_{4}}}V\left( 0 \right) {{\mathrm{e}}^{-\lambda t}}}. \end{aligned}$$

(61)

According to inequalities (59)–(61), it is stated that if system initial conditions are bounded, $V\left( 0 \right)$ is bounded, which means $v\left( s,t \right)$ and $\theta \left( s,t \right)$ are both bounded for $\forall \left( s,t \right) \in \left[ 0,l \right] \times \left[ 0,\infty \right)$.

Besides, from inequalities (59)–(61), one has

$$\begin{aligned} \lim \limits _{t\rightarrow \infty } \,\left| v\left( s,t \right) \right| , \lim \limits _{t\rightarrow \infty } \,\left| \theta \left( s,t \right) \right| =0 \quad for\quad \forall s\in \left[ 0,l \right] . \end{aligned}$$

(62)

Moreover, according to [35], we know that if initial conditions mentioned by Assumption 2 hold, output constraints $\left| v\left( {{l}_{1}},t \right) \right| \le {{k}_{1}}$, $\left| \theta \left( {{l}_{1}},t \right) \right| \le {{k}_{2}}$ can always be guaranteed for $\forall t\in \left[ 0,\infty \right)$ with control.

Therefore, the closed-loop system is exponentially stable under proposed control with output constraints, and Theorem 1 has been completely proven.

Remark 10

The selection method of control parameters is introduced in this remark. First, the designed control parameters should be chosen to satisfy conditions given below inequality (52). Then, by observing inequality (55), it is known that the convergence speed of the closed-loop system is directly proportional to $\lambda$. Therefore, control parameters ${{k}_{3}}$ and ${{k}_{4}}$ can be increased for improving convergent performance when ${{k}_{1}}$, ${{k}_{2}}$, $\alpha$ and $\beta$ are selected properly. However, large ${{k}_{3}}$ and ${{k}_{4}}$ may lead to the high gain of controller, which may have adverse effect on the actuator. In practical applications, we should choose control parameters properly according to the actual situation such that the satisfactory control performance can be satisfied.

3.2 Robust adaptive controller design for system with output constraints and actuator failures

This part aims at developing a robust adaptive compensation control algorithm to deal with actuator failures considering output constraints and disturbances. In view of stability and safety of whole system with actuator failures, actuator redundancy is applied in this section, and more than one actuator is used for each controlled variable in case complete failures occur to actuators.

Assume that there are ${{m}_{1}}$ actuators for deformation control whose output signals are denoted by ${{u}_{i}}\left( t \right)$, $i=1,2\ldots {{m}_{1}}$, and there are ${{m}_{2}}$ actuators for rotation control whose outputs are denoted by ${{\tau }_{j}}\left( t \right)$, $j=1,2\ldots {{m}_{2}}$.

Therefore, the total input signals from all actuators to the system can be represented by

$$\begin{aligned} u\left( t \right)&= \sum \limits _{i=1}^{{{m}_{1}}}{{{b}_{i}}{{u}_{i}}\left( t \right) } \end{aligned}$$

(63)

$$\begin{aligned} \tau \left( t \right)&=\sum \limits _{j=1}^{{{m}_{2}}}{{{c}_{j}}{{\tau }_{j}}\left( t \right) } \end{aligned}$$

(64)

where ${{b}_{i}}$ and ${{c}_{j}}$ are uncertain constants with known signs.

For each actuator, actuator fault is modeled by

$$\begin{aligned}&{{u}_{i}}\left( t \right) ={{f}_{i}}{{u}_{ci}}\left( t \right) +{{\bar{u}}_{i}}, \forall t\ge {{t}_{iF}} \end{aligned}$$

(65)

$$\begin{aligned}&{{f}_{i}}{{\bar{u}}_{i}} = 0, i=1,2,\ldots ,{{m}_{1}} \end{aligned}$$

(66)

or

$$\begin{aligned}&{{\tau }_{j}}\left( t \right) ={{h}_{j}}{{\tau }_{cj}}\left( t \right) +{{{\bar{\tau }}}_{j}}, \forall t\ge {{t}_{jH}} \end{aligned}$$

(67)

$$\begin{aligned}&{{h}_{j}}{{{\bar{\tau }}}_{j}} = 0, j=1,2,\ldots ,{{m}_{2}} \end{aligned}$$

(68)

where ${{u}_{ci}}\left( t \right)$ is input signal of the $i\text {th}$ actuator of $u\left( t \right)$ needing to be designed; ${{\tau }_{cj}}\left( t \right)$ is input signal of the $j\text {th}$ actuator of $\tau \left( t \right)$; ${{\bar{u}}_{i}}$ and ${{{\bar{\tau }}}_{j}}$ are both unknown constants; and ${{f}_{i}},{{h}_{j}}\in \left[ 0,1 \right)$.

Equation (65) shows that actuator failures suddenly occur to the $i\text {th}$ actuator of $u\left( t \right)$ from time ${{t}_{iF}}$ and Eq. (67) represents that the $j\text {th}$ actuator of $\tau \left( t \right)$ actuator fails at time ${{t}_{jH}}$.

An actuator is regarded as failure-free when its input equals its output, that is, ${{u}_{i}}\left( t \right) ={{u}_{ci}}\left( t \right)$, or ${{\tau }_{j}}\left( t \right) ={{\tau }_{cj}}\left( t \right)$, $i=1,2,\ldots {{m}_{1}}$, $j=1,2,\ldots {{m}_{2}}$. In other words, actuators working in failure-free condition can be written as ${{f}_{i}}=1$, ${{\bar{u}}_{i}}=0$ in Eq. (65), or ${{h}_{j}}=1$, ${{{\bar{\tau }}}_{j}}=0$ in Eq. (67).

Remark 11

As we note, Eqs. (66) and (68) indicate three cases including types of TLOE and PLOE as follows:

• (1) ${{f}_{i}}\ne \text {0}$ and ${{\bar{u}}_{i}}=0$, or ${{h}_{j}}\ne 0$ and ${{{\bar{\tau }}}_{j}}=0$ (PLOE). In this case, ${{u}_{i}}\left( t \right) ={{f}_{i}}{{u}_{ci}}\left( t \right)$ (${{\tau }_{j}}\left( t \right) ={{h}_{j}}{{\tau }_{cj}}\left( t \right)$), in which $0<{{f}_{i}}<1$ ($0<{{h}_{j}}<1$) for $i=1,2,\ldots {{m}_{1}}$ ($j=1,2,\ldots {{m}_{2}}$) denotes degree of loss of effectiveness of actuators. For instance, ${{f}_{i}}=0\text {.6}$ implies that the $i\text {th}$ actuator of $u\left( t \right)$ loses 40 $\%$ of its effectiveness, and ${{h}_{j}}=0\text {.3}$ means that the $j\text {th}$ actuator of $\tau \left( t \right)$ remains only 30 $\%$ of its effectiveness.

• (2) ${{f}_{i}}=0$ and ${{\bar{u}}_{i}}\ne 0$, or ${{h}_{j}}=0$ and ${{{\bar{\tau }}}_{j}}\ne 0$ (TLOE). In this case, ${{u}_{i}}\left( t \right)$ (${{\tau }_{j}}\left( t \right)$) is stuck at an uncertain value ${{\bar{u}}_{i}}$ (${{{\bar{\tau }}}_{j}}$) and cannot be affected by the actuator input any more.

• (3) ${{f}_{i}}=0$ and ${{\bar{u}}_{i}}=0$, or ${{h}_{j}}=0$ and ${{{\bar{\tau }}}_{j}}=0$. This condition refers to the float type of TLOE which is introduced by [38].

Before we design control laws, several assumptions are given for ensuring stability of the system.

Assumption 3

Assume that up to ${{m}_{1}}-1$ actuators of $u\left( t \right)$ and up to ${{m}_{2}}-1$ actuators of $\tau \left( t \right)$ are at state of TLOE at any time instant.

Assumption 4

${{b}_{i}}\ne 0$ and ${{c}_{j}}\ne 0$, and signs of ${{b}_{i}}$ and ${{c}_{j}}$, i.e., ${\mathrm{sgn}} \left( {{b}_{i}} \right)$ and ${\mathrm{sgn}} \left( {{c}_{j}} \right)$, are known for $i=1,2,\ldots ,{{m}_{1}}$ and $j=1,2,\ldots ,{{m}_{2}}$.

Remark 12

Since the fault times ${{t}_{iF}}$ and ${{t}_{jH}}$ in Eqs. (65) and (67) are unique, failure occurs only once on the $i\text {th}$ actuator of $u\left( t \right)$ and $j\text {th}$ actuator of $\tau \left( t \right)$. Therefore, the time instant of the last failure is finite.

If both failure type and failure value are known, control laws are designed as

$$\begin{aligned} {{u}_{ci}}\left( t \right)&=-{{k}_{1i}}{{\mu }_{1}}\left( t \right) -{{k}_{2i}} \end{aligned}$$

(69)

$$\begin{aligned} {{\tau }_{cj}}\left( t \right)&=-{{\bar{k}}_{1j}}{{\mu }_{2}}\left( t \right) -{{\bar{k}}_{2j}} \end{aligned}$$

(70)

where ${{k}_{1i}}$, ${{k}_{2i}}$, ${{\bar{k}}_{1j}}$, and ${{\bar{k}}_{2j}}$ are nonzero constants for $i=1,2,\ldots ,{{m}_{1}}$ and $j=1,2,\ldots ,{{m}_{2}}$.

Theorem 2

With Assumptions 1–4 and control laws in Eqs. (69) and (70), the boundedness of closed-loop signals of overhead crane bridge can be guaranteed subject to environmental disturbances if failure type and failure value are known. States of closed-loop system exponentially converge to zero with output constraints of the trolley, that is, $\lim \nolimits _{t\rightarrow \infty } \,v\left( s,t \right) = \lim \nolimits _{t\rightarrow \infty } \,\theta \left( s,t \right) =0$ holds for $\forall s\in \left[ 0,l \right]$ with $\left| v\left( {{l}_{1}},t \right) \right| <k_{1}^{{}}$, $\left| \theta \left( {{l}_{1}},t \right) \right| <k_{2}^{{}}$ for $\forall t\in \left[ 0,\infty \right)$.

Proof

The Lyapunov function of the system is defined as Eq. (37) with ${{V}_{1}}\left( t \right)$, ${{V}_{2}}\left( t \right)$, ${{V}_{3}}\left( t \right)$, ${{V}_{4}}\left( t \right)$ in Eqs. (32), (38)–(40), respectively, and ${{{\dot{V}}}_{2}}\left( t \right)$, ${{\dot{V}}_{3}}\left( t \right)$, ${{\dot{V}}_{4}}\left( t \right)$ are the same as ones in Eqs. (48)–(50).

Combining Eqs. (63)–(68), we have

$$\begin{aligned} u\left( t \right)&=\sum \limits _{i=1}^{{{m}_{1}}}{{{b}_{i}}\left( {{f}_{i}}{{u}_{ci}}\left( t \right) +{{{\bar{u}}}_{i}} \right) } \nonumber \\&=\sum \limits _{i=1}^{{{m}_{1}}}{\left( {{b}_{i}}{{f}_{i}}{{u}_{ci}}\left( t \right) +{{b}_{i}}{{{\bar{u}}}_{i}} \right) } \end{aligned}$$

(71)

$$\begin{aligned} \tau \left( t \right)&=\sum \limits _{j=1}^{{{m}_{2}}}{{{c}_{j}}\left( {{h}_{j}}{{\tau }_{cj}}\left( t \right) +{{{{\bar{\tau }}}}_{j}} \right) } \nonumber \\&=\sum \limits _{j=1}^{{{m}_{2}}}{\left( {{c}_{j}}{{h}_{j}}{{\tau }_{cj}}\left( t \right) +{{c}_{j}}{{{{\bar{\tau }}}}_{j}} \right) }. \end{aligned}$$

(72)

Substituting Eqs. (71), (72) and designed control laws in Eqs. (69) and (70) into ${{\dot{V}}_{1}}\left( t \right)$ in inequality (33), one has

$$\begin{aligned} {{{\dot{V}}}_{1}}\left( t \right)&\le -\beta {{k}_{3}}\eta _{3}^{2}\left( t \right) a\left( t \right) -\beta {{k}_{4}}\eta _{4}^{2}\left( t \right) b\left( t \right) +D\nonumber \\&\quad +\beta \eta _{3}^{{}}\left( t \right) \nonumber \\&\quad \left[ {{\mu }_{1}}\left( t \right) +\sum \limits _{i=1}^{{{m}_{1}}}{\left( {{b}_{i}}{{f}_{i}}{{u}_{ci}}\left( t \right) +{{b}_{i}}{{{\bar{u}}}_{i}} \right) } \right] a\left( t \right) \nonumber \\&\quad +\beta \eta _{4}^{{}}\left( t \right) \nonumber \\&\quad \left[ {{\mu }_{2}}\left( t \right) +\sum \limits _{j=1}^{{{m}_{2}}}{\left( {{c}_{j}}{{h}_{j}}{{\tau }_{cj}}\left( t \right) +{{c}_{j}}{{{{\bar{\tau }}}}_{j}} \right) } \right] b\left( t \right) . \end{aligned}$$

(73)

Assume there exist ${{k}_{1i}}$, ${{k}_{2i}}$, ${{\bar{k}}_{1j}}$, and ${{\bar{k}}_{2j}}$, $i=1,2,\ldots ,{{m}_{1}}$, $j=1,2,\ldots ,{{m}_{2}}$, satisfying

$$\begin{aligned}&\sum \limits _{i=1}^{{{m}_{1}}}{{{b}_{i}}{{f}_{i}}{{k}_{1i}}}=1, \sum \limits _{i=1}^{{{m}_{1}}}{{{b}_{i}}{{{\bar{u}}}_{i}}}= \sum \limits _{i=1}^{{{m}_{1}}}{{{b}_{i}}{{f}_{i}}{{k}_{2i}}} \end{aligned}$$

(74)

$$\begin{aligned}&\sum \limits _{j=1}^{{{m}_{2}}}{{{c}_{j}}{{h}_{j}}{{{\bar{k}}}_{1j}}}=1, \sum \limits _{j=1}^{{{m}_{2}}}{{{c}_{j}}{{{{\bar{\tau }}}}_{j}}}= \sum \limits _{j=1}^{{{m}_{2}}}{{{c}_{j}}{{h}_{j}}{{{\bar{k}}}_{2j}}}. \end{aligned}$$

(75)

Then, one has

$$\begin{aligned}&{{{\dot{V}}}_{1}}\left( t \right) \nonumber \\&\quad \le -\beta {{k}_{3}}\eta _{3}^{2}\left( t \right) a\left( t \right) -\beta {{k}_{4}}\eta _{4}^{2}\left( t \right) b\left( t \right) +D \nonumber \\&\qquad +\beta \eta _{3}^{{}}\left( t \right) \nonumber \\&\qquad \left[ {{\mu }_{1}}\left( t \right) +\sum \limits _{i=1}^{{{m}_{1}}}{\left( -{{b}_{i}}{{f}_{i}}{{k}_{1i}}{{\mu }_{1}}\left( t \right) -{{b}_{i}}{{f}_{i}}{{k}_{2i}}+{{b}_{i}}{{{\bar{u}}}_{i}} \right) } \right] \nonumber \\&\qquad a\left( t \right) +\beta \eta _{4}^{{}}\left( t \right) \nonumber \\&\qquad \left[ {{\mu }_{2}}\left( t \right) +\sum \limits _{j=1}^{{{m}_{2}}}{\left( -{{c}_{j}}{{h}_{j}}{{{\bar{k}}}_{1j}}{{\mu }_{2}}\left( t \right) -{{c}_{j}}{{h}_{j}}{{{\bar{k}}}_{2j}} +{{c}_{j}}{{{{\bar{\tau }}}}_{j}} \right) } \right] \nonumber \\&\qquad b\left( t \right) \nonumber \\&\quad =-\beta {{k}_{3}}\eta _{3}^{2}\left( t \right) a\left( t \right) -\beta {{k}_{4}}\eta _{4}^{2}\left( t \right) b\left( t \right) +D. \end{aligned}$$

(76)

Subsequent proving process of Theorem 2 is similar to Theorem 1, and finally, it can be obtained that with control laws in Eqs. (69) and (70), closed-loop system with certain failures is exponentially stable and output constraints of trolley can be ensured if system initial conditions are bounded. Consequently, Theorem 2 has been completely proven. $\square$

However, in practical engineering, actuator faults are sometimes uncertain, which greatly increases the difficulty of the control design. Thus, for dealing with aforementioned situation, a robust adaptive control scheme with failure compensation is developed as follows.

If ${{k}_{1i}}$, ${{k}_{2i}}$, ${{\bar{k}}_{1j}}$, ${{\bar{k}}_{2j}}$, ${{\bar{u}}_{i}}$, ${{{\bar{\tau }}}_{j}}$, ${{f}_{i}}$, ${{h}_{j}}$, $i=1,2,\ldots ,{{m}_{1}}$, $j=1,2,\ldots ,{{m}_{2}}$, are unknown, then we design control laws as

$$\begin{aligned} {{u}_{ci}}\left( t \right)&=-{{{\hat{k}}}_{1i}}{{\mu }_{1}}\left( t \right) -{{\hat{k}}_{2i}} \end{aligned}$$

(77)

$$\begin{aligned} {{\tau }_{cj}}\left( t \right)&=-{{\hat{\bar{k}}}_{1j}}{{\mu }_{2}}\left( t \right) -{{\hat{\bar{k}}}_{2j}} \end{aligned}$$

(78)

where

$$\begin{aligned} {{\dot{\hat{k}}}_{1i}}&={{\gamma }_{i}}{{\mu }_{1}}\left( t \right) {{\eta }_{3}}\left( t \right) a\left( t \right) {{\mathrm{sgn}} {({b}_{i})}} \end{aligned}$$

(79)

$$\begin{aligned} {{\dot{\hat{k}}}_{2i}}&={{\gamma }_{i}}{{\eta }_{3}}\left( t \right) a\left( t \right) {{\mathrm{sgn}} {({b}_{i})}} \end{aligned}$$

(80)

$$\begin{aligned} {{\dot{\hat{\bar{k}}}}_{1j}}&={{{\bar{\gamma }}}_{j}}{{\mu }_{2}}\left( t \right) {{\eta }_{4}}\left( t \right) b\left( t \right) {{\mathrm{sgn}} {({c}_{j})}} \end{aligned}$$

(81)

$$\begin{aligned} {{\dot{\hat{\bar{k}}}}_{2j}}&={{{\bar{\gamma }}}_{j}}{{\eta }_{4}}\left( t \right) b\left( t \right) {{\mathrm{sgn}} {({c}_{j})}} \end{aligned}$$

(82)

in which ${{\gamma }_{i}}$ and ${{{\bar{\gamma }}}_{j}}$ are positive constants for $i=1,2,\ldots ,{{m}_{1}}$ and $j=1,2,\ldots ,{{m}_{2}}$.

Theorem 3

Under Assumptions 1–4, control laws in Eqs. (77)–(78) and adaptive laws (79)–(82) can guarantee stability of closed-loop system with perturbations. Besides, system output constraints are always satisfied in the sense of $\lim \nolimits _{t\rightarrow \infty } \,v\left( s,t \right) = \lim \nolimits _{t\rightarrow \infty } \,\theta \left( s, t \right) =0$ for $\forall s\in \left[ 0,l \right]$, and $\left| v\left( {{l}_{1}},t \right) \right| <k_{1}^{{}}$, $\left| \theta \left( {{l}_{1}},t \right) \right| <k_{2}^{{}}$ for $\forall t\in \left[ 0,\infty \right)$.

Proof

As stated in Remark 12, the finite number of time instants ${{t}_{w}}$ exists for $w=1,2,\ldots ,n$ ($n\le {{m}_{1}}\text {+}{{m}_{2}}$) at which one or more of actuators of $u\left( t \right)$ and $\tau \left( t \right)$ fail. ${{t}_{w}}$ denotes the last time of actuator failure. Assume there are ${{p}_{w}}$ (${{p}_{w}}\ge 1$) failed actuators during time interval $\left[ {{t}_{w-1}},{{t}_{w}} \right)$, where $w=1,2,\ldots ,n\text {+}1$, ${{t}_{0}}=0$, and ${{t}_{n+1}}{=}\infty$. Define ${{\psi }_{1}},{{\psi }_{2}},\ldots {{\psi }_{{{p}_{w}}}}$ as ${{p}_{w}}$ failed actuators whose failure pattern does not change until time ${{t}_{w}}$. Among these ${{p}_{w}}$ failed actuators, ${{q}_{{{1}_{w}}}}$ actuators ${{\psi }_{1,1}},{{\psi }_{1,2}},\ldots ,{{\psi }_{1,{{q}_{{{1}_{w}}}}}}$ suffer from TLOE and ${{q}_{{{2}_{w}}}}$ actuators ${{\psi }_{2,1}},{{\psi }_{2,2}},\ldots ,{{\psi }_{2,{{q}_{{{2}_{w}}}}}}$ are subject to PLOE. A set ${{P}_{w}}$ and two subsets of ${{P}_{w}}$, namely ${{Q}_{{{1}_{w}}}}$ and ${{Q}_{{{2}_{w}}}}$, are defined as ${{P}_{w}}{=}\left\{ {{\psi }_{1}},{{\psi }_{2}},\ldots {{\psi }_{{{p}_{w}}}} \right\}$, ${{Q}_{{{1}_{w}}}}{=}\left\{ {{\psi }_{1,1}},{{\psi }_{1,2}},\ldots ,{{\psi }_{1,{{q}_{{{1}_{w}}}}}} \right\}$, and ${{Q}_{{{2}_{w}}}}{=}\left\{ {{\psi }_{2,1}},{{\psi }_{2,2}},\ldots ,{{\psi }_{2,{{q}_{{{2}_{w}}}}}} \right\}$, which satisfy ${{Q}_{{{2}_{w}}}}={{P}_{w}}-{{Q}_{{{1}_{w}}}}$.

A positive definite function ${{\bar{V}}_{w-1}}\left( t \right)$ during $\left[ {{t}_{w-1}},{{t}_{w}} \right)$ is proposed as

$$\begin{aligned} {{\bar{V}}_{w-1}}\left( t \right) =V\left( t \right) +{{V}_{5,w}}\left( t \right) \end{aligned}$$

(83)

where $V\left( t \right) ={{V}_{1}}\left( t \right) +{{V}_{2}}\left( t \right) +{{V}_{3}}\left( t \right) +{{V}_{4}}\left( t \right)$, $t\in \left[ {{t}_{w-1}},{{t}_{w}} \right)$, whose definition is the same as Eqs. (32), (38)–(40), and ${{V}_{5}}\left( t \right)$ is given as

$$\begin{aligned} {{V}_{5,w}}\left( t \right)&=\sum \limits _{i=1,i\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{1}}}{\beta \frac{\left| {{b}_{i}} \right| {{f}_{i}}}{2{{\gamma }_{i}}}}\left( {\tilde{k}}_{1i}^{2}+{\tilde{k}}_{2i}^{2} \right) \nonumber \\&\quad +\sum \limits _{j=1,j\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{2}}}{\beta \frac{\left| {{c}_{j}} \right| {{h}_{j}}}{2{{{{\bar{\gamma }}}}_{j}}}}\left( \tilde{\bar{k}}_{1j}^{2}+\tilde{{\bar{k}}}_{2j}^{2} \right) \end{aligned}$$

(84)

where ${\tilde{k}}_{1i}^{{}}{=}{\hat{k}}_{1i}^{{}}-k_{1i}^{{}}$, ${\tilde{k}}_{2i}^{{}}={\hat{k}}_{2i}^{{}}-k_{2i}^{{}}$, $\tilde{{\bar{k}}}_{1j}^{{}}{=}\hat{{\bar{k}}}_{1j}^{{}}-{\bar{k}}_{1j}^{{}}$, $\tilde{{\bar{k}}}_{2j}^{{}}{=}\hat{{\bar{k}}}_{2j}^{{}}-{\bar{k}}_{2j}^{{}}$.

Substituting designed control laws in Eqs. (77) and (78) into ${{\dot{V}}_{1}}\left( t \right)$ in Eq. (33), one has

$$\begin{aligned} {{{\dot{V}}}_{1}}\left( t \right)&\le -\beta {{k}_{3}}\eta _{3}^{2}\left( t \right) a\left( t \right) -\beta {{k}_{4}}\eta _{4}^{2}\left( t \right) b\left( t \right) +D \nonumber \\&\quad +\beta \eta _{3}^{{}}\left( t \right) \left( {{\mu }_{1}}\left( t \right) -\sum \limits _{i=1,i\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{1}}}{{{b}_{i}}{{f}_{i}}{{{\hat{k}}}_{1i}}}{{\mu }_{1}}\left( t \right) \right. \nonumber \\&\qquad \left. -\sum \limits _{i=1,i\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{1}}}{{{b}_{i}}{{f}_{i}}{{{\hat{k}}}_{2i}}}+\sum \limits _{i=1,i\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{1}}}{{{b}_{i}}{{{{\bar{u}}}}_{i}}} \right) a\left( t \right) \nonumber \\&\quad +\beta \eta _{4}^{{}}\left( t \right) \left( {{\mu }_{2}}\left( t \right) -\sum \limits _{j=1,j\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{2}}}{{{c}_{j}}{{h}_{j}}{{{\hat{\bar{k}}}}_{1j}}}{{\mu }_{2}}\left( t \right) \right. \nonumber \\&\qquad \left. -\sum \limits _{j=1,j\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{2}}}{{{c}_{j}}{{h}_{j}}{{{\hat{\bar{k}}}}_{2j}}}+\sum \limits _{j=1,j\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{2}}}{{{c}_{j}}{{{{\bar{\tau }}}}_{j}}} \right) b\left( t \right) . \end{aligned}$$

(85)

Differentiating Eq. (84) and substituting adaptive laws (79)–(82) yield

$$\begin{aligned} {{{\dot{V}}}_{5,w}}\left( t \right)&=\sum \limits _{i=1,i\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{1}}}{\beta \frac{\left| {{b}_{i}} \right| {{f}_{i}}}{{{\gamma }_{i}}}}\left( {\tilde{k}}_{1i}^{{}}\dot{{\hat{k}}}_{1i}^{{}} +{\tilde{k}}_{2i}^{{}}\dot{{\hat{k}}}_{2i}^{{}} \right) \nonumber \\&\quad +\sum \limits _{j=1,j\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{2}}}{\beta \frac{\left| {{c}_{j}} \right| {{h}_{j}}}{{{{{\bar{\gamma }}}}_{j}}}}\left( \tilde{{\bar{k}}}_{1j}^{{}}\dot{\hat{{\bar{k}}}}_{1j}^{{}}+ \tilde{{\bar{k}}}_{2j}^{{}}\dot{\hat{{\bar{k}}}}_{2j}^{{}} \right) \nonumber \\&=\sum \limits _{i=1,i\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{1}}}{\beta \frac{\left| {{b}_{i}} \right| {{f}_{i}}}{{{\gamma }_{i}}}} \nonumber \\&\quad \left( {\tilde{k}}_{1i}^{{}}{{\gamma }_{i}}{{\mu }_{1}}\left( t \right) {{\eta }_{3}}\left( t \right) a\left( t \right) {{\mathrm{sgn}} {({b}_{i})}} \right. \nonumber \\&\qquad \left. +{\tilde{k}}_{2i}^{{}}{{\gamma }_{i}}{{\eta }_{3}}\left( t \right) a\left( t \right) {{\mathrm{sgn}} {({b}_{i})}} \right) \nonumber \\&\qquad +\sum \limits _{j=1,j\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{2}}}{\beta \frac{\left| {{c}_{j}} \right| {{h}_{j}}}{{{{{\bar{\gamma }}}}_{j}}}} \nonumber \\&\quad \left( \tilde{{\bar{k}}}_{1j}^{{}}{{{{\bar{\gamma }}}}_{j}} {{\mu }_{2}}\left( t \right) {{\eta }_{4}}\left( t \right) b\left( t \right) {{\mathrm{sgn}} {({c}_{j})}} \right. \nonumber \\&\qquad \left. +\tilde{{\bar{k}}}_{2j}^{{}}{{{{\bar{\gamma }}}}_{j}}{{\eta }_{4}}\left( t \right) b\left( t \right) {{\mathrm{sgn}} {({c}_{j})}} \right) . \end{aligned}$$

(86)

Combining inequalities (85) and Eq. (86), and using Eqs. (74) and (75), one obtains

$$\begin{aligned}&{{{\dot{V}}}_{1}}\left( t \right) +{{{\dot{V}}}_{5,w}}\left( t \right) \nonumber \\&\quad \le -\beta {{k}_{3}}\eta _{3}^{2}\left( t \right) a\left( t \right) -\beta {{k}_{4}}\eta _{4}^{2}\left( t \right) b\left( t \right) +D \nonumber \\&\qquad +\beta \eta _{3}^{{}}\left( t \right) \left( {{\mu }_{1}}\left( t \right) -\sum \limits _{i=1,i\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{1}}}{{{b}_{i}}{{f}_{i}} {{{\hat{k}}}_{1i}}}{{\mu }_{1}}\left( t \right) \right. \nonumber \\&\qquad \qquad \left. -\sum \limits _{i=1,i\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{1}}}{{{b}_{i}}{{f}_{i}} {{{\hat{k}}}_{2i}}}+\sum \limits _{i=1,i\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{1}}}{{{b}_{i}}{{{\bar{u}}}_{i}}} \right) a\left( t \right) \nonumber \\&\qquad +\beta \eta _{4}^{{}}\left( t \right) \left( {{\mu }_{2}}\left( t \right) -\sum \limits _{j=1,j\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{2}}} {{{c}_{j}}{{h}_{j}}{{{\hat{\bar{k}}}}_{1j}}}{{\mu }_{2}}\left( t \right) \right. \nonumber \\&\qquad \qquad \left. -\sum \limits _{j=1,j\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{2}}}{{{c}_{j}}{{h}_{j}} {{{\hat{\bar{k}}}}_{2j}}}+\sum \limits _{j=1,j\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{2}}}{{{c}_{j}}{{{{\bar{\tau }}}}_{j}}} \right) b\left( t \right) \nonumber \\&\qquad +\beta \sum \limits _{i=1,i\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{1}}} \nonumber \\&\qquad {\left( {{f}_{i}}{{\mu }_{1}}\left( t \right) {{\eta }_{3}}\left( t \right) a\left( t \right) {{b}_{i}}{\tilde{k}}_{1i}^{{}}+{{f}_{i}} {\tilde{k}}_{2i}^{{}}{{\eta }_{3}}\left( t \right) a\left( t \right) {{b}_{i}} \right) } \nonumber \\&\qquad +\beta \sum \limits _{j=1,j\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{2}}} \nonumber \\&\qquad {\left( {{h}_{j}}\tilde{\bar{k}}_{1j}^{{}}{{\mu }_{2}}\left( t \right) {{\eta }_{4}}\left( t \right) b\left( t \right) {{c}_{j}}+{{h}_{j}}\tilde{{\bar{k}}}_{2j}^{{}}{{\eta }_{4}}\left( t \right) b\left( t \right) {{c}_{j}} \right) } \nonumber \\&\quad =-\beta {{k}_{3}}\eta _{3}^{2}\left( t \right) a\left( t \right) -\beta {{k}_{4}}\eta _{4}^{2}\left( t \right) b\left( t \right) +D \nonumber \\&\qquad +\beta \eta _{3}^{{}}\left( t \right) \left( {{\mu }_{1}}\left( t \right) +\sum \limits _{i=1,i\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{1}}}{{{b}_{i}}{{{{\bar{u}}}}_{i}}} \right) a\left( t \right) \nonumber \\&\qquad +\beta \eta _{4}^{{}}\left( t \right) \left( {{\mu }_{2}}\left( t \right) +\sum \limits _{j=1,j\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{2}}}{{{c}_{j}}{{{{\bar{\tau }}}}_{j}}} \right) b\left( t \right) \nonumber \\&\qquad +\beta \sum \limits _{i=1,i\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{1}}} \nonumber \\&\qquad {\left( -k_{1i}^{{}}{{f}_{i}}{{\mu }_{1}}\left( t \right) {{\eta }_{3}}\left( t \right) a\left( t \right) {{b}_{i}}-k_{2i}^{{}}{{f}_{i}}{{\eta }_{3}}\left( t \right) a\left( t \right) {{b}_{i}} \right) } \nonumber \\&\qquad +\beta \sum \limits _{j=1,j\notin {{Q}_{{{1}_{w}}}}}^{{{m}_{2}}} \nonumber \\&\qquad {\left( -{\bar{k}}_{1j}^{{}}{{h}_{j}}{{\mu }_{2}}\left( t \right) {{\eta }_{4}}\left( t \right) b\left( t \right) {{c}_{j}}-{\bar{k}}_{2j}^{{}}{{h}_{j}}{{\eta }_{4}}\left( t \right) b\left( t \right) {{c}_{j}} \right) } \nonumber \\&\quad =-\beta {{k}_{3}}\eta _{3}^{2}\left( t \right) a\left( t \right) -\beta {{k}_{4}}\eta _{4}^{2}\left( t \right) b\left( t \right) +D. \end{aligned}$$

(87)

From inequality (87) and Eqs. (48)–(50), time derivative of ${{\bar{V}}_{w-1}}\left( t \right)$ is reexpressed as

$$\begin{aligned} {{\dot{\bar{V}}}_{w-1}}\left( t \right) \le -\lambda V\left( t \right) . \end{aligned}$$

(88)

We define ${{\bar{V}}_{w-1}}\left( t_{w}^{-} \right) = \lim \nolimits _{\vartriangle t\rightarrow {{0}^{-}}} \,{{\bar{V}}_{w-1}}\left( t_{w}^{{}}+{\varDelta }t \right)$ and ${{\bar{V}}_{w-1}}\left( t_{w-1}^{+} \right) = \lim \nolimits _{\vartriangle t\rightarrow {{0}^{+}}} \,{{\bar{V}}_{w-1}}\left( t_{w-1}^{{}} +{\varDelta }t \right) ={{\bar{V}}_{w-1}}\left( t_{w-1}^{{}} \right)$. If a function ${\bar{V}}\left( t \right) ={{\bar{V}}_{w-1}}\left( t \right)$ is selected for $t\in \left[ {{t}_{w-1}},{{t}_{w}} \right)$, $w=1,2,\ldots ,n\text {+}1$, then ${\bar{V}}\left( t \right)$ is piecewise continuous. According to inequality (88), it is obvious that ${{\bar{V}}_{w-1}}\left( t \right)$ is nonincreasing during time interval $\left[ {{t}_{w-1}},{{t}_{w}} \right)$. Due to the boundedness of ${{\bar{V}}_{0}}\left( 0\right)$ and the infinite change causing by varying coefficients in front of ${\tilde{k}}_{1i}^{2}+{\tilde{k}}_{2i}^{2}$ and $\tilde{{\bar{k}}}_{1j}^{2}+\tilde{{\bar{k}}}_{2j}^{2}$, ${{\bar{V}}_{w}}\left( t_{w}^{+} \right)$ and ${{\bar{V}}_{w}}\left( t_{w+1}^{-} \right)$ are both bounded for $\left[ {{t}_{w}},{{t}_{w{+}1}} \right)$. As stated above, the boundedness of $v\left( s,t \right)$, $\theta \left( s,t \right)$, ${\tilde{k}}_{1i}^{{}}$, ${\tilde{k}}_{2i}^{{}}$, $\tilde{{\bar{k}}}_{1j}^{{}}$, and $\tilde{{\bar{k}}}_{2j}^{{}}$ can be guaranteed for $\left( s,t \right) \in \left[ 0,l \right] \times \left[ 0,\infty \right)$, $i=1,2,\ldots ,{{m}_{1}}$, and $j=1,2,\ldots ,{{m}_{2}}$. According to Eqs. (77) and (78), control signals ${{u}_{ci}}\left( t \right)$ and ${{\tau }_{cj}}\left( t \right)$ are also bounded.

Furthermore, since $V\left( t \right)$ is nonnegative and ${\dot{V}}\left( t \right)$ is bounded which can be deduced from aforementioned statement, it is attained that $\lim \nolimits _{t\rightarrow \infty } \,v\left( s,t \right) = \lim \nolimits _{t\rightarrow \infty } \,\theta \left( s,t \right) =0$ holds for $\forall s\in \left[ 0,l \right]$ inferring from Lemma 4, and $\left| v\left( {{l}_{1}},t \right) \right| <k_{1}^{{}}$, $\left| \theta \left( {{l}_{1}},t \right) \right| <k_{2}^{{}}$ can be always ensured for $\forall t\in \left[ 0,\infty \right)$. As a result, Theorem 3 has been proven. $\square$

4 Numerical simulations

To verify the performance of proposed control strategy, numerical simulations are done using the finite difference method [39]. Values of system parameters are chosen as: ${{\sigma }_{1}}=2.5~\mathrm{kg}/(\mathrm{ms})$, ${{I}_{p}}=2~{\mathrm{kg}}~{{\mathrm{m}}^{{2}}}$, ${\mathrm{EI}}=50~{\mathrm{N}}~{{\text {m}}^{\text {2}}}$, ${{\sigma }_{2}}=2.5\,{\hbox {kg}}/(\mathrm{ms})$, $M=60\,{\mathrm{kg}}$, $K=0.5~{\mathrm{N}}$, $J=2~\mathrm{kg}~{{\text {m}}^{{2}}}$, $\rho =2~{\mathrm{kg}}~{{\text {m}}^{-1}}$, ${{l}_{1}}=2~\text {m}$, ${{l}_{2}}=2~\text {m}$, and $l=4~\text {m}$. Initial conditions of $v\left( s,t \right)$ and $\theta \left( s,t \right)$ are, respectively, selected as $v\left( s,0 \right) =\left\{ \begin{array}{l} 0.03s,\quad {\mathrm{if}}\quad 0\le s<\text {}{{l}_{1}} \\ 0.03{{l}_{1}},\quad {\mathrm{if}}\quad s={{l}_{1}} \\ -0.03\frac{{{l}_{1}}}{{{l}_{2}}}\left( s-l \right) ,\quad {\mathrm{if}}\quad {{l}_{1}}<s\le l \\ \end{array} \right.$, $\theta \left( s,0 \right) =0$, ${\dot{v}}\left( s,0 \right) =0$, and ${\dot{\theta }}\left( s,0 \right) =0$. Assume that there, respectively, exist two actuators for control variables $v\left( s,t \right)$ and $\theta \left( s,t \right)$, which means ${{m}_{1}}={{m}_{2}}=2$ in Eqs. (63) and (64). External disturbances are presented as $d_{1}^{{}}\left( t \right) =0.05\sin \left( 0.1t \right)$ and $d_{2}^{{}}\left( t \right) =5\times \text {1}{{\text {0}}^{-4}}\sin \left( 0.5t \right)$. Let ${{b}_{1}}=0.7$, ${{b}_{2}}=0.3$, ${{c}_{1}}=0.7$, and ${{c}_{2}}=0.3$.

Actuator faults are then described by ${{f}_{1}}=1$, ${{\bar{u}}_{1}}=0$, ${{f}_{2}}=1$, ${{\bar{u}}_{2}}=0$ for $t<0.3\text { s}$, and ${{f}_{1}}=0\text {.5}$, ${{\bar{u}}_{1}}=0$, ${{f}_{2}}=0$, ${{\bar{u}}_{2}}=0.5$ for $t\ge 0.3\text { s}$, and ${{h}_{1}}=1$, ${{{\bar{\tau }}}_{1}}=0$, ${{h}_{2}}=1$, ${{{\bar{\tau }}}_{2}}=0$ for $t<0.6\text { s}$, and ${{h}_{1}}=0\text {.4}$, ${{{\bar{\tau }}}_{1}}=0$, ${{h}_{2}}=0$, ${{{\bar{\tau }}}_{2}}=0.2$ for $t\ge 0.6\text { s}$.

Fig. 3

Displacements $v\left( s,t \right)$ of the crane bridge

Control laws in Eqs. (77)–(82) are selected as ${{\gamma }_{1}}=200$, ${{\gamma }_{2}}=200$, ${{{\bar{\gamma }}}_{1}}=300$, ${{{\bar{\gamma }}}_{2}}=300$, $k_{1}^{{}}=0.06$, $k_{2}^{{}}=6\times {{10}^{-4}}$, ${{k}_{3}}=0.1$, ${{k}_{4}}=0.1$, ${{k}_{5}}=100$, ${{k}_{6}}=100$, $\alpha =1$, $\beta =10$, ${{\bar{D}}_{1}}=0\text {.05}$, ${{\bar{D}}_{2}}=5\times \text {1}{{\text {0}}^{-4}}$, where $k_{1}^{{}}$ and $k_{2}^{{}}$ are also limited values of $v\left( {{l}_{1}},t \right)$ and $\theta \left( {{l}_{1}},t \right)$, respectively.

For comparative analysis, the traditional PID control laws are proposed as follows

$$\begin{aligned} u\left( t \right)&=-{{k}_{a}}v\left( {{l}_{1}},t \right) -{{k}_{b}}{\dot{v}}\left( {{l}_{1}},t \right) -{{k}_{c}}\int _{0}^{t}{v\left( {{l}_{1}},q \right) \text {d}q} \end{aligned}$$

(89)

$$\begin{aligned} \tau \left( t \right)&=-{{k}_{d}}\theta \left( {{l}_{1}},t \right) -{{k}_{e}}{\dot{\theta }}\left( {{l}_{1}},t \right) -{{k}_{f}}\int _{0}^{t}{\theta \left( {{l}_{1}},q \right) \text {d}q} \end{aligned}$$

(90)

where ${{k}_{a}}$, ${{k}_{b}}$, ${{k}_{c}}$, ${{k}_{d}}$, ${{k}_{e}}$, ${{k}_{f}}$ are control parameters designed as ${{k}_{a}}=1$, ${{k}_{b}}=0.5$, ${{k}_{c}}=0.1$, ${{k}_{d}}=1$, ${{k}_{e}}=1$, and ${{k}_{f}}=0.2$.

Then, the following simulation analysis of the crane bridge includes three cases: without control, with PID control, and with the proposed control, to verify the control performance.

Figures 3 and 4 show the displacement $v\left( s,t \right)$ and rotation $\theta \left( s,t \right)$ of the crane bridge system in these three cases. Furthermore, dynamic responses of the system at several representative points, such as ${{v}_{L}}\left( \frac{{{l}_{1}}}{2},t \right)$, $v\left( {{l}_{1}},t \right)$, ${{v}_{R}}\left( {{l}_{1}}+\frac{{{l}_{2}}}{2},t \right)$, ${{\theta }_{L}}\left( \frac{{{l}_{1}}}{2},t \right)$, $\theta \left( {{l}_{1}},t \right)$, ${{\theta }_{R}}\left( {{l}_{1}}+\frac{{{l}_{2}}}{2},t \right)$, are clearly reflected in Figs. 5, 6, 7, and 8.

Fig. 4

Rotation $\theta \left( s,t \right)$ of the crane bridge

From Figs. 3, 4, 5, 6, 7, and 8, it is obvious that the system without control has serious vibration and rotation which need to be eliminated urgently. Besides, note from Figs. 3, 4, 5, 6, 7, and 8 that the tradition PID control also cannot stabilize the system because of lack of self-adaptive ability to compensate for undesirable effect caused by actuator failures, and thus it also cannot guarantee the required limitation of outputs of the system.

Compared with the PID control in Eqs. (89) and (90), the proposed control scheme in Eqs. (77)–(82) has a significant effect on vibration elimination, and states of the closed-loop system can gradually tend to zero even in the presence of actuator faults and environmental disturbances. Moreover, according to Figs. 3, 4, 5, 6, 7, and 8, it is obvious that the control laws in Eqs. (77)–(82) can always limit the displacement and rotation of the trolley into the given bounds, which means that output constraints $\left| v\left( {{l}_{1}},t \right) \right| <{{k}_{1}}$ and $\left| \theta \left( {{l}_{1}},t \right) \right| <{{k}_{2}}$ can always be satisfied without any violation.

Fig. 5

Displacements ${{v}_{L}}\left( \frac{{{l}_{1}}}{2},t \right)$ and ${{v}_{R}}\left( {{l}_{1}}+\frac{{{l}_{2}}}{2},t \right)$ of the crane bridge

Fig. 6

Displacement $v\left( {{l}_{1}},t \right)$ of the middle trolley

Fig. 7

Rotations ${{\theta }_{L}}\left( \frac{{{l}_{1}}}{2},t \right)$ and ${{\theta }_{R}}\left( {{l}_{1}}+\frac{{{l}_{2}}}{2},t \right)$ of the crane bridge

Figures 9 and 10 depict the control signals $u\left( t \right)$ and $\tau \left( t \right)$ designed in Eqs. (77)–(82) in the third case flowing into the system. Figures 9 and 10 indicate that actuators of ${{u}_{2}}\left( t \right)$ and ${{\tau }_{2}}\left( t \right)$ stuck at ${{u}_{2}}\left( t \right) =0.5\text { N}$ and ${{\tau }_{2}}\left( t \right) =0.2\text { N m}$ at $t=0.3\text { s}$ and $t=0.6\text { s}$, respectively, and partial faults separately occur to actuators of ${{u}_{1}}\left( t \right)$ and ${{\tau }_{1}}\left( t \right)$ at $t=0.3\text { s}$ and $t=0.6\text { s}$. Even under such two kinds of actuator faults, the stabilization can still be realized using the proposed control scheme in Eqs. (77)–(82).

Through the contrastive analysis of simulation results of three cases shown above, it is noteworthy that the actuator failure can be effectively compensated by the proposed control scheme with no knowledge of fault types and fault information, and states of the closed-loop system can be greatly restricted with the required output constraints of the trolley. Consequently, the simulation results in Figs. 3, 4, 5, 6, 7, 8, 9, and 10 show the validity of the developed control strategy in Eqs. (77)–(82).

Fig. 8

Rotation $\theta \left( {{l}_{1}},t \right)$ of the middle trolley

Fig. 9

Proposed control $u\left( t \right)$ in Eq. (77)

Fig. 10

Proposed control $\tau \left( t \right)$ in Eq. (78)

5 Conclusions

This paper uses PDEs to accurately describe dynamic properties of crane bridge system without any discretization, and thus spillover problem is avoided in controller design. Then, a robust adaptive fault-tolerant control algorithm is developed for realizing system stabilization even considering actuator faults, additional perturbations, and output constraints. With proposed control strategy, system displacement and rotation are eliminated even though there are uncertain actuator failures. In addition, output constraints of the central trolley can always be ensured in the course of control. Simulations are conducted for verifying effectiveness of proposed control protocol. In the future research, we plan to design neural control to deal with uncertainties of the crane bridge system [40].