Keywords

1 Introduction

3D crane is considered an underactuated system [1,2,3,4], which has attracted the attention of numerous researchers over the past two decades [5, 6]. Most of the previous studies focused on precisely controlling the trajectory and suppressing the oscillations of the cargo being swing angles [7, 8]; whilst, the vertical vibration originating from the elasticity of cable and steel structure is barely noticeable. The vertical oscillations, although much smaller than the horizontal oscillations, have a significant negative impact on the energy consumption and the life of the structure.

In some previous studies [9, 10], we proposed some control solutions with a new model of a 6-degree-of-freedom crane and gave relatively positive results. In this study, based on the newly built 6-degrees-of-freedom model, we will develop a simpler controller, energy-based coupling control (EBC), to reduce computational resources and re-experience the special characteristics of the dynamic model built based on the theory of Lagrangian dynamics. Comparisons with classical PID controllers are also made through simulation results. Eventually, the effectiveness of the whole work will be evaluated.

2 Dynamic Model

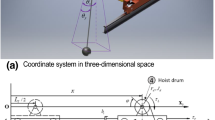
The physical model of an under-actuated indoor bridge crane is illustrated in Fig. 1. Here, the six DOFs corresponds to six generalized coordinates, specifically the trolley position along the girder \(x\left( t \right)\), the angle of the hoist cable \(\varphi_d \left( t \right)\), the displacement of the bridge along the rail \(y\left( t \right)\), the swing motions of the cargo in the Oxz and Oyz planes, and the vertical oscillation. Here, the angle of the angle \(\varphi_d \left( t \right)\) will determine the height of the cargo. Moreover, the first three generalized coordinates, \(x\left( t \right),\,y\left( t \right),\,\varphi_d \left( t \right)\), are considered as actuated states, and the last three, \(\theta_x \left( t \right),\,\theta_y \left( t \right),\,\delta \left( t \right)\), are un-actuated.

Fig. 1.
figure 1

Physical model of a bridge cran.

Full size image

The system consists of three masses: the cargo, the trolley with hoist, and the bridge, which are denoted as \(m_c\), \(m_t\), and \(m_b\), respectively. And we set the non-negative function \(E\) as the entire energy of the system. Depending on the particular working conditions and type of handled cargo, the carrying equipment is adjusted and its mass can be significant. In these cases, both the masses of the cargo and the lifting equipment are related to \(m_c\). Here, \(\Delta \delta\) denotes the initial elongation, \(k_e\) refers to the equivalent elastic coefficient. \(J_d\), and \(r_d\) represent the moment of inertia and radius of the payload-hoisting drum. \(b_m ,\,\,b_b ,\,\,b_t\) and \(b_r\) represent the damping factors of the hoisting mechanism, bridge, trolley, and inside wire rope, respectively. \(\tau_1\), \(\tau_2\), and \(\tau_3\) are active control inputs generated by the trolley, bridge moving, and payload-lifting mechanisms, respectively.

The physical features of the indoor bridge crane are characterized for full-state variables \({{\varvec{\chi}}}_s = \left[ {\begin{array}{*{20}c} {x\left( t \right)} & {y\left( t \right)} & {\varphi \left( t \right)} & {\theta_x \left( t \right)} & {\theta_y \left( t \right)} & {\delta \left( t \right)} \\ \end{array} } \right]^T\).

The system dynamics are provided in matrix form as [9]:

$$ {\varvec{M(\chi }}_s {\varvec{)\ddot{\chi }}}_s {\varvec{ + B\dot{\chi }}}_s {\varvec{ + C(\chi }}_s {\varvec{,\dot{\chi }}}_s {\varvec{)\dot{\chi }}}_s {\varvec{ + G(\chi }}_s {\varvec{) = U}}, $$
(1)

where \({\dot{\varvec{\chi }}}_s = \left[ {\begin{array}{*{20}c} {\dot{x}} & {\dot{y}} & {\dot{\varphi }} & {\dot{\theta }_x } & {\dot{\theta }_y } & {\dot{\delta }} \\ \end{array} } \right]^T\) and \({\varvec{\ddot{\chi }}}_s = \left[ {\begin{array}{*{20}c} {\ddot{x}} & {\ddot{y}} & {\ddot{\varphi }} & {\ddot{\theta }_x } & {\ddot{\theta }_y } & {\ddot{\delta }} \\ \end{array} } \right]^T\) are the first-order and second-order time derivatives of the system states, respectively; the input vector \({{\varvec{U}}}\) is \({{\varvec{U}}} = \left[ {\begin{array}{*{20}c} {{{\varvec{U}}}_s } & 0 & 0 & 0 \\ \end{array} } \right]^T\) with \({{\varvec{U}}}_s = \left[ {\begin{array}{*{20}c} {\tau_1 } & {\tau_2 } & {\tau_3 } \\ \end{array} } \right]^T\); the mass matrix \({\varvec{M(\chi }}_s {\varvec{)}} = {{\varvec{M}}}^T {\varvec{(\chi }}_s {\varvec{)}}\) is positive definite (PD); \({\varvec{C(\chi }}_s {\varvec{,\dot{\chi }}}_s {\varvec{)}}\) represents a Coriolis and centrifugal matrix; \({{\varvec{B}}}\) is a damping coefficient matrix; and \({\varvec{G(\chi }}_s {\varvec{)}}\) denotes a gravity vector.

3 Controller Design

The system dynamic can be divided into actuated and un-actuated parts by decoupling as

$$ {{\varvec{M}}}_{11} {\varvec{(\chi }}_s {\varvec{)\ddot{\chi }}}_{S1} {\varvec{ + M}}_{12} {\varvec{(\chi }}_s {\varvec{)\ddot{\chi }}}_{S2} {\varvec{ + B}}_{11} {\dot{\varvec{\chi }}}_a {\varvec{ + C}}_{11} {\varvec{(\chi }}_s {\varvec{,\dot{\chi }}}_s {\varvec{)\dot{\chi }}}_{S1} {\varvec{ + C}}_{12} {\varvec{(\chi }}_s {\varvec{,\dot{\chi }}}_s {\varvec{)\dot{\chi }}}_{S2} {\varvec{ + G}}_1 {\varvec{(\chi }}_s {\varvec{) = U}}_s , $$
(2)
$$\begin{aligned}& {{\varvec{M}}}_{21} {\varvec{(\chi }}_s {\varvec{)\ddot{\chi }}}_{S1} {\varvec{ + M}}_{22} {\varvec{(\chi }}_s {\varvec{)\ddot{\chi }}}_{S2} {\varvec{ + B}}_{22} {\dot{\varvec{\chi }}}_{S2} {\varvec{ + C}}_{21} {\varvec{(\chi }}_s {\varvec{,\dot{\chi }}}_s {\varvec{)\dot{\chi }}}_{S1} \\&\quad{\bf{ + C}}_{22} {\varvec{(\chi }}_s {\varvec{,\dot{\chi }}}_s {\varvec{)\dot{\chi }}}_{S2} {\bf{ + G}}_2 {\varvec{(\chi }}_s {\bf{) = }}\,0, \end{aligned}$$
(3)

where \({{\varvec{\chi}}}_{S1} = \left[ {\begin{array}{*{20}c} x & y & \varphi \\ \end{array} } \right]^T\), \({\dot{\varvec{\chi }}}_{S1} = \left[ {\begin{array}{*{20}c} {\dot{x}} & {\dot{y}} & {\dot{\varphi }} \\ \end{array} } \right]^T\), and \({\varvec{\ddot{\chi }}}_{S1} = \left[ {\begin{array}{*{20}c} {\ddot{x}} & {\ddot{y}} & {\ddot{\varphi }} \\ \end{array} } \right]^T\) are the vectors of the actuated states; \({{\varvec{\chi}}}_{S2} = \left[ {\begin{array}{*{20}c} {\theta_x } & {\theta_y } & \delta \\ \end{array} } \right]^T\), \({\dot{\varvec{\chi }}}_{S2} = \left[ {\begin{array}{*{20}c} {\dot{\theta }_x } & {\dot{\theta }_y } & {\dot{\delta }} \\ \end{array} } \right]^T\), and \({\varvec{\ddot{\chi }}}_{S2} = \left[ {\begin{array}{*{20}c} {\ddot{\theta }_x } & {\ddot{\theta }_y } & {\ddot{\delta }} \\ \end{array} } \right]^T\) are the vectors belonging to the un-actuated parts; and the block matrices \(\,{{\varvec{M}}}_{11} {\varvec{(\chi }}_s {\varvec{)}}\), \({{\varvec{M}}}_{12} {\varvec{(\chi }}_s {\varvec{)}}\), \({{\varvec{M}}}_{21} {\varvec{(\chi }}_s {\varvec{)}}\), \({{\varvec{M}}}_{22} {\varvec{(\chi }}_s {\varvec{)}}\), \({{\varvec{B}}}_{11}\), \({{\varvec{B}}}_{22}\), \({{\varvec{C}}}_{11} {\varvec{(\chi }}_s {\varvec{,\dot{\chi }}}_s {\varvec{)}}\), \({{\varvec{C}}}_{12} {\varvec{(\chi }}_s {\varvec{,\dot{\chi }}}_s {\varvec{)}}\), \({{\varvec{C}}}_{21} {\varvec{(\chi }}_s {\varvec{,\dot{\chi }}}_s {\varvec{)}}\), \({{\varvec{C}}}_{22} {\varvec{(\chi }}_s {\varvec{,\dot{\chi }}}_s {\varvec{)}}\), \({{\varvec{G}}}_1 {\varvec{(\chi }}_s {\varvec{)}}\), and \({{\varvec{G}}}_2 {\varvec{(\chi }}_s {\varvec{)}}\) are also given in [9].

The mass matrix \({\varvec{M(\chi }}_S {\varvec{)}}\) is positive definite, then we have

$$ {\varvec{\ddot{\chi }}}_S\, {\bf{ = M}}^{ - 1} {\varvec{(\chi }}_S {\varvec{)}}\left( {{{\varvec{U}}} - {\varvec{B\dot{\chi }}}_S - {\varvec{C(\chi }}_S {\varvec{,\dot{\chi }}}_S {\varvec{)\chi }}_S - {\varvec{G(\chi }}_S {\varvec{)}}} \right). $$
(4)

Also, \({\varvec{M(\chi }}_S {\varvec{)}} > 0\), \({{\varvec{\chi}}}_S^T {\varvec{M(\chi }}_S {\varvec{)\chi }}_S > 0\), \({{\varvec{M}}}_{11}^{ - 1} {\varvec{(\chi }}_S {\varvec{)}} = \left( {\det \left( {{{\varvec{M}}}_{11} {\varvec{(\chi }}_S {\varvec{)}}} \right)} \right)^{ - 1} {{\varvec{M}}}_{phk3} {\varvec{(\chi }}_S {\varvec{)}}\), and \({{\varvec{M}}}_{phk3} {\varvec{(\chi }}_S {\varvec{)}} > 0\) is the measurable auxiliary term

Let

$$ {\varvec{\ddot{\chi }}}_{S1} = \left( {\det ({\varvec{M(\chi }}_S {\varvec{)}})} \right)^{ - 1} ({{\varvec{W}}}_a {\varvec{ + P}}_a {{\varvec{U}}}_S ), $$
(5)

where

$$ {{\varvec{W}}}_a = - {{\varvec{M}}}_{phk3} {\varvec{(\chi }}_S {\varvec{)B\dot{\chi }}}_S - {{\varvec{M}}}_{phk3} {\varvec{(\chi }}_S {\varvec{)C(\chi }}_S {\varvec{,\dot{\chi }}}_S {\varvec{)\chi }}_S - {{\varvec{M}}}_{phk3} {\varvec{(\chi }}_S {\varvec{)G(\chi }}_S {\varvec{)}}, $$
(6)

and

$${{\varvec{P}}}_a = {{\varvec{M}}}_{phk3} {\varvec{(\chi }}_S {\varvec{)}}.$$
(7)

The mission of the controller is to force the system states \({{\varvec{\chi}}}_s\) to their target points \({{\varvec{\chi}}}_{ST} = \left[ {\begin{array}{*{20}c} {x_T } & {y_T } & {\varphi_T } & {\theta_{xT} } & {\theta_{yT} } & {\delta_T } \\ \end{array} } \right]^T\).

Define the tracking error being \({{\varvec{e}}}\left( t \right) = {{\varvec{\chi}}}_{S1} - {{\varvec{\chi}}}_{S1T}\), where \({{\varvec{\chi}}}_{S1T} = \left[ {\begin{array}{*{20}c} {x_T } & {y_T } & {\varphi_T } \\ \end{array} } \right]^T\). The controller of the system is computed as follow

$$ {\bf{U}}_S = \left\{ - k_D {\dot{\varvec{\chi }}}_{S1} - k_p {\bf{e}} - k_p {\bf{P}}_a^{\varvec{ - 1}} {\bf{W}}_a- \frac{1}{2}k_p \left[ \frac{d}{dt}\left( {\det ({\bf{M(}}{\varvec{\chi}}}_S {\varvec{)}}){\bf{P}}_a^{{\varvec{ - 1}}} \right) \right]{\dot{\varvec{\chi }}}_{S1}\right\}\left( {k_e {\varvec{ + }}k_p } \right)^{ - 1}$$
(8)

where, \(k_D\), \(k_e\), \(k_p\) are the positive controller coefficients.

Selecting the Lyapunov function as

$$ V_2 \left( t \right) = \frac{1}{2}k_p {\bf{e}}^{\bf{T}} {\bf{e}} + k_e E + \frac{1}{2}k_p {\dot{\varvec{\chi }}}_{S1}^T \left( {\det ({\bf{M(}}{\varvec{\chi }}_S {\bf{)}}){\bf{P}}_a^{ - 1}} \right){\dot{\varvec{\chi }}}_{S1} , $$
(9)

where, \(E\) is the entire energy of the system

Its first-order derivative with respect to time is

$$\begin{aligned} \dot{V}_2 \left( t \right) &= \frac{d}{dt}\left\{ {\frac{1}{2}k_p {{\bf{e}}}^{{\bf{T}}} {{\bf{e}}} + \frac{1}{2}k_p {\dot{\varvec{\chi }}}_{S1}^T \left( {\det ({\bf{M(}}\varvec{\chi} _S {\bf{)}}){{\bf{P}}}_a^{ - 1} } \right){\dot{\varvec{\chi }}}_{S1} } \right\} + k_e \dot{E} \\ &= k_e \left\{ {{\dot{\varvec{\chi }}}_S^T {\bf{M(}}{\varvec{\chi} }}_S {\bf{)}}\dot{\varvec{\chi} }_S {\bf{ + }}\frac{{1}}{{2}}{\dot{\varvec{\chi }}}_S^T {\dot{\bf{M(}}{\varvec{\chi }}_S {\varvec{)\dot{\chi }}}_S {\varvec{ + \dot{\chi }}}_S^T {\bf{G(}}{\varvec{\chi }}_S {\bf{)}}} \right\} + k_p {\dot{\varvec{\chi }}}_{S1}^T {{\bf{e}}} \\& + \frac{1}{2}k_p {\dot{\varvec{\chi }}}_{S1}^T \left[ {\frac{d}{dt}\left( {\det ({{\bf{M}}}){{\bf{P}}}_a^{ - 1} } \right)} \right]{\dot{\varvec{\chi }}}_{S1} + k_p {\dot{\varvec{\chi }}}_{S1}^T \left( {\det ({\bf{M(}}{\varvec{\chi }}_S {\bf{)}}){{\bf{P}}}_a^{ - 1} } \right){{\dot{\varvec{\chi} }}}_{S1} . \end{aligned}$$
(10)

With assumption that the influence of the dampers is smaller in the system, then

$$ \begin{aligned} \dot{V}_2 (t) = & k_e \left\{ \begin{gathered} {\varvec{\dot{\chi }}}_S^T {\bf{M(}}{\varvec{\chi }}_S ){\bf{M}}^{ - 1} {\varvec{(\chi }}_S {\bf{)}}\left( {\bf{U}} - {\bf{C(}}{\varvec{\chi }}_S ,{\varvec{\dot{\chi }}}_S {\varvec{)\chi }}_S - {\bf{G}}({\varvec{\chi }}_S {\bf{)}} \right) \hfill \\ + \frac{1}{2}{\varvec{\dot{\chi }}}_S^T {\dot{\bf{M}(}}{\varvec{\chi }}_S {\varvec{)\dot{\chi }}}_S + {\varvec{\dot{\chi }}}_S^T {\bf{G(}}{\varvec{\chi }}_S {\bf{)}} \hfill \\ \end{gathered} \right\} + k_p {\varvec{\dot{\chi }}}_{S1}^T {\bf{e}} \\ & + \frac{1}{2}k_p {\varvec{\dot{\chi }}}_{S1}^T \left[ {\frac{d}{{dt}}\left( {\det {\bf{(M}})P_a^{ - 1} } \right)} \right]{\varvec{\dot{\chi }}}_{S1} + k_p {\varvec{\dot{\chi }}}_{S1}^T \left( {\det {\bf{(M(}}{\varvec{\chi }}_S {\bf{))}}P_a^{ - 1} } \right){\varvec{\dot{\chi }}}_{S1} \\ & = k_e \left\{ {\varvec{\dot{\chi }}}_S^T \left( { - {\bf{C(}}{\varvec{\chi }}_S ,{\varvec{\dot{\chi }}}_S {\varvec{)\dot{\chi }}} - {\bf{G(}}{\varvec{\chi }}_S {\bf{)}} + {\bf{U}} + \frac{1}{2}{\dot{\bf{M}(}}{\varvec{\chi }}_S {\varvec{)\dot{\chi }}}_S } \right) + {\varvec{\dot{\chi }}}_S^T G{\varvec{(\chi }}_S ) \right \}+ k_p {\varvec{\dot{\chi }}}_{S1}^T {\bf{e}}\\ & + \frac{1}{2}k_p {\varvec{\dot{\chi }}}_S^T \left[ {\frac{d}{{dt}}\left( {\det {\bf{(}}M{\bf{)}}P_a^{ - 1} } \right)} \right]{\varvec{\dot{\chi }}}_{S1} + k_p {\varvec{\dot{\chi }}}_{S1}^T \left( {\det {\bf{(M(}}{\varvec{\chi }}_S {\bf{))}}P_a^{ - 1} } \right){\varvec{\dot{\chi }}}_{S1} \\ \end{aligned} $$
(11)

The matrix \({{\varvec{M}}}_c {\varvec{(\chi }}_S {\varvec{,\dot{\chi }}}_S {\varvec{)}} = {\varvec{\dot{M}(\chi }}_S {\varvec{) - }}2{\varvec{C(\chi }}_S {\varvec{,\dot{\chi }}}_S {\varvec{)}}\) is the skew symmetric matrix. Thus, we have

$$ \dot{V}_2 \left( t \right) = {\dot{\varvec{\chi }}}_S^T k_e {{\varvec{U}}} + {\dot{\varvec{\chi }}}_{S1}^T \left\{ \begin{gathered} + k_p \left( {\det ({\bf{M)}}{\varvec{\chi }}_S {\bf{)}}){{\bf{P}}}_a^{ - 1} } \right){\varvec{\dot{\chi }}}_{S1} + \frac{1}{2}k_p \left[ {\frac{d}{dt}\left( {\det ({\bf{M(}}{\varvec{\chi }}_S {\bf{)}}){{\bf{P}}}_a^{ - 1} } \right)} \right]{\dot{\varvec{\chi }}}_{S1} \hfill \\ + k_p {{\bf{e}}} \hfill \\ \end{gathered} \right\} $$
(12)
$$ \dot{V}_2 \left( t \right) = {\dot{\varvec{\chi }}}_{S1}^T \left\{ \begin{gathered} k_e {{\varvec{U}}}_S + k_p \left( {\det ({\varvec{M(\chi }}_S {\varvec{)}}){{\varvec{P}}}_a^{ - 1} } \right)\frac{1}{{\det ({\varvec{M(\chi }}_S {\varvec{)}})}}({{\varvec{W}}}_a {\varvec{ + P}}_a {{\varvec{U}}}_S ) \hfill \\ + \frac{1}{2}k_p \left[ {\frac{d}{dt}\left( {\det ({\varvec{M(\chi }}_S {\varvec{)}}){{\varvec{P}}}_a^{ - 1} } \right)} \right]{\dot{\varvec{\chi }}}_{S1} + k_p {{\varvec{e}}} \hfill \\ \end{gathered} \right\}. $$
(13)

Then, the function \(\dot{V}_2 \left( t \right)\) is computed as \(\dot{V}_2 \left( t \right) = - k_D {\dot{\varvec{\chi }}}_{S1}^T {\dot{\varvec{\chi }}}_{S1}\) based on control law (8). Furthermore, \(\,\dot{V}_2 \left( t \right) = - k_D \left\| {{\dot{\varvec{\chi }}}_{S1} } \right\|_2^2 \le 0,\,\left( {k_D > 0} \right)\), \(V_2 \left( t \right) < V_2 \left( 0 \right)\), and the function \(V_2 \left( t \right)\) is stable in the sense of Lyapunov and convert to zero since \(t \to \infty\), or \(\mathop {\lim }\limits_{t \to \infty } V_2 \left( t \right) = \mathop {\lim }\limits_{t \to \infty } \left[ {k_e E + \frac{1}{2}k_p {{\varvec{e}}}^{{\varvec{T}}} {{\varvec{e}}} + \frac{1}{2}k_p {\dot{\varvec{\chi }}}_{S1}^T \left( {\det ({\varvec{M(\chi }}_S {\varvec{)}}){{\varvec{P}}}_a^{ - 1} } \right){\dot{\varvec{\chi }}}_{S1} } \right] = 0\). It is inferred that \(\mathop {\lim }\limits_{t \to \infty } {{\varvec{e}}}\left( t \right) = 0\), \(\mathop {\lim }\limits_{t \to \infty } E\left( t \right) = 0\), \(\mathop {\lim }\limits_{t \to \infty } \cos \beta_m \left( t \right) = 1\). Eventually, \({{\varvec{\chi}}}_{S1}\) is compelled to \({{\varvec{\chi}}}_{S1T} = \left[ {\begin{array}{*{20}c} {\varphi_{lT} } & {\varphi_{rT} } & {\beta_{rT} } & {\gamma_{rT} } \\ \end{array} } \right]^T\), and \({{\varvec{\chi}}}_{S2}\) is converged to zero.

4 Simulation Implementation

The system parameters are obtained from a real crane system provided as: \(m_c\) = 5,000 kg, \(m_b\) = 2,316.5 kg, \(m_t\) = 371.9 kg, \(r_d\) = 0.31 m, \(J_d\) = 180 kg m2, \(b_t\) = 310 Nm/s, \(b_b\) = 350 Nm/s, \(b_m\) = 170 Nm/s, \(b_r\) = 260 Nm/s, \(g\) = 9.81 m/s2, \(k_e\) = 300,000 N/m, \(\Delta \delta\) = 0.01 m.

In order to clearly display the efficiency of the EBC controller, simulations are carried out for the EBC controller (shown by the solid purple line) and compared with the PID controller (shown by thes green dashed line). The simulation results are provided in Figs. 2–3.

Different from almost previous studies, the simulations were carried out with the parameters taken according to a real working crane with high lifting capacity and load. To ensure that the motors operate without overload as well as reduce the impact, the speed of the cargo movement in all directions should not exceed 0.6 m/s.

In Fig. 1, it can be seen that it takes about 18–25 s to drive the cargo to reach its desired position according to the spatial coordinates when using the EBC controller. In all three directions, these times are shorter than the PID control by more or less 5 s. Furthermore, the cargo movement speeds in the EBC case are maintained at a stable level (solid purple line), which can be compared with the PID controller (green dashed), as shown in Fig. 2b, d, f.

The superiority of the EBC controller is more evident when observing the oscillations in Fig. 3. Obviously, the amplitude of oscillation of the cargo when controlled by PID is larger, and it remains for more than 30 s. Meanwhile, the oscillation only appears with a small amplitude at the beginning and minimizes approximately 0 degrees during the movement until the end.

With the use of the EBC controller, not only is the cargo towed to its correct trajectory with minimized oscillations, but the travel speed is also limited to appropriate thresholds.

Fig. 2.
figure 2

Control the position of cargo

Full size image
Fig. 3.
figure 3

The system’s vibrations

Full size image

5 Conclusion

This study proposed a control issue for a new model of the 3D crane with 6 degrees of freedom, including the cargo's vertical vibration. Based on the computational model's decoupling and the mathematical model's special properties built on the basis of the Lagrangian theory dynamics, a controller based on the energy functions and the Lyapunov stability criterion was developed. The efficiency of the algorithm was investigated through simulations and comparisons with traditional PID controllers. The study results will be the premise to perform experiments on practical systems in the future.