Introduction

Cranes are special machinery for lifting heavy materials which is widely used in the field of mechanical engineering [1]. In terms of the structure and performance, cranes in practical application are mainly divided into four types: small light lifting equipment, bridge cranes, jib cranes, and cable cranes [2], in which the bridge crane is currently the most widely used. The girder of a bridge crane moves longitudinally along the elevated tracks lying on both sides with the trolleys transversely running along the tracks on the bridge [3]. Within a rectangular working area, the bridge crane can make full use of the space to lift the materials. By adding one more trolleys into the single trolley bridge crane, the double-trolley overhead traveling crane works with two independently controlled trolleys, which move individually or synchronously. A double-trolley overhead traveling crane with excellent stability and safe performance greatly improves the work efficiency, especially for longer objects with large spacing between two lifting points. Compared with the single trolley crane with equivalent tonnage, the double-trolley overhead traveling crane saves the raw steel by at least 10%, showing better economy.

As an important equipment in the field of mechanical engineering, the basic design requirements for the cranes are safety, reliability, and economy. Currently, it is commonly recognized that cranes should take on the lightweight road which attempts to reach an ideal match among the reliability, lifetime, weight, and cost [4]. Essentially, two main works are required according to the lightweight design conception: one is the prediction of the limit load-bearing and the other one is the optimization. Before the structure optimization which aims to achieve a perfect combination of favorable safety performance and low cost under a certain design condition, an initial exploration of the structural load-bearing capacity is required for reliable and economical design of the cranes.

However, existing studies on the double-trolley overhead traveling crane focuses only on the synchronization control of two trolleys [5], and structure design is performed usually by using the same design method to the single trolley crane with the same lifting weight and working-level. Little study about the strength analysis and optimization which specially aims at the double-trolley overhead traveling crane is reported. The cumbersome weight always exists which results in serious material waste and excessive energy consumption. In this case, an urgent task during the design stage is to reduce the crane weight to a large extent while guaranteeing the safe and reliable performance. Furthermore, approximately 60% of the crane weight comes from the main girder which is considered to be an important load-bearing part that affects the mechanical and operational performance [6, 7]. Thus, it is crucial to perform the strength analysis and optimal design on the main girder to reach the lightweight goal for the cranes.

In this paper, the strength analysis and optimal design of the main girder of the double-trolley overhead traveling crane is performed. First, the parametric finite element model is established using the finite element software ANSYS. The elastic–plastic stress analysis of the main girder under various loading conditions using the arc-length algorithm and nonlinear stabilization algorithm is performed respectively to predict the limit load-bearing ability of the main girder. Second, the optimal design is performed on the main girder based on the strength analysis to achieve the optimized weight. Finally, a software platform for the optimization of the main girder is developed using MATLAB. Based on the proposed strength and optimization methods, we implement the lightweight design conception which contributes to promoting the design level of generic cranes.

Parametric Modeling and Finite Element Analysis (FEA) of Main Girder

The parametric finite element modeling for the main girder is performed by considering the true structures and loads of cranes. Special codes are written using ANSYS parametric design language (APDL) based on ANSYS software and parametric finite element analysis is performed by taking a true crane in an engineering case for example.

Parametric Finite Element Modeling

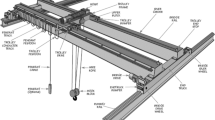
The overall structure of the double-trolley overhead traveling crane is shown in Fig. 1. The working-level is A3, and the rated lifting weight is 5 tons. The girder span is 16,420 mm. Figure 1 shows each end of the main girder has a tilted and contractive area, which has little effect on the loading condition and overall strength by preliminary stress analysis. Thus, it is reasonable to assume that the height of main girder is constant [8]. The simplified structure of main girder with geometric parameters is shown in Fig. 2.

Fig. 1
figure 1

Overall structure of double-trolley overhead traveling crane. (1) End beam, (2) main girder, (3) tonnage token device, (4) lifting trolley, (5) nameplate device, and (6) electrical equipment

Full size image
Fig. 2
figure 2

Girder structure. L the length of main girder, h the height of I-steel, b I-steel leg width, t 1 I-steel leg average thickness, d I-steel waist thickness, h 1 the height of lower cover plate in slant section, h 2 the distance between the bottom and I-steel to lower cover plate, h 3 the height of web plate in main girder both sides, h 4 seam length, l 1 upper cover plate width, l 2 the width of lower cover plate in horizontal section, t 2 web plate thickness, t 3 lower cover plate thickness, t 4 upper cover plate thickness, and t 5 stiffened plate thickness

Full size image

For parametric modeling, 20 geometric and loading parameters are extracted as the characteristic parameters: (1) the length of main girder, (2) the height of I-steel, (3) I-steel leg width, (4) I-steel leg average thickness, (5) I-steel waist thickness, (6) the height of lower cover plate in slant section, (7) the distance between the bottom of I-steel and lower cover plate, (8) the height of web plate in main girder both sides, (9) the seam length, (10) upper cover plate width, (11) the width of lower cover plate in horizontal section, (12) web plate thickness, (13) lower cover plate thickness, (14) upper cover plate thickness, (15) stiffened plate thickness, (16) the distance between the first stiffened plate and the end of main girder, (17) the spacing between stiffened plates except the first one, (18) the distance between one trolley and the end of main girder, (19) the distance between the other trolley and the end of main girder, and (20) the weight of lifting objects.

A parametric 3D finite element model is established using the finite element software ANSYS to perform the elastic–plastic stress analysis. The girder material is Q235 steel. The thicknesses of web plate and lower cover plate are both 5 mm. The 3D eight-node hexahedron solid element solid45 is adopted to mesh the structure. The finite element mesh model is shown in Fig. 3, which includes 58,444 nodes and 40,334 elements. The bilinear kinematic hardening model of material is employed.

Fig. 3
figure 3

Mesh model

Full size image

The main girder is usually considered as a simply supported beam in FEA [9]. Density is defined in material property, and the gravity is considered as the weight. According to the working conditions, the two trolleys are always symmetric with the midpoint of main girder, and the distance between the trolleys changes from L/4 to L/2 (L is the length of main girder). As shown in Fig. 4, the loads caused by the weight of the trolleys and lifting objects are applied as concentrated forces.

Fig. 4
figure 4

Boundary conditions and loads of main girder. Q concentrated load, G deadweight of main girder, L the length of main girder, and L 1 the distance between the trolley and the end of main girder

Full size image

Through the preliminary analysis for the practical operational properties of the crane, two extreme cases that the trolley is L/8 and L/4 away from the midpoint of main girder respectively are considered in section “Numerical Results for Limit Load-Bearing Analysis” to study the limit load-bearing ability. The finite element model with boundary conditions and loads is shown in Fig. 5.

Fig. 5
figure 5

Finite element model with boundary conditions and loads

Full size image

Solution Algorithms for Limit Load-Bearing Analysis

The elastic–plastic stress analysis of the structure could be conducted using the Newton–Raphson iterative algorithm. However, for the sudden plastic collapse behavior, the Newton–Raphson method cannot further track the load path and becomes invalid because the integrated structural stiffness matrices of the structure at the plastic collapse point are singular. To solve this problem, the arc-length algorithm and nonlinear stabilization algorithm are adopted respectively to track the nonlinear post-necking path and to predict the limit load-bearing ability of the main girder.

  1. (1)

    The finite element equation in the arc-length algorithm is given by [10–12]

    $$ \left[ K \right]\left[ u \right] = \lambda \left[ F \right] $$
    (1)

    where λ is a load factor within −1 and 1 which changes with the stiffness matrices [K] to ensure an accurate solution of displacement matrices [u]. The arc-length algorithm imposes another constraint, which is stated as

    $$ \sqrt {\varDelta u^{2} + \lambda^{2} } = R $$
    (2)

    where ∆u is the displacement increment and R is the arc-length radius.

  2. (2)

    The finite element equation in the nonlinear stabilization algorithm is

    $$ \left[ K \right]\left[ u \right] + \left[ C \right]\left[ u \right] = \left[ F \right] $$
    (3)

    where [K], [C], [F], and [u] are stiffness matrices, damping matrices, load matrices, and displacement matrices, respectively. As [K] becomes singular after the failure point, the elements in [C] increase to obtain the solution for [u] in such a way that the viscous forces introduced are sufficiently large to prevent instantaneous collapse but small enough not to affect the behavior significantly while the problem is stable.

It is generally recognized the arc-length algorithm can ensure highest solution precision though the calculations are relatively time-consuming. This arises mainly from the additional Eq 2 in the finite element analysis. In contrast, the nonlinear stabilization algorithm exhibits more rapid convergence velocity.

Parallel calculations are implemented on a high-performance computer and the main configurations are an Intel Xeon Central Processing Unit (CPU) with eight processors (the main frequency of each processor is 2.33 GHz) and 3.99 GB memory.

Numerical Results for Limit Load-Bearing Analysis

Figure 6 shows the distributions of Mises stress for the first case using two algorithms. The stress concentrations appear in such locations as the loading locations and the center of main girder, with the maximum value of 262.0 and 276.4 MPa, respectively, for the two algorithms. The maximum Mises stress does not reach the tensile strength 375 MPa, which indicates that a typical unstable load-bearing due to excess plastic deformation results in the collapse of the main girder. The calculated limit load-bearing for the first case is 16.3 and 17.9 tons using the arc-length algorithm and nonlinear stabilization algorithm, respectively.

Fig. 6
figure 6

Distributions of Mises stress using (a) arc-length algorithm and (b) nonlinear stabilization algorithm for the first case

Full size image

By comparison, the two algorithms lead to relatively consistent results and the nonlinear stabilization algorithm results in slightly stronger load-bearing ability than the arc-length algorithm. Table 1 compares the CPU time for two algorithms. The nonlinear stabilization algorithm costs less time than the arc-length algorithm, and the latter requires more calculation resources for complex problems. Thus, the nonlinear stabilization algorithm is a more preferable algorithm than the arc-length algorithms in terms of their calculation efficiency. Compared with these two algorithms, the conventional Newton–Raphson method cannot simulate the softening properties since it cannot deal with the negative stiffness matrix problems.

Table 1 CPU time for two algorithms and two loading locations (s)
Full size table

Figure 7 shows the distributions of Mises stress for the second case using two algorithms. The maximum Mises stress 255 MPa is smaller than 262.0 and 276.4 MPa for the first case. The calculated limit load-bearing is 26.3 and 26.6 tons, respectively. By comparing the two load cases above, we can find some common features that the overall stress distributions are similar and apparent stress concentrations appear in such the areas as the loading locations and the center of main girder. Table 2 lists the calculated limit load-bearing for the two loading cases using two algorithms. The first load case, with lower limit load-bearing than the second extreme case, is considered the most dangerous in all working conditions. From the point of view of conservation, the following stress analysis and optimal design are carried out under the first loading case, i.e., the trolley is L/8 away from the middle of main girder.

Fig. 7
figure 7

Distributions of Mises stress using (a) arc-length algorithm and (b) nonlinear stabilization algorithm for the second case

Full size image
Table 2 Calculated limit load-bearing (comparison of two algorithms and two loading locations) (103 kg)
Full size table

The predicted limit strength above provides a valuable reference for the evaluation of load-bearing abilities of the cranes. In general, there are many other undetermined factors affecting the safety performance of the crane, such as the operation status and operating environment. So, it is reasonable to ensure proper safety allowance by considering these undetermined factors. Taking the true double-trolley overhead traveling crane for example, the rated lifting weight is set as 5 tons with the calculated limit load-bearing of about 17t.

Stress Analysis of the Main Girder Under Working Conditions

Based on the limit load-bearing analysis above, the finite element analysis under normal working conditions, i.e., the trolley is L/8 away from the midpoint of the main girder with the payload of 5 tons, is performed. Figure 8 shows the distributions of Mises stress and displacement. Figure 8a shows the material still in the elastic range. The overall stress level of main girder is low, but the stress concentrations appear in some locations such as the loading locations and the center of main girder, with the maximum value of 130.7 MPa in loading locations. The maximum deflection occurs in the girder center with the value of 17.6 mm as shown in Fig. 8b. According to Chinese national standard GB/T 3811-2008 Design rules for cranes [13], the allowable stress and deflection for Q235 steel are calculated respectively as

$$ \begin{aligned} \left[ \sigma \right]& = 235\,{\text{MPa/}}1.48 = 158.8\,{\text{MPa,}} \\ \left[ \varepsilon \right] &= L /700 = 23.6\,{\text{mm}} .\\ \end{aligned} $$
(4)
Fig. 8
figure 8

Numerical results under working conditions. (a) Distributions of Mises stress and (b) distributions of displacement

Full size image

By Eq 4, both the strength and static stiffness of main girder meet the requirements.

Optimal Design of Main Girder

The lightweight design as a remarkable tendency that combines advanced numerical methods and manufacturing technique develops rapidly, and commits to improving the reliability and practicability of the crane. According to the FEA above, the strength and stiffness are much lower than the allowable values even in the most dangerous working condition, which results in the waste of material and energy. So it is necessary to perform the optimal design based on the parametric modeling and strength analysis.

Mathematical Model for Optimal Design

Optimal design aims to reach the optimal goal (such as weight, volume, and cost) under the premise of satisfying all the design requirements [14]. The optimal variables are generally divided into the design variables, the state variables and the objective functions. In terms of the crane, the optimal calculations are conducted by considering the girder weight as the objective function, and the allowable stress and deflection as the state variables, and the thickness and height of web plate as the design variables (x i , i = 1, 2) according to the results of strength analysis above. The proposed mathematical model for the optimal design is given by

$$ \begin{aligned} &\hbox{min} f(x) \\ &x_{i} ,\;x_{i}^{\text{L}} < x_{i} < x_{i}^{\text{U}} (i = 1,\,2) \\ &{\text{s}} . {\text{t}} .\,\sigma_{\hbox{max} } \le [\sigma ] \\ &\left| {\varepsilon_{\hbox{max} } } \right| \le \left[ \varepsilon \right] \end{aligned} $$
(5)

where f(x) is the objective function, \( x_{i}^{\text{L}} \) and \( x_{i}^{\text{U}} \) are the lower and upper bounds of design variables, σ max and ε max are the maximum stress and deflection, [σ] and [ε] are the allowable stress and deflection. The optimal variables are listed in Table 3.

Table 3 Optimal variables
Full size table

Optimization Methods

Currently, some advanced optimization methods are developed. The sub-problem approximation method and the first-order optimization method are used to accommodate a wide range of optimization problems in ANSYS. For both the sub-problem approximation and the first-order methods, the program performs a series of analysis–evaluation–modification cycles until all specified criteria are met [15, 16].

The sub-problem approximation method is an advanced zero-order method that can be efficiently applied to most engineering problems. In the sub-problem approximation method, the curve-fitting of the response functions about all optimal variables is achieved by numerical sampling for dependent variables (state variables and objective functions) [17, 18]. For the objective function, the fitting formula is given by

$$ f = a_{0} + \sum\limits_{i}^{n} {a_{i} } x_{i} + \sum\limits_{i}^{n} {\sum\limits_{i}^{n} {b_{ij} } } x_{i} x_{j} , $$
(6)

where a i and b ij are coefficients that are determined by the weighted least square method, x is design variable. In general, the constrained minimization problem is transformed into the unconstrained optimization problem using the penalty function for calculations. The formula is written as

$$ F\left( {x,p_{k} } \right) = f + f_{0} p_{k} \left[ {\sum\limits_{i}^{n} {X\left( {x_{i} } \right)} + \sum\limits_{i}^{{m_{1} }} {G\left( {g_{i} } \right)} + \sum\limits_{i}^{{m_{2} }} {H\left( {h_{i} } \right)} + \sum\limits_{i}^{{m_{3} }} {W\left( {w_{i} } \right)} } \right], $$
(7)

where f 0 is the reference value of objective function, p k is the response surface parameter, x i is the design variable, g i , h i , and w i are the state variables, and X, G, H, and W are the corresponding penalty functions. The penalty functions increase largely when the design variables or state variables reach their limits. The sequential unconstrained minimization technique (SUMT) is adopted to search the minimum value of objective function after the transformation. Most of the engineering problems can be handled using the sub-problem approximation method effectively.

The first-order optimization method is based on the design sensitivity, which uses the first-order partial derivatives of dependent variables. With higher precision, the first-order optimization method is especially suitable for large design space with many design variables.

The following optimal calculations are performed using two optimization methods above.

Numerical Results

The numerical calculations are performed on the DELUX computer with the main configurations: AMD Athlon™ II 645 CPU with two processors (the main frequency of each processor is 3.1 GHz) and 4 GB memory. The parallel numerical calculations using the two optimization methods last about 1 and 15 h, respectively.

Special codes are made using ANSYS-APDL language to perform the optimal design, and 30 iterations are set in the optimal calculations. Take the actual crane above for example, Figs. 9 and 10 show the distributions of Mises stress and displacement using two optimization methods. The stress concentrations appear in the local areas with the maximum stress values of 157.0 and 158.3 MPa for two optimization methods, respectively. The maximum deflections are 23.4 and 22.1 mm, respectively. So, the strength and static stiffness meet the requirements by Eq 4 according to GB/T 3811-2008 Design rules for cranes [13].

Fig. 9
figure 9

Optimization results using the sub-problem approximation method. (a) Distributions of Mises stress and (b) distributions of displacement

Full size image
Fig. 10
figure 10

Optimization results using the first-order optimization method. (a) Distributions of Mises stress and (b) distributions of displacement

Full size image

The comparative results for the optimal variables before and after optimization are listed in Table 4. Figure 11 shows the curve of the objective function with iterations using two optimization methods. From Table 4 and Fig. 11, with the decrease of web plate thickness and height, σ max is close to the allowable stress. This shows that the load-bearing ability of the structure can be made full use of by optimization. For the two optimization methods, the weights of main girder reduce by (2545.3 − 2139.2 kg)/2545.3 kg = 16.0% and (2545.3 − 2123.4 kg)/2545.3 kg = 16.6%, respectively. By comparison, similar optimization results for the main girder are obtained using two optimization methods, while the first-order method costs much more calculation time and space. Therefore, in the following work, the Sub-problem approximation method is adopted to carry out optimal design.

Table 4 Comparative results for the optimal variables before and after optimization
Full size table
Fig. 11
figure 11

Curve of objective function with iterations

Full size image

Software Platform for Optimal Design of Main Girder

In the following work, the software platform for optimal design is developed using MATLAB GUIDE in order to promote the practical application of the proposed optimization method for the lightweight design of cranes. The integrated parametric optimal design for this type of cranes can be conveniently implemented in this platform.

MATLAB Graphical User Interface (GUI)

As a set of high-performance numerical calculation and visualization software, MATLAB is officially launched in 1984 by the Mathworks Company. Users can conduct the matrix operation, the graphic drawing, the algorithm implementation and the generation of user interface using MATLAB. Among all the functions, graphical user interface (GUI) is an important tool and method to implement human–computer interaction. There are various graphical objects in GUI, which can cause the computer to act or change once they are selected or activated by users.

Design process of a GUI can be generally divided into two parts: (1) GUI structure design, including all dialog boxes, buttons and the location of objects, and (2) the implementations of GUI functions, i.e., the compilations of the callback programs [19]. In the GUI, users can conduct the corresponding projects conveniently according to the interface prompts, without the need to understand the internal working mechanism and the troublesome codes.

GUI Structure Design

Graphical user interfaces development environment (GUIDE) provides the developers with a development environment in MATLAB. Various common tools and menus in the GUIDE design panel are used to implement the GUI structure design. For example, the displayed content, the color of font and background as well as the size and position for a component can be modified by Property Inspector as shown in Fig. 12, and the relative positions of components are adjusted through the Align Objects. According to the requirements for the functions, the structures of the platform are designed as follows.

Fig. 12
figure 12

Property inspector

Full size image

The main interface is the first interface to appear when the platform is activated. By the main interface, users can access the platform by clicking on the enter button. The basic parameters before the optimization are shown in the next interface. Two function buttons are provided: one is to carry out the optimal calculations by calling ANSYS and the other one is to show optimization results. The optimization results of all variables can be obtained through the following interface, and the optimal process files can be checked and viewed by clicking on the corresponding button.

Implementation of GUI Function

The ultimate purpose to establish a GUI is to reach some functions, which can be implemented by compiling and executing the callback programs [20]. The compilations of callback programs in this platform mainly focus on the implementations of two functions, i.e., the calling of ANSYS and the output of results. Moreover, the following aspects should be considered:

  1. (1)

    The handles of various components should be acquired correctly.

  2. (2)

    There are two ways to accomplish the calling in MATLAB. Take the calling of a text document for example, !fname.txt and system(‘fname.txt’) are all valid (where fname is the name of the text document).

  3. (3)

    The background images can be inserted by invoking the commands of imread() and imshow(), and their sizes and positions in the interfaces can be set by Axes component.

  4. (4)

    The result files can be read through the command of importdata().

External Program

MATLAB GUIDE provides designers with a development environment relying on MATALB. In the following, the external program is generated to run the software platform with no need for the MATLAB environment. The generation of external program includes two main steps: the configuration for the compiler and the compilation for the script. Compiler LCC provided by MATLAB itself is selected as the compiler in this platform. In this way, the developed software platform which is independent of MATLAB shows better applicability and flexibility.

Engineering Case

Take the actual crane in engineering case in section “Parametric Finite Element Modeling” for example, the optimal design for the main girder is performed to test the developed software platform. The basic parameters are input into the software platform which is responsible for carrying out the optimal design integratedly and interactively. The corresponding interface is shown in Fig. 13. From Fig. 13c, the optimization results are consistent with those obtained in section “Numerical results.” It is shown that the developed software platform can carry out the parametric optimal design efficiently and conveniently.

Fig. 13
figure 13

Software platform. (a) Main interface, (b) interface for structure parameters, and (c) interface for optimal results

Full size image

Conclusions

With increasing application of the double-trolley overhead traveling crane in the field of mechanical engineering, the design requirements for reliability, practicability, and economy become higher. The lightweight design as a remarkable tendency that combines advanced numerical methods and manufacturing technique develops rapidly, and becomes an important means to improve the reliability and practicability of the crane. For the overhead traveling crane, the main girder is an important load-bearing part that affects the mechanical and operational performance largely. However, until now there is little study on the strength analysis and optimal design for the main girder of double-trolley overhead traveling crane which are involved in the lightweight design conception. The lightweight design aims to reduce the weight to the maximum extent under strength and stiffness constraints.

In this paper, we establish the parametric finite element model for the main girder and develop a set of numerical methods on the limit load-bearing analysis and optimal design using finite element analysis. Furthermore, a software platform for optimal design is developed using MATLAB GUIDE to preform optimal design efficiently. The limit load-bearing analysis and optimal design are performed on a true engineering crane using the proposed methods. The numerical results indicate that the rated lifting weight is reasonable with appropriate safety allowance, and the weight of the crane after optimization decreases by about 16%. Through the optimal design of the existing crane, we find that there is still large space for the decrease of the weight of cranes. By numerical analysis, the proposed numerical method implements the lightweight design conception efficiently as an optimal design platform. This work provides theoretical and technique support for promoting the safety evaluation and lightweight design of generic cranes.