1 Introduction

Chaotic maps are evolution functions which are deterministic, but their behavior is not predictable due to a great sensitivity to initial conditions [1]. Mixing, random-like behavior and ergodic behavior are also very important characteristics of chaotic maps. Due to the aforementioned features, chaotic maps are used in a wide range of disciplines which include cryptography, meteorology, sociology, physics, engineering, economics, biology and philosophy [2,3,4,5]. The application of chaos in cryptography was particularly popular in the past few decades which resulted in a great number of papers dealing with new cryptographic systems based on chaos and their security.

Low-dimensional chaotic maps have a simple structure and therefore could be easily implemented, which is a desirable property for cryptography. This is their main advantage over high-dimensional chaotic maps [6]. Some of the examples of simple one-dimensional chaotic maps are the logistic map [5], tent map [7] and sine map [8]. However, some low-dimensional chaotic maps are not resistant to some attacks such as the attacks based on the nonlinear prediction method [9] which are not efficient on high-dimensional chaotic maps. For this reason, development of new one-dimensional chaotic maps with better properties is needed.

Most of the existing one-dimensional chaotic maps have continuous space. However, discrete nature of digital devices is in contrast to continuous space on which these chaotic maps operate. Digital computers and devices are only able to use mappings from finite sets to finite sets [10], so approximations of continuous values to discrete values must be performed [11]. Such approximations of chaotic systems, defined on the continuous space, cause dynamical degradation on digital devices [12]. For this reason, a fully digital approach is necessary for the application of chaos in cryptography and other disciplines.

Recently, two one-dimensional discrete-space chaotic maps are proposed [13, 14] which completely solve the problem with dynamical degradation. Also, these maps do not have fixed points which is a desirable trait in cryptography. However, there are other characteristics of chaotic maps which affect their applicability in cryptography and other disciplines. Length of orbits of chaotic maps is very important characteristic when the application in cryptographic systems is in question. Both of discrete-space chaotic maps [13, 14] have a relatively short orbit lengths when they are set to operate with lower memory requirements. In order to increase the length of orbits, both maps [13, 14] should be used with parameter values which enable a larger space of these maps, but in this case computational complexity and memory requirements of both maps are increased. This situation could significantly affect the usability of these maps in lightweight devices which have limited memory and computational resources. Also, the increased computational complexity negatively influences the speed of implementation of chaotic map which is in contrast to requirement of fast encryption in real-time systems [15, 16].

For the above-mentioned reasons, there is a need for the development of new one-dimensional discrete-space chaotic maps which could improve orbit lengths without a great cost in increased computational complexity and memory requirements. In this paper, a new one-dimensional discrete-space chaotic map based on the multiplication of integer numbers and circular shift is proposed. This map preserves all desirable properties of previous discrete-space chaotic maps, while characteristics related to the orbit length, computational complexity and memory requirements are improved.

In recent years, the application of chaotic maps in cryptographic systems was very prominent in the S-box design [11, 17,18,19] and the design of pseudo-random number generators (PRNGs) [20, 21]. Design of good PRNGs proved to be very difficult task due to several aspects such as security and the requirement for generation of very long sequences of high randomness. Numerous papers have shown that PRNGs are very vulnerable to different cryptanalytic attacks if they are not carefully designed [22,23,24]. Also, not every chaotic map is suitable for the generation of such large quantity of pseudo-random data which are required in PRNG design [25]. On the other hand, S-box design methods do not require sequences of such length and quality as PRNGs and their security is not very vulnerable unlike the security of PRNGs. For this reason, in order to show an example of the application of the proposed map in cryptography, a random S-box design method will be presented.

S-box is an important nonlinear component which is used in block ciphers of substitution-permutation type in order to achieve the property of confusion [2]. Aims of the property of confusion are differently described depending on the type of cipher. In stream ciphers intended for image encryption, the confusion property is aimed at reducing high correlation between pixels [26, 27]. In order to achieve such aim, DNA coding [28], Chen system [26], PWLCM [29], perceptron model [30] and other approaches are used in image encryption. On the other hand, in block ciphers the confusion property is aimed at hiding the relationship between cipher-text and secret key. From the mathematical perspective, an \(p\times p\) S-box is a nonlinear mapping \(S: {\{0,1\}}^p \rightarrow {\{0,1\}}^p\), where \({\{0,1\}}^p\) represents the vector spaces of p elements from GF(2) [11].

One of the first chaos-based S-box design methods was based on exponential and logistic chaotic maps [3]. Afterward, many chaos-based S-box generation methods based on different chaotic maps were proposed. Some of these methods are based on 2D Baker map and Chebyshev map [31], tent map [32], Lorenz system [33], 3D four-wing autonomous chaotic system [34], chaotic scaled Zhongtang system [17], logistic-sine map [18], fractional-order chaotic Chen system [19], logistic and asymmetric tent map [35], etc. All aforementioned S-box design methods are based on chaotic maps, which are defined over the continuous space, whose implementation in digital devices causes dynamical degradation.

More recently, some chaos-based S-box design methods were proposed, which use chaotic maps defined over the discrete space and therefore are immune to dynamical degradation [11, 14]. Also, an efficient S-box design method based on composition is presented which can use any of the existing chaotic maps regardless of the space on which they are defined [36]. Bearing in mind that chaos is used in S-box design methods in order to provide pseudo-randomness, several random S-box generation methods based on different chaotic maps were compared in paper [37] in order to establish whether the selection of the chaotic map influences the quality of obtained S-boxes. Results of that research show that similar quality of S-boxes could be obtained by using different chaotic maps, under the condition that these maps are used properly [37]. Therefore, any chaotic map can be used in order to generate good S-boxes, but chaotic maps with longer periodic orbits and lower complexity are especially useful in enabling smooth generation of dynamical S-boxes.

The rest of this paper is organized as follows. In Sect. 2, the new one-dimensional discrete-space chaotic map based on the multiplication of integer numbers and circular shift is presented. In Sect. 3, dynamical properties of the proposed map are discussed. In Sect. 4, performance analysis of the proposed method regarding its applicability in cryptography and other disciplines is presented. A new S-box design method is proposed in Sect. 5. In Sect. 6. recommendations for future research are presented. Conclusions are drawn in Sect. 7.

2 The proposed one-dimensional discrete-space chaotic map

Let n denote the number of digits of a integer number x. Digits of the integer number x have an arbitrary base b that is greater than or equal to 2. Therefore, digits of the integer number x could have base 2 (binary digits), base 10 (decimal digits), base 16 (hexadecimal digits) or any other base bigger than one. However, when the implementation of the proposed chaotic map in digital computers and devices is in question, using binary digits is the most suitable. For this reason, an example of the binary implementation will be provided with the description of each part of this chaotic map.

The proposed one-dimensional discrete-space chaotic map is based on the multiplication of two parts of the integer number x. This number is divided into two parts which have \(\frac{n}{2}\) digits each when n is even. In the case, when n is odd, one part has one digit more than the other part. Let \(d_1d_2\ldots d_n\) denote digits of the integer number x and m denote the largest integer less than or equal to \(\frac{n}{2}\). Then, x is split into two parts \(p_1(x)=d_1d_2\ldots d_m\) and \(p_2(x)=d_{m+1}d_{m+2}\ldots d_n\).

When binary digits are used, the process of splitting the integer number x into two parts is very simple and fast by using integer division. In C\(++\) programming language, the operator / is used for the integer division, while the operator \(\%\) is used in order to obtain the remainder of the integer division. Therefore, binary integer x is split into two parts by using \(p_1(x)=x/2^m\) and \(p_2(x)=x\%2^m\).

The proposed one-dimensional discrete-space chaotic map is also based on the circular shift which will be denoted as function cshift(y). This function performs circular shift on digits of a integer number y. Number of positions by which y is shifted is dependent on this number in such way that y is shifted by \(y\%n\) positions.

Based on the above notation, the new one-dimensional discrete-space chaotic map is proposed by

$$\begin{aligned} x_{i+1}=cshift((p_1(x_i)+1)*(p_2(x_i)+1)+1). \end{aligned}$$
(1)

In the case when the number of digits of \((p_1(x_i)+1)*(p_2(x_i)+1)+1\) exceeds n, the most significant digit should be discarded. In most programming languages, this happens automatically when the number of binary digits n is equal to the number of bits of the integer type used to store x. Implementation of this chaotic map in C\(++\) programming language is very simple and may be carried out with the following code:

$$\begin{aligned} x=(z<< (z\%n))|(z>> (n - z\%n)); \end{aligned}$$
(2)

where \(z=(x/b^m+1)*(x\%b^m+1)+1\). Substitution of \((x/b^m+1)*(x\%b^m+1)+1\) with z in Eq. (2) is only performed in order to fit this code into one line of text, but it is not needed in C\(++\) programming language. This implementation does not consider memory requirements of integer types because the number of digits n is not set.

In order to provide an example with exact memory considerations, we can use unsigned long integer type which is 32 bits long to store variable x. In this case, we can consider that x have \(n=32\) binary digits (\(b=2\)). Integer number x is split into two parts which consist of \(m=16\) bits by using integer division with \(2^{16}=65{,}536\) and \(\%\) operator. These operations are equal to using regular (non-circular) left and right bitwise shifts by 16 positions. Implementation of this example in C\(++\) programming language is very simple and may be carried out with the following code:

$$\begin{aligned} x=(z<< (z\%32))|(z>> (32 - z\%32)); \end{aligned}$$
(3)

where \(z=(x/65{,}536+1)*(x\%65{,}536+1)+1\). Substitution with z in Eq. (3) is also only performed in order to fit this code into one line of text, but it is not needed in C\(++\) programming language. Besides this integer type, any other integer type which corresponds to the number of binary digits n can be used. The number of bits n (when the base b is equal to 2) completely determines the possible number of initial conditions (key space) of the proposed chaotic map which is equal to \(2^n\). In order to achieve bigger set in which the proposed map operates, the existing integer types such as \(\_int128\) could be used or implementations with even bigger number of bits could be created for \(n>128\) in order to achieve key space which is bigger than \(2^{128}\).

3 Dynamical properties of the proposed chaotic map

In the following text, we will deal with the dynamical properties of the proposed map. Due to the simplicity of exposition, analysis of dynamical properties will be mostly based on the example of the proposed map presented by Eq. (3).

Chaotic map f(x) has a fixed point if for some particular value of x, equation \(x=f(x)\) is correct. If \(x=cshift((p_1(x)+1)*(p_2(x)+1)+1)\), then the proposed map has a fixed point. Identification of fixed points for the proposed map is to some extent more complicated because of the cshift function, but due to fact that there are only n different positions by which number \((p_1(x)+1)*(p_2(x)+1)+1\) is circularly shifted, this problem can be divided into n equations which are easy to solve.

For example, if we consider the case when the integer number x consists of \(n=4\) binary digits, it is easy to find fixed point \(x=1010\) (\(x=10\) in decimal base). When n is smaller, there is a greater probability of the existence of fixed points. However, regardless of fixed points, it is recommended to use the proposed map for bigger n because space of \(2^n\) integer numbers is not large enough for the most applications when the n is smaller.

When the integer number x consists of \(n=32\) binary digits (Eq. 3), there are no fixed points. This is confirmed theoretically and experimentally by checking all \(2^{32}\) possible values of x. Therefore, we can conclude that the proposed map has fixed points for certain values of n, but it is easy to completely avoid them by selecting values of n for which it is determined (experimentally or theoretically) that there are no fixed points.

The proposed map is not bijective mostly due to commutative property of the multiplication operation, so \(f(a)=f(b)\) when \(p_1(a)=p_2(b)\) and \(p_1(b)=p_2(a)\). Function cshift also influences the bijective property of the proposed map.

Dynamical behavior of continuous-space chaotic maps with control parameters is usually verified by using bifurcation diagram and Lyapunov exponents [38, 39]. However, the proposed map does not have control parameters which could be used to obtain bifurcation diagram. Also, according to Kocarev et al [10], discrete Lyapunov exponent of chaotic maps defined over some finite discrete space is always a positive number except in some special cases such as identical mapping when the value of discrete Lyapunov exponent is equal to zero. For previously mentioned reasons, appropriate test for discrete-space chaotic maps should be used. In order to determine whether the proposed map exhibits chaotic behavior, the 0–1 test [40] was conducted. The example of the proposed map when \(n=32\) binary digits are used to represent the variable x (Eq. 3) is used to generate a sequence of length 1000. This sequence was tested with the 0–1 test, and the value of 0.998052 is obtained which is very close to the ideal value of 1. This result indicates that the proposed map is chaotic [40].

Lengths of the orbits and trajectories of the example of the proposed map from Eq. (3) (\(n=32\)) are experimentally obtained on the sample of one million randomly selected initial points. The minimal obtained length of orbit was 176 (more than \(2^{\frac{n}{4}-1}\)), while the maximal length of orbit including trajectory to that orbit was 36,103 (more than \(2^{\frac{n}{2}-1}\)). Distribution of orbit lengths of the proposed map is presented in Table 1.

Table 1 Distribution of orbit lengths of the proposed map
Full size table

Results from Table 1 show that the number of orbits shorter than 1000 is very small (under half percent), while almost 90 percent of orbits have length which is greater than 10, 000. These results show that length of orbits of the proposed map is very good in comparison with previous one-dimensional discrete-space chaotic maps [13, 14].

Qualitative behavior of the example of the proposed map (Eq. 3) is demonstrated by the cobweb plot diagrams when \(x_0=2000{,}000{,}000\). Due to large length of orbit for this initial point and limited length of the diagram, lines of cobweb plot are largely overlapping, which reduces the visibility of the diagram. For this reason, three cobweb plot diagrams for this initial point are presented with the different number of iterations. The first cobweb plot diagram presented in Fig. 1 shows only first 1000 iterations, the second cobweb plot diagram presented in Fig. 2 shows first 9364 iterations, while the third cobweb plot diagram shows all 19,364 iterations (Fig. 3).

Fig. 1
figure 1

Cobweb plot diagram for \(x_0=2000{,}000{,}000\), first 1000 iterations

Full size image
Fig. 2
figure 2

Cobweb plot diagram for \(x_0=2000{,}000{,}000\), first 9364 iterations

Full size image
Fig. 3
figure 3

Cobweb plot diagram for \(x_0=2000{,}000{,}000\), all 19,364 iterations

Full size image

4 Performance analysis

Chaotic maps are widely used in many different fields such as cryptography. Low-dimensional chaotic maps have some desirable characteristics for cryptography such as simple structure and relatively easy implementation [6]. For this reason, application of one-dimensional chaotic maps in cryptography is particularly interesting subject. Great number of continuous-space chaotic maps is used in cryptographic systems, especially for an S-box design. However, cryptographic systems are usually implemented in digital devices which cannot support continuous-space chaotic maps. For this reason, approximations of continuous-space chaotic maps are used which causes dynamical degradation. On the other hand, discrete-space chaotic maps [13, 14] are not affected by the dynamical degradation, but there are other characteristics of chaotic maps which affect their applicability in cryptographic systems. For the above-mentioned reasons, performance analysis of the proposed one-dimensional chaotic map is conducted in order to determine its applicability in cryptographic systems.

One-dimensional continuous-space chaotic maps are especially vulnerable to the dynamical degradation caused by their implementation on digital computers. The proposed map is fully based on integer numbers which means that it is not affected by dynamical degradation. This is clear advantage of the proposed map over the continuous-space chaotic maps when the application in cryptography is considered. Although certain methods using multiple-precision arithmetic are proposed with the aim to solve the problem with dynamical degradation of continuous-space chaotic maps [41], these methods can only reduce the effect of the digital degradation but cannot eliminate it completely. Previous one-dimensional discrete-space chaotic maps [13, 14] are also not affected by the dynamical degradation, same as the proposed chaotic map.

Available space of chaotic maps is very important for chaos-based cryptographic systems because it directly influences the key space of such systems. Even a random S-box design methods, which are not demanding as some other parts of cryptographic systems, require considerable key space in order to generate a sufficient number of S-boxes from which one or more good S-boxes could be selected [37]. Due to its discrete nature, the proposed map can achieve virtually unlimited space, same as other discrete-space chaotic maps [13, 14], limited only by the memory of the digital device in which it is implemented.

On the other hand, implementations of continuous-space chaotic maps suffer from limitations caused by available floating-point formats which lead to a limited space. If we consider one-dimensional continuous-space chaotic maps such as the logistic map [5] and tent map [7], both maps have one initial condition and one control parameter in their original form. According to IEEE standard for floating-point arithmetic [42], double precision format use 1 bit for sign, 11 bits for exponent and 52 bits for mantissa, which means that key space of one variable in double precision format has less than \(2^{64}\) possible values. Bearing in mind that values of initial conditions and parameters of one-dimensional maps are usually in the interval (0, 1) or some other interval of similar length, the number of different values for one variable is approximately \(2^{53}\) [23]. If we, in addition to the initial condition, include control parameter to the key space of one-dimensional continuous-space chaotic map, the total key space is about \(2^{53}\times 2^{53}=2^{106}\) which is less than \(2^{128}\). The proposed map can easily achieve key space of \(2^{128}\) for \(n=128\) which could be stored in integer type \(\_int128\). In order to avoid these limitations of continuous-space chaotic maps, certain procedures using multiple-precision arithmetic are proposed [41], but the use of such procedures is more complex than using discrete-space chaotic maps. Therefore, discrete-space chaotic maps have clear advantage over the continuous-space chaotic maps when the available space is considered.

However, available space of different discrete-space chaotic maps is not achieved with the same memory requirements. When a comparison of different discrete-space chaotic map is made, it is important to bear in mind that their characteristics such as orbit length, required memory and computational complexity depend on parameters which determine the size of space on which these maps operate. For this reason, examples of discrete-space chaotic maps with similar memory requirements should be compared with other chaotic maps of this type.

Previous one-dimensional discrete-space chaotic maps [13, 14] use permutations to represent the variable x and the parameter c of each map. If we consider the case when permutations of 8 elements are used, required memory for the variable and parameter of these discrete-space chaotic maps is \(3\times 8=24\) bits each. Therefore, each map requires 48 bits of memory for its variable and parameter. The proposed map does not has parameter c, so there are memory requirements only for the variable x. Although the proposed map can use variable represented with 48 bits, in order to highlight the advantages of this map we will use the example from Eq. (3) for the comparison which requires only 32 bits of memory.

When permutations of 8 elements are used, the available space on which chaotic maps [13, 14] operate have only \(8!=40{,}320\) elements (about \(2^{15.3}\)) which is very small compared to the space of the proposed map of \(2^{32}\) elements which is achieved on a smaller memory. The maximal orbit length reported in the paper [13] for this example is 214. This is very short compared to the example of the proposed map (Eq. 3) where the majority of orbits achieve length greater than 10, 000. Also, the maximal orbit length 36, 103 (plus trajectory) of this example of the proposed map is very close to the total size of the space of maps [13, 14]. Therefore, we can claim that length of orbits of the example of the proposed map is much greater than the length of orbits of maps [13, 14] achieved with similar memory requirements. Conversely, the proposed map can achieve similar space and orbit lengths as maps [13, 14], but with less required memory. Small memory requirement is especially desirable for the use in devices with limited memory space.

If we include parameter c in the key space of chaotic maps [13, 14] when permutations of 8 elements are used, total key space is only about \(2^{30.6}\) with 48 bits of memory required. The proposed map achieves key space of \(2^{32}\) with only 32 bits of memory required, while with the same memory requirement as previous discrete-space maps it achieves key space of \(2^{48}\).

The existence of fixed points is not a desirable trait of chaotic maps when it comes to their application in cryptography. Previous one-dimensional discrete-space chaotic maps do not have fixed points [13, 14]. The proposed map has fixed points for certain values of the parameter n, but this is not significant disadvantage in comparison with discrete-space chaotic maps [13, 14] because these fixed points could be easily avoided by selecting values of n for which it is determined (experimentally or theoretically) that there are no fixed points. One-dimensional continuous-space chaotic maps usually have fixed points regardless of values of theirs parameters. Also, it is very hard to identify all values of continuous-space chaotic maps which lead to fixed points and therefore it is very complicated or even impossible to avoid selection of initial points which lead to fixed points [22,23,24]. Easy identification of parameter n for which fixed points exist and ability to avoid them is advantage of the proposed map over mentioned continuous-space chaotic maps.

Most cryptographic applications require a large speed for their proper functioning. Therefore, it is desirable that chaotic maps have low complexity of their implementations which will result in a greater speed. One iteration of the proposed map has only one multiplication and three additions. Previous one-dimensional discrete-space chaotic maps [13, 14] require much more calculations per one iteration due to the use of the Lehmer code [43] whose computation time according to its definition is quadratic in number of elements of the permutation. Complexity of the proposed map is comparable to simpler one-dimensional continuous-space chaotic maps such as logistic map [5] which has two multiplications and one subtraction operation. For the above-mentioned reasons, we can conclude that the proposed chaotic map has several advantages over previous chaotic maps when we consider the application in cryptographic systems.

5 Random S-box design method based on the proposed map

The quality of an S-box is estimated according to the set of a widely used criteria which include bijection, nonlinearity, strict avalanche criterion, output bits independence criterion, equiprobable input/output XOR distribution and maximum expected linear probability [3, 11, 17,18,19, 31,32,33,34, 36]. When the random S-box generation is in question, there is no specific procedure aimed at creating an S-box which satisfies one or more mentioned criteria except for the bijective property. In order to generate an S-box which satisfies other criteria, random methods are aimed at generating a larger number of random S-boxes from which the best ones are selected according to the certain bounds [37].

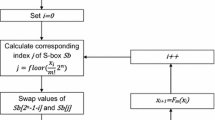
In this section, a simple example of a random \(p\times p\) bijective S-box design method, which is based on the example of the proposed map from Eq. (3), will be presented. First, the identical permutation \(Sb[j]=j\) for all \(0\le j < 2^p\) is used as an initial state of an S-box Sb. The initial value of the proposed discrete-space chaotic map x is selected from the set of integer values \([0,2^n-1]\) which is in the example of the proposed chaotic map from Eq. (3) equal to the set \([0,2^{32}-1]\).

After the initial value of an S-box is set and the initial value of the chaotic map is chosen, the S-box design procedure follows the simple Knuth shuffle [44]. For each \(0\le i < 2^p\), index \(j=floor(\frac{x_i}{2^n}\cdot 2^p)\) is obtained, values of \(Sb[2^p-1-i]\) and Sb[j] are swapped and the chaotic map (Eq. 3) is iterated one time in order to obtain value \(x_{i+1}\). The process of the generation of single S-box can be implemented by the following pseudo-code:

for \(0\le i < 2^p\)

swap values of \(Sb[2^p-1-i]\) and \(Sb[floor(\frac{x_i}{2^n}\cdot 2^p)]\)

\(x_{i+1}=F(x_i)\)

end for

where \(F(x_i)\) is Eq. (3). The proposed S-box generation method returns the \(p\times p\) S-box Sb. For example, if \(p=8\), \(n=32\) and \(x_0=4604{,}860\) then the \(8\times 8\) S-box from Table 2 is found. Although some more complex procedure could be applied in order to obtain a random S-box, it is not justified because the proposed chaotic map provides sequences of sufficient quality, so anything more than the simplest procedure will only reduce the efficiency of an S-box design process without any significant benefit for the quality of an S-box.

Table 2 The S-box generated by the algorithm based on the proposed chaotic map
Full size table

5.1 Performance analysis of the generated S-box

The example of an S-box generated with the approach based on the proposed discrete-space chaotic map was compared with some representative examples of random bijective chaos-based S-boxes from the references [11, 14, 17, 31, 33, 34, 36]. Also, some bounds used to measure the quality of \(8 \times 8\) S-boxes will be used as a benchmark.

An S-box generation method presented in this paper is designed in such way that only bijective S-boxes could be generated. The S-box from Table 2 has all different output values from the interval [0, 255], so it can be concluded that the bijective property is achieved [11].

The nonlinearity of an S-box is estimated according to the formula presented in the paper [45]. The nonlinearities of eight output bits of the generated S-box are 108, 108, 106, 106, 106, 106, 106 and 106. The minimum nonlinearity of 106 should be used as an indicator of the quality of an S-box according to this criterion, because an attacker will focus its attack on the weakest part of an S-box. The minimum nonlinearity of the generated S-box is better or equal to the most of random chaotic S-box examples from Table 3, and it satisfies the nonlinearity bound from the paper [37].

Table 3 Comparison of the random bijective chaotic S-boxes
Full size table

The description of the strict avalanche criterion can be found in the paper [46]. The dependence matrix of the S-box from Table 2 is presented in Table 4. The average offset of the dependence matrix elements from the ideal value of 0.5 is 0.02881 which satisfies the bound for SAC offset set in the paper [37]. The mean value of the dependence matrix is 0.501. The generated S-box has the second best SAC offset in the Table 3.

Table 4 The dependence matrix of the generated S-box
Full size table

BIC criteria refer to the nonlinearities of all pairs of output bits. According to these criteria, pairs of output bits should also satisfy the avalanche criterion [46]. The value of dynamic distance (DD) should be as small as possible integer in order for an S-box to satisfy the SAC for pairs of output bits [31]. The data regarding this criterion of the generated S-box are presented in Tables 5 and 6. The minimum value of BIC nonlinearity is 100, and the maximum value of DD is 10.

Table 5 BIC-nonlinearity criterion for the generated S-box
Full size table
Table 6 The DD of generated S-box (BIC-SAC criterion)
Full size table

The equiprobable input/output XOR distribution criterion refers to the maximum expected differential probability (MEDP) which is estimated on the basis of the formula from the paper [47]. The results of this test for the generated S-box are presented in Table 7 in which the maximal value is 10. This value is achieved by the most of S-boxes from Table 7.

Table 7 Input/output XOR distribution table of S-box generated by the proposed method
Full size table

The maximum expected linear probability criteria are described in papers [48, 49]). The S-box presented in this paper achieves value of 0.070557 according to these criteria which satisfies the bound set in [37].

The example of S-box generated by the method based on the proposed chaotic map satisfies all bounds set in the paper [37]. Therefore, we can claim that the proposed map can be used for the generation of S-boxes of high quality.

S-boxes of such quality could be used in block ciphers which use fixed S-box. Also, the proposed S-box design method could be used for generation of dynamical S-boxes under the condition that the number of digits n of the variable x of the proposed chaotic map is large enough to provide sufficient quantity of S-boxes. For example, the proposed S-box design method could be used for the generation of dynamical S-boxes in image encryption algorithm [35] instead of the step 3. In that image encryption algorithm, the logistic map and the asymmetric tent map were used in order to generate S-boxes, but the control parameter \(\mu \) of the logistic map has fixed value, so only two variables and one control parameter influence the key space of S-box generation method [35]. Therefore, the proposed S-box design method could be used in image encryption algorithm [35] when the value of n is bigger than \(3\times 64=192\), for example, for \(n=256\) and corresponding variable could be stored in integer types such as \(\_int256\). The proposed map could also be used in image encryption algorithm [35] instead of one of the two maps. For example, the proposed map could be used instead of the logistic map. Bearing in mind that the value of the control parameter of the logistic map is fixed in the paper [35], the proposed map with value of \(n=64\) should be sufficient.

6 Recommendations for future research

Realization of chaotic maps in hardware such as FPGA is very important issue due to the need to optimize such implementations in order to save resources [50]. Bearing in mind that the proposed discrete-space chaotic map can operate on variables presented with various number of digits and even on digits of arbitrary base, it could be implemented in various types of hardware. For this reason, future research should investigate in detail hardware implementations of the proposed chaotic map.

In this paper, one simple example of the application of the proposed map in S-box design is presented in order to demonstrate how this map can be used. However, chaos have been widely used in various applications from many fields including cryptography. In the last decade, many chaotic techniques have been used in various cryptographic applications such as PRNGs, image and video encryption, pattern recognition for biometric purposes such as voice recognition  [51]. For this reason, future research should investigate in detail whether the proposed map can be used in PRNG design which could consequently lead to its application in various types of the mentioned cryptographic systems. Also, the application of the proposed map in other fields should be explored.

7 Conclusion

In this paper, a new one-dimensional discrete-space chaotic map based on the multiplication of integer numbers and circular shift is presented. Dynamical properties of the proposed map are analyzed, and it exhibits chaotic behavior. The proposed map has fixed points for certain values of n, but it is easy to completely avoid them by selecting values of n for which it is determined that there are no fixed points. The proposed map is suitable for the application in fields where the fully digital approach is necessary because it is defined over a finite set and therefore does not require approximations of any kind. Compared to previous one-dimensional discrete-space chaotic maps, this map has improved characteristics related to the orbit length, computational complexity and memory requirements. Improvements regarding computational complexity and memory requirements can be particulary useful for the implementation in lightweight devices with limited memory and computational resources such as wireless sensor networks. As an example of the application of the proposed map in cryptography, an S-box design method based on this chaotic map is presented. The results of performance tests show that S-boxes with good cryptographic properties can be generated on the basis of this discrete-space chaotic map.