A novel method of S-box design based on discrete chaotic map

Abstract

A new method for obtaining random bijective S-boxes based on discrete chaotic map is presented. The proposed method uses a discrete chaotic map based on the composition of permutations. The obtained S-boxes have been tested on the number of criteria, such as bijection, nonlinearity, strict avalanche criterion, output bits independence criterion, equiprobable input/output XOR distribution and maximum expected linear probability. The results of performance test show that the S-box presented in this paper has good cryptographic properties. The advantage of the proposed method is the possibility to achieve large key space, which makes it suitable for generation of $n\times n$ S-boxes for larger values of n. Also, because this method uses discrete chaotic map based on the composition of permutations which has finite space domain, there is no need for discretization of continuous values of chaotic map, so the process of generation of S-boxes is not affected by approximations of any kind.

1 Introduction

Substitution box (S-box) is important nonlinear component used in block ciphers of substitution-permutation type which significantly affects their security [1]. Mathematically, an $n\times n$ S-box is a nonlinear mapping $S: {\{0,1\}}^n \rightarrow {\{0,1\}}^n$, where ${\{0,1\}}^n$ represents the vector spaces of n elements from GF(2). Secure block cipher should possess basic characteristics of cryptography like confusion and diffusion that make it resistant to various attacks, such as linear and differential cryptanalysis. Chaos has properties that make it suitable for use in cryptography such as mixing, random-like behavior, ergodic behavior and sensitivity to initial conditions. In recent years, a number of chaotic methods was used for the construction of S-boxes.

Jakimoski and Kocarev [2] proposed a S-box generation method based on exponential and logistic chaotic maps. Chen [3] presented S-box generation method based on 2D Baker map and Chebyshev map. Wang et al. proposed a dynamic S-Box generation method based on Tent map [4]. In [5], a method which uses the Lorenz system is proposed. In [6] several random S-box generation methods based on different chaotic maps were compared, and bounds for a number of criteria used to measure quality of S-boxes were proposed. An efficient algorithm for S-box design based on chaotic maps and composition method is presented in [7]. Later in [8], 3D four-wing autonomous chaotic system was used for S-box generation. S-box generation method based on Logistic map and Lorenz system were proposed in [9]. In [10] algorithm for generating S-boxes based on the six-dimensional compound hyperchaotic map was proposed. S-boxes are constructed using the chaotic scaled Zhongtang system in [11]. In [12] a method based on logistic-sine map is presented.

Besides these, there are many other methods for the generation of S-boxes based on various chaotic maps, which to our knowledge all have continuous space domain. However, digital computers cannot support the continuous nature of chaotic systems so the discretization of continuous values is necessary, or the discrete approximations of existing continuous systems are used. Implementation of the chaotic systems, which are built on the domain of infinite precision, on digital devices causes dynamical degradation [13]. Taking into account the high sensitivity to initial conditions of the chaotic maps, small differences caused by the use of approximations has a great influence on the obtained S-boxes. In [14] discrete chaotic map based on the composition of permutations is presented. Composition of permutations is widely used in encryption schemes [15]. This chaotic map [14] represents fully digital approach, so there is no need for discretization of continuous values.

In this paper, a new method to obtain random chaotic S-boxes is proposed. This method uses discrete chaotic map based on the composition of permutations [14] for obtaining a chaotic sequence which is used to determine order of the elements of the S-box. By using this chaotic map, the process of generation of S-boxes is not affected by approximations of any kind.

The rest of this paper is organized as follows. In Sect. 2, a discrete chaotic map based on the composition of permutations is presented. In Sect. 3, the novel method of S-box design is proposed and an example of the S-box generated by this method is presented. Criteria used to measure quality of S-boxes are introduced in Sect. 4, and the performance of the example S-box is evaluated and compared with other bijective chaos-based S-boxes. Conclusions are drawn in Sect. 5.

2 Discrete chaotic map based on the composition of permutations

Let $P=p_0p_1...p_{m-2}p_{m-1}$ denote a permutation of the set $\{0,1, . . . ,m-1\}$. Permutation $P^r=p_{m-1}p_{m-2}...p_1p_0$ is the reverse permutation of the permutation P.

The composition $h=f\circ g$ of two permutations f and g of the same set A is the permutation mapping each $x \in A$ into $h(x) = f(g(x))$.

Let $S_m$ denote the set of all permutations of the set $\{0,1, . . . ,m-1\}$. Lehmer code [16] is bijective function $l:S_m\rightarrow \{0,1,2,...,m!-1\}$. Function $l(P)=\sum _{0\le i <m}c_i\cdot (m-1-i)!$ where $P\in S_m$ and $c_i$ is the number of elements of the set $\{j>i | p_j < p_i\}$. Inverse Lehmer code is bijective function $l^{-1}:\{0,1,2,...,m!-1\}\rightarrow S_m$.

In [14] a one-dimensional discrete chaotic map is proposed by

$$\begin{aligned} X_{i+1}=X_i \circ f(X_i, C) \end{aligned}$$

(1)

where $X_i, C \in S_m$ and $f:S_m\rightarrow S_m$. If $x_i=l(X_i)$ and $c=l(C)$, this map can also be represented as

$$\begin{aligned} x_{i+1}=l[l^{-1}(x_i) \circ f(l^{-1}(x_i), l^{-1}(c))] \end{aligned}$$

(2)

where $x_i, c \in \{0,1,2,...,m!-1\}$ and $f:S_m\rightarrow S_m$. In [14], the special case of one-dimensional discrete chaotic map is considered in which

$$\begin{aligned} f(X_i, C)=l^{-1}(|l(C \circ X_i) - l((C \circ X_i)^r)|). \end{aligned}$$

(3)

On the basis of (1) and (3), we obtain map $F_m: \{0,1,2,...,m!-1\}\rightarrow \{0,1,2,...,m!-1\}$ by:

$$\begin{aligned} F_m(x)= & {} l(l^{-1}(x) \circ l^{-1}(|l(C \circ l^{-1}(x)) \nonumber \\&- l([C\circ l^{-1}(x)]^r)|)). \end{aligned}$$

(4)

This map can also be represented as

$$\begin{aligned} X_{i+1}=X_i \circ l^{-1}(|l(C \circ X_i) - l((C \circ X_i)^r)|). \end{aligned}$$

(5)

Fig. 1

Flowchart of the proposed S-box generation method

The special case of discrete chaotic map based on the composition of permutations (Eqs. 4 or 5) does not have fixed points which makes it suitable for application in cryptography. However, this map should be used with caution because length of the orbits could be very small for smaller values of m. Therefore, it is recommended that the map (Eq. 4) is used for $m \ge 8$.

Table 1 The S-box generated by proposed algorithm

3 Proposed S-box generation method

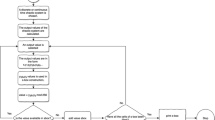
We now describe the proposed simple algorithm for generation of $n\times n$ S-boxes which uses discrete chaotic map based on the composition of permutations (Eq. 4). First, the initial state of S-box Sb is set to be equal to identical permutation, $Sb[j]=j$ for all $0\le j < 2^n$. After that, the initial value $x_0$ of chaotic map is chosen from the set $\{0,1,2,...,m!-1\}$. For each $0\le i < 2^n$ corresponding index $j=floor(\frac{x_i}{m!}\cdot 2^n)$ is calculated, swap of values of $Sb[2^n-1-i]$ and Sb[j] is performed and chaotic map is iterated one time in order to obtain value $x_{i+1}=F_m(x_i)$. The proposed S-box generation method is illustrated in Fig. 1. One S-box also can be generated by the following pseudocode:

      for $0\le i < 2^n$

      swap values of $Sb[2^n-1-i]$ and $Sb[floor(\frac{x_i}{m!}\cdot$

      $2^n)]$

      $x_{i+1}=F_m(x_i)$

      end for

Table 2 Comparison of the random bijective chaotic S-boxes and non-random S-boxes used in typical block ciphers

Proposed S-box generation method returns the $n\times n$ S-box Sb. For example, if $m=8,$ $c=722$ and $x_0=28087$ then the $8\times 8$ S-box from Table 1 is found.

4 Performance analysis of the generated S-box

A secure block cipher should be resistant to various attacks, such as linear and differential cryptanalysis. In substitution-permutation networks, this is generally achieved if the S-boxes satisfy a number of criteria, such as bijection, nonlinearity, strict avalanche criterion, output bits independence criterion, equiprobable input/output XOR distribution and maximum expected linear probability.

Some representative random bijective chaos-based S-boxes presented in references  [3, 5, 7,8,9, 11], are chosen to compare with S-box generated with proposed approach. In addition, performance values of modern non-random S-boxes such as AES, APA, Gray and Skipjack are presented in Table 2. In [6] several random S-box generation methods based on chaotic maps were compared. Bounds for criteria used to measure quality of S-boxes presented in that paper will also be used for comparison.

4.1 The bijective property and nonlinearity

An $n\times n$ S-box is bijective if it has all different output values from interval $[0, 2^n-1]$. Generated S-box has all different output values from interval [0, 255], so it satisfies the requirement of bijectivity.

Let $B=\{0,1\}$. The nonlinearity of a function $f: B^n \rightarrow B$ is defined by

$$\begin{aligned} N(f)=2^{n-1}-\frac{1}{2}\max _{a\in B^n} \left| \sum _{x\in B^n} (-1)^{f(x)+a\cdot x}\right| \end{aligned}$$

where $a \in B^n$ and $a\cdot x$ is the dot product between a and x (see [17] for example).

The nonlinearities of eight output bits of example of S-box generated by the proposed method are 108, 106, 106, 106, 106, 106, 108, 108. Minimum nonlinearity is an indicator of the quality of S-box according to this criterion, because the chain is only as strong as its weakest link. Minimum nonlinearity of generated S-box is 106, which is better than most of random chaotic S-boxes from Table 2. Also, our S-box satisfies bound set in [6] which indicates that it is highly nonlinear.

Table 3 The dependence matrix of the generated S-box

4.2 Strict avalanche criterion

The strict avalanche criterion (SAC) was introduced by Webster and Tavares [18]. If each output bit of some function should change with a probability of a half whenever a single input bit is complemented, then that function satisfies the strict avalanche criterion. The dependence matrix is used to test the SAC of an S-box. If each element $P_{i,j}$ of the matrix is close to the ideal value 0.5, the S-box nearly fulfills the SAC.

Table 4 BIC-nonlinearity criterion for the generated S-box

Let $e_i=[\delta _{i,1}\ \delta _{i,2}\ \ldots \delta _{i,n}]^T$, where

$$\begin{aligned} \delta _{i,j}=\left\{ \begin{array}{ll} 1, &{} i=j\\ 0, &{} i\ne j \end{array} \right. , \end{aligned}$$

and let $(\cdot )^T$ denote a matrix transpose. Then

$$\begin{aligned} P_{i,j}(f)=2^{-n}\sum _{x\in B^n} {f_j(x)\oplus f_j(x\oplus e_i)}. \end{aligned}$$

In addition, formula

$$\begin{aligned} S(f)=\frac{1}{n^2}\sum _{ 1\le i\le n}\sum _{ 1\le j\le n} | \frac{1}{2} - P_{i,j}(f) | \end{aligned}$$

is used to estimate offsets of the dependence matrices.

The dependence matrix of the generated S-box can be found in Table 3. The offset of the dependence matrix of S-box generated by proposed method is 0.02441, and the mean value is 0.5034 which is very close to the ideal value 0.5. However, the mean value is not always a reliable indicator of the fulfillment of the SAC criteria, because there are S-boxes that have a mean value close to 0.5, although elements of the dependence matrix have a great deviation from this ideal value. For this reason, the offset is a better indicator of the quality of S-box according to SAC criterion. The offsets of the dependence matrix of S-box presented in this paper and the S-boxes mentioned above are listed in Table 2. Based on the results, it can be concluded that S-box generated by proposed method has better property of SAC than other S-boxes from Table 2. Also, our S-box satisfies bound for SAC criteria set in [6].

4.3 Output bits independence criterion

Webster and Tavares [18] also presented the output bits independence criterion (BIC). S-box satisfying BIC criteria must be pair-wise independent for a given set of avalanche vectors generated by complementing a single plaintext bit. Let $f_1, f_2,..., f_n$ denote the Boolean functions in the S-box. If S-box satisfies BIC, $f_j\oplus f_k (j\ne k, 1\le j,k \le n)$ should be highly nonlinear and satisfy the avalanche criterion. Fulfillment of the SAC criterion of $f_j\oplus f_k$ can be tested with a dynamic distance [3]. The Dynamic Distance (DD) of a function f can be defined as

$$\begin{aligned}&DD(f)=\max _{d\in B^n, wt(d)=1}\frac{1}{2}\\&\quad \times \left| 2^{n-1}-\sum _{x=0}^{2^n-1} f(x)\oplus f(x\oplus d)\right| \end{aligned}$$

If the value of DD is a small integer and close to zero, the function f satisfies the SAC.

The results obtained from the generated S-box are shown in Tables 4 and 5. The minimum value of BIC-nonlinearity is 100 and maximum value of DD is 14 which indicates that our S-box satisfies bound for BIC criteria set in [6].

Table 5 The DD of generated S-box (BIC–SAC criterion)

Table 6 Input/output XOR distribution table of S-box generated by proposed method

4.4 Equiprobable input/output XOR distribution

This criterion is also known as maximum expected differential probability (MEDP). Differential cryptanalysis based on the imbalance of the input/output XOR distribution table of an S-Box was demonstrated by Biham and Shamir [19]. It is desirable for an S-box to have differential uniformity. Differential probability for a given map f can be calculated by measuring differential resistance as follows:

$$\begin{aligned} X(f)= & {} \max _{{\varDelta }x\in B^n\setminus \{0\},\ {\varDelta }y\in B^n} \{x\in B^n \mid f(x)\oplus \\&f(x\oplus {\varDelta }x) = {\varDelta }y\} \end{aligned}$$

The equiprobable input/output XOR distribution of generated S-box is presented in Table 6. Maximal value of S-box generated by proposed method is 10, which indicates that our S-box satisfies bound for the equiprobable input/output XOR distribution criteria set in [6].

4.5 Maximum expected linear probability

The maximum expected linear probability is the maximum value of the imbalance of an event [20, 21]). The parity of the input bits selected by the mask a is equal to the parity of the output bits selected by the mask b. Maximum expected linear probability (MELP) is defined by

$$\begin{aligned} L(f)=\max _{a,b\in B^n\setminus \{0\}}\left( 2^{-n}\sum _{x\in B^n} (-1)^{a\cdot x +b\cdot f(x)}\right) ^2 \end{aligned}$$

The maximal expected linear probability of the generated S-box is 0.070557 which satisfies bound set in [6].

5 Conclusion

In this paper, a new methodology for designing S-box is presented which uses discrete chaotic map. This chaotic map represents fully digital approach, so there is no need for discretization of continuous values and the process of generation of S-boxes is not affected by approximations of any kind. Also, proposed method uses chaotic map based on the composition of permutations of the set with an arbitrary number of elements m. Possibility of choosing any positive integer value for m enables almost unlimited key space up to $2^n!$. For that reason, proposed method is suitable for generation of $n\times n$ S-boxes for larger values of n. The S-box generated in this study is the only example of random chaotic S-box from Table 2 besides the S-box from [7], which satisfies all bounds set in [6]. Therefore, we can conclude that approach presented in this paper is effective in generating S-boxes with high performance.