A novel efficient S-box design algorithm based on a new chaotic map and permutation

Abstract

The substitution box (S-box) is one of the extremely important components in the design of block cipher. An excellent S-box is necessary for the block cipher algorithm, and its cipher strength directly affects the security of the cipher algorithm. The differential uniformity of the S-box generated by the chaotic system is 10 or 12, which cannot effectively resist differential cryptanalysis. Aiming at the high differential uniformity of the S-box constructed by the chaotic system, a novel efficient S-box construction scheme based on a new chaotic map and permutation is proposed in this paper. In this scheme, the chaotic matrix is generated by a new chaotic map, and then is replaced by permutation sequences to generate S-boxes. Comparative analysis shows that the generated S-boxes have high nonlinearity, low differential uniformity, and satisfy SAC and BIC criteria, which can improve the ability of the algorithm to resist differential cipher attacks and linear cryptographic analysis.

1 Introduction

In many block cipher algorithms, the S-box is the primary nonlinear part, and its quality directly determines the performance and security level of the encryption scheme. Therefore, the construction of the S-box with excellent performance has become an important research topic, which has attracted the attention of numerous scholars [1]. There are various methods for constructing an S-box, such as random generation construction [2], heuristic method [3], mathematical construction method [4], cellular automata [5] and other methods.

The chaotic system has superior characteristics of uncertainty [6, 7], ergodicity [8, 9], sensitivity [10, 11] and pseudo-randomness, which make it suitable for constructing nonlinear S-box in block ciphers. In a chaotic system, two initial values with an extremely small difference will also produce completely different chaotic sequences, and the state of the chaotic system at a certain moment is unpredictable. Therefore, the S-box constructed by the chaotic system has favorable confusion and nonlinear characteristics. A lot of schemes have used the chaotic system to construct S-box [12,13,14,15,16,17,18,19,20,21,22].

To improve the nonlinearity and confusion performance of the S-box, traditional one-dimensional (1D) chaotic maps have been used in lots of schemes to construct the S-box [23,24,25,26,27,28,29,30,31]. However, the range of chaotic parameters of 1D chaotic maps is small. Attackers can use signal estimation technology to predict the chaotic values of 1D chaotic systems, which are vulnerable to security threats [32]. Therefore, many schemes use more complex and higher-dimensional chaotic maps or combined chaotic maps to construct S-box [33,34,35,36,37,38,39,40,41,42,43,44,45]. Yan et al. [33] put forward a novel S-box dynamic design based on CLS produced by LNECS, and simulation analysis shows that S-box can resist well-known attacks and cryptanalysis. Ahmad et al. [34] present a new S-box evolution scheme, which used the dynamics of the fractional-order time-delayed two-state Hopfield neural network system. It has been shown that time delay plays a vital role in increasing the nonlinearity of the S-box. Zhu et al. [37] used the combination of Logistic and Tent maps to obtain chaotic sequences and get static S-boxes, and then the static S-boxes were used as seeds to dynamically generate new S-boxes under the control of the mixed chaotic system and fitness function. Wang et al. [42] proposed a chaotic S-box construction method based on a memorable simulated annealing algorithm (MSAA). Using the nonlinearity and randomness of dynamic iteration of digital cascade chaotic maps to generate chaotic S-box sets. Turk et al. [44] proposed a method to create dynamic, reliable and fast S-boxes based on the Tent map. The simulation shows that the generated S-boxes meet the design criteria of S-boxes. Zheng et al. [45] proposed a dynamic S-box encryption algorithm. By using the characteristics of the chaos map, the chaotic idea is integrated into the construction of the S-box, and a new dynamic S-box generation method is obtained.

The inherent characteristics of the chaotic system provide a good foundation for constructing S-box. The constructed S-box improves its nonlinearity to a certain extent and can obtain a higher security level. However, the S-boxes generated by chaotic systems still have high differential uniformity, which cannot achieve all expected performance indicators [23]. Therefore, Khan et al. [46] proposed constructing an S-box based on a traditional logistic map to reduce differential uniformity, but the parameter range of the chaotic system they used is small.

For the problem of high differential uniformity of S-boxes constructed by chaotic systems and the small parameter range of traditional one-dimensional chaotic maps, this paper proposes a new S-box construction scheme based on a new logistic map and permutation to improve the difference uniformity. We use a new logistic map to generate a chaotic matrix, which is replaced by the permutation sequences to generate S-boxes. Through performance comparison analysis, it is proved that this new logistic map has good chaotic performance, large enough parameter space, strong randomness, and high sensitivity. And the S-boxes constructed in this paper have strong nonlinearity and low differential uniformity, which can improve the ability of the algorithm to resist differential attacks and linear analysis. The innovations of this work are concluded as follows:

(1) A new logistic map is adopted, which has superior chaotic performance, large parameter space, and strong sensitivity. It can effectively resist brute force attacks and is more suitable for cryptography applications.

(2) A simple and effective S-box construction method using a new logistic map and permutation sequence is proposed to improve the difference uniformity, which can enhance the construction efficiency of the S-box.

(3) Compared with other S-boxes, the proposed S-boxes have higher nonlinearity and lower differential uniformity, indicating that the proposed S-boxes have obvious advantages in resisting the attacks of differential cryptanalysis and linear cryptanalysis.

The rest of this paper is organized as follows. Section 2 presents the basics used in this paper. The new logistic map is introduced and analyzed in Section 3. In Section 4, we introduce the S-box generation method. Section 5 presents some basic security analyses of proposing S-boxes. The conclusion is presented in Section 6.

2 Basic knowledge

2.1 S-box

The S-box is a nonlinear transformation. An S-box with an n-bit input mapped to m-bit output is called an $n\times m$ S-box, also commonly known as multi-output Boolean functions or vector functions. The $n\times m$ S-box is defined as

$$\begin{aligned} S(x)=(S(x_{1}),\ldots ,S(x_{m})):GF(2)^{n}\rightarrow GF(2)^{m} \end{aligned}$$

(1)

There are six common sizes of S-boxes, namely 4×4, 8×8, 8×32, 11×8, 13×8, 8×32. The most popular one is the 8×8 S-box.

2.2 Logistic map

Traditional 1D chaotic maps are simple in structure, easy to implement, and have excellent chaotic performance. The dynamical equation of the logistic map [47] is as follows

$$\begin{aligned} l_{n+1}=r_{l} \times l_{n} \times (1-l_{n}) \end{aligned}$$

(2)

where ${{l}_{n}}$ is the logistic sequence, and ${{l}_{n}}\in [0,1]$. ${{r}_{l}}$ is the chaotic parameter of the logistic map. When ${{r}_{l}}\in [3.5699465,4]$, this system is chaotic. The bifurcation diagram, Lyapunov exponential diagram, and iterative function diagram of the logistic map are shown in Figs.1(a), 2(a), and 3(a), respectively.

Fig. 1

Bifurcation diagram

2.3 Permutation

Let X be a non-empty set, and ${{\sigma }_{X}}$ be the set of all bijections from X to itself. On the composition of ${{\sigma }_{X}}$ map, $\circ$ constitutes a group, usually called ${{\sigma }_{X}}$ as a symmetric group on X, the element in ${{\sigma }_{X}}$ as the permutation on X, and the subgroup of ${{\sigma }_{X}}$ as a permutation group.

Let $\{{x_{0},x_{1},\ldots ,x_{k}}\}\subseteq \{0,1,\ldots ,n-1\}$, if the permutation f on $\{0,1,\ldots ,n-1\}$ is defined as

$$\begin{aligned} f(x)=\left\{ \begin{matrix} {{x}_{i+1}}\quad {mod}\quad k,\quad x\in \{{{x}_{0}},{{x}_{1}},\ldots ,{{x}_{k}}\} \\ {{x}_{i}},\qquad \qquad \qquad x\notin \{{{x}_{0}},{{x}_{1}},\ldots ,{{x}_{k}}\} \end{matrix} \right. \end{aligned}$$

(3)

Fig. 2

LEs analysis

Fig. 3

Iterative function diagram

3 New logistic map

3.1 Definition

The new logistic map used in this paper is defined by [48]

$$\begin{aligned} {{L}_{n+1}}=\bmod ({{b}_{L}}\times {{L}_{n}}\times (1-{{L}_{n}})-{{L}_{n}}^{2}/3)\times {{2}^{{{k}_{L}}}},1) \end{aligned}$$

(4)

where ${{L}_{n}}$ is a new logistic sequence, and ${{L}_{n}}\in [0,1]$. ${{b}_{L}}$ is the chaotic parameter. ${{k}_{L}}$ is the number of iterations. And $\bmod$ is the modulo function, which can control the value of the chaotic sequence within the range [0, 1]. ${{2}^{{{k}_{L}}}}$ is an adjustment function and iteratively removes transient effects by adjusting ${{2}^{{{k}_{L}}}}$. When ${{k}_{L}}\in \left[ 7,21 \right]$, and ${{b}_{L}}\in \left[ 0,30 \right]$, this system is completely chaotic.

3.2 Performance analysis

Matlab 2018a is used to test the performance of the new logistic map. The chaotic parameters of the new logistic map are set to ${{b}_{L}}\in [0,30]$, and ${{k}_{L}}=16$. And the initial values of the chaotic sequence of the traditional and new logistic maps are all set to 0.3.

3.2.1 Bifurcation diagram

The bifurcation diagram gives the idea of the stability boundary and quantifies the sensitive dependence on the control parameters. It is obtained by giving the initial value of bifurcation parameters, calculating the iterative sequence of the system under the corresponding parameters, and drawing the chaotic sequence.

We intuitively analyze the performance of the traditional and new logistic maps through bifurcation diagrams, as shown in Fig. 1. From Fig. 1, we know the new logistic map greatly increases the chaotic parameter range of the traditional logistic map, and it is in a completely chaotic state within the parameter range, so the chaotic performance is superior.

3.2.2 Lyapunov exponent (LE)

LE is used to measure the sensitivity of the chaotic system to its initial conditions. It points out that at least one measurement value of the chaotic system is positive. When LE is negative or 0, the region is a periodic region, which will interrupt the chaotic region, and the system is in a stable state. When LE is positive, the larger LE is, the more sensitive the chaotic system is to the initial value.

Figure 2 shows the LEs analysis of the traditional and new logistic maps, the LEs of the new logistic map are all positive, which proves its chaotic superior performance.

3.2.3 Iterative function diagram

For an iterative dynamic system ${{x}_{n+1}}=f({{x}_{n}})$, its iterative function diagram can be expressed as: when ${{x}_{n}}$ is the input, the output is ${{x}_{n+1}}$.

Figure 3 shows the iterative function diagrams of the traditional and new logistic maps. The iterative function diagram of the traditional logistic map is a regular curve, as shown in Fig. 3(a). The attacker can guess that it is a traditional logistic map from the curve in the iterative function diagram. However, the iterative function diagram of the new logistic map is randomly generated points without regularity. If the attacker gets the iterative function diagram in Fig. 3(b), the attacker cannot guess what kind of chaotic map it is. Therefore, the new logistic map has strong randomness and is difficult to predict.

3.2.4 Sensitivity analysis

The chaotic system is characterized by being sensitive to initial values. We judge the performance of the new logistic map by sensitivity analysis. We first set the initial value of the new logistic map to 0.5, and then reset the initial value to 0.500000000000001.

Figure 4 shows the sensitivity analysis of the new logistic map. The blue dotted line is the initial value of 0.5, and the double red line is the initial value of 0.500000000000001, although the initial value only differs by 1$^{-16}$, the chaotic curves of these two maps are quite different, which proves that the new logistic map has a strong sensitivity to the initial value.

Fig. 4

Sensitivity analysis. The initial value of 0.5 is the blue dotted line and the initial value of 0.500000000000001 is the double red line

Fig. 5

Generate S-box flow chart

4 Generate S-box

S-box plays a confusing role in the block cipher, and the sensitivity of chaotic to initial conditions is closely related to the confusion and diffusion characteristics of traditional cryptosystems [37]. Using a superior chaotic system can generate an S-box with excellent performance, which can improve the S-box capability of the algorithm.

In this paper, the new logistic map and permutation are used to generate 8-bit S-boxes. The new logistic map has excellent performance, which can improve the performance of the S-box in the algorithm. The steps of generating S-boxes are described as follows:

Step 1 Randomly select three numbers as the value of the chaotic parameter ${{b}_{L}}$, ${{k}_{L}}$, and the initial value ${{L}_{0}}$ of the new logistic map.

Step 2 Iterate the new logistic map for N times, delete the first 1500 values of the sequence and transform the selected numeric sequence L. Transform floating-point values of the numeric sequence L into integer sequences of 0$\sim$255 by using (5) to obtain the chaotic sequence $({{Z}_{1}},{{Z}_{2}},\ldots ,{{Z}_{N-1500}})$. The specific generation of the chaotic sequence is shown in Algorithm 1.

$$\begin{aligned} {{Z}_{i}}=(floor({{L}_{i+1500}}\times {{10}^{14}})) \bmod 256 \end{aligned}$$

(5)

where $i=1,2,\ldots ,N-1500$.

Table 1 Chaotic matrix

Algorithm 1

Generate chaotic sequence

Step 3 Arranging chaotic sequences to construct a 16×16 chaotic matrix. If there are duplicate values, only the first numerical value will be kept, and then the same value that appears later will be deleted. Finally, the 16×16 chaotic matrix is obtained, denoted by $({{Y}_{0}},{{Y}_{1}},\ldots ,{{Y}_{255}})$. Duplicate values are shown in (6). The concrete construction method is shown in Algorithm 2.

$$\begin{aligned} Y= unique\left( Z,^{\prime }stable^{\prime } \right) \end{aligned}$$

(6)

Algorithm 2

Chaotic matrix

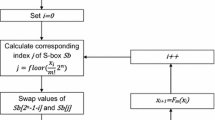
Step 4 According to the given permutation sequences, the chaotic matrix is permuted to generate the S-boxes. The construction method is shown in Algorithm 3. The flow chart of generating the S-box is shown in Fig. 5.

Algorithm 3

Generate S-box

In this scheme, the initial parameters of the chaotic sequence are ${{b}_{L}}=8$, ${{k}_{L}}=16$, and ${{L}_{0}}=0.321$ to generated a 16×16 chaotic matrix, as shown in Table 1.

Two permutation sequences are given in this paper, permutation sequence 1 and permutation sequence 2, which are used to generate S-box$_{1}$ and S-box$_{2}$, as shown in Tables 2 and 3, respectively.

Table 2 The S-box$_{1}$ generated by proposed algorithm

Permutation sequence 1:

( 0, 130, 230, 9, 121, 151, 100, 112, 104, 29, 178, 131, 153, 132, 4, 18, 127, 251, 34, 115, 88, 120, 150, 66, 105, 124, 110, 215, 232, 55, 14, 33, 48, 212, 217, 92, 117, 134, 23, 160, 42, 246, 77, 129, 182, 243, 79, 12, 255, 198, 108, 39, 191, 168, 216, 53, 190, 169, 136, 194, 27, 193, 45, 123, 141, 83, 174, 118, 204, 98, 60, 76, 35, 26, 207, 10, 143, 25, 43, 109, 227, 106, 44, 28, 175, 125, 85, 52, 111, 102, 221, 241, 145, 46, 32, 116, 89, 128, 68, 133, 38, 196, 170, 5, 213, 200, 63, 249, 74, 183, 186, 226, 67, 181, 57, 22, 70, 114, 176, 154, 93, 15, 205, 157, 237, 161, 239, 218) ( 1, 171, 197, 187, 238, 138, 155, 47, 96, 81, 253, 24, 37, 185, 97, 247, 71, 78, 17, 167, 3, 195, 188, 223, 208, 54, 94, 231, 147, 16, 248, 173, 75, 2, 184, 177, 69, 233, 144, 95, 211, 224, 201, 229, 245, 225, 163, 86, 250, 51, 158, 72, 119, 61, 142, 99, 101, 103, 180, 219, 164, 210, 149, 254, 82, 159, 148, 220, 36, 234, 126, 209, 214, 122, 40, 73, 31, 11, 172, 244, 56, 41, 240, 242, 65, 139, 189, 236, 135, 252, 192, 113, 62, 87, 80, 179, 206, 30, 202, 58, 199, 162, 140, 6, 84, 165, 235, 59, 20, 107, 91, 166, 19, 13, 156, 7, 49, 152, 21, 203, 90, 8, 146, 50, 64, 222, 228, 137 ).

Permutation sequence 2:

( 0, 242, 166, 250, 29, 65, 18, 113, 75, 136, 15, 50, 153, 119, 173, 126, 6, 198, 67, 93, 239, 46, 158, 151, 184, 196, 128, 200, 189, 108, 77, 3, 238, 167, 28, 105, 237, 204, 74, 154, 25, 30, 24, 244, 133, 64, 72, 41, 246, 218, 19, 202, 247, 205, 97, 145, 82, 107, 69, 228, 90, 14, 170, 220, 81, 99, 95, 130, 168, 219, 211, 53, 80, 230, 54, 109, 148, 38, 26, 37, 100, 201, 144, 175, 178, 7, 103, 137, 71, 87, 254, 63, 101, 47, 223, 122, 216, 225, 150, 140, 207, 31, 89, 10, 62, 58, 116, 180, 149, 57, 157, 76, 11, 169, 172, 83, 217, 22, 60, 48, 141, 88, 8, 162, 132, 115, 203, 193 ) ( 1, 2, 114, 13, 251, 5, 86, 243, 117, 177, 174, 229, 118, 73, 104, 213, 210, 106, 188, 227, 135, 78, 127, 147, 23, 35, 59, 236, 20, 42, 187, 231, 91, 111, 125, 155, 199, 235, 232, 40, 159, 123, 70, 226, 84, 94, 51, 68, 45, 163, 96, 249, 146, 27, 66, 110, 171, 142, 222, 124, 208, 49, 92, 186, 215, 98, 152, 233, 221, 176, 120, 85, 139, 21, 17, 182, 160, 4, 143, 34, 212, 134, 165, 255, 183, 164, 56, 190, 79, 224, 52, 16, 129, 138, 248, 32, 36, 240, 33, 12, 44, 234, 112, 9, 39, 194, 206, 102, 181, 191, 161, 197, 156, 209, 55, 241, 61, 43, 121, 245, 252, 185, 131, 179, 195, 192, 214, 253 ).

Table 3 The S-box$_{2}$ generated by proposed algorithm

Take generating a 4-bit S-box as an example:

1) The initial parameters of the chaotic sequence are ${{b}_{L}}=8$, ${{k}_{L}}=16$, and ${{L}_{0}}=0.321$ to generated a chaotic matrix.

2) Iterate the new logistic map 150 times, delete the first 50 values of the sequence and transform the selected numeric sequence L. Transform floating-point values of the numeric sequence L into integer sequences of 0$\sim$15 to obtain the chaotic sequence Z.

3) Arranging chaotic sequences to construct a 4×4 chaotic matrix Y. If there are duplicate values, only the first numerical value will be kept, and then the same value that appears later will be deleted. The chaotic matrix is Y = [11 6 9 5 13 10 4 7 12 15 14 0 3 8 1 2].

4) Permutation sequence is (4, 12, 9, 10, 14, 11, 5, 3, 13, 8, 6, 0, 15, 2, 7, 1).

It can be seen that the value 11 of the 0-th position of the initial S-box is replaced by the value 3 of the 12-th position, the value 6 of the 1-th position is replaced by the value 15 of the 9-th position, and so on, the value 2 of the 15-th position is replaced by the value 13 of the 4-th position, forming a cycle. Thus, the initial S-box Y = [11 6 9 5 13 10 4 7 12 15 14 0 3 8 1 2] is replaced by the permutation sequence (4, 12, 9, 10, 14, 11, 5, 3, 13, 8, 6, 0, 15, 2, 7, 1), and the new S-box generated after permutation is S-box= [3 15 14 1 0 10 5 8 12 4 11 2 9 7 6 13].

5 S-box performance analysis

To verify the performance of S-boxes constructed in this paper, this section will analyze the performance of S-boxes from bijectivity, nonlinearity, linear approximation probability, differential uniformity, strict avalanche criterion and bit independence criteria.

5.1 Bijectivity

Jakimoski et.al [49] proposed a test method for bijectivity. When $m=n$, the S-box satisfies the bijectivity if and only if the sum of the linear operations of each component Boolean function ${{f}_{i}}$ is ${{2}^{n-1}}$, that is

$$\begin{aligned} \omega t(\sum \limits _{i=1}^{n}{{{a}_{i}}{{f}_{i}}})={{2}^{n-1}} \end{aligned}$$

(7)

where $\omega t()$ is the Hamming weight, ${{a}_{i}}\in [0,1]$, and $({{a}_{1}},{{a}_{2}}, \ldots {{a}_{n}}) \ne (0,0,\ldots ,0)$. In other words, if (7) holds, each ${{f}_{i}}$ of the S-box is 0/1 balanced, and the S-box satisfies the bijective property.

According to the sufficient and necessary conditions for judging that the S-box satisfies the bijective characteristics, the average linear operation sum of the component Boolean functions of two 8-bit S-boxes constructed in this paper are 128, and each of the S-box is 0/1 balanced, which proves that S-boxes satisfy the bijectivity characteristics.

5.2 Nonlinearity

The nonlinearity is used to measure the ability of a cryptographic function to resist linear cryptanalysis. Nonlinearity is defined as

$f(x):F_{2}^{n}\rightarrow F_{2}^{{}}$ is an n-element Boolean function, and the nonlinearity of f(x) is [50]

$$\begin{aligned} N_{f}=\underset{{l\in {L_{n}}}}{min}\;{{d}_{H}}(f,l) \end{aligned}$$

(8)

where ${{L}_{n}}$ is the set of all-element linear and affine functions. ${{d}_{H}}(f,l)$ represents the Hamming distance between f and l.

If $S(x)={({f}_{1}}(x),\ldots ,{{f}_{m}}(x)):F_{2}^{n}\rightarrow F_{2}^{m}$ is a multi-output function, f(x) is generally converted into Walsh spectrum when calculating the nonlinearity, then

$$\begin{aligned} S{}_{\left\langle f \right\rangle }(\omega )=\sum \limits _{\omega \in GF(2^n)}{{{(-1)}^{f(x)\oplus x\cdot \omega }}} \end{aligned}$$

(9)

where $\omega \in GF(2^n)$, “.” represents the dot product operation, and $x\cdot \omega ={{x}_{1}}\cdot {{\omega }_{1}}\oplus {{x}_{2}}\cdot {{\omega }_{2}}\oplus \ldots \oplus {{x}_{n}}\cdot {{\omega }_{n}}$.

The nonlinearity expressed by the Walsh spectrum is

$$\begin{aligned} N_{f}={2}^{n-1}(1-{2}^{-n}\underset{{\omega \in GF(2^n)}}{max}\;|S{}_{\left\langle f \right\rangle }(\omega ) |) \end{aligned}$$

(10)

where $N_{f}$ is nonlinearity, and the greater its value, the stronger its ability to resist linear cryptanalysis.

To effectively resist linear attacks, the nonlinearity of a safe and effective S-box must be sufficiently large. Table 4 shows the nonlinearity of eight output Boolean functions of S-box$_{1}$ and S-box$_{2}$. The minimum nonlinearity of S-box$_{1}$ and S-box$_{2}$ is 108, the maximum nonlinearity is 112, and the nonlinearity of S-box$_{1}$ and S-box$_{2}$ is 104 and 106, respectively. Therefore, our S-boxes have good resistance to linear cryptanalysis.

Table 4 Nonlinearity and LP

5.3 Linear approximation probability

A secure cryptographic system should have strong confusion and diffusion effects. S-box with superior performance helps the cryptographic system to achieve strong confusion and diffusion effects through the nonlinear map between input and output data. Linear approximation probability (LP) is used to measure the resistance of the S-box to linear cryptanalysis, and its calculation formula is

$$\begin{aligned} LP=\underset{{{\alpha }_{x}},{{\beta }_{x}}\ne 0}{max}\;(\frac{\#\{x\in N\mid x\cdot {{\alpha }_{x}}=S(x)\cdot {{\beta }_{x}}\}}{{{2}^{n}}}-\frac{1}{2}) \end{aligned}$$

(11)

where $N=\{0,1,\ldots , 255\}$, ${{\alpha }_{x}}$ and ${{\beta }_{x}}$ are the corresponding input and output masks (${{\alpha }_{x}}\in N$ , ${{\beta }_{x}}\in N$), and $\#\{x\in N\mid X\}$represents the number of x satisfying condition X.

With the lower LP of the S-box, it is proved that the greater the nonlinearity of the S-box, the stronger the ability of the function to resist linear attacks, and vice versa. Table 4 shows the LP between the proposed S-box$_{1}$ and S-box$_{2}$. It can be seen that the LP of S-box$_{1}$ and S-box$_{2}$ are 0.093750 and 0.085938, and the maximum value of LP is only 0.093750, so our proposed S-boxes have good resistance to linear cryptanalysis.

5.4 Differential uniformity

Since the introduction of differential cryptanalysis, many scholars have focused on designing a “strong” S-box to enhance the security of block ciphers based on the S-box. The ability of the S-box to resist differential cryptanalysis essentially depends on the difference distribution table and differential uniformity (DU). The difference distribution table is defined as

${{2}^{n}}\times {{2}^{m}}$-order matrix $\Lambda (S)$ is the difference distribution table of the S-box defined by [51]

$$\begin{aligned} \Lambda (S)=\left( \begin{matrix} {{\lambda }_{00}} &{} {{\lambda }_{01}} &{} \ldots &{} {{\lambda }_{0({{2}^{m}}-1})} \\ {{\lambda }_{10}} &{} {{\lambda }_{11}} &{} \ldots &{} {{\lambda }_{1({{2}^{m}}-1})} \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ {{\lambda }_{{({2}^{\text {n}}}\text {-1)0}}} &{} {{\lambda }_{{({2}^{\text {n}}}\text {-1)}1}} &{} \ldots &{} {{\lambda }_{{({2}^{\text {n}}}\text {-1)}({{2}^{m}}-1})} \\ \end{matrix} \right) \end{aligned}$$

(12)

where ${{\lambda }_{ij}}=|\left\{ x\in GF{{(2)}^{n}}|S(x)+S(x+{{\alpha }_{i}})={{\beta }_{j}} \right\} |$. $i=0,1,\ldots , {{2}^{n}}-1$. $j=0,1,\ldots ,{{2}^{m}}-1$. ${{\alpha }_{i}}$ and ${{\beta }_{j}}$ are the binary representation of i, j, respectively. Obviously

$$\begin{aligned} {{\lambda }_{0j}}=\left\{ \begin{matrix} 2^{n}\quad (j=0) \\ 0 \quad (j\ne 0) \\ \end{matrix}\right. \end{aligned}$$

(13)

It must be pointed out that the distribution value of $\Lambda (S)$ is closely related to the operation on $GF{{(2)}^{n}}$, and only the case of bit-wise XOR is discussed here.

The key to differential analysis is to make use of special elements in the difference distribution table of the S-box. If the values of some elements are greater than those of other elements, the positions of these elements are particularly useful for differential attacks. Therefore, the concept of differential uniformity is introduced.

Suppose the difference distribution table of $n\times m$ S-box is $\Lambda (S)={{\lambda }_{ij}}$, then the DU of S-box is called ${{\delta }_{S}}$ [51], and the formula is as follows

$$\begin{aligned} {\delta _{S}}= & {} \max \{{{\lambda }_{ij}}|i=0,1,\ldots ,{{2}^{n}}-1,j=0,1,\ldots ,{{2}^{m}}-1\} \nonumber \\= & {} \underset{\underset{\beta \in GF{(2)^{m}}}{0\ne \alpha \in GF{(2)^{n}}}}{\max } {{\delta }_{S}}(\alpha ,\beta ) \end{aligned}$$

(14)

where ${{\delta }_{S}}(\alpha ,\beta )=|\left\{ x\in GF{{(2)}^{n}}:S(x\oplus \alpha )+S(x)=\beta \right\} |$ .

To resist differential cryptanalysis, the differential uniformity of the S-box should be as small as possible. The differential distribution tables of S-box$_{1}$ and S-box$_{2}$ are shown in Tables 5 and 6, respectively. The maximum value of the differential uniformity of our S-boxes is 6, which can effectively resist differential cryptanalysis.

5.5 Strict avalanche criterion

If a change in each input bit causes a change in each output bit with a probability of 0.5, then the map shown below satisfies the strict avalanche criterion (SAC)

$$\begin{aligned} S(x)=({{f}_{1}}(x),{{f}_{2}}(x),\ldots ,{{f}_{m}}(x)):F_{2}^{n}\rightarrow F_{2}^{m} \end{aligned}$$

(15)

Webster et.al [52] proposed to effectively judge whether the given $n\times m$ function f meets the SAC by constructing the correlation matrix. The value ${{a}_{i}}_{j}$ of each element of the correlation matrix is the correlation strength between the i-th bit of the ciphertext and the j-th bit of the plaintext. If each element of the correlation matrix has a value very close to 0.5, it can be said that the given function f satisfies the SAC.

The correlation matrices of the S-box$_{1}$ and S-box$_{2}$ are shown in Tables 7 and 8, respectively. It can be seen from the calculation that all elements of the correlation matrix are close to the theoretical value of 0.5.

5.6 Bit independence criteria

Webster et.al [52] proposed the bit independence criteria (BIC) of the S-box, as an important indicator for evaluating the performance of the S-box, which has good independence between bits and can effectively resist external attacks on the cryptographic system. The S-box can be regarded as a function $f:F_{2}^{n}\rightarrow F_{2}^{n}$, and its BIC calculation formula is as follows

$$\begin{aligned} BIC(f)=\underset{\underset{j\ne k}{1\le j,k\le n}}{\max } BIC({{b}_{j}},{{b}_{k}}) \end{aligned}$$

(16)

where $BIC({{b}_{j}},{{b}_{k}})=\underset{1\le i\le n}{\max }\; |corr(b_{j}^{{{e}_{i}}},b_{k}^{{{e}_{i}}'}) |$.

Table 5 Differential matrix for differential uniformity (DU) of S-box$_{1}$

Table 6 Differential matrix for differential uniformity (DU) of S-box$_{2}$

Adams et.al [53] presented a method for measuring the independence of output bits. For a given Boolean function ${{f}_{j}}\oplus {{f}_{k}}$ of two output bits in an S-box, if it has a high nonlinearity and satisfies SAC as much as possible, it can be ensured that each output bit pair has a correlation coefficient close to 0 when any single input bit is inverted. Therefore, it can be proved whether S-box satisfies BIC by measuring whether any ${{f}_{j}}\oplus {{f}_{k}}$ of the S-box satisfies the nonlinear characteristic and SAC.

By calculating the nonlinearity and correlation matrix of ${{f}_{j}}\oplus {{f}_{k}}$ between any two output bits of the S-box, when each element of the ${{f}_{j}}\oplus {{f}_{k}}$ correlation matrix has a value very close to 0.5, indicating that the ${{f}_{j}}\oplus {{f}_{k}}$ of the S-box satisfies the SAC. The nonlinearity of ${{f}_{j}}\oplus {{f}_{k}}$ is more than 100, which meets the nonlinear characteristics.

Table 7 SAC matrix of S-box$_{1}$

Table 8 SAC matrix of S-box$_{2}$

Table 9 BIC-SAC matrix of S-box$_{1}$

Table 10 BIC-SAC matrix of S-box$_{2}$

The BIC-SAC matrices of S-box$_{1}$ and S-box$_{2}$ are shown in Tables 9 and 10, and the BIC-Nonlinearity matrices are shown in Tables 11 and 12, respectively. All values of BIC-SAC are closed to 0.5, which satisfies the SAC. And all values of BIC-Nonlinearity are above 100, satisfying the nonlinear characteristics. Therefore, S-box$_{1}$ and S-box$_{2}$ have good independence between output bits.

Table 11 BIC-Nonlinearity matrix of S-box$_{1}$

Table 12 BIC-Nonlinearity matrix of S-box$_{2}$

5.7 Comparative analysis

To highlight the superior performance of the S-boxes proposed in this paper, the comparative analysis of the performance of S-box$_{1}$, S-box$_{2}$ and other S-boxes are compared and analyzed in terms of nonlinearity, linear approximation probability, differential uniformity, SAC and BIC, as shown in Table 13.

Table 13 Comparative analysis of S-boxes performance

In terms of nonlinearity, we find that the minimum value of S-box$_{1}$ and S-box$_{2}$ is 104, which is the largest in all comparative literature. It can be seen that the S-boxes constructed in this paper have good nonlinearity and are resistant to linear analysis.

Based on the comparative analysis of the LP, it can be observed that the LP of the proposed S-boxes is the smallest among all S-boxes, indicating that they have the strongest ability to resist linear cryptanalysis.

From the comparative analysis of the DU, it can be seen that the largest value of differential uniformity of our S-boxes is 6, which is the smallest of all compared S-boxes, proving that the S-boxes proposed in this paper can resist differential cryptanalysis.

According to the comparative analysis of SAC, the average value of SAC in S-box$_{1}$ is 0.5015 and the average value of SAC in S-box$_{2}$ is 0.5027. The average values of S-box$_{1}$ and S-box$_{2}$ are close to the ideal value of 0.5, indicating that S-box$_{1}$ and S-box$_{2}$ conform to SAC characteristics.

As can be seen from the comparative analysis of BIC, the BIC-SAC values of the S-box$_{1}$ and S-box$_{2}$ are all close to the ideal value of 0.5. The BIC-Nonlinearity values of S-box$_{1}$ and S-box$_{2}$ are 109.71 and 110.14. There are the greatest values in all comparative S-boxes, which proves that the BIC performance of the proposed S-boxes is excellent.

In summary, the proposed S-boxes have strong nonlinearity, small LP and DU, satisfy SAC characteristics and excellent BIC, which can resist linear cryptanalysis and differential cryptanalysis.

6 Conclusion

The design of the S-box in block cipher has always been an important research field in cryptography. Constructing S-box by the chaotic system can have strong randomness, but the differential uniformity of the generated S-box is 10 or 12. To solve this problem, this paper proposes a new efficient S-box construction scheme based on a new logistic map and permutation sequence. The chaotic matrix is generated by the new logistic map, and then is optimized by the permutation sequence to get the final S-box. Through performance analysis, proving that the new logistic map has strong chaotic performance, a large parameter space range, and high sensitivity to the initial value. The proposed S-boxes have high nonlinearity and their differential uniformity is only 6. They can enhance the ability of the cryptographic algorithm to resist differential cryptanalysis and linear cryptanalysis.