Bifurcations and dynamics of a plant disease system under non-smooth control strategy

Abstract

Mathematical models and analyses can assist in designing the control strategies to prevent the spread of infectious disease. The present paper investigates the bifurcations and dynamics of a plant disease system under non-smooth control strategy. The generalized Lyapunov approach is employed to perform the analysis of the plant disease model with non-smooth control. It is found that the controlled disease system can have three types of equilibria. The globally asymptotically attractor for each of three types of equilibria is determined by constructing Lyapunov functions and using Green’s Theorem. It is shown that the disease system can exhibit rich dynamic behaviors including globally stable equilibrium, stable pseudo-equilibrium and sliding mode bifurcations. The solution of the disease system can converge to the disease-free equilibrium, endemic equilibrium or sliding equilibrium on discontinuous surfaces. Biological implications of the obtained results are discussed for implementing the control strategies to the infectious plant diseases.

1 Introduction

Rapid development of modern industry has made negative impacts on the environment and air quality. Protecting plants is one of the important ways to improve the environment effectively. Therefore, we need to study the dynamical behavior of plants from time to time. Mathematical models and analysis have played an important role in the understanding and control of plant diseases. In the process of tree growth and forest development, if the external conditions are suitable for the growth of harmful organisms or the trees are infected by harmful organisms, then a series of abnormal pathological changes can occur in the organization and morphology of trees, which may result in poor quality or even the death of trees. This phenomenon has been referred to as forest disease in the literature.

In general, invasive and noninvasive diseases can coexist in plants, which undoubtedly makes the treatment complicated. At the same time, the shortage of treatment resources can seriously affect the implementation of a control strategy. Limited resources bring many challenges and difficulties to the control and prevention of plant infectious diseases. How to implement the best prevention and control measures using limited resources has become an important technical issue. Therefore, studying the control strategies for infected plants under limited resources is of biological significance and is meaningful.

If a very few individuals of plants are infected by an emerging infectious disease, then medical resources are sufficient for an early-stage treatment. However, some early symptoms are similar to the viral diseases, which make us hard to find the infected plants. At the same time, some infectious plant diseases have different viruses which may be treated differently (see [2, 3, 24, 25, 34]). A serious threat to forest may occur when the number of the infected plants increases. Different models of viral infections have been proposed to explain and control the spread of the virus (see [12, 20, 21, 28, 30]). On the other hand, different types of control strategies are constrained by the limited availability of medical resources for plant treatment, especially in the poor areas of some underdeveloped countries (see [2, 9, 20, 21, 23, 24, 28, 39]).

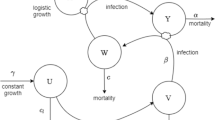
The basic model to be considered in this paper is the infectious disease model with the classic limited treatment capacity [7, 8, 11, 27, 34, 38], i.e.,

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}&= A-\mu S-\beta SI,&\\ \frac{\mathrm{d}I}{\mathrm{d}t}&=\beta SI-\mu _{1} I-v_{1}I-{\mathcal {H}}(I),&\\ \frac{\mathrm{d}R}{\mathrm{d}t}&=v_{1}I+{\mathcal {H}}(I) -\mu _{1}R, \end{aligned} \right. \end{aligned}$$

(1)

where S, I and R represent the numbers of susceptible, infective and recovered individuals. A denotes the recruitment rate of the susceptible individuals. $\beta$ is the transmission coefficient. $\mu$ represents the death rate of susceptible plants. $\mu _{1}$ represents the rate of death by diseases and natural causes. Obviously, $\mu _{1}>\mu$. In addition, ${\mathcal {H}}(I)=\frac{cI}{1+b_{1}I}$ denotes the function of treatment, with c being the maximum recovery rate and $b_{1}$ representing the effect of the medical resource limitation. And $v_{1}$ is the natural recovery rate with $v_{1}<c$.

It is often impossible to completely eradicate infected plants, which is either biologically or economically infeasible. One of the key goals of integrated disease management is to minimize losses and maximize returns. Integrated disease management allows for a tolerance threshold, called the economic threshold (ET), at which the damage to plants can be accepted. The control strategies are used only when the number of infected plants reaches ET.

Once plant disease occurs, we expect to control the number of the infected plants to an economic threshold within a limited time. (Below the threshold, no action is required.) In this aspect, the asymptotic behavior of infinite time would lose its practical significance to some extent. Therefore, it is necessary to study whether the infected plants can be controlled within a limited time by a threshold control method. The number of the infected plants was used as a reference index in applying the control strategy (see [24, 34]). When the number of the infected plants is below the threshold, the disease is regarded as manageable and the implementation of control methods is not required. However, if the number of the infected plants is beyond the threshold level, then the action of culling the infected plants must be taken immediately to control the spread of the disease before the situation becomes catastrophic or unmanageable. This control method has been referred to as the threshold control strategy [24, 34], which can be designed under the framework of discontinuous systems [2, 9, 26, 29, 35, 39]. The threshold control method is easily implemented in practical engineering. We use the number of infections as a threshold level to determine whether we need to implement control or not. When the number of infected plants is less than the threshold value, no action is required for the plant disease system. When it is higher than the threshold value, we need to remove the infected plants at the saturation treatment rate. It is found that the plant disease system can be successfully managed by the proposed non-smooth control strategy with its trajectory converging to the pseudo-equilibrium. The non-smooth infectious disease models were investigated by many researchers [1, 2, 6, 9, 14, 16,17,18, 22, 25, 27, 29, 34, 36, 37, 39, 40].

In the study of the infectious plant system, it is very natural to ask whether the system has a globally asymptotically stable periodic solution after a treatment is performed for the infectious plant system or additional control strategies are required to stabilize the plant system. Then three questions will be naturally raised for the plant disease system:

• 1. Is there any globally stable solution for the infectious system under the non-smooth control strategy?

• 2. What are the sliding mode domains of the system for the existence of equilibriums and their bifurcations?

• 3. How many types of sliding bifurcations can the system have?

This paper will address the above-mentioned three challenging questions for the dynamic behavior of the infectious plant disease system under non-smooth control strategy, by using the Lyapunov function and bifurcation technique.

In this paper, we apply the non-smooth threshold control strategy to the infectious model (1) which is expressed as:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}&= A-\mu S-\beta SI,&\\ \frac{\mathrm{d}I}{\mathrm{d}t}&=\beta SI-\mu _{1} I-v_{1}I-\frac{cI\psi (I)}{1+b_{1}I},&\\ \frac{\mathrm{d}R}{\mathrm{d}t}&=v_{1}I+\frac{cI\psi (I)}{1+b_{1}I} -\mu _{1}R,&\end{aligned} \right. \end{aligned}$$

(2)

where $\psi (I)$ is a non-smooth control function. According to the analysis of the discontinuous dynamical system (2), the dynamic behavior of the third equation can be determined by the properties of the first two equations. So we can simplify the analysis by studying the system governed by the first two equations:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}&= A-\mu S-\beta SI,&\\ \frac{\mathrm{d}I}{\mathrm{d}t}&= \beta SI-\mu _{1}I-v_{1}I-\frac{cI\psi (I)}{1+b_{1}I}.&\\ \end{aligned} \right. \end{aligned}$$

(3)

If the infected plant has a sudden infection after a treatment, then we need to perform multiple controls. By considering this actual situation, we propose a treatment control function satisfying the following assumption.

(H1):

The number of the infected plants is used as a reference index in implementing the control strategy by setting $\psi (I)=1$ when $I>\mathrm{ET}$, and $\psi (I)=0$ when $I<\mathrm{ET}$.

The rest of this paper is organized as follows. Section 2 presents some definitions and lemmas for the analysis. Section 3 discusses the existence of three types of equilibria and studies the properties of solutions. The qualitative analysis of system (3) is carried out in Sects. 4 and 5. The sliding bifurcations of the infectious system (3) are investigated in Sect. 6. Section 7 gives a brief conclusion.

2 Preliminaries

We consider a discontinuous dynamic system:

$$\begin{aligned} {\dot{u}}(t)=\left\{ \begin{aligned} f_{S_{1}}(u)&u\in S_{1},&\\ f_{S_{2}}(u)&u\in S_{2},&\\ \end{aligned} \right. \end{aligned}$$

(4)

where $f_{S_{1}}(u)=(A-\mu S-\beta SI,\beta SI-\mu _{1}I-v_{1}I)^{T}, f_{S_{2}}(u)=( A-\mu S-\beta SI, \beta SI-\mu _{1}I-v_{1}I-\frac{cI}{1+b_{1}I})^{T}$. We divide the plane $(S, I)\in R^{2}_{+}$ into two regions by controlling the threshold function

$$\begin{aligned} \left\{ \begin{aligned}S_{1}=\{u\in R^{2}_{+}\mid H(I)<0\},&\\ S_{2}=\{u\in R^{2}_{+}\mid H(I)>0\},&\\ \varPi =\{u\in R^{2}_{+}\mid H(I)=0\}.&\\ \end{aligned}\right. \end{aligned}$$

(5)

where $u=(S,I)^{T}\in R_{+}^{2}$. We choose the special function $H(I)=I-\mathrm{ET}$; here, ET describes the threshold value. The dynamic behavior of the subsystem determined by vector $f_{S_{1}}$ or $f_{S_{2}}$ can be studied by using the Filippov convex method [5, 12, 13, 23, 32] or Utkin’s equivalent control method [15, 19]. Let $\varTheta (u)=\langle H'(I),f_{S_{1}}(u)\rangle \langle H'(I), f_{S_{2}}(u)\rangle =f_{S_{1}}H'(I)\cdot f_{S_{2}}H'(I),$ where $\langle .\rangle$ represents the standard scalar product. For brevity, the notation $F_{S_{i}}H'(u)=\langle H'(I), f_{S_{i}}(u)\rangle$ will be used in the subsequent analysis.

From (5), the sliding mode domain is defined as $\varPi$, which can be divided into two regions [10, 20, 24, 30]:

(i) Escaping region $\varPi _{e}$: if $\langle H'(u),f_{S_{i}}(u)\rangle <0$ and $\langle H'(I), f_{S_{i}}(u)\rangle >0$

(ii) Sliding region $\varPi _{s}$: if $\langle H'(u),f_{S_{i}}(u)\rangle >0$ and $\langle H'(I), f_{S_{i}}(u)\rangle <0$.

The following definitions of the discontinuous system (4) are necessary throughout the paper [10, 20, 24, 30].

A point $u^{*}$ is termed as a pseudo-equilibrium if it is an equilibrium of the sliding mode of system (4), i.e., $F_{S}(u^{*})=\lambda f_{S_{1}}(u^{*})+(1-\lambda )f_{S_{2}}(u^{*})=0$, $H(I)=0$ and $0<\lambda <1$, where $\lambda =\frac{\langle H(I),f_{S_{2}}(u)\rangle }{\langle H(I), f_{S_{2}}(u)-f_{S_{1}}(u)\rangle }.$ The vector field of the discontinuous system (4) on sliding mode $\varPi _{S}$ is defined as : $\frac{du(t)}{dt}=F_{S}(u),u\in \varPi _{s},$ where $F_{S}(u)=\lambda f_{S_{1}}(u)+(1-\lambda )f_{S_{2}}(u)$.

A point $u^{*}$ is called a regular equilibrium of system (4) if $H(I)<0, f_{S_{1}}( u^{*})=0$, or $H(I)>0, f_{S_{2}}( u^{*})=0$.

Similarly, a point $u^{*}$ is referred to as a virtual equilibrium of system (4) if $H(I)<0, f_{S_{2}}( u^{*})=0$, or $H(I)>0, f_{S_{1}}( u^{*})=0$.

In addition, a point $u^{*}$ is called a tangent point of system (4), if $u^{*}\in \varPi _{s}$ and $[f_{S_{2}}H(I)][f_{S_{1}}H(I)]=0$.

A point $u^{*}$ is called a boundary equilibrium of system (4) if $H(I)=0, f_{S_{2}}(u^{*})=0$, or $H(I)=0, f_{S_{1}}(u^{*})=0$.

Express the solution from a given initial condition $u_{0}$ of Eq.(4) as $\xi (u_{0})$, the $\omega$ limit set as $\omega (u)$ and, for $G \in R^{2}_{+}$, $AG(t)\equiv \{u\in R^{2}_{+}|u=\xi _{u_{0}}(t)~~\mathrm {for}~~~u_{0}\in G\}, \xi (G)\equiv \bigcup \nolimits _{t\ge 0} AG(t)$ [40]. A function $V \in C^{1}(R^{2}_{+})$ is called a Lyapunov function of system (3) on $G\subset R^{2}$ if it is nonnegative on G and, for all $u\in G$, $V'(u)=\max \nolimits _{G\in f(u)}<V(u),G>\le 0$, where f(u) is given by:

$$\begin{aligned}f(u)=\left\{ \begin{aligned}&\{f_{S_{1}}(u)\}\mathrm {~if}~u\in S_{1},\\&\{\alpha _{1}f_{S_{1}}(u)+(1-\alpha _{1})f_{S_{2}}(u):0\leqslant \alpha _{1}\leqslant 1\}\mathrm {~if}u\in \varPi , \\&\{f_{S_{2}}(u)\}\mathrm {~if}~u\in S_{2}. \end{aligned} \right. \end{aligned}$$

Lemma 2.1

[4, 27] (LaSalle’s Invariance Principle) Assume that $G\subset R_{+}^{2}$ is an open set satisfying $\omega (G)=\bigcup \limits _{u\in G}\omega (u)\subset \xi (G)$. If every Filippov solution $u_{i}$; $u_{0}\in G$, of system (3) is unique, and V : $R_{+}^{2} \rightarrow R_{+}$ is a Lyapunov function of system (3) on $\xi (G)$, then $\omega (G)$ is a subset of the largest positive invariant subset of ${\overline{\varLambda }}$, where $\varLambda =\{u\in {\overline{G}}|V'(u)=0\}$.

Lemma 2.2

[4, 27] Suppose that G and V: $R^{2}_{+}\rightarrow R_{+}$ satisfy Lemma 2.1 and $R_{+}^{2}{\setminus } G$ is repelling such that all solutions stay in $R_{+}^{2} {\setminus } G$ for only a finite time. If $\omega (R_{+}^{2})=\omega (G)$ is bounded, then $\overline{\omega (R_{+}^{2})}$ is globally asymptotically stable.

3 Dynamic properties of the plant disease system with non-smooth control strategy

Proposition 3.1

(Positivity) Suppose that assumption H1 holds. Then there is a positive solution $u(t)=(S(t),I(t))^{T}>0$ for system (3) with the initial condition $u(0)=(S(0),I(0))^{T}>0$ for $t\in [0, T)$.

Proof

Under the condition of the hypothesis H1, we know that $\psi (0)$ is continuous at 0 (i.e., the function $\psi$ is continuous at $I = 0$). There exists a small positive number $\delta$ satisfying $|I|<\delta$. Then Eq. (3) becomes the following continuous system:

$$\begin{aligned} \frac{\mathrm{d}I}{\mathrm{d}t}=\left( \beta S-\mu _{1}-v_{1}-\frac{c\psi (I)}{1+b_{1}I}\right) I. \end{aligned}$$

(6)

If $I(0)=0$, then from Eq. (6) we know that $I(t)=0, t\in [0, T)$. If $I(0)\ne 0$, then we can state that $I(t)>0$ for all $t>0$. Otherwise, let $t_{1}=\mathrm {inf}\{t\mid I_{t}=0\}$, then $t_{1}> 0$ and $I(t_{1})>0$. We can easily find a positive constant $\theta _{1}$ such that $t_{1}-\theta _{1}>0$ and $0<I(t)<\delta _{1}$ for $t\in [t_{1}-\theta _{1},t_{1})$. Now, multiplying both sides of Eq.(6) by $I^{-1}$ for $t\in [t_{1}-\theta _{1},t_{1})$ and integrating over the interval $t\in [t_{1}-\theta _{1},t_{1})$, yields

$$\begin{aligned} 0{=}I(t_{1}){=}I(t_{1}{-}\theta _{1})\mathrm {e}^{\int ^{t_{1}}_{t_{1}-\theta _{1}}\beta S(t)-\mu _{1}-v_{1}-\frac{c\psi (I)}{1+b_{1}I(t)}dt}>0, \end{aligned}$$

which is a contradiction to the assumption. Thus, $I(t)>0$ for all $t\in [0,T)$.

By using same argument it can be proved that $S(t)>0$. If not, let $t_{1}$ be the first time when $S(t_{1})I(t_{1})=0$. Assume that $S(t_{1})=0,$ we know that $I(t)\geqslant 0$ for all $t\in [0,t_{1}]$. Then, from the first equation of (3), we can easily know that

$$\begin{aligned} \frac{dS(t)}{dt}|_{t=t_{1}}= A-\mu S(t_{1})-\beta S(t_{1})I(t_{1})=A>0. \end{aligned}$$

Since $S(t)>0$, for $S(t_{1})=0$, we must have $\frac{\mathrm{d}S}{\mathrm{d}t}|_{t=t_{1}}\leqslant 0$, which is a contradiction. This completes the proof. $\square$

Proposition 3.2

Suppose that assumption H1 holds. Then every solution (S(t), I(t)) of Eq. (3) is uniformly ultimately bounded.

Proof

As discussed in Proposition 3.1, the existence of the positive solution u(t) to Eq. (3) on [0, T) as $T\rightarrow +\infty$, with $u(0)=u_{0}$, is a straightforward consequence. Namely, $u(t)>0$ for all $t\in [0, T)$. From Eq. (3), we have

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}+\frac{\mathrm{d}I}{\mathrm{d}t}&= A-\mu S-\mu _{1} I-v_{1}I-\frac{c\psi (I)I}{1+b_{1}I}\\&\leqslant A-\ell (S+I)-\frac{c\psi (I)I}{1+b_{1}I}, \end{aligned} \end{aligned}$$

(7)

where $\ell =\mathrm {min}\{\mu ,v_{1}+\mu _{1}\}$.

From (7), for $\psi (I)=1$ or 0, if $S+I >\frac{A}{\ell }$ holds, then $A-\ell (S+I)-v\frac{c\psi (I)I}{1+b_{1}I}<0$. Therefore, $0\leqslant S+I \leqslant \mathrm {max}\{S_{0}+I_{0} ,\frac{A}{\ell }\}$, that is, the solution (S(t), I(t)) is bounded on [0, T). Using the continuation theorem, we can conclude that the solution (S(t), I(t)) is bounded on $[0, +\infty )$. The proof is completed.

By defining the sliding dynamic system as a convex combination of the two subsystems $S_{i}$,

$$\begin{aligned} F_{S}(u)=\lambda f_{S_{1}}(u)+(1-\lambda )f_{S_{2}}(u), \end{aligned}$$

we can obtain $\lambda =\frac{\langle H'(u),f_{S_{2}}(u)\rangle }{\langle H'(u), f_{S_{2}}(u)-f_{S_{1}}(u)\rangle },$ with $0\le \lambda \le 1$.

Equation $\lambda =1,0$ indicates that the flow is determined by $f_{S_{1}}$ or $f_{S_{2}}$, respectively. From the definition of the tangent point, two equations $\lambda =1$, $\lambda =0$ must be tangent to $\varPi _{S}$. Thus the sliding mode domain can be defined as $\varPi _{S}=\{u\in R^{2}_{+}\mid 0\le \lambda \le 1\}$, which is equivalent to $\varPi _{S}=\{u\in R^{2}_{+}\mid \varTheta \le 0\}$. Denote $\varPi _{S_{-}}=\{u\in R^{2}_{+}\mid \lambda = 0\}$ and $\varPi _{S_{+}}=\{u\in R^{2}_{+}\mid \lambda = 1\}$ as the boundaries of the sliding mode domains, then one of the vector fields is tangent to the boundary $\varPi _{S_{-}}$ or $\varPi _{S_{+}}$.

Based on H1, system (3) can be expressed as a continuous system in $S_{1}$

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}&= A-\mu S-\beta SI,&\\ \frac{\mathrm{d}I}{\mathrm{d}t}&=\beta SI-\mu _{1}I-v_{1}I , \end{aligned} \right. \end{aligned}$$

(8)

and in $S_{2}$ as

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}&= A-\mu S-\beta SI,&\\ \frac{\mathrm{d}I}{\mathrm{d}t}&= \beta SI-\mu _{1} I-v_{1}I-\frac{cI}{1+b_{1}I},&\\ \end{aligned} \right. \end{aligned}$$

(9)

where $S_{1}=\{u\in R^{2}_{+}\mid I<ET\}, S_{2}=\{u\in R^{2}_{+}\mid I>ET\},$ with $\varPi =\{u\in R^{2}_{+}\mid I=ET\}$.

The discontinuity boundary $\varPi$ separating the regions $S_{1}$ and $S_{2}$ is given by $\varPi =\{(S, I)\in R^{2}_{+}\mid I=ET\}$. According to the definitions given in Section 2, the sliding mode domains can be specified as $\varPi _{s}=\{u\in R^{2}_{+}\mid \varTheta (S,ET)\leqslant 0\}.$ Based on the definition of sliding region, from Eqs. (8) and (9), we can write

$$\begin{aligned} \begin{aligned}&\varTheta (S,I)\\&\quad = \left\{ (\beta S-\mu _{1}-v_{1})I\left( (\beta S-\mu _{1}-v_{1})I-\frac{cI}{1+b_{1}I}\right) \right\} , \end{aligned} \end{aligned}$$

where $I-\mathrm{ET}=0$. Using $\varTheta (S,ET) \leqslant 0$, we have

$$\begin{aligned} \begin{aligned}&\varTheta (S,ET)\\&\quad =(\beta S-\mu _{1}-v_{1})ET\times \\&\qquad \left( \beta SET-(\mu _{1}+v_{1})ET-\frac{cET}{1+b_{1}\mathrm{ET}}\right) \\&\quad \leqslant 0. \end{aligned} \end{aligned}$$

(10)

Therefore, from Eq. (10), the sliding domain $\varPi _{s}$ can be obtained as

$$\begin{aligned} \frac{\mu _{1}+v_{1}}{\beta }\leqslant S\leqslant \frac{(\mu _{1}+v_{1})(1+b_{1}ET)+c}{\beta (1+b_{1}ET)}. \end{aligned}$$

(11)

According to Eq.(3), the pseudo-equilibrium of sliding dynamic system is determined by

$$\begin{aligned} F_{S}(S,I)=\lambda F_{S_{1}}(S,I)+(1-\lambda ) F_{S_{2}}(S,I), \end{aligned}$$

(12)

from (12) and $H(I)=I-ET$, we have

$$\begin{aligned} \beta SI-\mu _{1}I-v_{1}I-\frac{c\lambda I}{1+b_{1}I}= 0, \end{aligned}$$

(13)

and, by substituting $I=ET$, we have

$$\begin{aligned} \lambda =(\beta S-\mu _{1} -v_{1})\frac{(1+b_{1}ET)}{c}, \end{aligned}$$

which simplifies the first equation of system (3) into $\frac{\mathrm{d}S(t)}{\mathrm{d}t}= F_{S}(S,I).$ From Eq. (3) and by sliding mode definition in Sect. 2, we have the sliding mode dynamic system

$$\begin{aligned} F_{S}(S,ET) =A-\mu S-\beta SET. \end{aligned}$$

(14)

For simplicity, we will use $E_{ir}^{-}$($E_{ir}^{+}$), $E_{iv}^{-}$($E_{iv}^{+}$), $E_{p}$, and $E^{B}_{j}(i=1,2,j=1,2)$ to represent the regular equilibrium (R-E), virtual equilibrium (V-E), pseudo-equilibrium (P-E), and boundary equilibrium (B-E), respectively. $\square$

Regular equilibrium (R-E): According to Eq. (3), for the subsystem $S_{1}$ with $I< ET$, the equilibriums of system (3) are the solutions of

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}&= A-\mu S-\beta SI,&\\ \frac{\mathrm{d}I}{\mathrm{d}t}&= \beta SI-(\mu _{1}+v_{1})I.&\\ \end{aligned} \right. \end{aligned}$$

The disease-free equilibrium and the endemic equilibrium are expressed as $E_{1}^{-}(S^{-}_{1},I^{-}_{1})$, $E_{2}^{-}(S^{-}_{2},I^{-}_{2})$, with

$$\begin{aligned} E_{1}^{-}{=}\left( \frac{A}{\mu },0\right) ,~ E_{2}^{-}{=}\left( \frac{\mu _{1}+v_{1}}{\beta }, \frac{A\beta -\mu (\mu _{1}+v_{1})}{\beta (\mu _{1}+v_{1})} \right) . \end{aligned}$$

We can easily obtain the following results. The basic reproduction number is ${\mathcal {R}}_{0}=\frac{\beta A}{(v_{1}+\mu _{1})\mu }$ (refer to [31]). If ${\mathcal {R}}_{0}<1$, the disease-free equilibrium $E_{1}^{-}$ is locally asymptotically stable. On the other hand, if ${\mathcal {R}}_{0} >1$, the equilibrium $E_{2}^{-}$ is locally asymptotically stable.

For subsystem $S_{2}$ with $I>ET$, the equilibriums of system (3) are the solutions of

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}&=A-\mu S-\beta SI,&\\ \frac{\mathrm{d}I}{\mathrm{d}t}&= \beta SI-\mu _{1}I-v_{1}I-\frac{cI}{1+ b_{1}I}.&\\ \end{aligned} \right. \end{aligned}$$

The disease-free equilibrium and the endemic equilibrium are expressed as $E_{1}^{+}(S^{+}_{1},I^{+}_{1})=\left( \frac{A}{\mu },0\right)$, and $E_{i}^{+}(S^{+}_{i},I^{+}_{i})(i=2,3)$ which is determined by

$$\begin{aligned} \begin{aligned}&(\mu _{1}+v_{1})\beta b_{1}I^{ 2}+ ((\mu _{1}+v_{1})(\beta +\mu b_{1})\\&\quad +\, c \beta -A\beta b_{1})I {+} ((\mu _{1}{+}v_{1})\mu + c\mu -A\beta ) = 0 , \end{aligned}\nonumber \\ \end{aligned}$$

(15)

where

$$\begin{aligned} \begin{aligned}&h _{1} = -\left( \frac{A\beta b_{1}-(\mu _{1}+v_{1})(\beta + \mu b_{1})- c \beta }{(\mu _{1}+v_{1}) \beta b_{1}}\right) ,\\&l _{1} = \frac{(\mu _{1}+v_{1})\mu + c\mu -A\beta }{(\mu _{1}+v_{1}) \beta b_{1}}. \end{aligned} \end{aligned}$$

For the convenience of explanation, from Eq. (15), we simply denote

$$\begin{aligned} \begin{aligned}&I_{2} ^{+} = \frac{-h_{1}+\sqrt{\varDelta _{1}}}{2},\\&I_{3} ^{+} = \frac{-h _{1}-\sqrt{\varDelta _{1}}}{2},\\&\varDelta _{1} = h ^{2}_{1}-4l_{1},\\&S _{i}^{+} = \frac{A}{\mu +\beta I_{i}^{+}}, i=2, 3. \end{aligned} \end{aligned}$$

If $\varDelta _{1}>0$, then the endemic equilibriums of the system are

$$\begin{aligned}&E_{2}^{+}(S^{+}_{2},I^{+}_{2})\\&\quad =\left( \frac{2A}{2\mu + \beta (-h_{1}+\sqrt{\varDelta _{1}})},\frac{-h _{1}+\sqrt{\varDelta _{1}}}{2}\right) , \end{aligned}$$

and

$$\begin{aligned}&E_{3}^{+}(S^{+}_{3},I^{+}_{3})\\&\quad =\left( \frac{2A}{2\mu + \beta (-h _{1} - \sqrt{\varDelta _{1}})},\frac{-h _{1} - \sqrt{\varDelta _{1}}}{2}\right) . \end{aligned}$$

The basic reproduction number of system (9) is ${\mathcal {R}}_{1}=\frac{\beta A}{(v_{1}+\mu _{1}+ c)\mu }$ (refer to [31]). We can easily obtain the following proposition.

Proposition 3.3

[11, 25, 33] System (9) always has a unique endemic equilibrium $E_{2}^{+}(S^{+}_{2}, I^{+}_{2} )$, if ${\mathcal {R}}_{1}>1$. In addition, if ${\mathcal {R}}_{1}=1$ and $h_{1}<0$, there exists a unique endemic equilibrium $E_{2}^{+}(S^{+}_{2}, I^{+}_{2} )$. On the other hand, if ${\mathcal {R}}_{1}=1$ and $h_{1}\ge 0$, there is no endemic equilibrium. Furthermore, if ${\mathcal {R}}_{1}<1, h_{1}<0$ and $\varDelta _{1}>0$, there exist two endemic equilibriums $E_{2}^{+}(S^{+}_{2}, I^{+}_{2} )$ and $E_{3}^{+}(S^{+}_{3}, I^{+}_{3})$. If ${\mathcal {R}}_{1}<1$, $h_{ 1} < 0$ and $\varDelta _{1}=0$, two endemic equilibriums $E_{2}^{+}(S^{+}_{2}, I^{+}_{2})$ and $E_{3}^{+}(S^{+}_{3}, I^{+}_{3})$ coalesce to form an endemic equilibrium of multiplicity 2. Moreover, if ${\mathcal {R}}_{1}<1, h_{1}<0$ and $\varDelta _{1}<0$, then there is no endemic equilibrium. If ${\mathcal {R}}_{1}<1$ and $h_{1}\ge 0$, there is no endemic equilibrium either.

Now we examine the stability of the endemic equilibrium of system (9). The corresponding characteristic equation for the endemic equilibrium $E^{+}_{i} (S ^{+}_{i}, I^{+}_{i} ), i = 2, 3$ is given by

$$\begin{aligned} \begin{aligned}&\lambda ^{2}+ Q(I_{i}^{+})\lambda + P(I^{+}_{i})=0, \end{aligned} \end{aligned}$$

(16)

where

$$\begin{aligned} \begin{aligned}&Q(I_{i}^{+})=\mu +\beta I _{i}^{+}-\frac{cb_{1}I ^{+}_{i}}{(1+b _{1}I _{i}^{+})^{2}},\\&P(I^{+}_{i})= \frac{A\beta ^{2} I^{+}_{i}}{\mu +\beta I^{ +}_{i}}-\frac{(\mu + \beta I^{+}_{i} )cb_{1}I^{+} _{i}}{(1+b_{1}I^{+}_{i})^{2}}. \end{aligned} \end{aligned}$$

We can obtain the following proposition from Eq. (16):

Proposition 3.4

[11, 25, 33] If ${\mathcal {R}}_{1}>1$ and $Q(I^{+}_{2})>0$, the endemic equilibrium $E^{+}_{2}$ of Eq. (9) is a stable node (or focus). If ${\mathcal {R}}_{1}>1$ and $Q(I_{2}^{+})<0$, then $E^{+}_{2}$ is a unstable node (or focus). If ${\mathcal {R}}_{1}>1$ and $Q(I_{2}^{+})=0$, then Eq. (9) has at least one closed orbit.

Pseudo-equilibrium (P-E): The corresponding sliding mode differential equation of system (3) becomes Eq. (14). By using the definition of the P-E point, we know that $E_{p}(\frac{A}{\mu +\beta ET}, ET).$ The stability of P-E $E_{p}$ can be investigated based on Eq. (14) on the sliding segment $\varPi _{S}$.

Theorem 3.1

Assume that in system (3) $I_{2}^{+}\leqslant ET\leqslant I_{2}^{-}$. Then the pseudo-equilibrium $E_{p}\left( \frac{A}{\mu +\beta ET},ET\right)$ of the system is locally stable.

Proof

Firstly, the sufficient condition on the existence of the P-E $E_{p}$ of Eq. (14) is investigated below. From the second equations of Eqs. (8) and (9), we obtain $S^{-}_{2}=\frac{\mu _{1}+v_{1}}{\beta }$ and $S^{+}_{2}=\frac{\mu _{1}+v_{1}+\frac{c}{1+b_{1}I^{+}_{2}}}{\beta }$, then $S^{-}_{2}<S^{+}_{2}$. By using the first equations of Eqs. (8) and (9), we have $I^{+}_{2}=\frac{A}{\beta S^{+}_{2}}-\frac{\mu }{\beta }$ and $I^{-}_{2}=\frac{A}{\beta S^{-}_{2}}-\frac{\mu }{\beta }$, then $I^{+}_{2}<I^{-}_{2}$.

By (11) and (12), under $I_{2}^{+}\leqslant ET\leqslant I_{2}^{-}$, we have

$$\begin{aligned} \frac{-h _{1}+\sqrt{\varDelta _{1}}}{2}\leqslant ET\leqslant \frac{A\beta -\mu (\mu _{1}+v_{1})}{\beta (\mu _{1}+v_{1})}, \end{aligned}$$

after an easy computation, we can obtain

$$\begin{aligned} \frac{\mu _{1}+v_{1}}{\beta }\leqslant \frac{A}{\mu +\beta ET}\leqslant \frac{(\mu _{1}+v_{1})(1+b_{1}ET)+c}{\beta (1+b_{1}ET)}. \end{aligned}$$

Then there exists the P-E $E_{p}$ of system (3) if $I_{2}^{+}\leqslant ET\leqslant I_{2}^{-}$.

Secondly, we consider $(F_{S}(S,I))_{S}'=-\mu -\beta I<0.$ We can obtain that $E_{p}(\frac{A}{\mu +\beta ET},ET)$ is locally stable. The proof is completed. $\square$

Boundary equilibrium (B-E): The boundary equilibrium of system (3) is governed by the equations

$$\begin{aligned} \left\{ \begin{aligned}&A-\mu S-\beta SI=0,&\\&\beta SI-\mu _{1} I-v_{1}I-\frac{c\psi (I)I}{1+ b_{1}I}=0,&\\&I=ET.&\\ \end{aligned} \right. \end{aligned}$$

(17)

From the first and second equations of system (17), we can obtain $\frac{A}{\mu +\beta ET} =(\mu _{1} +v_{1}+\frac{c\psi (I)}{1+ b_{1}ET})\frac{1}{\beta }.$ Now, let us denote $E_{1}^{B}$ as the B-E point for (17) with $\psi (I)=1$, i.e., $ET=I_{ 1}$ (if $I_{1}$ exists), and $E_{2}^{B}$ with $\psi (I) =0$, i.e., $ET =I_{2}$ (if $I_{2}$ exists), then we have boundary equilibriums:

$$\begin{aligned} \begin{aligned}&E_{1}^{B}=\left( ( \mu _{1} +v_{1}+\frac{c}{1+ b_{1}ET})\frac{1}{\beta }, ET \right) ;\\&E_{2}^{B}=\left( \frac{\mu _{1} +v_{1}}{\beta },ET\right) . \end{aligned} \end{aligned}$$

4 Global qualitative analysis of the plant disease subsystems (8) and (9)

In order to ensure that system (3) is asymptotically stable in each subspace, two cases for the threshold ET will be discussed. Moreover, the global dynamics of systems (8) and (9) will be investigated.

Lemma 4.1

If ${\mathcal {R}}_{0} <1$, the disease-free equilibrium $E_{1}^{-}(\frac{A}{\mu },0)$ of system (8) is globally asymptotically stable (G.A.S).

Proof

For the sake of simplicity, we first transfer the disease-free equilibrium $E_{1}^{-}$ to the origin by using $x=S-\frac{A}{\mu }$. Then system (8) becomes:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&=-\mu x-\beta xI- \frac{\beta A}{\mu }I,&\\ \frac{\mathrm{d}I}{\mathrm{d}t}&=\beta xI-\mu _{1}I-v_{1}I+ \frac{\beta A}{\mu }I.&\\ \end{aligned} \right. \end{aligned}$$

(18)

Considering the following Lyapunov function

$$\begin{aligned} V(x, I)=\frac{1}{2}x^{2}+\frac{A}{\mu }I \end{aligned}$$

and based on Eq. (18), we can obtain

$$\begin{aligned} \begin{aligned} \frac{d V(x, I)}{dt}&{=}-\mu x^{2}{-}\beta x^{2}I{-}\left( \mu _{1}I{+}v_{1}I{-} \frac{\beta A}{\mu }I\right) \frac{\beta A}{\mu }\\&\leqslant 0. \end{aligned} \end{aligned}$$

When ${\mathcal {R}}_{0}< 1$, we have $-\mu _{1}I-v_{1}I+\beta \frac{A}{\mu }I\leqslant 0$.

In other words, the disease-free equilibrium $E_{1}^{-}$ is G.A.S for (8 ) if ${\mathcal {R}}_{0}<1$. This completes the proof. $\square$

Lemma 4.2

Suppose that ${\mathcal {R}}_{0}>1$, the endemic equilibrium $E_{2}^{-}(S^{-}_{2},I^{-}_{2})$ of system (8) is G.A.S.

Proof

In order to apply LaSalle’s Invariance Principle, we first use $x = S-S^{-}_{2},y=I- I^{+}_{2}$ to transfer the equilibrium $E_{2}^{-}(S^{+}_{2}, I^{+}_{2})$ to the origin. We re-organize Eq. (8) as

$$\begin{aligned} \left\{ \begin{aligned} \frac{dx}{dt}&=-\mu x-\beta x( I_{2}^{-}+y)-(\mu _{1}+v_{1})y,&\\ \frac{dy}{dt}&=\beta x( I^{+}_{2}+y), \end{aligned} \right. \end{aligned}$$

(19)

and construct the Lyapunov function as

$$\begin{aligned} \begin{aligned}&V(x, y)=\frac{x^{2}}{2}+\frac{\mu _{1}+v_{1}}{\beta }\left( y- I^{+}_{2}ln\frac{ I^{+}_{2}+y}{ I^{+}_{2}}\right) . \end{aligned} \end{aligned}$$

Then based on Eq. (19), we have

$$\begin{aligned} \begin{aligned} \frac{d V(x, y)}{dt}&=-\mu x^{2}-\beta x^{2}( I^{+}_{2}+y)\leqslant 0. \end{aligned} \end{aligned}$$

Furthermore, when ${\mathcal {R}}_{0}>1$, the endemic equilibrium $E_{2}^{-}$ is G.A.S for (8), which implies that Lemma 4.2 holds.

When $I>ET$, system (3) becomes system (9) and its global stability behavior is investigated below. $\square$

Lemma 4.3

If ${\mathcal {R}}_{1} <1$, the disease-free equilibrium $E_{1}^{+}(\frac{A}{\mu },0)$ of system (9) is G.A.S.

Theorem 4.1

If ${\mathcal {R}}_{1}>1$ and $\mu _{1}+v_{1}-\frac{(\mu _{1}+v_{1}+c)^{2}}{4\mu }-\frac{\mu }{4}-(\frac{\mu _{1}+v_{1}+c}{\beta }) b_{1}c\geqslant 0$ , the endemic equilibrium $E_{2}^{+}(S^{+}_{2},I^{+}_{2})$ of system (9) is G.A.S.

Proof

We first use $x = S-S^{+}_{2},y=I- I^{+}_{2}$ to transfer the equilibrium $E_{2}^{+}(S^{+}_{2}, I^{+}_{2})$ to the origin. Then, system (9) is transformed to the following form:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&=-\mu x-\beta x( I^{+}_{2}+y)-(\mu _{1}+v_{1}+\frac{c}{1+b_{1} I^{+}_{2}})y,&\\ \frac{\mathrm{d}y}{\mathrm{d}t}&=\beta x( I^{+}_{2}+y)+\left( \frac{c}{1+ b_{1} I^{+}_{2}}-\frac{c}{1+ b_{1}( I^{+}_{2}+y)}\right) \\&\quad \times ( I^{+}_{2}+y), \end{aligned} \right. \end{aligned}$$

(20)

or

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&=-\mu x-\beta x( I^{+}_{2}+y)-\beta S^{+}_{2}y,&\\ \frac{\mathrm{d}y}{\mathrm{d}t}&=\beta (xy+xI^{+}_{2}+S^{+}_{2}y)-(\mu _{1}+v_{1})y\\&+\left( \frac{c I^{+}_{2}}{1+ b_{1} I^{+}_{2}}-\frac{c( I^{+}_{2}+y)}{1+ b_{1}( I^{+}_{2}+y)}\right) , \end{aligned} \right. \end{aligned}$$

(21)

where $\beta S^{+}_{2}y-(\mu _{1}+v_{1})y=\frac{cy}{1+ b_{1} I^{+}_{2}}$, $S^{+}_{2}=\frac{\mu _{1}+v_{1}+\frac{c}{1+b_{1} I^{+}_{2}}}{\beta }$.

Consider the following smooth Lyapunov function

$$\begin{aligned} \begin{aligned}&V_{2}(x, y)=V_{2}^{1}(x, y)+V_{2}^{0}(x, y)\\&\quad \frac{(x+y)^{2}}{2}+\frac{x^{2}}{2}\\&\quad +\,\frac{\mu _{1}+v_{1}+\frac{c}{1+b_{1} I^{+}_{2}}}{\beta }\left( y- I^{+}_{2}ln\frac{ I^{+}_{2}+y}{ I^{+}_{2}}\right) , \end{aligned} \end{aligned}$$

where $V_{2}^{0}(x, y){=}\frac{x^{2}}{2}+\frac{\mu _{1}+v_{1}+\frac{c}{1+b_{1} I^{+}_{2}}}{\beta } \left( y{-} I^{+}_{2}ln\frac{ I^{+}_{2}+y}{ I^{+}_{2}}\right) ,V_{2}^{1}(x, y)=\frac{(x+y)^{2}}{2}$.

For brevity, the right-hand side of Eqs. (20) or (21) is simply expressed as v(x, y).

$$\begin{aligned} \begin{aligned}&v_{01}(x,y)=\\&\quad \begin{pmatrix} &{}-\mu x-\beta x( I^{+}_{2}+y)-(\mu _{1}+v_{1}+\frac{c}{1+b_{1} I^{+}_{2}})y,&{} \\ &{}\beta x( I^{+}_{2}+y)+(\frac{c}{1+ b_{1} I^{+}_{2}}-\frac{c}{1+ b_{1}( I^{+}_{2}+y)})( I^{+}_{2}+y)\end{pmatrix} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&v_{02}(x,y)=\\&\quad \begin{pmatrix}&{}-\mu x-\beta x( I^{+}_{2}+y)-\beta S^{+}_{2}y,&{} \\ &{}\beta (xy+xI^{+}_{2}+S^{+}_{2}y)-(\mu _{1}+v_{1})y+(\frac{cI^{+}_{2}}{1+ b_{1} I^{+}_{2}}\\ {} &{}-\frac{c( I^{+}_{2}+y)}{1+ b_{1}( I^{+}_{2}+y)})&{}\\ \end{pmatrix} \end{aligned}. \end{aligned}$$

From this, we can calculate $\nabla V_{2}(x, y)v= \nabla V_{2}^{0}(x, y)v_{01}+\nabla V_{2}^{1}(x, y)v_{02}$ as

$$\begin{aligned} \begin{aligned}&\nabla V_{2}^{0}(x, y)v_{01}=\left( x, \frac{\mu _{1}+v_{1}+\frac{c}{1+b_{1} I^{+}_{2}}}{\beta }\frac{y}{ I^{+}_{2}+y}\right) \\&\quad \times \begin{pmatrix}&{}-\mu x-\beta x( I^{+}_{2}+y)-(\mu _{1}+v_{1}+\frac{c}{1+b_{1} I^{+}_{2}})y,&{} \\ &{}\beta x( I^{+}_{2}+y)+(\frac{c}{1+ b_{1} I^{+}_{2}}-\frac{c}{1+ b_{1}( I^{+}_{2}+y)})( I^{+}_{2}+y)\end{pmatrix} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\nabla V_{2}^{1}(x, y)v_{02}=\left( x+y, x+y\right) \\&\quad \times \begin{pmatrix}&{}-\mu x-\beta x( I^{+}_{2}+y)-\beta S^{+}_{2}y,&{} \\ &{}\beta (xy+xI^{+}_{2}+S^{+}_{2}y)-(\mu _{1}+v_{1})y+(\frac{cI^{+}_{2}}{1+ b_{1} I^{+}_{2}}\\ &{}-\frac{c( I^{+}_{2}+y)}{1+ b_{1}( I^{+}_{2}+y)})&{}\\ \end{pmatrix} \end{aligned}. \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned}&\nabla V_{2}(x, y)v=\nabla V_{2}^{0}(x, y)v_{01}+\nabla V_{2}^{1}(x, y)v_{02}\\&\quad =-\mu x^{2}-\beta x^{2}( I^{+}_{2}+y)+\left( \frac{\mu _{1}+v_{1}+\frac{c}{1+b_{1} I^{+}_{2}}}{\beta }\right) \\&\qquad \times \left( \frac{c}{1+b_{1} I^{+}_{2}}-\frac{c}{1+ b_{1}( I^{+}_{2}+y)}\right) y\\&\qquad -\,\mu x^{2}-(\mu _{1}+v_{1})xy\\&\qquad -\,\left( \frac{c (I^{+}_{2}+y)}{1+b_{1} (I^{+}_{2}+y)}-\frac{c I^{+}_{2}}{1+b_{1} I^{+}_{2}}\right) x\\&\qquad -\,(\mu _{1}+v_{1})y^{2}-\mu xy\\&\qquad -\,\left( \frac{c (I^{+}_{2}+y)}{1+b_{1} (I^{+}_{2}+y)}-\frac{c I^{+}_{2}}{1+b_{1} I^{+}_{2}}\right) y. \end{aligned} \end{aligned}$$

Using the differential mean value theorem, there exist $\tau ,\nu$ such that $K(y+ I^{+}_{2})-K(I^{+}_{2})=K'(\tau )y, f_{0}(y+ I^{+}_{2})-f_{0}(I^{+}_{2})=f_{0}'(\nu )y$, where $K(y+ I^{+}_{2})=\frac{c}{1+ b_{1}( I^{+}_{2}+y)}, f_{0}(y+ I^{+}_{2})=\frac{c( I^{+}_{2}+y)}{1+ b_{1}( I^{+}_{2}+y)}$, $K'(y+ I^{+}_{2})=\frac{-b_{1}c}{(1+ b_{1}( I^{+}_{2}+y))^{2}}, f_{0}'(y+ I^{+}_{2})=\frac{c}{(1+ b_{1}( I^{+}_{2}+y))^{2}}$. Then we have

$$\begin{aligned} \begin{aligned}&\nabla V_{2}(x, y)v<-\mu x^{2}-\beta x^{2}( I^{+}_{2}+y)\\&\qquad -\left( \frac{\mu _{1}+v_{1}+\frac{c}{1+b_{1} I^{+}_{2}}}{\beta }\right) \times K'(\tau )y^{2}\\&\qquad -\,\mu x^{2}-(\mu _{1}+v_{1})xy\\&\qquad -\,(f_{0}'(\nu ))yx-(\mu _{1}+v_{1})y^{2}-\mu xy-(f_{0}'(\nu ))y^{2}\\&\quad <-\mu \left( x+\frac{\left( f_{0}'(\nu )+\mu _{1}+v_{1}\right) y}{2\mu }\right) ^{2}-\mu \left( x+\frac{\mu y}{2\mu }\right) ^{2}\\&\qquad -\,\left[ \mu _{1}+v_{1}-\frac{(\mu _{1}+v_{1}+f_{0}'(\nu ))^{2}}{4\mu }-\frac{\mu }{4}+f_{0}'(\nu )\right. \\&\qquad \left. +\,\left( \frac{\mu _{1}+v_{1}+\frac{c}{1+b_{1}I^{+}_{2}}}{\beta }\right) K'(\tau )\right] y^{2}. \end{aligned} \end{aligned}$$

We know that $-b_{1}c\leqslant K'(\tau )<0, 0< f_{0}'(\nu )\leqslant c$ for all $-I^{+}_{2}\leqslant \tau ,\nu <\infty$. It is easy to obtain that $\mu _{1}+v_{1}-\frac{(\mu _{1}+v_{1}+c)^{2}}{4\mu }-\frac{(\mu )}{4}-\left( \frac{\mu _{1}+v_{1}+c}{\beta }\right) b_{1}c>\mu _{1}+v_{1}-\frac{(\mu _{1}+v_{1}+c)^{2}}{4\mu }-\frac{\mu }{4}-\left( \frac{\mu _{1}+v_{1}+\frac{c}{1+b_{1} I^{+}_{2}}}{\beta }\right) b_{1}c\geqslant 0$ .

Furthermore, when ${\mathcal {R}}_{1}>1$, and $\mu _{1}+v_{1}-\frac{(\mu _{1}+v_{1}+c)^{2}}{4\mu }-\frac{\mu }{4}-\left( \frac{\mu _{1}+v_{1}+c}{\beta }\right) b_{1}c\geqslant 0$ , $E_{2}^{+}$ is G.A.S for (9). The numerical results of Theorems 4.1 are shown in Fig 1. The proof is completed. $\square$

Fig. 1

Trajectory of the plant disease system (9) with the state variables S(t) and I(t); $A=3,v_{1}=0.2$, $\beta =1$, $b_{1}=0.1$, $c=0.3$, $\mu =1$, $\mu _{1}=1.1$

By setting $A=3,v_{1}=0.2$, $\beta =1$, $b_{1}=0.1$, $c=0.3$, $\mu =1$, $\mu _{1}=1.1$, it is straightforward to check that all the conditions of Theorem 4.1 are satisfied.

$$\begin{aligned} {\mathcal {R}}_{1}= & {} \frac{\beta A}{(v_{1}+\mu _{1}+ c)\mu }\\= & {} \frac{3\times 1}{(0.2+1.1+0.3)\times 1}\approx 1.875>1 \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\mu _{1}+v_{1}-\frac{(\mu _{1}{+}v_{1}+c)^{2}}{4\mu }-\frac{\mu }{4}-(\frac{\mu _{1}+v_{1}+c}{\beta }) b_{1}c\\&\quad =(1.1+0.2)-\frac{(1.1+0.2+0.3)^{2}}{4\times 1}-\frac{1}{4}\\&\qquad -\,\frac{(1.1+0.2+0.3)\times 0.1\times 0.3}{1}\geqslant 0.\end{aligned} \end{aligned}$$

Hence, the endemic equilibrium $E_{2}^{+}(S^{+}_{2},I^{+}_{2})$ of system (9) is G.A.S (see Fig. 1).

5 Global qualitative analysis of the plant disease system (3) with non-smooth control strategy

Theorem 5.1

Assume that assumption H1 holds. If ${\mathcal {R}}_{0}<1$, then the disease-free equilibrium $E^{-}_{1}$ is globally asymptotically stable.

Proof

The details of the proof are given in “Appendix A.”

By letting $A=2,v_{1}=0.2$, $\beta =0.2$, $b_{1}=1$, $c=5$, $\mu =1.2$, $\mu _{1}=1.4$, $ET=2.5$, it is easy to check that the conditions of Theorem 5.1 are satisfied. Hence, the disease-free equilibrium $E_{1}^{-}(S^{-}_{1},0)$ of system (3) is G.A.S (see Fig. 2). $\square$

Fig. 2

Trajectory of the plant disease system (9) with the state variables S(t) and I(t); $A=2,v_{1}=0.2$, $\beta =0.2$, $b_{1}=1$, $c=5$, $\mu =1.2$, $\mu _{1}=1.4$

Theorem 5.2

Assume that assumption H1 holds. If ${\mathcal {R}}_{1}<1<{\mathcal {R}}_{0}$ and $h_ {1} \geqslant 0$, then

• (i) the pseudo-equilibrium $E_{p}$ of system (3) is globally asymptotically stable if $0<ET<I_{2}^{-}$, or

• (ii) the endemic equilibrium $E^{-}_{2}$ is globally asymptotically stable if $I_{2}^{-}\leqslant ET$.

Proof

The proof is given in “Appendix A.”

By setting $A=3,v_{1}=0.2$, $\beta =1$, $b_{1}=1$, $c=5$, $\mu =1$, $\mu _{1}=1.1$, when the first control value $ET=0.9$, it is easy to find that the conditions of Theorem 5.2(i) are satisfied. Hence, the pseudo-equilibrium $E_{p}$ of system (3) is G.A.S (see Fig. 3a). When the second control value $ET=3.1$, the conditions of Theorem 5.1(ii) are satisfied. Hence, the endemic equilibrium $E_{2}^{-}(S^{-}_{2},I^{-}_{2})$ of system (3) is G.A.S (see Fig. 3b). $\square$

Fig. 3

Trajectory of the plant disease system (9) with the state variables S(t) and I(t); $A=3,v_{1}=0.2$, $\beta =1$, $b_{1}=1$, $c=5$, $\mu =1$, $\mu _{1}=1.1$. a$ET=0.9$, b$ET=3.1$

Corollary 5.1

Assume that assumption H1 holds. If ${\mathcal {R}}_{1}<1<{\mathcal {R}}_{0}$ and $h_ {1} <0$ and $\varDelta _ {1}<0$, then

• (i) the pseudo-equilibrium $E_{p}$ of system (3) is globally asymptotically stable if $0<ET<I_{2}^{-}$, or

• (ii) the endemic equilibrium $E^{-}_{2}$ is globally asymptotically stable if $I_{2}^{-}\leqslant ET$.

Proof

A similar procedure to that of Theorem 5.1 can be used to prove this Corollary 5.1, and we omit it here for brevity. $\square$

Fig. 4

Trajectory of the plant disease system (9) with the state variables S(t) and I(t); $A=363,v_{1}=0.2$, $\beta =0.5$, $b_{1}=1$, $c=14$, $\mu =12$, $\mu _{1}=13$. a$ET=2.6$, b$ET=4.5$

By setting $A=363,v_{1}=0.2$, $\beta =0.5$, $b_{1}=1$, $c=14$, $\mu =12$, $\mu _{1}=13$., when the third control value $ET=2.6$, it is easy to find that the conditions of Corollary 5.1(i) are satisfied. Hence, the pseudo-equilibrium $E_{p}$ of system (3) is G.A.S (see Fig. 4a). When the fourth control value $ET=4.5$, the conditions of Corollary 5.1(ii) are satisfied. Hence, the endemic equilibrium $E_{2}^{-}(S^{-}_{2},I^{-}_{2})$ of system (3) is G.A.S (see Fig. 4b).

Next, we consider the case of ${\mathcal {R}}_{1}>1$. Under which, the system (9) has a unique endemic equilibrium $E_{2}^{+}(S^{+} _{2}, I^{+}_{2})$. The basic reproduction number is found to be ${\mathcal {R}}_{0}=\frac{\beta A}{(v_{1}+\mu _{1})\mu }>{\mathcal {R}}_{1}=\frac{\beta A}{(v_{1}+\mu _{1}+ c)\mu }$. According to $S^{-}_{2}=\frac{\mu _{1}+v_{1}}{\beta }$ and $S^{+}_{2}=\frac{\mu _{1}+v_{1}+\frac{c}{1+b_{1}I^{+}_{2}}}{\beta }$, we have $S^{-}_{2}<S^{+}_{2}$, and by using the first equations of Eqs. (8) and (9), we can obtain $I^{-}_{2}=\frac{A}{\beta S^{-}_{2}}-\frac{\mu }{\beta }$ and $I^{+}_{2}=\frac{A}{\beta S^{+}_{2}}-\frac{\mu }{\beta }$, then, $I^{+}_{2}<I^{-}_{2}$. Based on Lemmas 4.1–4.3 and Theorem 4.1, we have the following results

Theorem 5.3

Assume that assumption H1 holds. If ${\mathcal {R}}_{1}>1$, then the function

$$\begin{aligned} V(S,I)= \frac{(S-S^{-}_{2})^{2}}{2}+\frac{\mu _{1}+v_{1}}{\beta }\left( I-I^{-}_{2}- I^{-}_{2}ln\frac{I}{ I^{-}_{2}}\right) \end{aligned}$$

is a Lyapunov function on $R_{+}^{2}$ for system (3) and the endemic equilibrium $E^{+}_{2}$ is globally asymptotically stable if $I_{2}^{+}<I_{2}^{-}\leqslant ET$.

Proof

Notice that the conditions of Lemma 2.1 and Lemma 2.2 introduced in Sect. 2 are all satisfied. By performing the analysis, we can have the following results: (1) If $(S,I)\in S_{1}$, then

$$\begin{aligned} \begin{aligned}&<\nabla V(S,I),f_{S_{1}}(S,I)>=\\&\quad -\mu (S-S^{-}_{2})^{2}-\beta (S-S^{-}_{2})^{2}I\leqslant 0. \end{aligned} \end{aligned}$$

(2) If $(S,I)\in \{(S,I)\in \varPi ; \mathrm { if }I= ET\}$, then

$$\begin{aligned} \begin{aligned}&<\nabla V(S,I),f_{S_{1}}(S,I)>=<V'_{S},V'_{I}> <f_{11},f_{12}>\\&\quad =V'_{S}f_{11}+V'_{I}f_{12}=-\mu (S-S^{-}_{2})^{2}-\beta (S-S^{-}_{2})^{2}I\\&\quad \leqslant 0, \end{aligned} \end{aligned}$$

where $f_{11}=A-\mu S-\beta SI, f_{12}=\beta SI-\mu _{1}I-v_{1}I$. Similarly,

$$\begin{aligned} \begin{aligned}&<\nabla V(S,I),f_{S_{2}}(S,I)>=<V'_{S},V'_{I}> <f_{21},f_{22}>\\&\quad =V'_{S}f_{11}+V'_{I}f_{22}=V'_{S}f_{11}+V'_{ I}f_{12}\\&\qquad +\,V'_{I}f_{22}-V'_{I}f_{12}\leqslant V'_{I}f_{22}-V'_{I}f_{12}\\&\quad =-\frac{cI}{1+ b_{1}I}\frac{S^{-}_{2}(I-I_{2}^{-})}{I},\\&\quad \leqslant 0, \end{aligned} \end{aligned}$$

where $I=ET>I_{2}^{-}, f_{11}= f_{21}= A-\mu S-\beta SI, f_{22}=\beta SI-\mu _{1}I-v_{1}I-\frac{cI}{1+b_{1}I}$. Then, we have $<\nabla V(S,I), f_{S_{2}}(S, I)> <0$. Hence,

$$\begin{aligned} \sup \limits _{0 \le \alpha _{1}\le 1}{<}\nabla V(S,I),\alpha _{1} f_{S_{1}}(S,I)+(1-\alpha _{1})f_{S_{2}}(S,I){>=}0. \end{aligned}$$

(3) If $(S,I)\in S_{2}$, due to $S^{-}_{2}=\frac{\mu _{1}+v_{1}}{\beta },S^{-}_{2}=\frac{\mu _{1}+v_{1}+\frac{c}{1+b_{1} I^{+}_{2}}}{\beta }$, $S^{-}_{2}<S^{+}_{2}$, then

$$\begin{aligned} \begin{aligned}&<\nabla V(S,I),f_{S_{2}}(S,I)>=<V'_{S},V'_{I}> <f_{21},f_{22}>\\&\quad =V'_{S}f_{11}+V'_{ I}f_{22}\\&\quad =V'_{S}f_{1}+V'_{I}f_{12}+V'_{I}f_{22}-V'_{I}f_{12}\\&\quad \leqslant V'_{I}f_{22}-V'_{I}f_{12}\\&\quad =-\frac{cI}{1+ b_{1}I}\frac{S^{-}_{2}(I-I_{2}^{-})}{I}. \end{aligned} \end{aligned}$$

If $I> ET$, we can obtain

$$\begin{aligned}<\nabla V(S,I),f_{S_{2}}(S,I)> <0. \end{aligned}$$

Hence, according to Lemmas 2.1–2.2, we know that the invariant subset is $\omega _{1}(R_{+}^{2})=\{(S,I)|V(S,I)\leqslant V(\frac{\mu _{1}+v_{1}}{\beta },ET)\} \subset S_{1}\cup (\frac{\mu _{1}+v_{1}}{\beta },ET)$, which is a subset of $\varOmega _{1}$. By considering the sliding mode behavior and the neutral stability of Lotka–Volterra cycles (see [4]) in $S_{1}$, $\omega _{1}(R_{+}^{2})$ can be shown as $\nabla V(S,I)$, which indicates that $\omega _{1}(R_{+}^{2})$ is closed. Therefore, $\omega _{1}(R_{+}^{2})$ is the global attractor for system (3) and the proof is completed. $\square$

By letting $A=3,v_{1}=0.2$, $\beta =1$, $b_{1}=0.1$, $c=0.3$, $\mu =1$, $\mu _{1}=1.1$, $ET=1.3076$, it is straightforward to check that all the conditions of Theorem 5.3 are satisfied. Hence, the endemic equilibrium $E^{+}_{2}$ is globally asymptotically stable if $I_{2}^{+}<I_{2}^{-}<ET$. The numerical results of Theorem 5.3 are shown in Fig. 5.

Fig. 5

Trajectory of the plant disease system (3) with the state variables S(t) and I(t); $A=3,v_{1}=0.2$, $\beta =1$, $b_{1}=0.1$, $c=0.3$, $\mu =1$, $\mu _{1}=1.1$, $ET=1.3076$

Lemma 5.1

If ${\mathcal {R}}_{1}>1$, $0\leqslant b_{1}<\frac{\beta }{c}$, then there is no closed orbit in regions $S_{i}(i=1,2)$.

Proof

By defining the Dulac function ${\mathcal {D}}_{1}=\frac{1}{I}$ for subsystem $S_{1}$, we have

$$\begin{aligned} \begin{aligned}&f_{11}(S,I){\mathcal {D}}_{1}=\frac{A}{I}- \frac{\mu S}{I}-\frac{\beta SI}{I};\\&f_{12}(S,I){\mathcal {D}}_{1}=\beta S-v_{1}-\mu _{1};\\&\quad \frac{\partial (f_{11}{\mathcal {D}}_{1})}{\partial S}+\frac{\partial (f_{12}{\mathcal {D}}_{1})}{\partial I}=\frac{\frac{A}{I}- \frac{\mu S}{I}-\frac{\beta SI}{I}}{\partial S} \\&\quad +\,\frac{\partial \beta S-v_{1}-\mu _{1}}{\partial I}=- \frac{\mu }{I}-\beta , \end{aligned} \end{aligned}$$

then, we can obtain $\frac{\partial (f_{11}D_{1})}{\partial S}+\frac{\partial (f_{12}D_{1})}{\partial I}<0$.

Similarly, for subsystem $S_{2}$, we have

$$\begin{aligned}&f_{21}(S,I){\mathcal {D}}_{1}=\frac{A}{I}- \frac{\mu S}{I}-\frac{\beta SI}{I};\\&f_{22}(S,I){\mathcal {D}}_{1}=\beta S-v_{1}-\mu _{1}-\frac{c}{1+ b_{1}I};\\&\frac{\partial (f_{21}{\mathcal {D}}_{1})}{\partial S}+\frac{\partial (f_{22}{\mathcal {D}}_{1})}{\partial I}=\frac{\partial (\frac{A}{I}- \frac{\mu S}{I}-\frac{\beta SI}{I})}{\partial S}\\&\qquad +\,\frac{\partial (\beta S-v_{1}-\mu _{1}-\frac{c}{1+ b_{1}I})}{\partial I} \\&\quad =- \frac{\mu }{I}-\beta +\frac{cb_{1}}{(1+b_{1}I)^{2}}. \end{aligned}$$

Again from Propositions 3.1 and 3.2, and $0\leqslant b_{1}<\frac{\beta }{c}$, we can obtain that

$$\begin{aligned} \begin{aligned}&\frac{\partial (f_{21}{\mathcal {D}}_{1})}{\partial S}+\frac{\partial (f_{22}{\mathcal {D}}_{1})}{\partial I} \\&\quad =- \frac{\mu }{I}{-}\beta {+}\frac{cb_{1}}{(1+b_{1}I)^{2}}\leqslant - \frac{\mu }{I}{-}\beta {+}\frac{\beta }{(1{+}b_{1}I)^{2}}\\&\quad \leqslant \frac{1}{I(1{+}b_{1}I)^{2}}(-\mu (1{+}b_{1}I)^{2}{-}\beta I (1{+}b_{1}I)^{2}-1){<}0 . \end{aligned} \end{aligned}$$

$\frac{\partial (f_{21}{\mathcal {D}}_{1})}{\partial S}+\frac{\partial (f_{22}{\mathcal {D}}_{1})}{\partial I}<0$. Hence, there is no closed orbit in regions $S_{i}$ (i=1,2) if ${\mathcal {R}}_{1}>1$ and $0\leqslant b_{1}<\frac{\beta }{c}$. The proof is completed. $\square$

Lemma 5.2

Assume that assumption H1 and the condition 1) of Proposition 3.4 hold. If $0\leqslant b_{1}<\frac{\beta }{c}$, then there is no closed orbit for system (3) containing part of the sliding domain $\varPi _{s}$.

Proof

From the sufficient condition on the existence of the pseudo-equilibrium of Theorem 3.1, we know that the pseudo-equilibrium of Eq. (14) is stable in the sliding domain $S_{2}^{-}\leqslant S_{p}\leqslant S_{2}^{+}$ or $I_{2}^{+}\leqslant ET\leqslant I_{2}^{-}$. It is easy to know that there is no closed orbit for system (3) containing part of $I_{2}^{+}<ET<I_{2}^{-}$. Next, we will prove that system (3) has no closed orbit containing part of the sliding domain $\varPi _{s}$ if $ET> I_{2}^{-}$ or $ET <I_{2}^{+}$.

Without loss of generality, if $ET > I_{2}^{-}$, by using the sliding mode dynamics (14), it is easy to show that $F'_{S}=-\mu -\beta ET<0$. Then, the solution moves from the right side to the left side in domain $\varPi _{s}$. Moreover, the solution of Eq.(3) starting from the point $E_{2}^{T}$ cannot touch the domain $\varPi _{s}$ again.

By using the condition 1) of Proposition 3.4, it is easy to know that the endemic equilibrium $E_{2}^{-}$ of Eq. (9) is a stable node or focus. Then the trajectory of system (3) intersects with the horizontal isocline $l_{1}$, where $l_{1}$ is defined at $\{(S,I)|S=\frac{\mu _{1}+v_{1}}{\beta },I<ET\}$, at the first point $N_{1}$, then the second point $N_{2}$. Hence we conclude that point $N_{2}$ locates on between the tangent point $E_{2}^{T}$ and the endemic equilibrium $E_{2}^{-}$. If not, the solution of system (3) may either coincide with the tangent point $E_{2}^{T}$ or intersect with the domain $\varPi _{s}$ at a certain point to the right side of tangent point $E_{2}^{T}$. If the previous hypothesis is true, then the trajectory exists a closed orbit which is tangent to the domain $\varPi _{s}$. The closed orbit is denoted by $\varUpsilon$. Then any solution of system (3) starting from a point out of the closed orbit $\varUpsilon$ cannot cross the cycle $\varUpsilon$, and certainly cannot tend to the endemic equilibrium $E_{2}^{-}$, which contradicts to the stability of the endemic equilibrium $E_{2}^{-}$. If the latter assumption is true, it indicates that there exists an unstable node or focus $E_{2}^{-}$, which also contradicts to the statement that $E_{2}^{-}$ is a stable equilibrium. Hence the orbit of system (3) starting from the tangent point $E_{2}^{T}$ cannot entre the domain $\varPi _{s}$, then the solution approaches the endemic equilibrium $E_{2}^{-}$.

Secondly, if $ET <I_{2}^{+}$, the proof process is similar to that for $ET > I_{2}^{-}$. Therefore, there is no closed orbit of system (3) containing part of the sliding domain $\varPi _{s}$. Hence, if ${\mathcal {R}}_{0}>1$, and under the condition 1) of Proposition 3.4, there is no closed orbit of system (3) containing part of the sliding domain $\varPi _{s}$. The proof is completed. $\square$

Fig. 6

Limit cycle $\varGamma$

Theorem 5.4

Assume that assumption H1 and the condition 1) of Proposition 3.4 hold. When $0\leqslant b_{1}<\frac{\beta }{c}$, the system (3) has a globally asymptotically stable pseudo-equilibrium $E_{p}$ if $I_{2}^{+}<ET<I_{2}^{-}$.

Proof

First we can prove that there is no closed trajectory in regions $S_{i}(i=1,2)$ and there exists no closed orbit for system (3) containing part of the sliding domain $\varPi _{s}$. If so, it is a contradiction to Lemmas 5.1 and 5.2.

Then we need to prove that there is no closed trajectory which contains the regions $S_{i}(i=1,2)$ and the sliding domain $\varPi _{s}$. If not, we assume that there is a closed orbit $\varGamma$ of system (3), which passes through the discontinuous manifold $\varPi$ and encloses the sliding domain $\varPi _{s}$. Additionally, the pseudo-equilibrium $E_{p}$ locates on $\varPi _{s}$, and the closed orbit has period T (see Fig.6). P and Q are the intersection points of $\varGamma$ and $\varPi$ (i.e., the line $I= ET$). Meanwhile, $P_{1} = P + a_{1}(\theta )$ and $Q_{1}=Q-a_{2}(\theta )$ represent the intersection points of $\varGamma$ and the line $I = ET-\theta$. Similarly, $P_{2} = P + b_{1}(\theta )$ and $Q_{2}=Q-b_{2}(\theta )$ are the intersection points of $\varGamma$ and the straight line $I = ET + \theta$, where $\theta > 0$ is sufficiently small. Moreover, $a_{1}(\theta ), a_{2}(\theta ), b_{1}(\theta )$ and $b_{2}(\theta )$ are continuous with respect to $\theta$ and $\lim \limits _{\theta \rightarrow 0}a_{i}(\theta )=\lim \limits _{\theta \rightarrow 0} b_{i}(\theta )=0$ for $i = 1, 2$.

The $\varGamma _{1}$ and segment $P_{1}Q_{1}$ locate in the region $S_{1}$. Similarly, the $\varGamma _{2}$ and segment $P_{2}Q_{2}$ locate in the region $S_{2}$ . Furthermore, the dynamics of the disease system with non-smooth control strategy in region $S_{1}$ are represented by $f_{11}$ and $f_{12}$. Let $\partial S_{1}$ denote the boundary of $S_{1}$. By using Green’s Theorem, we have

$$\begin{aligned} \begin{aligned}&\int \int _{S_{1}}\frac{\partial ({\mathcal {D}}_{1}f_{11})}{\partial S}+\frac{\partial ({\mathcal {D}}_{1}f_{12})}{\partial I}\mathrm{d}\sigma \\&\quad =\int \int _{S_{1}}\frac{\partial ({\mathcal {D}}_{1}f_{11})}{\partial S}\mathrm{d}\sigma +\int \int _{S_{1}}\frac{\partial (\mathcal {}D_{1}f_{12})}{\partial I}\mathrm{d}\sigma \\&\quad =\oint _{\partial S_{1}}({\mathcal {D}}_{1}f_{11})\mathrm{d}I -\oint _{\partial S_{1}}({\mathcal {D}}_{1}f_{12})\mathrm{d}S\\&\quad =\int _{\varGamma 1}{\mathcal {D}}_{1}f_{11}\mathrm{d}I +\int _{\overrightarrow{Q_{1}P_{1}}}{\mathcal {D}}_{1}f_{11}\mathrm{d}I\\&\qquad -\left( \int _{\varGamma 1}D_{1}f_{12}\mathrm{d}S+\int _{\overrightarrow{Q_{1}P_{1}}}{\mathcal {D}}_{1}f_{12}\mathrm{d}S\right) \\&\quad =\int _{\varGamma 1}({\mathcal {D}}_{1}f_{11} \cdot f_{12}- {\mathcal {D}}_{1}f_{12} \cdot f_{11})\mathrm{d}t\\&\qquad -\int _{\overrightarrow{Q _{1}P_{1}}}{\mathcal {D}}_{1}f_{12}\mathrm{d}S\\&\quad =-\int _{\overrightarrow{Q_{1}P_{1}}}{\mathcal {D}}_{1}f_{12}\mathrm{d}S, \end{aligned} \end{aligned}$$

(22)

where $\mathrm{d}S=f_{11}\mathrm{d}t, \mathrm{d}I=f_{12}\mathrm{d}t$, and there is no change of ET in the segment $Q_{1}P_{1}$, then we can obtain

$$\begin{aligned} \int _{\overrightarrow{Q_{1}P_{1}}} {\mathcal {D}}_{1}f_{11}\mathrm{d}I=\int _{ET-\theta }^{ET-\theta }{\mathcal {D}}_{1}f_{11}\mathrm{d}I= 0. \end{aligned}$$

Similarly, the dynamics in $S_{2}$ is represented by $f_{21}$ and $f_{22}$. By Green’s Theorem, we can find a $D_{1}$ function satisfying

$$\begin{aligned} \begin{aligned}&\int \int _{S_{2}}\frac{\partial ({\mathcal {D}}_{1}f_{21})}{\partial S}+\frac{\partial ({\mathcal {D}}_{1}f_{22})}{\partial I}\mathrm{d}\sigma \\&\quad =-\int _{\overrightarrow{P_{2}Q_{2}}}{\mathcal {D}}_{1}f_{22}\mathrm{d}S. \end{aligned} \end{aligned}$$

(23)

Suppose that $S_{20}\subset S_{2}$. Let

$$\begin{aligned} \begin{aligned} \xi&=\int \int _{S_{20}} \frac{\partial ({\mathcal {D}}_{1}f_{21})}{\partial S}+\frac{\partial ({\mathcal {D}}_{1}f_{22})}{\partial I} \mathrm{d}\sigma \\&=\oint _{\partial S_{20}}({\mathcal {D}}_{1}f_{21}\mathrm{d}I-{\mathcal {D}}_{1}f_{22}\mathrm{d}S)<0. \end{aligned} \end{aligned}$$

(24)

From Lemma 5.1, and based on Eq. (24), we have

$$\begin{aligned} \begin{aligned} 0> \xi > -\left( \int _{\overrightarrow{Q_{1}P_{1}}}{\mathcal {D}}_{1}f_{12}\mathrm{d}S +\int _{\overrightarrow{P_{2}Q_{2}}}{\mathcal {D}}_{1}f_{22}\mathrm{d}S\right) . \end{aligned}\nonumber \\ \end{aligned}$$

(25)

Then we take the limit $\theta \rightarrow 0$ of the sum of (22) and (23) as

$$\begin{aligned} \begin{aligned}&\lim _{\theta \rightarrow 0}\left( -\int _{\overrightarrow{Q_{1}P_{1}}}{\mathcal {D}}_{1}f_{12}\mathrm{d}S-\int _{\overrightarrow{P_{2}Q_{2}}}{\mathcal {D}}_{1}f_{22}\mathrm{d}S\right) \\&\quad =\lim _{\theta \rightarrow 0}\left[ \int _{Q-a_{2}(\theta )}^{P+a_{1}(\theta )}(\beta S -(\mu _{1} + v_{1}))\mathrm{d}S \right. \\&\left. \qquad {-}\!\,\int _{Q-b_{2}(\theta )}^{P+b_{1}(\theta )} \left( \beta S-(\mu _{1} {+} v_{1})){-}\frac{c}{1{+}b_{1}ET}\right) \mathrm{d}S\right] \\&\quad =\frac{b_{1}}{1+b_{1}ET}(Q- P) > 0. \end{aligned}\nonumber \\ \end{aligned}$$

(26)

From Fig. 6, we can easily see that $Q>P$. Then Eq. (26) holds, which contradicts to (25). Thus there is no closed orbit containing the sliding domain $\varTheta$ and the sliding equilibrium $E_{p}$. Therefore, $E_{p} \in \varTheta$ is globally asymptotically stable if $I_{2}^{+}<ET<I_{2}^{-}$ . The numerical results of Theorems 5.4 are shown in Fig. 7. The proof is completed. $\square$

Fig. 7

Trajectory of the plant disease system (3) with the state variables S(t) and I(t); $A=3,v_{1}=0.2$, $\beta =1$, $b_{1}=0.1$, $c=0.3$, $\mu =1$, $\mu _{1}=1.1$, $ET=1.1$

Fig. 8

Trajectory of the plant disease system (3) with the state variables S(t) and I(t); $A=3, v_{1}=0.2$, $\beta =1$, $b_{1}=0.1$, $c=0.3$, $\mu =1$, $\mu _{1}=1.1$, $ET=0.9046$

By setting $A=3$, $v_{1}=0.2$, $\beta =1$, $b_{1}=0.1$, $c=0.3$, $\mu =1$, $\mu _{1}=1.1$, and $ET=1.1$, it is easy to calculate the following parameters involved in the conditions of Theorem 5.4.

$$\begin{aligned}&{\mathcal {R}}_{1}=\frac{\beta A}{(v_{1}+\mu _{1}+ c)\mu }\\&\quad =\frac{3\times 1}{(1.1+0.2+0.3)\times 1}\approx 1.875>1. \end{aligned}$$

$I_{2} ^{+} = \frac{-h_{1}+\sqrt{\varDelta _{1}}}{2}=0.9046$, then $ET=1.1>I_{2} ^{+}=0.9046$. $I_{2} ^{-} =\frac{A\beta -\mu (\mu _{1}+v_{1})}{\beta (\mu _{1}+v_{1})}=1.3076$, then $ET=1.1<I_{2} ^{-}=1.3076$.

$$\begin{aligned} \begin{aligned} Q(I_{2}^{+})&=\mu +\beta I _{2}^{+}-\frac{cb_{1}I ^{+}_{2}}{(1+b _{1}I _{2}^{+})^{2}}\\ {}&=1+0.9046-\frac{0.3\times 0.1\times 0.9046}{(1+0.1\times 0.9046)^{2}}>0,\end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&0\leqslant b_{1}<\frac{\beta }{c}\Longleftrightarrow 0< 0.1<\frac{10}{3}.\end{aligned} \end{aligned}$$

Accordingly, the conditions of Theorem 5.4 are satisfied and thus the pseudo-equilibrium $E_{p}$ of system (3) is G.A.S (see Fig. 7).

Table 1 Main results of system (3)

Theorem 5.5

Assume that assumption H1 and the condition 1) of Proposition 3.4 hold. When $0\leqslant b_{1}<\frac{\beta }{c}$, the equilibrium $E_{2}^{+}(S^{+}_{2},I^{+}_{2})$ of system (3) is globally asymptotically stable if $ET\leqslant I^{+}_{2}<I_{2}^{-}$.

Proof

A similar procedure to that of Theorem 5.4 can be used to prove this theorem, and we omit it here for brevity. The results of Theorems 5.5 are shown in Fig. 8. $\square$

Now, we summarize the main results in Table 1.

Next we analyze the sliding bifurcation of system (3). According to the definition in Sect. 2, the tangent points $E_{i}^{T}(E_{i}^{B})$ on sliding segment $\varPi _{s}$ of the system coincide with the boundary equilibriums.

6 Sliding bifurcations of the disease system

This section discusses the regular/virtular equilibriums of boundary curves and the coexistence of virtual equilibriums for subsystems $S_{1}$ and $S_{2}$.

6.1 Bifurcations of regular/virtular equilibrium

System (3) can exhibit multiple equilibriums and sliding modes, which will be explored in this subsection. At first, $\mu$ and ET are chosen as bifurcation parameters to construct the bifurcation diagram, and the other parameters are same as those in Fig. 9a. Based on the solutions of equilibriums found in Sect. 3, we define the following lines to divide the first quadrant of the relevant parameter plane.

$$\begin{aligned}&L_{1}=\left\{ (\mu ,ET)\mid ET=I^{-}_{1}=0\right\} , \\&L_{2}=\left\{ (\mu ,ET)\mid ET=I^{-}_{2}=\frac{A\beta -\mu (\mu _{1}+v_{1})}{\beta (\mu _{1}+v_{1})}\right\} ,\\&L_{3}=\left\{ (\mu ,ET)\mid ET=I^{+}_{3}=\frac{(-h _{1} - \sqrt{\varDelta _{1}})}{2}\right\} ,\\&L_{4}=\left\{ (\mu ,ET)\mid ET=I^{+}_{2}=\frac{(-h _{1} +\sqrt{\varDelta _{1}})}{2}\right\} .\\&L_{5}=\left\{ (v_{1},ET)\mid ET=0\right\} ,\\&L_{6}=\left\{ (v_{1},ET)\mid ET=\frac{A\beta -\mu (\mu _{1}+v_{1})}{\beta (\mu _{1}+v_{1})}\right\} ,\\&L_{7}=\left\{ (v_{1},ET)\mid ET=\frac{(-h _{1} - \sqrt{\varDelta _{1}})}{2}\right\} ,\\&L_{8}=\left\{ (v_{1},ET)\mid ET=\frac{(-h _{1} + \sqrt{\varDelta _{1}})}{2}\right\} ,\\&L_{9}=\left\{ (A,ET)\mid ET=0\right\} ,\\&L_{10}=\left\{ (A,ET)\mid ET=\frac{A\beta -\mu (\mu _{1}+v_{1})}{\beta (\mu _{1}+v_{1})}\right\} ,\\&L_{11}=\left\{ (A,ET)\mid ET=\frac{(-h _{1} - \sqrt{\varDelta _{1}})}{2}\right\} ,\\&L_{12}=\left\{ (A,ET)\mid ET=\frac{(-h _{1}+ \sqrt{\varDelta _{1}})}{2}\right\} . \end{aligned}$$

The two solid lines $L_{2}$ and $L_{4}$ divide the $\mu -ET$ space into three parts. When $I_{2}^{-}>ET>I_{2}^{+}$ (i.e., the region $\varGamma ^{3}_{1}$, in Fig. 9a), the equilibria $E_{2}^{-}$ and $E_{2}^{+}$ are virtual (denoted by $E_{2v}^{-}$ and $E_{2v}^{+}$, respectively), and $E_{p}$ exists. When $ET\leqslant I_{2}^{+}$ (i.e., region $\varGamma ^{2}_{1}$, see Fig. 9a), the equilibrium $E_{2}^{+}$ is regular, while $E_{2}^{-}$ is virtual (denoted by $E_{2r}^{+}$ and $E_{2v}^{-}$, respectively), and $E_{p}$ does not exist. When $ET\geqslant I_{2}^{-}$(i.e., the region $\varGamma ^{1}_{1}$, see Fig. 9a), the equilibrium $E_{2}^{-}$ is regular, while $E_{2}^{+}$ is virtual (denoted by $E_{2r}^{-}$ and $E_{2v}^{+}$, respectively), and $E_{p}$ does not exist.

The equilibria of system (3) include those of $S_{1}$ or $S_{2}$, which may be regular or virtual equilibrium.

Fig. 9

Bifurcation set of system (3) with respect to $\mu$ and ET, $v_{1}$ and ET; a$v_{1}=0.2$, $\beta =1$, $\mu _{1}=1.1$, $b_{1}=0.1$, $c=0.3$, $A=30$, b$\mu =1$, $\mu _{1}=1.1$, $\beta =1$, $b_{1}=0.1$, $c=0.3$, $A=30$

From inequality (11), we can see that, with an increase of the threshold level ET , the sliding segment $\varPi _{s}$ reduces and may intersect with the boundary of the attraction region $\varPi$. As a result, a part of $\varPi$ may be either in the attraction region or out of the attraction region.

In practice, the main aim of infectious control is to make the total density of infectious or the other harmful plants to stabilize at a desired level ET or to prevent the possibility of multiple infectious outbreaks by applying appropriate control strategies. To achieve this goal, we can choose that the pseudo-equilibrium point is globally stable, and all the other equilibria of subsystems $S_{1}$ and $S_{2}$ are virtual. Therefore, we select a set of parameters for the only coexistence of pseudo-equilibrium as shown Figs. 12b, 13b for controlling the infectious plants. Some bifurcations occur in Figs. 10, 11. We change parameters $v_{1}$ and ET and fix the other parameters to construct the bifurcation diagram, as shown in Fig. 9b. The lines in Fig. 9 are defined as $L_{5}-L_{8}$. We also introduce the following lines to divide the first quadrant in the parameter plane.

$$\begin{aligned} \begin{aligned}&L_{13}=\left\{ (c,ET)\mid ET=0\right\} ,\\&L_{14}=\left\{ (c,ET)\mid ET=\frac{A\beta -\mu (\mu _{1}+v_{1})}{\beta (\mu _{1}+v_{1})}\right\} ,\\&L_{15}=\left\{ (c,ET)\mid ET=\frac{(-h _{1}- \sqrt{\varDelta _{1}})}{2}\right\} ,\\&L_{16}=\left\{ (c,ET)\mid ET=\frac{(-h _{1}+ \sqrt{\varDelta _{1}})}{2}\right\} ,\\&L_{17}=\left\{ (\beta ,ET)\mid ET=0\right\} ,\\&L_{18}=\left\{ (\beta ,ET)\mid ET=\frac{A\beta -\mu (\mu _{1}+v_{1})}{\beta (\mu _{1}+v_{1})}\right\} ,\\&L_{19}=\left\{ (\beta ,ET)\mid ET=\frac{(-h _{1} + \sqrt{\varDelta _{1}})}{2}\right\} ,\\&L_{20}=\left\{ (\beta ,ET)\mid ET=\frac{(-h_{1}-\sqrt{\varDelta _{1}})}{2}\right\} ,\\&L_{21}=\left\{ (b_{1},ET)\mid ET=0\right\} , \\&L_{22}=\left\{ (b_{1},ET)\mid ET=\frac{A\beta -\mu (\mu _{1}+v_{1})}{\beta (\mu _{1}+v_{1})}\right\} ,\\&L_{23}=\left\{ (b_{1}, ET)\mid ET=\frac{(-h_{1} - \sqrt{\varDelta _{1}})}{2}\right\} , \\&L_{24}=\left\{ (b_{1},ET)\mid ET=\frac{(-h _{1} + \sqrt{\varDelta _{1}})}{2}\right\} . \end{aligned} \end{aligned}$$

Fig. 10

Bifurcation of system (3) with respect to A and ET, c and ET; a$v_{1}=0.2$, $\beta =1$, $b_{1}=0.1$, $c=0.3$, $\mu =1$, $\mu _{1}=1.1$, b$v_{1}=0.2$, $\mu =1$, $\beta =1$, $b_{1}=0.1$, $\mu _{1}=1.1$, $A=30$

Parameters A, c and ET are changed to build the bifurcation diagrams shown in Fig. 10. The lines in Fig. 10 are determined by $L_{9}-L_{16}$. We let parameters $\beta$ and ET, $b_{1}$ and ET change to construct Fig. 11, where the lines are governed by $L_{17}-L_{24}$. If one or more parameters changes, boundary focus bifurcation and boundary node bifurcation can happen, which will be discussed in Sect. 6.2.

Fig. 11

Bifurcation of system (3) with respect to $\beta$ and ET, $b_{1}$ and ET; a$v_{1}=0.2$, $\mu _{1}=1.1$, $b_{1}=0.1$,$\mu =1$, $c=0.3$, $A=30$, b$v_{1}=0.1$, $\beta =1$, $\mu _{1}=1.1$,$\mu =1$, $c=0.3$, $A=30$

6.2 Boundary equilibrium (B-E) bifurcation

This subsection addresses the boundary node bifurcation, and boundary focus bifurcation of system (3) with non-smooth control strategy. The boundary equilibrium bifurcation is characterized by the collision of regular equilibrium, pseudo-equilibrium, and tangent point at the discontinuity surface when a bifurcation parameter reaches a certain critical value.

Remark 1

[24, 25] The B-E bifurcation occurs at $E_{i}^{B}$ if $f_{s_{ i}}(E_{i}^{B})$ is invertible (the eigenvalues of det($f_{s_{ i}}(E_{B})$ have nonzero real parts and $\langle H'(E_{i}^{B}),f_{s_{i}}(E_{i}^{B})\rangle \ne 0, i=1, 2$). These bifurcations have been classified as boundary node and boundary focus in [19].

Theorem 6.1

System (3) exists B-E bifurcation if the boundary equilibrium is visible.

Proof

System (3) may have boundary equilibrium $E_{1}^{B}(S^{*}_{B1}, I^{*}_{B1})$ and $E_{2}^{B}(S^{*}_{B2},I^{*}_{B2})$ if $I^{*}_{B1}$ and $I^{*}_{B2}$ exist. For the boundary equilibria $E_{1}^{B}$ and $E_{2}^{B}$, by simple calculations we have

$$\begin{aligned} \begin{aligned}&f_{s_{1}}H(E_{1}^{B})\\&\quad =(\beta S^{*}_{B1}-\mu _{1}-v_{1})I^{*}_{B1}\\&\quad =\left( \beta \frac{(\mu _{1} +v_{1})(1+ b_{1}I^{*}_{B1})+c}{(1+ b_{1}I^{*}_{B1})\beta }-\mu _{1}-v_{1}\right) I^{*}_{B1}\\&\quad =\left( \frac{c}{(1+ b_{1}I_{1}^{B})}\right) I^{*}_{B1}>0 \end{aligned} \end{aligned}$$

and

$$\begin{aligned}&f_{s_{2}}H(E_{2}^{B})\\&\quad =(\beta S^{*}_{B2}-\mu _{1}-v_{1}-\frac{c}{(1+ b_{1}I^{*}_{B2})})I^{*}_{B2}\\&\quad =\left( \beta \frac{\mu _{1} +v_{1}}{\beta }-\mu _{1}-v_{1}-\frac{c}{(1+ b_{1}I^{*}_{B2})}\right) I^{*}_{B2}\\&\quad =-\frac{c I^{*}_{B2}}{(1+ b_{1}I^{*}_{B2})}<0 \end{aligned}$$

and from the regular equilibrium of Eqs. (8) and (9), we know that det($f_{s_{_{ i}}} (E^{B}_{ i})$) has complex eigenvalues with nonzero real part $-Q(I^{*}_{Bi})/2,i=1,2,$ if $E_{i}^{B}$ is a saddle (a node, or a focus). According to Remark 1, a B-E bifurcation occurs at $E_{i}^{B},i= 1,2$. The proof is completed. $\square$

Fig. 12

Boundary node bifurcation for the infectious system under non-smooth control strategy (3) for the parameters $v_{1}=0.1$, $\beta =2$, $\mu =2$, $\mu _{1}=2.2$, $c=2.2$, $A=4$, $b_{1}=0.5$, a$ET=0.081$, b$ET=0.312$, and c$ET=0.713$

Fig. 13

Boundary focus bifurcation of the infectious system with non-smooth control strategy (3) for the parameters $v_{1}=0.2$, $\beta =1$, $\mu =0.3$, $\mu _{1}=0.8$, $c=1.8$, $A=1.8$, $b_{1}=1.5$, a$ET=0.081$, b$ET=0.553$, and c$ET=1.021$

Boundary node bifurcation (BNB) As shown in Fig. 12, the stable node point $E_{2}^{+}$ and a tangent point $E_{1}^{T}$ collide together, when the parameter is changed from the critical value $ET=0.081$ to $ET=0.713$. The BNB occurs at $E_{1}^{B}$, where the critical value $ET=0.081$. A stable node $E_{2}^{+}$ and a tangent point $E_{1}^{T}$ coexist, as shown in Fig. 12a, when $ET<I_{2}^{+}$. They collide at $ET=0.312$ (see Fig. 12b) and are replaced by a P-E point $E _{P}$ when $I_{2}^{+}<ET<I_{2}^{-}$, a tangent point $E_{1}^{T}$ and a virtual point $E _{2v}^{+}$ when $I_{2}^{-}\leqslant ET$ (see Fig. 12c with $ET=0.713$ for more details). From Fig. 12b, it is easy to notice that all the trajectories of the two regions of system (3) and the nonlinear threshold boundary can asymptotically converge to the pseudo-equilibrium point $E _{p}$ when appropriate control parameters are chosen.

Boundary focus bifurcation (BFB) If the P-E point, tangent point, and R-E point collide as the parameter ET reaches a threshold value, BFB may occur. For example, when parameter ET reaches the first economic threshold value $ET=1.021$, the R-E point $E_{2}^{-}$ and tangent point $E_{1}^{T}$ can collide (see Fig. 13c). The boundary equilibrium $E_{1}^{B}$ is an attractor as shown in Fig. 13b when $I_{2}^{-}\geqslant ET \geqslant I_{2}^{+}$. A stable focus $E_{2}^{+}$ and a tangent point $E_{1}^{T}$ coexist for $I_{2}^{+}\geqslant ET$, see Fig. 13a with $ET=0.081$. They collide at $ET=0.553$ to turn into a P-E point and a tangent point $E_{1}^{T}$ for $ET\geqslant I_{2}^{-}$(see Fig. 13C), with $ET=1.021$. Through this bifurcation, a stable focus becomes a stable P-E point. Another BFB occurs when parameter ET reaches the second critical value $ET=I_{2}^{-}$. A stable focus $E_{1}^{-}$ and a tangent point $E_{2}^{T}$ coexist for $ET<I_{2}^{+}$. They collide at $ET=I_{2}^{-}$ to evolve into a P-E point $E_{p}$ and a tangent point $E_{2}^{T}$ for $ET>I_{2}^{-}$.

In addition, this paper only discusses sliding bifurcation (boundary node and boundary focus bifurcations). Numerical simulations have also found the boundary-saddle bifurcation (see Ref.[26]) which is not given in this paper as it is hard to prove the existence of boundary-saddle bifurcation theoretically.

System (9) was found to have standard periodic trajectory lying entirely in area $S_{2}$(Ref. [11]). System (3) with non-smooth control strategy under investigation may have a new periodic trajectory in sliding area $\varPi _{s}$ (i.e., sliding periodic trajectory) which has isolated points only in common with $\varPi _{s}$ (i.e., crossing periodic trajectory). A crossing periodic trajectory may pass through the boundary of the sliding area $\varPi _{s}$. Accordingly, the orbits associated with periodic solutions will be a crossing loop.

Fig. 14

Grazing bifurcation of the infectious system with non-smooth control strategy (3) for the parameters $v_{1}=0.2$, $\beta =2$, $\mu =0.15$, $\mu _{1}=0.3$, $c=5$, $A=2$, $b_{1}=1$, a$ET=0.082$, b$ET=0.213$, and c$ET=0.6101$

Grazing bifurcation(GB) As discussed in refs. [25, 33], a standard periodic trajectory could collide, and this type of bifurcation was referred to as GB. System (3) with non-smooth control strategy has a stable periodic trajectory in region $S_{2}$, as shown in Fig. 14a for $ET=0.082$, and also has two tangent points $E_{1}^{T}$ and $E_{2}^{ T}$ which locate on the boundary of the sliding mode. The continuous system given by Eq. (9) has an unstable R-E point $E_{2r}^{+}$ while system (8) has one unstable V-E point $E_{2v}^{-}$. When the parameter ET increases and passes through the value of 0.082, a GB occurs as shown in Fig. 14a. The standard periodic trajectory of system (3) under non-smooth control strategy collides with its T-E point $E_{2}^{T}$. With a further increase of ET, the loop becomes a sliding loop, where a segment of sliding region is a part of the cycle, see Fig. 14b for $ET=0.213$.

Specifically, as the bifurcation parameter ET is increased to 0.6101, the stable periodic loop disappears, and P-E point $E_{ P}$ appears. At the same time, the regular equilibrium point $E_{2r}^{+}$ of the continuous system (9) becomes a V-E point $E_{2v}^{+}$, and the regular/virtual equilibrium point bifurcation occurs at $ET=0.6101$, as displayed in Fig. 14c. Meanwhile, Fig. 14c also shows that the P-E point of the discontinuous dynamical system cannot coexist with the regular equilibrium point.

7 Discussion and conclusion

This paper has investigated the plant disease system with non-smooth control strategy through studying the global dynamics and sliding bifurcations. By applying Filippov convex method, we first obtained the sliding dynamic system of the plant disease system with non-smooth control strategy and then studied the sliding mode dynamics and the local sliding bifurcations (see Figs. 9, 10, 11).

It was shown from the boundary node bifurcation diagram (Fig. 13b) that all the solutions of the two regions and can asymptotically converge to the pseudo-equilibrium point $E_{p}$ when the appropriate control parameters were selected.

The main results demonstrate that for the prevention and treatment of plants, the appropriate threshold ET (i.e., $ET<ET_{0}$) can be decided by using the proposed treatment strategy. That is to say, if the number of infected plants is larger than the economic threshold $ET_{0}$, we should take treatment immediately to the infected plants. Accordingly, the plant disease can be controlled at the early stage (as shown in Figs.12, 13). Meanwhile, the non-smooth control strategy can be applied to control the new emerging infectious disease.

In practice, our analysis suggests that the measure to reduce the disease plant density of infected plants is effective for controlling disease if the system parameters and the initial conditions are appropriately chosen. Based on the control measure, minimizing the number of the infected plants by disease plant density plays a leading role in controlling the disease and reducing the loss of the production.

It should be mentioned that the model discussed in the present paper can be extended to study the SIR epidemic [11, 25]. This paper only considered the dynamics of system (3) when $I=ET$. Under the condition $\frac{I}{S}<ET$ and by considering the other nonlinear factors induced from the practical protective measures, such as cutting out the weak or dying trees, removing the bottom branches of the seriously ill plants to reduce the spread of the disease, and creating mixed forests with different composition, the dynamic behavior of system (3) under such situations is not yet fully understood, which would be the topic of our future research.

Appendix A

The proof of Theorem 5.1

Notice that $h _{1} = -(\frac{A\beta b_{1}-(\mu _{1}+v_{1})(\beta + \mu b_{1})- c \beta }{(\mu _{1}+v_{1}) \beta b_{1}})$, if $h _{1}<0$ then we have $A\beta b_{1}-(\mu _{1}+v_{1})(\beta + \mu b_{1})- c \beta >0$. By simple calculations, we can obtain $\frac{A\beta }{(\mu _{1}+v_{1})\mu }>1+\frac{\beta }{b_{1}\mu }+\frac{c\beta }{(\mu _{1}+v_{1})\mu }$, which is a contradiction with ${\mathcal {R}}_{0}<1$. Then from Proposition 3.3, we know that If ${\mathcal {R}}_{1}<{\mathcal {R}}_{0}<1$ and $h_{1}\ge 0$, there is no endemic equilibrium for system (9). Then we consider Lyapunov function

$$\begin{aligned} V(S,I)= \frac{(S-S^{-}_{1})^{2}}{2}+\frac{A}{\mu }I \end{aligned}$$

(1) If $(S,I)\in S_{1}$, then

$$\begin{aligned} \begin{aligned}&<\nabla V(S,I),f_{S_{1}}(S,I)>=-\mu (S-S^{-}_{1})^{2}\\&\quad -\,\beta (S-S^{-}_{1})^{2}I-(\mu _{1}I+v_{1}I- \frac{\beta A}{\mu }I)\frac{\beta A}{\mu }\leqslant 0. \end{aligned} \end{aligned}$$

(2) If $(S,I)\in \{(S,I)\in \varPi ; \mathrm { if }I= ET\}$, then

$$\begin{aligned} \begin{aligned}&<\nabla V(S,I),f_{S_{1}}(S,I)>=<V'_{S},V'_{I}> <f_{11},f_{12}>\\&\quad =V'_{S}f_{11}+V'_{I}f_{12}\\&\quad =-\mu (S-S^{-}_{1})^{2}-\beta (S-S^{-}_{1})^{2}I\\&\qquad -\left( \mu _{1}I+v_{1}I- \frac{\beta A}{\mu }I\right) \frac{\beta A}{\mu }\\&\quad \leqslant 0, \end{aligned} \end{aligned}$$

where $f_{11}=A-\mu S-\beta SI, f_{12}=\beta SI-\mu _{1}I-v_{1}I$. Similarly,

$$\begin{aligned} \begin{aligned}&<\nabla V(S,I),f_{S_{2}}(S,I)>=<V'_{S},V'_{I}> <f_{21},f_{22}>\\&\quad \leqslant -\mu (S-S^{-}_{1})^{2}-\beta (S-S^{-}_{1})^{2}I\\&\qquad -(\mu _{1}I+v_{1}I- \frac{\beta A}{\mu }I)\frac{\beta A}{\mu },\\&\quad \leqslant 0, \end{aligned} \end{aligned}$$

where $I=ET>I_{2}^{-}, f_{21}= A-\mu S-\beta SI, f_{22}=\beta SI-\mu _{1}I-v_{1}I-\frac{cI}{1+b_{1}I}$. Then, we have

$$\begin{aligned}<\nabla V(S,I), f_{S_{2}}(S,I)> <0. \end{aligned}$$

Hence,

$$\begin{aligned}&\sup \limits _{0\le \alpha _{1}\le 1}<\nabla V(S,I),\alpha _{1} f_{S_{1}}(S,I)\\&\quad +\,(1-\alpha _{1})f_{S_{2}}(S,I)>=0. \end{aligned}$$

(3) If $(S,I)\in S_{2}$, then

$$\begin{aligned} \begin{aligned}&<\nabla V(S,I),f_{S_{2}}(S,I)>=<V'_{S},V'_{I}> <f_{21},f_{22}>\\&\quad \leqslant -\mu (S-S^{-}_{1})^{2}-\beta (S-S^{-}_{1})^{2}I\\&\qquad -(\mu _{1}I+v_{1}I- \frac{\beta A}{\mu }I)\frac{\beta A}{\mu },\\&\quad \leqslant 0,\end{aligned} \end{aligned}$$

If $I> ET$, we can obtain

$$\begin{aligned}<\nabla V(S,I),f_{S_{2}}(S,I)> <0. \end{aligned}$$

Hence, according to Lemmas 2.1, 2.2, we know that the invariant subset is $\omega _{0}(R_{+}^{2})=\{(S,I)|V(S,I)\leqslant V(\frac{A}{\mu },ET)\}\subset S_{1}\cup (\frac{ A}{\mu },ET)$, which is a subset of $\varOmega _{0}$. $E_{1}^{-}$ is globally asymptotically stable for system (3) and the proof is completed. $\square$

The proof of the case (i) of Theorem 5.2

A similar procedure to that of Theorem 5.4 can be used to prove this theorem, and we omit it here for brevity. $\square$

The proof of the case (ii) of Theorem 5.2

By using Proposition 3.1, if ${\mathcal {R}}_{1}<1<{\mathcal {R}}_{0}$ and $h_ {1} \geqslant 0$, then we know that there is no endemic equilibrium for the subsystem (9). We consider Lyapunov function

$$\begin{aligned}&V(S,I)= \frac{(S-S^{-}_{2})^{2}}{2}\\&\qquad +\frac{\mu _{1}+v_{1}}{\beta }\left( I-I^{-}_{2}- I^{-}_{2}ln\frac{I}{ I^{-}_{2}}\right) \end{aligned}$$

(1) If $(S,I)\in S_{1}$, then

$$\begin{aligned} \begin{aligned}&<\nabla V(S,I),f_{S_{1}}(S,I)>= \\&\quad -\mu (S-S^{-}_{2})^{2}-\beta (S-S^{-}_{2})^{2}I\leqslant 0. \end{aligned} \end{aligned}$$

(2) If $(S,I)\in \{(S,I)\in \varPi ; \mathrm { if }I= ET\}$, then

$$\begin{aligned} \begin{aligned}&<\nabla V(S,I),f_{S_{1}}(S,I)>=<V'_{S},V'_{I}> <f_{11},f_{12}>\\&\quad =V'_{S}f_{11}+V'_{I}f_{12}=-\mu (S-S^{-}_{2})^{2}-\beta (S-S^{-}_{2})^{2}I\\&\quad \leqslant 0, \end{aligned} \end{aligned}$$

where $f_{11}=A-\mu S-\beta SI, f_{12}=\beta SI-\mu _{1}I-v_{1}I$. Similarly,

$$\begin{aligned} \begin{aligned}&<\nabla V(S,I),f_{S_{2}}(S,I)>=<V'_{S},V'_{I}> <f_{21},f_{22}>\\ {}&=V'_{S}f_{11}+V'_{I}f_{22}=V'_{S}f_{11}+V'_{ I}f_{12}\\&\qquad +\,V'_{I}f_{22}-V'_{I}f_{12}\leqslant V'_{I}f_{22}-V'_{I}f_{12}\\&\quad =-\frac{cI}{1+ b_{1}I}\frac{S^{-}_{2}(I-I_{2}^{-})}{I},\\&\quad \leqslant 0, \end{aligned} \end{aligned}$$

where $I=ET>I_{2}^{-}, f_{21}= A-\mu S-\beta SI, f_{22}=\beta SI-\mu _{1}I-v_{1}I-\frac{cI}{1+b_{1}I}$. Then, we have

$$\begin{aligned}<\nabla V(S,I), f_{S_{2} }(S,I)> <0. \end{aligned}$$

Hence,

$$\begin{aligned} \sup \limits _{0\le \alpha _{1}\le 1}<\nabla V(S,I),\alpha _{1} f_{S_{1}}(S,I)+(1-\alpha _{1})f_{S_{2}}(S,I)>=0. \end{aligned}$$

(3) If $(S,I)\in S_{2}$, then

$$\begin{aligned} \begin{aligned}&<\nabla V(S,I),f_{S_{2}}(S,I)>=<V'_{S},V'_{I}> <f_{21},f_{22}>\\&\quad =V'_{S}f_{11}+V'_{I}f_{22}\\&\quad =V'_{S}f_{11}+V'_{ I}f_{12}+V'_{I}f_{22}-V'_{I}f_{12}\\&\quad \leqslant V'_{I}f_{22}-V'_{I}f_{12}\\&\quad =-\frac{cI}{1+ b_{1}I}\frac{S^{-}_{2}(I-I_{2}^{-})}{I}. \end{aligned} \end{aligned}$$

If $I> ET$, we can obtain

$$\begin{aligned}<\nabla V(S,I),f_{S_{2}}(S,I)> <0. \end{aligned}$$

Hence, according to Lemmas 2.1, 2.2, we know that the invariant subset is $\omega _{1}(R_{+}^{2})=\{(S,I)|V(S,I)\leqslant V(\frac{\mu _{1}+v_{1}}{\beta },ET)\}\subset S_{1}\cup (\frac{\mu _{1}+v_{1}}{\beta },ET)$, which is a subset of $\varOmega _{1}$. Then $E^{-}_{2}$ is globally asymptotically stable if $I_{2}^{-}\leqslant ET$, and the proof is completed. $\square$