Synchronization control of Markov jump neural networks with mixed time-varying delay and parameter uncertain based on sample point controller

Abstract

This paper put forward an improved synchronization problem for neural networks with Markov jump parameters. The traditional Markov jump neural network (MJNN) only considers the basic external time-varying delays, ignoring both the distributed and leakage delays in the internal transmission of the neural network and the small time-varying errors in the mode switching of Markov probability transition rates. In this paper, we focus on the synchronization of MJNN with mixed time-varying delay. And an improved Lyapunov–Krasovskii functional is constructed. The convergence of inequalities is solved by using affine Bessel–Legendre inequalities and Wirtinger double integral inequalities. At the same time, a new method is used to optimize the mathematical geometric area of the time-varying delay and reduce the conservativeness of the system. Finally, a sample point controller is constructed to synchronize the driving system and the corresponding system.

1 Introduction

The enlightenment stage of the neural network (NN) is in the middle and late 1980s. After decades of development, it gradually develops to a mature stage and has been extended to all areas of real life. This special nonlinear network which imitates the structure of human brain and the method of processing information have made amazing achievements in many aspects and can solve many problems that are difficult to solve by digital computers. In the past few decades, different kinds of NN have attracted attention. However, the simulation of human brain structure by artificial NN is still a low degree of research. Scholars have been looking for more accurate theories to imitate brain intelligence. Through continuous practice and theoretical research, people have found that chaos and time delay have been found in the nervous system, whether micro-neurons or macro-brain waves. Therefore, researchers focus on chaotic NN with time-varying delay [1, 10, 12, 33]. Chaotic NN is to apply the advantages of NN system to chaotic system, make up for each other’s shortcomings, and there is also a very large possibility of intelligent information processing. However, in traditional NN, only external time-varying delay is considered, and the distributed delay and leakage delay of information transmission within neurons are neglected. Therefore, the first problem that this paper focuses on is the chaotic perturbation of NN with mixed time-varying delay.

In recent years, the stability of NN with Markov jump has become a research hot spot. This model allows NN to have multiple modes, and different modes can be switched under the drive of a Markov chain. Therefore, the study of the stability of Markov jump model has more potential application value [13, 14, 18, 23, 25, 26, 29, 30]. In [25, 29], by constructing suitable LKF and using linear matrix inequality (LMI), the mean-square global exponential stability of a class of reaction-diffusion Hopfield MJNN and the global robust exponential stability of a class of time-varying delay MJNN are studied, respectively. However, the traditional probabilistic transfer matrix of Markov jump parameters often neglects the small time-varying errors in probability transition rates, which may make the switching process unstable and cause the system to collapse in severe cases. Therefore, the second problem that this paper focuses on is the time-varying probabilistic transfer parameters in MJNN.

Synchronization, as a nonlinear phenomenon, has appeared in many practical problems, such as physics, ecology and physiology. Therefore, the application of synchronization theory has been widely studied in different scientific fields. In particular since 1990s, Pecora and Carroll have paid attention to the importance of control and synchronization of chaotic systems. They put forward the concept of drive-response to achieve synchronization of chaotic systems. This method controls the response system by driving the external input of the system to achieve synchronization. So the theory of chaos synchronization and chaos control has been widely studied. In order to achieve synchronization, many control systems have been proposed, such as: synchronization method of driving-response [19]; active–passive synchronization method [20]; synchronization method based on mutual coupling [36]; adaptive synchronization method [9]; feedback control synchronization method [15]; projection synchronization control [11]; and impulse control [7]. Therefore, the third problem that this paper focuses on is how to construct a suitable sample point controller to synchronize MJNN drive system (MJNN-DS) and MJNN response system (MJNN-RS).

On the other hand, the synchronous analysis of MJNN usually constructs a suitable LKF and then converges the inequality. In recent years, scholars have proposed many useful inequality methods, such as: Jensen inequality [37], Wirtinger integral inequality [22], free matrix inequality [32], interactive convex inequality [34] and Bessel–Legendre inequalities [21]. These methods have effectively improved the convergence accuracy, but there is still room for improvement. Wirtinger double integral inequalities and affine Bessel–Legendre inequalities improve Wirtinger integral inequality and Bessel–Legendre inequality, respectively. Therefore, the fourth problem that this paper focuses on is how to use Wirtinger double integral inequalities and affine Bessel–Legendre inequalities to improve the convergence accuracy.

In addition, when discussing the interval range of time-varying delays, the defaults are $h_{1}\le h\le h_{2}$ and $d_{1}\le \dot{h}\le d_{2}$, which are conservative and can be optimized in two-dimensional space. Therefore, the fifth problem that this paper focuses on is to discuss the optimization of time-varying delay intervals based on two-dimensional level.

In summary, the contributions of this paper and the difficulties to be solved are as follows: Firstly, how to unify the mixed time-varying delay and time-varying probability transfer under one MJNN. Secondly, how to apply Wirtinger double integral inequalities and affine Bessel–Legendre inequalities to Lyapunov functional processing. Thirdly, how to synchronize MJNN-DS and MJNN-RS through the control of sample point controller. Fourthly, how to optimize the two-dimensional geometric area of time delay. In addition, these methods have the following advantages: the affine Bessel–Legendre inequalities improves the traditional Bessel–Legendre inequality, and with the increase in N, the optimization effect will be better. Compared with the traditional state feedback controller, the sample point controller can better transmit the effective information of the system and achieve better control effect. The traditional two-dimensional geometric area of time delay is a rectangle. We reduce the conservativeness of the system by reducing the area to a parallelogram.

Next, this paper will be based on the following four parts. The first part introduces MJNN-DS and MJNN-RS, sample point controller, and relevant useful lemmas. In the second part, the synchronous analysis of MJNN mixed-time-varying-delayed error system is carried out, and the convergence accuracy of LKF is improved by using Wirtinger double integral inequalities and affine Bessel–Legendre inequalities. In the third part, the range of time-varying delay in two-dimensional space is discussed, and the conservativeness of the system is reduced by reducing the two-dimensional geometric area. In the fourth part, a numerical example is constructed. The parameters of the sample point controller, the chaotic curve of MJNN system, Markov jump response curve, synchronization analysis response curve and error analysis response curve are obtained through actual simulation.

In this paper, “0” represents zero matrix of suitable dimension. $\mathbf {R}^{n}$ and $\mathbf {R}^{n\times m}$ represent n-dimensional and $n\times m$-dimensional Euclidean spaces, respectively. “T” represents the matrix transposition. $\{\varOmega , \digamma , \mathcal {P} \}$ represents the probability space.

2 Preliminaries

Consider the following MJNN-DS with mixed time-varying delay:

$$\begin{aligned} \dot{x}(t)= & {} -C(r(t))x(t-\sigma )+A(r(t))f(x(t))\nonumber \\&+B(r(t))f(x(t-d_{1}(t)))\nonumber \\&+D(r(t))\int ^{t}_{t-d_{2}(t)}f(x(s))ds+\mathcal {J} \end{aligned}$$

(1)

where $x(t)=(x_{1}(t),x_{2}(t),\cdots ,x_{n}(t))^\mathrm{T}\in \mathbf {R}^{n}$ is the neuron state vector. $A(\cdot )$, $B(\cdot )$, $C(\cdot )$ and $D(\cdot )$ are matrices of suitable dimensions with uncertainties, which are expressed as follows:

$$\begin{aligned} A(\cdot )= & {} \bar{A}(\cdot )+\varDelta A\quad B(\cdot )=\bar{B}(\cdot )+\varDelta B\\ C(\cdot )= & {} \bar{C}(\cdot )+\varDelta C\quad D(\cdot )=\bar{D}(\cdot )+\varDelta D \end{aligned}$$

where $\varDelta A$, $\varDelta B$, $\varDelta C$ and $\varDelta D$ are uncertain parameter terms, such as:

$$\begin{aligned} {[}\varDelta A, \varDelta B, \varDelta C, \varDelta D]=GF(t)[E_{1}, E_{2}, E_{3}, E_{4}] \end{aligned}$$

where G and $E_{i}(i=1,2,3)$ are real matrices of suitable dimensions, F(t) satisfies: $F^\mathrm{T}(t)F(t)\le I$.

$f(\cdot )$ is the neuron excitation function. $\mathcal {J}$ denotes external disturbances. r(t) represents a Markov jump subset on a finite state space $S=\{1,\cdot \cdot \cdot ,M\}$. Markov chain is defined in space $\{\varOmega , \digamma , \mathcal {P} \}$. The transfer rate matrix $\varPi (t)=(\mu _{ij})_{N \times N}$ is defined as follows:

$$\begin{aligned}&P\{r(t+\varDelta )=j|r(t)=i\}\\&\quad = \left\{ \begin{array}{lll}\mu _{ij}\varDelta +o(\varDelta ); if j\ne i,\\ 1+\mu _{ii}\varDelta +o(\varDelta ); if j=i\end{array}\right. \end{aligned}$$

where $\mu _{ij} \ge 0$, if $j\ne i$, $\mu _{ii}=-\sum ^{N}_{j=1,j\ne i}\mu _{ij}$. $\sigma$, $d_{1}(t)$ and $d_{2}(t)$ represent the leakage delay, the external time-varying delay and the distributed delay, respectively, and the time-varying delay ranges are as follows: $0\le d_{1}(t)\le d_{1}$, $h_{1}\le \dot{d}_{1}(t)\le h_{2}$, $0\le d_{2}(t)\le d_{2}$.

Remark 1

The first item on the right side of the equation is the stable negative feedback of the system, which is often referred to as the “leakage” item. Since the self-attenuation process of neurons is not instantaneous, when the neurons are cut off from the neural network and external inputs, it takes time to reset to the isolated static state. In order to describe this phenomenon, it is necessary to introduce a “leakage” delay. In this paper, $\sigma$ is called leakage delay.

Consider the following MJNN-RS with mixed time-varying delay:

$$\begin{aligned} \dot{y}(t)= & {} -C(r(t))y(t-\sigma )+A(r(t))f(x(t))\nonumber \\&+B(r(t))f(y(t-d_{1}(t)))\nonumber \\&+D(r(t))\int ^{t}_{t-d_{2}(t)}f(y(s))ds+u(t)+\mathcal {J} \end{aligned}$$

(2)

where $y(t)=(y_{1}(t),y_{2}(t),\cdots ,y_{n}(t))^\mathrm{T}\in \mathbf {R}^{n}$ is the neuron state vector. The meanings of other symbols are equivalent to MJNN driving system (1). u(t) represents the sample point controller, which is defined as follows:

$$\begin{aligned} u(t)=K(r(t_{k}))e(t_{k}),\quad t_{k}\le t<t_{k+1} \end{aligned}$$

where $K(\cdot )$ is the feedback gain matrix of the sample point controller, $e(t_{k})$ represents the discrete control function, and $t_{k}$ is the sample point and satisfies:

$$\begin{aligned} 0=t_{0}<t_{1}<\cdots<t_{k}<\cdots <\lim _{k\rightarrow +\infty }t_{k}=+\infty \end{aligned}$$

Assuming that the period of sample points is bounded, for any $k\ge 0$, there exists a normal quantity $d_{3}$ satisfying $t_{k+1}-t_{k}\le d_{3}$.

Remark 2

Obviously, due to the introduction of the discrete term $e(t_{k})$, the synchronization analysis of the system becomes more difficult. In this paper, the input delay method is used to deal with the discrete term. Define a smooth function:

$$\begin{aligned} d_{3}(t)=t-t_{k},\quad t_{k}\le t\le t_{k+1} \end{aligned}$$

Easy to get: $0\le d_{3}(t)\le d_{3}$. In summary, the sample point controller is converted as follows:

$$\begin{aligned} u(t){=}K(r(t_{k}))e(t_{k})\Longrightarrow u(t){=}K(r(t_{k}))e(t-d_{3}(t)) \end{aligned}$$

Let $e(t)=y(t)-x(t)$, $g(e(\cdot ))=f(y(\cdot ))-f(x(\cdot ))$. The MJNN error system with mixed time-varying delay is defined as follows:

$$\begin{aligned} \dot{e}(t)= & {} -C(r(t))e(t-\sigma )+A(r(t))g(e(t))\nonumber \\&+\,B(r(t))g(e(t-d_{1}(t)))\nonumber \\&+\,D(r(t))\int ^{t}_{t-d_{2}(t)}g(e(s))ds+u(t) \end{aligned}$$

(3)

Some lemmas are given below, which play a key role in the calculation of this paper.

Lemma 1

(Affine Bessel–Legendre inequalities)[8] If the function $x(\cdot )$ satisfies $x(\cdot ):[a,b]\rightarrow \mathbf {R}^{n}$ and $N\in \mathbf {N}$, given any positive definite matrix $R=R^\mathrm{T}$, there exists a matrix X such that the following relation holds

$$\begin{aligned} -\int ^{b}_{a}\dot{x}^\mathrm{T}(s)R\dot{x}(s)ds\le -\vartheta ^\mathrm{T}_{N}(t)\varOmega (X)\vartheta _{N}(t) \end{aligned}$$

where

$$\begin{aligned} \varOmega (X)= & {} XL_{N}+L^\mathrm{T}_{N}X^\mathrm{T}-(b-a)X\bar{R}X^\mathrm{T}\\ L_{N}= & {} [\varGamma ^\mathrm{T}_{N}(0)\quad \varGamma ^\mathrm{T}_{N}(1)\ldots \varGamma ^\mathrm{T}_{N}(N)]^\mathrm{T}\\ \bar{R}= & {} diag\left( R^{-1},\frac{1}{3}R^{-1},\ldots ,\frac{1}{2N+1}R^{-1}\right) \\ \vartheta _{N}= & {} \left\{ \begin{array}{lll} &{}&{}\left[ x^\mathrm{T}(b)\quad x^\mathrm{T}(a)\right] ^\mathrm{T} if N=0 \\ &{}&{}\left[ x^\mathrm{T}(b)\quad x^\mathrm{T}(a)\quad \frac{1}{b-a}\varPhi _{0}^\mathrm{T}\ldots \frac{1}{b-a}\varPhi _{N-1}^\mathrm{T}\right] ^\mathrm{T}if N>0 \end{array}\right. \\ \varGamma _{N}(k)= & {} \left\{ \begin{array}{lll} &{}&{}\left[ I\quad -I\right] ^\mathrm{T} \quad if\quad N=0 \\ &{}&{}\left[ I\quad (-1)^{k+1}I\quad \gamma ^{0}_{Nk}I\ldots \gamma ^{N-1}_{Nk}I\right] ^\mathrm{T} if N>0 \end{array}\right. \\ \varPhi _{k}= & {} \int ^{b}_{a}L_{k}(s)x(s)ds\\ \gamma ^{i}_{Nk}= & {} \left\{ \begin{array}{lll} &{}&{}-(2i+1)(1-(-1)^{k+i}) \quad if\quad i\le k \\ &{}&{}0\quad if\quad i\ge k+1 \end{array}\right. \\ L_{k}(u)= & {} (-1)^{k}\sum ^{k}_{l=0}\left[ (-1)^{l}\left( \begin{array}{lll} k\\ l \end{array}\right) \left( \begin{array}{lll} k+l \\ l \end{array}\right) \right] \left( \begin{array}{lll} \frac{u-a}{b-a} \end{array}\right) ^{l} \end{aligned}$$

Remark 3

Unlike the traditional Bessel–Legendre inequalities [21], the right side of the inequality of Lemma 1 is the affine of the length of the integral interval, so it can be easily dealt with by convexity. In addition, Lemma 1 can be transformed into existing inequalities in literature under special conditions, such as affine Jensen inequality [2] and affine Wirtinger integral inequality [6], which shows that the inequality of Lemma 1 is more general.

Remark 4

Lemma 1 has an additional decision variable of $(N+1)(N+2)n^{2}$ because of the addition of additional matrix X to the traditional Bessel–Legendre inequalities [21].

Lemma 2

(Wirtinger Double Integral inequalities)[17] If constants m and n satisfy $m<n$, for any positive definite matrix $\mathbb {H}$, and $x\in [m,n] \rightarrow \mathbf {R}^{n}$, the following inequalities hold

$$\begin{aligned}&(n-m)^{2}\int _{m}^{n}\int _{\theta }^{n}x^\mathrm{T}(u)\mathbb {H}x(u)dud\theta \\&\quad \geqslant 2\varTheta _{d1}^\mathrm{T}\mathbb {H}\varTheta _{d1}+4\varTheta _{d2}^\mathrm{T}H\varTheta _{d2} \end{aligned}$$

where

$$\begin{aligned} \left\{ \begin{array}{lll} \varTheta _{d1}&{}=&{}\int _{m}^{n}\int _{\theta }^{n}x(u)dud\theta \\ \varTheta _{d2}&{}=&{}-\int _{m}^{n}\int _{\theta }^{n}x(u)duds\\ &{}&{}+\frac{3}{s-r}\int _{m}^{n}\int _{\theta }^{n}\int _{u}^{n}x(u)dvduds \end{array}\right. \end{aligned}$$

Remark 5

Lemma 2 adds a multiple integral on the basis of Wirtinger integral inequality [22]. At the same time, $\varTheta _{d1}$ and $\varTheta _{d2}$ on the right side of the inequality contain more sub-terms. Therefore, Lemma 2 can express the internal information of the system more completely in the derivative deformation of Lyapunov functional, so it has lower conservativeness.

Lemma 3

[3]When has the $M-\varPi (t)$ transfer ratio matrix is located has the border area $\mathcal {D}$ apex, territory $\mathcal {D}_{1}$ by the following expression is composed:

$$\begin{aligned} \mathcal {D}_{1}= & {} \left\{ \varPi (r(t))|\varPi (r(t))\right. \nonumber \\= & {} \left. \sum ^{M}_{l=1}r_{l}(t)\varPi ^{(l)},\sum ^{M}_{l=1}r_{l}(t)=1,r_{l}(t)\ge 0 \right\} \end{aligned}$$

(4)

where $\varPi ^{(l)}(l=1,2,\cdot \cdot \cdot ,M)$ are vertices, r(t) is the parameter vector, it is assumed that the changes are known. As a result, $\dot{r}(t)$ is as follows:

$$\begin{aligned} \mathcal {D}_{2}= \left\{ \begin{array}{ll} -v_{l}{\le } \dot{r}_{l}(t){\le }v_{l},v_{l}{\ge } 0,l=1,2,\cdot \cdot \cdot ,M-1 \end{array}\right\} \nonumber \\ \end{aligned}$$

(5)

Remark 6

Easy to get $\sum ^{M}_{l=1}r_{l}(t)=1$ is equivalent to $\sum ^{M-1}_{l=1}\dot{r}_{l}(t)+\dot{r}_{M}(t)=0$. So $\dot{r}_{M}(t)$ is expressed by $\mid \dot{r}_{M}(t)\mid \le \sum ^{M-1}_{l=1}v_{l}$.

Lemma 4

[4] If the vector function x satisfies $x:[0,\varrho ]\rightarrow \mathbf {R}^{n}$, given any positive definite matrix $\mathcal {U}$ and positive scalar $\varrho$, the following relation holds

$$\begin{aligned}&\varrho ^{-1}\left[ \int ^{\varrho }_{0}x(s)ds\right] ^\mathrm{T}\mathcal {U}\left[ \int ^{\varrho }_{0}x(s)ds\right] \\&\quad \le \int ^{\varrho }_{0}x^\mathrm{T}(s)\mathcal {U}x(s)ds \end{aligned}$$

Lemma 5

[28] For any real matrices D, E, F and scalar $\varepsilon >0$, when $F^\mathrm{T}F\le I$ is satisfied, the following inequalities hold

$$\begin{aligned} DFE+E^\mathrm{T}F^\mathrm{T}D^\mathrm{T}\le \varepsilon DD^\mathrm{T}+\varepsilon ^{-1}E^\mathrm{T}E \end{aligned}$$

Assumption (A1) The neuron excitation function $f(\cdot )$ satisfies the following conditions:

$$\begin{aligned} 0<\frac{f_{i}(u_{i}-v_{i})}{u_{i}-v_{i}}\le l_{i}\quad (i=1,2\cdots ,N) \end{aligned}$$

where $u_{i}$ and $v_{i}$ are arbitrary real numbers, and $u\ne v$. $l_{i}$ are known constants.

3 Main results

Theorem 1

Given scalars $d_{i}>0,i=1,2,3$ and $\dot{d}_{1}(t)$, and satisfy, $d_{i}(t)\in [0,d_{i}],i=1,2,3$, $\dot{d}_{1}(t)\in [h_{1},h_{2}]$, for any delay d(t), MJNN-DS (1) and MJNN-RS (2) achieve complete synchronization, if there exist symmetry matrices $P_{P}^{(l)}>0\in \mathbf {R}^{7n}$, $Q_{i}>0,i=1,2,3,4\in \mathbf {R}^{n}$, $R_{i}>0,i=1,2\in \mathbf {R}^{n}$, $Z_{i}>0,i=1,2\in \mathbf {R}^{n}$, $S>0\in \mathbf {R}^{n}$, any matrices $X_{i},i=1,2,3,4\in \mathbf {R}^{4n\times 3n}$, $M_{1}$, $M_{2}$ and $\chi _{i}$ are matrices of suitable dimensions, such that the following hold:

$$\begin{aligned}&\varUpsilon _{P}^{(ls)}(d_{i}(t),\dot{d}_{1}(t))+\varUpsilon _{P}^{(sl)}(d_{i}(t),\dot{d}_{1}(t))<0\end{aligned}$$

(6)

$$\begin{aligned}&\varUpsilon _{P}^{(ls)}(d_{i}(t),\dot{d}_{1}(t))\nonumber \\&\quad =\begin{bmatrix} \varPsi _{P}(d_{i}(t),\dot{d}_{1}(t))&\varPi _{1}^\mathrm{T}X_{1}&\varPi _{2}^\mathrm{T}X_{2}&\varPi _{3}^\mathrm{T}X_{3}&\varPi _{4}^\mathrm{T}X_{4}&\varPhi _{1}&\varPhi _{2}\\ *&\varDelta _{22}&0&0&0&0&0\\ *&*&\varDelta _{33}&0&0&0&0\\ *&*&*&\varDelta _{44}&0&0&0\\ *&*&*&*&\varDelta _{55}&0&0\\ *&*&*&*&*&-\varepsilon I&0\\ *&*&*&*&*&*&-\frac{1}{\varepsilon }I \end{bmatrix} \end{aligned}$$

(7)

where

$$\begin{aligned}&\varDelta _{22}=-d_{1}(t)R_{1N}\quad \varDelta _{33}=-(d_{1}-d_{1}(t))R_{1N}\nonumber \\&\varDelta _{44}=-d_{3}(t)R_{2N}\quad \varDelta _{55}=-(d_{3}-d_{3}(t))R_{2N}\nonumber \\&R_{iN}=diag\{R_{i},3R_{i},5R_{i}\}\quad i=1,2\nonumber \\&\varPsi _{P}(d_{i}(t),\dot{d}_{1}(t))\nonumber \\&\quad =\varOmega _{P}^{(ls)}(d_{i}(t),\dot{d}_{1}(t))\nonumber \\&\qquad +\,e_{1}^\mathrm{T}\sum ^{4}_{i=1}Q_{i}e_{1}-(1-\dot{d}_{1}(t))e_{2}^\mathrm{T}Q_{1}e_{2}\nonumber \\&\qquad -\,e_{20}^\mathrm{T}Q_{2}e_{20}-e_{3}^\mathrm{T}Q_{3}e_{3}\nonumber \\&\qquad - \,e_{11}^\mathrm{T}Q_{4}e_{11}+e_{21}^\mathrm{T}(d_{1}R_{1}+d_{3}R_{2})e_{21}\nonumber \\&\qquad -\,\varPi _{1}^\mathrm{T}(X_{1}M+M^\mathrm{T}X_{1}^\mathrm{T})\varPi _{1}-\varPi _{2}^\mathrm{T}(X_{2}M\nonumber \\&\qquad + \,M^\mathrm{T}X_{2}^\mathrm{T})\varPi _{2}-\varPi _{3}^\mathrm{T}(X_{3}M+M^\mathrm{T}X_{3}^\mathrm{T})\varPi _{3}\nonumber \\&\qquad -\,\varPi _{4}^\mathrm{T}(X_{4}M+M^\mathrm{T}X_{4}^\mathrm{T})\varPi _{4}\nonumber \\&\qquad + \,e_{21}^\mathrm{T}\left[ \left( \frac{d_{1}^{2}}{2}\right) ^{2}Z_{1}+\left( \frac{d_{3}^{2}}{2}\right) ^{2}Z_{2}\right] e_{21}\nonumber \\&\qquad -\,\left[ d_{1}e_{1}-e_{16}\right] ^\mathrm{T}Z_{1}\left[ d_{1}e_{1}-e_{16}\right] -2\left[ -\frac{d_{1}}{2}e_{1}-e_{16}\right. \nonumber \\&\qquad \left. + \,\frac{3}{d_{1}}e_{17}\right] ^\mathrm{T}Z_{1}\left[ -\frac{d_{1}}{2}e_{1}-e_{16}+\frac{3}{d_{1}}e_{17}\right] \nonumber \\&\qquad -\,\left[ d_{3}e_{1}-e_{18}\right] ^\mathrm{T}Z_{2}\left[ d_{3}e_{1}-e_{18}\right] -2\left[ -\frac{d_{3}}{2}e_{1}\right. \nonumber \\&\qquad \left. -\,e_{18}+\frac{3}{d_{3}}e_{19}\right] ^\mathrm{T}Z_{2}\left[ -\frac{d_{3}}{2}e_{1}-e_{18}+\frac{3}{d_{3}}e_{19}\right] \nonumber \\&\qquad +\,d_{2}e_{1}^\mathrm{T}Se_{1} -\delta _{1}\left[ e_{23}^\mathrm{T}e_{23}-e_{1}^\mathrm{T}L^\mathrm{T}Le_{1}\right] \nonumber \\&\qquad -\,\delta _{2}\left[ e_{24}^\mathrm{T}e_{24}-e_{2}^\mathrm{T}L^\mathrm{T}Le_{2}\right] -\delta _{3}d_{2}^{-1}e_{22}^\mathrm{T}e_{22}+\varPhi _{3}\nonumber \\&\qquad \varOmega _{P}^{(ls)}(d_{i}(t),\dot{d}_{1}(t)) \end{aligned}$$

(8)

$$\begin{aligned}&=\,He\{T_{0}^\mathrm{T}(\dot{d}_{1}(t))P_{P}^{(l)}T_{1}(d_{1}(t))\}+T_{1}^\mathrm{T}(d_{1}(t))\nonumber \\&\qquad \sum ^{N}_{j=1}\mu _{ij}^{(l)}P_{j}^{(s)}T_{1}(d_{1}(t))\nonumber \\&\quad +\,T_{1}^\mathrm{T}(d_{1}(t))\sum ^{M-1}_{n=1}\pm (P_{P}^{(n)}-P_{P}^{(M)})T_{1}(d_{1}(t)) \end{aligned}$$

(9)

$$\begin{aligned}&\varPhi _{1}=col\{M_{1}G\quad \underbrace{0\cdots 0}_{19n}\quad M_{2}G\quad 0\quad 0\quad 0\} \end{aligned}$$

(10)

$$\begin{aligned}&\varPhi _{2}=col\{\underbrace{0\cdots 0 }_{19n}\quad -E_{3}^\mathrm{T}\quad 0\quad E_{4}^\mathrm{T}\quad E_{1}^\mathrm{T}\quad E_{2}^\mathrm{T}\} \end{aligned}$$

(11)

$$\begin{aligned}&M= \begin{bmatrix} I_{n}&-I_{n}&0_{n}&0_{n}\\ I_{n}&I_{n}&-2I_{n}&0_{n}\\ I_{n}&-I_{n}&6I_{n}&-12I_{n} \end{bmatrix} \end{aligned}$$

(12)

$$\begin{aligned}&\varPi _{1}=col\{e_{1}\quad e_{2}\quad e_{6}\quad e_{8}\} \nonumber \\&\varPi _{2}=col\{e_{2}\quad e_{3}\quad e_{7}\quad e_{9}\}\nonumber \\&\varPi _{3}=col\{e_{1}\quad e_{10}\quad e_{12}\quad e_{14}\} \nonumber \\&\varPi _{4}=col\{e_{10}\quad e_{11}\quad e_{13}\quad e_{15}\} \end{aligned}$$

(13)

$$\begin{aligned}&\varPhi _{3}=\begin{bmatrix} \underbrace{0\cdots 0}_{9n}&\chi _{i}&\underbrace{0\cdots 0}_{9n}&-\varepsilon _{1}M_{2}\bar{C}_{P}&-\varepsilon _{1}M_{2}&\varepsilon _{1}M_{2}\bar{D}_{P}&\varepsilon _{1}M_{2}\bar{A}_{P}&\varepsilon _{1}M_{2}\bar{B}_{P}\\ \underbrace{0\cdots 0}_{9n}&0&\underbrace{0\cdots 0}_{9n}&0&0&0&0&0\\ \vdots&\vdots&\vdots&\cdots&\cdots&\cdots&\cdots&\cdots \\ \underbrace{0\cdots 0}_{9n}&\chi _{i}&\underbrace{0\cdots 0}_{9n}&-M_{2}\bar{C}_{P}&-M_{2}-M_{2}^{T}&M_{2}\bar{D}_{P}&M_{2}\bar{A}_{P}&M_{2}\bar{B}_{P}\\ \underbrace{0\cdots 0}_{9n}&0&\underbrace{0\cdots 0}_{9n}&0&0&0&0&0\\ \underbrace{0\cdots 0}_{9n}&0&\underbrace{0\cdots 0}_{9n}&0&0&0&0&0\\ \underbrace{0\cdots 0}_{9n}&0&\underbrace{0\cdots 0}_{9n}&0&0&0&0&0 \end{bmatrix} \end{aligned}$$

(14)

$e_{i}(i=1,\cdots ,24)\in \mathbf {R}^{n\times 24n}$ are identity matrices. Sample point controller parameters can be obtained: $K_{i}=M_{2}^{-1}\chi _{i}$.

Proof

An improved LKFs are defined: $V(x(t),t,r(t))=V_{1}(t)+V_{2}(t)+V_{3}(t)+V_{4}(t)+V_{5}(t)$. where

$$\begin{aligned} V_{1}(t)= & {} \eta ^\mathrm{T}_{1}(t)P(r(t))\eta _{1}(t)\\ V_{2}(t)= & {} \int ^{t}_{t-d_{1}(t)}\!\!e^\mathrm{T}(s)Q_{1}e(s)ds{+}\int ^{t}_{t-\sigma }e^\mathrm{T}(s)Q_{2}e(s)ds\\&+\int ^{t}_{t-d_{1}}\!\!e^\mathrm{T}(s)Q_{3}e(s)ds{+}\int ^{t}_{t-d_{3}}\!\!e^\mathrm{T}(s)Q_{4}e(s)ds\\ V_{3}(t)= & {} \int ^{0}_{-d_{1}}\int ^{t}_{t+\theta }\dot{e}^\mathrm{T}(s)R_{1}\dot{e}(s)dsd\theta \\&\,+\int ^{0}_{-d_{3}}\int ^{t}_{t+\theta }\dot{e}^\mathrm{T}(s)R_{2}\dot{e}(s)dsd\theta \\ V_{4}(t)= & {} \frac{d_{1}^{2}}{2}\int ^{t}_{t-d_{1}}\int ^{t}_{\theta }\int ^{t}_{u}\dot{e}^\mathrm{T}(v)Z_{1}\dot{e}(v)dvdud\theta \\&+\,\frac{d_{3}^{2}}{2}\int ^{t}_{t-d_{3}}\int ^{t}_{\theta }\int ^{t}_{u}\dot{e}^\mathrm{T}(v)Z_{2}\dot{e}(v)dvdud\theta \\ V_{5}(t)= & {} \int ^{0}_{-d_{2}}\int ^{t}_{t+\theta }e^\mathrm{T}(s)Se(s)dsd\theta \end{aligned}$$

where

$$\begin{aligned} \eta _{1}(t)= & {} col\left\{ \quad e(t)\quad e(t-d_{1}(t))\quad e(t-d_{1})\right. \\&\quad \left. \int ^{t}_{t-d_{1}(t)}e(s)ds\quad \int ^{t-d_{1}(t)}_{t-d_{1}}e(s)ds\right. \\&\left. \frac{1}{d_{1}(t)}\int ^{0}_{-d_{1}(t)}\int ^{t}_{t+\theta }e(s)dsd\theta \quad \frac{1}{d_{1}-d_{1}(t)}\right. \\&\quad \left. \int ^{-d_{1}(t)}_{-d_{1}}\int ^{t-d_{1}(t)}_{t+\theta }e(s)dsd\theta \quad \right\} \end{aligned}$$

By deriving V(x(t), t, r(t)), meanwhile, Lemma 1 and Lemma 2 are used for $V_{3}(t)$ and $V_{4}(t)$ respectively, we get the following results

$$\begin{aligned} \dot{V}_{1}(t)= & {} He\{T_{0}^\mathrm{T}(\dot{d}_{1}(t))P_{P}T_{1}(d_{1}(t))\}+T_{1}^\mathrm{T}(d_{1}(t))\\&\sum ^{N}_{j=1}\mu _{ij}(r(t))P_{j}(r(t))T_{1}(d_{1}(t))\\&+\,T_{1}^\mathrm{T}(d_{1}(t))\left( \frac{dP_{P}(r(t))}{dt}\right) T_{1}(d_{1}(t))\\ \dot{V}_{2}(t)= & {} e_{1}^\mathrm{T}\sum ^{4}_{i=1}Q_{i}e_{1}-(1-\dot{d}_{1}(t))e_{2}^\mathrm{T}Q_{1}e_{2}\\&-\,e_{20}^\mathrm{T}Q_{2}e_{20}-e_{3}^\mathrm{T}Q_{3}e_{3}-e_{11}^\mathrm{T}Q_{4}e_{11}\\ \dot{V}_{3}(t)= & {} e_{21}^\mathrm{T}(d_{1}R_{1}+d_{3}R_{2})e_{21}-\int ^{t}_{t-d_{1}}\dot{e}^\mathrm{T}(s)R_{1}\dot{e}(s)ds\\&-\,\int ^{t}_{t-d_{3}}\dot{e}^\mathrm{T}(s)R_{2}\dot{e}(s)ds\\\le & {} e_{21}^\mathrm{T}(d_{1}R_{1}+d_{3}R_{2})e_{21}-\varPi _{1}^\mathrm{T}(X_{1}M+M^\mathrm{T}X^\mathrm{T}_{1}\\&-\,d_{1}(t)X_{1}R^{-1}_{1N}X^\mathrm{T}_{1})\varPi _{1}\\&- \,\varPi ^\mathrm{T}_{2}(X_{2}M+M^\mathrm{T}X^\mathrm{T}_{2}-(d_{1}-d_{1}(t))X_{2}R^{-1}_{1N}X^\mathrm{T}_{2})\varPi _{2}\\&- \,\varPi ^\mathrm{T}_{3}(X_{3}M+M^\mathrm{T}X^\mathrm{T}_{3}-d_{3}(t)X_{3}R^{-1}_{2N}X^\mathrm{T}_{3})\varPi _{3}\\&-\,\varPi ^\mathrm{T}_{4}(X_{4}M+M^\mathrm{T}X^\mathrm{T}_{4}\\&- \,(d_{3}-d_{3}(t))X_{4}R^{-1}_{2N}X^\mathrm{T}_{4})\varPi _{4}\\ \dot{V}_{4}(t)\le & {} e_{21}^\mathrm{T}\left[ \left( \frac{d_{1}^{2}}{2}\right) ^{2}Z_{1}+\left( \frac{d_{3}^{2}}{2}\right) ^{2}Z_{2}\right] \\&e_{21}-[d_{1}e_{1}-e_{16}]^\mathrm{T}Z_{1}[d_{1}e_{1}-e_{16}]\\&-\,2\left[ -\frac{d_{1}}{2}e_{1}\right. \\&\left. - e_{16}+\frac{3}{d_{1}}e_{17}\right] ^\mathrm{T}Z_{1}\left[ -\frac{d_{1}}{2}e_{1}-e_{16}+\frac{3}{d_{1}}e_{17}\right] \\&-\,[d_{3}e_{1}-e_{18}]^\mathrm{T}Z_{2}[d_{3}e_{1}-e_{18}]\\&-\,2\left[ -\frac{d_{3}}{2}e_{1}-e_{18}+\frac{3}{d_{3}}e_{19}\right] ^\mathrm{T}Z_{2}\\&\left[ -\frac{d_{3}}{2}e_{1}-e_{18}+\frac{3}{d_{3}}e_{19}\right] \\ \dot{V}_{5}(t)= & {} d_{2}e_{1}^\mathrm{T}Se_{1}-\int ^{t}_{t-d_{2}(t)}e^\mathrm{T}(s)Se(s)ds \end{aligned}$$

where

$$\begin{aligned}&T_{0}(\dot{d}_{1}(t))\\&\quad =col\left\{ \quad e_{21}\quad (1-\dot{d}_{1}(t))e_{4}\quad e_{5}\quad e_{1}-(1-\dot{d}_{1}(t))e_{2}\right. \\&\quad \left. (1-\dot{d}_{1}(t))e_{2}-e_{3}e_{1}-(1-\dot{d}_{1}(t))e_{6}\right. \\&\quad \left. -\,\dot{d}_{1}(t)e_{8}\quad (1-\dot{d}_{1}(t))e_{2}-e_{7}+\dot{d}_{1}(t)e_{9}\right\} \\&T_{1}(d_{1}(t))\\&=col\{\quad e_{1}\quad e_{2}\quad e_{3}\quad d_{1}(t)e_{6}\quad (d_{1}-d_{1}(t))e_{7}\quad d_{1}(t)e_{8}\\&\quad d_{1}-d_{1}(t))e_{9}\quad \} \end{aligned}$$

And the definitions of $\varPhi _{1}$, $\varPhi _{2}$, M, $\varPi _{1}$, $\varPi _{2}$, $\varPi _{3}$ and $\varPi _{4}$ are shown in (10)–(13). $\square$

The following inequalities are defined according to Assumption (A1)

$$\begin{aligned}&g^\mathrm{T}(e(t))g(e(t))-e^\mathrm{T}(t)L^\mathrm{T}Le(t)\le 0\\&g^\mathrm{T}(e(t-d_{1}(t)))g(e(t-d_{1}(t)))\\&\quad -e^\mathrm{T}(t-d_{1}(t))L^\mathrm{T}Le(t-d_{1}(t))\le 0\\&\int ^{t}_{t-d_{2}(t)}g^\mathrm{T}(e(s))g(e(s))ds\\&\quad -\int ^{t}_{t-d_{2}(t)}e^\mathrm{T}(s)L^\mathrm{T}Le(s)ds\le 0 \end{aligned}$$

where $L=diag\{l_{1},l_{2},\cdots ,l_{n}\}$. Meanwhile, given any positive constant: $\delta _{1}$, $\delta _{2}$ and $\delta _{3}$, the following inequalities can be obtained

$$\begin{aligned}&-\,\delta _{1}[g^\mathrm{T}(e(t))g(e(t))-e^\mathrm{T}(t)L^\mathrm{T}Le(t)]\ge 0 \end{aligned}$$

(15)

$$\begin{aligned}&-\,\delta _{2}[g^\mathrm{T}(e(t-d_{1}(t)))g(e(t-d_{1}(t)))\nonumber \\&\quad -e^\mathrm{T}(t-d_{1}(t))L^\mathrm{T}Le(t-d_{1}(t))]\ge 0 \end{aligned}$$

(16)

$$\begin{aligned}&-\,\delta _{3}[\int ^{t}_{t-d_{2}(t)}g^\mathrm{T}(e(s))g(e(s))ds\nonumber \\&\quad -\,\int ^{t}_{t-d_{2}(t)}e^\mathrm{T}(s)L^\mathrm{T}Le(s)ds]\ge 0 \end{aligned}$$

(17)

From Lemma 4, the following can be obtained

$$\begin{aligned}&-\delta _{3}\int ^{t}_{t-d_{2}(t)}g^\mathrm{T}(e(s))g(e(s))ds\nonumber \\&\quad \le -\delta _{3}d_{2}^{-1}\left[ \int ^{t}_{t-d_{2}(t)}g(e(s))ds\right] ^\mathrm{T}\nonumber \\&\quad \left[ \int ^{t}_{t-d_{2}(t)}g(e(s))ds\right] \end{aligned}$$

(18)

Given any constant $M_{1}$ and $M_{2}$, the following equation holds

$$\begin{aligned} 0= & {} 2[e^\mathrm{T}(t)M_{1}+\dot{e}^\mathrm{T}(t)M_{2}]\nonumber \\&\quad \left[ -\dot{e}(t)-C(r(t))e(t-\sigma )+A(r(t))g(e(t))\right. \nonumber \\&\left. + B(r(t))g(e(t-d_{1}(t)))+D(r(t))\right. \nonumber \\&\quad \left. \int ^{t}_{t-d_{2}(t)}g(e(s))ds+K(r(t))e(t-d_{3}(t))\right] \nonumber \\ \end{aligned}$$

(19)

Add (15)–(19) to $\dot{V}_{1}(t)$-$\dot{V}_{5}(t)$, and then deal with the items. Separating the definite items from the uncertain items in $A(\cdot )$, $B(\cdot )$, $C(\cdot )$ and $D(\cdot )$, the following results can be obtained:

$$\begin{aligned} \bar{\varPhi }_{3}= \begin{bmatrix} \underbrace{0\cdots 0}_{19n}&-M_{1}\varDelta C&0&M_{1}\varDelta D&M_{1}\varDelta A&M_{1}\varDelta B\\ \underbrace{0\cdots 0}_{19n}&0&0&0&0&0\\ \vdots&\cdots&\cdots&\cdots&\cdots&\cdots \\ \underbrace{0\cdots 0}_{19n}&-M_{2}\varDelta C&0&M_{2}\varDelta D&M_{2}\varDelta A&M_{2}\varDelta B\\ \underbrace{0\cdots 0}_{19n}&0&0&0&0&0\\ \underbrace{0\cdots 0}_{19n}&0&0&0&0&0\\ \underbrace{0\cdots 0}_{19n}&0&0&0&0&0 \end{bmatrix} \end{aligned}$$

where $\bar{\varPhi }_{3}$ is a matrix consisting of uncertain terms and $\varPhi _{3}$ is a matrix consisting of deterministic terms, as shown in (14). Next, lemma 5 is used for matrix $\bar{\varPhi }_{3}$, which can be obtained as follows:

$$\begin{aligned}&\begin{bmatrix} M_{1}G\\ 0\\ \vdots \\ 0\\ M_{2}G\\ 0\\ 0\\ 0 \end{bmatrix} F(t) \begin{bmatrix} 0\\ \vdots \\ 0\\ -E_{3}^\mathrm{T}\\ 0\\ E_{4}^\mathrm{T}\\ E_{1}^\mathrm{T}\\ E_{2}^\mathrm{T} \end{bmatrix}^\mathrm{T} + \begin{bmatrix} 0\\ \vdots \\ 0\\ -E_{3}^\mathrm{T}\\ 0\\ E_{4}^\mathrm{T}\\ E_{1}^\mathrm{T}\\ E_{2}^\mathrm{T} \end{bmatrix} F^\mathrm{T}(t) \begin{bmatrix} M_{1}G\\ 0\\ \vdots \\ 0\\ M_{2}G\\ 0\\ 0\\ 0 \end{bmatrix}^\mathrm{T} \nonumber \\&\quad \le \varepsilon ^{-1} \begin{bmatrix} M_{1}G\\ 0\\ \vdots \\ 0\\ M_{2}G\\ 0\\ 0\\ 0 \end{bmatrix} \begin{bmatrix} M_{1}G\\ 0\\ \vdots \\ 0\\ M_{2}G\\ 0\\ 0\\ 0 \end{bmatrix}^\mathrm{T} +\varepsilon \begin{bmatrix} 0\\ \vdots \\ 0\\ -E_{3}^\mathrm{T}\\ 0\\ E_{4}^\mathrm{T}\\ E_{1}^\mathrm{T}\\ E_{2}^\mathrm{T} \end{bmatrix} \begin{bmatrix} 0\\ \vdots \\ 0\\ -E_{3}^\mathrm{T}\\ 0\\ E_{4}^\mathrm{T}\\ E_{1}^\mathrm{T}\\ E_{2}^\mathrm{T} \end{bmatrix}^\mathrm{T}\nonumber \\ \end{aligned}$$

(20)

For convenience, let $M_{1}=\varepsilon _{1}M_{2}$ and $\chi _{i}=M_{2}K_{i}$, $\varepsilon _{1}$ is an arbitrary real number. To sum up, combined with (20), we can get:

$$\begin{aligned} \dot{V}(x(t),t,r(t))\le \xi ^{T}\varUpsilon (d_{i}(t),\dot{d}_{1}(t))\xi (t) \end{aligned}$$

(21)

where

$$\begin{aligned}&\varUpsilon (d_{i}(t),\dot{d}_{1}(t))\nonumber \\&\quad =\begin{bmatrix} \varPsi (d_{i}(t),\dot{d}_{1}(t))&\varPi _{1}^\mathrm{T}X_{1}&\varPi _{2}^\mathrm{T}X_{2}&\varPi _{3}^\mathrm{T}X_{3}&\varPi _{4}^\mathrm{T}X_{4}&\varPhi _{1}&\varPhi _{2}\\ *&\varDelta _{22}&0&0&0&0&0\\ *&*&\varDelta _{33}&0&0&0&0\\ *&*&*&\varDelta _{44}&0&0&0\\ *&*&*&*&\varDelta _{55}&0&0\\ *&*&*&*&*&-\varepsilon I&0\\ *&*&*&*&*&*&-\frac{1}{\varepsilon }I \end{bmatrix}\nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned}&\varPsi (d_{i}(t),\dot{d}_{1}(t))\nonumber \\&\quad =\varOmega (d_{i}(t),\dot{d}_{1}(t))+e_{1}^\mathrm{T}\sum ^{4}_{i=1}Q_{i}e_{1}\nonumber \\&\quad -(1-\dot{d}_{1}(t))e_{2}^\mathrm{T}Q_{1}e_{2}\nonumber \\&\quad -e_{20}^\mathrm{T}Q_{2}e_{20}-e_{3}^\mathrm{T}Q_{3}e_{3}\nonumber \\&\quad - e_{11}^\mathrm{T}Q_{4}e_{11}+e_{21}^\mathrm{T}(d_{1}R_{1}+d_{3}R_{2})e_{21}\nonumber \\&\quad -\varPi _{1}^\mathrm{T}(X_{1}M+M^\mathrm{T}X_{1}^\mathrm{T})\varPi _{1}-\varPi _{2}^\mathrm{T}(X_{2}M\nonumber \\&\quad + M^\mathrm{T}X_{2}^\mathrm{T})\varPi _{2}-\varPi _{3}^\mathrm{T}(X_{3}M+M^\mathrm{T}X_{3}^\mathrm{T})\varPi _{3}\nonumber \\&\quad -\varPi _{4}^\mathrm{T}(X_{4}M+M^\mathrm{T}X_{4}^\mathrm{T})\varPi _{4}\nonumber \\&\quad + e_{21}^\mathrm{T}\left[ \left( \frac{d_{1}^{2}}{2}\right) ^{2}Z_{1}+\left( \frac{d_{3}^{2}}{2}\right) ^{2}Z_{2}\right] e_{21}\nonumber \\&\quad -[d_{1}e_{1}-e_{16}]^\mathrm{T}Z_{1}[d_{1}e_{1}-e_{16}]\nonumber \\&\quad -2\left[ -\frac{d_{1}}{2}e_{1}-e_{16} + \frac{3}{d_{1}}e_{17}\right] ^\mathrm{T}\nonumber \\&\quad Z_{1}\left[ -\frac{d_{1}}{2}e_{1}-e_{16}+\frac{3}{d_{1}}e_{17}\right] \nonumber \\&\quad -[d_{3}e_{1}-e_{18}]^\mathrm{T}Z_{2}[d_{3}e_{1}-e_{18}]\nonumber \\&\quad -2\left[ -\frac{d_{3}}{2}e_{1}- e_{18}+\frac{3}{d_{3}}e_{19}\right] ^\mathrm{T}Z_{2}\left[ -\frac{d_{3}}{2}e_{1}-e_{18}\right. \nonumber \\&\quad \left. +\frac{3}{d_{3}}e_{19}\right] +d_{2}e_{1}^\mathrm{T}Se_{1}\nonumber \\&\quad -\delta _{1}[e_{23}^\mathrm{T}e_{23}-e_{1}^\mathrm{T}L^{T}Le_{1}]-\delta _{2}[e_{24}^\mathrm{T}e_{24}-e_{2}^\mathrm{T}L^\mathrm{T}Le_{2}]\nonumber \\&\quad -\delta _{3}d_{2}^{-1}e_{22}^\mathrm{T}e_{22}+\varPhi _{3}\end{aligned}$$

(23)

$$\begin{aligned}&\varOmega (d_{i}(t),\dot{d}_{1}(t))\nonumber \\&=He\{T_{0}^\mathrm{T}(\dot{d}_{1}(t))P_{P}(r(t))T_{1}(d_{1}(t))\}\nonumber \\&\quad +T_{1}^\mathrm{T}(d_{1}(t))\sum ^{N}_{j=1}\mu _{ij}P_{j}(r(t))T_{1}(d_{1}(t))\nonumber \\&\quad +T_{1}^\mathrm{T}(d_{1}(t))\left( \frac{dP_{P}(r(t))}{dt}\right) T_{1}(d_{1}(t)) \end{aligned}$$

(24)

$$\begin{aligned}&\xi (t)\nonumber \\&\quad = col\left\{ \quad e(t)\quad e(t-d_{1}(t))\quad e(t-d_{1})\right. \nonumber \\&\quad \left. \dot{e}(t-d_{1}(t))\quad \dot{e}(t-d_{1})\right. \nonumber \\&\quad \left. \frac{1}{d_{1}(t)}\int ^{t}_{t-d_{1}(t)}e(s)ds\quad \frac{1}{d_{1}-d_{1}(t)}\right. \nonumber \\&\quad \left. \int ^{t-d_{1}(t)}_{t-d_{1}}e(s)ds\quad \frac{1}{d_{1}^{2}(t)}\int ^{0}_{-d_{1}(t)}\int ^{t}_{t+\theta }e(s)dsd\theta \right. \nonumber \\&\quad \left. \frac{1}{(d_{1}-d_{1}(t))^{2}}\int ^{-d_{1}(t)}_{-d_{1}}\right. \nonumber \\&\quad \left. \int ^{t-d_{1}(t)}_{t+\theta }e(s)dsd\theta \quad e(t-d_{3}(t))\quad e(t-d_{3})\right. \nonumber \\&\quad \left. \frac{1}{d_{3}(t)}\int ^{t}_{t-d_{3}(t)}e(s)ds\quad \frac{1}{d_{3}-d_{3}(t)}\int ^{t-d_{3}(t)}_{t-d_{3}}e(s)ds\right. \nonumber \\&\quad \left. \frac{1}{d_{3}^{2}(t)}\right. \nonumber \\&\quad \left. \int ^{0}_{-d_{3}(t)}\int ^{t}_{t+\theta }e(s)dsd\theta \quad \right. \nonumber \\&\quad \left. \frac{1}{(d_{3}-d_{3}(t))^{2}}\int ^{-d_{3}(t)}_{-d_{3}}\int ^{t-d_{3}(t)}_{t+\theta }e(s)dsd\theta \right. \nonumber \\&\quad \left. \int ^{t}_{t-d_{1}}e(\theta )d\theta \quad \int ^{t}_{t-d_{1}}\int ^{t}_{\theta }e(s)dsd\theta \right. \nonumber \\&\quad \left. \int ^{t}_{t-d_{3}}e(\theta )d\theta \quad \int ^{t}_{t-d_{3}}\right. \nonumber \\&\quad \left. \int ^{t}_{\theta }e(s)dsd\theta \quad e(t-\sigma )\quad \dot{e}(t)\right. \nonumber \\&\quad \left. \int ^{t}_{t-d_{2}(t)}g(e(s))ds\quad g(e(t))\right. \nonumber \\&\quad \left. g(e(t-d_{1}(t)))\right\} \end{aligned}$$

(25)

Therefore, as long as satisfying (22) is negative definite, then $\dot{V}(x(t),t,r(t))$ is strictly negative definite in the interval $d_{1}(t)\in [0,d_{1}]$, $\dot{d}_{1}(t)\in [h_{1},h_{2}]$. According to Lyapunov stability theory, under the control of the sample point controller, the MJNN-DS (1) and the MJNN-RS (2) are completely synchronized. Sample point controller parameters can be obtained: $K_{i}=M_{2}^{-1}\chi _{i}$.

Remark 7

In (24), because of the existence of $\frac{dP_{P}(r(t))}{dt}$, we cannot directly calculate the results by MATLAB, so we use Lemma 3 to deform $P_{P}(r(t))$. The results are as follows:

$$\begin{aligned} \mathcal {D}_{1}= & {} \left\{ P_{P}(r(t))|P_{P}(r(t))\right. \nonumber \\&\left. =\sum ^{M}_{l=1}r_{l}(t)P_{P}^{(l)}, \sum ^{M}_{l=1}r_{l}(t)=1,r_{l}(t)\ge 0 \right\} \end{aligned}$$

(26)

where $P_{P}^{(l)}$ expresses respective polyhedron apex. The time-varying transition rates in $P_{P}(r(t))$ deforms as follows:

$$\begin{aligned} P_{P}(r(t))= & {} \sum _{l=1}^{M}r_{l}(t)P_{P}^{(l)}\Longrightarrow \frac{dP_{P}(r(t))}{dt}\\= & {} \sum _{l=1}^{M}\dot{r}_{l}(t)P_{P}^{(l)}=\sum _{n=1}^{M-1}\dot{r}_{n}(t)(P_{P}^{(n)}-P_{P}^{(M)}) \end{aligned}$$

According to (22), we have

$$\begin{aligned}&\varUpsilon (d_{i}(t),\dot{d}_{1}(t))\\&\quad =\sum _{l=1}^{M}r_{l}^{2}(t)\bar{\varUpsilon }_{P}^{(ll)}(d_{i}(t),\dot{d}_{1}(t))\\&\qquad +\sum _{l=1}^{M-1}\sum _{s=l+1}^{M}r_{l}(t)r_{s}(t)(\bar{\varUpsilon }_{P}^{(ls)}(d_{i}(t),\dot{d}_{1}(t))\\&\qquad + \bar{\varUpsilon }_{P}^{(sl)}(d_{i}(t),\dot{d}_{1}(t)))<0 \end{aligned}$$

where $\bar{\varUpsilon }_{P}^{(ls)}(d_{i}(t),\dot{d}_{1}(t))$ is equivalent to $\varUpsilon (d_{i}(t),\dot{d}_{1}(t))$ except $\bar{\varOmega }_{P}^{(ls)}(d_{i}(t),\dot{d}_{1}(t))$, it is expressed as follows:

$$\begin{aligned}&\bar{\varOmega }_{P}^{(ls)}(d_{i}(t),\dot{d}_{1}(t))\nonumber \\&\quad =He\{T_{0}^\mathrm{T}(\dot{d}_{1}(t))P_{P}^{(l)}T_{1}(d_{1}(t))\}\nonumber \\&\qquad +T_{1}^\mathrm{T}(d_{1}(t))\sum ^{N}_{j=1}\mu _{ij}^{(l)}P_{j}^{(s)}T_{1}(d_{1}(t))\nonumber \\&\qquad +T_{1}^\mathrm{T}(d_{1}(t))\sum ^{M-1}_{n=1}\dot{r}_{n}(t)(P_{P}^{(n)}-P_{P}^{(M)})T_{1}(d_{1}(t))\nonumber \\ \end{aligned}$$

(27)

We can get (6)–(9) by using the method of dealing with $\sum ^{M-1}_{n=1}\dot{r}_{n}(t)(P_{P}^{(n)}-P_{P}^{(M)})$ in [3]. Therefore, as long as (6) is satisfied, (22) is strictly negative definite. This completes the proof. $\square$

Remark 8

When using Lemma 1 to deal with $\dot{V}(t)$, we set the Legendre parameter $N=2$. If we take $N=1$, we just need to replace $\eta _{1}(t)$ with $\bar{\eta }_{1}(t)=[e^\mathrm{T}(t)\quad e^\mathrm{T}(t-d_{1}(t))\quad e^\mathrm{T}(t-d_{1})\quad \int ^{t}_{t-d_{1}(t)}e^\mathrm{T}(s)ds \int ^{t-d_{1}(t)}_{t-d_{1}}e^\mathrm{T}(s)ds]^\mathrm{T}$, and the rest of the processing is basically the same as Theorem 1.

Remark 9

If we increase the Legendre parameter N, we can get a stricter bound for the integral term in $\dot{V}_{3}(t)$. In this case, Lyapunov functions, especially $\eta _{1}(t)$ in $V_{1}$, should be changed appropriately in the order of increasing N to obtain a less conservative stability condition. $N=1$ and $N=2$ correspond to $\int ^{b}_{a}e(s)ds$ and $\frac{1}{(b-a)}\int ^{b}_{a}\int ^{b}_{\theta }e(s)dsd\theta$ in $\eta _{1}(t)$, respectively. When $N>2$, corresponding to the following: $\frac{1}{(b-a)^{N-1}}\int ^{b}_{a}\int ^{b}_{\alpha _{1}}\cdots \int ^{b}_{\alpha _{N-1}}e(\alpha _{N})d\alpha _{N}\cdots d\alpha _{2}d\alpha _{1}$.

Remark 10

When considering the range of time-varying delays, it is generally set to: $h_{1}\le h\le h_{2}$, $d_{1}\le \dot{h}\le d_{2}$. For the convenience of the next discussion, we present the delay and its derivatives in a two-dimensional plane as shown in Fig. 1.

Fig. 1

Area in general sense

Fig. 2

Area improved in this paper

The plane presents a rectangle, and the coordinates of its four vertices are: $(h_{1},d_{1})$, $(h_{1},d_{2})$, $(h_{2},d_{1})$ and $(h_{2},d_{2})$. The area of rectangle is the range of time-varying delays. It is improved by [21]. Change the four vertices into the following: (0, 0), $(h_{1},d_{2})$, $(h_{2},0)$ and $(h_{2},d_{1})$. The shape is shown in Fig. 2. It can be seen that in the same time-delay interval, the area of Fig. 2 is smaller than that of Fig. 1, which indicates that it is less conservative. Therefore, Theorem 1 can be optimized by this theory, and the results are as follows.

Theorem 2

Same as Theorem 1, MJNN-DS (1) and MJNN-RS (2) achieve complete synchronization, if the following hold:

$$\begin{aligned}&\varUpsilon _{P}^{(ls)}(0,0)+\varUpsilon _{P}^{(sl)}(0,0)<0 \end{aligned}$$

(28)

$$\begin{aligned}&\varUpsilon _{P}^{(ls)}(0,h_{2})+\varUpsilon _{P}^{(sl)}(0,h_{2})<0 \end{aligned}$$

(29)

$$\begin{aligned}&\varUpsilon _{P}^{(ls)}(d_{i},h_{1})+\varUpsilon _{P}^{(sl)}(d_{i},h_{1})<0 \end{aligned}$$

(30)

$$\begin{aligned}&\varUpsilon _{P}^{(ls)}(d_{i},0)+\varUpsilon _{P}^{(sl)}(d_{i},0)<0\quad i=1,3 \end{aligned}$$

(31)

where $\varUpsilon _{P}^{(ls)}(\cdot )+\varUpsilon _{P}^{(sl)}(\cdot )<0$ is defined in (6).

4 Numerical examples

Firstly, Examples 1 and 2 illustrate the validity of affine Bessel–Legendre inequalities and Wirtinger double integral inequalities. Secondly, Example 3 illustrates the effectiveness of optimizing two-dimensional space of time delay. Finally, Example 4 shows that under the control of sample point controller, MJNN-DS (1) and MJNN-RS (2) can achieve synchronization.

Example 1

Consider the following two modes and the matrix parameters[16]:

$$\begin{aligned} A_{1}= & {} \begin{bmatrix} 0.5&-1\\ 0&-3\\ \end{bmatrix} \quad A_{2}= \begin{bmatrix} -5&1\\ 1&0.2\\ \end{bmatrix}\\ B_{1}= & {} \begin{bmatrix} 0.5&-0.2\\ 0.2&0.3\\ \end{bmatrix} \quad B_{2}= \begin{bmatrix} -0.3&0.5\\ 0.4&-0.5\\ \end{bmatrix} \end{aligned}$$

with transition rates matrix

$$\begin{aligned} \varPi = \begin{bmatrix} -7&7\\ 3&-3\\ \end{bmatrix} \end{aligned}$$

Let $h_{2}=0$, $\mu _{11}=-7$. We compare the upper bounds of time-varying delays. The results are shown in Table 1. From Table 1, we can see that with the increase in N, the better the effect of affine Bessel–Legendre inequalities is.

Table 1 Different results to $d_{1}$ for Example 1

Example 2

The following two modes and the matrix parameters[16] are hold:

$$\begin{aligned} A_{1}= & {} \begin{bmatrix} -3.4888&0.8057\\ -0.6451&-3.2684\\ \end{bmatrix} \nonumber \\ A_{2}= & {} \begin{bmatrix} -2.4898&0.2895\\ 1.3396&-0.0211\\ \end{bmatrix}\\ B_{1}= & {} \begin{bmatrix} -0.8620&-1.2919\\ -0.6841&-2.0729\\ \end{bmatrix}\nonumber \\ B_{2}= & {} \begin{bmatrix} -2.8306&0.4978\\ -0.8436&-1.0115\\ \end{bmatrix} \end{aligned}$$

with transition rates matrix

$$\begin{aligned} \varPi = \begin{bmatrix} -0.1&0.1\\ 0.8&-0.8\\ \end{bmatrix} \end{aligned}$$

By setting different upper bounds of delay derivatives $h_{2}$, we obtain different upper bounds of delay as shown in Table 2. From Table 2, we can see that with the increase in N, the better the effect of affine Bessel–Legendre inequalities is.

Table 2 Different results to $d_{1}$ for Example 2

Example 3

Consider MJNN-DS (1) and MJNN-RS (2) with two modes and the matrix parameters:

$$\begin{aligned} A_{1}= & {} \begin{bmatrix} 0&0.6\\ 0&1\\ \end{bmatrix} \quad B_{1}= \begin{bmatrix} 0.5&0.9\\ 0&2\\ \end{bmatrix}\\ C_{1}= & {} \begin{bmatrix} 1&0\\ 1&0\\ \end{bmatrix} \quad D_{1}= \begin{bmatrix} 0.9&0\\ 1&1.6\\ \end{bmatrix}\\ A_{2}= & {} \begin{bmatrix} -4.5&2\\ -0.8&-4.3\\ \end{bmatrix} \quad B_{2}= \begin{bmatrix} -3.5&1.2\\ 1.0&-1.9\\ \end{bmatrix}\\ C_{2}= & {} \begin{bmatrix} 0.6&1.6\\ 1.8&-1.1\\ \end{bmatrix} \quad D_{2}= \begin{bmatrix} 1.6&0.5\\ -0.7&1.0\\ \end{bmatrix}\\ G= & {} \begin{bmatrix} 0.1&0\\ 0&0.1\\ \end{bmatrix} \quad E_{i}= \begin{bmatrix} 0.2&0\\ 0&0.2\\ \end{bmatrix}\\ i= & {} 1,2,3,4 \quad L= \begin{bmatrix} 0.1&0\\ 0&0.1\\ \end{bmatrix} \end{aligned}$$

Assume that the transition rate matrix is time-varying in the following vertex polyhedron $\varPi (t)=sin^{2}(t)\varPi ^{(1)}+cos^{2}(t)\varPi ^{(2)}$:

$$\begin{aligned} \varPi ^{(1)}= \begin{bmatrix} -0.8&0.8\\ 0.6&-0.6\\ \end{bmatrix} \quad \varPi ^{(2)}= \begin{bmatrix} -0.6&0.6\\ 0.8&-0.8\\ \end{bmatrix} \end{aligned}$$

Let $\delta _{1}=\delta _{2}=\delta _{3}=\varepsilon =\varepsilon _{1}=0.1$. When $N=2$, the time-varying delay range obtained from Theorem 1: $0\le d_{1}(t)\le 1.63$. Similarly, the time-varying delay range obtained from Theorem 2: $0\le d_{1}(t)\le 1.70$. It can be shown that Theorem 2 is effective in optimizing the two-dimensional geometric space of time delay.

Example 4

Consider MJNN-DS (1) and MJNN-RS (2) with two modes and the matrix parameters:

$$\begin{aligned}&A_{1}= \begin{bmatrix} 0&0.6\\ 0&1\\ \end{bmatrix} \quad B_{1}= \begin{bmatrix} 0.5&0.9\\ 0&2\\ \end{bmatrix}\\&C_{1}= \begin{bmatrix} 1&0\\ 1&0\\ \end{bmatrix} \quad D_{1}= \begin{bmatrix} 0.9&0\\ 1&1.6\\ \end{bmatrix}\\&A_{2}= \begin{bmatrix} -4.5&2\\ -0.8&-4.3\\ \end{bmatrix} \quad B_{2}= \begin{bmatrix} -3.5&1.2\\ 1.0&-1.9\\ \end{bmatrix}\\&C_{2}= \begin{bmatrix} 0.6&1.6\\ 1.8&-1.1\\ \end{bmatrix} \quad D_{2}= \begin{bmatrix} 1.6&0.5\\ -0.7&1.0\\ \end{bmatrix}\\&G= \begin{bmatrix} 0.1&0\\ 0&0.1\\ \end{bmatrix}\\&E_{i}= \begin{bmatrix} 0.2&0\\ 0&0.2\\ \end{bmatrix}\\&i=1,2,3,4 \quad L= \begin{bmatrix} 0.1&0\\ 0&0.1\\ \end{bmatrix} \end{aligned}$$

Fig. 3

Chaotic curve

Fig. 4

Time response of r(t)

Fig. 5

Time response of $x_{1}(t),y_{1}(t)$

Fig. 6

Time response of $x_{2}(t),y_{2}(t)$

Fig. 7

Time response of $e_{1}(t)$

Fig. 8

Time response of $e_{2}(t)$

Assume that the transition rate matrix is time-varying in the following vertex polyhedron $\varPi (t)=sin^{2}(t)\varPi ^{(1)}+cos^{2}(t)\varPi ^{(2)}$:

$$\begin{aligned} \varPi ^{(1)}= & {} \begin{bmatrix} -0.8&0.8\\ 0.6&-0.6\\ \end{bmatrix}\\ \varPi ^{(2)}= & {} \begin{bmatrix} -0.6&0.6\\ 0.8&-0.8\\ \end{bmatrix} \end{aligned}$$

Let $\delta _{1}=\delta _{2}=\delta _{3}=\varepsilon =\varepsilon _{1}=0.1$, the range of mixed time-varying delay is: $0\le d_{1}(t)\le 1.7$, $0\le d_{2}(t)\le 0.3$, $0\le d_{3}(t)\le 1.9$, $0.1\le \dot{d}_{1}(t)\le 0.6$. Substitute the above data into Theorem 2, we can get the parameters of the sample point controller as follows:

$$\begin{aligned} K_{1}= & {} \begin{bmatrix} -6.35965433&2.82331641\\ 2.82331676&-9.48809923\\ \end{bmatrix}\\ K_{2}= & {} \begin{bmatrix} -6.35965406&2.82331609\\ 2.82331651&-9.48809847\\ \end{bmatrix} \end{aligned}$$

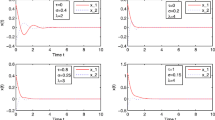
The neuron excitation function is $f(x)=tanhx$. The initial condition is $x_{0}(\theta )=[-0.3,2,1.2]$. As shown in Fig. 3, when MJNN (1) takes the above parameters, it shows obvious chaotic characteristics. Figure 4 is a Markov jump response curve with time-varying probability transition perturbations. Figures 5 and 6 describe the time state curves of MJNN-DS (1) and MJNN-RS (2). Figures 7 and 8 describe the convergence behavior of errors between MJNN-DS (1) and MJNN-RS (2). The numerical simulation shows the validity of the sample point controller for the complete synchronization of MJNN-DS (1) and MJNN-RS (2) with mixed time-varying delay and parameter uncertainties.

5 Conclusions

In this paper, a sample point controller is used to synchronize the DS and RS of MJNN with mixed time-varying delay and uncertain parameters. When dealing with error systems, Wirtinger double integral inequalities and affine Bessel–Legendre inequalities are introduced into Lyapunov functional to reduce conservativeness. In addition, when discussing the two-dimensional geometric area with time-varying delays, the conservativeness is reduced by changing the vertex of the polyhedron without changing the range of the delays. Finally, it is verified by numerical simulation that MJNN-DS and MJNN-RS are fully synchronized under the control of sample point controller, and the parameters of the controller are obtained.