Abstract
In this paper, the synchronization problem and its application in secret communication are investigated for two fractional-order chaotic systems with unequal orders, different structures, parameter uncertainty and bounded external disturbance. On the basis of matrix theory, properties of fractional calculus and adaptive control theory, we design a feedback controller for realizing the synchronization. In addition, in order to make it better apply to secret communication, we design an optimal controller based on optimal control theory. In the meantime, we propose an improved quantum particle swarm optimization (QPSO) algorithm by introducing an interval estimation mechanism into QPSO algorithm. Further, we make use of QPSO algorithm with interval estimation to optimize the proposed controller according to some performance indicator. Finally, by comparison, numerical simulations show that the controller not only can achieve the synchronization and secret communization well, but also can estimate the unknown parameters of the systems and bounds of external disturbance, which verify the effectiveness and applicability of the proposed control scheme.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Fractional calculus has a long history, which can be traced back to the end of the seventeenth century. As an ancient concept, the fractional calculus has not been paid more attention on account of its intrinsic complexity and lack of foreseen applications until it is applied to physics and engineering recently [1, 2]. Superficially, the fractional calculus is a generalization of the ordinary differentiation and integration to arbitrary order [3]. In fact, it has also its own characteristics. Researches have shown that many systems with memory feature and some complex materials can be more concisely and actually described by fractional-order derivatives, such as the diffusion process, the heat transfer process, viscoelastic systems, the dielectric polarization, electromagnetic waves and the effect of the frequency on induction machines [4,5,6]. Therefore, the fractional-order model can describe the real-world physical phenomena more reasonably and accurately than the classical integer-order one at times, which makes the fractional calculus play an important role in the research of complex dynamic systems [7].
In recent years, many investigations are focused on dynamic characteristics of fractional-order chaotic or hyperchaotic systems such as fractional-order Lorenz system [8], fractional-order Rössler system [9], fractional-order Chen system [10], fractional-order Lü system [11], fractional-order Chua’s system [12, 13], fractional-order Duffing system [14]. Chaotic phenomenon exists in nature and society widely. As an essential branch of chaotic systems, the fractional-order chaotic systems have been found in physics, biology, sociology, economy and so on. Due to the fact that there exist strong nonlinear dynamic characteristics, the fractional-order chaotic systems have been applied to many fields [15], such as signal processing, synchronization control, electronic circuits, encryption–decryption and secret communication [16,17,18,19], especially in the latter.
Up to now, how to design an appropriate controller to realize the synchronization between the drive system and response system has been a hot topic in the field of control. As a result, various control schemes are put forward and validated successfully, which include PID control [20], linear and nonlinear feedback control [21, 22], active control [23], state observer control [24, 25], projective control [26], sliding mode control [27, 28], impulsive control [29,30,31], phase synchronization[32], multi-scale synchronization[33, 34], robust control [35,36,37], adaptive control [38, 39] and so on.
Originally, the purpose for two same systems with different initial values is to make the response system track on the drive system completely [11, 40]. But considering the actual situation, the two systems are with different structures as usual. Then the synchronization between different systems is reached [41, 42], which promotes the further development of relevant research. However, the full or partial parameters of the two systems are likely to unknown in reality. Afterward, the research on parameter uncertainty has attracted much attention and made some progress [7, 43]. Nevertheless, most of the previous works are based on identical order from the drive system and response system. In fact, many problems are not with the above feature. Furthermore, as a matter of fact, the environment noise or external disturbance, mechanical vibration or oscillation, stochastic perturbation and other non-artificial factors will have also a negative effect on the systems. Although there have been some research results, such as the synchronization of nonidentical chaotic fractional-order systems with different orders of fractional derivatives [44], the disturbance observer-based robust synchronization control for a class of fractional-order chaotic systems [45] and the synchronization of two different fractional-order chaotic systems with fully unknown parameters and external disturbances [43], previous works include only the partial cases of them as above. If the factors are not taken into full consideration, there will exist certain deviation from the result. Meanwhile, most of the results are based on linearized models and methods, which makes them loss the generality. It is worth noting that the synchronized systems with minimum error can provide higher reliability and more efficient results for secure communication process. But, there exist much randomness such as parameter selection for the controller in previous methods, which cannot guarantee that the controller we designed is an optimal controller in a way.
Motivated by the above analysis, the contribution of this paper mainly displays in four aspects as follows: (i) a new controller is proposed on the basis of the knowledge including matrix theory, fractional calculus and adaptive control, which makes the synchronization problem with unequal orders, different structures, parameter uncertainty and unknown bounded external disturbance between the drive system and response system solved. (ii) In order to reduce the influence of external disturbance on synchronization error effectively, we further design an optimal controller based on optimization theory. (iii) Through bringing an interval estimation strategy into quantum particle swarm optimization (QPSO) algorithm, we put forward an improved QPSO algorithm named by QPSO algorithm with interval estimation (IEQPSO) according to the practical problem. Meanwhile, IEQPSO is used for optimizing the controller. (iv) The proposed controller is applied in the field of secret communication successfully, which makes the signal source encrypted well and decoded precisely. As an actual application, it conforms the generality and practicability of the proposed control scheme.
The rest of this paper is organized as follows. In Sect. 2, we introduce the relevant definitions of fractional calculus and some new operators. Besides, we state the problem to be solved. Combining with the property of fractional calculus, matrix theory and adaptive control theory, the controllers which can deal with many types of complicated synchronization problem are designed in two different cases, respectively, in Sect. 3. In the meantime, we give some extension of the controllers in this section. Based on optimal control theory, an optimal controller is proposed according to some performance indicator in Sect. 4. Furthermore, as an improved QPSO algorithm, IEQPSO algorithm is put forward and used to optimize the parameters in the controller in this section. In Sect. 5, we first verify the validity of IEQPSO algorithm by some benchmark functions. Besides, two numerical examples including the synchronization of fractional-order chaotic systems and its application in secret communication are conducted for the different cases, respectively, in this section. Finally, a summary to this paper is made in Sect. 6.
Notations In this paper, R stands for the set of real numbers, C for the set of complex numbers, \(Z^{+}\) for the set of positive real integers. For a matrix \(\varvec{A}\in R^{n\times n}\), \(\varvec{A}^{T}\) and \(\varvec{A}^{-1}\) denote the transpose and inverse of \(\varvec{A}\), respectively. As a special matrix, \(\varvec{I}_{n}\) stands for the unit matrix with n dimensions. Meanwhile, \(\varvec{1}_{n}\) is a column vector consisting of the diagonal elements of \(\varvec{I}_{n}\). For \(x\in R\), [x] denotes the largest integer no more than x, and |x| represents \(x\cdot \mathrm {sign}(x)\). Besides, \(\otimes \) stands for the Kronecker product. For convenience, \({}_{{{t}_{0}}}D_{t}^{q}\) and \({}_{{{t}_{0}}}J_{t}^{q}\) are simplified as \(D^{q}\) and \(J^{q}\), respectively. For the matrices \(\breve{\varvec{p}}=[\breve{p}_{1},\breve{p}_{2},\ldots ,\breve{p}_{n}]^{T}\) and \(\varvec{x}=[x_1,x_2,\ldots ,x_n]^{T}\), and a function \(\breve{f}(\cdot ):R \rightarrow R\), \(D^{\breve{\varvec{p}}}\varvec{x}\) and \(\breve{\varvec{f}}(\varvec{x})\) represent the operations \(D^{\breve{p}}\varvec{x}=[D^{\breve{p}_{1}}x_{1},D^{\breve{p}_{2}}x_{2},\ldots , D^{\breve{p}_{n}}x_{n}]^{T}\) and \(\breve{f}(\varvec{x})=[\breve{f}(x_{1}),\breve{f}(x_{2}),\ldots ,\breve{f}(x_{n})]^{T}\), respectively. In addition, for \(\breve{\varvec{p}}_{1}=[\breve{p}_{11},\breve{p}_{12},\ldots ,\breve{p}_{1n}]^{T}\) and \(\breve{\varvec{p}}_{2}=[\breve{p}_{21},\breve{p}_{22},\ldots , \breve{p}_{2n}]^{T}\) , we set that the operations \(\breve{\varvec{p}}_{1}\ne \breve{\varvec{p}}_{2}\), \(\breve{\varvec{p}}_{1}>\breve{\varvec{p}}_{2}\) and \(\breve{\varvec{p}}_{1}<\breve{\varvec{p}}_{2}\) mean \(\breve{p}_{1i}\ne \breve{p}_{2i}\), \(\breve{p}_{1i}>\breve{p}_{2i}\) and \(\breve{p}_{1i}<\breve{p}_{2i}\) for \(i=1,2,\ldots ,n\), respectively.
2 Preliminaries and problem statement
2.1 Theoretical basis
Definition 1
For \(q>0\), \(t\in [t_{0},t_{f}]\) and \(f(t)\in L_{1}[t_{0},t_{f}]\), the Riemann–Liouville fractional integral of the function f(t) is defined as
where \(J^{q}\) represents the fractional integral operator and \(\mathrm {\Gamma }(\cdot )\) is the Gamma function.
Definition 2
For \(m-1<q<m\) with \(m\in Z^{+}\), \(t\in [t_{0},t_{f}]\) and \(f^{(m)}(t)\in L_{1}[t_{0},t_{f}]\), the Caputo fractional derivative is described as
where \(D^{q}\) represents the fractional derivative operator. Moreover, it meets \(D^{q}c=0\) for a constant c. Next, we define a few operators for subsequent use.
Definition 3
For the vectors \(\varvec{a}=[a_{1},a_{2},\ldots ,a_{n}]^{T}\) and \(\varvec{b}=[b_{1},b_{2},\ldots ,b_{n}]^{T}\), the operator \(\overline{\varDelta }(\varvec{a},\varvec{b})\) is defined as
Definition 4
For \(\varvec{a}\) and \(\varvec{b}\) as above, if \(\varvec{b}\ne \varvec{0}\), the operator \(\underline{\varDelta }(\varvec{a},\varvec{b})\) is defined as
Definition 5
For the matrixes with same dimension \(\varvec{X}\) and \(\varvec{Y}^{T}\), the operator \(\mathrm {Ts}(\cdot )\) is defined as
Obviously, it meets \(\mathrm {Ts}^{T}(\varvec{X},\varvec{Y})=\mathrm {Ts}(\varvec{Y},\varvec{X})\).
2.2 Synchronization problem
For the synchronization problem between two fractional-order chaotic systems with unequal orders, different structures, parameter uncertainty and unknown external disturbance, the drive system is described as
where \(\varvec{p}=[p_{1},p_{2},\ldots ,p_{n}]^{T}\) and \(\varvec{x}=[x_{1},x_{2},\ldots ,x_{n}]^{T}\) are the fractional-order vector and state vector of the drive system, respectively, \(\varvec{f}(\cdot )=[f_{1}(\cdot ),f_{2}(\cdot ),\ldots ,f_{n}(\cdot )]^{T}\) is the function vector associated without the parameters in the drive system, \(\varvec{F}(\cdot )\in R^{n\times u}\) is the function matrix related to the parameters in the drive system, \(\varvec{\alpha }=[\alpha _{1},\alpha _{2},\ldots ,\alpha _{u}]^{T}\) is the parameter vector of the drive system, and \(\varvec{w}_{1}(t)=[w_{11}(t),w_{12}(t),\ldots ,w_{1n}(t)]^{T}\) is the unknown external disturbance vector of the drive system.
In the meantime, the response system is described as
where \(\varvec{q}=[q_{1},q_{2},\ldots ,q_{n}]^{T}\) and \(\varvec{y}=[y_{1},y_{2},\ldots ,y_{n}]^{T}\) are the fractional-order vector and state vector of the response system, respectively, \(\varvec{g}(\cdot )=[g_{1}(\cdot ),g_{2}(\cdot ),\ldots , g_{n}(\cdot )]^{T}\) is the function vector associated without the parameters in the response system, \(\varvec{G}(\cdot )\in R^{n\times v}\) is the function matrix related to the parameters in the response system, \(\varvec{\beta }=[\beta _{1},\beta _{2},\ldots ,\beta _{v}]^{T}\) is the parameter vector of the response system, and \(\varvec{w}_{2}(t)=[w_{21}(t),w_{22}(t), \ldots ,w_{2n}(t)]^{T}\) is the unknown external disturbance vector of the response system.
Definition 6
The synchronization error of the drive system and response system can be defined by
where \(\varvec{e}(t)=[e_{1}(t),e_{2}(t),\ldots ,e_{n}(t)]^{T}\) is the error vector with n dimensions. Obviously, if and only if \(\underset{t\rightarrow \infty }{\mathrm {lim}}\varvec{e}(t)=\varvec{0}\), the drive system and response system can achieve the synchronization. Namely, \(\varvec{y}(t)\rightarrow \varvec{x}(t)\) as \(t\rightarrow \infty \). So we need to design a controller on (7) for this purpose.
3 Controller design
Aiming at the proposed problem, we make the following assumptions firstly.
Assumption 1
There exist different orders between the drive system and response system. For fractional-order chaotic systems in reality, most of them are with orders less than \(\varvec{1}\). Therefore, it is assumed that \(\varvec{p}\ne \varvec{q}\) and \(\varvec{0}<\varvec{p},\varvec{q}<\varvec{1}\) in (6) and (7).
Assumption 2
For \(t\ge t_{0}\), \(\varvec{x}\in \varvec{\varOmega }_{1}\) and \(\varvec{y}\in \varvec{\varOmega }_{2}\), let \(\varvec{f}:[t_{0},\infty )\times \varvec{\varOmega }_{1}\rightarrow R^{n\times 1}\), \(\varvec{g}:[t_{0},\infty )\times \varvec{\varOmega }_{2}\rightarrow R^{n\times 1}\), \(\varvec{F}:[t_{0},\infty )\times \varvec{\varOmega }_{1}\rightarrow R^{n\times u}\) and \(\varvec{G}:[t_{0},\infty )\times \varvec{\varOmega }_{2}\rightarrow R^{n\times v}\) be all smooth functions. It is obvious that there exist the arbitrary-order derivative and integral for \(\varvec{f},\varvec{g},\varvec{F}\) and \(\varvec{G}\), where \(\varvec{x},\varvec{f}\) and \(\varvec{F}\) belong to (6), \(\varvec{y},\varvec{g}\) and \(\varvec{G}\) belong to (7).
Assumption 3
We assume that the unknown external disturbance is bounded. Namely, it meets \(|\varvec{w}_{1}(t)|\le \varvec{\xi }_{1}\) and \(|\varvec{w}_{2}(t)|\le \varvec{\xi }_{2}\) in (6) and (7), respectively. Meanwhile, it also satisfies \(|D^{\varvec{q}-\varvec{p}}\varvec{w}_{1}(t)|\le \varvec{\eta }_{1}\) for \(\varvec{0}<\varvec{p}<\varvec{q}<\varvec{1}\) and \(|D^{\varvec{p}-\varvec{q}}\varvec{w}_{2}(t)|\le \varvec{\eta }_{2}\) for \(\varvec{1}>\varvec{p}>\varvec{q}>\varvec{0}\). Therefore, \(|D^{\varvec{p}-\varvec{q}}\varvec{w}_{2}(t)-\varvec{w}_{1}(t)|\le \varvec{\xi }_{1}+\varvec{\eta }_{2}=\varvec{l}\) and \(|\varvec{w}_{2}(t)-D^{\varvec{q}-\varvec{p}}\varvec{w}_{1}(t)|\le \varvec{\eta }_{1}+\varvec{\xi }_{2}=\varvec{m}\), where \(\varvec{\xi }_{1},\varvec{\xi }_{2},\varvec{\eta }_{1},\varvec{\eta }_{2},\varvec{l},\varvec{m}\in R^{n\times 1}\) are constant vectors with n dimensions.
As to the complicated synchronization problem with different orders in the drive system and response system, the design of the controller is not very direct. Aiming at the problem, a new control scheme is proposed in this paper. On the basis of the size relationship of \(\varvec{p}\) and \(\varvec{q}\), the controllers are designed as follows.
3.1 Controller design as \(\varvec{1}>\varvec{p}>\varvec{q}>\varvec{0}\)
Lemma 1
[46] Let \(f:[t_{0},\infty )\rightarrow R\) be a smooth function. For \(n-1<p<n\), \(m-1<q<m\), \(p+q\le n\) and \(t\ge t_{0}\), the fractional derivative has the following relationship,
where \(n,m\in Z^{+}\), and \(m=[q]+1\).
Lemma 2
Let \(\varvec{x}(t)\in R^{n\times 1}\) be a continuous and derivable function vector, \(\varvec{A}\in R^{n\times n}\) is a positive definite matrix. For all \(t\ge t_{0}\) and \(\varvec{0}<\varvec{q}=[q_{1},q_{2},\ldots ,q_{n}]^{T}<\varvec{1}\), it follows
Proof
Since the positive definite matrix is with symmetry, there exists an orthogonal matrix \(\varvec{T}\in R^{n\times n}\) to make \(\varvec{T}^{-1}\varvec{A}\varvec{T}=\varvec{\varLambda }=\mathrm {diag}\{\lambda _{1},\lambda _{2},\ldots ,\lambda _{n}\}\) with \(\lambda _{i}>0\) for \(i=1,2,\ldots ,n\) according to matrix theory. Then \(\varvec{A}=\varvec{T}\varvec{\varLambda }\varvec{T}^{-1}=\varvec{T}\varvec{\varLambda }\varvec{T}^{T}\). Therefore, we have
Let \(\varvec{y}=\varvec{T}^{T}\varvec{x}=[y_{1},y_{2},\ldots ,y_{n}]^{T}\) and combine with Lemma 1 in [47], then (11) is equivalent to
So Lemma 2 is proved completely. \(\square \)
Theorem 1
For \(t\ge t_{0}\), there exist the diagonal positive definite matrix \(\varvec{M}\in R^{n\times n}\), positive definite matrices \(\varvec{N}\in R^{u\times u}\), \(\varvec{S}\in R^{n\times n}\), \(\varvec{U}\in R^{n\times n}\) and \(\varvec{V}\in R^{n\times n}\) to make system (6) and (7) synchronize if the conditions are satisfied as follows.
(i) The controller on system (7) is designed as
where \(\widetilde{\varvec{\alpha }}\in R^{u\times 1}\) and \(\widetilde{\varvec{\beta }}\in R^{v\times 1}\) are the estimates for \(\varvec{\alpha }\) and \(\varvec{\beta }\), respectively, \(\widetilde{\varvec{K}}=\mathrm {diag}\{\widetilde{k}_{1},\widetilde{k}_{2},\ldots ,\widetilde{k}_{n}\}\) and \(\widetilde{\varvec{L}}=\mathrm {diag}\{\widetilde{l}_{1},\widetilde{l}_{2},\ldots ,\widetilde{l}_{n}\}\) are the estimates for \(\varvec{K}=\mathrm {diag}\{k_{1},k_{2},\ldots ,k_{n}\}\) and \(\varvec{L}=\mathrm {diag}\{l_{1},l_{2},\ldots ,l_{n}\}\), respectively, and it satisfies \(k_{i}<0\) and \(l_{i}>0\) for \(i=1,2,\ldots ,n\). Furthermore, \(\varvec{e}=[e_{1},e_{2},\ldots ,e_{n}]^{T}\) is the error vector between the response system and drive system, \(\varvec{u}_{0}(t)\) and \(\varvec{r}_{1}(t)\) is, respectively, described as
(ii) Let \(\widetilde{\varvec{k}}=\widetilde{\varvec{K}}\cdot \varvec{1}_{n}\), \(\widetilde{\varvec{l}}=\widetilde{\varvec{L}}\cdot \varvec{1}_{n}\) and \(\varvec{E}=\mathrm {diag}\{\overline{\varDelta }(\varvec{e},\varvec{e})\}\cdot \varvec{1}_{n}\), then the unknown parameters to be estimated in the drive system can be updated by
where \(\widehat{\varvec{\alpha }}=\widetilde{\varvec{\alpha }}-\varvec{\alpha }\) and \(\widehat{\varvec{\beta }}=\widetilde{\varvec{\beta }}-\varvec{\beta }\) represents the estimation errors for \(\varvec{\alpha }\) and \(\varvec{\beta }\), respectively. Besides, \(\varvec{X}_{1}\in R^{u\times u}\) and \(\varvec{Y}_{1}\in R^{u\times n}\) comply with condition (iii).
The unknown parameters to be estimated in the response system can be updated by
where \(\varvec{X}_{2}\in R^{n\times u}\) and \(\varvec{Y}_{2}\in R^{n\times n}\) comply with condition (iii), and \(\varvec{m}(t)\) is presented as
The adaptive rate with uncertainty in the controller can be estimated by
The upper bound for the unknown external disturbances exists in the drive system and response system can be estimated by
(iii) \(\varvec{N}\varvec{X}_{1}<0\) and \(\varvec{S}\varvec{Y}_{2}<0\) are both negative definite matrixes with appropriate dimensions. In addition, it also satisfies the following condition.
Proof
For achieving a synchronization between (6) and (7), we bring \(\varvec{u}(t)\) into (7). Further, take \((\varvec{p}-\varvec{q})\)-order differential operation on both sides of it, which makes
where \(\varvec{U}(t)\) is described as
\(\square \)
Subtracting (6) from (22), we get
Let \(D^{\varvec{p}-\varvec{q}}(\varvec{G}(\varvec{y})\widehat{\varvec{\beta }})=\widehat{\varvec{B}}\), it holds
Let \(\varvec{k}=\varvec{K}\cdot \varvec{1}_{n}\) and \(\varvec{l}=\varvec{L}\cdot \varvec{1}_{n}\), and denote \(\widehat{\varvec{k}}=\widetilde{\varvec{k}}-\varvec{k}\) and \(\widehat{\varvec{l}}=\widetilde{\varvec{l}}-\varvec{l}\). The Lyapunov function is selected as
where \(V_{1}=\varvec{e}^{T}\varvec{M}\varvec{e}\), \(V_{2}=\widehat{\varvec{\alpha }}^{T}\varvec{N}\widehat{\varvec{\alpha }}\), \(V_{3}=\widehat{\varvec{B}}^{T}\varvec{S}\widehat{\varvec{B}}\), \(V_{4}=\widehat{\varvec{k}}^{T}\varvec{U}\widehat{\varvec{k}}\) and \(V_{5}=\widehat{\varvec{l}}^{T}\varvec{V}\widehat{\varvec{l}}\). So \(V=[\varvec{e}^{T},\widehat{\varvec{\alpha }}^{T},\widehat{\varvec{B}}^{T},\widehat{\varvec{k}}^{T},\widehat{\varvec{l}}^{T}]\cdot \mathrm {diag}\{\varvec{M},\varvec{N},\varvec{S},\varvec{U},\varvec{V}\}[\varvec{e}^{T}, \widehat{\varvec{\alpha }}^{T},\widehat{\varvec{B}}^{T},\widehat{\varvec{k}}^{T},\widehat{\varvec{l}}^{T}]^{T}\). Since \(\varvec{M}, \varvec{N},\varvec{S},\varvec{U},\varvec{V}>0\), it follows that \(\mathrm {diag}\{\varvec{M},\varvec{N},\varvec{S},\varvec{U},\varvec{V}\}>0\). Further, we have
In (27), it satisfies
Substituting (28) into (27), we obtain
Hence, the error system is asymptotically stable at the equilibrium point \(\varvec{0}\). Apparently, the synchronization problem to the two systems has been dealt, but the parameter identification question to \(\varvec{\beta }\) in the response system has not been solved yet.
Lemma 3
[3] Let \(f:[t_{0},\infty )\rightarrow R\) be a smooth function. For \(0<p\le q\), and \(t\ge t_{0}\), there exists the following relation between the fractional integral operator and fractional derivative operator
where \(m=[q]+1\).
Assumption 4
For the response system at \(t>T\), it is assumed as follows: (i) \(v=\mathrm {dim}(\varvec{\beta })\le n\); (ii) \(\varvec{G}(\varvec{y})\) is with full rank at some point; (iii) \(\varvec{G}(\varvec{y}_{1})-\varvec{G}(\varvec{y}_{2})\) is with full rank sometimes. As a matter of fact, most systems satisfy the assumption.
Theorem 2
For \(\widehat{\varvec{B}}=D^{\varvec{p}-\varvec{q}}(\varvec{G}(\varvec{y})\widehat{\varvec{\beta }})\) denoted as above and \(\underset{t\rightarrow \infty }{\mathrm {lim}}\widehat{\varvec{B}}(t)=\varvec{0}\) drawn the conclusion from Theorem 1, it satisfies \(\underset{t\rightarrow \infty }{\mathrm {lim}}\widehat{\varvec{\beta }}(t)=\varvec{0}\) such that \(\varvec{\beta }\) can be estimated by \(\widetilde{\varvec{\beta }}\) precisely.
Proof
Taking \((\varvec{p}-\varvec{q})\)-order integral operation on \(\widehat{\varvec{B}}\), we get
Since \(\underset{t\rightarrow \infty }{\mathrm {lim}}\widehat{\varvec{B}}(t)=\varvec{0}\) and \(\underset{t\rightarrow \infty }{\mathrm {lim}}(t-t_{0})^{\varvec{p}-\varvec{q}-\varvec{1}}=\varvec{0}\), there exist \(\widehat{\varvec{B}}(t)\rightarrow \varvec{0}\) as \(t\ge t_{M1}\) and \((t-t_{0})^{\varvec{p}-\varvec{q}-\varvec{1}}\rightarrow \varvec{0}\) as \(t\ge t_{M2}\). Let \(T=\mathrm {max}\{t_{M1},t_{M2}\}\), for \(t>T\), \(\underset{t\rightarrow \infty }{\mathrm {lim}}\varvec{G}(\varvec{y}(t))\widehat{\varvec{\beta }}(t)=\underline{\varDelta }(\int _{t_{0}}^{T}\overline{\varDelta }(\widehat{\varvec{B}}(\tau ),(t-\tau )^{\varvec{p}-\varvec{q}-\varvec{1}})\, d\tau ,\mathrm {\Gamma }(\varvec{p} -\varvec{q}))=\varvec{B}_{0}\).
Denote \(\varvec{G}(\varvec{y}(t_{i}))\widehat{\varvec{\beta }}(t_{i})=\varvec{G}_{i}\widehat{\varvec{\beta }}_{i}\). For different \(t_{i},t_{j}>T\) meet \(\varDelta t=t_{j}-t_{i}\rightarrow 0\), it follows that \(\varDelta \varvec{G}=\varvec{G}_{j}-\varvec{G}_{i}\rightarrow \varvec{0}\). Denote \(\varvec{G}_{j}=\varvec{G}_{i}+\varDelta \varvec{G}\) and \(\widehat{\varvec{\beta }}_{j}=\widehat{\varvec{\beta }}_{i}+\varDelta \widehat{\varvec{\beta }}\). Since \(\varvec{G}_{i}\widehat{\varvec{\beta }}_{i}\rightarrow \varvec{G}_{j}\widehat{\varvec{\beta }}_{j}\rightarrow \varvec{B}_{0}\), it satisfies \(\varvec{G}_{i}\widehat{\varvec{\beta }}_{i}\rightarrow \varvec{G}_{j}\widehat{\varvec{\beta }}_{j}=(\varvec{G}_{i}+\varDelta \varvec{G})(\widehat{\varvec{\beta }}_{i}+\varDelta \varvec{\beta })\). For \(\varDelta \varvec{G}\rightarrow \varvec{0}\), it follows that \(\varvec{G}_{i}\varDelta \varvec{\beta }\rightarrow \varvec{0}\). By \(\mathrm {rank}(\varvec{G}_{i})=\mathrm {min}\{v,n\}=v\), we know that \(\varDelta \varvec{\beta }\rightarrow \varvec{0}\). Namely, \(\widehat{\varvec{\beta }}_{i}\rightarrow \widehat{\varvec{\beta }}_{j}\). In turn, it can be calculated that \(\widehat{\varvec{\beta }}_{1}\rightarrow \widehat{\varvec{\beta }}_{2}\rightarrow \cdots \rightarrow \widehat{\varvec{\beta }}\) for \(t>T\). Combining with Assumption 4, there exist \(\varvec{G}_{k}\) and \(\varvec{G}_{l}\) to make \(\varvec{G}_{k}\widehat{\varvec{\beta }}_{k}\rightarrow \varvec{G}_{l}\widehat{\varvec{\beta }}_{l}\) for \(k,l=1,2,\cdots \) and \(k\ne l\). Therefore, \(\varvec{G}_{k}\widehat{\varvec{\beta }}_{k}-\varvec{G}_{l}\widehat{\varvec{\beta }}_{l}\rightarrow (\varvec{G}_{k}-\varvec{G}_{l})\widehat{\varvec{\beta }}\rightarrow \varvec{0}\). According to \(\mathrm {rank}(\varvec{G}_{k}-\varvec{G}_{l})=v\), it is known that \(\widehat{\varvec{\beta }}\rightarrow \varvec{0}\) for \(t>T\). That is to say, \(\underset{t\rightarrow \infty }{\mathrm {lim}}\widehat{\varvec{\beta }}(t)=\varvec{0}\) and \(\varvec{B}_{0}=\varvec{0}\). Then it shows that the estimate \(\widetilde{\varvec{\beta }}\) for \(\varvec{\beta }\) can be obtained precisely. So the prove for this theorem is complete. \(\square \)
In theory, we have proved the feasibility for the proposed controller completely. But it can be seen from the above that how to solve \(\widehat{\varvec{\beta }}\) or \(\widetilde{\varvec{\beta }}\) from \(\widehat{\varvec{B}}\) is still a difficult problem. Next, we will deal with the problem.
Definition 7
For \(t\ge t_{0}\) and \(h>0\), the Grunwald–Letnikov definition of the fractional calculus is described as
where h is the time step, and \(k=[(t-t_{0})/h]\). It is worth nothing that \(q>0\) and \(q<0\) for (32) represent the differential operation and integral operation, respectively.
The researches show that (32) has the following approximate form with the precision about o(h) at every time point \(t_{j}=t_{0}+jh\) for \(j=0,1,\ldots \) since h is small enough,
where \(w_{i}^{(q)}=(-1)^{i}C_{q}^{i}\) is the polynomial coefficient of the function \((1-z)^{q}\). Moreover, for \(i=1,2,\ldots \), \(w_{i}^{(q)}\) can be calculated by the following recursive relations.
Obviously, as a simple way, Definition 7 with the approximate form as (33) can be applied to work out the fractional-order integral of a given time series at every time point successfully. Let \(\varvec{G}(\varvec{y})\widehat{\varvec{\beta }}=\breve{\varvec{B}}\). For \(\widehat{\varvec{B}}\) solved from the error system by Adomian decomposition method (ADM) [48,49,50,51], \(J^{\varvec{p}-\varvec{q}}\widehat{\varvec{B}}\) can be calculated on the basis of (33). Further, \(\breve{\varvec{B}}\) can be calculated according to (31). Therefore, \(\widehat{\varvec{\beta }}\) can be calculated by
Remark 1
The methods for solving differential equation of the fractional-order chaotic system include mainly frequency domain method (FDM), Adams–Bashforth–Moulton method (ABMM) and ADM. Although the accuracy of FDM is within 2dB or 3dB, the approximation to real system can only be met in the desired frequency band. The truncation error of ABMM is \(o(h^{p})\) with \(p=\mathrm {min}\{2,1+q\}\), where h and q represent the time step and order of the differential equation. But ABMM consumes too many computer resources, and its calculation speed is very slow. Not only does ADM have simple operation and high speed, but also high precision, i.e., the truncation error of this method is less than \(\frac{c^{n}}{n!}\), where c is a positive bounded constant and n stands for the truncation number. Besides, Runge–Kutta method and Euler method can be used only if q is an integer.
Up to now, the synchronization problem with unknown parameters and bounded external disturbance between two fractional-order chaotic systems with different orders and structures has been dealt completely. Further, we can also draw the following conclusions.
Corollary 1
If there exist not the disturbance in the drive system and response system, we can know that \(\varvec{w}_{1}=\varvec{w}_{2}=\varvec{0}\) and \(\varvec{l}=\varvec{0}\). So the controller can be designed as
In addition, the update rules of unknown parameters and adaptive rate satisfy (16), (17) and (19).
Corollary 2
If the drive system and response system are with same structure, it will be obvious to satisfy \(\varvec{f}(\cdot )=\varvec{g}(\cdot )\) and \(\varvec{F}(\cdot )=\varvec{G}(\cdot )\). In the case of disturbance, the controller is designed as
Furthermore, the update rules of the controller meet (16), (17), (19) and (20).
Corollary 3
If the parameters \(\varvec{\alpha }\) and \(\varvec{\beta }\) of the systems are known in advance, we can design the controller as
Besides, conditions (19) and (20) are satisfied with the controller.
3.2 Controller design as \(\varvec{0}<\varvec{p}<\varvec{q}<\varvec{1}\)
Theorem 3
For \(t\ge t_{0}\), there exist the diagonal positive definite matrix \(\varvec{L}\in R^{n\times n}\), positive definite matrixes \(\varvec{N}\in R^{n\times n}\), \(\varvec{S}\in R^{v\times v}\), \(\varvec{U}\in R^{n\times n}\) and \(\varvec{V}\in R^{n\times n}\) to make system (6) and (7) synchronize if the conditions are satisfied as follows.
(i) The controller on system (7) is designed as
where what \(\widetilde{\varvec{\alpha }}\), \(\widetilde{\varvec{\beta }}\), \(\widetilde{\varvec{K}}\) and \(\varvec{e}\) represent is the same as that in Sect. 3.1, \(\widetilde{\varvec{M}}=\mathrm {diag}\{\widetilde{m}_{1},\widetilde{m}_{2},\ldots ,\widetilde{m}_{n}\}\) is the estimate for \(\varvec{M}=\mathrm {diag}\{m_{1},m_{2},\ldots ,m_{n}\}\), and it satisfies \(m_{i}>0\) for \(i=1,2,\ldots ,n\). Besides, \(\varvec{r}_{2}(t)\) is described as
(ii) Let \(\widetilde{\varvec{m}}=\widetilde{\varvec{M}}\cdot \varvec{1}_{n}\), then the update rule of unknown parameters in the drive system can be presented as
where \(\varvec{X}_{1}\in R^{n\times n}\) and \(\varvec{Y}_{1}\in R^{n\times v}\) comply with condition (iii), and \(\varvec{n}(t)\) is presented as
The update rule of unknown parameters in the response system can be presented as
where \(\varvec{X}_{2}\in R^{v\times n}\) and \(\varvec{Y}_{2}\in R^{v\times v}\) comply with condition (iii).
The adaptive rate with uncertainty in the controller can be estimated by
The upper bound of disturbances between the drive system and response system can be estimated by
where \(\widetilde{\varvec{k}}\) and \(\varvec{E}\) describe what as above.
(iii) The condition is the same as the third one in Sect. 3.1. But the corresponding dimensions of these matrixes are different from the above.
Proof
Taking \((\varvec{q}-\varvec{p})\)-order integral operation on both sides of (6), we have
\(\square \)
Then the synchronization problem to (6) and (7) is equivalent to design a controller on (7) for realizing a synchronization between (46) and (7). Therefore, it follows
Substituting (39) into (47) and subtracting (46) from (47), we obtain
Let \(D^{\varvec{q}-\varvec{p}}(\varvec{F}(\varvec{x})\widehat{\varvec{\alpha }})=\widehat{\varvec{A}}\), it holds
Let \(\varvec{m}=\varvec{M}\cdot \varvec{1}_{n}\), and denote \(\widehat{\varvec{m}}=\widetilde{\varvec{m}}-\varvec{m}\). The Lyapunov function is chosen as the same as (26), where \(V_{1}=\varvec{e}^{T}\varvec{L}\varvec{e}\) , \(V_{2}=\widehat{\varvec{A}}^{T}\varvec{N}\widehat{\varvec{A}}\), \(V_{3}=\widehat{\varvec{\beta }}^{T}\varvec{S}\widehat{\varvec{\beta }}\), \(V_{4}=\widehat{\varvec{k}}^{T}\varvec{U}\widehat{\varvec{k}}\) and \(V_{5}=\widehat{\varvec{m}}^{T}\varvec{V}\widehat{\varvec{m}}\). Moreover, \(\widehat{\varvec{k}}\) is defined as above. So, \(V=[\varvec{e}^{T},\widehat{\varvec{A}}^{T},\widehat{\varvec{\beta }}^{T},\widehat{\varvec{k}}^{T},\widehat{\varvec{m}}^{T}]\mathrm {diag}\{\varvec{L},\varvec{N},\varvec{S},\varvec{U},\varvec{V}\}[\varvec{e}^{T},\widehat{\varvec{A}}^{T}, \widehat{\varvec{\beta }}^{T},\widehat{\varvec{k}}^{T},\widehat{\varvec{m}}^{T}]^{T}\). Since \(\varvec{L},\varvec{N},\varvec{S},\varvec{U},\varvec{V}>0\), it follows that \(\mathrm {diag}\{\varvec{L},\varvec{N},\varvec{S},\varvec{U},\varvec{V}\}>0\). Besides, it follows
In (50), it meets
Substituting (51) into (50), we get
So the error system is asymptotically stable at the equilibrium point. Though the synchronization problem to the drive system and response system has been dealt in this case, but the parameter identification question to \(\varvec{\alpha }\) in the drive system has not been solved yet.
Assumption 5
For the drive system at \(t>T\), it is assumed as follows: (i) \(u=\mathrm {dim}(\varvec{\alpha })\le n\); (ii) \(\varvec{F}(\varvec{x})\) are with full rank at some point; (iii) \(\varvec{F}(\varvec{x}_{1})-\varvec{F}(\varvec{x}_{2})\) are with full rank sometimes. As a matter of fact, most systems satisfy the assumption.
Theorem 4
For \(\widehat{\varvec{A}}=D^{\varvec{q}-\varvec{p}}(\varvec{F}(\varvec{x})\widehat{\varvec{\alpha }})\) denoted as above and \(\underset{t\rightarrow \infty }{\mathrm {lim}}\widehat{\varvec{A}}(t)=\varvec{0}\) drawn the conclusion from Theorem 3, it meets \(\underset{t\rightarrow \infty }{\mathrm {lim}}\widehat{\varvec{\alpha }}(t)=\varvec{0}\) such that \(\varvec{\alpha }\) can be estimated by \(\widetilde{\varvec{\alpha }}\) accurately.
Proof
Taking \((\varvec{q}-\varvec{p})\)-order integral operation on \(\widehat{\varvec{A}}\), we obtain
Since \(\underset{t\rightarrow \infty }{\mathrm {lim}}\widehat{\varvec{A}}(t)=\varvec{0}\) and \(\underset{t\rightarrow \infty }{\mathrm {lim}}(t-t_{0})^{\varvec{q}-\varvec{p}-\varvec{1}}=\varvec{0}\), there exist \(\widehat{\varvec{A}}(t)\rightarrow \varvec{0}\) as \(t\ge t_{N1}\) and \((t-t_{0})^{\varvec{q}-\varvec{p}-\varvec{1}}\rightarrow \varvec{0}\) as \(t\ge t_{N2}\). Let \(T=\mathrm {max}\{t_{N1},t_{N2}\}\), for \(t>T\), \(\underset{t\rightarrow \infty }{\mathrm {lim}}\varvec{F}(\varvec{x}(t))\widehat{\varvec{\alpha }}(t)=\underline{\varDelta }(\int _{t_{0}}^{T}\overline{\varDelta }(\widehat{\varvec{A}}(\tau ),(t-\tau )^{\varvec{q}-\varvec{p}-\varvec{1}})\, d\tau ,\mathrm {\Gamma }(\varvec{q} -\varvec{p}))=\varvec{A}_{0}\).
Denote \(\varvec{F}(\varvec{x}(t_{i}))\widehat{\varvec{\alpha }}(t_{i})=\varvec{F}_{i}\widehat{\varvec{\alpha }}_{i}\). For different \(t_{i},t_{j}>T\) satisfy \(\varDelta t=t_{j}-t_{i}\rightarrow 0\), it follows that \(\varDelta \varvec{F}=\varvec{F}_{j}-\varvec{F}_{i}\rightarrow \varvec{0}\). Denote \(\varvec{F}_{j}=\varvec{F}_{i}+\varDelta \varvec{F}\) and \(\widehat{\varvec{\alpha }}_{j}=\widehat{\varvec{\alpha }}_{i}+\varDelta \widehat{\varvec{\alpha }}\). Since \(\varvec{F}_{i}\widehat{\varvec{\alpha }}_{i}\rightarrow \varvec{F}_{j}\widehat{\varvec{\alpha }}_{j}\rightarrow \varvec{A}_{0}\), it satisfies \(\varvec{F}_{i}\widehat{\varvec{\alpha }}_{i}\rightarrow \varvec{F}_{j}\widehat{\varvec{\alpha }}_{j}=(\varvec{F}_{i}+\varDelta \varvec{F})(\widehat{\varvec{\alpha }}_{i}+\varDelta \widehat{\varvec{\alpha }})\). For \(\varDelta \varvec{F}\rightarrow \varvec{0}\), it follows that \(\varvec{F}_{i}\varDelta \widehat{\varvec{\alpha }}\rightarrow \varvec{0}\). By \(\mathrm {rank}(\varvec{F}_{i})=\mathrm {min}\{u,n\}=u\), we know that \(\varDelta \widehat{\varvec{\alpha }}\rightarrow \varvec{0}\). Namely, \(\widehat{\varvec{\alpha }}_{i}\rightarrow \widehat{\varvec{\alpha }}_{j}\). In turn, it can be calculated that \(\widehat{\varvec{\alpha }}_{1}\rightarrow \widehat{\varvec{\alpha }}_{2}\rightarrow \cdots \rightarrow \varDelta \widehat{\varvec{\alpha }}\) for \(t>T\). Combining with Assumption 5, there exist \(\varvec{F}_{k}\) and \(\varvec{F}_{l}\) for \(k,l=1,2,\ldots \) and \(k\ne l\) to make \(\varvec{F}_{k}\widehat{\varvec{\alpha }}_{k}\rightarrow \varvec{F}_{l}\widehat{\varvec{\alpha }}_{l}\). So, \(\varvec{F}_{k}\widehat{\varvec{\alpha }}_{k}-\varvec{F}_{l}\widehat{\varvec{\alpha }}_{l}\rightarrow (\varvec{F}_{k}-\varvec{F}_{l})\widehat{\varvec{\alpha }}\rightarrow \varvec{0}\). According to \(\mathrm {rank}(\varvec{F}_{k}-\varvec{F}_{l})=u\), it is known that \(\widehat{\varvec{\alpha }}\rightarrow \varvec{0}\) for \(t>T\). Namely, \(\underset{t\rightarrow \infty }{\mathrm {lim}}\widehat{\varvec{\alpha }}(t)=\varvec{0}\) and \(\varvec{A}_{0}=\varvec{0}\). Then it shows that the estimate \(\widetilde{\varvec{\alpha }}\) for \(\varvec{\alpha }\) can be gained accurately. Theorem 4 is proved completely. \(\square \)
In addition, let \(\varvec{F}(\varvec{x})\widehat{\varvec{\alpha }}=\breve{\varvec{A}}\). Since \(\widehat{\varvec{A}}\) has been solved from the error system according to ADM, \(\breve{\varvec{A}}\) can be calculated by combining with (53) and (33). Consequently, \(\widehat{\varvec{\alpha }}\) can be calculated as follows.
Therefore, the synchronization problem can be achieved completely in this case. Based on Theorem 3, we can also summarize the following results.
Corollary 4
If there exist not the disturbance in the drive system and response system, we can know that \(\varvec{w}_{1}=\varvec{w}_{2}=\varvec{0}\) and \(\varvec{m}=\varvec{0}\). So the controller can be designed as
In addition, the update rules of unknown parameters and adaptive rate are satisfied with (41), (43) and (44).
Corollary 5
If the drive system and response system are with same structure, it will be obvious to satisfy \(\varvec{f}(\cdot )=\varvec{g}(\cdot )\) and \(\varvec{F}(\cdot )=\varvec{G}(\cdot )\). Under the disturbance, the controller is designed as
Moreover, the update rules of the controller meet (41), (43), (44) and (45).
Corollary 6
If the parameters \(\varvec{\alpha }\) and \(\varvec{\beta }\) of the two systems are known beforehand, we can design the controller as
Furthermore, conditions (44) and (45) are met with the controller.
Further, for some special situations implied in the above theorems and corollaries, we make comments as follows.
Remark 2
For one thing, we consider that \(\widetilde{\varvec{K}}\) is changing with the time in this paper. In fact, we may also give a constant matrix \(\widetilde{\varvec{K}}<0\), which make us reduce the design for the update rule of \(\widetilde{\varvec{k}}\). But it will bring us the blindness since it is very difficult for us to select an appropriate \(\widetilde{\varvec{K}}\). As a result, the convergence speed and robustness of the error system can be affected in a way. For another thing, as to the certainty and uncertainty of \(\varvec{\alpha }\), \(\varvec{\beta }\) or \(\widetilde{\varvec{k}}\), the existence and nonexistence of unknown bounded external disturbance \(\varvec{w}_{1}\) or \(\varvec{w}_{2}\), and whether the drive system and response system have same structure, we can design the controller by adjusting certain update rules in Theorems 1 and 3.
Remark 3
As a kind of complex synchronization problem to fractional-order chaotic systems, the case with orders \(\varvec{p}\ne \varvec{q}\) in the drive system and response system has been researched in this paper. Of course, if only one is equal to \(\varvec{1}\) between \(\varvec{p}\) and \(\varvec{q}\), the problem become a synchronization problem to integer-order chaotic system and fractional-order chaotic system. It is clear that the above theorems and corollaries are also suitable for the problem. However, if \(\varvec{p}=\varvec{q}\) holds, we need only let \(\varvec{r}_{1}(t)\) or \(\varvec{r}_{2}(t)\) and \(\varvec{m}(t)\) or \(\varvec{n}(t)\) be \(\varvec{0}\). Then for the synchronization problems under different cases as mentioned in Remark 2, we can design the controller to through applying Theorems 1 and 3.
Remark 4
In fact, the external disturbance has an important impact on system performance such as the stability, robustness and synchronization error. In this section, we can deal with the first two problems according to our theory. What we design is only a feasible controller by choosing an arbitrary positive definite matrix \(\varvec{V}\) with appropriate dimension, it cannot make sure that the controller is optimal one. Therefore, we propose an approach to optimize \(\varvec{V}\) to minimize the system error in Sect. 4, which can decrease the synchronization error and improve the decode precision in secret communization effectively.
4 Parameter optimization in the controller
As a matter of fact, this section is an improvement on the above designed controller, which reduces the system error effectively and enhances the control effect further.
4.1 Principle of parameter optimization
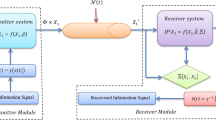
To improve synchronization performance between the drive system and response system, the key is appropriate selection for the positive definite matrix \(\varvec{V}\) related to the external disturbance in (20) or (45). Meanwhile, the matrices \(\varvec{M}\) or \(\varvec{L}\), \(\varvec{N}\), \(\varvec{S}\) and \(\varvec{U}\) are given in advance. For simplicity without loss of generality, we consider \(\varvec{V}\) as the diagonal matrix. Then, we transform the selection for \(\varvec{V}\) into a parameter optimization problem. The principle is shown in Fig. 1, where \(\mathrm {FOES}(\varvec{E}_{s},\widetilde{\varvec{V}})\) represents the fractional-order error system in Sects. 3.1 or 3.2, \(\widetilde{\varvec{V}}=\varvec{V}^{-1}\cdot \varvec{1}_{n}=[v_{1},v_{2},\ldots ,v_{n}]^{T}\), \(\varvec{e}_{s1}=\varvec{e}\), \(\varvec{e}_{s2}=\widehat{\varvec{\alpha }}\) or \(\varvec{e}_{s2}=\widehat{\varvec{A}}\), \(\varvec{e}_{s3}=\widehat{\varvec{B}}\) or \(\varvec{e}_{s3}=\widehat{\varvec{\beta }}\), \(\varvec{e}_{s4}=\widehat{\varvec{k}}\), and \(\varvec{e}_{s5}=\widehat{\varvec{l}}\) or \(\varvec{e}_{s5}=\widehat{\varvec{m}}\).
Figure 1 shows that the steady-state output of system under the action of parameter vector \(\widetilde{\varvec{V}}\) is
or
Constantly adjusting \(\widetilde{\varvec{V}}\) makes (58) or (59) have a minimum on the vectors including synchronization error, parameter identification error, adaptive rate error and disturbance estimation error. In addition, we choose \(K_{p}=1/\sqrt{5nL_{v}}\), where \(L_{v}=\mathrm {length}(\varvec{e})\). Therefore, the fitness function is set as a root mean square error (RMSE) of the above error vectors as follows.
or
So the parameter optimization problem is converted into a function optimization problem in the parameter space, that is to find the minimum of \(\overline{F}(\widetilde{\varvec{V}})\). At the same time, the corresponding independent variable is taken as
Since the fitness function is a multivariable function, there may be multiple local optimal solutions. Although there are many kinds of optimization methods, gradient descent (GD) method and artificial intelligent optimization algorithm represented by particle swarm optimization (PSO) algorithm are the two most commonly used methods. However, GD method not only operates complicatedly but also traps into the local optimal solution easily and converges slowly, which make this method unsuitable to use in this paper. As a parallel optimization algorithm, PSO algorithm is with two operators including the position variable and velocity variable, but this method is easy to get into an early maturity state and the convergence speed is also slow. As an improved method for PSO algorithm, QPSO algorithm makes up for the above defects. But the selection of search range has also an effect on the performance of this algorithm. Therefore, we put forward IEQPSO algorithm to improve QPSO algorithm and make use of it to optimize the parameter vector \(\widetilde{\varvec{V}}\).
4.2 IEQPSO algorithm
Individual thoughts are very complicated in a biotic community, where there exist various uncertainties just as particles have quantum behaviors. So the quantum theory is applied to PSO algorithm to make QPSO algorithm be proposed.
QPSO algorithm can be described as follows. We suppose that a population \(\breve{\varvec{X}}=[\breve{\varvec{X}}_{1},\breve{\varvec{X}}_{2},\ldots ,\breve{\varvec{X}}_{N}]^{T}\) is composed of N D-dimensional particles in the quantum space which represent the potential solution to problem, where \(\breve{\varvec{X}}_{i}=[x_{i1},x_{i2},\ldots ,x_{iD}]^{T}\) for \(i=1,2,\ldots ,N\). Furthermore, the individual and global optimal positions of particles are recorded as \(\varvec{P}_{i}=[p_{i1},p_{i2},\ldots ,p_{iD}]^{T}\) and \(\varvec{P}_{g}=[p_{g1},p_{g2},\ldots ,p_{gD}]^{T}\), respectively. Among them, the update rule of the current individual optimal position is
and the update rule of the current global optimal position is
where \(\overline{f}(\cdot )\) represents the evaluation function.
In the quantum space, the position and velocity of every particle cannot be determined simultaneously, and the state of it is ascertained by the wave function which is described as
In (65), \(\varvec{\delta }_{i}(t)\) is described as
where \(\varvec{\delta }_{i}=[\delta _{i1},\delta _{i2},\ldots ,\delta _{iD}]^{T}\), \(\breve{\varvec{L}}_{i}=[L_{i1},L_{i2},\ldots ,L_{iD}]^{T}\), and \(\varvec{\varPhi }_{i}=\mathrm {diag}\{\phi _{1},\phi _{2},\ldots ,\phi _{D}\}\) with \(\phi _{i}\in [0,1]\) for \(i=1,2,\ldots ,N\) represent the potential energy trap of \(\breve{\varvec{X}}_{i}\), the characteristic length of \(\varvec{\delta }_{i}\) and the state transition matrix, respectively. Obviously, it follows
The above formula shows that wherever the particle is originally, it will depend on the potential energy field to converge to the optimal position with probability 1, which is a good proof for the global convergence of this algorithm.
According to Monte Carlo’s rule, the evolution equation of particles from the tth to \((t+1)\)th algebra is
where \(\varvec{u}_{i}=[u_{i1},u_{i2},\ldots ,u_{iD}]^{T}\) is a random input vector with \(u_{id}\in [0,1]\) for \(i=1,2,\ldots ,N\) and \(d=1,2,\ldots , D\). In addition, \(\breve{\varvec{L}}_{i}(t)\) can be calculated by
where \(\varvec{P}_{m}\) represents the average optimal position, which can be computed by
and \(\alpha (t)\) is a compression–expansion factor. The effect is usually better with a linear decrease of \(\alpha \) from 1.0 to 0.5, so \(\alpha \) with the evolution algebra is selected as
where \(T_{f}\) represents the largest evolution algebra.
Therefore, on the basis of (68)–(71), we can obtain the evolution equation of particles and make the iteration continue until \(t>T_{f}\). Meanwhile, it can be seen from the above that QPSO algorithm has more simple operation and stronger search capability, which makes PSO algorithm be well improved in a way.
Remark 5
Since QPSO algorithm is with global convergence, the optimal solution can be got if we choose a large enough search space and appropriate parameters. In fact, in addition to the accuracy, the convergence speed is also an important test indicator for the algorithm. However, what has a significant effect on the convergence speed is a selection of the search space. In many cases, it is very difficult to choose an appropriate search interval. But in this paper, combining with the specific problem, we can estimate a smaller range of search interval beforehand, which is denoted as \([\underline{c},\overline{c}]\) for each component of the particle. So we call QPSO algorithm with this mechanism as IEQPSO algorithm. It is very obvious that it can shorten the search time and improve the convergence speed to some extent by using IEQPSO algorithm.
4.3 Algorithm flow
When IEQPSO algorithm is used to optimize the controller, the parameter vector \(\widetilde{\varvec{V}}=[v_{1},v_{2},\ldots ,v_{n}]^{T}\) is compared to a particle in the algorithm. Under the evaluation of the fitness function (60) or (61), the process is described as follows.
Step 1 According to the actual requirements of controller design, determining a big enough search interval which is denoted as \(\varvec{I}_{b}=[\underline{C},\overline{C}]\otimes \varvec{1}_{n}\), and divided into \(Q_{I}\) uniform intervals. Then, picking some points in those subintervals, and making use of them and (60) or (61) to draw the corresponding fitness function curve. Finally, based on the curve, a smaller search interval is decided, which is denoted as \(\varvec{I}_{s}=[\underline{c},\overline{c}]\otimes \varvec{1}_{n}\).
Step 2 Setting the evolution algebra \(T_{f}\), population size N, particle’s dimension D and initialing the position of particle swarm in \(\varvec{I}_{s}\) to be \(\breve{\varvec{X}}=[\breve{\varvec{X}}_{1},\breve{\varvec{X}}_{2},\ldots , \breve{\varvec{X}}_{N}]^{T}\) by random means, where \(\breve{\varvec{X}}_{i}=[x_{i1},x_{i2},\ldots ,x_{iD}]^{T}\) for \(i=1,2,\ldots ,N\), and \(D=\mathrm {dim}(\widetilde{\varvec{V}})\).
Step 3 Calculating the fitness value of every particle according to the fitness function as follows,
or
Step 4 Updating the position of all particles though (68)–(71) and computing the new fitness value of every particle as follows,
or
Step 5 Evaluating the individual optimal solution \(\varvec{P}_{i}\) and the global optimal solution \(\varvec{P}_{g}\) based on \(\overline{F}_{i}\), \(\overline{F}_{new,i}\), (63) and (64), then updating them.
Step 6 Judging whether the terminate condition is reached; if not, going to Step 3; otherwise, the evolution is over, and we let \(\widetilde{\varvec{V}}=\varvec{P}_{g}(T_{f})\) be the final result.
Therefore, in combination with the given matrices \(\varvec{M}\) or \(\varvec{L}\), \(\varvec{N}\), \(\varvec{S}\) and \(\varvec{U}\) and the above \(\widetilde{\varvec{V}}\), we can design the optimal controller.
5 Numerical simulation
Firstly, on the basis of several typical benchmark functions, we verify the effectiveness of IEQPSO algorithm through comparing to PSO algorithm with interval estimation (IEPSO).
5.1 Performance test on IEQPSO algorithm
The test functions are chosen as Schaffer function, Sphere function, Rosenbrock function and Griewank function, which are expressed by \(f(x_{1},x_{2})=0.5+\frac{\mathrm {cos}^{2}[\mathrm {sin}(|x_{1}^{2}-x_{2}^{2}|)]-0.5}{[1+0.001(x_{1}^{2}+x_{2}^{2})]^{2}}\), \(f(x_{1},x_{2})=\sum \nolimits _{i=1}^{2}x_{i}^{2}\), \(f(x_{1},x_{2},x_{3})=\sum \nolimits _{i=1}^{2}[100(x_{i+1}-x_{i}^{2})^{2}+(x_{i}-1)^{2}]\) and \(f(x_{1},x_{2},x_{3})=1+\frac{1}{4000}\sum \nolimits _{i=1}^{3}x_{i}^{2}-\prod \nolimits _{i=1}^{3}\mathrm {cos}(\frac{x_{i}}{\sqrt{i}})\), respectively, where \(x_{i}\in [-100,100]\) for \(i=1,2,3\). In the meantime, the corresponding independent variables of minimum points of the above functions are (0, ± 1.2531) (or (± 1.2531,0)), (0,0), (1,1,1) and (0,0,0), respectively. In the process of searching minimum point, we select \(T_{f}=20\), \(N=30\), \(D=2,2,3,3\), the velocity of IEPSO algorithm is set to \(\varvec{v}_{s}=[-\,0.2,0.2]\otimes \varvec{1}_{2},[-\,0.2,0.2]\otimes \varvec{1}_{2},[-\,0.2,0.2]\otimes \varvec{1}_{3},[- \,\,0.2,0.2]\otimes \varvec{1}_{3}\). For different functions, the search processes based on IEQPSO algorithm and IEPSO algorithm are shown in Figs. 2, 3, 4 and 5.
From Figs. 2, 3, 4 and 5, we can see that the fitness curves of IEQPSO algorithm drop faster than corresponding curves of IEPSO algorithm, which show strong search capability of the proposed method. It can be seen from the change process of the independent variable that the corresponding variable would converge to the real value by IEQPSO algorithm, but IEPSO algorithm may be either in precocious or slow convergence. Obviously, IEQPSO algorithm is well improved.
For quantitative analysis on the performance of IEQPSO algorithm, we give three performance indicators as follows: mean absolute error (MAE), worst absolute error (WAE) and functional absolute error (FAE). Letting \(x^{s}=\{x_{i}^{s}\}_{i=1}^{n}\) be the series consisting of minimum point search result, \(x^{*}=\{x_{i}^{*}\}_{i=1}^{n}\) for the real point, we define \(\text {MAE}=\frac{1}{n}\sum \limits _{i=1}^{n}|x_{i}^{s}-x_{i}^{*}|\), \(\text {WAE}=\underset{i=1,2,\ldots ,n}{\mathrm {max}}\{|x_{i}^{s}-x_{i}^{*}|\}\) and \(\text {FAE}=|f(x^{s})-f(x^{*})|\). Based on different search methods for the test functions, the corresponding performance evaluation is shown in Table 1.
According to Table 1, MAE and FAE relying on IEQPSO algorithm are about zero to two orders of magnitude lower than that of IEPSO algorithm, which confirm that IEQPSO algorithm has higher search precision. Meanwhile, WAE of IEQPSO algorithm is almost one-seventh to one-half of the corresponding indicator depending on comparison algorithm, which show that IEQPSO algorithm has stronger robustness. Visibly, IEQPSO algorithm strengthens the search performance. Through Figs. 2, 3, 4 and 5 and Table 1, the superiority and generalization of IEQPSO algorithm are illustrated.
Furthermore, in order to verify the effectiveness of the proposed control scheme in this paper, we take the following two simulation tests as examples to illustrate it.
5.2 Synchronization control for fractional-order chaotic systems
As to the case with \(\varvec{1}>\varvec{p}>\varvec{q}>\varvec{0}\), we take the fractional-order Lü chaotic system and fractional-order Lorenz chaotic system as the drive system and response system, respectively. Among them, the two systems are described in (76) and (77), respectively.
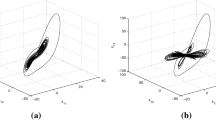
In the fractional-order Lü chaotic system, if it holds \(\varvec{p}=[p_{1},p_{2},p_{3}]^{T}=[0.95,0.95,0.95]^{T}\) and \(\varvec{\alpha }=[a_{1},b_{1},c_{1 }]^{T} =[36,3,20]^{T}\), the system will present the chaotic characteristic. Meanwhile, the chaotic attractor is shown in Fig. 6a.
In the fractional-order Lorenz chaotic system, we select \(\varvec{q}=[q_{1},q_{2},q_{3}]^{T}=[0.93,9.93,0.93]^{T}\) and \(\varvec{\beta }=[a_{2},b_{2},c_{2}]^{T}=[10,28,8/3]^{T}\). Further, the chaotic attractor in the system is shown in Fig. 6b.
In the simulation, for the controller, let \(\varvec{M},\varvec{N},\varvec{S},\varvec{U} =\varvec{I}_{3}\), \(\varvec{X}_{1}=\varvec{Y}_{2}=-\varvec{I}_{3}\) and \(\varvec{X}_{2}=\varvec{Y}_{1}=\varvec{0}_{3}\). As to bounded external disturbance, we set \(\varvec{w}_{1}(t)=[0.1\mathrm {cos}t, 0.1\mathrm {sin}t,-0.1\mathrm {cos}t]^{T}\) and \(\varvec{w}_{2}(t)=[-0.1\mathrm {cos}t,-0.1\mathrm {cos}t, 0.1\mathrm {sin}t]^{T}\). As to the initial conditions, let \(\varvec{x}_{0}=[6,-2,8]^{T}\), \(\varvec{y}_{0}=[1,2,3]^{T}\), \(\widehat{\varvec{\alpha }}_{0}=[-3,-1,2]^{T}\), \(\widehat{\varvec{B}}_{0}=[-5,6,8]^{T}\), \(\widetilde{\varvec{k}}_{0}=[0,0,0]^{T}\) and \(\widetilde{\varvec{l}}_{0}=[0,0,0]^{T}\). When the differential equations are solved according to ADM, the truncation number \(n=6\), the time step \(h=0.01\), and the time \(t\in [0,12]\). Further, we make use of IEQPSO algorithm to optimize \(\widetilde{\varvec{V}}\) for \(\varvec{V}\) in the controller. Firstly, we set a big enough search interval \(\varvec{I}_{b}=[0,60]\otimes \varvec{1}_{3}\) with a step \(h_{I}=3\). In addition, we let \(\widetilde{\varvec{V}}=[v_{0},v_{0},v_{0}]^{T}\) for the interval estimation. Then the interval estimation curve based on the fitness function is shown in Fig. 7.
According to Fig. 7, we select \(\varvec{I}_{s}=[0,10]\otimes \varvec{1}_{3}\) as the search interval for IEQPSO algorithm. To illustrate the effectiveness of IEQPSO algorithm, IEPSO algorithm is compared with it. In IEQPSO algorithm and IEPSO algorithm, the evolution algebra, population size and particle’s dimension are set to \(T_{f}=30\), \(N=20\) and \(D=3\), respectively. Besides, the velocity of IEPSO algorithm is limited to \(\varvec{v}_{s}=[-0.2,0.2]\otimes \varvec{1}_{3}\). Then the evolution curve based on the two algorithms is shown in Fig. 8.
According to Fig. 8, the fitness function curve of IEQPSO algorithm drops fast, and the solution of it converges to \(\widetilde{\varvec{V}}_{b}=[0.4774,0.4735,0.3675]^{T}\) quickly. Obviously, as an improved algorithm for IEPSO algorithm, IEQPSO algorithm improves the global search capability and convergence speed effectively. Next, we design the controller by \(\widetilde{\varvec{V}}_{b}\). Finally, the simulation curve is shown in Fig. 9.
Figure 9a shows that the synchronization error is close to be zero quickly, which shows that the response system can achieve the synchronization with the drive system fast. At the same time, we can see from Fig. 9b, c that the unknown parameters can be estimated accurately and quickly, which provide a new method for the parameter identification problem to complicated systems. In addition, Figure 9d, e shows that the relevant change rates can converge to certain values severally, which imply that the adaptive method plays an important role in the synchronization problem. So the example verifies the practicability of the proposed control scheme for the first case. To further illustrate its effectiveness, the quantitative analysis based on MAE is shown in Table 2.
We can see from Table 2 that MAE of synchronization error in the controller based on IEQPSO algorithm is basically less than corresponding indicator in contrast controllers, which verifies that the proposed control scheme improve the synchronization performance in accuracy. Meanwhile, it also confirms that IEQPSO algorithm has a stronger search capability than IEPSO algorithm.
5.3 Synchronization application to secret communication
For the case with \(\varvec{0}<\varvec{p}<\varvec{q}<\varvec{1}\), we take signal encryption–decryption process existing in secret communication as an example to illustrate the practicability of the proposed method. Here, the system containing an encrypted signal is regarded as the drive system described by (78), which is composed of the fractional-order Lorenz chaotic system and encrypted signal. As a decryption system, the fractional-order Wang hyperchaotic system with complicated dynamic characteristic is considered as the response system described by (79). In the meantime, the signal processing process is shown in Fig. 10.
In the drive system as above, the signal source is set to \(w_{s}=0.25\mathrm {sin}t\), the encryption coefficient is chosen as \(k_{s}=2\), if it meets \(\varvec{p}=[p_{1},p_{2},p_{3}]^{T}=[0.95,0.95,0.95]^{T}\) and \(\varvec{\alpha }=[a_{1},b_{1},c_{1}]^{T}=[10,28,8/3]^{T}\), the chaotic characteristic will emerge. At the same time, the chaotic attractor is shown in Fig. 11a.
In the response system as above, we choose \(\varvec{q}=[q_{1},q_{2},q_{3},q_{4}]^{T}=[0.98,9.98,0.98,0.98]^{T}\) and \(\varvec{\beta }=[\gamma _{1},\gamma _{2}, \gamma _{3},\gamma _{4}]^{T}=[10,40,25,10.6]^{T}\). Furthermore, the chaotic attractors are shown in Fig. 11b–d.
In the simulation, we let \(\varvec{L},\varvec{N},\varvec{S},\varvec{U}=\varvec{I}_{4}\), \(\varvec{X}_{1}=\varvec{Y}_{2}=-\varvec{I}_{4}\) and \(\varvec{X}_{2}=\varvec{Y}_{1}=\varvec{0}_{4}\) for the controller. Let \(\varvec{w}_{1}(t)=[0.2\mathrm {cos}t,-\,0.2\mathrm {sin}t,0.2\mathrm {sin}t]^{T}\) and \(\varvec{w}_{2}(t)=[0.3\mathrm {sin}t, 0.3\mathrm {cos}t,-\,0.2\mathrm {sin}t,-\,0.2\mathrm {cos}t]^{T}\) for bounded external disturbance, respectively. Let \(\varvec{x}_{0}=[3,-\,7,4]^{T}\), \(\varvec{y}_{0}=[-\,2,6,9,-\,10]^{T}\), \(\widehat{\varvec{A}}_{0}=[-\,4,-\,6,8,5]^{T}\), \(\widehat{\varvec{\beta }}_{0}=[-\,5,3,-\,8,7]^{T}\), \(\widetilde{\varvec{k}}_{0}=[0,0,0,0]^{T}\) and \(\widetilde{\varvec{m}}_{0}=[0,0,0,0]^{T}\) for the initial conditions. When the differential equations are solved by ADM, the truncation number is chosen as \(n=6\), the time step is set to \(h=0.01\), and the time is limited to \(t\in [0,16]\). Next, IEQPSO algorithm is used to optimize \(\widetilde{\varvec{V}}\) for \(\varvec{V}\) in the controller. First of all, we set a big enough search interval \(\varvec{I}_{b}=[0,60]\otimes \varvec{1}_{4}\) with a step \(h_{I}=3\). Besides, we let \(\widetilde{\varvec{V}}=[v_{0},v_{0},v_{0},v_{0}]^{T}\) for the interval estimation. Then the interval estimation curve based on the fitness function is shown in Fig. 12.
Based on Fig. 12, we select \(\varvec{I}_{s}=[0,10]\otimes \varvec{1}_{4}\) as the search interval for IEQPSO algorithm. In IEQPSO algorithm and IEPSO algorithm, the evolution algebra, population size and particle’s dimension are set to \(T_{f}=30\), \(N=20\) and \(D=4\), respectively. Furthermore, the velocity of IEPSO algorithm is limited to \(\varvec{v}_{s}=[-\,0.2,0.2]\otimes \varvec{1}_{4}\). Then the evolution curve about IEQPSO algorithm and IEPSO algorithm is shown in Fig. 13.
We can see from Fig. 13, the fitness function curve of IEQPSO algorithm goes down quickly, and the solution of it converges to \(\widetilde{\varvec{V}}_{b}=[0.3453,0.4256,0.3983,0.5150]^{T}\) fast. In comparison with IEPSO algorithm, it is very obvious that IEQPSO algorithm improves the global search capability and convergence speed effectively. Further, we design the controller by \(\widetilde{\varvec{V}}_{b}\). At last, the simulation curve is shown in Fig. 14.
We can see from Fig. 14a that the synchronization error converges to zero fast, which shows that the drive system and response system can realize the synchronization quickly. Meanwhile, Fig. 14b, c shows that the unknown parameters included in the drive system and response system can be identified fast and precisely, which offer a new way for the parameter identification problem to complicated systems. Furthermore, we can also see from Fig. 14d, e that the change rates existing in the error system can be close to certain values, respectively, which suggest that they are changing before the error system is stable. Obviously, the proposed method to the second case is well verified by the actual example. In addition, according to MAE of the synchronization error, the quantitative analysis is shown in Table 3.
Table 3 shows that the performance indicator of the controller based on IEQPSO algorithm is obviously less than that contrast controllers, which implies that the proposed control scheme improves effectively the synchronization performance in a way. Meanwhile, it also verifies that IEQPSO algorithm enhances the search capability compared to IEPSO algorithm. To make further illustration on secret communication, the signal source, encrypted signal and decryption signal are shown in Fig. 15. It can be seen that the proposed control scheme can achieve the encryption and decryption process for the signal source very well.
Remark 6
In secret communication, the encryption coefficient \(k_{s}\) plays an important role in matching the signal source s and signal to be added such as \(x_{1}\), which makes sure that the signal source is not distorted after being encrypted. Further, the bigger the synchronization error is, the harder it is to decrypt the signal source. From Tables 2 and 3, we can see the controller based on IEQPSO algorithm decreases the synchronization error about one to two orders of magnitude than contrast controllers, which improves effectively the accuracy of secret communication. In particular, the smaller the amplitude of the signal to be added is, the more obvious the superiority of the proposed controller is.
Remark 7
In order to enhance communication security further, secondary encryption of the signal is needed in some case. Thus the artificial noise \(\varvec{\varpi }\) is introduced into the encrypted signal \(\varvec{s}\), which makes \(\varvec{s}\) be protected by \(\varvec{r}_{s}=\mathcal {H}(\varvec{s}+\varvec{\varpi })\), where \(\mathcal {H}\) represents the linear operator. To avoid the impact on the main channel, \(\varvec{\varpi }\) is set in the null space of \(\mathcal {H}\), so that \(\varvec{\varpi }\in N(\mathcal {H})=\{\varvec{v}\in D(\mathcal {H})|\mathcal {H}\varvec{v}=\varvec{0}\}\), where \(D(\mathcal {H})\) stands for the domain of \(\mathcal {H}\). Letting \(\varvec{\varpi }\sim \mathcal {N}(\varvec{\mu },\overline{\varDelta }(\varvec{\sigma },\varvec{\sigma }))\), \(\varvec{\varpi }\) in the drive system and response system can be regarded as the bounded external disturbance. Meanwhile, it is noted that \(\varvec{r}_{s}=\mathcal {H}\varvec{s}\). Since the introduction of artificial noise makes no contribution to the structure of the whole system, the proposed method has little influence on the synchronization process and parameter identification in it. For convenience without loss of generality, we choose the unit operator \(\mathcal {I}\) in Sect. 5.3.
6 Conclusion
In this paper, we investigate the synchronization problem to different fractional-order chaotic systems with parameter uncertainty and bounded external disturbance. Combining with the matrix knowledge, theory on fractional calculus and adaptive method, we design a controller which can deal with the proposed problem in a way. Further, based on the optimal theory, we design an optimal controller according to some performance indicator. Meanwhile, we propose IEQPSO algorithm and apply it into the parameter optimization of the controller. Aiming at different cases, we design two types of optimal controllers. Furthermore, we give some corollaries and remarks, which broaden the scope of research. Finally, in two different cases, we take two couples of examples including synchronization control of fractional-order chaotic systems and synchronization application in secret communication to illustrate the effectiveness and practicability of proposed control schemes. As a future work, we can consider the problem and corresponding application that there exist the orders more than \(\varvec{1}\), different dimensions and time delay between the drive system and response system.
References
Hilfer, R.: Application of Fractional Calculus in Physics. World Scientific, Singapore (2000)
Wen, X.J., Wu, Z.M., Lu, J.G.: Stability analysis of a class of nonlinear fractional-order systems. IEEE Trans. Circuits Syst.-I 55, 1178–1182 (2008)
Podlubny, I.: Fractional Differential Equations. Academic, New York (1999)
Hua, C., Zhang, T., Li, Y., Guan, X.: Robust output feedback control for fractional order nonlinear systems with time-varying delays. IEEE/CAA J. Autom. Sin. 3, 477–482 (2016)
Lim, Y.-H., Oh, K.-K., Ahn, H.-S.: Stability and stabilization of fractional-order linear systems subject to input saturation. IEEE Trans. Autom. Control 5, 1062–1067 (2013)
Qustaloup, A., Levron, F., Mathieu, B., Nanot, F.M.: Frequency-band complex noninteger differentiator: characterization and synthesis. IEEE Trans. Circuits Syst. I 47, 25–39 (2000)
Wang, Q., Qi, D.-L.: Synchronization for fractional order chaotic systems with uncertain parameters. Int. J. Control Autom. Syst. 14, 211–216 (2016)
Grigorenko, I., Grigorenko, E.: Chaotic dynamics of the fractional Lorenz system. Phys. Rev. Lett. 91, 034101 (2003)
Chen, C.G., Chen, G.R.: Chaos and hyperchaos in the fractional-order Rössler equations. Phys. A 341, 55–61 (2004)
Li, C.G., Chen, G.R.: Chaos in the fractional order Chen system and its control. Chaos Solitons Fract. 3, 549–554 (2004)
Deng, W.H., Li, C.P.: Chaos synchronization of the fractional Lü system. Phys. A 353, 61–72 (2005)
Petras, I.: A note on the fractional-order Chua’s system. Chaos Solitons Fract. 38, 140–147 (2008)
Hartley, T.T., Lorenzo, C.F., Qammer, H.K.: Chaos in a fractional order Chuas system. IEEE Trans. Circuits Syst. I 42, 485–490 (1995)
Gao, X., Yu, J.B.: Chaos in the fractional order periodically forced complex Duffings oscillators. Chaos Solitons Fract. 24, 1097–1104 (2005)
Vaseghi, B., Pourmina, M.A., Mobayen, S.: Secure communication in wireless sensor networks based on chaos synchronization using adaptive sliding mode control. Nonlinear Dyn. 89, 1689–1704 (2017)
Muthukumar, P., Balasubramaniam, P., Ratnavelu, K.: Synchronization of a novel fractional order stretch-twist-fold (stf) flow chaotic system and its application to a new authenticated encryption scheme (aes). Nonlinear Dyn. 77, 1547–1559 (2014)
Xu, Y., Wang, H., Li, Y., Pei, B.: Image encryption based on synchronization of fractional chaotic systems. Commun. Nonlinear Sci. Numer. Simul. 19, 3735–3744 (2014)
N’Doye, I., Voos, H., Darouach, M.: Observer-based approach for fractional-order chaotic synchronization and secure communication. IEEE J. Emerg. Sel. Top. Circuits Syst. 3, 442–450 (2013)
Muthukumar, P., Balasubramaniam, P., Ratnavelu, K.: Sliding mode control for generalized robust synchronization of mismatched fractional order dynamical systems and its application to secure transmission of voice messages. ISA Trans. (2017). https://doi.org/10.1016/j.isatra.2017.07.007
Podlubny, I.: Fractional-order systems and PID-controllers. IEEE Trans. Autom. Control 44, 208–214 (1999)
Odibet, Z., Corson, N., Aziz-Alaoui, M.: Synchronization of fractional order chaotic systems via linear control. Int. J. Bifurc. Chaos 20, 81–97 (2010)
Zhu, H., Zhou, S.B., Zhang, J.: Chaos and synchronization of the fractional-order Chua’s system. Chaos Solitons Fract. 39, 1595–1603 (2009)
Taghvafard, H., Erjaee, G.H.: Phase and anti-phase synchronization of fractional order chaotic systems via active control. Commun. Nonlinear Sci. Numer. Simul. 16, 4079–4088 (2011)
Wu, X.J., Lu, H.T., Shen, S.L.: Synchronization of a new fractional-order hyperchaotic system. Phys. Lett. A 373, 2329–2337 (2009)
Li, C., Wang, J., Lu, J., Ge, Y.: Observer-based stabilisation of a class of fractional order non-linear systems for \(0<\alpha <2\) case. IET Control Theory Appl. 8, 1238–1246 (2014)
Wang, X.Y., Zhang, X.P., Ma, C.: Modified projective synchronization of fractional-order chaotic systems via active sliding mode control. Nonlinear Dyn. 69, 511–517 (2012)
Li, C.L., Su, K.L., Wu, L.: Adaptive sliding mode control for synchronization of a fractional-order chaotic system. J. Comput. Nonlinear Dyn. 8, 031005 (2013)
Aghababa, M.P.: Design of hierarchical terminal sliding mode control scheme for fractional-order systems. IET Sci. Meas. Technol. 9, 122–133 (2014)
Ma, T.D., Jiang, W.B., Fu, J.: Impulsive synchronization of fractional order hyperchaotic systems based on comparison system. Acta Phys. Sin. 61, 090503 (2012)
Maione, G.: Continued fractions approximation of the impulse response of fractional-order dynamic systems. IET Control Theory Appl. 2, 564–572 (2008)
Liu, J.-G.: A novel study on the impulsive synchronization of fractional-order chaotic systems. Chin. Phys. B 22, 060510 (2013)
Odibat, Z.: A note on phase synchronization in coupled chaotic fractional order systems. Nonlinear Anal. 13, 779–789 (2012)
Muthukumar, P., Balasubramaniam, P., Ratnavelu, K.: Synchronization and an application of a novel fractional order king cobra chaotic system, Chaos: an Interdisciplinary. J. Nonlinear Sci. 24, 033105 (2014)
Pan, L., Guan, Z., Zhou, L.: Chaos multiscale-synchronization between two different fractional-order hyperchaotic systems based on feedback control. Int. J. Bifurc. Chaos 23, 1350146 (2013)
Maheri, M., Arifin, N.M.: Synchronization of two different fractional-order chaotic systems with unknown parameters using a robust adaptive nonlinear controller. Nonlinear Dyn. 85, 825–838 (2016)
Lu, J.G., Chen, Y.Q.: Robust stability and stabilization of fractional-order interval systems with the fractional order \(\alpha \): the \(0<\alpha <1\) case. IEEE Trans. Autom. Control 55, 152–158 (2010)
Lu, J.G., Chen, G.: Robust stability and stabilization of fractional-order interval systems: an LMI Approach. IEEE Trans. Autom. Control 54, 1294–1299 (2009)
Pan, G., Wei, J.: Design of an adaptive sliding mode controller for synchronization of fractional-order chaotic systems. Acta Phys. Sin. 64, 040505 (2015)
Yin, C., Dadras, S., Zhong, S., Chen, Y.: Control of a novel of class of fractional-order chaotic systems via adaptive sliding mode control approach. Appl. Math. Model. 37, 2469–2483 (2013)
Zhou, P., Zhu, P.: A practical synchronization approach for fractional-order chaotic systems. Nonlinear Dyn. 89, 1719–1726 (2017)
Zhang, R.X., Yang, S.P.: Synchronization of fractional-order chaotic systems with different structures. Acta Phys. Sin. 57, 6852–6858 (2008)
Pan, L., Zhou, W., Zhou, L., Sun, K.: Chaos synchronization between two different fractional-order hyperchaotic systems. Commun. Nonlinear Sci. Numer. Simul. 16, 2628–2640 (2011)
Zhang, R., Yang, S.: Robust synchronization of different fractional-order chaotic systems with unknown parameters using adaptive sliding mode approach. Nonlinear Dyn. 71, 269–278 (2013)
Wang, Z., Huang, X., Zhao, Z.: Synchronization of nonidentical chaotic fractional-order systems with different orders of fractional derivatives. Nonlinear Dyn. 69, 999–1007 (2012)
Chen, M., Shao, S.Y., Shi, P., Shi, Y.: Disturbance-observer-based robust synchronization control for a class of fractional-order chaotic systems. IEEE Trans. Circuits Syst. II 64, 417–421 (2017)
Kilbas, A.A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier Science, New York (2006)
Aguila-Camacho, N., Duarte-Mermoud, M.A., Gallegos, J.A.: Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 19, 2951–2957 (2014)
Adomian, G.: A review of the decomposition method and some recent results for nonlinear equations. Math. Comput. Model. 13, 17–43 (1990)
Ray, S.S., Bera, R.K.: An approximate solution of a nonlinear fractional differential equation by Adomian decomposition method. Appl. Math. Comput. 167, 561–571 (2005)
Fatoorehchi, H., Abolghasemi, H., Zarghami, R., Rach, R.: Feedback control strategies for a cerium-catalyzed Belousov–Zhabotinsky chemical reaction system. Can. J. Chem. Eng. 93, 1212–1221 (2015)
Fatoorehchi, H., Rach, R., Sakhaeinia, H.: Explicit Frost-Kalkwarf type equations for calculation of vapour pressure of liquids from triple to critical point by the Adomian decomposition method. Can. J. Chem. Eng. 95, 2199–2208 (2017)
Acknowledgements
This work is supported by the National Natural Science Foundation of China under Grants 61522302.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Li, RG., Wu, HN. Adaptive synchronization control based on QPSO algorithm with interval estimation for fractional-order chaotic systems and its application in secret communication. Nonlinear Dyn 92, 935–959 (2018). https://doi.org/10.1007/s11071-018-4101-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-018-4101-9