1 Introduction

Nonlinearity can be found in any mechanical system [1,2,3,4,5]. The nonlinearity has been utilized in vibration control [6, 7], such as X-type nonlinear vibration controllers [8, 9], quasi-zero stiffness nonlinear vibration devices [10, 11], and the nonlinear energy sink (NES) [12, 13], which have been considered as promising ways to control vibration. However, introducing nonlinearity into the system may cause many unwanted vibrations, such as aperiodic vibrations and closed detached frequency responses. Therefore, it is critical to understand the effects of nonlinearity on structural dynamics behaviors.

The NES is an excellent vibration control device and can significantly dissipate vibration energy over a wide range of frequency [12, 14]. The traditional NES device has been well-performing and applied to the structures, such as single-DOF system [15, 16], multi-DOF system [17,18,19], elastic string [20], elastic beams [21, 22], truss core sandwich plate [23], hollow rotor [24], and whole-spacecraft [25]. Besides, in order to improve the performance of vibration control, some promising designs have been proposed, such as the parallel NES [26,27,28,29], inertial NES [30, 31], rotating NES [32, 33], asymmetric magnet-based NES [34], and lever-type NES (LNES) [35]. It is worth noting that while performing effective vibration control on the system, the NES may introduce an unstable closed detached resonance response branch due to the nonlinearity [36]. Zang et al. discovered that the appearance of the closed isolated response could significantly enhance the transmissibility [35]. Liu et al. proved that the unstable isolated branch could be eliminated by changing the geometric nonlinearity of the system [37]. Habib et al. explored the existence of the isolated resonance response in the SDOF system [38, 39]. Starosvetsky et al. discovered the upper stable branch response accompanied by the strongly modulated response [40]. Because of the practicality of vibration control, the investigations of closed detached resonance response should have received significant attention [41, 42].

When the stability of the structure changes, the system may appear bifurcation [43,44,45]. Due to the bifurcation, the dynamical behaviors of the structure may present quasiperiodic [46] or chaotic motion [47], which cause unwanted vibrations. Walter et al. verified the chaotic motion around the resonant frequency of the curved beam through the experiments [48]. Then, they found that the high sensitivity of the bridge flexural–torsional frequency is close to the critical condition via the bifurcation diagrams [1]. Ding et al. analyzed the nonlinear dynamic behaviors of an axially moving Timoshenko beam [49, 50]. Zhang et al. discussed the existence of chaos in the horseshoe sense for cantilevered pipe conveying pulsating fluid [51]. Guo et al. discovered the periodic and chaotic motions of a composite laminated plate by the global bifurcations [52, 53]. Zhang et al. proposed a novel method to settle the bifurcation and hysteresis nonlinear behavior of varying compliance vibrations of a rotor [54, 55]. Hou et al. investigated the stability and bifurcation of a rotor system driven by constant excitation and rub-impact [56]. For the system coupled with NES, Starosvetsky et al. predicted the periodic and quasiperiodic regimes of a structure via the averaging method [57]. Zang et al. proved that the introduction of the NES into the linear system might create dynamic complexity [58]. Detroux et al. proposed the bifurcation analysis of a satellite structure [59]. What is well known is that various NESs can have an excellent performance for vibration control. However, the introduction of nonlinearity may cause bifurcations of the system, which leads to the complicated dynamical behaviors of the system, resulting in periodic and aperiodic responses to the structure. In this paper, an LNES is taken as an example of various NESs to investigate the periodic and aperiodic motions caused by the bifurcations.

The organization of this manuscript is as follows. Section 2 introduces a fundamental system of a structure with an LNES. Section 3 proposed the numerical explorations of global bifurcation, and the dynamical behaviors are numerically identified. Section 4 illustrated the way to trace the frequency response of the system, especially the closed detached response curves, and then observed the stability and bifurcations around the resonate frequency. Section 5 concludes the manuscript (Fig. 1).

Fig. 1
figure 1

Linear oscillator based on an LNES

Full size image
Fig. 2
figure 2

Bifurcation analysis for the system responses with m changed: a the structure and b LNES

Full size image

2 A linear system coupled with an LNES

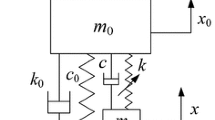
To consider a structure periodically excited and combined with an LNES, the structure, driven by harmonic force \(F(t)=A\cos (\omega t)\), is modeled as a linear SDOF system with linear stiffness \(k_{0}\), linear damping \(c_{0}\), and the mass \(m_{0}\). The LNES consists of a linear damper c, a nonlinear stiffness k, mass m, and a rigid massless lever. The equations of the dynamical system can be written by Newton’s second law as follows:

$$\begin{aligned}&m_0 \ddot{x}_0 +k_0 x_0 +(1-\alpha )k(x_{\mathrm{c}} -x)^{3}+c_{\mathrm{0}} {\dot{x}}_0 \nonumber \\&\quad +\,(1-\alpha )c({\dot{x}}_{\mathrm{c}} -\dot{x})+F\cos (\omega t)=0 \nonumber \\&\qquad m\ddot{x}+k(x-x_{\mathrm{c}} )^{3}+c({\dot{x}}-{\dot{x}}_{\mathrm{c}} )=0, \end{aligned}$$
(1)

where \(x_{0}\), x, and \(x_{\mathrm{c}}\) are the displacement responses of mass \(m_{0}\), mass m, and end C, respectively. The fulcrum location \(\alpha \) is the leveraged rate of length AC–AB. The response of \(m_{0}\) is the same as that at end A. Given a small relative motion, the vibration response \(x_{\mathrm{c}}\) of the lever could be written as

$$\begin{aligned} x_{\mathrm{c}} =(1-\alpha )x_0. \end{aligned}$$
(2)

The dynamical equations of the system can be rewritten as

$$\begin{aligned}&m_0 \ddot{x}_0 +k_0 x_0 +(1-\alpha )k((1-\alpha )x_0 -x)^{3}+c_{\mathrm{0}} {\dot{x}}_0 \nonumber \\&\quad +\,(1-\alpha )c((1-\alpha ){\dot{x}}_0 -{\dot{x}})+F\cos (\omega t)=0 \nonumber \\&\qquad m\ddot{x}+k(x-(1-\alpha )x_0 )^{3}{+}c({\dot{x}}-(1{-}\alpha ){\dot{x}}_0 )=0.\nonumber \\ \end{aligned}$$
(3)

3 Numerical explorations of global bifurcation

Nonlinear dynamical behaviors of the system with LNES will be revealed via numerical integrations in this section. The frequency of the periodic force is set as \(\omega =125.6649\,\hbox {rad/s}\). The time increment is defined as 0.005 of a period \(2\pi /\omega \). The bifurcation analysis of Poincaré map is introduced to identify dynamical behaviors. The response components within the time interval of [\(0,\,6000T\)] of the Poincaré maps will be obtained. To eliminate the transient responses, the displacement of the last 200 periods is focused. Choose the parameter values as \(m_{0}=72\,\hbox {kg}\), \(k_{0}=1137\,\hbox {kN/m}^{3}\), \(c_{0}=600\,\hbox {Ns/m}\), \(F=4000\,\hbox {N}\), \(m=2\,\hbox {kg}\), \(k=10{,}000\,\hbox {kN/m}^{3}\), \(c=100\,\hbox {Ns/m}\) and \(\alpha =3\). In the following investigation, three key design parameters of the LNES, namely mass m, nonlinear stiffness k, and fulcrum position \(\alpha \), are considered as the varying parameters, respectively. The time history response, phase portrait, Poincaré maps, and power spectra will be employed to identify the dynamical behaviors.

By varying the mass m for all other system parameters unchanged, Fig. 2 depicts the bifurcation diagrams analysis of the structure and the LNES. The numerical results reveal the periodic motions and complicated aperiodic motions (quasiperiodic or chaotic motion) of the structure, and the LNESs are exchanged alternately. The LNES induces such aperiodic motions because the linear structure can only behave periodically. For the periodic motion, as the attached mass m increases, the vibration of the structure is increased, until \(m=0.64\,\hbox {kg}\), then decreases, and finally increases after a few bursts of aperiodic motions. The vibration of the LNES is increased, till \(m=0.64\,\hbox {kg}\), and then decreases after a few complicated motions. It should be noted that the LNES has a passive option mass to minimize the vibration amplitude of the structure. Besides, Figs. 3 and 4 show that the structure and the LNES have the same dynamical behaviors. Specifically, when m is 1 kg in Figs. 3a and 4a, the structure and the LNESs are the period-1 motion. And when the m increases to 3.15 kg in Figs. 3b and 4b, the structure and LNES are the period-5 motion. Continually to increase m to 4 kg in Figs. 3c and 4c, the structure and the LNES change to be the quasiperiodic motion. Finally, when m is 4.8 kg in Figs. 3d and 4d, the structure and the LNES turn back to the period-1 motion.

Fig. 3
figure 3

Vibration of the structure varying the LNES mass under the description with time history response, phase portrait, Poincaré map, and the power spectra

Full size image
Fig. 4
figure 4

Vibration of the LNES varying the LNES mass under the description with time history response, phase portrait, Poincaré map, and the power spectra

Full size image

Figure 5 presents the bifurcation diagrams of the structure and the LNES varying the nonlinear stiffness k for all other system parameters unchanged. The structure and the LNES mainly exhibit periodic motion excepting an interval of complicated aperiodic motion with small and relatively sizeable nonlinear stiffness k. As the nonlinear stiffness k increases, the vibration of the structure is decreased and then increases after a few bursts of aperiodic motion. However, the vibration of the LNES decreases with the enhancement of the stiffness k for the periodic motion. Samples of periodic motion of the structure and the LNES are shown in Figs. 6a and 7a. The aperiodic motions are quasiperiodic as depicted in Figs. 6b and 7b.

Fig. 5
figure 5

Bifurcation analysis for the system responses with nonlinear stiffness k changed: a the structure and b LNES.

Full size image
Fig. 6
figure 6

Vibration of the structure varying the LNES nonlinear stiffness k under the description with time history response, phase portrait, Poincaré map, and the power spectra

Full size image
Fig. 7
figure 7

Vibration of the LNES varying the LNES nonlinear stiffness k under the description with time history response, phase portrait, Poincaré map, and the power spectra

Full size image

Figure 8 shows the bifurcation diagrams varying the fulcrum location \(\alpha \) for all other system parameters unchanged. The numerical results reveal the periodic motion and complicated aperiodic motion of the structure, and the LNESs are exchanged alternately. When complex aperiodic motions suddenly disappear, the periodic motion occurs again. With the gradual increase in the fulcrum position, the vibration of the structure and the LNES first decrease, then occurs aperiodic motion at \(\alpha =0.35\) and 1.65, and then gradually decreases at \(\alpha =2\). After a short period of aperiodic motion, the vibration amplitude is gradually reduced again. Besides, Figs. 9 and 10 show the dynamical behaviors of structure and the LNES. Specifically, when \(\alpha \) is 0.35 and 1.65 in Figs. 9a–c and 10a–c, the structure and the LNES are quasiperiodic motion. Continually to increase the fulcrum location \(\alpha \) to 6 in Figs. 9d and 10d, the structure and the LNES change to be the period-1 motion. It can be seen that direct utilization of the lever principle is not a suitable approach to determine the fulcrum location for the LNES.

Fig. 8
figure 8

Bifurcation diagram of the system response varying the fulcrum \(\alpha \): a the system and b LNES

Full size image
Fig. 9
figure 9

Vibration of the structure varying the LNES fulcrum \(\alpha \) under the description with time history response, phase portrait, Poincaré map, and the power spectra

Full size image
Fig. 10
figure 10

Vibration of the LNES varying the LNES fulcrum \(\alpha \) under the description with time history response, phase portrait, Poincaré map, and the power spectra

Full size image

4 The tracking and stability of frequency response curves

4.1 The basic step of harmonic balance method coupled with the arc-length tracking continuation

This section mainly focuses on the periodic motion and the bifurcation points from the perspective of the primary frequency response and the closed detached frequency response curves. The harmonic balance method is utilized to trace the curves. To apply the harmonic balance process, Eq. (3) is simplified to dimensionless forms as follows:

$$\begin{aligned}&{u}^{{\prime }{\prime }}_0 +u_0 +(1-\alpha )\beta l^{2}((1-\alpha )u_0 -u)^{3}\nonumber \\&\quad +\varsigma _0 {u}'_0 {+}(1{-}\alpha )\varsigma ((1{-}\alpha ){u}'_0 -{u}'){+}f\cos (\gamma \tau )=0 \nonumber \\&\qquad \lambda {u}''{+}\beta l^{2}(u{-}(1{-}\alpha )u_0 )^{3}{+}\varsigma ({u}'{-}(1{-}\alpha ){u}'_0 )=0,\nonumber \\ \end{aligned}$$
(4)

where

$$\begin{aligned} u_0= & {} \frac{x_0 }{l},u=\frac{x}{l},\tau =\omega _0 t,\lambda =\frac{m}{m_0 },\beta =\frac{k}{k_0 }, \nonumber \\ \varsigma _0= & {} \frac{c_0 }{m_0 \omega _0 },\varsigma =\frac{c}{m_{\mathrm{0}} \omega _0 },\gamma =\frac{\omega }{\omega _{\mathrm{0}} },f=\frac{F}{k_0 l}, \end{aligned}$$
(5)

in which the static deformation l of linear stiffness \(k_{0}\) is 100 times as the gravity of \(m_{0}\).

The responses of dynamical Eq. (4) can be expressed as follows:

$$\begin{aligned}&u_0 (\tau )=a_{0,0} +\sum \limits _{i=1}^n {\cos (i\gamma \tau )a_{0,i} } +\sum \limits _{i=1}^n {\sin (i\gamma \tau )b_{0,i} } \end{aligned}$$
(6)
$$\begin{aligned}&u(\tau )=a_0 +\sum \limits _{i=1}^n {\cos (i\gamma \tau )a_i } +\sum \limits _{i=1}^n {\sin (i\gamma \tau )b_i } \end{aligned}$$
(7)
$$\begin{aligned}&\mathbf{G}=[a_{0,0} ,a_{0,i} ,b_{0,i} ,a_0 ,a_i ,b_i ], \end{aligned}$$
(8)

where G is the coefficients to be defined for the corresponding harmonic term and i is the harmonic order, \(i=1, 2 {\ldots } n\).

Based on the method of harmonic balance, the harmonic coefficients of Eq. (4) can be obtained by solving a set of nonlinear algebraic equations with Newton–Raphson iteration. However, the method of Newton–Raphson will fail when passing cross the turning point, especially for the closed detached frequency response, because the iteration matrix is singular. To bridge over the problem, the arc-length tracking is utilized to cover with the method of harmonic balance [18, 58]. The nonlinear algebraic equations can be formulated as

$$\begin{aligned} \mathbf{f}(\lambda _{\mathrm{f}} ,\mathbf{G})=0, \end{aligned}$$
(9)

where \(\lambda _\mathrm{f}\) is an introduced parameter variable.

To track the solution branch of Eq. (9), the predictor–corrector procedure is carried out to obtain a valid initial value \((\lambda _{\mathrm{f}}, \mathbf{G})_{\mathrm{p}}\) from the starting point \((\lambda _{\mathrm{f}}, \mathbf{G})_{{0}}\). The tracing direction of the solution branch, namely the tangent vector, can be assumed as \(\mathbf{R}= \{R_{1},R_{2}{\ldots }R_{n+1}\}^{\mathrm{T}}\). The elements in vector \(\mathbf{R}\) can be obtained as follows:

$$\begin{aligned} R_i =(-1)^{i+1}\hbox {det}[\mathbf{C}_{\mathrm {-j}} (\lambda _{\mathrm{f}},\mathbf{G})], \end{aligned}$$
(10)

where the Jacobian matrix \(\mathbf{C}\left( {\lambda _{\mathrm{f}} ,\mathbf{G}} \right) =[{\partial \mathbf{f}}/{\partial \lambda _{\mathrm{f}}},{\partial \mathbf{f}}/{\partial \mathbf{G}}]\) and \(\mathbf{C}_{-j}(\lambda _\mathrm{f},\, \mathbf{G})\) is a submatrix given by deleting the jth column of the Jacobian matrix \(\mathbf{C}(\lambda _{\mathrm{f}},\,\mathbf{G})\). The det [.] is the determinant operator.

Then, the predictor value (\(\lambda _{\mathrm{f}},\,\mathbf{G})_{\mathrm{p}}\) can be given by the unit tangent vector \(\tau _{\mathrm{R}} =\mathbf{R}/\Vert \mathbf{R} \Vert \) as follows:

$$\begin{aligned} (\lambda _{\mathrm{f}} ,\mathbf{G})_{\mathrm{p}} =(\lambda _{\mathrm{f}} ,\mathbf{G})_0 +\tau _{\mathrm{R}} ((\lambda _{\mathrm{f}} ,\mathbf{G}))\Delta s, \end{aligned}$$
(11)

in which \(\Delta s\) is the basic increment of the arc-length. The \(\Delta s\) is a key factor to trace the solution branch of the system. When the curvature of the branch curve is large, especially if there is a closed detached response, the \(\Delta s\) should be small to ensure accuracy. The choice of the \(\Delta s\) is simple, namely \(\Delta {s}_{i}=\Delta {s}_{i-1}N_{\mathrm{p}}/I_{i-1}\). Here, \(\Delta {s}_{i}\) is the increment arc-length in the ith prediction step, \(N_{\mathrm{p}}\) is the presupposed number of the iterations, and \(I_{i-1}\) is the actual number of iterations.

Once the predictor value is determined, the Newton–Raphson iteration can be carried out and if the equations reach the iterative termination error value \(\varepsilon \), the solution branch can be given as

$$\begin{aligned} (\lambda _{\mathrm{f}} ,\mathbf{G})_i= & {} (\lambda _{\mathrm{f}} ,\mathbf{G})_{i-1} -\left[ {{\begin{array}{l} {\mathbf{C}(\lambda _{\mathrm{f}} ,\mathbf{G})_{i-1} } \\ {\mathbf{R}^{\mathrm {T}}(\lambda _{\mathrm{f}} ,\mathbf{G})_{i-1} } \\ \end{array} }} \right] ^{-1}\nonumber \\&\times \left[ {{\begin{array}{l} {\mathbf{f}(\lambda _{\mathrm{f}} ,\mathbf{G})_{i-1} } \\ 0 \\ \end{array} }} \right] \quad {(i=1,2\ldots n)}. \end{aligned}$$
(12)

4.2 The stability and bifurcation analysis via the Floquet theory

The Floquet theory [60] is utilized to settle the stability of periodic solutions above and determine the bifurcation points in the frequency response. Introducing the \(\mathbf{P}=[u_0 ,{u}^{\prime }_0 ,u,{u}^{\prime }]\) transforms Eq. (4) as follows:

$$\begin{aligned} \mathbf{{P}}^{\prime }(\tau )=\mathbf{F}(\mathbf{P}(\tau ),\tau ). \end{aligned}$$
(13)

Superposing the \(\Delta \mathbf{P}\) to perturb the assumed periodic solution \(\mathbf{P}^{*}\) of Eq. (13), we obtain

$$\begin{aligned} (\mathbf{P}^{*}+\Delta \mathbf{P})^{\prime }=\mathbf{F}(\mathbf{P}^{*}+\Delta \mathbf{P},\tau ). \end{aligned}$$
(14)

The stability of \(\mathbf{P}^{*}\) can be given with the linear stability of the system as follows:

$$\begin{aligned} \Delta \mathbf{{P}'}=\left( {{\partial \mathbf{F}(\mathbf{P}^{*},\tau )}/{\partial \mathbf{P}^{*}}} \right) \cdot \Delta \mathbf{P}=\mathbf{A}(\mathbf{P}^{*}(\tau ),\tau )\cdot \Delta \mathbf{P},\nonumber \\ \end{aligned}$$
(15)

where \(\mathbf{A}(\mathbf{P}(\tau ),\tau )={\partial \mathbf{F}(\mathbf{P}(\tau ),\tau )}/{\partial \mathbf{P}}\).

Based on the Hsu’s theory [61], the approximating monodromy matrix of Eq. (15) can be expressed as follows:

$$\begin{aligned} \mathbf{Q}=\prod _{n=N}^1 {\exp (\mathbf{A}_n \Delta T)} \approx \prod _{n=N}^1 \left( \mathbf{I}{+}\sum _k^{N_k } {\frac{(\mathbf{A}_n \Delta T)^{k}}{k!}} \right) ,\nonumber \\ \end{aligned}$$
(16)

where \(\mathbf{I}\) is the identity matrix and the period T of the solutions is segmented into N subintervals as \(\Delta T\). The \(N_{k}\) is the number of terms in the approximation of A\(_{n}\) exponential. Constant matrix \(\mathbf{A}_{n} = \mathbf{A}(\mathbf{P}^{*}(\tau _{n}))\) is taken to substitute the time-varying matrix \(\mathbf{A}(\mathbf{P}^{*}(\tau ))\) in the nth time interval, where \(\tau _{n}=n\Delta T/N\). If all the eigenvalues of Q (Floquet multipliers) are within a unit circle in the complex plane, the periodic solutions are stable. Otherwise, the periodic solutions are unstable, and the bifurcation points can be determined along with three regulations ruled under the Floquet multipliers [62].

  1. (i)

    If a multiplier escapes the unit circle at \(+\) 1 direction, the saddle-node (SN) bifurcation may occur.

  2. (ii)

    If a multiplier leaves the unit circle at − 1 direction, the period-doubling (PD) bifurcation may occur.

  3. (iii)

    If two complex conjugate multipliers cross out of the unit circle, the Neimark–Sacker (NS) bifurcation may occur.

Here, the SN bifurcation indicates a change in stability and leads to amplitude jumps that may result in possible significant changes in system response. The PD bifurcation means a new behavior with twice the period of the original system that may lead to the dynamical behaviors to chaos. The NS bifurcation represents the transformation of the motion state, leading the transition from periodic motion to quasiperiodic motion. The flowchart describing the arc-length continuity method and stability analysis is shown in Fig. 11.

Fig. 11
figure 11

Flowchart describing the arc-length continuity method and stability analysis

Full size image
Fig. 12
figure 12

Comparison between the analytical solutions and numerical results

Full size image
Fig. 13
figure 13

Frequency response curve of the structure varying the LNES mass \(\lambda \): a\(\lambda = 0.0139\), b\(\lambda = 0.0264\), c\(\lambda =0.0278\), d\(\lambda =0.0294\), e\(\lambda =0.0417\) and f\(\lambda = 0.0694\)

Full size image
Fig. 14
figure 14

Frequency response curve of the LNES varying the LNES mass \(\lambda \): a\(\lambda = 0.0139\), b\(\lambda = 0.0264\), c\(\lambda =0.0278\), d\(\lambda =0.0294\), e\(\lambda =0.0417\) and f\(\lambda = 0.0694\)

Full size image

To evaluate the dynamical behaviors of the structure coupled with the LNES in the frequency domain, the response of structure and LNES are redefined by the root mean square [18].

$$\begin{aligned}&u_{0r} =\frac{\sqrt{ 2 a_{0,0} ^{2}+a_{0,i} ^{2}+b_{0,i} ^{2}}}{2}\quad {(i=1,2\ldots n)} \end{aligned}$$
(17)
$$\begin{aligned}&u_r =\frac{\sqrt{ 2 a_0 ^{2}+a_i ^{2}+b_i ^{2}}}{2}\quad {(i=1,2\ldots n)}. \end{aligned}$$
(18)

4.3 Numerical examples

In this paper, the harmonic term is chosen to be three [58], the dimensionless parameters values are \(\omega _{0}=125.6649\), \(l=0.0621\), \(\zeta _{0}=0.0663\), \(\lambda =0.0278\), \(\beta =8.7951\), \(\zeta =0.0111\), \(f=0.0567\) and \(\alpha =3\). Figure 12 presents the analytical solutions compared with the numerical method. The black ball means numerical solutions, and the solid blue line represents the analytical solutions. It can be seen the analytical solutions highly correspond with the numerical results, even only an order 3 harmonic solution, and agree well with the numerical ones, which are used to check the accuracy of Eqs. (17) and (18).

Table 1 Ranges of bifurcation and the existence of closed detached frequency response varying the mass \(\lambda \)
Full size table
Fig. 15
figure 15

Frequency response curve of the structure varying the LNES nonlinear stiffness \(\beta \): a\(\beta = 0.0880\), b\(\beta =4.3975\), c\(\beta =8.4433\), d\(\beta =8.7951\), e\(\beta =9.2348\) and f\(\beta =26.3852\)

Full size image
Fig. 16
figure 16

Frequency response curve of the LNES varying the LNES nonlinear stiffness \(\beta \): a\(\beta {=}\,0.0880\), b\(\beta =4.3975\), c\(\beta =8.4433\), d\(\beta =8.7951\), e\(\beta =9.2348\) and f\(\beta =26.3852\)

Full size image

Figures 13 and 14 demonstrate the frequency response curves varying the mass \(\lambda \) attached. For a tiny mass \(\lambda \), the response curves are analogous to the linear stable case, which are shown in Figs. 13a and 14a. For a larger value of the mass \(\lambda \) in Figs. 13b and 14b, the response curves are distorted around the resonance frequency with two unstable branches. The first unstable branch is caused by SN bifurcation, within the frequency ranging from 0.8679 to 0.8961. The NS bifurcation induces the second unstable branch instability in the frequency interval of 1.003 to 1.079. For a moderate larger value of the mass \(\lambda \) in Figs. 13c and 14c, an outside closed detached frequency response curve appears caused by SN bifurcation within the frequency ranging from 0.8685 to 0.9049. The primary response curve still has an unstable branch induced by the NS bifurcation from 0.9888 to 1.0797. For large amounts of attached mass in Figs. 13d and 14d, the closed detached frequency response curve with SN bifurcation from 0.8747 to 0.8849 leaves apart from the primary response and turns to be small. The unstable branch range of the primary response curve induced by the NS bifurcation becomes larger from 0.9694 to 1.0799. For an extra increase in the value of the mass \(\lambda \) in Figs. 13e and 14e, the external closed detached frequency response disappears outside the primary curve. The unstable branch range of the primary response curve induced by the NS bifurcation continually becomes larger from 0.9260 to 1.0780. For a much increased value of the mass \(\lambda \) in Figs. 13f and 14f, the primary response curve turns to be stable without any bifurcation. It can be seen that as the mass attached increases, the SN bifurcation and the NS bifurcation may appear simultaneously in the system. When closed detached frequency response curves disappear, the NS bifurcation point of the structure characterizes the system with a quasiperiodic response near the resonance frequency. The ranges of bifurcation and the existence of closed detached frequency response varying the mass \(\lambda \) are shown in Table 1.

Table 2 Ranges of bifurcation and the existence of closed detached frequency response varying the stiffness \(\beta \)
Full size table
Fig. 17
figure 17

Frequency response curve of the structure varying the LNES fulcrum \(\alpha \): a\(\alpha =1.5\), b\(\alpha =1.65\), c\(\alpha =2.5\), d\(\alpha =3\), e\(\alpha =5\) and f\(\alpha =7\)

Full size image
Fig. 18
figure 18

Frequency response curve of the LNES varying the LNES fulcrum \(\alpha \): a\(\alpha =1.5\), b\(\alpha =1.65\), c\(\alpha =2.5\), d\(\alpha =3\), e\(\alpha =5\) and f\(\alpha =7\)

Full size image
Table 3 Ranges of bifurcation and the existence of closed detached frequency response varying the fulcrum \(\alpha \)
Full size table

Figures 15 and 16 show the frequency response curves changing with the nonlinear stiffness \(\beta \). In Figs. 15a and 16a, the dynamic characteristics of the system are stable. For a slightly larger stiffness shown in Figs. 15b and 16b, the response curve has an unstable branch induced by the NS bifurcation ranging from 0.9729 to 1.019. For a further larger stiffness shown in Figs. 15c and 16c, a closed detached frequency response curve with SN bifurcation ranging from 0.8811 to 0.8941 appears outside the primary response curve with NS bifurcation interval of 0.9844–1.076. The closed detached frequency response with SN bifurcation becomes larger and tends to attract the primary response curve with NS bifurcation in Figs. 15d and 16d. For a much increased stiffness in Figs. 15e and 16e, the closed detached frequency response merges with the primary response with two unstable branches. The first unstable branch is caused by the SN bifurcation ranging from 0.8590 to 0.8993, and the second unstable branch is induced by the NS bifurcation interval of 0.9947–1.083. Finally, in Figs. 15f and 16f, the dynamics of the system turn to be complex with three sections: SN bifurcation ranging from 0.6987 to 0.7094, 0.8879 to 0.9429, and 1.167 to 1.169, and one section NS bifurcation ranging from 1.083 to 1.167. It should be concerned that with an increase in the nonlinear stiffness, the dynamic behavior of the system tends to be complicated due to multiple sets of SN bifurcations and NS bifurcations, accompanied by the appearance of closed detached frequency response. Ranges of bifurcation and the existence of closed detached frequency response varying the stiffness \(\beta \) are shown in Table 2.

The last influencing factor of the frequency response curves is the fulcrum location \(\alpha \), shown in Figs. 17 and 18. In Figs. 17a and 18a, when the fulcrum \(\alpha \) is 1.5, the dynamic characteristics of the system are stable without any bifurcation. For a slightly increased value \(\alpha =1.65\) in Figs. 17b and 18b, an unstable branch with NS bifurcation appears within the range of 0.9908–1.006. With the increase in the fulcrum \(\alpha \) to 2.5 in Figs. 17c and 18c, the frequency response curves turn to be distorted with two unstable branches. The first unstable branch is induced by the SN bifurcation ranging from 0.9173 to 0.9302, and the second unstable branch is caused by the NS bifurcation 1.010–1.062. For a further fulcrum \(\alpha \), for example, \(\alpha =3\) in Figs. 17d and 18d, a closed detached frequency response curve with SN bifurcation ranging from 0.8685 to 0.9049 appears outside the primary response curve with NS bifurcation interval of 0.9888 to 1.080. Further increasing the fulcrum \(\alpha \) to 5 in Figs. 17e and 18e, the closed detached frequency response goes back and merges with the primary response curve, with two sections SN bifurcation ranging from 0.6147 to 0.6360 and 0.7556 to 0.7728 and one section NS bifurcation ranging from 0.9611 to 1.054. For a larger increase in fulcrum, \(\alpha =7\) in Figs. 17f and 18f, the frequency response curves turn back to stable. When the fulcrum position is small, the dynamic characteristics of the system are more complicated. However, when the fulcrum position increases to a certain extent, the dynamic region of the system is stable. Particularly, based on the illustrations from Figs. 13, 14, 15, 16, 17, and 18, it can be seen that when SN bifurcation and NS bifurcation occur simultaneously, it is a sign that the closed detached frequency response may appear. Ranges of bifurcation and existence of closed detached frequency response varying the fulcrum \(\alpha \) are shown in Table 3.

5 Conclusion

The dynamical behavior of a model combined with an LNES is proposed. The global bifurcations are numerically investigated by the Poincaré map. The time history response, phase trajectories, Poincaré maps, and amplitude spectra are used to identify dynamical behaviors. The basic steps of the harmonic balance method coupled with arc-length tracking continuation are introduced to trace the primary and close detached frequency response curves. The stabilities and bifurcation of frequency response curves have been settled via the Floquet theory. The investigation yields the following conclusions:

  1. 1.

    The quasiperiodic motion may occur. Actually, the bifurcation diagrams reveal the responses of the structure and LNESs are periodic motion except for the intermittency of quasiperiodic motion.

  2. 2.

    For small attached masses, close fulcrum, and large nonlinear stiffness, the dynamic behavior of the system is complex due to multiple sets of SN bifurcations and NS bifurcations.

  3. 3.

    When SN bifurcation and NS bifurcation occur simultaneously, it is a sign that the closed detached frequency response may appear.

  4. 4.

    When the closed detached frequency response disappears, the NS bifurcation on the primary branch of the system indicates that a quasiperiodic response occurs near the resonant frequency.

  5. 5.

    From the perspective of bifurcation, it can give a prediction for the frequency response and a base for the parameter optimization for the LNES absorber in engineering.