A new perspective on static bifurcations in the presence of viscoelasticity

Abstract

This manuscript explores the effect of viscoelasticity on static bifurcations: such as pitchfork, saddle-node, and transcritical bifurcations, of a single-degree-of-freedom mechanical oscillator. The viscoelastic behavior is modeled via a differential form, where the extra degree of freedom represents the internal force provided by the viscoelastic element. The governing equations are derived from a simplified lumped parameter model consisting of a rigid rod incorporating a viscoelastic element and subjected to axial and transverse forces at the free end, in addition to an external time-varying moment applied to the rod. In order to study the effect of viscoelasticity on bifurcation diagrams, the equations of motion are non-dimensionalized. Next, a review of static bifurcations in the absence of viscoelasticity is conducted, followed by an examination of the effect of viscoelasticity on the bifurcation diagrams. Finally, this paper investigates the effects of viscoelasticity on the transient behavior of the oscillator. Results show that the Deborah number, which measures the ratio of the viscoelastic time constant to the natural periodic time of the system, controls the duration of time needed to maintain oscillations around an unstable point before jumping to a stable equilibrium point.

1 Introduction

In recent years, many industries: such as the automotive, submarine, aviation, and aerospace, have continuously invested in the development of viscoelastic materials. Due to their damping characteristics, viscoelastic materials have been exploited to dissipate vibration energy in many systems. In particular, when high damping is required for lightweight applications. A simple way to understand a viscoelastic structure is by viewing a typical viscoelastic element consisting of a sandwich construction of a viscoelastic layer in between two elastic layers, as depicted in Fig. 1a.

Material scientists emphasize that all materials can be considered viscoelastic elements under certain conditions. Various levels of viscoelastic response behavior can be obtained by controlling the operating temperature. For lightweight and sensitive applications, a small alteration in the viscoelastic behavior may affect the dynamics of the system. One promising avenue of research is the development of mechanical metamaterials. These material systems may exhibit a viscoelastic response. In addition, they have tunable mechanical properties that allow the structure to undergo programmable responses [1, 2]. Figure 1b depicts a schematic of a flexible metamaterial structure incorporating an elastomeric structure with an embedded square arrangement of circular openings.

Fig. 1

a Illustration of a viscoelastic element, b schematic diagram of a metamaterial structure incorporating an elastomeric matrix with a square array of circular openings, and c characteristics of a viscoelastic material

Note that due to a simple harmonic excitation, a purely elastic material’s strain and stress are in-phase. On the other hand, for viscoelastic materials, the strain lags the stress in the material. In a linear viscoelastic material, this lag is evident in the elliptical hysteresis loops seen by plotting stress–strain under harmonic excitation. The hysteresis is also evident when examining the stress in the material versus time due to compressive loading. In a purely elastic material, the loading and unloading curve coincides, while in the viscoelastic case the material experiences hysteresis causing the two curves to deviate significantly. Creep is a phenomenon that can occur in viscoelastic materials. It happens when strain increases with time as stress is held constant. On the other hand, if the strain is held constant, and stress is found to be decreasing with time, the material exhibits what is called a viscoelastic relaxation. During slow loading, the relaxation of a viscoelastic material lasts for a longer period in time. Therefore, the peak stress due to a low loading rate is less than that of faster loading. These characteristics of a viscoelastic material, i.e., hysteresis, creep, stress relaxation, and loading rate effect, are shown in Fig. 1c.

Previous literature on viscoelasticity has focused on many aspects, including but not limited to: (i) examining the behavior of viscoelastic structures such as creep bending and creep buckling, (ii) obtaining mathematical models to describe the nonlinear stress–strain relation of viscoelastic elements, (iii) exploiting viscoelastic materials in vibration control applications, and (iv) studying the effect of damping of viscoelastic materials on the dynamic of snap-through criteria.

Numerous research efforts have focused on examining the behavior of viscoelastic elements. Kempner [3] studied numerically and experimentally the creep bending and buckling of linearly viscoelastic columns. In his study, a derived model was employed to estimate the creep bending deflection of a beam with initial sinusoidal deviation, where creep buckling of viscoelastic structures has been studied both experimentally and analytically by Minahen and Knauss [4]. The theory of linear viscoelasticity has been utilized to model polymeric column specimens under constant compressive loads.

Scientists have been developing nonlinear mathematical models that can be employed to understand the behavior of viscoelastic materials. A rheological model describing the nonlinear stress response for a viscoelastic material under a nonlinear strain history has been proposed by Monsia [5]. Results have demonstrated that the proposed model can be utilized to predict the stress–strain curve as a second-order polynomial. Nachbar and Huang [6] introduced two methods that can be applied to estimate buckling loads using potential energy curves and phase plane diagrams. The energy integral method was used to approximate the buckling load, while exact values were calculated by numerical integration of the governing equation. A study on understanding the nonlinear response of elastomeric materials under critical constraints has been conducted by Cui and Harne [7]. In their research, they have introduced an analytical approach to predict the response of elastomeric materials.

Due to the superior capability of viscoelastic structures in energy absorption, viscoelastic elements have been utilized in vibration and control applications. Flexural vibrations of sandwich beams with clamped ends have been studied theoretically and experimentally by Kovac et al. [8]. In their research, Galerkin’s procedure and the method of harmonic balance have been utilized to obtain a theoretical frequency–amplitude relation and then compared against experimental findings. An elementary theory of nonlinear vibrations of viscoelastic beams has been developed by Daya et al. [9]. They have exploited the method of harmonic balance coupled with a single-mode Galerkin’s analysis to study the response of free and forced vibrations of a viscoelastic beam. Furthermore, the change in damping of a post-buckled beam having geometric imperfections has been investigated by Kosmatka [10].

The role of damping in controlling vibration levels and its effect on the snap-through behavior has been studied by Murray and Gandhi [11]. It has been observed that applying the load for a longer time will allow energy to dissipate, as the system was not able to escape the energy barrier and continued in one stable state. Recently, Che et al. [12] presented an experimental and numerical study on a 3D printed viscoelastic meta-structures with snap-through instability. It has been demonstrated that the tunability of the time-dependent response behavior permits designing a meta-structure with the ability to alter its size, shape, or even its properties.

The influence of damping on snap-through dynamics has been examined by many researchers. It has been investigated by Johnson [13] for an impulsively loaded shallow circular arch by using Kelvin–Voigt representation. The influence of damping on oscillation’s response in the vicinity of various bifurcations of nonlinear systems has been investigated by Virgin and Wiebe [14]. It has been demonstrated that the damping ratio can be employed to predict the change in stability of the oscillator. Moreover, Weibe et al. [15] investigated the snap-through buckling of a single degree of freedom system. In their research, they introduced a method that can be used to distinguish between large and low amplitudes of the response based on the average total energy approach.

Reviewing the available literature, it is clear that various structural systems exhibit different instabilities, i.e., whether a fixed point or periodic solution behaves as an attractor or repeller to the flow. Incorporating a viscoelastic element increases the mathematical complexity of any model, by increasing the order of a mechanical system from a second-order system to third-order or higher. Depending on the number of differential equations used to capture the material response, or even change the mathematical model of the system to contain fractional derivatives, the prediction of the onset of the bifurcation in the system is complicated by balancing inertial forces and time-dependent elastic forces which may gradually creep until stability is lost. Not understanding the implications of the increased order of the system may lead to confusion.

Therefore, this paper aims to study the effect of viscoelasticity on static bifurcations such as saddle node (SN), subcritical pitchfork (PF), and transcritical (TC) bifurcations. To this end, the rest of the paper is organized as follows: Sect. 2 presents the governing equations of a lumped parameter model used to study the nonlinear behavior of a mechanical oscillator incorporating a viscoelastic element. A non-dimensionalized analysis using the Taylor series expansion of the governing equations is presented. Section 3 discusses static bifurcations of the system: first, in the absence of linear viscoelasticity and then with including linear viscoelasticity into the analysis. Section 4 explores the effect of the Deborah number on the duration of time needed to maintain oscillations around an unstable point before jumping to a stable equilibrium branch. Finally, Sect. 5 presents the relevant conclusions.

2 Governing equations

This manuscript presents a survey of the effects of viscoelasticity on different local bifurcations; saddle node, pitchfork, and transcritical bifurcations. These bifurcations establish the foundation to describe the nonlinear behavior of a single degree of freedom mechanical oscillator for finite amplitudes around an equilibrium.

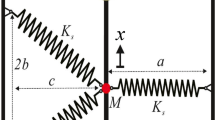
In order to gain insight into the effect of viscoelasticity on stability, we consider the model depicted in Fig. 2 The lumped parameter model is chosen to avoid restricting the analysis to a given geometry and a given set of geometric boundary conditions. The model consists of a rigid rod subjected to an axial force, $F_c$, and a transverse force, P, applied at the free end of the rod , and it can be viewed as the imperfection parameter. The viscoelastic material behavior is represented by the two-spring damper element attached to the free end of the rod. Additionally, an external time-varying moment, M(t), is applied to the rod along with a nonlinear rotational spring with nonlinear restoring $k_\mathrm{NL}$ [16,17,18,19]. The equation of motion for the system can be written as

$$\begin{aligned} I\ddot{\theta }+{\bar{M}}(\theta ;k_1,k_2,k_3)&= -f_\mathrm{v} L \cos \theta + F_CL \sin \theta \nonumber \\&\quad -PL\cos \theta +M \cos \varOmega t, \end{aligned}$$

(1)

where I is the mass moment of inertia of the rod, L is the length of the rod, $\varOmega$ is the frequency of the applied moment, t denotes the time, and ${\bar{M}}(\theta ;k_1,k_2,k_3)= k_1\theta +k_2\theta ^2+k_3\theta ^3$ is the nonlinear restoring moment. Here, $k_1$ is the linear stiffness of the rod, $k_2$ is the quadratic stiffness term which can account for nonlinearities due to asymmetries [20], $k_3$ is a cubic stiffness coefficient which accounts for geometric nonlinearities, and $\theta$ is the angular displacement of the rod. Finally, $f_\mathrm{v}$ is the internal force provided by the viscoelastic element, i.e., the force on the rod due to the two-spring dashpot element.

Fig. 2

Lumped parameter viscoelastic model with nonlinear stiffness, $k_\mathrm{NL}$ is the nonlinear restoring

2.1 Linear viscoelasticity

The examination will consider a system with geometric nonlinearity and linear viscoelastic material behavior. This behavior is found in applications ranging from elastomeric metamaterials [21, 22], which undergo large deflections but experience infinitesimal strain, viscoelastic strings [23, 24], skeletal muscles [25], and viscoelastic damping treatment of nonlinear beams [26]. Also, the results can be applied to systems that exhibit nonlinear elastic material behavior but linear viscoelasticity such as some polymer foams [27,28,29,30,31].

The viscoelastic behavior is modeled as a standard linear solid (SLS) element [32]. The SLS model consists of a spring with stiffness $(1-\beta )k$ and dashpot with damping coefficient $\eta$ connected in series. These two elements are connected in parallel to another spring of stiffness $\beta k$, where k represents the unparameterized stiffness coefficient of the SLS element and the variable $\beta$ is a dimensionless constant that lies in the interval $0\le \beta \le 1$, representing the difference in spring stiffnesses of the elastic elements in the SLS model. The viscoelastic force is described by the following differential equation

$$\begin{aligned}&\frac{{\dot{f}}_\mathrm{v}}{(1-\beta )k}+\frac{f_\mathrm{v}}{\eta }=\frac{\dot{\bar{\delta }}}{(1-\beta )}+\left( \frac{\beta k }{\eta }\right) \bar{\delta }, \nonumber \\&\quad \text {and}\quad \bar{\delta }=L\sin \theta . \end{aligned}$$

(2)

The symbol $\bar{\delta }$ denotes the displacement at the tip of the rod, and the dot represents a derivative with respect to time. It should be noted that the SLS model captures the behavior of two less-complex viscoelastic models: (i) the Kelvin–Voigt model, which captures the creep response, and (ii) the Maxwell model which accounts for both the stress relaxation and high loading rate response. Note that at $\beta = 0$ the viscoelastic element becomes that of a Maxwell material.¹ However, representing the material in this form can never capture the behavior of the Kelvin Voight material.

2.2 Dimensional analysis

The analysis of Eqs. (1) and (2) begins by using a Taylor series expansion of the trigonometric terms. The goal is to retain geometric nonlinearities while maintaining linear material behavior, a one-term expansion of $\sin \theta$ and $\cos \theta$ is required, i.e., $\sin \theta =\theta$ and $\cos \theta =1$. The result of this expansion can be written as

$$\begin{aligned}&I\ddot{\theta }+(k_1-F_CL)\theta +k_2\theta ^2+k_3\theta ^3= \nonumber \\&\quad =-f_\mathrm{v} L -PL+M \cos \varOmega t, \end{aligned}$$

(3)

$$\begin{aligned}&\frac{{\dot{f}}_\mathrm{v}}{(1-\beta )k}+\frac{f_\mathrm{v}}{\eta }=\frac{L{\dot{\theta }}}{(1-\beta )}+\left( \frac{\beta k }{\eta }\right) L\theta . \end{aligned}$$

(4)

Equations (3) and (4) can be non-dimensionalized in time using the following quantity

$$\begin{aligned} \quad T= \frac{t}{\tau } , \end{aligned}$$

(5)

where $\tau = {\eta }/{k}$ is the time constant of the viscoelastic system. Introducing the state variable $x=\theta$, we obtain the following system of governing equations that can be written as

$$\begin{aligned} D_e^{-2}x^{\prime \prime }&-f(x;\lambda ,\alpha _2,\alpha _3,\gamma )+\alpha _\mathrm{v} F_\mathrm{v}={M^*}\cos \omega T, \end{aligned}$$

(6)

$$\begin{aligned} \frac{{F}^{\prime }_\mathrm{v}}{(1-\beta )}&+F_\mathrm{v}=\frac{x^\prime }{(1-\beta )}+\beta x. \end{aligned}$$

(7)

where the constants are defined as

$$\begin{aligned} D_e&= {\omega _n}{\tau },\quad \lambda =\frac{F_CL}{k_1},\quad \alpha _2=\frac{k_2}{k_1},\quad \alpha _3=\frac{k_3}{k_1},\\ \alpha _\mathrm{v}&=\frac{kL}{k_1},\quad \gamma =\frac{PL}{k_1},\quad {M^*}=\frac{M}{k_1},\quad \text {and}\quad \omega =\frac{\varOmega \eta }{k}. \end{aligned}$$

where $\omega _n=\sqrt{k_1/I}$ is the natural frequency of the elastic system. The symbols $f(x;\lambda ,\alpha _2,\alpha _3,\gamma )=(\lambda -1) x-\alpha _2x^2-\alpha _3x^3 -\gamma$ represent the nonlinear restoring force function, $(\cdot )^\prime$ denotes the derivative $\hbox {d}(\cdot )/\hbox {d}T$, and $\alpha _2$ and $\alpha _3$ are the non-dimensional quadratic and cubic stiffness of the system, respectively. The symbol $\alpha _2$ accounts for nonlinearities due to asymmetries, and $\alpha _3$ represents geometric nonlinearities. The term $D_e$ denotes the Deborah number [33, 34]; it is a ratio of the timescale of stress relaxation to the characteristic timescale of the elastic oscillations of an effective linearized translational stiffness in terms of the length of the rod. It can be also viewed as the product of the time constant of the viscoelastic system, $\tau$, and the natural frequency of the elastic system. $F_\mathrm{v}$ is the non-dimensional viscoelastic force which can be defined as $F_\mathrm{v}=f_\mathrm{v}/(k L)$. The non-dimensional quantity $\lambda$ represents the loading bifurcation parameter, and $\gamma$ represents external loading and imperfections. Finally, $\alpha _\mathrm{v}$ may be viewed as the relative stiffness of the sum of the elastic components in the SLS element to an effective stiffness of the linear equivalent translation stiffness of the rotational spring. The Deborah number, $D_e$, controls the time-dependent behavior of the system, and $D_e^{-2}$ can be viewed as the effective mass of the system. The influence of the Deborah number on the dynamics of the system is discussed in Sect. 4.

3 Static bifurcations

Here, we utilize the non-dimensional analysis of the governing equations to generate and study various generic bifurcation diagrams. To this end, we divide this section into twofold: first, we start with the autonomous system, $M^*=0$, in the absence of viscoelasticity, i.e., $\alpha _\mathrm{v}=0$; and then we analyze the effect of viscoelasticity on the bifurcation diagrams.

Fig. 3

Bifurcation diagram for Case 1 with $\alpha _2=\gamma =0$, and $\alpha _3=0.1$. Subplot a indicates $\lambda$, x, V space, unstable branch is not indicated, blue lines represent the potential energy, purple lines represent the bifurcation diagram, and the red circles represent pitchfork bifurcation points. Subplot b indicates $\lambda$, $x_0$ space, and unstable branch is indicated by the dashed line . (Color figure online)

Table 1 Bifurcations types, control parameters, and Deborah number

3.1 Static bifurcations without linear viscoelasticity

It is important to recall that the nonlinear restoring force is described as

$$\begin{aligned} f(x;\lambda ,\alpha _2,\alpha _3,\gamma )=(\lambda -1) x-\alpha _2x^2-\alpha _3x^3 -\gamma .\nonumber \\ \end{aligned}$$

(8)

In the absence of viscoelasticity, the system can exhibit four generic static bifurcations of the fixed points when $\lambda$ is varied. The nature of these bifurcations, depending upon the values of $\alpha _2,~\alpha _3,~$and $\gamma$, can be identified by examining the shape of the potential function, i.e., $\displaystyle {\int }-f(x;\lambda ,\alpha _2,\alpha _3,\gamma ) \text {d} x$, which can be written as

$$\begin{aligned} V(x;\lambda ,\alpha _2,\alpha _3,\gamma )= & {} (1-\lambda ) \frac{x^2}{2}+\alpha _2\frac{x^3}{3}+\alpha _3\frac{x^4}{4}+\gamma x,\nonumber \\ \end{aligned}$$

(9)

and are described in the following paragraphs. Specifically, the manuscript examines four cases outlined in Table 1 and is detailed in the following paragraphs. When discussing the bifurcations in Case 1–3 in terms of linear elasticity, the parameters $\alpha _\mathrm{v}$, $\beta$, and $D_e$ are not relevant. In Case 4, Eqs. 6 and 7 are modified so that $\alpha _\mathrm{v}$ represents an elastic stiffness, and the damper no longer has an effect on the system.

Fig. 4

Bifurcation diagram for Case 2 with $\alpha _2 = 0.5,~\gamma =0$, and $\alpha _3 = 0.1$. Subplot a indicates $\lambda$, x, V space, unstable branches are not indicated, blue lines represent the potential energy, and purple line represents the bifurcation diagram. Subplot b indicates $\lambda$, $x_0$ space, and unstable branches are indicated by dashed lines. Orange circles represent saddle node bifurcation points, and blue circles represent transcritical bifurcation points. (Color figure online)

Fig. 5

Bifurcation diagram for Case 3 with $\alpha _2=0,~\gamma = - 0.1$, and $\alpha _3 = 0.1$. Subplot a indicates $\lambda$, x, V space, unstable branch is not shown, blue lines represent the potential energy, and purple lines represent the bifurcation diagram. Subplot b indicates $\lambda$, $x_0$ space, and unstable branch is indicated by the dashed line. Orange circles represent saddle node bifurcation points. (Color figure online)

Fig. 6

Bifurcation diagram for Case 4 with $\alpha _2=-1.5,~\gamma = 0.0$, $\alpha _3 = 0.5$, and $\beta = 1$. Subplot a indicates $\alpha _\mathrm{v}$, x, V space, unstable branch is not indicated, blue lines represent the potential energy, and purple lines represent the bifurcation diagram. Subplot b indicates $\alpha _\mathrm{v}$, $x_0$ space, and unstable branch is indicated by the dashed lines. Orange circles represent saddle node bifurcation points. (Color figure online)

• Case 1 The system can exhibit both subcritical and supercritical pitchfork bifurcations. However, this work will focus on the supercritical bifurcation which occurs when $\alpha _2=\gamma =0$ and $\alpha _3>0$. Equation (8) has one real solution for $\lambda <1$ and three real solutions for $\lambda >1$. As depicted in Fig. 3, the potential evolves from having one global minimum, i.e., a single-well potential when $\lambda <1$, to having one local maximum and two global minimum, i.e., a double-well potential for $\lambda >1$. The maximum occurs at $x=0$ indicates that this fixed point is unstable.

• Case 2 These parameters give rise to a compound bifurcation diagram consisting of both a saddle node and transcritical bifurcations. The saddle node bifurcation occurs when $\gamma =0$, and $\alpha _3,~\alpha _2> 0$ as depicted in Fig. 4. Under these conditions, when $\lambda <1$ the system is global-stable with one fixed point. At $\lambda =1-\alpha _2^2/(4\alpha _3)$, the potential function loses symmetry creating two additional fixed points, one stable and one unstable, at the point of these two branches coincide is the saddle node bifurcation. The transcritical bifurcation occurs under the same parameters as the saddle node bifurcation, i.e., $\gamma =0$, and $\alpha _3,~\alpha _2> 0$. This case again is depicted in Fig. 4. Recall, when $1-\alpha _2^2/(4\alpha _3)\le \lambda \le 1$, there are three solutions present: two stable and one unstable solution. The upper stable branch and the unstable branch collide at $\lambda =1$, where the two fixed points switch stability.

• Case 3 This is the second scenario in which the saddle node bifurcation occurs. Here, $\alpha _3> 0$, $\gamma <0$ and $\alpha _2=0$. As shown in Fig. 5, this saddle node appears as part of an asymmetrical bifurcation loosely referred to in this manuscript as an imperfect pitchfork bifurcation.² This corresponds to a loss of symmetry of the potential associated with the supercritical pitch fork bifurcation. The loss of symmetry is due to the presence of imperfection, in this case, a transverse force. Here, the primary stable branch persists for all values of the loading parameter, $\lambda$. As $\lambda$ is increased to approach $\lambda _{cr}$, a saddle node bifurcation occurs birthing two other branches, one stable and one unstable.

• Case 4 The last case that is examined where a saddle node bifurcation can occur is obtained by utilizing Eqs. (3) and (4), and by setting $\gamma =\lambda =0$, $\beta =1$. In this case, $\alpha _\mathrm{v}$ takes on a numerical value that varies or becomes the changing control parameters. These parameters correspond to no compressive load, and the viscoelastic element here morphed into a simple spring. In this scenario, the system behaves like a von Mises Truss [6, 33]. This purely elastic system has a potential which can be written as

  $$\begin{aligned} V(x;\alpha _2,\alpha _3,\alpha _\mathrm{v})&= (1+\alpha _\mathrm{v})\frac{x^2}{2}+\alpha _2\frac{x^3}{3}+\alpha _3\frac{x^4}{4}\nonumber \\&=0. \end{aligned}$$

  (10)

  Note, in this case, $\alpha _\mathrm{v}$ takes on the alternate definition as the measure of the strength of the elastic spring at the end of the rod. Figure 6 plots both potential energy and the bifurcation diagram for this case. Examining the fixed points when $\alpha _\mathrm{v}\le 0.125$ shows that there are three coexisting solutions: two stable solutions and one unstable solution. One stable solution is the null solution and it persist past $\alpha _\mathrm{v,cr}= 0.125$. The remaining solutions stable and unstable solutions annihilate each other at $\alpha _\mathrm{v,cr}$.

This rich dynamic behavior allows a detailed study of the effect of linear viscoelasticity on the stability of fixed points, as presented in the next subsection.

3.2 Static bifurcations with linear viscoelasticity

It is convenient in analyzing the effect of viscoelasticity to cast the system as a set of first order equations by letting $x_1=x$, $x_2=x^\prime$, and $x_3= F_\mathrm{v}$, leading to a set of matrix equations $\varvec{{\dot{x}}}={\varvec{F}}({\varvec{x}};{\varvec{M}})$ is a vector field that can be written as

$$\begin{aligned} {\varvec{F}}({\varvec{x}};{\varvec{M}})= \begin{pmatrix} x_2,\\ D_e^2 f(x_1;{\varvec{M}})-D_e^2\alpha _\mathrm{v} x_3,\\ -(1-\beta )x_3 + x_2+\beta (1-\beta )x_1 \end{pmatrix},\nonumber \\ \end{aligned}$$

(11)

where ${\varvec{x}}=(x_1,~x_2,~x_3)^T$ is the state vector, and ${\varvec{M}}=\left( \lambda , \gamma , \alpha _2, \alpha _3, \alpha _\mathrm{v}, \beta \right)$ is a vector of control parameters. The fixed points of the system are the solutions that satisfy

$$\begin{aligned} {\varvec{F}}(\varvec{x_0};{\varvec{M}})={\varvec{0}}, \end{aligned}$$

where $\varvec{x_0} =(x_{01},x_{02},x_{03})$ is the vector of equilibrium points. Setting the vector field to zero, one finds that $x_{02}=0$ and $x_{03}=\beta x_{01}$. Additionally, the nonlinear restoring force can be written as

$$\begin{aligned} f(x_{01};{\varvec{M}})&= -(1-\lambda +\alpha _\mathrm{v}\beta ) x_{01}-\alpha _2x_{01}^2-\alpha _3x_{01}^3-\gamma \nonumber \\&=0. \end{aligned}$$

(12)

The quantities $x_{01}$, $x_{02}$, and $x_{03}$ are the fixed points of the angular position of the rod, the angular velocity of the rod, and the force from the viscoelastic element, respectively.

Fig. 7

Depiction of viscoelastic system with a pitchfork bifurcation, Case 1. Subplot a presents the bifurcation diagram in the presence of viscoelasticity with $\alpha _2=\gamma =0$,  $\alpha _3=0.1,~\alpha _\mathrm{v} =1.0 ~ \beta = 0.5~\text {and}~D_e=1$. Dashed line represents unstable solution branch, and red circle represents pitchfork bifurcation point. Gray planes show the projections of the bifurcation diagram in $x_{01} - \lambda$ and $x_{03} - \lambda$ planes; small red and green dots represent, respectively, the start and end point of the path in the range considered. Subplot b indicates the locus of eigenvalues for equilibrium path A. Subplot c indicates the locus of eigenvalues for equilibrium path B. $\lambda$ is varied from 0 to 3. The bifurcation occurs at $\lambda _\mathrm{crit,PF}=1.5$. Subplot d $\tau _\mathrm{eff}$ and $\zeta _\mathrm{eff}$ versus $\lambda$ for stable portion of equilibrium solution path A. Subplot e $\tau _\mathrm{eff}$ and $\zeta _\mathrm{eff}$ versus $\lambda$ for equilibrium solution path B

3.2.1 Linear stability

The stability of the equilibrium points can be determined by examining the linearized dynamics around each point. This is accomplished by writing the state vector as ${\varvec{x}}={\varvec{x}}_0+\varvec{\delta }$, where ${\varvec{x}}_0$ is the vector of fixed points and $\varvec{\delta }$ represents the perturbations around the fixed point. Now the matrix equations $\varvec{{\dot{x}}}={\varvec{F}}({\varvec{x}};{\varvec{M}})$ can be linearized about an arbitrary fixed point as

$$\begin{aligned} \varvec{{\dot{\delta }}} =D_\mathbf{x }{\varvec{F}}({\varvec{x}}_0;{\varvec{M}})\varvec{\delta } +{\mathcal {O}}(||\varvec{\delta }||^2). \end{aligned}$$

(13)

Retaining only linear terms leads to linearized system $\dot{\varvec{\delta }}=\mathbf{A} \varvec{\delta }$. The matrix $\mathbf{A}$ is the matrix of partial derivatives of the vector field ${\varvec{F}}$, and it can be written as

$$\begin{aligned} \mathbf{A}&=D_\mathbf{x }{\varvec{F}}({\varvec{x}}_0;{\varvec{M}}) \nonumber \\&=\begin{bmatrix} 0 &{} \quad 1 &{} \quad \quad 0\\ De^{-2}f_x(x_{01};{\varvec{M}})&{} \quad 0 &{} \quad \quad -De^{-2}\alpha _\mathrm{v}\\ \beta (1-\beta ) &{} \quad 1 &{} \quad \quad -(1-\beta ) \end{bmatrix}, \end{aligned}$$

(14)

where $f_x(x_{01};{\varvec{M}})=\frac{d}{dx}f(x_{01};{\varvec{M}})$. The eigenvalues of the linearized system satisfy the third-order polynomial

$$\begin{aligned} \varLambda ^3+a_0\varLambda ^2+a_1\varLambda +a_2=0, \end{aligned}$$

(15)

where $\varLambda$ represents the eigenvalues of the linearized system, and the constants $a_i$ can be obtained from Eq. (14) and are defined in A.3. The fixed points are asymptotically stable under small perturbations provided that all eigenvalues have negative real parts. This analysis is used to determine the stability of the branches of the bifurcation diagrams presented in Sect. 3.2.3.

3.2.2 Pseudo-potential

Note that the system with its coupled viscoelastic nature system does not allow a true potential of the system. However, a pseudo-potential of the system can be formed by setting the time-dependent variables to $x^\prime =x^{\prime \prime }=F^\prime _\mathrm{v} =0$, eliminating the viscoelastic force in the restoring force, $F_\mathrm{v}=x_3$, and finally integrating with respect to $x_1$. The pseudo-potential, ${\bar{V}}$, can be written as

$$\begin{aligned} {\bar{V}}(x_1;{\varvec{M}})&= (1-\lambda +\alpha _\mathrm{v}\beta ) \frac{x_1^2}{2}+\alpha _2\frac{x_1^3}{3}+\alpha _3\frac{x_1^4}{4}+\gamma x_1\nonumber \\&=0, \end{aligned}$$

(16)

the corresponding viscoelastic force can be recovered as $F_\mathrm{v}=\beta x_1$. Examining the potential, the effects of the viscoelastic element can be captured by setting $\lambda _\mathrm{eff}=\lambda -\alpha _\mathrm{v}\beta$; therefore, the preceding discussion of stability applies when $\lambda$ is replaced by $\lambda _\mathrm{eff}$. The potential is not a function of the Deborah number, and therefore, the Deborah number does not change the asymptotic stability of the system. It does influence the path of the eigenvalues on the complex plane.

Fig. 8

Depiction of viscoelastic system with a saddle node and transcritical bifurcation, Case 2. Subplot a presents the bifurcation diagram in the presence of viscoelasticity with $\alpha _2 = 0.5,~\gamma =0$,  $\alpha _3=0.1,~\alpha _\mathrm{v} =1.0~ \beta = 0.5~\text {and}~D_e=1$. Dashed lines represent unstable solutions, orange circle represents saddle node bifurcation points, and blue circle represents transcritical bifurcation point; small red and green dots represent, respectively, the start and end point of the path in the range considered. Gray planes show the projections of the bifurcation diagram in ${x_{01} - \lambda }$ and $x_{03} - \lambda$ planes. Subplot b indicates the locus of eigenvalues for equilibrium path A. Subplot c indicates the locus of eigenvalues for equilibrium path $B_1$. Subplot d indicates the locus of eigenvalues for equilibrium path $B_2$. $\lambda$ is varied from 0 to 2. The bifurcation occurs for the saddle node point is at $\lambda _\mathrm{crit,~SN}=0.875$ and the for the transcritical point is at $\lambda _\mathrm{crit,TC}=1.5$. Subplot e $\tau _\mathrm{eff}$ and $\zeta _\mathrm{eff}$ versus $\lambda$ for stable portion of equilibrium solution path A. Subplot f $\tau _\mathrm{eff}$ and $\zeta _\mathrm{eff}$ versus $\lambda$ for equilibrium solution path $B_1$. Subplot g) $\tau _\mathrm{eff}$ and $\zeta _\mathrm{eff}$ versus $\lambda$ for equilibrium solution path $B_2$. (Color figure online)

Fig. 9

Depiction of viscoelastic system with an imperfect pitchfork bifurcation, Case 3. Subplot a presents the bifurcation diagram in the presence of viscoelasticity with $\alpha _2 = 0,~\gamma =-0.1$,  $\alpha _3=0.1,~\alpha _\mathrm{v} =1.0 ~ \beta = 0.5~\text {and}~D_e=1$. Dashed line represents unstable solution, and orange circle represents saddle node bifurcation point. Gray planes show the projections of the bifurcation diagram in ${x_{01} - \lambda }$ and $x_{03} - \lambda$ planes; small red and green dots represent, respectively, the start and end point of the path in the range considered. Subplot b indicates the locus of eigenvalues for equilibrium path A. Subplot c indicates the locus of eigenvalues for equilibrium path $B_1$. Subplot d indicates the locus of eigenvalues for equilibrium path $B_2$. $\lambda$ is varied from 0 to 2. The bifurcation occurs at $\lambda _\mathrm{crit,SN}=1.689$. Subplot e $\tau _\mathrm{eff}$ and $\zeta _\mathrm{eff}$ versus $\lambda$ for stable portion of equilibrium solution path A. Subplot f $\tau _\mathrm{eff}$ and $\zeta _\mathrm{eff}$ versus $\lambda$ for equilibrium solution path $B_1$

Fig. 10

Depiction of viscoelastic system with a saddle node bifurcation, Case 4. Subplot a presents the bifurcation diagram in the presence of viscoelasticity with $\lambda =0,~\alpha _2 = -1.5,~\gamma =0.0$,  $\alpha _3=0.5,~ \beta = 0.5~\text {and}~D_e=1$. Dashed line represents unstable solution, and orange circle represents saddle node bifurcation point. Gray planes show the projections of the bifurcation diagram in ${x_{01} - \alpha _\mathrm{v}}$ and $x_{03} - \alpha _\mathrm{v}$ planes; small and green dots represent, respectively, the start and end point of the path in the range considered. Subplot b indicates the locus of eigenvalues for equilibrium path A. Subplot c indicates the locus of eigenvalues for equilibrium path $B_1$. Subplot d indicates the locus of eigenvalues for equilibrium path $B_2$. $\alpha _\mathrm{v}$ is varied from 0 to 2. The bifurcation occurs at $\alpha _\mathrm{v,crit}=0.25$. Subplot e $\tau _\mathrm{eff}$ and $\zeta _\mathrm{eff}$ versus $\lambda$ for stable portion of equilibrium solution path A. Subplot f) $\tau _\mathrm{eff}$ and $\zeta _\mathrm{eff}$ versus $\lambda$ for equilibrium solution path $B_1$

3.2.3 Bifurcation diagrams

Figures 7, 8, 9, and 10 show the viscoelastic equivalents to the bifurcations shown in Figs. 3, 4, 5, and 6, respectively. The nature of the bifurcation does not change; however, the viscoelastic force is a state in the system, and the bifurcation diagram can be presented in a higher-dimensional space. The bifurcation diagrams resemble their elastic counterparts but have an additional equilibrium state $x_ {03}$, i.e., the equilibrium force in the viscoelastic element. Note that their dimensionality is increased, but their projections on the $x_{01}-\lambda$ plane retain the same general shape as their non-viscoelastic counterparts. As expected, both the pseudo-potential and the bifurcation diagram clearly show that the viscous component of the viscoelastic element does not fundamentally change the bifurcation type instead the equilibrium stiffness $\beta k$ acts in conjunction with the linear stiffness of the system.

3.2.4 Eigenvalues at bifurcation point

Before the complete discussion of the locus of eigenvalues on the complex plane, it is useful to examine Case 1 depicted in Fig. 7. The parameters for these plots are $\alpha _2 = 0,~\gamma =0$,  $\alpha _3=0.1,~\alpha _\mathrm{v} =1.0~ \beta = 0.5, ~\text {and}~D_e=1$. In fact, in the discussion of each case $D_e=1$. Figure 7a shows a perfect pitchfork bifurcation with an added viscoelastic component with respect to $\lambda$. In this case, each point on an equilibrium path, i.e., A, and B, has three associated eigenvalues denoted as $\mu =\alpha$, and $\mu = a\pm ib$, where $\alpha$, a and b are constants. Points on the equilibrium paths away from the bifurcation point have one real eigenvalue and two complex conjugate eigenvalues. This is in contrast to a second-order viscously damped system [14], which has two complex eigenvalues for a point on the equilibrium path away from the bifurcation point. In characterizing the effect of these eigenvalues on the response, the real eigenvalues for the stable equilibrium paths will be treated as the effective time constant denoted by $\tau _\mathrm{eff}$ from a first-order linearized system, whereas the complex conjugates will be examined by an effective damping ratio indicated by $\zeta _\mathrm{eff}$ from a second-order linearized system. These metrics can be written as follows

$$\begin{aligned} \tau _\mathrm{eff}=\frac{1}{\alpha }, \quad \zeta _\mathrm{eff}=\frac{-a}{\sqrt{a^2+b^2}}. \end{aligned}$$

In this case, the equilibrium path A is initially stable, as $\lambda$ is increased and passes through the bifurcation point, $\lambda _\mathrm{crit,PF}=1.5$, the path A becomes unstable. This instability can be seen on the locus of eigenvalues presented in Fig. 7b, when the eigenvalues cross the imaginary axis and become positive. Considering only stable segment equilibria, one sees that this movement of the eigenvalues on the complex plane causes the effective time constant, $\tau _\mathrm{eff}$ to grow toward infinity, while the effective damping ratio $\zeta _\mathrm{eff}$ shows only a slight increase (Fig. 7d).

The locus of eigenvalues associated with path B is presented in Fig. 7c. The eigenvalues have all negative real parts and move on the real axis. The complex conjugates’ eigenvalues primarily move toward the imaginary axis. Note that the effective time constant rapidly decreases as the path moves away from the critical $\lambda$, while the effective damping ratio for path B shows a slight decrease in value. This behavior is shown in Fig. 7e.

Fig. 11

Effect of Deborah number on snap through dynamics of imperfect pitchfork bifurcation, Case 3, when $\alpha _2 = 0.0$, $\alpha _3 = 0.1$, $\gamma = -0.1$, $\alpha _\mathrm{v}= 1.0$, $\lambda =1.69$ and $\beta = 0.50$: a $D_e$ =0.1, b $D_e$ = 1.0, c $D_e$ =10.0, and d $D_e$=100.0. Red lines indicate unstable equilibrium points, and blue lines indicate stable equilibrium point. Insets corresponded to shaded regions on plots. Subplot e shows locus of eigenvalues. Subplot f $\tau _\mathrm{eff}$and $\zeta _\mathrm{eff}$ versus $D_e$. (Color figure online)

Fig. 12

Effect of Deborah number on snap through dynamics experiencing the ghost of saddle node bifurcation, Case 4, when $\alpha _2 = 0.0$, $\alpha _3 = 0.1$, $\gamma = -0.1$, $\alpha _\mathrm{v}= \alpha _\mathrm{v,crit,SN}+0.001$, $\lambda =1.69$ and $\beta = 0.50$: a $D_e$ =0.1, b $D_e$ = 1.0, c $D_e$ =10.0, and d $D_e$=100.0. Opaque red lines indicate annihilated unstable equilibrium points, and opaque blue lines indicate annihilated stable equilibrium point. Insets corresponded to shaded regions on plots. (Color figure online)

Case 2, shown in Fig. 8a, has two bifurcations; a saddle node bifurcation, and a transcritical bifurcation. The parameters for this case are $\alpha _2 = 0.5,~\gamma =0$,  $\alpha _3=0.1,~\alpha _\mathrm{v} =1.0 ~\text {and}~ \beta = 0.5$. Here, the equilibrium paths are indicated by A, $B_1$, and $B_2$. The discussion will begin with path A, in this case, there is a transcritical bifurcation where path A becomes unstable, and path $B_2$ becomes stable. This occurs at a critical $\lambda _\mathrm{crit,TC} =1.5$. Interestingly, the eigenvalues presented in Fig. 8b that cross into the positive real plane are the real eigenvalues. As a result, the associated $\tau _\mathrm{eff}$ approaches infinity, while the associated $\zeta _\mathrm{eff}$ remains bounded and reaches a value of approximately 0.35. This behavior is depicted in Fig. 8e. The locus of eigenvalues associated with Path $B_1$ is presented in Fig. 8c. This path is stable and originates at the bifurcation $\lambda _\mathrm{crit,SN}=0.875$, i.e., the saddle node bifurcation point. Figure 8f shows that both the $\tau _\mathrm{eff}$ and $\zeta _\mathrm{eff}$ decreases from infinity as the eigenvalues move on the left-hand side of the complex plane. Finally, path $B_2$ began as the unstable path birthed from the saddle node bifurcation point. This is evident in Fig. 8d that the real eigenvalue starts at the origin and moves to the right-hand side on the positive real axis of the complex plane. As the solution nears the transcritical bifurcation point, the eigenvalue changes direction and crosses into the negative real axis, where the path becomes stable. The movement of the associated complex eigenvalues is always on the left-hand side of the imaginary axis. Initially, the complex parts of these eigenvalues move closer to the real axis, while the real parts become increasingly negative. As the solution moves toward the transcritical bifurcation point, the eigenvalues reverse direction and move toward the imaginary axis. As presented in Fig. 8g, this movement causes $\tau _\mathrm{eff}$ to decrease from infinity and the value $\zeta _\mathrm{eff}$ is the continuation of the $\zeta _\mathrm{eff}$ of the eigenvalues of path A.

The viscoelastic imperfect pitchfork bifurcation given in Case 3 is depicted in Fig. 9a. The parameters for this case are $\alpha _2 = 0, \gamma =-0.1$,  $\alpha _3=0.1,~\alpha _\mathrm{v} =1.0 ~\text {and}~ \beta = 0.5$. Note that A is stable for all values of the bifurcation parameter $\varLambda$ , However as path A nears the bifurcation point, $\lambda _\mathrm{crit,SN}=1.689$, both $\tau _\mathrm{eff}$, and $\zeta _\mathrm{eff}$ increases until they reach local maximum near the bifurcation point before decreasing (Fig. 9e). This is reflected in the locus of eigenvalues shown in Fig. 9b; the real eigenvalue approaches the origin and then changes direction and becomes increasingly negative as $\lambda$ is increased past the bifurcation point, while the complex eigenvalues approach the real axis where the real part becomes increasingly negative. Path $B_1$ originates from the $\textit{saddle node}$ bifurcation point at $\lambda _\mathrm{crit}=1.689$. Figure  9c shows the locus of eigenvalues of this path, the real eigenvalues becomes increasingly negative, and the complex eigenvalues approach the imaginary axis. As presented in Fig. 9f, this movement results in $\tau _\mathrm{eff}$ and $\zeta _\mathrm{eff}$ to decrease rapidly. Path $B_2$ is unstable; this is reflected in the associated real eigenvalues shown in Fig. 9d that move along the positive real axis. The remaining two eigenvalues remain on the left-hand side of the imaginary axis, yet they are initially real before converging and leaving the real axis to become complex conjugates.

Case 4 is the single saddle node bifurcation presented in Fig. 10a, which is common in von Mises trusses. In the previous cases, $\lambda$ is the bifurcation parameter, while in this case $\alpha _\mathrm{v}$ is the bifurcation parameter. Here, the parameters are $\lambda =0,~\alpha _2 = -1.5,~\gamma =0.0$,  $\alpha _3=0.5,~\text {and}~ \beta = 0.5$. Path A is the null solution path, and the eigenvalues of this path are shown in Fig. 10a. They lie on the left-hand side of the imaginary axis, the complex conjugate eigenvalues moves away from the imaginary axis, and the real eigenvalues approach the origin. By inspecting Fig. 10e, the effective time constant increases with $\alpha _\mathrm{v}$, and the effective damping ratio slightly increases with $\alpha _\mathrm{v}$. Path $B_1$ is stable and terminates at the saddle point. As illustrated in Fig. 10c, the complex eigenvalues approach the real axis, and the real eigenvalues move toward the origin. This causes $\tau _\mathrm{eff}$ and $\zeta _\mathrm{eff}$ shown in Fig. 10f to approach infinity as $\alpha _\mathrm{v}$ is increased to $\alpha _\mathrm{v,crit,SN}=0.25$.

4 Deborah number

Up to this point the manuscript has considered the presence and stability of equilibrium solutions of a viscoelastic material behavior in conjunction with geometric nonlinearities. The manuscript now focuses on the effects of viscoelasticity on the transient response due to changes in the Deborah number. Examining Eq. 6, $D_e^{-2}$ is an effective inertia of the non-dimensionalized system. Additionally, the Deborah number is defined as $D_e=\omega _n\tau$; thus, it is proportional to the ratio of viscoelastic time constant to the natural period of oscillation, i.e., $D_e\propto \tau /T_n$, where $T_n= 2\pi /\omega _n$.

The Deborah number does not affect the asymptotic stability of the system. However, it does affect eigenvalues of the system. The effect of the Deborah number can readily be seen near a saddle-node bifurcation depicted in Fig. 11. The Deborah number influences the duration of time an oscillation around an unstable point can be maintained before stability is lost and the response jumps to oscillations around a stable equilibrium point. Figure 11a plots the response when $D_e<<1$ this occurs when $\tau<< T_n$. In the case the effective inertia of the system $D_e^{-2}$ is large and the viscoelastic behavior resembles that of an underdamped system when it oscillates around the equilibrium points. Figure 11b shows the response when $\tau =T_n$. Here, the viscoelastic timescale is the same as the elastic timescale and the effective system behaves as if it is nearly critically damped. Figure 11c, d plots the snap-through response $D_e>>1$, i.e., this occurs when $\tau>>T_n$ and the elastic time scale is less than viscoelastic time scale. In both cases, there is a high-frequency elastic response near the unstable equilibrium point that is completely decayed as the system reaches the stable equilibrium point. This behavior can be readily understood by plotting the locus of eigenvalues for the stable equilibrium point. The locus is annotated with labels 1–4 corresponding to time traces in Fig. 11a–d, respectively. The equilibrium has two associated complex conjugate pairs that travel toward the origin on the complex plane and a real eigenvalue that moves to the left on the negative real axis as the Deborah number is increased (Fig. 11e). Figure 11f shows the effective damping ratio and time constant for this scenario. The effective time constant, $\tau _\mathrm{eff}$, decreases with Deborah number. The effective damping ratio $\zeta _\mathrm{eff}$ increases reaches a local maximum then subsequently decreases.

Combining Fig. 11e, f along with the time traces in Fig. 11a–c allows a complete understanding of this behavior. One sees that when $D_e=0.1$, the complex eigenvalues are dominant in the response and the presence of the real eigenvalue is obscured. In this case the system does not oscillate as it moves to the equilibrium point and then elastic response oscillations dominates. When $D_e$ is increased to 1.0, the effect of the real root on the response increases, while the effects of the complex conjugate eigenvalues decrease the combined effect is that the system appears to be near critically damped. Next, when $D_e$ is increased to 10.0 and 100.0, initially the complex conjugates eigenvalues are seen on the response and the system appears underdamped; initially, as time increases and the system approaches the stable equilibrium point, the real eigenvalue dominates the response.

The Deborah number also influences the presence of a ghost that occurs after a saddle node bifurcation [35]. Just after the stable and unstable fixed points collide and annihilate each other, a ghost that occurs causes a slow passage through a bottleneck. Figure 12a–d shows the length of the bottle neck for $D_e$ equal to 0.01, 1, 10, and 100, respectively. Note the bottleneck decreases in size until $D_e=1$ where it subsequently increases and remains nearly unchanged at $D_e=100$ when compared to $D_e$=0.1, the complex eigenvalues are dominant in the response, and hence the oscillation.

5 Conclusions

In this manuscript, we examined the effects of viscoelasticity on the various static bifurcation cases of a mechanical oscillator. To this end, a lumped parameter model was first obtained for a single degree of freedom system. The model consists of a viscoelastic rotating rod subjected to axial and transverse forces applied at the free end of the rod. Additionally, an external moment is applied along with a nonlinear rotational spring. The viscoelastic response was represented by the two-spring damper element connected to the free end of the rod. A non-dimensional analysis was performed on the governing equation to examine and generate multiple bifurcation diagrams, first for the oscillator without linear viscoelasticity, and then in the presence of a viscoelastic element. It was obvious that the nature of the bifurcation depends on the loading bifurcation parameter, the quadratic and cubic coefficients of the restoring force, and the external loading and imperfection parameter. Supercritical pitchfork, saddle-node, and transcritical bifurcation were investigated for different cases of the controlling parameters. By exploring the bifurcation diagrams in the presence of a viscoelastic element, it was evident that the nature of these diagrams does not change from the equivalent diagrams generated without linear viscoelasticity. Yet, results revealed that when introducing a viscoelastic element to the system, the bifurcation diagram included an additional equilibrium state representing the equilibrium force in the viscoelastic component. Furthermore, the manuscript analyzed the eigenvalues at bifurcation points of the various bifurcation cases considered in this study. The effective time constant of the oscillator and the effective damping was employed to characterize the effects of the eigenvalues on the response of the oscillator. Results revealed that this characterization can serve as a design guideline that can be utilized to create a system holding distinct effective damping and time constant by controlling the loading parameter. Finally, t he manuscript investigated the effects of viscoelasticity on the transient response of the oscillator. It was shown that the Deborah number can control the duration of time needed to maintain oscillation around an unstable branch before jumping to a stable branch.

Appendix

This appendix converts the linear standard viscoelastic element from stress–strain form to a force–displacement form. It presents an internal variable formulation of the governing equations of the system.

Fig. 13

Viscoelastic linear standard model with internal variable

1.1 Stress to force

In this work, the additional degree of freedom is the viscoelastic force in the system. Recall the viscoelastic relationship in the linear standard model can be written as

$$\begin{aligned} \frac{1}{E_1}{\dot{\sigma }}+\frac{1}{\mu }\sigma =\frac{E_1+E_2}{E_1}{\dot{\epsilon }}+\frac{E_2}{\mu }\epsilon . \end{aligned}$$

(A.1)

where $E_1$ and $E_2$ denote the modulus of the element and $\mu$ is the viscosity. Now if the moduli $E_1$ and $E_2$ are parameterized as $E_1=(1-\beta )E$ and $E_2=\beta E$, where E is a base elastic modulus and $\beta$ is a constant, the strain $\epsilon =L\sin \theta /b$ where A and b are the cross section area of length of the viscoelastic element, and $\sigma =f_\mathrm{v}A$, Eq. (A.1) can be written as

$$\begin{aligned}&\frac{{\dot{f}}_\mathrm{v}}{(1-\beta )k}+\frac{f_\mathrm{v}}{\eta }=\frac{\dot{\bar{\delta }}}{(1-\beta )}+\left( \frac{\beta k }{\eta }\right) \bar{\delta }, \nonumber \\&\text {where}~\bar{\delta }=L\sin \theta ,~k=EA/b,\text {and}~\eta =\mu A/b. \end{aligned}$$

(A.2)

1.2 Internal variable description

An alternate description can be obtained using the internal strain in the system. In this description the viscoelastic stress can be written as

$$\begin{aligned}&\sigma =(E_1+E_2)\epsilon -E_1\bar{\epsilon }, \end{aligned}$$

(A.3)

$$\begin{aligned}&\mu \dot{\bar{\epsilon }}+E_1(\bar{\epsilon }-\epsilon )=0, \end{aligned}$$

(A.4)

where $\bar{\epsilon }$ is the internal strain [36] and is shown in Fig. 13. These two descriptions are equivalent. This can be shown by taking the derivative of Eq. (A.3) to yield

$$\begin{aligned}&{\dot{\sigma }}=(E_1+E_2){\dot{\epsilon }}-E_2\dot{\bar{\epsilon }}. \end{aligned}$$

(A.5)

Now, Eqs. (A.5) and (A.3) can be plugged into Eq. (A.4) to yield

$$\begin{aligned} \frac{1}{E_1}{\dot{\sigma }}+\frac{1}{\mu }\sigma =\frac{E_1+E_2}{E_1}{\dot{\epsilon }}+\frac{E_2}{\mu }\epsilon . \end{aligned}$$

The additional dynamics of the system to viscoelasticity can be represented as $\sigma$ or $\bar{\epsilon }$.

The equation motion of the system in Fig. 2b can be written in terms of internal displacements ${\bar{x}}$ as

$$\begin{aligned}&I\ddot{\theta }+{\bar{M}}(\theta ;k_1,k_2,k_3) \end{aligned}$$

(A.6)

$$\begin{aligned}&\quad =\beta k L {\bar{x}} \cos \theta -kL^2\cos \theta \sin \theta + \nonumber \\&F_CL \sin \theta -PL\cos \theta +M \cos \varOmega t,\nonumber \\&\quad \eta \dot{{\bar{x}}}\beta k ({\bar{x}}-L\sin \theta )=0; \end{aligned}$$

(A.7)

when the functions $\sin \theta$ and $\cos \theta$ are expanded using a Taylor series, the equations of motion for the system can be written as

$$\begin{aligned}&I\ddot{\theta }+(k_1-F_CL)\theta +k_2\theta ^2+k_3\theta ^3\nonumber \\&\quad = kL(\beta x_i-L\theta )-PL+M \cos \varOmega t,\end{aligned}$$

(A.8)

$$\begin{aligned}&\eta {\dot{x}}_i+\beta k (x_i-L\theta )=0. \end{aligned}$$

(A.9)

Equations  in (A.8) and  (A.9) are the internal displacement equivalents of Equations (3) and (4).

1.3 Characteristic polynomial

The characteristic polynomial for the Jacobian defined in Eq. 14 can be written as

$$\begin{aligned} \varLambda ^3+a_0\varLambda ^2+a_1\varLambda +a_2=0, \end{aligned}$$

(A.10)

where

$$\begin{aligned} a_0&=1-\beta ,\end{aligned}$$

(A.11)

$$\begin{aligned} a_1&=\frac{1}{D_e^{-2}}\left( 1+\alpha _2 x_{01} +3\alpha _3^2 x_{01}-\lambda \right) ,~\text {and}\end{aligned}$$

(A.12)

$$\begin{aligned} a_2&=+\frac{1}{D_e^{-2}} \left( \beta \lambda - \alpha \beta ^2-\lambda \right) . \end{aligned}$$

(A.13)