Complex dynamics of a harmonically excited structure coupled with a nonlinear energy sink

Abstract

Nonlinear behaviors are investigated for a structure coupled with a nonlinear energy sink. The structure is linear and subject to a harmonic excitation, modeled as a forced single-degree-of-freedom oscillator. The nonlinear energy sink is modeled as an oscillator consisting of a mass, a nonlinear spring, and a linear damper. Based on the numerical solutions, global bifurcation diagrams are presented to reveal the coexistence of periodic and chaotic motions for varying nonlinear energy sink mass and stiffness. Chaos is numerically identified via phase trajectories, power spectra, and Poincaré maps. Amplitude-frequency response curves are predicted by the method of harmonic balance for periodic steady-state responses. Their stabilities are analyzed. The Hopf bifurcation and the saddle-node bifurcation are determined. The investigation demonstrates that a nonlinear energy sink may create dynamic complexity.

1 Introduction

Proposed in some pioneering works [1, 2], a nonlinear energy sink is an effective device to reduce mechanical and structural vibration passively [3, 4]. In contrast to early work dealing with the reduction of free vibration, much attention has been paid to suppress forced vibrations of structures subjected to external excitations. The structures were modeled as single-degree-of-freedom oscillators [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19], two-degree-of-freedom linear oscillators [20,21,22,23], linear strings [24, 25], linear beams [26, 27], and single-degree-of-freedom nonlinear oscillators [28]. A simplest model of a nonlinear energy sink is an essential nonlinear oscillator consisting of a small mass, a cubic stiffness, and a linear damper [5, 7, 8, 10, 15, 16, 20, 22,23,24,25,26,27,28].

Most available investigations focused on periodic steady-state responses [5, 8,9,10, 12, 13, 15,16,17,18,19,20, 22,23,28]. In addition to experimental works [5, 7, 16, 23] and numerical simulations [5, 6, 9,10,11,12,13,14, 17,18,19, 21,22,23, 26, 28], approximate analytical methods are a powerful approach to predict the steady-state responses by yielding amplitude-frequency response curves and examining their stabilities [5,6,7,8,9,10,11,12,13, 15,16,17,18,19,20,21, 24,25,28]. The most used approach is the complexification averaging method [5, 6, 9, 11,12,13, 16, 17, 19,20,21, 26,27,28]. In the applications of the method, it is difficult to solve numerically the resulting nonlinear algebraic equations. The difficulty can be overcome via an arc-length continuation technique [26,27,28]. The method of harmonic balance is also used to analyze the periodic steady-state response [8]. In addition, a mixed multiple scale/harmonic balance algorithm was proposed and applied for the two-degree-of-freedom nonlinear system [15] and the elastic strings considering the internally resonant [24] and non-resonant [25]. In addition to periodic motions, weakly quasiperiodic response [7, 8, 10, 21, 25], strongly modulated responses [9, 11, 12] with saddle-node bifurcation [12] and chaotic regimes [6, 8, 14] were also investigated.

The nonlinearity may change the dynamics of the system qualitatively as well as quantitatively. Specifically, the nonlinearity may lead to new complex dynamics such as chaos. The possibility of chaotic motion was initially revealed in Ref. [8], and chaos was examined by the Lyapunov exponent [6] and Melnikov’s methods [14]. It is well known that the route to chaos is essential and significant to understand nonlinear behaviors of a system. However, the route to chaos has not been researched for a system composed by a structure and a nonlinear energy sink. To address the lack of research in this aspect, the present work explores the route to chaos by examining global bifurcations in the Poincaré maps regarding two key design parameters of a nonlinear energy sink, namely the mass and the nonlinear stiffness. To present a complete view of dynamic complexity created by a nonlinear energy sink, amplitude-frequency response curves of periodic steady-state response curves are derived from the method of harmonic balance for different nonlinear energy sink masses and stiffness with the assistance of a pseudo arc-length continuation technique. The stabilities of the responses are analyzed with the emphasis on the locations of the Hopf bifurcations and the saddle-node bifurcations.

The manuscript is organized as follows. Section 2 presents a basic model of a structure with a nonlinear sink. In Sect. 3, global bifurcation diagrams are numerically calculated and chaos is numerically identified. In Sect. 4, the amplitude-frequency response curves are determined by the method of harmonic balance and supported by the direct numerical integrations. Section 5 ends the manuscript with concluding remarks.

2 A linear single-degree-of-freedom system with a nonlinear energy sink

Consider a harmonically excited structure coupled with a nonlinear energy sink. To highlight the dynamic complexity induced only by the nonlinear energy sink, the simplest model is used to represent the structure. Namely, the structure is a model as a linear single-degree-of-freedom system with stiffness $k_{1}$, linear damping coefficient $c_{1}$, the mass $m_{1}$, and excited by the periodic force $F({t})=A\hbox {cos}(\omega t)$. The nonlinear energy sink consists of $m_{2}$, cubic stiffness k, and linear damping c. Figure 1 shows the model.

Fig. 1

A linear oscillator with a nonlinear energy sink

Measured from their static equilibriums, the displacements of masses $m_{0}$ and m are denoted as $x_{0}$ and x, respectively. It should be remarked that both the effect of gravity and the pre-stress have been ignored. It works in the case of a structure coupled with a smooth nonlinear energy sink as shown in Fig. 1. If nonsmoothness is taken into account [17,18,19], the effects of gravity should be considered. Newton’s second law yields the dynamic equations of the system.

$$\begin{aligned}&m_0 \ddot{x}_0 +k_0 x_0 +c_0 \dot{x}_0 +c\left( {\dot{x}_0 -\dot{x}} \right) +k\left( {x_0 -x} \right) ^{3}\nonumber \\&\quad +\,A\cos \left( {\omega t} \right) =0 \nonumber \\&m\ddot{x}+k\left( {x-x_0 } \right) ^{3}+c\left( {\dot{x}-\dot{x}_0 } \right) =0. \end{aligned}$$

(1)

Fig. 2

The bifurcation diagram of the structure response for varying mass m

Fig. 3

The bifurcation diagram of the energy sink response for varying mass m

Fig. 4

Periodic vibration of the structure for $m=0.2496$ kg. a The time history. b The enlargement of the time history. c The phase portrait. d The Poincaré map

Fig. 5

Chaotic motion of the energy sink for $m=0.2496\,\hbox {kg}$. a The time history. b The amplitude spectrum. c The phase portrait. d The Poincaré map

Fig. 6

Period-1 motion of the structure for $m=0.3384\,\hbox {kg}$. a The time history. b The enlargement of the time history. c The phase portrait. d The Poincaré map

Fig. 7

Period-2 motion of the energy sink for $m=0.3384\,\hbox {kg}$. a The time history. b The enlargement of the time history. c The phase portrait. d The Poincaré map

Fig. 8

Chaotic motion of the structure for $m=0.72\,\hbox {kg}$. a The time history. b The amplitude spectrum. c The phase portrait. d The Poincaré map

Fig. 9

Chaotic motion of the energy sink for $m=0.72\,\hbox {kg}$. a The time history. b The amplitude spectrum. c The phase portrait. d The Poincaré map

3 Numerical explorations of global bifurcations: periodic and chaotic motions

This section examines nonlinear behaviors of the system based on the numerical integrations calculated via the Runge-Kutta scheme implemented by MATLAB [29, 30]. The time step is 0.01 of a period T which is the $2\uppi /\omega$ and the absolute error is $10^{-6}$. Choose the parameter values as $m_{0}=24\,\hbox {kg}$, $k_{0}=20\,\hbox {kN}/\hbox {m}$, $c_{0}= 1.2\,\text { N}\cdot \hbox {s}/\hbox {m}$, $c= 1.2\,\text { N}\cdot \hbox {s}/\hbox {m}$, $A=10\,\hbox {N}$, and $\omega =28.8675\,\hbox {rad}/\hbox {s}$. Two key design parameters of the nonlinear energy sink, namely, mass m and cubic stiffness k are considered as a varying parameter, respectively. Bifurcations in the Poincaré maps are employed to demonstrate the effect of the two parameters on dynamical behaviors. The displacement components in the Poincaré maps are focused. The first 4800 periods in the Poincaré maps are calculated, and only the last 200 periods are plotted in bifurcation diagrams to eliminate transient responses.

The varying mass m is focused with fixed $k=10{,}000\hbox {kN}/\hbox {m}^{3}$. Figures 2 and 3 depict the displacements components in the Poincaré maps of the structure response and the nonlinear energy sink response. The numerical results show that the responses of the structure and the energy sink are periodic except for a few bursts of chaotic motions. Such chaotic motions are dynamic complexity induced by the nonlinear energy sink, because linear structures behave periodically only. For the periodic responses, the vibrations of the structure and the energy decreases with the increasing energy sink mass, except for the very small energy sink mass. It should be remarked, the response of the energy sink seems more complex than that of the structure, as shown in Figs. 2 and 3. Specifically, Figs. 4 and 5 show that the structure vibrates periodically but the energy sink chaotically for $m=0.2496$ kg. Figures 6 and 7 show that the structure is with period-1 motion while the energy sink has period-2 motion, for $m=0.3384\,\hbox {kg}$, and the fact implies the occurrence the period-doubling bifurcation for the energy sink, also shown in Fig. 3. Figures 8 and 9 show vibrations of both the structure and the energy sink are possibly chaotic. In above-mentioned figures, chaos is identified by the time history, the amplitude spectrum, the phase portrait, and the Poincaré map, while periodic motion is demonstrated by the time history with its local enlargement, the phase portrait, and the Poincaré map.

Figures 10 and 11 present bifurcation diagrams of the displacement components in the Poincaré maps of the structure and the energy sink for varying cubic stiffness k for $m=0.5\,\hbox {kg}$. The structure and the energy sink vibrate periodically except for the bursts of chaos for the small and the large stiffness k. Samples of periodic motions of the structure and the energy sink are respectively shown in Figs. 12 and 13, and those of possibly chaotic motions can be found in Figs. 14 and 15. It may be expected that periodic motion and chaotic motion occur alternately for the further increase of the stiffness. The amplitude of the periodic motion of the structure increases with the stiffness, while that of the energy sink remains almost unchanged.

4 Amplitude-frequency response curves: harmonic balance analysis

This section focuses on periodical motion from the view of the amplitude-frequency response. The method of harmonic balance will be employed to predict the response under an excitation with a given frequency. To perform the harmonic balance analysis, Eq. (1) is cast into the dimensionless form.

$$\begin{aligned}&{u}_0^{''} +u_0 +\varsigma _0 {u}_0^{'} +\varsigma \left( {{u}_0^{'} -{u}^{'} } \right) +\beta \left( {u_0 -u } \right) ^{3}\nonumber \\&\quad +\,f\cos \left( {\gamma \tau } \right) =0, \nonumber \\&{u}^{''} +\lambda \beta \left( {u-u_0 } \right) ^{3}+\lambda \varsigma \left( {{u}^{'} -{u}_0^{'} } \right) =0, \end{aligned}$$

(2)

where the dimensionless displacements of the structure and the energy sink as well as the dimensionless time are

$$\begin{aligned} u_0 =\frac{x_0 }{l},\quad u=\frac{x}{l},\quad \tau =\omega _0 t, \end{aligned}$$

(3)

in which l is the static deformation of the linear structural spring $k_{0}$ per 1 kN, and the structural frequency, the mass ratio, the damping ratio of the structure and the energy sink, the dimensionless nonlinear stiffness, the frequency, as well as the dimensionless excitation amplitude are, respectively,

$$\begin{aligned} \omega _0^{2}= & {} \frac{k_0 }{m_0 },\lambda =\frac{m_0 }{m},\varsigma _0 =\frac{c_0 }{m_0 \omega _0 },\varsigma =\frac{c}{m_0 \omega _0 },\beta =\frac{kl^{2}}{\omega _0^{2}m_0 }, \nonumber \\ \gamma= & {} \frac{\omega }{\omega _{0} },f=\frac{A}{k_0 l}. \end{aligned}$$

(4)

Based on the harmonic balance method, the responses of the governing Eq. (2) can be approximated by a finite sum of low harmonic terms. Since the nonlinearity in this system is cubic, the responses contain the odd harmonics only. In order to check the numerical convergence of the harmonic expansion, the lowest three odd harmonics are considered. Then the responses can be expressed as follows

$$\begin{aligned} u_0 (\tau )= & {} a_{11} \cos (\gamma \tau )+b_{11} \sin (\gamma \tau )+a_{31} \cos (3\gamma \tau )\nonumber \\&+\,b_{31} \sin (3\gamma \tau )+a_{51} \cos (5\gamma \tau )+b_{51} \sin (5\gamma \tau ), \nonumber \\ u(\tau )= & {} a_{12} \cos (\gamma \tau )+b_{12} \sin (\gamma \tau )+a_{32} \cos (3\gamma \tau )\nonumber \\&+\,b_{32} \sin (3\gamma \tau )+a_{52} \cos (5\gamma \tau )+b_{52} \sin (5\gamma \tau ),\nonumber \\ \end{aligned}$$

(5)

where $a_{ij}$ and $b_{ij}$ ($i=1,3,5$ and $j=1,2$) are the coefficients of corresponding harmonic components to be determined.

Substituting Eq. (5) into Eq. (2) and equating the coefficients of each harmonic $\hbox {cos}(i\gamma \tau )$ and $\hbox {sin}(i\gamma \tau )$ ($i=1,3,5$) of the both hands of resulting equations yield a set of nonlinear algebraic equations, presented in “Appendix A” as Eq. (A1). Equation (A1) leads to a set of equations of the coefficients of the harmonic balance with the orders 1 and 3 by letting $a_{5j}$ and $b_{5j}\,(j=1,2)$ be all zero, and it further reduces to the equations for the harmonic balance with order 1 only by letting $a_{ij}$ and $b_{ij}\,(i=3,5\,\hbox {and }j=1,2)$ be all zero. For given parameters, Eq. (A1) and the degenerated cases can be numerically solved via a pseudo arc-length continuation technique. Thus, one can obtain the amplitude-frequency response curves.

In order to describe the amplitude-frequency response curves with the higher orders, the root mean squares of the responses could be calculated as

$$\begin{aligned} u_{0r}= & {} \sqrt{a_{11}^{2}+b_{11}^{2}+a_{31}^{2}+b_{31}^{2}+a_{51} ^{2}+b_{51}^{2}}, \end{aligned}$$

(6)

$$\begin{aligned} u_r= & {} \sqrt{a_{12}^{2}+b_{12}^{2}+a_{32}^{2}+b_{32}^{2}+a_{52} ^{2}+b_{52}^{2}}. \end{aligned}$$

(7)

Choose a set of parameters as $\omega _{0}=28.8675\,\hbox {rad}/\hbox {s}$, $\lambda =30$, $\varsigma _{0}=0.0017$, $\varsigma =0.0017$, $\beta =1.25$, and $f=0.01$. The amplitude-frequency response curve of the energy sink is shown in Fig. 16. As shown is the curve with its local enlargements, the results based on the harmonic balance solution up to order 5 agrees well with that of the solution up to order 3, and disagrees with that of the solution of order 1. Specifically, both the solutions up to order 3 and order 5 predict a loop with a small break for $\gamma$ between 0.978 and 0.984, while the first-order solution does not detect the loop. In addition the obvious qualitative difference, there is a not obvious qualitative difference of an additional loop for $\gamma$ between 0.978 and 0.984 or quantitative difference for $\gamma$ between 1.35 and 1.41. In all cases, the solutions up to order 3 and order 5 are completely coinciding, while they do not overlap with the first-order solution. Therefore, the harmonic balance up to order 3 seems sufficiently precise.

The harmonic balance solution up to order 3 is supported by the direct numerical integrations. The comparisons of the amplitude-frequency response curve of the nonlinear energy sink are shown in Fig. 17 for $\omega _{0}=28.8675\,\hbox {rad}/\hbox {s}$, $\lambda =160$, $\varsigma _{0}=0.0017$, $\varsigma =0.0017$, $\beta =1.25$, and $f=0.01$. Here, to highlight the jumping phenomenon in both sides, $\lambda =30$ is replaced by $\lambda =160$. Both in forwarded or reverse frequency sweeping, the analytical results (solid line) based on the solution up to order 3 is in good agreement with the numerical results (regular triangles for forwarded sweeping and inverted triangles for reverse sweeping). Thus, in the following investigation, the method of harmonic balance up to order 3 will be employed.

In order to examine the stability of solution, the responses are reformulated as

$$\begin{aligned} u_0 (\tau )= & {} a_{11} (\tau )\cos (\gamma \tau )+b_{11} (\tau )\sin (\gamma \tau )\nonumber \\&+\, a_{31} (\tau )\cos (3\gamma \tau )+b_{31} (\tau )\sin (3\gamma \tau ), \nonumber \\ u(\tau )= & {} a_{12} (\tau )\cos (\gamma \tau )+b_{12} (\tau )\sin (\gamma \tau )\nonumber \\&+\, a_{32} (\tau )\cos (3\gamma \tau )+b_{32} (\tau )\sin (3\gamma \tau ). \end{aligned}$$

(8)

Substituting Eq. (6) into Eq. (2) and equating the coefficients of each harmonic component in the resulting equationslead to a set of nonlinear differential-algebraic equations, which are presented in “Appendix B” as Eq. (B1). The fixed points of Eq. (B1) correspond to the steady-state response. For given parameters, the fixed points can be numerically located via a pseudo arc-length continuation technique. After the linearization at each fixed point, the set of nonlinear differential-algebraic equations are reduced to a set of linear differential equations. The stability of each fixed point can be determined by the eigenvalues of the Jacobian matrix of the linear differential equations. This approach yields the stability of the steady-state response. There may be Hopf bifurcation points and saddle-node points on the curves. At a Hopf bifurcation point, the real part of a pair of complex conjugate eigenvalues changes from the negative to the positive (referred to as the first type) or reversed (referred to as the second type). At a saddle-node point, a positive real eigenvalue occurs (referred to as the first type) or disappears (referred to as the second type).

Fig. 10

The bifurcation diagram of the structure response for varying the cubic stiffness k

Fig. 11

The bifurcation diagram of the energy sink for varying the cubic stiffness k

Fig. 12

Periodic vibration of the structure for $k=5600\,\hbox {kN}/\hbox {m}^{3}$. a The time history. b The enlargement of the time history. c The phase portrait. d The Poincaré map

Fig. 13

Periodic vibration of the energy sink for $k=5600\,\hbox {kN}/\hbox {m}^{3}$. a The time history. b The enlargement of the time history. c The phase portrait. d The Poincaré map

Fig. 14

Chaotic motion of the structure for $k=14{,}400\,\hbox {kN}/\hbox {m}^{3}$. a The time history. b The amplitude spectrum. c The phase portrait. d The Poincaré map

Fig. 15

Chaotic motion of the energy sink for $k=14{,}400\,\hbox {kN}/\hbox {m}^{3}$. a The time history. b The amplitude spectrum. c The phase portrait. d The Poincaré map

The method of harmonic balance yields amplitude-frequency response curves revealing effects of the cubic nonlinear term coefficient. Figures 18–20 depict the curves for $\beta =0.0125$, 0.125, 1.25 while other parameters are fixed as $\omega _{0}=28.8675\,\hbox {rad}/\hbox {s}$, $\lambda =48$, $\varsigma _{0}=0.0017$, $\varsigma =0.0017$, and $f=0.01$. The black solid line and the blue dash-dot line represent, respectively, the stable and the unstable portions of the curves. The green ball and the red triangle stand respectively for the Hopf bifurcation points and the saddle-node points. The case with $\beta =0.0125$ is demonstrated in Fig. 18. As shown in Fig. 18a, there is an unstable open loop at the peak part of the response curve of the structure. The loop begins at a first type Hopf bifurcation point at $\gamma =0.996501$ with another two second type Hopf bifurcations near $\gamma = 0.996555$ and $\gamma =0.996564$, then undergoes second type Hopf bifurcation points for $\gamma =1.029951$ with a nearby first type saddle-node point at $\gamma =1.032631$ by increasing the frequency, after that comes three second type Hopf bifurcations at $\gamma =1.013257$, $\gamma =1.013234$, and $\gamma =1.013195$ which the frequency turns back, and finally comes a second type Hopf bifurcation at $\gamma =1.011412$ followed by the ending point, the second saddle-node at $\gamma = 1.011412$. The amplitude-frequency response curve of the steady-state response of the system for $\beta =0.125$ is depicted in Fig. 19, in which the unstable branch begins at a first type Hopf bifurcation at $\gamma =0.975992$ followed by other two first type Hopf bifurcations $\gamma =0.976041$ and 0.976057. Specially, the first type Hopf bifurcation at $\gamma = 0.97966$ is close to the first type saddle-node at $\gamma = 0.97967$ at which the frequency begins to turn back. After passing through three second type Hopf bifurcations at $\gamma =0.971772$, 0.969014, 0.959331 and a second type saddle-node bifurcation at $\gamma =0.971772$, this branch ends in a saddle-node bifurcation at $\gamma =0.90675$. The second unstable branch begins with a Hopf bifurcation at $\gamma =0.978154$ followed by a first type Hopf bifurcation $\gamma =0.983675$ and a first type saddle-node $\gamma =0.988493$ with increase of frequency, then it undergoes two second type Hopf bifurcation $\gamma =0.987772$ and $\gamma =0.987497$, and finally ends at a second type saddle-node bifurcation $\gamma =0.987465$. The third unstable branch begins with a first type Hopf bifurcation at $\gamma =0.99439$ followed by another first type Hopf bifurcation at $\gamma =0.994868$, then undergoes two first type Hopf bifurcations $\gamma =1.004820$ and $\gamma =1.091698$ followed by a first type saddle-node bifurcation $\gamma =0.987772$, and finally comes three close second type Hopf bifurcations at ${\gamma }=1.031755$, 1.031695, 1.031666 and another second type Hopf bifurcation $\gamma =1.030376$ followed by the ending second type saddle-node bifurcation at $\gamma =1.030375$ where the frequency turns back. Figure 20 shows the amplitude-frequency response curve of the steady-state response for $\beta =1.25$. It is different from the curves in Figs. 18 and 19. There are two circle folds appearing between $\gamma =0.984$ and $\gamma =0.992$, and there are six unstable branches with increasing frequency. The first unstable branch begins with the first type Hopf bifurcation at $\gamma =0.900389$ followed by two other first type Hopf bifurcations at $\gamma =0.900527$ and $\gamma = 0.900662$, then it undergoes a first type saddle-node bifurcation at $\gamma =0.903502$ where the frequency starts to turn back to a first type Hopf bifurcation at $\gamma =0.903499$, further on appears three second type Hopf bifurcations at $\gamma =0.886521$, 0.885569, 0.880612, and then comes a second type saddle-node bifurcation at $\gamma =0.427613$ where the frequency changes to go forward followed by the ending second type Hopf bifurcation at $\gamma =0.519692$. The second unstable branch begins with a first type Hopf bifurcation at $\gamma =0.966910$ and ends with a second type Hopf bifurcation at $\gamma = 0.986591$. The third unstable branch begins with a first type Hopf bifurcation at $\gamma =0.987291$ followed by another first type Hopf bifurcation at $\gamma =0.987311$, then it undergoes a second type saddle-node at $\gamma =0.987311$ where the frequency turns back, and gets to a second type Hopf bifurcation at $\gamma =0.984231$ followed by the ending second type saddle-node at $\gamma =0.984218$. The fourth unstable branch begins with a first type Hopf bifurcation at $\gamma =0.990820$ followed by another first type Hopf bifurcation at $\gamma = 0.990837$, then it undergoes a second type saddle-node bifurcation at $\gamma =0.991051$ followed by a second type Hopf bifurcation at $\gamma = 0.991031$, then it goes through a first type Hopf bifurcation at $\gamma = 0.990598$, a second type Hopf bifurcation at $\gamma =0.990586$ and a first type Hopf bifurcation at $\gamma = 0.990583$, gets to a second type saddle-node bifurcation at $\gamma =0.990563$, and finally ends with a second type Hopf bifurcation at $\gamma =0.990566$. The fifth unstable branch begins with a first type Hopf bifurcation at $\gamma = 0.990662$, and ends with a second type Hopf bifurcation at $\gamma = 0.998331$. The sixth unstable branch begins with a first type Hopf bifurcation at $\gamma =1.057548$ followed by three first type Hopf bifurcations at $\gamma =1.065659$, 1.085802, 1.244552, goes through a first type saddle-node bifurcation at $\gamma =1.338758$ where the frequency turns back, and then undergoes a second type Hopf bifurcation at $\gamma =1.084814$ followed by a second type double Hopf bifurcation at ${\gamma }=1.084431$ and another second type Hopf bifurcation at $\gamma =1.082393$, and finally ends with a second type saddle-node bifurcation at $\gamma =1.082393$.

Fig. 16

The amplitude-frequency curves of the energy sink based on different order harmonic balance solutions

Fig. 17

Comparison of the amplitude-frequency curve of the energy sink based on the analytical and numerical methods

Fig. 18

The amplitude-frequency response curve of the steady-state response for $\beta =0.0125$. a The structure. b The nonlinear energy sink

Fig. 19

Amplitude-frequency response curve of the steady-state response with $\beta =0.125$. a The structure. b The nonlinear energy sink

Figures 21–23 show the amplitude-frequency response curves of the steady-state response for different mass ratio $\lambda$ while $\omega _{0}=28.8675\,\hbox {rad}/\hbox {s}$, $\beta =1.25$, $\varsigma _{0}=0.0017$, $\varsigma =0.0017$, and $f=0.01$. There are six unstable branches by increasing the frequency in each figure. In Fig. 21 with ${\lambda }=160$, the six unstable branches begin with the first type Hopf bifurcations at $\gamma = 0.807063$, 0.969513, 0.992771, 1.001971, 1.000845, 1.108926, respectively. The fourth and the sixth unstable branches end with the second type saddle-node bifurcations at $\gamma =1.000331$ and $\gamma =1.126458$. The other unstable branches end with the second type Hopf bifurcations at $\gamma =0.742804$, 0.992097, 0.990458, 1.019081. In Fig. 22 with $\lambda =63.1579$, two circles of the third and the fourth unstable branches are even more visible than those in Fig. 21. The six unstable branches begin with the first type Hopf bifurcations at $\gamma =0.880777$, 0.969011, 0.989561, 0.994257, 0.993705, 1.071969, respectively. The third and the sixth unstable branches end with the second type saddle-node bifurcations at $\gamma =0.986711$ and $\gamma =1.091146$. The other unstable branches end with the second type Hopf bifurcation at $\gamma =0.584962$, 0.988919, 0.993511, 1.004267. Notably, in Fig. 23 with $\lambda =30$, the first and the second unstable branches are very close to each other. In addition, the unstable branches are much more visible than that of in Figs. 20 and 21. The unstable branches begin with the first type Hopf bifurcation at $\gamma = 0.332037$, 0.928011, 0.959560, 0.981319, 0.982807, 1.025976, respectively. The first, the fourth and the sixth unstable branches end at the second type saddle-node bifurcations at $\gamma = 0.112208$, 0.977563, 1.069976. The other unstable branches end with the second Hopf bifurcations at ${\gamma }= 0.387639$, 0.980444, 0.985522.

Fig. 20

Amplitude-frequency response curve of the steady-state response with $\beta =1.25$. a The structure. b The nonlinear energy sink

Fig. 21

Amplitude-frequency response curve of the steady-state response with $\lambda =160$. a The structure. b The nonlinear energy sink

Fig. 22

Amplitude-frequency response curves of the steady-state response with $\lambda =63.1579$. a The structure. b The nonlinear energy sink

Fig. 23

Amplitude-frequency response curve of the steady-state response with $\lambda =30$. a The structure. b The nonlinear energy sink

5 Conclusions

The investigation treats steady-state response in forced vibration of a periodically excited linear structure coupled with a nonlinear energy sink. The global bifurcations are numerically examined via the Poincaré map. Phase trajectories power spectra and Poincaré maps are used to identify dynamical behaviors. For periodic steady-state response, the harmonic balance method is applied to determine the amplitude-frequency response curves and their stabilities. Especially the Hopf bifurcations and the saddle-node bifurcations in the response are located. The investigation finds that a nonlinear energy sink may introduce dynamic complexity. The dynamic complexity lies in the following aspects:

• (1) Chaotic motion may occur. Actually, the bifurcation diagrams reveal that the responses of the structure and the energy sink are periodic except a few bursts of chaotic motions.

• (2) The dynamic behaviors of the structure may be different from those of the nonlinear energy sink for appropriate parameters.

• (3) Even for the periodic steady-state responses, their amplitude-frequency response curves look complicated. There are more unstable portions defined by the Hopf bifurcations or the saddle-node bifurcations.

Appendices

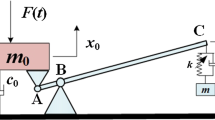
Appendix A

1.1 The nonlinear algebraic equations of the harmonic balance up to order 5

$$\begin{aligned}&-3/4\beta a_{11}^{2}b_{32} +3/4\beta a_{11}^{2}b_{31} +3/2\beta a_{51}^{2}b_{11} -3/2\beta a_{51}^{2}b_{12}\\&\quad -\,9/4\beta b_{11} ^{2}b_{12} +9/4\beta b_{11} b_{12}^{2}-3/4\beta a_{11}^{2}b_{12}+3/4\beta a_{11}^{2}b_{11} \\&\quad +\,3/4\beta a_{12}^{2}b_{11} -3/4\beta a_{12}^{2}b_{12}-3/2\beta a_{52} ^{2}b_{12} +3/2\beta a_{52}^{2}b_{11}\\&\quad -\,3/4\beta b_{12}^{2}b_{31} +\,3/4\beta b_{11}^{2}b_{32} -3/4\beta b_{11}^{2}b_{31} +3/4\beta a_{12}^{2}b_{31}\\&\quad -\,3/4\beta a_{12}^{2}b_{32} -3/2\beta b_{12} b_{51}^{2}-3/2\beta b_{12} b_{52}^{2}-\gamma \left( \zeta \right) a_{11} \\&\quad -\,\gamma \zeta _0 a_{11} +3/2\beta b_{11} b_{52}^{2}+3/2\beta b_{11} b_{51}^{2}+3/2\beta b_{11} b_{32}^{2}\\&\quad +\,3/2\beta b_{11} b_{31} ^{2}-3/4\beta a_{32}^{2}b_{51} +3/4\beta a_{32}^{2}b_{52} \\&\quad -\,3/2\beta a_{32}^{2}b_{12} +3/4\beta a_{31}^{2}b_{52} +3/2\beta a_{32}^{2}b_{11} -3/2\beta a_{31}^{2}b_{12}\\&\quad -3/4\beta a_{31} ^{2}b_{51} +3/2\beta a_{31}^{2}b_{11} +3/2\beta a_{32} a_{51} b_{11} \\&\quad -\,3/2\beta a_{32} a_{51} b_{12} -3/2\beta a_{32} a_{52} b_{11} +3/2\beta a_{32} a_{52} b_{12}\\&\quad -\,3/2\beta a_{32} a_{51} b_{31} +3/2\beta a_{32} a_{51} b_{32} +3/2\beta a_{32} a_{52} b_{31} \\&\quad +\,3/4\beta b_{12}^{2}b_{32} -3/2\beta a_{32} a_{52} b_{32} +3/2\beta a_{31} a_{52} b_{32}\\&\quad -\,3/2\beta a_{31} a_{52} b_{12} -3/2\beta a_{31} a_{52} b_{31} -3/2\beta a_{31} a_{51} b_{32} \\&\quad +\,3/2\beta a_{31} a_{52} b_{11} -3/2\beta a_{31} a_{32} b_{52} +3\beta a_{31} a_{32} b_{12} \\&\quad +\,3/2\beta a_{31} a_{32} b_{51} -3/4\beta b_{32}^{2}b_{52} +3/2\beta a_{31} a_{51} b_{12} \\&\quad +\,3/2\beta a_{31} a_{51} b_{31} -3/2\beta a_{31} a_{51} b_{11} +3/4\beta b_{32}^{2}b_{51}\\&\quad -\,3/4\beta b_{31}^{2}b_{52} +3/4\beta b_{31}^{2}b_{51} -3/2\beta b_{12} b_{32}^{2}\\&\quad -\,3/2\beta b_{12} b_{31}^{2} -3\beta b_{11} b_{51} b_{52} +3\beta b_{12} b_{31} b_{32}\\&\quad +\,3/2\beta b_{12} b_{31} b_{51}-\,3/2\beta b_{12} b_{31} b_{52} -3/2\beta b_{12} b_{32} b_{51}\\&\quad +\,3/2\beta b_{12} b_{32} b_{52}+3\beta b_{12} b_{51} b_{52}-\,3/2\beta b_{31} b_{32} b_{51}\\&\quad +\,3/2\beta b_{31} b_{32} b_{52} -3/2\beta b_{11} b_{32} b_{52}-3/2\beta a_{11} a_{12} b_{11}\\&\quad +\,3/2\beta a_{11} a_{12} b_{12} -3/2\beta a_{11} a_{12} b_{31}+3/2\beta a_{11} a_{12} b_{32} \\&\quad -\,3/2\beta a_{11} a_{31} b_{11} +3/2\beta a_{11} a_{31} b_{12}+3/2\beta a_{11} a_{31} b_{51} \\&\quad -\,3/2\beta a_{11} a_{31} b_{52} +3/2\beta a_{11} a_{32} b_{11}-3/2\beta a_{11} a_{32} b_{12} \\&\quad -3\beta a_{51} a_{52} b_{11} +3\beta a_{51} a_{52} b_{12}+3/2\beta b_{11} b_{12} b_{31} \\&\quad -\,3/2\beta b_{11} b_{12} b_{32} +b_{11} +3/2\beta a_{12} a_{52} b_{32}-3/2\beta a_{12} a_{52} b_{31} \\&\quad +\,3/2\beta a_{12} a_{51} b_{31} -3/2\beta a_{12} a_{51} b_{32}+3/2\beta a_{12} a_{32} b_{51}\\&\quad -\,3/2\beta a_{12} a_{32} b_{52} +3/2\beta a_{12} a_{31} b_{52}-3/2\beta a_{12} a_{31} b_{51} \\&\quad +\,3/2\beta a_{11} a_{52} b_{31} -3/2\beta a_{11} a_{52} b_{32}+3/2\beta b_{11} b_{32} b_{51} \\&\quad -\,3/2\beta a_{11} a_{32} b_{51} +3/2\beta a_{11} a_{32} b_{52}-3/2\beta a_{11} a_{51} b_{31} \\&\quad +\,3/2\beta a_{11} a_{51} b_{32} -3/2\beta b_{11} b_{31} b_{51}+3/2\beta b_{11} b_{31} b_{52} \\&\quad +\,3/4\beta b_{11}^{3}-b_{11} \gamma ^{2}-3/4\beta b_{12}^{3}-3/2\beta a_{12} a_{32} b_{11} \\&\quad +\,3/2\beta a_{12} a_{32} b_{12} -3\beta b_{11} b_{31} b_{32}+3/2\beta a_{12} a_{31} b_{11} \\&\quad -\,3/2\beta a_{12} a_{31} b_{12} -3\beta a_{31} a_{32} b_{11} =0, \end{aligned}$$

$$\begin{aligned}&f-3/2\beta a_{11} a_{31} a_{52} -3/2\beta a_{11} a_{32} a_{51} +3/2\beta a_{52} b_{11} b_{31} \\&\quad -\,3/2\beta a_{52} b_{11} b_{32} -3/2\beta a_{52} b_{12} b_{31}+3/2\beta a_{11} a_{32} a_{52} \\&\quad +\,3\beta a_{12} b_{31} b_{32} +3/2\beta a_{11} a_{12} a_{32}-3/2\beta a_{32} b_{32} b_{52}\\&\quad -\,3/2\beta a_{51} b_{11} b_{31} +3/2\beta a_{51} b_{11} b_{32}+3/2\beta a_{51} b_{12} b_{31} \\&\quad -\,3/2\beta a_{51} b_{12} b_{32} +3/2\beta a_{51} b_{31} b_{32}+3/2\beta a_{52} b_{12} b_{32}\\&\quad \,-3/2\beta a_{52} b_{31} b_{32} -3/2\beta a_{11} a_{12} a_{31}-3\beta a_{11} a_{31} a_{32} \\&\quad +\,3/2\beta a_{12} b_{31} b_{52}-3/2\beta a_{12} b_{31} b_{51}+3\beta a_{12} b_{51} b_{52}\\&\quad +\,3/2\beta a_{12} b_{32} b_{51} -3/2\beta a_{12} b_{32} b_{52}+3/2\beta a_{11} a_{31} a_{51} \\&\quad -\,3/2\beta a_{31} a_{32} a_{51}+3/2\beta a_{31} a_{32} a_{52}+3/2\beta a_{31} b_{11} b_{12}\\&\quad +\,3/2\beta a_{31} b_{11} b_{51} -3/2\beta a_{31} b_{11} b_{52}-3/2\beta a_{31} b_{12} b_{51} \\&\quad +\,3/2\beta a_{31} b_{12} b_{52}+3/2\beta a_{31} b_{31} b_{51}-3/2\beta a_{31} b_{31} b_{52} \\&\quad -\,3/2\beta a_{31} b_{32} b_{51} +3/2\beta a_{31} b_{32} b_{52}-3/2\beta a_{32} b_{11} b_{12} \\&\quad -\,3/2\beta a_{32} b_{11} b_{51} +3/2\beta a_{32} b_{11} b_{52}+3/2\beta a_{32} b_{12} b_{51} \\&\quad -\,3/2\beta a_{32} b_{12} b_{52} -3/2\beta a_{32} b_{31} b_{51}+3/2\beta a_{32} b_{31} b_{52} \\&\quad -\,3\beta a_{11} a_{51} a_{52} -3/2\beta a_{11} b_{11} b_{12}+3/2\beta a_{11} b_{11} b_{31} \\&\quad -\,3/2\beta a_{11} b_{11} b_{32} -3/2\beta a_{11} b_{12} b_{31}+3/2\beta a_{11} b_{12} b_{32} \\&\quad +\,a_{11} +\gamma \zeta _0 b_{11}+\gamma \left( \zeta \right) b_{11}+3\beta a_{12} a_{31} a_{32}\\&\quad -\,3\beta a_{11} b_{31} b_{32} +3/2\beta a_{12} b_{11} b_{32} -3/2\beta a_{12} b_{11} b_{31} \\&\quad +\,3/2\beta a_{12} b_{12} b_{31} +3/2\beta a_{12} b_{11} b_{12} -3/2\beta a_{12} a_{32} a_{52} \\&\quad +\,3\beta a_{12} a_{51} a_{52} -3/2\beta a_{12} a_{31} a_{51} +3/2\beta a_{12} a_{31} a_{52} \\&\quad +\,3/2\beta a_{12} a_{32} a_{51} -3/2\beta a_{11} b_{32} b_{51} +3/2\beta a_{11} b_{32} b_{52}\\&\quad -\,3\beta a_{11} b_{51} b_{52} -3/4\beta a_{12}^{2}a_{32} +3/4\beta a_{12}^{2}a_{31} \\&\quad +\,3/4\beta a_{52} b_{31}^{2}+3/2\beta a_{11} b_{51}^{2}+3/2\beta a_{11} b_{52}^{2}+3/4\beta a_{52} b_{32}^{2}\\&\quad +\,3/2\beta a_{11} b_{31} b_{51} -3/2\beta a_{11} b_{31} b_{52}-3/2\beta a_{12} b_{12} b_{32} \\&\quad +\,3/2\beta a_{32} b_{32} b_{51} -3/2\beta a_{12} b_{51}^{2}-3/2\beta a_{12} b_{52}^{2}\\&\quad +\,3/4\beta a_{31}^{2}a_{51} -3/4\beta a_{31}^{2}a_{52} -3/4\beta a_{31} b_{11}^{2}-3/4\beta a_{31} b_{12}^{2} \\&\quad +\,3/4\beta a_{32}^{2}a_{51} -3/4\beta a_{32}^{2}a_{52}+3/4\beta a_{32} b_{11}^{2}+3/4\beta a_{32}b_{12}^{2} \\&\quad -\,3/4\beta a_{51} b_{31}^{2}-3/4\beta a_{51} b_{32}^{2}-3/2\beta a_{12} b_{31}^{2}-3/2\beta a_{12} b_{32}^{2}\\&\quad -\,3/2\beta a_{12} a_{51}^{2}-3/2\beta a_{12} a_{52}^{2}-3/4\beta a_{12}b_{11}^{2}-3/4\beta a_{12} b_{12}^{2}\\&\quad +\,3/4\beta a_{11}^{2}a_{31}+9/4\beta a_{11} a_{12}^{2}+3/2\beta a_{11} a_{31}^{2}-3/4\beta a_{11}^{2}a_{32}\\&\quad -\,9/4\beta a_{11}^{2}a_{12}+3/2\beta a_{11}a_{51}^{2}+\,3/2\beta a_{11} a_{52}^{2}+3/4\beta a_{11} b_{11}^{2}\\&\quad +3/4\beta a_{11} b_{12}^{2}+\,3/2\beta a_{11} b_{31}^{2}+3/2\beta a_{11} b_{32}^{2}-3/2\beta a_{12} a_{31}^{2}\\&\quad -3/2\beta a_{12}a_{32}^{2}+\,3/2\beta a_{11} a_{32}^{2}+3/4\beta a_{11}^{3}-3/4\beta a_{12}^{3} \\&\quad -\,a_{11} \gamma ^{2}=0, \end{aligned}$$

$$\begin{aligned}&-3/2\beta a_{51} b_{51} b_{52} +3/2\beta a_{11} b_{31} b_{32} -3/2\beta a_{32} b_{12} b_{32} \\&\quad -\,3/2\beta a_{32} b_{11} b_{12} +3/2\beta a_{11} a_{12} a_{32} +3/2\beta a_{32} b_{12} b_{31} \\&\quad -\,3/2\beta a_{11} a_{12} a_{31} +3/2\beta a_{31} b_{11} b_{12} -3\beta a_{51} b_{31} b_{32}\\&\quad +3\beta a_{52} b_{31} b_{32} -3/2\beta a_{11} a_{31} a_{32} -3/2\beta a_{12} b_{31} b_{32}\\&\quad -\,3\beta a_{31}a_{32} a_{51}+\,3\beta a_{31} a_{32} a_{52} -3/2\beta a_{11} b_{11} b_{31}\\&\quad +\,3/2\beta a_{11} b_{11} b_{32}+3/2\beta a_{11} b_{12} b_{31}-3/2\beta a_{11} b_{12} b_{32}\\&\quad +3/2\beta a_{12} a_{31} a_{32}+\,3/2\beta a_{12} b_{11} b_{31}-3/2\beta a_{12} b_{11} b_{32} \\&\quad -\,3/2\beta a_{12} b_{12} b_{31} +3/2\beta a_{32} b_{11} b_{32}+3/2\beta a_{12} b_{12} b_{32} \\&\quad -\,3/2\beta a_{32} b_{11} b_{31} +3\beta a_{52} b_{11} b_{12}+3/2\beta a_{51} b_{12}^{2} \\&\quad -\,3/2\beta a_{52} b_{11}^{2}-3/2\beta a_{52} b_{12}^{2}+3/2\beta a_{12}^{2}a_{51}\\&\quad +\,3/2\beta a_{11} ^{2}a_{51} -3/2\beta a_{11}^{2}a_{52} +a_{51} -3/2\beta a_{52} b_{31}^{2} \\&\quad -\,3/2\beta a_{52} b_{32}^{2}+3/4\beta a_{51} b_{51}^{2}+9/4\beta a_{51} a_{52}^{2}+3/4\beta a_{51} b_{52}^{2}\\&\quad -\,3/4\beta a_{52} b_{51}^{2}-3/4\beta a_{52} b_{52}^{2}+5\gamma \left( \zeta \right) b_{51} +5\gamma \zeta _0 b_{51} \\&\quad -\,9/4\beta a_{51}^{2}a_{52} -3/2\beta a_{12}^{2}a_{52} -3/4\beta a_{12}^{2}a_{32} +3/4\beta a_{12}^{2}a_{31} \\&\quad +\,3/2\beta a_{51} b_{11}^{2}-3\beta a_{51} b_{11} b_{12} -3\beta a_{11} a_{12} a_{51} \\&\quad +\,3\beta a_{11} a_{12} a_{52} +3/2\beta a_{52} b_{51} b_{52} +3/2\beta a_{31} b_{11} b_{31} \\&\quad -\,3/2\beta a_{31} b_{11} b_{32} -3/2\beta a_{31} b_{12} b_{31} +3/2\beta a_{31} b_{12} b_{32} \\&\quad +\,3/2\beta a_{31}^{2}a_{51} -3/2\beta a_{31}^{2}a_{52} -3/4\beta a_{31} b_{11}^{2}-3/4\beta a_{31} b_{12}^{2}\\&\quad +\,3/2\beta a_{32} ^{2}a_{51} -3/2\beta a_{32}^{2}a_{52}+3/4\beta a_{32} b_{11}^{2}\\&\quad +\,3/4\beta a_{32} b_{12}^{2}+3/2\beta a_{51} b_{31}^{2}+3/2\beta a_{51} b_{32}^{2}+3/4\beta a_{12} b_{31}^{2}\\&\quad +\,3/4\beta a_{12} b_{32}^{2}+3/4\beta a_{11}^{2}a_{31} +3/4\beta a_{11} a_{31}^{2}\\&\quad -\,3/4\beta a_{11}^{2}a_{32} -3/4\beta a_{11} b_{31}^{2}-3/4\beta a_{11} b_{32}^{2}-3/4\beta a_{12} a_{31}^{2}\\&\quad -\,3/4\beta a_{12} a_{32}^{2}+3/4\beta a_{11} a_{32}^{2}+3/4\beta a_{51}^{3}-3/4\beta a_{52}^{3} \\&\quad -\,25a_{51} \gamma ^{2}=0, \end{aligned}$$

$$\begin{aligned}&3/2\beta a_{52}^{2}b_{31} +3/2\beta a_{11} a_{52} b_{11} -3/2\beta a_{11} a_{52} b_{12} \\&\quad +\,3/2\beta a_{12} a_{51} b_{11} -3/2\beta a_{12} a_{51} b_{12} +3/2\beta b_{11} b_{12} b_{51} \\&\quad -\,3/2\beta b_{11} b_{12} b_{52} -3\beta b_{31} b_{51} b_{52} +3\beta b_{32} b_{51} b_{52} \\&\quad -\,3/2\beta a_{12} a_{52} b_{11} +3/2\beta a_{12} a_{52} b_{12} -3/2\beta a_{31} a_{32} b_{31} \\&\quad +\,3/4\beta a_{11} ^{2}b_{51}+3/4\beta a_{12}^{2}b_{51} -3/4\beta a_{12}^{2}b_{52} -3/4\beta a_{11}^{2}b_{52} \\&\quad +\,3/2\beta a_{51}^{2}b_{31} -3/2\beta a_{51} ^{2}b_{32} -3/2\beta a_{52}^{2}b_{32} -3/4\beta b_{11}^{2}b_{51}\\&\quad +\,3/2\beta a_{31} a_{32} b_{32} -3\beta a_{51} a_{52} b_{31} +3\beta a_{51} a_{52} b_{32} \\&\quad -\,3/2\beta a_{11} a_{12} b_{51} +3/2\beta a_{11} a_{12} b_{52} -3/2\beta a_{11} a_{51} b_{11} \\&\quad +\,3/2\beta a_{11} a_{51}b_{12}-3/2\beta a_{11}^{2}b_{32} +3/2\beta a_{11}^{2}b_{31} +3/4\beta b_{11}^{2}b_{12} \\&\quad -\,3/4\beta b_{11} b_{12}^{2}-3/4\beta a_{11} ^{2}b_{12} +3/4\beta a_{11}^{2}b_{11} +3/4\beta a_{12}^{2}b_{11}\\&\quad -\,3/4\beta a_{12}^{2}b_{12} +3/2\beta a_{31} a_{51} b_{11} -3/2\beta a_{31} a_{51} b_{12} \\&\quad +\,3/2\beta b_{12}^{2}b_{31} -3/2\beta b_{11} ^{2}b_{32} +3/2\beta b_{11}^{2}b_{31} +3/2\beta a_{12}^{2}b_{31}\\&\quad -\,3/2\beta a_{12}^{2}b_{32} -3\gamma \left( \zeta \right) a_{31} -3\gamma \zeta _0 a_{31}-3/2\beta b_{32} b_{52}^{2} \\&\quad +\,3/4\beta a_{31}^{2}b_{31} +3/4\beta a_{32}^{2}b_{31} -3/4\beta a_{32}^{2}b_{32}+3/2\beta b_{31} b_{51}^{2} \\&\quad +\,3/2\beta b_{31} b_{52}^{2}+3/4\beta b_{12}^{2}b_{52}+3/4\beta b_{11}^{2}b_{52}-3/4\beta b_{12}^{2}b_{51} \\&\quad -\,3/4\beta a_{31}^{2}b_{32} +9/4\beta b_{31} b_{32}^{2}-9/4\beta b_{31}^{2}b_{32}-3/2\beta b_{32} b_{51}^{2}\\&\quad -\,3/2\beta b_{12}^{2}b_{32}-3/2\beta a_{31} a_{52} b_{11}+3/2\beta a_{31}a_{52} b_{12} \\&\quad -\,3/2\beta a_{32} a_{51} b_{11}+\,3/2\beta a_{32} a_{51} b_{12} +3/2\beta a_{32} a_{52} b_{11}\\&\quad -\,3/2\beta a_{32} a_{52} b_{12}-3/2\beta b_{12} b_{31} b_{51} +3/2\beta b_{12} b_{31} b_{52}\\&\quad +\,3/2\beta b_{12} b_{32} b_{51}-3/2\beta b_{12} b_{32} b_{52} +3/2\beta b_{11} b_{32} b_{52} \\&\quad -\,3/2\beta a_{11} a_{12} b_{11}+3/2\beta a_{11} a_{12} b_{12} -3\beta a_{11} a_{12} b_{31} \\&\quad +\,3\beta a_{11} a_{12} b_{32}+3/2\beta a_{11} a_{31} b_{51}-3/2\beta a_{11} a_{31} b_{52} \\&\quad -\,3\beta b_{11} b_{12} b_{31} +3\beta b_{11} b_{12} b_{32}+3/2\beta b_{11} b_{31} b_{51} \\&\quad -\,3/2\beta b_{11}b_{31} b_{52} -3/2\beta b_{11} b_{32} b_{51}-3/2\beta a_{11} a_{32} b_{51} \\&\quad +3/2\beta a_{11} a_{32} b_{52} -3/2\beta a_{11} a_{51} b_{31} +3/2\beta a_{11} a_{51} b_{32} \\&\quad +\,3/2\beta a_{11} a_{52} b_{31} -3/2\beta a_{11} a_{52} b_{32} -3/2\beta a_{12} a_{31} b_{51} \\&\quad +\,3/2\beta a_{12} a_{31} b_{52} +3/2\beta a_{12} a_{32} b_{51} -3/2\beta a_{12} a_{32} b_{52} \\&\quad +\,3/2\beta a_{12} a_{51} b_{31} -3/2\beta a_{12} a_{51} b_{32} -3/2\beta a_{12} a_{52} b_{31} \\&\quad +\,3/2\beta a_{12} a_{52} b_{32} +b_{31} -3/4\beta b_{32} ^{3}+3/4\beta b_{31}^{3}\\&\quad -\,9b_{31} \gamma ^{2}+1/4\beta b_{12} ^{3}-1/4\beta b_{11}^{3}=0, \end{aligned}$$

$$\begin{aligned}&-3/2\beta a_{11} a_{31} a_{52} -3/2\beta a_{11} a_{32} a_{51} -3/2\beta a_{31} b_{12} b_{52} \\&\quad -\,3/2\beta a_{52} b_{11} b_{31} +3/2\beta a_{52} b_{11} b_{32} +3/2\beta a_{52} b_{12} b_{31} \\&\quad +\,3/2\beta a_{11} a_{32} a_{52} +3\beta a_{32} b_{11} b_{12} +3/2\beta a_{32} b_{11} b_{51} \\&\quad +\,3\beta a_{11} a_{12} a_{32} +3/2\beta a_{51} b_{11} b_{31} -3/2\beta a_{51} b_{11} b_{32}\\&\quad -\,3/2\beta a_{51} b_{12} b_{31}+3/2\beta a_{51} b_{12} b_{32}+3/2\beta a_{31} b_{11} b_{52} \\&\quad -\,3/2\beta a_{52} b_{12} b_{32}-3\beta a_{11} a_{12} a_{31} +3/2\beta a_{12} b_{31} b_{52} \\&\quad -\,3/2\beta a_{12} b_{31} b_{51}+3/2\beta a_{12} b_{32} b_{51}-3/2\beta a_{12} b_{32} b_{52} \\&\quad +\,3/2\beta a_{11} a_{31} a_{51}+3/2\beta a_{31} b_{12} b_{51}-\,3/2\beta a_{31} b_{11} b_{51} \\&\quad -\,3\beta a_{31} b_{11} b_{12}-3/2\beta a_{32} b_{11} b_{52}-3/2\beta a_{32} b_{12} b_{51} \\&\quad +\,3/2\beta a_{32} b_{12} b_{52} +3/2\beta a_{11} b_{11} b_{12} +3/2\beta a_{11} b_{31} b_{51} \\&\quad -\,3/2\beta a_{11} b_{31} b_{52} -3/2\beta a_{11} b_{32} b_{51} +3/2\beta a_{11} b_{32} b_{52}\\&\quad -\,3/2\beta a_{12} a_{31} a_{51}+3/2\beta a_{12} a_{31} a_{52} +3/2\beta a_{12} a_{32} a_{51} \\&\quad -\,3/2\beta a_{12} a_{32} a_{52}-3/2\beta a_{12} b_{11} b_{12} -3/2\beta a_{12} b_{11} b_{51} \\&\quad +\,3/2\beta a_{12} b_{11} b_{52}+3/2\beta a_{12} b_{12} b_{51}-3/2\beta a_{12} b_{12} b_{52} \\&\quad -\,3\beta a_{31} a_{51} a_{52}-3/2\beta a_{52} b_{11} b_{12}-3/2\beta a_{31} b_{31} b_{32}\\&\quad -\,3\beta a_{31} b_{51} b_{52} +3\beta a_{32} a_{51} a_{52}+\,3/2\beta a_{32} b_{31} b_{32}\\&\quad +\,3\beta a_{32} b_{51} b_{52} -3/4\beta a_{51} b_{12}^{2}+3/4\beta a_{52} b_{11}^{2}+3\gamma \zeta _0 b_{31}\\&\quad +\,3/4\beta a_{52} b_{12} ^{2}+3/4\beta a_{12}^{2}a_{51} +3\gamma \left( \zeta \right) b_{31}+3/4\beta a_{11}^{2}a_{51}\\&\quad -\,3/4\beta a_{11}^{2}a_{52} -3/2\beta a_{32} a_{51}^{2}-9/4\beta a_{31}^{2}a_{32} \\&\quad -\,3/4\beta a_{12}^{2}a_{52} +3/2\beta a_{11} b_{12} b_{52} +3/2\beta a_{51} b_{11} b_{12} \\&\quad -\,3/2\beta a_{11} a_{12}a_{51}+3/2\beta a_{11} a_{12} a_{52} +3/2\beta a_{11} b_{11} b_{51}\\&\quad -\,3/2\beta a_{11} b_{11} b_{52}-3/2\beta a_{11} b_{12} b_{51} -3/2\beta a_{32} b_{51}^{2}\\&\quad -\,3/2\beta a_{32} b_{52}^{2}-3/2\beta a_{32} a_{52}^{2}-3/4\beta a_{32} b_{31}^{2}-3/4\beta a_{32} b_{32}^{2}\\&\quad +\,3/4\beta a_{31} b_{31}^{2}+3/4\beta a_{31} b_{32}^{2}+3/2\beta a_{31} b_{52}^{2}+3/2\beta a_{31} a_{51}^{2}\\&\quad +\,9/4\beta a_{31} a_{32}^{2}+3/2\beta a_{31} b_{51}^{2}+3/2\beta a_{31} a_{52}^{2}-3/4\beta a_{51} b_{11}^{2} \\&\quad +\,a_{31}+3/2\beta a_{12}^{2}a_{31} -3/2\beta a_{12}^{2}a_{32} +3/2\beta a_{31} b_{11}^{2}\\&\quad +\,3/2\beta a_{31} b_{12}^{2}-3/2\beta a_{32} b_{11}^{2}-3/2\beta a_{32} b_{12}^{2}+3/4\beta a_{12} b_{11}^{2}\\&\quad +\,3/4\beta a_{12} b_{12}^{2}+3/2\beta a_{11} ^{2}a_{31} +3/4\beta a_{11} a_{12}^{2}-3/2\beta a_{11}^{2}a_{32}\\&\quad -\,3/4\beta a_{11}^{2}a_{12} -3/4\beta a_{11} b_{11}^{2}-3/4\beta a_{11} b_{12}^{2}+3/4\beta a_{31}^{3}\\&\quad -\,3/4\beta a_{32}^{3}-9a_{31} \gamma ^{2}+1/4\beta a_{11}^{3}-1/4\beta a_{12}^{3}=0, \end{aligned}$$

$$\begin{aligned}&-3\beta a_{11} a_{12} b_{51} +3\beta a_{11} a_{12} b_{52} -3\beta b_{11} b_{12} b_{51} \\&\quad +\,3\beta b_{11} b_{12} b_{52} +3/2\beta a_{11} a_{31} b_{31} +3/2\beta a_{11}^{2}b_{51} \\&\quad +\,9/4\beta b_{51} b_{52}^{2}-5\gamma \zeta _0 a_{51} +3/4\beta a_{51}^{2}b_{51} -3/4\beta a_{51}^{2}b_{52} \\&\quad +\,3/2\beta a_{51} a_{52} b_{52} -3/2\beta a_{12} a_{32} b_{32} \\&\quad -3/2\beta a_{51} a_{52} b_{51}-3/2\beta a_{12} a_{31}b_{31}+3/2\beta a_{12} a_{31} b_{32} \\&\quad +\,3/2\beta a_{12} a_{32} b_{31}-3/2\beta a_{11} a_{31} b_{32}-3/2\beta a_{11} a_{32} b_{31}\\&\quad +\,3/2\beta a_{11} a_{32} b_{32} -5\gamma \left( \zeta \right) a_{51}\\&\quad +\,3/2\beta a_{12}^{2}b_{51}+3/4\beta a_{52}^{2}b_{51} -3/4\beta a_{52}^{2}b_{52} -9/4\beta b_{51}^{2}b_{52} \\&\quad +\,3/2\beta b_{11}^{2}b_{51} -3/2\beta b_{11} ^{2}b_{52} +3/2\beta b_{12}^{2}b_{51} \\&\quad -\,3/2\beta a_{12}^{2}b_{52}-3/2\beta a_{11}^{2}b_{52} +3/2\beta b_{12} b_{31} b_{32} -3/4\beta a_{11}^{2}b_{32} \\&\quad +\,3/4\beta a_{11}^{2}b_{31} -3/2\beta a_{31} a_{32} b_{12} -3/4\beta b_{12}^{2}b_{31}\\&\quad +\,3/4\beta b_{11} ^{2}b_{32} -\,3\beta a_{31} a_{32} b_{51} -3/4\beta b_{11}^{2}b_{31} +3/4\beta a_{12}^{2}b_{31} \\&\quad -\,3/4\beta a_{12}^{2}b_{32} +3\beta a_{31} a_{32} b_{52} -3\beta b_{31} b_{32} b_{51} -3/2\beta b_{12}^{2}b_{52} \\&\quad -\,3/4\beta b_{12} b_{32}^{2}-3/4\beta b_{12} b_{31}^{2}+3/2\beta b_{32}^{2}b_{51}\\&\quad -\,3/2\beta b_{32}^{2}b_{52} +3/2\beta b_{31} ^{2}b_{51} -3/2\beta b_{31}^{2}b_{52} +3/4\beta b_{11} b_{32}^{2}\\&\quad +\,3/4\beta b_{11} b_{31}^{2}-3/2\beta a_{32}^{2}b_{52} +3/2\beta a_{31}^{2}b_{51} \\&\quad -\,3/4\beta a_{32}^{2}b_{11} +3/2\beta a_{32} ^{2}b_{51} +3/4\beta a_{32}^{2}b_{12} -3/2\beta a_{31}^{2}b_{52}\\&\quad -\,3/4\beta a_{31}^{2}b_{11} +3/4\beta a_{31}^{2}b_{12} +3/4\beta b_{12}^{2}b_{32} \\&\quad +\,3\beta b_{31} b_{32} b_{52} -3/2\beta a_{11} a_{12} b_{31} +3/2\beta a_{11} a_{12} b_{32} \\&\quad +\,3/2\beta a_{11} a_{31} b_{11} \\&\quad -\,3/2\beta a_{11} a_{31} b_{12} -3/2\beta a_{11} a_{32} b_{11} +3/2\beta a_{11} a_{32} b_{12} \\&\quad +\,3/2\beta b_{11} b_{12} b_{31} -3/2\beta b_{11} b_{12} b_{32} -3/2\beta b_{11} b_{31} b_{32} \\&\quad -\,3/2\beta a_{12} a_{31} b_{11} +3/2\beta a_{12} a_{31} b_{12} +3/2\beta a_{12} a_{32} b_{11} \\&\quad -\,3/2\beta a_{12} a_{32} b_{12} +3/2\beta a_{31} a_{32} b_{11} +b_{51} -3/4\beta b_{52}^{3} \\&\quad +\,3/4\beta b_{51}^{3}-25b_{51} \gamma ^{2}=0, \end{aligned}$$

$$\begin{aligned}&-b_{12} \gamma ^{2}-3/2\beta \lambda a_{12} a_{51} b_{31} +3/2\beta \lambda a_{12} a_{51} b_{32}\\&\quad +3/2\beta \lambda a_{12} a_{52} b_{31} -3/2\beta \lambda a_{12} a_{52} b_{32} +3\beta \lambda a_{31} a_{32} b_{11} \\&\quad -\,3\beta \lambda a_{31} a_{32} b_{12} -3/2\beta \lambda a_{31} a_{32} b_{51} +3/2\beta \lambda a_{31} a_{32} b_{52}\\&\quad +\,3/2\beta \lambda a_{31} a_{51} b_{11} -3/2\beta \lambda a_{31} a_{51} b_{12} -3/2\beta \lambda a_{31} a_{51} b_{31} \\&\quad +\,3/2\beta \lambda a_{31} a_{51} b_{32} -3/2\beta \lambda a_{31} a_{52} b_{11} +3/2\beta \lambda a_{31} a_{52} b_{12}\\&\quad +3/2\beta \lambda a_{31} a_{52} b_{31} -3/2\beta \lambda a_{31} a_{52} b_{32} -3/2\beta \lambda a_{32} a_{51} b_{11} \\&\quad +\,3/2\beta \lambda a_{32} a_{51} b_{12} -3/2\beta \lambda a_{32} a_{51} b_{32} +3/2\beta \lambda a_{32} a_{52} b_{11}\\&\quad -3/2\beta \lambda a_{32} a_{52} b_{12} -3/2\beta \lambda a_{32} a_{52} b_{31} +3/2\beta \lambda a_{32} a_{52} b_{32} \\&\quad +\,3\beta \lambda a_{51} a_{52} b_{11} -3\beta \lambda a_{51} a_{52} b_{12} -3/2\beta \lambda b_{11} b_{12} b_{31}\\&\quad +3/2\beta \lambda b_{11} b_{12} b_{32} +3\beta \lambda b_{11} b_{31} b_{32} +3/2\beta \lambda b_{11} b_{31} b_{51} \\&\quad -\,3/2\beta \lambda b_{11} b_{31} b_{52} -3/2\beta \lambda b_{11} b_{32} b_{51} +3/2\beta \lambda b_{11} b_{32} b_{52} \\&\quad +\,3\beta \lambda b_{11} b_{51} b_{52} -3\beta \lambda b_{12} b_{31} b_{32} -3/2\beta \lambda b_{12} b_{31} b_{51} \\&\quad +\,3/2\beta \lambda b_{12} b_{31} b_{52} +3/2\beta \lambda b_{12} b_{32} b_{51} -3/2\beta \lambda b_{12} b_{32} b_{52}\\&\quad -\,3\beta \lambda b_{12} b_{51} b_{52} +3/2\beta \lambda b_{31} b_{32} b_{51} -3/2\beta \lambda b_{31} b_{32} b_{52} \\&\quad -\,3/2\beta \lambda a_{11} a_{12} b_{32} +3/2\beta \lambda a_{32} a_{51} b_{31} +3/2\beta \lambda a_{11} a_{12} b_{11}\\&\quad -\,3/2\beta \lambda a_{11} a_{12} b_{12} +3/2\beta \lambda a_{11} a_{12} b_{31} +3/2\beta \lambda a_{11} a_{31} b_{11} \\&\quad -\,3/2\beta \lambda a_{11} a_{31} b_{12} -3/2\beta \lambda a_{11} a_{31} b_{51} +3/2\beta \lambda a_{11} a_{31} b_{52}\\&\quad -\,3/2\beta \lambda a_{11} a_{32} b_{11} +3/2\beta \lambda a_{11} a_{32} b_{12} +3/2\beta \lambda a_{11} a_{32} b_{51} \\&\quad -\,3/2\beta \lambda a_{11} a_{32} b_{52} +3/2\beta \lambda a_{11} a_{51} b_{31} -3/2\beta \lambda a_{11} a_{51} b_{32}\\&\quad -\,3/2\beta \lambda a_{11} a_{52} b_{31} +3/2\beta \lambda a_{11} a_{52} b_{32} -3/2\beta \lambda a_{12} a_{31} b_{11} \\&\quad +\,3/2\beta \lambda a_{12} a_{31} b_{12} +3/2\beta \lambda a_{12} a_{31} b_{51} -3/2\beta \lambda a_{12} a_{31} b_{52} \\&\quad +\,3/2\beta \lambda a_{12} a_{32} b_{11}-3/2\beta \lambda a_{12} a_{32} b_{12} -3/2\beta \lambda a_{12} a_{32} b_{51} \\&\quad +\,3/2\beta \lambda a_{12} a_{32} b_{52} -3/2\beta \lambda a_{52} ^{2}b_{11} +3/2\beta \lambda a_{52}^{2}b_{12} \\&\quad +\,9/4\beta \lambda b_{11}^{2}b_{12} +3/4\beta \lambda a_{12}^{2}b_{32} -3/2\beta \lambda a_{31}^{2}b_{11} \\&\quad +\,3/2\beta \lambda a_{31}^{2}b_{12} +3/4\beta \lambda a_{31} ^{2}b_{51} -3/4\beta \lambda a_{31}^{2}b_{52}\\&\quad -\,3/2\beta \lambda a_{51}^{2}b_{11} +3/2\beta \lambda a_{51}^{2}b_{12} +3/4\beta \lambda b_{12}^{2}b_{31} \\&\quad +\,3/2\beta \lambda b_{12} b_{31}^{2} -3/2\beta \lambda a_{32}^{2}b_{11} +3/2\beta \lambda a_{32} ^{2}b_{12}+3/4\beta \lambda a_{32}^{2}b_{51} \\&\quad -3/4\beta \lambda a_{32}^{2}b_{52} -3/2\beta \lambda b_{11} b_{31}^{2}+3/4\beta \lambda b_{32}^{2}b_{52} -3/2\beta \lambda b_{11} b_{32}^{2}\\&\quad +3/2\beta \lambda b_{12} b_{51}^{2}-9/4\beta \lambda b_{11} b_{12} ^{2}+3/2\beta \lambda b_{12} b_{32}^{2}\\&\quad -\,3/2\beta \lambda b_{11} b_{51}^{2}-3/2\beta \lambda b_{11} b_{52}^{2}-3/4\beta \lambda b_{12}^{2}b_{32}\\&\quad +\,3/4\beta \lambda b_{11}^{2}b_{31} \\&\quad -\,3/4\beta \lambda b_{11}^{2}b_{32} +3/2\beta \lambda b_{12} b_{52} ^{2}-3/4\beta \lambda b_{31}^{2}b_{51} \\&\quad +\,3/4\beta \lambda b_{31} ^{2}b_{52} -3/4\beta \lambda b_{32}^{2}b_{51} -3/4\beta \lambda a_{11}^{2}b_{11}\\&\quad +3/4\beta \lambda a_{11}^{2}b_{12} \\&\quad -\,3/4\beta \lambda a_{11}^{2}b_{31} +3/4\beta \lambda a_{11} ^{2}b_{32} -3/4\beta \lambda a_{12}^{2}b_{11}\\&\quad +3/4\beta \lambda a_{12}^{2}b_{12} -3/4\beta \lambda a_{12}^{2}b_{31} -3/4\beta \lambda b_{11}^{3}\\&\quad +\,3/4\beta \lambda b_{12}^{3} \\&\quad +\,\gamma \lambda \zeta a_{11} -\gamma \lambda \zeta a_{12} =0, \end{aligned}$$

$$\begin{aligned}&3/2\beta \lambda a_{12} a_{32}^{2}+3/2\beta \lambda a_{12} a_{51} ^{2}+3/2\beta \lambda a_{12} a_{52}^{2}\\&\quad +\,3/4\beta \lambda a_{12} b_{11}^{2}+3/4\beta \lambda a_{12} b_{12}^{2}-3/2\beta \lambda a_{11} b_{31}^{2} \\&\quad -\,3/4\beta \lambda a_{11} b_{12}^{2}-3/2\beta \lambda a_{11} a_{52} ^{2}-3/4\beta \lambda a_{11} b_{11}^{2}\\&\quad -\,3/2\beta \lambda a_{11} a_{32}^{2}-3/2\beta \lambda a_{11} a_{51}^{2}-9/4\beta \lambda a_{11} a_{12}^{2} \\&\quad -\,3/2\beta \lambda a_{11} a_{31}^{2}-3/4\beta \lambda a_{11} ^{2}a_{31} +3/4\beta \lambda a_{11}^{2}a_{32} \\&\quad -\,3/4\beta \lambda a_{31}^{2}a_{51} +3/4\beta \lambda a_{31}^{2}a_{52} +3/4\beta \lambda a_{31} b_{11}^{2} \\&\quad +\,9/4\beta \lambda a_{11}^{2}a_{12} -3/2\beta \lambda a_{11} b_{52} ^{2}-3/4\beta \lambda a_{12}^{2}a_{31} \\&\quad +\,3/2\beta \lambda a_{12} b_{31}^{2}+3/2\beta \lambda a_{12} b_{32}^{2}+3/2\beta \lambda a_{12} b_{51}^{2} \\&\quad +\,3/2\beta \lambda a_{12} b_{52}^{2}-3/2\beta \lambda a_{11} b_{32} ^{2}-3/2\beta \lambda a_{11} b_{51}^{2}-a_{12} \gamma ^{2}\\&\quad -\,3/4\beta \lambda a_{52} b_{32}^{2}+3/4\beta \lambda a_{51} b_{32}^{2} \\&\quad -\,3/4\beta \lambda a_{52} b_{31}^{2}+3/4\beta \lambda a_{31} b_{12} ^{2}-3/4\beta \lambda a_{32}^{2}a_{51} \\&\quad +\,3/4\beta \lambda a_{32} ^{2}a_{52} -3/4\beta \lambda a_{32} b_{11}^{2}-3/4\beta \lambda a_{32} b_{12}^{2} \\&\quad +\,3/4\beta \lambda a_{51} b_{31}^{2}+3/4\beta \lambda a_{12} ^{2}a_{32} +3/2\beta \lambda a_{12} a_{31}^{2}\\&\quad +\,3/2\beta \lambda a_{32} b_{31} b_{51} -3/2\beta \lambda a_{32} b_{31} b_{52} -3/2\beta \lambda a_{32} b_{32} b_{51} \\&\quad +\,3/2\beta \lambda a_{32} b_{32} b_{52} +3/2\beta \lambda a_{51} b_{11} b_{31} -3/2\beta \lambda a_{51} b_{11} b_{32}\\&\quad -\,3/2\beta \lambda a_{51} b_{12} b_{31} +3/2\beta \lambda a_{51} b_{12} b_{32} -3/2\beta \lambda a_{51} b_{31} b_{32} \\&\quad -\,3/2\beta \lambda a_{52} b_{11} b_{31} +3/2\beta \lambda a_{52} b_{11} b_{32} -\gamma \lambda \zeta b_{11} \\&\quad +\,\gamma \lambda \zeta b_{12} +3/4\beta \lambda a_{12}^{3}-3/4\beta \lambda a_{11} ^{3}+3/2\beta \lambda a_{52} b_{12} b_{31} \\&\quad -\,3/2\beta \lambda a_{52} b_{12} b_{32} +3/2\beta \lambda a_{52} b_{31} b_{32} +3/2\beta \lambda a_{11} a_{32} a_{51}\\&\quad -\,3/2\beta \lambda a_{11} a_{32} a_{52} +3\beta \lambda a_{11} a_{51} a_{52} +3/2\beta \lambda a_{11} b_{11} b_{12} \\&\quad -\,3/2\beta \lambda a_{11} b_{11} b_{31} +3/2\beta \lambda a_{11} b_{11} b_{32} +3/2\beta \lambda a_{11} b_{12} b_{31}\\&\quad -\,3/2\beta \lambda a_{11} b_{12} b_{32} +3\beta \lambda a_{11} b_{31} b_{32} -3/2\beta \lambda a_{11} b_{31} b_{51} \\&\quad +\,3/2\beta \lambda a_{11} b_{31} b_{52} +3/2\beta \lambda a_{11} b_{32} b_{51} -3/2\beta \lambda a_{11} b_{32} b_{52} \\&\quad +\,3\beta \lambda a_{11} b_{51} b_{52} -3\beta \lambda a_{12} a_{31} a_{32} +3/2\beta \lambda a_{12} a_{31} a_{51} \\&\quad -\,3/2\beta \lambda a_{12} a_{31} a_{52} -3/2\beta \lambda a_{12} a_{32} a_{51} +3/2\beta \lambda a_{12} a_{32} a_{52}\\&\quad -3\beta \lambda a_{12} a_{51} a_{52} -3/2\beta \lambda a_{12} b_{11} b_{12} +3/2\beta \lambda a_{12} b_{11} b_{31} \\&\quad -\,3/2\beta \lambda a_{12} b_{11} b_{32} -3/2\beta \lambda a_{12} b_{12} b_{31} +3/2\beta \lambda a_{12} b_{12} b_{32}\\&\quad +3/2\beta \lambda a_{12} b_{31} b_{51} -3/2\beta \lambda a_{12} b_{31} b_{52} -3/2\beta \lambda a_{12} b_{32} b_{51} \\&\quad +\,3/2\beta \lambda a_{12} b_{32} b_{52} -3\beta \lambda a_{12} b_{51} b_{52} +3/2\beta \lambda a_{31} a_{32} a_{51}\\&\quad -\,3/2\beta \lambda a_{31} a_{32} a_{52} -3/2\beta \lambda a_{31} b_{11} b_{12} -3/2\beta \lambda a_{31} b_{11} b_{51} \\&\quad +\,3/2\beta \lambda a_{31} b_{11} b_{52} +3/2\beta \lambda a_{31} b_{12} b_{51} -3/2\beta \lambda a_{31} b_{12} b_{52} \\&\quad -\,3/2\beta \lambda a_{31} b_{31} b_{51} +3/2\beta \lambda a_{31} b_{31} b_{52} +3/2\beta \lambda a_{31} b_{32} b_{51} \\&\quad -\,3/2\beta \lambda a_{31} b_{32} b_{52} +3/2\beta \lambda a_{32} b_{11} b_{12} +3/2\beta \lambda a_{32} b_{11} b_{51} \\&\quad -\,3/2\beta \lambda a_{32} b_{11} b_{52} -3/2\beta \lambda a_{32} b_{12} b_{51} +3/2\beta \lambda a_{32} b_{12} b_{52} \\&\quad -\,3\beta \lambda a_{12} b_{31} b_{32} +3/2\beta \lambda a_{11} a_{12} a_{31} -3/2\beta \lambda a_{11} a_{12} a_{32} \\&\quad +\,3\beta \lambda a_{11} a_{31} a_{32} -3/2\beta \lambda a_{11} a_{31} a_{51} +3/2\beta \lambda a_{11} a_{31} a_{52} =0, \end{aligned}$$

$$\begin{aligned}&-9b_{32} \gamma ^{2}-3/2\beta \lambda a_{12} a_{51} b_{31} +3/2\beta \lambda a_{12} a_{51} b_{32} \\&\quad +\,3/2\beta \lambda a_{12} a_{52} b_{31} -3/2\beta \lambda a_{12} a_{52} b_{32} -3/2\beta \lambda a_{31} a_{51} b_{11} \\&\quad +\,3/2\beta \lambda a_{31} a_{51} b_{12} +3/2\beta \lambda a_{31} a_{52} b_{11} -3/2\beta \lambda a_{31} a_{52} b_{12} \\&\quad +\,3/2\beta \lambda a_{32} a_{51} b_{11} -3/2\beta \lambda a_{32} a_{51} b_{12} -3/2\beta \lambda a_{32} a_{52} b_{11} \\&\quad +\,3/2\beta \lambda a_{32} a_{52} b_{12} +3\beta \lambda b_{11} b_{12} b_{31} -3\beta \lambda b_{11} b_{12} b_{32} \\&\quad -\,3/2\beta \lambda b_{11} b_{31} b_{51} +3/2\beta \lambda b_{11} b_{31} b_{52} +3/2\beta \lambda b_{11} b_{32} b_{51} \\&\quad -\,3/2\beta \lambda b_{11} b_{32} b_{52} +3/2\beta \lambda b_{12} b_{31} b_{51} -3/2\beta \lambda b_{12} b_{31} b_{52} \\&\quad -\,3/2\beta \lambda b_{12} b_{32} b_{51} +3/2\beta \lambda b_{12} b_{32} b_{52} -3\beta \lambda a_{11} a_{12} b_{32} \\&\quad +\,3/2\beta \lambda a_{11} a_{12} b_{11} -3/2\beta \lambda a_{11} a_{12} b_{12} +3\beta \lambda a_{11} a_{12} b_{31} \\&\quad -\,3/2\beta \lambda a_{11} a_{31} b_{51} +3/2\beta \lambda a_{11} a_{31} b_{52} +3/2\beta \lambda a_{11} a_{32} b_{51} \\&\quad -\,3/2\beta \lambda a_{11} a_{32} b_{52} +3/2\beta \lambda a_{11} a_{51} b_{31} -3/2\beta \lambda a_{11} a_{51} b_{32} \\&\quad -\,3/2\beta \lambda a_{11} a_{52} b_{31} +3/2\beta \lambda a_{11} a_{52} b_{32} +3/2\beta \lambda a_{12} a_{31} b_{51} \\&\quad -\,3/2\beta \lambda a_{12} a_{31} b_{52} -3/2\beta \lambda a_{12} a_{32} b_{51} +3/2\beta \lambda a_{12} a_{32} b_{52} \\&\quad +\,3/2\beta \lambda a_{12}^{2}b_{32} -3/4\beta \lambda b_{11}^{2}b_{12} -3/2\beta \lambda b_{11}^{2}b_{31} \\&\quad +\,3/2\beta \lambda b_{11}^{2}b_{32} +3/4\beta \lambda b_{11} b_{12} ^{2}-3/2\beta \lambda b_{12}^{2}b_{31} \\&\quad +\,3/2\beta \lambda b_{12} ^{2}b_{32} -9/4\beta \lambda b_{31} b_{32}^{2}-3/4\beta \lambda b_{11}^{2}b_{52} \\&\quad -\,3/2\beta \lambda b_{31} b_{51}^{2}-3/4\beta \lambda b_{12} ^{2}b_{52} +9/4\beta \lambda b_{31}^{2}b_{32} \\&\quad -\,3/2\beta \lambda a_{12}^{2}b_{31} +3/4\beta \lambda b_{11}^{2}b_{51} -3/2\beta \lambda a_{52}^{2}b_{31} \\&\quad +\,3/2\beta \lambda a_{52}^{2}b_{32} +3/4\beta \lambda b_{12} ^{2}b_{51} +3/4\beta \lambda a_{11}^{2}b_{52} \\&\quad -\,3/4\beta \lambda a_{12}^{2}b_{51} +3/4\beta \lambda a_{12}^{2}b_{52} -3/4\beta \lambda a_{11}^{2}b_{51} \\&\quad -\,3/4\beta \lambda a_{32}^{2}b_{31} -3/4\beta \lambda a_{31} ^{2}b_{31} +3/4\beta \lambda a_{31}^{2}b_{32} \\&\quad +\,3/2\beta \lambda a_{11}^{2}b_{32} -3/4\beta \lambda a_{12}^{2}b_{11} +3/4\beta \lambda a_{12}^{2}b_{12} \\&\quad -\,3/4\beta \lambda a_{11}^{2}b_{11} +3/4\beta \lambda a_{11} ^{2}b_{12} -3/2\beta \lambda a_{11}^{2}b_{31} \\&\quad +\,3/2\beta \lambda a_{51}^{2}b_{32} +3/4\beta \lambda a_{32}^{2}b_{32} -3/2\beta \lambda a_{51}^{2}b_{31} \\&\quad +\,1/4\beta \lambda b_{11}^{3}-1/4\beta \lambda b_{12}^{3}-3/4\beta \lambda b_{31}^{3}-3/2\beta \lambda b_{31} b_{52}^{2}\\&\quad +\,3/2\beta \lambda b_{32} b_{51}^{2}+3/2\beta \lambda b_{32} b_{52} ^{2}+3/2\beta \lambda b_{11} b_{12} b_{52} \\&\quad -\,3/2\beta \lambda b_{11} b_{12} b_{51} -3\beta \lambda a_{51} a_{52} b_{32} +3\beta \lambda a_{51} a_{52} b_{31} \\&\quad -\,3/2\beta \lambda a_{31} a_{32} b_{32} +3/2\beta \lambda a_{31} a_{32} b_{31} -3/2\beta \lambda a_{12} a_{52} b_{12} \\&\quad +\,3/2\beta \lambda a_{12} a_{52} b_{11} +3/2\beta \lambda a_{12} a_{51} b_{12} -3/2\beta \lambda a_{12} a_{51} b_{11} \\&\quad +\,3/2\beta \lambda a_{11} a_{52} b_{12} -3/2\beta \lambda a_{11} a_{52} b_{11} -3/2\beta \lambda a_{11} a_{51} b_{12} \\&\quad +\,3/2\beta \lambda a_{11} a_{51} b_{11} +3/2\beta \lambda a_{11} a_{12} b_{51} -3/2\beta \lambda a_{11} a_{12} b_{52} \\&\quad +\,3\beta \lambda b_{31} b_{51} b_{52} -3\beta \lambda b_{32} b_{51} b_{52} +3/4\beta \lambda b_{32}^{3}-3\gamma \lambda \zeta a_{32} \\&\quad +\,3\gamma \lambda \zeta a_{31} =0, \end{aligned}$$

$$\begin{aligned}&-3/4\beta \lambda a_{12} b_{11}^{2}-3/4\beta \lambda a_{12} b_{12} ^{2}+3/4\beta \lambda a_{11} b_{12}^{2}\\&\quad +\,3/4\beta \lambda a_{11} b_{11}^{2}-3/4\beta \lambda a_{11} a_{12}^{2}-3/2\beta \lambda a_{11}^{2}a_{31} \\&\quad +\,3/2\beta \lambda a_{11}^{2}a_{32} -3/2\beta \lambda a_{31} b_{11} ^{2}+3/4\beta \lambda a_{11}^{2}a_{12} \\&\quad -\,9a_{32} \gamma ^{2}-3/2\beta \lambda a_{31} b_{12}^{2}+3/2\beta \lambda a_{32} b_{11}^{2}+3/2\beta \lambda a_{32} b_{12}^{2} \\&\quad +\,3/2\beta \lambda a_{12}^{2}a_{32} -3/2\beta \lambda a_{12} ^{2}a_{31} +3/4\beta \lambda a_{51} b_{12}^{2}\\&\quad -\,3/4\beta \lambda a_{52} b_{11}^{2}-3/4\beta \lambda a_{52} b_{12}^{2}-3/4\beta \lambda a_{11}^{2}a_{51} \\&\quad +\,3/4\beta \lambda a_{11}^{2}a_{52} -3/4\beta \lambda a_{12} ^{2}a_{51} +3/4\beta \lambda a_{12}^{2}a_{52} \\&\quad -\,3/4\beta \lambda a_{31} b_{31}^{2}-3/2\beta \lambda a_{31} a_{52}^{2}-3/4\beta \lambda a_{31} b_{32}^{2} \\&\quad +\,9/4\beta \lambda a_{31}^{2}a_{32} -9/4\beta \lambda a_{31} a_{32} ^{2}-3/2\beta \lambda a_{31} a_{51}^{2}\\&\quad -\,3/2\beta \lambda a_{32} b_{31} b_{32} +3\beta \lambda a_{31} b_{51} b_{52} -3\beta \lambda a_{32} a_{51} a_{52} \\&\quad +\,3/2\beta \lambda a_{11} b_{11} b_{52} -3/4\beta \lambda a_{31} ^{3}+3/4\beta \lambda a_{32}^{3}\\&\quad -\,3\gamma \lambda \zeta b_{31} +3\gamma \lambda \zeta b_{32} -3\beta \lambda a_{32} b_{51} b_{52} -3/2\beta \lambda a_{11} a_{12} a_{52} \\&\quad -\,3/2\beta \lambda a_{11} b_{11} b_{51} +3/2\beta \lambda a_{11} b_{12} b_{51} -3/2\beta \lambda a_{51} b_{11} b_{12} \\&\quad +\,3/2\beta \lambda a_{11} a_{12} a_{51} +3/4\beta \lambda a_{51} b_{11} ^{2}+3/2\beta \lambda a_{32} a_{52}^{2} \\&\quad +\,3/4\beta \lambda a_{32} b_{31}^{2}+3/4\beta \lambda a_{32} b_{32} ^{2}+3/2\beta \lambda a_{32} b_{51}^{2}\\&\quad +\,3/2\beta \lambda a_{32} b_{52}^{2}+3/2\beta \lambda a_{31} b_{31} b_{32} -3/2\beta \lambda a_{31} b_{51}^{2} \\&\quad -\,3/2\beta \lambda a_{31} b_{52}^{2}+3/2\beta \lambda a_{32} a_{51} ^{2}+3/2\beta \lambda a_{52} b_{11} b_{12} \\&\quad -\,3/2\beta \lambda a_{11} b_{12} b_{52} +3/2\beta \lambda a_{12} b_{11} b_{51} -3/2\beta \lambda a_{12} b_{11} b_{52} \\&\quad -\,3/2\beta \lambda a_{12} b_{12} b_{51} +3/2\beta \lambda a_{12} b_{12} b_{52} +3\beta \lambda a_{31} a_{51} a_{52} \\&\quad -\,1/4\beta \lambda a_{11}^{3}+1/4\beta \lambda a_{12}^{3}-3/2\beta \lambda a_{51} b_{11} b_{31} \\&\quad +\,3/2\beta \lambda a_{51} b_{11} b_{32} +3/2\beta \lambda a_{51} b_{12} b_{31} -3/2\beta \lambda a_{51} b_{12} b_{32} \\&\quad +\,3/2\beta \lambda a_{52} b_{11} b_{31} -3/2\beta \lambda a_{52} b_{11} b_{32} -3/2\beta \lambda a_{52} b_{12} b_{31} \\&\quad +\,3/2\beta \lambda a_{52} b_{12} b_{32} +3/2\beta \lambda a_{11} a_{32} a_{51} -3/2\beta \lambda a_{11} a_{32} a_{52} \\&\quad -\,3/2\beta \lambda a_{11} b_{11} b_{12} -3/2\beta \lambda a_{11} b_{31} b_{51} +3/2\beta \lambda a_{11} b_{31} b_{52} \\&\quad +\,3/2\beta \lambda a_{11} b_{32} b_{51} -3/2\beta \lambda a_{11} b_{32} b_{52} +3/2\beta \lambda a_{12} a_{31} a_{51} \\&\quad -\,3/2\beta \lambda a_{12} a_{31} a_{52} -3/2\beta \lambda a_{12} a_{32} a_{51} +3/2\beta \lambda a_{12} a_{32} a_{52} \\&\quad +\,3/2\beta \lambda a_{12} b_{11} b_{12} +3/2\beta \lambda a_{12} b_{31} b_{51} -3/2\beta \lambda a_{12} b_{31} b_{52} \\&\quad -\,3/2\beta \lambda a_{12} b_{32} b_{51} +3/2\beta \lambda a_{12} b_{32} b_{52} +3\beta \lambda a_{31} b_{11} b_{12} \\&\quad +\,3/2\beta \lambda a_{31} b_{11} b_{51} -3/2\beta \lambda a_{31} b_{11} b_{52} -3/2\beta \lambda a_{31} b_{12} b_{51} \\&\quad +\,3/2\beta \lambda a_{31} b_{12} b_{52} -3\beta \lambda a_{32} b_{11} b_{12} -3/2\beta \lambda a_{32} b_{11} b_{51} \\&\quad +\,3/2\beta \lambda a_{32} b_{11} b_{52} +3/2\beta \lambda a_{32} b_{12} b_{51} -3/2\beta \lambda a_{32} b_{12} b_{52} \\&\quad +\,3\beta \lambda a_{11} a_{12} a_{31} -3\beta \lambda a_{11} a_{12} a_{32} -3/2\beta \lambda a_{11} a_{31} a_{51} \\&\quad +\,3/2\beta \lambda a_{11} a_{31} a_{52} =0, \end{aligned}$$

$$\begin{aligned}&-25b_{52} \gamma ^{2}-3/2\beta \lambda a_{31} a_{32} b_{11} +3/2\beta \lambda a_{31} a_{32} b_{12} \\&\quad +\,3\beta \lambda a_{31} a_{32} b_{51} -3\beta \lambda a_{31} a_{32} b_{52} -3/2\beta \lambda b_{11} b_{12} b_{31} \\&\quad +\,3/2\beta \lambda b_{11} b_{12} b_{32} +3/2\beta \lambda b_{11} b_{31} b_{32} -3/2\beta \lambda b_{12} b_{31} b_{32} \\&\quad +\,3\beta \lambda b_{31} b_{32} b_{51} -3\beta \lambda b_{31} b_{32} b_{52} -3/2\beta \lambda a_{11} a_{12} b_{32} \\&\quad +\,3/2\beta \lambda a_{11} a_{12} b_{31} -3/2\beta \lambda a_{11} a_{31} b_{11} +3/2\beta \lambda a_{11} a_{31} b_{12} \\&\quad +\,3/2\beta \lambda a_{11} a_{32} b_{11} -3/2\beta \lambda a_{11} a_{32} b_{12} \\&\quad +\,3/2\beta \lambda a_{12} a_{31} b_{11} -3/2\beta \lambda a_{12} a_{31} b_{12} -3/2\beta \lambda a_{12} a_{32} b_{11} \\&\quad +\,3/2\beta \lambda a_{12} a_{32} b_{12} -3/2\beta \lambda a_{11} a_{31} b_{31} \\&\quad +\,3/2\beta \lambda a_{11} a_{31} b_{32} -3/4\beta \lambda b_{11} b_{32}^{2}-3/4\beta \lambda b_{11} b_{31}^{2}\\&\quad +\,3/2\beta \lambda b_{32}^{2}b_{52} +3/4\beta \lambda a_{12}^{2}b_{32} -3/2\beta \lambda a_{32}^{2}b_{51} \\&\quad +\,3/2\beta \lambda a_{32}^{2}b_{52} -3/4\beta \lambda a_{31} ^{2}b_{12} -3/2\beta \lambda a_{31}^{2}b_{51} \\&\quad +\,3/2\beta \lambda a_{31}^{2}b_{52} +3/4\beta \lambda a_{32}^{2}b_{11} -3/4\beta \lambda a_{32}^{2}b_{12} \\&\quad +\,3/4\beta \lambda a_{31}^{2}b_{11} +3/4\beta \lambda b_{12} b_{31} ^{2}+3/4\beta \lambda b_{12} b_{32}^{2}\\&\quad +\,3/4\beta \lambda b_{12} ^{2}b_{31} -3/2\beta \lambda a_{51} a_{52} b_{52} +3/2\beta \lambda a_{51} a_{52} b_{51} \\&\quad -\,3/2\beta \lambda a_{12} a_{32} b_{31} +3/2\beta \lambda a_{12} a_{32} b_{32} +3/2\beta \lambda a_{12} a_{31} b_{31} \\&\quad -\,3/2\beta \lambda a_{12} a_{31} b_{32} +3/2\beta \lambda a_{11} a_{32} b_{31} \\&\quad -\,3/2\beta \lambda a_{11} a_{32} b_{32} -3/4\beta \lambda b_{12} ^{2}b_{32} +3/4\beta \lambda b_{11}^{2}b_{31} \\&\quad -\,3/4\beta \lambda b_{11}^{2}b_{32} -3/4\beta \lambda a_{51}^{2}b_{51} +3/4\beta \lambda a_{51}^{2}b_{52} \\&\quad -\,3/4\beta \lambda a_{52}^{2}b_{51} +3/4\beta \lambda a_{52} ^{2}b_{52} +3/2\beta \lambda b_{11}^{2}b_{52}\\&\quad +\,3/2\beta \lambda b_{12}^{2}b_{52} -3/4\beta \lambda a_{12}^{2}b_{31} +9/4\beta \lambda b_{51}^{2}b_{52} \\&\quad -\,9/4\beta \lambda b_{51} b_{52}^{2}-5\gamma \lambda \zeta a_{52} -3/2\beta \lambda b_{11}^{2}b_{51} \\&\quad -\,3\beta \lambda b_{11} b_{12} b_{52} +3\beta \lambda b_{11} b_{12} b_{51} +3\beta \lambda a_{11} a_{12} b_{51} \\&\quad -\,3\beta \lambda a_{11} a_{12} b_{52} \\&\quad -\,3/2\beta \lambda b_{12}^{2}b_{51} +3/2\beta \lambda a_{11} ^{2}b_{52} -3/2\beta \lambda a_{12}^{2}b_{51} \\&\quad +\,3/2\beta \lambda a_{12}^{2}b_{52} -3/2\beta \lambda a_{11}^{2}b_{51} +3/4\beta \lambda a_{11}^{2}b_{32} \\&\quad -\,3/4\beta \lambda a_{11}^{2}b_{31} -3/2\beta \lambda b_{31} ^{2}b_{51} +3/2\beta \lambda b_{31}^{2}b_{52} \\&\quad -\,3/2\beta \lambda b_{32}^{2}b_{51} +5\gamma \lambda \zeta a_{51} -3/4\beta \lambda b_{51}^{3}+3/4\beta \lambda b_{52}^{3}=0, \end{aligned}$$

$$\begin{aligned}&-3/4\beta \lambda a_{11}^{2}a_{31} +3/4\beta \lambda a_{11} ^{2}a_{32} +3/4\beta \lambda a_{31} b_{11}^{2}\nonumber \\&\quad +\,3/2\beta \lambda a_{52} b_{32}^{2}-3/2\beta \lambda a_{51} b_{32}^{2}+3/2\beta \lambda a_{52} b_{31}^{2} \nonumber \\&\quad +\,3/4\beta \lambda a_{31} b_{12}^{2}-3/2\beta \lambda a_{32} ^{2}a_{51} +3/2\beta \lambda a_{32}^{2}a_{52} \nonumber \\&\quad -\,3/4\beta \lambda a_{32} b_{11}^{2}-3/4\beta \lambda a_{32} b_{12}^{2}-3/2\beta \lambda a_{51} b_{31}^{2} \nonumber \\&\quad +\,3/4\beta \lambda a_{12}^{2}a_{32} +3/4\beta \lambda a_{12} a_{31} ^{2}-3/4\beta \lambda a_{12}^{2}a_{31} \nonumber \\&\quad -\,3/2\beta \lambda a_{51} b_{12}^{2}+3/2\beta \lambda a_{52} b_{11}^{2}+3/2\beta \lambda a_{52} b_{12}^{2} \nonumber \\&\quad +\,3/4\beta \lambda a_{11} b_{32}^{2}-3/4\beta \lambda a_{11} a_{32} ^{2}+3/4\beta \lambda a_{11} b_{31}^{2}\nonumber \\&\quad -\,25a_{52} \gamma ^{2}+3/4\beta \lambda a_{12} a_{32}^{2}-3/4\beta \lambda a_{12} b_{31}^{2} \nonumber \\&\quad -\,3/4\beta \lambda a_{12} b_{32}^{2}-3/2\beta \lambda a_{31} ^{2}a_{51} +3/2\beta \lambda a_{31}^{2}a_{52} \nonumber \\&\quad -\,3/4\beta \lambda a_{11} a_{31}^{2}-3/2\beta \lambda a_{52} b_{51} b_{52} -3/2\beta \lambda a_{32} b_{12} b_{31} \nonumber \\&\quad +\,3/2\beta \lambda a_{32} b_{12} b_{32} +3/2\beta \lambda a_{51} b_{51} b_{52} +3/2\beta \lambda a_{31} b_{12} b_{31} \nonumber \\&\quad -\,3/2\beta \lambda a_{31} b_{11} b_{31} -3/2\beta \lambda a_{31} b_{12} b_{32} +3/2\beta \lambda a_{32} b_{11} b_{31} \nonumber \\&\quad -\,3/2\beta \lambda a_{11}^{2}a_{51} +3/2\beta \lambda a_{11} ^{2}a_{52} -3/2\beta \lambda a_{12}^{2}a_{51} \nonumber \\&\quad +\,3/2\beta \lambda a_{12}^{2}a_{52} -5\gamma \lambda \zeta b_{51} +5\gamma \lambda \zeta b_{52} +9/4\beta \lambda a_{51}^{2}a_{52} \nonumber \\&\quad -\,9/4\beta \lambda a_{51} a_{52}^{2}+3/4\beta \lambda a_{52} ^{3}-3/4\beta \lambda a_{51}^{3}\nonumber \\&\quad -\,3/4\beta \lambda a_{51} b_{51} ^{2}-3/4\beta \lambda a_{51} b_{52}^{2}+3/4\beta \lambda a_{52} b_{51}^{2} \nonumber \\&\quad -\,3/2\beta \lambda a_{32} b_{11} b_{32} +3/2\beta \lambda a_{31} b_{11} b_{32} +3/4\beta \lambda a_{52} b_{52}^{2}\nonumber \\&\quad -\,3/2\beta \lambda a_{51} b_{11}^{2}+3\beta \lambda a_{51} b_{11} b_{12} -3\beta \lambda a_{52} b_{11} b_{12} \nonumber \\&\quad +\,3\beta \lambda a_{11} a_{12} a_{51} -3\beta \lambda a_{11} a_{12} a_{52} +3\beta \lambda a_{51} b_{31} b_{32} \nonumber \\&\quad -\,3\beta \lambda a_{52} b_{31} b_{32} +3/2\beta \lambda a_{11} b_{11} b_{31} -3/2\beta \lambda a_{11} b_{11} b_{32} \nonumber \\&\quad -\,3/2\beta \lambda a_{11} b_{12} b_{31} +3/2\beta \lambda a_{11} b_{12} b_{32} -3/2\beta \lambda a_{11} b_{31} b_{32} \nonumber \\&\quad -\,3/2\beta \lambda a_{12} a_{31} a_{32} -3/2\beta \lambda a_{12} b_{11} b_{31} +3/2\beta \lambda a_{12} b_{11} b_{32} \nonumber \\&\quad +\,3/2\beta \lambda a_{12} b_{12} b_{31} -3/2\beta \lambda a_{12} b_{12} b_{32} +3\beta \lambda a_{31} a_{32} a_{51} \nonumber \\&\quad -\,3\beta \lambda a_{31} a_{32} a_{52} -3/2\beta \lambda a_{31} b_{11} b_{12} +3/2\beta \lambda a_{32} b_{11} b_{12} \nonumber \\&\quad +\,3/2\beta \lambda a_{12} b_{31} b_{32} +3/2\beta \lambda a_{11} a_{12} a_{31} -3/2\beta \lambda a_{11} a_{12} a_{32}\nonumber \\&\quad +\,3/2\beta \lambda a_{11} a_{31} a_{32} =0. \end{aligned}$$

(A1)

Appendix B

1.1 The nonlinear differential-algebraic equations of the harmonic balance up to order 3

$$\begin{aligned}&-f-3/2b_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta +3/2b_{11} \left( \tau \right) b_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \\&\quad -\,3a_{31} \left( \tau \right) a_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \\&\quad -\,3/2b_{31} \left( \tau \right) a_{12} \left( \tau \right) b_{12} \left( \tau \right) \beta -3b_{31} \left( \tau \right) a_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \\&\quad +\,3/2a_{12} \left( \tau \right) b_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \\&\quad -\,3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) b_{31} \left( \tau \right) \beta +3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) b_{12} \left( \tau \right) \beta \\&\quad +\,3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) b_{32} \left( \tau \right) \beta \\&\quad +\,3/2a_{11} \left( \tau \right) a_{31} \left( \tau \right) a_{12} \left( \tau \right) \beta +3a_{11} \left( \tau \right) a_{31} \left( \tau \right) a_{32} \left( \tau \right) \beta \\&\quad +\,3/2a_{11} \left( \tau \right) b_{31} \left( \tau \right) b_{12} \left( \tau \right) \beta \\&\quad +\,3a_{11} \left( \tau \right) b_{31} \left( \tau \right) b_{32} \left( \tau \right) \beta -3/2a_{11} \left( \tau \right) a_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \\&\quad -\,3/2a_{11} \left( \tau \right) b_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \\&\quad -\,3/2b_{11} \left( \tau \right) a_{31} \left( \tau \right) b_{12} \left( \tau \right) \beta +3/2b_{11} \left( \tau \right) b_{31} \left( \tau \right) a_{12} \left( \tau \right) \beta \\&\quad -\,3/2b_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{12} \left( \tau \right) \beta \\&\quad -\,2\left( {\frac{\hbox {d}}{\hbox {d}\tau }b_{11} \left( \tau \right) } \right) \gamma -3/4\left( {a_{11} \left( \tau \right) } \right) ^{3}\beta -\left( {\frac{\hbox {d}}{\hbox {d}\tau }a_{11} \left( \tau \right) } \right) \zeta _0 \\&\quad +\,a_{11} \left( \tau \right) \gamma ^{2}+3/4\left( {a_{12} \left( \tau \right) } \right) ^{3}\beta \\&\quad -\,\left( {\frac{\hbox {d}}{\hbox {d}\tau }a_{11} \left( \tau \right) } \right) \left( \zeta \right) +3/2a_{12} \left( \tau \right) \left( {a_{32} \left( \tau \right) } \right) ^{2}\beta \\&\quad +\,3/2a_{12} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta -3/4\left( {b_{12} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \\&\quad -\,\gamma b_{11} \left( \tau \right) \left( \zeta \right) -\gamma b_{11} \left( \tau \right) \zeta _0 -3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}a_{31} \left( \tau \right) \beta \\&\quad -\,3/2a_{11} \left( \tau \right) \left( {a_{32} \left( \tau \right) } \right) ^{2}\beta -3/4a_{11} \left( \tau \right) \left( {b_{11} \left( \tau \right) } \right) ^{2}\beta \\&\quad +\,3/2\left( {a_{31} \left( \tau \right) } \right) ^{2}a_{12} \left( \tau \right) \beta +3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}a_{12} \left( \tau \right) \beta \\&\quad +\,9/4\left( {a_{11} \left( \tau \right) } \right) ^{2}a_{12} \left( \tau \right) \beta -3/2a_{11} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta \\&\quad +\,3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}a_{31} \left( \tau \right) \beta -3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \\&\quad -\,3/2a_{11} \left( \tau \right) \left( {a_{31} \left( \tau \right) } \right) ^{2}\beta -3/2a_{11} \left( \tau \right) \left( {b_{31} \left( \tau \right) } \right) ^{2}\beta \\&\quad -\,9/4a_{11} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta -3/4a_{11} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta \\&\quad +\,3/4a_{31} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta +3/2\left( {b_{31} \left( \tau \right) } \right) ^{2}a_{12} \left( \tau \right) \beta \\&\quad +\,3/4\left( {a_{12} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta +3/4a_{12} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta \\&\quad -\,3/4a_{31} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta +3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \\&\quad -\,a_{11} \left( \tau \right) -\frac{\hbox {d}^{2}}{\hbox {d}\tau ^{2}}a_{11} \left( \tau \right) =0, \end{aligned}$$

$$\begin{aligned}&-3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{11} \left( \tau \right) \beta -3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{31} \left( \tau \right) \beta \\&\quad +\,3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta +3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \\&\quad +\,3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}b_{31} \left( \tau \right) \beta +9/4\left( {b_{11} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta \\&\quad -\,3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta -3/2b_{11} \left( \tau \right) \left( {a_{31} \left( \tau \right) } \right) ^{2}\beta \\&\quad -\,3/2b_{11} \left( \tau \right) \left( {b_{31} \left( \tau \right) } \right) ^{2}\beta -3/4b_{11} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta \\&\quad -\,9/4b_{11} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta -3/2b_{11} \left( \tau \right) \left( {a_{32} \left( \tau \right) } \right) ^{2}\beta \\&\quad -\,3/2b_{11} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta +3/2\left( {a_{31} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta \\&\quad +\,3/2\left( {b_{31} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta -3/4b_{31} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta \\&\quad +\,3/4b_{31} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta +3/4\left( {a_{12} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta \\&\quad +\,3/4\left( {a_{12} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta -3/4\left( {b_{12} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \\&\quad +\,3/2b_{12} \left( \tau \right) \left( {a_{32} \left( \tau \right) } \right) ^{2}\beta +3/2b_{12} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta \\&\quad +\,\gamma a_{11} \left( \tau \right) \left( \zeta \right) +\gamma a_{11} \left( \tau \right) \zeta _0 +3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) a_{31} \left( \tau \right) \beta \\&\quad +\,3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) a_{12} \left( \tau \right) \beta -3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) a_{32} \left( \tau \right) \beta \\&\quad -\,3/2a_{11} \left( \tau \right) a_{31} \left( \tau \right) b_{12} \left( \tau \right) \beta \\&\quad +\,3/2a_{11} \left( \tau \right) b_{31} \left( \tau \right) a_{12} \left( \tau \right) \beta -3/2a_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{12} \left( \tau \right) \beta \\&\quad -\,3/2a_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta +3/2a_{11} \left( \tau \right) b_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \\&\quad -\,3/2b_{11} \left( \tau \right) a_{31} \left( \tau \right) a_{12} \left( \tau \right) \beta +3b_{11} \left( \tau \right) a_{31} \left( \tau \right) a_{32} \left( \tau \right) \beta \\&\quad -\,3/2b_{11} \left( \tau \right) b_{31} \left( \tau \right) b_{12} \left( \tau \right) \beta +3b_{11} \left( \tau \right) b_{31} \left( \tau \right) b_{32} \left( \tau \right) \beta \\&\quad +3/2b_{11} \left( \tau \right) a_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta +3/2b_{11} \left( \tau \right) b_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \\&\quad +\,3/2a_{31} \left( \tau \right) a_{12} \left( \tau \right) b_{12} \left( \tau \right) \beta -3a_{31} \left( \tau \right) b_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \\&\quad -\,3b_{31} \left( \tau \right) b_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta -3/2a_{12} \left( \tau \right) b_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \\&\quad +\,b_{11} \left( \tau \right) \gamma ^{2}-3/4\left( {b_{11} \left( \tau \right) } \right) ^{3}\beta -\left( {\frac{\hbox {d}}{\hbox {d}\tau }b_{11} \left( \tau \right) } \right) \zeta _0 \\&\quad +\,3/4\left( {b_{12} \left( \tau \right) } \right) ^{3}\beta -\left( {\frac{\hbox {d}}{\hbox {d}\tau }b_{11} \left( \tau \right) } \right) \left( \zeta \right) +2\left( {\frac{\hbox {d}}{\hbox {d}\tau }a_{11} \left( \tau \right) } \right) \gamma \\&\quad -\,b_{11} \left( \tau \right) -\frac{\hbox {d}^{2}}{\hbox {d}\tau ^{2}}b_{11} \left( \tau \right) =0, \end{aligned}$$

$$\begin{aligned}&-9/4a_{31} \left( \tau \right) \left( {a_{32} \left( \tau \right) } \right) ^{2}\beta -3/4a_{31} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta \\&\quad +\,3/4\left( {b_{31} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta +9/4\left( {a_{31} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \\&\quad -\,3/4a_{31} \left( \tau \right) \left( {b_{31} \left( \tau \right) } \right) ^{2}\beta -3\gamma b_{31} \left( \tau \right) \left( \zeta \right) \\&\quad -\,3\gamma b_{31} \left( \tau \right) \zeta _0 +3/4a_{32} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta \\&\quad -\,3b_{11} \left( \tau \right) b_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \\&\quad -\,3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) b_{12} \left( \tau \right) \beta +3a_{11} \left( \tau \right) a_{31} \left( \tau \right) a_{12} \left( \tau \right) \beta \\&\quad -\,3a_{11} \left( \tau \right) a_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta +3b_{11} \left( \tau \right) a_{31} \left( \tau \right) b_{12} \left( \tau \right) \beta \\&\quad +\,3/2b_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{12} \left( \tau \right) \beta -\left( {\frac{\hbox {d}}{\hbox {d}\tau }a_{31} \left( \tau \right) } \right) \left( \zeta \right) \\&\quad -\,6\left( {\frac{\hbox {d}}{\hbox {d}\tau }b_{31} \left( \tau \right) } \right) \gamma -\left( {\frac{\hbox {d}}{\hbox {d}\tau }a_{31} \left( \tau \right) } \right) \zeta _0 +3/4\left( {a_{32} \left( \tau \right) } \right) ^{3}\beta \\&\quad +\,9a_{31} \left( \tau \right) \gamma ^{2}-3/4\left( {a_{31} \left( \tau \right) } \right) ^{3}\beta -1/4\left( {a_{11} \left( \tau \right) } \right) ^{3}\beta \\&\quad +\,1/4\left( {a_{12} \left( \tau \right) } \right) ^{3}\beta +3/2\left( {b_{12} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \\&\quad -\,3/2\left( {a_{11} \left( \tau \right) } \right) ^{2}a_{31} \left( \tau \right) \beta +3/4a_{11} \left( \tau \right) \left( {b_{11} \left( \tau \right) } \right) ^{2}\beta \\&\quad -\,3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}a_{12} \left( \tau \right) \beta +3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}a_{12} \left( \tau \right) \beta \\&\quad -\,3/2\left( {b_{11} \left( \tau \right) } \right) ^{2}a_{31} \left( \tau \right) \beta +3/2\left( {b_{11} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \\&\quad -\,3/4a_{11} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta +3/4a_{11} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta \\&\quad -\,3/2a_{31} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta +3/2\left( {a_{12} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \\&\quad -\,3/4a_{12} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta -3/2a_{31} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta \\&\quad +\,3/2\left( {a_{11} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta -a_{31} \left( \tau \right) \\&\quad +\,3/2a_{31} \left( \tau \right) b_{31} \left( \tau \right) b_{32} \left( \tau \right) \beta \\&\quad -\,3/2b_{31} \left( \tau \right) a_{32} \left( \tau \right) b_{32} \left( \tau \right) \beta -\frac{\hbox {d}^{2}}{\hbox {d}\tau ^{2}}a_{31} \left( \tau \right) =0, \end{aligned}$$

$$\begin{aligned}&-3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{11} \left( \tau \right) \beta -3/2\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{31} \left( \tau \right) \beta \\&\quad +\,3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta +3/2\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \\&\quad -\,3/2\left( {b_{11} \left( \tau \right) } \right) ^{2}b_{31} \left( \tau \right) \beta -3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta \\&\quad +\,3/2\left( {b_{11} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta -3/4b_{11} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta \\&\quad +\,3/4b_{11} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta -3/2b_{31} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta \\&\quad -\,3/2b_{31} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta +3/4\left( {a_{12} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta \\&\quad +\,3/2\left( {a_{12} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta +3/2\left( {b_{12} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \\&\quad +\,3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) a_{12} \left( \tau \right) \beta +3a_{11} \left( \tau \right) b_{31} \left( \tau \right) a_{12} \left( \tau \right) \beta \\&\quad -\,3/2a_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{12} \left( \tau \right) \beta -3a_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \\&\quad +\,3b_{11} \left( \tau \right) b_{31} \left( \tau \right) b_{12} \left( \tau \right) \beta -3b_{11} \left( \tau \right) b_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \\&\quad -\,3/4b_{31} \left( \tau \right) \left( {a_{32} \left( \tau \right) } \right) ^{2}\beta -9/4b_{31} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta \\&\quad +\,3/4\left( {a_{32} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta +3\gamma a_{31} \left( \tau \right) \left( \zeta \right) +3\gamma a_{31} \left( \tau \right) \zeta _0 \\&\quad -\,3/4\left( {a_{31} \left( \tau \right) } \right) ^{2}b_{31} \left( \tau \right) \beta +3/4\left( {a_{31} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \\&\quad +\,9/4\left( {b_{31} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta +9b_{31} \left( \tau \right) \gamma ^{2}-\left( {\frac{\hbox {d}}{\hbox {d}\tau }b_{31} \left( \tau \right) } \right) \zeta _0 \\&\quad -\,\left( {\frac{\hbox {d}}{\hbox {d}\tau }b_{31} \left( \tau \right) } \right) \left( \zeta \right) +6\left( {\frac{\hbox {d}}{\hbox {d}\tau }a_{31} \left( \tau \right) } \right) \gamma \\&\quad -\,3/4\left( {b_{31} \left( \tau \right) } \right) ^{3}\beta +3/4\left( {b_{32} \left( \tau \right) } \right) ^{3}\beta +1/4\left( {b_{11} \left( \tau \right) } \right) ^{3}\beta \\&\quad -\,1/4\left( {b_{12} \left( \tau \right) } \right) ^{3}\beta \\&\quad -\,b_{31} \left( \tau \right) +3/2a_{31} \left( \tau \right) b_{31} \left( \tau \right) a_{32} \left( \tau \right) \beta \\&\quad -\,3/2a_{31} \left( \tau \right) a_{32} \left( \tau \right) b_{32} \left( \tau \right) \beta -\frac{\hbox {d}^{2}}{\hbox {d}\tau ^{2}}b_{31} \left( \tau \right) =0, \end{aligned}$$

$$\begin{aligned}&-\gamma b_{12} \left( \tau \right) \lambda \zeta +3/4\left( {a_{11} \left( \tau \right) } \right) ^{3}\beta \lambda -3/4\left( {a_{12} \left( \tau \right) } \right) ^{3}\beta \lambda \\&\quad +\,\gamma b_{11} \left( \tau \right) \lambda \zeta -2\left( {\frac{\hbox {d}}{\hbox {d}\tau }b_{12} \left( \tau \right) } \right) \gamma +a_{12} \left( \tau \right) \gamma ^{2} \\&\quad +\,\left( {\frac{\hbox {d}}{\hbox {d}\tau }a_{11} \left( \tau \right) } \right) \lambda \zeta -\left( {\frac{\hbox {d}}{\hbox {d}\tau }a_{12} \left( \tau \right) } \right) \lambda \zeta \\&\quad +3/2b_{11} \left( \tau \right) a_{31} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda -3/2b_{11} \left( \tau \right) b_{31} \left( \tau \right) a_{12} \left( \tau \right) \beta \lambda \\&\quad +\,3/2b_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda +3/2b_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda \\&\quad -\,3/2b_{11} \left( \tau \right) b_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \lambda \\&\quad +\,3a_{31} \left( \tau \right) a_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \lambda +3/2b_{31} \left( \tau \right) a_{12} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda \\&\quad +3b_{31} \left( \tau \right) a_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda \\&\quad -\,3/2a_{12} \left( \tau \right) b_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda +3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) b_{31} \left( \tau \right) \beta \lambda \\&\quad -\,3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda \\&\quad -\,3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda -3/2a_{11} \left( \tau \right) a_{31} \left( \tau \right) a_{12} \left( \tau \right) \beta \lambda \\&\quad -\,3a_{11} \left( \tau \right) a_{31} \left( \tau \right) a_{32} \left( \tau \right) \beta \lambda -3/2a_{11} \left( \tau \right) b_{31} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda \\&\quad -\,3a_{11} \left( \tau \right) b_{31} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda +3/2a_{11} \left( \tau \right) a_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \lambda \\&\quad +\,3/2a_{11} \left( \tau \right) b_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda +3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}a_{31} \left( \tau \right) \beta \lambda \\&\quad -\,9/4\left( {a_{11} \left( \tau \right) } \right) ^{2}a_{12} \left( \tau \right) \beta \lambda \\&\quad -\,3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \lambda +3/4a_{11} \left( \tau \right) \left( {b_{11} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad +\,3/2a_{11} \left( \tau \right) \left( {a_{31} \left( \tau \right) } \right) ^{2}\beta \lambda +3/2a_{11} \left( \tau \right) \left( {b_{31} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad +\,9/4a_{11} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta \lambda +3/4a_{11} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad +\,3/2a_{11} \left( \tau \right) \left( {a_{32} \left( \tau \right) } \right) ^{2}\beta \lambda +3/2a_{11} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad -\,3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}a_{31} \left( \tau \right) \beta \lambda -3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}a_{12} \left( \tau \right) \beta \lambda \\&\quad +\,3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \lambda -3/2\left( {a_{31} \left( \tau \right) } \right) ^{2}a_{12} \left( \tau \right) \beta \lambda \\&\quad +\,3/4a_{31} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta \lambda -3/4a_{31} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad -\,3/2\left( {b_{31} \left( \tau \right) } \right) ^{2}a_{12} \left( \tau \right) \beta \lambda -3/4\left( {a_{12} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \lambda \\&\quad -\,3/4a_{12} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta \lambda -3/2a_{12} \left( \tau \right) \left( {a_{32} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad -\,3/2a_{12} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta \lambda +3/4\left( {b_{12} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \lambda \\&\quad -\,\frac{\hbox {d}^{2}}{\hbox {d}\tau ^{2}}a_{12} \left( \tau \right) =0, \end{aligned}$$

$$\begin{aligned}&-\gamma a_{11} \left( \tau \right) \lambda \zeta +3/4\left( {b_{11} \left( \tau \right) } \right) ^{3}\beta \lambda -3/4\left( {b_{12} \left( \tau \right) } \right) ^{3}\beta \lambda \\&\quad +\,\gamma a_{12} \left( \tau \right) \lambda \zeta -\left( {\frac{\hbox {d}}{\hbox {d}\tau }b_{12} \left( \tau \right) } \right) \lambda \zeta \\&\quad +\,\left( {\frac{\hbox {d}}{\hbox {d}\tau }b_{11} \left( \tau \right) } \right) \lambda \zeta +2\left( {\frac{\hbox {d}}{\hbox {d}\tau }a_{12} \left( \tau \right) } \right) \gamma \\&\quad +\,b_{12} \left( \tau \right) \gamma ^{2}+3/2a_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda \\&\quad -\,3/2a_{11} \left( \tau \right) b_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \lambda +3/2b_{11} \left( \tau \right) a_{31} \left( \tau \right) a_{12} \left( \tau \right) \beta \lambda \\&\quad -\,3b_{11} \left( \tau \right) a_{31} \left( \tau \right) a_{32} \left( \tau \right) \beta \lambda \\&\quad +\,3/2b_{11} \left( \tau \right) b_{31} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda -3b_{11} \left( \tau \right) b_{31} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda \\&\quad -\,3/2b_{11} \left( \tau \right) a_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \lambda \\&\quad -\,3/2b_{11} \left( \tau \right) b_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda -3/2a_{31} \left( \tau \right) a_{12} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda \\&\quad +\,3a_{31} \left( \tau \right) b_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \lambda \\&\quad +\,3b_{31} \left( \tau \right) b_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda +3/2a_{12} \left( \tau \right) b_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \lambda \\&\quad -\,3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) a_{31} \left( \tau \right) \beta \lambda \\&\quad -\,3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) a_{12} \left( \tau \right) \beta \lambda +3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) a_{32} \left( \tau \right) \beta \lambda \\&\quad +\,3/2a_{11} \left( \tau \right) a_{31} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda \\&\quad -\,3/2a_{11} \left( \tau \right) b_{31} \left( \tau \right) a_{12} \left( \tau \right) \beta \lambda +3/2a_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda \\&\quad -\,3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \lambda \\&\quad -\,3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}b_{31} \left( \tau \right) \beta \lambda -3/4b_{31} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad -\,3/4\left( {a_{12} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta \lambda \\&\quad -\,3/4\left( {a_{12} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \lambda +3/4\left( {b_{12} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \lambda \\&\quad -\,3/2b_{12} \left( \tau \right) \left( {a_{32} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad -\,3/2b_{12} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta \lambda -9/4\left( {b_{11} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta \lambda \\&\quad +\,3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \lambda \\&\quad +\,3/2b_{11} \left( \tau \right) \left( {a_{31} \left( \tau \right) } \right) ^{2}\beta \lambda +3/2b_{11} \left( \tau \right) \left( {b_{31} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad +\,3/4b_{11}\left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad +\,9/4b_{11} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta \lambda +3/2b_{11} \left( \tau \right) \left( {a_{32} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad +\,3/2b_{11} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad -\,3/2\left( {a_{31} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta \lambda -3/2\left( {b_{31} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta \lambda \\&\quad +\,3/4b_{31} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad +\,3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{11} \left( \tau \right) \beta \lambda +3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{31} \left( \tau \right) \beta \lambda \\&\quad -\,3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta \lambda \\&\quad -\,\frac{\hbox {d}^{2}}{\hbox {d}\tau ^{2}}b_{12} \left( \tau \right) =0, \end{aligned}$$

$$\begin{aligned}&3\gamma b_{31} \left( \tau \right) \lambda \zeta -3\gamma b_{32} \left( \tau \right) \lambda \zeta +3/4\left( {a_{31} \left( \tau \right) } \right) ^{3}\beta \lambda \\&\quad -\,3/4\left( {a_{32} \left( \tau \right) } \right) ^{3}\beta \lambda +1/4\left( {a_{11} \left( \tau \right) } \right) ^{3}\beta \lambda \\&\quad -\,1/4\left( {a_{12} \left( \tau \right) } \right) ^{3}\beta \lambda +\left( {\frac{\hbox {d}}{\hbox {d}\tau }a_{31} \left( \tau \right) } \right) \lambda \zeta \\&\quad -\,6\left( {\frac{\hbox {d}}{\hbox {d}\tau }b_{32} \left( \tau \right) } \right) \gamma +9a_{32} \left( \tau \right) \gamma ^{2}-\left( {\frac{\hbox {d}}{\hbox {d}\tau }a_{32} \left( \tau \right) } \right) \lambda \zeta \\&\quad -\,3/2a_{31} \left( \tau \right) b_{31} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda +3/2b_{31} \left( \tau \right) a_{32} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda \\&\quad -\,3/4\left( {b_{31} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \lambda \\&\quad -\,3/4a_{32} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta \lambda -9/4\left( {a_{31} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \lambda \\&\quad +\,3/4a_{31} \left( \tau \right) \left( {b_{31} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad +\,9/4a_{31} \left( \tau \right) \left( {a_{32} \left( \tau \right) } \right) ^{2}\beta \lambda +3/4a_{31} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad -\,3b_{11}\left( \tau \right) a_{31} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda \\&\quad -\,3/2b_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda +3b_{11} \left( \tau \right) b_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \lambda \\&\quad +\,3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda \\&\quad -\,3a_{11} \left( \tau \right) a_{31} \left( \tau \right) a_{12} \left( \tau \right) \beta \lambda +3a_{11} \left( \tau \right) a_{12} \left( \tau \right) a_{32} \left( \tau \right) \beta \lambda \\&\quad +\,3/2\left( {a_{11} \left( \tau \right) } \right) ^{2}a_{31} \left( \tau \right) \beta \lambda \\&\quad -\,3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}a_{12} \left( \tau \right) \beta \lambda -3/2\left( {a_{11} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \lambda \\&\quad -\,3/4a_{11} \left( \tau \right) \left( {b_{11} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad +\,3/4a_{11} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta \lambda -3/4a_{11} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad +\,3/2\left( {b_{11} \left( \tau \right) } \right) ^{2}a_{31} \left( \tau \right) \beta \lambda \\&\quad +\,3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}a_{12} \left( \tau \right) \beta \lambda -3/2\left( {b_{11} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \lambda \\&\quad +\,3/2a_{31} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad +\,3/2a_{31} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta \lambda -3/2\left( {a_{12} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \lambda \\&\quad +\,3/4a_{12} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta \lambda \\&\quad -\,3/2\left( {b_{12} \left( \tau \right) } \right) ^{2}a_{32} \left( \tau \right) \beta \lambda -\frac{\hbox {d}^{2}}{\hbox {d}\tau ^{2}}a_{32} \left( \tau \right) =0, \end{aligned}$$

$$\begin{aligned}&-3\gamma a_{31} \left( \tau \right) \lambda \zeta +3\gamma a_{32} \left( \tau \right) \lambda \zeta +3/4\left( {b_{31} \left( \tau \right) } \right) ^{3}\beta \lambda \nonumber \\&\quad -\,3/4\left( {b_{32} \left( \tau \right) } \right) ^{3}\beta \lambda -1/4\left( {b_{11} \left( \tau \right) } \right) ^{3}\beta \lambda \nonumber \\&\quad +\,1/4\left( {b_{12} \left( \tau \right) } \right) ^{3}\beta \lambda -\left( {\frac{\hbox {d}}{\hbox {d}\tau }b_{32} \left( \tau \right) } \right) \lambda \zeta +9b_{32} \left( \tau \right) \gamma ^{2}\nonumber \\&\quad +\,6\left( {\frac{\hbox {d}}{\hbox {d}\tau }a_{32} \left( \tau \right) } \right) \gamma +\left( {\frac{\hbox {d}}{\hbox {d}\tau }b_{31} \left( \tau \right) } \right) \lambda \zeta \nonumber \\&\quad -\,3/2a_{31} \left( \tau \right) b_{31} \left( \tau \right) a_{32} \left( \tau \right) \beta \lambda +3/2a_{31} \left( \tau \right) a_{32} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda \nonumber \\&\quad +\,3/4\left( {a_{31} \left( \tau \right) } \right) ^{2}b_{31} \left( \tau \right) \beta \lambda -3/4\left( {a_{31} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \lambda \nonumber \\&\quad -\,9/4\left( {b_{31} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \lambda +3/4b_{31} \left( \tau \right) \left( {a_{32} \left( \tau \right) }\right) ^{2}\beta \lambda \nonumber \\&\quad +\,9/4b_{31} \left( \tau \right) \left( {b_{32} \left( \tau \right) } \right) ^{2}\beta \lambda -3/4\left( {a_{32} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \lambda \nonumber \\&\quad +\,3a_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda \nonumber \\&\quad -\,3b_{11} \left( \tau \right) b_{31} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda +3b_{11} \left( \tau \right) b_{12} \left( \tau \right) b_{32} \left( \tau \right) \beta \lambda \nonumber \\&\quad -\,3/2a_{11} \left( \tau \right) b_{11} \left( \tau \right) a_{12} \left( \tau \right) \beta \lambda \nonumber \\&\quad -\,3a_{11} \left( \tau \right) b_{31} \left( \tau \right) a_{12} \left( \tau \right) \beta \lambda +3/2a_{11} \left( \tau \right) a_{12} \left( \tau \right) b_{12} \left( \tau \right) \beta \lambda \nonumber \\&\quad -\,3/2\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \lambda \nonumber \\&\quad +\,3/2\left( {b_{11} \left( \tau \right) } \right) ^{2}b_{31} \left( \tau \right) \beta \lambda +3/2b_{31} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta \lambda \nonumber \\&\quad -\,3/4\left( {a_{12} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta \lambda \nonumber \\&\quad -\,3/2\left( {a_{12} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \lambda -3/2\left( {b_{12} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \lambda \nonumber \\&\quad +\,3/4\left( {b_{11} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta \lambda \nonumber \\&\quad -\,3/2\left( {b_{11} \left( \tau \right) } \right) ^{2}b_{32} \left( \tau \right) \beta \lambda +3/4b_{11} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta \lambda \nonumber \\&\quad -\,3/4b_{11} \left( \tau \right) \left( {b_{12} \left( \tau \right) } \right) ^{2}\beta \lambda \nonumber \\&\quad +\,3/2b_{31} \left( \tau \right) \left( {a_{12} \left( \tau \right) } \right) ^{2}\beta \lambda +3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{11} \left( \tau \right) \beta \lambda \nonumber \\&\quad +\,3/2\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{31} \left( \tau \right) \beta \lambda \nonumber \\&\quad -\,3/4\left( {a_{11} \left( \tau \right) } \right) ^{2}b_{12} \left( \tau \right) \beta \lambda -\frac{\hbox {d}^{2}}{\hbox {d}\tau ^{2}}\hbox {b}_{32} \left( \tau \right) =0. \end{aligned}$$

(B1)