A higher-order coupled nonlinear Schrödinger system: solitons, breathers, and rogue wave solutions

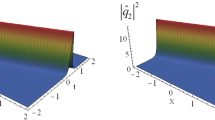
Abstract

Under investigation in this paper is a generalized coupled nonlinear Schrödinger system with higher-order terms, which describes the propagation properties of ultrashort solitons in two ultrashort optical fields. Based on the 3$\times$3 lax pair, the N-fold Darboux transformation (DT) has been constructed. Several kinds of solitons, breathers, and rogue wave solutions are generated on the vanishing and nonvanishing backgrounds by virtue of the DT. Figures are plotted to reveal the dynamic features of those solutions: (1) elastic interactions between two solitons; (2) mutual attractions and repulsions of bound solitons; (3) propagation properties of Ma-breathers, Akhmediev breathers, two-breathers, and rogue waves. The results show that the rogue waves can result from two different ways: the limit process of Ma-breathers and Akhmediev breathers.

1 Introduction

During the past decades, investigations on the nonlinear Schrödinger (NLS) system have attracted much research interest because the propagation of slowly varying amplitude electromagnetic waves in a single-mode fiber can be described by the NLS system [1–10]

$$\begin{aligned} i\,q_{t}\pm \frac{1}{2}\,q_{xx}+|q|^2\,q=0, \end{aligned}$$

(1.1)

where q denotes the slowly varying complex envelope of the wave, and subscripts x and t are the longitudinal distance and retarded time, respectively. However, when increasing the bit rates, it is necessary to decrease the pulse width, and the NLS system will become inadequate when the pulse lengths become comparable; then, the higher-order terms have to be considered, including the third-order dispersion (TOD), self-steepening (SS), and stimulated raman scattering terms [11–20]. In addition, in the case of achieving wavelength division multiplexing, one have to consider more than one field simultaneously [21–28]. Especially, the wave dynamics of simultaneous propagation of two ultrashort optical fields in a fiber is governed by the coupled NLS system with higher-order terms as [29, 30]

$$\begin{aligned}&i\,q_{1t}+q_{1xx}+2\left( \sigma _{1}|q_{1}|^{2}+\sigma _{2}|q_{2}|^{2}\right) q_{1}+i\varepsilon \left[ q_{1xxx}\right. \nonumber \\&\quad \left. +\,3\left( \sigma _{1}|q_{1}|^{2}+\sigma _{2}|q_{2}|^{2}\right) q_{1x}\right. \nonumber \\&\quad \left. +\,3\left( \sigma _{1}q_{1}^{*}q_{1x} +\sigma _{2}q_{2}^{*}q_{2x}q_{1}\right) \right] =0, \end{aligned}$$

(1.2a)

$$\begin{aligned}&i\,q_{2t}+q_{2xx}+2\left( \sigma _{1}|q_{1}|^{2}+\sigma _{2}|q_{2}|^{2}\right) q_{2}+i\varepsilon \left[ q_{2xxx}\right. \nonumber \\&\quad \left. \ +\,3\left( \sigma _{1}|q_{1}|^{2}+\sigma _{2}|q_{2}|^{2}\right) q_{2x}\right. \nonumber \\&\quad \left. +\,3\left( \sigma _{1}q_{1}^{*}q_{1x}+\sigma _{2}q_{2}^{*}q_{2x}q_{2}\right) \right] =0, \end{aligned}$$

(1.2b)

where $q_{1}$ and $q_{2}$ are the field functions; $\sigma _{1}$ and $\sigma _{2}$ refer to self-phase modulation (SPM) and cross-phase modulation (XPM), respectively; $\varepsilon$ denotes the strength of higher-order linear and nonlinear effects.

System (1.2) is a completely integrable model, and some properties of System (1.2) have been analyzed recently. Tasgal and Potasek [29] have obtained one-soliton solutions by the inverse scattering method; Wang et al. [30] have reported the Lax integrable property and derived bright soliton solutions by the Riemann Hilbert formulation. The soliton solutions obtained in Refs. [29, 30] are all deduced on the vanishing backgrounds. In common cases, vanishing backgrounds can generate soliton solutions, while nonvanishing backgrounds can generate breather and rogue wave solutions. Thus, the aim of this paper was to analyze the dynamic behaviors of soliton solutions, derive several kinds of breather and rogue wave solutions on vanishing and nonvanishing backgrounds, and to analyze how the solutions are affected by higher-order terms for System (1.2).

This paper will be organized as follows: In Sect. 2, we will present 3$\times$3 Lax pair and construct the Darboux transformation (DT) for System (1.2). In Sect. 3, using the DT obtained, we will derive soliton solutions on vanishing backgrounds. In Sect. 4, breather and rogue wave solutions will be discussed on nonvanishing backgrounds, and the dynamic behaviors of those solutions will be analyzed with some graphical illustration. Finally, our conclusions will be addressed in Sect. 5.

2 Lax pair and Darboux transformation

Employing the Ablowitz–Kaup–Newell–Segur procedure [31], one can derive the 3$\times$3 Lax pair associated with System (1.2) as [30]

$$\begin{aligned}&\varPsi _{x}=F \varPsi =(\lambda \,F_{1}+F_{0})\,\varPsi , \end{aligned}$$

(2.1a)

$$\begin{aligned}&\varPsi _{t}=G \varPsi =\left( \lambda ^{3}\,G_{3}+\lambda ^{2}\,G_{2}+2\,\lambda \,G_{1}+G_{0}\right) \,\varPsi , \end{aligned}$$

(2.1b)

where $\lambda$ is the spectral parameter, $\varPsi =(\psi _{1},\psi _{2},\psi _{3})^T$ (T denotes the transpose of a vector) is the vector eigenfunction, and

$$\begin{aligned} F_{0}= & {} \left( \begin{array}{ccc} 0 &{} \quad q_{1} &{} \quad q_{2}\\ -\sigma _{1}\,q_{1}^{*} &{} \quad 0 &{} \quad 0\\ -\sigma _{2}\,q_{2}^{*} &{} \quad 0 &{} \quad 0 \end{array} \right) ,\ \ F_{1}\!=\!\left( \begin{array}{ccc} i &{} \quad 0 &{} \quad 0\\ 0 &{} \quad -i &{} \quad 0\\ 0 &{} \quad 0 &{} \quad -i \end{array} \right) ,\ G_{3}=4\,\varepsilon F_{1},\\ G_{2}= & {} \left( \begin{array}{ccc} -2i &{} \quad 4\,\varepsilon \,q_{1} &{} \quad 4\,\varepsilon \,q_{2}\\ -4\,\varepsilon \,\sigma _{1}\,q^{*}_{1} &{} \quad 2i &{} \quad 0\\ -4\,\varepsilon \,\sigma _{2}\,q^{*}_{2} &{} \quad 0 &{} \quad 2i \end{array} \right) ,\ \ \ G_{0}=\left( \begin{array}{ccc} A_{1} &{} \quad A_{2} &{} \quad A_{3}\\ B_{1} &{} \quad B_{2} &{} \quad B_{3}\\ C_{1} &{} \quad C_{2} &{} \quad C_{3} \end{array} \right) ,\\ G_{1}= & {} \left( \begin{array}{ccc} i\,\varepsilon \,\left( \sigma _{1}\,|q_{1}|^{2}+\sigma _{2}\,|q_{2}|^{2}\right) &{} \quad -q_{1}-i\,\varepsilon \,q_{1x} &{} \quad -q_{2}-i\,\varepsilon \,q_{2x}\\ \sigma _{1}q^{*}_{1}-i\,\varepsilon \,\sigma _{1}q^{*}_{1x} &{} \quad i\,\varepsilon \,\sigma _{1}|q_{1}|^{2} &{} \quad i\,\varepsilon \,\sigma _{1}\,q_{1}^{*}\,q_{2}\\ \sigma _{2}q^{*}_{2}-i\,\varepsilon \,\sigma _{2}q^{*}_{2x} &{} \quad i\,\varepsilon \,\sigma _{2}q_{1}\,q_{2}^{*} &{} \quad i\,\varepsilon \,\sigma _{2}|q_{2}|^{2} \end{array} \right) , \end{aligned}$$

with

$$\begin{aligned}&A_{1}=\sigma _{1}\left( i\,|q_{1}|^{2}-\varepsilon \,q_{1x}\,q_{1}^{*} +\varepsilon \,q_{1x}^{*}\,q_{1}\right) \\&\quad +\,\sigma _{2}\left( i\,|q_{2}|^{2}-\varepsilon \,q_{2x} \,q_{2}^{*}+\varepsilon \,q_{2x}^{*}\,q_{2}\right) ,\\&A_{2}=i\,q_{1x}-\varepsilon \,q_{1xx}-2\,\varepsilon \,q_{1} \left( \sigma _{1}|q_{1}|^{2}+\sigma _{2}|q_{2}|^{2}\right) ,\\&A_{3}=i\,q_{2x}-\varepsilon \,q_{2xx}-2\,\varepsilon \,q_{2}\left( \sigma _{1}|q_{1}|^{2}+\sigma _{2}|q_{2}|^{2}\right) ,\\&B_{1}=i\,\sigma _{1}\,q_{1x}^{*}+\varepsilon \,\sigma _{1} \,q_{1xx}^{*}+2\,\varepsilon \,\sigma _{1}\,q_{1}^{*}\left( \sigma _{1}\,|q_{1}|^{2} +\sigma _{2}\,|q_{2}|^{2}\right) ,\\&B_{2}=\varepsilon \,\sigma _{1}\,q_{1x}\,q_{1}^{*} -i\,\sigma _{1}\,|q_{1}|^{2}-\varepsilon \,\sigma _{1}\,q_{1x}^{*}\,q_{1},\\&B_{3}=\varepsilon \,\sigma _{1}\,q_{2x}\,q_{1}^{*} -i\,\sigma _{1}\,q_{1x}^{*}\,q_{2}-i\,\sigma _{1}\,q_{2}\,q_{1}^{*},\\&C_{1}=i\,\sigma _{2}\,q_{2x}^{*}+\varepsilon \,\sigma _{2}\,q_{2xx}^{*} +2\,\varepsilon \,\sigma _{2}\,q_{2x}^{*}\,\left( \sigma _{1}|q_{1}|^{2} +\sigma _{2}|q_{2}|^{2}\right) ,\\&C_{2}=\varepsilon \, \sigma _{2}\,q_{1x}\,q_{2}^{*} -\varepsilon \, \sigma _{2}\,q_{2x}^{*}\,q_{1}-i\,\sigma _{2} \,q_{1}\,q_{2}^{*},\\&C_{3}=\varepsilon \, \sigma _{2}\,q_{2x}\,q_{2}^{*}-\varepsilon \,\sigma _{2}\,q_{2x}^{*}\,q_{2}-i\,\sigma _{2}\,|q_{2}|^{2}. \end{aligned}$$

Through direct computation, one can find that the compatibility condition $U_{t}-V_{x}+U\,V-V\,U=0$ will give rise to System (1.2).

DT technique is a method which can derive multi-soliton solutions from trivial seeds in a purely algebraic procedure for the integrable nonlinear evolution equations (NLEEs) [32, 33]. Main feature of DT is that the Lax pair associated with the NLEE remains covariant under the gauge transformation [34, 35]. By using Lax pair (2.1), we construct the DT for System (1.2) as

$$\begin{aligned}&\varPsi ^{\prime }=T\varPsi =(\lambda \,I+S)\varPsi , \nonumber \\&\varPsi ^{\prime }_{x}=F^{\prime }\varPsi ^{\prime },\ \ \varPsi ^{\prime }_{t}=G^{\prime }\varPsi ^{\prime }, \end{aligned}$$

(2.2)

where I denotes the identity matrix, $F^{\prime }$ and $G^{\prime }$ have the same forms as F and G except that $q_{1}$ and $q_{2}$ are replaced by $q_{1}^{\prime }$ and $q_{2}^{\prime }$, respectively. Defining $S=-H\, \varLambda \, H^{-1}$ and

$$\begin{aligned}&\varLambda =\left( \begin{array}{ccc} \lambda _{1} &{} \quad 0 &{} \quad 0\\ 0 &{} \quad \lambda _{1}^{*} &{} \quad 0\\ 0 &{} \quad 0 &{} \quad \lambda _{1}^{*} \end{array} \right) ,\quad H=\left( \begin{array}{ccc} \phi _{1} &{} \quad \varphi _{1}^{*} &{} \quad \psi _{1}^{*}\\ \varphi _{1} &{} \quad -\sigma _{1}\phi _{1}^{*} &{} \quad 0\\ \psi _{1} &{} \quad 0 &{} \quad -\sigma _{2}\phi _{1}^{*} \end{array} \right) , \end{aligned}$$

where the vector $(\phi _{1},\varphi _{1},\psi _{1})^{T}$ is the solution of Lax pair (2.1) associated with the eigenvalue $\lambda _{1}$, we can obtain the transformation between potential functions $q_{1}^{\prime }$, $q_{2}^{\prime }$ and $q_{1}$, $q_{2}$ as

$$\begin{aligned} q_{1}^{\prime }= & {} q_{1}+2\,i\,\left( \lambda _{1}-\lambda _{1}^{*}\right) \nonumber \\&\frac{\sigma _{2}\,\phi _{1}\,\varphi _{1}^{*}}{\sigma _{1} \,\sigma _{2}|\phi _{1}|^{2}+\sigma _{2}|\varphi _{1}|^{2} +\sigma _{1}|\psi _{1}|^{2}}, \end{aligned}$$

(2.3a)

$$\begin{aligned} q_{2}^{\prime }= & {} q_{2}+2\,i\,\left( \lambda _{1}-\lambda _{1}^{*}\right) \nonumber \\&\frac{\sigma _{1}\,\phi _{1}\,\psi _{1}^{*}}{\sigma _{1} \,\sigma _{2}|\phi _{1}|^{2}+\sigma _{2}|\varphi _{1}|^{2} +\sigma _{1}|\psi _{1}|^{2}}. \end{aligned}$$

(2.3b)

For the convenience of calculation, we can rewrite the DT (2.3) as the following determinant representations:

$$\begin{aligned}&q_{1}^{\prime }=q_{1}-2\,i\,\frac{|\varOmega _{1}|}{|\varOmega _{2}|},\ \ \ \ q_{2}^{\prime }=q_{2}-2\,i\,\frac{|\varOmega _{3}|}{|\varOmega _{2}|}, \end{aligned}$$

(2.4)

where

$$\begin{aligned}&\varOmega _{1}=\left( \begin{array}{ccc} \phi _{1} &{} \quad -\lambda _{1}\,\phi _{1} &{} \quad \psi _{1}\\ \varphi _{1}^{*} &{} \quad -\lambda _{1}^{*}\,\varphi _{1}^{*} &{} \quad 0\\ \psi _{1}^{*} &{} \quad -\lambda _{1}^{*}\,\psi _{1}^{*} &{} \quad -\sigma _{2}\,\phi _{1}^{*} \end{array} \right) ,\\&\varOmega _{3}=\left( \begin{array}{ccc} \phi _{1} &{} \quad \varphi _{1} &{} \quad -\lambda _{1}\,\phi _{1}\\ \varphi _{1} &{} \quad -\sigma _{1}\phi _{1}^{*} &{} \quad -\lambda _{1}^{*}\,\varphi _{1}^{*}\\ \psi _{1} &{} \quad 0 &{} \quad -\lambda _{1}^{*}\,\psi _{1}^{*} \end{array} \right) ,\\&\varOmega _{2}=\left( \begin{array}{ccc} \phi _{1} &{} \quad \varphi _{1} &{} \quad \psi _{1}\\ \varphi _{1}^{*} &{} \quad -\sigma _{1}\phi _{1}^{*} &{} \quad 0\\ \psi _{1}^{*} &{} \quad 0 &{} \quad -\sigma _{2}\,\phi _{1}^{*} \end{array} \right) . \end{aligned}$$

The DT investigated above is of degree one. Now, we will discuss the DT of higher degree for System (1.2). In fact, the DT of higher degree can be regarded as a superposition of that of degree one. Now, we define

$$\begin{aligned}&T_{n}=T_{n}(\lambda ; \lambda _{1}, \lambda _{2},\ldots ,\lambda _{n})=\sum _{k=0}^{n}S_{n-k}\lambda ^{k},\nonumber \\&S_{0}=I, \end{aligned}$$

(2.5)

where $S_{i}\, (i=1,2,\ldots ,n \,(n\geqslant 2))$ are $3\times 3$ matrices, the elements of which are some functions depending on the variables x and t.

Using Expression (2.5), we can obtain

$$\begin{aligned}&\varPsi ^{[n]}=T_{n}\varPsi =\left( \sum _{k=0}^{n}S_{n-k}\lambda ^{k}\right) \varPsi , \end{aligned}$$

(2.6a)

$$\begin{aligned}&U_{0}^{(n)}=U_{0}+S_{n-1}\,U_{1}-U_{1}^{\prime }\,S_{n-1}. \end{aligned}$$

(2.6b)

By using Expressions (2.6), we can deduce the potential formula

$$\begin{aligned}&q_{1}^{(n)}=q_{1}-2\,i\,(S_{n-1})_{12}, \end{aligned}$$

(2.7a)

$$\begin{aligned}&q_{2}^{(n)}=q_{2}-2\,i\,(S_{n-1})_{13}, \end{aligned}$$

(2.7b)

where

$$\begin{aligned} (S_{n-1})_{12}=\frac{|\varDelta _{1n}|}{|\varDelta _{2n}|}, \ \ \ (S_{n-1})_{13}=\frac{|\varDelta _{3n}|}{|\varDelta _{2n}|}, \end{aligned}$$

with

$$\begin{aligned}&\varDelta _{1n}=\left( \begin{array}{ccc} \varXi _{1} &{} \quad \cdots &{} \quad \alpha _{1}\\ \cdots &{} \quad \cdots &{} \quad \cdots \\ \varXi _{n} &{} \quad \cdots &{} \quad \alpha _{n} \end{array} \right) ,\quad \varDelta _{3n}=\left( \begin{array}{ccc} \varTheta _{1} &{} \quad \cdots &{} \quad \alpha _{1}\\ \cdots &{} \quad \cdots &{} \quad \cdots \\ \varTheta _{n} &{} \quad \cdots &{} \quad \alpha _{n} \end{array} \right) ,\\&\varDelta _{2n}=\left( \begin{array}{ccc} \varGamma _{1} &{} \quad \cdots &{} \quad \alpha _{1}\\ \cdots &{} \quad \cdots &{} \quad \cdots \\ \varGamma _{n} &{} \quad \cdots &{} \quad \alpha _{n} \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned}&\varXi _{1}=\left( \begin{array}{ccc} \lambda _{1}^{n-1}\phi _{1} &{} \quad -\lambda _{1}^{n}\phi _{1} &{} \quad \lambda _{1}^{n-1}\psi _{1}\\ (\lambda _{1}^{*})^{n-1}\varphi _{1}^{*} &{} \quad -(\lambda _{1}^{*})^{n}\varphi _{1}^{*} &{} \quad 0\\ (\lambda _{1}^{*})^{n-1}\psi _{1}^{*} &{} \quad -(\lambda _{1}^{*})^{n}\psi _{1}^{*} &{} \quad -\sigma _{2}(\lambda _{1}^{*})^{n-1}\phi _{1}^{*} \end{array} \right) ,\\&\varXi _{n}=\left( \begin{array}{ccc} \lambda _{n}^{n-1}\phi _{n} &{} \quad -\lambda _{n}^{n}\phi _{n} &{} \quad \lambda _{n}^{n-1}\psi _{n}\\ \left( \lambda _{n}^{*}\right) ^{n-1}\varphi _{n}^{*} &{} \quad -\left( \lambda _{n}^{*}\right) ^{n}\varphi _{n}^{*} &{} \quad 0\\ \left( \lambda _{n}^{*}\right) ^{n-1}\psi _{n}^{*} &{} \quad -\left( \lambda _{n}^{*}\right) ^{n}\psi _{n}^{*} &{} \quad -\sigma _{2}\left( \lambda _{n}^{*}\right) ^{n-1}\phi _{n}^{*} \end{array} \right) ,\\&\alpha _{1}=\left( \begin{array}{ccc} \phi _{1} &{} \quad \varphi _{1} &{} \quad \psi _{1}\\ \varphi _{1}^{*} &{} \quad -\sigma _{1}\phi _{1}^{*} &{} \quad 0\\ \psi _{1}^{*} &{} \quad 0 &{} \quad -\sigma _{2}\phi _{1}^{*} \end{array} \right) ,\\&\alpha _{n}=\left( \begin{array}{ccc} \phi _{n} &{} \quad \varphi _{n} &{} \quad \psi _{n}\\ \varphi _{n}^{*} &{} \quad -\sigma _{1}\phi _{n}^{*} &{} \quad 0\\ \psi _{n}^{*} &{} \quad 0 &{} \quad -\sigma _{2}\phi _{n}^{*} \end{array} \right) ,\\&\varTheta _{1}=\left( \begin{array}{ccc} \lambda _{1}^{n-1}\phi _{1} &{} \quad \lambda _{1}^{n-1}\varphi _{1} &{} \quad -\lambda _{1}^{n}\phi _{1}\\ (\lambda _{1}^{*})^{n-1}\varphi _{1}^{*} &{} \quad -\sigma _{1}(\lambda _{1}^{*})^{n-1}\phi _{1}^{*} &{} \quad 0\\ (\lambda _{1}^{*})^{n-1}\psi _{1}^{*} &{} \quad 0 &{} \quad -\sigma _{2}(\lambda _{1}^{*})^{n-1}\phi _{1}^{*} \end{array} \right) ,\\&\varTheta _{n}=\left( \begin{array}{ccc} \lambda _{n}^{n-1}\phi _{n} &{} \quad \lambda _{n}^{n-1}\varphi _{n} &{} \quad -\lambda _{n}^{n}\phi _{n}\\ \left( \lambda _{n}^{*}\right) ^{n-1}\varphi _{n}^{*} &{} \quad -\sigma _{1}\left( \lambda _{n}^{*}\right) ^{n-1}\phi _{n}^{*} &{} \quad 0\\ \left( \lambda _{n}^{*}\right) ^{n-1}\psi _{n}^{*} &{} \quad 0 &{} \quad -\sigma _{2}\left( \lambda _{n}^{*}\right) ^{n-1}\phi _{n}^{*} \end{array} \right) ,\\&\varGamma _{1}=\left( \begin{array}{ccc} \lambda _{1}^{n-1}\phi _{1} &{} \quad \lambda _{1}^{n-1}\varphi _{1} &{} \quad \lambda _{1}^{n-1}\psi _{1}\\ (\lambda _{1}^{*})^{n-1}\varphi _{1}^{*} &{} \quad -\sigma _{1}(\lambda _{1}^{*})^{n-1}\phi _{1}^{*} &{} \quad -(\lambda _{1}^{*})^{n}\varphi _{1}^{*}\\ (\lambda _{1}^{*})^{n-1}\psi _{1}^{*} &{} \quad 0 &{} \quad -(\lambda _{1}^{*})^{n}\psi _{1}^{*} \end{array} \right) ,\\&\varGamma _{n}=\left( \begin{array}{ccc} \lambda _{n}^{n-1}\phi _{n} &{} \quad \lambda _{n}^{n-1}\varphi _{n} &{} \quad \lambda _{n}^{n-1}\psi _{n}\\ \left( \lambda _{n}^{*}\right) ^{n-1}\varphi _{n}^{*} &{} \quad -\sigma _{1}\left( \lambda _{n}^{*}\right) ^{n-1}\phi _{n}^{*} &{} \quad -\left( \lambda _{n}^{*}\right) ^{n}\varphi _{n}^{*}\\ \left( \lambda _{n}^{*}\right) ^{n-1}\psi _{n}^{*} &{} \quad 0 &{} \quad -\left( \lambda _{n}^{*}\right) ^{n}\psi _{n}^{*} \end{array} \right) , \end{aligned}$$

and $\varPsi _{j}=\varPsi (x,t,\lambda )|_{\lambda =\lambda _{j}}=(\phi _{j}, \varphi _{j},\psi _{j})^{T}$ is the basic solutions of the Lax pair (2.1) corresponding to $\lambda =\lambda _{i}\, (i=1,2,\ldots ,n)$.

3 Soliton solutions on vanishing backgrounds for System (1.2)

In this section, we will construct soliton solutions for System (1.2) by using the obtained DT on vanishing backgrounds, i.e., $q_{1}=q_{2}=0$, including one-soliton, two-soliton, and bound-soliton solutions.

Case 3.1 Under the seeds as $q_{1}=q_{2}=0$, from Lax pair (2.1), we can obtain $\phi _{1}=c_{1}\,\mathrm{exp}\,\theta _{1},\ \varphi _{1}=c_{2}\,\mathrm{exp}\,(-\theta _{1}),\ \psi _{1}=c_{3}\,\mathrm{exp}\,(-\theta _{1})$, here $\theta _{1}=i\,\lambda _{1}\,x+(-2\,i\,\lambda _{1}^{2} +4i\,\varepsilon \,\lambda _{1}^{3})\,t$ and $c_{1},\ c_{2},\ c_{3}$ are complex parameters and $\lambda _{1}=a+i\,b$. Then, Eq. (2.3) can give one-soliton solutions for System (1.2) as

$$\begin{aligned} q_{1}^{\prime }&=2i\left( \lambda _{1}-\lambda _{1}^{*}\right) \frac{\sigma _{2}}{2\sqrt{(\sigma _{1} +\sigma _{2})\sigma _{1}\sigma _{2}}}\nonumber \\&\quad \times \mathrm{sech}\left( \theta _{1}+\theta _{1}^{*} +\mathrm{ln\sqrt{\frac{\sigma _{1}\sigma _{2}}{\sigma _{1}+\sigma _{2}}}}\right) \,\mathrm{exp}\left( \theta _{1}-\theta _{1}^{*}\right) , \end{aligned}$$

(3.1a)

$$\begin{aligned} q_{2}^{\prime }&=2i\left( \lambda _{1}-\lambda _{1}^{*}\right) \frac{\sigma _{1}}{2\sqrt{(\sigma _{1} +\sigma _{2})\sigma _{1}\sigma _{2}}}\nonumber \\&\quad \times \mathrm{sech}\left( \theta _{1}+\theta _{1}^{*} +\mathrm{ln\sqrt{\frac{\sigma _{1}\sigma _{2}}{\sigma _{1}+\sigma _{2}}}}\right) \,\mathrm{exp}\left( \theta _{1}-\theta _{1}^{*}\right) . \end{aligned}$$

(3.1b)

Moreover, through symbolic computation, one can conclude some physical quantities for $q_{1}$ and $q_{2}$ via Solutions (3.1) as portrayed in Table 1.

Table 1 Physical quantities of solitons for $q_{1}$ and $q_{2}$ via Solutions (3.1)

From Table 1, one can remarkably find that the soliton amplitudes, widths, and initial phases are independent to the parameter $\varepsilon$, i.e., the higher-order terms do not influence the soliton amplitude, widths, and initial phases. However, the soliton velocities become a complicated mix of the eigenvalues and the higher-order term parameters, so the higher-order terms will influence the soliton velocities.

Case 3.2 Taking $n=2$ in Eq. (2.7), choosing two sets of solutions for Lax Pair (2.1): $\varPsi _{1}=\varPsi (x,t,\lambda )|_{\lambda =\lambda _{1}} =(\phi _{1},\varphi _{1},\psi _{1})^{T}$ and $\varPsi _{2}=\varPsi (x,t,\lambda )|_{\lambda =\lambda _{2}}=(\phi _{2},\varphi _{2}, \psi _{2})^{T}$, through direct computations, we obtain two-soliton solutions for System (1.2) as

$$\begin{aligned} q_{1}^{(2)}=q_{1}-2\,i\,\frac{|\varDelta _{12}|}{|\varDelta _{22}|},\ \ \ \ q_{2}^{(2)}=q_{2}-2\,i\,\frac{|\varDelta _{32}|}{|\varDelta _{22}|},\nonumber \\ \end{aligned}$$

(3.2)

where

$$\begin{aligned} \varDelta _{12}= & {} \left( \begin{array}{cccccc} \lambda _{1}\phi _{1} &{} \quad -\lambda _{1}^{2}\phi _{1} &{} \quad \lambda _{1}\psi _{1} &{} \quad \phi _{1} &{} \quad \varphi _{1} &{} \quad \psi _{1}\\ \lambda _{1}^{*}\varphi _{1}^{*} &{} \quad -\lambda _{1}^{*2}\varphi _{1}^{*} &{} \quad 0 &{} \quad \varphi _{1}^{*} &{} \quad -\sigma _{1}\phi _{1}^{*} &{} \quad 0\\ \lambda _{1}^{*}\psi _{1}^{*} &{} \quad -\lambda _{1}^{*2}\psi _{1}^{*} &{} \quad -\sigma _{2}\lambda _{1}^{*}\phi _{1}^{*} &{} \quad \psi _{1}^{*} &{} \quad 0 &{} \quad -\sigma _{2}\phi _{1}^{*}\\ \lambda _{2}\phi _{2} &{} \quad -\lambda _{2}^{2}\phi _{2} &{} \quad \lambda _{2}\psi _{2} &{} \quad \phi _{2} &{} \quad \varphi _{2} &{} \quad \psi _{2}\\ \lambda _{2}^{*}\varphi _{2}^{*} &{} \quad -\lambda _{2}^{*2}\varphi _{2}^{*} &{} \quad 0 &{} \quad \varphi _{2}^{*} &{} \quad -\sigma _{1}\phi _{2}^{*} &{} \quad 0\\ \lambda _{2}^{*}\psi _{2}^{*} &{} \quad -\lambda _{2}^{*2}\psi _{2}^{*} &{} \quad -\sigma _{2}\lambda _{2}^{*}\phi _{2}^{*} &{} \quad \psi _{2}^{*} &{} \quad 0 &{} \quad -\sigma _{2}\phi _{2}^{*} \end{array} \right) ,\\ \varDelta _{32}= & {} \left( \begin{array}{cccccc} \lambda _{1}\phi _{1} &{} \quad \lambda _{1}\varphi _{1} &{} \quad -\lambda _{1}^{2}\phi _{1} &{} \quad \phi _{1} &{} \quad \varphi _{1} &{} \quad \psi _{1}\\ \lambda _{1}^{*}\varphi _{1}^{*} &{} \quad -\sigma _{1}\lambda _{1}^{*}\phi _{1}^{*} &{} \quad 0 &{} \quad \varphi _{1}^{*} &{} \quad -\sigma _{1}\phi _{1}^{*} &{} \quad 0\\ \lambda _{1}^{*}\psi _{1}^{*} &{} \quad 0 &{} \quad -\sigma _{2}\lambda _{1}^{*}\phi _{1}^{*} &{} \quad \psi _{1}^{*} &{} \quad 0 &{} \quad -\sigma _{2}\phi _{1}^{*}\\ \lambda _{2}\phi _{2} &{} \quad \lambda _{2}\phi _{2} &{} \quad -\lambda _{2}^{2}\phi _{2} &{} \quad \phi _{2} &{} \quad \varphi _{2} &{} \quad \psi _{2}\\ \lambda _{2}^{*}\varphi _{2}^{*} &{} \quad -\sigma _{1}\lambda _{2}^{*}\phi _{2}^{*} &{} \quad -\lambda _{2}^{*2}\varphi _{2}^{*} &{} \quad \varphi _{2}^{*} &{} \quad -\sigma _{1}\phi _{2}^{*} &{} \quad 0\\ \lambda _{2}^{*}\psi _{2}^{*} &{} \quad 0 &{} \quad -\lambda _{2}^{*2}\psi _{2}^{*} &{} \quad \psi _{n}^{*} &{} \quad 0 &{} \quad -\sigma _{2}\phi _{2}^{*} \end{array} \right) ,\\ \varDelta _{22}= & {} \left( \begin{array}{cccccc} \lambda _{1}\phi _{1} &{} \quad \lambda _{1}\varphi _{1} &{} \quad \lambda _{1}\psi _{1} &{} \quad \phi _{1} &{} \quad \varphi _{1} &{} \quad \psi _{1}\\ \lambda _{1}^{*}\varphi _{1}^{*} &{} \quad -\sigma _{1}\lambda _{1}^{*}\phi _{1}^{*} &{} \quad -\lambda _{1}^{*2}\varphi _{1}^{*} &{} \quad \varphi _{1}^{*} &{} \quad -\sigma _{1}\phi _{1}^{*} &{} \quad 0\\ \lambda _{1}^{*}\psi _{1}^{*} &{} \quad 0 &{} \quad -\lambda _{1}^{*2}\psi _{1}^{*} &{} \quad \psi _{1}^{*} &{} \quad 0 &{} \quad -\sigma _{2}\phi _{1}^{*}\\ \lambda _{2}\phi _{2} &{} \quad \lambda _{2}\phi _{2} &{} \quad \lambda _{2}\psi _{2} &{} \quad \phi _{2} &{} \quad \varphi _{2} &{} \quad \psi _{2}\\ \lambda _{2}^{*}\varphi _{2}^{*} &{} \quad -\sigma _{1}\lambda _{2}^{*}\phi _{2}^{*} &{} \quad 0 &{} \quad \varphi _{2}^{*} &{} \quad -\sigma _{1}\phi _{2}^{*} &{} \quad 0\\ \lambda _{2}^{*}\psi _{2}^{*} &{} \quad 0 &{} \quad -\sigma _{2}\lambda _{2}^{*}\phi _{2}^{*} &{} \quad \psi _{2}^{*} &{} \quad 0 &{} \quad -\sigma _{2}\phi _{2}^{*} \end{array} \right) . \end{aligned}$$

Figure 1 describes the interactions of two bright solitons with different amplitudes and velocities expressed via Eq. (3.2), and as depicted in Fig. 1, the main feature of the collisions is that the shapes, amplitudes, and pulse widths of the solitons all reserve invariant except for slightly visible phase shifts after the process of interaction; that is to say, the interactions are elastic. In addition, one can observe that the interaction between the two solitons is centered at the origin (0, 0) due to the choice of the phase $\phi =0$.

Fig. 1

Elastic interactions between the two-soliton solutions. Parameters are: $\lambda _{1}=1+0.5i$, $\lambda _{2}=-1+0.6i$, $\sigma _{1}=1$, $\sigma _{2}=2$ and $\varepsilon =0.1$

Now, we introduce a special type of two-soliton solutions for System (1.2) named bound solitons [36]. Considering the initial pulses as $q_{1}(0,t)=q_{2}(0,t)=\mathrm{sech}\,(t-t_{0})+\mathrm{sech}\,(t+t_{0})$, $t_{0}$ is the initial separations of two solitons, we will investigate the interaction scenarios between two neighboring solitons.

Calculated from Lax pair (2.1), the real parts of the eigenvalues $\lambda _{1},\ \lambda _{2}$ will be zero, i.e., $\lambda _{1}=i\,\varrho _{1},\ \lambda _{2}=i\,\varrho _{2}$, by using the Taylor series of $q_{1}(0,t),\ q_{2}(0,t)$, the expressions of the two-soliton solutions (3.2) and the first conservative law of System (1.2)

$$\begin{aligned} \int _{-\infty }^{\infty }\left( |q_{1}|^{2}-|q_{2}|^{2}\right) \mathrm{d}t=2(\varrho _{1}+\varrho _{2}), \end{aligned}$$

(3.3)

we can deduce that

$$\begin{aligned}&\varrho _{1,2}=1+\frac{2\,t_{0}}{\mathrm{sinh}(2\,t_{0})}\pm \mathrm{sech}\,t_{0}. \end{aligned}$$

(3.4)

When $t_{0}=3.5$, Eq. (3.4) results in $\lambda _{1}=1.07311\,i,\ \lambda _{2} =0.95243\,i$; then, we can obtain the bound solitons which periodically propagate as shown in Fig. 2. Main feature of the bound soliton is that when the two solitons propagate along their own trajectories, the mutual attraction between them takes place, and consequently, the two solitons merge. At the spot of the interaction, the amplitudes of solitons get higher instantly. After the interaction, the mutual repulsion between the two solitons occur, and this repulsion causes that the two solitons separate. However, once they separate, the mutual attraction takes place again, and the process will repeat periodically.

Fig. 2

Periodically mutual attractions and repulsions of bound-soliton solution. Parameters are: $\lambda _{1}=1.07311\,i,\ \lambda _{2}=0.95243\,i$, $\sigma _{1}=\sigma _{2}=1$ and $\varepsilon =0$

However, when $t_{0}=8.1$, Eq. (3.4) results in $\lambda _{1}=1.00061\,i,\ \lambda _{2}=0.99994\,i$; then, the mutual attractions and repulsions between two solitons disappear, and the two solitons will eventually separate owing to their different velocities. In addition, if we choose $\varrho _{1}=0.5, \varrho _{2}=-0.501$, then the two solitons will propagate in parallel without any effect on each other even if the propagation distance grows long enough as shown in Fig. 3. So we can suppress the effects between bound solitons by virtue of adjusting the values of $\varrho _{1}$ and $\varrho _{2}$.

Fig. 3

Parallel propagation of two-soliton solutions. Parameters are: $\lambda _{1}=0.5\,i,\ \lambda _{2}=-0.501\,i$, $\sigma _{1}=\sigma _{2}=1$ and $\varepsilon =0.1$

4 Breather and rogue wave solutions on nonvanishing backgrounds for Eq. (1.2)

In this section, we will construct one- and two-breather and rogue wave solutions for System (1.2) on nonvanishing backgrounds: the continuous wave (cw) backgrounds as $q_{1}=a\,\mathrm{exp}\,i\,(\kappa \, x+\omega t), \ q_{2}=b\,\mathrm{exp}\,i\,(\kappa \, x+\omega t)$.

Substituting the nonvanishing seeds $q_{1}=a\,\mathrm{exp}\,i\,(\kappa \, x+\omega t), \ q_{2}=b\,\mathrm{exp}\,i\,(\kappa \, x+\omega t)$ into Lax pair (2.1) and setting $\phi _{1}=f_{1},\ \varphi _{1}=f_{2}\,\mathrm{exp}\,[-i\,(\kappa \, x+\omega t)],\ \psi _{1}=f_{3}\,[-i\,(\kappa \, x+\omega t)]$, one can obtain

$$\begin{aligned}&f_{1x}=i\,\lambda _{1} \,f_{1}+a\,f_{2}+b\,f_{3}, \end{aligned}$$

(4.1a)

$$\begin{aligned}&f_{2x}+i\,\lambda _{1} \,f_{2}=-a\,\sigma _{1} \,f_{1}+i\,\kappa \,f_{2}, \end{aligned}$$

(4.1b)

$$\begin{aligned}&f_{3x}+i\,\lambda _{1} \,f_{3}=-b\,\sigma _{2} \,f_{1}+i\,\kappa \,f_{3}, \end{aligned}$$

(4.1c)

$$\begin{aligned}&f_{1t}=\gamma \,f_{1}-a\,\alpha \,f_{2}-b\,\alpha \,f_{3},\end{aligned}$$

(4.1d)

$$\begin{aligned}&f_{2t}-i\,\omega \,f_{2}=a\,\sigma _{1}\,\alpha \,f_{1}+[i\,a^{2} \sigma _{1}(\beta +2\,\varepsilon \,\kappa )\nonumber \\&\quad -2\,i\,\beta \,\lambda _{1}^{2}]f_{2} +i\,a\,b\,\sigma _{1}\,(\beta +2\,\varepsilon \,\kappa )f_{3},\end{aligned}$$

(4.1e)

$$\begin{aligned}&f_{3t}-i\,\omega \,f_{3}=b\,\sigma _{2}\,\alpha \,f_{1} +i\,a\,b\,\sigma _{2}\,(\beta +2\,\varepsilon \,\kappa )f_{2}\nonumber \\&\quad +[i\,b^{2}\sigma _{1}(\beta +2\,\varepsilon \,\kappa )-2\,i\,\beta \,\lambda _{1}^{2}]f_{3}, \end{aligned}$$

(4.1f)

where $\alpha =\kappa -\kappa ^{2}\,\varepsilon -2\kappa \,\varepsilon \,\lambda _{1} +2(\lambda _{1}-2\varepsilon \,\lambda _{1}^{2}+\varepsilon \,a^{2}\sigma _{1} +\varepsilon \,b^{2}\,\sigma _{2}),\ \ \beta =2\varepsilon \,\lambda _{1},\ \ \gamma =i[2\,\beta \,\lambda _{1}^{2}-(a^{2}\sigma _{1}+\,b^{2}\,\sigma _{2}) (\beta +2\varepsilon \,\kappa )].$

Supposing $\lambda _{1}=\kappa _{s}+i\,A_{s}=\kappa /2+i\,A_{s}$ and through direct computations, we can obtain

$$\begin{aligned} \phi _{1}&=\frac{i\,(\mu _{1}-2\lambda _{1})}{2\,b\,\sigma _{2}}\,\mathrm{exp}\,(\mu _{1}\,x+\vartheta _{1}\,t)\nonumber \\&\quad +\frac{i\,(\mu _{2}-2\lambda _{1})}{2\,b\,\sigma _{2}}\,\mathrm{exp}\,(\mu _{2}\,x+\vartheta _{2}\,t), \end{aligned}$$

(4.2a)

$$\begin{aligned} \varphi _{1}&=\frac{a\,\sigma _{1}}{b\,\sigma _{2}}\,\mathrm{exp}\,(\mu _{1}\,x+\vartheta _{1}\,t)+\frac{a\,\sigma _{1}}{b\,\sigma _{2}}\,\mathrm{exp}\,(\mu _{2}\,x+\vartheta _{2}\,t)\nonumber \\&\quad -\frac{b}{a}\,\mathrm{exp}\,(\mu _{3}\,x+\vartheta _{3}\,t), \end{aligned}$$

(4.2b)

$$\begin{aligned} \psi _{1}&=\mathrm{exp}\,(\mu _{1}\,x+\vartheta _{1}\,t)+\mathrm{exp}\,(\mu _{2}\,x+\vartheta _{2}\,t)\nonumber \\&\quad +\mathrm{exp}\,(\mu _{3}\,x+\vartheta _{3}\,t), \end{aligned}$$

(4.2c)

where $\mu _{1}=i(\kappa +s)/2, \ \mu _{2}=i(\kappa -s)/2,\ \mu _{3}=i(\kappa -\lambda _{1}),\ \nu _{1}=k_{1}\,\mu _{1}+k_{0},\ \nu _{2}=k_{1}\,\mu _{2}+k_{0},\ \nu _{3}=i(\omega +2\,\lambda _{1}^{2}-4\,\varepsilon \,\lambda _{1}^{3})$ and $s=2\sqrt{a^{2}\,\sigma _{1}+b^{2}\,\sigma _{2}-A_{s}^{2}},\ k_{1}=i[\kappa -\kappa ^{2}\varepsilon -2\kappa \,\varepsilon \,\lambda _{1}+2(\lambda _{1}-2\varepsilon \lambda _{1}^{2}+a^{2}\,\sigma _{1}\,\varepsilon +b^{2}\,\sigma _{2}\,\varepsilon )]/2, \ k_{0}=i[\omega +\kappa ^{2}\,\varepsilon \,\lambda _{1}-a^{2}\,\sigma _{1}-b^{2}\,\sigma _{2}+\kappa (-\lambda _{1}+2\,\varepsilon \,\lambda _{1}^{2}+2\,a^{2}\,\varepsilon \,\sigma _{1}+2\,b^{2}\,\varepsilon \,\sigma _{2})]$. Substituting the above conclusions into Eq. (2.3), we can obtain three types of solutions for System (1.2). Now, we will analyze the novel properties of those solutions under three different cases.

Case 4.1 When $a^{2}\,\sigma _{1}+b^{2}\,\sigma _{2}=A_{s}^{2}$, then the solutions will have nothing to do with x and t, and in this case, the solutions are not significant.

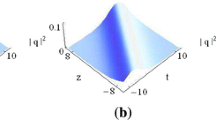
Case 4.2 In case of $a^{2}\,\sigma _{1}+b^{2}\,\sigma _{2}>A_{s}^{2}$, taking $s=\zeta +i\,\eta$, then $\zeta =2\sqrt{a^{2}\,\sigma _{1}+b^{2}\,\sigma _{2}-A_{s}^{2}},\ \eta =0$. Substituting the above conclusions into Eqs. (4.2) and (2.3), one can derive the Ma-breather solutions for System (1.2) as shown in Fig. 4. One can observe from Fig. 4 that the breathers time periodically propagate on cw backgrounds, i.e., they are the Ma-breathers [37].

Fig. 4

Evolution of the Ma-breather solutions. Parameters are: $a=1$, $b=1.2$, $\kappa =1$, $A_{s}=1$, $\sigma _{1}=\sigma _{2}=1$ and $\varepsilon =0.1$

In addition, defining $A_{s}=\sqrt{a^{2}\,\sigma _{1}+b^{2}\,\sigma _{2}}-\epsilon ^{2}$ and taking $\epsilon \rightarrow 0$, that is to say, $A_{s}\rightarrow (\sqrt{a^{2}\,\sigma _{1}+b^{2}\,\sigma _{2}})^{-}$, we can derive rogue wave solutions for System (1.2) as shown in Fig. 5.

Fig. 5

Evolution of the rogue wave solutions. Parameters are: $a=1$, $b=1.2$, $\kappa =1$, $A_{s}=1$, $\sigma _{1}=\sigma _{2}=1$ and $\varepsilon =0.1$

Case 4.3 In case of $a^{2}\,\sigma _{1}+b^{2}\,\sigma _{2}<A_{s}^{2}$, taking $s=\zeta +i\,\eta$, then $\zeta =0,\, \eta =2\sqrt{A_{s}^{2}-a^{2}\,\sigma _{1}-b^{2}\,\sigma _{2}}$. Substituting the above conclusions into Eqs. (4.2) and (2.3), one can derive the Akhmediev breather solutions for System (1.2) as shown in Fig. 6. From Fig. 6, one can find that the Akhmediev breathers [38] are periodic in the space coordinate and aperiodic in the time coordinate. Generally, the time-aperiodic solution can be regarded as a homoclinic or separatrix trajectory in the infinite-dimension phase space of the solutions for System (1.2) with periodic boundary conditions in space. Through numerical simulation, one can gain the facts that in Fig. 6:

(1) the periods are in inverse proportion to the value of $A_{s}^{2}-a^{2}\,\sigma _{1}-b^{2}\,\sigma _{2}$, so the group velocities of the Akhmediev breathers are dependent on parameters $A_{s}, a,\ b,\ \sigma _{1}$ and $\sigma _{2}$;

Fig. 6

Evolution of the Akhmediev breather solutions. Parameters are: $a=1$, $b=0.6$, $\kappa =2.2$, $A_{s}=1.4$, $\sigma _{1}=\sigma _{2}=1$ and $\varepsilon =0.1$

(2) parameters a and b can affect the amplitudes.

Similarly, Case 4.2, defining $A_{s}=\sqrt{a^{2}\,\sigma _{1}+b^{2}\,\sigma _{2}}+\epsilon ^{2}$ and taking $\epsilon \rightarrow 0$, that is to say, $A_{s}\rightarrow (\sqrt{a^{2}\,\sigma _{1}+b^{2}\,\sigma _{2}})^{+}$, we can derive another rogue wave solutions for System (1.2) as shown in Fig. 7.

Fig. 7

Evolution of the rogue wave solutions. Parameters are: $a=1$, $b=0.6$, $\kappa =2.2$, $A_{s}=1.4$, $\sigma _{1}=\sigma _{2}=1$ and $\varepsilon =0.1$

Comparing with Figs. 5 and 7, one can observe that the rogue wave solitons can be resulted from two different processes: the localized process of the Akhmediev breathers and the reduction process of the Ma-breathers.

Case 4.4 Choosing $\lambda _{2}=\kappa /2+i\,B_{s}$ and through direct computations, we can obtain

$$\begin{aligned} \phi _{2}&=\frac{i\,(\varrho _{1}-2\lambda _{2})}{2\,b\,\sigma _{2}}\,\mathrm{exp}\,(\varrho _{1}\,x+\delta _{1}\,t)\nonumber \\&\quad +\frac{i\,(\varrho _{2}-2\lambda _{2})}{2\,b\,\sigma _{2}}\,\mathrm{exp}\,(\varrho _{2}\,x+\delta _{2}\,t), \end{aligned}$$

(4.3a)

$$\begin{aligned} \varphi _{2}&=\frac{a\,\sigma _{1}}{b\,\sigma _{2}}\,\mathrm{exp}\,(\varrho _{1}\,x+\delta _{1}\,t)+\frac{a\,\sigma _{1}}{b\,\sigma _{2}}\,\mathrm{exp}\,(\varrho _{2}\,x+\delta _{2}\,t)\nonumber \\&\quad -\frac{b}{a}\,\mathrm{exp}\,(\varrho _{3}\,x+\delta _{3}\,t), \end{aligned}$$

(4.3b)

$$\begin{aligned} \psi _{2}&=\mathrm{exp}\,(\varrho _{1}\,x+\delta _{1}\,t)+\mathrm{exp}\,(\varrho _{2}\,x+\delta _{2}\,t)\nonumber \\&\quad +\mathrm{exp}\,(\varrho _{3}\,x+\delta _{3}\,t), \end{aligned}$$

(4.3c)

where $\varrho _{1}=i(\kappa +\theta )/2, \ \varrho _{2}=i(\kappa -\theta )/2,\ \varrho _{3}=i(\kappa -\lambda _{2}),\ \delta _{1}=m_{1}\,\varrho _{1}+m_{0},\ \delta _{2}=m_{1}\,\varrho _{2}+m_{0},\ \delta _{3}=i(\omega +2\,\lambda _{2}^{2}-4\,\varepsilon \,\lambda _{2}^{3})$ and $\theta =2\sqrt{a^{2}\,\sigma _{1}+b^{2}\,\sigma _{2}-B_{s}^{2}},\ m_{1}=i[\kappa -\kappa ^{2}\varepsilon -2\kappa \,\varepsilon \,\lambda _{2} +2(\lambda _{2}-2\varepsilon \lambda _{2}^{2}+a^{2}\,\sigma _{1} \,\varepsilon +b^{2}\,\sigma _{2}\,\varepsilon )]/2, \ m_{0}=i[\omega +\kappa ^{2}\,\varepsilon \,\lambda _{2}-a^{2} \,\sigma _{1}-b^{2}\,\sigma _{2}+\kappa (-\lambda _{2} +2\,\varepsilon \,\lambda _{2}^{2}+2\,a^{2}\,\varepsilon \,\sigma _{1} +2\,b^{2}\,\varepsilon \,\sigma _{2})]$. Substituting the above conclusions into Eq. (3.2), we can obtain two-breather solutions for System (1.2) as shown in Fig. 8.

Fig. 8

Evolution of the two-breather solutions. Parameters are: $a=1$, $b=0.6$, $\kappa =2.2$, $A_{s}=1.4$, $B_{s}=1.7$ $\sigma _{1}=\sigma _{2}=1$ and $\varepsilon =1.3$

5 Conclusions

Our main attention has focused on System (1.2) which governs the propagation properties of ultrashort solitons in two ultrashort optical fields. We have obtained constructed N-fold DT based on 3$\times$ 3 lax pair for System (1.2). In addition, we have derived one- and two-soliton solutions on vanishing backgrounds and breather and rogue wave solutions on nonvanishing backgrounds for System (1.2). Figures have been plotted to display the dynamic features of those solutions. By the graphical analysis of Figs. 1, 2, 3, 4, 5, 6, 7, and 8, we have discussed the following characteristics of the solitons in the propagation:

• Elastic interactions of two solitons.

• Mutual attractions and repulsions of bound solitons.

• Propagation properties of Ma-breathers, Akhmediev breathers, two-breathers, and rogue waves.