1 Introduction

Liquid sloshing phenomena play an important role in automotive, civil, marine, and aerospace engineering. Several analytical and numerical methods have been developed in the literature to study the static and dynamic properties of fluids moving in partially filled containers. The development of analytical methods for the analysis of liquid sloshing is very challenging because dynamic boundary conditions at the free surface are nonlinear and the position time history of the liquid free surface is not known a priori. For these reasons, the analytical methods developed in the literature are more suited to simplified scenarios characterized by regular geometric tank shapes and a small-amplitude sloshing motion [34, 35].

Most of the numerical methods developed to solve liquid sloshing problems are based on two different approaches, namely Lagrangian and Eulerian. In the former approach, the mesh is attached to the fluid material points, while in the latter approach the domain under investigation is discretized using a stationary mesh. Eulerian techniques are particularly suited for the study of turbulent flow, but the identification of the fluid free surface is not straightforward and requires using a very refined mesh. On the other hand, Lagrangian methods are accurate in predicting the location of the fluid free surface, but the loss in numerical accuracy resulting from severe deformations requires the use of adaptive remeshing algorithms. In order to address the difficulties encountered by grid-based numerical methods in the study of physical systems which exhibit very large deformations, such as liquid sloshing, several mesh-free methods have been developed [42].

Among the most popular mesh-free methods, the smoothed particle hydrodynamic (SPH) has been widely used in the field of fluid dynamics to study complex systems characterized by turbulence and multiphase flow. The level of difficulty in the analysis of liquid sloshing problems increases considerably when the container is component of a complex mechanical system such as a tanker truck, a railroad vehicle, or a spacecraft. A recently proposed total Lagrangian continuum-based liquid sloshing approach based on the absolute nodal coordinate formulation (ANCF) allows for a systematic integration of fluid and vehicle models using multibody system (MBS) algorithms [78].

In the field of ocean and coastal engineering, hydrodynamic impact loads due to liquid sloshing can have an effect on the structural integrity of marine systems. The study of breaking waves has been the subject of several investigations in the field of liquefied natural gas (LNG) vessels and Naval engineering [8, 10,11,12, 16, 23, 33, 61, 64]. In the field of vehicle system dynamics, on the other hand, the main concern is not the effect of liquid sloshing on the structural integrity of the containers, but rather on the vehicle dynamics and stability. In order to analyze the effect of liquid sloshing on the vehicle dynamics and stability, the average liquid motion inside the container and the time-varying fluid inertia forces are the main focus. For this reason, simple approaches based on models with rigid bodies representing the fluid motion are often used when the vehicle or container dynamics and stability are the main concern. Continuum-based ANCF sloshing formulations have been recently proposed for the implementation in MBS algorithms to study the effect of liquid sloshing on vehicle dynamics. In sloshing scenarios, however, turbulence may occur, and therefore, it is necessary to quantify and evaluate its effect on the average nominal motion of the fluid. Several researchers investigated the breaking wave effects induced by nonlinear sloshing motion using the finite element and finite difference methods [15, 31, 39,40,41, 44, 46, 47, 74]. In this paper, the effect of breaking waves on the average nominal motion of the fluid is examined by developing two different models; a continuum-based ANCF model that can accurately represent the nominal motion, but does not capture the effect of turbulence; and a mesh-free SPH model that can capture the turbulence effect. Comparison between the results of these two models will shed light on the significance of the turbulence effect in sloshing scenarios. It will also shed light on the model accuracies as well as the computational cost.

The main goal of this paper is to perform for the first time a detailed comparative quantitative study of the effect of turbulence and wave breaking phenomena on liquid sloshing using the SPH and ANCF methods. This paper makes the following specific contributions:

  1. (1)

    The paper describes the ANCF and SPH discretization to obtain the discrete dynamic equations which govern liquid sloshing phenomena. Based on this description, the fundamental differences between the ANCF and SPH approaches are discussed.

  2. (2)

    A detailed quantitative comparison between the ANCF and SPH approaches when solving sloshing problems is performed. The comparative numerical study is focused on evaluating both the accuracy and computational cost of the two different approaches. To this end, two benchmark examples are used; the dam break and sloshing tank benchmark problems. These two benchmark problems are solved for different motion scenarios in order to compare the results of different ANCF and SPH models.

  3. (3)

    The effects of breaking waves on liquid sloshing dynamics are investigated. The good agreement between the ANCF and SPH results in the case of light and moderate turbulence scenarios demonstrates that ANCF finite elements can accurately predict the nominal fluid motion and inertia forces. In case of severe turbulence, it is found that the ANCF approach overpredicts the amplitude of oscillations of the fluid center of mass as compared to the SPH method, due to the absence of mechanical energy dissipation associated with the fluid mixing.

  4. (4)

    The ANCF liquid sloshing results are validated against experimental data, and verified using the results of the SPH models. The validation and verification of the ANCF liquid sloshing approach are necessary in order to justify using such a new approach in future liquid sloshing investigations, particularly when complex motion scenarios are considered.

The paper is organized as follows. In Sect. 2, the basic governing equations of the liquid sloshing phenomena are presented, while the solution procedures used in this investigation for solving these equations using the SPH and ANCF approaches are presented in Sects. 3 and 4, respectively. Section 5 provides a summary of the fundamental differences between the SPH and ANCF approaches. In Sect. 6, the numerical results obtained for the two benchmark problems are validated against experimental data, and the effects of breaking waves on liquid sloshing dynamics are discussed. Section 7 presents a summary and the main conclusions drawn from this study.

2 Basic governing equations

The dynamic behavior of fluids is governed by the Navier–Stokes equations, derived by combining the continuity and momentum balance equations. The continuity equation is written as

$$\begin{aligned} \frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathbf{v})=0 \end{aligned}$$
(1)

where \(\rho \) is the mass density, t is time, and v is the velocity vector. In the case of incompressible materials, Eq. 1 reduces to \(\nabla \cdot \mathbf{v}=0\). The momentum balance equation can be written as

$$\begin{aligned} \rho \mathbf{a}=\nabla \cdot {\varvec{\upsigma }}+\mathbf{b} \end{aligned}$$
(2)

where \(\mathbf{a}={d\mathbf{v}}/{dt}\) is the absolute acceleration vector, b is the body force vector, and \({\varvec{\upsigma }}\) is the Cauchy stress tensor. In the case of isotropic Newtonian fluids, the fluid constitutive equations can be written as

$$\begin{aligned} {\varvec{\upsigma }}=-\left[ {p+\lambda \hbox {tr}(\mathbf{D})} \right] \mathbf{I}+2\mu \mathbf{D} \end{aligned}$$
(3)

where p is the hydrostatic pressure, \(\mathbf{D }=\left( \nabla \mathbf{v }+\left( {\nabla \mathbf{v }} \right) ^{T}\right) {/}2\) is the rate of deformation tensor, \(\nabla \mathbf{v }\) is the gradient of the velocity vector, \(\hbox {tr}\) is the trace operator, \(\mathbf{I }\) is the \(3\times 3\) identity matrix, and \(\lambda \) and \(\mu \) are viscosity coefficients. Substituting the expression of the stress defined in Eq. 3 into Eq. 2, one obtains the Navier–Stokes equations

$$\begin{aligned} \rho \mathbf{a}=-\nabla \cdot \left( {p\mathbf{I}} \right) +\lambda \nabla \cdot \left( {\hbox {tr}(\mathbf{D})\mathbf{I}} \right) +2\mu \nabla \cdot \mathbf{D}+\mathbf{b} \end{aligned}$$
(4)

In the case of incompressible fluids, Eq. 4 reduces to

$$\begin{aligned} \mathbf{a}=-\frac{\nabla p}{\rho }+\frac{\mu }{\rho } \nabla ^{2}{} \mathbf{v}+\frac{\mathbf{b}}{\rho } \end{aligned}$$
(5)

where \(\nabla ^{2}\) is the Laplace operator. In the following sections, the ANCF and SPH formulations and procedures used to obtain the solution of Eq. 4 are discussed. This discussion will shed light on the fundamental differences between the two approaches.

3 SPH approach

The smoothed particle hydrodynamics (SPH) method is a mesh-free, particle-based, Lagrangian numerical technique first introduced by Lucy [53] and Gingold and Monaghan [22]. The SPH method was successfully applied to complex problems, such as fracture, blast, penetration, impact and fluid free surface [6, 7, 9, 24, 25, 38, 42, 43, 45, 48, 65, 76]. The analysis of liquid sloshing problems using the SPH method has been studied by modifying the spatial derivative and by accounting for the boundary particles [17, 70]. Several investigations on multiphase flow and surface tension problems have been performed using the SPH method [26, 32, 58, 60].

While the SPH method has several advantages, it also has its own technical drawbacks. Wen et al. [79] developed the conservative smoothing approach as a cure for tensile instability. The SPH method also has difficulty in enforcing boundary conditions, which was later rectified by Randles and Libersky [66]. The stability and convergence analysis of mesh-free methods have been studied by Belytschko et al. [3,4,5]. The first SPH penalty contact algorithm was developed by Vignjevic and Campbell [75]. However, it was shown that this approach often excited zero energy modes. Beissel and Belytschko [2] proposed an alternative method to stabilize nodal integration, referred to as the least square stabilization method. Chen et al. [14] and Chen and Beraun [13] proposed a corrective smoothed particle method (CSPM) to improve the calculation accuracy.

The SPH method can be developed using the kernel estimate. A function \(A\left( \mathbf{x}\right) \) can be approximated by smoothing kernel functions \(\phi _{h} \left( \mathbf{x}-\mathbf{x}_{j}\right) \) centered around \(\mathbf{x}\) as

$$\begin{aligned} A\left( \mathbf{x} \right) \approx \sum \nolimits _{j=1}^N {\phi _h \left( {\mathbf{x}-\mathbf{x}_j } \right) A\left( {\mathbf{x}_j } \right) \Delta V_j } , \forall \mathbf{x}_j \in \Omega _{s} \end{aligned}$$
(6)

where \(\Omega _{s}\) is the domain, \(\Delta V_j ={m_j }/\rho _j,m_{j},\rho _{j} \), and \(\mathbf{x}_{j}\) are the nodal volume, mass, mass density, and position of particle j, respectively, and N is the total number of particles within the support domain of the smoothing function at \(\mathbf{x}\). If the kernel selected is sufficiently smooth, the gradient of the approximation function \(A\left( \mathbf{x} \right) \) is calculated as

$$\begin{aligned} \nabla A\left( \mathbf{x} \right) \approx \sum \nolimits _{j=1}^N {\nabla \phi _h \left( {\mathbf{x}-\mathbf{x}_j } \right) A\left( {\mathbf{x}_j } \right) \Delta V_{j}} \end{aligned}$$
(7)
Fig. 1
figure 1

Schematic illustration of a SPH smoothing kernel function in the three-dimensional case

Full size image

Several smoothing kernel functions can be used, such as the cubic spline function defined as

$$\begin{aligned} \phi _{h} \left( q \right) =\frac{C}{h^{n}}\left\{ {{\begin{array}{c@{\quad }c} {1-\frac{3}{2}q^{2}+\frac{3}{4}q^{3}}&{} {0\le q\le 1} \\ {\frac{1}{4}\left( {2-q} \right) ^{3}}&{} {1\le q\le 2} \\ 0&{} \hbox {otherwise} \\ \end{array} }} \right. \end{aligned}$$
(8)

where h is the smoothing length or support size, \(q={\left\| {\mathbf{x}-\mathbf{x}_j } \right\| }/h, n\) is the space dimension, and C is a normalization factor, defined as

$$\begin{aligned} C=\left\{ {{\begin{array}{l@{\quad }l} {2/3}&{} {n=1} \\ {{10}/7\pi }&{} {n=2} \\ {1/\pi }&{} {n=3} \\ \end{array} }} \right. \end{aligned}$$
(9)

An illustration of an SPH smoothing kernel function in the three-dimensional case is shown in Fig. 1. Using the SPH approximations given in Eqs. 6 and 7 with Eq. 1, the Lagrangian description leads to

$$\begin{aligned} \frac{d\rho _i }{dt}=\rho _i \sum \nolimits _{j=1}^N {\frac{m_j }{\rho _j }(\mathbf{v}_i -\mathbf{v}_j )\nabla \phi _{ij} } \end{aligned}$$
(10)

where \(\phi _{ij} \equiv \phi _h \left( {\mathbf{x}_i -\mathbf{x}_j} \right) \), and \(\mathbf{v}={d\mathbf{x}}/{dt}\) is the velocity vector. The incompressible Navier–Stokes equations can be discretized as

$$\begin{aligned} \dfrac{d\mathbf{v}_i }{dt}= & {} -\sum \nolimits _{j=1}^N {m_j \left( {\frac{p_i }{\rho _i^2 }+\frac{p_j }{\rho _j^2 }+\prod \nolimits _{ij} } \right) \nabla \phi _{ij} } \nonumber \\&+\,\mu \sum \nolimits _{j=1}^N {\frac{m_j }{\rho _j }\left( {\mathbf{v}_i -\mathbf{v}_j } \right) \nabla ^{2}\phi _{ij} } +\frac{b_i }{\rho _i } \end{aligned}$$
(11)

where \(\prod _{ij} \) is an artificial viscosity term, defined as

$$\begin{aligned} \Pi _{ij} =\left\{ {{\begin{array}{c@{\quad }c} {\dfrac{Q_2 \mu _{ij}^2 -Q_1 c_{ij} \mu _{IJ} }{\rho _{ij} }}&{} {\hbox {if}\;(\mathbf{v}_i -{} \mathbf{v}_j )\cdot (\mathbf{x}_i -{} \mathbf{x}_j )<0\;} \\ 0&{} {\hbox {otherwise}} \\ \end{array} }} \right. \end{aligned}$$
(12)

In the above equation, \(Q_1\) and \(Q_2\) are the linear and quadratic bulk viscosity coefficients, respectively, \(c_i\) is the speed of sound at \(\mathbf{x}_i \), \(\rho _{ij} ={(\rho _i +\rho _j )}/2\), \(\mu _{ij} ={\left[ {h_{ij} (\mathbf{v}_i -\mathbf{v}_j )\cdot (\mathbf{x}_i -\mathbf{x}_j )} \right] }/{\left[ {(\mathbf{x}_i -\mathbf{x}_j )^{2}+0.01 h_{ij} } \right] }\), \(h_{ij} ={(h_i +h_j )}/2\), and \(c_{ij} ={(c_i +c_j )}/2\) [57].

4 ANCF approach

As previously mentioned, in studying the effect of liquid sloshing on vehicle dynamics and stability, the main concern is predicting the average time-varying fluid inertia forces. Simple rigid-body pendulum models are often used to obtain an estimate of the fluid inertia forces and their effect on the vehicle dynamics and stability. In this investigation, the continuum-based FE absolute nodal coordinate formulation (ANCF), which allows for developing a total Lagrangian non-incremental solution procedure suited for the nonlinear analysis of large-rotation and large-deformation problems, is used [69]. The ANCF method was originally developed for solving solid mechanics problems, but it has also been successfully applied for predicting the fluid average inertia properties in liquid sloshing problems. Wei et al. [78] developed a total Lagrangian continuum-based ANCF liquid sloshing formulation which can be systematically integrated with MBS algorithms. The ANCF liquid sloshing method addresses the deficiencies of the low-order continuum-based liquid sloshing formulation proposed by Wang et al. [77], which cannot describe large fluid displacements. ANCF liquid sloshing models were used by Shi et al. [72] with MBS railroad vehicle algorithms that allow for wheel/rail separation and by Nicolsen et al. [59] with a fully nonlinear tanker truck vehicle model. The validation of the ANCF liquid sloshing solution procedure was performed by Grossi and Shabana [27], who compared the results of this method with numerical and experimental data published in the literature. Grossi and Shabana [28] also generalized the continuum-based ANCF liquid sloshing approach to the analysis of non-Newtonian fluids and studied the effect of crude oil sloshing on railroad vehicle dynamics and stability.

In the ANCF description, the vector of element nodal coordinates includes both absolute position and gradient coordinates, allowing for describing arbitrarily complex fluid shapes and correctly capturing rigid-body motion. The use of position vector gradients as ANCF nodal coordinates allows for modeling the interaction between the fluid and the external environment in a straightforward manner; ensures the continuity of the gradient vectors and their time derivative, strains, and stresses at the nodal points; and leads to a constant mass matrix and zero centrifugal and Coriolis forces. Furthermore, because a small number of ANCF elements can be used to describe very complex fluid shapes, models with significantly fewer degrees of freedom (DOF) than what is required by other existing methods can be developed to achieve the same accuracy [27]. Because the ANCF liquid sloshing method is based on a total Lagrangian approach, the mesh moves with the fluid material points and allows for predicting the location of the fluid free surface with higher degree of accuracy. The ability to correctly capture highly deformed fluid shapes is necessary in order to have an accurate estimate of the fluid inertia forces. It is important to point out that in the case of severe mesh distortion, an adaptive mesh refinement algorithm should be used to prevent loss of the solution accuracy. Another important feature of the ANCF liquid sloshing method is that it can be systematically integrated with MBS solvers without the need for the use of a co-simulation approach. However, due to the use of a continuum-based Lagrangian mesh, the ANCF method does not capture turbulence, splashing effects, and the motion of solids through fluids.

The position field of an ANCF element j can be written as \(\mathbf{r}^{j}\left( {\mathbf{x}^{j},t} \right) =\mathbf{S}^{j}\left( {\mathbf{x}^{j}} \right) \mathbf{e}^{j}\left( t \right) \), where \(\mathbf{r}^{j}\) is the global position vector of an arbitrary point on the element j, \(\mathbf{S}^{ j}\) is the shape function matrix that depends on the element spatial coordinates \(\mathbf{x}^{j}=\left[ {x_{1}^{j} \;x_{2}^{j} \;x_{3}^{j} } \right] ^{T}\) and \(\mathbf{e}^{j}\) is the vector of time-dependent element nodal coordinates [69]. The vector of nodal coordinates of element j at node k is defined for a fully parameterized three-dimensional element as \(\mathbf{e}^{j}=\left[ {{\begin{array}{llll} {\left( {\mathbf{r}^{jk}} \right) ^{T}}&{} {\left( {\mathbf{r}_{x_1 }^{jk} } \right) ^{T}}&{} {\left( {\mathbf{r}_{x_2 }^{jk} } \right) ^{T}}&{} {\left( {\mathbf{r}_{x_3 }^{jk} } \right) ^{T}} \\ \end{array} }} \right] ^{T}\), where \(\mathbf{r}^{jk}\) is the absolute position vector of node k of the element j and \(\mathbf{r}_{x_l }^{jk} \) is the gradient vector obtained by differentiation with respect to the element spatial coordinates \(x_l \), \(l=1,2,3\). The use of the ANCF total Lagrangian formulation allows for simply writing the absolute acceleration vector as \(\mathbf{a}^{j}=\mathbf{S}^{j}{\ddot{\mathbf{e}}}^{j}\), where \({\ddot{\mathbf{e}}}^{j}\) is the second time derivative of the nodal coordinate vector \(\mathbf{e}^{j}\). Similarly, the absolute velocity vector is defined as \(\mathbf{v}^{j}=\mathbf{S}^{j}{\dot{\mathbf{e}}}^{j}\). The fluid partial differential equations of motion shown in Eq. 4 can be reduced to a set of second-order ordinary differential equations using the principle of virtual work and the ANCF displacement field as

$$\begin{aligned} \mathbf{M}^{j}{\ddot{\mathbf{e}}}^{j}=\mathbf{Q}_b^j +\mathbf{Q}_t^j +\mathbf{Q}_C^j -\mathbf{Q}_P^j +\mathbf{Q}_v^j \end{aligned}$$
(13)

where \(\mathbf{M}^{j}=\int _{V^{j}} {\rho ^{j}\left( {\mathbf{S}^{j}} \right) ^{T}{} \mathbf{S}^{j}\mathrm{{d}}V^{j}} \) is a constant symmetric mass matrix, \(V^{j}\) is the element volume, \(\mathbf{Q}_b^j =\int _{V^{j}} {\left( {\mathbf{S}^{j}} \right) ^{T}{} \mathbf{b}^{j}\mathrm{{d}}V^{j}} \) is the vector of generalized body forces, \(\mathbf{Q}_t^j =\int _{s^{j}} {\left( {\mathbf{S}^{j}} \right) ^{T}{\varvec{\upsigma }}^{j}{} \mathbf{n}^{j}ds^{j}} \) is the vector of generalized surface traction forces, \(s^{j}\) is the surface area, \(\mathbf{n}^{j}\) is the unit outward vector normal to \(s^{j}\), \(\mathbf{Q}_C^j =\left( {\mathbf{S}^{j}} \right) ^{T}{} \mathbf{F}_C^j \) is the vector of generalized contact forces, \(\mathbf{F}_C^j \) is a penalty force vector, \(\mathbf{Q}_v^j =-\int _{V^{j}} {2\mu \left[ {\left( {\mathbf{C}_r^j } \right) ^{-1}{\varvec{{\dot{\upvarepsilon }}}}^{j}\left( {\mathbf{C}_r^j } \right) ^{-1}} \right] } :\left( {{\partial {{\varvec{\upvarepsilon }}}^{j}}/{\partial \mathbf{e}^{j}}} \right) \mathrm{{d}}V^{j}\) is the vector of generalized viscous forces, \(\mathbf{C}_r^j =\left( {\mathbf{J}^{j}} \right) ^{T}{} \mathbf{J}^{j}\) is the right Cauchy–Green deformation tensor, \(\mathbf{J}^{j}\) is the matrix of position vector gradients, \({\varvec{{\upvarepsilon }}}^{j}=1/{2\left( {\mathbf{C}_r^j -\mathbf{I}} \right) }\) is the Green-Lagrange strain tensor, \(\mathbf{Q}_P^j =\int _{V^{j}} {\left( {{\partial U^{j}}/{\partial \mathbf{e}^{j}}} \right) } \mathrm{{d}}V^{j}\) is the vector of generalized penalty forces, and \(U^{j}\) is a penalty strain energy function [27, 78].

5 Formulation differences

Based on the summary of the SPH and ANCF equations presented in the preceding two sections, the following basic differences between the two formulations can be identified:

  1. 1.

    The SPH formulation is a particle-based approach, while ANCF is a continuum-based approach. Particle kinematics is concerned with discrete points, while in a continuum approach, a distributed-matter description is used. Smoothing the region using splines or other polynomials or functions is not equivalent to using polynomial descriptions for elements with boundaries well defined by nodal points and geometries in the reference configuration. For this reason, the assumed kinematic descriptions are not same.

  2. 2.

    The SPH and ANCF approaches for describing the geometry in the reference configurations are fundamentally different. For ANCF elements, the matrix of position vector gradients in the reference configuration plays a fundamental role.

  3. 3.

    In the SPH approach, a nodal mass is predefined and used to formulate the inertia forces, which is equivalent to using a lumped-mass formulation. Such an approach can be used to describe an arbitrarily large displacement. A diagonal lumped-mass matrix cannot, however, be used with ANCF elements since such a lumping scheme does not allow for correctly describing the rigid-body motion. A consistent mass formulation must be used with ANCF elements.

  4. 4.

    The interaction between the ANCF elements is defined using linear algebraic constraint equations, and this results in constraint (reaction) forces at the nodal points. The use of the constraint connectivity conditions does not require assuming penalty force coefficients. In the SPH approach, the interaction between particle-based regions is defined using a penalty formulation.

  5. 5.

    The use of the discrete inertia representation and the penalty contact formulation to describe the SPH particle interaction has the advantage of allowing for mesh distortions that cannot be conveniently captured using the continuum-based ANCF approach. This, however, comes at the expense of the need for much larger model dimensions that require larger array spaces and costly computational time.

  6. 6.

    The SPH and ANCF formulations of the elastic and/or viscous forces are not equivalent. Different kinematic descriptions are used in the two different approaches. Integration over the element volume and standard FE assembly procedure are required in the ANCF elastic and/or viscous force formulations, while summation over the number of particles is required for the SPH approach (Eq. 11). The standard FE assembly procedure is based on the algebraic connectivity conditions at the element nodes, and this ensures the continuity of the ANCF strains and stresses at the nodal points.

In the following section, a comparative study is performed based on numerical results obtained using the two fundamentally different approaches (SPH and ANCF). This comparative study sheds light on the accuracy and computational efficiency of the two approaches when used for solving liquid sloshing problems. The performance of the SPH particle-based approach and the ANCF continuum-based approach in different sloshing scenarios, and under different excitation conditions is evaluated.

6 Numerical results

In this section, two benchmark problems are considered to compare the performance of the ANCF and SPH methods and evaluate the wave breaking effect in liquid sloshing problems. The first benchmark problem is the dam break example [54, 55], while the second benchmark problem is the sloshing tank example [19], in which liquid sloshing motion is generated in a rectangular tank subjected to horizontal excitation. In both problems, the fluid considered is water, which is assumed to have mass density and dynamic viscosity coefficients of \(1000\;\hbox {kg/m}^{3}\) and \(0.001\;\hbox {Pa}\cdot \hbox {s}\), respectively. The SPH simulations are performed using the commercial software LS-DYNA, while the ANCF results are obtained using the general-purpose MBS software SIGMA/SAMS (Systematic Integration of Geometric Modeling and Analysis for the Simulation of Articulated Mechanical Systems). The numerical time integration methods used to solve the fluid equations of motion in case of the SPH and ANCF methods are the central difference scheme and the third-order Implicit Adams method [29], respectively. The simulations are performed on a computer with an Intel Core i7, 3.4 GHz processor and 8 GB RAM. For both benchmark problems, the convergence rates from the ANCF and SPH methods are studied and the CPU simulation times versus the number of degrees of freedom (DOF) are compared. The numerical errors in the convergence study are calculated using the normalized root-mean square error (NRMSE), \(e_{{n}}\), defined as \(e_n =\sqrt{{\sum _{i=1}^{N_m } {\left( {s_i^c -s_i^r } \right) ^{2}} }/{\sum _{i=1}^{N_m } {\left( {s_i^r } \right) ^{2}} }}\), where \(s_i^c\) and \(s_{i}^{r}\) are the ith computed and reference data points, respectively, and \(N_{m}\) is the total number of data points.

Fig. 2
figure 2

Schematic diagram of dam break problem

Full size image

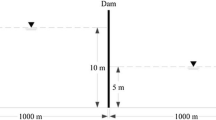
6.1 Dam break benchmark problem

In the dam break problem, the fluid assumes an initially square configuration with side dimension \(H_{w} =0.5\) m, as shown in Fig. 2. The column of fluid collapses over the rigid ground under the effect of gravity, and the position of the water front as a function of time is measured. Dam break flows are encountered in many industrial and environmental processes, and they are well suited for testing the capability of numerical methods of describing complex fluid free surface shapes. The ANCF solution is obtained using a mesh of rectangular ANCF elements, which have cubic shape functions and 6 degrees of freedom per node [62]. Unilateral constraints at the contact interface with the rigid walls are introduced using the same penalty contact algorithm as described by Grossi and Shabana [27]. For the SPH model, the wall rigid boundaries are defined using four-noded Belytschko–Tsay shell elements, whereas the fluid is modeled using SPH nodes. The water constitutive model is defined using a “Null material” with Grüneisen equation of state [30, 56]. The algorithm used to define the contact between the fluid and the rigid boundary is “Automatic Nodes to Surface” [52]. The numerical results and mesh convergence for this problem are presented in terms of the dimensionless time and position coordinates \(t^{*}=t\sqrt{g/{H_{w}}}\) and \(x^{*}={x_f }/{H_{w} }\), respectively, where \(g=9.81\;\hbox {m}/{\hbox {s}^{2}}\) is the gravity constant and \(x_{f}\) is the position of the water front. The converged solution for each method is obtained by calculating the normalized error \(e_{n}\) between two successively refined meshes until \(e_n \le 0.005\). It is found that the converged solution can be obtained using a mesh of \(10\times 10\) ANCF rectangular elements, while a grid of \(125\times 125\) particles is required when using the SPH method. Figure 3 shows a comparison between the SPH and ANCF converged solutions, the experimental results produced by Martin and Moyce [54, 55], and the analytical solution of Ritter [67]. It is clear that the SPH and ANCF solutions are in good agreement. The deviation from the experimental results is partly due to experimental uncertainties and partly to some physical effects which are not accounted for in the numerical results, such as the interaction between the fluid and surrounding air, as discussed in the literature [1, 17, 49]. The evolution of the fluid free surface and the horizontal displacement field are shown at different time instants in Fig. 4, while the convergence is presented in Fig. 5, which shows the normalized error \(e_{{n}}\) versus the number of degrees of freedom (DOF). The reference solutions used to calculate \(e_n \) for the ANCF and SPH methods are a mesh of \(10\times 10\) rectangular ANCF elements and a grid of \(125\times 125\) SPH particles, respectively. It is observed that the ANCF method has a faster convergence rate when compared to the SPH method for this problem. Furthermore, the number of degrees of freedom employed in the converged ANCF solution is nearly 35 times less than that required to obtain the SPH converged solution. Figure 6 shows the simulation time required by the ANCF and SPH models as the number of degrees of freedom is increased. It is observed that the SPH and ANCF curves are almost parallel, indicating that the rate of increase in the CPU time resulting from mesh refinement is similar for both methods. It is interesting to notice that if nearly the same number of degrees of freedom is employed in both the ANCF and SPH models, the SPH approach requires less simulation time but leads to a significant deterioration of the solution accuracy. Furthermore, the CPU time required to obtain the ANCF converged solution is 70% less than the CPU time required by the converged SPH solution. The SPH and ANCF error and CPU time as a function of the model degrees of freedom are presented in Table 1.

Fig. 3
figure 3

Wave front comparisons between ANCF, SPH, Ritter solutions, and experimental data ( ANCF, SPH, Ritter, experimental). (Color figure online)

Full size image
Fig. 4
figure 4

SPH solution of the fluid deformed shape at different dimensionless times (\(125\times 125\) particles; horizontal displacement is in meters). (Color figure online)

Full size image
Fig. 5
figure 5

Convergence of the SPH and ANCF solutions for the dam break problem ( ANCF, SPH). (Color figure online)

Full size image
Fig. 6
figure 6

CPU time for the dam break problem ( ANCF, SPH). (Color figure online)

Full size image
Table 1 Normalized root-mean square error (NRMSE) and CPU time obtained for the broken dam problem
Full size table

6.2 Sloshing tank benchmark problem

Fig. 7
figure 7

Schematic diagram of the sloshing tank problem

Full size image
Fig. 8
figure 8

Wave height predicted using different methods ( ANCF, SPH, experimental). (Color figure online)

Full size image
Fig. 9
figure 9

ANCF solution of the fluid deformed shape

Full size image

The initial configuration and geometry of the sloshing tank problem is shown in Fig. 7. This initial configuration is based on the experiment of Faltinsen and Timokha [19], where the tank length is \(L_{{t}} =1.73\;\hbox {m}\), the water depth is \(H_{{w}} =0.6\;\hbox {m}\), and the tank height is \(H_{{t}} =1.15\;\hbox {m}\). The horizontal harmonic tank motion is defined as \(x_{{{t}}} =A \cos \left( {{2\uppi \, t}/T} \right) \), where \(x_{{t}}\) is the location of the tank, and \(A=0.032\;\hbox {m}\) and \(T=1.5\,\hbox {s}\) are, respectively, the amplitude and period of oscillation. Numerical simulations are performed to compute the value of \(H_{w}\) at a measurement point \(P_{{m}}\), located \(0.05\;\hbox {m}\) away from the left tank wall. The ANCF solution is obtained using a mesh of ANCF brick (solid) elements, which have cubic shape functions and 12 degrees of freedom per node [63]. The rigid rectangular tank is modeled using the ANCF reference node [68]. The SPH model is developed using the procedures and assumptions previously described in this section. Figure 8 shows the wave height measured at the measurement point using a \(12\times 8\) ANCF mesh and a \(340\times 120\) SPH grid. Overall, the numerical results agree well with the experimental data in terms of both amplitude and frequency of oscillation. The smaller peak amplitudes predicted using the SPH method can be explained considering that the SPH solid boundary conditions require a specialized treatment in order to obtain suitable repulsive forces [71]. The fluid deformed shape at different time instants calculated using the ANCF method is shown in Fig. 9. The normalized error \(e_n \) calculated with respect to the set of experimental data provided by Faltinsen and Timokha [19] and the simulation times are shown in Table 2. In agreement with the results obtained for the dam break problem, the ANCF solution, using 1932 degrees of freedom, can be obtained using nearly 40 times fewer coordinates than the number of coordinates required to obtain the SPH solution (81600 coordinates). Furthermore, the CPU time required to obtain the ANCF solution is nearly 25% less than that required to obtain the SPH solution, as reported in Table 2. Figure 10 shows the position of the fluid center of mass calculated with respect to the geometric center of the tank. Overall, the numerical results are in good agreement with the experimental data. It is observed that the SPH method underpredicts the oscillations in the location of the center of mass as compared to experimental measurement. With regard to the convergence characteristic of each method, Fig. 11 shows that the convergence rate of the ANCF method is slower than the SPH one. Figure 12 shows the simulation time obtained using the ANCF and SPH methods as a function of mesh refinement. In agreement with the results obtained for the dam break problem, the rate of increase in CPU time resulting from mesh refinement is similar for both methods.

Table 2 Normalized root-mean square error (NRMSE) and CPU time obtained for the sloshing tank problem
Full size table
Fig. 10
figure 10

Position of the fluid center of mass ( ANCF, SPH, experimental). (Color figure online)

Full size image
Fig. 11
figure 11

Convergence of the SPH and ANCF solutions for the sloshing tank problem ( ANCF, SPH). (Color figure online)

Full size image
Fig. 12
figure 12

CPU time for the sloshing tank problem ( ANCF, SPH). (Color figure online)

Full size image

6.3 Breaking wave effect

In this section, the effect of breaking waves on liquid sloshing dynamics is studied. As the result of sloshing motion, turbulent regions can develop in the fluid and at the interface between the fluid and the container. These regions, which are characterized by irregular fluid fluctuations and mixing, can be accurately captured using Eulerian-based methods or mesh-free Lagrangian formulations, such as SPH. On the other hand, the continuum-based ANCF method cannot be used to capture vortices and wave breaking phenomena. Figure 13 shows localized turbulent regions obtained for the sloshing tank problem described in Sect. 6.2, using the SPH method. For the sloshing scenario considered in Sect. 6.2, the effect of turbulence is negligible, and the results obtained using the ANCF method are in good agreement with the experimental and SPH results. In order to initiate significant turbulence motion, the period and amplitude of excitation of the tank in the sloshing tank problem are changed. Using the values of the excitation amplitude, namely \(A=0.032\;\hbox {m}, 0.084\;\hbox {m}, 0.136\;\hbox {m}\), three different turbulence scenarios are defined as light, moderate and severe, respectively. For each value of excitation amplitude, the effect of varying the excitation frequency on liquid sloshing dynamics is investigated. The time histories of the fluid free surface shape obtained at different time instants for the moderate and severe turbulent scenarios is shown in Figs. 14 and 15, respectively. It is clear that while in the moderate turbulence case the turbulent regions are mainly confined to the fluid free surface, in case of severe turbulence, vorticial flows are generated within the entire fluid volume. Figure 16 shows the x-displacement of the fluid center of mass obtained using the ANCF and SPH methods for each turbulent scenario considering three different values of excitation frequency \(\omega _{{e}} =1.12\omega _{{ 0}} ,\;1.48\omega _{{ 0}} ,\;2.22\omega _{{ 0}} \), where \(\omega _{{ 0}} =0.6\;\hbox {Hz}\) is the first frequency of the free oscillations. The sloshing oscillation frequency can be calculated for a rectangular tank using the analytical relationship \(\omega _n^2 =gk_n \tanh \left( {k_n H_{{w}} } \right) \), where \(\omega _{n}\) is the nth sloshing oscillation frequency, g is the gravity constant, \(k_n ={\left( {2n+1} \right) \pi }/{L_{{t}} }\) is the wave number, and n is the sloshing mode number [19, 21, 50, 51, 73, 80]. It is important to point out that the equation \(\omega _n^2 =gk_n \tanh \left( {k_n H_{{w}} } \right) \) is valid under the assumptions of inviscid, incompressible, irrotational flow and negligible surface tension. Figure 16 shows that in the case of light and moderate turbulence, the ANCF and SPH solutions are in good agreement. These results show that the ANCF continuum-based method is capable of accurately averaging the fluid inertia properties, thus leading to an accurate calculation of the position of the fluid center of mass. As the effects of the breaking waves increase, the ANCF method does not capture the increase in mechanical energy dissipation; and the amplitude of the fluid oscillation computed using the ANCF method overpredicts the SPH solution. This behavior is observed mainly in the case of moderate turbulence with excitation frequency \(\omega _{{e}} =2.22\omega _{{ 0}} \), and in the three severe turbulent scenarios with \(A=0.136\;\hbox {m}\). The maximum x-displacement of the fluid center of mass as a function of the frequency ratio \({\omega _{{e}} }/{\omega _{{ 0}} }\) is shown for the light, moderate, and severe turbulent scenarios in Figs. 17, 18 and 19, respectively. The maximum x-displacement of the fluid center of mass is normalized with respect to the value of maximum x-displacement obtained in the case of excitation frequency \(\omega _{{e}} =0.5\;\hbox {Hz}\). The x-position of the fluid center of mass can be calculated analytically using the asymptotic nonlinear multimodal approach as \(x_C \left( t \right) =-{2}/{\pi ^{2}h^{*}}\sum _{i=1}^{n_{{f}} } {\beta _i \left( t \right) \frac{1}{i^{2}}\left( {1+\left( {-1} \right) ^{i+1}} \right) } \), where \(h^{*}={2H_{{w}} }/{L_{{t}} }\), \(n_{{f}} \) is the number of Fourier terms, \(\beta _i \) is a generalized modal coordinate, and t is time [20, 21]. It is important to point out that the use of the preceding equation for \(x_C \) is limited to the case of small fluid response amplitude to fluid depth ratio and in the case of negligible wave breaking effects. From the results shown in Fig. 17, it is clear that in the case of light turbulence, the ANCF and SPH results agree well with the analytical solution. Figure 18 shows that in case of moderate turbulence, a good agreement is observed between the SPH and analytical solutions, while the ANCF solution deviates from the reference solution as the excitation frequency increases. In case of severe turbulence, the asymptotic nonlinear multimodal approach cannot be used, and the SPH results are considered as the reference solution. In agreement with the results obtained for the moderate turbulent scenario, the ANCF solution shown in Fig. 19 deviates from the reference SPH solution as the excitation frequency increases. The non-monotonic behavior of the ANCF curves shown in Figs. 18 and 19 is expected because the ANCF method does not account for the energy dissipation due to the wave breaking. In order to identify the frequencies of the fundamental modes of displacement and the contribution of each mode to the sloshing response, the power spectral density associated with the results shown in Fig. 16 is calculated using the fast Fourier transform (FFT). The power spectrum \(\hbox {S}(\omega )\) is calculated considering three different levels of excitation frequency \(\omega _{{e}} =1.12\omega _{{ 0}} ,\;1.48\omega _{{ 0}} ,\;2.22\omega _{{ 0}} \), and three excitation amplitudes \(A=0.032\;\hbox {m}, 0.084\;\hbox {m}, 0.136\;\hbox {m}\). Figure 20 shows the power spectrum based on the results obtained in the first 6 seconds of simulation. It is observed that when the excitation frequency is close to the fundamental frequency, i.e., \(\omega _{{e}} =1.12\omega _{{ 0}} \), the sloshing response is dominated by the fundamental sloshing mode \(\omega _{{ 0}} \). When the excitation frequency is larger than the fundamental frequency, i.e., \(\omega _{{e}} =\;1.48\omega _{{ 0}} \) and \(\omega _{{e}} =\;2.22\omega _{{ 0}} \), two dominant frequencies, namely the excitation frequency \(\omega _{{e}} \) and the fundamental frequency \(\omega _{{ 0}} \), can be identified. In the case of excitation frequency \(\omega _{{e}} =\;2.22\omega _{{ 0}} \), the responses at the higher sloshing oscillation frequencies \(\omega _1 \) and \(\omega _2 \) are also visible. It is observed that by increasing the excitation amplitude, the mechanical energy dissipation due to the wave breaking significantly affects the energy content of the sloshing modes associated with the sloshing oscillation frequencies. Consequently, the transient response of the fluid is rapidly damped out when the SPH method is used, while it remains in the ANCF solution. The use of the ANCF method, which does not account for the hydrodynamic damping effects due to the wave breaking, leads to overpredicting the energy of the fundamental sloshing mode. On the other hand, a good agreement is found between the ANCF and SPH methods in predicting the stable steady-state fluid response associated with the excitation frequency. In the case of excitation amplitude \(A=0.084\;\hbox {m}\), the effect of the excitation frequency on the hydrodynamic loads is studied. Figure 21 shows the variation of the hydrodynamic force acting on the container at different levels of excitation frequency. In Fig. 21, the value of the hydrodynamic force is normalized with respect to the fluid mass. It is observed that as the excitation frequency gets closer to the fundamental sloshing oscillation frequency, the value of the hydrodynamic load increases. However, the wave breaking effects resulting from an increase in the excitation frequency do not lead to an increase in the maximum value of the hydrodynamic force.

Fig. 13
figure 13

Small turbulent regions obtained using the SPH method

Full size image
Fig. 14
figure 14

SPH prediction of the moderate turbulence scenario (\(A=0.084\;\hbox {m}\), \(T=0.75\;\hbox {s})\)

Full size image
Fig. 15
figure 15

SPH prediction of the severe turbulence scenario (\(A=0.136\;\hbox {m}\), \(T=1.125\;\hbox {s})\)

Full size image
Fig. 16
figure 16

x-displacement of the fluid center of mass for different excitation frequencies and amplitudes ( ANCF, SPH). (Color figure online)

Full size image
Fig. 17
figure 17

Normalized maximum amplitude of the fluid center of mass for \(A=0.032\;\hbox {m}\) ( ANCF, SPH, analytical). (Color figure online)

Full size image
Fig. 18
figure 18

Normalized maximum amplitude of the fluid center of mass for \(A=0.084\;\hbox {m}\) ( ANCF, SPH, analytical). (Color figure online)

Full size image
Fig. 19
figure 19

Normalized maximum amplitude of the fluid center of mass for \(A=0.136\;\hbox {m}\) ( ANCF, SPH). (Color figure online)

Full size image
Fig. 20
figure 20

Power spectrum of the sloshing response ( ANCF, SPH). (Color figure online)

Full size image
Fig. 21
figure 21

Hydrodynamic load calculated using the SPH method (\({\omega _{{e}} }/{\omega _{{ 0}}}=2.22\), \({\omega _e }/{\omega _{{ 0}} }=1.48\), \({\omega _{{e}} }/{\omega _{{ 0}}}=1.12)\). (Color figure online)

Full size image

7 Conclusion

This paper is focused on the study of breaking wave effects in liquid sloshing problems using the ANCF and SPH methods. The fundamental differences between the two formulations are presented, and the advantages and limitations of each method are discussed. The dam break and sloshing tank benchmark problems are used to assess the performance of both formulations in capturing the fluid dynamic behavior resulting from sloshing excitations. In the dam break problem, a good agreement is observed between the ANCF and SPH converged solutions. Moreover, it is found that the ANCF converged solution requires 35 times fewer degrees of freedom than the SPH solution. In the sloshing tank problem, while the ANCF solution agrees well with the experimental results, it is found that the SPH solution underpredicts the amplitude of the wave height at the point of interest and the lateral displacement of the fluid center of mass. In agreement to what is found for the dam break problem, the ANCF solution requires nearly 40 times fewer degrees of freedom as compared to the SPH solution. In case of the dam break problem, the CPU time required by the ANCF method to converge to the reference solution is 70% less than that required by the SPH method; in the sloshing tank problem, the CPU time saving obtained using the ANCF method is 25%. In both benchmark problems, it is observed that the rate of increase in simulation time resulting from mesh refinement is comparable when the ANCF and SPH methods are used. The effects of breaking waves on liquid sloshing dynamics are investigated for the sloshing tank problem by varying the excitation frequency and amplitude. It is shown that in the case of light and moderate turbulence, the continuum-based ANCF method leads to an accurate prediction of the position of the fluid center of mass by averaging the fluid inertia properties. In case of severe turbulence, the mechanical energy dissipation due to vorticial flows and wave breaking, which is not captured using the ANCF method, leads to damping out the fluid response. Severe sloshing scenarios, which cannot be captured using the ANCF method, can be accurately described using the particle-based SPH formulation.

It is important to point out that because of the use of two fundamentally different algorithms in the ANCF and SPH model simulations, less weight should be given to the CPU time comparison, while more weight should be given to the number of degrees of freedom of the models. This is mainly due to the fact that different optimization and parallelization methods are used in the two software employed in this study. Future investigations will focus on the study of fundamental sloshing issues, some of which are discussed in more recent investigations [36, 37].