1 Introduction

Fluid–structure interaction (FSI) is a phenomenon frequently encountered in varied engineering topics, e.g., hydrodynamic slamming of marine vessels, wave/tsunami surge impact on offshore/coastal structures, and sloshing in liquid containers [1, 2]. FSI problems contain a variety of challenges involving violent fluid motions, rapidly moving interfaces, and deformable solid boundaries. Considering the lack of comprehensive analytical solutions and the limitations in experimental studies, numerical models play a significant role in the analysis of such problems [3, 4].

Smoothed particle hydrodynamics (SPH) is a mesh-free particle method developed originally for astrophysics [5, 6]. The method can easily handle large deformations and rapidly moving interfaces through its meshless fully Lagrangian nature. Many researchers have successfully applied SPH to various fluid flow simulations [7,8,9,10,11,12,13]. With the success of the method in the numerical modeling of fluid flows, many researchers purposing to utilize the capabilities of SPH in complex FSI problems have performed numerical analyses based on the coupling of SPH with other numerical frameworks (e.g., finite element method (FEM) [14,15,16], discrete element method (DEM) [17], element bending group (EBG) [18], and peridynamics (PD) [19, 20]). In parallel, some researchers have focused on coupling SPH with rigid multi-body systems involving mechanical constraints to simulate elastic FSI problems [21, 22]. In such partitioned approaches, while SPH is commonly used to simulate the fluid phase, a separate solver is employed for modeling the solid one.

An alternative way to simulate FSI problems is to use the SPH technique in both the fluid and solid phases. Such numerical models allow a precise and consistent imposition of fluid–structure interface boundary conditions [23] and can be classified based on SPH forms used for problem subdomains [4]. In early works, the conventional SPH model was commonly used for solid dynamics. Several researchers used WCSPH-SPH [24, 25] and ISPH-SPH [26] couplings in FSI simulations. Khayyer et al. [23] employed the coupling of ISPH with a newly developed SPH-based structure model for various FSI problems and later extended that model using a multi-resolution scheme [27].

The conventional SPH-based structure models have three drawbacks named inconsistency, tensile instability, and hourglass mode [3, 4, 28]. In this regard, many researchers have proposed several improvements to overcome these drawbacks. A detailed brief can be found in the work of Zhan et al. [4]. The total Lagrangian SPH (TLSPH) framework suggested by Belytschko et al. [29] provides a suitable structure for the solid phase of coupled SPH models for FSI problems. The method avoids tensile instability using material coordinates in the initial configuration and restores high-order consistency with the corrected kernel implementation. In addition, an hourglass control technique proposed by Ganzenmüller [30] can be used to eliminate the hourglass mode resulting in distorted particle distribution in the TLSPH analyses.

In recent years, TLSPH has started to be used in the solid phase of fully integrated SPH models developed for FSI problems. He et al. [31] presented a TL-WCSPH model for hydroelasticity analyses. Sun et al. [32] introduced a numerical model coupling multi-phase WCSPH with TLSPH. In their work, they used adaptive-particle-refinement (APR) technique to improve the numerical efficiency of the model. Zhan et al. [4] proposed a three-dimensional GPU-accelerated TL-WCSPH model stabilized by an hourglass control scheme. Lyu et al. [33] introduced a coupled TL-WCSPH model modified with tensile instability control (TIC) and particle shifting technique (PST) formulations. Sun et al. [34] extended the TL-WCSPH model of Sun et al. [32] with a combination of TIC and PST for complex three-dimensional FSI problems. O’Connor and Rogers [3] presented a unified TL-WCSPH model with hourglass control implemented within the open-source SPH code DualSPHysics [35]. Meng et al. [36] developed a TL-WCSPH model based on the Riemann solver for two- and three-dimensional hydroelasticity analyses.

In this work, we developed a numerical model based on the TL-WCSPH coupling for challenging fluid–elastic structure interaction problems. In the proposed model, while the fluid phase is simulated using the WCSPH framework, a TLSPH formulism stabilized by the hourglass control scheme based on the work of Ganzenmüller [30] is used for modeling the solid phase. In addition, the proposed TLSPH model contains an artificial viscosity term to treat possible stability issues except for hourglass mode. The performance of the proposed numerical model is verified using varied benchmark cases in the literature. At first, an analytical solution of a free oscillating cantilever plate is used to validate the proposed TLSPH model. Later, the present coupling scheme is validated by well-known benchmark cases, including a hydrostatic water column on an aluminum plate and the interaction of the dam-break wave with an elastic gate. Two relatively new benchmark cases based on the interaction of dam-break flows in dry and wet beds with deformable baffles confined by different boundary conditions are also used to investigate the numerical accuracy of the present coupling scheme. In addition, the effect of time integration on the solution accuracy is investigated using two different time-integration schemes in the literature with/without a predictor–corrector stage required for multiple calculations in each time step.

2 Numerical model

2.1 WCSPH model for fluid dynamics

The governing equations of fluid motion can be described by following conservation of mass and momentum equations:

$$ \frac{D\rho }{{Dt}} = - \rho \nabla \cdot {\varvec{v}} $$
(1a)
$$ \frac{{D{\varvec{v}}}}{Dt} = - \frac{1}{\rho }\nabla P + {\Gamma } + {\mathbf{g}} $$
(1b)

where \(\rho\) is the density, \({\varvec{v}}\) is velocity, \(P\) is pressure, \({\Gamma }\) is the dissipative term, and \({\mathbf{g}}\) is the gravitational acceleration. In WCSPH, the fluid domain is modeled as weakly compressible, and an equation of state, calculating fluid pressure based on particle density, is adopted to close the governing equations [7, 37]:

$$ P = \frac{{c_{0}^{2} \rho_{0} }}{\gamma }\left[ {\left( {\frac{\rho }{{\rho_{0} }}} \right)^{\gamma } - 1} \right] $$
(2)

where \(\rho_{0}\) is the reference fluid density and \(c_{0}\) is the numerical sound speed in the fluid. \(\gamma\) is a constant, which is taken as 7 for fluids. To ensure the weakly compressible condition, \(c_{0}\) is determined by:

$$ c_{0} \ge 10{\text{max}}\left( {V_{{{\text{max}}}} , \sqrt {P_{{{\text{max}}}} /\rho_{0} } } \right) $$
(3)

where \(V_{{{\text{max}}}}\) and \(P_{{{\text{max}}}}\) are the maximum anticipated fluid velocity and pressure, respectively.

In SPH approximation, the continuum is represented by a set of discrete particles, and conservation equations for particle a can be written in the discretized form of a summation of the neighboring particles b:

$$ \frac{{D\rho_{a} }}{Dt} = \rho_{a} \mathop \sum \limits_{b} \frac{{m_{b} }}{{\rho_{b} }}{\varvec{v}}_{ab} \cdot \nabla_{a} W_{ab} + {\mathcal{D}}_{a} $$
(4a)
$$ \frac{{D{\varvec{v}}_{a} }}{Dt} = - \mathop \sum \limits_{b} m_{b} \left( {\frac{{P_{a} + P_{b} }}{{\rho_{a} \rho_{b} }} + {\Pi }_{ab} } \right)\nabla_{a} W_{ab} + {\mathbf{g}} $$
(4b)

where \(m\) is the mass, \({\varvec{v}}_{ab} = {\varvec{v}}_{{\varvec{a}}} - {\varvec{v}}_{{\varvec{b}}}\), and \(\nabla_{a} W_{ab}\) is the gradient of the kernel function \(W\):

$$ \nabla_{a} W_{ab} = \frac{{{\varvec{x}}_{ab} }}{{x_{ab} }} \frac{{\partial W_{ab} }}{{\partial x_{ab} }} $$
(5)

where \({\varvec{x}}\) is the position vector, \({\varvec{x}}_{ab} = - {\varvec{x}}_{ba} = {\varvec{x}}_{a} - {\varvec{x}}_{b}\), and \(x_{ab} = \left| {{\varvec{x}}_{ab} } \right|\). The performance of an SPH model depends heavily on the choice of the kernel function [38]. In this work, the fifth-order quintic kernel [39] is adopted. \({\mathcal{D}}_{a}\) is the density diffusion term [40], implemented to limit pressure oscillations faced in WCSPH simulations:

$$ {\mathcal{D}}_{a} = \delta hc_{0} \mathop \sum \limits_{b} \frac{{m_{b} }}{{\rho_{b} }} \psi_{ab} \cdot \nabla_{a} W_{ab} $$
(6a)
$$ \psi_{ab} = 2\left( {\rho_{b} - \rho_{a} } \right)\frac{{{\varvec{x}}_{ba} }}{{x_{ab}^{2} + \eta^{2} }} $$
(6b)

where \(h\) is the smoothing length defining the size of the compact support domain of the kernel function. \(\delta\) is a constant that controls the intensity of the diffusion term and is set to \(\delta = 0.1\) in this work. \(\eta = 0.1h\), which is used to prevent numerical singularities. \({\Pi }_{ab}\) is the artificial viscosity term [41] used for numerical stabilization:

$$ {\Pi }_{ab} = \left\{ {\begin{array}{*{20}c} { - \left( {\frac{{\alpha c_{0} }}{{\overline{\rho }_{ab} }}} \right)\left( {\frac{{h{\varvec{v}}_{ab} \cdot {\varvec{x}}_{ab} }}{{x_{ab}^{2} + \eta^{2} }}} \right)} & {{\varvec{v}}_{ab} \cdot {\varvec{x}}_{ab} < 0} \\ 0 & {{\varvec{v}}_{ab} \cdot {\varvec{x}}_{ab} \ge 0} \\ \end{array} } \right. $$
(7)

where \(\alpha\) is the artificial viscosity constant and \(\overline{\rho }_{ab} = 0.5\left( {\rho_{a} + \rho_{b} } \right)\).

2.2 TLSPH model for solid dynamics

In TLSPH formulation, the mass and momentum conservation equations are given by:

$$ \rho^{{\text{s}}} J = \rho_{0}^{{\text{s}}} $$
(8a)
$$ \frac{{D{\varvec{v}}}}{Dt} = \frac{1}{{\rho_{0}^{s} }}\nabla_{0} \cdot {\varvec{P}} + {\mathbf{g}} $$
(8b)

where the zero subscripts represent the quantities calculated considering reference configuration, \(\rho^{{\text{s}}}\) is the density of the solid, \(J\) is the Jacobian determinant of deformation gradient tensor \({\varvec{F}}\), and \({\varvec{P}}\) is the first Piola–Kirchhoff (PK1) stress tensor:

$$ {\varvec{P}} = J\user2{\sigma F}^{ - T} ; {\varvec{F}} = \frac{{{\text{d}}{\varvec{x}}}}{{{\text{d}}{\varvec{X}}}} $$
(9)

where \({\varvec{\sigma}}\) is the Cauchy stress tensor, and \({\varvec{x}}\) and \({\varvec{X}}\) are the current and reference positions, respectively. The superscript –T denotes the inverse of the transposed tensor. In TLSPH, the momentum equation (Eq. 8b) only depends on the initial density \(\left( {\rho_{0}^{s} } \right)\), and therefore, solving the continuity equation is unnecessary [34]. The Cauchy stress tensor, considering the linear–elastic constitutive model based on the plane-strain assumption in two dimensions, is expanded as:

$$ \left[ {\begin{array}{*{20}c} {\sigma^{11} } \\ {\sigma^{22} } \\ {\sigma^{12} } \\ \end{array} } \right] = \frac{E}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left[ {\begin{array}{*{20}c} {1 - \nu } & \nu & 0 \\ \nu & {1 - \nu } & 0 \\ 0 & 0 & {1 - 2\nu } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon^{11} } \\ {\varepsilon^{22} } \\ {\varepsilon^{12} } \\ \end{array} } \right] $$
(10)

where \(E\) is Young’s modulus, \(\nu\) is Poisson ratio, and \({\varvec{\varepsilon}}\) is Euler strain tensor expressed as:

$$ {\varvec{\varepsilon}} = {\varvec{F}}^{ - T} {\varvec{EF}}^{T} $$
(11)

where \({\varvec{E}}\) is the Green–Lagrange strain tensor given by:

$$ {\varvec{E}} = \frac{1}{2}\left[ {{\varvec{U}} + {\varvec{U}}^{T} + {\varvec{U}}^{T} {\varvec{U}}} \right];\user2{ U} = {\varvec{F}} - {\varvec{I}} $$
(12)

where \({\varvec{U}}\) is the displacement gradient tensor and \({\varvec{I}}\) is the identity matrix.

In the TLSPH framework, the discrete forms of the momentum equation and deformation gradient are written as follows:

$$ \frac{{D{\varvec{v}}_{{\varvec{a}}} }}{Dt} = \frac{1}{{\rho_{0a}^{{\text{s}}} }}\mathop \sum \limits_{b} \frac{{m_{b}^{{\text{s}}} }}{{\rho_{0b}^{{\text{s}}} }}\left( {{\varvec{P}}_{a} {\varvec{L}}_{a}^{ - 1} + {\varvec{P}}_{b} {\varvec{L}}_{b}^{ - 1} + {\varvec{P}}_{ab}^{v} {\varvec{L}}_{a}^{ - 1} } \right){ }\nabla_{0a} W_{0ab} + {\mathbf{g}} $$
(13a)
$$ {\varvec{F}}_{a} = \mathop \sum \limits_{b} \frac{{m_{b}^{{\text{s}}} }}{{\rho_{0b}^{{\text{s}}} }}\left( {{\varvec{x}}_{b} - {\varvec{x}}_{a} } \right) \otimes {\varvec{L}}_{a}^{ - 1} { }\nabla_{0a} W_{0ab} $$
(13b)
$$ {\varvec{L}}_{a} = \mathop \sum \limits_{b} \frac{{m_{b}^{{\text{s}}} }}{{\rho_{0b}^{{\text{s}}} }}\left( {{\varvec{X}}_{b} - {\varvec{X}}_{a} } \right) \otimes \nabla_{0a} W_{0ab} $$
(13c)

where \(m^{s}\) and \(\rho_{0}^{s}\) are the mass and initial density of the solid particles, respectively, \({\varvec{L}}\) is the kernel gradient correction matrix, and \({\varvec{P}}_{ab}^{v}\) is the artificial viscous force used for numerical stabilization:

$$ {\varvec{P}}_{ab}^{v} = J_{a} {\Pi }_{ab}^{{\text{s}}} {\varvec{F}}_{a}^{ - T} $$
(14a)
$$ {\Pi }_{ab}^{s} = \left\{ {\begin{array}{*{20}c} {\alpha_{s} c_{0}^{{\text{s}}} h_{s} \rho_{0}^{{\text{s}}} \frac{{{\varvec{v}}_{ab} \cdot {\varvec{x}}_{ab} }}{{x_{ab}^{2} + 0.01h_{s}^{2} }}} & {{\varvec{v}}_{ab} \cdot {\varvec{x}}_{ab} < 0} \\ 0 & {{\varvec{v}}_{ab} \cdot {\varvec{x}}_{ab} \ge 0} \\ \end{array} } \right. $$
(14b)

where \({\Pi }_{ab}^{{\text{s}}}\), \(c_{0}^{{\text{s}}}\), \(h_{s}\), and \(\alpha_{{\text{s}}}\) denote the artificial viscosity term, speed of sound, smoothing length, and artificial viscosity constant for the solid, respectively.

Although TLSPH restores first-order consistency and avoids tensile instability, the method with its current form suffers from hourglass mode. Some researchers tried to suppress that issue by using only artificial viscous force (Eq. 14a) [31,32,33,34]. However, this treatment lacks theoretical background and often results in excessive energy dissipation [4]. In this work, an hourglass control scheme proposed by Ganzenmüller [30] is employed to treat the hourglass mode. The illustration of the idea of mentioned hourglass control scheme starts with the definition of ideal linear separation between particle a and its neighboring particle b:

$$ {\varvec{x}}_{ab}^{a} = {\varvec{F}}_{a} {\varvec{X}}_{ab} $$
(15)

However, the actual separation is determined based on the current positions of particles as \({\varvec{x}}_{ab} = {\varvec{x}}_{a} - {\varvec{x}}_{b}\). The error vector, which is the pairwise symmetric difference between the idealized linear and actual separations, is expressed as:

$$ {\varvec{e}}_{ab} = \frac{1}{2}\left( {{\varvec{x}}_{ab}^{a} - {\varvec{x}}_{ab} + {\varvec{x}}_{ab}^{b} - {\varvec{x}}_{ab} } \right) = \frac{1}{2}\left( {{\varvec{F}}_{a} + {\varvec{F}}_{b} } \right){\varvec{X}}_{ab} - {\varvec{x}}_{ab} $$
(16)

To stabilize the system and suppress the hourglass modes, the magnitude of the error vector needs to be minimized [30]. In this regard, a correction force in line with \({\varvec{x}}_{ab}\), proportional to the magnitude of the error vector, is used:

$$ {\varvec{f}}_{a}^{{{\text{HG}}}} = \kappa \mathop \sum \limits_{b} \frac{{m_{a}^{{\text{s}}} }}{{\rho_{0a}^{{\text{s}}} }} \frac{{m_{b}^{{\text{s}}} }}{{\rho_{0b}^{{\text{s}}} }} E_{ab} \frac{{{\varvec{e}}_{ab} \cdot {\varvec{x}}_{ab} }}{{X_{ab}^{2} }} \frac{{\user2{ x}_{ab} }}{{x_{ab}^{2} }} W_{0ab} $$
(17)

where \(\kappa\) is a coefficient determining the magnitude of penalty force and \(E_{ab} = 0.5\left( {E_{a} + E_{b} } \right)\). The hourglass force calculated by Eq. 17 is added into the momentum equation, and the total acceleration of particle a, thereby, can be written as:

$$ \begin{aligned} \frac{{D{\varvec{v}}_{{\varvec{a}}} }}{Dt} & = \frac{1}{{\rho_{0a}^{{\text{s}}} }}\mathop \sum \limits_{b} \frac{{m_{b}^{{\text{s}}} }}{{\rho_{0b}^{{\text{s}}} }}\left( {{\varvec{P}}_{a} {\varvec{L}}_{a}^{ - 1} + {\varvec{P}}_{b} {\varvec{L}}_{b}^{ - 1} + {\varvec{P}}_{ab}^{v} {\varvec{L}}_{a}^{ - 1} } \right)\\ &\quad \nabla_{0a} W_{0ab} + \frac{{{\varvec{f}}_{a}^{{{\text{HG}}}} }}{{m_{a}^{{\text{s}}} }} + {\mathbf{g}}\end{aligned} $$
(18)

2.3 Boundary condition and fluid–structure coupling

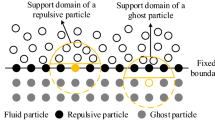
In the present work, the dummy particle method, proposed by Adami et al. [42], is employed for both boundary treatment and fluid–structure coupling. In this method, the cut of the kernel support domain of fluid particles near the boundary and solid domains is prevented by representing the boundary and structure domains with dummy fluid particles contributing to the governing equations. In this regard, pressures of boundary and structure particles are obtained firstly by a summation of all contributions of neighboring fluid particles using the kernel function:

$$ P_{s} = \frac{{\mathop \sum \nolimits_{f} W_{{{\text{s}}f}} + \left[ {\rho_{f} \left( {{\mathbf{g}} - {\varvec{a}}_{{\text{s}}} } \right) \cdot {\varvec{x}}_{{{\text{s}}f}} + P_{f} } \right]}}{{\mathop \sum \nolimits_{f} W_{{{\text{s}}f}} }} $$
(19)

where the subscripts f and s represent the fluid and boundary/structure particles, respectively. \({\varvec{x}}_{{{\text{s}}f}} = {\varvec{x}}_{{\text{s}}} - {\varvec{x}}_{f}\) and \({\varvec{a}}_{s}\) is the acceleration of the boundary/structure particles. Following the pressure calculation, densities of the boundary and structure particles are obtained using the equation of state:

$$ \rho_{{\text{s}}} = \rho_{0} \left[ {\frac{{P_{{\text{s}}} \gamma }}{{c_{0}^{2} \rho_{0} }} + 1} \right]^{{\frac{1}{\gamma }}} $$
(20)

Obtained density and pressure values of boundary/structure particles are used in the computation of density change and acceleration of fluid particles and, in addition, the determination of the external forces on solid particles caused by the fluid domain. However, this step is unnecessary for boundary particles because they remain fixed and do not move without any imposed or assigned motion function. Consequently, the total acceleration of fluid and structure particles can be written in a discrete form as follows:

$$ \begin{gathered} \left. {\frac{{D{\varvec{v}}_{a} }}{Dt}} \right|_{{{\text{fluid}}}} = - \mathop \sum \limits_{{b \in {\text{fluid}}}} m_{b} \left( {\frac{{P_{a} + P_{b} }}{{\rho_{a} \rho_{b} }} + {\Pi }_{ab} } \right)\nabla_{a} W_{ab} \hfill \\ - \mathop \sum \limits_{{b \in {\text{bound}}}} m_{b} \left( {\frac{{P_{a} + P_{b} }}{{\rho_{a} \rho_{b} }} + {\Pi }_{ab} } \right)\nabla_{a} W_{ab} \\ \quad - \mathop \sum \limits_{{b \in {\text{solid}}}} m_{b}^{H} \left( {\frac{{P_{a} + P_{b} }}{{\rho_{a} \rho_{b}^{H} }} + {\Pi }_{ab} } \right)\nabla_{a} W_{ab} + {\mathbf{g}} \hfill \\ \end{gathered} $$
(21a)
$$\begin{gathered}\left.{\frac{{D{\varvec{v}}_{a} }}{Dt}} \right|_{{{\text{solid}}}} =\frac{1}{{\rho_{0a}^{s} }}\mathop \sum\limits_{{b \in {\text{solid}}}} \frac{{m_{b}^{s} }}{{\rho_{0b}^{s} }}\left( {{\varvec{P}}_{a} {\varvec{L}}_{a}^{ - 1} + {\varvec{P}}_{b} {\varvec{L}}_{b}^{ - 1} + {\varvec{P}}_{ab}^{v} {\varvec{L}}_{a}^{ - 1} } \right) { }\nabla_{0a} W_{0ab}\hfill \\ + \frac{{{\varvec{f}}_{a}^{HG} }}{{m_{a}^{s} }} - \frac{{m_{a}^{H} }}{{m_{a}^{s} }}\mathop \sum\limits_{{b \in {\text {fluid}}}} m_{b} \left( {\frac{{P_{a} + P_{b} }}{{\rho_{a}^{H} \rho_{b} }} + {\Pi }_ {ab} } \right)\nabla_{a} W_{ab} + {\mathbf{g}} \hfill \\ \end{gathered}$$
(21b)

It should be noted that the superscript H denotes a hydrodynamic definition of mass and density variables of solid particles, which are not physical quantities and are used only in the treatment of fluid–structure coupling [3].

In the dummy particles method, the implementation of the free-slip or no-slip boundary condition depends on the treatment of viscous forces between the fluid and boundary/solid particles. A free-slip boundary condition is applied by simply omitting viscous effects between fluid and boundary/solid particles [42]. For a no-slip boundary condition, viscous forces between fluid and boundary/solid particles are calculated considering the extrapolated smoothed velocity field assigned to boundary/solid particles. A detailed brief can be found in the work of Adami et al. [42]. In this work, a free-slip boundary condition is adopted. In this regard, it should be noted that because of the free-slip assumption, viscous effects between fluid and boundary/solid particles in Eqs. 21a and 21b are neglected, and only viscous forces between fluid particles take into consideration in simulations.

2.4 Time integration

2.4.1 Symplectic time-integration scheme

The symplectic time-integration scheme [35, 43] with second-order accuracy in time involves a predictor and corrector stage. During the predictor stage, the position and velocity of the fluid and solid particles are calculated as [35]:

$$ {\varvec{x}}_{a}^{{n + \frac{1}{2}}} = {\varvec{x}}_{a}^{n} + \frac{\Delta t}{2}{\varvec{v}}_{a}^{n} $$
(22a)
$$ {\varvec{v}}_{a}^{{n + \frac{1}{2}}} = {\varvec{v}}_{a}^{n} + \frac{\Delta t}{2}\frac{{D{\varvec{v}}_{a} }}{Dt}^{n} $$
(22b)

and in the corrector stage, predicted values are used to calculate the corrected velocity and position of fluid and solid particles:

$$ {\varvec{v}}_{a}^{n + 1} = {\varvec{v}}_{a}^{n} + \Delta t\frac{{D{\varvec{v}}_{a} }}{Dt}^{{n + \frac{1}{2}}} $$
(23a)
$$ {\varvec{x}}_{a}^{n + 1} = {\varvec{x}}_{a}^{n} + \Delta t\frac{{\left( {{\varvec{v}}_{a}^{n + 1} + {\varvec{v}}_{a}^{n} } \right)}}{2} $$
(23b)

The density of fluid particles is also calculated using the following predictor and corrector stages as follows:

$$ \rho_{a}^{{n + \frac{1}{2}}} = \rho_{a}^{n} + \frac{\Delta t}{2}\frac{{D\rho_{a} }}{Dt}^{n} $$
(24a)
$$ \rho_{a}^{n + 1} = \rho_{a}^{n} \frac{{2 - \varepsilon_{a}^{{n + \frac{1}{2}}} }}{{2 + \varepsilon_{a}^{{n + \frac{1}{2}}} }} $$
(24b)

where \(\varepsilon_{a}^{{n + \frac{1}{2}}} = - \left( {\frac{{D\rho_{a} }}{Dt}^{{n + \frac{1}{2}}} /\rho_{a}^{{n + \frac{1}{2}}} } \right)\Delta t\).

2.4.2 Verlet/One-step Euler time-integration scheme

Following the work of O’Connor and Rogers [3], two separate approaches for the fluid and solid phases are used in this section for time integration. For the fluid phase, Verlet [44] scheme is applied to calculate field variables in each time step as:

$$ {\varvec{v}}_{a}^{n + 1} = {\varvec{v}}_{a}^{n - 1} + 2\Delta t\frac{{D{\varvec{v}}_{a} }}{Dt}^{n} $$
(25a)
$$ {\varvec{x}}_{a}^{n + 1} = {\varvec{x}}_{a}^{n} + \Delta t{\varvec{v}}_{a}^{n} + \frac{1}{2}\Delta t^{2} \frac{{D{\varvec{v}}_{a} }}{Dt}^{n} $$
(25b)
$$ \rho_{a}^{n + 1} = \rho_{a}^{n - 1} + 2\Delta t\frac{{D\rho_{a} }}{Dt}^{n} $$
(25c)

To prevent the divergence of the integrated values, for every \(N_{s}\) time step (which \(N_{s} = 40\) is recommended [35]), field variables are calculated according to:

$$ {\varvec{v}}_{a}^{n + 1} = {\varvec{v}}_{a}^{n} + \Delta t\frac{{D{\varvec{v}}_{a} }}{Dt}^{n} $$
(26a)
$$ {\varvec{x}}_{a}^{n + 1} = {\varvec{x}}_{a}^{n} + \Delta t{\varvec{v}}_{a}^{n} + \frac{1}{2}\Delta t^{2} \frac{{D{\varvec{v}}_{a} }}{Dt}^{n} $$
(26b)
$$ \rho_{a}^{n + 1} = \rho_{a}^{n} + \Delta t\frac{{D\rho_{a} }}{Dt}^{n} $$
(26c)

This scheme provides a lower computational cost compared to predictor–corrector schemes as it does not require multiple calculations in each time step [38]. For the solid phase, a one-step semi-implicit Euler scheme is employed [3]:

$$ {\varvec{v}}_{a}^{n + 1} = {\varvec{v}}_{a}^{n} + \Delta t\frac{{D{\varvec{v}}_{a} }}{Dt}^{n} $$
(27a)
$$ {\varvec{x}}_{a}^{n + 1} = {\varvec{x}}_{a}^{n} + \Delta t{\varvec{v}}_{a}^{n + 1} $$
(27b)

2.5 Time stepping

In the present coupling, the time step \(\Delta t\) is limited based on the fluid and solid phases. For the fluid phase, \(\Delta t^{{\text{f}}}\) is calculated depending on the Courant–Friedrich–Levy (CFL) condition, force per unit mass on fluid particles \(\left( {\Delta t_{f} } \right)\), and viscous diffusion term \((\Delta t_{{{\text{cv}}}} )\) [35, 45]:

$$ \Delta t_{f}^{f} = C_{{\text{CFL }}} {\text{min}}\left( {\sqrt {h/\left| {\frac{{D{\varvec{v}}_{a} }}{Dt}} \right|} } \right) $$
(28a)
$$ \Delta t_{{{\text{cv}}}}^{f} = C_{{\text{CFL }}} {\text{min}}\left( {\frac{h}{{c_{0}^{f} + {\text{max}}\left( {\frac{{\left| {h{\varvec{v}}_{ab} \cdot {\varvec{x}}_{ab} } \right|}}{{x_{ab}^{2} + \eta^{2} }}} \right)}}} \right) $$
(28b)

where \(C_{{\text{CFL }}}\) is a constant of CFL condition and is taken as \(C_{{{\text{CFL}}}} = 0.2\) in this work. The time step for the solid phase \(\left( {\Delta t^{s} } \right)\) also bounded by the following CFL condition is calculated:

$$ \Delta t^{{\text{s}}} = 0.6\frac{{h_{{\text{s}}} }}{{c_{0}^{{\text{s}}} }}; c_{0}^{s} = \sqrt {K_{{\text{s}}} /\rho_{0}^{{\text{s}}} } $$
(29)

where \(K_{s}\) is the bulk modulus of the solid, defined as \(K_{s} { } = E/\left[ {3\left( {1 - 2\nu } \right)} \right]\). Consequently, the new time step criterion of system \(\Delta t\) is determined as:

$$ \Delta t = {\text{min}}\left( {\Delta t_{{\text{f}}}^{{\text{f}}} , \Delta t_{{{\text{cv}}}}^{{\text{f}}} ,\Delta t^{{\text{s}}} } \right) $$
(30)

3 Numerical validations

In this section, the performance of the proposed numerical model is verified using various benchmark cases in the literature. At first, the solution accuracy of the TLSPH model is investigated using an analytical solution of a free oscillating cantilever plate. Later, the TL-WCSPH coupling is validated using various benchmark cases, including hydrostatic water column on an elastic plate, dam-break flow through an elastic gate, and dam-break wave impact in dry and wet beds on deformable baffles confined by different boundary conditions. In addition, the effect of the time integration on the solution accuracy of the proposed TL-WCSPH coupling is investigated using two different time-integration schemes described in Sect. 2.3.

In all numerical simulations, the smoothing length for both WCSPH and TLSPH models is set to hf = hs = 1.35dp. The dimensionless hourglass coefficient is chosen as \(\kappa = 50\) following the suggestion of Ganzenmüller [30] for beam bending problems, and a slight artificial viscous force with \(\alpha_{{\text{s}}} = 0.03\) is adopted to prevent possible numerical instabilities.

3.1 Free oscillation of a cantilever plate

An analytical solution of a free oscillating cantilever plate [46] is used to investigate the solution accuracy of the present TLSPH model. A schematic view of the solution domain is shown in Fig. 1. The length of the cantilever plate is Ls = 0.2 m, the thickness ts = 0.02 m, Young’s modulus of E = 2 MPa, and the Poisson ratio of ν = 0.3975. The cantilever plate is subjected to an initial velocity distribution defined as:

$$ v_{y} \left( x \right) = \xi c_{s} \frac{f\left( x \right)}{{f\left( L \right)}} $$
(31a)
$$ f\left( x \right) = \left( {\cos k_{w} L + \cosh k_{w} L} \right)\left( {\cosh k_{w} x - \cos k_{w} x} \right) + \left( {\sin k_{w} L - \sinh k_{w} L} \right)\left( {\sinh k_{w} x - \sin k_{w} x} \right) $$
(31b)

where \(\xi = 0.01\) is the velocity amplification factor; \(k_{w}\) is wave number satisfying \(k_{w} L = 1.875\) for the first mode of vibration.

Fig. 1
figure 1

Schematic view of benchmark case (lengths in cm)

Full size image

Numerical analysis is performed with three different particle resolutions as ts/dp = 20, 40, and 80. The one-step Euler time-integration scheme is adopted in numerical simulations considering the lower computational cost. Note that the symplectic time-integration scheme is also tested in preliminary works, and quite similar results are obtained. The numerical analyses are performed for t = 1 s simulation time, and the snapshots of numerical results at different time instants are shown in Fig. 2. It can be seen from the figure that the proposed model provides a smooth stress field on the plate section.

Fig. 2
figure 2

Snapshots of numerical result at t = 0.57 s (top) and t = 0.7 s (bottom) for ts/dp = 80

Full size image

Time histories of plate tip point deflection reproduced by the proposed TLSPH model are shown in Fig. 3 compared with the analytical solution. It can be observed that the proposed TLSPH model computations are in good agreement with the analytical solution. Table 1 presents the root-mean-squared error (RMSE) for numerically reproduced deflections. Results show that the solution accuracy of the proposed model increases in proportion to the particle resolution.

Table 1 RMSE of free oscillating plate numerical computations
Full size table
Fig. 3
figure 3

Time histories of free oscillating plate tip point deflections

Full size image

3.2 Hydrostatic water column on an elastic plate

The accuracy of the present coupling scheme is investigated using a benchmark case based on the hydrostatic water column on an elastic plate [16]. The initial configuration of the benchmark case is shown in Fig. 4. The water column has a height of H0 = 2 m and a width of W0 = 1 m. An aluminum plate with a length of Ls = 1 m, a thickness of ts = 0.05 m, a density of ρ = 2700 kg/m3, Young’s modulus of E = 67.5 GPa, and a Poisson ratio of ν = 0.34 is located at the bottom of the initially still water column.

Fig. 4
figure 4

Schematic view of solution domain and measurement point M1 (lengths in cm)

Full size image

Numerical analyses are performed using the initial particle spacing dp = 6.25 × 10–3 m, corresponding to ts/dp = 8 and H0/dp = 320. For the fluid phase, the artificial viscosity constant is set to α = 0.1. A snapshot of the numerical computations is shown in Fig. 5. It can be seen from the figure that, for both time-integration schemes, the proposed model reproduced smooth pressure and stress fields for the fluid and solid phases, respectively.

Fig. 5
figure 5

Snapshots of numerical results at t = 0.3 s

Full size image

Figure 6 shows the mid-span (M1) deflection (δ) history comparisons. The present model computations are compared with the analytical solution (δ = 6.85 × 10–5 m [16]) and the ISPH-SPH results of Khayyer et al. [23] with the same ts/dp ratio. Results indicate that the proposed model computations obtained with both time-integration schemes showed quite similar oscillations at the initial stage and reached the equilibrium state early than the ISPH-SPH results of Khayyer et al. [23]. After the equilibrium state, the proposed model reproduced plate deflection consistent with ISPH-SPH results and showed reasonable accuracy with the analytical solution. In addition, it is observed that while numerical computations obtained by Verlet/One-step Euler time integration showed some deviations at the equilibrium state, symplectic time integration provides higher stability in computations.

Fig. 6
figure 6

Comparisons of mid-span deflections at M1

Full size image

3.3 Interaction of a dam-break wave with elastic gate

A well-known benchmark case based on the deformation of the elastic gate subjected to water pressure is used to validate the present model. Figure 7 shows the initial geometry of the solution domain. The height and width of the still water column have dimensions of H0 = 0.14 m and W0 = 0.1 m, respectively. An elastic gate with a length of Ls = 0.079 m, a thickness of ts = 0.005 m, Young’s modulus of E = 7.8 MPa, and a Poisson ratio of ν = 0.4 is fixed from the upper side, and the downside is free. The solution domain is discretized using the initial particle spacing dp = 5 × 10–4 m corresponding to ts/dp = 10 and H0/dp = 280. For the fluid phase, the artificial viscosity constant is taken as α = 0.01.

Fig. 7
figure 7

Schematic view of solution domain and measurement point M1 (lengths in cm)

Full size image

The snapshots of the present model computations at different time intervals comparatively with experimental photographs are shown in Fig. 8. Results indicate that the proposed model results computed by both time-integration schemes provided smooth pressure and stress fields for fluid and solid phases, respectively, without an unphysical gap in the fluid–structure interface.

Fig. 8
figure 8

Comparisons of experimental photographs with snapshots of present model computations

Full size image

Figure 9 shows the displacement comparisons at the measurement point M1. The present model results are compared with the experimental measurements of Antoci et al. [24] and the numerical results of Zhang et al. [47], Gao et al. [48], and Yao and Huang [49], which used the same Young’s modulus of E = 7.8 MPa. Results indicate that the proposed model reproduced almost the same gate displacement with both of the time-integration schemes and showed well agreement with other numerical model results. However, there is a fewer agreement with experimental measurement. Authors consider that it is caused by the uncertainties in the mechanical properties of the elastic plate used in the experiment. Some researchers used less stiff material models such as hyperelasticity and obtained better agreements with experimental measurements [14].

Fig. 9
figure 9

Displacement comparisons at M1

Full size image

3.4 Interaction of a dam-break wave in wet bed with an elastic baffle

In this section, the present numerical model is validated using the interaction of a dam-break flow in wet bed with an elastic baffle, which is studied first experimentally and numerically by Yilmaz et al. [21]. Figure 10 presents a schematic illustration of the experimental setup. The experiment is conducted in a rectangular tank with a length of 1.5 m and a height of 0.25 m. The rectangular tank is divided into two parts, upstream and downstream, using a rigid plate of 0.003 m thickness. The upstream and downstream are filled initially with the water height of H0 = 0.15 m and H0t = 0.03 m, respectively. An elastic baffle with a length of Ls = 0.08 m and thickness of ts = 0.007 m embedded into a rigid foundation of 0.047 m in width and 0.016 in height is placed at a distance of 0.3 m from upstream. The material of the baffle corresponds with the density of ρ = 1250 kg/m3, Young's modulus of E = 5.7 MPa, and the Poisson ratio of ν = 0.4.

Fig. 10
figure 10

Schematic illustration of experimental setup and measurement point M1 (lengths in cm)

Full size image

The solution domain is discretized using initial particle spacing of dp = 0.001 m corresponding to ts/dp = 7 and H0/dp = 150. The artificial viscosity constant for the WCSPH model is chosen as α = 0.04. Figure 11 shows the snapshots of numerical results with pressure and stress fields for fluid and solid subdomains, respectively, at different time instants comparatively with experimental results. It is observed that the proposed model with both of the time-integration schemes reproduced free-surface profiles consistent with experiments and obtained a smooth pressure field in the fluid phase and around the fluid–structure coupling without any unphysical gap. In addition, it is seen from the figure that the proposed model smoothly reproduced the stress field of the elastic baffle section in both time-integration schemes.

Fig. 11
figure 11

Snapshots of numerical results at different time instants

Full size image

Figure 12 shows time variations of horizontal displacements at the measurement point M1. Results indicate that the proposed model reproduces quite similar displacement computations with both of the time-integration schemes, consistent with the numerical and experimental results of Yilmaz et al. [21]. Also, it should be noted that there is an over-prediction in displacements computed by both numerical models at first contact (around t = 0.3 s) compared with experimental data. Yilmaz et al. [21] reported that the difference in wave-front shape, developing in a wet-bed condition, in numerical computations can cause that displacement difference.

Fig. 12
figure 12

Time histories of horizontal displacements at measurement point (M1)

Full size image

3.5 Interaction of a dam-break wave with an elastic sluice gate

The interaction of a dam-break flow with an elastic sluice gate is used for the present model validation. The phenomenon is first studied experimentally and numerically by Yilmaz et al. [15]. Figure 13 shows a schematic illustration of the experimental setup. A rectangular tank with a length of 1.508 m and a height of 0.25 m is used in the experiment. The upstream and downstream are divided using a rigid plate with a thickness of 0.003 m. The upstream part is filled initially by the water with a height of H0 = 0.2 m and a width of W0 = 0.5 m. An elastic sluice gate with a length of Ls = 0.125 m, a thickness of ts = 0.007 m, a density of ρ = 1250 kg/m3, Young's modulus of E = 4 MPa, and the Poisson ratio of ν = 0.4 is placed at a distance of 0.3 m from upstream.

Fig. 13
figure 13

Schematic illustration of experimental setup and measurement point M1 (lengths in cm)

Full size image

The solution domain is discretized using dp = 0.001 m corresponding to ts/dp = 7 and H0/dp = 200. For the fluid phase, the artificial viscosity constant is set to α = 0.03. Figure 14 presents snapshots of numerical computations comparatively with experimental photographs. It is observed that the proposed model with both of the time-integration schemes reproduced free-surface profiles and structure deformations consistent with experimental results and provided a smooth pressure field for the fluid phase without any unphysical gap around the fluid–structure interface. Once again, it is seen from the figure that, for both of the time-integration schemes, the proposed model smoothly reproduced the stress field in the elastic sluice gate.

Fig. 14
figure 14

Snapshots of numerical results at different time instants

Full size image

Figure 15 shows the comparison of horizontal displacements at measurement point M1. The results indicate that the present model computations obtained with both of the time-integration schemes captured a reasonable accuracy with the experimental measurements [15] and numerical results of Yilmaz et al. [21] and Meng et al. [36]. However, it is observed that there are oscillations in displacement computations after t = 1 s. The present validation case includes chaotic fluid motions with a hydraulic jump that resulted in violent air entrainment around the fluid–structure coupling. Figure 16 shows the vortex evolution in the proposed model computations at the mentioned oscillation period. Authors consider that vortexes evolving in fluid–structure interface caused those oscillations in displacement computations. In addition to time-integration schemes used in this work, it is detected that the dynamics of mentioned oscillation period also differ depending on the numerical parameters used in analyses (e.g. artificial viscosity constant and smoothing length). A similar situation is also reported in the work of Yilmaz et al. [21]. For a more detailed investigation of the effects of the air entrainment and vortex evolution around the coupling on solution accuracy, a set of numerical analyses based on the multi-phase flow conditions can be conducted in future works.

Fig. 15
figure 15

Time histories of horizontal displacements at measurement point M1

Full size image
Fig. 16
figure 16

Vortex evolution in numerical results at specified time instants

Full size image

4 Conclusions

In this work, a coupled TL-WCSPH model is proposed for complex elastic FSI problems. In the proposed model, while the fluid phase is modeled by the WCSPH scheme, the solid phase is modeled based on a TLSPH framework stabilized by the hourglass control scheme and artificial viscous force. The performance of the proposed model is verified by a set of benchmark cases involving free oscillation of a cantilever plate, hydrostatic water column on an elastic plate, dam-break flow through an elastic gate, the interaction of the dam-break flow in wet bed with an elastic baffle, and the interaction of dam-break flow with an elastic sluice gate. The effect of the time integration on the solution accuracy of the proposed TL-WCSPH model is also investigated using two different time-integration schemes.

For all considered cases, the proposed model reproduced a smooth fluid pressure field for both of the time-integration schemes without numerical instabilities and an unphysical gap around the fluid–structure coupling. In addition, the stress field in the solid domain was also reproduced smoothly with both of the time-integration schemes without any numerical instability and distorted particle distribution thanks to hourglass control and artificial viscous force improvements.

The Verlet/One-step Euler and Symplectic time-integration schemes used in this work provided quite similar computations for considered FSI benchmark cases. Authors consider that Verlet/One-step Euler time-integration scheme for the proposed TL-WCSPH model provides a useful structure considering the low computational costs. However, it should be noted that the symplectic time-integration scheme with a predictor–corrector stage provides more stable computations in the case of the hydrostatic water column on an elastic plate, which includes high fluid pressure load and solid bulk modulus values.