1 Introduction

During the last two decades, a considerable number of researchers have contributed in large deformation formulations for multibody applications. There are several approaches that account for large displacements. The floating reference frame formulation takes an arbitrary motion of the body-fixed reference frame into account [1, 2]. This approach employs rigid-body degrees of freedom in addition to nodal variables used in structural mechanics and uses the same stiffness matrix to obtain elastic forces. The mass matrix, centrifugal and Coriolis inertia forces and generalized gravity forces appear to be highly nonlinear. Local displacements of a flexible body are supposed to be small and do not allow for the simulation of large deformations. The incremental finite element approach [3, 4] is free from this disadvantage, but it uses infinitesimal rotation angles as nodal variables. Thus, the kinematic equations are linearized and rigid-body displacements cannot be exactly described. The large rotation vector formulation [5, 6] was also proposed for large deformation problems. It employs finite rotation angles and can correctly represent an arbitrary rigid-body motion. All three approaches exhibit highly nonlinear terms in the equations of motion because of the use of a local reference frame fixed to a flexible body. Various methods were reviewed by Shabana [7].

Another approach in flexible dynamics is the absolute nodal coordinate formulation (ANCF) introduced by Shabana [8]. In this finite element nonincremental formulation, a global reference frame is used to describe the nodal coordinates. The orientation of elements is described by the global slopes instead of the rotation angles. The ANCF does not linearize the kinematic equations. Beam, plate, and shell elements, which are usually considered as non-isoparametric elements in classical finite element formulations [9], become isoparametric when the ANCF approach is implemented. A distinctive feature of the ANCF is that, in contrast to other large deformation formulations, the equations of motion contain a constant mass matrix and constant generalized gravity forces. The centrifugal and Coriolis inertia forces vanish. In general, the ANCF leads to simple expressions for the inertia forces and highly non-linear expressions for the elastic forces.

The ANCF has undergone extensive development over the last decades. It has been started with the known abstractions of beam and plate. The spatial ANCF beam element considering the rotary inertia, shear, and torsion effects was first proposed by Shabana and Yakoub [10]. Gerstmayr and Shabana considered a higher order beam element not suffering from locking effect [11]. The 3D beam element using Euler-Bernoulli model was proposed by Dombrowski [12]. Fully parameterized beam elements were developed, also [13]. The detailed comparison between a Timoshenko beam element, a fully parameterized ANCF beam element and an ANCF element using an elastic line approach was performed by Schwab and Meijaard [14]. Recently, a new 3D beam element based on the Bernoulli–Euler theory and free of singularities was proposed by Nachbagauer et al. [15]. Mikkola and Shabana [16] considered a thick plate element employing ANCF, and Dmitrochenko and Pogorelov [17] described a generalization of plate finite elements, in which nodal displacements, slope vectors, and second-order slope vectors are used as a set of nodal coordinates. The elements accounting for transverse shear deformation and effects of shear locking associated with such elements have been studied by Omar and Shabana [18], Sopanen and Mikkola [19], Garcia-Vallejo et al. [20]. New locking-free formulation for planar, shear deformable, linear, and quadratic beam elements have been proposed by Nachbagauer et al. [21]. The use of 3D solid elements in multibody system has been also studied. The adaptation of the hexahedral solid element based on the fully nonlinear formulation for modeling solid bodies in multibody systems was performed by Kubler et al. [22]. Gerstmayr and Schoberl [23] proposed a 3D finite element method in which the total Lagrange formulation is adopted, and the strain tensor is linearized with respect to a corotational frame. Two 3D solid elements employing nodal displacements and slope vectors as nodal coordinates were introduced by the authors [24]. Currently, many applications of various finite elements using the ANCF have been developed from scratch or adopted from conventional FEM formulations to the ANCF. It has been shown that all known ANCF elements can be derived from conventional FEM elements using a universal transform [25]. General purpose elements, such as spatial plates are employed in many applications and demonstrate high accuracy. The problems associated with this is one of the reasons why at present ANCF elements has been used widely in many scientific and applied problems, e.g., dynamics of belt drives [26], simulations for knee joint ligaments [27], ligament/bone insertion site constraints [28], contact problem for contact wire and pantograph [29], investigations of the deformed insect wings dynamic [30]. However, such finite elements incur significant computational costs. At the same time, there are many problems which can be solved successfully in 2D formulation. For example, a long beam can be simulated using planar elements under certain conditions. For a number of highly nonlinear problems of statics and dynamics, the simulation in 3D is not required because of the planar nature of the problems. The solutions for axisymmetric problems with large deflections can also be obtained using two-dimensional elements. It is noteworthy that in case of using the ANCF the simulation may require considerably smaller number of elements (compared to the conventional FEM approach) for obtaining quite accurate solution of the highly nonlinear problem and reduce computational costs significantly. Surprisingly, only a small amount of attention has been allotted to 2D elements using the ANCF. In this paper, the authors propose four 2D elements and consider their performance in numerical simulations.

2 Using universal numerical code in element notations

A great amount of finite element types have been developed since the introduction of the finite element method in 1941 by Hrennikoff [31]. The finite element method is extensively applied to various fields of physics, including structural and fluid mechanics as well as coupled problems. However, a general system for identifying finite elements does not currently exist. For example, one can discuss a rectangular three-dimensional four-noded element with three degrees of freedom at each node, translation in z direction, and rotations about the x,y axes (a bending plate without in-plane strain) [32]. The formal description of the element is long and inconvenient when discussing many elements of different types. For an element that can be described simply by 12 degrees of freedom, kinematical indicators of this element are still lacking. The names of the element types used in commercial software also do not give detailed information about the element features. Thus, a consistent system of brief designations would be very helpful in many cases.

The digital code describing conventional element types was introduced by Dmitrochenko and Mikkola [33]. This code uses three digits: dnc. The first digit d denotes the element dimension (1 for a beam, 2 for a plate or shell, and 3 for a solid element). The second digit in the code reflects the number of nodes n. Finally, the last digit c shows the number of coordinates per node; it is the number of derivatives of the field variable starting with zero-th derivative, or the variable itself. In terms of this paper, c=1 if only translational degree of freedom Z is used, c=3 if the variable and its two derivatives are used in addition to translation: \(Z,\tfrac{\partial Z}{\partial x},\tfrac{\partial Z}{\partial y}\), and so on. An element encoded by dnc has n⋅c degrees of freedom.

ANCF elements require the fourth digit. This is a multiplier m, which describes the procedure of vectorization and allows the transformation of a conventional finite element to an ANCF element. The ANCF concept uses identical interpolation polynomials for all coordinates. For example, in the two-dimensional case, the multiplier m=2 shows that two coordinates are interpolated using the same polynomial. The conventional 3D solid element with four nodes having 3 degrees of freedom at each node has a dnc code 243, and its number of degrees of freedom is 12. Transforming this element to the ANCF, the fourth digit (m=3) should be added to the digital sequence to show the number of components of the global nodal vector r which are interpolated using the same polynomial. The resulting nomenclature code containing the modification (dncm) will be 2433. The total number of degrees of freedom after applying the transition procedure is be n⋅c⋅m, and the element provides a complete strain set including in-plane strain. In this paper, the dncm nomenclature code is used for designating the elements.

3 Formulation of the elements

3.1 Kinematics of the elements

Dmitrochenko and Pogorelov reduced the order of the plate element with 36 degrees of freedom (dncm 2433) [17]. This element can be derived from the plate element with 48 degrees of freedom (dncm code 2443). Dufva and Shabana presented an extensive investigation of the 2433 element and provided a number of numerical examples [34]. The rectangular 2432 element can be derived directly from the reduced 2433 spatial element by eliminating the components that are responsible for the motion in the third (out of plane) direction.

The global vector r defining the position of an arbitrary point P within the plate element is calculated using the element shape functions and the vector of nodal coordinates:

$$ \mathbf{r} = \mathbf{S}( x,y ) \cdot\mathbf{e}, $$
(1)

where S is the matrix of shape functions depending on the coordinates x and y, constructed as follows:

$$ \mathbf{S}(x,y) = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\ }|@{\ }c@{\ }|@{\ }c@{\quad}c@{\quad}c@{\quad}c} S_{1,0}^{2nc}\mathbf{I} & S_{1,1}^{2nc}\mathbf{I} & \ldots & S_{1,c - 1}^{2nc}\mathbf{I} & \ldots & S_{n,0}^{2nc}\mathbf{I} & S_{n,1}^{2nc}\mathbf{I} & \ldots & S_{1,c - 1}^{2nc}\mathbf{I} \\\end{array} \right ], $$
(2)

and e is the vector of nodal coordinates including positions of nodes and slope coordinates. In Eq. (2) I is a 2×2 identity matrix, n is a number of nodes of the element. For a node with a number k, the vector of nodal coordinates is

$$ \mathbf{e}_{k} = \biggl\{ \begin{array}{c@{\quad}c@{\quad}c} \mathbf{r}_{k}^{\mathrm{T}} & \displaystyle \frac{\partial \mathbf{r}_{k}^{\mathrm{T}}}{\partial x} & \displaystyle \frac{\partial \mathbf{r}_{k}^{\mathrm{T}}}{\partial y} \\\end{array} \biggr\}^{\mathrm{T}}. $$
(3)

The vector of nodal coordinates for the whole element can be written as follows:

$$ \mathbf{e} = \left \{ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{e}_{1}^{\mathrm{T}} & \mathbf{e}_{2}^{\mathrm{T}} & \mathbf{e}_{3}^{\mathrm{T}} & \mathbf{e}_{4}^{\mathrm{T}} \\\end{array} \right \}^{\mathrm{T}}. $$
(4)

The element is formulated with employing the shape functions shown in the set of expressions (5). The same set of the shape functions was used for the 2433 element [34], but in the two-dimensional case z coordinate is omitted and only x and y coordinates are interpolated.

(5)

where ξ=x/l, η=y/w,l and w are length and width of the undeformed rectangular element accordingly.

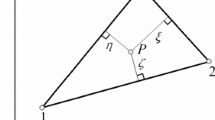
The triangular element using both translational degrees of freedom and slopes (dncm 2432) is based on Specht’s shape functions [35, 36]. The triangular area coordinates are used to obtain the set of the shape functions. The triangle can be described by the coordinates of its vertices (x i ,y i ), as shown in Fig. 1. The coordinates x and y of any point inside a triangular area can be expressed as follows:

$$ \begin{array}{@{}l} x = x_{1}\Delta_{1} + x_{2}\Delta_{2} + x_{3}\Delta_{3}, \\[4pt] y = y_{1}\Delta_{1} + y_{2}\Delta_{2} + y_{3}\Delta_{3}, \\ \end{array} $$
(6)

where Δ1,Δ2,Δ3 are the triangular coordinates with a range of values between 0 and 1, if the following constraint equation is satisfied:

$$ \Delta_{1} + \Delta_{2} + \Delta_{3} = 1. $$
(7)
Fig. 1
figure 1

Triangular coordinates definition

Full size image

In Eq. (6), the coordinates Δ1,Δ2,Δ3 are the dimensionless areas of triangles \(\Delta_{1}^{*}, \Delta_{2}^{*}, \Delta_{3}^{*}\) (Fig. 1) and can be calculated as follows:

$$ \Delta_{i} = \frac{\Delta_{i}^{*}}{\Delta} ,\quad i = 1,2,3, $$
(8)

where Δ is the area of the triangle, \(\Delta_{i} = \tfrac{1}{2}(x_{1}y_{2} - x_{2}y_{1} + x_{2}y_{3} - x_{3}y_{2} + x_{3}y_{1} - x_{1}y_{3})\). The triangular coordinates can be found from the Eq. (6) under the condition (7):

$$ \Delta_{i} = \frac{( c_{i1}x + c_{i2}y + c_{i3} )}{2\Delta}\quad ( i = 1,2,3), $$
(9)

where

$$ c_{i1} = y_{j} - y_{k},\qquad c_{i2} = x_{k} - x_{j},\qquad c_{i3} = x_{j}y_{k} - x_{k}y_{j}. $$
(10)

The lengths of the triangle’s edges before deformation are calculated using the coefficients from the expression (10): \(l_{i}^{2} = c_{i1}^{2} + c_{i2}^{2}\). Finally, the shape functions can be expressed in terms of triangular coordinates as follows:

(11)

where

(12)

The elements with translational degrees of freedom (Figs. 2 and 3) have two components in the vector for the node with a number k:e k =r k . The shape functions of the elements with dncm 2412 and 2312 are described by the sets of Eqs. (13) and (14), respectively [35].

Fig. 2
figure 2

Elements with dncm 2332 and 2432

Full size image
Fig. 3
figure 3

Elements with dncm 2312 and 2412

Full size image

for element 2412:

$$ S_{1,0}^{241} = \frac{(l - x)(w - y)}{lw},\qquad S_{2,0}^{241} = \frac{x(w - y)}{lw}, \qquad S_{3,0}^{241} = \frac{xy}{lw},\qquad S_{4,0}^{241} = \frac{y(l - x)}{lw}. $$
(13)

for element 2312: (13)

(14)

In fact, the elements with dncm 2412 and 2432 only use nodal Cartesian coordinates in global coordinate system, hence they strictly speaking, cannot be considered as truly ANCF elements. Nevertheless, these elements can be used together with other ANCF elements under certain conditions.

3.2 Formulation of the elastic forces

The elastic forces can be calculated using a continuum mechanics approach. The strain energy is determined by the integral:

(15)

where

(16)

is a Voigt representation of nonlinear Green–Lagrange strain tensor,

$$ \mathbf{E} = \frac{E}{1 - \nu^{2}}\left [ \begin{array}{c@{\quad}c@{\quad}c} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & 2(1 - \nu) \\\end{array} \right ] $$
(17)

is the matrix of elastic constants, which includes Young’s modulus E and Poisson’s ratio ν, and, finally, h is the thickness of the element. The integral describing the strain energy (15) can be evaluated analytically or numerically using Gaussian quadratures. Analytical evaluation can be performed symbolically, for example, using Maple software, but the expressions for the vector of the elastic forces can be quite complicated and incur significant computational costs. Thus, numerical integration becomes more preferable. The vector of the generalized elastic forces can be determined as a gradient of the strain energy:

(18)

and the derivatives of vector ε are computed as follows:

(19)

where \(\mathbf{S}'_{x}\) and \(\mathbf{S}'_{y}\) are derivatives of the matrix of shape functions S.

3.3 Equations of motion

Using Eq. (1) leads to a constant mass matrix of the element and zero centrifugal and Coriolis forces. Kinetic energy of the element can be obtained by differentiating Eq. (1) with respect to time:

$$ T = \frac{1}{2}h\iint_{A} \rho \dot{\mathbf{r}}^{\mathrm{T}} \cdot\dot{\mathbf{r}}\,\mathrm{d}x\,\mathrm{d}y, $$
(20)

where \(\dot{\mathbf{r}}\) is the velocity of an arbitrary point within the plane element, ρ is the specific weight of the material and A is the area of the undeformed element. Equation (20) allows the acquisition of the mass matrix, which remains constant under an arbitrary large displacement of the element. The mass matrix is defined as follows:

$$ \mathbf{M} = h\iint_{A} \rho\mathbf{S}^{\mathrm{T}} \cdot\mathbf{S}\,\mathrm{d}x\,\mathrm{d}y. $$
(21)

The equation of motion is formulated using the constant mass matrix M, the vector of nonlinear elastic nodal forces Q and the vector of external forces Q e [8]:

$$ \mathbf{M} \cdot\ddot{\mathbf{e}} + \mathbf{Q} = \mathbf{Q}_{e}, $$
(22)

where \(\ddot{\mathbf{e}}\) is the vector of nodal accelerations.

4 Numerical results

The main purpose of developing two-dimensional elements was to create a tool that provides an efficient solution of particular applied problems of statics in which high geometrical nonlinearity is observed. However, these elements can also be used in a flexible system dynamics simulation. In order to check the performance of the elements, several test problems were simulated using the elements with dncm 2312, 2412, 2332, and 2432. For the elements using slopes as nodal coordinates a simple cantilever beam subjected to small and large bending was considered. The results of numerical simulation were compared to the exact analytical solution of the Elastica problem for beam obtained using Maple software and with the Timoshenko solution accounting for bending and shear strain [37]. Several dynamics problems, such as the motion of a flexible pendulum and ellipsograph, were simulated, and the solutions were compared to similar results obtained using other element types. For all the simulations described in this section, the equations of motion were solved in MATLAB software using the integrator ode45.

For obtaining solutions in problems of statics, a damping factor of the value close to critical was introduced in the equations of motion. The following approach was used for determining the damping factor value. First, the test simulation was performed and the vibration period T was evaluated. Then the equation of motion in the form (23) was solved.

$$ \mathbf{M} \cdot\ddot{\mathbf{e}} + \mathbf{D} \cdot\dot{ \mathbf{e}} + \mathbf{Q}(\mathbf{e}) = \mathbf{Q}_{e}, $$
(23)

where

$$ \mathbf{D} = \frac{4\pi}{T}\mathbf{M}. $$
(24)

Calculating exact values of damping coefficients is not necessary in test simulations, because the only purpose of using damping in this case is to save the calculation time. That is why using the simplest approach gives satisfactorily results in this case.

4.1 Small deformations for the cantilever beam

The cantilever beam subjected to small bending was considered. The length of the beam was L=0.5 m, the height and width of its rectangular cross-section were h=0.05 m and b=0.01 m, respectively, Young’s modulus was E=2 MPa, and Poisson’s ratio was ν=0.3. Equal vertical concentrated forces P=0.025 N were applied in two nodes of the free-end cross-section. Gravity forces were not taken into account in this solution. The vertical deflection δ V of the free-end cross-section centroid was evaluated numerically and by using the Timoshenko solution for beam including the terms due to pure bending and due to pure shear [37]. The free-end vertical deflection is

$$ \delta_{V} = \frac{PL^{3}}{3EI} + \frac{PL}{kGA}, $$
(25)

where I and A is the inertia moment and the area of the cross-section respectively, k=5/6 is the shear factor and G=E/(2(1+ν)) is the shear modulus. Table 1 illustrates the difference Δ T between the Timoshenko solution and the solution obtained using ANCF for the model with different number n of the elements with dncm 2432. The solution accounting for pure bending only and the difference in deflections Δ b is shown as well.

Table 1 Small deformation for the cantilever beam
Full size table

The validation shows satisfactorily accuracy of the ANCF solution. It should be noted that the computational error can affect the solution for a larger number of finite elements because of a large amount of calculations performed using bulk expressions for the elastic force components in case of using analytical integration of the Eq. (15).

4.2 Cantilever beam subjected to large bending

The vertical load applied by two equal concentrated forces at the nodes of the cantilever beam free-end cross-section caused a large displacement (Fig. 4). The parameters of beam were the same as for the case of small deformations in the previous section. Gravity was not taken into account in this solution. The magnitude of the vertical load P was selected to provide certain values of the dimensionless force parameter p=PL 2/EI, where I is the second moment of area of the beam’s cross-section. The horizontal δ H and the vertical δ V deflections of the centroid of the free-end beam cross-section were evaluated. Figure 4 illustrates that a small number of elements employing finite slopes is capable to represent large deformations. In this case, the beam includes only two finite elements with dncm 2432. In Table 2, the values of deflections are given for the model constructed using different numbers of elements n with dncm 2432. The difference between the solutions Δ is shown, also. The elements using translational degrees of freedom were not used for such simulation due to shear locking effect.

Fig. 4
figure 4

The deformed shape of the beam (two 2432 elements)

Full size image
Table 2 Large deflection of the cantilever beam
Full size table

4.3 Motion of a flexible pendulum

The motion of a flexible pendulum was simulated using different element types. For this particular problem, the shear locking effect of simple 2312 and 2412 elements did not affect the result significantly.

In the Fig. 5, the positions of the model in different moments of time are presented. In this simulation, the beam length L=0.5 m, the cross-section height and width are h=0.1 m and b=0.01 m accordingly, the Young’s modulus E=2×105 Pa, Poisson’s ratio ν=0.3 and the specific weight ρ=7800 kg/m3; no damping was used. Figure 6 depicts a diagram of the vertical deflection of the pendulum’s point A (see Fig. 5) for several models with the same parameters, but the damping factor α=0.5 is introduced. Model I is formed using two 2432 elements (represented by a solid line at the figure), model II consists of four 2412 elements (deflection is shown by “x” markers) and, finally, model III includes eight 2312 elements (“o” markers at the plot). Similarly to the well-known “flying spaghetti” problem [38], this flexible pendulum can be referred to as “flying lasagna.”

Fig. 5
figure 5

The positions of a pendulum (two 2432 elements are used in the model)

Full size image
Fig. 6
figure 6

Vertical deflection of the point A (see Fig. 5) of the pendulum

Full size image

4.4 Motion of a flexible ellipsograph

Figures 7, 8, and 9 illustrate the motion of a heavy elastic beam. The model of the beam includes two 2432 elements (Fig. 7). The length of the beam is L=1 m, height and width of its rectangular cross-section are h=0.02 m and b=0.01 m respectively, specific gravity ρ=7800 kg/m3, Young’s modulus E=108 Pa, Poisson’s ratio ν=0.3; 1 second of motion was simulated. The vertical displacement of the left end of the beam and the horizontal displacement of its right end are constrained. The solid curves in Figs. 8 and 9 show the horizontal and vertical displacements of the centroid of the beam’s middle cross-section. In order to validate the result, a similar problem was simulated using thin beam element with dncm 1222 [8]. The solutions obtained for thin beam element are shown with “o” and “x” markers at Fig. 8 and Fig. 9. The program package Universal Mechanism [39], was used for this calculation.

Fig. 7
figure 7

Positions of a flexible ellipsograph at different moments of time

Full size image
Fig. 8
figure 8

Horizontal deflection of the middle point of the ellipsograph during motion

Full size image
Fig. 9
figure 9

Vertical deflection of the middle point of the ellipsograph during motion

Full size image

5 Conclusions

The presented quadrilateral and triangular planar finite elements employing absolute nodal coordinate formulation can be successfully used for investigating flexible system dynamics that allow the reduction to the 2D case, or initially formulated in 2D. Although the elements using translational degrees of freedom only, cannot be considered as truly ANCF elements, they can be a useful complement to more complex elements that utilizes both displacements of nodes and slopes. Using the reduced elements significantly decreases computational costs, and consequently, allows investigation the problems containing a larger number of elements. The test problems have demonstrated that the elements using translation of nodes and finite slopes as nodal coordinates can be used in the simulation for the flexible system subjected to large bending.