1 Introduction

In numerical analysis, dam-break is the immediate release of an initially stationary water body by removing a vertical obstacle. When a dam is broken, flash flooding occurs as the impounded water flees through the opening in the downstream river. The dynamics of dam-break shock waves is rather complex, and its behavior does not meet the terms of the conventional assumptions of the steady and gradually varied open-channel flows. This fact is probably the major factor in the lag of investigations of dam-break flows compared to other free surface problems. The difficulty is to choose an appropriate technique for capturing the abrupt changes in the bore formation and flow velocity values while the wave propagates. To comply with these constraints, the employed numerical model must be founded on advanced techniques that inherent non-oscillatory advection [1].

In recent years, developing shock-capturing models has been the center of attention for engineers. There is a significant amount of literature dedicated to the satisfactory solutions of the shallow water equations for shock-dominated problems. These include the finite-difference method (FDM) [2–5], finite-volume method (FVM) [6, 7], finite-element method (FEM) [8–11], and smoothed hydrodynamic particle (SPH) models [12, 13]. For example, Zhang et al. [14] developed a hydrodynamic and sediment transport model for dam-break flow simulation using an explicit FVM based on the shallow water equation (SWE) system. FEM has also been effectively applied to similar flow problems [15, 16]. An attentive historical report of FEMs in this context is reported by Wang et al. [17] employing the Galerkin scheme to solve wave equations. Wang et al. [17] showed that the classic FEM is more efficient than the ordinary FDMs due to its rigorous mathematical theory and efficiency of creating complex geometries. Moreover, isogeometric analysis (IA) is superior to the SPH models for the imposition of boundary conditions [5]. However, Wang et al.’s [17] study was conducted using classic techniques, which results in fluctuations in the sharp discontinuities.

Accordingly, employing advanced numerical methods with the shock-capturing ability was inevitable. These techniques were later implemented by researchers such as Sheu and Fang [18] who merged the FEM and flux-corrected transport (FCT) methods and applied it to the SWEs. Later, Ortiz [9] also developed a finite-element model based on the FCT technique for shallow water flows to predict the evolution of coastlines.

The total-variation-diminishing (TVD) model is another shock-capturing scheme, which was initiated by Harten [19] to describe oscillations in the calculated results. The scheme was employed by Wang et al. [20] through a second-order Lax–Wendroff method in conjunction with an FDM to discretize the two-dimensional SWEs. More recently, Boulahia et al. [21] employed a similar TVD scheme for the numerical simulation of a one-dimensional flow for an inert gas mixture. Many other relevant works on applying this technique to the engineering applications of shock-dominated flow problems have been published [3, 22–24]. However, no work has been reported so far on a combination of the FEM and TVD models to investigate the engineering problems with abrupt changes in the results, especially for the SWEs. Most of these studies are limited to the implementation of the TVD scheme along with the FDMs. Accordingly, this study proposes a finite-element model founded in the TVD concept based on Van Leer’s flux-limiter. Here, the basal idea of the TVD method is to correct the algorithms with large oscillation errors in the water elevation, and velocity fields with anti-oscillation contributions using a local criterion to flag and correct the nodes for the maximum and minimum fluxes. The simulations are conducted in two-dimensional domains to demonstrate the features of the developed scheme. Here the topographic effects are ignored to simplify the validation process of the model. The accuracy of the obtained results is compared against the pre-existing analytical and numerical results as a validation process to the model [25, 26].

The rest of this paper is organized as follows. In Sect. 2, the governing equation system is presented and discussed. Section 3 describes the developed numerical procedure. In Sect. 4, four regularly used benchmarks are considered and employed to validate the developed model. Finally, Sect. 5 summarizes the findings of the study.

2 Mathematical theory

SWEs are typically derived by depth averaging the Navier–stokes equations under the hydrostatic and Boussinesq approximations. Here, the resulting system yields the two-dimensional SWEs.

$$U_{t} + F_{x} + G_{y} + S = 0$$
(1)

in which U represents the solution vector of conservative variables, F and G denote the flux vectors; S accounts for the topographical and frictional source terms, and the subscripts t, x and y represent the partial derivatives of the time and space, respectively.

$$U = \left\{ \begin{aligned} h \hfill \\ uh \hfill \\ vh \hfill \\ \end{aligned} \right\}$$
(2)
$$F = \left\{ \begin{aligned} & uh \hfill \\ &u^{2} h + gh^{2}/2 \hfill \\ &uvh \hfill \\ \end{aligned} \right\}$$
(3)
$$G = \left\{ \begin{aligned} &vh \hfill \\ &uvh \hfill \\ &v^{2} h + gh^{2}/2 \hfill \\ \end{aligned} \right\}$$
(4)
$$S = \left\{ \begin{aligned} &0 \hfill \\ &gh(S_{bx} - S_{fx} ) \hfill \\ &gh(S_{by} - S_{fy} ) \hfill \\ \end{aligned} \right\},$$
(5)

where u and v are the depth-integrated velocity components in the x- and y-directions; respectively. g is gravity, h denotes the water depth, S bx and S by are defined by the depth gradients while S fx and S fy correspond to the friction slopes along the x- and y-directions, respectively.

$$S_{fx} = \frac{{n^{2} u(u^{2} + v^{2} )^{1/2} }}{{h^{4/3} }}$$
(6)
$$S_{fy} = \frac{{n^{2} v(u^{2} + v^{2} )^{1/2} }}{{h^{4/3} }},$$
(7)

where n denotes manning’s roughness coefficient.

To simplify the validation process, the homogeneous case is considered [25].

$$U_{t} + AU_{x} + BU_{y} = 0$$
(8)

in which

$$A = \frac{{{\text{d}}F(U)}}{{{\text{d}}U}} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ { - u^{2} + c^{2} } & {2u} & 0 \\ { - uv} & v & u \\ \end{array} } \right]$$
(9)
$$B = \frac{{{\text{d}}G(U)}}{{{\text{d}}U}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ { - uv} & v & u \\ { - v^{2} + c^{2} } & 0 & {2v} \\ \end{array} } \right],$$
(10)

where

$$c = \sqrt {gh} .$$
(11)

3 Numerical scheme and resolution techniques

The process is the standard scientific approach to the computational fluid dynamics. The scheme is first order in space and second-order in time. In a view to discretize the governing equations in time, the following Taylor series expansion in its weak form was used in the time increment \(\Delta t\) [27].

$$\begin{aligned} \int\limits_{\varOmega } {\varPsi_{i} \Delta U{\text{d}}\varOmega } = - \Delta t\left[ {\int\limits_{\varOmega } {\varPsi_{i} \left( {\left. {\frac{\partial F}{\partial x}} \right|^{n} + \left. {\frac{\partial G}{\partial y}} \right|^{n} } \right){\text{d}}\varOmega } } \right] \hfill \\ + \frac{{\Delta t^{2} }}{2}\left\{ {\int\limits_{\varOmega } {\varPsi_{i} \frac{\partial }{\partial x}\left[ {A^{n} \left( {\left. {\frac{\partial F}{\partial x}} \right|^{n} + \left. {\frac{\partial G}{\partial y}} \right|^{n} } \right)} \right]{\text{d}}\varOmega } + \int\limits_{\varOmega } {\varPsi_{i} \frac{\partial }{\partial y}\left[ {B^{n} \left( {\left. {\frac{\partial F}{\partial x}} \right|^{n} + \left. {\frac{\partial G}{\partial y}} \right|^{n} } \right)} \right]{\text{d}}\varOmega } } \right\} \hfill \\ \end{aligned}$$
(12)

in which \(\varPsi_{i}\) is the set of basis functions.

Conducting the Taylor series expansion of the fluxes, and combining the expressions into the second-order time derivative:

$$\left. {\frac{{\partial^{2} U}}{{\partial t^{2} }}} \right|^{n} = \frac{\partial }{\partial t}\frac{\partial U}{\partial t} = - \frac{\partial }{\partial t}\left( {\frac{\partial F}{\partial x} + \frac{\partial G}{\partial y}} \right)^{n} = - \frac{2}{\Delta t}\left[ {\frac{\partial }{\partial x}(F^{n + 1/2} - F^{n} ) + \frac{\partial }{\partial y}(G^{n + 1/2} - G^{n} )} \right]$$
(13)

Here, applying the Gauss theorem to the weak form of Eq. (8) yields:

$$\begin{aligned} \int\limits_{\varOmega } {\varPsi_{i} } U^{n + 1} {\text{d}}\varOmega &= \int\limits_{\varOmega } {\varPsi_{i} } U^{n} {\text{d}}\varOmega + \Delta t\left[ {\int\limits_{\varOmega } {\frac{\partial }{\partial x}\varPsi_{i} } F^{n + 1/2} {\text{d}}\varOmega + \int\limits_{\varOmega } {\frac{\partial }{\partial y}\varPsi_{i} } G^{n + 1/2} {\text{d}}\varOmega } \right. \hfill \\ &\quad \left. { + \int\limits_{\varOmega } {\varPsi_{i} } \frac{\partial }{\partial n}F^{n + 1/2} {\text{d}}\varGamma + \int\limits_{\varOmega } {\varPsi_{i} \frac{\partial }{\partial n}} G^{n + 1/2} {\text{d}}\varGamma } \right] \hfill \\ \end{aligned}$$
(14)

This equation was discretized in space using the Bubnov–Galerkin method. However, the solution may suffer from spurious oscillations in the results near the sharp changes in the flow conditions. The strategy is to add a new term to the system functioning as a flux-limiter [28]:

$$\int\limits_{\varOmega } {\varPsi_{i} U_{i}^{n + 1} } {\text{d}}\varOmega = \int\limits_{\varOmega } {\varPsi_{i} U_{i} } {\text{d}}\varOmega + {\text{RH}}_{i}^{n} + \sum\limits_{k} {d_{ik} K_{ik} (U_{k}^{n} - U_{i}^{n} )} ,$$
(15)

where d is a coefficient, which is varied within the range [0, 1], and \(K_{ij} = \sum\nolimits_{l} {\int_{{T_{i}^{l} }} {\varPsi_{i} \varPsi_{j} {\text{d}}\varOmega } }\). RH is the combination of the integral terms of the weak form equations’ right-hand side terms.

3.1 Flux-limiter

The second-order TVD scheme was obtained here through identifying the location of the probable oscillations and inserting a new term to reduce the dissipation. In a two-dimensional case, using the extrapolated points \(\left\{ {i*} \right\}\) and \(\left\{ {k*} \right\}\), the following variations were produced for each segment [29]:

$$\Delta_{i*} q = q_{i} - q_{i*} ;\,\quad \Delta_{ik} q = q_{k} - q_{i} ;\quad \Delta_{k*} q = q_{k*} - q_{k} ,$$
(16)

where q i is the unknown parameter. \(q_{i*} = q_{k} - 2\overrightarrow {\nabla } q_{i} .\overrightarrow {\eta }\) and \(q_{k*} = q_{i} + 2\overrightarrow {\nabla } q_{k} .\overrightarrow {\eta }\) are the extrapolated unknowns in direction \(\overrightarrow {\eta } = (x_{k} - x_{i} ;y_{k} - y_{i} )\). Moreover, d ik is defined as follows:

$$d_{ik} = \left\{ {\begin{array}{*{20}l} 0 &\quad {{\text{if }}{\kern 1pt} r^{ + } < 0\quad {\text{or}}\quad r^{ - } < 0\;({\text{extremum}})} \\ {1 - B(r_{s}^{ + } ,r_{s}^{ - } )} &\quad {\text{otherwise}} \\ \end{array} } \right.,$$
(17)

where

$$r^{ + } = \frac{{\hbox{min} \left( {\left| {\Delta_{k*} q} \right|,\left| {\Delta_{ik} q} \right|} \right)}}{{\hbox{max} \left( {\left| {\Delta_{k*} q} \right|,\left| {\Delta_{ik} q} \right|} \right)}};\quad r^{ - } = \frac{{\hbox{min} \left( {\left| {\Delta_{i*} q} \right|,\left| {\Delta_{ik} q} \right|} \right)}}{{\hbox{max} \left( {\left| {\Delta_{i*} q} \right|,\left| {\Delta_{ik} q} \right|} \right)}}$$
(18)
$$B(r_{s}^{ + } ,r_{s}^{ - } ) = \hbox{min} [B(r_{s}^{ + } ),B(r_{s}^{ - } )]$$
(19)

in which \(B(r)\) is Van Leer’s limiter, which varies within the range \(\left[ { 0 , 1} \right]\):

$$B(r) = \hbox{min} \left( {\frac{2r}{1 + r},1} \right)$$
(20)

The dissipation coefficient was identical throughout the governing equations, while water depth was the main variable to obtain the sensor. Moreover, due to the explicit nature of the calculations, the Courant–Friedrichs–Lewy (CFL) criterion was honored as the stability condition [30]. According to this criterion, the time step ∆t fulfill the following inequality:

$${\text{CFL}} = \frac{\Delta t}{{h_{\text{e}} }}\left| {\left( {c + \sqrt {u^{2} + v^{2} } } \right)} \right|_{\hbox{max} } \le 1,$$
(21)

where h e is the element size.

4 Results and discussion

The developed TVD Taylor–Galerkin (TVD-TG) model was applied to four typical test cases, namely the one-dimensional dam-break considering both the sub- and supercritical flows, and the asymmetric and circular dam-break problems. The MATLAB software was devised to code the numerical procedure. Two constant relative water depths were defined as the Dirichlet boundary condition at the inlet and outlet sets. All other boundaries are defined as solid walls and described by a combination of Dirichlet and Neumann boundary conditions by the integrations in the weak form of the equations.

4.1 One-dimensional dam-break problem (subcritical flow)

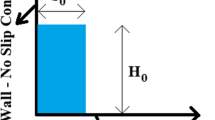
In this benchmark, the assumption of the immediate and complete dam break is considered, which is suitable for a reinforced concrete arch dam. The test demonstrates the flow field at \(t = 36\;{\text{s}}\). The computational domain is a \(2000 \times 200\;{\text{m}}^{2}\) horizontal and rectangular channel discretized by 2000 linear triangular elements. The chosen time step for the time discretization is \(\Delta t = 0.39\;{\text{s}}\). The dam is located in the middle of a horizontal channel, and the water body is assumed stationary with unequal depths on both sides of the dam (Fig. 1). The normal velocities along the boundary are assumed zero.

Fig. 1
figure 1

Initial conditions for the dam-break problem

Full size image

Figure 2 depicts the finite-element grid form of the computational domain.

Fig. 2
figure 2

The employed grid form

Full size image

The subcritical and supercritical flow regimes were obtained by changing the up- to downstream water depth ratios. For example, \(\frac{{h_{0} }}{{h_{1} }} = \frac{5}{10}\) denotes the subcritical flow regime while \(\frac{{h_{0} }}{{h_{1} }} = \frac{1}{10}\) represents a supercritical flow. The obtained results were compared with Stoker’s [25] analytical solution, obtained by solving the following polynomial equations.

$$u(x,t) = \left\{ {\begin{array}{*{20}l} 0 & \quad {{\text{if}}\;\;x < \frac{L}{2} - t\sqrt {gh_{\text{L}} } } \\ {\frac{1}{3t}\left( {2\left( {x + t\sqrt {gh_{L} } } \right) - L} \right)} & \quad {{\text{if}}\;\frac{L}{2} - t\sqrt {gh_{\text{L}} } \le x \le (u_{2} - c_{2} )t + \frac{L}{2}} \\ {u_{2} } & \quad {{\text{if}}\;(u_{2} - c_{2} )t + \frac{L}{2} < x \le st + \frac{L}{2}} \\ 0 & \quad {{\text{if}}\;\;x > st + \frac{L}{2}} \\ \end{array} } \right.$$
(22)
$$h(x,t) = \left\{ {\begin{array}{*{20}l} {h_{\text{L}} } & \quad {\;{\text{if}}\;\;x < \frac{L}{2} - t\sqrt {gh_{\text{L}} } } \\ {\frac{1}{9g}\left( {2\sqrt {gh_{\text{L}} } - \frac{1}{2t}\left( {2x - L} \right)} \right)^{2} } & \quad {{\text{if}}\;\frac{L}{2} - t\sqrt {gh_{L} } \le x \le (u_{2} - c_{2} )t + \frac{L}{2}} \\ {\frac{{h_{\text{R}} }}{2}\left( {\sqrt {1 + \frac{{8s^{2} }}{{gh_{\text{R}} }}} - 1} \right)} & \quad {{\text{if}}\;(u_{2} - c_{2} )t + \frac{L}{2} < x \le st + \frac{L}{2}} \\ {h_{\text{R}} } & \quad {{\text{if}}\;\;x > st + \frac{L}{2}} \\ \end{array} } \right.,$$
(23)

where

$$u_{2} = S - \frac{{gh_{\text{R}} }}{4S}\left( {1 + \sqrt {1 + \frac{{8s^{2} }}{{gh_{\text{R}} }}} } \right)$$
(24)
$$c_{2} = \sqrt {\frac{{gh_{\text{R}} }}{2}\left( {\sqrt {1 + \frac{{8s^{2} }}{{gh_{\text{R}} }}} - 1} \right)}$$
(25)

in which s is the positive root of (\(u_{2} + 2c_{2} - 2\sqrt {gh_{\text{L}} }\)), where \(L\) is the length of the domain, \(h_{\text{L}}\) is water depth on the left-hand side of the dam, and \(h_{\text{R}}\) denotes the water depth in the downstream channel.

To demonstrate the model’s efficiency, the results were also compared with two ideal FDM solutions regularly used for dam-break modeling. Accordingly, considering the same initial and boundary conditions, the SWEs were solved by the Lax–Wendroff and MacCormack procedures (Figs. 3, 4). All computations, including the numerical and analytical solutions, were performed in MATLAB 7.0.4.

Fig. 3
figure 3

One-dimensional dam-break flow problem (\(h_{1} = 10\;{\text{m}}\), \(h_{0} = 5\;{\text{m}}\) and \(t = 36\;{\text{s}}\))

Full size image
Fig. 4
figure 4

Flow velocity results for the analytical and numerical simulation of the one-dimensional dam-break problem (\(h_{1} = 10\;{\text{m}}\), \(h_{0} = 5\;{\text{m}}\) and \(t = 36\;{\text{s}}\))

Full size image

Figures 3 and 4 show that the proposed TVD model produces the best fitting results comparing with the analytic solution. Moreover, it can be seen that the developed model is successful in predicting the formation of the shock and rarefaction waves without showing spurious fluctuations.

4.2 One-dimensional dam-break problem (supercritical flow)

Accurate simulation of supercritical flows is often complicated. Most of the numerical models introduced in the literature suffer from severe fluctuations in the abrupt changes of the flow conditions [13, 31, 32]. In this section, the capability of the developed model is assessed and compared to the analytical, FDM, and Chang et al.’s [13] SPH models. Figure 5 demonstrates the solution of a supercritical flow induced by dam-break, where the water depth ratio is 0.1.

Fig. 5
figure 5

Dam-break flow water depth results of the analytical solution with the current model, MacCormack, and the results of Chang et al. [13]

Full size image

It can be seen that there is a deformation in the waveform in the MacCormack predictions. Moreover, the SPH model was not able to capture the shock formation. However, the developed model produces acceptable results.

4.3 Partial dam-break problem

The purpose of this benchmark is to evaluate the capability of the TVD-TG model to resolve the two-dimensional wave propagation. There is no analytical solution to this problem. However, its numerical solutions are available in the literature [33–36]. Figure 6 depicts the geometric dimensions of the computational domain used for the flow simulation. Initially, the upstream discharge is assumed zero while the water depths are 10 m in the upstream, and 5 m in the downstream sections. The domain dimension is 200 × 200 m2, divided by 3200 triangular elements.

Fig. 6
figure 6

The geometry of the partial dam-break problem

Full size image

After the removal of the barrier, water sets free to flow through the downstream channel reach. The shock and rarefaction waves are formed in the domain propagating in reverse directions. Figure 7 demonstrates the water surface, water depth contours, and the velocity field at t = 7.2, respectively.

Fig. 7
figure 7

The partial dam-break problem; a water surface elevation (m), b depth contours (m)

Full size image

According to the results, the shock and rarefaction waves propagation to the right and left side of the breached dam are evidently predicted. Figure 8 depicts the velocity vectors in the flow region.

Fig. 8
figure 8

The partial dam-break problem. Velocity field at t = 7.2 s

Full size image

4.4 Circular dam-break problem

The developed model was also validated using the scenario of a circular dam break, as described by [33, 37, 38]. This case considers the breaking of a cylindrical dam to study the properties of the model to preserve symmetry. The initial condition is comprised of two regions of stationary water bodies, which are separated by a thin-walled cylinder of diameter 22 m located in the center of a \(50 \times 50\;{\text{m}}^{2}\) horizontal and frictionless channel (Fig. 9). The domain was discretized by 5000 triangular elements. The water depth inside and outside the wall are 10 and 1 m, respectively.

Fig. 9
figure 9

The initial conditions for the circular dam-break problem

Full size image

Figure 10 represents the obtained depth contours and velocity vectors.

Fig. 10
figure 10

Circular dam-break flow using the TVD–Taylor–Galerkin method at t = 0.69 s. a Three-dimensional view of the water elevation (m), b contours of water depth (m), c velocity field

Full size image

The model shows the symmetry preserving and shock-capturing characteristics. However, some variations of water depth in the form of isles are notable in Fig. 10a, b, which are the negative features of using a Cartesian coordinate system in this particular case. The model is comparable to Zachariah’s [26] solution.

5 Conclusions

A mixed TVD Taylor–Galerkin model was developed and applied to the shallow water equations. The performance of the model was evaluated by various benchmarks, including the one-dimensional, asymmetric, and circular dam-break flows. The following conclusions were drawn:

  • The developed finite-element model has shown to act as an effective shock-capturing model.

  • The model is tested to simulate both the sub- and supercritical dam-break flows with the water depth ratios of 0.5 and 0.1. Comparing the predicted results with the results of other researchers, it was noticed that the current model performs better, in terms of accuracy, especially in the supercritical flow regimes.

  • Regarding the ability of the TVD-TG model to predict supercritical flows, this model can be used with some approximations to predict flows with dry beds. Accordingly, new models can be carried out by considering lower depth ratios while ignoring the corresponding source terms in the SVEs. This can result in faster calculations.

  • The partial dam-break case revealed the scheme’s efficiency to predict the salient features of a two-dimensional flow emanating from an asymmetric dam-break. On the other hand, the circular dam-break benchmark confirms the model’s symmetry-conserving capability.

It can be seen that the combination of the TVD and Taylor–Galerkin schemes presented here can be a valuable practical tool for engineers to mitigate the spurious oscillations in the shock-dominated problems. Here, the TVD scheme operates when it is required to. Therefore, this approach can be useful in terms of time and computational costs, in order to maintain larger time steps than the CFL criterion, which can be further investigated in future works.