Quasi-periodically Actuated Capacitive MEMS

Abstract

This work reports on the effect of a quasi-periodic (QP) voltage on the dynamics of a resonant capacitive micro-electro-mechanical system (MEMS) under DC and AC actuations. We consider that the AC actuation is composed of resonant AC and non resonant AC voltages. The microstructure device is modelled as a lumped mass-spring-damper system. Averaging technique and the method of multiple scales are performed to obtain the modulation equations of the slow dynamic near the primary resonance. The influence of the amplitude and the frequency of a high frequency voltage (HFV) on the occurrence of bistability and jumps in the frequency response is examined and the safe basin of attraction is explored. The results of this work indicate that when the mechanical parameters of the MEMS device are fixed and cannot be tuned, a HFV can be used for controlling the dynamic of the resonant capacitive MEMS.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Analysis of nonlinear vibrations of MEMS such as resonators, sensors and switches is an active research topic with applications in many engineering fields such as communications, automotive and robotics, to name just a few. One of the most critical issues in the design of MEMS is their reliability, life time, survivability and stability under mechanical, thermal and electrical loads. From dynamical point of view one of the key performances of MEMS is the repeatability and the reproducibility in terms of uniquely determined dynamics. However, this property is affected by nonlinearities, especially hysteresis and pull-in phenomena. Indeed, in capacitive MEMS devices hysteresis and pull-in instability constitutes one of the main way to the device failure [1].

Various theoretical and experimental works investigated the dynamic of MEMS actuated by DC and AC resonant voltages. For instance, Mestrom et al. [2] measured the effects of AC voltage on the hysteresis interval. Sahai et al. [3] used a laser beam focused on a MEMS structure to tune its nonlinear behavior from softening to hardening. Nayfeh and co-workers [4, 5] studied the mechanisms leading to the dynamic pull-in of MEMS resonators actuated by a resonant AC voltage. They showed that AC resonant voltage lowers drastically the pull-in threshold caused by the jumps phenomena. Alsaleem et al. [6] studied analytically and experimentally nonlinear resonances and dynamic pull-in of a microbeam. Rhoads et al. [7] studied parametrically excited MEMS oscillators, while Lakrad and Belhaq [8, 9] investigated the effect of a HFV on the pull-in in a microstructure actuated by mechanical shocks and electrostatic forces and the effect of a HF AC tension on the pull-in induced by a DC. Kacem et al. [10] analyzed the nonlinear dynamics of micro- and nanoelectromechanical resonant sensors around the primary resonance. For a comprehensive review on nonlinear static and dynamics of MEMS, the reader can refer to [1].

All the previously cited works deal with periodically driven MEMS. In the present paper, the effect of a QP voltage on a capacitive MEMS is investigated. The QP actuation is composed of a resonant AC voltage and a nonresonant AC one.

The rest of the paper is organized as follows: In Sect. 2, we describe the model, we perform an averaging technique [11] and then we use the method of multiple scales [12] to approximate the QP solutions of the MEMS device. In Sect. 3, analytical results are compared to numerical simulations, QP resonance curves are plotted and the effects of the control parameters are discussed. The dynamic integrity and basin erosion are also computed and commented. Section 4 concludes the work.

2 Equation of Motion and Perturbation Analysis

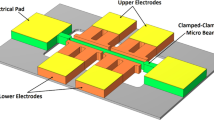
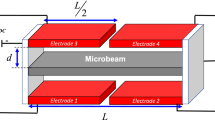
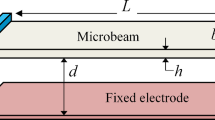
A single-degree-of-freedom model depicted in Fig. 1 is considered to represent a MEMS device employing DC and AC voltages as actuators. The movable electrode is modelled as a linear mass-spring-damper system. This linearity is valid when the thickness of the movable electrode is greater than the initial gap with the stationary electrode. We suppose that the only nonlinearity exhibited by the MEMS device is caused by the electric actuation. Thus, the equation of motion can be written as

$$\begin{aligned} m \ddot{x}+ c \dot{x} + k x =\frac{\varepsilon S}{2(d-x)^2} V^2(t) \end{aligned}$$

(1)

Fig. 1

A single-degree-of-freedom model used to model the capacitive MEMS

where x(t) is the displacement of the movable mass m, c and k are the damping and stiffness of the system, respectively, $\varepsilon$ is the dielectric constant of the gap medium, d is the initial capacitor gap width, S is the area of the cross section, and V(t) is the electric load.

The electric tension V(t) is taken as square root of a QP function as follows

$$\begin{aligned} V(t) = \sqrt{V_0^2 +U_1^2 \cos {(\omega ^* t)}+U_2^2 \cos {(\varOmega ^* t)}} \end{aligned}$$

(2)

where $V_0$ is the DC voltage, $U_1$ and $\omega ^*$ are the amplitude and the frequency of the AC resonant actuation, respectively, while $U_2$ and $\varOmega ^*$ denote the amplitude and the frequency of the nonresonant voltage, respectively. The specific form of the input voltage (2) is chosen in order to decouple the effects of DC and AC voltages, to avoid the occurrence of other harmonics and to principally prevent coupling with harmonic resonances. Note that a square root of a harmonic voltage was used in [13, 14] to decouple parametric and harmonic excitation.

By setting $X=\frac{x}{d}$, $\tau =\omega _0 t$, $\omega _0=\sqrt{\frac{k}{m}}$, $\xi =\frac{c}{2m\omega _0}$, $\omega =\frac{\omega ^*}{\omega _0}$ and $\varOmega =\frac{\varOmega ^*}{\omega _0}$, where the displacement is normalized with respect to the gap and the frequencies are normalized with respect to the natural frequency $\omega _0$ of the mass-spring system, the nondimensional equation of motion reads

$$\begin{aligned} X''+ 2 \xi X' + X =\frac{\alpha }{(1-X)^2} +\frac{\beta \cos {(\omega \tau )}}{(1-X)^2} +\frac{\gamma \cos {(\varOmega \tau )}}{(1-X)^2} \end{aligned}$$

(3)

Here the primes denote the derivatives with respect to the normalized time $\tau$, and the parameters

$$\begin{aligned} \alpha= & {} \frac{\varepsilon S V_0^2}{2 m \omega _0^2 d^3} \end{aligned}$$

(4)

$$\begin{aligned} \beta= & {} \frac{\varepsilon S U_1^2}{2 m \omega _0^2 d^3} \end{aligned}$$

(5)

$$\begin{aligned} \gamma= & {} \frac{\varepsilon S U_2^2}{2 m \omega _0^2 d^3} \end{aligned}$$

(6)

represent the contribution of the DC voltage, the resonant AC and the nonresonant AC voltages, respectively. It should be pointed out that the parameters $\alpha , \beta$ and $\gamma$ have to be chosen such that the electric tension V(t) in (2) is real.

Equation (3) is a quasi-periodically driven system both externally and parametrically. In what follows $\varOmega$ is taken larger than $\omega$ and the corresponding voltage is referred to as HFV.

In the absence of the AC voltages, the application of a DC voltage $\alpha$ causes an attractive electrostatic force between the two electrodes that causes a permanent displacement of the mass towards the stationary electrode. The static equilibria $X_s$ are given by solving the following algebraic equation

$$\begin{aligned} X_s = \frac{\alpha }{(1-X_s)^2} \end{aligned}$$

(7)

Note that $X_s=1$ corresponds to the static pull-in phenomenon which leads to the contact between the two electrodes. This contact is desirable, for instance, for capacitive switches and undesirable for sensors. In this latter, it can cause stiction, plastic deformations of the movable electrode or even its failure.

A static analysis reveals that the pull-in occurs for $\alpha _p =\frac{4}{27} \approx 0.148$ which corresponds to a steady state displacement $X_s=1/3$. Figure 2 shows the classical variation of the static equilibria $X_s$ with the DC voltage $\alpha$. The stable (lower) branch and the unstable (upper) branch of equilibrium points collide in a saddle-node bifurcation, resulting in the disappearance of both branches. In order to avoid the static pull-in, the DC voltage $\alpha$ should be taken below 0.148 and the initial conditions should be taken inside the homoclinic loop of the saddle equilibrium. It is worth noting that the pull-in phenomenon could happen for values of $\alpha$ lower $\alpha _p$, statically determined, due to the transient dynamics and to the modification of the basin of attraction .

Fig. 2

Static equilibria $X_s$ versus the DC voltage $\alpha$. Solid lines stable, dashed lines unstable

2.1 Fast Flow Dynamic

The expression of the electric tension $V(\tau )$ used in (3) contains a slow dynamic which describes the main motion at time-scale of the microstructure natural vibration and a fast dynamic at time scale of the HFV. In what follows the two-step perturbation method is used to approximate QP solutions of (3).

To obtain the main equation governing the slow dynamic of the device, we implement the method of direct partition of motion [11] by introducing two different time-scales: a fast time $T_{-1} = \eta ^{-1} \tau$ and a slow time $T_0 = \tau$. Then, the displacement of the mass $X(\tau )$, around a stable static equilibrium $X_s$, can be split up into a slow part $Z(T_0)$ and a fast part $\phi (T_{-1},T_0)$ as follows

$$\begin{aligned} X(\tau ) = X_{s}+ Z(T_0) + \phi (T_{-1},T_0) \equiv X_{s} + \eta \tilde{Z}(T_0) + \eta ^2 \tilde{\phi }(T_{-1},T_0) \end{aligned}$$

(8)

Here the positive parameter $\eta$ is introduced to measure the smallness of other parameters $(0<\eta \ll 1)$. The slow part $Z(T_0)$ takes into account the transient motion composed of the natural damped motion of the microstructure and the response to the resonant actuation. In order to give a physical meaning to the perturbation parameter $\eta$, the high-frequency is chosen as $\varOmega =\eta ^{-1}$. The fast motion and its derivatives are assumed to be $2\pi$-periodic functions of the fast time $T_0$ with zero mean value with respect to it [11]. Thus, $\langle X(\tau ) \rangle =Z(T_0)$ where $\langle . \rangle = \frac{1}{2\pi } \int _0^{2\pi } (.) dT_{-1}$ defines the fast time-averaging operator. Introducing $D_m^n=\frac{\partial ^n }{\partial T_m^n}$ yields

$$\begin{aligned} \frac{d }{d \tau }= & {} \eta ^{-1} D_{-1}+D_0 +\eta D_1 +\eta ^2 D_2 +O(\eta ^3) \end{aligned}$$

(9)

$$\begin{aligned} \frac{d^2 }{d \tau ^2}= & {} \eta ^{-2} D_{-1}^2+\eta ^{-1} 2D_{-1}D_0+D_0^2 +O(\eta ) \end{aligned}$$

(10)

Setting $\beta =\eta ^3 \tilde{\beta }$ and $\xi =\eta ^2 \tilde{\xi }$ where the parameters with tildes are of order O(1) and substituting (9) and (10) into (3), we obtain up to $O(\eta ^4)$ order the following equation

$$\begin{aligned}&(D_{-1}^2\tilde{\phi })+X_s+\eta [2(D_{-1}D_0\tilde{\phi })+ (D_0^2\tilde{Z})+ \tilde{Z}] + \eta ^2 [(D_0^2\tilde{\phi })+2(D_{-1}D_1\tilde{\phi })+\tilde{\phi }+2(D_0D_1\tilde{Z})] \nonumber \\+ & {} \eta ^3 [2(D_{-1}D_2\tilde{\phi })+2(D_0D_1\tilde{\phi })+2(D_0D_2\tilde{Z})+(D_1^2\tilde{Z}) + 2\tilde{\xi } (D_{-1}\tilde{\phi })+2\tilde{\xi }(D_0\tilde{Z})] \nonumber \\= & {} \frac{1}{(1-X_s)^2} \left\{ \bigg [ \alpha +\gamma \cos {(T_{-1})}\bigg ]+\eta \left[ \frac{2 \tilde{Z}}{(1-X_s)}(\alpha + \gamma \cos {(T_{-1})}) \right] \right. \\+ & {} \eta ^2 \left[ (\frac{3 \tilde{Z}^2}{(1-X_s)^2}+\frac{2 \tilde{\phi }}{(1-X_s)}) (\alpha +\gamma \cos {(T_{-1})}) \right] \nonumber \\+ & {} \left. \eta ^3 \left[ (\frac{4 \tilde{Z}^3}{(1-X_s)^3}+\frac{6 \tilde{Z} \tilde{\phi }}{(1-X_s)^2}) (\alpha + \gamma \cos {(T_{-1})})+\tilde{\beta } \cos {(\omega T_0)} \right] \right\} + O(\eta ^4) \nonumber \end{aligned}$$

(11)

The dominant terms dependent on $T_{-1}$ up to the order $O(\eta )$ in (11) are

$$\begin{aligned} (D_{-1}^2\tilde{\phi }) = \frac{\gamma }{(1-X_s)^2} \cos {(T_{-1})} \end{aligned}$$

(12)

Thus, up to this leading order, the fast motion is given by

$$\begin{aligned} \tilde{\phi }(T_{-1},T_0) =- \frac{\gamma }{(1-X_s)^2} \cos {(T_{-1})}+O(\eta ) \end{aligned}$$

(13)

This fast motion $\phi$ increases by increasing the amplitude $\gamma$ of the HFV and by considering larger values of static equilibrium $X_s$ which implies having a large DC voltage $\alpha$.

2.2 Slow Flow Dynamic

To approximate the equation of the slow dynamic, Eq (11) is averaged over a period of the fast time scale $T_{-1}$. One obtains the following equation up to the order $O(\eta ^3)$

$$\begin{aligned} (D_0^2\tilde{Z})+ \omega _1^2 \tilde{Z} = \eta [\alpha _1 \tilde{Z}^2 - \gamma _1 ] + \eta ^2 [ \alpha _2 \tilde{Z}^3 - \gamma _2 \tilde{Z} -2 \tilde{\xi } (D_0\tilde{Z})+\tilde{\beta }_1 \cos {(\omega T_0)} ] \end{aligned}$$

(14)

where

$$\begin{aligned} \alpha _1=\frac{3\alpha }{(1-X_s)^4}, \alpha _2 = \frac{4 \alpha }{(1-X_s)^5}, \tilde{\beta }_1 = \frac{\tilde{\beta }}{(1-X_s)^2}, \gamma _1 =\frac{\gamma ^2}{(1-X_s)^5}, \gamma _2 = \frac{3 \gamma ^2}{(1-X_s)^6} \end{aligned}$$

The parameters $\alpha _i (i=1,2)$, $\tilde{\beta }_1$ and $\gamma _i (i=1,2)$ represent the effects of the DC actuation, the AC resonant actuation and the HFV, respectively. The fast dynamic influences the slow one, in (14), through a biasing term $\eta \gamma _1$ and a linear term $\eta ^2 \gamma _2 \tilde{Z}$.

The normalized natural frequency of the mass actuated by the DC voltage is given by

$$\begin{aligned} \omega _1^2 = 1 - \frac{2 \alpha }{(1-X_s)^3} \end{aligned}$$

(15)

In Fig. 3 the natural frequency $\omega _1$ given in (15) is plotted versus the DC voltage $\alpha$. In the same figure are plotted in circles the numerically obtained natural frequencies of (3) in the absence of the AC voltages ($\beta =\gamma =0$) and damping. In this case the system is Hamiltonian and the physically acceptable solutions are centers that are confined inside a homoclinic loop corresponding precisely to the static pull-in phenomenon. It should be noted that the fundamental frequency of orbits near the centers is computed numerically using a fast Fourier transformation analysis. It can be seen from Fig. 3 that the natural frequency is decreasing with respect to $\alpha$ till reaching zero which corresponds to the pull-in instability.

Fig. 3

Natural frequency $\omega _1$ versus $\alpha$. Continuous line (given by (15)) and circles (given by numerical simulation of (3))

In order to obtain approximations of periodic solutions of the slow dynamic, we use the multiple scales method [12] up to the second order near the primary resonance i.e., $\omega = \omega _1 + \sigma$ where the small detuning parameter $\sigma =\eta ^2 \tilde{\sigma }$ is introduced to measure the closeness of the excitation frequency $\omega$ to the natural frequency $\omega _1$. New time scales are introduced $T_n=\eta ^n \tau$, where n is a positive integer. Then, equating terms of like power of $\eta$ in (14), we obtain the following hierarchy of problems:

• Order O(1)

  $$\begin{aligned} D_0^2 \tilde{Z}_0 + \omega _1^2 \tilde{Z}_0 =0 \end{aligned}$$

  (16)

The solution is written as

$$\begin{aligned} \tilde{Z}_0(T_0,T_1,T_2) = \tilde{A}(T_1,T_2) \exp {(i \omega _1 T_0)}+ c.c \end{aligned}$$

(17)

where cc denotes the complex conjugate of the preceding terms. The complex amplitude $\tilde{A}(T_1,T_2)$ has to be determined by eliminating the secular terms at the next level of approximations.

• Order $O(\eta )$

  $$\begin{aligned} D_0^2\tilde{Z}_1 + \omega _1^2 \tilde{Z}_1 = \alpha _1 \tilde{Z}_0^2 - \gamma _1 -2(D_0D_1\tilde{Z}_0) \end{aligned}$$

  (18)

The secular terms elimination condition is given by

$$\begin{aligned} D_1\tilde{A} = 0 \end{aligned}$$

(19)

and the particular solution up to order $O(\eta )$ reads

$$\begin{aligned} \tilde{Z}_1 = \frac{\alpha _1}{\omega _1^2} \tilde{A}\bar{\tilde{A}} -\frac{\gamma _1}{2\omega _1^2} -\frac{\alpha _1 \tilde{A}^2}{3\omega _1^2} \exp {(i2\omega _1 T_0)} +c.c \end{aligned}$$

(20)

• Order $O(\eta ^2)$

  $$\begin{aligned} D_0^2\tilde{Z}_2+\omega _1^2 \tilde{Z}_2 =&-2(D_0D_2\tilde{Z}_0)-(D_1^2\tilde{Z}_0)+2\alpha _1 \tilde{Z}_0 \tilde{Z}_1 \nonumber \\&+\, \alpha _2 \tilde{Z}_0^3 -\gamma _2 \tilde{Z}_0- 2 \xi (D_0\tilde{Z}_0)+\frac{\tilde{\beta }_1}{2} e^{(i\omega T_0)} \end{aligned}$$

  (21)

Elimination of secular terms leads to

$$\begin{aligned} i2\omega _1 (D_2 \tilde{A}) = -i2 \tilde{\xi } \omega _1 \tilde{A}+ \varGamma _1 \tilde{A} + L_2 \tilde{A}^2\bar{\tilde{A}}+\frac{\tilde{\beta }_1}{2} e^{i \sigma T_0} \end{aligned}$$

(22)

where $\varGamma _1=-\frac{2 \alpha _1 \gamma _1}{\omega _1^2} -\gamma _2$ and $L_2=\frac{10 \alpha _1^2}{3\omega _1^2}+3\alpha _2$. The particular solution at this order is given by

$$\begin{aligned} \tilde{Z}_2 = -\frac{1}{8 \omega _1^2} \left( \alpha _2 - \frac{2\alpha _1^2}{3\omega _1^2} \right) \tilde{A}^3 e^{(i3\omega _1 T_0)} +cc \end{aligned}$$

(23)

Using the polar form $\tilde{A}=(\tilde{a}/2) \exp {(i \theta )}$, where $\tilde{a}$ and $\theta$ are the amplitude and the phase, respectively, separating real and imaginary parts in (22) leads to the following modulation equations of amplitude and phase

$$\begin{aligned} \frac{d \tilde{a}}{d\tau }= & {} -\xi \tilde{a} + \eta ^2 \frac{\tilde{\beta }_1}{2\omega _1} \sin {(\psi )} \end{aligned}$$

(24)

$$\begin{aligned} \tilde{a} \frac{d \psi }{d\tau }= & {} \sigma \tilde{a}+\eta ^2 \left[ \varGamma _1 \frac{\tilde{a}}{2\omega _1}+ L_2\frac{\tilde{a}^3}{8\omega _1}+ \frac{\tilde{\beta }_1}{2\omega _1} \cos {(\psi )} \right] \end{aligned}$$

(25)

with $\psi =\tilde{\sigma } T_2-\theta$. One should point out that stationary solutions of (24) and (25) i.e., $\dot{a}=\dot{\psi }=0$ correspond to periodic solutions of the slow flow (14) and consequently to the QP vibrations of the original system (3). In fact, with $Z = \eta \tilde{Z}$ and $a = \eta \tilde{a}$, the amplitude a of these periodic solutions is obtained by solving the following algebraic equation

$$\begin{aligned} \xi ^2 a^2+ \left[ \sigma a+ \eta ^2 \varGamma _1 \frac{a}{2\omega _1}+L_2\frac{a^3}{8\omega _1} \right] ^2 = \left( \frac{\beta _1}{2\omega _1} \right) ^2 \end{aligned}$$

(26)

It can be seen that HFV influences the amplitude a through the parameter $\varGamma _1$. The approximated QP solution of (3), up to the leading order, is then given by

$$\begin{aligned} X(\tau )= & {} X_s -\frac{\gamma }{\varOmega ^2 (1-X_s)^2} \cos (\varOmega \tau ) + a \cos {(\omega \tau +\psi )} \nonumber \\&+ \frac{\alpha _1}{2\omega _1^2} \frac{a^2}{\varOmega ^2} -\frac{\gamma _1}{\varOmega ^2 \omega _1^2}-\frac{\alpha _1 }{6\omega _1^2} a^2 \cos {(2\omega \tau -2\psi )} \nonumber \\&- \frac{1}{32 \omega _1^2} (\alpha _2-\frac{2\alpha _1^2}{3\omega _1^2}) a^3 \cos {(3\omega \tau - 3 \psi )} +O(\eta ^4) \end{aligned}$$

(27)

3 Main Results

In this section, we analyze the effect of different actuations on the dynamic of the micro-system. To validate the analytical prediction, we compare the analytical approximation given by (27) with the results obtained by numerical simulations of (3) using a Fehlberg fourth-fifth order Runge-Kutta method.

Next, attention will be paid on the regions where the behavior of the micro-system is QP precluding the chaotic regions. Indeed, (3) represents a four-dimensional dynamical system in the space $R^2 \times T^2$ and can be written in the form

$$\begin{aligned} X'= & {} Y \nonumber \\ Y'= & {} -2\xi Y - X +\frac{\alpha + \beta \cos {(\varPhi )} + \gamma \cos {(\varTheta )}}{(1-X)^2} \nonumber \\ \varPhi '= & {} \omega \\ \varTheta '= & {} \varOmega \nonumber \end{aligned}$$

(28)

A visual representation of the attractors in the four-dimensional flow (28) can be achieved using Poincaré map by strobing on the fast-evolving phase $\varTheta$. The corresponding mapping $(X_n, X'_n, \varPhi _n) \rightarrow (X_{n+1}, X'_{n+1}, \varPhi _{n+1})$ is three dimensional.

In all numerical computations the damping coefficient $\xi =0.0002$. In Fig. 4 we show the time histories of (3) obtained analytically (27) and numerically for various parameters of control. One can observe from these figures a good match between the analytical and the numerical results.

In Fig. 5 are depicted the power spectra and the Poincaré map of the attractors (shown in Fig. 4a, b) projected on the plane $(X_n,\varPhi _n)$, with $\varPhi _n$ is computed modulo $\frac{2\pi }{\omega }$. These plots show that the attractors are QP.

Fig. 4

Time histories for $\alpha =0.12, \xi =0.0002, \sigma =0$ and $\gamma =0.119$. Gray line (analytical solution (27)) and black line (numerical solution of (3)). a $\beta = {2.10}^{-6}$ and $\varOmega$ = 7.1, b $\beta = {10}^{-5}$ and $\varOmega$ = 4.1, c $\beta = {5.10}^{-5}$ and $\varOmega$ = 4.1

Fig. 5

Projection of the Poincaré map in the plane $(X, \varPhi )$ and the power spectra for the attractors of Fig. 4a, b. a $\beta = {2.10}^{-6}$ and $\varOmega$ = 7.1, b $\beta = {10}^{-5}$ and $\varOmega$ = 4.1

3.1 Case with Resonant Actuation Only

In the absence of the nonresonant voltage ($\gamma =0$), the system is subject to a DC and an AC resonant voltages. Figure 6 shows, for different values of the static voltage $\alpha$, the amplitude-frequency response of the mass, as given by (26). The numerical values of the amplitude a of the periodic solutions are obtained by solving the algebraic equation (26). It can be seen from this figure that increasing the static voltage $\alpha$ increases the softening behavior of the system.

In Fig. 7, we show for fixed DC voltage $\alpha =0.12$, the frequency response for different values of resonant AC voltage $\beta$. One observes that increasing $\beta$ leads to the softening behavior, hysteresis as well as dynamic pull-in instability [5] for larger values of $\beta$.

The bifurcation curves delimiting the existence regions of solutions are shown in Fig. 8 in the plane of the resonant voltage parameters. It is clear that the region of multiplicity of solutions (zone I) increases with increasing $\beta$. This results is in agreement with the softening effect of increasing $\beta$ shown in Fig. 7.

Fig. 6

Resonance curves for various values of $\alpha$, for $\gamma =0$, $\xi =0.0002$ and $\beta =0.00001$. Lines Analytical solutions (24) and (25): continuous for stable and dashed for unstable. The stars, triangles and circles for numerical solutions of (3)

Fig. 7

Resonance curves for various values of $\beta$, for $\gamma =0$, $\xi =0.0002$ and $\alpha =0.12$. Continuous lines for stable, dashed lines to unstable analytic solutions. The stars are numerically computed amplitude

Fig. 8

Number of solutions in the plane $(\sigma , \beta )$ for $\gamma =0$, $\alpha =0.12$ and $\xi =0.0002$: zone I three solutions and zone II one solution

3.2 Effects of the Nonresonant Voltage

In this subsection we investigate the effect of adding the nonresonant AC voltage on the frequency response of the moving mass. In particular, we shall investigate how this voltage can affect the domain of bistability. First, assume that the parameters of the system are chosen in zone I of Fig. 8 $(\sigma =-0.002, \beta =0.00001)$ where bistability exists. In Fig. 9 we show in the parameter plane $(\gamma , \varOmega )$ of the HFV the region where the bistability can be eliminated (the gray region). Figure 9 indicates that the elimination zone of bistability is optimal for moderate values of the frequency $\varOmega$ and high values of the amplitude $\gamma$ of the HFV.

Fig. 9

Number of solutions in the plane $(\varOmega , \gamma )$ for $\alpha =0.12$, $\sigma =-0.002$, zone I three solutions, zone II one solution

Fig. 10

Analytical resonance curves given by (26) versus the shift of the resonance $\sigma$ for various values of $\gamma$. $\alpha =0.12$ and $\varOmega =7.1$

Figure 10 shows, for fixed $\varOmega =7.1$ and $\alpha =0.12$, the influence of the amplitude $\gamma$ on the resonance frequency of the slow dynamic obtained analytically in (26). This figure shows that increasing the amplitude $\gamma$ causes the nonlinear resonance frequency to shift towards higher frequencies. Figure 10 also indicates that by tuning the amplitude of the HFV, the amplitude of the resonant mass response might be increased or decreased to a desirable value of operation.

In Fig. 11 are shown the numerically computed resonance curves of the original equation (3) for various values of $\gamma$. This figure shows the maximum values of the stationary solution of the QP attractors, after disregarding 6600 resonant period, during 600 times of the resonant period. This figure confirms the analytically obtained results of Fig. 10. The effect of the amplitude $\gamma$ and frequency $\varOmega$ of the nonresonant voltage on the resonance shift is presented in Fig. 12. This figure shows that the amplitude $\gamma$ and the frequency $\varOmega$ cause opposite effects on the shift of resonance. Indeed, increasing $\gamma$ increases the shift, while increasing $\varOmega$ decreases it towards the case $\gamma =0$.

Fig. 11

Numerical resonance curves for different values of $\gamma$ and $\varOmega =7.1$ of (3). $\beta =0.00001, \xi =0.0002, \alpha =0.12$

Fig. 12

Shift of the resonance versus the amplitude of the HF voltage $\gamma$ for various values of $\varOmega$

3.3 Dynamic Integrity and Basin Erosion

It is agreed that the safety of a nonlinear system depends not only on the stability of its solutions but also on the uncorrupted basin surrounding each solution [15]. Indeed, by performing numerical simulations of trajectories from different starting points we are able to detect any significant change in the safe basin of attraction . In this section we analyze and approximate numerically the safe basin of attraction.

Fig. 13

Basins of attraction for various values of $\beta$ and for $\alpha =0.13, \sigma =-0.001$ and $\gamma =0$. a $\beta =0$. b $\beta =0.003$. c $\beta =0.007$. d $\beta =0.01$.

The chosen phase space window is $X(\tau ) \in [0,0.5]$ and $X'(\tau ) \in [-0.2,0.15]$ which contains the compact part of the safe basins of attractions. Figures 13 show the basins evolution for increasing value of the AC voltage $\beta$ in the absence of HFV. The safe basins correspond to the black regions and the corrupted areas correspond to the white regions. These latter regions correspond precisely to the occurrence of the dynamic pull-in phenomenon. The erosion of the safe basins for increasing resonant voltage amplitude $\beta$ is depicted in Fig. 13.

Figure 14 shows that the safe basin of attraction can be increased by adding a HFV with $\gamma = 0.12$ and $\varOmega = 5.1$. The effect of adding the nonresonant voltage on the basins of attractions is given in Fig. 15. It shows the global integrity measure, representing the normalized area of the safe basin [15], versus the amplitude of the resonant voltage amplitude $\beta$ for various $\gamma$. One observes that increasing the amplitude $\gamma$ may increase the safe basin of attraction for $\beta <0.005$ while the amplitude of the HFV has no effect on the global integrity measure beyond $\beta =0.005$. Indeed, increasing the safe basin offers the movable electrode of the capacitive MEMS to gain stability and to operate in larger intervals.

Fig. 14

Basins of attraction for $\alpha =0.13, \beta =0.00001, \xi =0.0002, \sigma =-0.001$ and $\varOmega =5.1$. The gray zone corresponds to $\gamma =0$ and the black zone to $\gamma =0.12$

Fig. 15

Global integrity measure versus $\beta$ for various values of $\gamma$ and for $\alpha =0.13, \xi =0.0002, \sigma =-0.001$ and $\varOmega =5.1$

4 Conclusion

The dynamics of a quasi-periodically actuated capacitive MEMS is studied analytically and numerically. The MEMS is modelled by a lumped single degree of freedom system actuated by DC and AC electrical voltages. The AC actuation is QP and is composed of a resonant AC voltage and a non resonant fast AC voltage. The QP attractors are approximated by using the two-step perturbation technique. The method of direct partition of motion was performed to approximate the slow dynamic of the device and the multiple scales method was used to obtain the amplitude-frequency response of the slow dynamic near the primary resonance.

The results shown that adding a HFV to the resonant AC actuation shifts the frequency response toward higher frequencies, thereby retarding the occurrence of bistability and jumps in the response amplitude. It was also shown that for appropriate values of the amplitude and the frequency of the HFV, jumps phenomena can be eliminated. Moreover, by tuning the amplitude of the HFV, the amplitude of the resonant mass might be increased or decreased to a desirable value of operation which can be of interest for sensing specific mechanical parameters. It was also shown that for appropriate amplitude and frequency of the HFV the safe basin of attraction is increased and consequently the dynamic integrity of the device is improved.

The present work reveals that in certain operations where the original mechanical characteristics of the MEMS device are assigned and cannot be tuned, HFV can be considered as a practical alternative for controlling the dynamic of the resonant capacitive MEMS.