1 Introduction

The growing requirements for high-performance, single-chip, multi-band and reconfigurable radio-frequency (RF) solutions for wireless communication systems, mechanical resonators have been widely explored in recent years. Because of their high quality-factor (QF), quartz-crystal and surface-acoustic-wave (SAW) resonators have been generally employed as the frequency setting elements in oscillators-based circuitry. Nevertheless, these conventional oscillators can only provide a relatively small frequency tuning whose magnitude is limited up to a few megahertz. Consequently, to cover a larger frequency bandwidth, the need for mechanical micro-resonators turned into a tremendous interest to the RF wireless design society. Moreover, with the need of high-QF, more metal–oxide–semiconductor (CMOS) compatibility and multi-frequency operation on a chip, microelectromechanical system (MEMS) based resonators provide a feasible alternative to the bulky quartz crystal and SAW based old resonators. Also, MEMS resonators represent the best possibility for integration as oscillators for wider band transceiver applications (Wu et al. 2020; Chen et al. 2018; Rinaldi et al. 2011; Zuo et al. 2010).

To be compatible with various applications, MEMS structures were mainly characterized based on their focal actuation mechanisms (Azimloo et al. 2014). Even though many unique actuation methods are developed, the conventional mechanisms can be generally categorized into Electrostatic and Piezoelectric actuation (Wu et al. 2020). Indeed, the electrostatic parallel-plates based actuation process is the most executed mechanism in MEMS which benefits the systems to have the lowest excitation control, the largest changes in the measured capacitance, a relatively easier fabrication process and better performance over the different other methods (Nayfeh et al. 2007; Siahpour et al. 2018). The micro-resonator consists mainly of a flexible/movable beam (bridge) suspended over a fixed/stationary conductor (electrode) (Ghayesh et al. 2013; Feng et al. 2019) where a combination of DC and AC voltages are assumed for actuating/resonating purposes. Nevertheless, this method suffers from certain non-linear behaviors (Alsaleem et al. 2010; Zhang et al. 2014; Masoumi et al. 2021) including hysteresis, sudden jumps in the response, the pull-in instability, etc.…. These nonlinear trends were shown to be useful under certain conditions within systems requiring low frequency applications such as earthquake detectors and energy vibration based harvesting structures (Ghasemi et al. 2020). In such cases, the static DC voltage can be used to tune the natural frequency of the micro-resonator to lower values and hence form a certain type of system called tunable resonator.

Generally, MEMS structures have an unlimited number of oscillating modes due to the distributed mechanical parameters of the micro-beams, which are necessary to label the vibration type of the micro-resonator and particularly depends on the arrangement/shape of the actuating electrodes. By differently shaping and arranging these electrodes, the electric actuating load can be fashioned to trigger a certain mode of vibration. However, any of these vibrating systems usually resonate at first lowest mode of vibration also known as the fundamental mode, a proper selection of the mode of excitation/actuation, the resonating condition of the microsystem can be tuned to a desired wider range of frequency bandwidth. Indeed, numerous scholars (Prak et al. 1992; Gil et al. 2012) have studied selective mode of excitations but they conducted that microbeams assuming electrostatic actuation, the first mode of vibration is more likely to be excited as compared to the other higher-order modes, resulting in an oscillator resonating in a narrow band of frequencies ranging from the first fundamental frequency to the frequency corresponding to approximately 60–70% of dynamic pull-in voltage of the first mode.

In the literature, one can find several attempts, such as (Yao and MacDonald 1995; Pourkamali et al. 2003; Jensen et al. 2003; Lee et al. 2007, 2008; Morgan and Ghodssi 2008; Zine-El-Abidine and Yang 2009; Mobki et al. 2013; Madinei et al. 2015; Ghasemi et al. 2020), to design smart and innovative electrostatic based actuation mechanism for MEMS devices through shaping the stationary actuating electrodes. An increase of 5–25% in the frequency tuning range were reported in the designs of Yao and MacDonald (1995), Pourkamali et al. (2003), Lee et al. (2007), Morgan and Ghodssi (2008). On the other hand, there are also attempts to achieve a wider frequency tuning range. For instance, in the effort of Mobki et al. (2013) and Madinei et al. (2015), and by placing the actuating electrodes asymmetrically on both sides of the microbeam, the second mode (asymmetric) of vibration has been excited more than other modes and the frequency range of oscillation increased accordingly.

Despite these cited numerous efforts devoted into improving the tuning domain of electrically actuated MEMS based resonators, there is a need for a comprehensive study possibly covering wider frequency tuning applications ranging from low-to-high band of frequencies. As a case study, the configuration used in this paper consists of a doubly-clamped flexible microbeam placed between two stationary electrodes with different symmetric and asymmetric arrangements. Herein, to attain the first fundamental frequency, both stationary electrodes have an equal length with the movable microbeam, whereas the second oscillating mode is excited when the immovable electrodes are half the length of the microbeam and placed asymmetrically on both sides of the microbeam. A numerical/analytical model is developed, based on multimode Galerkin-based reduced-order model to solve the static and eigenvalue problems of the micro-beam under these various electrostatic actuation arrangements and distributions. A wider range of tunability behavior when controlling the actuation arrangement are to be analyzed and compared accordingly. Finite element analysis based on COMSOL Multiphysics software has been used to validate the obtained results. The results show that the obtained tuning range are very sensitive to the actuation scheme, which can be very supportive for sensing and harvesting applications. On the other hand, the proposed analytical model can be used as a guideline for designing micro-sensors and micro-actuators with low power consumption, high sensitivity, and wide tuning range of electrostatically actuated MEMS.

2 Model description

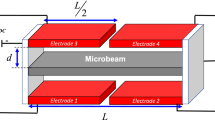
A schematic drawing of a MEMS resonator illustrated in Fig. 1 consists of a micro-beam clamped from both sides at the anchors and is arranged in between two symmetric upper and lower actuating electrodes. In this study, four different arrangements of the actuating excited electrodes, ranging from single-sided or double-sided configurations, will be considered depending on which resonating mode is to be exited:

  • Arrangement #1: in the classical model, system consisting of single-sided electrodes, assuming same DC voltage applied on lower electrodes (1 and 2) or the higher electrodes (3 and 4). In this case, the first fundamental mode of the microbeam will be excited.

  • Arrangement #2: system consisting of double-sided electrodes assuming a DC voltage applied simultaneously to all actuating electrodes (1, 2, 3 and 4). Therefore another kind of electrostatic excitation can be obtained (Mobki et al. 2013; Rezazadeh et al. 2012); here as well, the first mode of natural frequency will be excited accordingly.

  • Arrangement #3: system consisting of double-sided electrodes but here assuming an asymmetric DC actuation to one pair of the lower and upper electrodes (electrodes 1 and 4 or electrodes 2 and 3). This actuation skeleton causes the second mode of vibration more likely to be excited as compared to the other modes.

  • Arrangement #4: system consisting of double-sided electrodes through connecting the lower and upper electrodes with a cross-shape arrangement into the DC power supplies (electrodes 1 and 4 and electrodes 2 and 3). Here as well, the second mode of vibration will be mainly the dominant mode to be triggered.

Fig. 1
figure 1

Schematic of electrostatically actuated doubly-clamped microbeam resonator

Full size image

Consequently, the above suggested actuating arrangements will be mainly used to examine the multi-frequency based micro-resonator capabilities with a possible wider frequency tuning range. Another objective of this work is to possibly lower the excited micro-resonator’s modes of vibration. For this, an increase of the total length of the microbeam is one possibility which results into a decrease of the overall stiffness of the microbeam and consequently decrease in its natural frequencies. Nevertheless, in this case, the microbeam will be more prominent to undergo an earlier pull-in instability.

3 Mathematical modeling

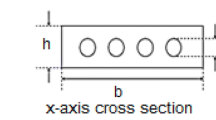
In this section, the equations governing the behavior of an electrostatically actuated microbeam, Fig. 1, are derived. The microbeam has a length L, width b and thickness h. It is assumed to be made from a silicon on insulator (SOI) wafer layer (isotropic material) with an affective young modulus of E = 169 GPa, Poisson’s ratio of \(\nu\) = 0.22, and mass density of \(\rho\) = 2328 kg/m3 (Sharpe et al. 1997). A static DC voltage VDC is applied between the movable microbeam and its lower and upper actuating electrodes. This difference of voltage results into a uniformly and equally distributed electrostatic force on the microbeam’s length. This attractive force causes the movable electrode to move toward the actuating electrodes and therefore resulting into a change in the structure effective stiffness. Assuming a nonlinear Euler–Bernoulli beam model superimposed to a couple-stress theory, the structural in-plane behavior of the movable electrode of Fig. 1 is governed by the following equation and respective boundary conditions (Younis et al. 2003):

$$\left\{\begin{array}{c}\left(EI+\mu A{l}^{2}\right)\frac{{\partial }^{4}w(x,t)}{\partial {x}^{4}}+\rho A\frac{{\partial }^{2}w(x,t)}{\partial {t}^{2}}+c\frac{\partial w(x,t)}{\partial t}={F}_{e}\left(V,w(x,t)\right);\\ w\left(x=0,t\right)=w\left(x=L,t\right)=0; \frac{\partial w(x=0,t)}{\partial x}=\frac{\partial w(x=L,t)}{\partial x}=0;\end{array}\right.$$
(1)

where \(w(x,t)\) denotes the microbeam’ in-plane deflection in the y-direction, function of space variable x and time t, \(A=bh\) and \(I=b{h}^{3}/12\) are respectively the cross-sectional area and moment of inertia, c is the coefficient of viscous damping due to the squeeze film damping, E and \(\mu\) are young’s modulus and shear modulus respectively, \(l\) = 170 nm (Miandoab et al. 2014) represents the length scale parameter. The term on the left-hand-side of the Eq. (1) denotes the parallel-plate electric forces assuming complete overlap area between the microbeam and the stationary electrode. This resultant electrostatic force, which has mainly a space-dependent profile, can be written for the four different arrangements of Fig. 1, respectively as follows in Table 1 (Madinei et al. 2015; Younis et al. 2003):

Table 1 Associated force from actuation type
Full size table

Regarding Table 1, \(H\left[x\right]\) is the Heaviside function, \({V}_{DC}\) represents the applied voltage between the micro-beam and the upper or downer electrodes, \({g}_{0}\) is the initial air gap between the electrodes and the non-deformed micro-beam, \({a}_{1}\) and \({a}_{2}\) parameters express the voltage distribution over the driven electrodes to study their excitation in desired frequency mode, \({\varepsilon }_{0}=8.85\times {10}^{-12}({F.m}^{-1})\) is the permittivity of free space. For convenience, the dimensionless variables are defined as follows:

$$\widetilde{w}=\frac{w}{{g}_{0}}, \widetilde{x}=\frac{x}{L}, {\widetilde{a}}_{1}=\frac{{a}_{1}}{L}, {\widetilde{a}}_{2}=\frac{{a}_{2}}{L}, \widetilde{t}=t\sqrt{\frac{EI}{\rho bh{L}^{4}}}$$
(2)

By substituting Eq. (2) in Eq. (1) and considering the associated force as actuation type #3, the result can be written as the following form:

$$\frac{{\partial }^{2}\widetilde{w}}{\partial {\widetilde{t}}^{2}}+{\beta }_{1}\frac{\partial \widetilde{w}}{\partial \widetilde{t}}+\left(1+{\beta }_{2}\right)\frac{{\partial }^{4}\widetilde{w}}{\partial {\widetilde{x}}^{4}}=\gamma {V}_{DC}^{2}\left(\frac{H\left[{\widetilde{a}}_{1}-\widetilde{x}\right]}{{\left(1-\widetilde{w}\right)}^{2}}-\frac{H\left[\widetilde{x}-{\widetilde{a}}_{2}\right]}{{\left(1+\widetilde{w}\right)}^{2}}\right)+f(\omega ,t)$$
(3)

The parameters appeared in Eq. (3) are:

$${{\beta }_{1}=\frac{c{L}^{4}}{EI\sqrt{\frac{\rho A{L}^{4}}{EI}}}, \beta }_{2}=\frac{\mu A{l}^{2}}{EI}, \gamma =\frac{6{\varepsilon }_{0}{L}^{4}}{E{h}^{3}{g}_{0}^{3}}$$
(4)

4 Numerical approach

In this section, the resultant equation governed by substituting electrostatic force expressions (Table 1) into Eq. (1) is numerically discretized using the modal expansion reduced-order modeling technique (Younis et al. 2003). For this, the microbeam in-plane deflection can be expanded as follows:

$$w\left(x,t\right)=\sum_{k=1}^{N}{\Psi }_{k}\left(x\right){q}_{k}(t)$$
(5)

where \({\Psi }_{k}\left(x\right)\) represents the mode-shape of an un-forced and un-damped doubly-clamped straight beam and \({q}_{k}(t)\) is the corresponding unknown time-dependent modal coordinate amplitude. By substituting Eq. (5) in Eq. (3), the resultant outcome is then multiplied by the mode-shape functions \({\Psi }_{j}(1\le j\le N)\) and the subsequent N-equations are then integrated from 0-L. This produces N ordinary-differential equations (ODEs) in \({\mathrm{q}}_{k}(1\le k\le N)\) forming a reduced-order-model (ROM). A convergence analysis was carried out and it was found that five modes (N = 5) is sufficient for convergence.

The derived ROM can be used to calculate the microresonator natural frequencies. Toward this, the static deflection of the beam upon the electrostatic actuation is first caudated. For this, we calculate the stationary deflection by setting all time dependent terms in the ROM based ODEs equal to zero. So the outcome equation for the static deflection of Eq. (3) is expressed as:

$$\left(1+{\beta }_{2}\right)\frac{{\partial }^{4}\widetilde{w}(x)}{\partial {\widetilde{x}}^{4}}=\gamma {V}_{DC}^{2}\left(\frac{H\left[{\widetilde{a}}_{1}-\widetilde{x}\right]}{{\left(1-\widetilde{w}(x)\right)}^{2}}-\frac{H\left[\widetilde{x}-{\widetilde{a}}_{2}\right]}{{\left(1+\widetilde{w}(x)\right)}^{2}}\right)$$
(6)

Due to the nonlinearity of the governing equation, the analytical solution methods cannot be used to obtain the results; therefore, it is better to linearize the equation. To solve the non-linear Eq. (6), the first step is taken by applying step by step linearization method. According to this method it is assumed that \({w}_{i}\) is the beam displacement due to the applied voltage \({V}_{i}\). Therefore, by increasing the voltage to the new value, the displacement of the micro-beam can be written as follows:

$${w}_{i+1}={w}_{i}+\delta w={w}_{i}+\Psi \left(x\right)$$
(7)

where:

$${V}_{i+1}={V}_{i}+\delta v$$
(8)

So Eq. (6) in \({(i)}^{th}\) and \({(i+1)}^{th}\) steps can be written as follows:

$$\left(1+{\beta }_{2}\right)\frac{{d}^{4}{w}_{i}}{d{x}^{4}}=\gamma {{V}_{i}}^{2}\left(\frac{H\left[{a}_{1}-x\right]}{{\left(1-{w}_{i}\right)}^{2}}-\frac{H\left[x-{a}_{2}\right]}{{\left(1+{w}_{i}\right)}^{2}}\right)$$
(9)
$$\left(1+{\beta }_{2}\right)\frac{{d}^{4}{w}_{i+1}}{d{x}^{4}}=\gamma {{V}_{i+1}}^{2}\left(\frac{H\left[{a}_{1}-x\right]}{{\left(1-{w}_{i+1}\right)}^{2}}-\frac{H\left[x-{a}_{2}\right]}{{\left(1+{w}_{i+1}\right)}^{2}}\right)$$
(10)

Substituting Eq. (7) in Eq. (10) yields to:

$$\left(1+{\beta }_{2}\right)\frac{{d}^{4}{w}_{i}}{d{x}^{4}}+\left(1+{\beta }_{2}\right)\frac{{d}^{4}\Psi }{d{x}^{4}}=\gamma {{V}_{i+1}}^{2}\left(\frac{H\left[{a}_{1}-x\right]}{{\left(1-{w}_{i}-\Psi \left(x\right)\right)}^{2}}-\frac{H\left[x-{a}_{2}\right]}{{\left(1+{w}_{i}+\Psi \left(x\right)\right)}^{2}}\right)$$
(11)

Using the calculus of variation theory and Taylor expansion, neglecting the higher-order term of the Taylor series, the right side of the obtained Eq. (11) can be rewritten as follows:

$$\begin{aligned} \left( {1 + \beta_{2} } \right)\frac{{d^{4} w_{i} }}{{dx^{4} }} & + \left( {1 + \beta_{2} } \right)\frac{{d^{4} \Psi }}{{dx^{4} }} \\ & = \gamma V_{i}^{2} \left( {\frac{{H\left[ {a_{1} - x} \right]}}{{\left( {1 - w_{i} } \right)^{2} }} - \frac{{H\left[ {x - a_{2} } \right]}}{{\left( {1 + w_{i} } \right)^{2} }}} \right) + 2\gamma V_{i}^{2} \left( {\frac{{H\left[ {a_{1} - x} \right]}}{{\left( {1 - w_{i} } \right)^{3} }} + \frac{{H\left[ {x - a_{2} } \right]}}{{\left( {1 + w_{i} } \right)^{3} }}} \right)\Psi \\ & + 2\gamma V_{i} \left( {\frac{{H\left[ {a_{1} - x} \right]}}{{\left( {1 - w_{i} } \right)^{2} }} - \frac{{H\left[ {x - a_{2} } \right]}}{{\left( {1 + w_{i} } \right)^{2} }}} \right)\delta v \\ \end{aligned}$$
(12)

By simplifying the Eq. (12), the linear equation to calculate \(\Psi \left(x\right)\) is obtained as the following form:

$$\begin{gathered} \left( {1 + \beta_{2} } \right)\frac{{d^{4} \Psi }}{{dx^{4} }} - 2\gamma V_{i}^{2} \left( {\frac{{H\left[ {a_{1} - x} \right]}}{{\left( {1 - w_{i} } \right)^{3} }} + \frac{{H\left[ {x - a_{2} } \right]}}{{\left( {1 + w_{i} } \right)^{3} }}} \right)\Psi \hfill \\ = 2\gamma V_{i} \left( {\frac{{H\left[ {a_{1} - x} \right]}}{{\left( {1 - w_{i} } \right)^{2} }} - \frac{{H\left[ {x - a_{2} } \right]}}{{\left( {1 + w_{i} } \right)^{2} }}} \right)\delta v \hfill \\ \end{gathered}$$
(13)

The solution of Eq. (13) belongs to infinite Hilbert space and can be expressed versus its basis functions. Since Eq. (13) is an equation with variable coefficients and finding a complete orthogonal basis that leads to a separable Hilbert space is laborious (difficult), therefore, the infinite Hilbert space is projected to a finite space based on the Galerkin decomposition method. To attain the approximate solution according to the Galerkin method, \(\Psi (x)\) is expressed in terms of a linear combination of a set of linear independent shape functions \({\varphi }_{n}\left(x\right)\) satisfying the boundary conditions.

$$\Psi \left( x \right) \cong \mathop \sum \limits_{n = 1}^{N} s_{n} \varphi_{n} \left( x \right)$$
(14)

By substituting Eq. (14) into Eq. (13) and multiplying the outcome by \({\varphi }_{m}(x)\) as a weight function of Galerkin method and integrating the output from \(x=0\) to 1, a set of linear algebraic equations can be obtained as follows:

$$\mathop \sum \limits_{m = 1}^{N} \left( {K_{mech} - K_{elec} } \right)s_{n} = F_{n} n = 1, \ldots ,N$$
(15)

where:

$$K_{mech} = \left( {1 + \beta_{2} } \right)\mathop \int \limits_{0}^{1} \varphi_{n}^{IV} \varphi_{m} dx$$
(16)
$$K_{elec} = 2\gamma V_{i}^{2} \mathop \int \limits_{0}^{1} \left( {\frac{{H\left[ {a_{1} - x} \right]}}{{\left( {1 - w_{i} } \right)^{3} }} + \frac{{H\left[ {x - a_{2} } \right]}}{{\left( {1 + w_{i} } \right)^{3} }}} \right)\varphi_{n} \varphi_{m} dx$$
(17)
$$F_{n} = {\text{~}}2\gamma V_{i} \mathop \int \limits_{0}^{1} \left( {\frac{{H\left[ {a_{1} - x} \right]}}{{\left( {1 - w_{i} } \right)^{2} }} - \frac{{H\left[ {x - a_{2} } \right]}}{{\left( {1 + w_{i} } \right)^{2} }}} \right)\delta v\varphi _{n} dx$$
(18)

At each step, by substituting calculated \(\Psi (x)\) in Eq. (7), \({w}_{i}(x)\) will be determined for a given specific \({V}_{i}\). According to Eq. (15) by increasing the applied DC voltage, the equivalent stiffness of the structure will be reduced and in case the stiffness of the structure reaches zero, the solution of the problem will gain an unstable value called Pull-in.

Furthermore, the eigenvalue problem of the micro-resonator is solved through perturbing the response around the calculated static position and considering only the linear part of the ROM. It is worth saying that the stability of each equilibrium solution is inspected through calculating the eigenvalues of the Jacobian matrix of the ROM.

5 Results and discussion:

As a case study, a micro-beam with length \(L=350\, \upmu m\), width \(b=20\, \upmu m\), thickness \(h=2\, \upmu m\), and same upper and lower gap size of \({g}_{0}=1\, \upmu m\), is considered. The shape functions satisfying the boundary conditions take the following form Rao (2019):

$$\varphi_{n} \left( x \right) = \left( {\cos \left( {A_{n} x} \right) - \cosh \left( {A_{n} x} \right)} \right) - B_{n} {*}\left( {\sin \left( {A_{n} x} \right) - \sinh \left( {A_{n} x} \right)} \right)$$
(19)

where \({B}_{n}\) and \({A}_{n}\) for the clamped–clamped structure are expressed as:

$$B_{n} = \frac{{\left( {\cos \left( {A_{n} } \right) - \cosh \left( {A_{n} } \right)} \right)}}{{\left( {\sin \left( {A_{n} } \right) - \sinh \left( {A_{n} } \right)} \right)}},{ }A_{n} = \left[ {4.7300,7.8532,10.9956,14.1372} \right].$$
(20)

To validate the results of this study, an attempt done to simulate the results of Madinei et al. (2015) to compare with; considering the first and the second arrangements in Table 1, the ROM results are displayed in Table 2. These two simulations validate the ROM and shows an acceptable agreement with the reported results in the literature. Also, the effect of index N in shape function on the static pull-in voltage for different step sizes is compared in Table 3.

Table 2 Validation of analysis process
Full size table
Table 3 Comparison of obtained results to the index N in shape function
Full size table

Figure 2 is related to static analysis of the single-side actuated microbeam (Arrangement #1). Since the diagram is plotted in dimensionless scale, the micro-beam after goes through about a third of the air gap, for classical parallel-plates model the pull-in phenomenon is occurred in \({V}_{pull-in}=11.12\, {\rm V}\). The simulation results for the deflection of the classical beam are shown through a dashed line with a stared marker. According to COMSOL results, the deflection of the microbeam is raised by increasing the applied DC voltage until \({V}_{DC}=10.99\, {\rm V}\). The COMSOL results diverge for voltages greater than \({V}_{DC}=10.99\, {\rm V}\). Therefore, \({V}_{DC}=10.99\, {\rm V}\) is considered as pull-in voltage in the COMSOL model, which are closely agreed with the results of numerical results. The pull-in voltage that is obtained from the COMSOL model is smaller than the distributed model. In COMSOL modeling, the fringing field effect is taken into account, which is neglected in our model, thereby increasing the applied force to the microbeam.

Fig. 2
figure 2

Pull-in voltage for static analysis of single-side actuated beam

Full size image

As can be seen in Fig. 3, the graph is plotted for the proposed model in Arrangement #2. In the ideal case (T-shape graph) the air gap between the electrodes and micro-beam is the same quietly. Accordingly, due to an equal upper and lower electrostatic field in both sides of the microbeam, a net resultant force will be zero and therefore the microstructure won’t deflect till the initiation of a pitch-fork type (Madinei et al. 2015) of the pull-in instability at around 14.83 V with two options for the microbeam to suddenly jump toward the upper or lower electrodes. However, due to the fabrication process, it might exist a little gap difference between the microbeam and electrodes or a small difference between voltage suppliers on both sides. In that case, with a lower distance to the microbeam or a higher amount of voltage applied, there is very little displacement toward the electrodes. Hence the dashed line and dash-dotted line in Fig. 3 are plotted for different gap values and its curvature becomes more visible as the micro-beam will jump toward the electrode with a less distance to the microbeam. Regarding the double-sided system, the force applied to both sides to bring the structure to the critical value requires a stronger electrical field, hence in the double-sided structure, the value of static pull-in voltage is more than the single-sided type, equals here \(14.45\, {\rm V}\).

Fig. 3
figure 3

Pull-in voltage for static analysis of double-side actuated beam in different gaps

Full size image

Whereas one pair of the electrodes [the electrodes (1–4) or electrodes (2–3)] are connected to a power supply (Arrangement #3), the clamp-clamp microbeam is excited in the second mode of frequency, as shown by solid lines in Fig. 4. Implementation of this case is possible by the value of \({a}_{1} , {a}_{2}=0.5\) in Heaviside function. Concerning the highest amount of displacement that occurred in the neighborhood of 0.29 and 0.71 of the micro-beam lengths, Fig. 4 shows the displacement of the beam in these points with increasing the voltage value. Calculation shows that the voltage of static instability which is occurred in the second mode of frequency is\(30.77\, {\rm V}\). In the case of the proposed actuation system in Arrangement #4, displacement dependency of the electrostatic force is eliminated which results in an increment in the pull-in voltage up to \(39.85\, {\rm V}\), as shown with a dash-dotted line in Fig. 4. The COMSOL finite element analysis results of the displacement magnitude across the clamped–clamped microbeam resonator under four different electrostatic actuation types are presented in Fig. 5.

Fig. 4
figure 4

Static analysis of two type double-side actuated beam structures in the second mode

Full size image
Fig. 5
figure 5

Deflection of the microbeam simulated by COMSOL

Full size image

Micro-structures, being small in size and rigid in mechanical properties, they commonly possess high natural frequencies and this particularity maybe unpractical for several applications such as seismographs, where it is required to operate the sensor in low frequency regime. Lowering their natural frequencies could be possible by increasing the effective mass or reducing the structural stiffness.

As discussed earlier, this work suggests the use of double-sided structure to possibly decrease the natural frequency of the micro-resonator via altering the bias DC voltage assuming four different arrangements without the need of changing the dimensions neither material properties of the structure. As a result, it’s possible to design MEMS resonators with a very wide frequency tuning range. Therefore, to investigate the performance of the micro-resonator, natural frequencies to DC voltage dependency is to be examined. Thus, the linearized eigenvalue problem of the microbeam based micro-resonator is computed through perturbing its vibrational response around the above obtained static positions and while considering only the linear part of the ROM (Azimloo et al. (2020). This process is mainly linearizing the nonlinear beam equations around the static equilibrium position at a given exciting DC load. Then, through evaluating the eigenvalue problem of the linearized system by substituting the stable equilibrium solution, result into pairs of pure imaginary eigenvalues. Taking the real value of each imaginary pair yields the natural frequencies of each mode of the investigated configuration of the micro-resonator.

Firstly, the efficacy of the double-sided structure in frequency tunability compared to the single-sided structures is investigated for the first mode of frequency. As can be seen in Fig. 6 the natural frequency of the first mode for both cases is \(146 \, \mathrm{kHz}\). The graph shown with a dashed line is the indicator expressing changes of the resonant frequency by increasing the bias voltage in a single-sided structure. The graph has two regions with a low slope and sudden changes. In the low slop region by changing the bias voltage up to 70% of the pull-in value, 9.8% of frequency tunability would be possible, but in sudden changes region due to the sudden changes of frequency around the pull-in voltage and reducing the amount of structure controllability, the possibility of frequency tuning around the pull-in voltage will be very difficult. The diagram shown with the solid line represents frequency changes in the double-sided structure which has a milder slope in comparison to the classical structure. So, by enhancing the bias voltage up to 70% of the pull-in voltage, 26.8% of resonant frequency tunability will be obtained in the double-side actuated system. For the case of double-sided one, and due to the elimination of the displacement dependency with the electrostatic force, the variation of the system fundamental frequency versus the applied DC voltage shows a reasonable trend, making it possible to further increase the applied actuating load continuously up to approximately 95% of the pull-in voltage, and with an increase to about 61.8% tunability range of the first natural frequency.

Fig. 6
figure 6

Frequency versus voltage in the first natural frequency mode

Full size image

Figure 7 shows resonant frequency variation of the proposed structure versus bias voltage changes when the structure is excited in the second mode of vibration. Since the excitation in the second mode is done by double-sided structure, the comparison between two different methods of voltage distribution among the electrodes is investigated. According to work done by Madinei et al. (2015), while the bias voltage (V) is applied to the electrodes 1 and 4 (Arrangement #3), as shown with the dashed line, the system has similar behavior with the single-sided structure that excited in the first mode of frequency. In this case, the range of tunability is limited by 70% of the pull-in voltage in the second natural frequency and a 9.7% tuning ratio is achieved. According to arrangement #4, the electrodes (1–4) and electrodes (2–3) are connected to the supply voltages V1 and V2 respectively. If both of the supply voltages V1 and V2 have the same amounts equal to V, assuming very small differences between them in view of non-ideal supply voltage conditions, distribution of the electrical force on both sides of the structure occurred or applied in a way that the excitation of the structure happens in the second mode of natural frequency. Regarding Fig. 7, the natural frequency in the second mode of vibration for both cases is \(401.3 \, \mathrm{kHz}\). By considering the 70% of pull-in voltage, 26.7% of frequency tuning ratio will be achievable in the Type #4 double-side actuated system. On the other hand, as mentioned before in the double-side actuated system the effect of non-linearity is decreased. Therefore, it becomes possible to access 61.8% of resonant frequency tuning by applying high bias voltage close to 95% of the pull-in voltage of the second mode.

Fig. 7
figure 7

Frequency versus voltage in the second mode of natural frequency

Full size image

Utilizing selective mode excitation in the proposed structure provides the possibility of increasing the frequency bandwidth and tunability. According to Fig. 8, it can be seen while the structure is actuated in the second mode of vibration and the bias voltage is increased according to arrangement #4, the rate of frequency variation proportional to the voltage changes has a mild slope. This process continues until the natural frequency of the structure is closed to the first mode of frequency. Then, by changing the voltage distribution according to arrangement #2, by increasing the bias voltage from zero to 95% of pull-in voltage of the first mode, a wide frequency range can be covered thoroughly. Accordingly, the resonant frequency will be tuned from + 174.8% to – 61.8% of the first mode of vibration. This procedure allows tuning resonators with a higher degree of controllability than previous cases. Table 4 indicates a comparison of the current state of the art MEMS tunable resonator with the micro-resonator found in the literature. This comparison presents the high tuning range, low power consumption and easier design process that can be achieved with the proposed tuning method.

Fig. 8
figure 8

Frequency tuning by selective mode excitation

Full size image
Table 4 Comparison of the current state of the art MEMS tunable resonator
Full size table

6 Conclusion

In this study, the proposed model consists of a clamp-clamp micro-beam that is placed between two electrodes and each electrode is equally divided into two sections. Electrode’s arrangement presented in this study provides the possibility of a different form of voltage application between the electrodes. Consequently, this enables the structure to have selectively different modes of excitation. To solve governing differential equation and investigate the mechanical behavior of the micro-structure assuming the different forms of the actuation, a Galerkin modal expansion-based method was applied to discretize the equation into reduced-order model equations that can then be numerically integrated using Newton–Raphson method.

It was shown that with the uniform voltage distribution between the electrodes on both sides of the beam, structure excitation occurred in the first mode of frequency. Also in the case of connecting the electrodes as a cross shape into the power supplies with the same voltage distribution, the resonator was excited in the second mode of frequency. By solving the static bending equations, stable areas of the micro-beam in single-sided and double-sided structures were calculated. It was shown that in the double-sided structure due to equal electric field in both sides of the micro-beam, the occurred displacement in the ideal case (same gap value and same applied voltage) is close to zero. So, in the double-sided structure, applying a high bias DC voltage leading system to have a very low natural frequency is capable. Therefore, the double-sided structure in comparison to the single-sided structure is very sensitive to low-frequency excitations.

The paper showed that by using the design of double-sided structures in MEMS resonators and increasing the bias voltage to approximately 95% of the pull-in value, the tunable frequency range could be increased up to about 62% of the first natural frequency, while for the classical model (single-sided) it equals to 9.8%. Also, by using a combination of double-sided structure and selective mode excitation, the expansion of tuning ratio from + 174.8% to – 61.8% of the first mode of vibration, without changing the dimensions of the structure, is feasible.