1 Introduction

Nonlinear mathematical physics equations play a significant role in real-life applications. The nonlinear Schrödinger equations, in particular, are widely applied across various fields, including nonlinear optics, quantum mechanics, fluid mechanics, and other areas of nonlinear dynamics [1,2,3,4]. Algorithms based on solitons offer a promising avenue for exploring solutions to nonlinear practical problems [1, 5,6,7,8,9]. In the past decades, the studies of nonlocal integrable equations in nonlinear mathematical physics have attracted a lot of attention. Certain soliton equations demonstrate a fascinating characteristic whereby the evolution of their solutions is not simply affected by time and spatial coordinates, but is also influenced by nonlocal interactions. This important concept derives from the parity-time symmetry in quantum mechanics, which was first proposed by Bender and Boettcher [10]. As a result of the broad utilization of parity-time symmetry in multiple domains, it is naturally combined with the integrable system. Since then, many types of nonlocal integrable equations have also been derived [11,12,13,14,15]. One of the most typical examples is the nonlocal nonlinear Schrödinger equation [16]

$$\begin{aligned} iq_t(x,t)-q_{xx}(x,t)-2\mu q(x,t)q^{*}(-x,t)q(x,t)=0, \qquad \mu =\pm 1. \end{aligned}$$
(1)

Fokas developed high-dimensional variants of the equation above and suggested the nonlocal DS equation [17,18,19]. Subsequently, some new nonlocal multidimensional equations were investigated [20, 21].

Research on nonlocal integrable equations is meaningful because their solutions possess intriguing characteristics, such as the phenomenon where solutions blow up at a finite time and the coexistence of kink and soliton solutions [22, 23]. These features enrich the solutions of nonlinear evolution equations. Various established methods exist for solving integrable equations, including the Darboux transformation approach [24], the inverse scattering transform method [25], and the KP reduction method [26,27,28]. Among these techniques, the KP reduction method is particularly advantageous, as it can produce straightforward exact solutions.

The main idea of the KP reduction method is to first obtain the bilinear forms of the nonlinear evolution system. Then, it involves finding similar bilinear equations within the KP hierarchy and connecting these two sets of equations through appropriate variable transformations. Finally, the exact solutions of the Gram determinant are derived. Compared with other methods, the KP reduction method can directly bypass the spectral problem of nonlinear evolution equations, which is more concise and effective for gaining higher-order (semi-)rational solutions [29]. However, the finiteness of the bilinear equations within the KP hierarchy means that not all variable substitutions are successful in reducing the original bilinear equations.

As an integrable extension of the KP equation, the Mel’nikov equation introduces an addition of the complex field [30,31,32,33]:

$$\begin{aligned} \begin{aligned}&u_{xxxx}+u_{xt}+3(u^2)_{xx}-3u_{yy}+\lambda (\varphi \varphi ^*(x,y,t))_{xx}=0,\\&i\varphi _y=u\varphi +\varphi _{xx}, \end{aligned} \end{aligned}$$
(2)

in which \(\varphi \) indicates the complex short wave, u represents a real long wave, and \(\lambda \) is a real parameter. In many physical domains, soliton equations with self-consistent sources represent a crucial class of models. Wave interactions on the x, y plane were initially investigated by Mel’nikov. His groundbreaking research revealed the emergence of the KP equation with self-consistent sources as an integrable extension of soliton equations [34,35,36]. Inspired by this, Ma et al. considered a \((3+1)\)-dimensional Mel’nikov equation [37]

$$\begin{aligned} \begin{aligned}&u_{yy}-u_{zz}-u_{xt}-[3u^2+u_{xx}+2\lambda \varphi \varphi ^*]_{xx}=0,\\&i\varphi _y=2u\varphi +2\varphi _{xx},\\&i\varphi _z=u\varphi +\varphi _{xx}.\\ \end{aligned} \end{aligned}$$
(3)

In fact, the Eq. (3) is a high-dimensional generalization of the KP equation with self-consistent sources.

In this present work, we propose the \((3+1)\)-dimensional nonlocal Mel’nikov equation in the form

$$\begin{aligned} \begin{aligned}&u_{yy}-u_{zz}-u_{xt}-[3u^2+u_{xx}+2\lambda \varphi (x,y,z,t)\varphi (x,-y,-z,t)]_{xx}=0,\\&i\varphi _y=2u\varphi +2\varphi _{xx},\\&i\varphi _z=u\varphi +\varphi _{xx}. \end{aligned} \end{aligned}$$
(4)

The nonlocal Eq. (4) is derived by employing the reduction \(\varphi ^*(x,y,z,t)=\varphi (x,-y,-z,t)\) in the \((3+1)\)-dimensional local Eq. (3). In the case of conjugate reduction \(\varphi (x,y,z,t)=\varphi ^*(-x,y,z,-t),\) Cao and his group have studied the soliton and rational solutions against a constant background [38]. The key contributions of our work are as follows:

(i) Multi-soliton and rational solutions on a periodic wave and a constant background are constructed. This result is mainly achieved by imposing two parameter restrictions on the solution of the \(\tau \) function in the KP hierarchy.

(ii) The breather of the \((3+1)\)-dimensional nonlocal Mel’nikov equation is obtained for the first time. In contrast to Ref. [38], we add the case of degenerate antidark-soliton and degenerate dark-soliton.

(iii) Compared with previous work, when N is even, some results are similar to those in Refs. [39,40,41]. However, for odd values of N, both soliton and rational solutions coexist in two different backgrounds. In contrast to the findings in Refs. [39, 40], where lumps always appeared in pairs, this paper demonstrates that an odd or even number of lumps can emerge.

The following summarizes the general organization of this work. In Sect. 2, we establish the framework for constructing soliton solutions and provide the accompanying proofs. Sections 3 and 4 delve into the analysis of the dynamic behaviors exhibited by soliton solutions. In Sect. 5, the rational solutions within two kinds of backgrounds are generated. Finally, we conclude with a summary of our findings in Sect. 6.

2 Soliton Solutions in Two Different Backgrounds

For the purpose of constructing soliton solutions, through introducing bilinear transformation

$$\begin{aligned} \varphi =\frac{g}{f},\qquad u=2(\ln f)_{xx}, \end{aligned}$$
(5)

under the condition

$$\begin{aligned} f(x,y,z,t)=f(x,-y,-z,t), \end{aligned}$$
(6)

where g represents a complex-valued function and f is real, then Eq. (4) could be cast into the bilinear equations

$$\begin{aligned} \begin{aligned}&(2D_x^2-iD_y)g\cdot f=0,\\&(D_x^2-iD_z)g\cdot f=0,\\&(D_x^4+D_xD_t-D_y^2+D_z^2-2\lambda )f\cdot f=-4\lambda g(x,y,z,t)g(x,-y,-z,t), \end{aligned} \end{aligned}$$
(7)

in which D represents the Hirota operator [42].

Theorem 2.1

The nonlocal Eq. (4) admits soliton solutions

$$\begin{aligned} \varphi =\frac{g}{f},\qquad u=2(\ln f)_{xx}, \end{aligned}$$
(8)

where

$$\begin{aligned} f=\mathop {det}\limits _{1\le i,j\le N}(M_{i,k}^{(0)}),\qquad g=\mathop {det}\limits _{1\le i,j\le N}(M_{i,k}^{(1)}), \end{aligned}$$

and the components of the matrix include

$$\begin{aligned} M_{i,k}^{(n)}=\mu _{ik}e^{-\xi _i-\psi _k}+\frac{1}{p_i+q_k}\left( -\frac{p_i}{q_k}\right) ^n \end{aligned}$$
(9)

with

$$\begin{aligned} \begin{aligned} \xi _i=p_ix-(iz+2iy)p_i^2+\left( \frac{\lambda }{p_i}-4p_i^3\right) t+\xi _{i0},\\ \psi _k=q_kx+(iz+2iy)q_k^2+\left( \frac{\lambda }{q_k}-4q_k^3\right) t+\psi _{k0}.\\ \end{aligned} \end{aligned}$$

Here N defines an integer, and \(p_i\), \(q_k\) represent random complex constants.

Further, there are two parameter conditions to consider:

(I) Assume N is even, i.e. \(N=2L\), by choosing

$$\begin{aligned} \begin{aligned}&\mu _{ik}=\mu _{L+i,L+k},\qquad \mu _{L+i,k}=\mu _{i,L+k},\qquad p_k=q_{L+k},\qquad q_i=p_{L+i},\\&\xi _{k0}=\psi _{L+k,0},\qquad \psi _{i0}=\xi _{L+i,0},\\ \end{aligned} \end{aligned}$$
(10)

in which \(i,k=1,2,...,L\).

(II) Assume N is odd, i.e. \(N=2L+1\), by considering

$$\begin{aligned} p_{2L+1}=q_{2L+1}, \qquad \mu _{2L+1,L+i}=\mu _{i,2L+1},\qquad \xi _{2L+1,0}=\psi _{2L+1,0}, \end{aligned}$$
(11)

where \(i=1,2,...,2L+1\).

Proposition 2.1

In Theorem (2.1), by taking \(\mu _{ik}=\sigma _{i,k}\mu _i\), we obtain the nonsingular solutions (8) under the condition

$$\begin{aligned} q_i=p_i^*, \end{aligned}$$
(12)

where \(\sigma _{i,k}\) is the Kronecker delta.

To get soliton solutions with a nonzero background, we take the parameter restriction that is distinct from the one given in Theorem (2.1).

Theorem 2.2

The nonlocal Eq. (4) admit soliton solutions

$$\begin{aligned} \varphi =\frac{g}{f},\qquad u=2(\ln f)_{xx}, \end{aligned}$$
(13)

where

$$\begin{aligned} f=\mathop {det}\limits _{1\le i,j\le N}(M_{i,k}^{(0)}),\qquad g=\mathop {det}\limits _{1\le i,j\le N}(M_{i,k}^{(1)}), \end{aligned}$$

with the components of the matrix have the following forms

$$\begin{aligned} M_{i,k}^{(n)}=\mu _{i}\sigma _{i,k}e^{-\xi _i-\psi _k}+\frac{1}{p_i+q_k}\left( -\frac{p_i}{q_k}\right) ^n, \end{aligned}$$
(14)

with

$$\begin{aligned} \begin{aligned} \xi _i=p_ix-(iz+2iy)p_i^2+\left( \frac{\lambda }{p_i}-4p_i^3\right) t+\xi _{i0},\\ \psi _k=q_kx+(iz+2iy)q_k^2+\left( \frac{\lambda }{q_k}-4q_k^3\right) t+\psi _{k0}.\\ \end{aligned} \end{aligned}$$

Here, \(\mu _{i}\), \(p_i\), \(q_k\) are arbitrary complex constants and require

$$\begin{aligned} p_i=q_i. \end{aligned}$$
(15)

2.1 Evidence Supporting Theorems (2.1) and (2.2)

Lemma 2.1

The bilinear Eq. (7) are transformed from the bilinear forms in KP hierarchy [43]

$$\begin{aligned} \begin{aligned}&(D_{x_1}^4-4D_{x_1}D_{x_3}+3D_{x_2}^2)\tau _n\cdot \tau _n=0,\\&(D_{x_1}D_{x_{-1}}-2)\tau _n\cdot \tau _n=-2\tau _{n+1}\cdot \tau _{n-1},\\&(D_{x_1}^2-D_{x_2})\tau _{n+1}\cdot \tau _n=0,\\ \end{aligned} \end{aligned}$$
(16)

which possess a Gram determinant solution

$$\begin{aligned} \tau _n=|M_{i,k}^{(n)}|_{1\le i,k\le N}. \end{aligned}$$
(17)

Here, \(M_{i,k}^{(n)}\) is defined as follows:

$$\begin{aligned} \begin{aligned}&M_{i,k}^{(n)}=\mu _{ik}+\frac{1}{p_i+q_k}\phi _i^{(n)}\chi _k^{(n)},\\&\phi _i^{(n)}=p_i^ne^{\xi _i},\\&\chi _k^{(n)}=(-q_k)^{-n}e^{\psi _k},\\ \end{aligned} \end{aligned}$$
(18)

with

$$\begin{aligned} \xi _i=\frac{1}{p_i}x_{-1}+p_ix_1+p_i^2x_2+p_i^3x_3+\xi _{i0},\\ \psi _k=\frac{1}{q_k}x_{-1}+q_k x_1-q_k^2x_2+q_k^3x_3+\psi _{k0}. \end{aligned}$$

Notably, set \(x_{-1}=\lambda t\), \(x_1=x\), \(x_2=-iz-2iy\), \(x_3=-4t\), then Eq. (16) can be cast into Eq. (7).

Proof of Theorem (2.1). We rewrite \(\tau ^{(n)}\) as \(e^{\xi _i+\psi _k}\widetilde{M_{i,k}^{(n)}}\) and impose restrictions on the parameters. Based on (10) and (11), it is possible to derive

$$\begin{aligned} \begin{aligned}&(\xi _{L+i}+\psi _{L+k})(x,-y,-z,t)=(\psi _i+\xi _k)(x,y,z,t),\\&(\xi _{2L+1}+\psi _{2L+1})(x,-y,-z,t)=(\xi _{2L+1}+\psi _{2L+1})(x,y,z,t).\\ \end{aligned} \end{aligned}$$
(19)

According to the above results, we can obtain the following relations:

$$\begin{aligned} \begin{aligned}&\widetilde{M_{i,k}^{(n)}(x,y,z,t)}=\widetilde{M_{L+k,L+i}^{-(n)}(x,-y,-z,t)},\\&\widetilde{M_{L+i,k}^{(n)}(x,y,z,t)}=\widetilde{M_{L+k,i}^{-(n)}(x,-y,-z,t)},\\&\widetilde{M_{i,L+k}^{(j,l)}(x,y,z,t)}=\widetilde{M_{k,L+i}^{-(n)}(x,-y,-z,t)},\\&\widetilde{M_{i,2L+1}^{(j,l)}(x,y,z,t)}=\widetilde{M_{2L+1,L+i}^{-(n)}(x,-y,-z,t)},\\&\widetilde{M_{2L+1,k}^{(j,l)}(x,y,z,t)}=\widetilde{M_{L+k,2L+1}^{-(n)}(x,-y,-z,t)},\\&\widetilde{M_{L+i,2L+1}^{(j,l)}(x,y,z,t)}=\widetilde{M_{2L+1,i}^{-(n)}(x,-y,-z,t)},\\&\widetilde{M_{2L+1,L+k}^{(j,l)}(x,y,z,t)}=\widetilde{M_{k,2L+1}^{-(n)}(x,-y,-z,t)},\\&\widetilde{M_{2L+1,2L+1}^{(j,l)}(x,y,z,t)}=\widetilde{M_{2L+1,2L+1}^{-(n)}(x,-y,-z,t)}.\\ \end{aligned} \end{aligned}$$
(20)

In summary, we yield \(\tau ^{(n)}(x,y,z,t)=\tau ^{-(n)}(x,-y,-z,t)\) whether N is odd or even, and when \(n=0\), the condition (6) holds. Regarding the proof of Proposition (2.1), we omit it here as it is similar to that in Ref. [44].

Proof of Theorem (2.2). Based on the condition (15), when \(i=k\), then we know

$$\begin{aligned} (\xi _i+\psi _i)(x,y,z,t)= & {} 2p_ix+2 \left( \frac{\lambda }{p_i}-4p_i^3\right) t +\xi _{i0}+\psi _{i0}\nonumber \\= & {} (\xi _i+\psi _i)(x,-y,-z,t), \end{aligned}$$
(21)

furthermore, the following result could be deduced

$$\begin{aligned} \begin{aligned} M_{i,i}^{(n)}(x,y,z,t)&=\mu _ie^{(-\xi _i-\psi _i)(x,y,z,t)}+\frac{1}{2p_i}(-1)^{(n)} \\&=\mu _ie^{(-\xi _i-\psi _i)(x,-y,-z,t)}+\frac{1}{2p_i}(-1)^{-(n)} \\&=M_{i,i}^{-(n)}(x,-y,-z,t). \end{aligned} \end{aligned}$$
(22)

For another case, where \(i\ne k\), we get

$$\begin{aligned} M_{i,k}^{(n)}(x,y,z,t)= & {} \frac{1}{p_i+q_k} \left( -\frac{p_i}{q_k}\right) ^{(n)}\nonumber \\= & {} \frac{1}{q_i+p_k}\left( -\frac{p_k}{q_i}\right) ^{-(n)}\nonumber \\= & {} M_{k,i}^{-(n)}(x,-y,-z,t). \end{aligned}$$
(23)

In conclusion, the following condition holds for any integer N

$$\begin{aligned} \tau ^{(n)}(x,y,z,t)=\tau ^{-(n)}(x,-y,-z,t), \end{aligned}$$
(24)

this completes the proof.

3 Dynamical Behavior of Multi-solitons on a Constant Background

By setting \(N=1\), one-soliton solution is obtained

$$\begin{aligned} M_{1,1}^{(n)}=\mu _{11}e^{-\xi _1-\psi _1}+\left( -\frac{p_1}{q_1}\right) ^{(n)}\frac{1}{p_1+q_1}, \end{aligned}$$
(25)

with

$$\begin{aligned} -\xi _1-\psi _1=-((p_1+q_1)x+(iz+2iy)(q_1^2-p_1^2)+ \left( \frac{\lambda }{p_1}-4p_1^3 +\frac{\lambda }{q_1}-4q_1^3\right) t+\xi _{10}+\psi _{10}). \end{aligned}$$

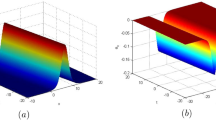
Since \(p_1=q_1\), the solution is independent of y, z. We construct two types of behaviors based on the situations in which \(p_1\) is a real number and a pure imaginary number (see Fig. 1):

When \(p_1\) assumes a real value, the solutions for the \(|\varphi |\) component include both dark solitons, characterized by a real \(\mu _{11}\), and antidark solitons, characterized by a complex \(\mu _{11}\). Conversely, when \(p_1\) is an pure imaginary number, the \(|\varphi |\) and |u| components display periodic wave solutions.

Fig. 1
figure 1

Three types of one-soliton solutions when \(\lambda =1\): a Antidark soliton for \(\varphi \) with \(p_1=1, \mu _{11}=-1+i\). b Dark soliton for \(\varphi \) with \(p_1=1, \mu _{11}=10\). c Periodic wave solution for \(\varphi \) with \(p_1=i, \mu _{11}=10\)

Full size image

The exact solution (8) for the two solitons can be obtained by taking the form

$$\begin{aligned} \varphi =\frac{g}{f},\qquad u=2(\ln f)_{xx} \end{aligned}$$

with

$$\begin{aligned} f&=\left| \begin{matrix} \mu _{11}e^{-\xi _1-\psi _1}+\frac{1}{p_1+q_1}&{}\qquad \frac{1}{p_1+q_2} \\ \frac{1}{p_2+q_1}&{}\qquad \mu _{22}e^{-\xi _2-\psi _2}+\frac{1}{p_2+q_2} \end{matrix}\right| ,\\ g&=\left| \begin{matrix} \mu _{11}e^{-\xi _1-\psi _1}-\frac{p_1}{q_1(p_1+q_1)} &{}\qquad -\frac{p_1}{q_2(p_1+q_1)} \\ -\frac{p_2}{q_1(p_2+q_1)}&{}\qquad \mu _{22}e^{-\xi _2-\psi _2}-\frac{p_2}{q_2(p_2+q_2)} \end{matrix}\right| . \end{aligned}$$

Here, we mainly consider the asymptotic properties of \(\varphi \). Within the constraints of Proposition (2.1), we take \(p_1=q_1^{*}=e^{i\theta }\) to prevent singularities. Consequently, f and g are represented as

$$\begin{aligned} f= & {} (\mu _{11}^2-\mu _{12}^2)e^{-\xi _1-\psi _1-\xi _2-\psi _2}+\frac{\mu _{11}}{2\cos \theta }(e^{-\xi _1-\psi _1}+e^{-\xi _2-\psi _2})\nonumber \\{} & {} -\frac{\mu _{12}}{2}(e^{-\xi _1-\psi _2+i\theta }+e^{-\xi _2-\psi _1-i\theta })+\frac{\sin ^2\theta }{4\cos \theta ^2},\nonumber \\ g= & {} (\mu _{11}^2-\mu _{12}^2)e^{-\xi _1-\psi _1-\xi _2-\psi _2}-\frac{\mu _{11}}{2\cos \theta }(e^{-\xi _1-\psi _1-2i\theta }+e^{-\xi _2-\psi _2+2i\theta })\nonumber \\{} & {} +\frac{\mu _{12}}{2}(e^{-\xi _1-\psi _2+i\theta }+e^{-\xi _2-\psi _1-i\theta })+\frac{\sin ^2\theta }{4\cos \theta ^2}. \end{aligned}$$
(26)

Next, to delve deeper into the collision characteristics exhibited by the two solitons, we make asymptotic analysis [45,46,47,48] of the above solution:

(I) Before collision (\(t\rightarrow -\infty \))

Soliton 1 (\(-\xi _2-\psi _2\rightarrow -\infty , -\xi _1-\psi _1\approx 0\)):

$$\begin{aligned} \varphi _1^{-}\simeq e^{-2i\theta }\frac{-\mu _{11}+\frac{\sin ^2\theta e^{\xi _1+\psi _1+2i\theta }}{2\cos \theta }}{\mu _{11}+\frac{\sin ^2\theta e^{\xi _1+\psi _1}}{2\cos \theta }}, \end{aligned}$$

Soliton 2 (\(-\xi _2-\psi _2\rightarrow 0, -\xi _1-\psi _1\approx +\infty \)):

$$\begin{aligned} \varphi _2^{-}\simeq \frac{\frac{\mu _{11}^2-\mu _{12}^2}{\mu _{11}}-\frac{e^{\xi _2+\psi _2-2i\theta }}{2\cos \theta }}{\frac{\mu _{11}^2-\mu _{12}^2}{\mu _{11}}+\frac{e^{\xi _2+\psi _2}}{2\cos \theta }}, \end{aligned}$$

(I) After collision (\(t\rightarrow +\infty \))

Soliton 1 (\(-\xi _2-\psi _2\rightarrow +\infty , -\xi _1-\psi _1\approx 0\)):

$$\begin{aligned} \varphi _1^{+}\simeq \frac{\frac{\mu _{11}^2-\mu _{12}^2}{\mu _{11}}-\frac{e^{\xi _1+\psi _1+2i\theta }}{2\cos \theta }}{\frac{\mu _{11}^2-\mu _{12}^2}{\mu _{11}}+\frac{e^{\xi _1+\psi _1}}{2\cos \theta }}, \end{aligned}$$

Soliton 2 (\(-\xi _2-\psi _2\rightarrow 0, -\xi _1-\psi _1\approx -\infty \)):

$$\begin{aligned} \varphi _2^{+}\simeq e^{2i\theta }\frac{-\mu _{11}+\frac{\sin ^2\theta e^{\xi _2+\psi _2-2i\theta }}{2\cos \theta }}{\mu _{11}+\frac{\sin ^2\theta e^{\xi _2+\psi _2}}{2\cos \theta }}. \end{aligned}$$

When \(\mu _{12}=0\), an elastic collision will occur between the two solitons. At this point, their amplitudes satisfy \(|\varphi _i^{+}(-\xi _i-\psi _i)|=\sin ^2\theta |\varphi _i^{-}(-\xi _i-\psi _i)|, i=1,2\). By taking different parameters, several types of two-soliton solutions are derived. The images of these specific exact solutions are depicted in the (x, z) plane in Fig. 2 and in the (x, t) plane in Fig. 3, respectively. It is interesting to note that the two solitons interact with each other within the (x, z) plane, yet they remain parallel to one another within the (x, t) plane.

Fig. 2
figure 2

Five different types of two-soliton solutions in the (x, z) plane with \(\lambda =1, t=0, p_1=1+i\): a \(\mu _{11}=i\). b \(\mu _{11}=-\frac{1}{2}+\frac{i}{3}\). c \(\mu _{11}=2\). d \(\mu _{11}=1+i\). e \(\mu _{11}=-1+i\)

Full size image
Fig. 3
figure 3

Five different types of two-soliton in the (x, t) plane with \(\lambda =1, t=1, p_1=1+i\): a \(\mu _{11}=i\). b \(\mu _{11}=-\frac{1}{2}+\frac{i}{3}\). c \(\mu _{11}=2\). d \(\mu _{11}=1+i\). e \(\mu _{11}=-1+i\)

Full size image

In addition, to obtain the two-soliton solutions on the periodic background, one can consider taking \(N=3\) and letting \(p_3\) be a pure imaginary number (see Fig. 4).

Fig. 4
figure 4

Two-soliton solutions on a periodic wave background with \(\lambda =1, t=0, p_1=1+i, p_3=2i\): a \(\mu _{11}=i, \mu _{33}=2i\). b \(\mu _{11}=2, \mu _{33}=2\). c \(\mu _{11}=-\frac{1}{2}+\frac{i}{3}, \mu _{33}=2i\). d \(\mu _{11}=1+i, \mu _{33}=2i\). e \(\mu _{11}=-1+i, \mu _{33}=2i\)

Full size image

For getting three-soliton solutions, we choose \(N=3\) and rewrite \(\mu _{ij}=\sigma _{ij}\mu _i\). Figure 5 shows four different kinds of three-soliton solutions.

Fig. 5
figure 5

Four kinds of three-soliton in the (x, z) plane with \(\lambda =1, t=0, p_1=1+i, p_3=2\): a \(\mu _{1}=2, \lambda _{3}=2\). b \(\mu _{1}=2i, \mu _{3}=2\). c \(\mu _{1}=-\frac{1}{2}+\frac{i}{3}, \mu _{3}=2\). d \(\mu _{1}=-\frac{1}{2}+\frac{i}{4}, \mu _{3}=-\frac{1}{2}+i\)

Full size image

4 Dynamical Behavior of Multi-solitons and Breather on a Periodic Background

Different from Theorem (2.1), the dynamic behaviors of soliton solutions in Theorem (2.2) will be analyzed here. According to the parameter selection in (15), we know

$$\begin{aligned} -\xi _i-\psi _i=-\left( 2p_ix+2\left( \frac{\lambda }{p_i}-4p_i^3\right) t+\xi _{i0}+\psi _{i0}\right) , \end{aligned}$$
(27)

the above condition shows that the solutions are independent of y, z. By dividing the real and imaginary parts of p, various soliton solutions can be obtained.

For the one-soliton solutions, we get the same figure as shown in Fig. 1. When \(N=2\), the solutions of Eq. (4) are

$$\begin{aligned} \varphi =\frac{g}{f},\qquad u=2(\ln f)_{xx}, \end{aligned}$$
(28)

where

$$\begin{aligned} f= & {} \mu _1\mu _2e^{-\xi _1-\psi _1-\xi _2-\psi _2}+\frac{\mu _1e^{-\xi _1-\psi _1}}{2p_2}+\frac{\mu _2e^{-\xi _2-\psi _2}}{2p_1}+\frac{1}{4p_1p_2}-\frac{1}{(p_1+p_2)^2},\nonumber \\ g= & {} \mu _1\mu _2e^{-\xi _1-\psi _1-\xi _2-\psi _2}-\frac{\mu _1e^{-\xi _1-\psi _1}}{2p_2}-\frac{\mu _2e^{-\xi _2-\psi _2}}{2p_1}+\frac{1}{4p_1p_2}-\frac{1}{(p_1+p_2)^2}.\nonumber \\ \end{aligned}$$
(29)

When \(p_1\), \(p_2\) are real numbers, the constant background yields the two-soliton solutions. Next, if we take \(p_1\) to be a real number and let \(p_2\) be purely imaginary, we derive one-soliton solutions on a periodic wave background. By comparing these two-soliton solutions with those obtained in Theorem (2.1), the solutions presented here are depicted on the (x, t) plane. Figure 6 displays three kinds of two-soliton and two kinds of one-soliton.

Fig. 6
figure 6

Two-soliton within the constant background with \(\lambda =1, t=1, p_1=1, p_2=2\): a \(\mu _{1}=1, \mu _{2}=1\). b \(\mu _{1}=-1+i, \mu _{2}=1\). c \(\mu _{1}=-1+i, \mu _{2}=-1+i\). One soliton within the periodic wave background with \(\lambda =1, p_1=1, p_2=3i\): d \(\mu _{1}=-1+i, \mu _{2}=10\). e \(\mu _{1}=2, \mu _{2}=10\)

Full size image

For \(N\ge 3\), the corresponding multi-soliton solutions on both constant and periodic backgrounds can be obtained. As shown in Fig. 7, there are three different types of two-soliton on the periodic wave background and three different forms of three-soliton on the constant background.

Fig. 7
figure 7

Three-soliton solutions on the constant background with \(\lambda =1, t=1, p_1=1, p_2=\frac{1}{2}, p_3=3\): a \(\mu _{1}=-1+i, \mu _{2}=-1+i, \mu _3=1\). b \(\mu _{1}=1, \mu _{2}=1, \mu _3=1\). c \(\mu _{1}=-1+i, \mu _{2}=-1+i, \mu _3=-1+i\). Two-soliton solutions on the periodic wave background with \(\lambda =1, p_1=1, p_2=3, p_3=2i\): d \(\mu _{1}=1, \mu _{2}=1, \mu _3=6\). e \(\mu _{1}=-1+i, \mu _{2}=1, \mu _3=6\). (f)\(\mu _{1}=-1+i, \mu _{2}=-1+i, \mu _3=6\)

Full size image

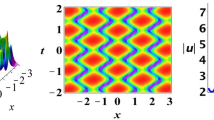
In what follows, when \(p_1\), \(p_2\) are imaginary numbers at the same time, the line breather solutions would be yielded. Figure 8 illustrates breather solutions on two backgrounds, respectively.

Fig. 8
figure 8

Breather in the constant background with \(\lambda =1, p_1=\frac{i}{10}, p_2=\frac{2i}{5}\): a \(\mu _{1}=1, \mu _{2}=2\). Breather within the periodic wave background with \(\lambda =1, p_1=\frac{i}{10}, p_2=\frac{3i}{5}, p_3=\frac{3i}{2}\): b \(\mu _{1}=1, \mu _{2}=2, \mu _3=1\)

Full size image

5 Rational Solutions of the \((3+1)\)-dimensional Nonlocal Mel’nikov Equation

This part will finish discussing the evidence and create rational solutions for Eq. (4). First, we select the matrix elements in the \(\tau \) function as

$$\begin{aligned} \begin{aligned}&m_{sj}^{(n)}=\mu _s\sigma (s,j)+A_sB_j\left( \frac{1}{p_s+q_j} \left( -\frac{p_s}{q_j}\right) ^{n} e^{\xi _s+\psi _j}\right) ,\\&\xi _s=\frac{1}{p_s}x_{-1}+p_sx_1+p_s^2x_2+p_s^3x_3,\\&\psi _j=\frac{1}{q_j}x_{-1}+q_jx_1-q_j^2x_2+q_j^3x_3, \end{aligned} \end{aligned}$$
(30)

with differential operators \(A_s\) and \(B_j\) denote

$$\begin{aligned} A_s=\sum _{k=0}^{n_s}c_{sk}(p_s\partial _{p_s})^{n_s-k},\qquad B_j=\sum _{l=0}^{n_j}d_{jl}(q_j\partial _{q_j})^{n_j-l}. \end{aligned}$$
(31)

Then, after substitution calculation, \(m_{sj}^{(n)}\) can be rewritten as

$$\begin{aligned} m_{sj}^{(n)}= & {} \left( -\frac{p_s}{q_j}\right) ^ne^{\xi _s+\psi _j}\left[ \sum _{k=0}^{n_0}c_{sk}(p_s\partial p_s+\xi _i'+n)^{n_0-k}\right. \nonumber \\{} & {} \quad \left. \times \sum _{l=0}^{n_0}d_{jl}(q_j\partial q_j+\psi _j'-n)^{n_0-l}\right] \frac{1}{p_i+q_j}+\mu _s\sigma (s,j). \end{aligned}$$
(32)

where

$$\begin{aligned} \begin{aligned}&\xi _s=p_sx-(iz+2iy)p_s^2+\left( \frac{\lambda }{p_s}-4p_s^3\right) t,\\&\psi _j=q_jx+(iz+2iy)q_j^2+\left( \frac{\lambda }{q_j}-4q_j^3\right) t,\\&\xi _s'=p_sx-2(iz+2iy)p_s^2-\left( \frac{\lambda }{p_s}+12p_s^3\right) t,\\&\psi _j'=q_jx+2(iz+2iy)q_j^2-\left( \frac{\lambda }{q_j}+12q_j^3\right) t,\\ \end{aligned} \end{aligned}$$

and \(\sigma (s,j)\) is the Kronecker delta, \(c_{sk}\), \(d_{jl}\), \(\mu \), \(p_i\), \(q_k\) are arbitrary complex constants.

Lemma 5.1

On the basis of Theorem (2.1), when N is even, take

$$\begin{aligned} n_{L+s}=n_s, \qquad c_{L+s,k}=d_{sk}, \qquad d_{L+j,l}=c_{jl}, \end{aligned}$$
(33)

and when N is odd, take

$$\begin{aligned} c_{2L+1,k}=d_{2L+1,k}, \end{aligned}$$
(34)

at this time, \(\tau \) function satisfies \(\tau _n(x,-y,-z,t)=\tau _{-n}(x,y,z,t).\)

Lemma 5.2

Whether N is odd or even, based on Theorem (2.2), add the condition

$$\begin{aligned} c_{sk}=d_{sk}, \end{aligned}$$
(35)

still leads to the establishment of \(\tau _n(x,-y,-z,t)=\tau _{-n}(x,y,z,t)\).

Proof

Rewrite \(m_{sj}^{(n)}\) as \(e^{\xi _s+\psi _j}\widetilde{M_{sj}^{(n)}}\), where \(\widetilde{M_{sj}^{(n)}}\) stands for

$$\begin{aligned} \widetilde{M_{sj}^{(n)}}=\mu _s\sigma (s,j)e^{-\xi _s-\psi _j}+ \left( -\frac{p_s}{q_j}\right) ^nA_s'B_j'\frac{1}{p_s+q_j}, \end{aligned}$$
(36)

with

$$\begin{aligned} \begin{aligned} A_s'=\sum _{k=0}^{n_i}c_{sk}(p_s\partial _{p_s}+\xi _s'+n)^{n_i-k},\\ B_j'=\sum _{l=0}^{n_j}d_{jl}(q_j\partial _{q_j}+\psi _j'-n)^{n_j-l}. \end{aligned} \end{aligned}$$
(37)

According to the Eqs. (10), (32)–(33), it is easy to find

$$\begin{aligned} \xi _{L+s}'(x,-y,-z,t)=\psi _s'(x,y,z,t),\qquad \psi _{L+j}'(x,-y,-z,t)=\xi _j'(x,y,z,t), \end{aligned}$$
(38)

then we have

$$\begin{aligned} \widetilde{M_{L+s,L+j}^{(n)}}(x,-y,-z,t)=\widetilde{M_{js}^{(-n)}}(x,y,z,t). \end{aligned}$$

Furthermore, based on the previous proof process for (19), one can deduce that \(\tau _n(x,-y,-z,t)=\tau _{-n}(x,y,z,t).\)

When \(N=2L+1\), based on the above conditions (11), (34), we know that \(\xi _{2L+1}'(x,-y,-z,t)=\psi _{2L+1}'(x,y,z,t).\) Then, the conclusion of \(\tau _n(x,-y,-z,t)=\tau _{-n}(x,y,z,t)\) is completed. We disregard Lemma (5.2)’s evidence because it is identical to Lemma (5.1). \(\square \)

5.1 Two Backgrounds with Rational Solutions

In the case of \(N=1\) and \(p_1=q_1\), we have

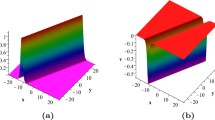
$$\begin{aligned}{} & {} \widetilde{M_{11}^{(n)}}=\left( -\frac{p_1}{q_1}\right) ^{(n)}\nonumber \\{} & {} \quad \left[ \frac{p_1q_1}{(p_1+q_1)^2}+\left( \frac{-p_1}{p_1+q_1}+\xi _1'+n+a_{11}\right) \left( \frac{-q_1}{p_1+q_1}+\psi _1'-n+b_{11}\right) \right] \frac{1}{p_1+q_1},\nonumber \\ \end{aligned}$$
(39)

then \((3+1)\)-dimensional nonlocal Mel’nikov equation has one-lump solution \(\varphi =\frac{g}{f}\), as shown in Fig. 9. The bright lump is located in the (x, z) plane and also present in the (x, y) plane.

Fig. 9
figure 9

One-lump on the constant background with \(\lambda =1, t=0, p_1=1, a_{11}=0, n_0=1\)

Full size image

When \(N=2\), under \(p_2=q_1, q_2=p_1,q_1=p_1^*\), we can conclude three different kinds of lump solutions including bright lump (\(p_{1R}^2>3p_{1I}^2\)), bi-peak lump (\(\frac{1}{3}p_{1R}^2\le p_{1I}^2\le 3p_{1R}^2\)) and dark lump (\(p_{1I}^2>3p_{1R}^2\)). Figure 10 illustrates the existence of the lump and W-type soliton in distinct planes.

Fig. 10
figure 10

Rational solutions within a constant background to the Eq. (4) with \(\lambda =1, a_{11}=0, t=0.5\): a \(p_1=3+i\). b \(p_1=1+i\). c \(p_1=1+2i\). d \(p_1=2+i\)

Full size image

For the rational solutions within another background, we consider \(N=2\), then one-lump and M-type soliton in different planes are generated (see Fig. 11).

Fig. 11
figure 11

Rational solutions to the Eq. (4) with \(\lambda =1, t=1, a_{11}=0, p_1=\frac{1}{2}, p_2=i, c_2=1+3i\). a One-lump on the periodic wave background when \(y=0\). b–c M-type soliton when \(x=0\)

Full size image

When \(N=3, n_1=n_2=1, p_3, q_3\) are purely imaginary values, dark-lump and bi-model lump are obtained (see Fig. 12).

Fig. 12
figure 12

Rational solutions to the Eq. (4) on the periodic wave background with \(\lambda =1, t=0.5, a_{11}=0, p_2=i, p_3=2i, c_3=8+8i\). a Dark-lump when \(p_1=1+i\). b Bi-model lump when \(p_1=1+2i\)

Full size image

6 Conclusion

By utilizing the KP reduction method, the soliton solutions and rational solutions of the \((3+1)\)-dimensional nonlocal Mel’nikov equation in the constant and periodic wave background are studied. Through the imposition of two parameter constraints on the \(\tau \) function, we can derive soliton solutions on both the constant background and the periodic wave background. These soliton patterns encompass various types, including anti-dark solitons, dark solitons, periodic wave solutions, and degenerate solitons. Notably, our study introduces breather of the \((3+1)\)-dimensional nonlocal Mel’nikov equation for the first time, representing a novel discovery.

In addition, we take another form of \(\tau \) function to get the rational solutions, which contains lump and M(W)-type soliton. Unlike the case described in Ref. [38, 39], where lumps appear in pairs, the lumps presented here can be either odd or even. This demonstrates that the dynamic behavior of the nonlocal model in partial reverse-space is more richer. These new discoveries greatly advance our comprehension of nonlocal equations and warrant further investigation into these intriguing physical phenomena.