General bright–dark soliton solution to (2 + 1)-dimensional multi-component long-wave–short-wave resonance interaction system

Abstract

In this paper, we derive a general mixed (bright–dark) multi-soliton solution to a two-dimensional (2D) multi-component long-wave–short-wave resonance interaction (LSRI) system, which include multi-component short waves (SWs) and one-component long wave (LW) for all possible combinations of nonlinearity coefficients including positive, negative and mixed types. With the help of the KP hierarchy reduction method, we firstly construct two types of general mixed N-soliton solution (two-bright–one-dark soliton and one-bright–two-dark one for SW components) to the 2D three-component LSRI system in detail. Then by extending the corresponding analysis to the 2D multi-component LSRI system, a general mixed N-soliton solution in Gram determinant form is obtained. The expression of the mixed soliton solution also contains the general all bright and all dark N-soliton solution as special cases. In particular, for the soliton solution which include two-bright–one-dark soliton for SW components in three-component LSRI system, the dynamics analysis shows that solioff excitation and solioff interaction appear in two SW components which possess bright soliton, while V-type solitary and interaction take place in the other SW component and LW one.

1 Introduction

It is of considerable interest to investigate multi-component system of nonlinear partial differential equations in the theory of nonlinear waves. For instance, in the integrable coupled nonlinear Schrödinger (NLS) equation, namely the celebrated Manakov model [1], it has recently been found that the solitons exhibit certain novel inelastic collision properties, which have not been observed in single-component counterpart [2]. Furthermore, the vector solitons undergoing shape changing (inelastic) collision identified in the generalized multi-component NLS equation can be used in developing logic gates and in all-optical digital computations [3,4,5,6,7].

The long-wave–short-wave resonance interaction (LSRI) is a strong nonlinear interaction phenomenon that occurs when the phase velocity $v_\mathrm{p}$ of the short wave (high-frequency wave) and the group velocity $v_\mathrm{g}$ of the long wave (low-frequency wave) satisfy the Zakharov–Benny condition $v_\mathrm{p}=v_\mathrm{g}$ [8]. This model appear in various contexts such as water waves, plasma physics, nonlinear optics, bio-physics and Bose–Einstein condensates [8,9,10,11,12,13,14,15,16,17,18]. Indeed, the theoretical study of such resonant nonlinear wave interaction originates from investigation the dynamics of Langmuir and ion acoustic waves in plasma by Zakharov [9]. In the case of long waves propagating in a single direction, the Zakharov system is reduced to the Yajima–Oikawa equations [10]. Yajima and Oikawa [10] showed that these equations are integrable using the method of the inverse scattering transformation and admit multi-soliton solutions.

In two-dimensional (2D) case, the LSRI system for the resonant interaction between a long surface wave and a short internal wave in a two-layer fluid was proposed in Ref. [19] and the bright and dark soltion solutions are provided by using the Hirota’s direct method. By applying the reductive perturbation method, Ohta et al. [20] derived an integrable two-component analog of the 2D LSRI system as a governing equation for the interaction of the nonlinear dispersive waves and the $(N;M;N +M)$ bright soliton solution expressed by the Wronskian was reported. The Painlevé test for the single- and two-component 2D LSRI systems was carried out, and some special solutions such as positons, dromions, instantons and periodic wave solutions were constructed [21, 22]. Later, Kanna et al. have obtained the bright N-soliton solutions in the Gram-type determinant form for the multi-component LSRI system and analyzed the bright soliton bound states in detail [23, 24]. In particular, these authors have shown that such bright multi-soliton solution display a fascinating energy-sharing (shape changing) collision in 2D multi-component LSRI system [23]. Moreover, they have derived the general 2D multi-component LSRI system as the evolution equation for propagation of N-dispersive waves in weak Kerr-type nonlinear medium in the small-amplitude limit [25]. The corresponding set of general governing equations with arbitrary nonlinearity coefficients is given by

$$\begin{aligned}&i \left( S^{(\ell )}_t + S^{(\ell )}_y\right) - S^{(\ell )}_{xx}+ L S^{(\ell )}=0,\ \ \ell =1,2,\ldots , M,\ \ \ \ \ \nonumber \\&\quad L_t=2\sum ^M_{\ell =1}\sigma _\ell |S^{(\ell )}|^2_x, \end{aligned}$$

(1)

where $\sigma _\ell =\pm 1$, $S^{(\ell )}$ and L indicate the $\ell$th short-wave and long-wave components, respectively. The general multi-component LSRI system is shown to be integrable by performing the Painlevé analysis and its exact bright multi-soliton solution was constructed in [27]. In Ref. [25], the mixed (bright–dark) one- and two-soliton solutions of a particular 2D multi-component LSRI system, namely the general LSRI system with same nonlinearity coefficients, were also obtained and their propagation properties and collision dynamics were discussed. However, the general representation of the mixed multi-soliton solution for this particular LSRI system is missing. More importantly, as the detailed analysis provided in [27] involving the dynamics of the bright soliton, the arbitrariness of nonlinearity coefficients $\sigma _\ell$ gives an additional freedom resulting in rich soliton dynamics. Thus, it is still worth seeking for the explicit formulation of the mixed multi-soliton solution for the general 2D multi-component LSRI system.

The KP hierarchy reduction for deriving soliton solutions of integrable systems is an elegant and effective method, which was first proposed by the Kyoto school in the 1970s [28]. Such method has been applied to study the bright soliton solutions in various equations such as the NLS equation, the modified KdV equation and the Davey–Stewartson equation. In fact, the multi-component YO system in one-dimensional case with same nonlinearity coefficients $\sigma _\ell$ was reduced from the KP hierarchy in Ref. [29,30,31] and its corresponding bright soliton solution was obtained directly. Recently, general dark–dark soliton solution was derived in a two-component NLS equation with the focusing–defocusing coupling by using the KP hierarchy reduction method [32]. Very recently, one of our authors [33] has constructed general bright–dark N-soliton solution to the vector NLS equation of all possible combinations of nonlinearities including all focusing, all-defocusing and mixed types. Similarly, we have obtained the two different expressions of the dark N-soliton solution, the Gram and Wronski determinants, for the 2D multi-component LSRI system [34]. General bright–dark multi-soliton solution to the 1D multi-component LSRI system was derived in [35]. Meanwhile, exact explicit rational solutions in terms of Gram determinant of the 2D multi-component LSRI system were investigated in Ref. [36]. Breather solutions were calculated by the Hirota bilinear method, and rogue wave modes were obtained from the breathers through a long-wave limit for the 1D multi-component LSRI system [38]. In addition, an integrable semi-discrete analog of the 1D multi-component LSRI system was proposed and both the bright and dark soliton solutions in terms of Pfaffians were constructed [37]. In this study, we will be devoted to consider the general formulation of the mixed multi-soliton solution for the 2D multi-component LSRI system.

The goal of this paper is to construct general bright–dark multi-soliton solution to the 2D multi-component LSRI system (1). The rest of the paper is organized as follows. In Sect. 2, we deduce two types of general mixed soliton solution, which include two-bright–one-dark and one-bright–two-dark soliton for SW components, to the three-component LSRI system by using the KP hierarchy reduction technique. In Sect. 3, general bright–dark soliton solution consisting of m bright solitons and $M-m$ dark solitons to the multi-component YO system is obtained by generalizing our analysis. We summarize the paper in Sect. 4.

2 General mixed soliton solution to the 2D three-component LSRI system

In order to have a clear picture of the procedure to derive the general mixed soliton solution, we first restrict our treatment to a 2D three-component LSRI system [i.e., Eqs. (1) with the number of the short-wave components $M = 3$],

$$\begin{aligned}&i \left( S^{(\ell )}_t + S^{(\ell )}_y\right) - S^{(\ell )}_{xx}+ L S^{(\ell )}=0,\ \ \ell =1,2,3,\ \ \ \ \ \nonumber \\&\quad L_t=2(\sigma _1|S^{(1)}|^2+\sigma _2|S^{(2)}|^2+\sigma _3|S^{(3)}|^2)_x, \end{aligned}$$

(2)

where $\sigma _\ell =\pm 1$ for $\ell =1,2,3$. In this case, the mixed soliton can be divided into bright and dark parts among the three short-wave components in two different ways: two-bright–one-dark soliton and one-bright–two-dark one. Hence, we will construct these two types of soliton solutions in the subsequent two subsections, respectively.

2.1 Two-bright–one-dark soliton for SW components

In this case, we assume that the SW components $S^{(1)}$ and $S^{(2)}$ are of bright type and the SW component $S^{(3)}$ is of dark type. By introducing the dependent variable transformations

$$\begin{aligned} S^{(1)}= & {} \frac{g^{(1)}}{f},\ \ S^{(2)}=\frac{g^{(2)}}{f},\ \ \nonumber \\ S^{(3)}= & {} \rho _1\frac{h^{(1)}}{f} \mathrm{e}^{\mathrm{i}\left[ \alpha _1 x+ \beta _1y-\left( \beta _1-\alpha ^2_1\right) t\right] },\ \ L=-2(\log f)_{xx},\nonumber \\ \end{aligned}$$

(3)

the three-component LSRI system (2) is converted into the following bilinear equations:

$$\begin{aligned}&\left[ i (D_t+D_y)-D^2_x \right] g^{(k)}\cdot f=0,\ \ k=1,2,\nonumber \\&\quad \left[ i (D_t+D_y-2\alpha _1D_x)-D^2_x \right] h^{(1)}\cdot f=0,\ \ \nonumber \\&\quad \left( D_tD_x-2\sigma _3\rho ^2_1\right) f\cdot f= -2\sum ^2_{k=1}\sigma _k g^{(k)}g^{(k)*}\nonumber \\&\quad -2\sigma _3\rho ^2_1 h^{(1)}h^{(1)*}, \end{aligned}$$

(4)

where $g^{(1)},g^{(2)}$ and $h^{(1)}$ are complex-valued functions, f is a real-valued function, $\alpha _1,\beta _1$ and $\rho _1 (\rho _1>0)$ are arbitrary real constants and ${}^*$ denotes the complex conjugation hereafter. The Hirota’s bilinear differential operators are defined by

$$\begin{aligned} D^n_xD^m_t(a\cdot b)= & {} \bigg ( \frac{\partial }{\partial x} - \frac{\partial }{\partial x'} \bigg )^n \bigg (\frac{\partial }{\partial t} - \frac{\partial }{\partial t'} \bigg )^m\\&\quad a(x,t)b(x',t')\bigg |_{x=x',t=t'} . \end{aligned}$$

In what follows, we provide the detailed process that the bilinear form of three-component LSRI system is reduced from the three-component KP hierarchy by suitable reductions and its mixed multi-soltion solution is also obtained correspondingly. To this end, we start from the following bilinear equations in KP hierarchy,

$$\begin{aligned}&(D_{x_2}-D^2_{x_1})\tau _{1,0}(k_1)\cdot \tau _{0,0}(k_1)=0,\nonumber \\&(D_{x_2}-D^2_{x_1})\tau _{0,1}(k_1)\cdot \tau _{0,0}(k_1)=0,\nonumber \\&(D_{x_2}-D^2_{x_1}-2c_1D_{x_1})\tau _{0,0}(k_1+1)\cdot \tau _{0,0}(k_1)=0,\nonumber \\&D_{x_1}D_{y^{\hbox {{(1)}}}_1}\tau _{0,0}(k_1)\cdot \tau _{0,0}(k_1)=-2 \mu _1 \tau _{1,0}(k_1)\tau _{-1,0}(k_1),\nonumber \\&D_{x_1}D_{y^{\hbox {(2)}}_1}\tau _{0,0}(k_1)\cdot \tau _{0,0}(k_1)=-2 \mu _2 \tau _{0,1}(k_1)\tau _{0,-1}(k_1),\nonumber \\&(D_{x_1}D_{x^{\hbox {(1)}}_{-1}}-2)\tau _{0,0}(k_1)\cdot \tau _{0,0}(k_1)\nonumber \\&\quad =-2 \tau _{0,0}(k_1+1)\tau _{0,0}(k_1-1). \end{aligned}$$

(5)

Based on the classical Sato theory [28], the above equations have the solution given by the Gram determinant form

$$\begin{aligned} \tau _{0,0}({k_1})= & {} \left| \begin{array}{ccc} A &{} I \\ -I &{} B \end{array} \right| , \end{aligned}$$

(6)

$$\begin{aligned} \tau _{1,0}(k_1)= & {} \left| \begin{array}{ccc} A &{} I &{} \varPhi ^T \\ -I &{} B &{} \mathbf 0 ^T\\ \mathbf 0 &{} -\bar{\varPsi } &{} 0 \end{array} \right| ,\nonumber \\ \tau _{-1,0}(k_1)= & {} \left| \begin{array}{ccc} A &{} I &{} \mathbf 0 ^T \\ -I &{} B &{} \varPsi ^T\\ -\bar{\varPhi } &{} \mathbf 0 &{} 0 \end{array} \right| , \end{aligned}$$

(7)

$$\begin{aligned} \tau _{0,1}(k_1)= & {} \left| \begin{array}{ccc} A &{} I &{} \varPhi ^T \\ -I &{} B &{} \mathbf 0 ^T\\ \mathbf 0 &{} -\bar{\varUpsilon } &{} 0 \end{array} \right| ,\nonumber \\ \tau _{0,-1}(k_1)= & {} \left| \begin{array}{ccc} A &{} I &{} \mathbf 0 ^T \\ -I &{} B &{} \varUpsilon ^T\\ -\bar{\varPhi } &{} \mathbf 0 &{} 0 \end{array} \right| , \end{aligned}$$

(8)

where I is an $N\times N$ identity matrix, A and B are $N\times N$ matrices defined as

$$\begin{aligned} A_{ij}(k_1)= & {} \frac{1}{p_i+\bar{p}_j} \left( -\frac{p_i-c_1}{\bar{p}_j+c_1} \right) ^{k_1} \mathrm{e}^{\xi _i+\bar{\xi }_j},\nonumber \\ B_{ij}= & {} \frac{\mu _1}{q_i+\bar{q}_j} \mathrm{e}^{\eta _i+\bar{\eta }_j} + \frac{\mu _2}{r_i+\bar{r}_j} \mathrm{e}^{\chi _i+\bar{\chi }_j}, \end{aligned}$$

and $\mathbf 0$ is a N-component zero-row vector, $\varPhi ,\varPsi ,\varUpsilon ,\bar{\varPhi },\bar{\varPsi }$ and $\bar{\varUpsilon }$ are N-component row vectors given by

$$\begin{aligned} \varPhi= & {} (\mathrm{e}^{\xi _1}, \mathrm{e}^{\xi _2}, \ldots , \mathrm{e}^{\xi _N} ),\ \ \varPsi =(\mathrm{e}^{\eta _1}, \mathrm{e}^{\eta _2}, \ldots , \mathrm{e}^{\eta _N} ),\\ \varUpsilon= & {} (\mathrm{e}^{\chi _1}, \mathrm{e}^{\chi _2}, \ldots , \mathrm{e}^{\chi _N} ),\\ \bar{\varPhi }= & {} (\mathrm{e}^{\bar{\xi }_1}, \mathrm{e}^{\bar{\xi }_2}, \ldots , \mathrm{e}^{\bar{\xi }_N} ),\\ \bar{\varPsi }= & {} (\mathrm{e}^{\bar{\eta }_1}, \mathrm{e}^{\bar{\eta }_2}, \ldots , \mathrm{e}^{\bar{\eta }_N} ),\ \ \bar{\varUpsilon }=(\mathrm{e}^{\bar{\chi }_1}, \mathrm{e}^{\bar{\chi }_2}, \ldots , \mathrm{e}^{\bar{\chi }_N} ),\ \ \end{aligned}$$

with

$$\begin{aligned} \xi _i= & {} \frac{1}{p_i-c_1}x^{(1)}_{-1}+p_ix_1+p^2_ix_2+\xi _{i0},\\ \bar{\xi }_j= & {} \frac{1}{\bar{p}_j+c_1}x^{(1)}_{-1}+\bar{p}_jx_1-\bar{p}^2_jx_2+\bar{\xi }_{j0},\\ \eta _i= & {} q_i y^{(1)}_1 +\eta _{i0},\\ \bar{\eta }_j= & {} \bar{q}_j y^{(1)}_1 +\bar{\eta }_{j0}, \ \ \chi _i=r_i y^{(2)}_1 +\chi _{i0}, \\ \bar{\chi }_j= & {} \bar{r}_j y^{(2)}_1 +\bar{\chi }_{j0}. \end{aligned}$$

Here $p_i, \bar{p}_j, q_i, \bar{q}_j, r_i, \bar{r}_j, \xi _{i0}, \bar{\xi }_{j0}, \eta _{i0}, \bar{\eta }_{j0}, \chi _{i0}, \bar{\chi }_{j0}$ and $c_1$ are complex parameters.

Next, by setting $x_1$, $x^{(1)}_{-1}$, $y^{(1)}_1$, $y^{(2)}_1$, $\mu _1$ and $\mu _2$ are real, $x_2$, $c_1$ are pure imaginary and by letting $p^*_j=\bar{p}_j$, $q^*_j=\bar{q}_j=r^*_j=\bar{r}_j$, $\xi ^*_{j0}=\bar{\xi }_{j0}$, $\eta ^*_{j0}=\bar{\eta }_{j0}$ and $\chi ^*_{j0}=\bar{\chi }_{j0}$, it is easy to check that

$$\begin{aligned} A_{ij}(k_1)= A^*_{ji}(k_1),\ \ B_{ij}= B^*_{ji}. \end{aligned}$$

Thus, we can define

$$\begin{aligned} f= & {} \tau _{0,0}(0),\ \ g^{(1)}=\tau _{1,0}(0),\ \ g^{(2)}=\tau _{0,1}(0), \\ h^{(1)}= & {} \tau _{0,0}(1),\\ g^{(1)*}= & {} -\tau _{-1,0}(0),\ \ g^{(2)*}=-\tau _{0,-1}(0), \\ h^{(1)*}= & {} \tau _{0,0}(-1), \end{aligned}$$

and then the bilinear Eq. (5) become

$$\begin{aligned}&(D_{x_2}-D^2_{x_1})g^{(k)}\cdot f=0,\nonumber \\&\quad D_{x_1}D_{y^{\tiny (k)}_1}f\cdot f=2 g^{(k)}g^{(k)*},\ \ k=1,2,\nonumber \\&\quad (D_{x_2}-D^2_{x_1}-2c_1D_{x_1})h^{(1)}\cdot f=0,\nonumber \\&\quad (D_{x_1}D_{x^{\hbox {(1)}}_{-1}}-2)f\cdot f=-2 h^{(1)}h^{(1)*}. \end{aligned}$$

(9)

Furthermore, by considering the independent variables changes

$$\begin{aligned}&x_1=x,\ \ x_2=-\mathrm{i}y,\ \ y^{(k)}_1=-\nu _k(t-y),\\&x^{(1)}_{-1}=\sigma _3\rho ^2_1(t-y),\ \ k=1,2, \end{aligned}$$

i.e.,

$$\begin{aligned} \partial _x= & {} \partial _{x_1},\ \ \partial _y=-\mathrm{i}\partial _{x_2}+\sum ^2_{k=1}\nu _k\partial _{y^{(k)}_1}-\sigma _3\rho ^2_1\partial _{x^{(1)}_{-1}},\nonumber \\ \partial _t= & {} -\sum ^2_{k=1}\nu _k\partial _{y^{(k)}_1}+\sigma _3\rho ^2_1\partial _{x^{(1)}_{-1}}, \end{aligned}$$

with $c_1=\mathrm{i}\alpha _1$ and $\nu _1,\nu _2$ are real constants, Eqs. (9) are transformed into the bilinear Eq. (4) of the three-component LSRI system.

Finally, the general mixed soliton (two-bright–one-dark soliton for SW components) solution to 2D three-component LSRI system reads

$$\begin{aligned} f= & {} \left| \begin{array}{ccc} A &{} I \\ -I &{} B \end{array} \right| ,\nonumber \\ h^{(1)}= & {} \left| \begin{array}{ccc} A^{(1)} &{} I \\ -I &{} B \end{array} \right| ,\nonumber \\ g^{(k)}= & {} \left| \begin{array}{ccc} A &{} I &{} \phi ^T \\ -I &{} B &{} \mathbf 0 ^T\\ \mathbf 0 &{} \psi ^{(k)} &{} 0 \end{array} \right| , \end{aligned}$$

(10)

where A, $A^{(1)}$ and B are $N\times N$ matrices defined as

$$\begin{aligned} A_{ij}= & {} \frac{1}{p_i+p^*_j} \mathrm{e}^{\varXi _i+\varXi ^*_j},\\ A^{(1)}_{ij}= & {} \frac{1}{p_i+p^*_j} \left( -\frac{p_i-\mathrm{i}\alpha _1}{p^*_j +\mathrm{i}\alpha _1} \right) \mathrm{e}^{\varXi _i+\varXi ^*_j},\\ B_{ij}= & {} \frac{1}{q_i+q^*_j} \sum ^2_{k=1} \mu _k\mathrm{e}^{\varTheta ^{(k)}_{i}+\varTheta ^{(k)*}_{j} }, \end{aligned}$$

and $\phi$ and $\psi ^{(k)}$ are N-component row vectors given by

$$\begin{aligned} \phi= & {} (\mathrm{e}^{\varXi _1}, \mathrm{e}^{\varXi _2}, \ldots , \mathrm{e}^{\varXi _N}),\\ \psi ^{(k)}= & {} -(\mathrm{e}^{\varTheta ^{(k)*}_1 }, \mathrm{e}^{\varTheta ^{(k)*}_2 }, \ldots , \mathrm{e}^{\varTheta ^{(k)*}_N } ),\ \ \end{aligned}$$

with

$$\begin{aligned} \varXi _i= & {} \frac{1}{p_i-\mathrm{i}\alpha _1}\sigma _3\rho ^2_1(t-y)+p_ix-\mathrm{i}p^2_iy+\xi _{i0},\\ \varTheta ^{(k)}_i= & {} -\nu _k q_i(t-y)+\theta ^{(k)}_{i0}. \end{aligned}$$

Here $\sigma _k=\mu _k\nu _k$, $p_i$, $q_i$, $\xi _{i0}$ and $\theta ^{(k)}_{i0}$ $(i=1,2,\ldots ,N; k=1,2)$ are arbitrary complex parameters.

2.1.1 One-soliton solution

To obtain the single soliton solution, we take $N=1$ in the formula (10). The Gram determinants read

$$\begin{aligned} f= & {} \left| \begin{array}{ccc} A_{11} &{} 1 \\ -1 &{} B_{11} \end{array} \right| ,\nonumber \\ h^{(1)}= & {} \left| \begin{array}{cccc} A^{(1)}_{11} &{} 1 \\ -1 &{} B_{11} \end{array} \right| ,\nonumber \\ g^{(k)}= & {} \left| \begin{array}{ccccc} A_{11} &{} 1 &{} \mathrm{e}^{\varXi _1} \\ -1 &{} B_{11} &{} 0 \\ 0 &{} -\mathrm{e}^{\varTheta ^{(k)*}_1 } &{} 0 \end{array} \right| , \end{aligned}$$

(11)

where $A_{11}=\frac{1}{p_1+p^*_1} \mathrm{e}^{\varXi _1+\varXi ^*_1}, A^{(1)}_{11}=\frac{1}{p_1+p^*_1} \left( -\frac{p_1-\mathrm{i}\alpha _1}{p^*_1+\mathrm{i}\alpha _1} \right) \mathrm{e}^{\varXi _1+\varXi ^*_1}$ and $B_{11}=\frac{1}{q_1+q^*_1} \sum ^2_{k=1} \mathrm{e}^{\varTheta ^{(k)}_{1}+\varTheta ^{(k)*}_{1} }$ for $k=1,2$. Then one can write the above tau functions as

$$\begin{aligned} f= & {} 1+\frac{\mathrm{e}^{2\varXi _{1R}} }{4p_{1R}q_{1R}} \sum ^2_{k=1} \mu _k\mathrm{e}^{2\varTheta ^{(k)}_{1R} }, \end{aligned}$$

(12)

$$\begin{aligned} g^{(1)}= & {} -\mathrm{e}^{\varXi _1+\varTheta ^{(1)*}_1},\ \ g^{(2)}=-\mathrm{e}^{\varXi _1+\varTheta ^{(2)*}_1}, \end{aligned}$$

(13)

$$\begin{aligned} h^{(1)}= & {} 1- \frac{p_1-\mathrm{i}\alpha _1}{p^*_1+\mathrm{i}\alpha _1} \frac{\mathrm{e}^{2\varXi _{1R}} }{4p_{1R}q_{1R}} \sum ^2_{k=1}\mathrm{e}^{2\varTheta ^{(k)}_{1R} }, \end{aligned}$$

(14)

where the suffixes R and I denote the real and imaginary parts, respectively.

To obtain nonsingular soliton solution, we always choose $p_{1R}q_{1R}>0$ and $\mu _1=\mu _2=1$. Then one-soliton solutions can be classified into the following three cases (only for $\sigma _1$ and $\sigma _2$): (i) positive nonlinearity coefficients [$(\sigma _1,\sigma _2)=(1,1)$, then $\nu _1=\nu _2=1$]: This case have been discussed in Ref. [25]; (ii) negative nonlinearity coefficients [$(\sigma _1,\sigma _2)=(-1,-1)$, then $\nu _1=\nu _2=-1$]: For the choice, the LSRI system admits a similar type of propagation and even collision behaviors as that of the positive nonlinearity coefficients [26, 27]; (iii) mixed-type nonlinearity coefficients: Without loss of generality, we take $(\sigma _1,\sigma _2)=(1,-1)$ and fix $\sigma _3=1$, then $\nu _1=-\nu _2=1$ and tau functions in (12)–(14) can be rewritten as

$$\begin{aligned}&f=1+\mathrm{e}^{\varOmega _1+\varOmega ^*_1+R_1}+\mathrm{e}^{\varOmega _2+\varOmega ^*_2+R_2}, \end{aligned}$$

(15)

$$\begin{aligned}&g^{(1)}=-\mathrm{e}^{\varOmega _1+\mathrm{i}\varGamma _1 +\theta ^{(1)}_{10R}},\nonumber \\&g^{(2)}=-\mathrm{e}^{\varOmega _2+\mathrm{i}\varGamma _2 +\theta ^{(2)}_{10R}},\end{aligned}$$

(16)

$$\begin{aligned}&h=1+\mathrm{e}^{\varOmega _1+\varOmega ^*_1+R_1+2\mathrm{i}\phi }+\mathrm{e}^{\varOmega _2+\varOmega ^*_2+R_2+2\mathrm{i}\phi } \end{aligned}$$

(17)

with $\varOmega _k=\varOmega _{kR}+\mathrm{i}\varOmega _{kI}$, $\varOmega _{kR}=p_{1R}x+(-w_{kR}+2p_{1R}p_{1I})y + w_{kR} t$, $\varOmega _{kI}=p_{1I}x-[w_{kI}+(p^2_{1R}-p^2_{1I})]y + w_{kI} t$, $\varGamma _k=2(-1)^{k+1}q_{1I}(t-y)-\theta ^{(k)}_{10I}$, $w_{kR}=\frac{\rho ^2_1p_{1R}}{p^2_{1R}+(p_{1I}-\alpha _1)^2}+(-1)^kq_{1R}$, $w_{kI}=-\frac{\rho ^2_1(p_{1I}-\alpha _1)}{p^2_{1R}+(p_{1I}-\alpha _1)^2}+(-1)^kq_{kI}$, $\mathrm{e}^{R_k}=\frac{1}{4p_{1R}q_{1R}} \mathrm{e}^{2\xi _{10R}+2\theta ^{(k)}_{10R}}$ and $\mathrm{e}^{2\mathrm{i}\phi }=-\frac{p_1-\mathrm{i}\alpha _1}{p^*_1+\mathrm{i}\alpha _1}$ for $k=1,2$.

From the expressions (15)–(17) of tau functions, the single soliton solution actually represents two-soliton resonance solution. In the following, we carry out the asymptotic analysis for this kind of soliton resonance solution. We assume $p_{1R}>0, p_{1I}>0$, $q_{1R}>0, q_{1I}>0$ and $\frac{\rho ^2_1p_{1R}}{p^2_{1R}+(p_{1I}-\alpha _1)^2} < q_{1R}$, then $w_{1R}<0$ and $w_{2R}>0$. In the limit $x,y\rightarrow \pm \infty$ and a fixed t, the soliton resonance solution takes the following asymptotic forms.

(a) Before collision ($x,y\rightarrow -\infty$):

soliton 1 ($\varOmega _{1R}\simeq 0$, $\varOmega _{2R}\rightarrow -\infty$)

$$\begin{aligned}&S^{(1)} \simeq -\frac{\sqrt{p_{1R}q_{1R}}}{\mathrm{e}^{\xi _{10R}}} \mathrm{e}^{\mathrm{i}(\varOmega _{1I}+\varGamma _1)} \mathrm{sech}(\varOmega _{1R}+\frac{R_1}{2}),\\&\quad S^{(2)} \simeq 0,\\&\quad S^{(3)} \simeq \frac{\rho _1}{2} \mathrm{e}^{\mathrm{i}[\alpha _1 x+ \beta _1y -(\beta _1-\alpha ^2_1)t]} [1+\mathrm{e}^{2\mathrm{i}\phi }\\&\quad -(1-\mathrm{e}^{2\mathrm{i}\phi })\tanh (\varOmega _{1R}+\frac{R_1}{2})], \\&\quad L \simeq -2 p^2_{1R} \mathrm{sech}^2\left( \varOmega _{1R}+\frac{R_1}{2}\right) , \end{aligned}$$

soliton 2 ($\varOmega _{2R}\simeq 0$, $\varOmega _{1R}\rightarrow -\infty$)

$$\begin{aligned}&S^{(1)} \simeq 0,\\&\quad S^{(2)} \simeq -\frac{\sqrt{p_{1R}q_{1R}}}{\mathrm{e}^{\xi _{10R}}} \mathrm{e}^{\mathrm{i}(\varOmega _{2I}+\varGamma _2)} \mathrm{sech}(\varOmega _{2R}+\frac{R_2}{2}),\\&\quad S^{(3)} \simeq \frac{\rho _1}{2} \mathrm{e}^{\mathrm{i}\left[ \alpha _1 x+ \beta _1y-\left( \beta _1-\alpha ^2_1\right) t\right] } \left[ 1+\mathrm{e}^{2\mathrm{i}\phi }\right. \\&\quad -\left. (1-\mathrm{e}^{2\mathrm{i}\phi })\tanh (\varOmega _{2R}+\frac{R_2}{2})\right] , \\&\quad L \simeq -2 p^2_{1R} \mathrm{sech}^2\left( \varOmega _{2R}+\frac{R_2}{2}\right) , \end{aligned}$$

(b) After collision ($x,y\rightarrow +\infty$):

soliton 1 ($\varOmega _{1R}\simeq 0$, $\varOmega _{2R}\rightarrow +\infty$)

$$\begin{aligned}&S^{(1)} \simeq 0,\\&S^{(2)} \simeq 0,\\&S^{(3)} \simeq \rho _1 \mathrm{e}^{\mathrm{i}\left[ \alpha _1 x+ \beta _1y -\left( \beta _1-\alpha ^2_1\right) t+2\phi \right] }, \\&L \simeq 0, \end{aligned}$$

Fig. 1

Mixed one-soliton (two-bright–one-dark soliton for SW components) solution in three-component LSRI system at time $t=0$

soliton 2 ($\varOmega _{2R}\simeq 0$, $\varOmega _{1R}\rightarrow +\infty$)

$$\begin{aligned}&S^{(1)} \simeq 0,\\&S^{(2)} \simeq 0,\\&S^{(3)} \simeq \rho _1 \mathrm{e}^{\mathrm{i}\left[ \alpha _1 x+ \beta _1y-\left( \beta _1-\alpha ^2_1\right) t+2\phi \right] }, \\&L \simeq 0, \end{aligned}$$

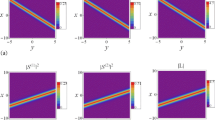
As reported in Ref. [26, 27], the formation of this special soliton solution is due to the mixed-type nonlinearity coefficients. In this case, we illustrate one-soliton solution in Fig. 1 with the parameters $\mu _1=\mu _2=\nu _1=-\nu _2=\rho _1=1$, $\alpha _1=2$, $p_1=1+\frac{1}{2}\mathrm{i}$, $q_1=2+\mathrm{i}$, $\mathrm{e}^{\xi _{10}}=1+3\mathrm{i}$, $\mathrm{e}^{\theta ^{(1)}_{10}}=1+\frac{1}{2}\mathrm{i}$ and $\mathrm{e}^{\theta ^{(2)}_{10}}=\frac{1}{2}+2\mathrm{i}$. One can observe that the bright solitons in SW components $S^{(1)}$ and $S^{(2)}$ are solitoffs, while the dark soliton of the SW component $S^{(3)}$ and the bright one of the LW component $-L$ are “V” solitary wave. In Ref. [39], the authors have derived the solitoff solution for the single-component LSRI system (only one SW component). For the multi-component LSRI system, the formation of such soliton is ascribed to the mixed-type nonlinearity coefficients $\sigma _l$, as expressed in (12). This situation also hits that the fact reported in [27] the arbitrariness of nonlinearity coefficients $\sigma _\ell$ in the general multi-component LSRI system increases the freedom resulting in rich mixed soliton dynamics.

Fig. 2

Mixed two-soliton (two-bright–one-dark soliton for SW components) solution in three-component LSRI system at time $t=0$

2.1.2 Two-soliton solution

By taking $N=2$ in (10), we deduce the Gram determinant forms for the mixed two-soliton solution as

$$\begin{aligned} f= & {} \left| \begin{array}{cccc} A_{11} &{} A_{12} &{} 1 &{} 0 \\ A_{21} &{} A_{22} &{} 0 &{} 1 \\ -1 &{} 0 &{} B_{11} &{} B_{12} \\ 0 &{} -1 &{} B_{21} &{} B_{22} \\ \end{array} \right| ,\nonumber \\ h^{(1)}= & {} \left| \begin{array}{cccc} A^{(1)}_{11} &{} A^{(1)}_{12} &{} 1 &{} 0 \\ A^{(1)}_{21} &{} A^{(1)}_{22} &{} 0 &{} 1 \\ -1 &{} 0 &{} B_{11} &{} B_{12} \\ 0 &{} -1 &{} B_{21} &{} B_{22} \\ \end{array} \right| ,\end{aligned}$$

(18)

$$\begin{aligned} g^{(k)}= & {} \left| \begin{array}{ccccc} A_{11} &{} A_{12} &{} 1 &{} 0 &{} \mathrm{e}^{\varXi _1} \\ A_{21} &{} A_{22} &{} 0 &{} 1 &{} \mathrm{e}^{\varXi _2}\\ -1 &{} 0 &{} B_{11} &{} B_{12} &{} 0 \\ 0 &{} -1 &{} B_{21} &{} B_{22} &{}0 \\ 0 &{} 0 &{} -\mathrm{e}^{\varTheta ^{(k)*}_1 } &{} -\mathrm{e}^{\varTheta ^{(k)*}_2 } &{} 0 \end{array} \right| , \end{aligned}$$

(19)

where $A_{ij}=\frac{1}{p_i+p^*_j} \mathrm{e}^{\varXi _i+\varXi ^*_j}, A^{(1)}_{ij}=\frac{1}{p_i+p^*_j} \left( -\frac{p_i-\mathrm{i}\alpha _1}{p^*_j+\mathrm{i}\alpha _1} \right) \mathrm{e}^{\varXi _i+\varXi ^*_j}$ and $B_{ij}=\frac{1}{q_i+q^*_j} \sum ^2_{k=1} \mu _k \mathrm{e}^{\varTheta ^{(k)}_{i}+\varTheta ^{(k)*}_{j} }$ for $k=1,2$.

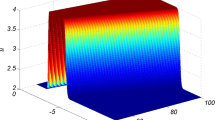
For the same nonlinearity coefficients $(\sigma _1,\sigma _2,\sigma _3)=(1,-1,1)$, we show an example in Fig. 2 which displays the bright solitoff interaction appearing in SW components $S^{(1)}$ and $S^{(2)}$ and the V-type soliton interaction for dark soliton in SW component $S^{(3)}$ and bright one in LW component $-L$, respectively. The parameters are chosen as $\mu _1=\mu _2=\nu _1=-\nu _2=1$, $\rho _1=2, p_1=1+\frac{1}{2}\mathrm{i}, p_2=\frac{2}{3}+\frac{3}{2}\mathrm{i}, q_1=1+\mathrm{i}, q_2=\frac{1}{2}+\frac{2}{3}\mathrm{i}, \mathrm{e}^{\xi _{10}}=1+3\mathrm{i}, \mathrm{e}^{\xi _{20}}=\frac{3}{2}+\frac{1}{2}\mathrm{i}, \mathrm{e}^{\theta ^{(1)}_{10}}=1+\frac{1}{2}\mathrm{i}, \mathrm{e}^{\theta ^{(1)}_{20}}=1+\frac{1}{5}\mathrm{i}, \mathrm{e}^{\theta ^{(2)}_{10}}=\frac{2}{3}+\mathrm{i}$ and $\mathrm{e}^{\theta ^{(2)}_{20}}=\frac{1}{4}+\frac{1}{3}\mathrm{i}$.

2.2 One-bright–two-dark soliton for SW components

In this subsection, we let SW component $S^{(1)}$ is of bright type and SW components $S^{(2)}$ and $S^{(3)}$ are of dark type. Using the dependent variable transformations

$$\begin{aligned} S^{(1)}= & {} \frac{g^{(1)}}{f},\ \ S^{(2)}=\rho _1\frac{h^{(1)}}{f} \mathrm{e}^{\mathrm{i}[\alpha _1 x+ \beta _1y-(\beta _1-\alpha ^2_1)t]},\nonumber \\ S^{(3)}= & {} \rho _2\frac{h^{(2)}}{f} \mathrm{e}^{\mathrm{i}[\alpha _2 x+ \beta _2y-(\beta _2-\alpha ^2_2)t]} ,\ \ L=-2(\log f)_{xx},\nonumber \\ \end{aligned}$$

(20)

leads three-component LSRI Eqs. (2) into the following bilinear equations:

$$\begin{aligned}&\left[ i (D_t+D_y)-D^2_x \right] g^{(1)}\cdot f=0,\nonumber \\&\quad \left[ i (D_t+D_y-2\alpha _lD_x)-D^2_x \right] h^{(l)}\cdot f=0,\ \ l=1,2, \nonumber \\&\quad \left( D_tD_x-2 \sum ^2_{l=1}\sigma _{l+1}\rho ^2_l \right) f\cdot \nonumber \\&\quad f= -2\sigma _1 g^{(1)}g^{(1)*}-2\sum ^2_{l=1}\sigma _{l+1}\rho ^2_l h^{(l)}h^{(l)*}, \end{aligned}$$

(21)

where $g^{(1)},h^{(1)}$ and $h^{(2)}$ are complex-valued functions, f is a real-valued function, $\alpha _l,\beta _l$ and $\rho _l (\rho _l>0,l=1,2)$ are arbitrary real constants.

Similar to the previous subsection, the bilinear equations of three-component LSRI system (21) are viewed as a reduction of two-component KP hierarchy. Specifically, we consider the bilinear equations in two-component KP as follows,

$$\begin{aligned}&(D_{x_2}-D^2_{x_1})\tau _{1}(k_1,k_2)\cdot \tau _{0}(k_1,k_2)=0,\nonumber \\&\quad (D_{x_2}-D^2_{x_1}-2c_1D_{x_1})\tau _{0}(k_1+1,k_2)\cdot \nonumber \\&\qquad \tau _{0}(k_1,k_2)=0,\nonumber \\&\quad (D_{x_2}-D^2_{x_1}-2c_2D_{x_1})\tau _{0}(k_1,k_2+1)\cdot \nonumber \\&\qquad \tau _{0}(k_1,k_2)=0,\nonumber \\&\quad D_{x_1}D_{y^{(1)}_1}\tau _{0}(k_1,k_2)\cdot \nonumber \\&\qquad \tau _{0}(k_1,k_2)=-2 \mu _1 \tau _{1}(k_1,k_2)\tau _{-1}(k_1,k_2),\nonumber \\&\quad (D_{x_1}D_{x^{\hbox {(1)}}_{-1}}-2)\tau _{0}(k_1,k_2)\cdot \nonumber \\&\qquad \tau _{0}(k_1,k_2)=-2 \tau _{0}(k_1+1,k_2)\tau _{0}(k_1-1,k_2),\nonumber \\&\quad (D_{x_1}D_{x^{\hbox {(2)}}_{-1}}-2)\tau _{0}(k_1,k_2)\cdot \nonumber \\&\qquad \tau _{0}(k_1,k_2)=-2 \tau _{0}(k_1,k_2+1)\tau _{0}(k_1,k_2-1).\nonumber \\ \end{aligned}$$

(22)

On the basis of the Sato theory for the KP hierarchy, the tau functions in above bilinear equations can be expressed by the following Gram determinant

$$\begin{aligned} \tau _{0}(k_1,k_2)= & {} \left| \begin{array}{ccc} A &{} I \\ -I &{} B \end{array} \right| ,\end{aligned}$$

(23)

$$\begin{aligned} \tau _{1}(k_1,k_2)= & {} \left| \begin{array}{ccc} A &{} I &{} \varPhi ^T \\ -I &{} B &{} \mathbf 0 ^T\\ \mathbf 0 &{} -\bar{\varPsi } &{} 0 \end{array} \right| ,\nonumber \\ \tau _{-1}(k_1,k_2)= & {} \left| \begin{array}{ccc} A &{} I &{} \mathbf 0 ^T \\ -I &{} B &{} \varPsi ^T\\ -\bar{\varPhi } &{} \mathbf 0 &{} 0 \end{array} \right| , \end{aligned}$$

(24)

where $\varPhi ,\varPsi ,\bar{\varPhi },\bar{\varPsi }$ are N-component row vectors defined previously, A and B are $N\times N$ matrices defined as

$$\begin{aligned} A_{ij}(k_1,k_2)= & {} \frac{1}{p_i+\bar{p}_j} \left( -\frac{p_i-c_1}{\bar{p}_j+c_1} \right) ^{k_1}\nonumber \\&\left( -\frac{p_i-c_2}{\bar{p}_j+c_2} \right) ^{k_2} \mathrm{e}^{\xi _i+\bar{\xi }_j},\\ B_{ij}= & {} \frac{\mu _1}{q_i+\bar{q}_j} \mathrm{e}^{\eta _i+\bar{\eta }_j} , \end{aligned}$$

with

$$\begin{aligned} \xi _i= & {} \frac{1}{p_i-c_1}x^{(1)}_{-1}+\frac{1}{p_i-c_2}x^{(2)}_{-1} +p_ix_1+p^2_ix_2+\xi _{i0},\\ \bar{\xi }_j= & {} \frac{1}{\bar{p}_j+c_1}x^{(1)}_{-1} +\frac{1}{\bar{p}_j+c_2}x^{(2)}_{-1}+\bar{p}_jx_1-\bar{p}^2_jx_2+\bar{\xi }_{j0},\\ \eta _i= & {} q_i y^{(1)}_1 +\eta _{i0},\ \ \bar{\eta }_j=\bar{q}_j y^{(1)}_1 +\bar{\eta }_{j0}. \end{aligned}$$

Here $p_i, \bar{p}_j, q_i, \bar{q}_j, \xi _{i0}, \bar{\xi }_{j0}, \eta _{i0}, \bar{\eta }_{j0}, c_1$ and $c_2$ are complex parameters.

Next, we present the reduction process to obtain the bilinear Eq. (21) from the ones in two-component KP hierarchy. We first perform the complex conjugate reduction by setting $x_1$, $x^{(1)}_{-1}$, $x^{(2)}_{-1}$, $y^{(1)}_1$ and $\mu _1$ are real, $x_2$, $c_1$ $c_2$ are pure imaginary and by letting $p^*_j=\bar{p}_j$, $q^*_j=\bar{q}_j$, $\xi ^*_{j0}=\bar{\xi }_{j0}$, and $\eta ^*_{j0}=\bar{\eta }_{j0}$. Then, it is easy to see that

$$\begin{aligned} A_{ij}(k_1,k_2)=A^*_{ji}(-k_1,-k_2),\ \ B_{ij}=B^*_{ji}. \end{aligned}$$

(25)

Thus, if we define

$$\begin{aligned} f= & {} \tau _{0}(0,0),\ \ g^{(1)}=\tau _{1}(0,0), \ \ h^{(1)}=\tau _{0}(1,0),\\ h^{(2)}= & {} \tau _{0}(0,1), \\ g^{(1)*}= & {} -\tau _{-1}(0,0), \ \ h^{(1)*}=\tau _{0}(-1,0),\\ h^{(2)*}= & {} \tau _{0}(0,-1), \end{aligned}$$

the bilinear Eq. (22) become

$$\begin{aligned}&(D_{x_2}-D^2_{x_1})g^{(1)}\cdot f=0,\nonumber \\&\quad (D_{x_2}-D^2_{x_1}-2c_1D_{x_1})h^{(1)}\cdot f=0,\nonumber \\&\quad (D_{x_2}-D^2_{x_1}-2c_2D_{x_1})h^{(2)}\cdot f=0,\nonumber \\&\quad D_{x_1}D_{y^{(1)}_1}f\cdot f=2 \mu _1 g^{(1)}g^{(1)*},\nonumber \\&\quad (D_{x_1}D_{x^{\hbox {(1)}}_{-1}}-2)f\cdot f=-2 h^{(1)}h^{(1)*},\nonumber \\&\quad (D_{x_1}D_{x^{\hbox {(2)}}_{-1}}-2)f\cdot f=-2 h^{(2)}h^{(2)*}. \end{aligned}$$

(26)

Furthermore, by using the independent variables transformations

$$\begin{aligned}&x_1=x,\ \ x_2=-\mathrm{i}y,\ \ y^{(1)}_1=-\nu _1(t-y),\\&x^{(l)}_{-1}=\sigma _{l+1}\rho ^2_l(t-y),\ \ l=1,2, \end{aligned}$$

i.e.,

$$\begin{aligned} \partial _x= & {} \partial _{x_1},\ \ \partial _y=-\mathrm{i}\partial _{x_2}+\nu _1\partial _{y^{(1)}_1}-\sum ^2_{l=1}\sigma _{l+1}\rho ^2_l\partial _{x^{(l)}_{-1}},\\ \partial _t= & {} -\nu _1\partial _{y^{(1)}_1}+\sum ^2_{l=1}\sigma _{l+1}\rho ^2_l\partial _{x^{(l)}_{-1}}, \end{aligned}$$

and $c_1=\mathrm{i}\alpha _1$, $c_2=\mathrm{i}\alpha _2$, we can arrive at the bilinear Eq. (21).

Consequently, we are able to construct the general mixed soliton (one-bright–two-dark soliton for SW components) solution to 2D three-component LSRI system,

$$\begin{aligned} f= & {} \left| \begin{array}{ccc} A &{} I \\ -I &{} B \end{array} \right| ,\nonumber \\ h^{(l)}= & {} \left| \begin{array}{ccc} A^{(l)} &{} I \\ -I &{} B \end{array} \right| ,\nonumber \\ g^{(1)}= & {} \left| \begin{array}{ccc} A &{} I &{} \phi ^T \\ -I &{} B &{} \mathbf 0 ^T\\ \mathbf 0 &{} \psi ^{(1)} &{} 0 \end{array} \right| , \end{aligned}$$

(27)

where A, $A^{(k)}$ and B are $N\times N$ matrices defined as

$$\begin{aligned}&A_{ij}=\frac{1}{p_i+p^*_j} \mathrm{e}^{\varXi _i+\varXi ^*_j},\\&A^{(l)}_{ij}=\frac{1}{p_i+p^*_j} \left( -\frac{p_i-\mathrm{i}\alpha _l}{p^*_j+\mathrm{i}\alpha _l} \right) \mathrm{e}^{\varXi _i+\varXi ^*_j},\\&B_{ij}=\frac{1}{q_i+q^*_j} \mathrm{e}^{\varTheta ^{(1)}_{i}+\varTheta ^{(1)*}_{j} }, \end{aligned}$$

and $\phi$ and $\psi ^{(1)}$ are N-component row vectors given by

$$\begin{aligned} \phi= & {} (\mathrm{e}^{\varXi _1}, \mathrm{e}^{\varXi _2}, \ldots , \mathrm{e}^{\varXi _N} ),\\ \psi ^{(1)}= & {} -(\mathrm{e}^{\varTheta ^{(1)*}_1 }, \mathrm{e}^{\varTheta ^{(1)*}_2 }, \ldots , \mathrm{e}^{\varTheta ^{(1)*}_N } ),\ \ \end{aligned}$$

with

$$\begin{aligned} \varXi _i= & {} \sum ^2_{l=1} \frac{1}{p_i-\mathrm{i}\alpha _l} \sigma _{l+1}\rho ^2_l(t-y)+p_ix-\mathrm{i}p^2_iy+\xi _{i0},\\&\varTheta ^{(1)}_i=-\nu _1 q_i(t-y)+\theta ^{(1)}_{i0}. \end{aligned}$$

Here $\sigma _1=\mu _1\nu _1$, $p_i$, $q_i$, $\xi _{i0}$ and $\theta ^{(1)}_{i0}$ $(i=1,2,\ldots ,N; l=1,2)$ are arbitrary complex parameters.

2.2.1 One-soliton solution

By taking $N=1$ in the formula (27), we get the Gram determinants

$$\begin{aligned} f= & {} \left| \begin{array}{cccc} A_{11} &{} 1 \\ -1 &{} B_{11} \\ \end{array} \right| ,\nonumber \\ h^{(l)}= & {} \left| \begin{array}{cccc} A^{(l)}_{11} &{} 1 \\ -1 &{} B_{11} \\ \end{array} \right| ,\nonumber \\ g^{(1)}= & {} \left| \begin{array}{ccccc} A_{11} &{} 1 &{} \mathrm{e}^{\varXi _1} \\ -1 &{} B_{11} &{} 0 \\ 0 &{} -\mathrm{e}^{\varTheta ^{(1)*}_1 } &{} 0 \end{array} \right| , \end{aligned}$$

(28)

where $A_{11}=\frac{1}{p_1+p^*_1} \mathrm{e}^{\varXi _1+\varXi ^*_1}, A^{(l)}_{11}=\frac{1}{p_1+p^*_1} \left( -\frac{p_1-\mathrm{i} \alpha _l}{p^*_1+\mathrm{i}\alpha _l} \right) \mathrm{e}^{\varXi _1+\varXi ^*_1}$ and $B_{11}=\frac{1}{q_1+q^*_1} \mathrm{e}^{\varTheta ^{(1)}_{1}+\varTheta ^{(1)*}_{1} }$ for $l=1,2$. The above tau functions can be written as

$$\begin{aligned}&f=1+\frac{\mathrm{e}^{2\varXi _{1R} +2\varTheta ^{(1)}_{1R}} }{4p_{1R}q_{1R}},\ \ g^{(1)}=-\mathrm{e}^{\varXi _1+\varTheta ^{(1)*}_1},\end{aligned}$$

(29)

$$\begin{aligned}&h^{(l)}=1- \frac{p_1-\mathrm{i}\alpha _l}{p^*_1+\mathrm{i}\alpha _l} \frac{\mathrm{e}^{2\varXi _{1R} +2\varTheta ^{(1)}_{1R}} }{4p_{1R}q_{1R}},\ \ l=1,2. \end{aligned}$$

(30)

As an example, we show such one-soliton solution in Fig. 3 under the nonlinear coefficients $(\sigma _1,\sigma _2,\sigma _3)=(1,1,-1)$. The parameters are chosen as $\mu _1=\nu _1=\rho _1=\rho _2=1$, $\alpha _1=0,\alpha _2=1$ $p_1=1$, $q_1=1+\mathrm{i}$ and $\mathrm{e}^{\xi _{10}}=\mathrm{e}^{\theta ^{(1)}_{10}}=1$. Here, $\alpha _l$-parameter affects the depth of dark part in mixed soliton solution. This fact can be evidenced from Fig. 3 in which $S^{(2)}$ is a dark soliton, whereas $S^{(3)}$ is a gray one.

Fig. 3

One-bright–two-dark mixed one-soliton solution in three-component LSRI system at time $t=0$.

Fig. 4

Mixed two-soliton bound state (one-bright–two-dark soliton for SW components) in three-component LSRI system at time $t=0$

2.2.2 Two-soliton solution

When $N=2$ in (27), we have the mixed two-soliton solution in Gram determinant form as follows

$$\begin{aligned} f= & {} \left| \begin{array}{cccc} A_{11} &{} A_{12} &{} 1 &{} 0 \\ A_{21} &{} A_{22} &{} 0 &{} 1 \\ -1 &{} 0 &{} B_{11} &{} B_{12} \\ 0 &{} -1 &{} B_{21} &{} B_{22} \\ \end{array} \right| ,\nonumber \\ h^{(l)}= & {} \left| \begin{array}{cccc} A^{(l)}_{11} &{} A^{(l)}_{12} &{} 1 &{} 0 \\ A^{(l)}_{21} &{} A^{(l)}_{22} &{} 0 &{} 1 \\ -1 &{} 0 &{} B_{11} &{} B_{12} \\ 0 &{} -1 &{} B_{21} &{} B_{22} \\ \end{array} \right| ,\end{aligned}$$

(31)

$$\begin{aligned} g^{(1)}= & {} \left| \begin{array}{ccccc} A_{11} &{} A_{12} &{} 1 &{} 0 &{} \mathrm{e}^{\varXi _1} \\ A_{21} &{} A_{22} &{} 0 &{} 1 &{} \mathrm{e}^{\varXi _2}\\ -1 &{} 0 &{} B_{11} &{} B_{12} &{} 0 \\ 0 &{} -1 &{} B_{21} &{} B_{22} &{}0 \\ 0 &{} 0 &{} -\mathrm{e}^{\varTheta ^{(1)*}_1 } &{} -\mathrm{e}^{\varTheta ^{(1)*}_2 } &{} 0 \end{array} \right| , \end{aligned}$$

(32)

where $A_{ij}=\frac{1}{p_i+p^*_j} \mathrm{e}^{\varXi _i+\varXi ^*_j}, A^{(l)}_{ij}=\frac{1}{p_i+p^*_j} \left( -\frac{p_i-\mathrm{i}\alpha _l}{p^*_j+\mathrm{i}\alpha _l} \right) \mathrm{e}^{\varXi _i+\varXi ^*_j}$ and $B_{ij}=\frac{\mu _1}{q_i+q^*_j} \mathrm{e}^{\varTheta ^{(1)}_{i}+\varTheta ^{(1)*}_{j} }$ for $l=1,2$.

The soliton interaction can be analyzed in parallel with the same type of soliton solution to LSRI system with the same nonlinearity coefficients $\sigma _\ell =1,\ell =1,2,3$. Interestingly, two-soliton bound state can be acquired from this mixed soliton solution by restricting solitons moving with a common speed. For this purpose, we rewrite $\varXi _{iR}+\varTheta ^{(1)*}_{iR}=p_{iR} x + (2p_{iR}p_{iI}-w_{iR})y +w_{iR} t+\xi _{i0R}+\theta ^{(1)}_{i0R}$ and $\varXi _{iI}+\varTheta ^{(1)*}_{iI}=p_{iI} x + (p^2_{iI}-p^2_{iR} -w_{iI})y +w_{iI} t +\xi _{i0I}-\theta ^{(1)}_{i0I}$ with $w_{iR}= \sum ^2_{l=1}\frac{\sigma _{l+1}\rho ^2_l p_{iR}}{p^2_{iR} +(p_{iI}-\alpha _l)^2 } -\nu _1q_{iR}$ and $w_{iI}=-\sum ^2_{l=1}\frac{\sigma _{l+1}\rho ^2_l (p_{iI}-\alpha _l)}{p^2_{iR} +(p_{iI}-\alpha _l)^2 }+\nu _1q_{iI}$. Then conditions $p_{1I}=p_{2I}$ and $\frac{w_{1R}}{p_{1R}}=\frac{w_{2R}}{p_{2R}}$ will result in two-soliton bound state, which is illustrated in Fig. 4 with $(\sigma _1,\sigma _2,\sigma _3)=(-1,1,-1)$. The parameters are $\mu _1=-\nu _1=\rho _1=1,\rho _2=2$, $\alpha _1=0,\alpha _2=1$, $p_1=2+\mathrm{i}$, $p_2=3+\mathrm{i}$, $q_1=\frac{131}{45},q_2=3+2\mathrm{i}$, $\mathrm{e}^{\xi _{10}}=1+3\mathrm{i},\mathrm{e}^{\xi _{20}}=3+2\mathrm{i}$, $\mathrm{e}^{\theta ^{(1)}_{10}}=2+\frac{1}{2}\mathrm{i}$ and $\mathrm{e}^{\theta ^{(1)}_{20}}=\frac{1}{2}+5\mathrm{i}$.

3 General N-soliton solution to 2D multi-component LSRI system

In the same spirit as the three-component LSRI system, the general mixed-type soliton solution to the 2D multi-component LSRI system can be derived via the KP hierarchy reduction method. It is known that the multi-bright soliton solutions can be derived from the reduction of the multi-component KP hierarchy, whereas the multi-dark soliton solutions are obtained from the reduction of the single KP hierarchy but with multiple copies of shifted singular points. Therefore, if we consider a general mixed soliton solution consisting of m bright solitons and $M-m$ dark solitons to the 2D multi-component LSRI system (1), we need to start from an $(m+1)$-component KP hierarchy with $M-m$ copies of shifted singular points in the first component. The details are omitted here, and we present only the results for the 2D multi-component LSRI system (1).

3.1 N-bright–dark soliton solution

To seek for mixed multi-soliton solution consisting of m bright solitons and $M-m$ dark solitons for SW components, the 2D multi-component LSRI system is first converted to the following bilinear form

$$\begin{aligned}&\left[ i (D_t+D_y)-D^2_x \right] g^{(k)}\cdot f=0,\ \ k=1,2,\ldots ,m,\nonumber \\&\quad \left[ i (D_t+D_y-2\alpha _lD_x)-D^2_x \right] h^{(l)}\cdot \nonumber \\&\quad f=0,\ \ l=1,2,\ldots ,M-m, \nonumber \\&\quad \left( D_tD_x-2 \sum ^{M-m}_{l=1}\sigma _{l+m}\rho ^2_l \right) f\cdot \nonumber \\&\quad f=-2 \sum ^m_k\sigma _k g^{(k)}g^{(k)*}-2\sum ^{M-m}_{l=1}\sigma _{l+m}\rho ^2_l h^{(l)}h^{(l)*},\nonumber \\ \end{aligned}$$

(33)

through the dependent variable transformations:

$$\begin{aligned} S^{(k)}= & {} \frac{g^{(k)}}{f},\nonumber \\ S^{(l)}= & {} \rho _l\frac{h^{(l)}}{f} \mathrm{e}^{\mathrm{i}[\alpha _l x + \beta _ly-(\beta _l-\alpha ^2_l)t]},\nonumber \\ L= & {} -2(\log f)_{xx}, \end{aligned}$$

(34)

where $\alpha _l$, $\beta _l$ and $\rho _l$ $(\rho _l>0)$ are real constants for $k=1,\ldots m$ and $l=1,\ldots ,M-m$.

Similar to the procedure discussed in Sect. 2, taking into account the Gram determinant solutions of the $(m + 1)$-component KP hierarchy, one can obtain mixed multi-soliton solution as follows:

$$\begin{aligned} f= & {} \left| \begin{array}{ccc} A &{} I \\ -I &{} B \end{array} \right| ,\nonumber \\ h^{(l)}= & {} \left| \begin{array}{ccc} A^{(l)} &{} I \\ -I &{} B \end{array} \right| ,\nonumber \\ g^{(k)}= & {} \left| \begin{array}{ccc} A &{} I &{} \phi ^T \\ -I &{} B &{} \mathbf 0 ^T\\ \mathbf 0 &{} \psi ^{(k)} &{} 0 \end{array} \right| , \end{aligned}$$

(35)

where A, $A^{(l)}$ and B are $N\times N$ matrices defined as

$$\begin{aligned}&A_{ij}=\frac{1}{p_i+p^*_j} \mathrm{e}^{\varXi _i+\varXi ^*_j},\\&A^{(l)}_{ij}=\frac{1}{p_i+p^*_j} \left( -\frac{p_i-\mathrm{i}\alpha _l}{p^*_j+\mathrm{i}\alpha _l} \right) \mathrm{e}^{\varXi _i+\varXi ^*_j},\\&B_{ij}=\frac{1}{q_i+q^*_j} \sum ^m_{k=1} \mu _k \mathrm{e}^{\varTheta ^{(k)}_{i}+\varTheta ^{(k)*}_{j} }, \end{aligned}$$

and $\phi$ and $\psi ^{(k)}$ are N-component row vectors given by

$$\begin{aligned} \phi= & {} (\mathrm{e}^{\varXi _1}, \mathrm{e}^{\varXi _2}, \ldots , \mathrm{e}^{\varXi _N}),\\ \psi ^{(k)}= & {} -(\mathrm{e}^{\varTheta ^{(k)*}_1 }, \mathrm{e}^{\varTheta ^{(k)*}_2 }, \ldots , \mathrm{e}^{\varTheta ^{(k)*}_N } ),\ \ \end{aligned}$$

with

$$\begin{aligned} \varXi _i= & {} \sum ^{M-m}_{l=1} \frac{1}{p_i-\mathrm{i}\alpha _l}\sigma _{l+1}\rho ^2_l(t-y)\\&+p_ix-\mathrm{i}p^2_iy+\xi _{i0},\\ \varTheta ^{(k)}_i= & {} -\nu _k q_i(t-y)+\theta ^{(k)}_{i0}. \end{aligned}$$

Here $\sigma _k=\mu _k\nu _k$, $p_i$, $q_i$, $\xi _{i0}$ and $\theta ^{(k)}_{i0}$ $(i=1,2,\ldots ,N; k=1,2,\ldots ,m; l=1,2,\ldots ,M-m)$ are arbitrary complex parameters.

Particularly, when all $\nu _k=1$, we have general mixed soliton solution of the following form by performing row and column operations,

$$\begin{aligned} f= & {} \left| \begin{array}{ccc} A' &{} I \\ -I &{} B' \end{array} \right| ,\nonumber \\ h^{(l)}= & {} \left| \begin{array}{ccc} A'^{(l)} &{} I \\ -I &{} B' \end{array} \right| ,\nonumber \\ g^{(k)}= & {} \left| \begin{array}{ccc} A' &{} I &{} \phi '^T \\ -I &{} B' &{} \mathbf 0 ^T\\ \mathbf 0 &{} C &{} 0 \end{array} \right| , \end{aligned}$$

(36)

where $A'$, $A'^{(l)}$ and $B'$ are $N\times N$ matrices defined as

$$\begin{aligned}&A'_{ij}=\frac{1}{p_i+p^*_j} \mathrm{e}^{\varXi '_i+\varXi '^*_j},\\&A'^{(l)}_{ij}=\frac{1}{p_i+p^*_j} \left( -\frac{p_i-\mathrm{i}\alpha _l}{p^*_j+\mathrm{i}\alpha _l} \right) \mathrm{e}^{\varXi '_i+\varXi '^*_j},\\&B'_{ij}=\frac{1}{q_i+q^*_j} \sum ^m_{k=1} \sigma _k c^{(k)}_ic^{(k)*}_j, \end{aligned}$$

and $\phi$ and $\psi ^{(k)}$ are N-component row vectors given by

$$\begin{aligned}&\phi '=(\mathrm{e}^{\varXi '_1}, \mathrm{e}^{\varXi '_2}, \ldots , \mathrm{e}^{\varXi '_N} ),\\&C=-(c^{(k)*}_1, c^{(k)*}_2, \ldots , c^{(k)*}_N ), \end{aligned}$$

where $\varXi '_i=\sum ^{M-m}_{l=1} \frac{1}{p_i-\mathrm{i}\alpha _l}\sigma _{l+1}\rho ^2_l(t-y)+p_ix-\mathrm{i}p^2_iy -q^*_i(t-y) +\xi _{i0}$ and $c^{(k)}_i=\mathrm{e}^{\theta ^{(k)}_{i0}}$, $p_i$, $q_i$, $\xi _{i0}$ and $\theta ^{(k)}_{i0}$ $(i=1,2,\ldots ,N; k=1,2,\ldots ,m; l=1,2,\ldots ,M-m)$ are arbitrary complex parameters.

For the 2D multi-component LSRI system (1) with all $\sigma _\ell =1$, the explicit one- and two-mixed soliton solutions have been obtained by using the perturbation expansion method [25]. Here the general mixed soliton solution can be expressed by the determinant form (36).

3.2 N-bright soliton solution

General N-bright soliton solution to 2D multi-component LSRI system (1) can be derived from the KP hierarchy reduction method. More precisely, the dependent variable transformations

$$\begin{aligned} S^{(k)}=\frac{g^{(k)}}{f},\ \ L=-2(\log f)_{xx},\ \ k=1,\ldots ,M, \end{aligned}$$

(37)

first convert Eqs. (1) into the following bilinear equations

$$\begin{aligned}&\left[ i (D_t+D_y)-D^2_x \right] g^{(k)}\ldots f=0,\ \ k=1,2,\ldots , M,\nonumber \\&\quad D_tD_x f\ldots f= -2 \sum ^M_k\sigma _k g^{(k)}g^{(k)*}. \end{aligned}$$

(38)

Then, starting from the $(M + 1)$-component KP hierarchy, one can construct general N-bright soliton solution expressed by Gram determinant in the same way. The tau functions of f and $g^{(k)}$ take the same form as in (43)

$$\begin{aligned} f= & {} \left| \begin{array}{ccc} A &{} I \\ -I &{} B \end{array} \right| ,\nonumber \\ g^{(k)}= & {} \left| \begin{array}{ccc} A &{} I &{} \phi ^T \\ -I &{} B &{} \mathbf 0 ^T\\ \mathbf 0 &{} \psi ^{(k)} &{} 0 \end{array} \right| , \end{aligned}$$

(39)

where A, $A^{(k)}$ and B are $N\times N$ matrices defined as

$$\begin{aligned} A_{ij}= & {} \frac{1}{p_i+p^*_j} \mathrm{e}^{\varXi _i+\varXi ^*_j},\\ B_{ij}= & {} \frac{1}{q_i+q^*_j} \sum ^M_{k=1} \mu _k \mathrm{e}^{\varTheta ^{(k)}_{i}+\varTheta ^{(k)*}_{j} } \end{aligned}$$

and $\phi$ and $\psi ^{(k)}$ are N-component row vectors given by

$$\begin{aligned} \phi= & {} (\mathrm{e}^{\varXi _1}, \mathrm{e}^{\varXi _2}, \ldots , \mathrm{e}^{\varXi _N} ),\\ \psi ^{(k)}= & {} -(\mathrm{e}^{\varTheta ^{(k)*}_1 }, \mathrm{e}^{\varTheta ^{(k)*}_2 }, \ldots , \mathrm{e}^{\varTheta ^{(k)*}_N } ),\ \ \end{aligned}$$

with

$$\begin{aligned} \varXi _i= & {} \sum ^{M-m}_{l=1} \frac{1}{p_i-\mathrm{i}\alpha _l}\sigma _{l+1}\rho ^2_l(t-y)\\&+p_ix-\mathrm{i}p^2_iy+\xi _{i0},\\ \varTheta ^{(k)}_i= & {} -\nu _k q_i(t-y)+\theta ^{(k)}_{i0}. \end{aligned}$$

Here $\sigma _k=\mu _k\nu _k$, $p_i$, $q_i$, $\xi _{i0}$ and $\theta ^{(k)}_{i0}$ $(i=1,2,\ldots ,N; k=1,2,\ldots ,m; l=1,2,\ldots ,M-m)$ are arbitrary complex parameters.

When all $\nu _k=1$, we have general bright soliton solution of the following form,

$$\begin{aligned} f= & {} \left| \begin{array}{ccc} A' &{} I \\ -I &{} B' \end{array} \right| ,\nonumber \\ g^{(k)}= & {} \left| \begin{array}{ccc} A' &{} I &{} \phi '^T \\ -I &{} B' &{} \mathbf 0 ^T\\ \mathbf 0 &{} C &{} 0 \end{array} \right| , \end{aligned}$$

(40)

where $A'$, $A'^{(l)}$ and $B'$ are $N\times N$ matrices defined as

$$\begin{aligned} A'_{ij}= & {} \frac{1}{p_i+p^*_j} \mathrm{e}^{\varXi '_i+\varXi '^*_j},\\ B'_{ij}= & {} \frac{1}{q_i+q^*_j} \sum ^M_{k=1} \sigma _k c^{(k)}_ic^{(k)*}_j, \end{aligned}$$

and $\phi$ and $\psi ^{(k)}$ are N-component row vectors given by

$$\begin{aligned} \phi '= & {} (\mathrm{e}^{\varXi '_1}, \mathrm{e}^{\varXi '_2}, \ldots , \mathrm{e}^{\varXi '_N} ),\\ C= & {} -(c^{(k)*}_1, c^{(k)*}_2, \ldots , c^{(k)*}_N ), \end{aligned}$$

where $\varXi '_i=p_ix-\mathrm{i}p^2_iy -q^*_i(t-y) +\xi _{i0}$ and $c^{(k)}_i=\mathrm{e}^{\theta ^{(k)}_{i0}}$, $p_i$, $q_i$, $\xi _{i0}$ and $\theta ^{(k)}_{i0}$ $(i=1,2,\ldots ,N; k=1,2,\ldots ,M)$ are arbitrary complex parameters.

3.3 N-dark soliton solution

To find general N-dark soliton solution to 2D multi-component LSRI system (1), we use the dependent variable transformations

$$\begin{aligned} S^{(k)}= & {} \frac{g^{(k)}}{f},\ \ S^{(l)}=\rho _l\frac{h^{(l)}}{f} \mathrm{e}^{\mathrm{i}\left[ \alpha _l x+ \beta _ly-\left( \beta _l-\alpha ^2_l\right) t\right] },\nonumber \\ L= & {} -2(\log f)_{xx}, \end{aligned}$$

(41)

Eqs.(1) become the following bilinear form,

$$\begin{aligned}&\left[ i (D_t+D_y-2\alpha _lD_x)-D^2_x \right] h^{(l)}\cdot f=0,\nonumber \\&\quad l=1,2,\ldots ,M, \left( D_tD_x-2 \sum ^{M}_{l=1}\sigma _{l}\rho ^2_l \right) f\cdot \nonumber \\&\quad f=-2\sum ^{M}_{l=1}\sigma _{l}\rho ^2_l h^{(l)}h^{(l)*}, \end{aligned}$$

(42)

where $\alpha _l$, $\beta _l$ and $\rho _l$ $(\rho _l>0)$ are real constants for $l=1,\ldots ,M$.

Similar to the procedure discussed in Sect. 2, taking into account the Gram determinant solutions of the $(m + 1)$-component KP hierarchy, one can obtain mixed multi-soliton solution as follows:

$$\begin{aligned} f= & {} \left| \begin{array}{ccc} A &{} I \\ -I &{} B \end{array} \right| ,\nonumber \\ h^{(l)}= & {} \left| \begin{array}{ccc} A^{(l)} &{} I \\ -I &{} B \end{array} \right| ,\ \end{aligned}$$

(43)

where A, $A^{(l)}$ and B are $N\times N$ matrices defined as

$$\begin{aligned} A_{ij}= & {} \frac{1}{p_i+p^*_j} \mathrm{e}^{\varXi _i+\varXi ^*_j},\\ A^{(l)}_{ij}= & {} \frac{1}{p_i+p^*_j} \left( -\frac{p_i-\mathrm{i}\alpha _l}{p^*_j+\mathrm{i}\alpha _l} \right) \mathrm{e}^{\varXi _i+\varXi ^*_j},\\ B_{ij}= & {} \delta _{ij}, \end{aligned}$$

with

$$\begin{aligned} \varXi _i= & {} \sum ^{M-m}_{l=1} \frac{1}{p_i-\mathrm{i}\alpha _l} \sigma _{l+1}\rho ^2_l(t-y)\\&+p_ix-\mathrm{i}p^2_iy+\xi _{i0}, \end{aligned}$$

Here $p_i$, $\xi _{i0}$ and $\theta ^{(k)}_{i0}$ $(i=1,2,\ldots ,N; l=1,2,\ldots ,M)$ are arbitrary complex parameters.

Due to a simple determinant identity shown in [33],

$$\begin{aligned} \left| \begin{array}{ccc} A &{} I \\ -I &{} I \end{array} \right| =|I+A|, \end{aligned}$$

this form of dark soliton solution coincides with the one in [34].

In summary, we obtain general mixed (bright–dark) multi-soliton solution to two-dimensional multi-component LSRI system with all possible combinations of nonlinearity coefficients including positive, negative and mixed types. Compared with the study in Ref. [25], we need to emphasize that: (i) Kanna et. al have only provided mixed one- and two-soliton solutions for $\sigma _\ell =1$; here, we present N-soliton solutions in terms of determinant, which even include general bright and dark soliton solution. (ii) Starting from $\tau$ functions and the relevant bilinear equations in the KP hierarchy, N-soliton solutions for the 2D multi-component LSRI system are derived through the direct reduction. In other words, we give the complete proof of N-soliton solutions but the Ref. [25] have constructed the mixed one- and two-soliton solutions by using power series expansions. (iii) More importantly, the nonlinearity coefficients in (1) are always $\sigma _\ell =\pm 1$ [under line of formula (1)], which like coupled NLS equations, and include focusing, defocusing and focusing–defocusing cases. In fact, the result of [25] corresponds to the focusing case $\sigma _\ell =1$; thus, N-soliton solution for this case is just a special case of our formulae [see in detail Eq. (36)]. Besides, although the spirit of our derivation is same as the vector NLS equation [33] and the 1D YO system [35], the different model leads to the completely different reduction condition and then brings the distrinct solution expression.

4 Conclusion

In this paper, we have constructed general bright–dark multi-soliton solution to two-dimensional multi-component LSRI system describing the nonlinear resonant interaction of M-component short waves with a long wave. This solution exists in the original system for all possible combinations of nonlinearity coefficients including positive, negative and mixed types. Taking the three-component LSRI system as an example, we have deduced two kinds of the general mixed N-soliton solution (two-bright–one-dark soliton and one-bright–two-dark one for SW components) in the form of Gram determinant by using the KP hierarchy reduction method. The same analysis was extended to obtain the general mixed solution consisting of m bright solitons and $M-m$ dark ones for SW components in the 2D multi-component LSRI system. The expression of the mixed solution also contains the general bright and dark N-soliton solution. In particular, for the soliton solution which include two-bright–one-dark soliton for SW components in three-component LSRI system, the dynamics analysis showed that solioff excitation and solioff interaction appear in two SW components which possess bright soliton, while V-type solitary and interaction occur in the other SW component and LW one. In addition, the related mixed soliton bound states in 2D three-component LSRI system were exhibited graphically.